Discrimination methods for dispersivity of fine-grained soils based on dispersive mechanisms
-
摘要: 针孔、碎块、双密度计、孔隙水可溶性阳离子和交换性钠离子百分比等现有评价细粒土分散性的5种常规试验方法,操作过程繁琐,耗时耗力。基于细粒土分散机理,通过人工配制不同黏粒含量、不同碳酸钠质量分数的土样,研究细粒土分散性常规判别试验方法的适用性,提出快速准确评价细粒土分散性的方法。试验结果表明,分散土可分为物理性分散土(可称之为低凝聚性土)、化学性分散土、物理-化学复合型分散土,其中黏粒含量10%是细粒土产生物理性分散的界限。泥球、孔隙水可溶性阳离子和交换性钠离子百分比试验适用于所有细粒土,针孔和双密度计试验适用于黏粒含量不低于10%的细粒土。当黏粒含量低于10%时,采用泥球试验的判别结果作为判别依据;当黏粒含量不低于10%时,以泥球和针孔试验的判别结果作为综合判别依据,并且以最强的分散性判别结果为准。双密度计、孔隙水可溶性阳离子、交换性钠离子百分比和酸碱度试验仅作为细粒土分散机理的解释性试验,不参与综合判别。Abstract: The crumb tests, the pinhole tests, the double-hydrometer tests, the pore water soluble cation tests and the exchangeable sodium ion percentage tests are the common methods for identifying the dispersivity of the fine-grained soils, which are complex and time-consuming. Based on the dispersive mechanisms of the fine-grained soils, the soil samples with different clay contents and sodium carbonate mass fractions are prepared artificially to analyze the suitability of the conventional discrimination methods for dispersivity and to propose a rapid and accurate discrimination method. The results show that the dispersive soils can be divided into physical dispersive soils which can be called low cohesive soils, chemical dispersive soils and physical-chemical composite dispersive soils. It also can be found that 10% of the clay content is the upper limit of physical dispersivity of the fine-grained soils. The mud ball tests, the pore water soluble cation tests and the exchangeable sodium ion percentage tests can be applied to all fine-grained soils, and the pinhole tests and the double-hydrometer tests are suitable for the fine-grained soils with a clay content no lower than 10%. The results of the mud ball tests should be used as the discrimination criterion for dispersivity if the clay content is lower than 10%, otherwise the discrimination criterion for dispersivity should be the strongest dispersivity results of the mud ball tests and the pinhole tests. The double-hydrometer tests, the pore water soluble cation tests, the exchangeable sodium ion percentage tests, and the pH tests are used as the explanatory tests for the dispersive mechanisms of the fine-grained soils, which have no influences on the comprehensive discrimination.
-
0. 引言
岩质边坡在形成的过程中往往会产生软弱夹层,在降雨、地震等外部因素作用下边坡极易沿力学性质相对薄弱的结构面产生滑坡等破坏,软弱夹层结构面一定程度上决定着岩体的整体稳定性[1-2]。大量工程实例表明软弱结构面大多都具有显著的时效性,岩体破坏时应力并未达到岩体的极限强度,而是经过时间效应累积突破长期强度破坏。剪切蠕变破坏主要发生在大型岩质边坡中,其边坡滑动都不是瞬间破坏,而是经过长期的变形积累,内部软弱结构面贯通造成滑坡失稳破坏[3-4]。自然界中,大多数软弱夹层处于岩体内部且表现为非贯通状态,其滑移变形机理亟待深入研究。
对于非贯通结构面的研究,前人已经开展了大量工作并取得相关成果。Zhang等[5]研究发现规则锯齿结构面在蠕变过程中表现为非稳态,用改进Burgers模型呈现此类结构面的蠕变特性。张治亮等[6]对含砂岩软弱结构面进行研究,通过改进非线性元件和开尔文模型组合表征蠕变特性。Wu等[7]提出NVPRM模型对预制结构面的砂岩进行了研究。熊良宵等[8]通过FLAC3D的二次本构开发功能验证了其建立的六元件模型对于岩石黏弹塑性蠕变特性的有效性。陈兴周等[9]在西元模型的基础上考虑损伤效应,建立了一种岩石损伤蠕变特性本构。Zhang等[10]考虑了非线性剪切流变的影响,以Nishihara为原型进行串联,较好的反映了岩石加速蠕变的细观特性。李任杰等[11]通过云母片模拟软弱结构面,推导了此类结构面的蠕变特性本构模型。此外,前人对岩体长期荷载作用下的岩体损伤变形机制展开了相关的研究。王建明等[12]从断裂力学的单裂隙附加应变能增量和损伤应变能量释放思路出发,推导了断续裂隙细观损伤张量表达式。王中强等[13]采用辛普生积分推导了混凝土能量损伤公式。张强勇等[14]以FLAC3D软件为平台,引入损伤变量到本构模型的修正,通过数值模拟验证了损伤变量对岩体长期强度的作用。杨圣奇等[15]将损伤力学引入岩石流变模型中,推导了两阶段岩体损伤演化方程,说明了考虑损伤变量的必要性。
目前对于隐伏非贯通软弱夹层结构面的剪切蠕变特性影响因素的研究还不充分,且大多采用相似材料模拟软弱结构面。本次以工程现场软弱夹层为样本设计缩尺含软弱夹层岩体制备方法,考虑夹层埋藏深度、倾角和含水率因素分析隐伏非贯通软弱夹层岩体剪切蠕变特性,考虑多参数渐变损伤分阶段推导适用于此类岩体的剪切蠕变本构模型,通过相似模拟试验验证本构模型正确性,并阐明隐伏非贯通含软弱夹层边坡稳定性。
1. 剪切蠕变试验
1.1 试验设备
本次试验设备采用辽宁工程技术大学土木工程实验室TAW2000三轴试验仪剪切试验系统,见图 1。通过电脑控制不同法向应力,推动剪切上盘进行剪切蠕变试验。
1.2 样本制备
在隐伏型岩质边坡中,对于含软弱结构面的地段确定其蠕变滑移特性十分不易。因此,采用室内模拟的方法加以推测验证具有合理性和必要性。
此次试验设计以混凝土试块模拟硬质岩层,取现场软弱夹层样本制备试块中软弱夹层结构面。经基础力学试验测得软弱夹层c=3.24 MPa,φ=29°。试验配置硬岩材料主要为石英砂∶重晶石粉∶水泥∶石膏∶水=3∶3∶2∶2∶2.1,再加入1%甘油。模具采用三联标准混凝土试模(100 mm×100 mm×100 mm),考虑软弱夹层在岩体内厚度,在相似原理基础上自制软弱夹层预制双面贯通模具(50 mm×50 mm×2 mm)。试块制备见图 2。
具体步骤主要包括①底部浇筑:将调制好的硬岩砂浆导入模具并分层振捣浇筑3 cm;②软弱夹层制作:分别按照固定级配的原岩样本进行不同含水率的配置,将调制好的夹层倒入双面贯通的模具中如图 2(b);③软弱夹层在试块内定位:在模具内通过测量确定软弱夹层角度及位置,采用薄铁片将预制夹层移入模具,待夹层初步凝固取出双面贯通模具;④上层浇筑:待取出模具后进行顶部硬岩的浇筑,浇筑时四周进行充分振捣,顶部完全覆盖后整体振捣确保密实性;⑤试块在模具内静置24 h后脱模,将试件于水中养护21 d。分别以岩层倾角和软弱夹层含水率为变量进行影响因素试验,每个试件制备4个,共计64个试件。
1.3 试验设计
目前室内剪切蠕变试验加载方式主要分为两种,一种是在一组试样上施加相同的正应力,在不同试样上施加不同剪应力直至试样破坏;另外一种为陈宗基先生提出的相对省时的试验方法,即在一组试样上施加不同正应力,在不同试样上逐级增加剪切荷载直至剪坏[16]。对比上述两者方法,最终决定采用第二种试验方法进行岩体蠕变特性的研究。
为研究软弱夹层不同含水率和岩层倾角对隐伏式非贯通岩质边坡的剪切蠕变破坏特性,以软弱夹层含水率15%,18%,21%,23%,岩层倾角0°,35°,50°,65°进行正交试验,考虑软弱夹层所处岩层深度,以不同法相应力进行试验。为明确含软弱夹层岩体试块受力特征,单独浇筑一组纯硬岩配比试件作为对照组,测得该组试件在法相应力2.4,2.9,3.4 MPa作用下,最大剪应力分别为10.86,13.69,15.84 MPa。试验组切向应力根据室内直剪试验确定不同参变量下的最大剪应力,再根据最大剪应力的20%,40%,60%,80%,90%,100%进行逐级加载,每次加载时间持续48 h,最后一级试样破坏即停止加载。不同试件加载工况如表 1。
表 1 隐伏式含软弱夹层边坡室内模拟加载工况参数表Table 1. Indoor simulation loading condition parameters of concealed slope with weak interlayer编号 含水率 夹层倾角/(°) 法相应力/MPa 最大剪应力/MPa 1 15% 0 2.40 5.46 2 35 2.90 5.98 3 50 3.40 6.26 4 65 3.90 6.39 5 18% 0 2.40 5.12 6 35 2.90 5.32 7 50 3.40 5.42 8 65 3.90 5.89 9 0 2.40 5.09 10 35 2.90 5.12 11 50 3.40 5.32 12 65 3.90 5.48 13 0 2.40 4.86 14 35 2.90 4.91 15 50 3.40 4.96 16 65 3.90 5.09 2. 剪切蠕变结果分析
通过室内直剪试验确定每组试块最大剪应力,在上述不同工况下进行剪切-蠕变试验。试验数据分析可得,试验中出现瞬时应变、衰减蠕变、稳态蠕变和加速蠕变阶段。在不同条件下的剪切蠕变破坏情况均有明显差异,本文仅取含水率为15%和软弱夹层倾角为0°两种情况进行分析说明。
2.1 破坏裂纹情况
随着试验的持续进行,最后试块破坏时的外部特征展现出不同的情况。图 3中以内部软弱夹层含水率为15%时不同倾角下的破坏情况进行总结。图 3(a)中软弱夹层倾角是0°,即试块剪断时沿其夹层角度受力,从图中可以看出剪断裂纹呈水平状态和岩层倾角保持一致且裂纹上部完全开裂下部有较小的细微裂纹。图 3(b)中软弱夹层倾角为35°,试件剪断破坏时裂纹出现较小的倾角约30°向上发展,且后部展开一条向下扩展的裂纹并未完全贯通。图 3(c)中软弱夹层倾角50°,试件破坏时展现出两条明显向上倾斜的裂纹角度较图 3(b)中更加大。图 3(d)中软弱夹层倾角为65°,试件破坏过程中展现两条裂纹,上部裂纹倾角约60°、下部倾角趋于水平且软弱夹层外有突出倾向。
从以上试验现象可以发现,同一含水率情况下不同软弱夹层岩层倾角的岩体在剪切蠕变破坏时主要破坏区域在岩体软弱夹层处,且软弱夹层上节理面相对于更加容易滑动开裂。这是由于岩体在受力过程中岩体产生一定弯矩上部岩体有向下倾倒趋势,在软弱夹层节理面上部力学承载相对较快,在同一弯矩作用效果相同时下部需要更大的力。即岩体试件剪切蠕变破坏可以符合实际含软弱夹层岩质边坡滑移情况。
2.2 破坏断面情况
为确保养护21 d后软弱夹层内部含水率的变化情况,需要对剪切破坏后的软弱夹层进行含水率测定,对应不同含水率下的剪断断面如图 4。从图 4中可以发现经过养护后的软弱夹层还是保持着原本的含水率,水分的流失在误差预计范围之内,可以达到试验的目的。从各断面破坏后的形态特征可以发现,试样在剪切蠕变的过程中主要承力部位是硬岩部分,内部软弱夹层在受力过程中逐步压缩,内部结构在外力的作用下重组,在无法承载外力后内部产生黏性变形,剪断时软弱夹层断面结构变得松散极不稳定。
2.3 剪切-蠕变影响因素分析
(1)同一含水率情况下
为研究软弱夹层在岩体内倾角对整体剪切蠕变破坏的影响,本节选用软弱夹层含水率为15%时的不同情况进行分析。
该含水率下采用分五级加载的方式进行剪切蠕变试验,通过图 5可以发现在荷载初步加载时即产生约0.4 mm的位移,在后续加载过程中均出现瞬时位移较大之后趋于平缓的现象,这是由于在加载过程中在极短的时间内相当于对其加入动荷载,在动荷载加入时其岩体内部软弱夹层内摩擦力转化为动摩擦力,在动摩擦力作用下岩体要发生滑动相对需要较小的应力,内部软弱夹层突然受力压缩外部表现为位移突然增加,在受力稳定后,动摩擦力再次转化为静摩擦力,岩体产生位移变化再次需要更大的应力,同时外部硬岩应力重新分布稳定,整体曲线显示出瞬时增大之后趋于稳定状态,在稳定过程中产生的位移则很小,曲线趋于平缓[17]。
在图 6中对不同岩层倾角下试验结果对比发现,在相同情况下岩体内软弱夹层的倾角变化随角度的增加岩体剪切蠕变滑移位移减小,这是由于其内部软弱夹层剪切面的减小导致的。不同倾角的软弱夹层受剪切面依次减小,外部硬岩厚度增加岩体趋于更加稳定,即在相同荷载下剪切位移更小。这也说明在隐伏式含软弱夹层边坡中,软弱夹层和山体硬岩平行时由于降雨等原因导致上部荷载增加时,沿软弱夹层滑动的危险性更高,软弱夹层和硬岩产生相对角度时岩体边坡相对稳定。
在实际施工过程中对硬岩和软弱夹层平行的顺层边坡治理时应相对于其他更加着重考虑岩层倾角问题,并进行支护设计。
(2)同一岩层倾角情况下
为研究软弱夹层含水率对边坡整体稳定的影响,以最危险岩层倾角0°进行研究。从图 7中可以发现,随着含水率的增加试块在剪切蠕变试验过程中所需要的最大荷载明显减小,且各级荷载增加时岩体剪切位移变化明显,说明含水率相对于岩层倾角对含软弱夹层边坡滑移破坏影响程度更大。这是由于随着含水率的增加其内部软弱夹层逐渐失去承载能力,其内部静摩擦力转化为动摩擦所需要力更小,在试块外部受力过程中内部软弱夹层由于含水率的不同对外产生不同的渗透力,随含水率增加外部岩体受力后对内部压力增加内部软弱夹层产生向外的力,促进了岩体的破坏。
在实际边坡中,由于降雨导致内部软弱夹层软化含水率增加,岩体对其应力增加的同时软弱夹层内部也产生静水压力,导致降雨后一段时间不稳定岩质边坡容易产生蠕变滑移,最终导致山体滑坡等灾害。
(3)蠕变速率影响分析
以正应力2.4 MPa下岩层试件剪切蠕变状况进行分析含软弱夹层试件在剪应力作用下的蠕变速率变化情况。本文取软弱夹层含水量正常和饱和情况下一级加载蠕变速率情况进行分析,如图 8,9。
由图 8,9可得含软弱夹层岩石在软弱夹层含水率不同剪切蠕变试验过程中各个工况下均表现为衰减蠕变、稳态蠕变和加速蠕变3个阶段后随着时间的增长而破裂。相对应的时间-蠕变速率曲线在初始阶段有一定速率并逐步减小在稳态阶段速率变得相对稳定,在蠕变加速阶段速率增加迅速。
3. 多参数渐变损伤剪切蠕变本构模型
3.1 多参数损伤变量引入
实际工程中的岩体在持续荷载作用下岩体的剪切模量、强度、黏性系数等相关的岩体力学参数在其受力荷载未达到岩体长期强度时会下降部分值[18],相关研究已证实其过程中损伤衰减过程的作用存在。根据损伤力学理论,损伤变量主要从结构有效承载面积和能量损伤中按变形参数变化两方面定义,并指出材料变形参数的劣化是材料损伤的主要因素。根据陈兴周等[9]提出的材料损伤衰减规律,认为剪切模量的损伤演化可以用下式表达:
D(t)=E0−E∞E0(1−e−αt)。 (1) 式中:E0为初始弹性模量;E∞为任意时刻弹性模量;α为与材料损伤程度相关的系数;t为时间。
由此可推导任意时刻流变参数损伤为
A(t)=A0(1−Dt)=A0[E0e−αt+E∞(1−e−αt)E0]。 (2) 式中:A0表示材料初始值。
可得能量损伤和黏性损伤分别为
E(t)=E0(1−Dt)=E0e−αt+E∞(1−e−αt), (3) η(t)=η0(1−Dt)=η0E0e−αt+E∞(1−e−αt)E0。 (4) 式中:η0为黏性参数。
岩石的剪切强度和时间的相关关系为
τ(t)=(τ0−τ∞)e−mt+τ∞。 (5) 式中:τ(t)表示水平剪应力;τ0为瞬时剪切强度;τ∞为任意时间(极大)的剪切强度,接近于岩石强度;m为材料参数
3.2 损伤条件判别
在综合考虑3个主应力的影响下,以等效应变定义材料的损伤阈值。定义岩体随蠕变的进行,计损伤应变εe,阈值应变εt。由弹性力学可知ε3−J1ε2+ J2ε−J3=0的3个根ε1,ε2,ε3可表示3个主应变。经过数学计算可得
εe=√ε12+ε22+ε32=√J12−2J2。 (6) 式中:J1=εx+εy+εz;
J2=εxεy+εyεz+εzεx−14(γ2xy+γ2yz+γ2xz)。 当应变大于确定的阈值即εe>εt时岩体进入损伤阶段。损伤阈值对应于应力峰值处的损伤,通过试验数据加速蠕变阶段曲线确定,定义此阶段开始时间应变为阈值应变。
3.3 剪切蠕变损伤本构模型的建立
本文以西原模型为基础, 考虑软弱夹层内含水率随时间变化导致的黏性损伤劣化效应Dt,以及非线性的加速蠕变阶段引起的能量损伤Et[19],综合以上因素有弹性元件、黏性元件、黏塑性元件,提出一个新的黏弹塑性剪切蠕变本构模型,如图 10。
(1)当σ<σs,此时蠕变参数损伤只考虑时间效应引起的损伤劣化效应Dt,其蠕变本构方程表达为
ε=τG1(1−Dt)+τG2[1−exp(−G2η2t)]+η3(1−Dt)ε4′ntn−1。 (7) 式中:σs为屈服应力;ε4′为非线性黏性体应变的一阶导数;n为流变指数;ε为应变;ε∗为加速蠕变的初始值。
(2)当σ⩾σs,ε<ε∗时,考虑岩体弹性和蠕变参数的损伤劣化效应Dt,此时蠕变损伤本构方程为
ε=τG1(1−Dt)+τG2[1−exp(−G2η2t)]+τη3t。 (8) (3)当σ⩾σs,ε⩾ε∗时,考虑岩体弹性材料参数和蠕变参数以及加速蠕变变化引起的损伤劣化效应Dt,此时蠕变损伤本构模型为
ε=τG1(1−Dt)+τG2[1−exp(−G2η2t)]+τη3t+η3(1−Dt)ε4′ntn−1。 (9) 综合以上本构方程可描述含软弱夹层岩质边坡在降雨后一段时间岩体内软弱夹层随时间的材料损伤劣化效应和加速蠕变变化的损伤劣化效应。所建立本构方程可以反映岩体力学参数损伤的瞬时、衰减及稳态蠕变阶段,还可以反映高剪应力下的加速蠕变状态。
3.4 长期强度预测
岩石的蠕变破坏通常有两个拐点表征岩石状态的变化,第一个拐点为衰减蠕变阶段进入稳态蠕变阶段,第二个拐点是稳态蠕变阶段进入到加速蠕变阶段[20]。因此,可通过确定两个拐点时间并反映到同一个应力-应变关系图中,中间水平阶段反映岩土体长期强度。长期强度荷载下岩土时效损伤和材料损伤下,满足以下关系:
Dc=D∞+DE。 (10) 将式(3)和式(5)代入式(10)可得岩体损伤
Ev=13m((2α+√6√6−α−1)+6√R(d)χ√6−α)−αd√R(d)χ。 (11) 式中:χ=μmη2+α2km2η1,R(d)=Dc2ξ1+ξ2,ξ=D/Dc对损伤变量d进行求导以及边界条件式(6)可得长期强度Q∞的表达式
Q∞=2α+√6√6−αQ3+6√R(D∞)χ√6−α, (12) 对应时刻瞬时损伤D∞=ξDc。
4. 边坡相似模拟验证
分析发现含软弱夹层隐伏式岩质边坡在破坏前夕有明显的预兆,可通过加速蠕变来反映。在前期试验基础上取饱和含水率下岩层倾角水平状态进行实际工程边坡相似模拟验证,根据相似性原理确定相似比为20∶1开展试验。
4.1 模型搭建
结合广西巴马-凭祥公路某段边坡滑移情况进行隐伏式软弱夹层相似模拟验证,边坡搭建如图 11。本次试验根据相似理论及室内试件试验确定软弱夹层采用重晶石粉∶石英砂∶高强石膏∶甘油∶水=2.6∶5.7∶0.3∶0.1∶1.3调制而成。硬质岩层采用重晶石粉、石英砂、水泥、高强石膏、甘油、水按配比制备。边坡两侧采用实验室长3 m宽10 cm槽钢逐级固定支撑,待每层夯实之后再加下一级。为防止软弱夹层向其他硬质岩层渗水造成试验效果不明显,采取15 cm×30 cm塑料薄膜充当防水层。为模拟雨水在软弱夹层渗流并加快渗流速率采用自吸水棉线进行引导,每层两根共4根棉线,共计10 m。沿软弱夹层方向每层软弱夹层均匀布置土压力采集点,反映含水率对软弱夹层的压力影响。为防止雨水下渗过程中向硬岩渗水,采用自吸水棉线穿过塑料软管直至两层软弱夹层,共计软管5 m。
计算相似比例确定实际边坡经转换后得边坡底部最长270 cm,边坡高130 cm,边坡顶部长85 cm,边坡台阶长60 cm,边坡面为60°坡面。其中软弱夹层1长67 cm,软弱夹层2长118 cm,夹层角度和实际边坡取值相同均取46°,软弱夹层隐伏于边坡表面内部。边坡堆砌完成后拆除单面模板各关键组成如图 12。
4.2 滑移情况分析
在经过12 h的持续渗水试验,在注水速率20 mL/min下边坡内软弱夹层达到饱和状态,如图 13。
在12.5 h边坡发生滑移破坏,如图 14,15,此时边坡在后缘渗水情况下从边坡顶部开始滑移,且边坡断面上部首先开始出现剪断裂纹,上层软弱夹层首先向下滑移,下层软弱夹层随之产生裂纹但是并没有完全滑移。这是由于软弱夹层随着含水率的增加,软弱夹层内部力学性能降低、强度丧失,失去对边坡的整体承载力导致逐步滑坡,软弱夹层2由于软弱夹层1的下滑导致其上部荷载降低从而重新达到稳定状态,下部分裂隙是由于软弱夹层1下滑力带动产生。结合以上试验现象验证了剪切蠕变试验的合理性。
从图 16,17可知,在向软弱夹层注水的过程中,随着软弱夹层含水率依次升高,各测点剪切位移也随之增加,达到饱和后剪切位移趋于稳定增长,在后期滑坡产生时测点位移快速增加,与剪切蠕变试验加速蠕变阶段相对应,整体表现出各测点均有初始衰减蠕变、稳态蠕变和最后滑移前加速蠕变,其中加速蠕变阶段初始边坡坡角出现剪出口之后边坡断面裂纹进一步扩展直至整体滑移。
4.3 蠕变损伤模型试验验证
为验证所推导蠕变损伤本构模型的正确合理性,根据相似模拟试验数据进行拟合分析[21]。由试验参数可知此时正应力3.4 MPa,最大剪应力5.26 MPa。由图 14,15可知含软弱夹层在岩层内部所处位置在3.4 MPa正应力下发生剪切蠕变时根据损伤判别公式ε=5.26 MPa⩾ε∗=4.7 MPa,故采用式(9)进行拟合运算验证。在试验开始t=0时确定初始剪切模量G1,通过稳态等速蠕变阶段剪切蠕变试验数据代入式(8)可求得参数G2,η3;通过衰减蠕变阶段数据代入式(7)可确定η2;最后通过加速蠕变阶段数据代入式(9)以求得n。可得到边坡剪切蠕变损伤参数如表 2。
表 2 含软弱夹层岩体蠕变损伤模型参数Table 2. Creep damage model parameters of rock mass with weak interlayer剪应力/MPa G1/(MPa⋅mm−1) G2/(MPa⋅mm−1) G3/(MPa⋅mm−1) η1/(MPa⋅h⋅mm−1) η2/(MPa⋅h⋅mm−1) η3/(MPa⋅h⋅mm−1) n Dt R2 2.3 289546.26 7.69 186.96 0.12 6.32 78634.95 0.16 0.06 0.985 2.9 39.86 386.21 12.64 12.36 15.96 3532.64 0.26 0.02 0.968 3.5 16.98 15.69 756.32 53.69 48.61 1597.68 0.39 0.05 0.986 4.1 7.95 795.64 35.91 2.39 189.37 48316.26 1.23 0.26 0.974 4.7 13.69 298.79 141.26 138.41 46.96 225.61 1.28 0.81 0.963 取测点1-2分阶段本构拟合,可得反映蠕变过程的完整曲线及拟合效果曲线图 18。
图 18中t1时刻蠕变速率骤增即边坡开始滑移,软弱夹层进入加速蠕变阶段,t2时刻剪切位移呈直线增长,边坡完全失稳滑移。由图 18可得试验数据和本构模型拟合各个阶段拟合度均大于0.96,即该模型可以反映含软弱夹层隐伏式非贯通岩质边坡的剪切蠕变特性,对衰减蠕变、稳态蠕变和加速蠕变阶段解释准确,具有较高的可信度。
5. 结论
(1)隐伏式非贯通含软弱夹层岩体在剪切蠕变过程中,软弱夹层倾角、埋深和岩体稳定性正相关;夹层含水率和岩体稳定性负相关;随着软弱夹层所处深度的增加岩体稳定性减小,但存在一定临界值。
(2)考虑多参数岩体渐变损伤,分蠕变阶段建立对应本构模型,可以较好的反映岩体剪切蠕变过程中瞬时蠕变、衰减蠕变、稳态蠕变和加速蠕变阶段。
(3)通过相似模拟试验揭示隐伏非贯通含软弱夹层岩质边坡的启滑机制,拟合验证蠕变本构模型的适用性,对实际边坡滑移起到实际参考效果。
-
表 1 土样的物理性质
Table 1 Physical properties of soils
取土
地点颗粒相对质量密度 液限
/%塑限
/%最大干密度
/
(g·cm-3)最优含水率
/%颗粒组成/% 土样
分类砂粒
(2~0.075 mm)粉粒
(0.075~
0.005 mm)黏粒
(≤0.005 mm)延安 2.71 30.3 18.0 1.78 16.0 1.4 81.2 17.4 低液限黏土(CL) 表 2 针孔试验判别结果
Table 2 Discriminated results of pinhole tests
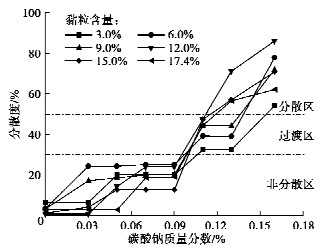
黏粒含量/% 碳酸钠质量分数/% 0 0.03 0.05 0.07 0.09 0.11 0.13 0.16 3.0 分 分 分 分 分 分 分 分 6.0 分 分 分 分 分 分 分 分 9.0 分 分 分 分 分 分 分 分 12.0 非 非 非 过 过 过 分 分 15.0 非 非 非 非 非 过 过 分 17.4 非 非 非 非 非 过 过 分 注:(1)“分”表示分散土,“过”表示过渡土,“非”表示非分散土;(2)判别标准:分散土,在50 mm水头下针孔迅速扩大1.5倍以上,水流混浊;过渡土,在180,380 mm水头下针孔扩大,水流混浊;非分散土,在1020 mm水头下针孔没有变化,水流清澈。 表 3 泥球试验判别结果
Table 3 Discriminated results of mud ball tests
黏粒
含量/%碳酸钠质量分数/% 0 0.03 0.05 0.07 0.09 0.11 0.13 0.16 3.0 非 过 分 分 分+ 分+ 分+ 分+ 6.0 非 过 过 分 分 分+ 分+ 分+ 9.0 非 过 过 过 分 分+ 分+ 分+ 12.0 非 非 非 过 分 分+ 分+ 分+ 15.0 非 非 非 非 过 分+ 分+ 分+ 17.4 非 非 非 非 过 分+ 分+ 分+ 注:①“分+”表示强分散土,“分”表示分散土,“过”表示过渡土,“非”表示非分散土。②判别标准:非分散土,土水之间没有反应,土-水界面清晰。过渡土,土水之间轻微反应,土-水界面轻微模糊。分散土,土水之间中等反应,土-水界面模糊。强分散土,土水之间严重反应,土-水界面完全模糊。 表 4 双密度计试验判别结果
Table 4 Discriminated results of double hydrometer tests
黏粒含量/% 碳酸钠质量分数/% 0 0.03 0.05 0.07 0.09 0.11 0.13 0.16 3.0 非 非 非 非 非 过 过 分 6.0 非 非 非 非 非 过 过 分 9.0 非 非 非 非 非 过 过 分 12.0 非 非 非 非 非 过 分 分 15.0 非 非 非 非 非 过 分 分 17.4 非 非 非 非 非 过 分 分 注:①“分”表示分散土,“过”表示过渡土,“非”表示非分散土。②判别标准:一般认为其判别标准应为:非分散土(D < 30%);过渡土(30% ≤ D ≤ 50%);分散土(D > 50%)。 表 5 孔隙水可溶性阳离子试验判别结果
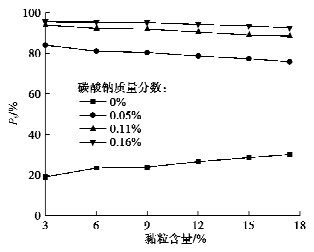
Table 5 Discriminated results of pore water soluble cation tests
黏粒
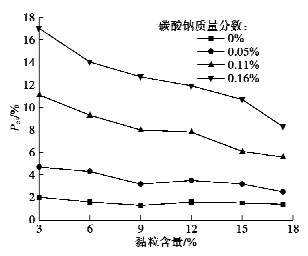
含量/%碳酸钠质量分数/% 0 0.05 0.11 0.16 3.0 非 分 分 分 6.0 非 分 分 分 9.0 非 分 分 分 12.0 非 分 分 分 15.0 非 分 分 分 17.4 非 分 分 分 注:①“分”表示分散土,“过”表示过渡土,“非”表示非分散土。②判别标准:当孔隙水中阳离子总量(TDS)≥ 1 1/n mmol/L时,非分散土,Ps < 40%;过渡土,40% ≤Ps < 60%;分散土,Ps ≥ 60%。 表 6 交换性钠离子百分比试验判别结果
Table 6 Discriminated results of exchangeable sodium ion percentage tests
黏粒
含量/%碳酸钠质量分数/% 0 0.05 0.11 0.16 3.0 非 非 分 分 6.0 非 非 过 分 9.0 非 非 过 分 12.0 非 非 过 分 15.0 非 非 非 分 17.4 非 非 非 过 注:①“分”表示分散土,“过”表示过渡土,“非”表示非分散土。②判别标准:非分散土,Pes < 7;过渡土,7 ≤ Pes < 10;分散土,Pes ≥ 10。 表 7 5种分散性试验判别结果汇总
Table 7 Summary of discriminated results of 5 kinds of dispersivity tests
黏粒
含量/%碳酸钠质量分数/% 0 0.05 0.11 0.16 泥 针 双 孔 交 泥 针 双 孔 交 泥 针 双 孔 交 泥 针 双 孔 交 3.0 非 — — 非 非 分 — — 分 非 分 — — 分 分 分 — — 分 分 6.0 非 — — 非 非 过 — — 分 非 分 — — 分 过 分 — — 分 分 9.0 非 — — 非 非 过 — — 分 非 分 — — 分 过 分 — — 分 分 12.0 非 非 非 非 非 非 非 非 分 非 分 过 过 分 过 分 分 分 分 分 15.0 非 非 非 非 非 非 非 非 分 非 分 过 过 分 非 分 分 分 分 分 17.4 非 非 非 非 非 非 非 非 分 非 分 过 过 分 非 分 分 分 分 过 注:①“分”表示分散土,过表示过渡土,“非”表示非分散土。②“泥”表示泥球试验,“针”表示针孔试验,“双”表示双密度计试验,“孔”表示孔隙水可溶性阳离子试验,“交”表示交换性钠离子百分比试验。③由于针孔试验和双密度计试验不适用黏粒含量低于10%的土样,故表中没有列出试验结果。 -
[1] 樊恒辉, 赵高文, 李洪良. 分散性黏土研究现状与展望[J]. 岩土力学, 2010, 31(增刊1): 108-114. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2010S1020.htm FAN Henghui, ZHAO Gaowen, LI Hongliang. Current researches and prospects of dispersive clay[J]. Rock and Soil Mechanics, 2010, 31(S1): 108-114. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2010S1020.htm
[2] Standard Test Methods for Identification and Classification of Dispersive Clay Soils by the Pinhole Test: ASTM D4647[S]. ASTM, 2010.
[3] Standard Test Methods for Determining Dispersive Characteristics of Clayey Soils by the Crumb Test: ASTM D6572[S]. ASTM, 2021.
[4] Standard Test Method for Dispersive Characteristics of Clay Soil by Double Hydrometer: ASTM D4221[S]. ASTM, 2018.
[5] Standard Test Methods for Pore Water Extraction and Determination of the Soluble Salt Content of Soils by Refractometer: ASTM D4542[S]. ASTM, 2022.
[6] Standard Test Method for Measuring the Exchange Complex and Cation Exchange Capacity of Inorganic Fine-Grained Soils: ASTM D7503[S]. ASTM, 2018.
[7] 樊恒辉, 赵高文, 路立娜, 等. 分散性土的综合判别准则与针孔试验方法的改进[J]. 水力发电学报, 2013, 32(1): 248-253, 262. https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201301041.htm FAN Henghui, ZHAO Gaowen, LU Lina, et al. Comprehensive criterion of dispersive soil and improvement of pinhole test[J]. Journal of Hydroelectric Engineering, 2013, 32(1): 248-253, 262. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201301041.htm
[8] BS 1377: Part: 5, British standard methods of test for soils for civil engineering purposes, Part 5. compressibility, permeability and durability tests[S].
[9] 彭文明, 李建, 张延亿, 等. 一种低液限黏土的分散性试验研究[J]. 岩土工程学报, 2020, 42(增刊1): 121-126. doi: 10.11779/CJGE2020S1024 PENG Wenming, LI Jian, ZHANG Yanyi, et al. Experimental study on dispersion of one kind of low liquid limit clay[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(S1): 121-126. (in Chinese) doi: 10.11779/CJGE2020S1024
[10] INGLES O G, AITCHISON G D. Soil-water disequilibrium as cause of subsidence in natural soils and earth embankments[C]//Proceedings of the Tokyo Symposium on Land Subsidence, 1969.
[11] SHERARD J L, DECKER R S, RYKEN R L. Piping in earth of dispersive clay[C]//Proceedings of the ASCE Specialty Conference on the Performance of Earth-supported Structure, Purdue University, 1972: 589-626.
[12] MOHANTY S, ROY N, SINGH S P, et al. Estimating the strength of stabilized dispersive soil with cement clinker and fly ash[J]. Geotechnical and Geological Engineering, 2019, 37(4): 2915-2926. doi: 10.1007/s10706-019-00808-1
[13] CHOROM M, RENGASAMY P, MURRAY R S. Clay dispersion as influenced by pH and net particle charge of sodic soils[J]. Soil Research, 1994, 32(6): 1243. doi: 10.1071/SR9941243
[14] 魏迎奇, 温彦锋, 蔡红, 等. 分散性黏土鉴定试验的可靠性分析[J]. 中国水利水电科学研究院学报, 2007, 5(3): 186-190, 195. doi: 10.3969/j.issn.1672-3031.2007.03.005 WEI Yingqi, WEN Yanfeng, CAI Hong, et al. Reliability analysis of identification test of dispersive clay[J]. Journal of China Institute of Water Resources and Hydropower Research, 2007, 5(3): 186-190, 195. (in Chinese) doi: 10.3969/j.issn.1672-3031.2007.03.005
[15] 王观平. 黏土矿物与分散性粘土[J]. 黑龙江水专学报, 1994(3): 21-25. WANG Guanping. Clay mineral and dispersive clay[J]. Journal of Heilongjiang Hydraulic Engineering College, 1994(3): 21-25. (in Chinese)
[16] 赵高文, 樊恒辉, 陈华, 等. 蒙脱石对黏性土分散性的影响[J]. 岩土工程学报, 2013, 35(10): 1928-1932. http://cge.nhri.cn/cn/article/id/15316 ZHAO Gaowen, FAN Henghui, CHEN Hua, et al. Influence of montmorillonite on dispersivity of clayey soils[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1928-1932. (in Chinese) http://cge.nhri.cn/cn/article/id/15316
[17] 刘杰. 土石坝渗流控制理论基础及工程经验教训[M]. 北京: 中国水利水电出版社, 2006. LIU Jie. Seepage Control of Earth-Rock Dams Theoretical Basis, Engineering Experiences and Lessons[M]. Beijing: China Water & Power Press, 2006. (in Chinese)
[18] FAN H H, KONG L W. Empirical equation for evaluating the dispersivity of cohesive soil[J]. Candian Geotechnical Journal, 2013, 50(9): 989-994
[19] 樊恒辉, 孔令伟. 分散性土研究[M]. 北京: 中国水利水电出版社, 2012: 118-156. FAN Henghui, KONG Lingwei. Study Dispersive Clay[M]. Beijing: China Water & Power Press, 2012: 118-156. (in Chinese)
[20] 土工试验方法标准: GB/T 50123—2019[S]. 北京: 中国计划出版社, 2019. Standard for Soil Test Method: GB/T 50123—2019[S]. Beijing: China Planning Press, 2019.
[21] 蒋以超, 张一平. 土壤化学过程的物理化学[M]. 北京: 中国科学技术出版社, 1993: 323-328. JIANG Yichao, ZHANG Yiping. Physical Chemistry of Soil Chemical Process[M]. Beijing: China Science and Technology Press, 1993: 323-328. (in Chinese)
[22] 黄昌勇, 徐建明. 土壤学[M]. 3版. 北京: 中国农业出版社, 2010: 163. HUANG Changyong, XU Jianming. Agrology[M]. 3rd ed. Beijing: China Agriculture Press, 2010: 163. (in Chinese)
[23] 熊顺贵. 基础土壤学[M]. 北京: 中国农业大学出版社, 2001: 206-207. XIONG Shungui. Basic Soil Science[M]. Beijing: China Agricultural University Press, 2001: 206-207. (in Chinese)
[24] 樊恒辉, 李洪良, 赵高文. 黏性土的物理化学及矿物学性质与分散机理[J]. 岩土工程学报, 2012, 34(9): 1740-1745. http://cge.nhri.cn/cn/article/id/14705 FAN Henghui, LI Hongliang, ZHAO Gaowen. Relation among dispersive mechanism, physical-chemical and mineral properties of clayey soil[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(9): 1740-1745. (in Chinese) http://cge.nhri.cn/cn/article/id/14705
[25] VOLK G M. Method of determination of degree of dispersion of the clay fraction of soils[C]//Proceedings, Soil Science Society of American, 1937.
-
期刊类型引用(2)
1. 周斌,张弘,林春秀,付冬平. 降雨条件下基坑坡度和平台宽度对稳定性的影响. 广东土木与建筑. 2025(02): 28-31 .  百度学术
百度学术
2. 樊鸿志,王光进,蓝蓉,刘明生. 露天矿山岩质边坡软弱夹层赋存状态影响边坡稳定性规律研究. 重庆大学学报. 2024(04): 22-33 .  百度学术
百度学术
其他类型引用(2)




 下载:
下载: