考虑非饱和渗透系数随机场统计特征的库岸老滑坡稳定性分析

王长虹; 杜昊东; 柳伟; 宗振邦; 胡世韬

doi:10.11779/CJGE20211273

考虑非饱和渗透系数随机场统计特征的库岸老滑坡稳定性分析 English Version

王长虹^1,,
杜昊东¹,
柳伟^{2, 3, ,},
宗振邦¹,
胡世韬¹

1.
上海大学力学与工程科学学院土木工程系, 上海 200444
2.
华东交通大学江西省岩土工程基础设施安全与控制重点实验室, 江西南昌 330013
3.
江西交通职业技术学院建筑工程学院, 江西南昌 330013

详细信息

作者简介:
王长虹(1978—)，上海高校特聘教授，主要从事随机岩土力学-贝叶斯方法研究。E-mail: changhong_wang@163.com

通讯作者:
柳伟，E-mail: xjxlw1979@163.com

中图分类号: TU443
计量
- 文章访问数: 289
- HTML全文浏览量: 51
- PDF下载量: 91
出版历程
- 收稿日期: 2021-12-06
- 网络出版日期: 2023-02-23
- 刊出日期: 2023-01-31

Stability analysis of old reservoir bank landslide by considering spatial random field characteristics of unsaturated hydraulic conductivity

1.
School of Mechanics and Engineering Science, Shanghai University, Shanghai 200444, China
2.
Jiangxi Key Laboratory of Infrastructure Safety and Control in Geotechnical Engineering, East China Jiaotong University, Nanchang 330013, China
3.
Department of Architectural Engineering, Jiangxi V & T College of Communications, Nanchang 330013, China

摘要

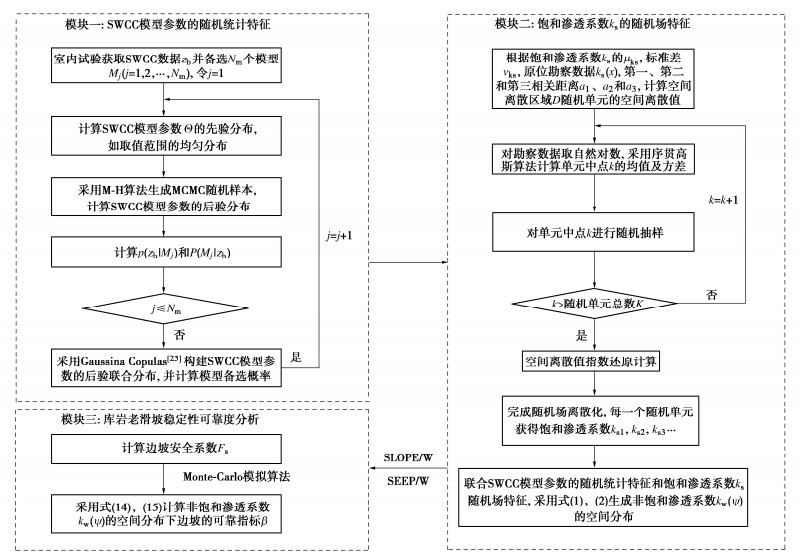
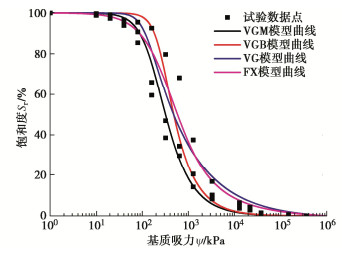
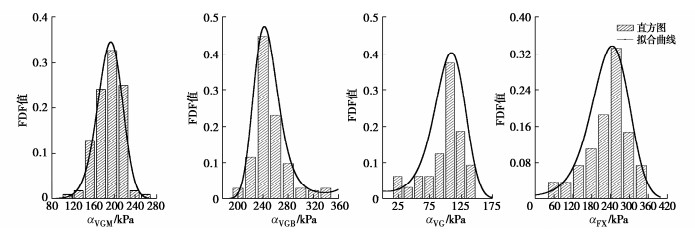
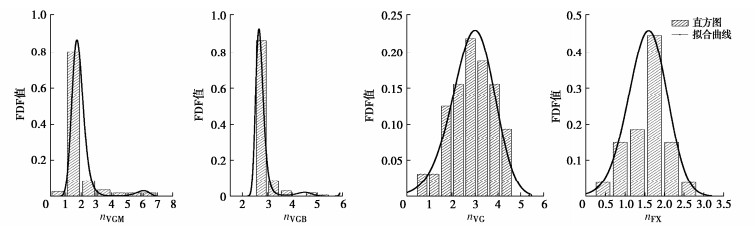
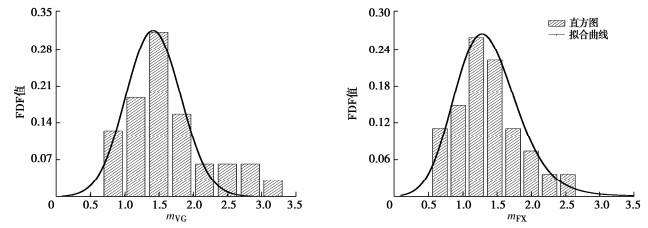
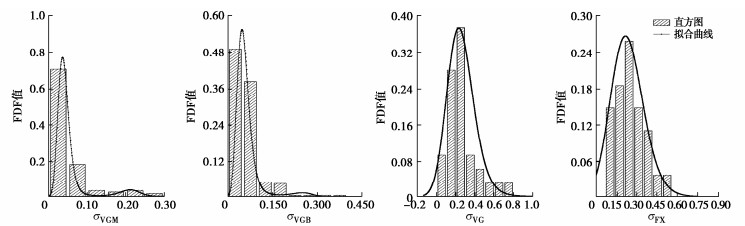
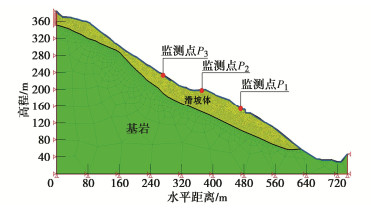
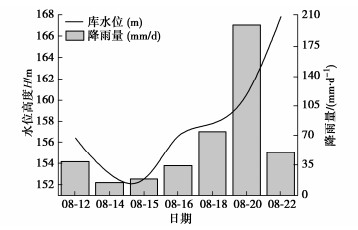
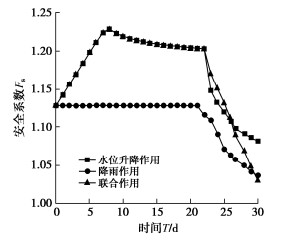
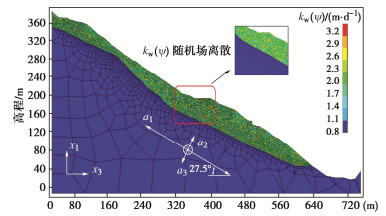
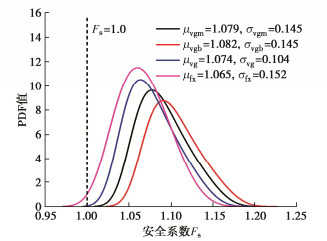
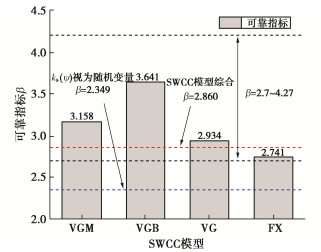
摘要: 库岸边坡如果在历史上发生过滑坡灾害，计算所得的安全系数将略高于临界状态值1.0，仅以安全系数评价库岸老滑坡的稳定性，将导致预测结果与边坡稳定状态不相符合。提出以土水特征曲线和非饱和渗透系数为核心的水力参数联合随机（场）统计特征为基础，建立库岸边坡稳定性的可靠度分析方法。首先根据有限的室内土水特征关系试验数据，采用贝叶斯理论校准土水特征曲线VGM、VGB、VG和FX模型参数的随机统计特征，并得到模型备选组合的概率。其次根据饱和渗透系数的随机场统计特征，联合土水特征曲线的随机统计特征，生成库岸边坡非饱和渗透系数的随机场空间分布。最后分析仅考虑土水特征曲线随机统计特征的库岸边坡稳定性失效概率，以及综合考虑非饱和渗透系数随机场统计特征的可靠指标。针对三峡库区石榴树包老滑坡在2020年强降雨和长江水位快速升降的工程背景，开展考虑渗流作用的非饱和土边坡稳定性可靠度分析。研究结果表明，虽然边坡稳定性的安全系数较低，但是可靠指标满足规范不小于2.70的要求，无需采取额外的边坡工程加固措施，建议继续开展边坡的长期健康监测。
- 库岸老滑坡 /
- 土水特征曲线 /
- 非饱和渗透系数 /
- 贝叶斯方法 /
- 可靠度分析
Abstract: If a reservoir bank landslide happenes in the history, the factor of safety of slope stability will approach the critical value 1.0, which cannot indicate the realistic stable situation of the reservoir bank slope. Based on the combined random (field) statistical characteristics of the hydraulic parameters, which consist of the soil-water characteristic curve (SWCC) and the saturated hydraulic conductivity, a reliability analysis method for the old reservoir bank landslide is established. Firstly, according to the limited laboratory test data of saturation-matrix suction, the statistical characteristics of the SWCC properties, such as VGM, VGB, VG, and FX model parameters, are calibrated by the Bayesian method, and the applied probabilities of SWCC model combination are determined through the laboratory measurements. Secondly, combining the random field characteristics of the saturated hydraulic conductivity with the random characteristics of the SWCC models, the spatial distributions of the unsaturated hydraulic conductivity are generated in the slide body. Finally, the reliability analysis will calculate the failure probability of the old reservoir bank landside only considering the random characteristics of the SWCC models, and the reliability index results of the spatial random field statistical characteristics of the unsaturated hydraulic conductivity. Under the conditions of heavy rainfall and rapid rise and fall of the Yangtze River water level in 2020, the reliability analysis of the old Shiliushubao landslide is carried out in the Three Gorges Reservoir area. The results indicate that the factor of safety of the slope stability is low, but the reliability index meets the minimum requirement of 2.70 according to the specification. None of the additional reinforcement measures are required. Nevertheless, the long-term slope monitoring program is suggested to be continued.
- old reservoir bank landslide /
- soil-water characteristic curve /
- unsaturated hydraulic conductivity /
- Bayesian method /
- reliability analysis

HTML全文

0. 引言

露天矿边坡在降雨和爆破开挖等外界荷载作用下，会在边坡坡顶和局部平台顶部形成一定规模张拉裂隙，这在实际工程中较为常见。进一步的岩体开挖所引发的应力调整和卸荷扰动会使这些张拉裂隙不断扩展，进而导致边坡突发性失稳，给周围人员生命及财产造成极大威胁。此类岩质边坡的特点为在边坡前缘存在近水平或缓倾坡外的结构面（常为层面或软弱夹层），后缘存在张拉裂隙，前缘缓倾结构面和后缘裂隙之间的区域对边坡稳定性起控制作用^[1-2]。为此研究开挖卸荷作用下前后裂隙之间的扩展贯通机理具有重要理论与工程意义。

目前，有关含后缘裂隙边坡失稳破坏机制的研究已取得了一定研究成果。黄达等^[3]利用模型试验和数值模拟研究了不同后缘裂隙倾角边坡破坏模式和裂隙扩展演化规律。Wu等^[4]从断裂力学的角度分析了不同后缘裂隙长度下危岩型边坡破坏演化规律。Zhang等^[5]以三峡太白岩悬崖为工程实例，定义了基于断裂力学的边坡稳定性系数。王来贵等^[6]分析了含后缘裂隙边坡在爆破荷载作用下的滑面导通机制。钟助等^[7]推导了边坡中部锁固段控制型边坡稳定性系数计算公式。

针对开挖卸荷作用下边坡失稳机制的研究，吴永等^[8]构建了开挖卸荷作用下边坡滑面形成的力学模型。常远等^[9]研究了露天矿高边坡的开挖损伤过程。Chang等^[10]给出了卸荷作用下裂隙边坡的临界失稳高度计算模型。李明等^[11]、习朝辉等^[12]、Zhu等^[13]利用模型试验探讨了开挖卸荷作用下边坡破坏机制与模式。李韬等^[14]、李新坡等^[15]利用数值模拟手段，研究了岩质边坡在开挖过程中的变形特征和稳定性状态。

关于含后缘裂隙岩质边坡的研究，主要集中在针对不同后缘裂隙几何分布下的边坡破坏研究。在边坡卸荷方面的研究，主要为通过模型试验和数值模拟手段来研究。针对含后缘裂隙岩质边坡在开挖卸荷作用下的理论方面研究较少。基于此，本文利用断裂力学理论，给出了卸荷作用下边坡后缘裂隙尖端应力强度因子和临界失稳高度计算方程，考虑分支裂隙扩展长度，构建了边坡岩体裂隙扩展贯通力学模型，阐明了边坡岩体断裂破坏机理，提出了边坡稳定性系数计算方法，并通过工程算例来验证，研究结论可为此类边坡的开挖稳定性评价提供理论支撑。

1. 卸荷诱发边坡失稳的力学基础

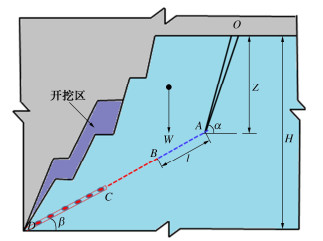
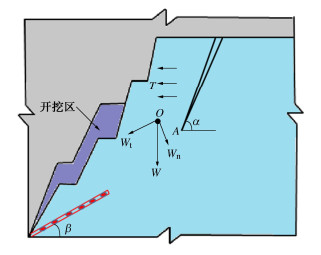
露天矿的不断开挖会使得岩体内的裂隙不断扩展贯通，具体作用机制为：随着开挖岩体表面的法向应力卸荷至0，而卸荷会使岩体产生差异回弹变形，这种变形会使坡体内产生方向指向开挖面的拉应力T^[16]，在拉应力T和滑体自重应力共同作用下，后缘裂隙起裂扩展。图 1为露天矿含后缘裂隙边坡滑动力学模型。

图 1 边坡滑动力学模型

Figure 1. Dynamic model for slope slip

下载: 全尺寸图片幻灯片

图 1中，A为后缘裂隙尖端，O为滑体重心位置，W_t为滑体在平行于下部裂隙方向的力，W_n为滑体在垂直于下部裂隙方向的力，将其分解到边坡后缘裂隙切向和法向的力分别为

，

${W}_{\text{t}}=W\mathrm{sin}\beta \text{ }\text{，}$

(1)

，

${W_{\text{n}}} = W\cos \beta \text{，}$

(2)

，

${W_\tau } = {W_{\text{t}}}\cos (\alpha - \beta ) + {W_{\text{n}}}\sin (\alpha - \beta ) \text{，}$

(3)

，

${W_\sigma } = {W_{\text{t}}}{\text{sin}}(\alpha - \beta ) - {W_{\text{n}}}\cos (\alpha - \beta ) \text{，}$

(4)

。

$W = \gamma V 。$

(5)

式中： $\alpha$ 为后缘裂隙与水平方向的夹角； $\beta$ 为下部裂隙与水平方向的夹角；W为滑体重量； ${W_\tau }$ 为后缘裂隙的切向力； ${W_\sigma }$ 为后缘裂隙的法向力； $\gamma$ 为岩体重度； $V$ 为滑体体积；T为卸荷拉应力。

本文在采用上述力学模型进行理论分析时作出如下假设：①不考虑爆破荷载的影响；②不考虑水对岩体的弱化作用；③不考虑降雨荷载影响，这里主要分析边坡在自重和开挖卸荷作用的影响。

随着开挖的不断向下进行，卸荷拉应力和滑体重力在后缘裂隙上的法向分力使裂隙宽度不断增加，切向分力使裂隙长度不断增加，后缘裂隙最终扩展至下部裂隙，在二者之间发生剪断破坏，造成边坡失稳。边坡频繁的开挖卸荷会引起边坡内应力场的变化，同时卸荷拉应力会对边坡的潜在滑动面造成一定影响，所以分析卸荷拉应力作用下的裂隙扩展对分析边坡的稳定性有着重要意义。

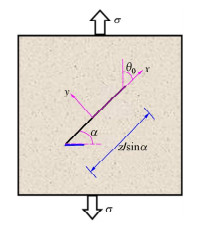
边坡后缘裂隙的受力模型，可简化为受到复杂应力和卸荷拉应力作用下的一个拉剪裂隙，属于Ⅰ-Ⅱ复合型断裂，其二维力学模型如图 2所示，裂隙尖端极坐标应力分量^[17]表达式为

$\left. \begin{array}{l}{\sigma }_{rr}=\frac{1}{2\sqrt{2\text{π}r}}\left[{K}_{{\rm I}}\text{(}3-\mathrm{cos}\theta \text{)}\mathrm{cos}\frac{\theta }{2}+{K}_{{\rm I}{\rm I}}(3\mathrm{cos}\theta -1)\mathrm{sin}\frac{\theta }{2}\right]\text{，}\\ {\sigma }_{\theta \theta }=\frac{1}{2\sqrt{2\text{π}r}}\mathrm{cos}\frac{\theta }{2}\left[{K}_{{\rm I}}(1+\mathrm{cos}\theta )-3{K}_{{\rm I}{\rm I}}\mathrm{sin}\theta \right]\text{ }\text{，}\\ {\tau }_{r\theta }=\frac{1}{2\sqrt{2\text{π}r}}\mathrm{cos}\frac{\theta }{2}\left[{K}_{{\rm I}}\mathrm{sin}\theta +{K}_{{\rm I}{\rm I}}(3\mathrm{cos}\theta -1)\right]\text{ }。\end{array} \right\}$

(6)

图 2 拉剪裂隙

Figure 2. Tension-shear crack

下载: 全尺寸图片幻灯片

式中： ${\sigma _{rr}}$ 为径向应力； ${\sigma _{\theta \theta }}$ 为轴向应力； ${\tau _{r\theta }}$ 为剪切应力； $\theta$ 裂隙尖端扩展方向； $r$ 为裂隙尖端到裂隙上点的距离； ${K_{\rm I}}$ 为裂隙尖端Ⅰ型应力强度因子； ${K_{{\rm I}{\rm I}}}$ 为裂隙尖端Ⅱ型应力强度因子。

根据最大周向拉应力准则，不考虑奇异应力项（T应力）影响，Ⅰ-Ⅱ复合型裂隙会沿着最大拉应力 ${\sigma _{\theta \theta \max }}$ 的方向扩展，岩体裂隙扩展起裂角 ${\theta _0}$ 方向^[18]满足

${K}_{{\rm I}}\mathrm{sin}{\theta }_{0}+{K}_{\text{II}}\text{(}3\mathrm{cos}{\theta }_{0}-1\text{)}=0\text{ }。$

(7)

当边坡裂隙尖端应力强度因子满足

$\left[ {{K_{\rm I}}{\text{co}}{{\text{s}}^2}\frac{{{\theta _0}}}{2} - \frac{3}{2}{K_{{\text{II}}}}\sin {\theta _0}} \right]{\text{cos}}\frac{{{\theta _0}}}{2}{\text{ = }}{K_{{\rm I}C}}$

(8)

时，裂隙起裂扩展，其中， ${K_{{\rm I}C}}$ 为岩体断裂韧度。

2. 卸荷坡体后缘裂隙扩展力学模型

2.1 卸荷作用下后缘裂隙的起裂扩展

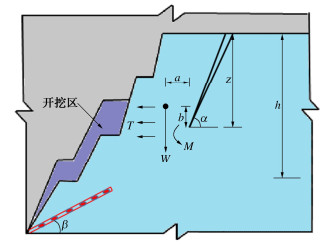
边坡下部岩体未开挖之前，后缘张拉裂隙只受滑体自重的作用，随着开挖的进行，在坡体内产生方向由坡体指向坡面的卸荷拉应力T，裂隙尖端应力强度因子增加，当其达到岩体断裂韧度时，裂隙起裂扩展。如图 3所示为边坡后缘裂隙扩展概化模型，W为滑体重量，h为后缘裂隙未贯通岩体及其上部岩体的平均高度，z为裂隙垂直高度，a为滑体重心到裂隙尖端水平距离，b为滑体重心到裂隙尖端垂直距离，M为滑体和卸荷拉应力对裂隙尖端产生的弯矩。

图 3 边坡后缘裂隙扩展概化模型

Figure 3. Generalized model for crack propagation at trailing edge of slope

下载: 全尺寸图片幻灯片

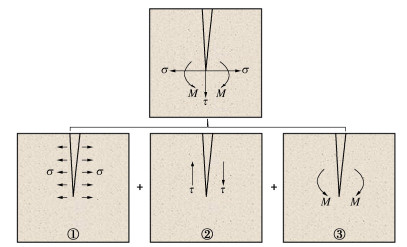
根据应力强度因子叠加原理，上部滑体自重和卸荷拉应力作用下后缘裂隙尖端应力强度因子可分解为如图 4的结果，图 4中①~③分别为拉应力、剪应力和弯矩，其裂隙尖端应力强度因子为

${K_{{\rm I}1}} = \sigma \sqrt {{\text{π (}}z/\sin \alpha {\text{)}}/2} \text{，}$

(9)

${K_{{\rm I}2}} = {\sigma _{\max }}\sqrt {{\text{π }}(z/\sin \alpha )/2} \text{，}$

(10)

${K_{{\rm I}{\rm I}3}} = \tau \sqrt {{\text{π }}(z/\sin \alpha )/2} \text{，}$

(11)

$\sigma = {W_\sigma }{\text{sin}}\alpha /h + T\sin \alpha \text{，}$

(12)

$\tau = {W_\tau }{\text{sin}}\alpha /h + T\cos \alpha \text{，}$

(13)

${\sigma _{\max }} = {\text{6}}M/{h^2} 。$

(14)

图 4 边坡后缘裂隙尖端应力强度因子的叠加原理示意图

Figure 4. Schematic diagram of superposition principle of stress intensity factor at the tip of crack at the back edge of slope

下载: 全尺寸图片幻灯片

式中： $\sigma$ 为裂隙面上的拉伸应力； $\tau$ 为裂隙面上的剪切应力； ${\sigma _{\max }}$ 为最大拉应力； $M = Wa + Thb$ 。

因此，卸荷条件下边坡岩体后缘裂隙尖端应力强度因子为

$\left. \begin{array}{l}{K}_{{\rm I}}={K}_{{\rm I}1}+{K}_{{\rm I}2}\text{ }\text{，}\\ {K}_{{\rm I}{\rm I}}={K}_{{\rm I}{\rm I}3}\text{ }。\end{array} \right\}$

(15)

将式（9）~（14）计算结果代入式（15）可得卸荷条件下边坡后缘裂隙尖端应力强度因子为

$\left. \begin{array}{l}{K}_{{\rm I}}=\{\left[\gamma V\mathrm{sin}\beta \text{sin}(\alpha -\beta )-\gamma V\mathrm{cos}\beta \mathrm{cos}(\alpha -\beta )\right]\text{sin}\alpha /h+\\ \text{ }T\mathrm{sin}\alpha +\text{6(}\gamma Va+Thb\text{)}/{h}^{2}\}\sqrt{\text{π}(z/\mathrm{sin}\alpha )/2}\text{ }\text{，}\\ {K}_{{\rm I}{\rm I}}=\{\left[\gamma V\mathrm{sin}\beta \mathrm{cos}(\alpha -\beta )+\gamma V\mathrm{cos}\beta \mathrm{sin}(\alpha -\beta )\right]\text{sin}\alpha /h+\\ \text{ }T\mathrm{cos}\alpha \}\sqrt{\text{π}(z/\mathrm{sin}\alpha )/2}\text{ }。\end{array} \right\}$

(16)

由式（16）可知，卸荷拉应力增大，边坡后缘裂隙尖端的Ⅰ和Ⅱ型应力强度因子都增大。

将式（16）代入式（7）化解可得

$\begin{gathered} \left\{ {\left[ {\gamma V\sin \beta {\text{sin}}(\alpha - \beta ) - \gamma V\cos \beta \cos (\alpha - \beta )} \right]{\text{sin}}\alpha /h + } \right. \hfill \\ \left. {T\sin \alpha + {\text{6}}(\gamma Va + Thb)/{h^2}} \right\} \cdot {\text{\{ }}[\gamma V\sin \beta \cos (\alpha - \beta ) + \hfill \\ \gamma V\cos \beta \sin (\alpha - \beta )]{\text{sin}}\alpha /h + T\cos \alpha {{\text{\} }}^{ - {\text{1}}}}{\text{ = }}\frac{{1 - 3\cos {\theta _0}}}{{\sin {\theta _0}}} 。 \end{gathered}$

(17)

令式（17）中等号左边等于R，则可进一步求得裂隙起裂角 ${\theta _0}$ 为

${\theta _0}{\text{ = }}\arccos \frac{{3 + \sqrt {{R^4} + 8{R^2}} }}{{{R^2} + 9}} 。$

(18)

由式（18）可得卸荷状态下边坡后缘裂隙起裂角。

根据前文分析，边坡后缘裂隙处于拉剪应力状态，裂隙起裂与否取决于岩石的Ⅰ型断裂韧性 ${K_{{\rm I}C}}$ ，将式（16）代入式（8）可得卸荷条件下后缘裂隙尖端复合应力强度因子 ${K_{{\text{Ic}}}}$ ：

$\begin{gathered} {K_{{\rm I}{\text{c}}}} = \left\{ {\left[ {\gamma V\sin \beta {\text{sin}}(\alpha - \beta ) - \gamma V\cos \beta \cos (\alpha - \beta )} \right]{\text{sin}}\alpha /h + } \right. \hfill \\ {\text{ }}\left. {T\sin \alpha + {\text{6}}(\gamma Va + Thb)/{h^2}} \right\}{\text{co}}{{\text{s}}^3}\frac{{{\theta _0}}}{2}\sqrt {{\text{π }}(z/\sin \alpha )/2} + \hfill \\ {\text{ }}\sin {\theta _0}{\text{cos}}\frac{{{\theta _0}}}{2}\left\{ {\left[ {\gamma V\sin \beta \cos (\alpha - \beta ) + \gamma V\cos \beta \sin (\alpha - \beta )} \right] \cdot } \right. \hfill \\ \text{sin}\alpha /h+T\mathrm{cos}\alpha \}\sqrt{\text{π}(z/\mathrm{sin}\alpha )2}\text{ }。 \end{gathered}$

(19)

式（19）为边坡后缘裂隙起裂扩展的充要条件，当 ${K_{{\rm I}{\text{c}}}}$ ≥ ${K_{{\rm I}C}}$ ，裂隙起裂扩展。进一步对式（17）化解可求得卸荷作用下后缘裂隙处于临界扩展状态时的垂直高度 ${Z}_{临界}$ 为

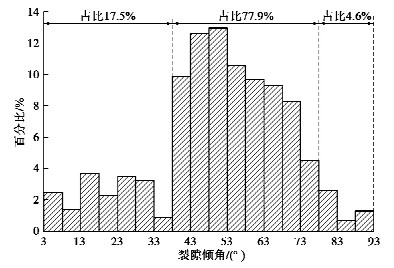
$\begin{array}{l}{z}_{临界}=2\mathrm{sin}\alpha {K}_{{\rm I}C}^{2}\cdot \{\text{π}\{[\gamma V\mathrm{sin}\beta \text{sin}(\alpha -\beta )-\\ \gamma V\mathrm{cos}\beta \mathrm{cos}(\alpha -\beta )]{\text{sin}\alpha /h+T\mathrm{sin}\alpha +\text{6}(\gamma Va+Thb)/{h}^{2}\}}^{2}\cdot \\ {\text{cos}}^{6}\frac{{\theta }_{0}}{2}+\text{π}{\mathrm{sin}}^{2}{\theta }_{0}{\text{cos}}^{2}\frac{{\theta }_{0}}{2}\{[\gamma V\mathrm{sin}\beta \mathrm{cos}(\alpha -\beta )+\\ {\left. {{{\left. {\left. {\gamma V\cos \beta \sin (\alpha - \beta )} \right]{\text{sin}}\alpha /h + T\cos \alpha } \right\}}^2}} \right\}^{ - {\text{1}}}} 。\end{array}$

(20)

通过上述边坡力学模型可以分析后缘裂隙几何参数对裂隙临界失稳高度和裂隙起裂角的影响，从式（17），（20）可以看出。直接关系到边坡的稳定性状态的主要因素有平均高度、裂隙倾角和卸荷拉应力，其他因素为岩体固有属性。根据现场坍塌剖面地质调查结果绘制后缘裂隙形态分布如图 5所示，该矿山地层结构简单，岩体在外界环境荷载作用下裂隙较为发育。后缘裂隙倾角主要集中在38°~78°，其余角度裂隙随机不规则散布在群集之间。下部裂隙角度β为43°，岩体断裂韧性为1.2 MPa·m^1/2，岩石重度25 kN/m³，滑体体积V约为8×10 m³。本次分析采用控制变量法，通过现场调查，定义后缘裂隙倾角α在40°~90°变化，平均高度h在20~115 m变化。

图 5 岩体裂隙形态分布情况

Figure 5. Distribution of cracks in rock mass

下载: 全尺寸图片幻灯片

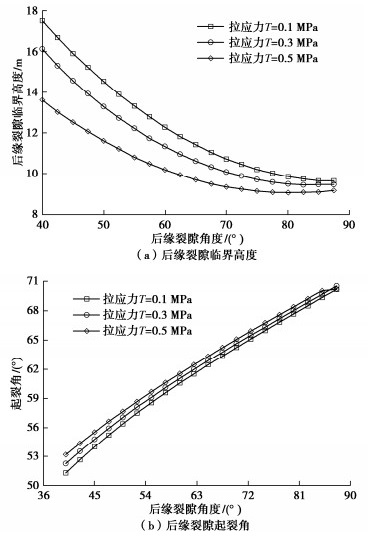
将上述数据代入式（18），（20）便可得到后缘裂隙临界高度和起裂角随后缘裂隙倾角和拉应力T的变化关系，如图 6所示。图 6（a）为裂隙临界高度与裂隙倾角的变化关系，裂隙临界高度随裂隙倾角的增大而逐渐减小直至趋于稳定，其曲率逐渐降低直至趋于0。说明后缘裂隙倾角为90°时，裂隙最容易起裂扩展，当裂隙倾角较小时，上部滑体重量在垂直于裂隙方向上分解了一部分力，其尖端应力强度因子变小，当裂隙垂直时，滑体重力水平分力与卸荷拉应力全部作用于裂隙面，其尖端应力强度因子最大，裂隙最容易扩展，所对应的临界扩展高度最小。图 6（b）是后缘裂隙起裂角与裂隙倾角的关系图，从图 6（b）可以看出，起裂角与裂隙倾角近似呈现出线性关系，裂隙起裂角随裂隙倾角的增加而增大，说明裂隙倾角越大，裂隙越来越趋向于边坡坡面扩展，随着滑面的长度在增加，边坡稳定性增加。从图 6还可以看出，随着水平方向卸荷拉应力的增加，后缘裂隙临界扩展高度变小，起裂角变大，这二者的都是向边坡不稳定的方向变化。

图 6 后缘裂隙临界高度与起裂角随裂隙倾角变化关系图

Figure 6. Relationship between critical height and initiation angle of trailing edge crack with dip angle of crack

下载: 全尺寸图片幻灯片

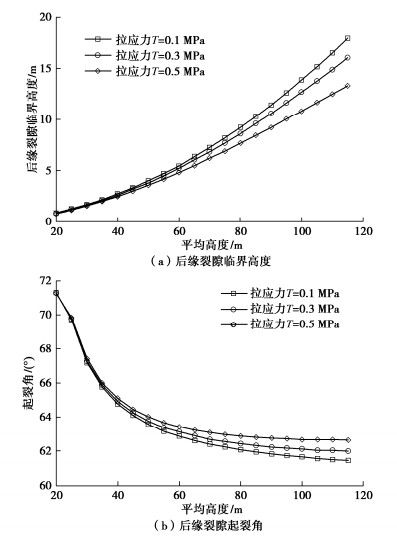
将上述数据代入式（18），（20）便可得到后缘裂隙临界高度和起裂角随平均高度和拉应力T的变化关系，如图 7所示。后缘裂隙临界高度随平均高度变化关系如图 7（a）所示，裂隙临界高度随平均高度的增大而逐渐增大，其曲率逐渐增大，说明平均高度越大，裂隙尖端应力强度因子越小，裂隙越不容易扩展，所对应的扩展临界高度就大，边坡越稳定。图 7（b）是后缘裂隙起裂角与平均高度的关系图，裂隙起裂角随平均高度的增加而减小，其曲率逐渐减小直至为零。说明平均高度越大，裂隙越来越偏离边坡坡面扩展，导致滑面的长度增加，边坡稳定性增强。从图 7还可以看出，随着水平方向卸荷拉应力的增加，后缘裂隙临界扩展高度变小，起裂角变大，这二者的变化都是向边坡不稳定的方向变化。

图 7 后缘裂隙临界高度与起裂角随平均高度变化关系图

Figure 7. Relationship between critical height and initiation angle of trailing edge fracture with average height

下载: 全尺寸图片幻灯片

2.2 开挖坡体裂隙扩展长度计算

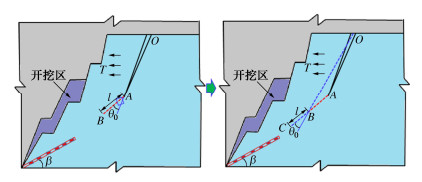
前文就边坡后缘裂隙在开挖卸荷作用下的起裂条件和扩展方向进行了计算与分析，下面就裂隙起裂后如何扩展与贯通进行解释。边坡岩体在爆破和开挖等外界荷载扰动下形成如所示的后缘裂隙OA，在边坡开挖卸荷作用下不断扩展，最终与下部裂隙贯通，造成边坡滑坡的发生。第一次边坡开挖时，当后缘裂隙尖端的应力强度因子在滑体自重应力和卸荷拉应力共同作用下大于岩体断裂韧度时，裂隙按起裂角 ${\theta _0}$ 起裂扩展一定长度AB，随后坡体应力场调整结束，岩体整体处于平衡状态，裂隙停止扩展。第二次开挖，在边坡岩体内应力场作用下，裂隙以初始等效长度OB为基础再次起裂扩展一定长度BC，这样，边坡岩体每开挖一次，裂隙就扩展一次，扩展长度不断累积，最终与下部裂隙贯通。

图 8 边坡后缘裂隙扩展贯通示意图

Figure 8. Schematic diagram of crack extension and penetration at back edge of slope

下载: 全尺寸图片幻灯片

边坡岩体后缘裂隙扩展属于拉剪扩展，拉剪应力作用下分支裂隙尖端应力强度因子为^[18]

${K_{\text{I}}}(l) = \frac{{5.18(z/\sin \alpha )\tau \cos \alpha }}{{\sqrt {{\text{π }}l} }} \text{，}$

(21)

式中，l为分支裂隙扩展长度。

卸荷拉应力增加了分支裂隙尖端的应力强度因子。在滑体自重应力和卸荷拉应力作用下，分支裂隙尖端的应力强度因子 ${K_{\text{I}}}(l)$ 随着裂隙长度增加而增加，当增加到 ${K_{\text{I}}}(l)$ = ${K_{{\rm I}C}}$ 时，分支裂隙就会不稳定扩展。随着边坡岩体内应力场的调整，当分支裂隙尖端的应力强度因子 ${K_{\text{I}}}(l)$ ＜ ${K_{{\rm I}C}}$ 时，裂隙停止扩展。于是可获得分支裂隙扩展的长度为

$l = {\left[ {5.18(z/\sin \alpha )\cos \alpha } \right]^2} \cdot \left\{ {\left[ {\gamma V\sin \beta \cos (\alpha - \beta ) + } \right.} \right. \\ {\left. {\gamma V\cos \beta \left. {\sin (\alpha - \beta )} \right]{\text{sin}}\alpha /h + T\cos \alpha } \right\}^2}{{/(\pi }}K_{{\rm I}C}^2{)^{ - 1}}{\text{ }} 。$

(22)

3. 含后缘裂隙边坡稳定性分析

3.1 边坡安全系数推导

第2节计算了开挖卸荷作用下边坡岩体发生损伤破坏时分支裂隙扩展长度，本节从宏观角度进一步对边坡安全系数的求解进行推导。文献[8]关于边坡开挖前后坡体内应力状态可知，不论开挖后裂隙的应力状态如何，单元体内的裂隙会沿着最大主应力方向扩展，即裂隙会沿着跟边坡开挖面近似平行的方向扩展，当扩展到一定规模时，边坡后缘裂隙和下部裂隙相当于岩体中两个较大的优势裂隙，边坡岩体在开挖卸荷扰动下，其中规模较大的优势裂隙首先发生贯通，所以，本文为计算更进一步简化，认为后缘裂隙将沿近似下部裂隙方向扩展贯通，如图 9所示，边坡高度为H，滑面倾角为β，分支裂隙扩展长度为l。

图 9 边坡滑面贯通受力示意图

Figure 9. Schematic diagram of penetration force on sliding surface of slope

下载: 全尺寸图片幻灯片

滑体重量G沿滑面和垂直滑面的分量为

${W}_{\text{T}}\text{=}W\mathrm{sin}\beta \text{，}{W}_{\text{N}}\text{=}W\mathrm{cos}\beta 。$

(23)

滑面AD上的平均法向应力为

${\sigma _{\text{N}}} = \frac{{W\cos \beta }}{{{L_{AD}}}} 。$

(24)

在自重力作用下，滑面AD上的所能承受的最大剪切力为

${F_{\text{T}}} = {\text{(}}c + {\sigma _{\text{N}}}\tan \varphi {\text{)}}{L_{BC}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\; ({c_i} + {\sigma _{\text{N}}}\tan {\varphi _i}){L_{AB}} + ({c_j} + {\sigma _{\text{N}}}\tan {\varphi _j}){L_{CD}} 。$

(25)

式中：c和 $\varphi$ 为岩体的黏聚力和内摩擦角； ${c_i}$ 和 ${\varphi _i}$ 为已扩展裂隙面的黏聚力和内摩擦角； ${c_j}$ 和 ${\varphi _j}$ 为原下部裂隙面上的黏聚力和内摩擦角。

则考虑卸荷作用下裂隙扩展长度的边坡安全系数K的表达式为

$K = \frac{{{F_{\text{T}}}}}{{{W_{\text{T}}}}} = \left\{ {(c + {\sigma _{\text{N}}}\tan \varphi ){L_{BC}} + ({c_i} + {\sigma _{\text{N}}}\tan {\varphi _i}){L_{AB}} + } \right.\\ \;\;\;\;\;\;\;\; ({c}_{j}+{\sigma }_{N}\mathrm{tan}{\varphi }_{j}){L}_{CD}\}/(W\mathrm{sin}\beta )\text{ }。$

(26)

当K＞1时，说明岩桥所能承受最大剪切力大于作用于结构面的下滑力，边坡处于稳定状态；当K＜1时，说明岩桥所能承受最大剪切力小于作用于结构面的下滑力，边坡处于不稳定状态；当K＝1时，说明岩桥所能承受最大剪切力等于作用于结构面的下滑力，边坡处于极限平衡状态。

3.2 影响因素分析

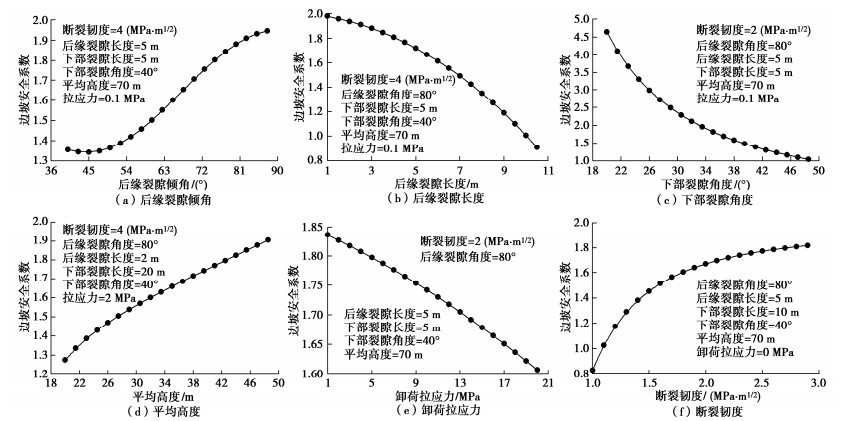
根据式（26）可知安全系数主要与后缘裂隙倾角、后缘裂隙长度、平均高度、起裂角、断裂韧度、下部裂隙角度和卸荷拉应力等因素有关，具体变化关系如图 10所示。起裂角通过后缘裂隙几何参数求得。从图 10（a）可以看出边坡安全系数随裂隙倾角的增加而增大，但在局部存在一定波动，这是由于上部结构面拉应力和剪应力随裂隙倾角的变化而交替变化所导致。从图 10（b）可以看出边坡安全系数随裂隙长度的增加而减小，其曲率呈逐渐增加趋势，这是因为裂隙越长，其尖端应力强度因子越大，分支裂隙扩展长度越大，边坡越不稳定。从图 10（c）可以看出边坡安全系数下部裂隙角度的增加而减小，其曲率呈逐渐减小趋势，这是因为裂隙角度越大，滑动面长度越小，边坡越不稳定。从图 10（d）可以看出边坡安全系数随平均高度的增加而增加，近似呈线性关系，这是因为平均高度越大，滑动面长度越大，边坡越稳定。从图 10（e）可以看出边坡安全系数随卸荷拉应力的增加而减小，近似呈线性关系，这是因为卸荷拉应力越大，裂隙扩展长度越大，边坡越不稳定。从图 10（f）可以看出边坡安全系数随断裂韧度的增加而增加，其曲率呈逐渐减小趋势，这是因为断裂韧度越大，分支裂隙扩展长度越小，边坡越稳定。

图 10 边坡安全系数的影响因素分析结果

Figure 10. Analysis results of factors affecting factor of safety of slope

下载: 全尺寸图片幻灯片

4. 工程实例分析

齐大山铁矿位于辽河冲积平原的边缘地带，矿区东部为千山山脉。该矿年生产铁矿石达1700×10⁴ t，东帮边坡已开采到-230 m水平，整体坡角达52°，目前开采还在不断向深部进行，已逐渐成为深凹露天矿。受边坡开挖卸荷和两次滑坡牵引作用，在东帮-40 m平台处出现后缘拉裂隙，对边坡稳定性产生严重影响。本文以齐大山铁矿该区域边坡为工程背景来验证上述理论模型的合理性。

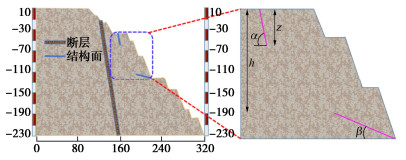
本局部边坡之前已经发生两次小规模牵引式滑坡，如图 11（a）所示，且在-40 m平台出现规模较大的后缘裂隙，如图 11（b）所示。随下部采场采掘加深，存在大范围的边坡滑坡发生的可能。经现场勘察发现，该边坡滑体体积V约为4.4×10³ m³，边后缘存在一条长度达460 m，深度约13 m，方向近似垂直的拉裂隙，平均高度达86 m，重心到裂隙尖端的水平距离a为0.8 m。通过已经发生滑坡区域发现在下部坡脚位置存在剪出口，其结构面长度约35 m，倾角为38°左右。卸荷拉应力的取值通过室内真三轴卸荷试验近似获得，将现场裂隙试样加载到原岩应力状态，开始侧向卸荷，随着卸载的持续进行，水平向拉应力 ${\sigma _3}$ 在不断变化，可通过式 ${\sigma _3} = {\sigma _0} - {\sigma _{{\text{3t}}}}$ 求得，其中 ${\sigma _0}$ 为开始卸载时刻的水平应力值， ${\sigma _{{\text{3t}}}}$ 为在试验过程中的高速摄影记录下裂隙起时刻所对应的水平应力值^[19]，大小为0.5 MPa。通过现场取样和相关岩石力学试验得到具体岩体相关物理力学参数如表 1所示。该东帮边坡地质剖面图和概化后的裂隙边坡计算力学模型如图 12所示。

图 11 边坡破坏现状图

Figure 11. Current situation of slope failure

下载: 全尺寸图片幻灯片

表 1 岩体物理力学参数

Table 1. Physical and mechanical parameters of rock mass

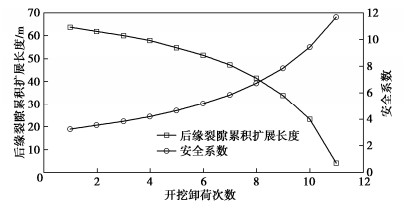
断裂韧性/ (MPa·m^1/2)	重度/ (kN·m^-3)	黏聚力/ MPa	内摩擦角/(°)	裂隙面黏聚力/ MPa	裂隙面内摩擦角/(°)
1.2	26	5.332	43.6°	0.112	24.6

下载: 导出CSV

| 显示表格

图 12 齐大山铁矿东帮边坡地质剖面及概化力学模型图

Figure 12. Geological profile and simplified mechanical model diagram of east slope of Qidashan Iron Mine

下载: 全尺寸图片幻灯片

将上述相关参数代入式（20）可以求得裂隙扩展临界高度为2.24 m。这表明此处后缘裂隙高度已经远远超过其临界扩展高度，在卸荷扰动作用下，裂隙极易发生扩展失稳。将所求起裂角代入式（22）可求得分支裂隙扩展长度，进一步代入式（26）可求得开挖完每一步后边坡安全系数，计算结果如图 13所示。

图 13 计算结果图

Figure 13. Calculated results

下载: 全尺寸图片幻灯片

从图 13可知，随着卸荷次数的增加，安全系数逐渐降低，开挖次数越多，安全系数降低的速度越快。这表明卸荷扰动次数越多，边坡越容易发生突变失稳。

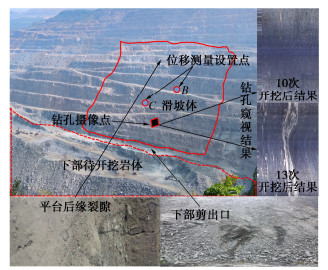
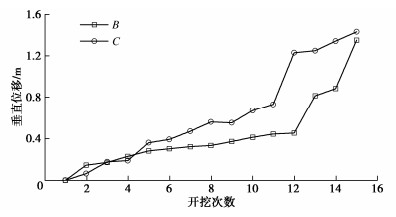
为更进一步确定本文所提方法的正确性和合理性，通过现场钻孔摄像和位移连续监测来进行验证。钻孔摄像可清楚观察到随着爆破开挖次数的增加，裂隙扩展贯通情况。位移连续监测可明确边坡岩体是否发生位移突变。相关监测设置如图 14所示，位移监测结果如图 15所示。

图 14 现场测点布置与钻孔窥视结果

Figure 14. Layout of site survey point and borehole peeping results

下载: 全尺寸图片幻灯片

图 15 位移监测结果

Figure 15. Monitoring results of displacement

下载: 全尺寸图片幻灯片

从现场钻孔窥视结果可以明显看出，在13次开挖以后出现明显的滑移带，图 15位移监测结果也表明12次开挖后，垂直位移发生突变，表明边坡此时已经发生滑坡，而理论计算结果表明11次开挖以后，边坡安全系数小于1，计算结果偏保守，上述结果表明本文所提方法安全可靠。

5. 结论

（1）基于断裂力学理论，推导了卸荷作用下后缘裂隙起裂方向与临界扩展高度计算公式。后缘裂隙尖端复合应力强度因子随着卸荷拉应力的增加而增加，表明开挖卸荷作用会降低边坡稳定性。

（2）临界高度随裂隙倾角的增大而逐渐减小直至趋于稳定。起裂角随裂隙倾角的增加而增大，说明裂隙倾角越大，裂隙越来越趋向于边坡坡面扩展，随着滑面的长度在增加，边坡稳定性增加。

（3）临界高度随平均高度的增大而逐渐增大，说明平均高度越大，裂隙尖端应力强度因子越小，所对应的扩展临界高度就大，边坡越稳定。起裂角随平均高度的增加而减小，说明平均高度越大，裂隙越来越偏离边坡坡面扩展，导致滑面的长度增加，边坡稳定性增强。

（4）给出了考虑分支裂隙扩展长度的边坡安全系数计算公式。裂隙倾角、平均高度和断裂韧度会增加边坡稳定性，裂隙长度、下部裂隙角度和卸荷拉应力会降低边坡稳定性。最后基于齐大山东帮边坡验证了理论计算模型的合理性。

图 1 非饱和土边坡稳定性计算流程图

Figure 1. Flow chart of stability analysis of slopes of unsaturated soils

下载: 全尺寸图片幻灯片

图 2 SWCC模型的试验数据和拟合曲线

Figure 2. Laboratory test data and fitting models of SWCC

下载: 全尺寸图片幻灯片

SWCC模型参数 $\alpha$ 的后验分布

Posterior distributions of SWCC model parameter $\alpha$

下载: 全尺寸图片幻灯片

图 4 SWCC模型参数n的后验分布

Posterior distributions of SWCC model parameter $n$

下载: 全尺寸图片幻灯片

图 5 SWCC模型VG和FX参数m的后验分布

Posterior distributions of SWCC model (i.e., VG and FX) parameter $m$

下载: 全尺寸图片幻灯片

SWCC模型误差 $\sigma$ 的后验分布

Posterior distributions of SWCC model error $\sigma$

下载: 全尺寸图片幻灯片

图 7 数值计算模型

Figure 7. Numerical model

下载: 全尺寸图片幻灯片

图 8 2020年三峡库区第5波洪峰水文图

Figure 8. Hydrograph of fifth wave of flood arriving at Three Gorges Reservoir in 2020

下载: 全尺寸图片幻灯片

图 9 边坡安全系数变化图

Figure 9. Variation of factor of safety of slopes

下载: 全尺寸图片幻灯片

图 10 非饱和渗透系数随机场离散化赋值

Figure 10. Spatial discretization of unsaturated hydraulic conductivity

下载: 全尺寸图片幻灯片

图 11 SWCC模型对应边坡稳定性安全系数的PDF曲线

Figure 11. PDFs of factor of safety of 4 SWCC models

下载: 全尺寸图片幻灯片

图 12 不同SWCC模型的可靠指标

Figure 12. Reliability indices of 4 SWCC models

下载: 全尺寸图片幻灯片

参考文献(24)

[1]	李松林, 许强, 汤明高, 等.库水位升降作用下不同滑面形态老滑坡响应规律[J].工程地质学报, 2017, 25(3): 841-852. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201703032.htm LI Songlin, XU Qiang, TANG Minggao, et al. Response patterns of old landslides with different slipsurface shapes triggered by fluctuation of reservoir water level[J]. Journal of Engineering Geology, 2017, 25(3): 841-852. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201703032.htm
[2]	李梦姿, 蔡国庆, 李昊, 等.考虑抗拉强度剪断的非饱和土无限边坡稳定性分析[J].岩土工程学报, 2020, 42(4): 705-713. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18177.shtml LI Mengzi, CAI Guoqing, LI Hao, et al. Stability of infinite unsaturated soil slopes with tensile strength cut-off[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(4): 705-713. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18177.shtml
[3]	傅方, 赵成刚, 李伟华, 等.地震荷载作用下非饱和土边坡稳定性数值模拟[J].岩土工程学报, 2013, 35(增刊2): 408-414. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract15417.shtml FU Fang, ZHAO Chenggang, LI Weihua, et al. Numerical simulation of stability of unsaturated soil slopes under earthquakes[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 408-414. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract15417.shtml
[4]	邓志平, 李典庆, 曹子君, 等.考虑地层变异性和土体参数变异性的边坡可靠度分析[J].岩土工程学报, 2017, 39(6): 986-995. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16921.shtml DENG Zhiping, LI Dianqing, CAO Zijun, et al. Slope reliability analysis considering geological uncertainty and spatial variability of soil parameters[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(6): 986-995. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16921.shtml
[5]	蒋水华, 刘贤, 黄发明, 等.考虑多参数空间变异性的降雨入渗边坡失稳机理及可靠度分析[J].岩土工程学报, 2020, 42(5): 900-907. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18202.shtml JIANG Shuihua, LIU Xian, HUANG Faming, et al. Failure mechanism and reliability analysis of soil slopes under rainfall infiltration considering spatial variability of multiple soil parameters[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(5): 900-907. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18202.shtml
[6]	RAHIMI A, et al. Effect of hydraulic properties of soil on rainfall-induced slope failure[J]. Engineering Geology, 2010, 114(3/4): 135-143.
[7]	唐栋, 祁小辉, 蒋水华, 等.不同前期降雨与土–水特征曲线对边坡稳定的影响[J].岩土工程学报, 2015, 37(增刊1): 148-155. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16232.shtml TANG Dong, QI Xiaohui, JIANG Shuihua, et al. Effect of different antecedent rainfalls and SWCCs on slope stability[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S1): 148-155. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16232.shtml
[8]	王林, 李典庆, 曹子君, 等.基于贝叶斯理论的土水特征曲线模型选择与参数识别方法[J].应用基础与工程科学学报, 2019, 27(6): 1269-1284. https://www.cnki.com.cn/Article/CJFDTOTAL-YJGX201906008.htm WANG Lin, LI Dianqing, CAO Zijun, et al. Bayesian approaches for model selection and parameter identification of soil-water characteristic curve[J]. Journal of Basic Science and Engineering, 2019, 27(6): 1269-1284. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YJGX201906008.htm
[9]	VANMARCKE E H. Probabilistic modeling of soil profiles[J]. Journal of the Geotechnical Engineering Division, 1977, 103(11): 1227-1246.
[10]	GUI S X, ZHANG R D, TURNER J P, et al. Probabilistic slope stability analysis with stochastic soil hydraulic conductivity[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(1): 1-9.
[11]	SRIVASTAVA A, et al. Influence of spatial variability of permeability property on steady state seepage flow and slope stability analysis[J]. Engineering Geology, 2010, 110(3/4): 93-101. https://www.sciencedirect.com/science/article/pii/S0013795209002968
[12]	ZHU H, ZHANG L M, ZHANG L L, et al. Two-dimensional probabilistic infiltration analysis with a spatially varying permeability function[J]. Computers and Geotechnics, 2013, 48: 249-259. https://www.sciencedirect.com/science/article/pii/S0266352X12001620
[13]	HUANG M L, SUN D A, WANG C H, et al. Reliability analysis of unsaturated soil slope stability using spatial random field-based Bayesian method[J]. Landslides, 2021, 18(3): 1177-1189.
[14]	MUALEM Y. A new model for predicting the hydraulic conductivity of unsaturated porous media[J]. Water Resources Research, 1976, 12(3): 513-522.
[15]	BURDINE N T. Relative permeability calculations from pore size distribution data[J]. Journal of Petroleum Technology, 1953, 5(3): 71-78.
[16]	VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898. https://eurekamag.com/research/004/556/004556517.php
[17]	FREDLUND D G, XING A Q. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 521-532.
[18]	LU N, GODT J W, WU D T. A closed-form equation for effective stress in unsaturated soil[J]. Water Resources Research, 2010, 46(5): 567-573. doi: 10.1029/2009WR008646
[19]	RICHARDS L A. Capillary conduction of liquids through porous mediums[J]. Physics, 1931, 1(5): 318-333.
[20]	CHEN Z Y, MORGENSTERN N R. Extensions to the generalized method of slices for stability analysis[J]. Canadian Geotechnical Journal, 1983, 20(1): 104-119. http://www.geoeng.iwhr.com/ytgcyjs/rootfiles/2015/10/28/1445241321868136-1445565535446448.pdf
[21]	刘源.基于贝叶斯方法的岩土参数随机反演及边坡可靠度分析[D].南昌: 南昌大学, 2020. LIU Yuan. Stochastic Back Analysis of Geotechnical Parameters and Reliability Analysis for Slope Using Bayesian Method[D]. Nanchang: Nanchang University, 2020. (in Chinese)
[22]	王长虹, 朱合华, 徐子川, 等.考虑岩土参数空间变异性的盾构隧道地表沉降分析[J].岩土工程学报, 2018, 40(2): 270-277. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17281.shtml WANG Changhong, ZHU Hehua, XU Zichuan, et al. Ground surface settlement of shield tunnels considering spatial variability of multiple geotechnical parameters[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(2): 270-277. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17281.shtml
[23]	KRIGE D. A statistical approach to some basic mine valuation problems on the Witwatersrand[J]. Journal of the Southern African Institute of Mining and Metallurgy, 1951, 52(6): 119-139.
[24]	高游, 孙德安.单峰和双峰土水特征曲线基本参数的确定[J].岩土工程学报, 2017, 39(10): 1884-1891. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17044.shtml GAO You, SUN De'an. Determination of basic parameters of unimodal and bimodal soil water characteristic curves[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(10): 1884-1891. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17044.shtml

施引文献(10)

期刊类型引用(6)

1.	邓东平，石柱，彭文耀. 卸荷损伤效应下开挖边坡稳定性极限平衡分析. 工程地质学报. 2025(01): 327-340 . 百度学术
2.	王超，伍永平，赵自豪，曹健，段会强，杨盼盼. 三点弯曲载荷下岩体偏置斜裂隙的应力强度因子. 金属矿山. 2024(02): 114-122 . 百度学术
3.	宋洋，马旭琪，赵常青，谢志辉，王富成，牛凯. 隐伏非贯通软弱夹层岩质边坡剪切蠕变特征及稳定性研究. 岩土工程学报. 2024(04): 755-763 . 本站查看
4.	徐树强，李营作，姜海涛，王智涛，李斌. 别斯库都克煤矿南帮边坡破坏机理及致灾模式. 露天采矿技术. 2023(02): 13-15+19 . 百度学术
5.	于远祥，秦光，陈盼. 露天矿烧变岩高边坡卸荷机理与稳定性研究. 西安科技大学学报. 2023(05): 941-951 . 百度学术
6.	李佳航，郭明伟，杨智. 基于边坡下滑方向的传递系数法. 岩石力学与工程学报. 2023(S2): 4261-4270 . 百度学术