Model test and simulation on saltwater up-coning process caused by pumping of horizontal well
-
摘要: 滨海地区的海水入侵使地下水呈上层淡水、下层咸水的分布结构,在开采地下水时易发生咸水锥进现象,使抽取的地下水发生咸化。水平井能有效延迟深层咸水的锥进过程,可有效避免上层地下淡水的污染。开发了模拟水平抽水井抽水引起的咸水锥进过程的试验设备,实现了水平抽水井以恒定流量抽水所导致的咸水锥进过程；然后基于Dagan和Bear竖直井的解析解（DB模型）,推导出了水平井抽取无限侧边界地下水引起的咸水锥进过程的解析解,解析解显示咸淡水界面为初始水平、中间突出、向上锥进至井口的锥进过程,与试验过程的中间阶段的锥进过程较为符合；随后利用TOUGH2/T2DM模拟了水平井抽水引起的咸水锥进过程的试验,数值模拟得到的咸淡水界面向上锥进的模拟结果与试验结果拟合较好；在数值模拟的基础上,进一步分析了边界条件和介质的非均质性对咸水锥进过程的影响。研究通过模型试验、解析解模型和数值模拟模型研究了试验室尺度的咸水锥进过程,可为咸水锥进问题的进一步研究提供技术支撑。Abstract: In coastal areas, fresh water is stored in the upper aquifer, and saltwater is in the lower aquifer caused by seawater intrusion. The phenomenon of saltwater up-coning is easy to occur when exploiting fresh groundwater, making the extracted groundwater salinized. Horizontal well can effectively postpone the time of up-coning, thereby avoiding the pollution of the upper freshwater. A test for simulating the process of saltwater up-coning caused by pumping of horizontal well is performed in this research, and the saltwater up-coning process caused by pumping of horizontal well with a constant flow rate is obtained. Then based on the analytical solutions of Dagan & Bear, the analytical solution of the saltwater up-coning process caused by pumping of horizontal well with infinite lateral boundaries is derived. The analytical solution shows that the interface is horizontal initially, protruding subsequently, and tapering around the well, which is consistent with the middle stage of the model tests. TOUGH2/T2DM is then used to simulate the test process of saltwater up-coning caused by pumping of horizontal well. The up-coning processes of saltwater-freshwater interface obtained by numerical simulation fit well with the model test results. Based on the proposed numerical model, the effects of boundary conditions and heterogeneity of media on saltwater up-coning process are analyzed. The saltwater up-coning process in laboratory scale studied by model tests, DB analytical solutions and numerical simulation model in this research can provide technical supports for further researches on saltwater up-coning in coastal aquifer.
-
Keywords:
- saltwater up-coning /
- horizontal well /
- model test /
- DB model /
- numerical simulation
-
0. 引言
滨海含水层中,海平面上升或地下水位下降都会引起海水入侵的发生。人为超量开采地下水,海水与淡水之间的水动力平衡遭到破坏,许多沿海含水层遭受海水入侵,形成地下水呈上层淡水、下层咸水的分布结构。滨海地区的淡水资源比较匮乏,许多城市会通过抽取地下淡水来满足水资源的需求,不合理的抽水过程容易造成“咸水锥进”的现象,即下层咸水向抽水井口处运移,咸淡水界面呈向井口锥进的现象。咸水锥进将进一步压缩滨海地区有限的淡水资源,产生一系列环境地质问题[1-2]。因此,避免或减缓抽水过程中下层咸水向抽水井锥进的研究对于保护滨海地区宝贵的淡水资源具有重要的意义。
对于抽水可能引发的咸水锥进过程的研究方法主要分为两大类：①试验研究,包括野外试验和室内模型试验；②模拟研究,常用的模拟模型包括解析解模型和数值模拟模型。室内模型试验比较灵活,容易操作,很多学者选择室内砂箱试验的方法对咸水锥进过程进行研究。比如,Simmons等[3]在砂箱中进行了密度依赖流动的试验,主要集中在不稳定的盐羽垂直向下移动,使用饱和和不饱和多孔介质设置。Goswami等[4]使用砂箱试验来为侧向咸水侵入案例开发稳态、侵入和后退界面条件情况的模型基准测试结果。Werner等[5]使用砂箱进行了竖直井抽水引起的咸水锥进试验,试验分析了咸淡水二维剖面的变化过程。模拟模型主要分为两类：①第一类为咸淡水界面为突变界面模型；②第二类为咸淡水没有明确的分界,咸淡水中间由咸水和淡水组成的混合区来过渡,叫做混溶模型。突变界面模型假设混合区的影响很小,可以忽略不计,简化了研究过程,其解析解研究得到发展。比如Dagan等[6]的DB模型,可以计算出咸淡水界面的剖面形状。Muskat[7]基于Ghyben-Herzerg模型开发的模型可以计算出咸淡水界面的临界高度。考虑密度变化的咸淡水运移溶混模型主要基于有限元、有限差分和有限体积等数值方法。Sun等[8]在前人的基础上,采用数学模型模拟出由于水平井抽水引起的咸水锥进三维过程,并分析了不同井长、井的位置、初始界面位置、抽水速率对临界锥进高度、临界时间等的影响,证明水平井可以有效推迟临界锥进时间。相比数学模型来说,物理模型可以对试验过程有全面和直观的表达；结合数值模拟,又可以更加方便快捷地研究不同的影响因素对锥进过程的影响。
本文研究开发了模拟水平井抽水引起咸水锥进过程的试验设备,进行了咸水锥进过程的砂箱模型试验,然后基于Dagan和Bear竖直井的解析解（DB模型）,推导出了水平井抽取无限侧边界地下水引起的咸水锥进过程的解析解,随后用TOUGH2/T2DM模型模拟了砂箱的咸水锥进过程,并分析了边界条件和介质的非均质性等因素对咸水锥进过程的影响,深入研究了抽水井抽水引起的咸水锥进过程的规律。
1. 砂箱模型试验
1.1 试验设备与方法
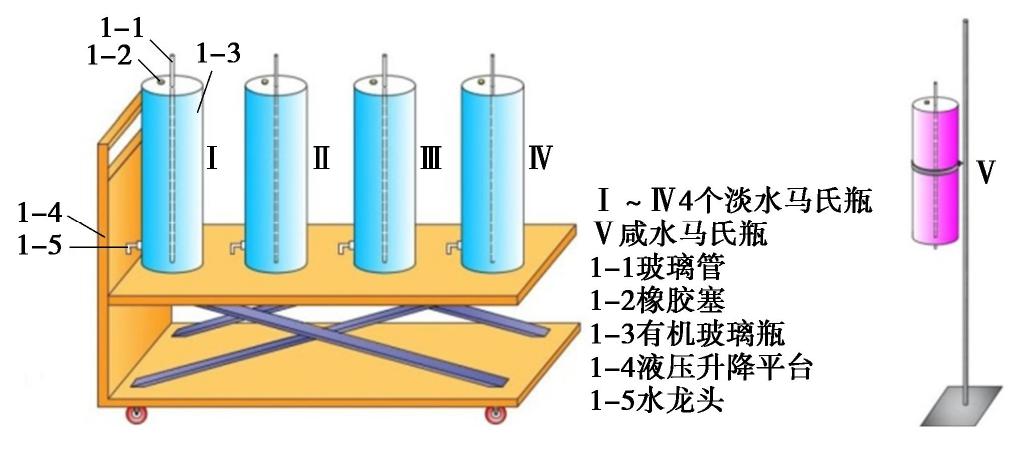
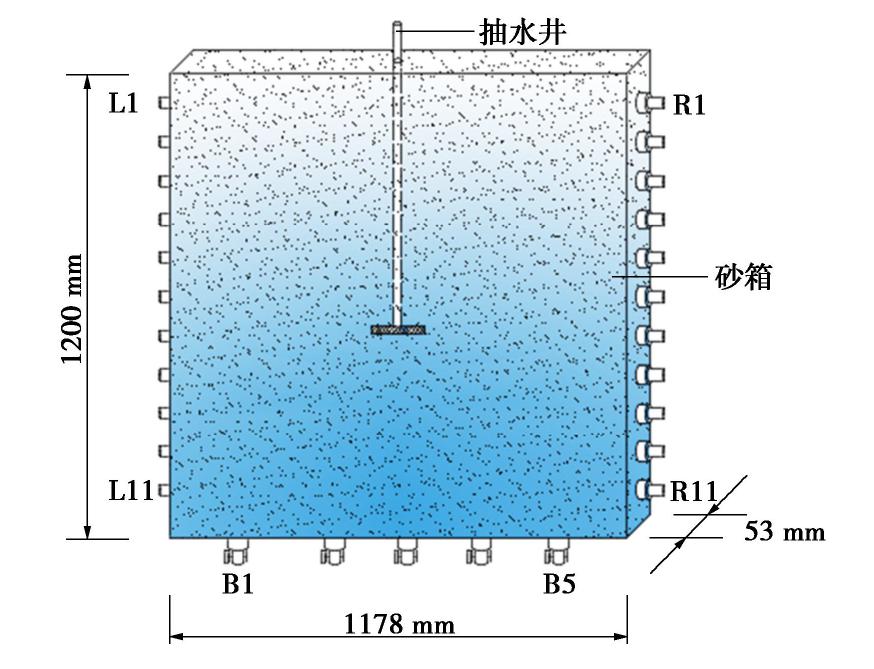
模拟水平井抽水引起的咸水锥进过程的试验设备由砂箱（图1）、咸淡水供水装置（图2）、抽水系统和观测设备组成。
砂箱由厚15 mm的有机玻璃板制成,为防止砂箱变形,四周与面板用铁质箍架作支撑。砂箱内径尺寸为长1178 mm,宽53 mm,高1200 mm。砂箱左右两侧每隔100 mm打孔（L1—L11、R1—R11）,用于砂箱不同高度恒定水头咸/淡水的供给和测压管的连接,在砂箱内侧壁供水孔处铺设土工布,防止堵塞。砂箱底部有5个均匀布设的孔（B1—B5）,用于对砂土进行自下而上的饱和和测压管的连接。在距砂箱底部55 cm处布置水平井,抽水井由内径8 mm的钢管制成,水平井正中间与竖直钢管焊接在一起,组成倒“T”状。
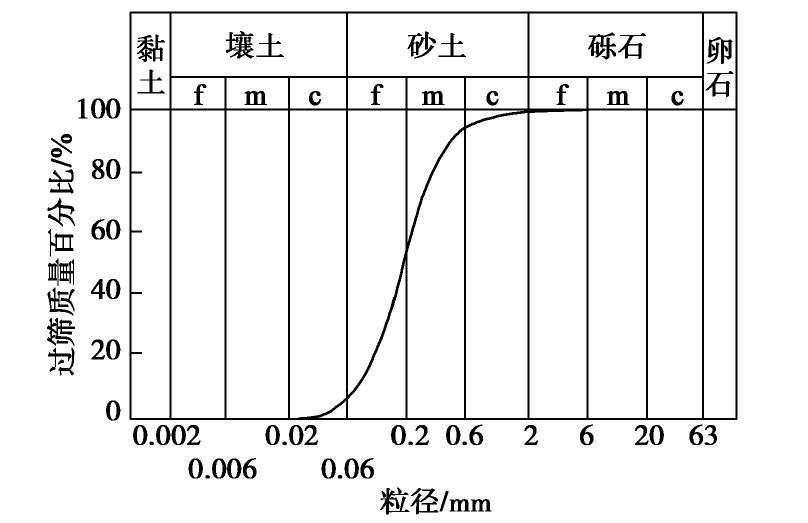
首先在砂箱内分层装入水洗标准细砂,标准细砂的级配如图3所示。细砂的颗粒密度为2.65 g/cm3,填装后预定的干密度为1.75 g/cm3,每层填装的厚度为5 mm,根据预定的干密度和层厚计算每层干砂的重量,按照《土工试验方法标准》[9]统一标准装填,装填后的孔隙度为0.353。另外进行装填干密度为1.75 g/cm3砂柱的常水头渗透系数试验,测得饱和渗透系数范围为0.0001～0.0002 m/s,平均值为0.00016 m/s。在距砂箱底部55 cm处埋入水平井,井外包有防止堵塞的细金属网,井的有效抽水长度为100 mm。T型井上端与内径为8 mm的橡胶软管连接,软管另一端与蠕动泵相连。
将砂箱底部连接淡水供水装置,并对标准砂进行淡水饱和。将图2所示的淡水马氏瓶Ⅰ—Ⅳ灌满蒸馏水,分别与B1,B2,B4和B5相连,打开底孔上的止水阀门,通过逐步提升淡水马氏瓶的高度,将砂箱内的干砂进行自下而上的淡水饱和,饱和过程中控制高于淡水马氏瓶相应高度处的侧向阀门进行排气,B3,L4,L11,R4,R10连接测压管。饱和过程完成后,关闭B1,B2,B4,B5止水阀。将4个淡水马氏瓶导管分别换接至L3/R3,L5/R5,L7/R7,L9/R9入流孔处,并保持淡水马氏瓶的水头高度1.2 m（假设砂箱底部为0压面）不变,静置24 h。
配置试验所用的咸水溶液,为添加Rhodamine WT染色试剂的CaCl2溶液,Rhodamine WT染色剂的浓度为500 mg/L,CaCl2溶液的浓度为35‰。Rhodamine WT试剂是一种染色后几乎不改变溶液密度的染色剂,其使用方法参考Schincariol[10]和 Simmons等[3]的试验研究。
连接咸水马上瓶,获得咸淡水平衡状态。咸淡水平衡态的咸、淡水水头高度差首先根据淡水和咸水的密度,通过等效淡水压头计算初步确定。然后根据淡水马氏瓶的高度,调整好咸水马氏瓶的高度。再将咸水溶液通过B1,B2,B4,B5入流孔小心通入砂箱至咸淡水界面达到预定的平衡高度,即距砂箱底10 mm处,接着关闭B1,B2,B4,B5和咸水溶液出流阀门,将咸水马氏瓶出流软管换接至L11,R11入流孔,打开咸水溶液出流阀门,观察测压管水头变化,利用测压管对边界压头变化的响应来平衡咸水和淡水边界压头,进行咸淡水界面微调。静置12 h,直到得到水平清晰的咸淡水平衡界面,如图4（a）所示。
进行抽水试验,调整蠕动泵的抽水速率,将抽水速率设置为恒定的3.8 mL/s。按下蠕动泵的开始按钮,试验开始计时。每隔等时间段对抽取的水样进行电导度测定。将砂箱置于遮光幕布内部,与拍摄设备保持一定的拍摄距离,砂箱与拍摄设备中间布设头顶荧光灯管。砂箱中咸淡水界面的变化,B3,L4,L11,R4,R11连接的测压管水头变化过程,淡水马氏瓶Ⅰ～Ⅳ和咸水马氏瓶内的液面高度变化过程均通过不同的高清摄像机进行延时拍摄记录下来。
1.2 试验结果及分析
本次水平井抽水试验共进行了435 min,咸淡水界面形状稳定并且盐羽颜色不再变化后,试验结束。图4给出了试验过程中特征时刻,即0,30,60,78,90,130,162 min和试验结束435 min的咸淡水界面形状。图4（a）为试验开始时刻的初始状态,咸淡水界面大致呈水平状态,位于距砂箱底部10 cm的位置；抽水30 min后,见图4（b）,咸淡水界面呈整体上升,靠近砂箱两端界面上升速度较快,中央位置的界面上升速度较慢,咸淡水界面在两端上升了约10 cm,中央仅上升了1 cm；抽水60 min后,见图4（c）,咸淡水界面继续上升,但中央上升的速度有所加快,咸淡水界面在砂箱两端附近接近水平,与初始界面相比上升了约13 cm,中央位置处的界面上升了约8 cm；抽水78 min后,见图4（d）,咸淡水界面继续上升,砂箱两边的界面上升高度约14 cm,由两端向砂箱内部界面逐渐向上倾斜,但中央仍存在微小下凹；抽水90 min后,见图4（e）,咸淡水界面继续上升,但两端上升速度很慢,由两端向内部向上倾斜的程度增大,中央位置界面呈水平；抽水130 min后,见图4（f）,咸淡水界面呈锥状凸起,中央的顶点到达水平井底,上升高度为45 cm,界面在砂箱两端的上升高度为15cm,盐羽在中央位置有一条颜色较淡的“线”,可能是由于填砂时密度不均匀引起的,在中央的砂由于方便捣实密度稍大导致的；抽水162 min后,见图4（g）,咸淡水界面仍为锥状凸起,与130 min时相比界面形状几乎没有变化,只是盐羽的颜色有所加深；抽水435 min后,见图4（h）,咸淡水界面形状基本稳定,在水平井底端形成一条水平的短线,盐羽的颜色也由浅变深,持续不变,试验结束。
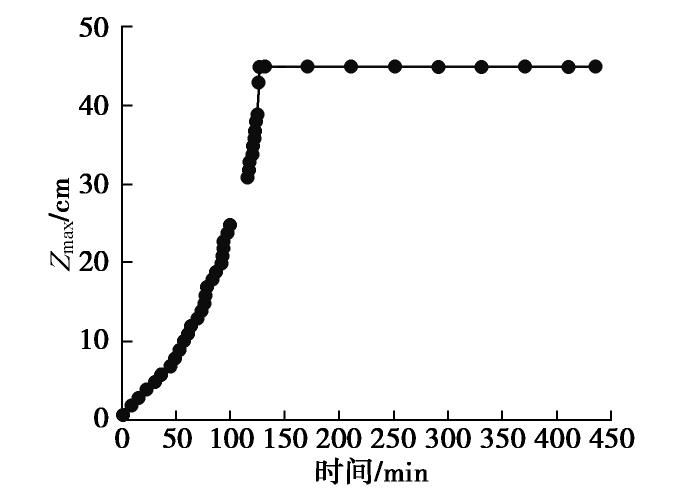
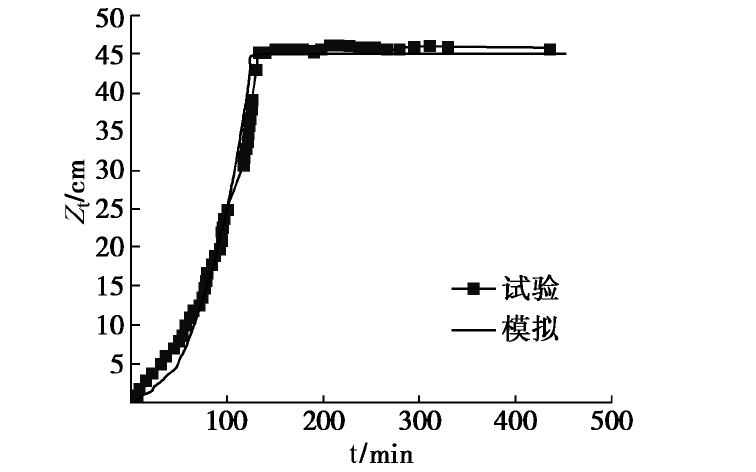
图5给出了咸水锥进过程中咸淡水界面的中心点距初始水平咸淡水界面的垂直高度随时间的变化,记为Z(t)。由Z(t)的变化可见,咸淡水界面的中心点在前130 min随时间逐渐升高,并且升高的速度在初期比较缓慢,然后逐渐加快,其中在100～115 min,图像部分被支架遮挡,在130 min时到达水平井底部后几乎保持不变。
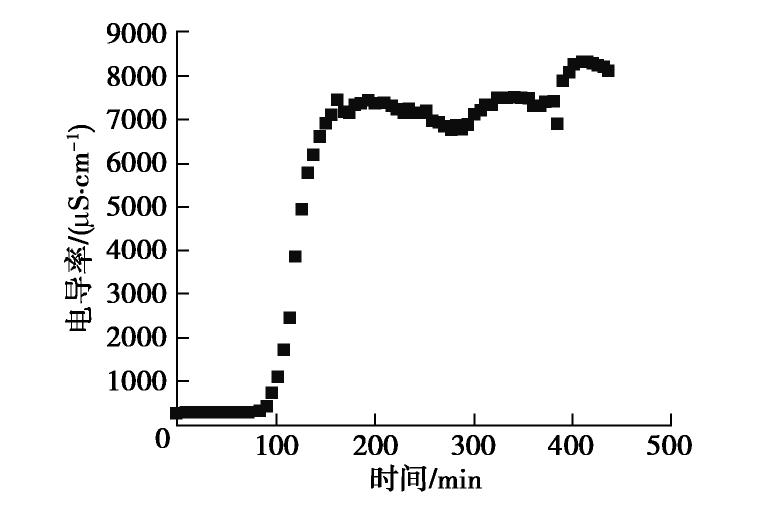
图6给出了抽水过程中所抽取出的水的电导率随时间的变化过程。由图6可见,所抽出水的电导率在抽水过程的前78 min几乎保持不变,78 min以后抽出水的电导率开始上升,说明此时已经有咸水被抽出,结合图4（d）所示的78 min时咸淡水界面的图像,此时肉眼可见的咸淡水界面距砂箱底部约30 cm,距离初始咸淡水界面的高度为15 cm,说明肉眼可见的盐羽界面盐度小于1.0（假设咸水溶液的浓度为1.0）,Jakovovic等[11]认为肉眼可见的盐羽界面处的盐度约为0.5。在抽水130 min后,抽出的咸水的电导率逐渐增大,此时肉眼可见的盐羽顶点到达水平井底部,但电导率还没到达峰值,在试验162 min左右抽出水的电导率达到第一个峰值,之后电导率开始出现小范围波动。通过比较130 min（约4000 μS/cm）和163 min（约8000 μS/cm）的电导率相对值,可基本判断肉眼可见的盐羽界面处的盐度约为0.5。
2. DB解析模型
基于Dagan和Bear的竖直井解析解数学模型（DB模型）,推导出水平井抽水引起的界面向上锥进的解析解。DB模型为不考虑咸淡水混合的界面突变模型,计算简洁,可模拟出咸淡水界面的二维剖面。
2.1 数学模型的假设条件
（1）采用的多孔介质为均质介质,具有水平方向上的各向同性和垂直方向上的各向异性。
（2）假定两种流体的界线清晰,或者两种流体的混合区很小,可以忽略不计。
（3）不考虑区域流。
（4）模型的上下边界远离进水口和咸淡水界面,即具有足够厚的含水层。
（5）侧向边界距离井无限远。
2.2 咸淡水界面方程
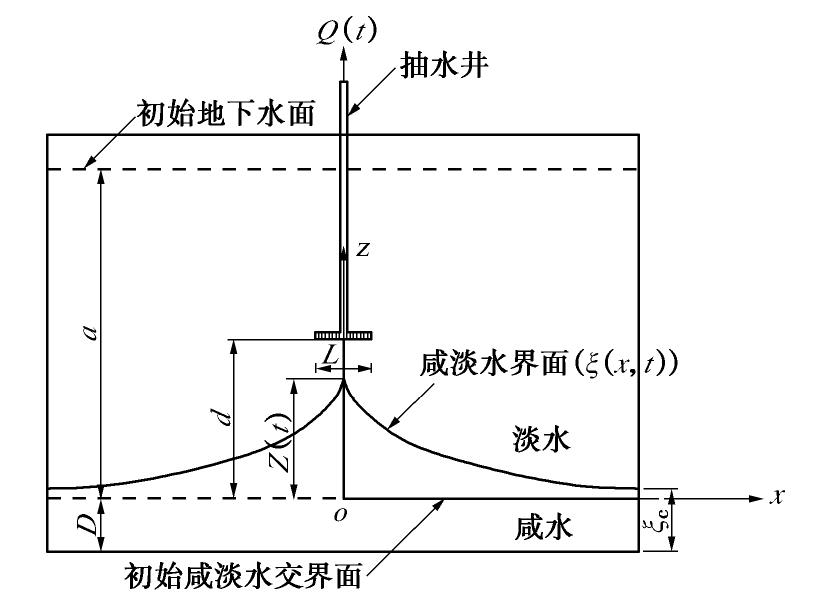
水平井抽水引起咸水锥进的概念模型如图7所示,Q(t)为抽水井抽取地下水的速率（m3/s）,a为初始地下水面与初始咸淡水交界面的距离（m）,D为初始咸淡水交界面与含水层底板的距离（m）,ζ(x, t)为随时间变化的咸淡水界面形状（以井口正下方的初始交界面处为原点,水平向右为x坐标,竖直向上为z坐标）,d为井底与初始咸淡水交界面的距离（m）,Z为盐羽顶点距初始咸淡水界面的高度（m）,
ζc 为随时间变化的侧边盐羽距离含水层底板的高度（m）,L为水平井的长度（m）。![]()
图 7 水平井抽水引起咸水锥进的概念模型Figure 7. Conceptual model for saltwater up-coning caused by pumping of horizontal well根据Dagan等[6]的研究结果来看,咸淡水界面的二维剖面可以用数学方程式来表达,此方程与时间和距抽水口的距离有关。DB模型的表达式为
ζ(r,t)=Q2π(Δγ/γ)Kxd[1(1+R′2)12−1[(1+γ′)2+R′2]12]。 (1) 式中
R′=rd(KzKx)12 ,γ′=(Δγ/γ)Kz2ndt ,r为咸淡水界面上的点距井的距离,这里r=x−x′ ；t为抽水时间；γ 为淡水相对质量密度；Δγ 为两液体的相对质量密度差；Kx,Kz为多孔介质横向和纵向渗透率；n为含水层的孔隙度。由于本试验所用抽水井为水平井,故将原DB模型表达式从井的左端至右端积分,得到水平井的咸淡水界面的二维剖面表达式为
ζ(r,t)=1LL/2∫−L/2Q2π(Δγ/γ)Kxd⋅[1(1+R′2)12−1[(1+γ′)2+R′2]12]dx′ 。 (2) 积分结果为
ζ(x,t)=Q2π(Δγ/γ)L√KxKz⋅{ln|√Kz/Kxd(x−L2)+√(1+γ′)2+KzKxd(x−L2)2|−ln|√Kz/Kxd(x+L2)+√(1+γ′)2+KzKxd(x+L2)2|−ln|√Kz/Kxd(x−L2)+√1+KzKxd(x−L2)2|+ln|√Kz/Kxd(x+L2)+√1+KzKxd(x+L2)2|}。 (3) 2.3 模型参数的选取与计算
数学模型中,根据砂箱试验装置设置确定相关参数的取值：抽水流量Q取常数,为3.8×10-6 m3/s；
γ 为淡水的相对质量密度,为1.0 g/cm3；Δγ 为两液体的相对质量密度差,为0.025 g/cm3；纵向渗透率Kz取0.00162 m/s；纵向横向渗透率比Kz/Kx取1.0；d为井底与初始咸淡水交界面的距离,取0.45 m；n为孔隙度,取0.0353。2.4 解析解模拟结果分析
根据式（3）进行计算,得到不同时刻的咸淡水界面。DB模型计算得到的咸淡水界面形状“中间凸起,两边渐进水平”,整体界面位置随时间不断上移。将计算结果与试验对比,见图8,解析解的计算结果与试验第二阶段的图像比较符合,即试验历时在90～120 min、咸淡水界面锥进高度在15～25 cm时解析解比较适用于推求水平井抽水的锥进过程。
![]()
图 8 特征时刻试验过程的盐羽图像及解析解结果对比Figure 8. Comparison of saltwater plume images and analytical solution at characteristic times通过提取试验过程中咸淡水界面
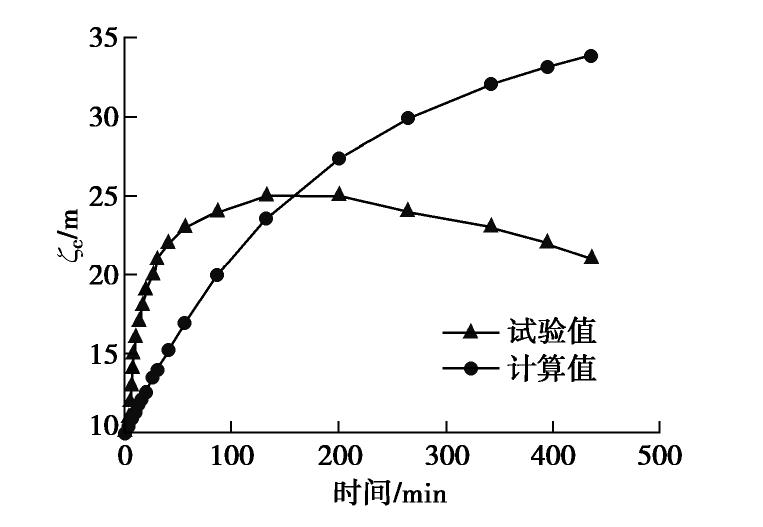
ζ 的右侧最低处距砂箱底部的距离ζc ,得到不同时间ζc 的试验数据与解析解数据对比结果,见图9,试验中盐羽右侧最低处距砂箱底部的距离ζc 在开始时快速上升,至距砂箱底部25 cm的位置后缓慢下降,而在解析解结果中,ζc 随试验进行逐渐增大。造成这种差别的主要原因是侧边界条件,试验中淡水通过马氏瓶固定高度并与砂箱侧面相连接,淡水连接点的高度分别为0.3,0.5,0.7,0.9 m,当抽水引起砂箱内部压力下降后,在水头差的作用下,淡水通过连接口向砂箱流动,因此试验过程中当ζc 上升到25 cm时受侧向淡水入流的影响逐渐回退,咸淡水界面向中心聚拢。而解析解模型中,假设侧向边界距离井中心无限远,解析解得到的是咸淡水界面沿整个含水层的上升情况,边界淡水的效应没有反映出来,边界条件的影响将在第4节进行详细讨论。![]()
图 9 不同时间ζc的试验数据与模拟数据的对比Figure 9. Comparison of experimental data and simulating data of ζc at different times2.5 解析解适用性的讨论
由于水平井抽水试验中,咸水锥进的界面受到很多因素的影响,比如砂土材料、试验的控制条件、抽水速率等,DB解析解模型不能完全反映这些因素的影响,因此采用解析解模型来推求试验中的咸淡水界面的适用性受到一定的限制。
Dagan等[6]通过小扰动方法得到在排水条件下的咸淡水界面上升的非稳态数学解,通过砂箱试验证明该解适用于咸淡水界面顶部的上升高度低于d/2～d/3范围内。Werner等[5]利用砂箱进行了4组竖直井抽水引起的咸水锥进的试验,将结果与DB模型的解析解界面进行了对比,咸淡水界面顶部的上升高度低于d/3时拟合结果较好,并且随着咸淡水密度差的增大而拟合结果逐渐变差。
从本研究的结果看,对于水平井抽水引起咸水锥进问题,推导的改进DB模型解析解在咸淡水界面顶部的上升高度在d/2～d/3范围时与试验界面拟合较好。
3. 数值模拟
本节将利用TOUGH2/T2DM模块模拟上述砂箱模型试验得到的水平井抽水引起的咸水锥进过程,并进一步研究各种可能的因素对咸水锥进的影响规律。开源程序TOUGH2/T2DM（TOUGH2 Dispersion Module）可用于求解气、液二相流体和空气、淡水、咸水三种组分在饱和-非饱和多孔介质/裂隙介质中的运移问题,详细的基本控制方程、本构方程及数值求解方法见文献[12,13]。
3.1 模型的建立
数学模型的范围与砂箱内部尺寸相同,长1.178 m（X方向）、宽0.053 m（Y方向）、高1.2 m（Z方向）。X方向上的网格剖分关于中轴线对称,X方向网格范围为0.008～0.03 m,最中央的网格宽度最小0.008 m；因为砂箱很薄,可近似二维问题,Y方向只有一个网格；Z方向的剖分需要考虑距砂箱底部0.55 m处的水平抽水井,抽水井的内径为0.008 m,Z方向网格范围为0.008～0.02 m。模型共分为2790个单元,5796个节点,如图10所示。模型参数取值参考室内模型试验的测试的参数值,如表1所示,由于试验中淡水马氏瓶的高度与砂箱顶齐平,试验过程中砂箱均为水相饱和,因此未设置标准砂的非饱和水力学参数。
表 1 数学模型计算参数Table 1. Parameters used in numerical model参数 取值 砂土渗透率 0.00016 m/s 分子扩散系数 1.0×10-9 m2/s 纵向弥散系数 0.002 横向弥散系数 0.0001 孔隙率 0.353 水动力黏滞系数 1.009×10-3 Pa s 固有渗透系数 1.7×10-11 m2 淡水密度 1000 kg/m3 咸水密度 1025 kg/m3 3.2 初始平衡态的数值模拟
模型的顶边界为大气边界,初始平衡态计算时侧面边界无水气流动,底边界为给定咸水水头边界。以及初始咸淡水平衡态界面的位置（距离砂箱底0.1 m）,可以确定底部咸水边界的咸水压力水头为1.173 m（以砂箱底部为0压面,下同）。模型计算的初始条件为细砂淡水饱和,为水相单相流静水平衡态。模型的计算时间设置为足够长,根据上述边界条件和初始条件运行模型,达到平衡态后计算自动停止,计算得到106.95 d后达到咸淡水平衡状态,如图11（a）所示。试验初始时,肉眼可见的咸淡水界面距离砂箱底约0.1 m,如图11（b）所示。
![]()
图 11 各特征时刻模拟结果与试验图像对比Figure 11. Comparison between simulated results and model test ones at characteristic times3.3 抽水过程的数值模拟
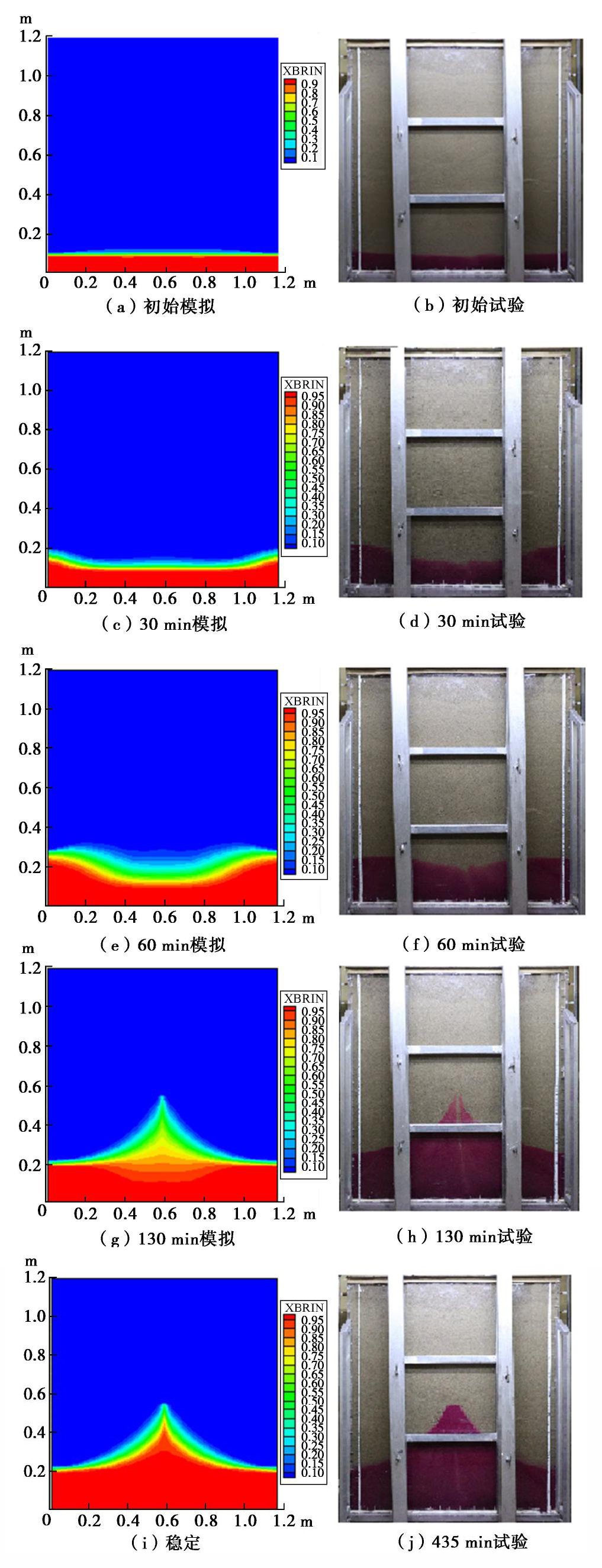
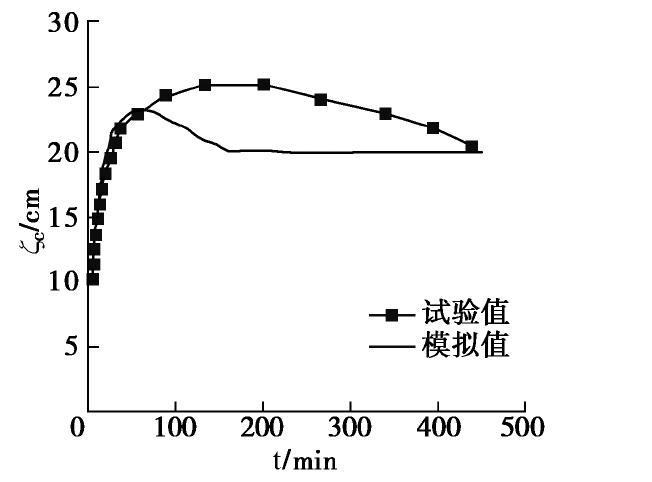
以上述初始平衡状态的模拟结果作为初始条件,保持顶部大气边界条件不变,侧边在与试验连接淡水和咸水马氏瓶的相应位置处设置淡水水头边界和咸水水头固定边界,淡水压力根据淡水马氏瓶的高度1.2 m和淡水密度1000 kg/m3计算确定,咸水水头根据物理模型试验中咸水马氏瓶的高度变化过程：试验开始至60 min咸水马氏瓶液面距离砂箱底1.19 m,60 min以后至试验结束咸水水头持续1.173 m,以及咸水密度1025 kg/m3来确定。抽水井单元采用源项来模拟,源强根据抽水速率3.8 ml/s来计算确定。得到各个特征时刻的模拟盐羽分布与相应时刻试验的盐羽图像对比见图11（c）,（d）,（e）,（f）,（g）,（h）,（i）,（j）。砂箱两端处咸淡水界面距离砂箱底部的高度
ζc 的变化过程与试验过程的对比见图12,咸淡水界面中央处距离初始咸淡水界面的高度Z(t)的变化过程与试验过程的对比见图13。![]()
图 12 0.5盐度等值线在砂箱两侧的高度变化Figure 12. Variation of height from bottom of sand box of 0.5 salinity isoline at lateral boundary of sand box![]()
图 13 0.5盐度等值线在砂箱中央处距离初始界面的高度变化Figure 13. Variation of height from initial interface of saltwater/freshwater of 0.5 salinity isoline at center line of sand box综合比较分析图11～13,考虑到边界条件的近似性和介质的不均匀性,数值模拟结果与试验过程拟合较好,试验过程中的盐羽分布不均匀,可能是由于介质分布的不均匀导致的,在第4节将详细讨论。
4. 影响因素分析
4.1 边界条件的影响
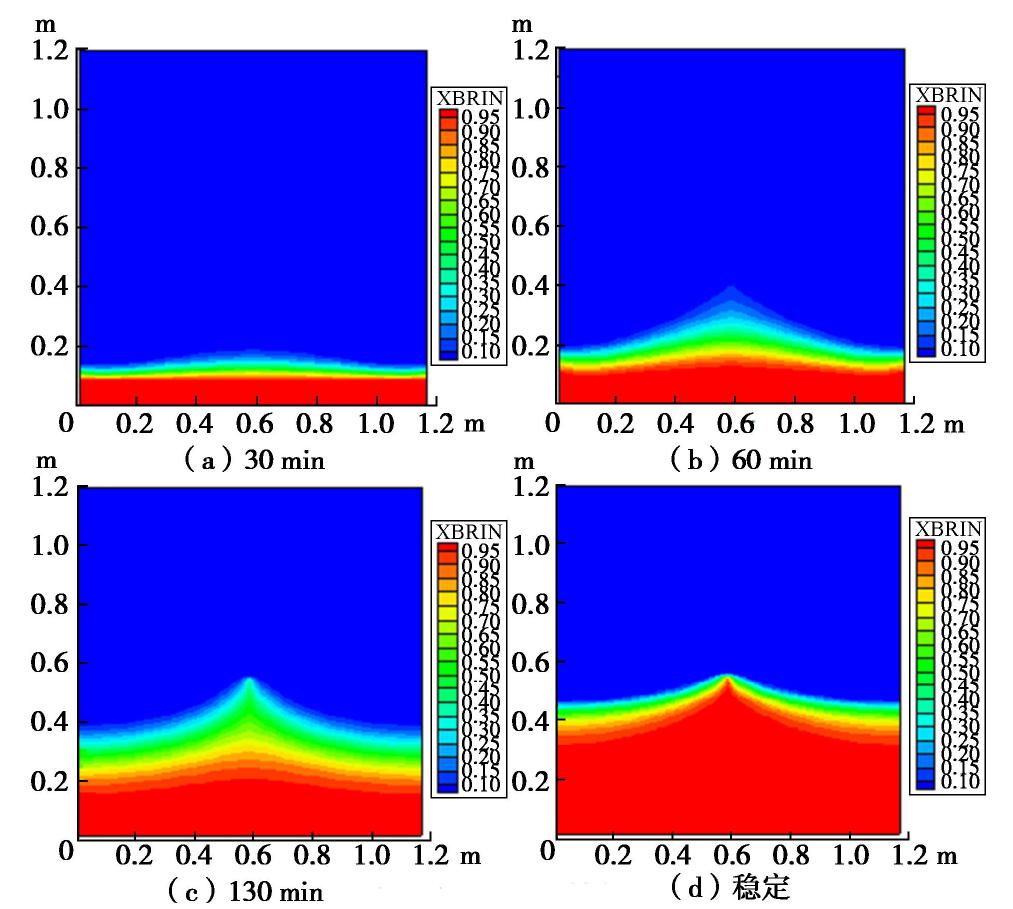
在第3节中,DB模型计算得到的咸淡水界面形状为“中间凸起,两边渐进水平”,且呈整体上升的趋势,而试验结果中,咸淡水界面的形状为初始“两端高、中间凹”,在砂箱两侧咸淡水界面上升的速度速度初始较快,然后逐渐回落,咸淡水界面的形状后来为“中间凸起,两边渐进水平”,可能的原因是试验过程中咸水水头初始60 min内比较大,然后60 min后逐渐减小。为了分析侧边淡水边界条件的影响,利用数学模型模拟分析DB模型边界条件下的咸水锥进过程：顶部为零压水头边界,侧边界为不透水边界,底边界设置咸水水头为1.173 m。初始条件为图11（a）所示的咸淡水平衡状态,模拟得到30,60,130 min和稳定状态的咸淡水界面分布如图14所示。
![]()
图 14 DB模型边界条件下各特征时刻模拟结果Figure 14. Simulated results at characteristic time under boundary conditions of DB model对比图14与图8所示的DB模型边界条件下的数值模拟结果和解析解结果,可见当数值模拟的边界条件与DB解析解的边界条件一致时,数值模拟的结果与解析解所示的咸淡水界面形状及发展过程拟合较好,说明室内模型试验的结果与DB解析解在初始和最终差别较大的原因主要是试验中咸/淡水边界条件的影响。
4.2 介质非均质性的影响
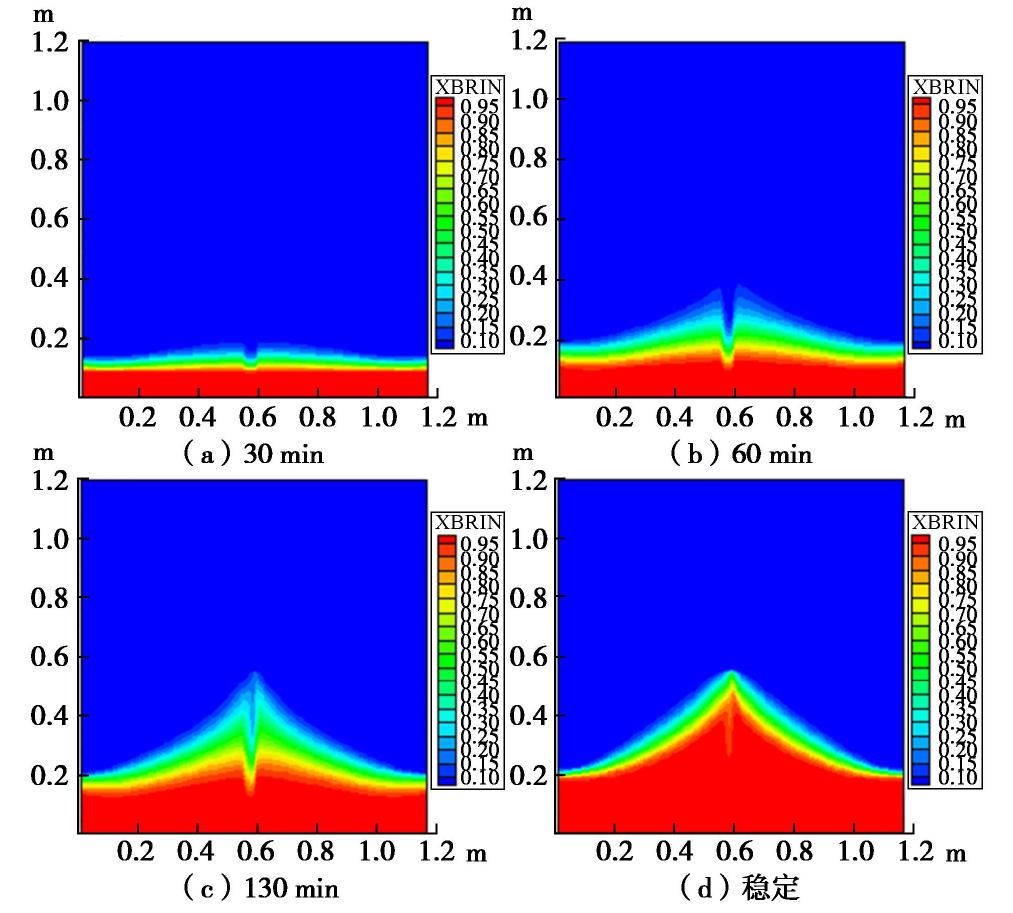
试验过程中,盐羽在中央位置有一条颜色较淡的“线”,初步分析可能是由于填砂时密度不均匀引起的,在中央的砂由于方便捣实密度稍大或者淡水饱和时产生了不均匀沉降导致的。为了分析介质非均质性的影响,利用数学模型模拟分析砂箱中部（水平坐标0.567～0.589 m）介质的渗透率较小,假设为原渗透率的0.5倍时的咸水锥进过程。顶部边界仍为大气边界,侧边淡水边界条件保持不变,为方便起见,固定侧边咸水水头为1.173 m保持不变,初始条件仍为图11（a）所示的咸淡水平衡状态,模拟得到30,60,130 min和稳定状态的咸淡水界面分布如图15所示。
![]()
图 15 非均质条件下各特征时刻模拟结果Figure 15. Simulated results at characteristic time under inhomogeneous medium由图15所示的咸水锥进过程各特征时刻的盐羽分布,可知由于中部砂的渗透性较小,盐度较低,出现了与试验结果相类似的“淡”盐羽分布区,说明试验过程中盐羽在中央位置所形成的颜色较淡的“线”,是由于砂非均质性造成的。
5. 结论
本文主要研究了砂箱尺度的水平井抽水引起的咸水锥进过程,比较分析了采用砂箱模型试验、DB解析解模型和数值模拟模型3种研究方法得到的咸水锥进过程,得出5点结论。
（1）通过开发模拟水平井抽水引起咸水锥进过程的试验设备,可以实现水平井以恒定流量抽取地下水所导致的咸水锥进过程。试验显示咸水锥进过程初始阶段的咸淡水界面形状为“两端高、中间凹”,在砂箱两侧咸淡水界面上升的速度速度初始较快,然后逐渐回落,咸淡水界面的形状后来为“中间凸起,两边渐进水平”,主要原因是试验过程中咸水水头初始60 min内比较大,60 min后逐渐减小。说明试验过程中的咸淡水水头的分布与变化对试验的影响较大。
（2）基于DB竖直井解析解模型,推导出了水平井抽水引起的咸淡水界面随时间和距原点的横向距离的解析解,解析解显示咸淡水界面为初始水平、中间突出、向上锥进至井口的锥进过程,与试验过程的咸淡水界面顶部的上升高度在d/3～d/2范围时拟合较好。室内模型试验的结果与DB解析解在初始和最终差别较大的原因主要是试验中咸/淡水边界条件的影响,通过数值模拟DB边界条件下的咸水锥进过程证实了这个结论。
（3）利用TOUGH2/T2DM开源软件建立了模拟水平井抽水引起的咸水锥进过程的数值模拟模型,将数值模拟结果与砂箱试验结果对比,两者拟合较好。
（4）利用所建立的数值模拟模型,模拟分析了DB解析解边界条件下的咸水锥进过程,证实了室内模型试验的结果与DB解析解在初始和最终差别较大的原因主要是试验中咸/淡水边界条件的影响。
（5）利用所建立的数值模拟模型,模拟分析了砂的非均质性的影响,证实了砂箱模型试验过程中盐羽在中央位置所形成的颜色较淡的“线”,由于填砂时密度不均匀引起的,在砂箱中部由于方便捣实密度稍大或者淡水饱和时产生了不均匀沉降导致渗透性降低。
-
![]()
图 7 水平井抽水引起咸水锥进的概念模型
Figure 7. Conceptual model for saltwater up-coning caused by pumping of horizontal well
![]()
图 8 特征时刻试验过程的盐羽图像及解析解结果对比
Figure 8. Comparison of saltwater plume images and analytical solution at characteristic times
![]()
图 9 不同时间ζc的试验数据与模拟数据的对比
Figure 9. Comparison of experimental data and simulating data of ζc at different times
![]()
图 11 各特征时刻模拟结果与试验图像对比
Figure 11. Comparison between simulated results and model test ones at characteristic times
![]()
图 12 0.5盐度等值线在砂箱两侧的高度变化
Figure 12. Variation of height from bottom of sand box of 0.5 salinity isoline at lateral boundary of sand box
![]()
图 13 0.5盐度等值线在砂箱中央处距离初始界面的高度变化
Figure 13. Variation of height from initial interface of saltwater/freshwater of 0.5 salinity isoline at center line of sand box
![]()
图 14 DB模型边界条件下各特征时刻模拟结果
Figure 14. Simulated results at characteristic time under boundary conditions of DB model
![]()
图 15 非均质条件下各特征时刻模拟结果
Figure 15. Simulated results at characteristic time under inhomogeneous medium
表 1 数学模型计算参数
Table 1 Parameters used in numerical model
参数 取值 砂土渗透率 0.00016 m/s 分子扩散系数 1.0×10-9 m2/s 纵向弥散系数 0.002 横向弥散系数 0.0001 孔隙率 0.353 水动力黏滞系数 1.009×10-3 Pa s 固有渗透系数 1.7×10-11 m2 淡水密度 1000 kg/m3 咸水密度 1025 kg/m3 
下载: 导出CSV
-
[1] Food and Agriculture Organization of the United States. Seawater Intrusion in Coastal Aquifers. Guidelines for Study, Monitoring and Control[R]. Water Reports No. 11. Rome: Food and Agriculture Organization of the United States, 1997.
[2] CHANG Y W, HU B X, XU Z X, et al. Numerical simulation of seawater intrusion to coastal aquifers and brine water/freshwater interaction in south Coast of Laizhou Bay, China[J]. Journal of Contaminant Hydrology, 2018, 215: 1-10. doi: 10.1016/j.jconhyd.2018.06.002
[3] SIMMONS C T, PIERINI M L, HUTSON J L. Laboratory investigation of variable-density flow and solute transport in unsaturated-saturated porous media[J]. Transport in Porous Media, 2002, 47(2): 215-244. doi: 10.1023/A:1015568724369
[4] GOSWAMI R R, CLEMENT T P. Laboratory-scale investigation of saltwater intrusion dynamics[J]. Water Resources Research, 2007, 43(4): W04418.
[5] WERNER A D, JAKOVOVIC D, SIMMONS C T. Experimental observations of saltwater up-coning[J]. Journal of Hydrology, 2009, 373(1/2): 230-241.
[6] DAGAN G, BEAR J. Solving the problem of local interface upconing in A coastal aquifer by the method of small perturbations[J]. Journal of Hydraulic Research, 1968, 6(1): 15-44. doi: 10.1080/00221686809500218
[7] MUSKAT M. The Flow of Homogeneous Fluids through Porous Media[M]. Boston: International Human Resources Development Corporation, 1982.
[8] SUN D M. Seawater upconing under a pumping horizontal well in a confined coastal aquifer[J]. International Journal of Environmental Sciences & Natural Resources, 2017, 2(1): 555-579. doi: 10.19080/ijesnr.2017.02.555579.
[9] 土工试验方法标准：GB/T50123—2019[S]. 2019. Standard for Soil Test Method: GB/T50123—2019[S]. 2019. (in Chinese)
[10] SCHINCARIOL R A. Migration of Dense Aqueous Phase Liquids in Homogeneous and Heterogeneous Porous Media[D]. Edmonton: University of Alberta, 1989.
[11] JAKOVOVIC D, WERNER A D, SIMMONS C T. Numerical modelling of saltwater up-coning: Comparison with experimental laboratory observations[J]. Journal of Hydrology, 2011, 402(3/4): 261-273.
[12] PRUESS K, OLDENBURG C M, MORIDIS G J. TOUGH2 user's guide version 2[R]. Oak Ridge: Office of Scientific and Technical Information (OSTI), 1999.
[13] OLDENBURG C M, PRUESS K. A two-dimensional dispersion module for the TOUGH2 simulator[R]. Oak Ridge: Office of Scientific and Technical Information (OSTI), 1993.
计量
- 文章访问数: 177
- HTML全文浏览量: 17
- PDF下载量: 95
