Deformation and acoustic emission characteristics of dry and saturated rock fractures
-
摘要: 天然岩体处于各类复杂的地质环境中,定量描述岩石裂隙在各种条件下的变形破坏行为是开展各类与岩石裂隙力学特性相关研究的基础。通过单轴压缩试验和弹塑性接触数值计算研究了两种具有不同岩性的岩石裂隙在干燥与饱和状态下的受压变形破坏行为,并对试验过程中的声发射信号进行了采集分析。结果表明:试验与数值计算得到的法向应力-位移曲线和塑性破坏区域皆基本吻合,验证了弹塑性接触计算方法的可靠性;塑性变形均值增量up随法向应力σn的增长呈现变化速率降低的非线性减小关系,利用力学及几何参数建立的拟合公式可较好地预测该关系;声发射源位置与试验及数值模拟得到的损伤破坏区域基本匹配,干燥状态下两种岩石声发射振铃计数、累计计数均高于饱和状态;声发射振铃计数与塑性变形均值增量的变化趋势基本一致。研究结果定量地揭示了岩石基本力学参数和裂隙表面特征对其受压变形破坏行为的控制作用。Abstract: The natural rock masses are situated in various complex geological conditions. Quantitative description of the deformation and failure behaviors of rock fractures under these conditions is of fundamental importance for the studies related to their mechanical behaviors. In this study, the unconfined compression tests and the elastic-plastic contact numerical simulations are implemented to study the compressive deformation and failure behavior of two kinds of rock fractures under dry and saturated conditions, together with acoustic emission detection and analysis. The results show that the normal stress-displacement curves and the plastic failure areas obtained from the experiment and the numerical simulation agree well with each other, which verifies the reliability of the contact method. The mean increment of plastic deformation decreases nonlinearly with the increasing normal stress with a decreasing rate, and a fitting formula is established using mechanical and geometric parameters. The position of acoustic emission (AE) sources matches with the damage area obtained from the experiment and the numerical simulation. Both the AE ringing count and the cumulative count are higher in dry rocks than those in saturated rocks. The AE ringing count and the mean increment of plastic deformation follow an identical changing trend. These results reveal the controlling role played by the fundamental mechanical parameters and geometric properties in the deformation and failure behaviors of rock fractures.
-
Keywords:
- rock fracture /
- deformation /
- elastic-plastic contact /
- acoustic emission /
- normal stress
-
0. 引言
不同应力条件下岩石孔隙结构演化对其渗透特性的影响规律,对二氧化碳地质封存、油气藏开采、水利水电工程都有着重要的理论指导意义。目前,国内外学者开展了一系列应力–渗流耦合试验来研究应力条件与岩石渗透率之间的演化关系。如王如宾等[1]、Emmanue等[2]、张俊文等[3]对砂岩开展不同荷载组合下渗透试验,结果表明优势渗流通道的扩展及有效连通是渗透率演化的重要特征;王彪等[4]等为研究不同深埋隧道岩石渗透率的变化规律,进行了在0~8 MPa围压下砂岩的渗透率测试,结果发现在围压加载过程中,岩石渗透率逐渐减小且存在一个拐点;Ma等[5]分析了岩石中有效应力变化引起的渗透率变化规律,发现相较于围压,岩石渗透特性对孔隙压力变化更为敏感;李克钢等[6]研究了白云岩在不同卸荷围压比和不同孔隙压力下的三轴卸荷渗透特性,指出孔隙水压的存在加速了岩石内部裂隙的产生和扩展,孔隙水压力越大,岩石渗透率越大;Civan[7]用弯曲的圆柱状弹性管束模拟非均质多孔岩石中的优势流动通道,从理论上描述了多孔岩石孔隙度和渗透率的应力依赖关系,表明岩体渗透性与其结构改变密切相关。但以上研究主要从岩石宏观变形、孔隙率等方面研究渗透演化机制,忽略了岩石内部多尺度孔隙分布特征对渗透率的影响。
核磁共振(NMR)技术作为一种无损、快速、安全的测试手段,能够实时监测岩石内部孔隙结构变化。基于核磁共振建立的SDR和Coates渗透率模型被国内外学者用来评价渗透率与孔隙度之间的演化关系。但模型中的经验系数难以确定,对具有复杂孔隙结构的岩石渗透率具有挑战性[8];且模型预测结果过度依赖T2截止值的选取,这使得利用现有模型来估算岩石渗透率还存在一定局限性[9]。在此基础上,国内外学者对常规模型进行改进或创新,肖亮等[10]、葛新民等[11]认为对于致密砂岩,T2截止值复杂多变,选用固定单截止值显然难以满足计算岩石渗透率的要求;姚艳斌等[12]、范宜仁等[13]提出基于饱和流体和束缚流体双T2截止值的SDR渗透率计算模型;周尚文等[14]在SDR模型的基础上,建立了一种适合于页岩的单参数“T2g”渗透率模型;Aghda等[15]、Alghamdi等[16]对TC模型和SDR模型中的系数进行了修正,建立了适合低渗透碳酸盐岩的渗透模型;Mao等[17]将核磁测井数据与毛管压力相结合,构建了Swanson参数与岩石渗透率的关系模型,但值得注意的是该模型适用于低孔低渗岩层;韩玉娇等[18]、Xu等[19]提出了对核磁共振T2谱不同组分进行划分的方法,但该方法没有深入研究储集层的孔隙结构特征,划分的依据不够充分。
综上所述,以上方法都有其各自的局限性,考虑孔隙结构演化的岩石渗透率评价模型还有待改进和提升。与常规储层相比,低孔低渗的砂岩储层孔隙结构复杂,孔径分布呈现强烈的非均质性特征,且不同尺度孔隙在应力作用下变形差异明显。这种不同尺度孔隙压缩敏感性对岩石渗透率的影响机理还需进一步研究。因此,本文针对砂岩开展不同应力条件下的渗流–应力耦合试验,利用核磁共振耦合渗流试验系统实现应力加载过程中渗透率、孔隙结构的实时监测,系统地研究不同应力条件下岩石的孔隙结构、渗透规律的变化特征,揭示不同尺度孔隙压缩敏感性对渗透特性的影响规律。
1. 砂岩渗透特性试验方案
1.1 岩心试样
试验所用岩心取自湖南某水库隧洞,孔隙率为8.31%,岩样矿物主要以石英为主,占总体的82.72%,其次是黏土矿物占14.85%,方解石占0.97%,锐钛矿占0.87%,菱铁矿仅占0.59%。参照《水利水电工程岩石试验规程》(SL/T 264—2020),将钻取的岩心切割打磨成直径为2.5 cm,高为5 cm的圆柱体岩样。
1.2 试验装置及原理
本文的岩石细观耦合渗流核磁共振在线分析系统如图 1(a)所示,主要包括计算机伺服控制系统、岩心夹持器、围压控制系统、轴压控制系统、渗压控制系统。各系统之间的作用关系如图 1(b)所示,通过核磁共振与三轴渗流装置的耦合,能够实时观测渗透过程中岩心孔隙结构以及渗流特性的变化。
本试验利用核磁共振弛豫原理反演得到T2弛豫时间。对于低频磁场,总弛豫机制以表面弛豫为主,而表面弛豫时间T2取决于表面弛豫速率与孔隙的比表面积。因此,根据T2弛豫时间可以得到孔隙的尺寸分布如下[20-21]:
1T2≈ρ2SV=ρ2FS1rc。 (1) 式中ρ2为T2表面弛豫强度(μm/s),与岩石性质有关;S/V为孔隙表面积与体积之比,与孔隙尺寸有关;FS为几何形状因子,管状模型FS取2;rc为孔隙平均半径(μm)。
1.3 试验方案
试样开展不同应力条件的应力–渗流耦合试验,主要步骤如下:
(1)将岩心试样放入真空饱和仪中24 h至完全饱和,随后将岩心取出用湿毛巾擦干表面水分放入岩心夹持器上进行渗透试验。
(2)在试验开始前,用CPMG序列进行测试,调节参数为:TE=0.1 ms,TW=3000 ms,回波数为18000。
(3)利用伺服监控系统依次设置围压、轴压、渗压条件见表 1,打开温控系统,试验过程中保持温度为30℃。
表 1 试验工况Table 1. Test conditions工况Ⅰ 围压/MPa 渗压/MPa 轴压/MPa 工况Ⅱ 围压/MPa 渗压/MPa 轴压/MPa Ⅰ-1 1.7 1.0 3.7 Ⅱ-1 1.5 0.5 3.7 Ⅰ-2 2.7 1.0 3.7 Ⅱ-2 1.5 0.6 3.7 Ⅰ-3 3.7 1.0 3.7 Ⅱ-3 1.5 0.7 3.7 Ⅰ-4 4.7 1.0 3.7 Ⅱ-4 1.5 0.8 3.7 Ⅰ-5 5.7 1.0 3.7 Ⅱ-5 1.5 0.9 3.7 Ⅰ-6 6.7 1.0 3.7 Ⅱ-6 1.5 1.0 3.7 (4)打开核磁成像模块,将岩心成像方向设置为轴向。
(5)试验间隔1 h,利用尾端天平测量系统测量流体出渗量。
(6)达到渗流平衡后记录渗透率,多组试验工况如表 1所示。
2. 试验结果与分析
为研究应力–渗流作用下砂岩试样内部孔隙结构以及渗透率的演化规律,采用岩石细观耦合渗流核磁共振在线分析系统,对砂岩试样S1、S2进行不同应力工况下的渗透试验,实时监测并记录试验结果。
2.1 不同围压作用下砂岩的孔隙结构演化规律
(1)孔径分布曲线演化规律
图 2(a)展示了不同围压条件下的砂岩孔径分布。可以发现,孔径主要分布在0.001~20 μm,孔径分布曲线面积随着围压增大而减小,T2谱从单峰分布变成双峰分布。这表明保持渗压不变、增大围压的过程中,孔隙体积减小,孔隙连通性变差;此外,孔径分布曲线出现向左移动的现象,这是由于围压作用主要集中于大孔,致使大孔隙受压闭合,而小孔和中孔基本不变。
(2)矿物离子浓度演化规律
应力–渗流耦合过程中,砂岩试样还会发生一系列复杂的物理化学反应,致使渗透液中矿物成分不断变化。委托江苏省地质勘察中心采用电感耦合等离子体发射光谱仪对渗出液进行离子成分分析,主要离子浓度变化曲线见图 2(b)。其中Ca2+浓度变化最为显著,表明砂岩渗流过程中主要是碳酸钙与水发生溶解反应。
CaCO3+2H+=Ca2++H2O+CO2↑ 低围压阶段,离子浓度迅速下降,高围压阶段,离子浓度趋于稳定,表明随着围压增加,反应速率开始降低。这是因为大孔隙提供了主要的渗流通道,而试验初期大孔隙压敏效应强,有效渗流通道变窄,反应表面积变小,阻止了反应的发生。进一步增加围压,此时大孔隙大部分已经闭合,孔隙压缩敏感性降低,达到渗流稳定状态,致使反应速率趋于稳定。
(3)砂岩核磁共振剖面图像分析
利用核磁共振成像技术,获得不同围压条件下试样的核磁共振图像。图中蓝色像素点为背景颜色,红色像素点表示充满流体的孔隙空间,颜色越深表示孔径越大,面积越大表示孔隙体积越大。
不同围压条件下核磁共振剖面图像如图 2(c)所示。随着围压增大,红色像素点面积逐渐减小,表明围压增大促使孔隙率减小;红色像素点逐渐变浅,由聚集分布变成分散分布,表明围压增大导致大孔隙明显闭合,孤立孔隙增多,渗流通道连通性变差,这与孔径分布曲线变化规律一致。
2.2 不同渗压作用下砂岩的孔隙结构演化规律
(1)孔径分布曲线演化规律
图 3(a)为不同渗压作用下的孔径分布曲线。与增加围压变化趋势相反,随着渗压增大,总孔隙度增加,主要表现为小孔隙增多。相较于小孔的体积变化,中孔、大孔的体积变化幅度相对较小,表明渗压主要促使储层岩石内部小孔发育,渗流通道扩展。
(2)矿物离子浓度演化规律
图 3(b)为不同渗压作用下的离子浓度变化规律。随着试验的进行,离子浓度演化有3个明显阶段:迅速增加—缓慢降低—趋于平稳。这是因为试验初期渗压增大促使孔隙发育,渗流通道的连通性增加,水岩反应的表面积增大,反应速率增强;试验中期,随着渗压的持续增加,渗流速度大于水岩反应速率,使得反应不充分导致反应速率减慢,矿物离子浓度下降;试验后期,小孔隙不再发育扩展,孔隙中的水岩反应达到平衡状态,离子浓度变化趋于稳定。
(3)砂岩核磁共振剖面图像分析
不同渗压条件下的砂岩剖面图像如图 3(c)所示。随着渗压增大,红色像素点由分散分布变成集中相连,表示渗压作用促使孔隙发育,渗流通道扩展,岩样内孔隙流体增多;当渗压增大到0.7 MPa时,剖面出现大量斑驳的浅色像素点,表明在渗压的作用下,孔隙变化主要表现为小孔隙数量增多,再次验证了孔径分布曲线的结果,渗压增加促使小孔发育。
综上所述,不同应力条件对于孔隙结构作用不同,进而对砂岩试样渗透率的影响差异显著:围压作用导致孔隙闭合,主要集中于大孔变小,孔隙连通性减弱,渗透率降低;渗压促使孔隙扩展,主要集中于小孔发育,孔隙连通性增强,渗透率变大。因此,量化不同尺度孔隙的压缩敏感性,研究多尺度孔隙压缩系数对砂岩的渗透特性影响至关重要。
3. 基于多尺度孔隙压缩系数的渗透率计算方法
以往对岩石渗透特性的研究多是为了获得岩石渗透率与孔隙率之间的宏观关系,例如Kozeny-Carman关系、Verma-Puress关系、幂律关系。但宏观的渗透率–孔隙率关系忽略了渗透–应力耦合过程中岩石内部孔隙结构演化对渗透率的影响。因此,本小节将提出基于多尺度孔隙压缩系数的渗透率计算方法,探讨孔隙结构演化对砂岩渗透特性的影响规律。
以往的研究表明,砂岩储层渗透率在有效应力作用下呈现负指数降低规律,孔隙压缩系数是表征降低程度的关键参数,其关系式满足[22]:
k/k0=e−αCfΔσ, (2) 式中,k0,k分别为初始渗透率和加载不同有效应力后的渗透率(cm2),Cf为岩样的孔隙压缩系数(MPa-1),Δσ为压力差(MPa),σ为介质变形系数,本文采用SHI[22]建立的经典孔隙模型中,σ=3。Cf为岩样的平均孔隙压缩系数(MPa-1),定义为
Cf=−1Vb0dVbdσ, (3) 式中,dσ为加载的应力差值(MPa),Vb0为试样的初始总孔隙体积(cm3),dVb为每一级应力作用下孔隙体积变化量(cm3)。
根据核磁共振的基本原理,T2弛豫时间代表孔隙大小。因此,孔隙压缩体积可以通过不同有效应力下T2松弛分布面积的变化来计算[23],
Cf=−1Vb0(Vbi−Vb0σi−σ0−)=−1Sb0(Sbi−Sb0σi−σ0), (4) 式中,σ0为初始应力(MPa),σi为第i级应力(MPa),Sb0、Sbi分别为初始、第i级孔径分布面积,代表孔隙体积(cm3)。
与孔隙连通性强的常规储层不同,砂岩孔隙结构复杂,孔隙连通性差的纳米级孔隙发育良好,大小孔隙尺寸相差5个数量级。因此,根据本文选用岩样特点,并结合Zhang等[24]、闫建平等[25]的孔隙分类法,将孔隙分为3种类型,即大孔(r>1 μm)、中孔(0.1 μm<r<1 μm)、小孔(r<0.1 μm),各尺度孔隙分量见表 2,3,则有
Vb=VSP+VMP+VLP , (5) 表 2 不同围压作用下不同尺度孔隙变化率及压缩系数Table 2. Change rates and compression coefficients of pores at different scales under different confining pressures围压/MPa VP VSP ΔVSP/V0 VMP ΔVMP/V0 VLP ΔVLP/V0 CSP CMP CLP Ce 1.7 6.22 4.10 — 1.95 — 0.66 — — — — — 2.7 6.04 4.31 5.12 1.77 -9.23 0.47 -28.79 -0.049 0.092 0.288 0.262 3.7 5.92 4.24 3.41 1.78 -8.72 0.38 -42.42 -0.017 0.045 0.210 0.177 4.7 5.76 4.24 3.41 1.69 -13.33 0.29 -56.06 -0.011 0.046 0.185 0.158 5.7 5.73 4.24 3.41 1.69 -13.33 0.27 -59.09 -0.008 0.034 0.147 0.124 6.7 5.68 4.22 2.93 1.67 -14.36 0.24 -63.64 -0.006 0.029 0.127 0.106 表 3 不同渗压作用下不同尺度孔隙变化率及压缩系数Table 3. Change rates and compression coefficients of pores at different scales under different osmotic pressures渗压/MPa VP VSP ΔVSP/V0 VMP ΔVMP/V0 VLP ΔVLP/V0 CSP CMP CLP Ce 0.5 6.07 2.70 — 2.63 — 0.73 — — — — — 0.6 6.25 3.12 15.33 2.63 0.20 0.70 -4.69 -1.533 -0.020 0.469 -0.635 0.7 6.42 3.50 29.41 2.49 -5.36 0.60 -18.41 -1.471 0.268 0.921 -0.428 0.8 6.70 3.65 35.23 2.46 -6.27 0.58 -20.57 -1.174 0.209 0.686 -0.349 0.9 6.93 3.78 39.75 2.49 -5.23 0.66 -10.12 -0.994 0.131 0.253 -0.355 1.0 7.07 3.84 42.29 2.49 -5.25 0.66 -10.35 -0.846 0.105 0.207 -0.306 将式(5)左右两侧对有效应力微分
dVbdσ=dVSPdσ+dVMPdσ+dVLPdσ, (6) 并在上式两侧同时除以总孔隙Vb0,则有
1Vb0dVbdσ=VSP0Vb01VSP0dVSPdσ+VMP0Vb0⋅1VMP0dVMPdσ+VLP0Vb01VLP0dVLPdσ, (7) 将式(7)代入孔隙压缩系数式(3)中,最终得到考虑多尺度的孔隙压缩系数
Ce=VSP0Vb0CSP+VMP0Vb0CMP+VLP0Vb0CLP, (8) 式中,CSP,CMP,CLP分别为有效应力引起岩样中小孔、中孔、大孔的压缩系数(MPa-1),分别表示为
CSP=−1VS0dVSidσi,CMP=−1VM0dVMidσi,CLP=−1VL0dVLidσi, dVSi,dVLi,dVMi分别为每一级应力对应的小孔、中孔、大孔的孔隙体积变化量。σ为对岩样施加的有效应力(MPa);Vi,V0分别为有效应力σi,σ0下的孔隙体积(cm3)。
不同围压作用下不同尺度孔隙变化率及孔隙压缩系数计算结果见表 2。随着围压增加,小孔隙的变化率增加2.93%,中孔隙减少14.36%,大孔隙减少63.64%,孔隙分量变化幅度:大孔>中孔>小孔,说明大孔隙的压缩敏感性最强。不同渗压作用下不同尺度孔隙变化率及孔隙压缩系数计算结果见表 3。随着渗压增大,小孔隙的变化率增加了42.29%,中孔隙减少了5.25%,大孔隙减少了10.35%,小孔变化幅度最大,表明渗压作用促使小孔发育扩展。根据不同尺度下的孔隙分量,分别计算小孔、中孔、大孔的孔隙压缩系数,将结果代入式(8),计算得到考虑多尺度的孔隙压缩系数。可以发现,随着有效应力增大,多尺度孔隙压缩系数的绝对值逐渐减小。
分别采用平均孔隙压缩系数以及多尺度孔隙压缩系数来计算砂岩渗透率,对比结果如图 4所示。不同围压作用下渗透率对比结果见图 4(a),渗透率随着围压增大而减小,基于Shi等[22]模型的平均孔隙压缩系数计算的渗透率数值大于试验结果,误差在两倍以上,而基于多尺度孔隙压缩系数计算的渗透率结果更加接近试验值,这是由于平均孔隙压缩系数低估了大孔隙的闭合作用致使系数偏小,进而导致渗透率计算结果偏大;不同渗压作用下渗透率对比结果见图 4(b),渗透率随着渗压增大而增大,基于平均孔隙压缩系数的渗透率计算数值小于试验结果,这是因为低估了小孔发育对渗流的作用,致使平均孔隙压缩系数偏大,进而导致渗透率的计算结果与试验值偏小。
因此,不难发现,传统的渗透率计算公式适合描述孔隙连通性较好的常规储层的渗透率与孔隙压缩性关系,而对于低渗砂岩储层,孔隙连通性较差,孔径结构复杂,孔径之间最大相差5个数量级,不同孔隙可压缩性之间存在着本质的差异,砂岩中孔隙结构对渗透率的影响更为复杂。基于多尺度孔隙压缩系数计算的渗透率方法能更加合理地表征不同尺度孔隙对渗透率的贡献差异,可显著提高砂岩储层的渗透率计算精度。
4. 结论
本文以砂岩为研究对象,开展不同围压和渗压工况下的渗流–应力耦合试验研究。利用岩石细观耦合渗流核磁共振在线分析系统,实时监测渗流过程中试样孔隙结构以及渗透率的演化规律,主要结论如下:
(1)不同尺度孔隙的压缩性不同,当围压加载到6.7 MPa时,大孔、中孔、小孔的孔隙率变幅分别为63.3%,14.4%,2.9%,变化幅度:大孔>中孔>小孔,说明孔径越大,孔隙的围压敏感性越强。
(2)当渗压加载到1.0 MPa时,大孔、中孔、小孔的孔隙率变幅分别为10.35%,5.25%,42.29%,小孔变化幅度最大,说明孔径越小,孔隙的渗压敏感性越强。
(3)不同应力条件对多尺度孔隙作用机制不同,围压增大导致大孔隙明显闭合,而渗压增大促使小孔隙发育扩展。
(4)针对非均质性较强、孔隙结构复杂的砂岩而言,考虑多尺度孔隙压缩系数的渗透率计算方法,能够显著提高储层渗透率的预测精度。
-
表 1 岩样的基本性质
Table 1 Fundamental properties of rock samples
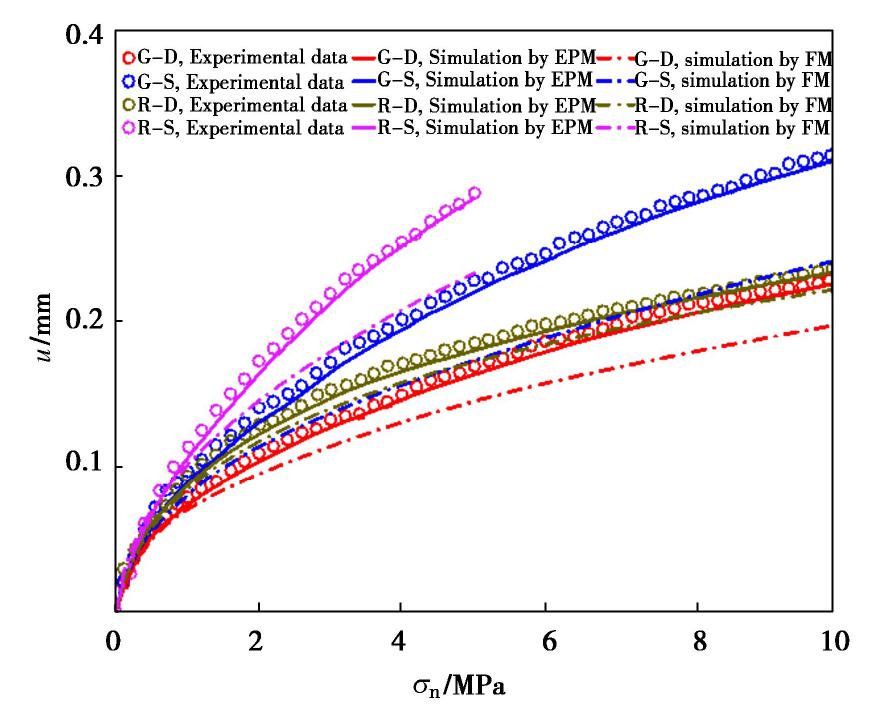
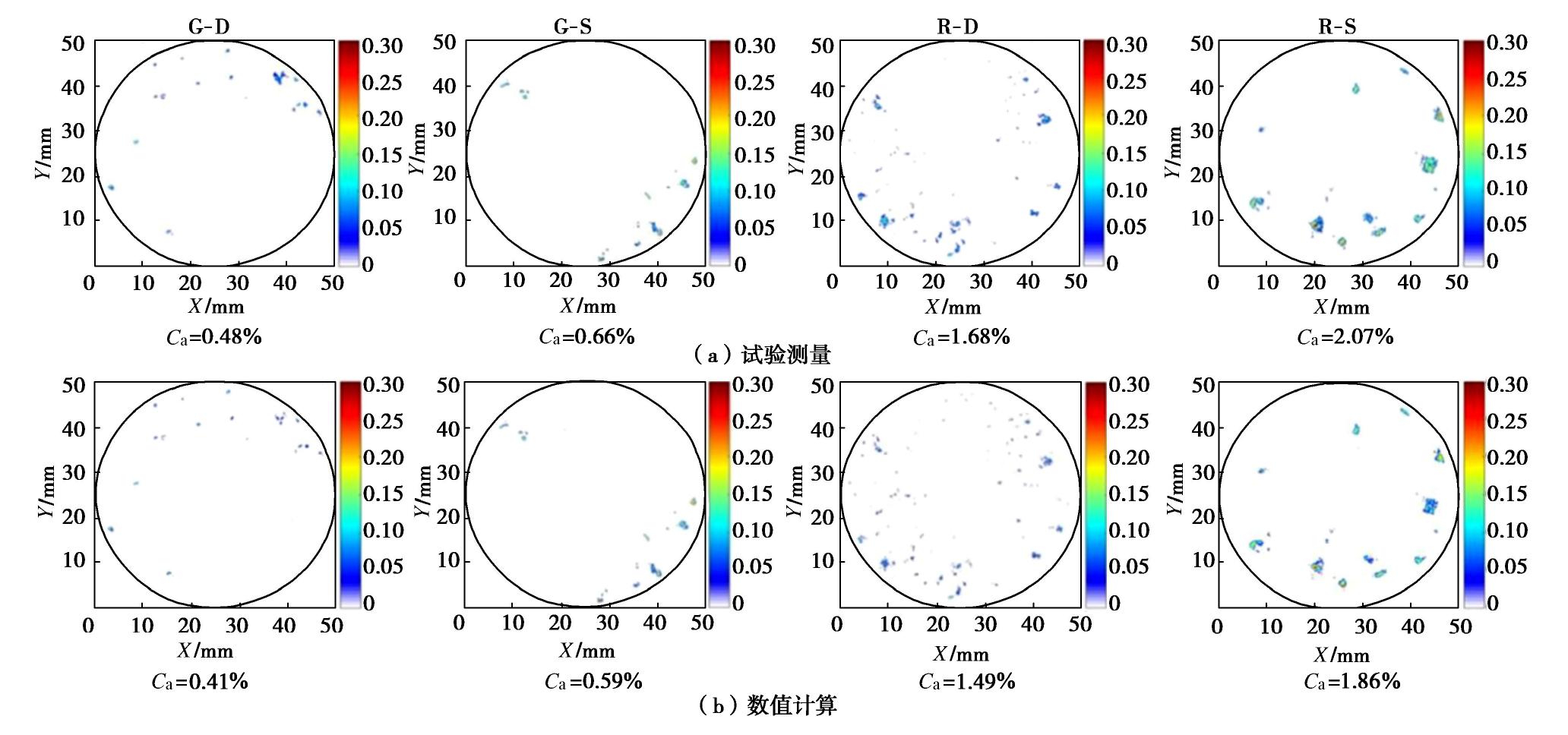
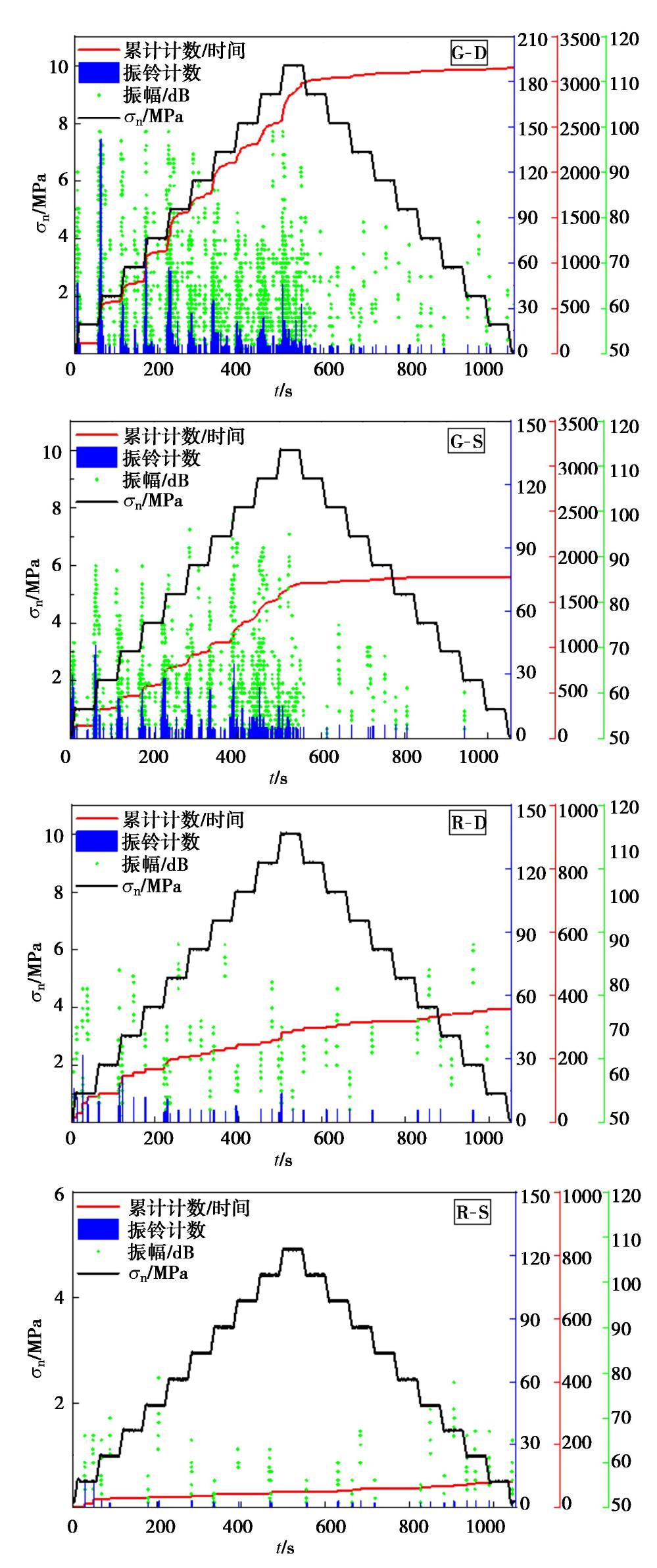
试样编号 UCS/MPa 弹性模量/GPa 泊松比 P波波速/(m/s) 旋转角度/(°) G-D 148.94 47.33 0.24 3179 6.11 G-S 133.20 44.99 0.23 4292 6.80 R-D 71.45 15.10 0.40 2689 3.49 R-S 39.98 11.20 0.35 3022 14.77 注: G为花岗岩,R为红砂岩,D为干燥,S为饱和。表 2 试样加卸载方案
Table 2 Loading and unloading plans
试样编号 加载速率/(MPa·s-1) 目标应力/MPa 卸载速率/(MPa·s-1) 保载时间/s G-D 0.1 10 0.1 45 G-W 0.1 10 0.1 45 R-D 0.1 10 0.1 45 R-W 0.05 5 0.05 45 -
[1] ERGULER Z A, ULUSAY R. Water-induced variations in mechanical properties of clay-bearing rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(2): 355-370. doi: 10.1016/j.ijrmms.2008.07.002
[2] RAJABZADEH M A, MOOSAVINASAB Z, RAKHSHANDEHROO G. Effects of rock classes and porosity on the relation between uniaxial compressive strength and some rock properties for carbonate rocks[J]. Rock Mechanics and Rock Engineering, 2012, 45(1): 113-122. doi: 10.1007/s00603-011-0169-y
[3] WONG L N Y, MARUVANCHERY V, LIU G. Water effects on rock strength and stiffness degradation[J]. Acta Geotechnica, 2016, 11(4): 713-737. doi: 10.1007/s11440-015-0407-7
[4] BANDIS S C, LUMSDEN A C, BARTON N R. Fundamentals of rock joint deformation[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1983, 20(6): 249-268.
[5] PEI L, HYUN S, MOLINARI J F, et al. Finite element modeling of elasto-plastic contact between rough surfaces[J]. Journal of the Mechanics & Physics of Solids, 2005, 53(11): 2385-2409.
[6] LAVROV A. Fracture permeability under normal stress: a fully computational approach[J]. Journal of Petroleum Exploration and Production Technology, 2017, 7(1): 181-194. doi: 10.1007/s13202-016-0254-6
[7] TIAN X F, BHUSHAN B. A numerical three-dimensional model for the contact of rough surfaces by variational principle[J]. Journal of Tribology, 1996, 118(1): 33-42. doi: 10.1115/1.2837089
[8] HOPKINS D L. The Effect of Surface Roughness on Joint Stiffness, Aperture, and Acoustic Wave Propagation[D]. Berkeley: University of California, 1991.
[9] LI B, ZHAO Z H, JIANG Y J, et al. Contact mechanism of a rock fracture subjected to normal loading and its impact on fast closure behavior during initial stage of fluid flow experiment[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(13): 1431-1449. doi: 10.1002/nag.2365
[10] GREENWOOD J A, WILLIAMSON J B P P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society of London, 1966, 295(1442): 300-319.
[11] KLING T, VOGLER D, PASTEWKA L, et al. Numerical simulations and validation of contact mechanics in a granodiorite fracture[J]. Rock Mechanics and Rock Engineering, 2018, 51(9): 2805-2824. doi: 10.1007/s00603-018-1498-x
[12] ZOU L C, LI B, MO Y Y, et al. A high-resolution contact analysis of rough-walled crystalline rock fractures subject to normal stress[J]. Rock Mechanics and Rock Engineering, 2020, 53(5): 2141-2155. doi: 10.1007/s00603-019-02034-w
[13] RUDAJEV V, VILHELM J, LOKAJÍČEK T. Laboratory studies of acoustic emission prior to uniaxial compressive rock failure[J]. International Journal of Rock Mechanics and Mining Sciences, 2000, 37(4): 699-704. doi: 10.1016/S1365-1609(99)00126-4
[14] 陈国庆, 陈毅, 孙祥, 等. 开放型岩桥裂纹贯通机理及脆性破坏特征研究[J]. 岩土工程学报, 2020, 42(5): 908-915. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202005018.htm CHEN Guo-qing, CHEN Yi, SUN Xiang, et al. Crack coalescence and brittle failure characteristics of open rock bridges[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(5): 908-915. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202005018.htm
[15] LIU S M, LI X L, WANG D K, et al. Mechanical and acoustic emission characteristics of coal at temperature impact[J]. Natural Resources Research, 2019, 29(4): 1755-17772.
[16] 龚囱, 李长洪, 赵奎. 红砂岩短时蠕变声发射b值特征[J]. 煤炭学报, 2015, 40(增刊1): 85-92. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB2015S1013.htm GONG Cong, LI Chang-hong, ZHAO Kui. Study on b-value characteristics of acoustic emission of red sandstone during short-time creep process[J]. Journal of China Coal Society, 2015, 40(S1): 85-92. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB2015S1013.htm
[17] 王春来, 廖泽锋, 李长峰, 等. 花岗岩岩爆声发射时空熵值动态特征实验研究[J]. 采矿与安全工程学报, 2019, 36(3): 626-633. https://www.cnki.com.cn/Article/CJFDTOTAL-KSYL201903027.htm WANG Chun-lai, LIAO Ze-feng, LI Chang-feng, et al. Experimental investigation of dynamic characteristics of AE spatio-temporal entropy for granitic rockburst[J]. Journal of Mining & Safety Engineering, 2019, 36(3): 626-633. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KSYL201903027.htm
[18] LI L R, DENG J H, ZHENG L, et al. Dominant frequency characteristics of acoustic emissions in white marble during direct tensile tests[J]. Rock Mechanics and Rock Engineering, 2017, 50(5): 1337-1346. doi: 10.1007/s00603-016-1162-2
[19] 赵兴东, 李元辉, 袁瑞甫, 等. 基于声发射定位的岩石裂纹动态演化过程研究[J]. 岩石力学与工程学报, 2007, 26(5): 944-950. doi: 10.3321/j.issn:1000-6915.2007.05.011 ZHAO Xing-dong, LI Yuan-hui, YUAN Rui-pu, et al. Study on crack dynamic propagation process of rock samples based on acoustic emission location[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(5): 944-950. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.05.011
[20] 刘建坡, 徐世达, 李元辉, 等. 预制孔岩石破坏过程中的声发射时空演化特征研究[J]. 岩石力学与工程学报, 2012, 31(12): 2538-2547. doi: 10.3969/j.issn.1000-6915.2012.12.018 LIU Jian-po, XU Shi-da, LI Yuan-hui, et al. Studies of AE time-space evolution characteristics during failure process of rock specimens with prefabricated holes[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(12): 2538-2547. (in Chinese) doi: 10.3969/j.issn.1000-6915.2012.12.018
[21] DONG L J, HU Q C, TONG X J, et al. Velocity-free MS/AE source location method for three-dimensional hole-containing structures[J]. Engineering, 2020, 6(7): 827-834. doi: 10.1016/j.eng.2019.12.016
[22] GEIGER L. Probability method for determination of earthquake epicenters form arrival time only[J]. Bulletin of Saint Louis University, 1912, 8: 60-71.
[23] 赵兴东, 刘建坡, 李元辉, 等. 岩石声发射定位技术及其实验验证[J]. 岩土工程学报, 2008, 30(10): 1472-1476. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200810012.htm ZHAO Xing-dong, LIU Jian-po, LI Yuan-hui, et al. Experimental verification of rock locating technique with acoustic emission[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(10): 1472-1476. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200810012.htm
[24] BOUSSINESQ J. Application des potentiels: à l'étude de l'équilibre et du mouvement des solides élastiques[J]. Gauthier-Villard, Paris, 1885.
[25] MOMBER A W. Fracture toughness effects in geomaterial solid particle erosion[J]. Rock Mechanics and Rock Engineering, 2015, 48(4): 1573-1588.
[26] PRADHAN P S, KING R L, YOUNAN N H, et al. Estimation of the number of decomposition levels for a wavelet-based multiresolution multisensor image fusion[J]. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(12): 3674-3686.
[27] BROWN S R, SCHOLZ C H. Closure of rock joints[J]. Journal of Geophysical Research: Solid Earth, 1986, 91(B5): 4939-4948.
[28] 王笑然, 李楠, 王恩元, 等. 岩石裂纹扩展微观机制声发射定量反演[J]. 地球物理学报, 2020, 63(7): 2627-2643. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX202007013.htm WANG Xiao-ran, LI Nan, WANG En-yuan, et al. Microcracking mechanisms of sandstone from acoustic emission source inversion[J]. Chinese Journal of Geophysics, 2020, 63(7): 2627-2643. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX202007013.htm
[29] YAO Q L, CHEN T, JU M H, et al. Effects of water intrusion on mechanical properties of and crack propagation in coal[J]. Rock Mechanics and Rock Engineering, 2016, 49(12): 4699-4709.
-
期刊类型引用(3)
1. 谭智勇,王超林,龙安发. 外部水源作用下岩石液氮冻结试验研究. 岩土工程学报. 2024(02): 415-425 .  本站查看
本站查看
2. 杨帅,毛海涛,刘畅,王晓菊. 中高强混凝土抗压强度与气孔分布特征关系模型研究. 长江科学院院报. 2024(04): 194-202 .  百度学术
百度学术
3. 林键,杨溢,曹广勇,刘洋,邵晚行. 静水压作用下砂岩渗透特性及渗透率模型改进. 地下空间与工程学报. 2024(03): 776-787 .  百度学术
百度学术
其他类型引用(5)




 下载:
下载: