Discrete element simulation of collapse characteristics of particle column considering gradation and shape
-
摘要: 颗粒形态和级配情况等是影响碎屑颗粒流(如滑坡、泥石流、岩崩等)运动的重要因素。基于沃洛诺伊镶嵌原理的随机生成方法创建了不同长细比不同级配的多面体颗粒,引入势粒子算法用于考虑颗粒间的接触作用,根据室内试验确定了离散元接触模型的各项参数,对考虑级配和形态的颗粒柱坍塌特性开展数值试验,研究结果表明:①颗粒柱的归一化堆积高度随颗粒的长细比和中值粒径d50的减小而减小,归一化跑出距离则随其减小而增加。②堆积过程中不同工况的相对静止角
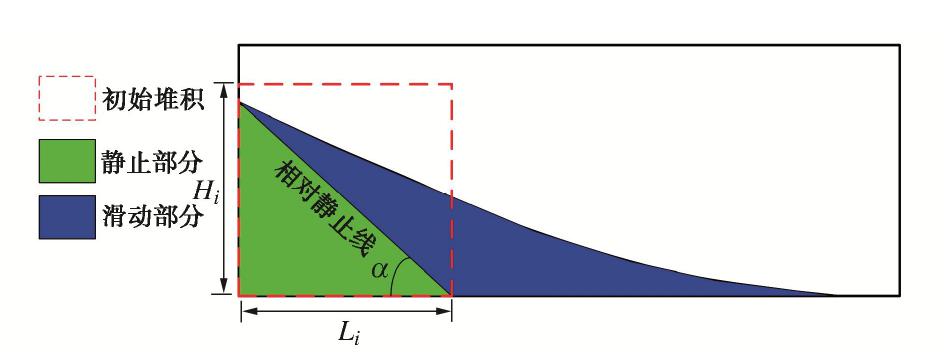
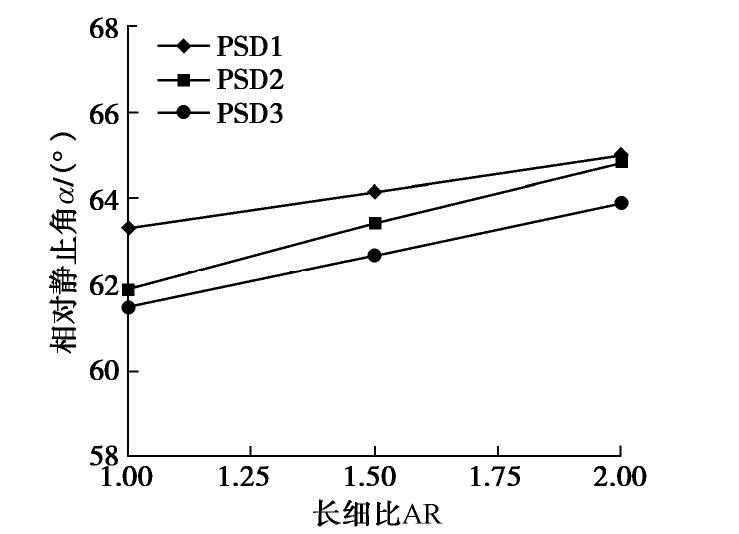
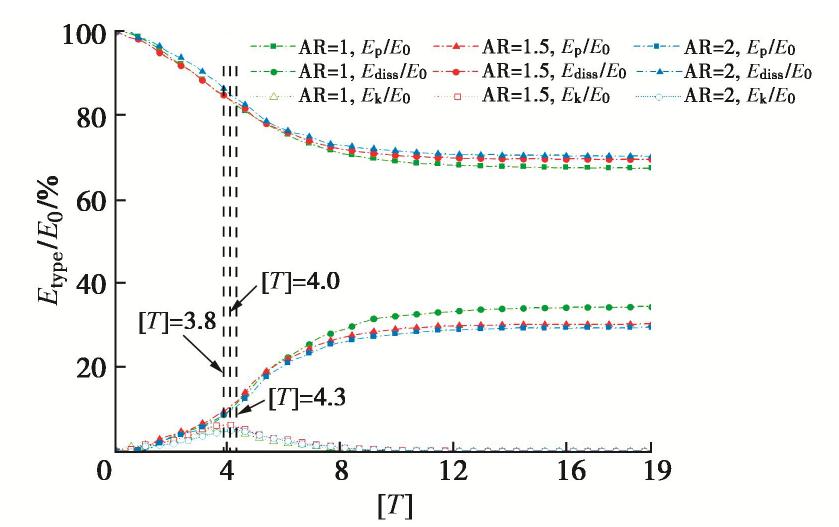
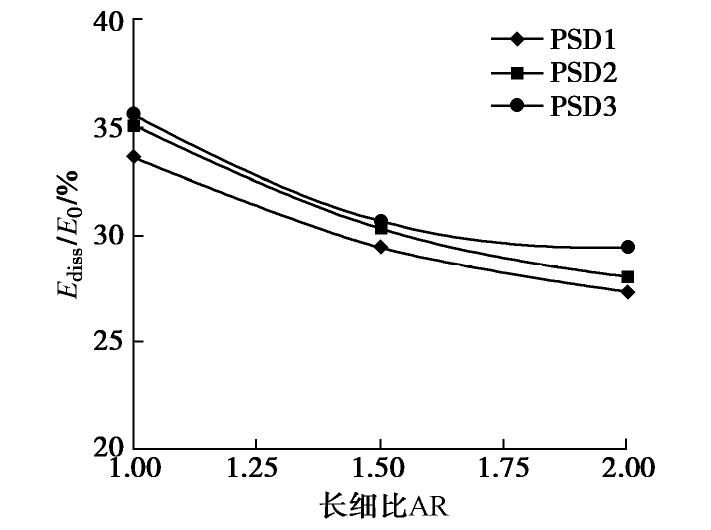
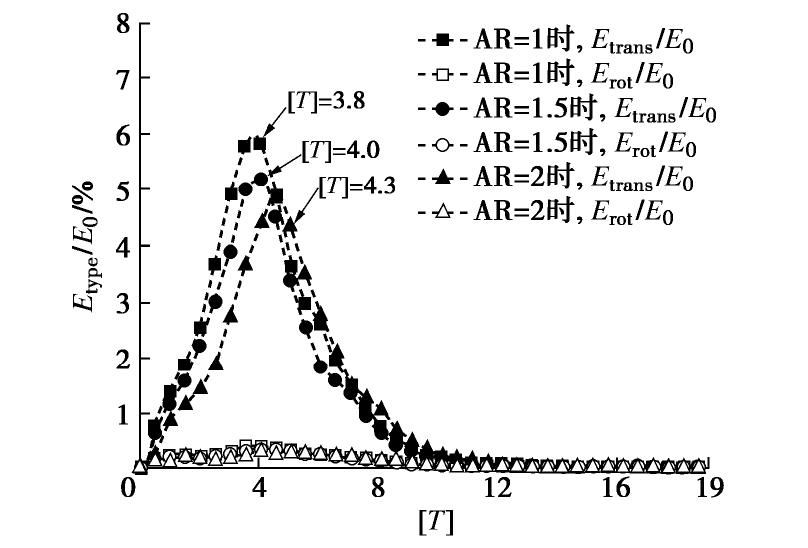
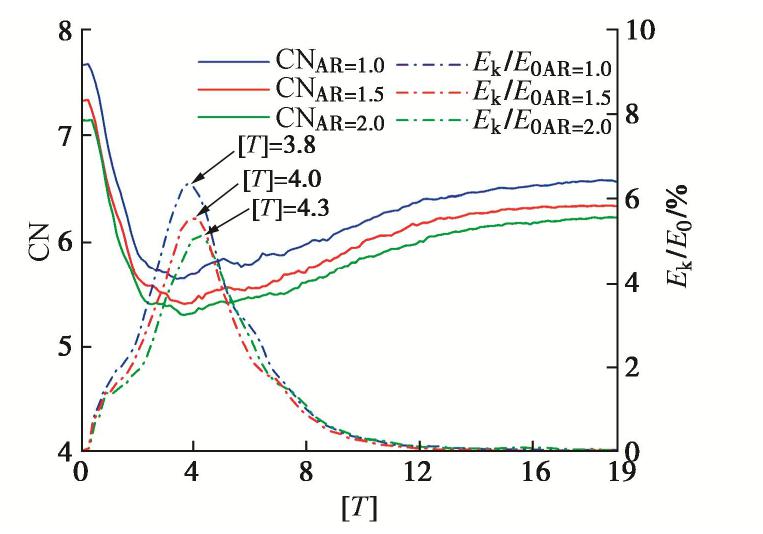
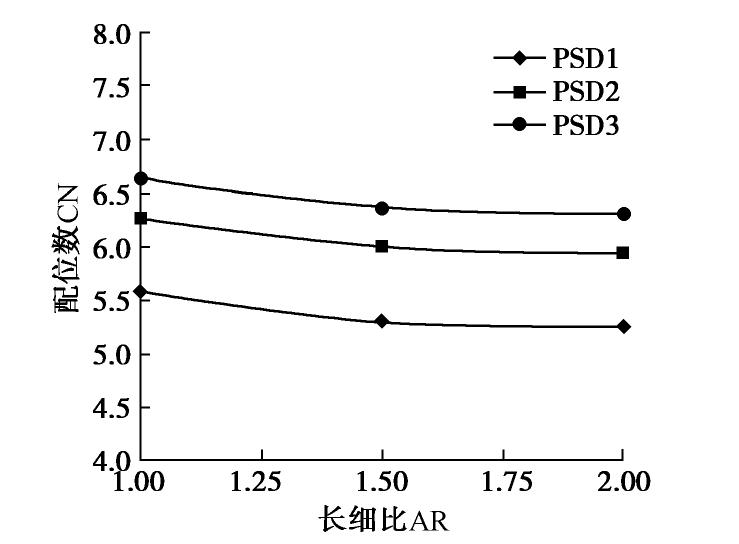
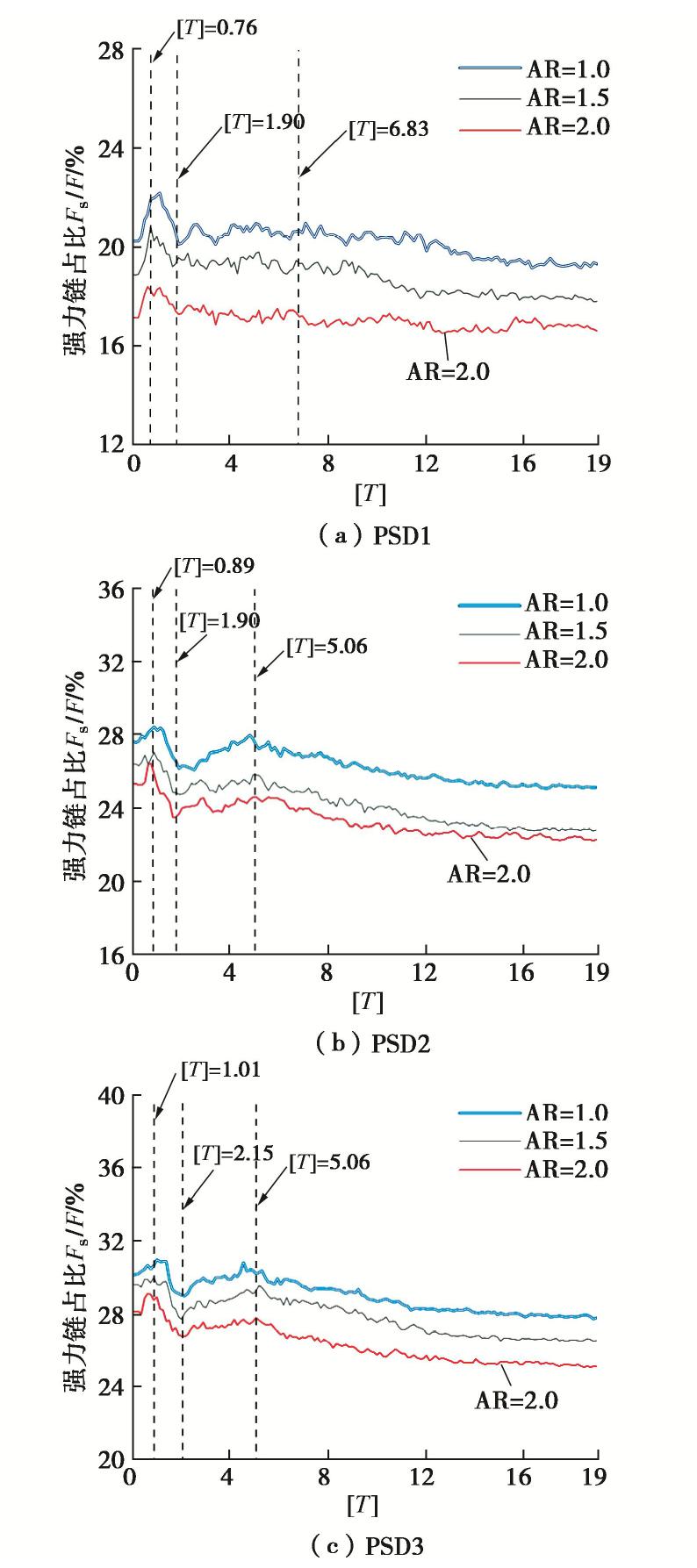
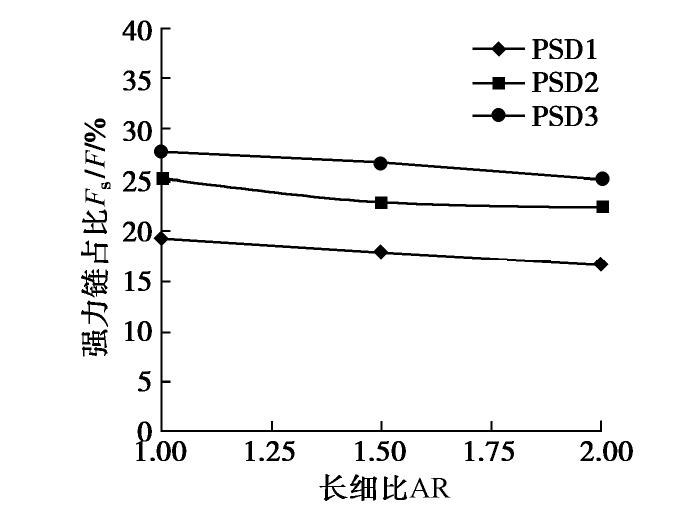
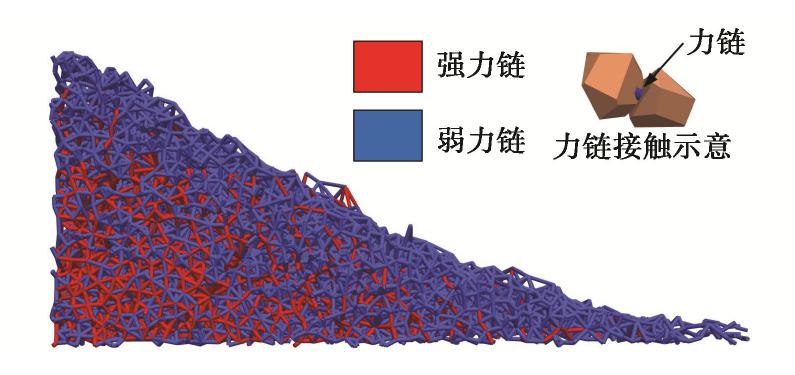
α 为61.49°~64.99°,且变化规律与归一化堆积高度变化一致。③不同工况的归一化能量耗散为27.1%~35.5%,且转动动能仅占平动动能的8.20%~9.05%。④归一化动能和颗粒配位数呈现负相关的关系,归一化动能达到峰值时颗粒配位数也达到最小值。⑤崩塌过程中强力链一般分布在滑动堆积体的中下部区域,形成力链传递的“拱效应”。中值粒径d50和长细比增大会减少强力链的数量,接触力传递的路径少而集中,从而限制颗粒在堆积过程中的运动。Abstract: Particle shape and gradation are the important factors affecting the movement of debris particle flows (such as landslides, debris flows, rock slides, etc.). The random generation method based on the Voronoi tessellation creates polyhedral particles with different aspect ratios and gradations. The potential particle algorithm is introduced to consider the contact effect between particles. The parameters of the contact model of discrete element are determined according to the indoor tests. For the item parameters, numerical experiments are carried out on the collapse characteristics of the particle column considering the gradation and morphology. The research results show that: (1) The normalized stacking height of the particle column decreases with the decrease of the aspect ratio and the median diameter (d50) of the particles, and the normalized run-out distance increases with the decrease. (2) The relative angle of repose under different working conditions during the accumulation process is in the range of 61.49°~64.99°, and the change rule is consistent with the change of the normalized accumulation height. (3) The normalized energy dissipation range under different working conditions is between 27.1%~35.5%, and the rotational kinetic energy only accounts for 8.20%~9.05% of the translational kinetic energy. (4) The normalized kinetic energy has a negative correlation with the particle coordination number, and the particle coordination number reaches the minimum when the normalized kinetic energy reaches its peak. (5) In the process of collapse, the strong chain is generally distributed in the middle and lower areas of the sliding accumulation body, forming the "arch effect" of the transmission of the force chain. The increase in the median particle size (d50) and the slenderness ratio will reduce the number of strong chains, and the paths of contact force transmission will be small and concentrated, thereby restricting the movement of particles during the accumulation process.-
Keywords:
- particle column /
- gradation /
- aspect ratio /
- potential particle /
- collapse process /
- discrete element method
-
0. 引言
传统弹塑性模型由于隐含了共轴性假设,无法模拟土体变形的非共轴特性[1-3]。针对这一问题,国内外学者从不同角度入手,提出了多种形式的非共轴模型。一些研究将土体的非共轴行为归因于其细观结构的各向异性,并基于土体细观结构的演化规律,采用多尺度的方法建立非共轴模型[4-9]。另一方面,通过直接采用数学公式描述宏观试验现象来构建土体本构模型也是一种非常有效的方法,因此,一些研究者也采用引入非共轴塑性理论的方式建立土体本构模型[10-13]。Rudnicki等[14]在研究裂隙岩体分叉行为时,为了提高理论预测的精确性,引入了非共轴应力率引发的塑性变形,由此提出了原始的非共轴理论。但这一早期理论是在二维应力空间内所建立,并不适用于三维化的模型。后来,Hashiguchi等[15]通过重新定义非共轴应力率表达式,建立了三维形式的非共轴理论。钱建固等[16]采用Gram-Schimidt张量正交化理论,将第三应力不变量的影响加入到了非共轴理论中。基于钱建固等[16]的研究,李学丰等[17],陈洲泉等[18]分别采用非共轴模型对空心圆柱扭剪试验中砂土的力学响应进行了模拟。刘元雪等[13]研究了三维条件下主应力轴旋转加载过程中应力率的数学描述问题,并在此基础上建立了考虑非共轴塑性变形的本构模型。这些研究表明,通过将非共轴理论引入已有的共轴模型中,可以一定程度上再现单剪试验与空心圆柱试验中的非共轴现象。
分析已有研究结果可以发现,传统非共轴理论均采用从总应力率减去所谓共轴应力率的方式定义非共轴应力率,不同理论中定义的非共轴应力率之间的区别还没有被明确地探讨过。最近,Li等[19]从纯数学角度对两个张量之间的非共轴性进行了研究,但与传统非共轴理论同样地采用从总量减去所谓共轴量的方式定义非共轴量,这种定义方式一定程度上给非共轴应力率的理解带来了困难。另一方面,虽然传统非共轴理论在模拟土体变形方面取得了一些成功,但非共轴塑性应变率与非共轴应力率之间通常采用线性假设并且二者始终同向,这与土体的实际变形特性不符。针对上述问题,本文在总结已有理论基础上,通过建立一种针对对称二阶张量的分解法将应力率进行了正交分解,由此可从另一角度对非共轴应力率进行表述。进一步地,在Zienkiewicz[20]建立的广义塑性力学基础上,针对诱发非共轴塑性变形的每一分量应力率建立相应的非线性加载机制,提出了广义形式的非共轴理论。然后,基于该理论建立了一个非共轴模型并采用两种数值试验对模型的合理性进行了检验,以期广义非共轴理论能够为土体非共轴模型的构建提供更为广阔的理论基础。
1. 传统的非共轴理论
首先需要说明的是,本文对于非共轴理论的介绍均是基于小变形假设。因此,对于采用了Jaumann应力率的非共轴理论,本文在介绍时均采用普通应力率代替。
在Rudnicki等[14]提出的早期非共轴理论中,总应变率
˙ε 被分解为弹性应变率˙εe ,共轴塑性应变率˙εcp 与非共轴塑性应变率˙εnp 三者之和:˙ε=˙εe+˙εcp+˙εnp, (1) Rudnicki等[14]认为非共轴塑性应变率
˙εnp 与静水压力部分无关,其方向与s 正交,由此将˙εnp 表示为˙snc=˙s−s:˙ss:ss, (2a) ˙εnp=1Ht˙snc, (2b) 式中,
Ht 为非共轴塑性模量,s 为偏应力,˙s 为偏应力率,˙snc 为非共轴应力率。然而式(2a),(2b)由于没有考虑第三应力不变量的影响,并不适用于一般化的三维模型。Hashiguchi等[15]通过假设非共轴塑性应变率与屈服面偏切线方向的应力率同向且二者之间为线性关系,将非共轴塑性应变率
˙εnp 的表达式修正为˙εnp=TE−1:˙snc。 (3) 式中
T 为一个无量纲的标量系数;E 为弹性刚度张量;˙snc 为˙snc=Ιt:˙σ, (4a) 式中
Ιt=I−131⊗1−f′σ‖f′σ‖⊗f′σ‖f′σ‖, (4b) f′σ=fσ−13tr(fσ)1, (4c) 其中,
σ 为应力,˙σ 为应力率,Ιt 为偏切线投影张量,I 为对称转换张量,其分量形式为Iijkl= (δikδjl+δilδjk)/2 ,δij 为Kronecker符号,f′σ 为屈服函数梯度的偏量部分,fσ=∂f/∂σ 表示屈服函数的梯度(本文中fa=∂f/∂a ,下文不再说明),1 为二阶单位张量,其分量为δij 。钱建固等[16]为考虑第三应力不变量的影响提出了另一种三维化的非共轴理论。在该理论中,非共轴塑性应变率的表达式与式(2b)相同,但非共轴应力率
˙snc 的表达式修改为˙snc=˙s−s:˙ss:ss−S:˙sS:SS, (5a) S=s2−23J21−32J3J2s。 (5b) 式中
S 为二阶张量,分别正交于1 和s ;J2=tr(s2)/2 为偏应力第二不变量;J3=tr(s3)/3 为偏应力第三不变量。分析上述非共轴理论可知,非共轴应力率的定义均采用从总应力率中减去所谓共轴应力率的方式,这与Li等[19]对于两个张量之间非共轴性的定义方式相类似。但这种定义方式不能说明非共轴应力率是由多项正交应力率分量所构成这一事实。为了对此问题进行更加清楚的解释,有必要对应力率的分量表达形式进行研究。
2. 非共轴应力率的正交分解
令3个单位基矢量
ˆe1 ,ˆe2 ,ˆe3 分别代表3个主应力σ1 ,σ2 ,σ3 所在的方向。则在这一坐标系中,应力张量σ 可为σ=σ1ˆe1⊗ˆe1+σ2ˆe2⊗ˆe2+σ3ˆe3⊗ˆe3。 (6) 3个主应力
σ1 ,σ2 ,σ3 分别为σ1=p+23qsin(θ+23π), (7a) σ2=p+23qsin(θ), (7b) σ3=p+23qsin(θ−23π)。 (7c) 式中
p 为平均应力,p=tr(σ)/3 ;q 为广义剪应力,q=√3s:s/2 ;θ 为罗德角,θ=−[sin−1(27J3/2q3)]/3 。现假设
σ 经过微小的增量Δσ 变化为σ∗ ,则可以采用如下取极限的方式定义一个与σ 相关的方向量:n=limσ∗→σσ∗−σ‖σ∗−σ‖。 (8) 进一步地,假设
Δσ 由平均应力变化Δp 引发,令Δp→0+ ,则根据式(8)可得到方向ˆnp 为ˆnp=√33ˆe1⊗ˆe1+√33ˆe2⊗ˆe2+√33ˆe3⊗ˆe3。 (9) 同理,当
Δσ 分别是由广义剪应力q 和罗德角θ 的独立变化所引发时,令Δq→0+ 和Δθ→0+ 可分别得到方向ˆnq 和ˆnθ 为ˆnq=√63sin(θ+23π)ˆe1⊗ˆe1+√63sin(θ)ˆe2⊗ˆe2+√63sin(θ−23π)ˆe3⊗ˆe3, (10) ˆnθ=√63cos(θ+23π)ˆe1⊗ˆe1+√63cos(θ)ˆe2⊗ˆe2+√63cos(θ−23π)ˆe3⊗ˆe3。 (11) 进一步地,假设
σ∗ 是由σ 经过绕σ1 轴旋转α 角所得,则σ∗ 可表示为σ∗=Q⋅σ⋅QT ,相应的正交变换张量Q 为Qij=[1000cos(α)sin(α)0−sin(α)cos(α)]。 (12) 将
σ∗=Q⋅σ⋅QT 和式(12)代入式(8),令Δα→0+ 可得方向ˆnr1 为ˆnr1=√22ˆe2⊗ˆe3+√22ˆe3⊗ˆe2。 (13) 假设
σ∗ 分别由σ 绕σ2 轴和σ3 轴旋转所得,经过与前述相同的运算,可以得到方向ˆnr2 ,ˆnr3 为ˆnr2=√22ˆe1⊗ˆe3+√22ˆe3⊗ˆe1, (14) ˆnr3=√22ˆe1⊗ˆe2+√22ˆe2⊗ˆe1, (15) 可以证明,这样得到的6个方向
ˆnp ,ˆnq ,ˆnθ ,ˆnr1 ,ˆnr2 ,ˆnr3 是相互正交的(本文中任意两个方向量a 与b 正交意味着a:b=0 )并且6个方向量与对称转换张量I 存在如下关系:I=ˆnp⊗ˆnp+ˆnq⊗ˆnq+ˆnθ⊗ˆnθ+ˆnr1⊗ˆnr1+ˆnr2⊗ˆnr2+ˆnr3⊗ˆnr3。 (16) 当应力
σ 处于屈服面上时,并假设屈服函数具有f(p,q,θ) =0的形式,则其偏法线方向ˆnf 可以表示为ˆnf=(fqqnq+fθnθ)/√(fqq)2+fθ2。 (17) 屈服面的偏切线方向
ˆnt 为ˆnt=(fqqˆnθ−fθˆnq)/√(fqq)2+fθ2。 (18) 容易证明,6个方向量
ˆnp ,ˆnf ,ˆnt ,ˆnr1 ,ˆnr2 ,ˆnr3 之间也是相互正交的并满足关系:I=ˆnp⊗ˆnp+ˆnf⊗ˆnf+ˆnt⊗ˆnt+ˆnr1⊗ˆnr1+ˆnr2⊗ˆnr2+ˆnr3⊗ˆnr3。 (19) 需注意的是,上述讨论都是限制在主应力空间内进行的。为将式(19)推广至一般应力空间,现假设
e1 ,e2 ,e3 为一般应力空间的3个单位基矢量,令单位正交张量Q 表示主应力空间与一般应力空间之间的转换,则Q 可表示为Q=Qijˆei⊗ˆej, (20a) Qij=ˆei•ej。 (20b) 在一般应力空间中,定义方向
np=QT⋅ˆnp⋅Q ,nq=QT⋅ˆnq⋅Q ,nθ=QT⋅ˆnθ⋅Q ,nf=QT⋅ˆnf⋅Q ,nt=QT⋅ˆnt⋅Q ,nr1=QT⋅ˆnr1⋅Q ,nr2=QT⋅ˆnr2⋅Q ,nr3=QT⋅ˆnr3⋅Q 。则可以证明,np ,nq ,nθ ,nf ,nt ,nr1 ,nr2 ,nr3 与对称转换张量I 之间存在关系:I=np⊗np+nq⊗nq+nθ⊗nθ+ nr1⊗nr1+nr2⊗nr2+nr3⊗nr3 =np⊗np+nf⊗nf+nt⊗nt+nr1⊗nr1+nr2⊗nr2+nr3⊗nr3。 (21) 利用式(21),可将应力率
˙σ 表示为˙σ=I:˙σ=˙σp+˙σq+˙σθ+˙σr1+˙σr2+˙σr3=˙σp+˙σf+˙σt+˙σr1+˙σr2+˙σr3。 (22) 式中
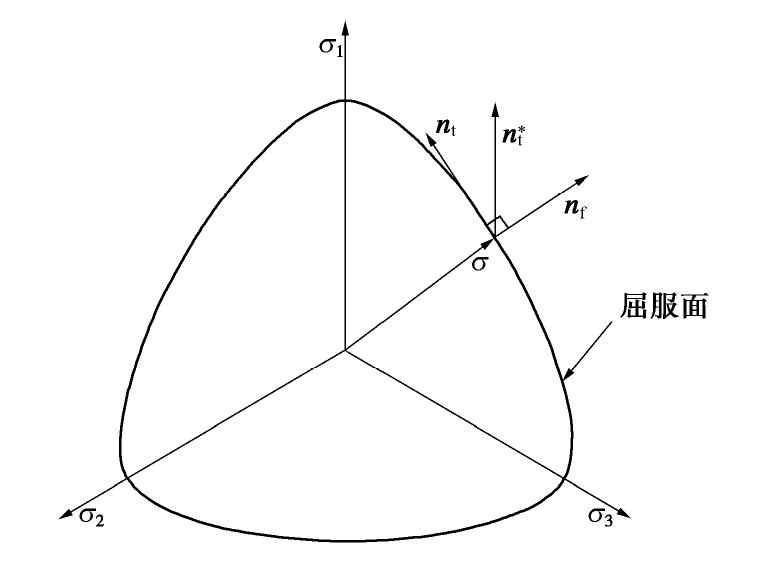
˙σp=(˙σ:np)np ,˙σq=(˙σ:nq)nq ,˙σθ=(˙σ: nθ)nθ ,˙σf=(˙σ:nf)nf ,˙σt=(˙σ:nt)nt ,˙σr1=(˙σ: nr1)nr1 ,˙σr2=(˙σ:nr2)nr2 ,˙σr3=(˙σ:nr3)nr3 。式(22)表明,总应力率˙σ 既可以分解为˙σp ,˙σq ,˙σθ ,˙σr1 ,˙σr2 ,˙σr3 之和,也可以分解为˙σp ,˙σf ,˙σt ,˙σr1 ,˙σr2 ,˙σr3 之和,并且上述分解方式适用于任意的对称二阶张量。此外,从上述推导过程可知,应力率分量˙σp ,˙σq ,˙σθ ,˙σf ,˙σt 都是由主应力大小的改变所引发,而˙σr1 ,˙σr2 ,˙σr3 3个应力率分量是由主应力方向的改变所引发。进一步地,nq=limΔq→0+σ∗−σ‖σ∗−σ‖=∂q/∂σ‖∂q/∂σ‖=s√s:s, (23) nθ=limΔθ→0+σ∗−σ‖σ∗−σ‖=∂θ/∂σ‖∂θ/∂σ‖=S√S:S。 (24) 利用式(22)~(24),可将Rudnicki等[14]定义的非共轴应力率表示为
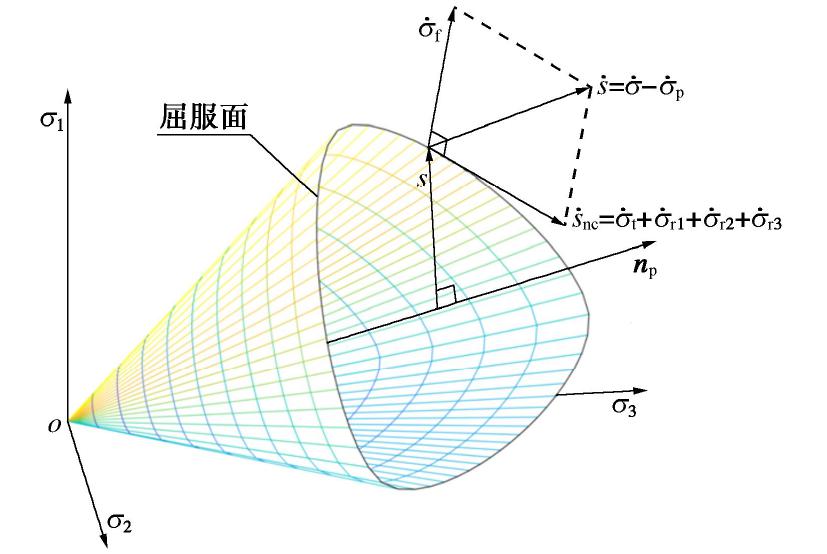
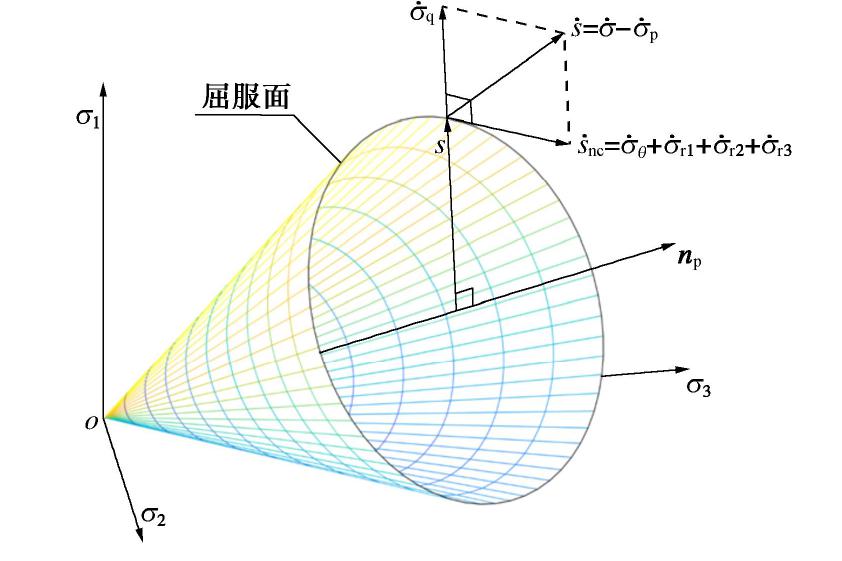
˙snc=˙σ−˙σp−˙σq=˙σθ+˙σr1+˙σr2+˙σr3。 (25) 式(25)的几何解释如图1所示。
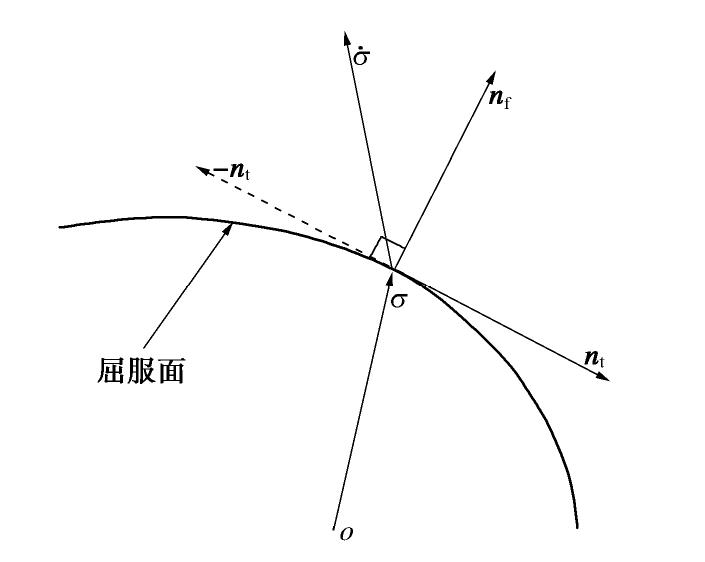
同理,可将Hashiguchi等[15]定义的非共轴应力率表示为
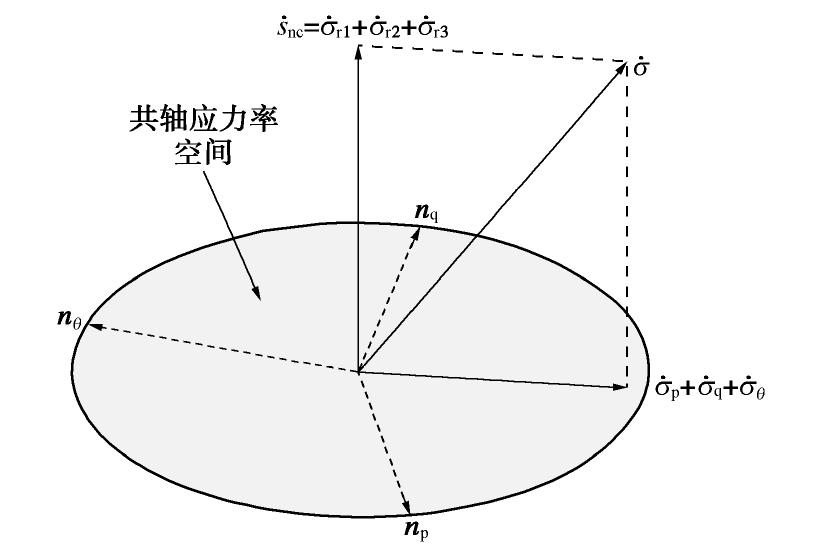
˙snc=˙σ−˙σp−˙σf=˙σt+˙σr1+˙σr2+˙σr3。 (26) 式(26)的几何解释如图2所示。
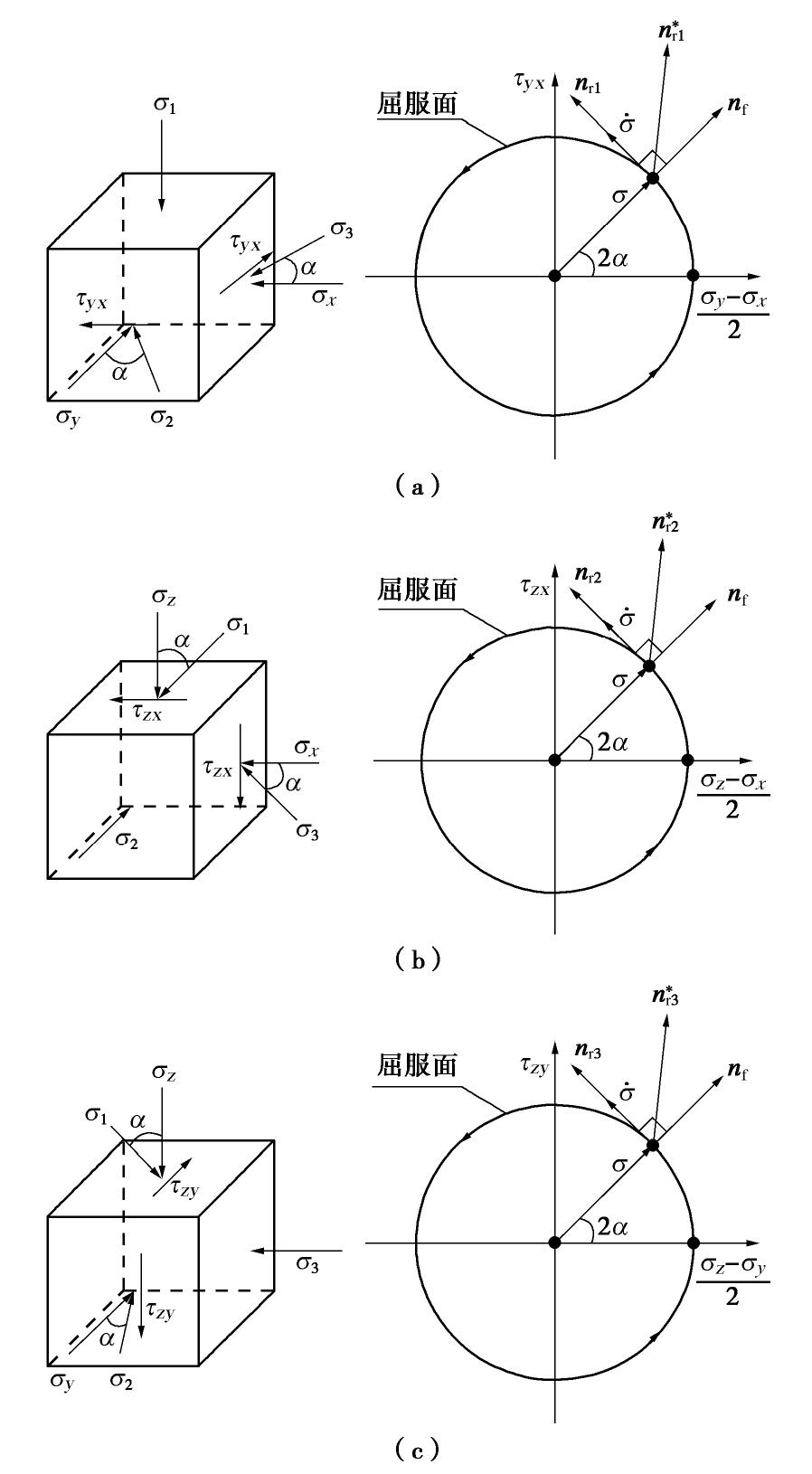
而钱建固等[16]定义的非共轴应力率可重新表示为
˙snc=˙σ−˙σp−˙σq−˙σθ=˙σr1+˙σr2+˙σr3。 (27) 式(27)的几何解释如图3所示。
通过上述分析可清楚得知,Rudnicki等[14]定义的非共轴应力率包含
˙σθ ,˙σr1 ,˙σr2 ,˙σr3 共4项正交分量,Hashiguchi等[15]定义的非共轴应力率包含˙σt ,˙σr1 ,˙σr2 ,˙σr3 共4项正交分量,而钱建固等[16]给出非共轴应力率包含˙σr1 ,˙σr2 ,˙σr3 共3项正交分量。其中,Rudnicki等[14]理论与Hashiguchi等[15]理论的主要区别体现在˙σθ 和˙σt 的不同。而钱建固等[16]定义的非共轴应力率仅包含主应力方向改变引发的应力率˙σr1 ,˙σr2 ,˙σr3 ,从而完全排除了主应力大小改变的影响,这是其区另外两种非共轴理论的标志。需要指出的是,上述结论是基于式(8)定义的方向量和式(22)表示的应力率的正交分解基础上推出的,而基于传统非共轴理论以及Li等[19]研究给出的非共轴应力率的表述方式难以得出类似结论。
3. 广义非共轴理论
传统弹塑性理论[21]中通常将加载强度指标
L 定义为L=1Kp∂f∂σ:˙σ, (28) 式中,
Kp 为塑性模量。利用应力率的分解式(22)并根据分量之间的正交关系,可将式(28)表示为L=1Kp∂f∂σ:˙σ=1Kp∂f∂σ(˙σp+˙σf)。 (29) 由式(29)可知,传统弹塑性模型中仅考虑了应力率分量
˙σp 与˙σf 诱发的塑性变形,而忽略了非共轴应力率分量˙σt ,˙σr1 ,˙σr2 ,˙σr3 的影响。尽管Hashiguchi等[15]非共轴理论可以反映这4项的影响,但该理论将非共轴塑性应变率与非共轴应力率之间表示为了线性关系并且二者始终同向,这一假设与岩土材料的试验结果不相符。例如,Gutierrez等[22]在对Toyoura砂进行空心圆柱扭剪试验时发现,在主应力幅值保持不变而方向连续改变的旋转加载条件下,非共轴塑性应变率显著偏离了非共轴应力率的方向。此外,砂土试验结果[23-26]表明,非共轴应力率所诱发的塑性变形不仅包括偏应变也包括体应变,而且砂土的非共轴塑性应变率还受当前孔隙比、应力状态和各向异性等因素的影响。此外,需要注意的是,˙σt 表示主应力大小的改变,而˙σr1 ,˙σr2 ,˙σr3 三项代表了主应力方向的改变,因而˙σt 与˙σr1 ,˙σr2 ,˙σr3 代表了两类不同的加载机制。为了精确描述非共轴应力率的影响,本文建议针对每一分量应力率建立独立的非线性加载机制。首先以分量
˙σt 为例,本文将与其相关的加载称为第一类非共轴加载。参考Zienkiewicz等[20]提出的广义塑性力学,通过直接定义加载强度指标、塑性模量和塑性流动方向,可将相应的加载机制表示为Lt=1Ktp(nt:˙σ)=1Ktp(nt:˙σt), (30a) ˙εpt=L1(n∗t+13Dt√2/3), (30b) Ktp=Ktp(σ,ψ,C), (30c) Dt=Dt(σ,ψ,C)。 (30d) 式中
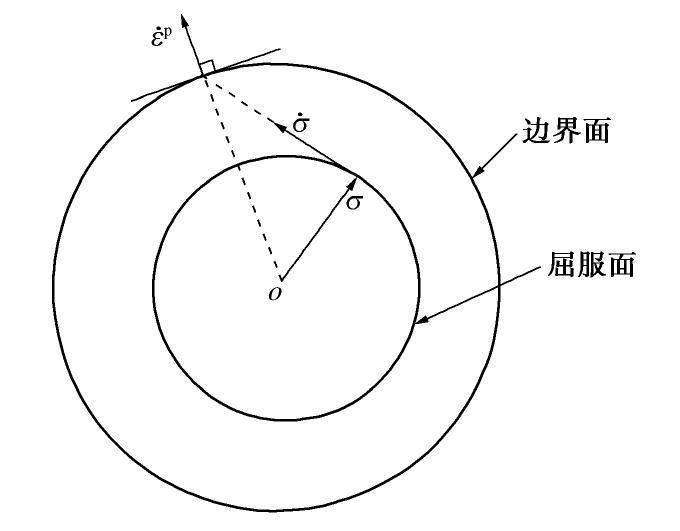
Lt 为nt 方向的加载强度指标;˙εpt 为分量˙σt 诱发的塑性应变率;n∗t 为˙σt 诱发的塑性偏应变率的方向;Ktp ,Dt 为与˙σt 对应的塑性模量和剪胀系数,二者可表示为前应力σ 、状态参数ψ 和代表材料特性的一组参数C 的函数。考虑到当前的研究普遍认为非共轴性源于材料的各向异性,因此参数C 中应当包括代表各向异性程度的幅值参量,并且当材料为各向同性时,需满足塑性模量Ktp=+∞ ,以保证nt 方向的应力率不会诱发塑性变形。注意到,在Gutierrez等[22]进行的主应力轴纯旋转加载试验中,随着应力比的增加,砂土变形的非共轴性会相应减弱,且当应力状态接近临界状态时,非共轴性几乎消失。基于这一规律,Gutierrez等[22]建议用应力率与边界面交点处的外法线方向表示塑性流动方向,如图4所示。关于
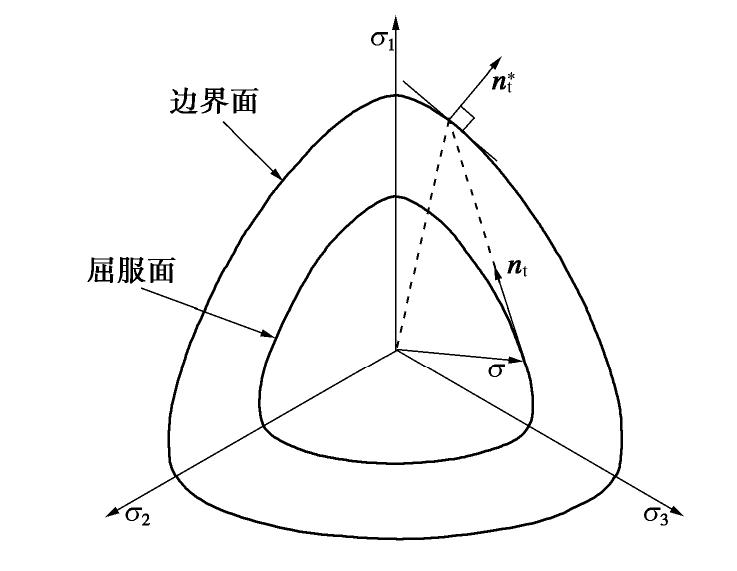
n∗t 方向的确定,这里采用与Gutierrez等[22]相似的方法,将˙σt 诱发的塑性偏应变率方向定义为nt 与边界面交点处的外法线方向,该方法的几何解释如图5所示。此外,也可以采用如下的方式定义
n∗t 为nt∗=√1−χnt+√χnf, (31) 式中,
χ 称为方向系数且0≤χ≤1 。理论上,通过将χ 表示为随应力状态变化的函数也可达到与上述几何映射方法相似的描述效果,如图6所示。另一方面,从几何角度可知,
nt 和−nt 均表示偏平面上屈服函数的切线方向。关于加载过程中nt 和−nt 的选择,可类比于传统弹塑性模型中加卸载的概念,引入加载与反向加载的概念,如图7所示。在弹塑性加载过程中,首先按照弹性变形计算试探应力率
˙σtrial ,若˙σtrial:nt≥0 ,选用nt 计算;相反,若˙σtrial:nt<0 ,选用−nt 代替式(30)中的nt 进行计算。至此,完成了对应于分量
˙σt 的加载机制的描述。采用同样的方式,可以将对应于分量˙σr1 ,˙σr2 ,˙σr3 的加载称为第二类非共轴加载,并将相应的加载机制表示为Lri=1Krip(nri:˙σ)=1Krip(nri:˙σt), (32a) ˙εpri=Lri(n∗ri+13Dri√2/3), (32b) Krip=Krip(σ,ψ,C), (32c) Dri=Dri(σ,ψ,C)。 (32d) 式中指标
ri 分别取r1 ,r2 ,r3 ;Lri 为nri 方向的加载强度指标;˙εpri 为分量˙σri 诱发的塑性应变率;n∗ri 为˙σri 诱发的塑性偏应变率的方向;Krip ,Dri 为与˙σri 对应的塑性模量和剪胀系数,二者同样地都可以表示为当前应力σ 、状态参数ψ 和代表材料特性参数C 的函数。3个加载机制的示意图如图8所示。其中,非共轴塑性流动方向
n∗ri 可为nri∗=√1−χnri+√χnf。 (33) 也可采用图5所示的映射方法确定,只需将图中的
nt 理解为nri 即可。将非共轴应力率进行正交分解并参考Zienkiewicz等[20]的广义塑性力学,通过直接定义塑性指标变量建立了多重非线性加载机制,用于描述每一非共轴应力率分量诱发的塑性变形。通过采用边界面理论中的几何映射法则或采用方向插值系数法可描述非共轴塑性流动方向在屈服面偏切线方向与偏法线方向之间连续变化。因而相较于传统理论,本理论在描述土体的非共轴塑性变形方面具有更强的灵活性。
4. 数值试验
为了评估本文建立的非共轴理论在分析岩土材料非共轴变形方面的合理性,结合该理论与Li等[27]发展的状态相关模型,建立砂土的非共轴本构模型。模型中的状态变量定义为
ψ=e−ec=e−[eΓ−λc(p/pa)ξ]。 (34) 式中
e 为当前孔隙比;ec 为临界孔隙比;eΓ ,λc ,ξ 均为材料常数;pa 为大气压力。剪切模量
G 和体积模量K 为G=G0(2.97−e)21+e√ppa, (35) K=G2(1+ν)3(1−2ν), (36) 式中,
G0 为材料常数,ν 为泊松比。屈服函数
f 为f=q−Mg(θ)p=0, (37) 式中,
M 为硬化内变量,g(θ) 为角隅函数[10],g(θ)=√(1+c2)2+4(1−c2)sin3θ−(1+c2)2(1−c)sin3θ, (38) 其中,
c 为三轴拉伸与压缩条件下极限应力比的比值。塑性模量
Kp 为Kp=hGenψ[Mcg(θ)e−nψη−1]。 (39) 式中
Mc 为临界状态应力比;应力比η=q/p ;n 为材料常数;h=h1−h2e ,h1 ,h2 为2个材料常数。剪胀系数D 和塑性势函数g 为D=d0Mcg(θ)[Mcg(θ)emψ−η], (40a) g=q−d0Mcg(θ)emψpd0−Mcg(θ)[1−(pp0)d0Mcg(θ)−1], (40b) 其中,
d0 ,m 为2个材料常数,p0 为塑性势面与p 轴的交点。基于小变形假设,将总应变率
˙ε 分解为弹性应变率˙εe 、共轴塑性应变率˙εcp 与非共轴塑性应变率˙εpt ,˙εpr1 ,˙εpr2 ,˙εpr3 之和:˙ε=˙εe+˙εcp+˙εpt+˙εpr1+˙εpr2+˙εpr3。 (41) 式(41)中的共轴塑性应变率
˙εcp 由传统位势理论确定,而非共轴塑性应变率˙εpt ,˙εpr1 ,˙εpr2 ,˙εpr3 由多重非共轴加载机制确定。令L1=L ,L2=Lt ,L3=Lr1 ,L4=Lr2 ,L5=Lr3 ,N1=∂f/∂σ ,N2= nt ,N3=nr1 ,N4=nr2 ,N5=nr3 ,N∗1=∂g/∂σ ,N∗2=n∗t+Dt√2/31/3 ,N∗3=n∗r1+Dr1√2/31/3 ,N∗4= n∗r2+Dr2√2/31/3 ,N∗5=n∗r3+Dr3√2/31/3 。利用弹性本构关系与式(30),(32),(41)可得˙σ=E:˙ε−5∑I=1LIE:N∗I。 (42) 令
K1p=Kp ,K2p=Ktp ,K3p=Kr1p ,K4p=Kr2p ,K5p=Kr3p ,分别用N1 ,N2 ,N3 ,N4 ,N5 双点积式(42),则可得(KIp+NI:E:N∗I)LI+5∑J=1,J≠INI:E:N∗JLJ=NI:E:˙εe。 (43) 式(43)是关于加载强度指标
LI 的一组线性方程,令Λ 表示LI 的系数矩阵,求解该方程组可得LJ=5∑I=1bIΛ∗IJ/det(Λ)。 (44) 式中
bI=NI:E:˙εe ;Λ∗ 为Λ 的伴随矩阵;det(Λ) 为Λ 的行列式。将式(44)代入式(42),可得非共轴本构关系式:˙σ=[Ee−Ee:(5∑I=1N∗I⊗MI):Ee]:˙ε, (45a) MJ=5∑I=1NIΛ∗IJ/det(Λ)。 (45b) 为了评估模型描述砂土本构反应的合理性,本文设计了应力与应变两种探测试验。如图8(b)所示,应力探测试验模拟主应力绕中主应力
σ2 的纯旋转加载。材料假设为Toyoura砂,共轴模型参数取自文献[2],并假设
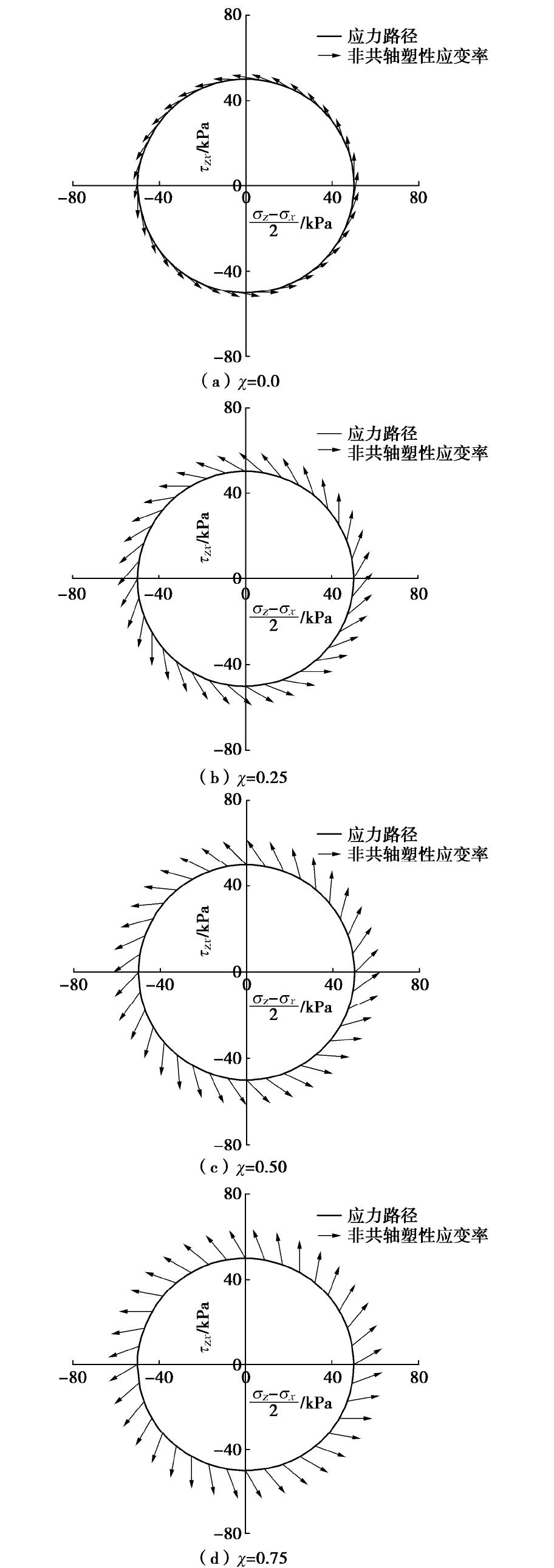
Ktp=Kr1p=Kr2p=Kr3p=Kp ,Dt=Dr1= Dr2= Dr3=D 。初始时刻平均应力p= 98 kPa,剪应力q= 50 kPa,罗德角θ= 0.0,初始孔隙比e0 =0.78。加载过程中,大主应力方向角α 从0°连续增加至180°。非共轴塑性流动方向采用式(31)确定,方向系数χ 分别为0.0,0.25,0.5,0.75,模拟结果如图9所示。图9表明,当
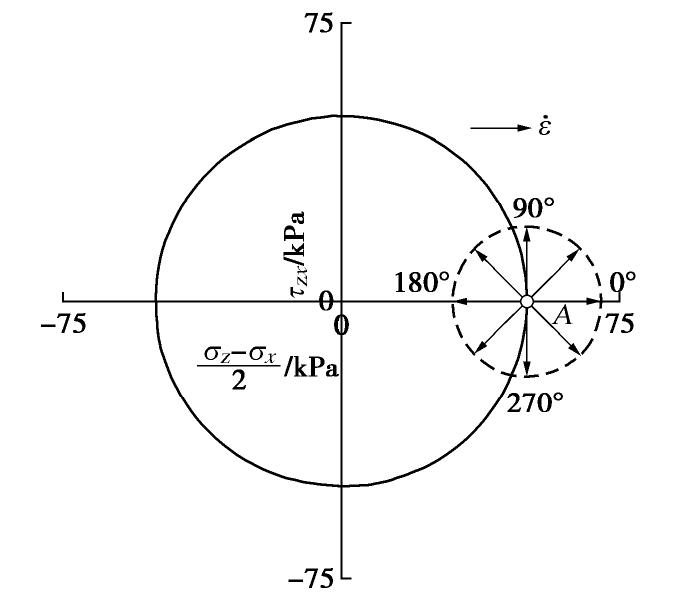
χ=0.0 时,计算的非共轴塑性应变率方向与应力路径正切;当χ≠0.0 时,计算的非共轴塑性应变率方向处于应力路径的切线方向与法线方向之间,更符合试验结果。随着χ 的增大,非共轴塑性增量方向由切线方向逐渐向法线方向靠近。因此,基于广义非共轴理论建立的模型可以更加真实的反映砂土的变形特点。如图10所示,在应变探测试验中,初始时刻的应力状态用A点表示,并假设与前述应力探测试验中的初始状态相同。然后在二维空间内,沿任意方向施加应变率幅值
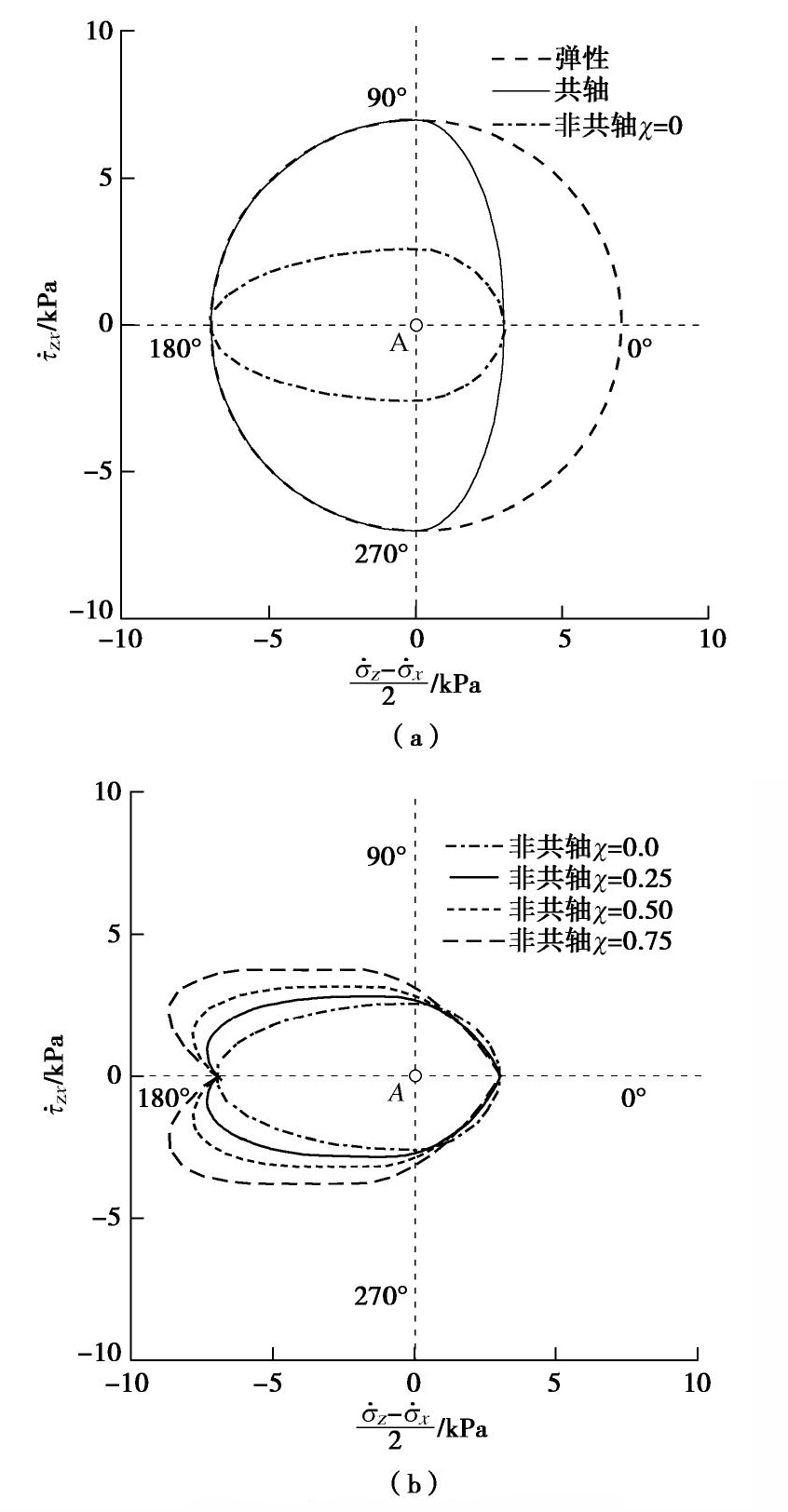
‖˙ε‖ 为0.0001的应变荷载。Gudehus[28]首先提出了应变探测方法,并认为合理的应力率响应包络线应满足的基本条件是连续性。图11(a)展示了弹性模型、共轴弹塑性模型和非共轴弹塑性模型(
χ=0.0 )计算的应力率响应包络线。显然,3种模型预测的包络线满足连续性要求。此外,由图11(a)可知,沿着0°方向和180°方向加载,非共轴模型(χ=0.0 )与共轴模型计算的应力率相同,而沿其他方向加载,非共轴模型(χ=0.0 )的计算结果显示出更加软化的力学响应。图11(b)展示了不同χ 条件下,非共轴模型计算的应力率包络线。由图11可知,随着χ 的增加,在90°~180°~270°范围内,模型展示出了相对硬化的力学响应,而在270°~0°~90°范围内,χ 对包络线的影响并不明显。此外,不同χ 条件下,模型计算的包络线均满足连续性要求。应变探测试验结果初步表明,基于广义非共轴理论建立的模型满足数值计算的稳定性要求。5. 结论
(1)传统非共轴理论将非共轴应力率定义为总应力率减去所谓共轴应力率的剩余部分,无法说明非共轴应力率由多项正交分量构成的事实。本文通过严格的数学推导证明了总应力率可以分解为6项正交应力率分量之和。在此基础上,对于已有的非共轴理论进行了总结和比较,指出,Rudnicki等与Hashiguchi等定义的非共轴应力率包含4项正交的应力率分量,而钱建固等定义的非共轴应力率包含3项正交的应力率分量。
(2)传统非共轴理论假设非共轴塑性应变率与非共轴应力率之间为线性关系并且二者始终同向,这与试验结果不相符。将非共轴应力率正交分解为4项,然后采用多重非线性加载机制描述每一非共轴应力率分量诱发的塑性变形,而总的非共轴塑性变形视为分量非共轴塑性变形之和,从而建立了一种广义形式的非共轴理论。新建理论能够描述非共轴应力率与非共轴塑性应变率之间的非线性关系,同时也能描述二者方向之间的非一致性。
(3)推导了基于广义非共轴理论建立弹塑性模型时的应力-应变关系式。然后用两种数值试验评估了模型的合理性,结果表明,基于广义非共轴理论建立的模型预测的应力率响应包络线满足连续性要求,在描述砂土非共轴变形方面具有更强的灵活性。数值试验结果初步显示了广义非共轴理论在砂土本构建模方面的优越性和合理性,表明该理论能够为土体非共轴模型的构建提供更为广阔的理论基础。
-
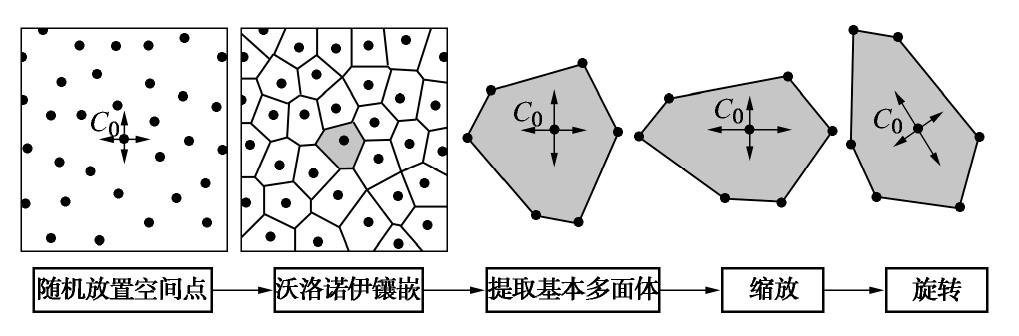
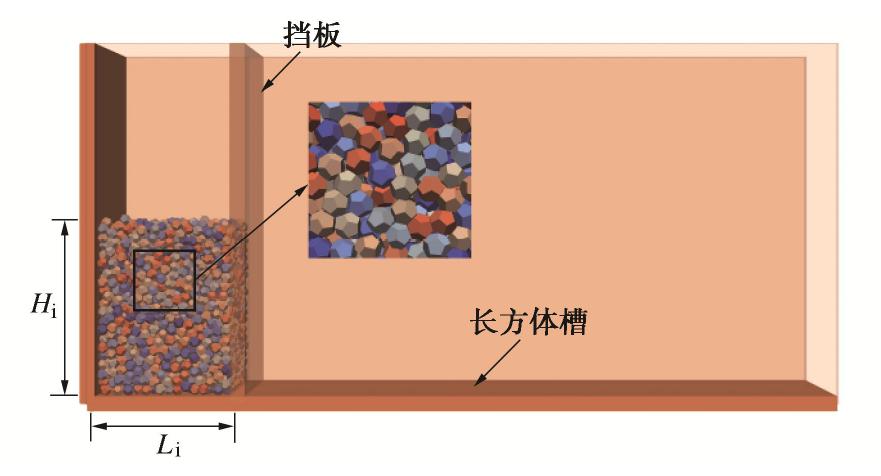
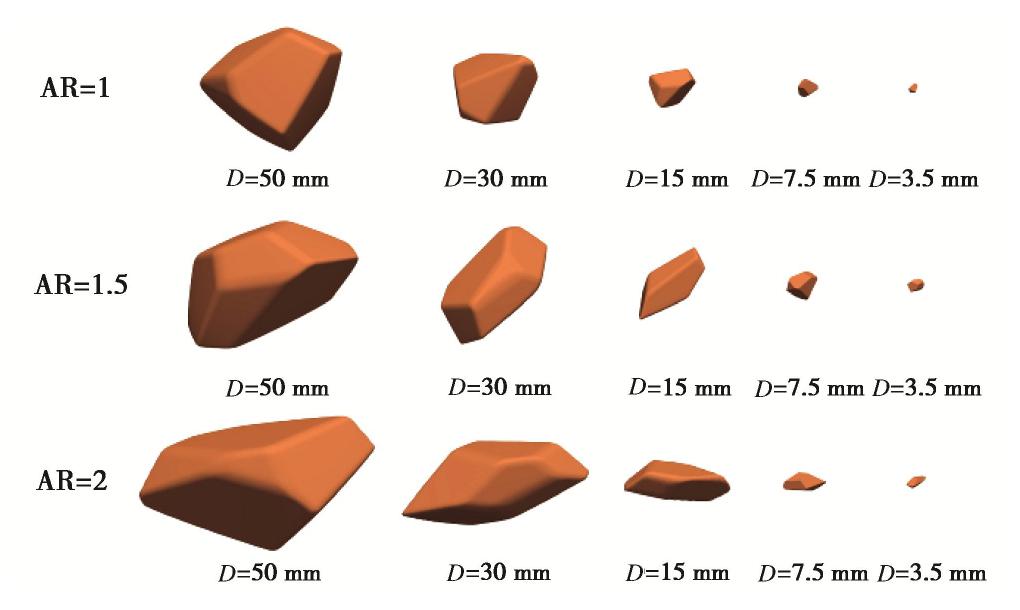
图 1 随机形态多面生成方法[13]
Figure 1. Random shape multi-faceted generation method
表 1 离散元参数表
Table 1 Parameters of discrete elements
类别 密度/(kg·m³) 摩擦角/(°) 法向刚度 Kn /(108 N·m-1)切向刚度 Ks /(108N·m-1)局部阻尼系数 十二面体 2500 30 1 1 0.4 长方体槽 3500 35 1 1 0.4 表 2 摩擦系数表
Table 2 Friction coefficients
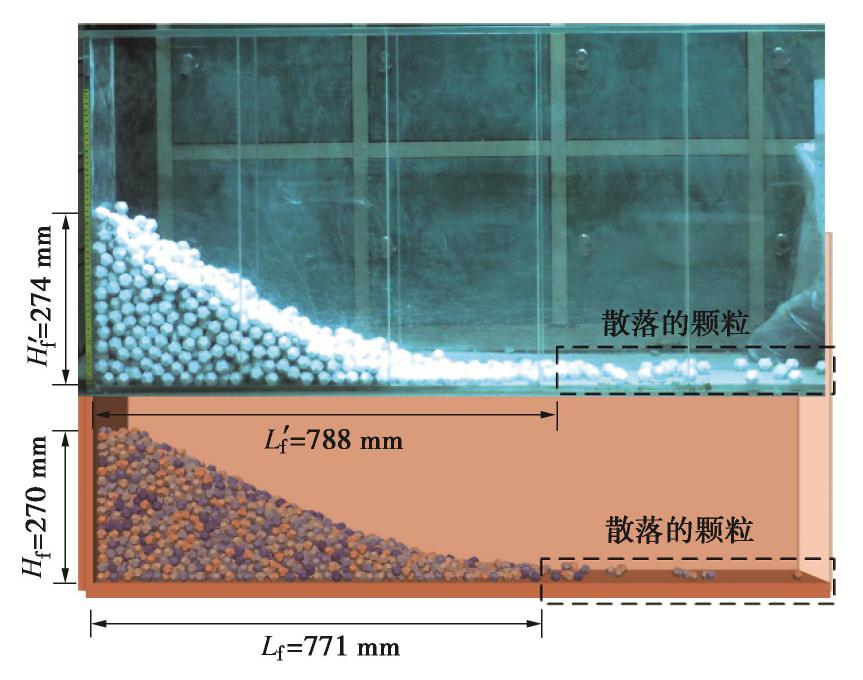
类别 摩擦系数 颗粒-挡板 0.24 颗粒-底板 0.25 表 3 室内试验和数值模拟结果对比
Table 3 Comparison between indoor tests and numerical simulations
校准参数 最大跑出距离 Lf /mm最终堆积高度 Hf /mm相对静止角 α /(°)滑动体积占比w/% 室内试验 788 274 47.62 56.97 数值试验 771 270 47.20 53.11 相对误差/% 2.16 1.46 0.88 6.7 表 4 不同级配颗粒的中值粒径
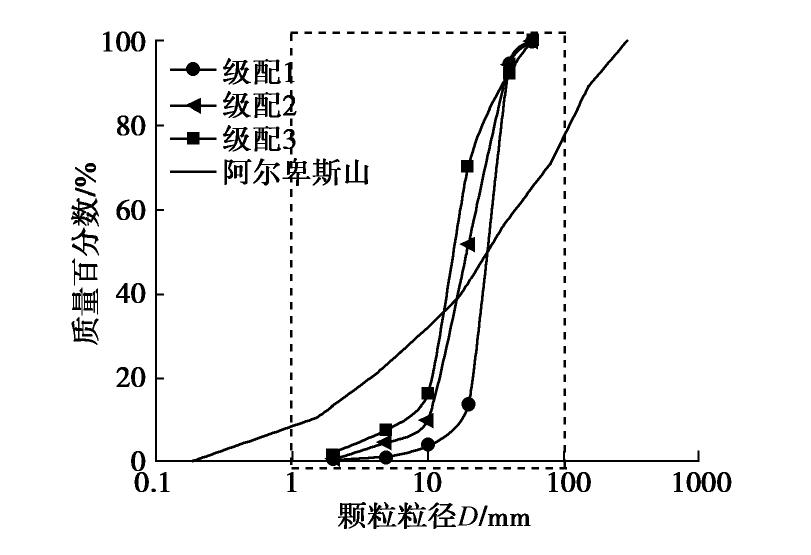
Table 4 Median particle sizes of different graded particles
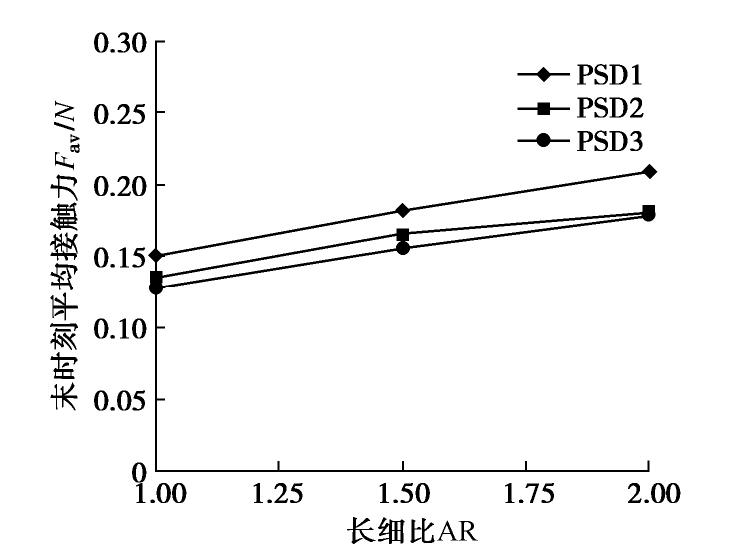
级配 PSD1 PSD2 PSD3 中值粒径d50/mm 27.75 19.52 15.49 -
[1] 刘广煜, 徐文杰, 佟彬, 等. 基于块体离散元的高速远程滑坡灾害动力学研究[J]. 岩石力学与工程学报, 2019, 38(8): 1557-1566. doi: 10.13722/j.cnki.jrme.2019.0158 LIU Guang-yu, XU Wen-jie, TONG Bin, et al. Study on dynamics of high-speed and long Run-out landslide hazards based on block discrete element method[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(8): 1557-1566. (in Chinese) doi: 10.13722/j.cnki.jrme.2019.0158
[2] MARKS B, ROGNON P, EINAV I. Grainsize dynamics of polydisperse granular segregation down inclined planes[J]. Journal of Fluid Mechanics, 2012, 690: 499-511. doi: 10.1017/jfm.2011.454
[3] 张雪, 盛岱超. 一种模拟土体流动的连续体数值方法[J]. 岩土工程学报, 2016, 38(3): 562-569. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201603025.htm ZHANG Xue, SHENG Dai-chao. Continuum approach for modelling soil flow in geotechnical engineering[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(3): 562-569. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201603025.htm
[4] OREFICE L, KHINAST J G. Deformable and breakable DEM particle clusters for modelling compression of plastic and brittle porous materials—Model and structure properties[J]. Powder Technology, 2020, 368: 90-104. doi: 10.1016/j.powtec.2020.04.035
[5] ZENIT R. Computer simulations of the collapse of a granular column[J]. Physics of Fluids, 2005, 17(3): 31703. doi: 10.1063/1.1862240
[6] LUBE G, HUPPERT H E, SPARKS R S J, et al. Collapses of two-dimensional granular columns[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2005, 72(4 Pt 1): 041301.
[7] UTILI S, ZHAO T, HOULSBY G T. 3D DEM investigation of granular column collapse: Evaluation of debris motion and its destructive power[J]. Engineering Geology, 2015, 186: 3-16. doi: 10.1016/j.enggeo.2014.08.018
[8] PHILLIPS J C, HOGG A J, KERSWELL R R, et al. Enhanced mobility of granular mixtures of fine and coarse particles[J]. Earth and Planetary Science Letters, 2006, 246(3/4): 466-480.
[9] 张成功, 尹振宇, 吴则祥, 等. 颗粒形状对粒状材料圆柱塌落影响的三维离散元模拟[J]. 岩土力学, 2019, 40(3): 1197-1203. doi: 10.16285/j.rsm.2017.2065 ZHANG Cheng-gong, YIN Zhen-yu, WU Ze-xiang, et al. Three-dimensional discrete element simulation of influence of particle shape on granular column collapse[J]. Rock and Soil Mechanics, 2019, 40(3): 1197-1203. (in Chinese) doi: 10.16285/j.rsm.2017.2065
[10] ŠMILAUER V. Yade Documentation[M]. 2nd ed. 2015. The Yade Project. doi: 10.5281/zenodo.34073 (http://yade-dem.org/doc/)
[11] CUNDALL P A, STRACK O D L. Discussion: a discrete numerical model for granular assemblies[J]. Géotechnique, 1980, 30(3): 33-336.
[12] LANDAUER J, KUHN M, NASATO D S, et al. Particle shape matters - Using 3D printed particles to investigate fundamental particle and packing properties[J]. Powder Technology, 2020, 361: 711-718. doi: 10.1016/j.powtec.2019.11.051
[13] ELIÁŠ J. Simulation of railway ballast using crushable polyhedral particles[J]. Powder Technology, 2014, 264: 458-465. doi: 10.1016/j.powtec.2014.05.052
[14] BOON C W, HOULSBY G T, UTILI S. A new algorithm for contact detection between convex polygonal and polyhedral particles in the discrete element method[J]. Computers and Geotechnics, 2012, 44: 73-82. doi: 10.1016/j.compgeo.2012.03.012
[15] BOYD S, VANDENBERGHE L. Convex Optimization[M]. Cambridge: Cambridge University Press, 2004.
[16] COETZEE C J. Review: Calibration of the discrete element method[J]. Powder Technology, 2017, 310: 104-142. doi: 10.1016/j.powtec.2017.01.015
[17] ZHAO S W, ZHOU X W, LIU W H. Discrete element simulations of direct shear tests with particle angularity effect[J]. Granular Matter, 2015, 17(6): 793-806. doi: 10.1007/s10035-015-0593-x
[18] MINDLIN R D. Compliance of elastic bodies in contact[J]. Journal of Applied Mechanics, 1949, 16(3): 259-268. doi: 10.1115/1.4009973
[19] LI Y J, XU Y, THORNTON C. A comparison of discrete element simulations and experiments for ‘sandpiles’ composed of spherical particles[J]. Powder Technology, 2005, 160(3): 219-228. doi: 10.1016/j.powtec.2005.09.002
[20] 王玉峰, 程谦恭, 朱圻. 汶川地震触发高速远程滑坡-碎屑流堆积反粒序特征及机制分析[J]. 岩石力学与工程学报, 2012, 31(6): 1089-1106. doi: 10.3969/j.issn.1000-6915.2012.06.002 WANG Yu-feng, CHENG Qian-gong, ZHU Qi. Inverse grading analysis of deposit from rock avalanches triggered by Wenchuan earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(6): 1089-1106. (in Chinese) doi: 10.3969/j.issn.1000-6915.2012.06.002
[21] 边学成, 李伟, 李公羽, 等. 基于颗粒真实几何形状的铁路道砟剪切过程三维离散元分析[J]. 工程力学, 2015, 32(5): . https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201505010.htm BIAN Xue-cheng, LI Wei, LI Gong-yu, et al. Three-dimensional discrete element analysis of railway ballast's shear process based on particles' real geometry[J]. Engineering Mechanics, 2015, 32(5): . (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201505010.htm
[22] 杨舒涵, 周伟, 马刚, 等. 粒间摩擦对岩土颗粒材料三维力学行为的影响机制[J]. 岩土工程学报, 2020, 42(10): 1885-1893. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202010018.htm YANG Shu-han, ZHOU Wei, MA Gang, et al. Mechanism of inter-particle friction effect on 3D mechanical response of granular materials[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(10): 1885-1893. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202010018.htm
[23] ZHAO X L, EVANS T M. Numerical analysis of critical state behaviors of granular soils under different loading conditions[J]. Granular Matter, 2011, 13(6): 751-764. doi: 10.1007/s10035-011-0284-1
[24] 孙其诚, 王光谦. 静态堆积颗粒中的力链分布[J]. 物理学报, 2008, 57(8): 4667-4674. doi: 10.3321/j.issn:1000-3290.2008.08.007 SUN Qi-cheng, WANG Guang-qian. Force distribution in static granular matter in two dimensions[J]. Acta Physica Sinica, 2008, 57(8): 4667-4674. (in Chinese) doi: 10.3321/j.issn:1000-3290.2008.08.007
[25] 戴北冰, 杨峻, 刘锋涛, 等. 散粒土自然堆积的宏细观特征与形成机制[J]. 岩土工程学报, 2019, 41(增刊2): 57-60. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S2016.htm DAI Bei-bing, YANG Jun, LIU Feng-tao, et al. Macro-and micro-properties and formation mechanisms of granular piles[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S2): 57-60. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S2016.htm



 下载:
下载: