颗粒形状和压实度对炉渣颗粒土力学特性的影响

吴杨; 黄锦盛; 崔杰; 吉本正宪

doi:10.11779/CJGE202112008

颗粒形状和压实度对炉渣颗粒土力学特性的影响 English Version

1.
广州大学土木工程学院,广东　广州　510006
2.
山口大学工学部,山口　宇部　7538511

基金项目:

国家自然科学基金项目 51908153

广东省基础与应用基础研究基金项目 2021A1515012096

广州市科技计划项目 201904010278

广州市科技计划项目 202102010380

中国工程院重点咨询项目 2019-XZ-18

详细信息

作者简介:
吴杨(1985— ),男,副教授,博士,主要从事颗粒材料和天然气水合物沉积物力学性质等方面的研究。E-mail：yangwu@gzhu.edu.cn

通讯作者:
崔杰, E-mail：jcui2009@hotmail.com

中图分类号: TU43
计量
- 文章访问数: 246
- HTML全文浏览量: 20
- PDF下载量: 199
出版历程
- 收稿日期: 2021-02-02
- 网络出版日期: 2022-11-30
- 刊出日期: 2021-11-30

Inﬂuences of particle shape and degree of compaction on shear response of clinker ash

1.
School of Civil Engineering, Guangzhou University, Guangzhou 510006, China
2.
Faculty of Engineering, Yamaguchi University, Ube 7538511, Japan

摘要

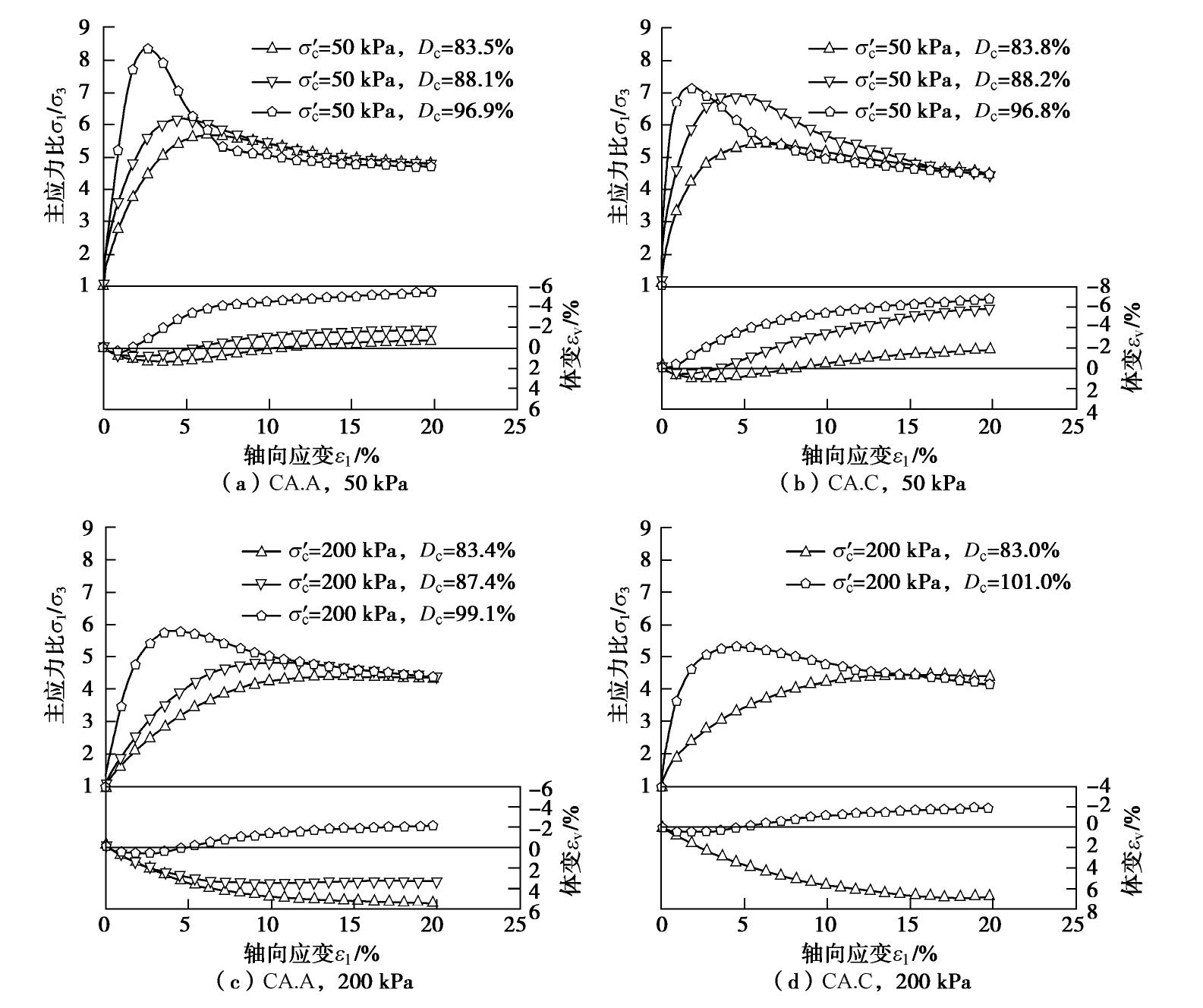
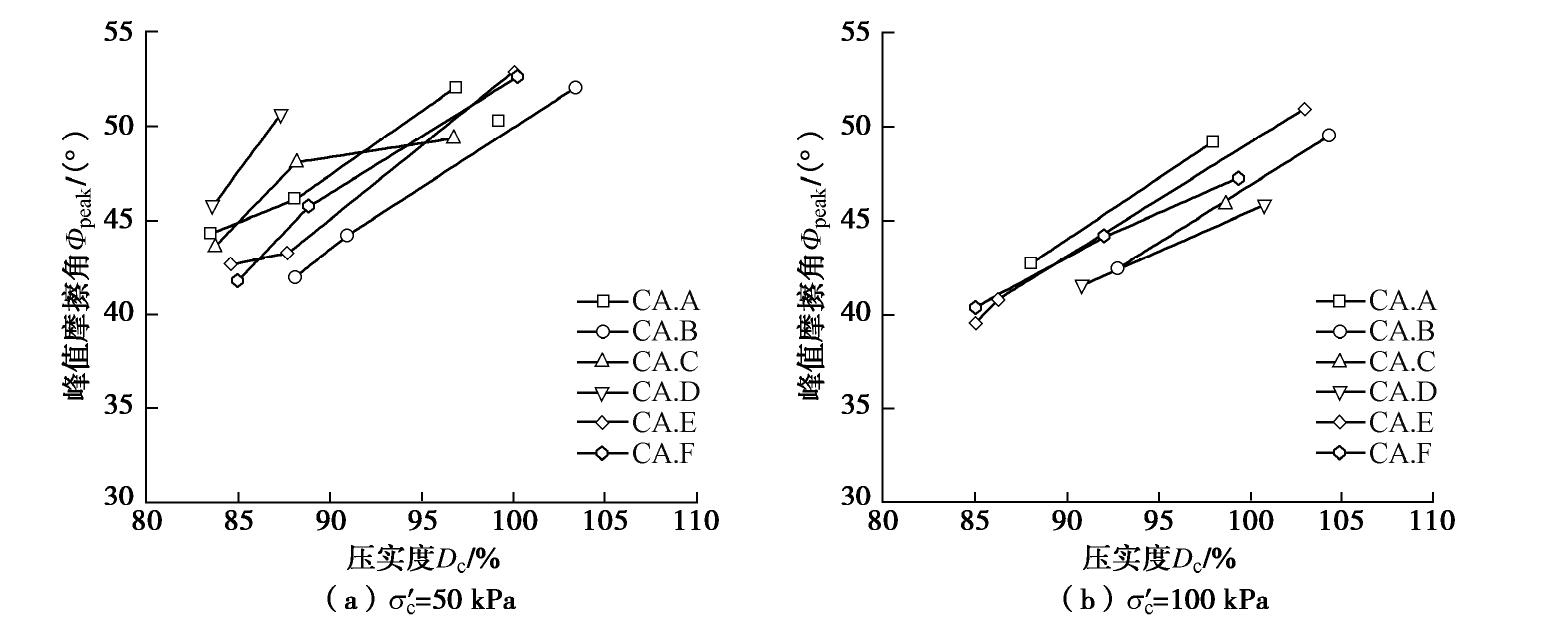
摘要: 炉渣颗粒土是火电厂发电过程中煤炭燃烧产生的一种颗粒废弃物,近年来经常作为边坡和路基回填材料在工程建设中使用。对6种不同产地的炉渣颗粒土进行了单颗粒破碎试验,发现炉渣颗粒土的单颗粒强度显著低于天然砂土,具有较大的破碎性。随后,开展了一系列排水三轴剪切试验,研究了颗粒形状、压实度和围压对其剪切特性的影响。三轴试验结果表明,压实度可以显著提高炉渣颗粒土的初始刚度及峰值抗剪强度。相较于自然砂土,炉渣颗粒土拥有较大的峰值摩擦角,作为回填材料可提供较大的承载力。另外,炉渣颗粒土的峰值摩擦角随着围压的增大而降低。分析结果揭示颗粒形状和单颗粒强度均是影响炉渣颗粒土抗剪强度的重要因素。在不同的围压水平,两者对峰值抗剪强度的影响程度有所不同。另外,通过图像分析法获取了不同种类炉渣颗粒土的多种形状参数,发现炉渣颗粒土的圆度和球度都显著小于大部分自然砂土,表明该类颗粒材料拥有较为复杂的颗粒形状。分析结果还表明炉渣颗粒土的临界状态摩擦角与炉渣颗粒土的各个形状参数都存在一定程度的关联性。采用了一个新的能够考虑多种颗粒形状因素影响的综合指标,建立了其与临界状态强度和临界状态线位置参数的经验关系表达式。
- 颗粒形状 /
- 炉渣颗粒土 /
- 临界状态 /
- 压实度 /
- 摩擦角
Abstract: The clinker ash is a kind of granular waste produced after the combustion of coal. It has been used in slope and foundation engineering as backfill materials. The single-particle crushing tests on the clinker ash from six different origins are carried out. The results indicate that the clinker ash particles own much lower single-particle strength than the natural sands and exhibit larger crushability. A series of drained triaxial shear tests are performed on the clinker ash to examine the effects of particle shape, degree of compaction and effective confining pressure on its shear characteristics. An increase in the degree of compaction strengthens the initial stiffness and the peak shear strength of the clinker ash. Compared to the natural sands, the clinker ash possesses larger peak friction angle and provides higher bearing capacity as foundation materials. As the effective confining pressure increases, the peak friction angle of the clinker ash gradually decreases. The results suggest that both the particle shape and the single-particle strength are important factors affecting the shear strength of the clinker ash. In addition, several particle shape parameters of the clinker ash are decided using the digital image analysis method. The clinker ash has smaller roundness and sphericity indexes due to its complex particle shape. The analysis results show that the critical state friction angle is well correlated with the particle shape parameters. A general and new particle shape index is employed to correlate with the relevant parameters associated with the critical state and its position.
- particle shape /
- clinker ash /
- critical state /
- degree of compaction /
- friction angle

HTML全文

0. 引言

岩土工程、水利工程、道路桥梁工程等的附存环境或对象相当大一部分是由离散形式的颗粒材料组成,如砂土、碎石、粗粒土等,可统称为岩土颗粒材料。岩土颗粒材料的力学特性直接影响地（路）基、堤防、堆石坝等工程的设计、施工和运行。颗粒材料看似简单,但其物理力学性质复杂,存在压硬性、剪胀性、应力路径相关性等复杂力学特性^[1-2]。这些复杂的力学行为与其离散性、多尺度和能量耗散机制有关^[1]。对颗粒材料进行宏观唯象建模不足以反映其所有力学特性^[3-4],颗粒材料的微观动力学行为、接触网络、介观结构、细观组构等为揭示颗粒材料复杂的宏细观力学特性提供了新的途径^[5-7]。

细观尺度下颗粒材料的研究手段主要包括物理实验和数值模拟两大类。物理实验方面,常用的观测手段有光弹实验、扫描电镜技术、CT（computed tomography）扫描技术、DIC（digital image correlation）成像技术等^[4]。数值分析方法有离散单元法（discrete element method,DEM）^[5-6]、连续-离散耦合分析方法（combined finite and discrete method,FDEM）^[8-9]等。其中,颗粒离散单元法（DEM）发展迅速,计算简便,已广泛应用于岩土类颗粒材料的研究中,经过不断改进能够对颗粒形状^[10]、颗粒破碎^[11]、以及颗粒材料的临界状态^[12-13]、剪胀^[13]、细观接触^[14]和组构^{[6, 14]}等特性进行表征。

岩土颗粒材料是多体相互作用的耗散体系,颗粒间摩擦是耗散外力功的主要途径之一,是颗粒材料宏观剪切强度的主要来源之一,也是其变形和破坏特性的重要内部控制因素^[4]。颗粒间摩擦特性会影响颗粒间接触力的大小分布和颗粒重排列,进而引起颗粒体系宏观力学特性的变化。Dai等^[15]采用玻璃珠进行了一系列直剪试验,发现颗粒间摩擦对颗粒材料剪切行为的影响显著。Sandeep等^[16]指出颗粒间的摩擦系数与杨氏模量和表面粗糙度成反比。Senetakis等^[17]采用破碎的石灰石颗粒进行微观力学滑动实验并对颗粒间的摩擦系数进行量化。

细观数值模拟方面,Rothenburg等^[12]采用离散单元法研究了不同摩擦系数的试样孔隙比与配位数之间的关系；Antony等^[5]分析了摩擦特性对颗粒材料宏观抗剪强度的影响；Huang等^[18]评估了颗粒材料的临界状态对颗粒间摩擦的敏感性；Barreto等^[19]认为摩擦系数影响了强接触力链的稳定性。尽管关于颗粒间摩擦系数对颗粒材料宏细观力学特性的影响研究较多,但摩擦特性对颗粒材料在三维复杂加载路径下力学行为的影响,以及不同颗粒间摩擦系数下各类细观结构对宏观抗剪强度和体积变形的作用机制,还有待进一步的研究。

颗粒间接触形成的接触力网络是一个高度非均质、强非线性的的复杂网络。颗粒体系内大部分的力是通过相对稀疏的链状网络（称之为“力链”）传递^[20]。Radjai等^[21]、Thornton等^[22]将颗粒体系的接触网络划分为两个互补的子接触网络：强接触网络和弱接触网络。大于系统平均接触力的接触形成的强接触网络是传递力的主要通道；弱接触网络中的接触力小于系统平均接触力,为强接触网络的稳定提供支撑^[22]。分别对强弱接触网络的配位数、组构等细观参量进行分析,是研究颗粒材料强度和变形的有效途径^{[5, 23-24]}。

本文将基于岩土颗粒材料真三轴离散元数值试验,分析细观滑动摩擦与颗粒体系强度、变形之间的关系,研究不同摩擦系数下强、弱接触网络的配位数分布、接触力、组构张量及各向异性的特征,探讨强、弱接触网络对颗粒材料宏观应力-应变关系的贡献,揭示细观尺度摩擦特性对宏观力学行为的作用机制。

1. DEM数值试验

1.1 数值试验及参数

本文利用开源软件LIGGGHTS进行离散元模拟^[25]。进行真三轴加载路径的DEM模拟之前,需要制备各向同性且具有一定围压的立方体数值试样。制样时,在400 mm×400 mm×400 mm的立方体空间中随机生成粒径服从Gaussian分布的圆球颗粒,共计31253个。为了避免制样产生各向异性,在试样的各个方向采用位移控制等速地压缩试样直至目标大小。随后,施加三向等压应力进行各向同性固结,直至达到预定的围压值0.5 MPa,得到试样的初始孔隙比为0.582。采用Hertz-Mindlin非线性接触模型^[26]描述颗粒间的接触力,颗粒间滑移服从库仑摩擦定律,即颗粒间发生滑动的条件为｜F_t｜≥μ｜F_n｜,μ为颗粒间的滑动摩擦系数。加载过程中的μ值分别取0.05,0.1,0.2,0.3,0.4,0.5。其它DEM模拟参数如表1所示。

表 1 数值模拟细观参数

Table 1. Microscopic parameters of numerical simulation

参数	值
密度ρ/(kg·m^-3)	2600
颗粒粒径d/mm	2.25~8.25
弹性模量E/GPa	65.0
泊松比 $ν$	0.12
恢复系数e	0.95
滑动摩擦系数μ	0.05,0.1,0.2,0.3,0.4,0.5

下载: 导出CSV

| 显示表格

1.2 真三轴加载路径

采用等p（围压）等b（中主应力系数）加载路径对各向同性试样进行加载。加载时,为了消除边界效应,避免应变局部化,采用周期性边界^[27]。加载过程中,轴向加载速度为-0.01 mm/s。采用周期性边界的伺服机制,使试样的应力状态达到预定的值以满足真三轴应力路径^{[13, 27]},试样中主应力 $σ_{2}$ 和小主应力 $σ_{3}$ 的控制条件^[13]分别为

$σ_{2} = b σ_{1} + (1 - b) \frac{3 p - σ_{1} (1 + b)}{(2 - b)}$ ,

(1)

$σ_{3} = \frac{3 p - σ_{1} (1 + b)}{(2 - b)}$ 。

(2)

颗粒材料的广义剪应力q,平均静水压力p,体积应变 $ε_{v}$ ,广义剪应变 $ε_{d}$ 均可由应力应变张量主值导出：

$p = \frac{σ_{1} + σ_{2} + σ_{3}}{3}$ ,

(3)

$q = \frac{1}{\sqrt{2}} \sqrt{{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}}$ ,

(4)

$ε_{v} = ε_{1} + ε_{2} + ε_{3}$ ,

(5)

$ε_{d} = \frac{\sqrt{2}}{3} \sqrt{[{(ε_{1} - ε_{2})}^{2} +(ε_{2} - ε_{3})^{2} + {(ε_{3} - ε_{1})}^{2}]}$ 。

(6)

2. 细观摩擦与宏观强度

2.1 加载过程中的应力应变

不同的摩擦系数下,剪应力q,体积应变 $ε_{v}$ 随剪应变 $ε_{d}$ 在三轴压缩路径下（b=0）的演化曲线如图1所示。图中体积应变以剪缩为正,剪胀为负。随着颗粒间摩擦系数μ的增大,峰值剪应力逐渐增大,且峰值后的应变软化程度愈加明显。体积响应表现为：随着μ值的增加,试样更快进入剪胀状态,且试样体积膨胀程度越明显。

图 1 应力应变曲线（b=0.0）

Figure 1. Curves of stress-strain relationship（b=0.0）

下载: 全尺寸图片幻灯片

将不同摩擦系数下等p等b真三轴数值试验得到的峰值应力状态点绘制在π平面,如图2所示,为大小不同的三角锥形。π平面内的应力演化反映出不同b值,μ值条件下,试样剪应力峰值的大小,可以看出,试样的剪应力峰值随着b值的增大而减小,随着μ值的增大而不断增大,且μ值较大时,试样对滑动摩擦系数的敏感度减弱,体现在剪应力的增加幅度逐渐减小。

图 2 不同摩擦系数下剪应力峰值状态

Figure 2. Peak states of deviatoric stress of samples under different friction coefficients

下载: 全尺寸图片幻灯片

2.2 三维强度准则

对于无黏结的颗粒材料,其抗剪强度 $τ_{f}$ = $σ_{n}$ tan( $φ_{mob}$ ),其中 $σ_{n}$ 是破坏面上的垂直压力, $φ_{mob}$ =sin^-1 $(σ_{1} - σ_{3})$ / $(σ_{1} + σ_{3})$ 是宏观内摩擦角,是颗粒材料的抗剪强度指标,反映了颗粒材料的宏观摩擦特性。Skinner等^[28]指出峰值状态的宏观内摩擦角 $φ_{max}$ 随着颗粒间摩擦系数μ的增大而增大。图3总结了多个学者得出的 $φ_{max}$ 与粒间摩擦系数μ的关系^{[19, 28-32]}。结合本文所得不同b值下的峰值内摩擦角,可以发现随着摩擦系数μ的增大,峰值内摩擦角 $φ_{max}$ 的增大变化幅度反而减小,与宏观抗剪强度的变化吻合（如图2所示）。当b=0.5时,峰值内摩擦角 $φ_{max}$ 较大,且 $φ_{max}$ 在三轴拉伸路径（b=1.0）下的值大于^{[23, 32]}三轴压缩路径（b=0.0）,与已有的DEM和物理试验研究结果基本一致。

图 3 峰值内摩擦角φ_max与滑动摩擦系数μ的关系

Figure 3. Relationship between peak internal friction angle φ_max and inter-particle friction coefficient μ

下载: 全尺寸图片幻灯片

岩土材料的强度理论中,最常采用的是Mohr-Coulomb^[33]和Drucker-Prager^[34]强度准则,但Mohr-Coulomb准则没有考虑中主应力对强度的影响,Drucker-Prager准则不能反映三轴拉伸和压缩应力状态下抗剪强度的不同。于是,国内外学者^[35-38]基于岩土材料的真三轴试验结果提出了更多的三维强度准则,其中常见的有Lade-Duncan准则^[35]和Mastsuoka- Nakai准则^[36]。为了探讨不同摩擦系数下各个强度准则的预测能力,以便于选取一个预测精准且形式简单的强度准则,定义以下指标反映强度准则的预测能力：

$error = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(\frac{σ_{predicated}^{i} - σ_{measured}^{i}}{σ_{measured}^{i}})}^{2}}$ ,

(7)

式中, $σ_{predicated}^{i}$ 为第i个中主应力系数时的预测值, $σ_{measured}^{i}$ 为相应数值试验得到的应力破坏值。

将不同摩擦系数下各强度准则的预测误差列于表2,并绘制摩擦系数为0.05,0.2和0.5时各强度准则以及数值模拟所得的破坏应力在π平面的破坏迹线^[37-38],如图4所示。图中TC和TE分别表示三轴压缩（triaxial compression）和三轴拉伸（triaxial extension）应力路径。Mohr-Coulomb准则的破坏迹线为不等边三角形,比较靠近静水压力轴,是所有强度准则中最保守的。Drucker-Prager准则在π平面的破坏迹线是一个圆,由于其过高的估计了中主应力对强度的贡献,导致其预测的强度与数值模拟结果相差较大,但随着摩擦系数的减小,其预测误差逐渐降低。Mastsuoka-Nakai准则预测的破坏点在b=0和b=1时与Mohr-Coulomb准则重合,在0<b<1区间内,Mastsuoka-Nakai准则破坏迹线随着摩擦系数的减小逐渐外凸。Lade-Duncan准则在μ=0.5时与数值试验结果最为接近,误差值只有0.95%。当μ≤0.2时,摩擦特性对不同b值下的强度影响较小,各强度准则在π平面的破坏迹线逐渐向Drucker-Prager准则靠拢,此时各强度准则的预测能力相差不大。当0.2<μ≤0.4时,Mastsuoka-Nakai准则预测能力较好。当0.4<μ≤0.5时,Lade-Duncan准则的预测精度较高。由于岩土颗粒材料属于摩擦性颗粒材料,其细观摩擦系数大约在0.3～0.5之间^{[18, 27]},上述关于强度准则的对比,进一步说明了Mastsuoka- Nakai准则和Lade-Duncan准则在一般岩土材料中的适用性。

表 2 三维强度准则预测误差表

Table 2. Prediction errors of three-dimensional strength criteria

摩擦系数	误差/%
摩擦系数	Drucker-Prager	Mohr-Coulomb	Lade-Duncan	Mastsuoka-Nakai
0.05	6.32	5.18	3.33	2.57
0.10	10.57	6.64	7.86	6.81
0.20	13.60	7.00	8.57	5.46
0.30	15.16	8.05	5.94	1.88
0.40	15.75	10.03	3.91	1.23
0.50	16.33	12.05	0.95	5.07

下载: 导出CSV

| 显示表格

图 4 破坏面在π平面上的迹线

Figure 4. Trace of failure surface on π plane

下载: 全尺寸图片幻灯片

3. 摩擦特性与细观结构演化

3.1 强弱接触网络内的配位数分布

按照Radjai等^[21]提出的方法,用平均接触力将颗粒体系的总接触网络划分为强接触网络和弱接触网络。本文以Г_all,Г_strong,Г_weak分别表示总、强、弱接触网络。图5表明不同加载路径下峰值状态强、弱接触网络中平均法向和切向接触力比值与摩擦系数μ的关系基本不受b值的影响。由接触力比值可知,强接触网络对总接触网络平均接触力的贡献较大。随着μ值的增加,强弱接触网络平均法向接触力的比值随之增大,而平均切向接触力的比值随之减小,这是因为μ值的增加使得强接触网络中平均法向接触力明显增大,而弱接触网络中平均法向接触力增加较小。

图 5 强弱接触网络之间平均接触力的比值

Figure 5. Stress ratios of average contact stress between strong and weak contact networks

下载: 全尺寸图片幻灯片

峰值状态下,强、弱和总接触网络的配位数分布情况如图6所示。图中的配位数是指单个颗粒的接触数目,与之对应的颗粒数目是指接触网络中具有相同配位数的颗粒个数。Bratberg等^[41]研究了二维状态下颗粒材料内部的接触连通性,结果表明配位数越少的颗粒所受约束少,各向异性程度高；相应配位数越多的颗粒越稳定,各向异性程度低。在总接触网络中,随着μ值的增大,配位数众数由5减小为4,且配位数大于5或小于4的分布曲线均发生左移,试样整体的平均配位数减小,各向异性程度增加。弱接触网络中颗粒配位数分布与总接触网络的分布规律相似,但配位数众数由4减小为3。

图 6 峰值状态配位数的分布

Figure 6. Distribution of coordination numbers at peak stress

下载: 全尺寸图片幻灯片

值得注意的是,强接触网络的配位数分布与总网络差异较大,μ值的改变对强接触网络配位数为1,2的颗粒数目影响甚微,这些颗粒是构成“力链”末端及“力链”主体的颗粒群^{[23, 41]},此现象间接印证了强接触网络中“力链”的存在,而且表明在峰值状态下,试样内形成“力链”的颗粒数目不随μ值的改变而波动,或许意味着此时“力链”结构已经达到最优的颗粒分配状态。同时,配位数大于3的颗粒数目减少,说明摩擦系数越大,试样内传递力的强接触网络越稀疏,接触各向异性越明显。因而试样宏观抗剪强度增加的原因可以认为是强接触网络法向接触力的明显增大。

对比不同加载路径下强、弱和总接触网络配位数的分布曲线,发现其基本表现出与加载路径无关的特性,与刘嘉英等^[6]的研究结果一致。在既定的加载路径下,总接触网络配位数的分布中弱接触网络占主导位置,弱接触网络中配位数高的颗粒数目较多,结合配位数与颗粒材料体积变形的关系,可以推断弱接触网络对试样整体的体积变形贡献较大。

3.2 组构张量及其偏值在π平面的分布

岩土颗粒材料的宏观力学特性与加载过程中细观组构的演化规律密切相关^[42]。文章采用Satake^[43]和Oda^[44]提出的组构张量表达方式：

$Φ_{i j} = \frac{1}{N_{c}} \sum_{c = 1}^{N_{c}} n_{i} n_{j}$ ,

(8)

式中,n是沿着颗粒间接触面法线方向的单位矢量,N_c为颗粒体系中的接触总数。组构张量偏张量 ${Φ^{'}}_{i j}$ 的第二不变量可以表征颗粒体系接触方向的各向异性,用等效各向异性系数A计算如下：

$A = \sqrt{\frac{3}{2} {Φ^{'}}_{i j}^{} {Φ^{'}}_{i j}^{}} = \sqrt{3 J_{2}^{Φ}}$ 。

(9)

强接触网络的组构张量定义为

$Φ_{i j}^{s} = \frac{1}{N_{s}} \sum_{s = 1}^{N_{s}} n_{i}^{s} n_{j}^{s}$ ,

(10)

式中, $n_{i}^{s}$ 是单位法向量在第s个强接触处的第i个分量。N_s是颗粒体系中的强接触总数。强接触网络的等效各向异性系数A^s如下表示：

$A^{s} = \sqrt{\frac{3}{2} Φ_{i j}^{s^{'}} Φ_{i j}^{s^{'}}} = \sqrt{3 J_{2}^{Φ^{s}}}$ 。

(11)

类比于广义剪应力q和平均应力p的定义, $Φ_{d}$ 和 $Φ_{m}$ 可以表示为

$Φ_{d} = \frac{1}{\sqrt{2}} \sqrt{{(Φ_{11} - Φ_{22})}^{2} + {(Φ_{22} - Φ_{33})}^{2} + {(Φ_{33} - Φ_{11})}^{2}}$ ,

(12)

$Φ_{m} = (Φ_{11} + Φ_{22} + Φ_{33}) / 3$ 。

(13)

而强接触网络中 $Φ_{d}^{s}$ 和 $Φ_{m}^{s}$ 分别定义为

$Φ_{d}^{s} = \frac{1}{\sqrt{2}} \sqrt{{(Φ_{11}^{s} - Φ_{22}^{s})}^{2} + {(Φ_{22}^{s} - Φ_{33}^{s})}^{2} + {(Φ_{33}^{s} - Φ_{11}^{s})}^{2}}$ ,

(14)

$Φ_{m}^{s} = (Φ_{11}^{s} + Φ_{22}^{s} + Φ_{33}^{s}) / 3$ 。

(15)

图7是峰值状态下总接触网络和强接触网络组构张量各向异性不变量A和A^s在π平面的分布。总接触网络的组构张量不变量A在π 平面内呈现出倒三角锥形,与应力张量分布（如图2）的形状相反。而强接触网络组构张量不变量A^s在π平面内的分布表现出与宏观应力响应较好的一致性,说明强接触网络对宏观应力的贡献更为显著。在剪切变形中,不同b值和μ值的峰值应力的变化主要是由强接触网络的组构各向异性主导。Thornton等^{[29, 45]}指出总接触网络的组构各向异性程度小于强接触网络（对比图7（a）,7（b））。这是由颗粒体系的传力方式造成的,强接触承担颗粒体系大部分的力,会选择有利的接触方向以平衡外荷载的施加,使得强接触的传力网络呈现出强烈的方向各向异性。

图 7 π平面峰值状态组构张量偏张量不变量

Figure 7. Anisotropy invariants of fabric tensors on

$π$ plane for peak stress states

下载: 全尺寸图片幻灯片

应力比q/p与强接触网络组构比 $Φ_{d}^{s}$ / $Φ_{m}^{s}$ 的关系见图8。不同μ值下,q/p与 $Φ_{d}^{s}$ / $Φ_{m}^{s}$ 的比值始终约为1。Sazzad等^[24]指出不同加载路径下,应力比与强接触网络的组构比亦约为1。说明当只考虑强接触网络时,宏观应力比q/p与细观组构比 $Φ_{d}^{s}$ / $Φ_{m}^{s}$ 之间的关系始终呈线性唯一,该特性与粒间摩擦和加载路径均无关。同时也证明了颗粒体系的宏观力学特性与强接触网络组构各向异性的密切性。结合图2和图7可知,颗粒体系宏观抗剪强度随粒间摩擦的增大可能是由细观强接触网络组构各向异性的加强引起的。

图 8 不同μ值下q/p和

$Φ_{d}^{s}$ /

$Φ_{m}^{s}$ 的关系（b=0.0）

Figure 8. Relationship between q/p and

$Φ_{d}^{s}$ /

$Φ_{m}^{s}$ for different values of μ（b=0.0）

下载: 全尺寸图片幻灯片

3.3 强弱接触网络各向异性的特征及其演化

Yimsiri等^[46]在定量分析颗粒体系的各向异性时,定义了两类不同机理的各向异性：几何各向异性和力学各向异性。颗粒材料的几何各向异性可以用接触法向向量和枝向量的分布表示,此外组构张量的表示形式还可以如下所示^[43-44]：

$Φ_{i j} = \int_{Θ} E (Θ) n_{i} n_{j} d Θ$ ,

(16)

式中,Θ表示域内n的方向分布,E(Θ)是概率分布函数。一般采用E(Θ)的傅立叶展开式描述接触法向：

$E (Θ) = \frac{1}{4 π} (1 + a_{i j}^{c} n_{i} n_{j})$ ,

(17)

其中二阶各向异性张量 $a_{i j}^{c}$ 是一个偏张量,表征接触方向的各向异性程度。表达方式为

$a_{i j}^{c} = 15 / 2 {Φ^{'}}_{i j}$ ,

(18)

式中, ${Φ^{'}}_{i j}$ 是 $Φ_{i j}$ 的偏张量。

由于本文数值模拟采用的是理想圆球颗粒,枝向量几乎与接触法向同向,且颗粒尺寸分布相对较窄,故枝向量各向异性对总强度的贡献很小。力学各向异性包括法向接触力引起的法向接触力各向异性aⁿ和切向接触力引起的切向接触力各向异性a^t,其具体定义详见文献[47]。

试样初始状态是各向同性的,外荷载的施加使得试样内部结构急剧变化,因而,初期试样各向异性系数均随剪应变的增加而迅速增大,且摩擦系数μ越大,强接触网络各向异性系数增加速率越快,这是由于颗粒间摩擦越大,越能积极有效地调动强接触网络的颗粒参与外力的抵抗。从强、弱接触网络中a^c,aⁿ的演化曲线（如图9）可知,强接触网络中a^c,aⁿ值均大于弱接触网络,且均随着摩擦系数的增加而增大,说明强接触力沿加载方向的支撑作用明显,强接触网络的各向异性对总接触网络的各向异性贡献较大。

图 9 强弱接触网络中各向异性系数的演化

Figure 9. Evolution of anisotropic coefficient in strong-weak contact system

下载: 全尺寸图片幻灯片

4. 结论

（1）在颗粒体系真三轴加载条件下,随着摩擦系数的增大,宏观颗粒体系的剪应力峰值增大,进入剪胀状态更迅速,且后期剪胀程度更明显。当摩擦系数μ≤0.2时,Mohr-Coulomb、Drucker-Prager、Lade- Duncan和Matsuoka-Nakai准则的预测能力相差不大；当摩擦系数为0.2<μ≤0.5时,Lade-Duncan和Matsuoka-Nakai准则能较好地拟合不同加载路径下的数据点,更适用于一般岩土颗粒材料。

（2）粒间滑动摩擦对颗粒体系中强、弱接触网络的配位数分布影响差异明显。在三维加载条件下,各接触网络的配位数分布表现出与加载路径无关的特性。在剪应力峰值状态,弱接触网络的配位数分布受μ值的影响较大,但强接触网络中参与形成“力链”的颗粒数目基本保持不变。此外,强接触网络的组构张量偏不变量在π平面内的分布表现出与宏观应力响应较好的一致性,且颗粒体系宏观应力比q/p与细观强接触网络组构比 $Φ_{d}^{s}$ / $Φ_{m}^{s}$ 的关系呈线性唯一,与粒间摩擦和加载路径均无关,说明颗粒体系中的强接触网络在应力传递过程中发挥了重要且恒定的作用。

（3）滑动摩擦系数对强、弱接触网络的细观接触力及其组构各向异性影响显著。颗粒间摩擦系数的增加显著提高了强接触网络的法向接触力以及各接触网络的各向异性系数,其中强接触网络的法向接触力各向异性对整体力学各向异性贡献显著。

图 1 炉渣颗粒土粒度分布曲线

Figure 1. Grain-size distribution curves of clinker ash

下载: 全尺寸图片幻灯片

图 2 电子显微镜下炉渣颗粒土典型颗粒图像

Figure 2. Electron scanning images of typical clinker ash grains

下载: 全尺寸图片幻灯片

图 3 炉渣颗粒土和天然砂土的平均单颗粒破碎强度

Figure 3. Mean crushing strengths of clinker ash and natural sands

下载: 全尺寸图片幻灯片

图 4 炉渣颗粒土干密度随含水率的变化规律

Figure 4. Variation in dry density of clinker ash with water content

下载: 全尺寸图片幻灯片

图 5 炉渣颗粒土在不同试验条件下的应力-应变关系曲线

Figure 5. Stress-strain curves for clinker ash under different test conditions

下载: 全尺寸图片幻灯片

图 6 不同压实度条件下炉渣颗粒土的应力-应变关系

Figure 6. Stress-strain curves for clinker ash under different degrees of compaction

下载: 全尺寸图片幻灯片

图 7 不同压实度条件下炉渣颗粒土的峰值摩擦角

Figure 7. Variation in peak friction angle of clinker ash with varying degrees of compaction

下载: 全尺寸图片幻灯片

图 8 颗粒形状参数对临界状态摩擦角的影响

Figure 8. Effects of particle shape parameters on critical state friction angle of different granular materials

下载: 全尺寸图片幻灯片

图 9 炉渣颗粒土平均规则性ρ与临界状态角的关系

Figure 9. Relationship between mean regularity of particles and critical state friction angle for clinker ash

下载: 全尺寸图片幻灯片

图 10 炉渣颗粒土的临界状态线

Figure 10. Critical state lines of clinker ash

下载: 全尺寸图片幻灯片

图 11 炉渣颗粒土和天然砂土的平均规则性ρ与临界状态线位置参数的关系

Figure 11. Relationship between mean regularity of particles and critical state line position parameters of clinker ash and other natural sands

下载: 全尺寸图片幻灯片

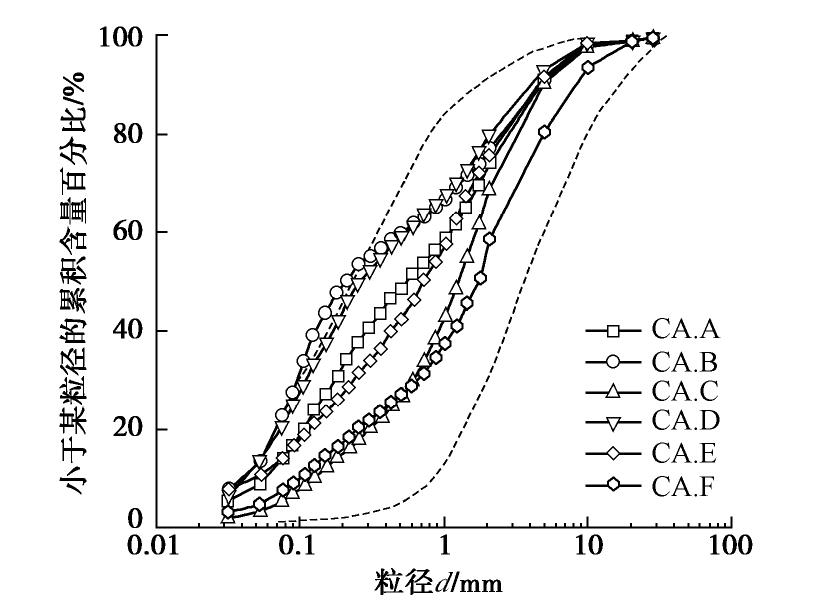
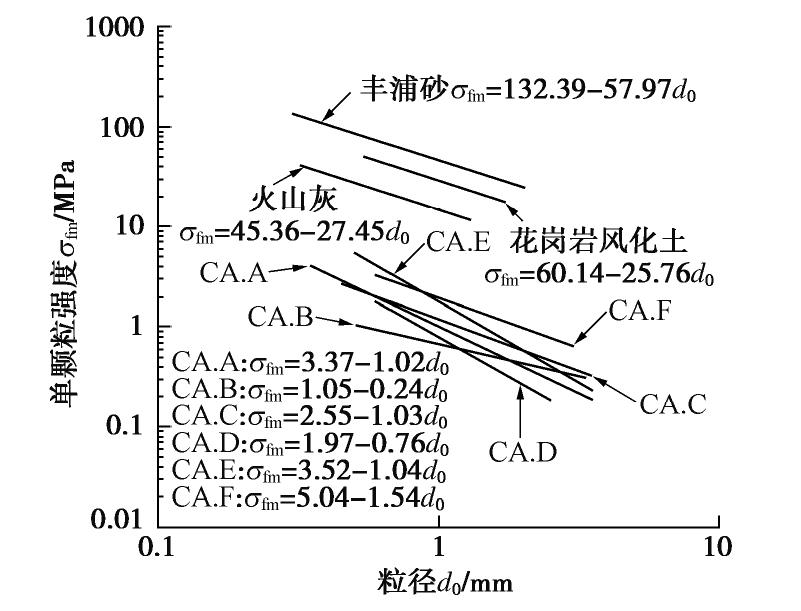
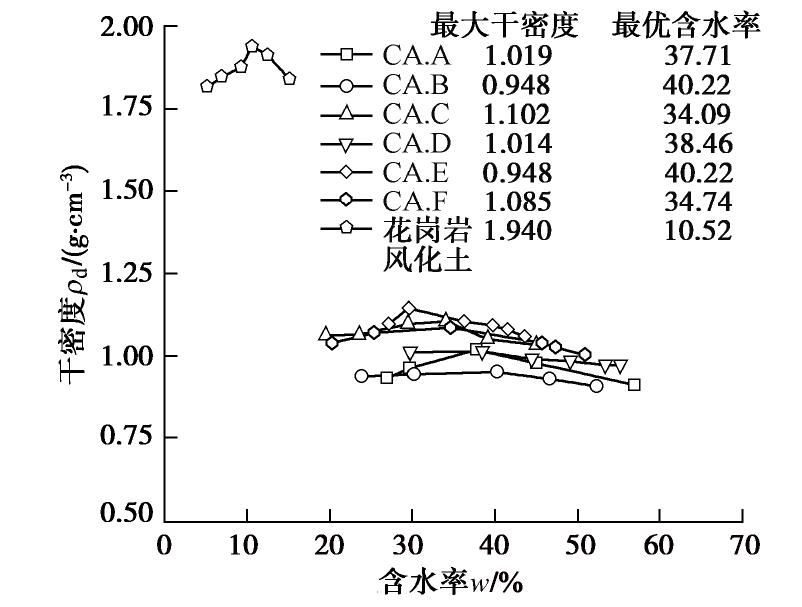
表 1 炉渣颗粒土物理性质

Table 1 Physical properties of clinker ash

试样	颗粒相对质量密度G_s	最大孔隙比 $e_{\max}$	最小孔隙比 $e_{\min}$	不均匀系数 $C_{u}$	平均粒径 $d_{50}$ /mm	平均单颗粒强度 $σ_{fm}$ /MPa
CA.A	2.072	1.748	0.949	20.3	0.570	4.27
CA.B	2.151	1.646	1.010	12.5	0.210	1.99
CA.C	2.173	1.618	0.883	13.8	1.300	2.56
CA.D	2.132	1.488	0.887	21.2	0.220	1.04
CA.E	2.151	1.422	0.752	26.7	0.710	4.75
CA.F	2.110	1.425	0.769	21.0	1.750	3.12

下载: 导出CSV

表 2 炉渣颗粒土的颗粒形状参数

Table 2 Particle shape parameters of clinker ash

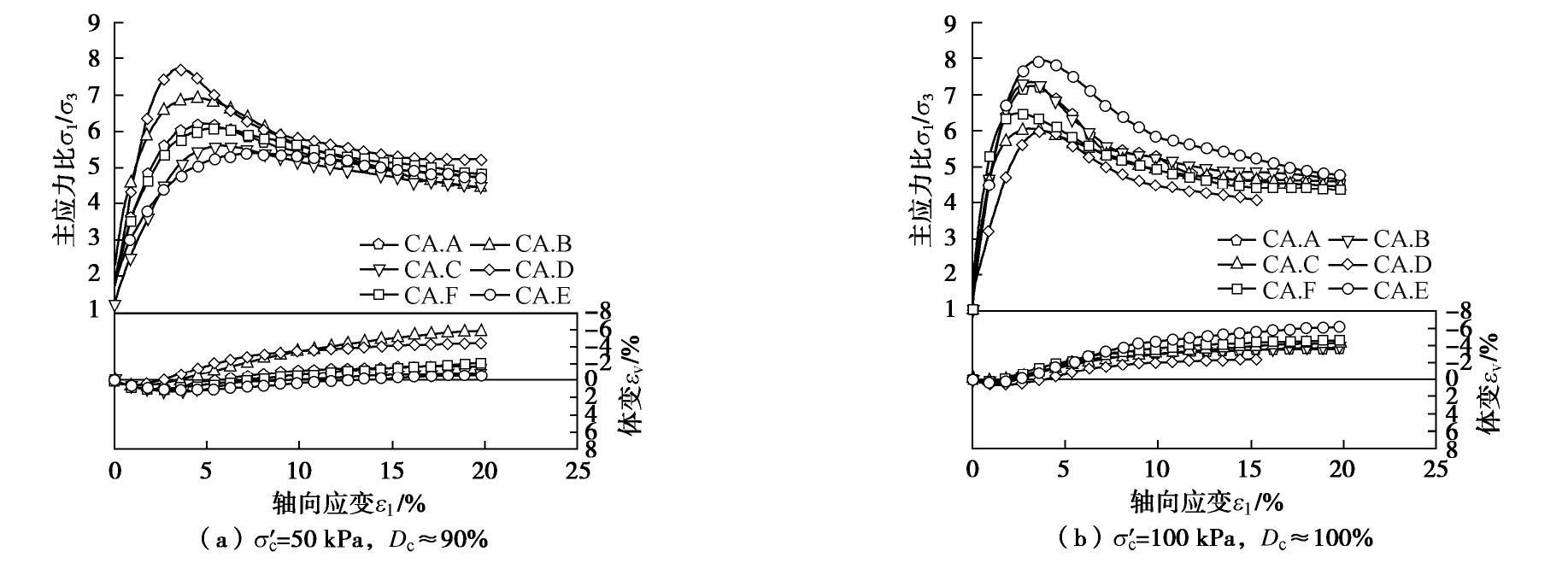
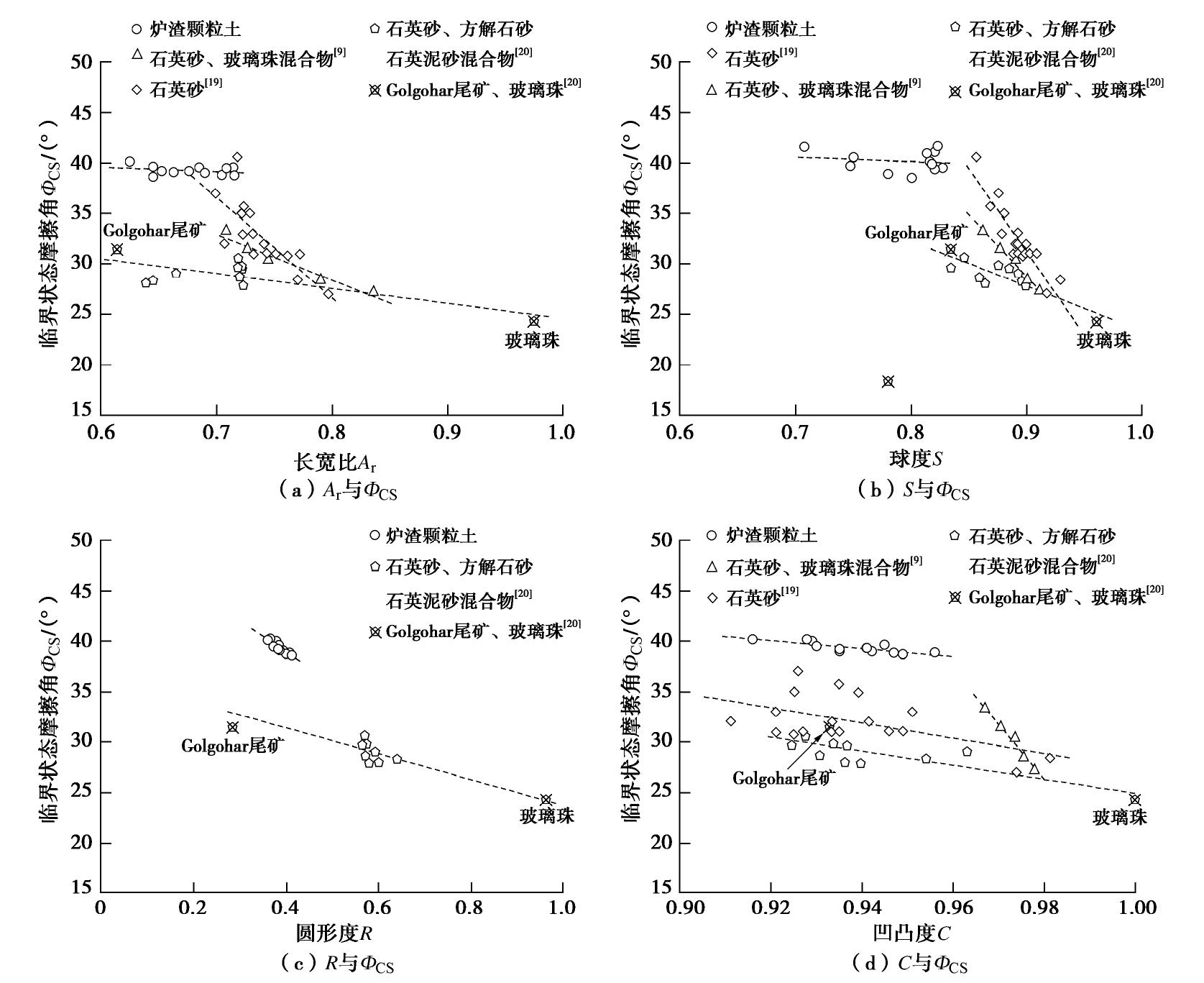
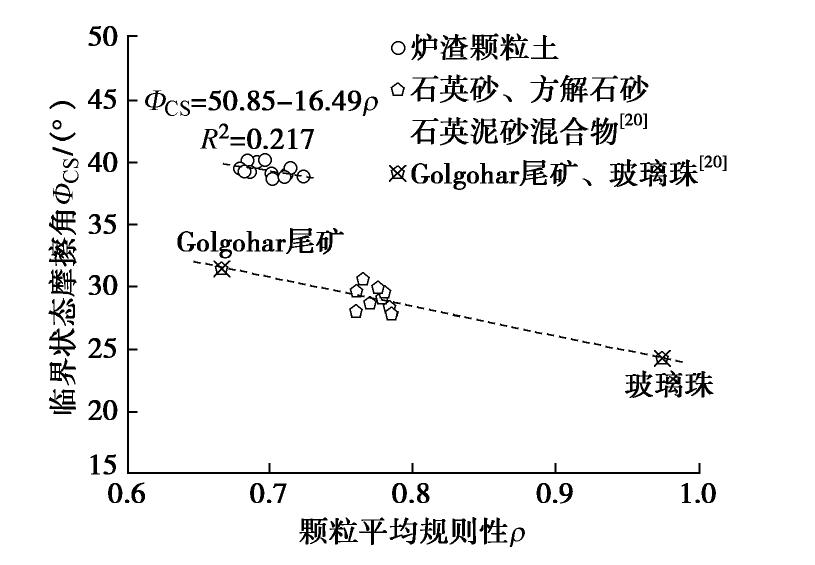
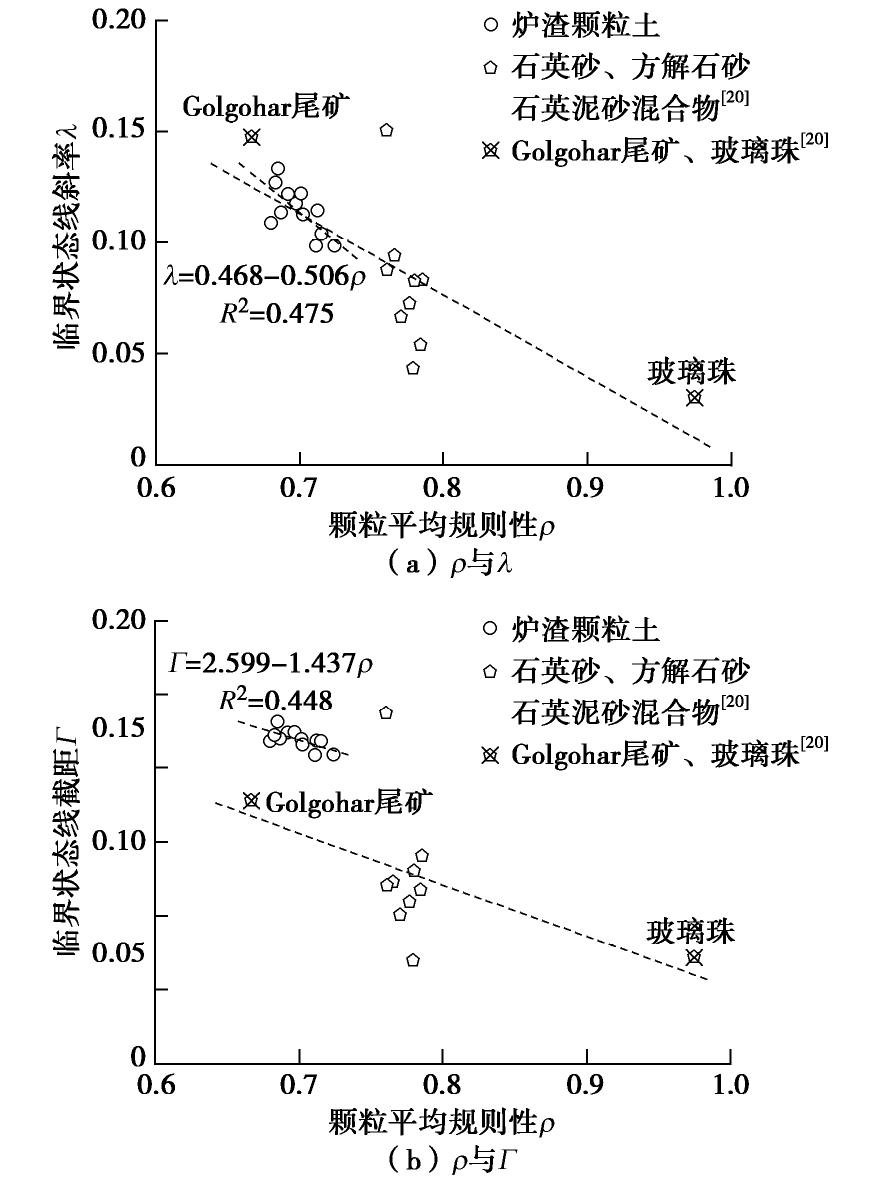
试样	圆形度R	长宽比 $A_{f}$	球度S	凹凸度C	平均规则性 $ρ$
CA.a	0.402	0.715	0.781	0.947	0.711
CA.b	0.375	0.708	0.707	0.930	0.680
CA.c	0.389	0.663	0.810	0.935	0.701
CA.d	0.414	0.645	0.801	0.949	0.702
CA.e	0.388	0.676	0.747	0.935	0.686
CA.f	0.387	0.652	0.751	0.941	0.682
CA.A	0.379	0.645	0.814	0.929	0.691
CA.B	0.366	0.684	0.822	0.916	0.697
CA.C	0.408	0.704	0.820	0.956	0.723
CA.D	0.362	0.625	0.823	0.928	0.684
CA.E	0.396	0.689	0.821	0.942	0.712
CA.F	0.384	0.714	0.817	0.945	0.715

下载: 导出CSV

表 3 三轴排水剪切试验条件

Table 3 Experimental conditions for drained triaxial shear tests

试样	${σ^{'}}_{c}$ /kPa	实际压实度D_c/%			试样	${σ^{'}}_{c}$ /kPa	实际压实度D_c/%
CA.A	50	83.5	88.1	96.9	CA.D	50	83.6	87.3
	100		88	97.9		100		90.8	100.7
	200	83.4	87.4	99.1		200	85.0		101.4
CA.B	50	88.1	90.1	103.4	CA.E	50	84.6	87.7	100.1
	100		92.7	104.2		100	85.0	86.2	102.9
	200	86.0	93.7	104.9		200		90.0	98.0
CA.C	50	83.8	88.2	96.8	CA.F	50	85.0	88.9	100.3
	100			98.6		100	85.0	92.0	99.3
	200	83.0		101.0		200			99.9
注：目标压实度D_c为85%,90%,100%。

下载: 导出CSV

表 4 炉渣颗粒土临界状态摩擦角与临界状态线几何参数

Table 4 Critical state friction angles and geometrical parameters of critical state line for clinker ash

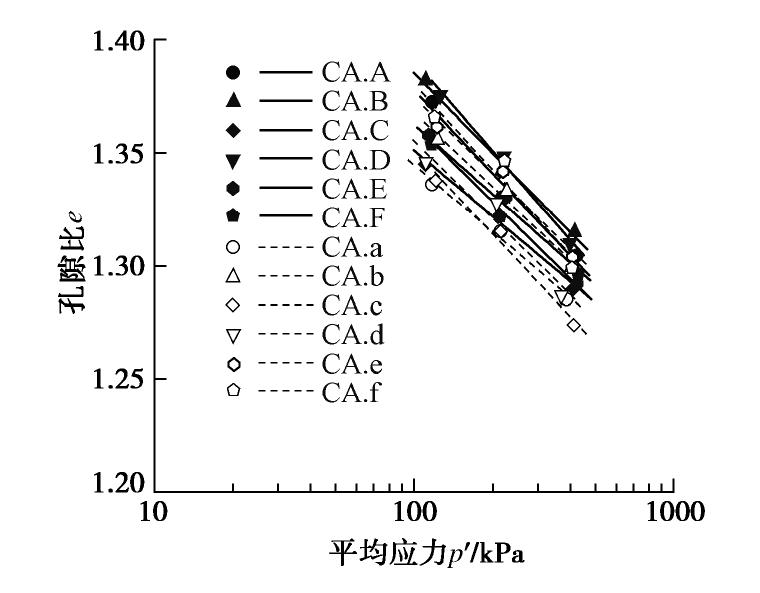
试样	临界状态摩擦角 $Φ_{cs}$	截距Γ	斜率 $λ$
CA.A	39.95	1.541	0.121
CA.B	40.15	1.589	0.117
CA.C	38.82	1.596	0.097
CA.D	40.10	1.576	0.132
CA.E	39.02	1.598	0.114
CA.F	39.54	1.609	0.102
CA.a	38.77	1.619	0.098
CA.b	39.45	1.621	0.108
CA.c	39.04	1.545	0.121
CA.d	38.60	1.655	0.114
CA.e	39.16	1.591	0.111
CA.f	39.21	1.589	0.127

下载: 导出CSV

参考文献(31)

[1]	闫澍旺, 李嘉, 张京京, 等. 石灰炉渣轻质混合料处理地基试验研究及工程应用[J]. 岩土工程学报, 2015, 37(增刊1): 6-10. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2015S1003.htm YAN Shu-wang, LI Jia, ZHANG Jing-jing, et al. Experimental research and engineering application of lime-slag mixed materials used in foundation treatment[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S1): 6-10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2015S1003.htm
[2]	刘传孝, 田鸿业, 张加旺, 等. 炉渣置换软土地基的注浆均质度影响试验研究[J]. 岩土工程学报, 2010, 32(增刊2): 517-520. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2010S2127.htm LIU Chuan-xiao, TIAN Hong-ye, ZHANG Jia-wang, et al. Test on grouting homogeneity degree of slag to replace soft soil foundation[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(S2): 517-520. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2010S2127.htm
[3]	章定文, 曹智国. 工业废渣加固土强度特性[J]. 岩土力学, 2013, 34(增刊1): 54-59. doi: 10.16285/j.rsm.2013.s1.004 ZHANG Ding-wen, CAO Zhi-guo. Strength characteristics of stabilized soils using industrial by-product binders[J]. Rock and Soil Mechanics, 2013, 34(S1): 54-59. (in Chinese) doi: 10.16285/j.rsm.2013.s1.004
[4]	CONSOLI N C, HEINECK K S, COOP M R, et al. Coal bottom ash as a geomaterial: influence of particle morphology on the behavior of granular materials[J]. Soils and Foundations, 2007, 47(2): 361-373. doi: 10.3208/sandf.47.361
[5]	WAKATSUKI Y, HYODO M, YOSHIMOTO N, et al. Particle characteristics and strength, deformation characteristics of loose clinker ash[J]. Doboku Gakkai Ronbunshuu C, 2009, 65(4): 897-914. doi: 10.2208/jscejc.65.897
[6]	WINTER M, SUESHIMA T, YOSHIMOTO N, et al. Effect of particle characteristics on the shear strength of clinker ash[M]//Geomechanics from Micro to Macro. Macro: CRC Press, 2014: 1099-1104.
[7]	CHO G C, DODDS J, SANTAMARINA J C. Particle shape effects on packing density, stiffness, and strength: natural and crushed sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(5): 591-602. doi: 10.1061/(ASCE)1090-0241(2006)132:5(591)
[8]	刘清秉, 项伟, BUDHU M, 等. 砂土颗粒形状量化及其对力学指标的影响分析[J]. 岩土力学, 2011, 32(增刊1): 190-197. doi: 10.16285/j.rsm.2011.s1.121 LIU Qing-bing, XIANG Wei, BUDHU M, et al. Study of particle shape quantification and effect on mechanical property of sand[J]. Rock and Soil Mechanics, 2011, 32(S1): 190-197. (in Chinese) doi: 10.16285/j.rsm.2011.s1.121
[9]	YANG J, LUO X D. Exploring the relationship between critical state and particle shape for granular materials[J]. Journal of the Mechanics and Physics of Solids, 2015, 84: 196-213. doi: 10.1016/j.jmps.2015.08.001
[10]	ZHOU B, WANG J, WANG H. Three-dimensional sphericity, roundness and fractal dimension of sand particles[J]. Géotechnique, 2018, 68(1): 18-30. doi: 10.1680/jgeot.16.P.207
[11]	ZHAO S W, ZHAO J D. A poly-superellipsoid-based approach on particle morphology for DEM modeling of granular media[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2019, 43(13): 2147-2169. doi: 10.1002/nag.2951
[12]	NIE J Y, LI D Q, CAO Z J, et al. Probabilistic characterization and simulation of realistic particle shape based on sphere harmonic representation and Nataf transformation[J]. Powder Technology, 2020, 360: 209-220. doi: 10.1016/j.powtec.2019.10.007
[13]	孔亮, 彭仁. 颗粒形状对类砂土力学性质影响的颗粒流模拟[J]. 岩石力学与工程学报, 2011, 30(10): 2112-2119. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201110020.htm KONG Liang, PENG Ren. Particle flow simulation of influence of particle shape on mechanical properties of quasi-sands[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(10): 2112-2119. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201110020.htm
[14]	张程林, 周小文. 砂土颗粒三维形状模拟离散元算法研究[J]. 岩土工程学报, 2015, 37(增刊1): 115-119. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2015S1024.htm ZHANG Cheng-lin, ZHOU Xiao-wen. Algorithm for modelling three-dimensional shape of sand based on discrete element method[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S1): 115-119. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2015S1024.htm
[15]	常晓林, 马刚, 周伟, 等. 颗粒形状及粒间摩擦角对堆石体宏观力学行为的影响[J]. 岩土工程学报, 2012, 34(4): 646-653. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201204011.htm CHANG Xiao-lin, MA Gang, ZHOU Wei, et al. Influences of particle shape and inter-particle friction angle on macroscopic response of rockfill[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(4): 646-653. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201204011.htm
[16]	MA G, ZHOU W, REGUEIRO R A, et al. Modeling the fragmentation of rock grains using computed tomography and combined FDEM[J]. Powder Technology, 2017, 308: 388-397. doi: 10.1016/j.powtec.2016.11.046
[17]	HUANG Q S, ZHOU W, MA G, et al. Experimental and numerical investigation of Weibullian behavior of grain crushing strength[J]. Geoscience Frontiers, 2020, 11(2): 401-411. doi: 10.1016/j.gsf.2019.07.007
[18]	康馨, 陈植欣, 雷航, 等. 基于3D打印研究颗粒形状对砂土宏观力学性质的影响[J]. 岩土工程学报, 2020, 42(9): 1765-1772. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202009030.htm KANG Xin, CHEN Zhi-xin, LEI Hang, et al. Effects of particle shape on mechanical performance of sand with 3D printed soil analog[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(9): 1765-1772. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202009030.htm
[19]	ALTUHAFI F N, COOP M R, GEORGIANNOU V N. Effect of particle shape on the mechanical behavior of natural sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(12): 4016071. doi: 10.1061/(ASCE)GT.1943-5606.0001569
[20]	LASHKARI A, FALSAFIZADEH S R, SHOURIJEH P T, et al. Instability of loose sand in constant volume direct simple shear tests in relation to particle shape[J]. Acta Geotechnica, 2020, 15(9): 2507-2527. doi: 10.1007/s11440-019-00909-4
[21]	JIS A 1224. Test Method for Minimum and Maximum Densities of Gravels[S]. 2009.
[22]	YOSHIMURA Y, OGAWA S. A simple quantification method of grain shape of granular materials such as sand[J]. Doboku Gakkai Ronbunshu, 1993, 1993(463): 95-103. doi: 10.2208/jscej.1993.463_95
[23]	ZHENG J, HRYCIW R D. Traditional soil particle sphericity, roundness and surface roughness by computational geometry[J]. Géotechnique, 2015, 65(6): 494-506. doi: 10.1680/geot.14.P.192
[24]	NAKATA Y, HYODO M, HYDE A F L, et al. Microscopic particle crushing of sand subjected to high pressure one-dimensional compression[J]. Soils and Foundations, 2001, 41(1): 69-82. doi: 10.3208/sandf.41.69
[25]	MCDOWELL G R, BOLTON M D. On the micromechanics of crushable aggregates[J]. Géotechnique, 1998, 48(5): 667-679. doi: 10.1680/geot.1998.48.5.667
[26]	KIM B, PREZZI M, SALGADO R. Geotechnical properties of fly and bottom ash mixtures for use in highway embankments[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(7): 914-924. doi: 10.1061/(ASCE)1090-0241(2005)131:7(914)
[27]	BOPP P A, LADE P. Relative density effects on drained sand behavior at high pressures[J]. Soils and Foundations, 2005, 45: 15-26. doi: 10.3208/sandf.45.15
[28]	YAO Y P, HOU W, ZHOU A N. UH model: three-dimensional unified hardening model for overconsolidated clays[J]. Géotechnique, 2009, 59(5): 451-469. doi: 10.1680/geot.2007.00029
[29]	YAO Y P, SUN D A, MATSUOKA H. A unified constitutive model for both clay and sand with hardening parameter independent on stress path[J]. Computers and Geotechnics,2008, 35(2): 210-222. doi: 10.1016/j.compgeo.2007.04.003
[30]	YAO Y P, ZHOU A N. Non-isothermal unified hardening model: a thermo-elasto-plastic model for clays[J]. Géotechnique, 2013, 63(15): 1328-1345. doi: 10.1680/geot.13.P.035
[31]	YAO Y P, LU D C, ZHOU A N, et al. Generalized non-linear strength theory and transformed stress space[J]. Science in China Series E: Technological Sciences, 2004, 47: 691-709. doi: 10.1360/04ye0199

施引文献(28)

期刊类型引用(15)

1.	杨舒涵，漆天奇，刘嘉英. 堆石料宏细观力学特性离散元分析. 人民长江. 2024(02): 203-210 . 百度学术
2.	LI Shuai，GU Tianfeng，WANG Jiading，WANG Fei，LI Pu. Regulation effect of the grille spacing of a funnel-type grating water–sediment separation structure on the debris flow performance. Journal of Mountain Science. 2024(07): 2283-2304 . 必应学术
3.	王辉，钮新强，马刚，周伟. 干湿循环作用下堆石料宏细观力学特性的离散元模拟研究. 岩土力学. 2024(S1): 665-676 . 百度学术
4.	张江浩，冀鸿兰，杨震，李志军，刘晓民. 冻融循环下黄河堤岸砂质壤土宏细观破坏过程. 河海大学学报(自然科学版). 2024(06): 69-80 . 百度学术
5.	黄志刚，王轩，傅力，童立红. 加载速率和摩擦系数对颗粒材料系统剪切强度的影响研究. 力学季刊. 2024(04): 1032-1042 . 百度学术
6.	栗培龙，宿金菲，孙胜飞，王霄，马云飞. 多级矿料-沥青体系的颗粒特性、界面效应及迁移行为研究进展. 中国公路学报. 2023(01): 1-15 . 百度学术
7.	王伟，张志义，赵博. 煤矿井下风积沙箱式充填体侧向约束机理数值研究. 新疆大学学报(自然科学版)(中英文). 2023(03): 367-372 . 百度学术
8.	肖浩波，漆天奇，杨舒涵，周伟，刘嘉英. 椭球颗粒体系宏、细观特性的3维离散元分析. 工程科学与技术. 2023(06): 78-86 . 百度学术
9.	张革，曹玲，王成汤. 考虑各向异性影响的冻土修正线性黏结接触模型开发及应用. 岩土力学. 2023(S1): 645-654 . 百度学术
10.	郑虎，牛文清，毛无卫，黄雨. 颗粒材料双轴压缩试验的光弹测试. 同济大学学报(自然科学版). 2023(11): 1719-1724 . 百度学术
11.	王怡舒，刘斯宏，沈超敏，陈静涛. 接触摩擦对颗粒材料宏细观力学特征和能量演变规律的影响. 岩石力学与工程学报. 2022(02): 412-422 . 百度学术
12.	雷云，刘源，徐同桐，何子苗. 粒间摩擦和层厚比对二维分层颗粒系统底部响应的影响. 科学技术与工程. 2022(07): 2585-2591 . 百度学术
13.	刘嘉英，周伟，姬翔，魏纲，袁思莹，李欣骏. 基于细观拓扑结构演化的颗粒材料剪胀性分析. 力学学报. 2022(03): 707-718 . 百度学术
14.	蒋明杰，栗书亚，吉恩跃，张小勇，朱俊高. 粗粒土大型静止侧压力系数测定试验的颗粒流模拟. 科学技术与工程. 2021(25): 10867-10872 . 百度学术
15.	崔溦，魏杰，王超，王枭华，张社荣. 考虑颗粒级配和形态的颗粒柱坍塌特性离散元模拟. 岩土工程学报. 2021(12): 2230-2239 . 本站查看