高温下饱和冻土一维融化热固结模型及解答

周扬; 武子寒; 许程; 卢萌盟; 周国庆

doi:10.11779/CJGE202112005

高温下饱和冻土一维融化热固结模型及解答 English Version

周扬^{1, 2,},
武子寒²,
许程²,
卢萌盟^{1, 2},
周国庆²

1.
中国矿业大学力学与土木工程学院,江苏　徐州　221116
2.
中国矿业大学深部岩土力学与地下工程国家重点实验室,江苏　徐州　221116

基金项目:

国家自然科学基金项目 51878657

国家自然科学基金项目 51204164

详细信息

作者简介:
周扬(1982— ),男,江苏扬州人,博士,副教授,从事矿山建设、冻土物理学方面的研究。E-mail：tod2006@126.com

中图分类号: TU445
计量
- 文章访问数: 323
- HTML全文浏览量: 49
- PDF下载量: 265
出版历程
- 收稿日期: 2020-11-29
- 网络出版日期: 2022-11-30
- 刊出日期: 2021-11-30

One-dimensional thaw thermo-consolidation model for saturated frozen soil under high temperature and its solution

1.
School of Mechanics & Civil Engineering, China University of Mining & Technology, Xuzhou 221116, China
2.
State Key Laboratory for Geomechanics and Deep Underground Engineering, China University of Mining & Technology, Xuzhou 221116, China

摘要

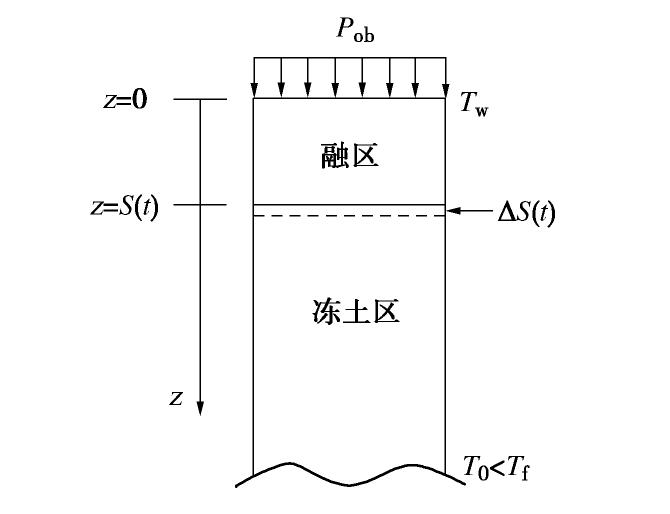
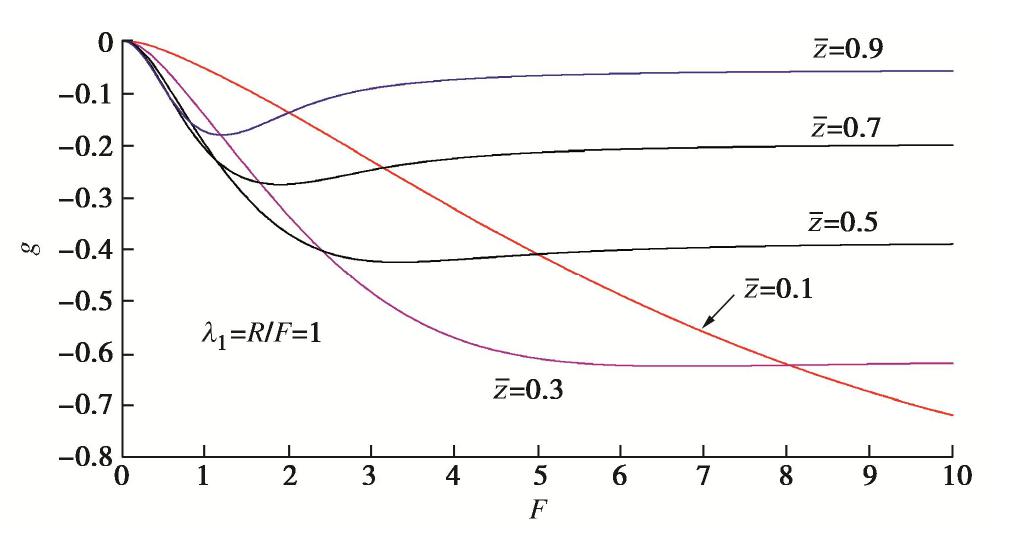
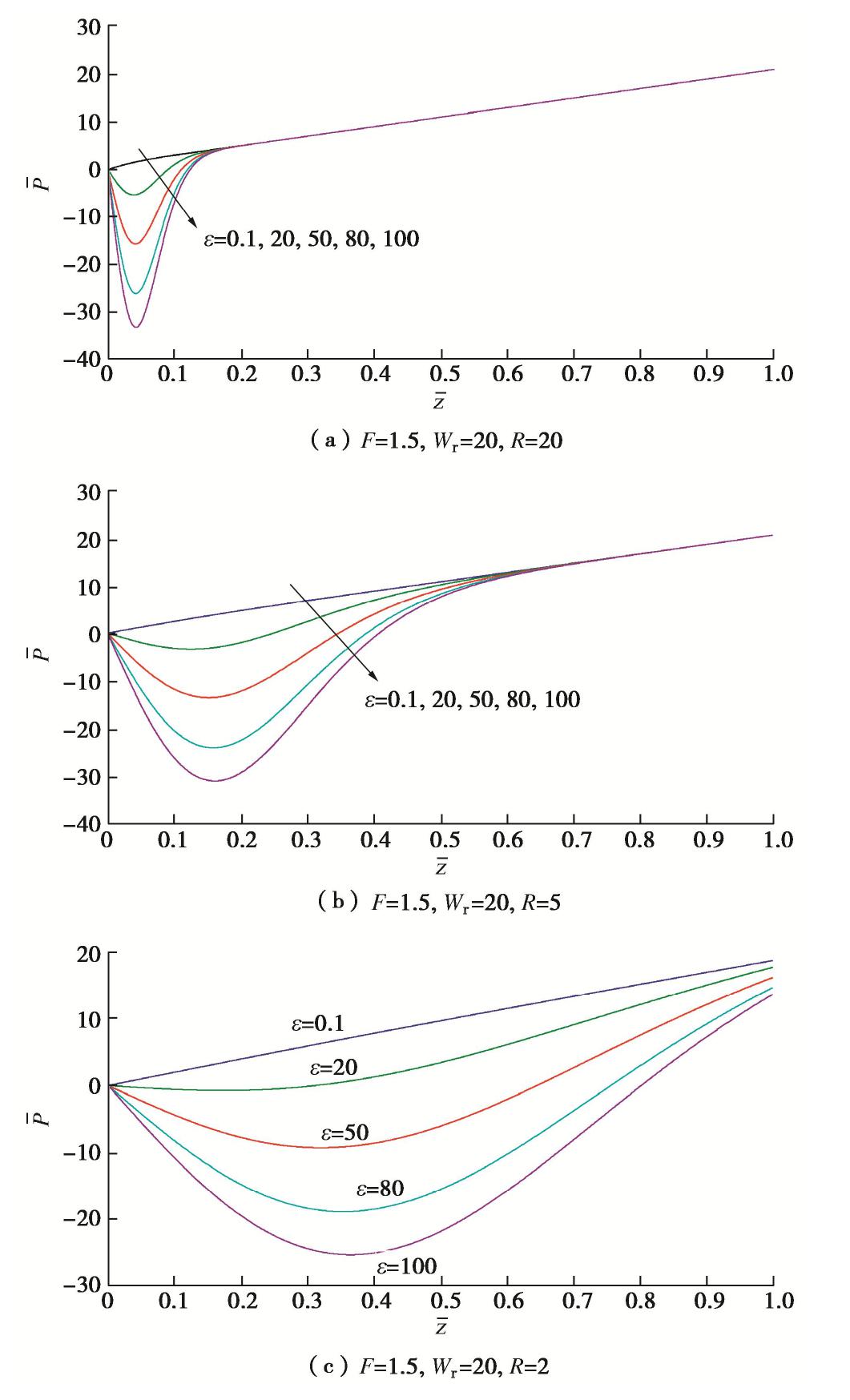
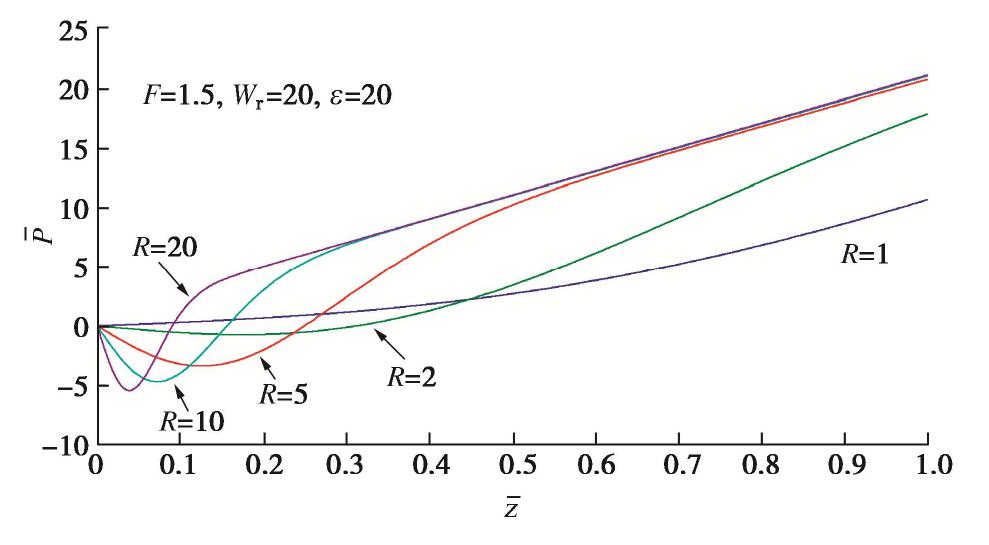
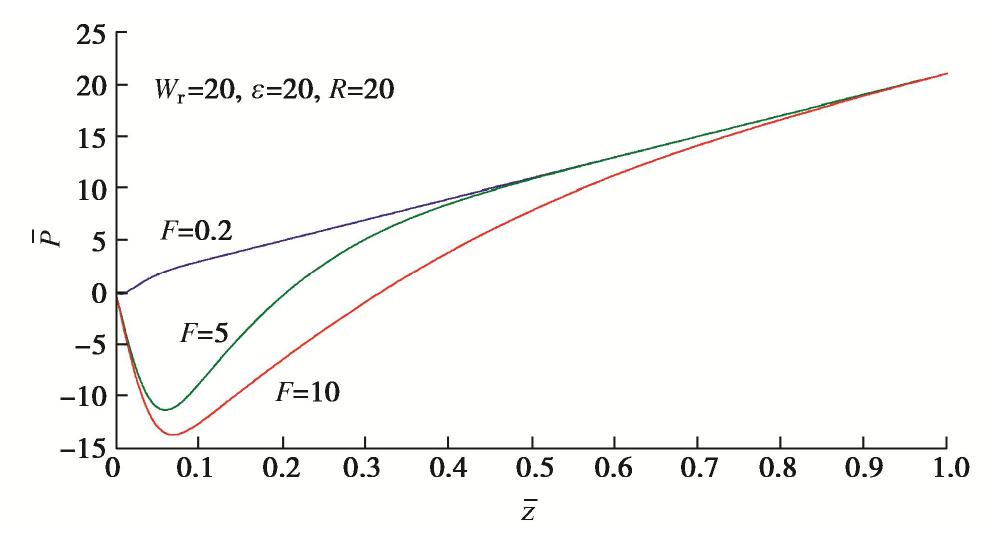
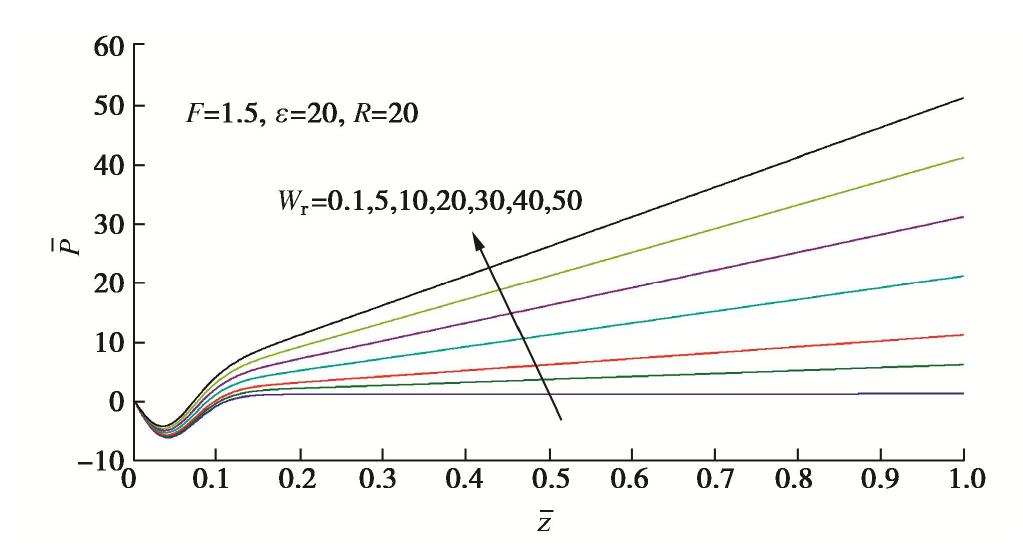
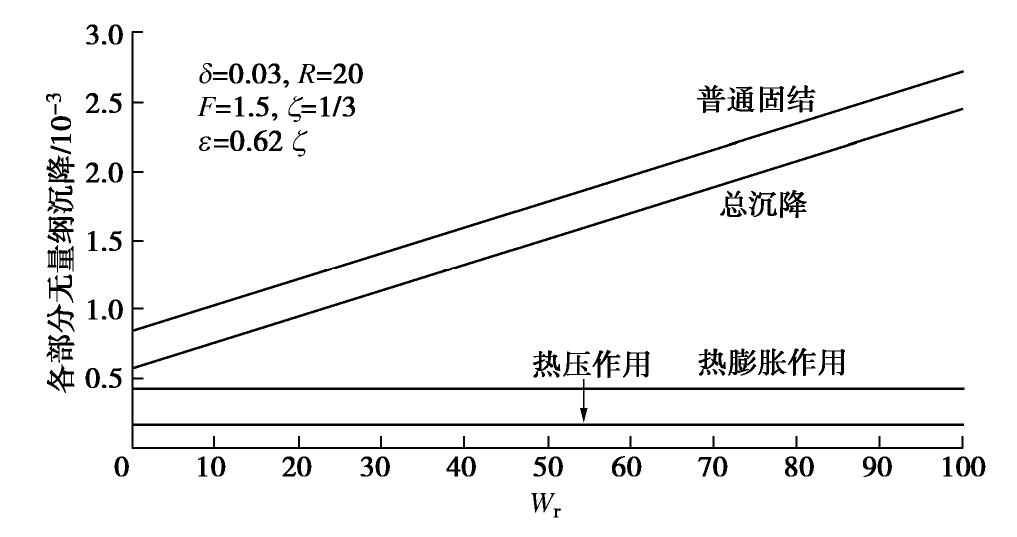
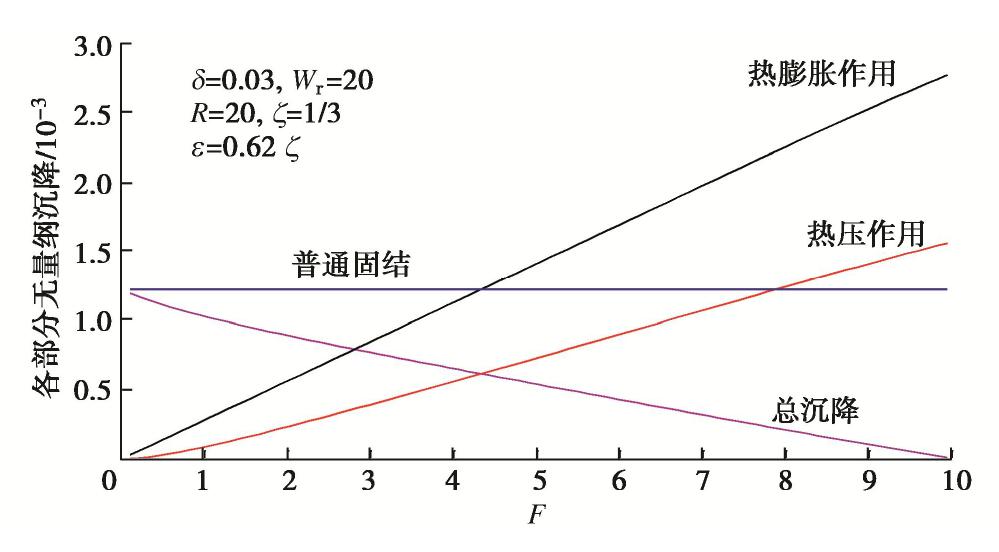
摘要: 冻结法应用及寒区施工中常采用高温热水强制融化冻土,针对饱和冻土在高温下的一维融化过程,建立了理论模型并给出了模型的解析解答。模型包含传热及热固结两部分,前者为全区域考虑未冻水的相变热传导过程,后者为融区内土体在温度、荷载及自重作用下的热固结过程。传热部分在文献中已有温度场、融化界面的解析解答,而融区内超静孔压的解析解答由本文推导获得。在忽略土颗粒、水的热膨胀作用后,模型和解答可以退化为Morgenstern和Nixon的经典冻土一维融化固结模型。利用模型解答对冻土在高温下一维融化过程中超静孔压、沉降进行了计算分析,结果表明：热压作用在热固结强度因子ε为正时会减小超静孔压,该效果随着ε增加而增强；减小融化固结比R或增大导温固结比F均扩大热压作用的相对影响范围,但前者使热压作用在融区内趋于均匀,后者会增加整体的热压作用；增加自重时间因子W_r几乎不改变热压作用强度及相对影响范围；高温的净效果使融土产生膨胀,但其影响小于普通固结沉降,因此总体效果仍表现为沉降。
- 饱和冻土 /
- 融化固结 /
- 高温融化 /
- 热固结 /
- 解析解
Abstract: During the application of artificial ground freezing technique and construction in cold regions, high-temperature hot water is often used to melt the frozen soil manually. For the one-dimensional thawing process of saturated frozen soil under high temperature, a theoretical model describing the process is established and an analytical solution is developed for the model. The model comprises a heat transfer part and a thermo-consolidation part. The former is a heat conduction process of frozen soil with phase change of pore ice considering the unfrozen water effect, while the latter is a thermo-consolidation process of soil in the thawed region under the effects of high temperature, external load and self-weight. The temperature field and the melting interface for the heat transfer part have already been deduced in the existing literatures, which are adopted directly. For the excessive pore water pressure in the thawed region, an analytical solution is developed. By neglecting the thermal expansion of soil grains and water, the proposed model and the developed solution may degenerate to those of the classical one-dimensional thaw consolidation model for frozen soil developed by Morgenstern and Nixon. The analytical solution is then used to analyze the excessive pore water pressure and the settlement for one-dimensional thawing process of frozen soil under high temperature. The results show that the effect of thermal pressure reduces the excessive pore water pressure if the thermo-consolidation intensity factor ε is positive, and this effect increases with the increasing ε. Reducing the thaw consolidation ratio R or increasing the diffusion consolidation ratio F will expand the relative influence zone of the thermal pressure. However, the former leads to a more uniform thermal pressure effect in the thawed region, while the latter generally increases the thermal pressure effect in the thawed region. Increasing the self-weight time factor W_r barely changes the intensity and the relative influence zone of the thermal pressure. The net effect of high temperature is to expand the thawed soil, but it is weaker than the effect of normal consolidation settlement, thus the general effect is still settlement.
- saturated frozen soil /
- thaw consolidation /
- thaw under high temperature /
- thermal consolidation /
- analytical solution

HTML全文

0. 引言

中国西北、西南地区河流河床及河岸滩地等区域多有覆盖层发育，砂砾料储量丰富，是一种较好的筑坝材料。相应地，在西北和西南水利水电开发中，砂砾石坝成为一种重要的坝型^[1-3]。目前，砂砾料已经成为新疆等地区常用的筑坝材料，如新疆阿尔塔什水利枢纽中的混凝土面板砂砾石坝、新疆大石门水利枢纽沥青混凝土心墙砂砾石坝等^[1]。与另外一种常见的爆破堆石料相比，其开采成本低，施工方便，压实后具有更高的强度和变形模量，而且具有在高应力环境下强度衰变小，变形稳定时间短等优点^[4-5]。

对于筑坝填料而言，其物理力学特性参数的确定，主要取决于颗粒组成，即级配对物理力学特性（密度、渗透系数、强度参数及变形特性参数）具有重要的影响^[6]。因此，研究砂砾料在一定压实度条件下的力学特性，首先应对砂砾料颗粒级配进行深入研究。从国内外相关文献来看，目前针对粗粒土级配开展的研究主要集中在土体级配对其物理力学特性方面的影响，以及粗粒土在缩尺之后对其力学性质的影响。如李罡等^[7]在研究粒状材料颗粒级配对临界状态影响时，引入了C_u开展相关的研究工作；蒋明镜等^[8]通过试验研究不同颗粒级配对火山灰力学性质影响，分析了某种级配曲线对压缩性及强度指标的影响；朱晟等^[9]细致开展了粗粒土级配特征对粗粒土的物理力学特性的影响。而在级配表示方法方面，研究相对较少，主要的研究结果包括朱晟等^[10]提出的基于分形方法的土体颗粒组成表达；朱俊高等^[11]提出了适用于连续级配土的级配方程并验证了该级配方程对多种土料实际级配的适用性。然而现有的研究成果大多是利用不均匀系数C_u与曲率系数C_c来评价粗粒土的级配优劣，其并未直接表达粗粒土中颗粒尺寸和完整的级配特征，因此也就难以进行级配特征与土体物理力学特征之间的定量表达。

砂砾石料的级配特性，主要受母岩特性、产生原因、空间分布等不确定因素的影响。由于无黏性粗粒土力学参数的离散程度与细粒土相比较大，现有分析方法在计算精度方面及砾石填料适用性上尚存在不足。因此试验方法仍然是当前确定其参数最直接、最可靠的方法，也是大多数理论和经验估值的重要依据。充分利用有限的试验数据，结合概率统计方法探索颗粒级配与力学参数间的关系，是目前较为实用的途径^[12]。

通过实际工程经验也可知，碾压完成后的砂砾石坝体力学强度特征参数，与坝料级配特征参数有着明显的关系，但是碾压区域坝料质量检测数据极少，仅3~5组。根据前期大量的地质勘探资料分析可知，心墙坝坝壳填筑所用的坝料，来源于同一地质时期形成的层位，该坝料堆积形成的历史成因是相同的，所经历的地质运动也是相同的，同一个区域内的砂砾石，在其物理力学特性上具有强烈的概率统计特性，可以认为他们都是来源于同一个大母体分布中服从某一种概率分布的随机变量，因此可以通过前期积累的大量现场挖坑检测的数据形成先验分布，结合后续单元工程中挖坑检测得到的试验数据样本，可较为合理地评价大坝填筑施工质量。根据已有的样本数据去推断总体分布时，一般需要将数据拟合成具体的概率分布模型，并估计其相应的分布参数，在数理统计分析中一般采用多维正态分布，但正态分布往往难以得到小样本条件下土体力学参数分布的最优估计，且不能反映有偏样本和截尾样本的分布特点，甚至有时不能通过检验^[13]。而威布尔分析模型弥补了正态分布的这些缺陷，对各种类型试验数据有极强的适应能力，不仅能够适用于大样本数据，对小样本数据也有较好的适用性，广泛用于研究机械、化工、电气、电子、材料、航天，甚至医学研究。威布尔分布模型由其形状、尺度（范围）和位置3个参数决定。其中形状参数是最重要的参数，决定分布密度曲线的基本形状，通过改变其形状参数可以近似表达其他分布，如正态、对数正态、指数等分布。尺度参数起放大或缩小曲线的作用，但不影响分布的形状。

通过设计模型试验获取数据进行统计分析的方法，由于试验中数据量较少且未能考虑施工中的不确定性因素的影响，试验数据往往较为理想，所得方法用于拟合实际工程中的问题时通常难以较好的描述。在本研究中，结合新疆大石门水利枢纽工程施工过程中获取的大量检测试验数据，在大量统计的基础上，通过分析各参数与干密度间的相关性，在砂砾石填料区选取了与干密度相关性最密切的3个级配特征参数为砾石含量、曲率系数C_c、最大粒径；在过渡料填料区选取了与干密度相关性最密切的3个特征参数为砾石含量、曲率系数C_c、含泥量（小于0.075 mm），并对其分别构建了一维威布尔分布模型，求出对应模型的3个控制参数为位置参数μ、尺度参数 $\sigma$ 、形状参数 $\xi$ ，得到了在一定保证率条件下的粗粒土级配参数估计值。在此基础上，进一步推导出了三维威布尔分布函数表达式，建立了能够利用以上3个级配特征参数间相关关系反映砂砾石料和过渡料填料区干密度的三维威布尔分布模型，使干密度的表征方法更具综合性，可用于砂砾坝填料的质量评估和预测。

1. 威布尔分布模型

1.1 一维威布尔分布模型

Weibull分布自1939年由瑞典工程师提出后，因能够以小样本准确可靠地进行预测而被广泛采用^[14]。目前一维威布尔概率分布已发展成为工程中应用最广的概率分布类型之一，能够较好的拟合数据样本点，可适用于完全样本、有偏样本和截尾样本的拟合。Weibull分布包括传统的二参数分布和三参数分布，前者可理解为后者的特例。

（1）概率分布函数

一维威布尔概率分布函数的表达式可表示为^[15-18]

$F(x)=1-\mathrm{exp}\left[-{\left(\frac{x-\mu }{\sigma }\right)}^{\xi }\right](x\ge \mu )\text{，}$

(1)

其密度函数为

$f(x) = \frac{\xi }{\sigma }{\left( {\frac{{x - \mu }}{\sigma }} \right)^{\xi - 1}}\exp \left[ { - {{\left( {\frac{{x - \mu }}{\sigma }} \right)}^\xi }} \right]\text{，}$

(2)

式中，F(x)为分布函数，f (x)为密度函数，x为随机变量，x ≥ μ；ξ为形状参数（斜率），ξ ≥ 0，其决定威布尔分布曲线的形状； $\sigma$ 为尺度参数， $\sigma$ ≥ 0，是一种平均效应，表征威布尔分布中点的大致位置；μ为位置参数，表征威布尔分布的起算位置，当μ = 0时，三参数威布尔分布便退化为二参数威布尔分布。

（2）参数计算

威布尔分布参数计算常用的方法是极大似然法和最小二乘法^[19-20]。虽然极大似然法精度高，但需要在实数范围内，搜索求解极大似然超越方程，求解计算复杂；最小二乘法求解相对简单，可简单的求出位置数据，使求得的数据与实际数据之间误差的平方和最小。因此，本研究采用最小二乘法进行求解，为计算威布尔分布中的3个参数，需将式（1）两边取2次自然对数得到：

$\ln {\text{ln}}\frac{1}{{1 - F(x)}} = \xi {\text{ln}}(x - \mu ) - {\text{ln}}{\sigma ^\xi }。$

(3)

令 $Y = \ln \ln \frac{1}{{1 - F(x)}}$ ， $X = \ln (x - \mu )$ ， $A = \ln {\sigma ^\xi }$ ，则式（3）变为线性方程：

$Y = \xi X - A。$

(4)

由于μ表示威布尔分布模型的起算位置，因此可取一个小于试验数据最小值的数μ₀（或者取为0）作为起始值（已知值）进行初步计算，得出X_i = ln (x_i - μ₀)；计算Y_i时需要先计算出累计概率F(x_i)，目前常用的方法：将n个变量（试验数据）由小到大排序为x₁ ≤ x₂≤ x₃ ≤……≤ x_n，对应的累计失效概率为F(x₁) ≤ F(x₂) ≤ F(x₃) ≤……≤ F(x_n)，其中第i个累计失效概率F(x_i)可用中位秩算法求得^[21]：

$F({x_i}) = \frac{{i - 0.3}}{{n + 0.4}}。$

(5)

进一步选用最小二乘法对上式线性方程进行参数计算^[22]，进而可求出线性方程中的斜率ξ和截距A：

$\xi = \frac{{\sum\limits_{i = 1}^n {{X_i}{Y_i} - \frac{1}{n} \cdot \left( {\sum\limits_{i = 1}^n {{X_i}} } \right) \cdot \left( {\sum\limits_{i = 1}^n {{Y_i}} } \right)} }}{{\sum\limits_{i = 1}^n {X_i^2 - \frac{1}{n} \cdot {{\left( {\sum\limits_{i = 1}^n {X_i^{}} } \right)}^2}} }}\text{，}$

(6)

$A = \frac{1}{n} \cdot \sum\limits_{i = 1}^n {Y_i^{} - \frac{\xi }{n} \cdot \sum\limits_{i = 1}^n {{X_i}} } \text{，}$

(7)

进而求出尺度参数 $\sigma = \exp \left( {\frac{A}{\xi }} \right)$ 。

在计算式（6），（7）的同时，也可同时计算出表征拟合直线的相关系数r：

$r = \frac{{\sum\limits_{i = 1}^n {{X_i}{Y_i} - \frac{1}{n} \cdot \left( {\sum\limits_{i = 1}^n {{X_i}} } \right) \cdot \left( {\sum\limits_{i = 1}^n {{Y_i}} } \right)} }}{{\sqrt {\left( {\sum\limits_{i = 1}^n {X_i^2 - \frac{1}{n} \cdot {{\left( {\sum\limits_{i = 1}^n {{X_i}} } \right)}^2}} } \right) \cdot \left( {\sum\limits_{i = 1}^n {Y_i^2 - \frac{1}{n} \cdot {{\left( {\sum\limits_{i = 1}^n {{Y_i}} } \right)}^2}} } \right)} }}。$

(8)

计算效果的优劣可用相关系数r表征，其绝对值越接近1，说明线性拟合的效果越好。由于在初始计算时μ为任意小于试验数据最小值的数，计算得出的r往往并非接近于1，因此需要对μ进行优化，以得出最接近于1的r。

因此，可设目标函数U = Max | r (μ₀) |，以μ₀为变量，进行迭代计算，使目标函数U趋近于1时的μ₀即为最优值，其可作为一维威布尔分布函数的位置参数μ，同时也可对应计算出形状参数ξ和尺度参数 $\sigma$ 。此时，一维威布尔分布函数的3个参数已全部求出。

（3）可靠度条件下的估计值

在实际应用时，往往需要给出在一定可靠度条件下的参数估计值，因此，设参数估计的可靠度为R²，分布函数与可靠度R²的关系为^[23]

${R^2}(x) = 1 - F(x)\text{，}$

(9)

即

${R^2}(x) = \exp \left[ { - {{\left( {\frac{{x - \mu }}{\sigma }} \right)}^\xi }} \right]\text{，}$

(10)

$\frac{1}{{{R^2}(x)}} = \exp {\left( {\frac{{x - \mu }}{\sigma }} \right)^\xi }。$

(11)

再对式（11）两边取对数得

${x_{{R^2}}} = \mu + \sigma \ln {\left( {\frac{1}{{{R^2}}}} \right)^{\frac{1}{\xi }}}\text{，}$

(12)

式中， ${x_{{R^2}}}$ 为一维威布尔分布在可靠度R²条件下的估计值，利用已经得出的3个参数，代入式（12）即可计算出 ${x_{{R^2}}}$ 。

1.2 三维威布尔分布模型

实际工程中坝料级配的描述，是一系列颗粒粒径及其含量的表达，这些参数在一定的尺度范围内存在着随机性和符合统计规律的自相似性，且某些参数间存在着明显的相关性^[24]。因此，难以采用一维概率分布进行全面描述，但目前多维概率分布中参数、相关系数确定以及假设检验仍存在困难，限制了多维概率分布在坝料级配特性表达中的应用。

近年来不少研究者逐步完善了多维复合极值分布理论并将其成功应用于极端海况以及台风预测中^[25-27]，为坝料级配特性的多维概率表达提供了新的思路。已有研究以离散型随机变量是Poisson分布为基础，推导得出了Poisson-Nested-Logistic三维复合极值分布模型^[28-31]，表达式为

$G(x,y,z)=\mathrm{exp}\left\{-{\left[（{S}_{1}^{1/(\alpha \beta )}+{S}_{2}^{1/(\alpha \beta )}{）}^{\beta }+{S}_{3}^{1/\alpha }\right]}^{\alpha }\right\}\text{，}$

(13)

式中， ${S_j} = {\left( {1 + {\xi _j}\frac{{{x_j} - {\mu _j}}}{{{\sigma _j}}}} \right)^{ - 1/{\xi _j}}}$ ，j = 1, 2, 3。本研究受上述离散型多维复合极值分布模型建立思想的启发，在一维威布尔分布的基础上，通过对坝料级配曲线中参数的相关性拟合分析，结合干密度概率分布，构建了基于威布尔分布的多维复合分布函数模型，一维威布尔概率函数如式（1）所示，对于三维威布尔分布而言，其概率分布函数应该是每个变量的边缘函数的组合，考虑三维威布尔概率分布中变量之间的相关系数，通过公式推导与数值拟合，得出的三维威布尔分布模型概率函数的数学表达式为

$\begin{aligned} G(x, y, z)= & \left\{\left[\left(1-\exp \left(\frac{x-\mu_1}{\sigma_1}\right)^{\xi_1}\right) \cdot\left(1-\exp \left(\frac{y-\mu_2}{\sigma_2}\right)^{\xi_2}\right)\right]^{\beta / \sqrt[3]{\alpha \beta}} .\right. \\ & \left.\left(1-\exp \left(\frac{z-\mu_3}{\sigma_3}\right)^{\xi_3}\right)\right\}^{\alpha / \sqrt[3]{\alpha \beta}}。 \end{aligned}$

(14)

式中，ξ_j，μ_j，σ_j (j=1，2，3)分别为x，y，z的边缘分布形状参数、位置参数和尺度参数，0 ≤ α，β ≤ 1为由相关系数r得到的相关参数，α，β均为1时，x，y，z相互独立。史道济^[32]通过矩估计法，给出了相关参数 $\alpha$ ， $\beta$ 的显式表达式：

$\left.\begin{array}{l} \alpha=\frac{\sqrt{1-r_{1,3}}+\sqrt{1-r_{2,3}}}{2} \\ \beta=\frac{\sqrt{1-r_{1,2}}}{\alpha}, \end{array}\right\}$

(15)

式中，r_ij为线性相关系数，i，j = 1, 2, 3，i < j。

式（14）中3个变量的分层结构（ $\alpha$ 为外层， $\beta$ 为内层）代表xy之间比xz和yz之间有着更强的相关性；式中 $\sqrt[3]{{}}$ 是通过迭代优化的方法得到的。最后对推导的三维威布尔分布模型的合理性进行显著水平为0.05的K-S检验。

根据模拟数据的拟合分析可知，当三维威布尔分布中3个参数中任意两个参数间的相关系数小于0.15时，可认为该三维威布尔分布中的参数相互独立，此时三维威布尔分布表达式可直接用边缘分布相乘，这样得到的拟合效果要较考虑参数之间相关系数后，即利用式（14），计算得到的效果更准确。

1.3 威布尔分布的假设检验

模型假设检验是为了评价所得概率分布模型的拟合精度，在统计分析中常用的检验方法有：卡方检验、D检验和K-S检验，其中K-S检验(Kolmogorov-Smirnov) 在威布尔分布中广泛采用，是比较一个频率分布G(x)与理论概率分布F(x)的检验方法^[33]。其假设H₀为两个数据分布一致或者数据符合理论分布。计算公式为

${D}_{n}^{}=\mathrm{max}\left\{{D}_{n}^{+}\text{，}{D}_{n}^{-}\right\} \text{，}$

(16)

式中，

$D_n^ + = \max \left\{ {\frac{i}{n} - {F_0}\left( {{x_i}} \right)} \right\}\text{，}$

(17)

$D_n^ - = \max \left\{ {{F_0}\left( {{x_i}} \right) - \frac{{i - 1}}{n}} \right\}。$

(18)

若实际观测值 $D_n^{}$ > D (n，α)，则拒绝H₀，否则接受H₀假设。

2. 基于威布尔分布的砂砾石坝填料颗粒级配概率模型构建

2.1 工程背景

本研究的工程背景为新疆车尔臣河大石门水利枢纽工程，其位于巴州且末县境内的车尔臣河干流上，距乌鲁木齐约1200.0 km，建设工程为防洪、发电和灌溉等综合利用。水库总库容1.27×10⁹ m³，正常蓄水位2300.0 m，电站装机容量60.0 MW。主要由大坝、泄水建筑物、发电引水系统和地面厂房等建筑物组成，施工总工期为48个月。

挡水大坝采用沥青混凝土心墙坝，其标准横剖面图如图 1所示。坝顶高程2304.5 m，最大坝高128.8 m，坝顶宽度12.0 m，坝长205.0 m。坝体填筑材料主要分区为上游砂砾料填筑区、下游砂砾料填筑区、心墙上下游过渡料填筑区、岸坡过渡料填筑区、上游围堰砂砾石填筑区、沥青混凝土心墙、利用堆石料填筑区。主要工程量：砂砾料填筑量约312.8×10⁴ m³，过渡料约16.1×10⁴ m³，沥青混凝土约1.4×10⁴ m³，可利用料约18.5×10⁴ m³。

图 1 大石门水利枢纽沥青混凝土心墙坝标准横剖面图

Figure 1. Standard horizontal section of sand-gravel dam with asphalt concrete core wall of Dashimen project

下载: 全尺寸图片幻灯片

2.2 砂砾石坝料干密度主要影响因素的相关性分析

大坝填筑最重要的控制因素是压实后的干密度，影响坝料干密度的因素较多，主要包括坝料压实功作用（碾压速度、遍数、振动频率、吨位等综合作用）、坝料级配、母岩强度、含水率等。大坝压实功基本都是通过碾压试验确定，对于母岩来源一致的坝料而言，级配参数、含水率是碾压施工结束后干密度的主要控制因素。筑坝砂砾填料干密度具有级配相关性，但在砂砾填料施工质量控制中，目前主要以含砾量表征级配对干密度的影响，未考虑级配形状、最大粒径、不均匀系数、曲率系数的影响。已有研究表明，砂砾料干密度受这些因素的影响较为显著，而简化的室内实验难以准确描述现场原级配料的干密度。在此基础上推导出来的外延公式缺乏普遍适用性，应用时存在较大的误差。为了研究这些参数对其敏感性，本研究借助数理统计的方法，基于施工过程中大量的检测试验数据，建立试验参数间的关系，选择与干密度相关性最紧密的3个因素，并对这3个因素通过威布尔分布进行拟合分析，推导出在一定保证率条件下的估计值。

在大石门水利枢纽工程堆石坝工程施工过程中，堆石坝工程检测资料主要为上游砂砾填筑料（453组）、下游砂砾填筑料（473组）、心墙上下游过渡料（908组）、岸坡过渡料（183组），共2017组试验。

上述试验数据会有部分组数的参数数据缺失，经统计上游砂砾填筑料的有效试验组数（级配参数与干密度数据均存在）为345组，下游砂砾填筑料的有效试验组数为358组，心墙上下游过渡料的有效试验组数为455组，下游砂砾填筑料的有效试验组数为183组，本研究采用数据处理软件SPSS 22对以上有效试验数据进行相关性分析，研究挖坑检测试验数据中与干密度关系最密切的参数。计算所得的干密度与其他特征参数的相关性r见表 1，具体的实现过程详见李申等^[34]的研究。由表可知，在上下游砂砾石填料区含泥量（小于0.075 mm）、不均匀系数C_u、含水率与干密度间表现出明显的不相关或负相关，砾石含量、曲率系数C_c、最大粒径与干密度间表现出明显的相关性；而在过渡料填料区不均匀系数C_u、最大粒径、含水率与干密度间表现出明显的不相关或负相关，砾石含量、曲率系数C_c、含泥量（小于0.075 mm）与干密度间表现出明显的相关性。根据相关性分析结果，最后在砂砾石填料区选取了与干密度相关性最密切的3个级配特征参数为砾石含量、曲率系数C_c、最大粒径；在过渡料填料区选取了与干密度相关性最密切的3个特征参数为砾石含量、曲率系数C_c、含泥量（小于0.075 mm）。

表 1 试验数据相关性分析

Table 1. Correlation analysis of test data

填料区	相关系数r	砾石含量/%	含泥量(小于0.075 mm)/%	曲率系数C_c	不均匀系数C_u	最大粒径/mm	含水率/%
上游砂砾填筑料	干密度/(g·cm^-3)	0.665	-0.028	0.522	-0.004	0.331	-0.123
下游砂砾填筑料	干密度/(g·cm^-3)	0.793	0.015	0.441	-0.076	0.473	0.027
心墙上下游过渡料	干密度/(g·cm^-3)	0.363	-0.093	0.193	0.003	0.020	-0.036
岸坡过渡料	干密度/(g·cm^-3)	0.527	-0.144	0.312	-0.038	-0.025	0.010

下载: 导出CSV

| 显示表格

2.3 基于一维威布尔分布的砂砾石级配参数拟合

根据1.1节推导的威布尔分布拟合公式，编制EXCEL规划算法，对与干密度最为相关的级配特征参数逐个进行拟合，进而计算出威布尔分布的3个参数，构建一维威布尔概率分布模型。分别对各参数的实际有效数据进行一维威布尔分布拟合，限于篇幅，仅列出上游、下游砂砾填筑料的拟合结果，心墙上下游过渡料、岸坡过渡料的拟合结果不再一一列出。上下游砂砾填筑料的拟合结果见图 2~9，对应的威布尔分布参数见表 2，3，从拟合结果可以看出，威布尔分布拟合结果的相关系数r均超过0.98，拟合结果较为可观。然后利用K-S检验法分别对本文威布尔分布拟合得到的干密度、砾石含量、曲率系数以及最大粒径的概率分布进行检验，K-S检验法结果如表 2，3所示，从表中可看出在在显著性水平α =0.05条件下，威布尔分布拟合得到的各项级配参数的概率密度函数都通过了拟合良好性检验，能够真实反映随机变量的概率分布情况。说明本研究的威布尔分布模型能够较好的适用于坝体填料试验数据的描述及参数估计，具有较好的应用前景。

图 2 上游砂砾填筑料干密度一维威布尔分布拟合

Figure 2. One-dimensional Weibull distribution fitting of dry density in upstream sand-gravel materials

下载: 全尺寸图片幻灯片

图 3 上游砂砾填筑料砾石含量一维威布尔分布拟合

Figure 3. One-dimensional Weibull distribution fitting of gravel content in upstream sand-gravel materials

下载: 全尺寸图片幻灯片

图 4 上游砂砾填筑料曲率系数一维威布尔分布拟合

Figure 4. One-dimensional Weibull distribution fitting of curvature coefficient in upstream sand-gravel materials

下载: 全尺寸图片幻灯片

图 5 上游砂砾填筑料最大粒径一维威布尔分布拟合

Figure 5. One-dimensional Weibull distribution fitting of maximum particle size in upstream sand-gravel materials

下载: 全尺寸图片幻灯片

图 6 下游砂砾填筑料干密度一维威布尔分布拟合

Figure 6. One-dimensional Weibull distribution fitting of dry density in downstream sand-gravel materials

下载: 全尺寸图片幻灯片

图 7 下游砂砾填筑料砾石含量一维威布尔分布拟合

Figure 7. One-dimensional Weibull distribution fitting of gravel content in downstream sand-gravel materials

下载: 全尺寸图片幻灯片

图 8 下游砂砾填筑料曲率系数一维威布尔分布拟合

Figure 8. One-dimensional Weibull distribution fitting of curvature coefficient in downstream sand-gravel materials

下载: 全尺寸图片幻灯片

图 9 下游砂砾填筑料最大粒径一维威布尔分布拟合

Figure 9. One-dimensional Weibull distribution fitting of maximum particle size in downstream sand-gravel materials

下载: 全尺寸图片幻灯片

表 2 上游砂砾填筑料级配威布尔分布模型参数

Table 2. Parameters of Weibull distribution model for gradation of upstream sand-gravel materials

统计指标	样本总数n	位置参数μ	尺度参数σ	形状参数ξ	相关系数r	显著性水平α	临界值D (n，α)	D_n	估计值F(N)
干密度/(g·cm^-3)	453	2.256	0.124	7.824	0.989	0.05	0.0639	0.0384	2.349
砾石含量/%	345	64.000	10.759	5.691	0.998	0.05	0.0732	0.0534	71.245
曲率系数	345	1.500	3.369	2.314	0.988	0.05	0.0732	0.0259	2.774
最大粒径/mm	345	160.000	159.674	2.856	0.996	0.05	0.0732	0.0564	232.621

下载: 导出CSV

| 显示表格

表 3 下游砂砾填筑料级配威布尔分布模型参数

Table 3. Parameters of Weibull distribution model for gradation of downstream sand-gravel materials

统计指标	样本总数n	位置参数μ	尺度参数σ	形状参数ξ	相关系数r	显著性水平α	临界值D (n，α)	D_n	估计值F(N)
干密度/(g·cm^-3)	473	2.016	0.364	19.533	0.984	0.05	0.0625	0.0437	2.341
砾石含量/%	473	57.967	16.907	7.580	0.997	0.05	0.0625	0.0492	70.532
曲率系数	358	1.231	3.469	2.184	0.994	0.05	0.0719	0.0418	2.507
最大粒径/mm	473	110.434	213.426	3.560	0.993	0.05	0.0625	0.0581	223.851

下载: 导出CSV

| 显示表格

从概率密度函数曲线还可以看出，威布尔分布模型具有可偏、截尾、有界的特性，能够推断出一定保证率条件下的参数估计值，且较好的适用于无黏性粗粒土力学参数离散程度大的特点。

在实际工程中，大坝填筑施工质量控制的最关键指标是在标准大坝填筑碾压施工之后，利用挖坑灌水或灌砂法测定干密度。结合统计分析得到的在保证率为90%的条件下坝料级配特征参数的概率分布模型，能够用于碾压之后坝料干密度预测，可为大坝填筑中质量控制提供重要的参考与借鉴。

2.4 基于三维威布尔分布的砂砾石级配参数拟合

通过对干密度主要影响因素的相关性分析，得出了在砂砾石填料区与干密度相关性最密切的砾石含量、曲率系数C_c和最大粒径3个因素，但这3个参数间还同时存在着相关性。基于此，将这3个参数利用推导出的式（14）建立三维威布尔分布模型，其中，r₁₂为砾石含量与曲率系数相关系数，r₂₃为曲率系数与最大粒径相关系数，进而可求出α，β；ξ_j，μ_j，σ_j分别为3个参数在对应的一维威布尔分布中的形状参数、位置参数和尺度参数，将以上值代入式（14）即可求出三维威布尔分布函数G(x, y, z)。其中，此时的频率分布不再是一维威布尔分布中的单个参数的频率，而是同时满足3个参数时的频率。

计算结果见图 10~13，图中横坐标表示三维变量分组的个数，纵坐标表示分布函数值，图 10，11是砂砾石填料区基于砾石含量、曲率系数C_c、最大粒径间相关关系建立的三维威布尔分布模型，图 12，13是心墙上下游过渡料和岸坡过渡料填料区基于砾石含量、曲率系数C_c、含泥量（小于0.075 mm）间相关关系建立的三维威布尔分布模型。由图可知，三维威布尔分布较好地拟合了试验结果，能够同时考虑三个参数对干密度的影响，使干密度的表征方法更具综合性。

图 10 上游砂砾填筑料三维威布尔分布拟合

Figure 10. Three-dimensional Weibull distribution fitting of upstream sand-gravel materials

下载: 全尺寸图片幻灯片

图 11 下游砂砾填筑料三维威布尔分布拟合

Figure 11. Three-dimensional Weibull distribution fitting of downstream sand-gravel materials

下载: 全尺寸图片幻灯片

图 12 心墙上下游过渡料三维威布尔分布拟合

Figure 12. Three-dimensional Weibull distribution fitting of upstream and downstream transition materials on core wall

下载: 全尺寸图片幻灯片

图 13 岸坡过渡料三维威布尔分布拟合

Figure 13. Three-dimensional Weibull distribution fitting of transition materials on bank slope

下载: 全尺寸图片幻灯片

从拟合结果可以看出，使用本研究提出的多维威布尔分布概率模型对新疆大石门水库砂砾石坝料的级配特征参数检验时，其拟合效果相对较好。然后利用K-S检验法分别对不同填料区建立的三维威布尔分布模型进行检验，K-S检验法结果如所示，从表中可看出在在显著性水平 $\alpha$ =0.05条件下，本文构建的三维威布尔概率分布函数模型都通过了拟合良好性检验，能够真实反映随机变量的概率分布情况。

表 4 不同填料区三维威布尔分布模型的K-S检验

Table 4. K-S tests of three-dimensional Weibull distribution models in different packing areas

填料区	样本数n	显著性水平α	临界值D (n，α)	D_n
上游砂砾填筑料	11	0.05	0.391	0.3093
下游砂砾填筑料	11	0.05	0.391	0.2976
心墙上下游过渡料	11	0.05	0.391	0.3424
岸坡过渡料	11	0.05	0.391	0.3137

下载: 导出CSV

| 显示表格

通过每个变量边缘分布的规划求解，得到边缘分布密度函数参数，结合不同变量间相关系数，进而得到与以干密度相关的级配特征为主要因素的多维威布尔分布概率函数。随着大坝填筑施工智能化程度越来越高，越来越多地采用智能化监控设备进行大坝碾压施工过程的实时监控。每一个单元工程或碾压仓位，可积累数十万条海量施工数据，因此利用大坝填筑过程中挖坑检测积累的坝料级配特征数据，整理得到坝料级配的三维威布尔分布模型作为先验分布，结合拟分析的单元工程检测样本，可以推求该单元工程中随机位置的坝料级配后验分布，可为施工过程中海量数据与挖坑检测数据之间的耦合分析提供重要途径与桥梁。

3. 结论

针对土石坝来说，坝料级配控制是坝料压实特性、力学强度及变形参数控制的最重要的指标之一，针对同一来源的砂砾石坝填料，其颗粒组成具有明显的规律性，服从一定的概率分布规律，因此，利用多维的威布尔概率分布对砂砾石坝填料级配的重要特征参数进行拟合研究，对于大坝填筑碾压施工质量控制、压实后坝体材料力学参数估计及坝体变形分析与预测都具有重要的基础意义。通过系统的概率理论推导研究，并结合大石门水利枢纽真实坝料筛分试验结果，进行了砂砾石坝填料多维概率分布拟合研究与应用探讨，主要得到3点结论。

（1）采用数据处理软件SPSS 22对新疆大石门水库砂砾石坝料的级配特征参数进行了相关性分析，分别得出了在砂砾石填料区和过渡料填料区与干密度相关性最密切的3个级配特征参数。

（2）给出了一维威布尔概率分布模型的详细推导过程，结合大石门大坝工程施工过程中得到的施工质量检测资料，对上、下游砂砾填料级配特征参数进行了威布尔分布概率拟合，得到的不同级配特征参数的拟合结果与经验值之间的相关系数均大于0.98，取得了较好的拟合效果。结果表明，一维威布尔分布能够较好的描述砾石填料的参数特征，并能预测出在一定保证率条件下的参数估计值，可以用于碾压之后的坝料干密度预测，为大坝填筑中质量控制提供参考与借鉴。

（3）推导了三维威布尔分布函数表达式，建立了能够利用颗粒砾石含量、最大粒径及曲率系数C_c间的相关关系反映砂砾石填料区干密度的三维威布尔分布模型，以及利用颗粒砾石含量、曲率系数C_c、含泥量（小于0.075 mm）间的相关关系反映过渡料填料区干密度的三维威布尔分布模型，该模型能够同时考虑三个参数对干密度的影响，使干密度的表征方法更具综合性，可用于砂砾填料的质量评估和预测。

在后续的研究中，本文将利用上述整理得到坝料级配的多维威布尔分布模型作为先验分布，结合拟分析的某单元工程检测样本，推求该单元工程中随机位置的坝料级配后验分布，然后通过同一母体中的多维威布尔分布先验与后验分析，得到某一单元工程中的任意部位在一定分位数条件下服从多维概率分布的随机数，通过相关研究得到的该点的工程力学参数，进而实现真正的大坝拟真实性态的应力变形分析。

图 1 高温下饱和冻土一维融化过程示意图

Figure 1. Schematic diagram of 1-D thawing process of saturated frozen soil under high temperature

下载: 全尺寸图片幻灯片

图 2 超静孔压解答中g函数的变化

Figure 2. g function in analytical solution of excessive pore water pressure

下载: 全尺寸图片幻灯片

图 3 ε对 $\bar{P}$ 影响

Figure 3. Effects of ε on $\bar{P}$

下载: 全尺寸图片幻灯片

图 4 R对 $\bar{P}$ 影响

Figure 4. Effects of R on $\bar{P}$

下载: 全尺寸图片幻灯片

图 5 F对 $\bar{P}$ 影响

Figure 5. Effects of F on $\bar{P}$

下载: 全尺寸图片幻灯片

图 6 W_r对 $\bar{P}$ 影响

Figure 6. Effects of W_r on $\bar{P}$

下载: 全尺寸图片幻灯片

图 7 各部分无量纲沉降随W_r的变化

Figure 7. Variation of different dimensionless settlements with W_r

下载: 全尺寸图片幻灯片

图 8 各部分无量纲沉降随F的变化

Figure 8. Variation of different dimensionless settlements with F

下载: 全尺寸图片幻灯片

图 9 各部分无量纲沉降随R的变化

Figure 9. Variation of different dimensionless settlements with R

下载: 全尺寸图片幻灯片

表 1 文献[29]中材料参数及A的计算值

Table 1 Material parameters and computed values of A in Ref.[29]

材料 a_w/(10^-4℃^-1) a_s/(10^-6℃^-1) a_sm/(10^-6℃^-1) n E/MPa v A/(10^-4MPa℃^-1)

A 3 3 3 0.25 5.0 0.2 -4.2083
B 3 3 3 0.375 2.880 0.2 -3.6120

下载: 导出CSV

参考文献(36)

[1]	李国玉, 马巍, 王学力, 等. 中俄原油管道漠大线运营后面临一些冻害问题及防治措施建议[J]. 岩土力学, 2015, 36(10): 2963-2973. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201510034.htm LI Guo-yu, MA Wei, WANG Xue-li, et al. Frost hazards and mitigative measures following operation of Mohe-Daqing line of China-Russia crude oil pipeline[J]. Rock and Soil Mechanics, 2015, 36(10): 2963-2973. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201510034.htm
[2]	牛富俊, 程国栋, 赖远明, 等. 青藏高原多年冻土区热融滑塌型斜坡失稳研究[J]. 岩土工程学报, 2004, 26(3): 402-406. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200403024.htm NIU Fu-jun, CHENG Guo-dong, LAI Yuan-ming, et al. Instability study on thaw slumping in permafrost regions of Qinghai-Tibet Plateau[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(3): 402-406. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200403024.htm
[3]	陈瑞杰, 程国栋, 李述训, 等. 人工地层冻结应用研究进展和展望[J]. 岩土工程学报, 2000, 22(1): 40-44. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200001006.htm CHEN Rui-jie, CHENG Guo-dong, LI Shu-xun, et al. Development and prospect of research on application of artificial ground freezing[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(1): 40-44. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200001006.htm
[4]	胡向东, 李忻轶, 吴元昊, 等. 拱北隧道管幕冻结法管间冻结封水效果实测研究[J]. 岩土工程学报, 2019, 41(12): 2207-2214. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201912008.htm HU Xiang-dong, LI Xin-yi, WU Yuan-hao, et al. Effect of water-proofing in Gongbei Tunnel by freeze-sealing pipe roof method with field temperature data[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(12): 2207-2214. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201912008.htm
[5]	周洁, 李泽垚, 万鹏, 等. 组合地层渗流对人工地层冻结法及周围工程环境效应的影响[J]. 岩土工程学报, 2021, 43(3): 471-480. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202103013.htm ZHOU Jie, LI Ze-yao, WAN Peng, et al. Effects of seepage in clay-sand composite strata on artificial ground freezing and surrounding engineering environment[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(3): 471-480. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202103013.htm
[6]	张升, 颜瀚, 滕继东, 等. 一个冻土的渗透系数模型及其验证[J]. 岩土工程学报, 2020, 42(11): 2146-2152. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202011026.htm ZHANG Sheng, YAN Han, TENG Ji-dong, et al. New model for hydraulic conductivity of frozen soils[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(11): 2146-2152. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202011026.htm
[7]	程桦, 陈汉青, 曹广勇, 等. 冻土毛细-薄膜水分迁移机制及其试验验证[J]. 岩土工程学报, 2020, 42(10): 1790-1799. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202010004.htm CHENG Hua, CHEN Han-qing, CAO Guang-yong, et al. Migration mechanism of capillary-film water in frozen soil and its experimental verification[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(10): 1790-1799. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202010004.htm
[8]	周扬, 周国庆, 周金生, 等. 饱和土冻结透镜体生长过程水热耦合分析[J]. 岩土工程学报, 2010, 32(4): 578-585. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201004018.htm ZHOU Yang, ZHOU Guo-qing, ZHOU Jin-sheng, et al. Ice lens growth process involving coupled moisture and heat transfer during freezing of saturated soil[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(4): 578-585. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201004018.htm
[9]	周扬, 周国庆, 王义江. 饱和土水热耦合分离冰冻胀模型研究[J]. 岩土工程学报, 2010, 32(11): 1746-1751. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201011021.htm ZHOU Yang, ZHOU Guo-qing, WANG Yi-jiang. Separate ice frost heave model for coupled moisture and heat transfer in saturated soils[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1746-1751. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201011021.htm
[10]	ZHOU Y, ZHOU G Q. Intermittent freezing mode to reduce frost heave in freezing soils—experiments and mechanism analysis[J]. Canadian Geotechnical Journal, 2012, 49(6): 686-693. doi: 10.1139/t2012-028
[11]	梁波, 张贵生, 刘德仁. 冻融循环条件下土的融沉性质试验研究[J]. 岩土工程学报, 2006, 28(10): 1213-1217. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200610006.htm LIANG Bo, ZHANG Gui-sheng, LIU De-ren. Experimental study on thawing subsidence characters of permafrost under frost heaving and thawing circulation[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(10): 1213-1217. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200610006.htm
[12]	王天亮, 卜建清, 王扬, 等. 多次冻融条件下土体的融沉性质研究[J]. 岩土工程学报, 2014, 36(4): 625-632. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201404006.htm WANG Tian-liang, BU Jian-qing, WANG Yang, et al. Thaw subsidence properties of soils under repeated freeze-thaw cycles[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(4): 625-632. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201404006.htm
[13]	王效宾, 杨平, 张婷. 人工冻土融沉特性试验研究[J]. 南京林业大学学报(自然科学版), 2008, 32(4): 108-112. WANG Xiao-bin, YANG Ping, ZHANG Ting. Study on thaw settlement behaviour of artificial freezing soil[J]. Journal of Nanjing Forestry University (Natural Sciences Edition), 2008, 32(4): 108-112. (in Chinese)
[14]	赵贵涛, 韩仲, 邹维列, 等. 干湿、冻融循环对膨胀土土-水及收缩特征的影响[J]. 岩土工程学报, 2021, 43(6): 1139-1146. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202106024.htm ZHAO Gui-tao, HAN Zhong, ZOU Wei-lie, et al. Influences of drying-wetting-freeze-thaw cycles on soil-water and shrinkage characteristics of expansive soil[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(6): 1139-1146. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202106024.htm
[15]	MORGENSTERN N R, NIXON J F. One-dimensional consolidation of thawing soils[J]. Canadian Geotechnical Journal, 1971, 8(4): 558-565.
[16]	MORGENSTERN N R, SMITH L B. Thaw-consolidation tests on remoulded clays[J]. Canadian Geotechnical Journal, 1973, 10(1): 25-40.
[17]	NIXON J F, MORGENSTERN N R. Thaw-consolidation tests on undisturbed fine-grained permafrost[J]. Canadian Geotechnical Journal, 1974, 11(1): 202-214.
[18]	ZHOU Y, ZHANG L Y, XU C, et al. Analytical solution for classical one-dimensional thaw consolidation model considering unfrozen water effect and time-varying load[J]. Computers and Geotechnics, 2020, 122: 103513.
[19]	FORIERO A, LADANYI B. FEM assessment of large-strain thaw consolidation[J]. Journal of Geotechnical Engineering, 1995, 121(2): 126-138.
[20]	GIBSON R E, SCHIFFMAN R L, CARGILL K W. The theory of one-dimensional consolidation of saturated clays. II. Finite nonlinear consolidation of thick homogeneous layers[J]. Canadian Geotechnical Journal, 1981, 18(2): 280-293.
[21]	YAO X L, QI J L, WU W. Three dimensional analysis of large strain thaw consolidation in permafrost[J]. Acta Geotechnica, 2012, 7(3): 193-202.
[22]	YAO X L, QI J L, LIU M X, et al. Pore water pressure distribution and dissipation during thaw consolidation[J]. Transport in porous media, 2017, 116(2): 435-451.
[23]	QI J L, YAO X L, YU F, et al. Study on thaw consolidation of permafrost under roadway embankment[J]. Cold Regions Science and Technology, 2012, 81: 48-54.
[24]	WANG S H, QI J L, YU F, et al. A novel method for estimating settlement of embankments in cold regions[J]. Cold Regions Science and Technology, 2013, 88: 50-58.
[25]	WANG L M, WANG W L, YU F. Thaw consolidation behaviours of embankments in permafrost regions with periodical temperature boundaries[J]. Cold Regions Science and Technology, 2015, 109: 70-77.
[26]	DUMAIS S, KONRAD J M. One-dimensional large-strain thaw consolidation using nonlinear effective stress-void ratio-hydraulic conductivity relationships[J]. Canadian Geotechnical Journal, 2018, 55(3): 414-426.
[27]	王涛, 岳丰田, 姜耀东, 等. 井筒冻结壁强制解冻技术的研究与实践[J]. 煤炭学报, 2010, 35(6): 918-922. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201006012.htm WANG Tao, YUE Feng-tian, JIANG Yao-dong, et al. Research and practice on forced thaw technology applied to frozen wall of mine shaft[J]. Journal of China Coal Society, 2010, 35(6): 918-922. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201006012.htm
[28]	袁云辉, 杨平, 王海波. 人工水平冻结冻土帷幕强制解冻温度场数值分析[J]. 南京林业大学学报(自然科学版), 2011, 35(4): 117-120. https://www.cnki.com.cn/Article/CJFDTOTAL-NJLY201104027.htm YUAN Yun-hui, YANG Ping, WANG Hai-bo. Thermal field numerical analysis of artificial thawing of horizontal freezing soil wall[J]. Journal of Nanjing Forestry University (Natural Sciences Edition), 2011, 35(4): 117-120. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-NJLY201104027.htm
[29]	ZHOU Y, RAJAPAKSE R K N D, GRAHAM J. A coupled thermoporoelastic model with thermo-osmosis and thermal-filtration[J]. International Journal of Solids and Structures, 1998, 35(34/35): 4659-4683.
[30]	白冰. 岩土颗粒介质非等温一维热固结特性研究[J]. 工程力学, 2005, 22(5): 186-191. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200505033.htm BAI Bing. One-dimensional thermal consolidation characteristics of geotechnical media under non-isothermal condition[J]. Engineering Mechanics, 2005, 22(5): 186-191. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200505033.htm
[31]	吴瑞潜, 谢康和, 程永锋. 变荷载下饱和土一维热固结解析理论[J]. 浙江大学学报(工学版), 2009, 43(8): 1532-1537. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC200908034.htm WU Rui-qian, XIE Kang-he, CHENG Yong-feng. Analytical theory for one-dimensional thermal consolidation of saturated soil under time-dependent loading[J]. Journal of Zhejiang University (Engineering Science), 2009, 43(8): 1532-1537. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC200908034.htm
[32]	钮家军, 凌道盛, 王秀凯, 等. 饱和单层土体一维热固结精确解[J]. 岩土工程学报, 2019, 41(9): 1715-1723. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909018.htm NIU Jia-jun, LING Dao-sheng, WANG Xiu-kai, et al. Exact solutions for one-dimensional thermal consolidation of single-layer saturated soil[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1715-1723. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909018.htm
[33]	ZHOU Y, ZHOU J, SHI X Y, et al. Practical models describing hysteresis behavior of unfrozen water in frozen soil based on similarity analysis[J]. Cold Regions Science and Technology, 2019, 157: 215-223.
[34]	ZHOU Y, WANG Y J, BU W K. Exact solution for a Stefan problem with latent heat a power function of position[J]. International Journal of Heat and Mass Transfer, 2014, 69: 451-454.
[35]	ZHOU Y, HU X X, LI T, et al. Similarity type of general solution for one-dimensional heat conduction in the cylindrical coordinate[J]. International Journal of Heat and Mass Transfer, 2018, 119: 542-550.
[36]	涂新斌, 戴福初. 土体一维传热方程解析解及热扩散系数测定[J]. 岩土工程学报, 2008, 30(5): 652-657. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200805007.htm TU Xin-bin, DAI Fu-chu. Analytical solution for one-dimensional heat transfer equation of soil and evaluation for thermal diffusivity[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(5): 652-657. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200805007.htm

施引文献(19)

期刊类型引用(11)

1.	邢玮，朱锐，张晨，王羿，周峰. 高寒地区供水渠道水热特征及其长期演化规律. 南京工业大学学报(自然科学版). 2024(01): 93-102 . 百度学术
2.	柴石玉，张凌凯. 干湿-冻融循环对碱激发粉煤灰-矿粉改性膨胀土力学特性的损伤机理研究. 工程力学. 2024(11): 157-167 . 百度学术
3.	张晨，陈红永，王羿，蔡正银. 寒区工程离心模型试验地基表面换热特性及热边界设置方法研究. 水利学报. 2023(06): 729-738 . 百度学术
4.	凌松耀，蹇永明，张智勇，李卓，黄翀垚，郭兴会，张奇. 融雪-降雨型滑坡失稳机理. 科学技术与工程. 2023(21): 8980-8987 . 百度学术
5.	蔡正银，朱洵，张晨，黄英豪. 高寒区膨胀土渠道边坡性能演变规律. 中南大学学报(自然科学版). 2022(01): 21-50 . 百度学术
6.	朱锐，郭万里. 寒区渠道粉土质砂换填料力学特性试验研究. 中南大学学报(自然科学版). 2022(04): 1461-1471 . 百度学术
7.	蔡正银，张晨，朱洵，黄英豪，王羿. 高寒区长距离供水工程能力提升与安全保障技术. 岩土工程学报. 2022(07): 1239-1254 . 本站查看
8.	李燕，王斯海，朱锐. 复杂边界条件下膨胀土的体变特性与抗压强度研究. 水利水运工程学报. 2022(04): 106-113 . 百度学术
9.	朱锐，蔡正银，黄英豪，张晨，郭万里，朱洵. 湿干冻融循环下渠水入渗特性的离心模型试验和现场试验研究（英文）. Journal of Central South University. 2021(05): 1519-1533 . 百度学术
10.	朱锐，蔡正银，黄英豪，张晨，郭万里. 冻融过程对高寒区渠道基土力学特性的影响. 农业工程学报. 2021(14): 108-116 . 百度学术
11.	陈永，黄英豪，朱洵，吴敏，王硕，朱锐. 冻融循环对膨胀土变形和力学特性的影响研究. 水利水运工程学报. 2021(05): 112-119 . 百度学术