对“稳定安全系数计算公式中荷载与抗力错位影响探讨”质疑的答复

付文光

doi:10.11779/CJGE202111025

对“稳定安全系数计算公式中荷载与抗力错位影响探讨”质疑的答复 English Version

付文光

1.
深圳市工勘岩土集团有限公司,广东　深圳　518063
2.
广东省岩土与地下空间工程技术研究中心,广东　深圳　518063

详细信息

作者简介:
付文光(1970— ),男,北京人,教授级高级工程师,主要从事岩土工程设计咨询、工程实践与试验研究等工作。E-mail：zgjy1992@126.com

中图分类号: TU43
计量
- 文章访问数: 256
- HTML全文浏览量: 12
- PDF下载量: 252
出版历程
- 收稿日期: 2021-04-25
- 网络出版日期: 2022-12-01
- 刊出日期: 2021-10-31

Reply to query about "Discussion of dislocation phenomena of resistance and load in formula for stability safety factor"

FU Wen-guang

1.
Shenzhen GongKan Geotechnical Group Co., LTD, Shenzhen 518063, China
2.
Guangdong Engineering and Technology Research Center for Geotechnique and Underground Space, Shenzhen 518063, China

摘要

HTML全文

孙建生老师对敝人《稳定安全系数计算公式中荷载与抗力错位影响探讨》^[1]（以下简称原文）提出了宝贵的指导及讨论意见,非常感谢！

业界普遍认为边坡稳定安全系数目前主要有两种定义方法：①为抗滑力矩与下滑力矩之比（通常可简化为抗力荷载比）,相应的稳定安全系数计算方法一般采用单一安全系数法（原文即采用此法）,以瑞典条分法为代表；②定义为滑动面上的抗剪强度与实际产生的剪应力之比,相应的稳定安全系数计算方法一般采用强度（抗剪强度）折减法,以毕肖普法（Bishop）及简布法（Janbu）为代表。宋二祥等^[2]倾向于第二种定义。孙文中 $\sum R \div K = \sum S$ ,对所有抗滑力除以了同一安全系数K、即均进行了折减,从公式表达来看与单一安全系数法没什么不同,与强度折减法仅对岩土体的抗剪强度进行折减明显不同。

但文献[3]认为“抗滑稳定安全系数K是表达……实际……滑动力 $\sum S$ 与理论极限（虚拟概念）抗滑力 $\sum R$ 的极限平衡接近程度”,之后的论述绕此展开。“实际滑动力”、“理论极限抗滑力”及“极限平衡接近程度”等用语是理解文献[3]观点的关键。

第②种定义中的“抗剪强度”及“剪应力”也可表达为“抗力”及“荷载”或“抗滑力”及“滑动力”,从文献[3]角度来看,极限抗滑力是理论的,故是“虚拟概念”；实际滑动力即实际发生的荷载,与抗滑力相等时则土体处于极限平衡状态；在安全系数K计算过程中通过逐步折减而逼近极限平衡状态,表达了实际滑动力与抗滑力的接近程度,故文献[3]更适合从第②种定义及强度折减法的角度去理解。倘若如此,则：

（1）文献[3]认为原文极限平衡力学基本概念混淆、错误、缺失。笔者认为,原文没有明示但实质上依据的是第一种定义,文献[3]讨论的实质上属于第②种定义,两种定义中的概念不同是正常现象。

（2）文献[3]认为“分子与分母加减项的变化必然影响到安全系数计算结果,但这绝不是极限平衡概念的滑动力荷载与极限抗滑力概念错位问题的探讨依据”,笔者同意。“分子与分母加减项的变化必然影响到安全系数计算结果”正是原文目的,原文探讨的就是加减项中的那些不合理项导致的按第一种定义编写的安全系数计算公式有时并不完全符合第一种定义这种现象；“计算结果……不是概念错位问题的探讨依据”,因为定义形式不同,当然不能把根据第一种定义获得的计算结果当作探讨第二种定义概念的依据。

（3）文献[3]认为抗滑力是虚拟受力。笔者认为,抗滑力大于滑动力时可如此认为,小于时（处于极限平衡状态或滑坡时）则不是虚拟的、而是实际发生的。

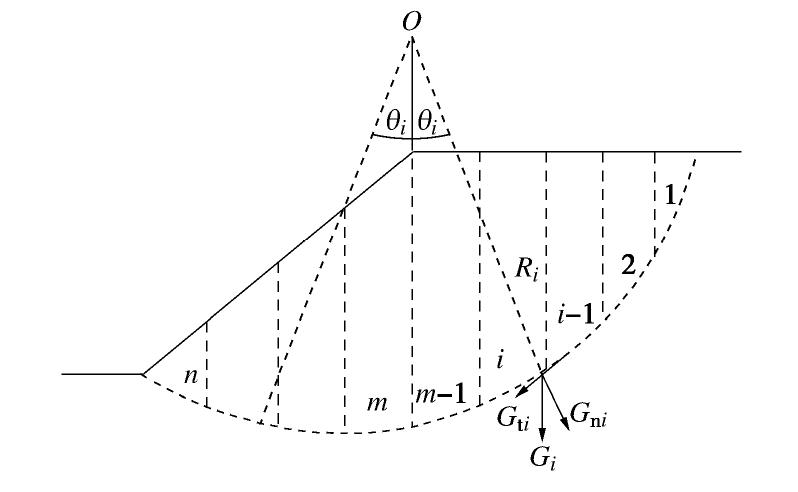
（4）文献[3]认为“在 $K = \frac{\sum R}{\sum S}$ 公式中,分子抗滑力 $\sum R$ 包含所有极限虚拟概念状态的抗滑力因素,不论正负......分母滑动力 $\sum S$ 包含所有实际切向滑动力因素,不论正负”,笔者没有理解。①所有的抗滑力均应是同向、即“正”的,“负抗滑力”指的是什么呢?如果是负的,与抗滑力反向的,就应该是滑动力；但如果是滑动力,就应该如第②种定义及文献[3]前述,是实际发生的,那么就不是“虚拟概念”的,因为“虚拟概念”的是抗滑力；但如果是抗滑力,就应该与其它“正”抗滑力同向、不应为负,故“负抗滑力”到底是什么力,很难理解；②同理,所有的滑动力均应是同向、即“正”的,“负滑动力很难理解；③假定部分滑动力也可以“虚拟概念”、即作为“负抗滑力”计入分子 $\sum R$ ,部分抗滑动可以实际发生、即作为“负滑动力”计入分母 $\sum S$ ,那么,哪些滑动力可以计入分子、哪些抗滑力可以计入分母?

仍以瑞典条分法为例,当滑弧中心点O位于边坡上方时,如图1所示,土条1~（m-1）的重力产生滑动力 $\sum_{i = 1}^{m - 1} G ti$ ,土条m~n的重力产生抗滑力 $\sum_{i = m}^{n} G ti$ ,两者作用方向相反,围绕着两者关系如何处理产生4种稳定安全系数K计算公式,其中前2种工程应用广泛：

$K = \frac{\sum_{i = 1}^{n} (G_{n i} \tan φ_{i} + c_{i} l_{i})}{\sum_{i = 1}^{m - 1} G_{t i} - \sum_{i = m}^{n} G_{t i}}$ ,

(1)

$K = \frac{\sum_{i = 1}^{n} (G_{n i} \tan φ_{i} + c_{i} l_{i})}{\sum_{i = 1}^{m - 1} G_{t i} + \sum_{i = m}^{n} G_{t i}}$ ,

(2)

$K = \frac{\sum_{i = 1}^{n} (G_{n i} \tan φ_{i} + c_{i} l_{i}) - \sum_{i = m}^{n} G_{t i}}{\sum_{i = 1}^{m - 1} G_{t i}}$ ,

(3)

$K = \frac{\sum_{i = 1}^{n} (G ni \tan φ i + c i l i) + \sum_{i = m}^{n} G ti}{\sum_{i = 1}^{m - 1} G ti}$ 。

(4)

图 1 瑞典条分法边坡稳定分析简图

Figure 1. Sketch about slope stability analysis by Swedish Slicing Method

下载: 全尺寸图片幻灯片

式（1）～（4）从文献[3]角度来看：①式（1）将 $\sum_{i = m}^{n} G_{t i}$ 放在分母与滑动力 $\sum_{i = 1}^{m - 1} G_{t i}$ 相减,可认为是 $\sum S$ 中的“负滑动力”；②式（2）将之放在分母与滑动力相加,可认为是 $\sum S$ 中的“正滑动力”；③式（3）将之放在分子与抗滑力 $\sum_{i = 1}^{n} （ G_{n i} tan φ_{i} + c_{i} l_{i} ）$ 相减,可认为是 $\sum R$ 中的“负抗滑力”；④式（4）将之放在分子与抗滑力相加,可认为是 $\sum R$ 中的“正抗滑力”。那么, $\sum_{i = m}^{n} G_{t i}$ 到底是“负滑动力”、“正滑动力”、“负抗滑力”还是“正抗滑力”?这个问题文献[3]没有指明如何处理,却正是原文所讨论的核心内容,换句话说,在这个问题上原文所讨论的内容与孙文观点是互补的。

（4）其余意见详见笔者对文献[2]的回复意见,不再赘述。

总结：①业界对边坡稳定安全系数的主要定义形式有两种,原文依据的是第一种,孙文实质上依据的是第二种,故概念有所不同；②文献[3]提出了“负抗滑力”及“负滑动力”等观点但没有提出实现方法,没有解决原文讨论的安全系数计算公式中抗力与荷载错位（从文献[3]角度可理解为抗滑力与滑动力应用不当）的问题。

笔者对文献[3]理解不准确及本回复意见不妥之处,敬请孙老师及读者们谅解及继续批评指正。

图 1 瑞典条分法边坡稳定分析简图

Figure 1. Sketch about slope stability analysis by Swedish Slicing Method

下载: 全尺寸图片幻灯片

参考文献(3)

[1]

付文光, 陈双, 王振威. 稳定安全系数计算公式中荷载与抗力错位影响探讨[J]. 岩土工程学报, 2021, 43(3): 556-563. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202103023.htm

FU Wen-guang, CHEN Shuang, WANG Zhen-wei. Discussion of dislocation phenomena of resistance and load in formula for stability safety factor[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(3): 556-563. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202103023.htm

[2]

宋二祥. 条分法计算边坡稳定安全系数的定义——关于“稳定安全系数计算公式中荷载与抗力错位影响探讨”的讨论[J]. 岩土工程学报, 2021, 43(11): 2142-2143. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202111025.htm

SONG Er-xiang. On the safety factor definition of slope stability calculated by the slices method — Discussion on “Discussion of dislocation phenomena of resistance and load in formula for stability safety factor”[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(11): 2142-2143. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202111025.htm

[3]

孙建生. 关于“稳定安全系数计算公式中荷载与抗力错位影响探讨”的质疑[J]. 岩土工程学报, 2021, 43(11): 2146. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202111028.htm

SUN Jian-sheng. Query about “Discussion of dislocation phenomena of resistance and load in formula for stability safety factor”[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(3): 2146. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202111028.htm

施引文献(2)

期刊类型引用(2)

1.	王卫星，潘大荣，陈立. 某地铁车站基坑外车道超载安全性分析. 江苏建筑. 2023(04): 112-114+125 . 百度学术
2.	谷浩源，韩流，张健，刘世宝，高志强，吴锋锋. 水-热耦合下露天矿冻结期靠帮开采边坡稳定性研究. 煤矿安全. 2023(12): 159-166 . 百度学术