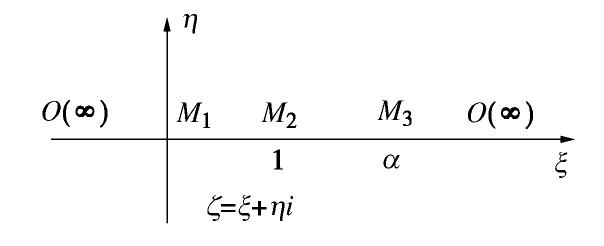Simplified calculation and design method of multi-well system for anti-uplifting based on intercepting and discharging water
-
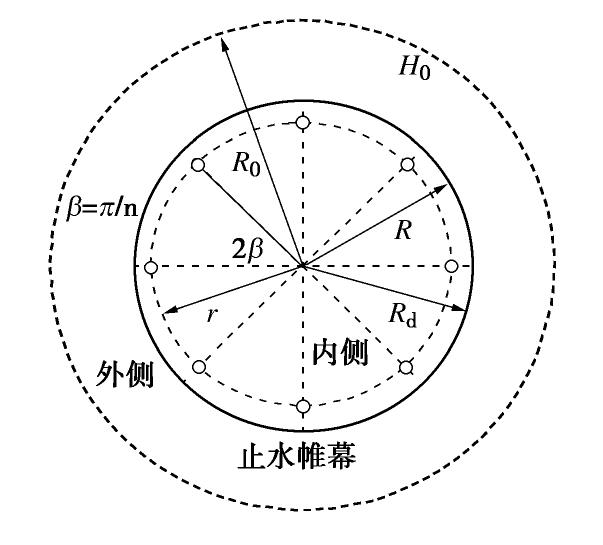
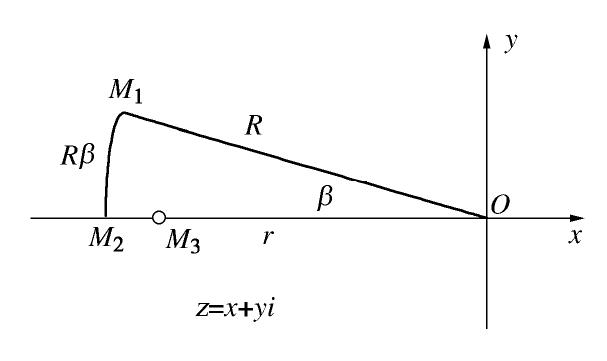
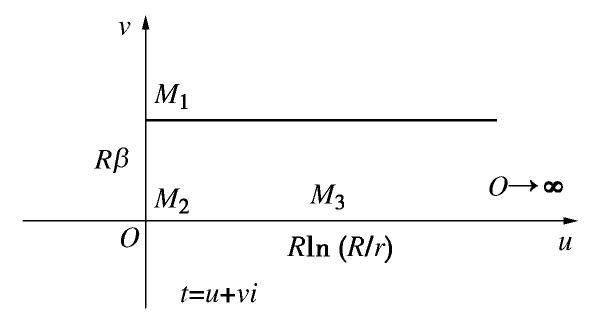
摘要: 对于截排减压抗浮系统中的减压井群（多井系统）,目前除采用数值法进行渗流分析外,尚无实用的简化计算方法,不利于推广使用。鉴于此,提出了简化计算方法：对于圆形止水帷幕内侧均匀分布的多井系统,假定止水帷幕内侧边界水头为常数,通过共形映射推导得到多井系统的水头分布；对于非圆形止水帷幕,可将其等效为圆形近似求解；采用阻力系数法,在考虑止水帷幕透水和绕渗的基础上,将止水帷幕内外侧渗流场串联起来,求解得到总流量。经算例验证,简化算法与有限元法相比结果差距较小,且仅需提供不多的几何参数,即可求得较精确的结果。在排水减压抗浮设计时,控制板底水头和井周水力坡降是关键,为兼顾安全性和经济性,需对参数n,r,hw及rw反复调整以达到最佳效果。Abstract: For the multi-well system in the anti-uplifting system based on intercepting and discharging water, there is no practical simplified method except the numerical method for seepage analysis, which is not conducive to its application. In view of this, a simplified method is proposed. The idea is as follows: for the multi-well system with even distribution inside the circular cut-off wall, the hydraulic head on the inside boundary of the cut-off wall is assumed to be constant, and the distribution of the hydraulic head of the multi-well system is deduced through conformal mapping. For the non-circular cut-off wall, it can be equivalent to a circle to obtain an approximate solution.The resistance coefficient method is adopted to connect the inner and outer seepage fields of the cut-off wall in series on the basis of considering the water leakage and by-pass seepage of the cut-off wall, and the total flow can be obtained. After verification, a comparison with the finite element method shows that the difference between the simplified algorithm and the finite element method is smaller, and it only needs to provide a few geometric parameters to get more accurate results. The control of the hydraulic head at the bottom of the floor and the hydraulic slope around the well are the key points in the anti-uplifting design process based on drainage decompression. Moreover, in order to give consideration of both safety and economy, parameters n, r, hw and rw need to be adjusted repeatedly to achieve the best effect.
-
Keywords:
- anti-uplifting /
- seepage /
- multi-well system /
- cut-off wall /
- conformal mapping
-
0. 引言
桩基因其承载力高、沉降小等特点,而广泛应用于桥梁、建筑、码头、海上风电等重大工程中。桩基础承载力的可靠性直接关乎上部结构的安全,承载力直接确定方法主要是桩顶静载试验。针对承载力高、现场试验条件复杂等测试难题,而后也发展出O-cell法或自平衡法,极大地推动了对桩基础的承载机理研究。但实际工程中,桩基础的初步设计及承载力预估主要依赖于基本的岩土试验参数,如SPT(标注贯入试验)、CPT(静力触探试验)、PMT(旁压试验)等试验方法确定的参数。不同国家及不同行业领域规范也会偏重于某一岩土试验方法,如法国规范(NF P94-150-1)[1]主要采用PMT法,采用法国规范的地区一般进行PMT试验,而很少做其他岩土参数试验。
旁压试验参数既能用于工程场地地质评价,也能对浅基础的地基承载力进行设计和桩基础承载力设计[2-3]。彭柏兴[4]对长沙某工程44根嵌岩桩进行统计分析,认为按照旁压试验计算的软质裂隙岩体的允许承载力,其安全度能满足工程设计要求。王哲威等[5]对阿尔及利亚东西高速公路桥梁工程进行了现场旁压试验,分别应用法国规范和中国规范对桩基承载力进行计算,发现两者差别较小。杨石飞等[6]对上海软土地区30多项旁压试验及133组静载试验进行统计分析,提出了根据旁压试验确定挤土桩和非挤土桩的承载力计算公式。此外,Schlosser等[7]对突尼斯湖Rades桥深厚黏土场地进行现场旁压试验,采用旁压试验预测了桩基承载力,与实测承载力较接近。Boumedi等[8]利用旁压试验对尼罗河下游的LNG储油罐桩基础竖向和水平承载力进行预测,发现与实测结果吻合较好。
既有文献大多数利用旁压试验对嵌岩及黏性土中桩基进行承载力预测,但很少有对深厚砂性土中桩基承载力进行预测,也缺少现场静载试验对比。为了揭示深厚砂性地层中的桩基承载特性,以下选取了非洲某大桥主桥试桩进行竖向静载试验,对比分析了旁压试验方法与其他不同方法的承载力计算结果,为类似工程设计提供有益参考。
1. 旁压试验确定桩基承载力的方法
旁压试验是利用可侧向膨胀的旁压仪,通过对钻孔孔壁周围土体施加径向压力的原位测试方法。根据孔壁压力与变形量的关系,计算地基土承载力、压缩模量。该原位试验方法适用土层较广泛,可应用于软弱土层,也可用于软岩地层,且试验深度可达到100 m以上。Baguelin等[9]认为旁压试验比较接近桩周土受力模型,Briaud[10]认为旁压试验是一种很好的分析桩基承载力和桩基沉降的试验方法。根据欧洲规范(BS EN 1997—2)及法国规范,桩基竖向承载力可通过现场旁压试验进行计算,推荐采用Menard方法,公式如下：
(1) 
(2) 
(3) 式中Q为单桩竖向承载力；A为桩端截面积；k为抗压承载力系数,与桩端持力层性质以及桩类型有关,可根据规范查表得到,对于非挤土桩k为1.0~1.8,对于挤土桩k为1.4~4.2;
(4) 
(5) 
(6) 式中z为土层深度,D为桩径；L为桩入土长度；h为桩端以上持力层厚度。
此外,Baguelin采用如下公式计算侧摩阻力qs和端阻力qb:
(7) 
(8) 2. 工程应用及试桩承载力对比
2.1 工程概述及地质条件
非洲科特迪瓦某新建桥梁全长630 m,主桥为主跨200 m独塔斜拉桥,跨越运河,主梁为钢混组合梁型式。连接线采用34.2 m跨连续梁结构,全线桥梁下部结构采用桩基础。为得到桩的极限承载力及对应沉降,本项目对主线桥及法国大街立交桥进行桩基荷载试验。
为了有效推进该大桥的设计工作,自平衡法被推荐为基桩承载力检测的静载试验方法,选取了2根主桥P3和P7桥墩附近的基桩进行静载试验。其中试桩TP-1位于主桥P3轴线上,距离P3墩台外边缘7 m；试桩TP-2位于主桥P7墩顺桥方向轴线上,距离P7墩系梁外边缘7 m。桩长范围主要为细砂及中砂类砂性土,两根试桩及其地层剖面如图1所示。
2.2 桩基静载试验结果与分析
(1)荷载位移分析
根据设计要求,试验按照法国规范[1]分两次循环加卸载。两根试桩均采用双荷载箱(如图1所示),试验先加载下荷载箱,再加载上荷载箱,通过加载上下两个荷载箱可得到桩基承载力。通过向上向下荷载位移曲线,可按照自平衡规范[11]等效转换得到桩顶的荷载位移曲线,如图2所示。
从图2可知,试桩TP-1和TP-2第1次循环加载至峰值时等效得到的桩顶荷载分别为18032 kN和20676 kN,对应的位移分别34.65 mm和89.15 mm。而试桩第2次循环加载至极限时,等效得到的荷载分别为21832 kN和23076 kN,对应的位移分别为46.97 mm和109.37 mm。说明第1次循环加载沉降量较显著,可能因为砂性地层桩端密实性较差,存在一定厚度的沉渣影响,通过第1次循环加载可使得桩端土进一步压密,从而第2次循环加载位移趋于平缓。试桩TP-2的沉降量远大于试桩TP-1,说明试桩TP-1的施工质量更好,可能因为TP-2钻孔深度大于TP-1钻孔深度,成孔时间长,影响成桩质量。由于该试桩桩径为2.0 m,根据法国标准(NF P94—150—1)[1]及欧洲规范(EN 1997—2)[12],极限位移可取为0.1D(D为桩径),即为200 mm。但是,为了设计保守,建议取为实际最大极限加载值等效桩顶荷载作为试桩的极限承载力。
(2)桩侧摩阻力分析
为了获得桩身不同位置的轴力及土层侧摩阻力,在不同截面埋设了应变计,如图1所示。应变计考虑了温差影响,每级加载阶段桩身截面的应变计应变变化量计算公式如下：
(9) 式中εi和ε0分别为第i级加载时的测量应变值、初始应变值,单位为με;Ti和T0分别为第i等级加载时的测量温度、初始温度；F应变计和F混凝土分别为12.2 με/℃和10 με/℃。
根据计算的桩身轴力及实测位移,可推算得到桩侧摩阻力和桩身某一截面的位移。为了分析不同土层侧摩阻力发挥机理,将两根试桩桩身各区段侧摩阻力位移关系曲线绘制如图3所示,限于篇幅,图中仅提供了下荷载箱测试分析结果。由图3可知,随着位移的增加,桩侧的摩擦力逐渐发挥,越靠近桩端的密实土层,极限摩阻力越大,且极限摩阻力的临界位移也越大。通过对桩端附近土侧摩阻力位移曲线分析,发现桩端附近土侧摩阻力出现硬化增长现象,可能受桩端阻力影响。而其他土层的侧阻力位移则表现为快速增长和平稳变化形态。其中TP-1试桩侧阻力快速增长阶段的剪切位移主要为5 mm以内,而平稳阶段主要为5~10 mm。但TP-2试桩的两阶段的剪切位移范围均比TP-1试桩的偏大,如平稳阶段的剪切位移达到10~30 mm。这可能因为TP-2试桩桩长大于TP-1桩长,使得TP-2钻孔暴露时间更长,砂层也较厚,泥浆护壁时间也较长,增加桩侧泥皮厚度,泥皮的黏滞特性会使摩阻力发挥所需的剪切位移增大。
(3)桩端阻力分析
根据现场测试,可获得桩端阻力和桩端位移,如图4所示。由图4可知,两根试桩的端阻力增长规律相似,均没有出现明显陡变现象。由于受桩端沉渣影响,桩端阻力出现软化和硬化现象,软化主要表现为沉渣压密过程,桩端位移增长较快；而硬化主要表现为沉渣厚度在充分压缩后,颗粒的稳定性开始逐渐增强、承载能力不断强化,逐渐由桩端持力层发挥承载。
根据两根试桩端阻力-位移曲线结果,虽然最终未出现极限破坏状态,为安全设计考虑,两根试桩均以最终加载获得的端阻力作为极限端阻力,试桩TP-1和TP-2最大端阻力分别为3971 kPa和4304 kPa,对应的极限位移分别为36.5 mm和87.1 mm。从端阻力位移结果也可以看出TP-2试桩的桩端沉渣厚度大于TP-1,说明桩端沉渣会显著影响桩基的沉降,从现场施工记录来看,TP-2成孔过程出现过塌孔现象,发现桩底沉渣也较厚,本次试验也证实了沉渣问题。
2.3 试桩承载力计算分析
本工程地勘均采用欧洲规范,现场对不同钻孔均进行了旁压试验,其中临近主桥试桩TP-1和TP-2位置的钻孔SP4和SP9旁压试验参数随试验深度的变化关系如图5所示。
从图5可知,旁压净极限压力
根据旁压净极限压力
此外,根据不同土性,该图中也给出了公路桥涵规范(JTG 3363—2019)[13]推荐的土层侧摩阻力值,与欧洲规范旁压试验计算值差别较小,但明显比实测值偏大。上段和中段桩侧阻力实测值比公路桥涵规范摩阻力标准值小37%~52%,若考虑上段和中段桩侧摩阻力为负摩阻力的影响,按照自平衡技术规程(JT/T738—2009)[11],黏性土侧阻力一般按照0.8的系数进行修正,砂性土按照0.7的修正系数。经过修正后得到的侧阻力比公路桥涵规范摩阻力标准值小11%~31%。说明按照公路桥涵规范进行承载力设计,会高估桩侧摩阻力,使承载力偏于不安全。
两根试桩的侧阻力远比欧洲规范和公路桥涵规范小,除了受成孔质量影响和正负摩阻力效应影响外,还可能与土层温度效应影响有关。公路桥涵规范主要对中国地区的不同地层进行统计,提出的侧阻力标准值在中国国内工程应用具有一定的普适性,但对于科特迪瓦热带地区国家的地层,存在显著的温度差异。已有研究表明[14-15],黏土及砂土的抗剪强度会随温度的增加而有所降低,表现出热软化现象。本工程TP-1试桩在测试阶段已发现地层温度普遍较高,达到30℃~45℃,如图7所示。
从图7可以看出,浅层土的温度达到40℃左右,65 m深度的土层温度也达到了30℃以上,该温度明显高于中国区域土体温度。因此,直接采用中国公路桥涵规范侧阻力推荐值会存在一定的偏差。
根据欧洲规范旁压试验结果,可计算得到桩端阻力,由于桩端持力层为中密实砂层,抗压承载力系数k取为1.2。不同方法计算得到的端阻力如表1所示。
表 1 不同方法端阻力计算值Table 1. Base resistances obtained by different methods试桩 试桩实测最大值 欧洲规范旁压试验计算值 公路桥涵规范(JTG 3363—2019) 数值 差异比/% 数值 差异比/% TP-1 3971 6072 52.91 5594 40.87 TP-2 4304 7476 73.70 5594 29.97 从表1可以看出,两根试桩实测获得的最大端阻力均明显小于欧洲规范旁压试验计算值以及公路桥涵规范计算值。其中欧洲规范计算得到的端阻力约为实测端阻力的1.5~1.7倍。因此,若按照欧洲规范旁压试验结果进行估算桩端阻力需进行一定的修正。
3. 基于旁压试验三折线预测桩基承载力
为了分析桩侧阻力、桩端阻力与旁压净极限压力之间的关系,以下对两根试桩结果进行统计,如图8所示。根据实测统计结果,以下提出了分段线性拟合方法,对旁压净极限压力进行三段线性分类,可得到较合理的计算桩侧摩阻力的计算公式,如公式(10)所示。该分段公式克服了Baguelin方法高估桩侧摩阻力的不安全问题。
![]()
图 8 侧摩阻力与旁压净极限压力的关系Figure 8. Relationship between skin friction and pressuremeter net ultimate pressure
(10) 而对于端阻力,由于两根试桩持力层的平均旁压净极限压力分别为5.06 MPa和6.23 MPa,通过实测端阻力可换算得到两根试桩的端阻力与旁压净极限压力的比值分别为0.78和0.69,均大于Baguelin方法提出的系数。此工程的桩端持力层均为中密实砂层,建议该比值采用平均值,即为0.73。
通过两根试桩测试结果,可得到不同方法单桩极限承载力及端阻力、侧阻力组成情况,见表2。
表 2 不同方法桩基承载力结果Table 2. Bearing capacities of pile foundation by different methods试桩 工况 试验实测结果 欧洲规范(BS EN 1997—2)旁压试验 公路桥涵规范(JTG 3363—2019) 旁压试验分段函数法 数值 比例/% 数值 比例/% 数值 比例/% 数值 比例/% TP-1 桩侧阻力(kN) 9355 43 23625 55 22406 56 14216 55 桩端阻力(kN) 12477 57 19075 45 17573 44 11604 45 承载力(kN) 21832 — 42700 — 39979 — 25820 — TP-2 桩侧阻力(kN) 9554 41 31814 58 29070 62 22970 62 桩端阻力(kN) 13522 59 23486 42 17573 38 14288 38 承载力(kN) 23076 — 55300 — 46643 — 37258 — 从表2中可知,实测获得的侧阻力为承载力的41%~43%,欧洲规范(BS EN 1997—2)旁压试验得到侧阻力所占比例为55%~58%,公路桥涵规范(JTG 3363—2019)得到的侧阻力所占比例为56%~62%。而欧洲规范计算得到的承载力为实测承载力的1.95~2.4倍,公路桥涵规范计算得到的承载力为实测承载力的1.83~2.02倍,两种规范计算结果差别较小。该工程采用欧洲规范旁压试验计算方法会明显高估了单桩承载力,采用该欧洲规范旁压试验方法时需进行一定的修正。而如果采用旁压试验分段函数法,计算得到的承载力均比欧洲规范和公路桥涵规范得到的承载力小,与实测承载力更为接近,近似为实测承载力的1.18~1.61倍。由于本工程两根试桩结果忽略了上段桩正负摩阻力影响,以及桩端阻力未达到极限,实测承载力在一定程度上存在富余。因此,采用旁压试验分段函数法对本工程桩基承载力进行预测更为合理。
4. 结论
结合非洲某工程桩基现场试验及旁压试验,研究了深厚砂性土中桩基承载特性。主要结论如下：
(1)砂层的厚度会影响成桩质量,钻孔穿越砂层越厚,桩端更容易出现沉渣问题。通过试桩两次循环加载的沉降变化也证实了沉渣问题,且桩端沉渣会显著影响桩基沉降,使桩端阻力产生弱化和强化特性。
(2)两根试桩的侧阻力远比欧洲规范和公路桥涵规范小,除了受成孔质量影响和正负摩阻力效应影响外,还可能与土层温度效应影响有关,温度越高,会使土体抗剪强度表现热软化特性,降低侧摩阻力。
(3)通过对旁压试验进行三段线性分类,可得到旁压试验预测桩基承载力方法,相较于欧洲规范和公路桥涵规范更适用于深厚砂层桩基承载力预测。
-
![]()
图 6 不同井数量n时OM1的水头分布
Figure 6. Distribution hydraulic head of OM1 with different numbers of wells
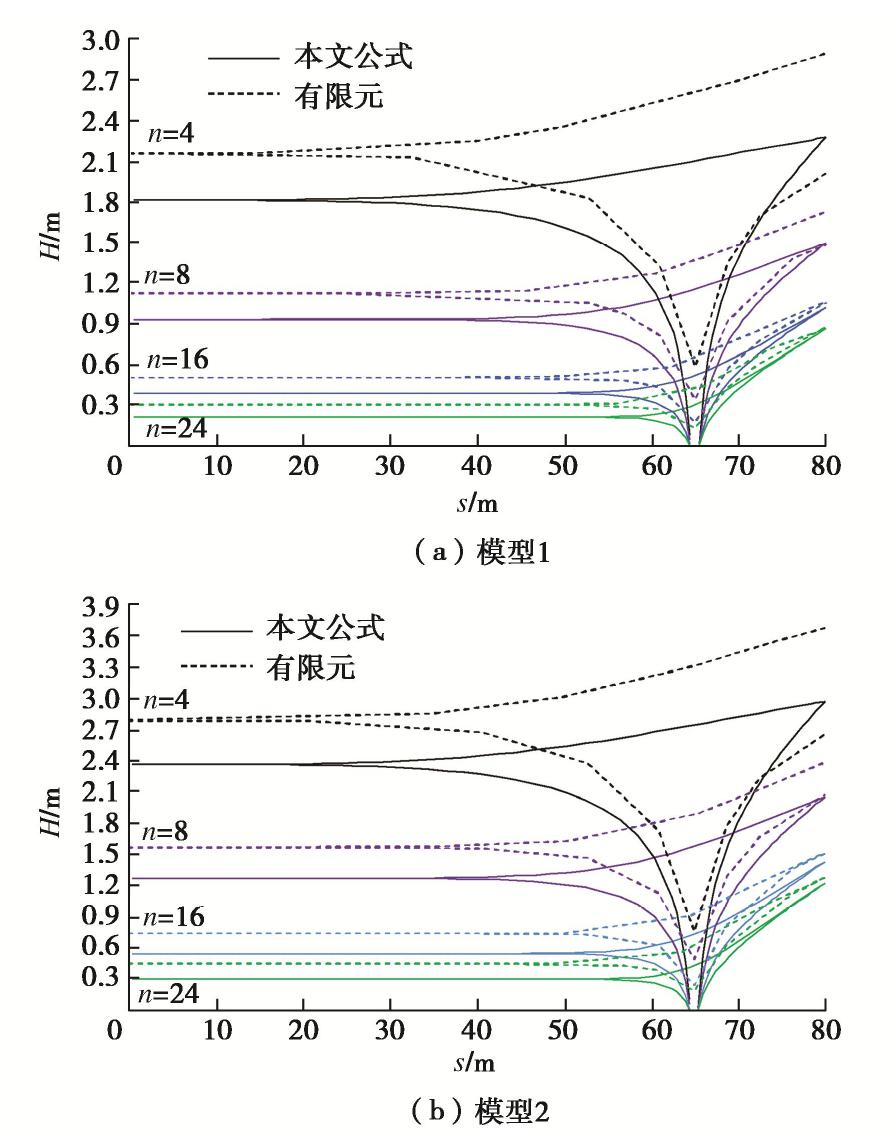
表 1 计算结果比较
Table 1 Comparison of calculated results
n 模型1 模型2 Q/(m3·d-1) Hd/m HR/m(M1) HR/m(M2) Q/(m3·d-1) Hd/m HR/m(M1) HR/m(M2) 本文 有限元 本文 有限元 本文 有限元 本文 有限元 本文 有限元 本文 有限元 本文 有限元 本文 有限元 4 606 560 5.3 5.2 2.3 2.9 2.3 2.0 392 368 5.3 5.4 3.0 3.7 3.0 2.7 8 741 717 5.2 4.9 1.5 1.7 1.5 1.5 503 504 5.1 5.2 2.1 2.1 2.1 2.1 16 823 802 5.1 4.9 1.0 1.1 1.0 1.1 574 586 5 5 1.4 1.5 1.4 1.5 24 850 836 5.1 4.8 0.9 0.9 0.9 0.9 597 611 5 5 1.2 1.3 1.2 1.3 332 862 851 5.1 4.8 0.8 0.8 0.8 0.8 607 627 5 4.9 1.1 1.2 1.1 1.2 
下载: 导出CSV
-
[1] 朱东风, 曹洪, 骆冠勇, 等. 截排减压抗浮系统在抗浮事故处理中的应用[J]. 岩土工程学报, 2018, 40(9): 1746-1752. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201809026.htm ZHU Dong-feng, CAO Hong, LUO Guan-yong, et al. Application of interception and drainage anti-floating system in treatment of uplift accidents[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(9): 1746-1752. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201809026.htm
[2] 曹洪, 潘泓, 骆冠勇. 地下结构截排减压抗浮概念及应用[J]. 岩石力学与工程学报, 2016, 35(12): 2542-2548. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201612019.htm CAO Hong, PAN Hong, LUO Guan-yong. A new anti-floatation method by drainage: concept and application[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(12): 2542-2548. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201612019.htm
[3] 安徽省水利科学研究所. 多层地基和减压沟井的渗流计算理论[M]. 北京: 水利出版社, 1980. Anhui Water Resources Research Institute. Theory of Seepage Flow for Calculating Layered Media and Relief Ditches and Relief Wells[M]. Beijing: Water Resources Press, 1980. (in Chinese)
[4] 毛昶熙. 渗流计算分析与控制[M]. 2版. 北京: 中国水利水电出版社, 2003. MAO Chang-xi. Seepage Computation Analysis & Control[M]. 2nd ed. Beijing: China Water Power Press, 2003. (in Chinese)
[5] U.S. Army Corps of Engineers. Design, Construction, and Maintenance of Relief Wells (Engineer Manual No. 1110-1914)[M]. Washington D.C.: Department of the Army, 1992.
[6] 吴林高. 工程降水设计施工与基坑渗流理论[M]. 北京: 人民交通出版社, 2003. WU Lin-gao. Design and Execution of Dewatering & Theory of Seepage in Deep Excavation[M]. Beijing: China Communications Press, 2003. (in Chinese)
[7] 曹洪, 朱东风, 范泽, 等. 止水帷幕缝隙渗漏变化过程试验研究[J]. 水利学报, 2019, 50(6): 699-709. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201906005.htm CAO Hong, ZHU Dong-feng, FAN Ze, et al. Laboratory study of leakage process for cut-off wall with crack[J]. Journal of Hydraulic Engineering, 2019, 50(6): 699-709. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201906005.htm
[8] 王仁东. 略去流床板桩厚度对滤流(渗流)计算的影响[J]. 浙江大学学报, 1957(3): 9-27. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC195703001.htm WANG Ren-dong. The influence on seepage calculation without considering sheet pile thickness[J]. Journal of Zhejiang University, 1957(3): 9-27. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC195703001.htm
[9] 胡瑶. 考虑基坑防渗结构的井的计算方法研究[D]. 广州: 华南理工大学, 2018. HU Yao. Study on Calculation Method of Well Considering Impervious Structure of Foundation Pit[D]. Guangzhou: South China University of Technology, 2018. (in Chinese)
[10] 钟玉泉. 复变函数论[M]. 3版. 北京: 高等教育出版社, 2004. ZHONG Yu-quan. Complex Function Theory[M]. 3rd ed. Beijing: China Higher Education Press, 2004. (in Chinese)
[11] 朱东风. 地下结构截排减压抗浮法渗控关键问题研究[D]. 广州: 华南理工大学, 2019. ZHU Dong-feng. A Study on Seepage Control Issues of Anti-uplift Method for Underground Structures Based on Intercepting and Discharging Water[D]. Guangzhou: South China University of Technology, 2019. (in Chinese)
[12] 阿拉文, 努麦诺夫. 滤流理论[M]. 王仁东译.北京: 高等教育出版社.1959. Аравин , Нуменов . Percolation Theory[M]. WANG Ren-dong trans. Beijing: Higher Education Press.1959. (in Chinese)
[13] ZHU D F, CAO H, PAN H, et al. Laboratory study of retention and clogging performance of no-fines concretes[J]. European Journal of Environmental and Civil Engineering, 2021, 25(8): 1471-1490. doi: 10.1080/19648189.2019.1581664
[14] 刘杰. 土的渗透破坏及控制研究[M]. 北京: 中国水利水电出版社, 2014. LIU Jie. Piping and seepage control of soil[M]. Beijing: China Water Power Press, 2014. (in Chinese)
计量
- 文章访问数: 234
- HTML全文浏览量: 37
- PDF下载量: 96
