Nonlinear analysis of load transfer of grouting branch-type anchor
-
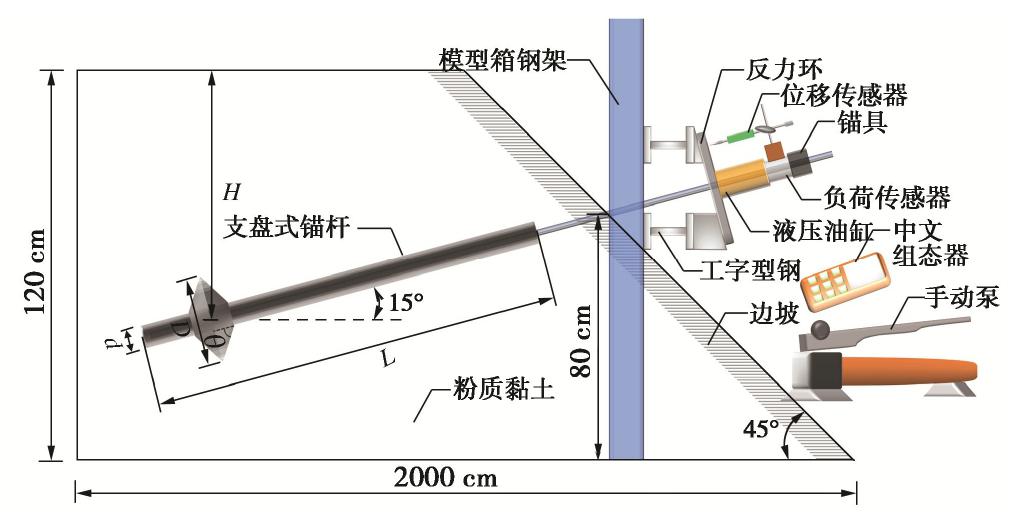
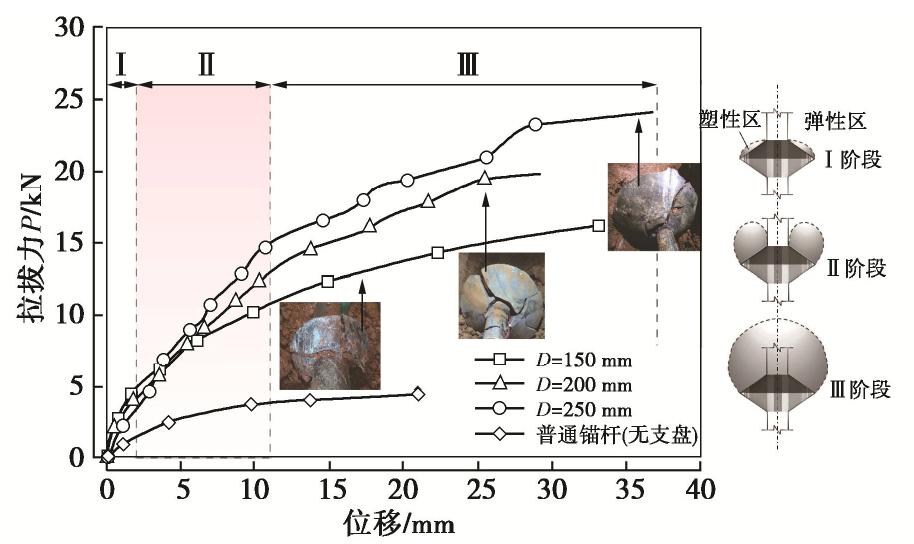
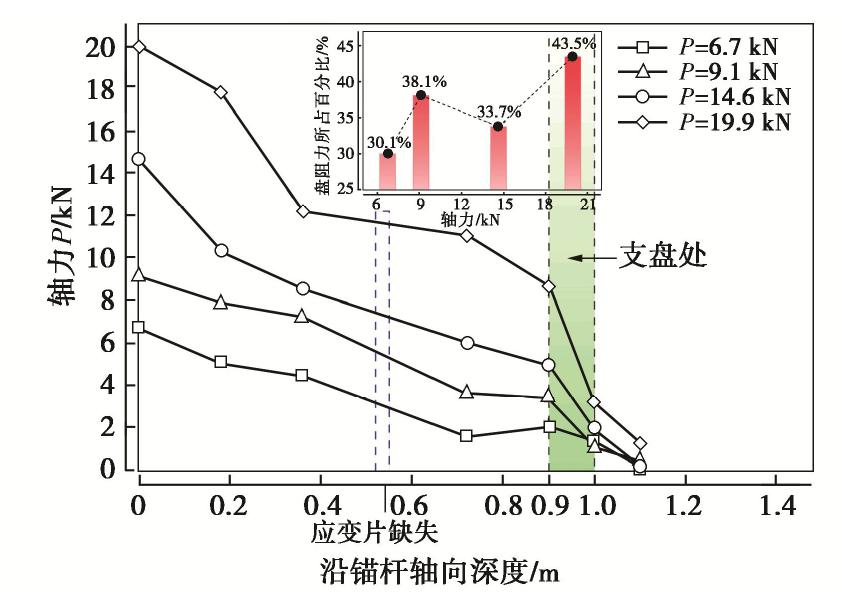
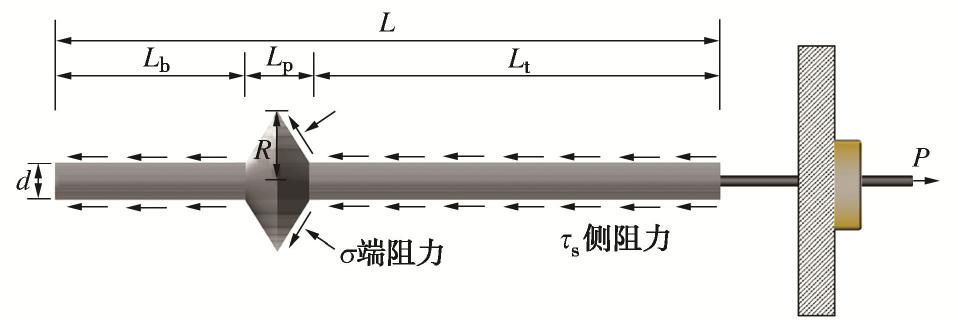
摘要: 基于支盘式锚杆室内模型拉拔试验,探究荷载-位移曲线的变化特征和轴力传递特性,然后在此基础上探讨支盘式锚杆的力学模型,推导出盘端阻力的理论计算公式,结合锚-土界面的双曲线非线性模型,采用分段变形协调迭代算法建立荷载传递计算模型,并与实测数据进行对比验证,最后对极限扩孔压力分布、支盘挤扩角等参数进行敏感性分析。研究结果表明,荷载-位移曲线可划分为三阶段,轴力分布沿锚固体深度呈减小趋势且在支盘处发生台阶状突变,荷载比也不断增长；计算模型所得结果与室内实测数据基本一致,验证了本模型的有效性；支盘的极限扩孔压力沿支盘径向先快速非线性增长后缓慢减小,其峰值随着位移增大而增大并以支盘中心为圆点径向外移,整体分布由“锥台状”发展为“圆柱状”；挤扩角大于50°时,对锚杆承载性状影响显著。研究结果对支盘式锚杆的受力分析和设计具有重要的理论及实际意义。Abstract: Based on the indoor model pull-out tests on the branch-type anchor, the variation characteristics of the load-displacement curve and the axial force transmission characteristics are studied. Then, the mechanical model for the anchor is discussed, and the theoretical formula for the end resistance of disc is derived. Combined with the hyperbolic nonlinear model for the anchor-soil interface, the load transfer model is established by using the sectional deformation coordinated iterative algorithm. Finally, the sensitivity analysis of the parameters such as the ultimate pressure of cavity expansion distribution and the squeezing angle of the branch disc is performed. The results show that the load displacement curve can be divided into three stages. The axial force distribution decreases along the anchor depth and the step mutation occurs at the branch disc, and the load ratio also increases continuously. The calculated results are basically consistent with the indoor measured data, which verifies the validity of the model. The ultimate pressure of cavity expansion increases rapidly and nonlinearly along the radial direction of the branch disc and then decreases slowly. The peak value increases with the displacement and moves radially outward with the center of the branch disc as the circular point. The overall distribution changes from "cone platform" to "cylinder". When the squeezing angle is greater than 50°, the ultimate drawing force significantly increases. The research results are of important theoretical and practical significance for the analysis and design of the force of the branch-type anchor.
-
Keywords:
- branch-type anchor /
- cavity theory expansion /
- nonlinearity /
- load transfer /
- numerical calculation
-
0. 引言
土的渗透特性是土重要的工程性质之一,影响着土木工程的施工。目前无黏性土渗透特性的试验研究,多是采用竖向圆柱体模型槽进行,试验中土体受到的水流的作用方向是由下至上的竖直方向,而对于土体承受水平向渗流时土体渗透特性的研究不多[1],渗流方向对土体渗流变形特性的研究还尚未给予足够重视。对土渗流的研究表明,实际施工中渗流的优势方向往往是水平方向,通常土体水平向的渗透性大于竖向,而抵抗水平向渗透破坏的能力低于抵抗竖向渗透破坏的能力[2-6]。
本文针对粉砂竖向和水平向渗透特性研究存有的不足,利用自主设计的实验装置,对粉砂开展竖向和水平向渗流试验,对比分析了两种不同方向渗流场下粉砂的渗透特性。基于室内模拟试验,建立三维离散元与计算流体力学耦合的细观力学模型,对粉砂在竖向和水平向的渗流情况进行分析和计算。通过数值计算结果,对竖向和水平向渗流作用下的粉砂内部接触力、渗流速度及流场的分布规律进行细观分析,将数值模拟与室内试验的结果进行分析、比较。
1. 不同渗流方向下粉砂渗透变形室内试验模拟
1.1 试验仪器和方法
（1）试验仪器
粉砂的竖向渗透变形试验借助实验室自主设计的圆柱形渗流试验仪进行,该装置示意图如图1所示。粉砂水平向渗流渗透变形特性的研究是在自主设计的水平渗流试验装置中进行的,见图2。模型由进水系统,装样区及排水系统3个主要部分组成。进水系统可以通过对进水水头高度的调节自由选择水头加载高度。
![]()
图 1 圆柱形渗流试验仪示意图Figure 1. Schematic diagram of instrument for cylindrical seepage tests（2）试验方法及步骤
粉砂烘干并分层装样。称样烘干24 g取出装样,每10 cm分为一层进行装样；排气饱和。装样完成,分次提升水箱供水高度对试验土样进行饱和,最后一次使水头抬升至与试样顶端齐平,静置24 h；逐级调整水头进行试验。逐级抬升水头高度,对测压管水头高度读数并记录,同时量测渗流量大小,记录试验进程中的渗流现象,直至该级渗流稳定,转入下一级水头；当试验过程中,流量忽然增大,并出现明显的渗流通道,可以认定为试样发生渗透破坏,不再继续加大水头高度,试验完成。
1.2 粉砂竖向和水平向渗流试验结果分析
对粉砂在竖向渗流下的渗透流速受水力梯度影响下的变化规律进行研究,得到渗流速度随水力梯度变化的关系曲线,如图3所示。对粉砂在水平向渗流作用下的临界水力梯度进行研究,结果如图4所示。
![]()
图 3 竖向渗流下渗流速度随水力梯度变化曲线Figure 3. Relationship between seepage velocity and vertical hydraulic gradient![]()
图 4 水平向渗流下渗流速度随水力梯度变化曲线Figure 4. Relationship between seepage velocity and critical hydraulic gradient由图3得到,在水力梯度
<0.787时,渗流速度随水力梯度呈近似线性的变化,此时土样处于渗流稳定阶段；当水力梯度为1.1时,渗流速度忽然增大,粉砂颗粒流失量也徒增,此时土体发生渗透变形。图4粉砂在水平向渗流下的变化规律显示：水力梯度小于0.45时,粉砂土渗透流速随着水力梯度的增大呈线性增长,水流清澈,粉砂流出较少。当水力梯度增至0.52时,试样整体的流速瞬间增大,粉砂流出量明显增多且呈持续流失状态,此时粉砂土样内部颗粒运移不再规律,试样开始发生渗透破坏。 表1给出粉砂在两种渗流方向下的渗透系数、临界坡降与破坏坡降。粉砂在竖向渗流时的临界水力梯度为0.787,破坏水力梯度为1.10；而水平向渗流中,所能承受的临界水力梯度为0.45。在影响因素诸如种类、级配、密度、孔隙大小等相同的前提下,粉砂竖向渗流的临界水力梯度比水平向高出近44%。由于土体在受到水平向渗流时,平均渗透系数取决于最透水土层的厚度和渗透性；而对于竖向渗流,其平均渗透系数取决于最不透水土层的渗透性。加之,竖向渗流中重力作用与渗流方向一致,会产生对土层的压密作用,使得该渗流方向下的渗透系数小于水平向,而土体能够承受的水头高于水平向的渗流。
表 1 不同渗流方向下粉砂渗透系数、临界坡降和破坏坡降Table 1. Datat of permeability coeffieient of silt, critical slope and failure slope under different seepage directions渗流方向 渗透系数/(10-4 cm·s-1) 临界水力梯度 破坏水力梯度 竖向 6.13 0.787 1.10 水平 6.25 0.450 0.52 2. 不同渗流方向下粉砂渗透变形颗粒流模拟
对于固相颗粒,通过求解运动和动量方程模拟颗粒运动,采用离散元的颗粒流理论进行模拟；对于液相介质,采用均一化流体计算技术模拟其在孔隙中的运动,也就是通过求解平均Navier-Stokes方程模拟孔隙中流体的运动[7-9]。
2.1 数值模型
对粉砂土不同向渗流形态的模拟中,边界条件的界定也略有不同。竖向渗流下,颗粒周边的边界为固壁边界条件,上下为压力边界条件。水平向渗流下,模型的前后和上下边界为固壁边界条件,左右设置为压力边界条件和自由边界条件。生成的土体模型如图5所示。
对于竖向的渗流,按照试验中模型,上覆为自由边界,没有压重。对于水平向的渗流,试样在重力和浮力作用下保持平衡,当作用渗流力后,土中小颗粒将从模型右侧流出,因此在试样右侧设置了相互交叉垂直的线墙,如图6所示。
2.2 数值计算流程
采用PFC3D对流固耦合问题进行计算流程如图7所示。
2.3 数值模拟结果
（1）粉砂土竖向和水平向渗流下渗透变形情况
a）粉砂竖向渗流下的渗透变形情况
图8给出了粉砂在竖向渗流作用下,土样随水力梯度的变化情况。
![]()
图 8 竖向渗流下粉砂土随水力梯度变化情况Figure 8. Variation of silty sand with gradient under vertical seepage水力梯度从0.1,0.2,0.3,...,逐级增加,水力梯度施加至0.7时,粉砂几乎无变化；当水力梯度增至0.8时,土样出现从底部被整体抬升的趋势,发生少量细小颗粒流失的现象；水力梯度继续增至1.0时,土体发生了整体的抬升,土体表面颗粒簇发生整体迁移的现象。模拟结果表明,试样的临界水力梯度在0.8左右。
b）粉砂水平向渗流下的渗透变形情况
粉砂土的水平向渗流中水力梯度也是由0.1,0.2,0.3依次逐级抬升,图9给出了粉砂土在水平向渗流下试样随水力梯度变化的情况。
![]()
图 9 水平向渗流下粉砂土随水力梯度变化情况Figure 9. Variation of silt with gradient under horizontal seepage从图9中可以看出,当水力梯度增至0.3时,试样底部细小颗粒也开始发生迁移,水力梯度继续增大至0.4,此时试样发生颗粒成团的流失,土体发生了渗透变形。水力梯度加载至0.5时,土体颗粒发生了更加显著的整体性渗流破坏。根据模拟结果,得到粉砂土水平向渗流的临界水力梯度在0.4左右。
（2）粉砂土竖向和水平向渗流下配位数变化情况分析
土体的配位数表示了颗粒间的接触数,是表达土颗粒间接触情况的参数之一,总配位数是颗粒与颗粒之间以及颗粒与墙之间的平均接触数,反映出试样的压密程度；力学配位数为颗粒与颗粒之间接触数大于2时的颗粒接触数,反映额土骨架的压密程度。图10,11给出了粉砂土在竖向和水平向渗流作用下,配位数随水力梯度的变化情况。
![]()
图 10 竖向渗流下粉砂配位数随水力梯度变化Figure 10. Variation of coordination number with gradient under vertical seepage![]()
图 11 水平向渗流粉砂配位数随水力梯度变化Figure 11. Variation of coordination number with gradient under horizontal seepage图10,11可以看出,当竖向渗流的水力梯度为0.8,水平向渗流水力梯度为0.4时,土体的两个配位数都发生迅速的下降,说明此时的土体状态发生了较大的变化,即渗透变形发生。图中,总配位数和力学配位数都在随着水力梯度的增大而不断降低,总的配位数较力学配位数下降更快速,幅度也更大。这是由于水力梯度增大,颗粒发生了移动,颗粒的接触数减小,但在水力梯度增加至土体渗透变形前的整个过程中,总配位数下降幅度明显大于力学配位数,说明发生移动的多为小颗粒,小颗粒的运移使土体中接触数减少,随之小颗粒填充至骨架颗粒孔隙间,与大颗粒发生接触,保持了力学配位数的大小。
3. 结论
（1）粉砂在水平向能承受的渗流破坏作用一般低于竖向渗流。
（2）数值模拟结果与模拟试验过程中粉砂的渗流变化过程相符,数值方法所测得的临界水力梯度与试验测得的结果亦较为吻合。
（3）竖向和水平向渗流下,粉砂的总配位数和力学配位数均随着水力梯度的抬升而衰减,当土体发生渗透破坏,土体配位数出现迅速降低。
-
![]()
图 5 支盘式锚杆（D=200 mm）沿轴向深度的轴力分布图
Figure 5. Distribution of axial force of branch-type anchor (D = 200 mm) along axial depth
![]()
图 6 支盘式锚杆（D=250 mm）沿轴向深度的轴力分布图
Figure 6. Distribution of axial force of branch-type anchor (D = 250 mm) along axial depth
![]()
图 12 支盘式锚杆荷载传递分析模型示意图
Figure 12. Scheme of load transfer analysis model for branch-type anchor
![]()
图 13 分段变形协调迭代算法流程图
Figure 13. Flow chart of sectional deformation coordinated iterative algorithm
![]()
图 15 支盘式锚杆（D=200 mm）轴力分布对比分析图
Figure 15. Comparative analysis of distribution of axial force of branch-type anchor (D=200 mm)
![]()
图 16 不同位移下盘-土界面的极限扩孔压力分布示意图
Figure 16. Scheme of ultimate pressure of cavity expansion at plate-soil interface under different displacements
![]()
图 17 不同支盘挤扩角下的荷载位移曲线对比分析图
Figure 17. Comparative analysis of load-displacement curves under different squeezing angles
表 1 锚杆试验参数
Table 1 Test parameters for anchor
支盘直径R/mm 锚杆长度L/mm 锚杆直径d/mm 挤扩角θ/(°) 平行试验次数 — 1100 50 — 2 150 1100 50 60 2 200 1100 50 60 2 250 1100 50 60 2 
下载: 导出CSV
表 2 土的基本力学性质
Table 2 Basic mechanical properties of soil
密度ρ/(g·cm-3) 含水率w/% 黏聚力c/kPa 内摩擦角 /(°) 弹性模量E/(kN·m2) 泊松比 1.90 25.2 21 15.6 7400 0.31
下载: 导出CSV
-
[1] 程良奎, 张培文, 王芳. 岩土锚固工程的若干力学概念问题[J]. 岩石力学与工程学报, 2015, 34(4): 668-682. CHENG Liang-kui, ZHANG Pei-wen, WANG Fang. Several mechanical concepts for anchored structures in rock and soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(4): 668-682. (in Chinese)
[2] 简文彬, 黄炜, 罗金妹, 等. 多支盘锚固结构[P]. CN211256969U, 2020-08-14. JIAN Wen-bin, HUANG Wei, LUO Jin-mei, et al. Multi-branch Anchor Structure: CN211256969U[P]. 2020-08-14. (in Chinese)
[3] 简文彬, 杨坚, 罗金妹, 等. 一种多支盘锚固体系扩孔设备及施工方法[P]. CN110700760A, 2020-01-17. JIAN Wen-bin, YANG Jian, LUO Jin-mei, et al. Hole Reaming Equipment and Construction Method of Multi- Branch Anchor Solid System[P]. CN110700760A. 2020-01-17. (in Chinese)
[4] 杨坚, 简文彬, 黄炜, 等. 注浆支盘式锚杆拉拔试验及极限承载力计算[J]. 岩土力学, 2021, 42(4): 1126-1132. YANG Jian, JIAN Wen-bin, HUANG Wei, et al. Pull-out test and ultimate bearing capacity calculation of grouting branch-type anchor[J]. Rock and Soil Mechanics, 2021, 42(4): 1126-1132. (in Chinese)
[5] NIE W, ZHAO Z Y, NING Y J, et al. Numerical studies on rockbolts mechanism using 2D discontinuous deformation analysis[J]. Tunnelling and Underground Space Technology, 2014, 41(1): 223-233.
[6] MA S Q, NEMCIK J, AZIZ N. An analytical model of fully grouted rock bolts subjected to tensile load[J]. Construction and Building Materials, 2013, 49(8): 519-526.
[7] NEMCIK J, MA S, AZIZ N, et al. Numerical modelling of failure propagation in fully grouted rock bolts subjected to tensile load[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 71(10): 293-300.
[8] MA S Q, ZHAO Z Y, NIE W, et al. An analytical model for fully grouted rockbolts with consideration of the pre- and post-yielding behavior[J]. Rock Mechanics and Rock Engineering, 2017, 50(11): 3019-3028.
[9] NI P, SONG L, MEI G, et al. Generalized nonlinear softening load-transfer model for axially loaded piles[J]. International Journal of Geomechanics, 2017, 17(8): 04017019.
[10] BRYSON L S, GIRALDO J R. Analysis of case study presenting ground anchor load-transfer response in shale stratum[J]. Canadian Geotechnical Journal, 2020, 57(1): 85-99.
[11] 陈建功, 陈晓东. 基于小波函数的锚杆拉拔全过程分析[J]. 岩土力学, 2019, 40(12): 4590-4596. CHEN Jian-gong, CHEN Xiao-dong. Analysis of whole process of bolt pulling based on wavelet function[J]. Rock and Soil Mechanics, 2019, 40(12): 4590-4596. (in Chinese)
[12] 黄明华, 赵明华, 陈昌富. 锚固长度对锚杆受力影响分析及其临界值计算[J]. 岩土力学, 2018, 39(11): 4033-4041. HUANG Ming-hua, ZHAO Ming-hua, CHEN Chang-fu. Influence of anchorage length on stress in bolt and its critical value calculation[J]. Rock and Soil Mechanics, 2018, 39(11): 4033-4041. (in Chinese)
[13] 匡政, 白晓宇, 张明义, 等. 考虑锚固体不均匀及杆体脱黏效应的GFRP抗浮锚杆杆体荷载分布函数[J]. 岩石力学与工程学报, 2019, 38(6): 1158-1171. KUANG Zheng, BAI Xiao-yu, ZHANG Ming-yi, et al. Load distribution function of GFRP anti-floating anchors considering the anchorage body unevenness and the anchor debonding effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(6): 1158-1171. (in Chinese)
[14] 土工试验标准方法：GB/T50123—2019[S]. 2019. Standard for Soil Test Method: GB/T50123—2019[S]. 2019. (in Chinese)
[15] 建筑基坑支护技术规程：JGJ 120—2012[S]. 2012. Technical Specification for Building Foundation Pit Support: JGJ 120—2012[S]. 2012. (in Chinese)
[16] LIU J, LIU M, ZHU Z. Sand deformation around an uplift plate anchor[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2012, 138(6): 728-737.
[17] 胡伟, 孟建伟, 姚琛, 等. 浅埋平板圆锚竖向拉拔极限承载力计算方法[J]. 岩土力学, 2020, 41(9): 3049-3055. HU Wei, MENG Jian-wei, YAO Chen, et al. Calculation method of vertical pullout ultimate bearing capacity of shallow circular anchor plate[J]. Rock and Soil Mechanics, 2020, 41(9): 3049-3055. (in Chinese)
[18] 史旦达, 毛逸瑶, 杨勇, 等. 基于DIC技术的砂土中圆形锚板上拔土体变形特性试验研究[J]. 岩土力学, 2020, 41(10): 3201-3213. SHI Dan-da, MAO Yi-yao, YANG Yong, et al. Experimental study on the deformation characteristics of soils around uplift circular plate anchors using digital image correlation technology[J]. Rock and Soil Mechanics, 2020, 41(10): 3201-3213. (in Chinese)
[19] VESIC A S. Expansion of cavities in infinite soil mass[J]. Journal of the Soil Mechanics and Foundations Division, 1972, 98(3): 265-290.
[20] 刘裕华, 陈征宙, 彭志军, 等. 应用圆孔柱扩张理论对预制管桩的挤土效应分析[J]. 岩土力学, 2007, 28(10): 2167-2172. LIU Yu-hua, CHEN Zheng-zhou, PENG Zhi-jun. Analysis of pile driving effect of precast tubular pile using cylindrical cavity expansion theory[J]. Rock and Soil Mechanics, 2007, 28(10): 2167-2172. (in Chinese)
[21] 王伟堂, 裘华君, 詹红琴. 压桩挤土位移的预估与防治的研究[J]. 岩土工程学报, 2001, 23(3): 378-379. WANG Wei-tang, QIU Hua-jun, ZHAN Hong-qin. Study on prediction and prevention for soil displacement caused by the statically pressed piles[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(3): 378-379. (in Chinese)
[22] 郑颖人, 龚晓南. 岩土塑性力学基础[M]. 北京: 中国建筑工业出报社, 1989. ZHENG Ying-ren, GONG Xiao-nan. Fundamentals of Geotechnics Plasticity[M]. Beijing: China Architecture & Building Press, 1989. (in Chinese)
[23] FARMER I W. Stress distribution along a resin grouted rock anchor[J]. International Journal of Rock Grouted Rock Mechanics Mining Science & Geomechanics Abstract, 1975, 12(11): 347-351.
[24] 赵明华, 黄炎杰, 黄明华. 基于有限差分法的锚杆荷载传递非线性计算方法研究[J]. 铁道科学与工程学报, 2018, 15(8): 1963-1970. ZHAO Ming-hua, HUANG Yan-jie, HUANG Ming-hua. Study on nonlinear calculation method of load transferring along tensile anchor rod base on finite difference method[J]. Journal of Railway Science and Engineering, 2018, 15(8): 1963-1970. (in Chinese)
[25] 张季如, 唐保付. 锚杆荷载传递机理分析的双曲函数模型[J]. 岩土工程学报, 2002, 24(2): 188-192. KUANG Zheng, ZHANG Ji-ru, TANG Bao-fu, et al. Hyperbolic function model to analyze load transfer mechanism on bolts[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(2): 188-192. (in Chinese)
[26] RANDOLPH M F, WROTH C P. An analysis of vertical deformation of piles groups[J]. Géotechnique, 1979, 29(4): 423-439.
-
期刊类型引用(4)
1. 应宏伟，陈雨，王阳扬，刘冠. 含碎石芯软黏土复合试样大三轴试验研究. 湖南大学学报(自然科学版). 2024(11): 104-114 . 
百度学术
2. 邱俊峰，叶晨峰，陈峰，郑铖杰. 镍铁渣粉水泥固化砂土剪切强度与应力应变关系研究. 湖南文理学院学报(自然科学版). 2023(02): 78-82+95 . 百度学术
3. 殷天军，宁华宇，寇晓强. 深中通道沉管基础水下深层水泥搅拌桩应用全过程探讨. 中国港湾建设. 2022(07): 11-16 . 百度学术
4. 张振，郑文强，叶观宝，陈勇. 循环荷载下水泥土桩复合单元体变形特性及其地基长期沉降计算方法. 中国公路学报. 2022(11): 21-29 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 243
- HTML全文浏览量: 24
- PDF下载量: 131
- 被引次数: 6
