基于逆可靠度分析的隧道开挖面极限支护压力优化设计

姬建; 张哲铭; 夏嘉诚; 闵凡路; 吴志军

doi:10.11779/CJGE202110008

基于逆可靠度分析的隧道开挖面极限支护压力优化设计 English Version

姬建^{1, 2,},
张哲铭^{1, 2},
夏嘉诚^{1, 2},
闵凡路^{1, 2},
吴志军³

1.
河海大学岩土力学与堤坝工程教育部重点实验室,江苏　南京　210024
2.
河海大学土木与交通学院,江苏　南京　210024
3.
武汉大学土木与建筑工程学院,湖北　武汉　430072

基金项目:

国家自然科学基金项目 51879091

国家自然科学基金项目 52079045

详细信息

作者简介:
姬建(1983— ),男,博士,教授,主要从事岩土工程可靠度、边坡工程、地下空间风险分析等领域的科研与教学工作。E-mail：JI0003AN@e.ntu.edu.sg

中图分类号: TU431
计量
- 文章访问数: 262
- HTML全文浏览量: 24
- PDF下载量: 164
出版历程
- 收稿日期: 2021-02-05
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-09-30

Inverse reliability-based design of limit support pressure for tunnel face stability

JI Jian^{1, 2,},
ZHANG Zhe-ming^{1, 2},
XIA Jia-cheng^{1, 2},
MIN Fan-lu^{1, 2},
WU Zhi-jun³

1.
Key Laboratory of Geomechanics and Embankment Engineering, Ministry of Education, Hohai University, Nanjing 210024, China
2.
College of Civil and Transportation Engineering, Hohai University, Nanjing 210024, China
3.
College of Civil Engineering, Wuhan University, Wuhan 430072, China

摘要

摘要: 探讨了采用一阶可靠度方法（FORM）的逆形式对浅埋圆形隧道开挖面极限支护压力进行可靠度优化设计（RBD）的可能性。逆可靠度分析的计算过程可以在随机变量的原始空间中实现,并且可以直接提供一些满足目标可靠度指标的设计信息。针对隧道开挖面的坍塌和隆起破坏模式,通过三维有限元极限分析（FELA）计算极限支护压力的确定性解,由此建立极限状态方程并进行逆可靠度设计。在概率研究中,逆可靠度方法通过与蒙特卡罗模拟的结果对比显示出足够的准确性。在此基础上,本研究针对不同工况进行了一系列支护压力的可靠度优化设计和概率分析,获得相应的RBD结果。最后,讨论了土体抗剪强度参数的空间变异性对支护压力的影响。
- 隧道开挖面稳定 /
- 反分析 /
- 有限元极限分析 /
- 概率设计 /
- 空间变异性
Abstract: The possibility of reliability-based design (RBD) for shallow circular tunnels is explored using the simplified inverse first-order reliability method (FORM). The inverse reliability analysis can directly offer some design information that meets the targeted reliability index, and the calculation procedure can be easily implemented in the original space of random variables. In the tunnel face stability analysis, the deterministic results of the support pressures are obtained through the three-dimensional finite element limit analysis (FELA), and the limit state functions are established for the collapse and blow-out failure modes of the excavated face, respectively. In the probabilistic study, the inverse reliability method shows adequate accuracy by comparing with Monte Carlo simulations. On this basis, a series of probability analysis and RBD of the limit support pressures for maintaining the tunnel face stability in cohesive soil and sandy soil strata are carried out. Some insightful RBD results are obtained with respect to different scenarios of shear strength uncertainties. Finally, the effects of spatial variability of shear strength parameters of soils on the required support pressures of tunnel face are discussed.
- tunnel face stability /
- inverse analysis /
- finite element limit analysis /
- probabilistic design /
- spatial variability

HTML全文

0. 引言

隧道开挖安全问题主要来自3个方面：隧道开挖面的稳定性,不同时期的地面沉降以及衬砌结构的受力^[1]。在盾构隧道掘进过程中,开挖面支护压力的大小决定开挖面的稳定性。开挖面支护压力过小会导致开挖面发生坍塌破坏（collapse）,支护压力过大会导致地表发生隆起破坏（blow-out）。因此合理地确定支护压力是掘进施工中的关键问题,评估和控制隧道开挖面稳定性具有重要意义^[2]。

目前,针对隧道开挖稳定性的研究方法主要有极限平衡法、极限分析法、有限元强度折减法、稳定系数法和试验研究等。吕玺琳等^[3]在村山氏极限平衡法的基础上推导了维持开挖面稳定的最小极限支护压力公式。Wilson等^[4]基于刚性块上限法和有限元极限分析方法计算出极限支护压力的上下界,并采用稳定系数N的形式来评价开挖面稳定程度。Zhang等^[5]基于极限分析的运动学方法,采用带环包络线的连续速度场给出了坍塌和隆起两种情况下支护压力的上界。Xiang等^[6]通过透明土模型试验技术和PFC^3D数值模拟,研究了开挖面的破坏机理。虽然这些方法对于破坏机制和极限支护压力研究具有重要参考价值,但仍处于确定性的范畴,无法考虑岩土体参数不确定性的影响。相比之下,概率分析可以系统地评估设计中使用的输入变量的不确定性对工程安全性的影响。因此,一系列针对工程安全评估的可靠度方法应运而生,比如蒙特卡罗模拟（MCS）、一阶/二阶可靠度方法（FORM/FOSM）、响应面法（RSM）和神经网络等。Low等^[7]采用FORM和FOSM对均质地层中圆形隧道进行了可靠性设计。然而,FORM/FOSM通常需要显式的极限状态控制方程,若控制方程为隐式,则需要RSM等方法来近似模拟极限状态方程。Lü等^[8]采用FORM和RSM分析了隧道支护系统的可靠性,并提基于可靠度的优化设计方案。Mollon等^[9]将随机响应面法与FLAC^3D数值模型相结合,对圆形隧道稳定性进行了概率分析。Pan等^[10]考虑了土体参数的空间变异性,基于稀疏多项式混沌展开对隧道工作面进行了全局灵敏度分析。蒋水华等^[11]提出了隧道开挖面可靠度分析的非侵入式随机有限差分法,为分析低概率水平下盾构隧道开挖可靠度问题提供了一个有效的工具。

以往的研究大多是正向的可靠度分析,收敛速度慢且计算量大,本研究在FORM的基础上提出一种逆向的可靠度算法,该算法可以根据目标可靠度指标反算出合理的支护压力和一些设计信息,可较大幅度降低计算成本,其中隐式极限状态控制方程通过有限元极限分析进行数值求解。最后,针对不同砂性土和黏性土中浅埋圆形隧道开挖面极限支护压力提出一系列的可靠度优化设计和概率分析。

1. 一阶可靠度基本概念和算法实现

1.1 一次二阶矩可靠度指标

可靠度指标是评估系统失效概率的指标,可以考虑输入参数固有的不确定性。传统的Hasofer-Lind可靠度指标β计算公式如下：

$β = \underset{x \in F}{mi} n \sqrt{{(x - μ)}^{T} C^{- 1} (x - μ)}$ ,

(1)

式中,x表示由n个随机参数组成的列向量,μ为其对应均值组成的向量,C为协方差矩阵,F表示失效域。在相互独立标准正态分布的随机变量空间中,可靠度指标的物理意义可以解释为空间坐标原点到极限状态面的最短距离。

对于岩土参数,其概率分布通常不完全遵循标准正态分布,并且会存在一定的相关性。此时,将非正态随机变量转化为正态随机变量对于传统的FORM算法是必不可少的步骤,导致一些额外计算工作量。为简化计算,Low等^[12]在原始空间内重新解读了β计算的物理意义：

$β = \sqrt{{[\frac{x_{i}^{*} - μ_{i}^{N}}{σ_{i}^{N}}]}^{T} R^{- 1} [\frac{x_{i}^{*} - μ_{i}^{N}}{σ_{i}^{N}}]}$ ,

(2)

式中,x_i^*为第i个随机变量的设计点,μ_i^N 和 σ_i^N分别是随机变量的等效均值和标准差, $R$ 是协方差矩阵。其中μ_i^N 和 σ_i^N由Rackwitz-Fiessler转换^[13]所得。

进一步,FORM失效概率 $P_{f}$ 和可靠度指标β关系如下：

$P_{f} \approx Φ (- β)$ ,

(3)

式中,Ф(·)为标准正态变量的累计分布函数。

1.2 HLRF-x迭代算式求解随机参量设计点

Hasofer-Lind-Rackwits-Fiessler (HLRF)迭代计算是一种求解FORM可靠度指标的高效算法,其不需要近似极限状态面的显式形式,因此适合用来实现可靠度分析与其他数值模拟方法的一体化。Ji等^[14]提出了原始空间内的HLRF算法,即HLRF-x算法。为了改善其收敛性,可通过引入步长来重新构造,得到一种改进的iHLRF-x算法,具体表达如下^[15]：

$x_{k + 1} = x_{k} + λ_{k} d_{k}$ ,

(4)

$d_{k} = μ_{k}^{N} + \frac{[\nabla g {(x_{k}]}^{T} (x_{k} - μ_{k}^{N}) - g (x_{k}) T_{k} \nabla g (x_{k})}{\nabla g {(x_{k})}^{T} T_{k} \nabla g (x_{k})} - x_{k} ，$

(5)

式中, $λ_{k}$ 和 $d_{k}$ 分别为步长和搜索方向, $x_{k}$ 为第k步的迭代计算点,g( $x_{k}$ )和 $\nabla$ g( $x_{k}$ )为 $x_{k}$ 处的极限状态方程和梯度向量。 $T_{k} = {[σ_{k}^{N}]}^{T} R [σ_{k}^{N}]$ 为第k步的迭代计算点处的修正协方差矩阵,其中对角矩阵 $[σ_{k}^{N}] =$ $[\begin{matrix} σ_{k, 1}^{N} & \dots & 0 \\ ⋮ & σ_{k, i}^{N} & ⋮ \\ 0 & \dots & σ_{k, m}^{N} \end{matrix}]$ , $σ_{k, i}^{N}$ 为 $x_{k}$ 处第i个随机变量的等效正态标准差。

对于标准正态变量,当 $λ_{k}$ =1时,iHLRF-x可退化为传统的HLRF算法。

1.3 逆可靠度算法

逆可靠度分析旨在快速获取某概率水平下的不确定性设计参数,即可靠度优化设计（RBD）。理论上,可以采用正向分析的可靠度分析如上述FORM算法,尝试计算来进行RBD。这种方式需要大量的经验性重复计算。为克服其局限性,本文介绍一种基于HLRF的逆可靠度分析算法。

逆可靠度问题定义为

$θ ： min {|| x || |g(x, θ) = 0} = β_{t}$ ,

(6)

式中,θ是极限状态方程g(x,θ)的一个阈值, $β_{t}$ 为目标可靠度指标。式（6）的解为

$x_{k + 1} = - β_{t} \frac{Τ_{k} \nabla x g (x_{k}, θ k)}{| | \nabla x | |} + μ_{k}^{N}$ ,

(7)

$θ_{k + 1} = θ_{k} + \frac{{[\nabla x g (x_{k}, θ_{k})]}^{T} (x_{k} - μ_{k}^{N}) - g (x_{k}, θ_{k}) + β_{t} | | \nabla x | |}{\partial g (x_{k}, θ_{k}) / \partial θ}$ 。

(8)

引入迭代步长 $λ$ 和搜索方向d_k,即

$(\begin{matrix} x_{k}_{+ 1} \\ θ_{k + 1} \end{matrix}) = (\begin{matrix} x_{k} \\ θ_{k} \end{matrix}) + λ d_{k}^{x}$ ,

(9)

$d_{k}^{x} = (\begin{matrix} (- β_{t} \frac{T_{k} \nabla x g (x_{k}, θ_{k})}{| | \nabla x | |} + μ_{k}^{N} - x_{k} \\ \frac{{[\nabla x g (x_{k}, θ_{k})]}^{T} (x_{k} - μ_{k}^{N}) - g (x_{k}, θ_{k}) + β_{t} | | \nabla x | |}{\partial g (x_{k}, θ_{k}) / \partial θ}) \end{matrix}) 。$

(10)

逆可靠度算法的收敛性可以通过优化方程和Armijo规则来调整,有关更多详细信息,请参见Ji等^[15]的论文。

1.4 隧道开挖面稳定的极限状态

本文将采用逆可靠度分析方法进行浅埋圆形隧道开挖面稳定性的优化设计。为了针对坍塌和隆起两种破坏模式分别建立极限状态方程：

$g_{1} (x) = σ_{t} - σ_{c}$ ,

(11)

$g_{2} (x) = σ_{t} - σ_{b}$ ,

(12)

式中,g(x)是极限状态方程,x是输入随机参数组成的向量, $σ_{t}$ 为隧道开挖面上施加的支护压力, $σ_{c}$ 为发生坍塌破坏临界支护压力, $σ_{b}$ 为发生隆起破坏的临界支护压力。当g(x)>0时,开挖面稳定；当g(x)<0时,开挖面破坏。

2. 三维有限元极限分析

2.1 数值模型

隧道开挖面的稳定性本质上是一个三维问题,因此需要进行全面的三维分析。现有的三维数值模拟方法有离散元法（DEM）、有限差分法（FDM）、有限元法（FEM）等,但采用以上方法建立三维隧道开挖模型并计算非常耗时。目前,三维有限元极限分析（FELA）技术已经成功应用于岩土工程中各种稳定性问题,FELA结合了有限元模型和经典的极限分析方法的优点,计算效率显著提高。

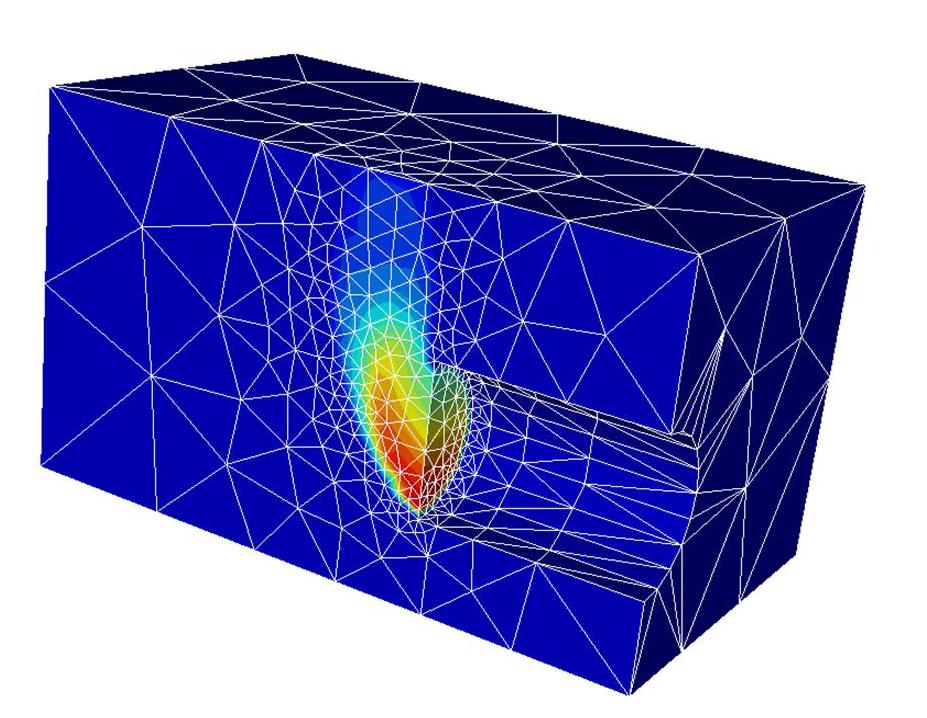
考虑隧道结构的对称性,取半圆形隧道进行建模,如图1所示。掘进隧道模型尺寸及相关物理量基于文献报道^[16]。模型四周边界为法向约束,底部采用固定约束,顶部地面可以自由移动。掘进隧道周围采用法向约束,模拟刚性衬砌的效果。隧道直径为D,埋深为C。均质土层为Mohr-Coulomb材料,黏聚力为c,摩擦角为φ,重度为 $γ$ 。除了这些强度参数外,还需要定义土层变形参数,如泊松比和弹性模量。

图 1 隧道模型示意图

Figure 1. Schematic diagram of tunnel model

下载: 全尺寸图片幻灯片

为了平衡隧道开挖面的水土压力,仅依靠土体自身强度是不够的。在开挖过程中,有必要在开挖面上提供适当的支护压力 $σ_{t}$ 以保持其稳定性。 $σ_{t}$ 通过荷载乘数法施加在开挖面,该方法的原理是 $σ_{t}$ 从较小的初始值开始逐渐增加,直到满足有限元控制方程进而获取临界支护压力值。

为了提高精度,模型计算时采用网格自适应优化技术^[17],即在能量耗散率较大的区域适当增加单元密度,以减小数值离散误差；而在能量耗散率较小的区域适当减小单元密度,以确保整体计算效率。网格划分效果如图2所示。

图 2 数值模型及网格划分

Figure 2. Numerical model and meshes

下载: 全尺寸图片幻灯片

2.2 极限分析准则

传统的极限分析准则包括上限准则和下限准则。其最主要的特点就是能够在严格的条件下求解极限荷载。当然,也存在很多其他的准则能够减少控制方程的数量。与上限和下限法则的特点不同,混合准则的主要优势并不在于在严格的准则下进行求解,而在于能够提供很多折中的解,相比上下限解更能够接近真实解。详细原理和信息可以查阅Optum软件手册^[18]。

为了进一步评估该方法的准确性,本文同时采用了FLAC^3D针对相同模型进行计算并比较。表1中给出了两种不同工况各自计算结果的对比,由于计算原理的不同,FELA的结果略高于FLAC^3D,差异在可接受范围内。然而对于图2这样的模型,FLAC^3D计算需要耗费十几小时的计算时间,而FELA仅需要1～2 min。基于以上情况,本文采用OptumG3进行隧道开挖面极限支护压力的可靠度优化设计。

表 1 坍塌模式下极限支护压力对比(C/D=1, γ = 18 kN/m³)

Table 1. Comparison of critical collapse pressures

C/D	c = 7 kPa,φ = 17°		c = 10 kPa,φ = 25°
C/D	FLAC^3D	OptumG3	FLAC^3D	OptumG3
0.6	36.8	38.6	11.7	13.2
0.8	37.2	39.5	12.1	13.3
1.0	37.3	40.1	12.2	13.1
1.5	37.3	41.0	12.2	12.9
2.0	37.4	41.4	12.2	13.0
注：表中极限支护压力单位为kPa。

下载: 导出CSV

| 显示表格

3. iHLRF-x算法在隧道开挖面可靠度分析中的应用

3.1 逆可靠度分析流程

iHLRF-x算法的优势之一在于其可以与任何解析解或数值软件相结合。本研究将其与三维有限元极限分析结合,根据目标可靠度指标来反算出合理的支护压力,并通过处理土体参数的统计信息来对支护压力进行概率评估。步骤总结如下：

（1）确定参数的概率分布类型和相关系数。指定初始输入参数x（通常取均值）。

（2）通过数值软件计算初始支护压力,根据式（11）和式（12）建立极限状态方程g(x_k)。

（3）将x_k替换为x_k+1(x_k+1= x_k+∆x),获得梯度向量 $\nabla$ g(x_k)。

（4）设定目标可靠度指标 $β_{t}$ ,通过iHLRF计算d_k并得到新的输入参数矩阵x_k+1和相应可靠度指标β。

（5）输入新的x_k+1并重复步骤1～4直到同时满足 $β$ = $β_{t}$ 和 |g(x_new)| ≤ $ε$ 。其中 $ε$ 为预先设定的阈值。

在本文工作中,上述算法和过程在Microsoft Excel Visual Basic平台实现编程计算。

3.2 算例验证

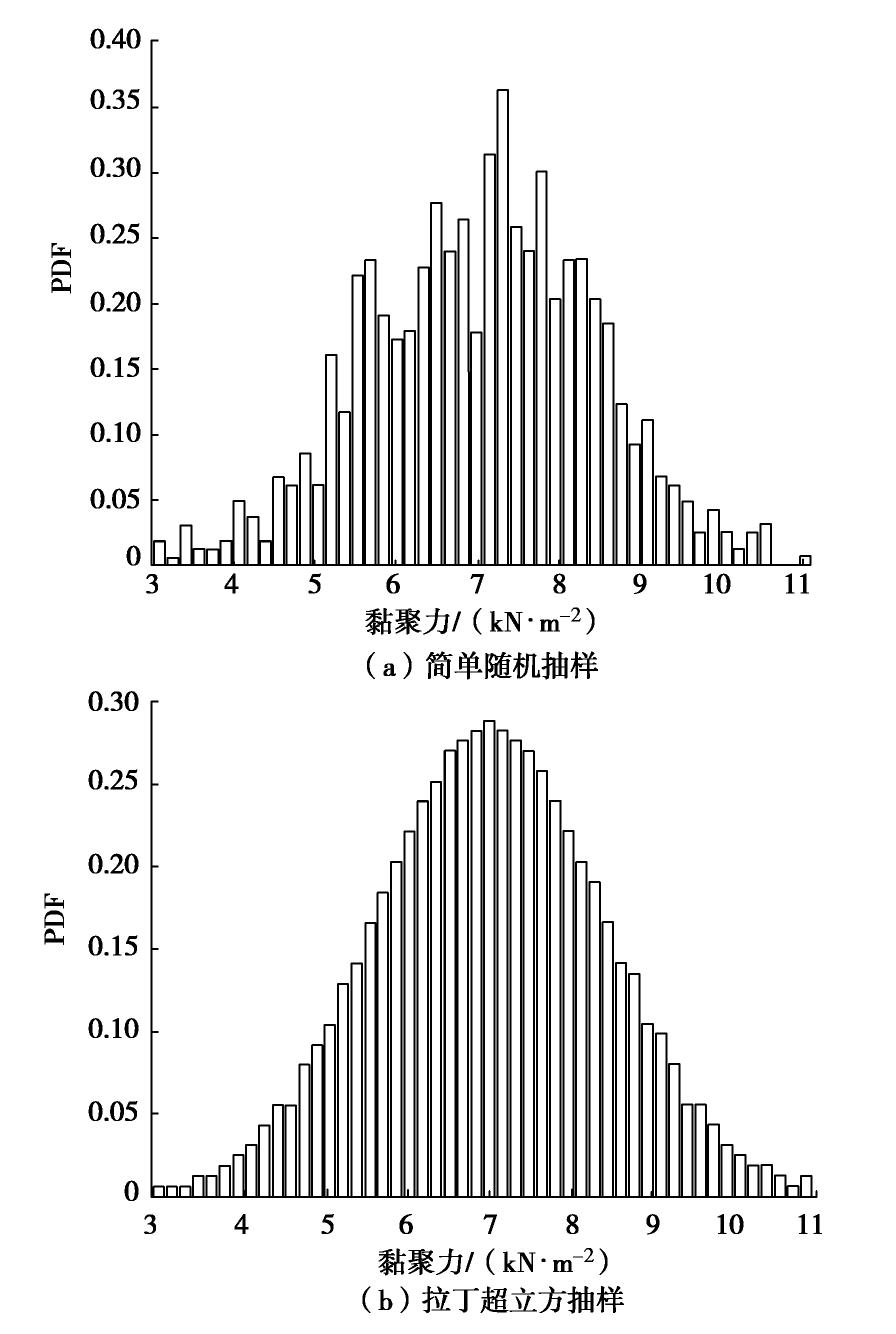
为了验证逆可靠度分析方法的准确性,本文对同一案例进行了蒙特卡罗模拟（Monte Carlo simulation,简称 MCS）,并进行了结果对比。所选案例隧道直径为10 m,埋深为10 m。土体本构采用Mohr-Coulomb模型,黏聚力c和摩擦角φ均假设为正态分布变量（μ_c = 7 kPa,μ_φ = 17°,COV_c = 20%,COV_φ = 10%）。对于MC模拟,要达到失效概率P_f= 10^-k的精度,需要进行的模拟次数为10^k+2次^[10],为了提高抽样效率,本文采用拉丁超立方抽样技术（LHS）^[19]。如图3所示,对于2000个样本,LHS的概率密度曲线（PDF）比简单随机抽样平滑得多。通常,使用LHS获得2000个样本的分析结果,可以达到简单随机抽样方法10000个样本的分析效果,减少了大量的计算时间,提高了效率。

图 3 不同抽样方法对比

Figure 3. Comparison of different sampling methods

下载: 全尺寸图片幻灯片

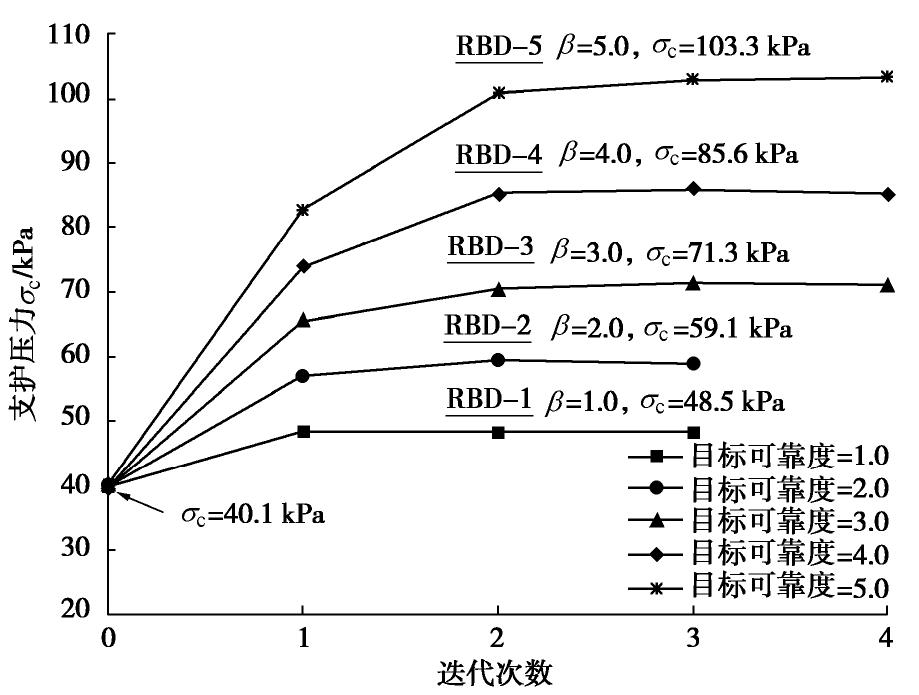
针对开挖面坍塌失效模式,逆可靠度分析的目的是通过设定的可靠度指标或风险水平对极限支护压力进行可靠度优化设计。如图4所示,通过改变目标可靠度指标 $β_{t}$ ,极限支护压力由初始的40.1 kPa迭代至对应的支护压力值,并由此绘制出开挖面失效概率随支护压力的变化关系曲线。从图5中可以看出,分别由iHLRF-x与MCS绘制的失效概率曲线非常吻合。例如,要达到目标可靠度指标 $β_{t}$ =3.0（即失效概率为0.13%）,通过iHLRF-x逆可靠度分析所得的支护压力为71.3 kPa,而该值在MCS结果中对应的失效概率为0.10%,误差为0.03%。相比之下,MCS需要耗费大约10 h的计算时间,而iHLRF-x仅仅需要几分钟的时间进行3～4步迭代就可以达到收敛值,大大节约了计算成本,并且可通过设定目标可靠度指标灵活使用,避免多余计算。

图 4 坍塌模式下支护压力的RBD

Figure 4. RBD for support pressures

下载: 全尺寸图片幻灯片

图 5 开挖面失效概率随支护压力的变化关系曲

Figure 5. Relationship curves of failure probability of excavation face with support pressures

下载: 全尺寸图片幻灯片

4. 开挖面极限支护压力可靠度设计

4.1 基于逆可靠度分析的支护压力概率结果

隧道开挖面极限支护压力可靠度优化设计的目的是根据不同可靠度指标给出建议的支护压力值。规范JCSS中对于最终极限状态（ULS）建议的可靠度指标为3.1～4.7,对于正常使用极限状态建议的可靠度指标为1.2～2.3。欧标（Eurocode 7）中对于ULS建议的可靠度指标为3.8^[20]。因此,本文将iHLRF-x算法与隧道三维有限元极限分析模型相结合,对3种典型土体类型下隧道开挖面不同破坏模式的极限支护压力进行逆可靠度分析,可靠度指标涵盖上述标准建议值。在逆可靠度分析中,选用岩土参数黏聚力和内摩擦角作为随机变量,并考虑其分布类型和变异系数。表2总结了每种工况下的参数的统计信息,该数据来自于文献调研^[21-22]。

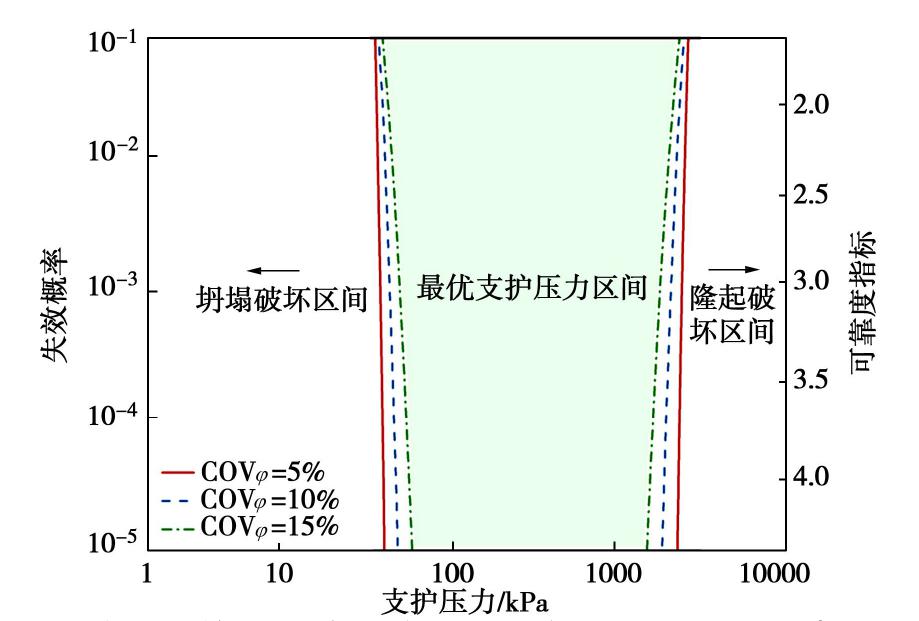
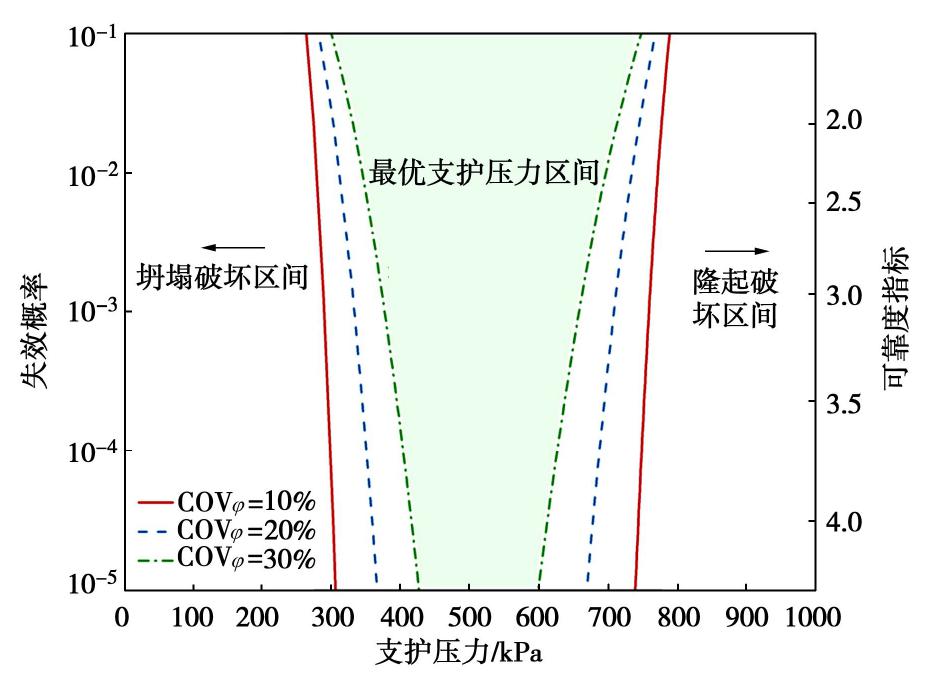
表 2 参数的统计信息

Table 2. Statistical information of variables

土类	参数	分布类型	均值	变异系数/%	相关性
砂性土	φ/(°)	正态	30	5/10/15	N/A
砂性土	γ/(kN·m^-3)	—	18	—	N/A
纯黏性土	c/kPa	正态	30	10/20/30	N/A
纯黏性土	γ/(kN·m^-3)	—	25	—	N/A
黏性土	c/kPa	正态/对数正态	正态/对数正态	20/30	不相关/相关ρ = ‒0.5
	φ/(°)	7	17	10/20
	γ/(kN·m^-3)	—	18	—

下载: 导出CSV

| 显示表格

图6～8分别给出了砂性土、纯黏性土、黏性土的失效概率随支护压力变化关系曲线。在每一幅图中,左边的曲线对应坍塌的失效模式,右边的曲线对应隆起的失效模式。在坍塌失效模式下,支护压力越大,失效概率越小；在隆起失效模式下,支护压力越大,失效概率越大。以指定失效概率作为界限值（例如10^-5）,坍塌失效模式和隆起失效模式之前存在一个区间,称为最优支护压力区间。通过对比可以发现,砂性土的支护压力安全区间比黏性土土的支护压力安全区间大得多,并且发生隆起破坏时的支护压力过高,超过大多数增压盾构设备的承受范围,这说明在砂性土的情况下,隆起的失效模式是极不可能的。针对砂性土和纯黏性土来说,参数的变异系数越大,支护压力的安全区间宽度越窄,如图6,7所示。对于黏性土来说,同时考虑黏聚力和内摩擦角的变异系数,在相同失效概率的情况下,内摩擦角的微小变化会极大地影响支护压力。显然,其不确定性越大,失效概率越高。相比之下,支护压力对黏聚力的变化不是很敏感。这意味着当对隧道开挖面进行逆可靠度分析时,准确评估内摩擦角的不确定性对于支护压力的调整非常重要。

图 6 开挖面失效概率随支护压力的变化关系曲线（砂性土）

Figure 6. Relationship curves of failure probability of excavation face with support pressures (sandy soils)

下载: 全尺寸图片幻灯片

图 7 开挖面失效概率随支护压力的变化关系曲线（纯黏性土）

Figure 7. Relationship curves of failure probability of excavation face with support pressures (pure cohesive soils)

下载: 全尺寸图片幻灯片

图 8 开挖面失效概率随支护压力的变化关系曲线（黏性土）

Figure 8. Relationship curves of failure probability of excavation face with support pressures (cohesive soils)

下载: 全尺寸图片幻灯片

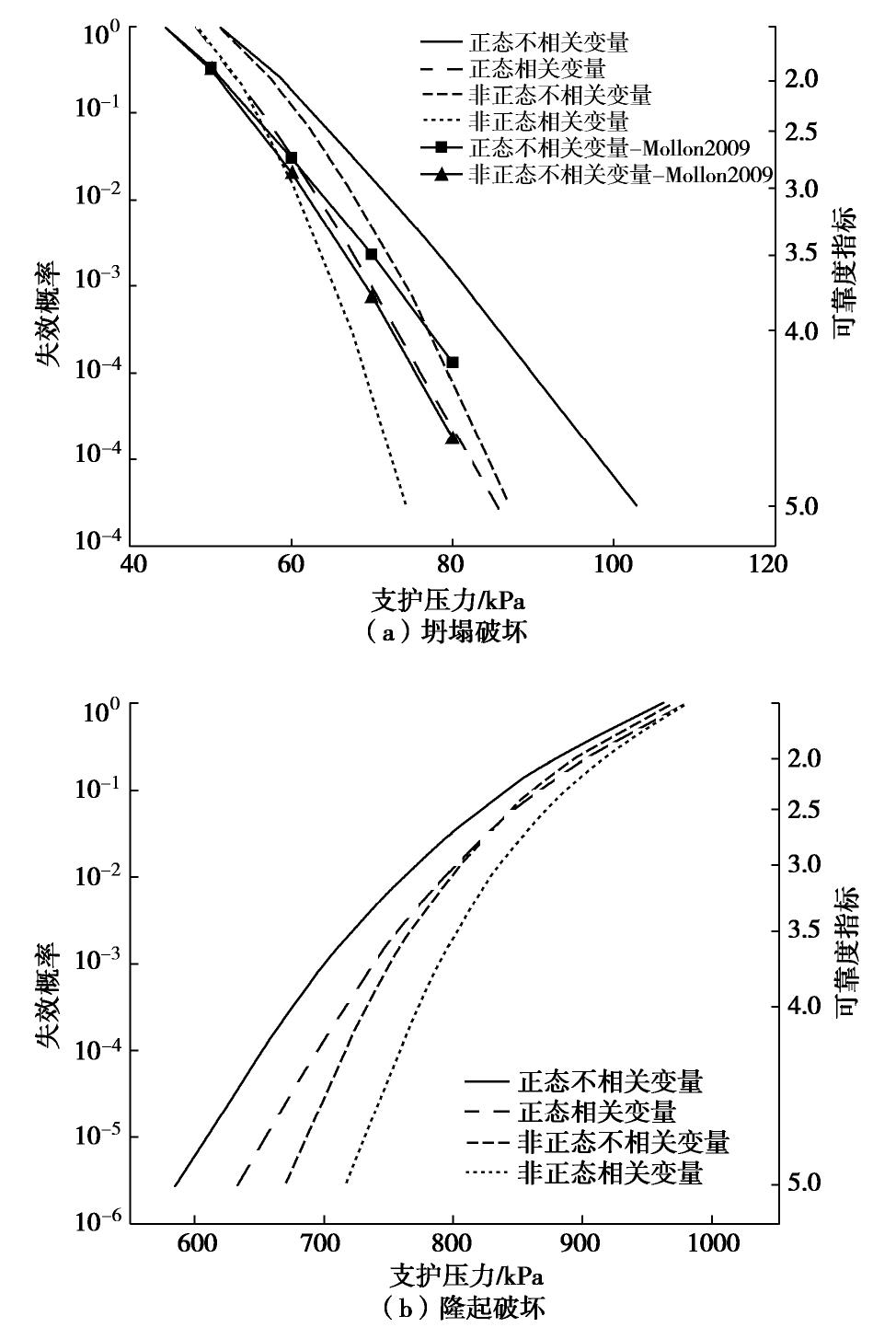
对于大多数工程可靠度问题,基本随机变量可能不服从标准正态分布。相反,其他各种形式的统计分布,甚至随机变量之间通常存在的一定的相关性。图9给出了4种不同变量分布类型下失效概率随支护压力变化关系曲线,并与Mollon等^[9]采用响应面法的结果进行对比。可以看出,不同方法之间存在一定的差异,但曲线的趋势很吻合。本文的结果相对保守,该误差是由于不同方法计算隧道开挖面支护压力造成的。以坍塌破坏模式为例,正态不相关变量和正态相关变量的结果对比表明,在相同的失效概率下,不相关变量所对应的支护压力大于负相关变量的结果。隆起破坏模式亦是如此,负相关变量的结果相对保守。以目标可靠度 $β_{t}$ =3.0举例来说,当变量服从正态分布时,支护压力为71.28 kPa,若变量负相关,支护压力62.64 kPa；当变量处于非正态分布时,参数不相关与参数负相关的结果分别为67.17和67.23 kPa。由此可见,变量的分布类型也影响着支护压力的大小。

图 9 参数不同分布类型下失效概率曲线（黏性土）

Figure 9. Curves of failure probability under different distribution types of parameters (cohesive soils)

下载: 全尺寸图片幻灯片

4.2 可靠度指标、设计点及分项安全系数

根据逆可靠度分析出的设计点值（ $c *$ and $φ *$ ）,可按下式得出不同参数的分项安全系数：

$F_{c} = \frac{μ_{c}}{c *}$ ,

(13)

$F_{φ} = \frac{\tan (μ_{φ})}{\tan φ *}$ 。

(14)

表3列出了黏性土坍塌失效模式下不同目标可靠度指标和相应的设计点下4种类型变量的安全系数。可以发现,摩擦角分项安全系数F_φ随着可靠度指标的提高而提高,但是黏聚力分项安全系数F_c相对不太敏感,且其变化规律不够一致。Eurocode7中可靠度指标为3.8时,建议的F_c和F_φ分别为1.6和1.25。本文所得出4种变量类型的F_c介于1.3～1.6,正态相关变量除外,F_φ介于1.2～1.5。可以看出,逆可靠度分析可以更具体地得出不同设计参数的安全系数。

表 3 可靠度指标,设计点及分项安全系数

Table 3. Reliability indexes, design points and partial safety factors

变量类型	β	$σ_{t}$ /kPa	c*/kPa	φ*/(°)	F_c	F_φ
正态不相关变量	2.0	59.07	5.65	14.02	1.24	1.22
	2.5	64.60	5.49	13.17	1.28	1.31
	3.0	71.28	5.13	12.43	1.36	1.39
	3.8	82.79	4.93	11.05	1.42	4.57
非正态不相关变量	2.0	57.78	5.78	14.13	1.21	1.21
	2.5	62.46	5.40	13.6	1.30	1.26
	3.0	67.17	5.22	12.97	1.34	1.33
	3.8	75.28	5.37	11.82	1.30	1.46
正态相关变量	2.0	53.59	6.31	14.57	1.11	1.18
	2.5	58.01	6.50	13.66	1.08	1.26
	3.0	62.64	6.71	12.77	1.04	1.35
	3.8	70.70	6.88	11.48	1.02	1.51
非正态相关变量	2.0	58.2	5.58	14.26	1.25	1.20
	2.5	62.62	5.55	13.51	1.26	1.27
	3.0	67.23	5.35	12.89	1.31	1.34
	3.8	66.36	5.82	12.80	1.20	1.35

下载: 导出CSV

| 显示表格

5. 土体参数空间变异性对开挖面支护压力的影响

概率方法根据其所采用的土体参数随机模型可以分为两类：随机变量法和随机场法。随机变量法,顾名思义,将某个不确定性土体参数视为单一随机变量,进行简单的不确定性描述,但其对该随机变量的空间分布变异性描述不够充分,而随机场法可以描述土体参数的空间变异性^[23]。

5.1 KL展开法（Karhunen-Loeve expansion）

目前,随机场的生成有多种方法,例如局部平均法,乔列斯基分解法以及KL展开法^[24]。由于KL展开法具有指数相关函数的解析解,使用方便。本文采用KL展开法生成黏聚力c和摩擦角φ的各向异性随机场。

对于二维随机场,指数相关函数可以表示为

$C_{X} (s, t) = σ_{X}^{2} \exp (\frac{- | x_{1} - x_{2} |}{θ_{x}} + \frac{- | y_{1} - y_{2} |}{θ_{y}})$ ,

(15)

式中,s和t为空间任意两点,坐标分别为(x₁, x₂)和(y₁, y₂),θ为相关距离。KL展开随机场的关键是获得相关函数的特征值 $λ$ 和特征函数f(x),即式（15）的解：

$\int C_{X} (s, t) f (s) = λ f (t)$ ,

(16)

具体求解过程详见参考文献[25]。

5.2 空间变异自相关距离的影响

本文将KL展开随机场与有限元极限分析相结合,对4.1节中黏性土的案例进行了空间变异性分析。考虑到三维随机分析需要耗费大量的时间,故采用简化的二维模型进行计算,如图10所示。为了研究空间变异性对支护压力的影响,抗剪强度参数水平自相关距离θ_x设置为10～40 m,竖向自相关距离θ_y设置为1.5～3 m。

图 10 黏聚力二维随机场模拟结果

Figure 10. Modeling of two-dimensional random field of cohesion of soils

下载: 全尺寸图片幻灯片

图11展示了不同自相关距离下支护压力的PDF曲线。从图中可以看出,自相关距离越大,PDF曲线越宽,表明所需要的支护压力的概率分布越分散。两幅图的对比表明,所需支护压力的PDF曲线对竖直自相关距离的变化更为敏感。

图 11 空间变异性对概率密度函数的影响

Figure 11. Influences of spatial variability on probability density functions

下载: 全尺寸图片幻灯片

此外,随机变量情况下的PDF曲线最为分散,这一结果同文献报道相一致^[10]。对这一现象的解释如下,当自相关距离θ趋于无穷大时,土体抗剪强度的某次概率实现在空间上趋于恒定,但在不同的实现中仍会发生变化,此时与随机变量的情况一致。相反,当自相关距离θ趋于0时,土体抗剪强度随机场的某次实现将变得非常不平整,各离散单元的抗剪强度差异很大,但随机场的整体平均抗剪强度变化小于前者,这也导致了支护压力的变异性较小,即PDF曲线较窄。

由此可见,用随机变量来描述土体参数不确定性是随机场的一种极端情况,使得支护压力的概率分布最为分散。

6. 结论与展望

本文探讨了土体强度参数不确定和空间变异因素下的浅埋圆形隧道开挖面稳定性问题,将简化逆可靠度算法（iHLRF-x算法）与三维有限元极限分析模型相结合,对隧道开挖面极限支护压力进行了一系列概率反演分析和可靠度优化设计。主要结论如下：

（1）对于给定的目标可靠度指标,逆可靠度算法仅需要迭代计算3,4步即可获得相应的隧道开挖面支护压力,实现了高效概率化优化设计。

（2）在砂性土情况下,隧道开挖引起地表隆起破坏模式几乎不存在；塌陷是唯一可能的破坏模式；在纯黏性土中,两种情况都有可能。进一步的概率分析表明,土体强度参数不确定性越大,开挖面失效概率越大。在黏性土中,失效概率对内摩擦角的不确定性更为敏感。同时,随机参数的概率分布类型显著影响最优支护压力的大小,参数的变异系数对支护压力的大小也有一定的影响。

（3）土体参数的空间变异性对支护压力概率分布特征有着重要影响,随着土体自相关距离的增大,所需要的支护压力概率分布越分散。当自相关距离趋于无穷时,等价于用随机变量描述土体参数不确定性。

（4）本文展示的隧道开挖面支护压力逆可靠度求解问题是实现其概率优化设计的基础,文中结果可为研究隧道开挖稳定性问题提供参考。

图 1 隧道模型示意图

Figure 1. Schematic diagram of tunnel model

下载: 全尺寸图片幻灯片

图 2 数值模型及网格划分

Figure 2. Numerical model and meshes

下载: 全尺寸图片幻灯片

图 3 不同抽样方法对比

Figure 3. Comparison of different sampling methods

下载: 全尺寸图片幻灯片

图 4 坍塌模式下支护压力的RBD

Figure 4. RBD for support pressures

下载: 全尺寸图片幻灯片

图 5 开挖面失效概率随支护压力的变化关系曲

Figure 5. Relationship curves of failure probability of excavation face with support pressures

下载: 全尺寸图片幻灯片

图 6 开挖面失效概率随支护压力的变化关系曲线（砂性土）

Figure 6. Relationship curves of failure probability of excavation face with support pressures (sandy soils)

下载: 全尺寸图片幻灯片

图 7 开挖面失效概率随支护压力的变化关系曲线（纯黏性土）

Figure 7. Relationship curves of failure probability of excavation face with support pressures (pure cohesive soils)

下载: 全尺寸图片幻灯片

图 8 开挖面失效概率随支护压力的变化关系曲线（黏性土）

Figure 8. Relationship curves of failure probability of excavation face with support pressures (cohesive soils)

下载: 全尺寸图片幻灯片

图 9 参数不同分布类型下失效概率曲线（黏性土）

Figure 9. Curves of failure probability under different distribution types of parameters (cohesive soils)

下载: 全尺寸图片幻灯片

图 10 黏聚力二维随机场模拟结果

Figure 10. Modeling of two-dimensional random field of cohesion of soils

下载: 全尺寸图片幻灯片

图 11 空间变异性对概率密度函数的影响

Figure 11. Influences of spatial variability on probability density functions

下载: 全尺寸图片幻灯片

表 1 坍塌模式下极限支护压力对比(C/D=1, γ = 18 kN/m³)

Table 1 Comparison of critical collapse pressures

C/D	c = 7 kPa,φ = 17°		c = 10 kPa,φ = 25°
C/D	FLAC^3D	OptumG3	FLAC^3D	OptumG3
0.6	36.8	38.6	11.7	13.2
0.8	37.2	39.5	12.1	13.3
1.0	37.3	40.1	12.2	13.1
1.5	37.3	41.0	12.2	12.9
2.0	37.4	41.4	12.2	13.0
注：表中极限支护压力单位为kPa。

下载: 导出CSV

表 2 参数的统计信息

Table 2 Statistical information of variables

土类	参数	分布类型	均值	变异系数/%	相关性
砂性土	φ/(°)	正态	30	5/10/15	N/A
砂性土	γ/(kN·m^-3)	—	18	—	N/A
纯黏性土	c/kPa	正态	30	10/20/30	N/A
纯黏性土	γ/(kN·m^-3)	—	25	—	N/A
黏性土	c/kPa	正态/对数正态	正态/对数正态	20/30	不相关/相关ρ = ‒0.5
	φ/(°)	7	17	10/20
	γ/(kN·m^-3)	—	18	—

下载: 导出CSV

表 3 可靠度指标,设计点及分项安全系数

Table 3 Reliability indexes, design points and partial safety factors

变量类型	β	$σ_{t}$ $σ_{t}$ /kPa	c*/kPa	φ*/(°)	F_c	F_φ
正态不相关变量	2.0	59.07	5.65	14.02	1.24	1.22
	2.5	64.60	5.49	13.17	1.28	1.31
	3.0	71.28	5.13	12.43	1.36	1.39
	3.8	82.79	4.93	11.05	1.42	4.57
非正态不相关变量	2.0	57.78	5.78	14.13	1.21	1.21
	2.5	62.46	5.40	13.6	1.30	1.26
	3.0	67.17	5.22	12.97	1.34	1.33
	3.8	75.28	5.37	11.82	1.30	1.46
正态相关变量	2.0	53.59	6.31	14.57	1.11	1.18
	2.5	58.01	6.50	13.66	1.08	1.26
	3.0	62.64	6.71	12.77	1.04	1.35
	3.8	70.70	6.88	11.48	1.02	1.51
非正态相关变量	2.0	58.2	5.58	14.26	1.25	1.20
	2.5	62.62	5.55	13.51	1.26	1.27
	3.0	67.23	5.35	12.89	1.31	1.34
	3.8	66.36	5.82	12.80	1.20	1.35

下载: 导出CSV

参考文献(25)

[1]	VERMEER P A, RUSE N, MARCHER T. Tunnel heading stability in drained ground[J]. Felsbau, 2002, 20(6): 8-18.
[2]	李伟平, 李兴, 薛亚东, 等. 砂卵石地层浅埋盾构隧道开挖面稳定模型试验[J]. 岩土工程学报. 2018, 40(增刊2): 199-203. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2018S2042.htm LI Wei-Ping, LI Xing, XUE Ya-dong, et al. Model tests on face stability of shallow shield tunnels in sandy cobble strata[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(S2): 199-203. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2018S2042.htm
[3]	吕玺琳, 王浩然, 黄茂松. 盾构隧道开挖面稳定极限理论研究[J]. 岩土工程学报, 2011, 33(1): 57-62. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201101012.htm LÜ Xi-lin, WANG Hao-ran, HUANG Mao-song. Limit theoretical study on face stability of shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 57-62. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201101012.htm
[4]	WILSON D W, ABBO A J, SLOAN S W, et al. Undrained stability of a circular tunnel where the shear strength increases linearly with depth[J]. Canadian Geotechnical Journal, 2011, 48(9): 1328-1342. doi: 10.1139/t11-041
[5]	ZHANG F, GAO Y, WU Y, et al. Face stability analysis of large-diameter slurry shield-driven tunnels with linearly increasing undrained strength[J]. Tunnelling and Underground Space Technology, 2018, 78: 178-187. doi: 10.1016/j.tust.2018.04.018
[6]	XIANG Y, LIU H, ZHANG W, et al. Application of transparent soil model test and DEM simulation in study of tunnel failure mechanism[J]. Tunnelling and Underground Space Technology, 2018, 74: 178-184. doi: 10.1016/j.tust.2018.01.020
[7]	LOW B K, EINSTEIN H H. Reliability analysis of roof wedges and rockbolt forces in tunnels[J]. Tunnelling and Underground Space Technology, 2013, 38: 1-10. doi: 10.1016/j.tust.2013.04.006
[8]	LÜ Q, XIAO Z, JI J, et al. Reliability based design optimization for a rock tunnel support system with multiple failure modes using response surface method[J]. Tunnelling and Underground Space Technology, 2017, 70: 1-10. doi: 10.1016/j.tust.2017.06.017
[9]	MOLLON G, DIAS D, SOUBRA A H. Probabilistic analysis of circular tunnels in homogeneous soil using response surface methodology[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(9): 1314-1325. doi: 10.1061/(ASCE)GT.1943-5606.0000060
[10]	PAN Q J, DIAS D. Probabilistic evaluation of tunnel face stability in spatially random soils using sparse polynomial chaos expansion with global sensitivity analysis[J]. Acta Geotechnica, 2017, 12(6): 1415-1429. doi: 10.1007/s11440-017-0541-5
[11]	蒋水华, 刘贤, 曾绍慧, 等. 盾构隧道开挖面稳定非侵入式可靠度分析[J]. 地下空间与工程学报, 2019, 15(增刊2): 583-589. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE2019S2012.htm JIANG Shui-hua, LIU Xian, ZENG Shao-hui, et al. Non-intrusive reliability analysis on excavation face stability of shield-driven tunnels[J]. Chinese Journal of Underground Space and Engineering, 2019, 15(S2): 583-589. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BASE2019S2012.htm
[12]	LOW B K, TANG W H. Reliability analysis using object- oriented constrained optimization[J]. Structural Safety, 2004, 26(1): 69-89. doi: 10.1016/S0167-4730(03)00023-7
[13]	RACKWITZ R, FLESSLER B. Structural reliability under combined random load sequences[J]. Computers & Structures, 1978, 9(5): 489-494.
[14]	JI J, KODIKARA J K. Efficient reliability method for implicit limit state surface with correlated non-Gaussian variables[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 39(17): 1898-1911. doi: 10.1002/nag.2380
[15]	JI J, ZHANG C, GAO Y, et al. Reliability-based design for geotechnical engineering: an inverse FORM approach for practice[J]. Computers and Geotechnics, 2019, 111: 22-29. doi: 10.1016/j.compgeo.2019.02.027
[16]	SHIAU J, AL-ASADI F. Determination of critical tunnel heading pressures using stability factors[J]. Computers and Geotechnics, 2020, 119: 103345. doi: 10.1016/j.compgeo.2019.103345
[17]	赵明华, 张锐. 有限元上限分析网格自适应方法及其工程应用[J]. 岩土工程学报, 2016, 38(3): 537-545. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201603021.htm ZHAO Ming-hua, ZHANG Rui. Adaptive mesh refinement of upper bound finite element method and its applications in geotechnical engineering[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(3): 537-545. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201603021.htm
[18]	Optum CE[CP]. Optum Computational Engineering, 2019. https://www.optumce.com.
[19]	ZHANG W, MENG F, CHEN F, et al. Effects of spatial variability of weak layer and seismic randomness on rock slope stability and reliability analysis[J]. Soil Dynamics and Earthquake Engineering, 2021, 146: 106735. doi: 10.1016/j.soildyn.2021.106735
[20]	LIU H, LOW B K. Reliability-based design of tunnelling problems and insights for Eurocode 7[J]. Computers and Geotechnics, 2018, 97: 42-51. doi: 10.1016/j.compgeo.2017.12.005
[21]	MOLLON G, DIAS D, SOUBRA A. Range of the safe retaining pressures of a pressurized tunnel face by a probabilistic approach[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(11): 1954-1967. doi: 10.1061/(ASCE)GT.1943-5606.0000911
[22]	程红战, 陈健, 胡之锋, 等. 考虑砂土抗剪强度空间变异性的盾构开挖面稳定性分析[J]. 岩土力学, 2018, 39(8): 3047-3054. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201808040.htm CHENG Hong-zhan, CHEN Jian, HU Zhi-feng, et al. Face stability analysis for a shield tunnel considering spatial variability of shear strength in sand[J]. Rock and Soil Mechanics, 2018, 39(8): 3047-3054. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201808040.htm
[23]	ZHANG W, JI J, GAO Y, et al. Spatial variability effect of internal friction angle on the post-failure behavior of landslides using a random and non-Newtonian fluid based SPH method[J]. Geoscience Frontiers, 2020, 11(4): 1107-1121. doi: 10.1016/j.gsf.2020.02.003
[24]	仉文岗, 王琦, 刘汉龙, 等. 岩体空间变异性对隧道拱顶失效概率的影响[J]. 岩土力学, 2021, 42(5): 1462-1472. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202105028.htm ZHANG Wen-gang, WANG Qi, LIU Han-long, et al. Influence of rock mass spatial variability on probability of tunnel roof wedge failure[J]. Rock and Soil Mechanics, 2021, 42(5): 1462-1472. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202105028.htm
[25]	HUANG J, LYAMIN A V, GRIFFITHS D V, et al. Quantitative risk assessment of landslide by limit analysis and random fields[J]. Computers and Geotechnics, 2013, 53: 60-67.

施引文献(22)

期刊类型引用(9)

1.	周文朋，王开军，冯宏朝，高锋，高梁，徐荣超. 超高特大矩形顶管始发端掌子面稳定性计算. 水利与建筑工程学报. 2025(01): 144-153 . 百度学术
2.	郝鹏，杨浩，冯少军，王博 . 高置信水平结构逆可靠度分析与优化方法研究进展. 力学学报. 2024(02): 310-326 . 百度学术
3.	钟华，韩玉，陶志刚，刘能源. 软岩隧道NPR锚索主动控制关键技术. 地下空间与工程学报. 2024(02): 587-596+605 . 百度学术
4.	黄阜，陈晶晶，王勇涛，杨云强，谭瑞. 基于极限分析理论的复合地层中双模盾构开挖面稳定性研究. 土木与环境工程学报(中英文). 2024(06): 89-99 . 百度学术
5.	熊先勇，曾亚林，付慧建，曾威. 基于支持向量机和改进粒子群算法的钢管混凝土拱桥可靠度分析. 公路工程. 2023(02): 55-61 . 百度学术
6.	李天胜，何川，方砚兵，周子寒，包烨明，陈子全，白国峰. 基于围岩变形失效的隧道结构可靠度设计方法. 西南交通大学学报. 2023(03): 613-621 . 百度学术
7.	孙望成. 考虑Hoek–Brown准则的盾构隧道掌子面稳定性分析. 湖南文理学院学报(自然科学版). 2023(03): 32-36+43 . 百度学术
8.	吴兴征，刘赫. 土工构筑物的逆几何可靠性分析算法. 土木与环境工程学报(中英文). 2023(05): 106-115 . 百度学术
9.	徐中秋，杨扬，鲁芬婷. 顶管施工对始发端土体影响的分析与研究. 新乡学院学报. 2022(09): 69-72 . 百度学术

其他类型引用(13)

资源附件(0)

图(11) / 表(3)

计量

文章访问数: 262
HTML全文浏览量: 24
PDF下载量: 164
被引次数: 22

0. 引言
1. 一阶可靠度基本概念和算法实现
1.1 一次二阶矩可靠度指标
1.2 HLRF-x迭代算式求解随机参量设计点
1.3 逆可靠度算法
1.4 隧道开挖面稳定的极限状态
2. 三维有限元极限分析
2.1 数值模型
2.2 极限分析准则
3. iHLRF-x算法在隧道开挖面可靠度分析中的应用
3.1 逆可靠度分析流程
3.2 算例验证
4. 开挖面极限支护压力可靠度设计
4.1 基于逆可靠度分析的支护压力概率结果
4.2 可靠度指标、设计点及分项安全系数
5. 土体参数空间变异性对开挖面支护压力的影响
5.1 KL展开法（Karhunen-Loeve expansion）
5.2 空间变异自相关距离的影响
6. 结论与展望

0. 引言
1. 一阶可靠度基本概念和算法实现
1.1 一次二阶矩可靠度指标
1.2 HLRF-x迭代算式求解随机参量设计点
1.3 逆可靠度算法
1.4 隧道开挖面稳定的极限状态
2. 三维有限元极限分析
2.1 数值模型
2.2 极限分析准则
3. iHLRF-x算法在隧道开挖面可靠度分析中的应用
3.1 逆可靠度分析流程
3.2 算例验证
4. 开挖面极限支护压力可靠度设计
4.1 基于逆可靠度分析的支护压力概率结果
4.2 可靠度指标、设计点及分项安全系数
5. 土体参数空间变异性对开挖面支护压力的影响
5.1 KL展开法（Karhunen-Loeve expansion）
5.2 空间变异自相关距离的影响
6. 结论与展望

参考文献(25)

施引文献(22)

资源附件(0)

基于逆可靠度分析的隧道开挖面极限支护压力优化设计 English Version

作者简介: 姬建(1983— ),男,博士,教授,主要从事岩土工程可靠度、边坡工程、地下空间风险分析等领域的科研与教学工作。E-mail：JI0003AN@e.ntu.edu.sg

计量

出版历程

Inverse reliability-based design of limit support pressure for tunnel face stability

0. 引言

1. 一阶可靠度基本概念和算法实现

1.1 一次二阶矩可靠度指标

1.2 HLRF-x迭代算式求解随机参量设计点

1.3 逆可靠度算法

1.4 隧道开挖面稳定的极限状态

2. 三维有限元极限分析

2.1 数值模型

2.2 极限分析准则

3. iHLRF-x算法在隧道开挖面可靠度分析中的应用

3.1 逆可靠度分析流程

3.2 算例验证

4. 开挖面极限支护压力可靠度设计

4.1 基于逆可靠度分析的支护压力概率结果

4.2 可靠度指标、设计点及分项安全系数

5. 土体参数空间变异性对开挖面支护压力的影响

5.1 KL展开法（Karhunen-Loeve expansion）

5.2 空间变异自相关距离的影响

6. 结论与展望

期刊类型引用(9)

其他类型引用(13)

计量

出版历程

目录

0. 引言

1. 一阶可靠度基本概念和算法实现

1.1 一次二阶矩可靠度指标

1.2 HLRF-x迭代算式求解随机参量设计点

1.3 逆可靠度算法

1.4 隧道开挖面稳定的极限状态

2. 三维有限元极限分析

2.1 数值模型

2.2 极限分析准则

3. iHLRF-x算法在隧道开挖面可靠度分析中的应用

3.1 逆可靠度分析流程

3.2 算例验证

4. 开挖面极限支护压力可靠度设计

4.1 基于逆可靠度分析的支护压力概率结果

4.2 可靠度指标、设计点及分项安全系数

5. 土体参数空间变异性对开挖面支护压力的影响

5.1 KL展开法（Karhunen-Loeve expansion）

5.2 空间变异自相关距离的影响

6. 结论与展望

作者简介:
姬建(1983— ),男,博士,教授,主要从事岩土工程可靠度、边坡工程、地下空间风险分析等领域的科研与教学工作。E-mail：JI0003AN@e.ntu.edu.sg