局部冲刷场地桩基桥梁地震响应简化分析及离心振动台验证

梁发云; 梁轩; 张浩

doi:10.11779/CJGE202110002

局部冲刷场地桩基桥梁地震响应简化分析及离心振动台验证 English Version

1.
同济大学地下建筑与工程系,上海　200092
2.
上海师范大学建筑工程学院,上海　201418

基金项目:

国家自然科学基金面上项目 51878487

国家自然科学基金面上项目 41672266

详细信息

作者简介:
梁发云(1976— ),男,博士,教授,主要从事土力学与基础工程的教学科研工作。Email：fyliang@tongji.edu.cn

中图分类号: TU435
计量
- 文章访问数: 281
- HTML全文浏览量: 54
- PDF下载量: 242
出版历程
- 收稿日期: 2020-12-16
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-09-30

Simplified analysis of dynamic response of pile-supported bridge under local scour and verification by centrifugal shaking tests

1.
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
2.
College of Civil Engineering, Shanghai Normal University, Shanghai 201418, China

摘要

摘要: 冲刷导致桩周土体流失,改变了场地的地震动特性,同时影响了桥梁的抗震性能。为研究局部冲刷下桩基桥梁动力特性及潜在破坏风险,探讨了冲刷场地的地震动特性,给出局部冲刷场地的地震动快速计算方法；并在此基础上提出局部冲刷后桩基桥梁地震分析简化模型,通过振型叠加法计算桥梁的墩底、桩身剪力和最大位移,用以快速评估局部冲刷后桩基桥梁的破坏风险,进而确定临界破坏冲刷深度；为验证模型的正确性,开展了50g重力下桩基桥梁离心振动台试验,桥梁上部结构简化为质量块,基础采用3×3群桩。按照冲刷深度分为3个工况,每个工况下输入白噪声和El-Centro波。研究表明,一般冲刷使得场地周期减小,但局部冲刷对场地周期影响不明显,局部冲刷坑坡角对场地的地震动几乎没有影响；局部冲刷场地与一般冲刷场地的地震动差别较大,但与原场地的地震响应基本相似；桥梁响应最大时的冲刷深度取决于桥梁频率与地震波主要波频的关系。该简化方法计算的桥梁反应与试验结果相近,因此,可用于局部冲刷条件下桥梁的地震反应快速计算、震害风险评估和临界破坏冲刷深度确定。
- 冲刷效应 /
- 桥梁工程 /
- 双质点模型 /
- 地震动输入 /
- 离心振动台试验
Abstract: Scour causes the erosion of soil, changes the seismic response of site, and also influences the seismic properties of bridge. To investigate the dynamic behavior and damage potential of pile-supported bridges at local scour site, the effects of scour on the ground motion of site are firstly discussed, and a fast calculation method for calculating ground motion is presented. Next, a simplified model describing the bridge response is put forward, which considers the ground motion changes caused by local scour. Then the shear force at the pier bottom and pile head, and the maximum displacement of bridge are calculated by the modal superposition method so as to quickly evaluate the damage potential of bridge after scour and further determine the critical damage scour depth. Finally, the centrifugal shaking tests on the pile-supported bridge are conducted under 50g to verify the accuracy of this model. The superstructure of the bridge supported by 3×3 pile-group foundation is simplified as a mass block. There are 3 scour depth conditions. It is found that the site period obviously decreases under general scour, and hardly changes under local scour. The slope angle of local scour hole has virtually no impact on the ground motions of site. The motions at local scour sites are quite different from those at general scour sites, but similar to those at the original free site at the same depth. The scour depth, where the bridge reaches the greatest response, depends on the interrelation between bridge period and dominant frequency of the earthquake. The centrifuge tests further prove that the proposed model can be applied to the fast calculation of seismic response, the assessment of potential of scoured bridge and the critical scour depth under earthquakes.
- scour effect /
- bridge engineering /
- 2-DOF model /
- ground motion input /
- centrifugal shaking table test

HTML全文

0. 引言

在桥梁服役期间,冲刷和地震导致桥梁破坏的重要因素^[1]。实际工程中,冲刷深度一般可达几米至十几米,研究资料表明,最大冲刷深度可能会超过20 m^[2],冲刷导致的桩基过度裸露严重影响了桥梁的承载力及抗震性能^[3-4],同时改变了初始场地条件。世界上有很多桥梁修建于地震和洪水频发的地区,如美国西海岸、中国西南山区和东南沿海地区等。相比于单一灾害,冲刷和地震双重灾害作用下的桥梁更容易发生破坏^[5]。然而,国内已有的设计规范,如《城市桥梁抗震规范》（CJJ166—2011）和《公路工程水文勘测设计规范》（JTG C30—2015）,均通过增加承台埋深抵消冲刷效应,未考虑实际工程中过度冲刷导致的桩基裸露情况和场地初始设计地震动改变的影响。另外,冲刷条件下桩基桥梁的动力特性尚不清晰,缺乏快速准确的震害风险评估方法。因此,有必要开展冲刷条件下桩基桥梁的抗震特性及其破坏风险评估研究。

关于冲刷后桥梁动力特性和震害风险评估的研究可分为3个方面：

（1）通过试验研究冲刷后桥梁抗震性能,如Wang等^[6]通过1g振动台试验,针对简化的桩-柱式桥梁模型的抗震性能开展研究,发现随着冲刷深度的增加,桩和桥墩的弯矩分布模式发生变化,由此可能导致桥梁破坏机理发生转变；梁发云等^[7]基于离心机振动台研究了整层冲刷下群桩基础的弯矩分布规律；Wang等^[8]对比了液化场地和非液化场地冲刷后桩基桥梁的地震反应,发现浅层土液化可导致桥梁损伤位置从墩底或桩身转移到桩头。试验方法可以很好地模拟桥梁的动力响应规律,但耗时耗力难易快速评估桥梁冲刷后的破坏风险。

（2）基于数值计算方法,通过建立全桥模型,能更全面地模拟桩-土-上部结构的相互作用。Prasad等^[9]建立了不同冲刷深度下混凝土桥有限元模型进行了非线性时程分析,Wang等^[10]通过OpenSees建立不同类型桥梁的有限元模型,认为不同类型桥梁结构对冲刷深度的敏感性不同；Klinga等^[11]则建立了考虑非线性土桩结构相互作用、桥台和桥墩非线性响应的桥梁模型,发现桩身弯矩、桩身变形随冲刷深度增大。但由于数值建模难度大、计算耗时长,每个冲刷深度下均需重复建模计算,难以适应快速评估冲刷后桥梁抗震性能的需求。

（3）近年来,有学者提出了简化的双质点理论模型,从力学及运动学角度分析冲刷前后的振型特征和评估桥梁地震损伤潜力。叶爱君等^[12]通过建立两质点单墩模型,分析了不同冲刷深度下高桩承台基础与桥墩的动力相互作用规律；Xu等^[13]从定性角度分析冲刷深度的影响,发现随着冲刷深度增大,桥梁动力反应可能先增大后减小；Song等^[14]则进一步采用双质点模型分析桩基桥梁在冲刷条件下的内力变化规律。上述双质点模型较好地描述了承台与上部结构的相互作用规律,但均忽略了冲刷效应引起的场地的地震动改变,尤其对于冲刷坑较深的场地情况,其影响不可忽略。

因此,本文在双质点模型研究的基础上,通过数值方法分析冲刷对场地地震动的影响,给出局部冲刷后场地的地震动快速计算方法；并从弹性地震需求和承载力角度分析了冲刷后桥梁的动力特性及临界破坏冲刷深度；通过离心振动台试验验证桥梁简化地震分析模型的准确性,研究结果为现有简支桥梁桩基允许最大裸露长度的计算、冲刷条件下桥梁的设计与安全评估提供了一种快捷有效的方法。

1. 局部冲刷场地的地震动特性

1.1 局部冲刷坑形态分析

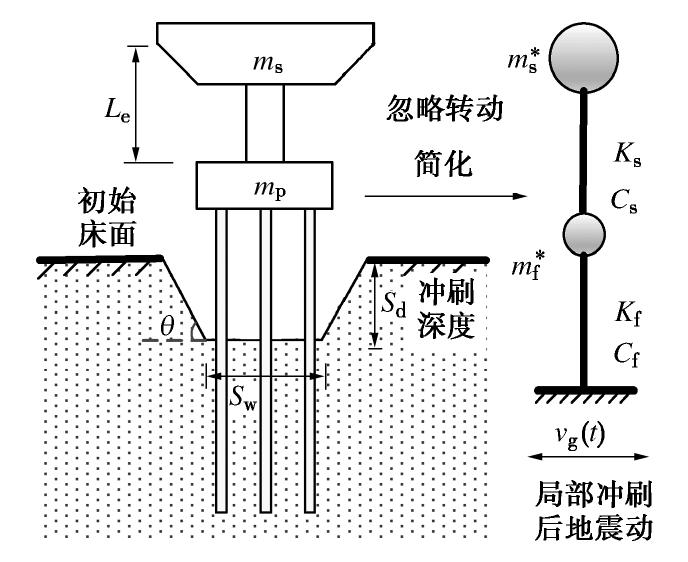
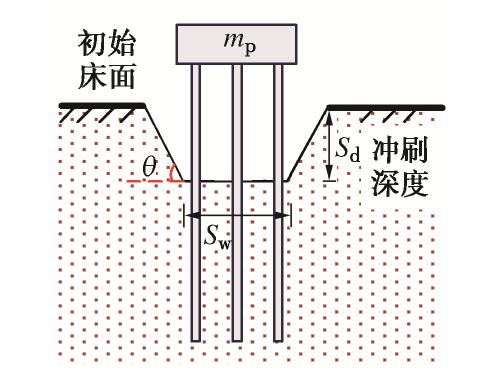
冲刷通常分为一般冲刷、收缩冲刷和局部冲刷,其中,局部冲刷产生的影响最大,其深度远大于一般冲刷和收缩冲刷^[1]。现场实测的局部冲刷坑形态一般近似“C”型或倒锥形态^[15],很多学者为研究方便,一般将其简化为如图1所示的局部冲刷模型^[16-18]。参考Amini等^[19]关于小间距群桩冲刷试验结论,以及何泓男等^[16]关于局部冲刷下桩基水平承载试验,本文同样采用如图1所示梯形截面冲刷坑形式。

图 1 局部冲刷坑形态

Figure 1. Shape of local scour hole

下载: 全尺寸图片幻灯片

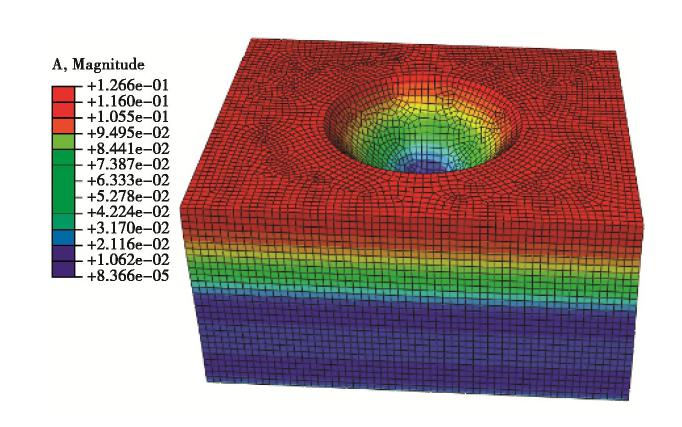
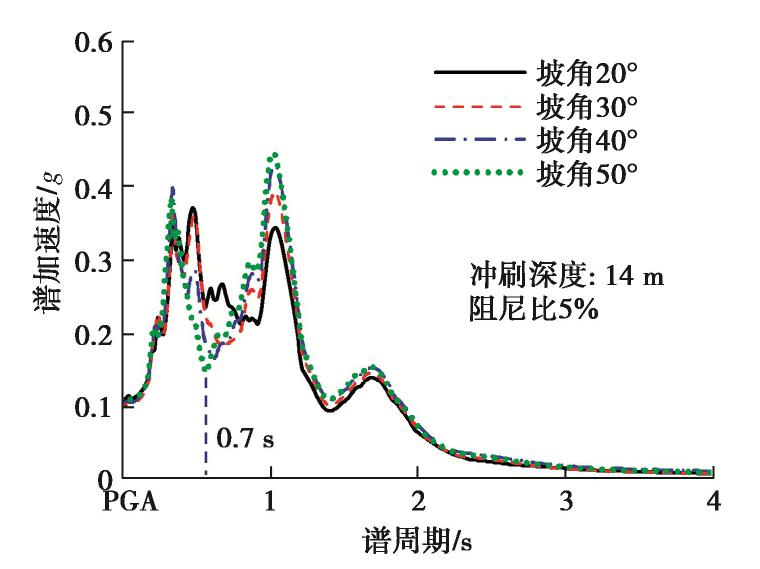
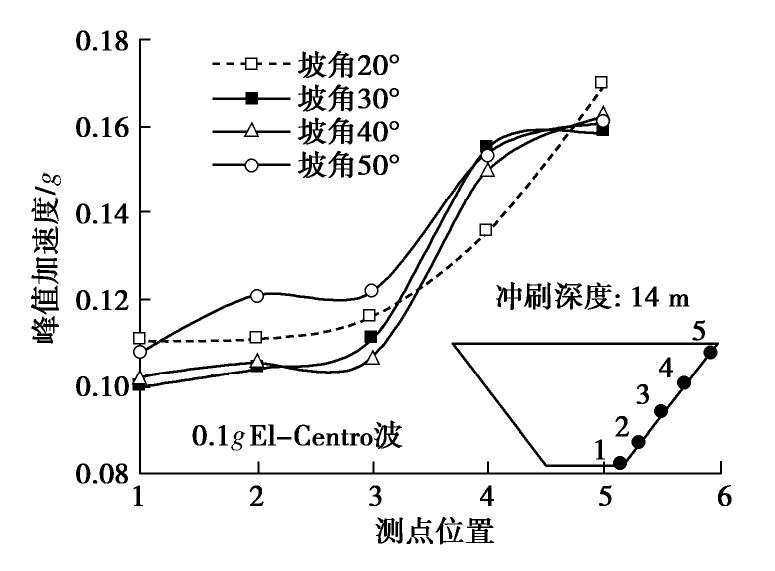
Lin等^[17]和Zhang等^[18]认为砂土场地冲刷坑坡度一般为20°～50°。因此,本文分别建立坡度为20°、30°、40°、50°的局部冲刷场地三维有限元模型如图2,以研究冲刷坑形态对地震动的影响。其中冲刷深度取较大值14 m,土体采用线弹性模型,弹性模量50 MPa,密度1450 kg/m³,泊松比0.3,土层厚度28 m,土体瑞利阻尼系数α=0.3158,β=0.0078,模型采用黏弹性边界^[20]。为保证动力分析的准确性,Lee等^[21]认为网格尺寸 $Δ l$ 要满足 $Δ l$ ≤ $λ_{\min} / 10$ ,其中 $λ_{\min}$ 为输入波的最短波长。本文采用El-Centro 地震波作为基岩输入波,波频范围0.1～10 Hz,没有过高频率,且考虑了上述网格尺寸及分析步长限制,计算结果比较可靠。

图 2 局部冲刷场地数值模型

Figure 2. Numerical mode for local scour site

下载: 全尺寸图片幻灯片

图3为0.1g El-Centro波作用下局部冲刷场地坑底的加速度反应谱,可以看出冲刷坑的坡角对坑底的地震动反应影响很小,仅在0.7～1.0 s区间稍有差异,可能是由于不同坡角的斜坡对波的散射作用不同所造成的。图4为局部冲刷坑斜坡上不同位置处的峰值加速度,显然,峰值加速度随位置升高而增大,但同一高度位置处的加速度峰值随坡角变化不大（不超过20%）。

图 3 冲刷坑坡角对坑底加速度反应谱的影响

Figure 3. Influences of slope angle on acceleration spectrum at bottom of scour hole

下载: 全尺寸图片幻灯片

图 4 冲刷坑斜坡上的峰值加速度

Figure 4. Peak accelerations of slope

下载: 全尺寸图片幻灯片

Khanbabazadeh等^[22]在研究盆地效应时,同样发现盆地边缘坡角的变化对盆地中心处地震动的影响很小。Lin^[23]对冲刷坑的深度、宽度及坡度进行因素分析时,发现冲刷深度对水平桩承载性能的影响最大,坡度的影响可以忽略。因此,本文在研究冲刷深度对场地地震影响时,对于坡脚的影响不予以考虑,坡角取均值30°常数。

1.2 局部冲刷深度的影响

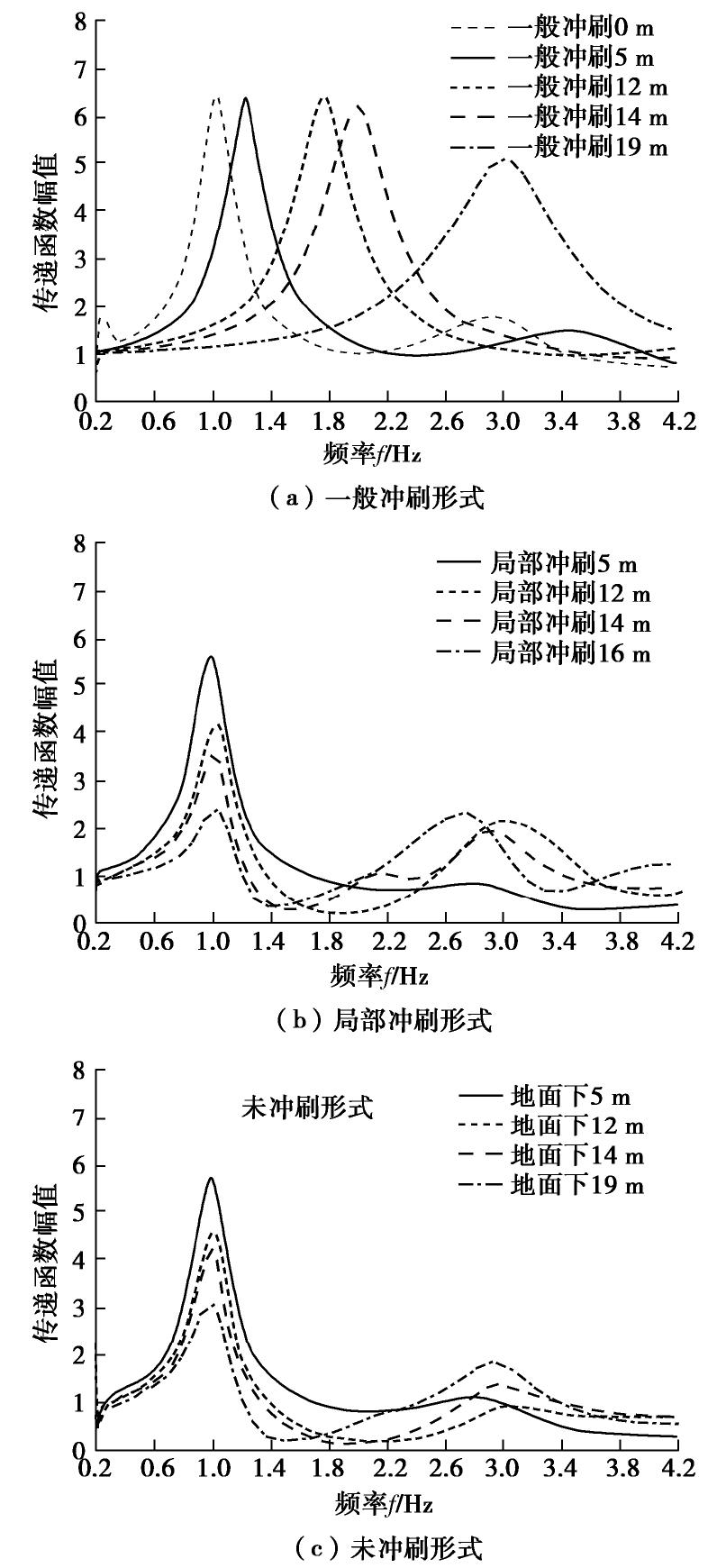
图5为任一地震波作用下,基岩到冲刷坑底部（或某深度处）的加速度传递函数（其反映了场地对波频的放大效应,若不考虑土体非线性,其形状与地震波类型无关,本文以0.1g Lander波作为激励,波频涵盖0.2～25 Hz）。其中,图5（a）为一般冲刷（整层土冲刷）场地传递函数,很明显,随着冲刷深度增加场地卓越频率由1.0 Hz增大到3.0 Hz,当冲刷深度超过12 m时,传递函数幅值也显著降低。图5（b）所示的局部冲刷场地和图5（c）未冲刷场地地面下同等深度处的传递函数在低频段几乎一致,而在2.6～4.2 Hz段稍有差异,其主要由冲刷坑侧壁的对地震波的折射、反射造成。和一般冲刷场地的传递函数明显不同的是：局部冲刷场地卓越周期（频率）几乎不变,这意味着局部冲刷对场地周期的影响很小,但传递函数幅值随冲刷深度递减；局部冲刷场地的传递函数幅值明显小于一般冲刷场地,从而局部冲刷场地的加速度更小。

图 5 基岩到冲刷面（或地面）加速度传递函数

Figure 5. Transfer function for acceleration from site bottom to erosional basal surface

下载: 全尺寸图片幻灯片

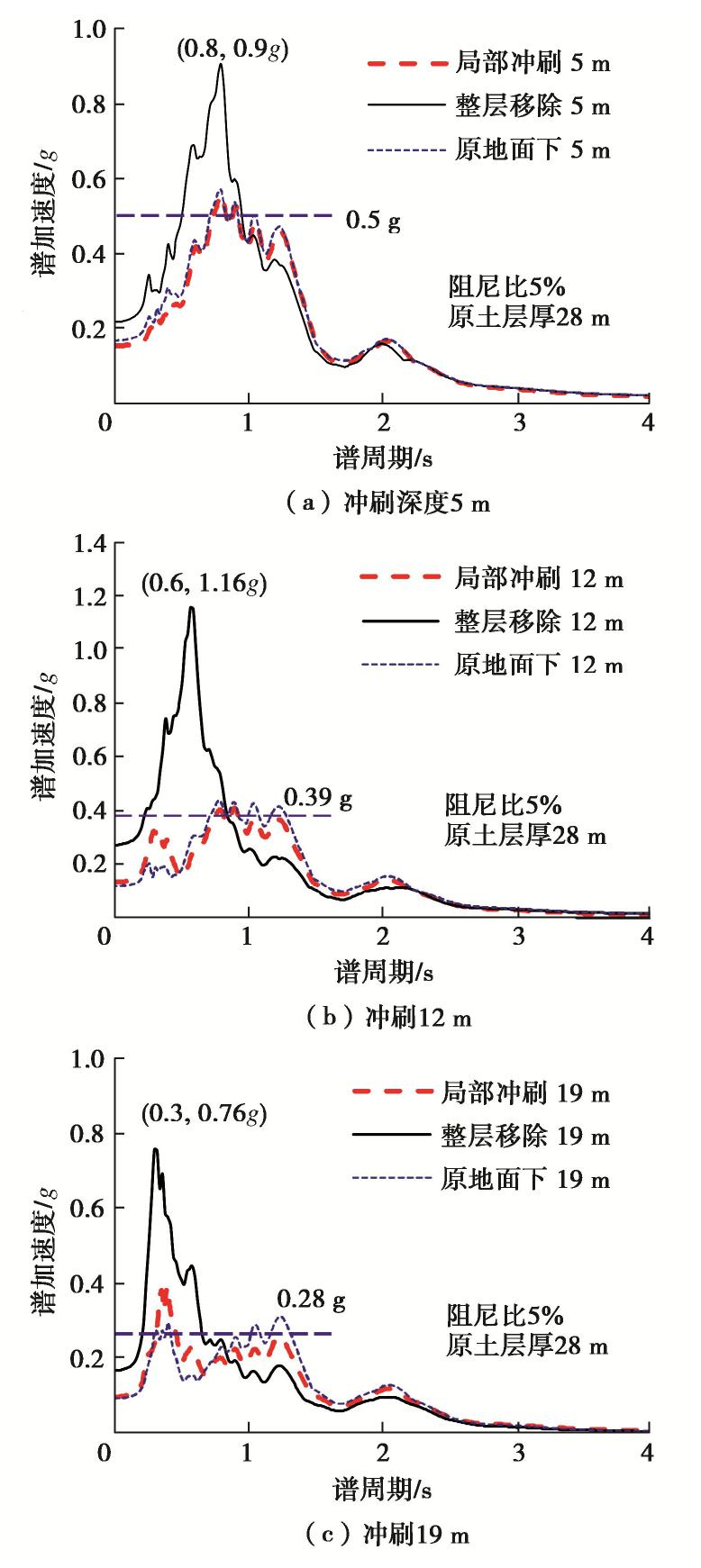
图6为0.1g El-Centro波作用下场地反应谱,很明显未冲刷场地同等深度处的加速度反应谱和局部冲刷坑底的反应谱几乎相同；另一方面,局部冲刷场地反应谱峰值远小于一般冲刷场地,且随冲刷深度的增大,局部冲刷场地的谱加速度峰值从0.5g逐渐减小至0.28g,但一般冲刷场地的谱加速度峰值从0.9g先增大到1.16g再减小至0.76g,其主要原因是一般冲刷场地周期显著减小,当接近地震波的卓越周期时,动力放大系数先增大后减小。

图 6 0.1g El-Centro波作用下场地加速度反应谱

Figure 6. Acceleration spectra of site under El-Centro waves

下载: 全尺寸图片幻灯片

由图5,6可知,一般冲刷场地和局部冲刷场地的地震动差异显著,但和原未冲刷场地深度处的响应近似。因此,在进行局部冲刷后桥梁的地震反应分析时,不能直接用一般冲刷场地或原场地土表的地震动作为输入荷载。简化起见,可以用未冲刷场地同等深度处加速度时程代替。

1.3 局部冲刷场地的地震动计算

上述分析结论可知,对于非线性较弱的均质局部冲刷场地,其地震动可采用未冲刷场地地面下同等深度处的加速度时程（或反应谱）代替。其中,均质自由场地z深度处的加速度可采用Makris等^[24]的一维自由场反应公式快速得到,即

$a_{ff} (z) = \frac{a_{g}}{\cos ((ω / V_{s}) H_{soil})} \cos (\frac{ω}{V_{s}} z) = a_{s} \cos (\frac{ω}{V_{s}} z)$ ,

(1)

式中, $a_{ff} (z)$ 为z深度处的频域内加速度, $V_{s}$ 为土体的剪切波速,H_soil为土层厚度,ω为圆频率, $a_{g}$ 和 $a_{s}$ 分别为基岩和地表的频率内加速度。对于任一地表加速度时程a(t)可经Fourier变换成频率 $a_{g}$ (ω),将其带入上式可得到冲刷后加速度 $a_{ff} (z)$ ,再经Fourier逆变换,得到局部冲刷场地的地震时程；而对于设计反应谱,则可经地震波模拟软件转换为人工波,再通过上述步骤得到局部冲刷后地震动时程,进而得到局部冲刷后的反应谱。

2. 局部冲刷后桥梁地震简化分析

采用多跨简支梁和群桩基础支撑的跨江海桥梁,其相邻梁跨的横向刚度约束相对较小,桥梁质量主要集中在上部结构以及承台,为简化起见,可忽略上部结构及承台的转动自由度及橡胶垫的约束。参考Xu等^[13]和Song等^[14]将此类桥梁简化为图7所示的双质点模型,其中群桩基础等效为底部固定约束的悬臂杆。局部冲刷场地的地震动采用1.3节方法计算。通过求解地震作用下的桥梁运动方程（2）获得桥梁弹性地震需求,以桥墩和桩基临近屈服对应的墩底和桩头的水平抗力作为其承载力,并将其应用于局部冲刷后桩基桥梁临界冲刷深度的计算和地震风险的快速评估。

图 7 考虑冲刷导致地震动改变的简化模型

Figure 7. A simplified model for bridge considering scour induced ground motion changes

下载: 全尺寸图片幻灯片

$m \ddot{v} (t) + c \dot{v} (t) + k v (t) = - m {\ddot{x}}_{g} (t)$ ,

(2)

式中,m,c,k分别为质量矩阵、阻尼矩阵、刚度矩阵,v(t)为位移, ${\ddot{x}}_{g} (t)$ 为冲刷后场地的加速度时程。

2.1 模型等效参数

如图7所示,m_s和m_p分别为上部结构和承台质量；K_s,K_f分别为桥墩和群桩基础的等效刚度；C_s,C_f分别为桥墩和群桩基础的等效阻尼,一般取5% 和10%。对于桥墩质量相对较小且为等截面立柱的情况,将其质量的影响部分集中到上部结构和承台处,根据Priestley等^[25]的简化原则,上部结构的等效质量如下式所示：

$m_{s}^{*} = m_{s} + N_{c} L_{c} {\bar{m}}_{c} / 3$ ,

(3)

承台的等效质量如下式所示：

$m_{f}^{*} = m_{p} + N_{c} L_{c} {\bar{m}}_{c} / 3 + N_{f} h {\bar{m}}_{f} / 3$ ,

(4)

式中, $m_{s}$ , $m_{p}$ 分别为桥面和承台质量, ${\bar{m}}_{f}$ , ${\bar{m}}_{c}$ 为桩和桥墩的单位长度质量,N_c,N_f分别为墩柱和桩的数量,L_c为桥墩高度,h为桩基出露高度。

桥墩的等效刚度K_s根据Priestley等^[25]方法计算：

$K_{s} = \frac{N_{c} α_{c} E I_{c}}{L_{e}^{3}}$ ,

(5)

式中,EI_c为立柱抗弯刚度,N_c为桥墩立柱数目,α_c为桥墩边界条件系数,对于单立柱桥墩可取3,多柱桥墩取12,L_e为上部结构形心到承台面的距离。

群桩基础的等效刚度K_f,本文参考Song等^[14]基于高桩承台基础试验的经验公式计算,其中通过地基反力折减系数描述群桩相互作用,以边界系数描述承台约束。

$K_{f} = {\begin{cases} \sum_{i = 1}^{N_{r}} \frac{{(N_{p})}_{i}}{0.083 ζ_{i}^{3} + 0.353 ζ_{i}^{2} + 0.5 ζ_{i} + 0.71} \frac{E I_{p}}{D_{i}^{3}} (黏土) \\ \sum_{i = 1}^{N_{r}} \frac{{(N_{p})}_{i}}{0.083 ζ_{i}^{3} + 0.44 ζ_{i}^{2} + 0.86 ζ_{i} + 0.94} \frac{E I_{p}}{D_{i}^{3}} (砂土) \end{cases} 。$

(6)

式中,N_r为桩排数,N_p为每排桩数,EI_p为桩的抗弯刚度, $ζ_{i}$ 为i排桩基出露有效高度,ζ_i=h/D_i,h为冲刷深度,D_i为i排桩的固嵌深度,可由下式计算：

$D_{i} = {\begin{cases} \sqrt[4]{E I_{p} / k_{n}^{*}} (黏土) \\ \sqrt[5]{E I_{p} / k_{c}^{*}} (砂土) \end{cases}$ ,

(7)

式中, $k_{n}^{*} = n_{i} k_{n}$ 为黏土等效地基反力系数, $k_{c}^{*} = n_{i} k_{c}$ 为砂土地基等效地基反力系数,n_i为i排桩折减系数, $k_{c}$ 和 $k_{n}$ 分别为黏土和砂土地基反力系数。

2.2 桥梁频率和阻尼

一般认为系统阻尼仅影响系统反应峰值,对自振周期及振型无影响,因此可通过求解无阻尼的双质点自由振动方程（8）可获得系统周期及振型参数。

$[\begin{matrix} m_{1} & 0 \\ 0 & m_{2} \end{matrix}] \ddot{v} (t) + [\begin{matrix} k_{11} & k_{12} \\ k_{21} & k_{22} \end{matrix}] v (t) = 0$ ,

(8)

其中系统一阶、二阶圆频率为

$ω_{1 ， 2}^{2} = \frac{1}{2} (\frac{k_{11}}{m_{1}} + \frac{k_{22}}{m_{2}}) \pm \sqrt{\frac{1}{4} {(\frac{k_{11}}{m_{1}} + \frac{k_{22}}{m_{2}})}^{2} - \frac{k_{11} k_{22} - k_{12} k_{21}}{m_{1} m_{2}}}$ 。

(9)

一阶振型和二阶振型可分别表示为

$ϕ_{1} = {[\frac{v_{11}}{v_{21}}, 1]}^{T}, ϕ_{2} = {[\frac{v_{12}}{v_{22}} ， 1]}^{T}$ ,

(10a)

$\frac{v_{11}}{v_{21}} = - \frac{k_{12}}{k_{11} - ω_{1}^{2} m_{1}} ， \frac{v_{12}}{v_{22}} = - \frac{k_{12}}{k_{11} - ω_{2}^{2} m_{1}}$ 。

(10b)

第n振型等效阻尼 $ξ_{n}$ ,可由Hwang等^[26]计算,

$ξ_{n} = \frac{\sum_{j = 1}^{2} K_{j} ϕ_{n j}^{2} C_{j}}{ϕ_{n}^{T} K ϕ_{n}}$ 。

(11)

K_j,C_j为子结构的刚度和阻尼,即K₁=K_f,C₁=C_f,K₂=K_s,C₂=C_s；K为体系刚度矩阵； $ϕ_{n j}$ 表示第n振型中j结构的振型位移。由式（8）,（10）,（11）,可得

$ξ_{1} = \frac{K_{f} C_{f} + K_{s} {(\frac{v_{21}}{v_{11}} - 1)}^{2} C_{s}}{K_{f} C_{f} + K_{s} {(\frac{v_{21}}{v_{11}} - 1)}^{2}}$ ,

(12a)

$ξ_{2} = \frac{K_{f} C_{f} + K_{s} {(\frac{v_{12}}{v_{22}} - 1)}^{2} C_{s}}{K_{f} C_{f} + K_{s} {(\frac{v_{12}}{v_{22}} - 1)}^{2}}$ 。

(12b)

2.3 地震波作用下的桥梁响应

根据振型的正交特性,地震作用下有阻尼多自由度体系的运动方程可表示为

$M_{n} {\ddot{Y}}_{n} (t) + C_{n} \dot{Y} (t) + K_{n} Y_{n} (t) = ϕ_{n}^{T} m r {\ddot{v}}_{g} (t)$ ,

(13)

式中,广义质量 $M_{n} = ϕ_{n}^{T} m ϕ_{n}$ ,广义阻尼 $C_{n} = ϕ_{n}^{T} c ϕ_{n}$ ,广义刚度 $K_{n} = ϕ_{n}^{T} k ϕ_{n}$ ,广义位移 $Y_{n} (t) = ϕ_{n}^{T} m v (t) /$ $(ϕ_{n}^{T} m ϕ_{n})$ ,r表示单位列向量。

采用振型叠加法可得结构的时程总反应 $v (t) = \sum ϕ_{n} Y_{n} (t)$ 。而工程上主要关注结构最大响应,对于第n振型的最大加速度 $a_{n}$ ,可由下式计算：

$a_{n} = ϕ_{n} \cdot M P F_{n} \cdot S_{n} (T)$ ,

(14)

式中, ${MPF}_{n} = (ϕ_{n}^{T} m r) / (ϕ_{n}^{T} m ϕ_{n})$ ,为振型参与系数； $S_{n} (T)$ 为地震动作用下周期为T对应的反应谱加速度,对于地震波 $S_{n} (T) = k β (T) g$ ,k为地震影响系数,β(T)为地震放大系数,对于单位谐波 ${\ddot{v}}_{g} (t) = \sin (\bar{ω} t)$ , $S_{n} (T) = D_{n} =$ ${[{(1 - β_{n}^{2})}^{2} + {(2 ξ_{n} β_{n})}^{2}]}^{- 1 / 2}$ ,D_n为动力放大系数。

第n振型在m₁,m₂处引起的惯性力P_1n,P_2n由下式计算

$P_{1 n} = \frac{v_{1 n}}{v_{2 n}} {MPF}_{n} m_{1} S_{n} (T) ， P_{2 n} = {MPF}_{n} m_{2} S_{n} (T)$ 。

(15)

第n振型引起的墩底剪力V_n、桩头剪力V_pn、墩顶位移 $Δ_{n}$ 以及群桩冲刷面处总弯矩M_pn分别为

$V_{n} = P_{2 n} ， V_{p n} = P_{1 n} + P_{2 n} ， Δ_{n} = \frac{P_{1 n} + P_{2 n}}{K_{1}} + \frac{P_{2 n}}{K_{2}}$ ,

(16a)

$M_{p n} = P_{1 n} H_{e} + P_{2 n} (L_{e} + H_{e})$ ,

(16b)

采用SRSS组合方法,可求得各项地震最大反应

$R_{\max} = \sqrt{\sum_{n = 1}^{2} R_{n}^{2}}$ ,

(16c)

R_n即为上面的V_n,V_pn, $Δ_{n}$ 。

3. 局部冲刷后桥梁动力分析

以一简支混凝土桥为例,梁跨结构及桥墩等效质量m₂=287500 kg,桥墩等效刚度K₂=2.5×10⁴ kN/m,墩身单位长度质量8655 kg,墩底到桥面中心距离L_e=7 m,桥墩抗弯刚度EI_c=3114000 kN·m²,墩底弯曲强度M_c=11970 kN·m。承台及墩身等效质量m₁=97500 kg。桩直径0.7 m,单位长度962 kg,抗弯刚度EI_p=449375 kN·m²,单桩弯曲强度M_p=1100 kN·m。采用3×3布置形式,桩间距为2.5倍桩径。场地为细砂地层,地基反力系数1080 kN/m³,群桩等效刚度K₁根据式（6）算。桥墩和群桩阻尼C_s,C_f分别取5%,10%。

3.1 冲刷后场地的设计反应谱

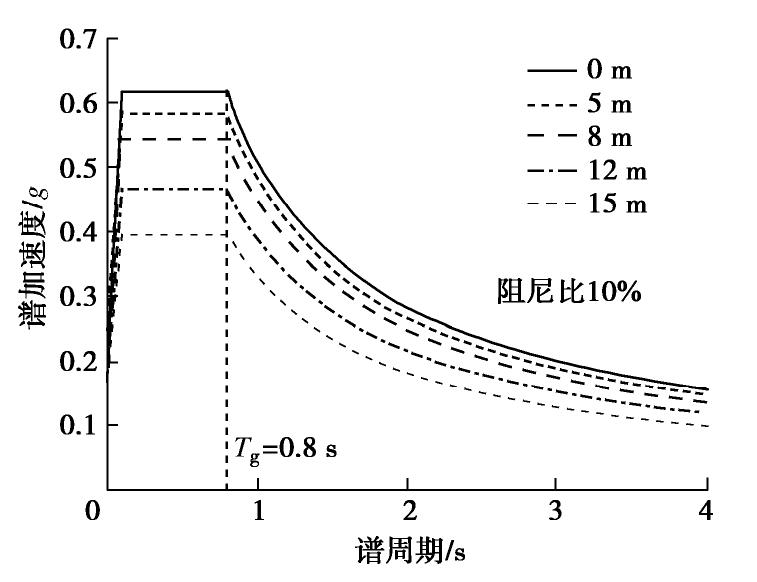
假设场地为软弱细砂,剪切波速140 m/s,土层厚度28 m,场地周期0.8 s。桥梁设防烈度7级（0.15g）,按照《城市桥梁抗震设计规范》（CJJ166—-2011）的初始设计反应谱,根据式（1）计算地面下任意深度处加速度,并经傅里叶变换和平滑处理可得到不同深度的局部冲刷场地的反应谱曲线,如图8所示。

图 8 场地在局部冲刷下的地震动反应谱

Figure 8. Acceleration response spectra of site under local scour

下载: 全尺寸图片幻灯片

3.2 冲刷对桥梁动力特性的影响

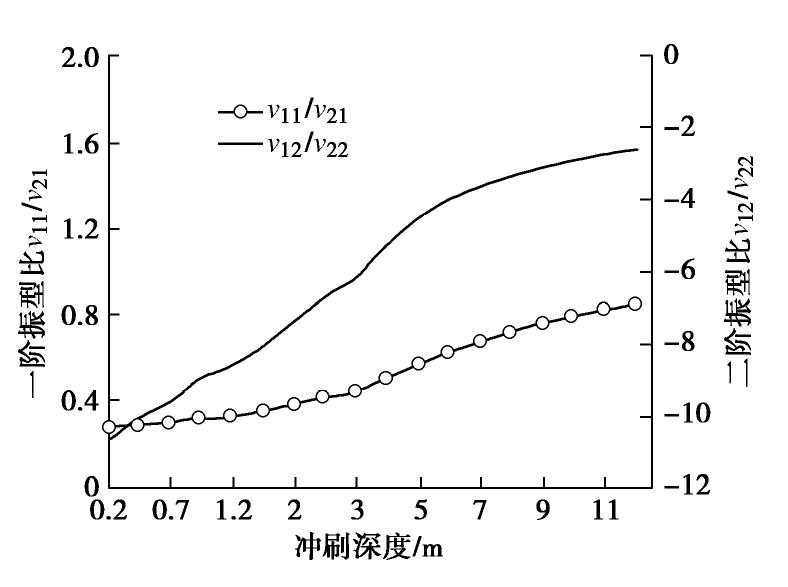
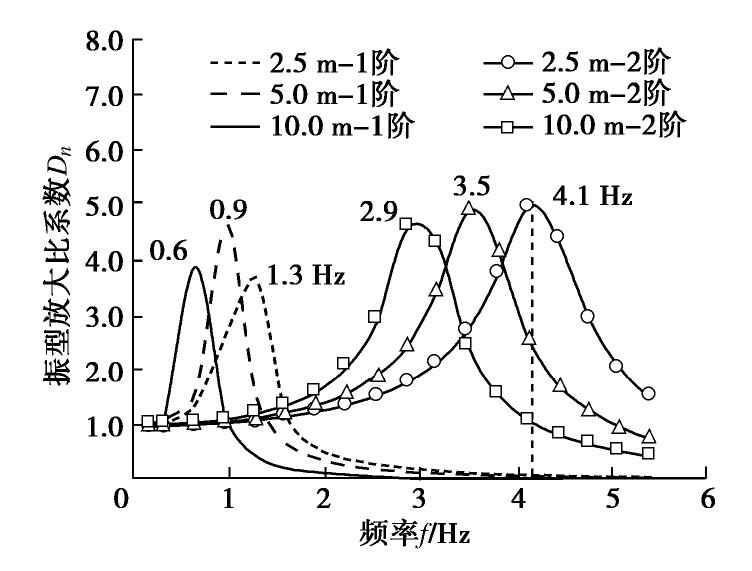
由式（14）可知,对于冲刷条件下的体系反应,某一振型的重要程度取决于3个参数：①振型,其随冲刷深度变化如图9所示,二阶振型位移的绝对值有减小趋势；②振型参与系数,按照案例桥梁的参数计算出振型参与系数MPF₁在1.06～1.18之间,MPF₂在-0.06～-0.14之间,几乎保持不变；③放大系数,是影响桥梁反应的主要因素,其大小主要取决于荷载频率与振型频率的关系。图10为案例桥梁在0～6Hz 单位谐波作用下的振型放大系数D_n。可看出,冲刷深度增加振型放大系数D₁,D₂峰值均向低频偏移,这是冲刷导致桥梁周期增大造成的。当冲刷达10 m时,D₁,D₂共振频率分别从1.3,4.1 Hz减小到0.6,2.9 Hz。而一般地震波波频范围为0～20 Hz,主要频率集中在1～3 Hz,这使得冲刷后的桥梁在低频成分丰富的地震波作用下承台的惯性作用显著增大,破坏风险增加。

图 9 冲刷深度对振型的影响

Figure 9. Effects of scour vibration mode

下载: 全尺寸图片幻灯片

图 10 谐波作用下振型放大系数

Figure 10. Mode amplification factor under harmonic waves

下载: 全尺寸图片幻灯片

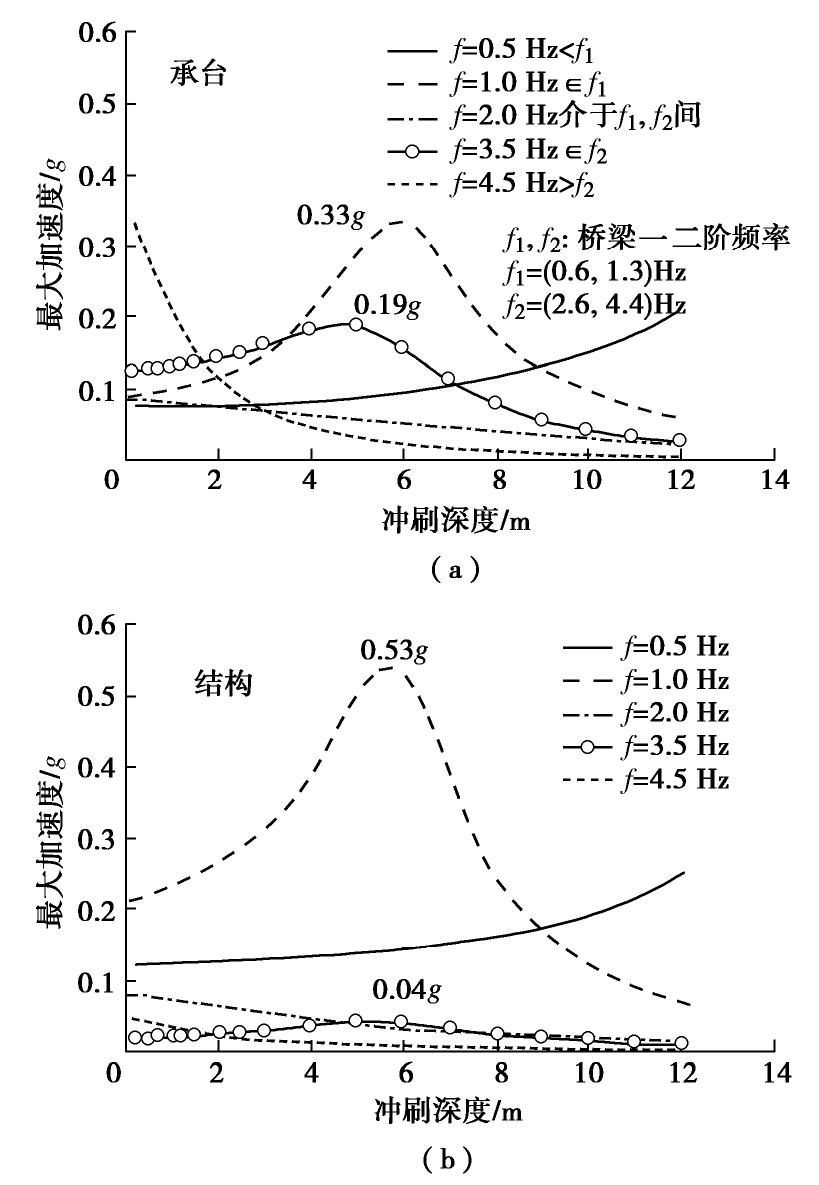
桥梁的动力响应一定程度上取决于地震波的卓越周期（或主要波频成分）和振型频率的相互关系。图11给出了桥梁在谐波 ${\ddot{v}}_{g} (t) = 0.1 \sin (2 π f t)$ 作用下上部结构与承台处最大加速度随冲刷深度的变化曲线。当冲刷深度逐渐增大到12 m时,桥梁一二阶固有频率f₁f₂分别从1.3,4.4 Hz减小至0.6,2.6 Hz。由图11可知,当荷载频率f小于桥梁在最大冲刷深度时的一阶频率f₁时,桥梁反应随冲刷深度增大而增大；当f介于f₁或f₂的范围内,桥梁反应随冲刷深度先增大后减小；当f₁< f<f₂或f > f₂时,桥梁整体反应随冲刷深度减小。另外,在低频荷载作用下桥梁结构的峰值加速度（0.53g）大于承台处峰值反应（0.33g）,当荷载频率大于2.0 Hz时,承台处峰值加速度更大。总的来说,冲刷后桥梁动力响应取决于荷载频率与桥梁固有频率之间的相互关系,即在低频波作用下,桥梁一阶振型占主导作用,且上部结构反应大于承台反应；在高频波作用下,二阶振型占主导作用,且承台反应大于上部结构反应。对于特定地震波,当地震波主要波频包含桥梁一二阶频率变化范围时,随冲刷深度的增加先增大后减小,到达某一冲刷深度时,桥梁反应最为强烈,不利于桥梁抗震。

图 11 谐波作用下桥梁的最大加速度

Figure 11. Maximum accelerations of bridge under harmonic waves

下载: 全尺寸图片幻灯片

3.3 桥墩与桩头的水平承载力

一般桥梁设计时桥墩、桩的抗剪强度应适当高于柱、桩的屈服破坏时所对应的剪力,而冲刷使得桥梁桩基侧向刚度减小,相同剪力下更容易发生弯曲破坏而非剪切破坏；另外,冲刷后桩基础也具有足够的竖向承载力和抗失稳能力。因此本文以桩身和桥墩发生弯曲屈服时对应的墩底水平剪力、桩头水平剪力作为桥梁承载力指标,并通过与桥梁的弹性地震需求比较评估桥梁的破坏风险。

通常前排桩弯矩较大,在受力时先屈服,以前排桩屈服时对应的桩头最大水平位移 $Δ_{f}$ ,计算桩头处水平承载力V_f= $Δ_{f}$ K₁,其中桩头极限位移可采用Song 等^[27]的经验公式：

$Δ_{f} = \frac{0.083 ζ_{1}^{4} + 0.58 ζ_{1}^{3} + 1.62 ζ_{1}^{2} + 2.43 ζ_{1} + 1.62}{0.5 ζ_{1}^{2} + 1.75 ζ_{1} + 1.62} \frac{M_{p} R_{1}^{2}}{E I_{p}} ，$

(17)

式中,R₁=(EI_p/n_h)^0.2为前排桩固嵌深度,n_h为地基反力系数,ζ₁=h/R₁桩基等效出露长度,h为冲刷深度,M_p为单桩的弯矩承载力,其与配筋、桩径等因素相关,但对于确定桥梁桩基为常数值,本文按算例取1100 kN·m,EI_p为桩基截面抗弯刚度。

桥墩以墩底屈服时对应最大水平剪力V_c作为其承载力,计算如下：

$V_{c} = \frac{N_{c} M_{c}}{{L^{'}}_{e}}$ ,

(18)

式中,N_c为桥墩立柱数量,M_c为单墩立柱抗弯刚度,本例取11280 kN·m, ${L^{'}}_{e}$ 为墩柱塑性铰到上部结构形心距离,本例取6 m。

3.4 临界破坏冲刷深度

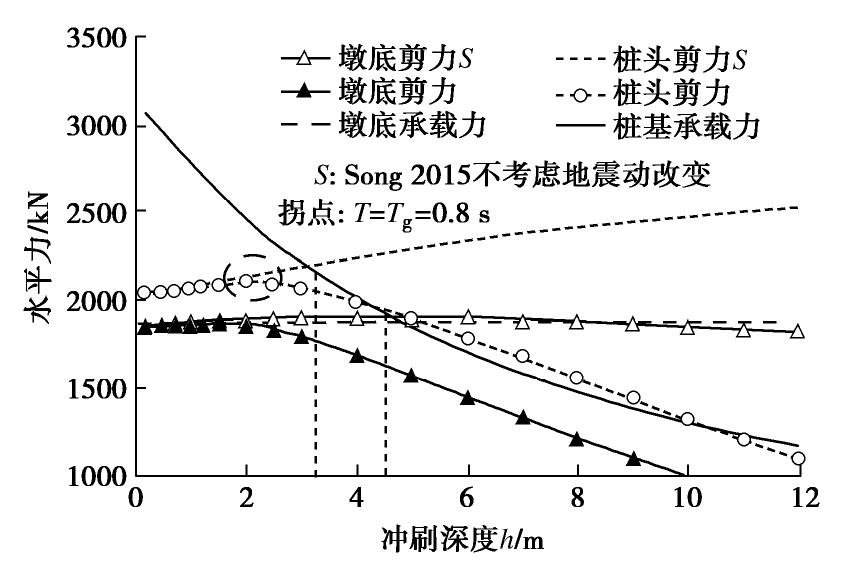
由图8知,局部冲刷场地的峰值加速度随冲刷深度增大而减小,有利于结构抗震；而桩基承载力随冲刷深度增大降低,不利于结构抗震；同时从图11可知,桥梁随冲刷深度增大可能会出现一个峰值响应,这说明可能存在一个冲刷深度,使得桥梁在冲刷和地震作用下的发生破坏。根据式（6）,（16）,（17）和图8中加速度反应谱,绘制墩底、桩头剪力和承载力曲线如图12。很明显,按照Song等^[14]方法计算的桥墩底部剪力几乎不随冲刷深度改变。而考虑冲刷场地的地震动变化后,墩底剪力随冲刷深度增大而减小,说明冲刷对于桥墩抗震有利,这和Wang等^[6]的单桩冲刷试验以及Wang等^[10]的数值模拟结论一致。另一方面,桩基承载力随冲刷深度增大迅速减小,而桩头剪力随冲刷深度增大有先增大后减小的趋势,总体上,桩基破坏风险随冲刷深度增大而增加,两曲线的交点对应的冲刷深度即为临界破坏冲刷深度。其中桩头剪力曲线的下降段主要是由于桥梁一阶周期超过场地特征周期T_g=0.8 s时,一阶振型的输入地震动S₁(T)迅速减小所致（见图8）。而不考虑地震动输入的改变,按照Song等^[14]方法计算,得到的桩头剪力随冲刷深度线性增大,显著高估了桩基受力状态,达到桩基破坏时冲刷深度更小。

图 12 桥梁地震需求与承载力曲线

Figure 12. Seismic demand and bearing curves of bridge

下载: 全尺寸图片幻灯片

本文根据桥梁的地震峰值响应与承载力曲线角度得到的临界破坏冲刷深度,可以用来计算现有桥梁容许的桩基裸露长度以及评估桥梁在现有冲刷条件下的潜在破坏风险。临界冲刷深度大小与场地周期、桥梁自振频率、地震波频谱特征等相关。

4. 离心振动台试验验证

为验证简化模型在计算桩身、墩底内力及结构位移的准确性,以上述案例中的桥梁为背景,开展了50g条件下离心机振动台试验,试验采用同济大学TLJ-150型岩土离心试验机。

4.1 模型设计

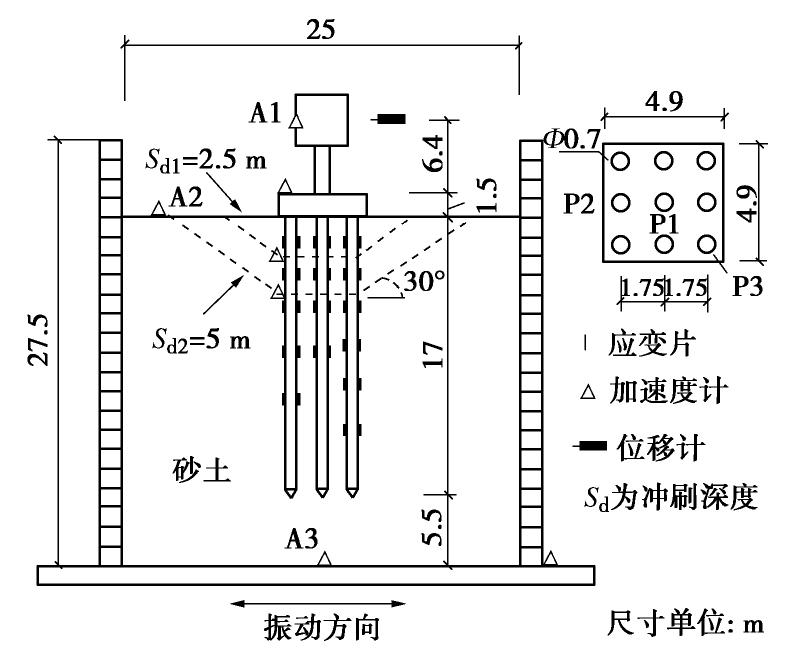
根据本文案例的桥梁参数及重力相似准则进行模型设计。其中桥梁结构主要以桥面质量、承台质量、自振周期为控制参数进行设计,并将上部结构简化为集中质量,如图13。桩则以抗弯刚度和截面尺寸为主控参数进行比例缩放,具体参数见表1。试验采用干细砂土,平均粒径0.1 mm,不均匀系数2.4,填土平均密度1.30 g/cm³。砂土场地受地震荷载一般会产生“震陷”现象。为减少影响,在正式试验前进行了多次白噪声扫频,使得砂土振密,直至场地不再沉降,场地周期稳定在0.5 s,此时测得砂土平均密度1.45 g/cm³,土层厚度22.5 m（原型）,平均剪切波速180 m/s。

图 13 试验模型剖面

Figure 13. Lateral view of bridge model

下载: 全尺寸图片幻灯片

表 1 模型设计相似比例

Table 1. Scale of design model

部件	参数	模型	原型	比例
桩	刚度/(N·m²)	71.9	44937500	1∶50⁴
	外径/m	0.014	0.7	1∶50
	弹模/GPa	70	—	—
承台	质量/kg	0.78	97500	1∶50³
上部	质量/kg	2.31	288500	1∶50³
结构	周期/s	0.009	0.51	1∶50

下载: 导出CSV

| 显示表格

4.2 试验工况

由于剪切箱尺寸限制如图13,冲刷深度S_d取5 cm,10 cm两种工况,对应原型冲刷深度分别为2.5 m,5.0 m。冲刷坑形态采用梯形截面形式,坡度取30°。如表2,在每个工况下输入白噪声、El-Centro波并采集结构加速度、位移、弯矩等参数以研究冲刷条件下桥梁的频率特性和地震响应。

表 2 试验工况

Table 2. Testing programs

冲刷深度/m	峰值加速度/g
冲刷深度/m	白噪声	El-Centro波
0	0.05	0.1, 0.2, 0.3
2.5	0.05	0.1, 0.2, 0.3
5.0	0.05	0.1, 0.2, 0.3

下载: 导出CSV

| 显示表格

4.3 结果对比分析

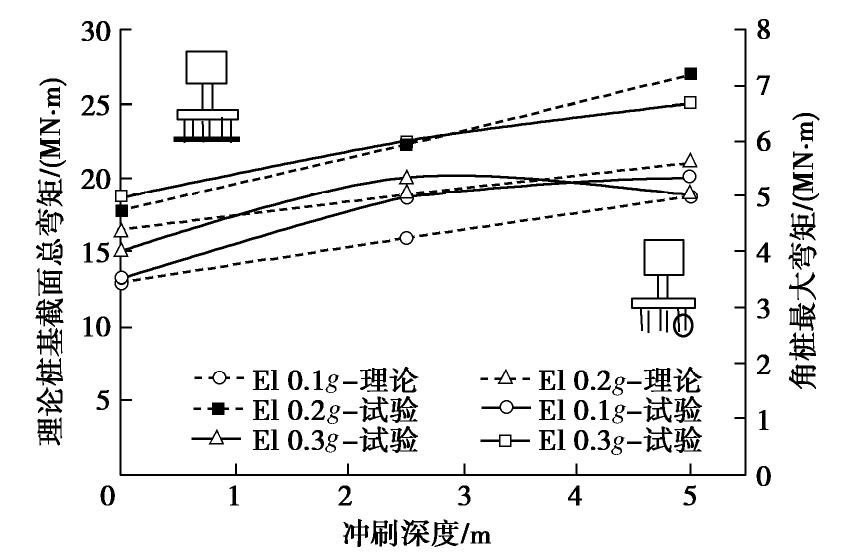
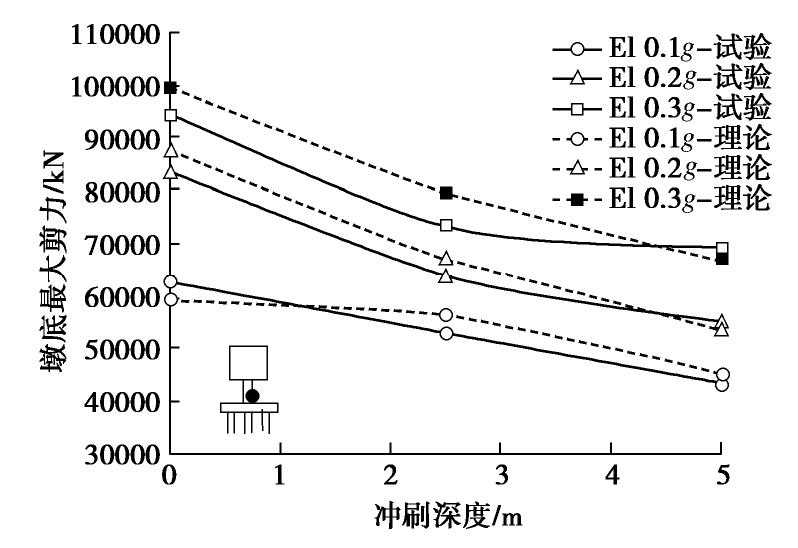
Wang等^[6]关于冲刷后桩基桥梁振动台试验表明,桩身最大弯矩位置（反弯点）随冲刷深度增加而降低,但总体在冲刷面以下3倍桩径处。同一地震荷载水平下,弯矩反弯点位置相对冲刷面固定,因此,可用冲刷面处群桩截面弯矩近似反映桩身最大弯矩的变化趋势。图14,15分别为桥梁在EL-Centro地震波作用下得到的桩身最大弯矩和墩底最大剪力曲线,其中理论桩身弯矩为冲刷面处群桩截面的总弯矩,所用地震波为冲刷面处地震波,而试验弯矩为角桩应变片测得的最大桩身弯矩；如图15,本文理论计算的墩底最大剪力与试验结果吻合,表现为随冲刷深度增加而减小。对比图14,15可以看出桥梁的破坏模式可能由桥墩向桩基转变,这和Wang等^[6]的试验结果以及Wang等^[10]数值结果吻合。

图 14 桩身弯矩对比

Figure 14. Comparison of bending moments of piles

下载: 全尺寸图片幻灯片

图 15 墩底剪力对比

Figure 15. Comparison of shear forces at pier bottom

下载: 全尺寸图片幻灯片

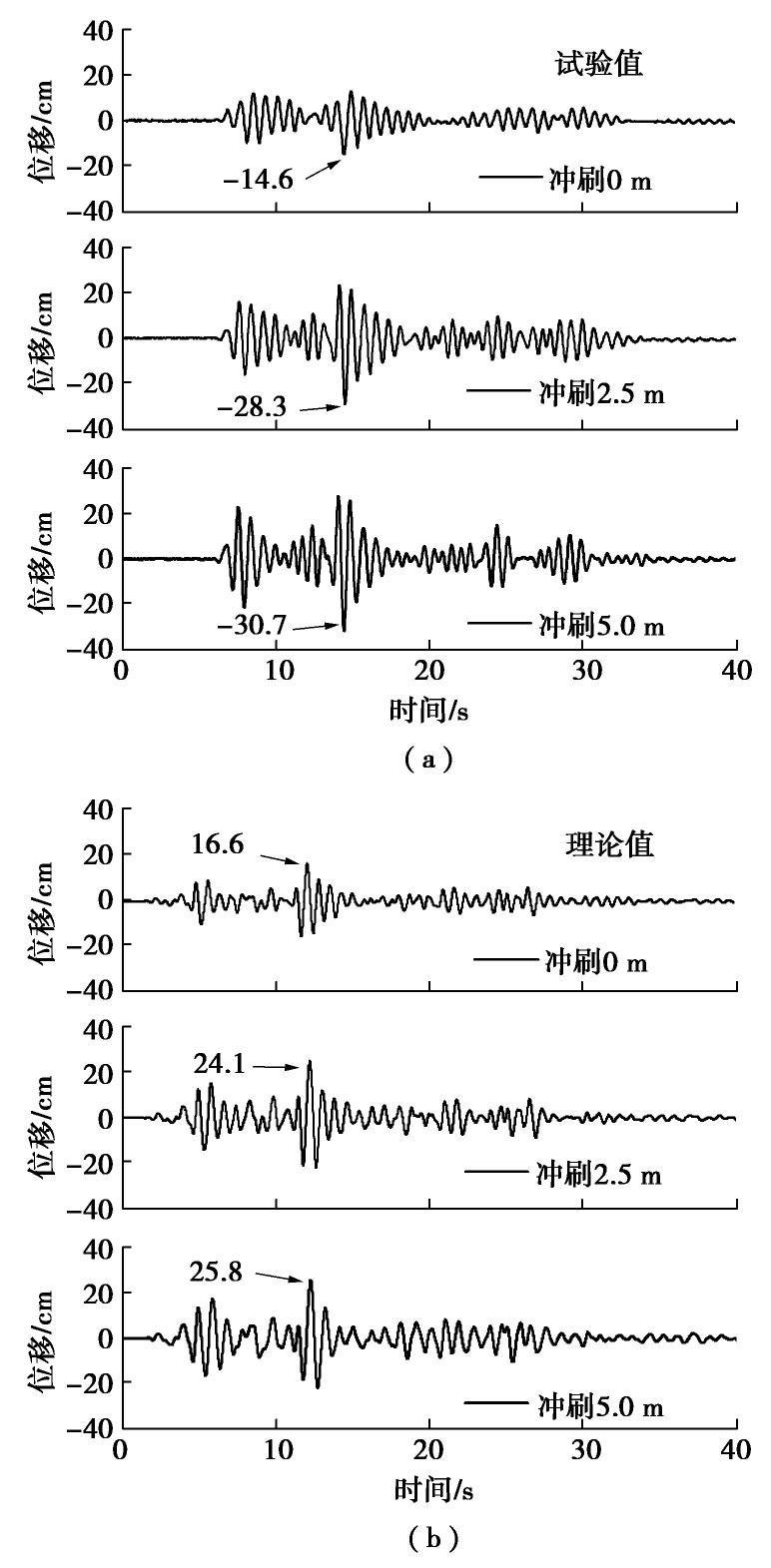
图16为0.2g峰值加速度的El-centro波作用下,桥梁上部结构位移变化时程,其中理论值通过Matlab数值求解公式（13）得到。很明显理论求得位移时程趋势和试验值相同,但在2.5 m及5 m冲刷深度时,理论值小于试验值,可能由于实际中上部质量块的摇摆分量造成。另一方面,上部结构位移随冲刷深度显著增大,因此在进行冲刷后桥梁地震风险分析时,除了评估墩底及桩身受力,还应当评估落梁灾害发生的可能性。

图 16 0.2g El-Centro作用上部结构的位移

Figure 16. Displacements of superstructure under 0.2g El Centro waves

下载: 全尺寸图片幻灯片

5. 结论

（1）一般冲刷（整层土冲刷）使得场地周期减小,但局部冲刷几乎不会改变场地卓越周期,且局部冲刷坑的坡角对场地的地震动几乎没有影响。

（2）冲刷使得场地的地震动减小,局部冲刷场地的地震动明显小于一般冲刷场地,但和未冲刷的自由场地同等深度处地震响应相似,可用原自由场地同深度处加速度或其谱加速度作为简化模型输入地震动。

（3）对于特定地震波,桥梁响应最大的冲刷深度取决于桥梁频率与地震波主要波频的关系,当地震波主要波频包含桥梁一二阶频率变化范围时,当到达某一冲刷深度时,桥梁反应最为强烈,不利于桥梁抗震。

（4）本文简化模型计算值和离心机试验吻合较好,模型计算的桥梁临界破坏冲刷深度,可用于计算现有桥梁的容许最大桩基裸露长度以及评估桥梁在现有冲刷条件下的潜在破坏风险。

图 1 局部冲刷坑形态

Figure 1. Shape of local scour hole

下载: 全尺寸图片幻灯片

图 2 局部冲刷场地数值模型

Figure 2. Numerical mode for local scour site

下载: 全尺寸图片幻灯片

图 3 冲刷坑坡角对坑底加速度反应谱的影响

Figure 3. Influences of slope angle on acceleration spectrum at bottom of scour hole

下载: 全尺寸图片幻灯片

图 4 冲刷坑斜坡上的峰值加速度

Figure 4. Peak accelerations of slope

下载: 全尺寸图片幻灯片

图 5 基岩到冲刷面（或地面）加速度传递函数

Figure 5. Transfer function for acceleration from site bottom to erosional basal surface

下载: 全尺寸图片幻灯片

图 6 0.1g El-Centro波作用下场地加速度反应谱

Figure 6. Acceleration spectra of site under El-Centro waves

下载: 全尺寸图片幻灯片

图 7 考虑冲刷导致地震动改变的简化模型

Figure 7. A simplified model for bridge considering scour induced ground motion changes

下载: 全尺寸图片幻灯片

图 8 场地在局部冲刷下的地震动反应谱

Figure 8. Acceleration response spectra of site under local scour

下载: 全尺寸图片幻灯片

图 9 冲刷深度对振型的影响

Figure 9. Effects of scour vibration mode

下载: 全尺寸图片幻灯片

图 10 谐波作用下振型放大系数

Figure 10. Mode amplification factor under harmonic waves

下载: 全尺寸图片幻灯片

图 11 谐波作用下桥梁的最大加速度

Figure 11. Maximum accelerations of bridge under harmonic waves

下载: 全尺寸图片幻灯片

图 12 桥梁地震需求与承载力曲线

Figure 12. Seismic demand and bearing curves of bridge

下载: 全尺寸图片幻灯片

图 13 试验模型剖面

Figure 13. Lateral view of bridge model

下载: 全尺寸图片幻灯片

图 14 桩身弯矩对比

Figure 14. Comparison of bending moments of piles

下载: 全尺寸图片幻灯片

图 15 墩底剪力对比

Figure 15. Comparison of shear forces at pier bottom

下载: 全尺寸图片幻灯片

图 16 0.2g El-Centro作用上部结构的位移

Figure 16. Displacements of superstructure under 0.2g El Centro waves

下载: 全尺寸图片幻灯片

表 1 模型设计相似比例

Table 1 Scale of design model

部件	参数	模型	原型	比例
桩	刚度/(N·m²)	71.9	44937500	1∶50⁴
	外径/m	0.014	0.7	1∶50
	弹模/GPa	70	—	—
承台	质量/kg	0.78	97500	1∶50³
上部	质量/kg	2.31	288500	1∶50³
结构	周期/s	0.009	0.51	1∶50

下载: 导出CSV

表 2 试验工况

Table 2 Testing programs

冲刷深度/m	峰值加速度/g
冲刷深度/m	白噪声	El-Centro波
0	0.05	0.1, 0.2, 0.3
2.5	0.05	0.1, 0.2, 0.3
5.0	0.05	0.1, 0.2, 0.3

下载: 导出CSV

参考文献(27)

[1]	WANG C, YU X, LIANG F Y. A review of bridge scour: mechanism, estimation, monitoring and countermeasures[J]. Natural Hazards, 2017, 87(3): 1881-1906. doi: 10.1007/s11069-017-2842-2
[2]	曹圣华. 苏通大桥巨型群桩基础冲刷防护研究[D]. 南京: 河海大学, 2006. CAO Sheng-hua. Research of Sutong Bridge Huge Pile Foundation Scour[D]. Nanjing: Hohai University, 2006. (in Chinese)
[3]	LIN C, BENNETT C, HAN J, et al. Scour effects on the response of laterally loaded piles considering stress history of sand[J]. Computers and Geotechnics, 2010, 37(7/8): 1008-1014.
[4]	FOTI S, SABIA D. Influence of foundation scour on the dynamic response of an existing bridge[J]. Journal of Bridge Engineering, 2011, 16(2): 295-304. doi: 10.1061/(ASCE)BE.1943-5592.0000146
[5]	ALIPOUR A, SHAFEI B, SHINOZUKA M. Reliability-based calibration of load factors for design of reinforced concrete bridges under multiple extreme events: scour and earthquake[J]. Journal of Bridge Engineering, 2013, 18(5): 362-371. doi: 10.1061/(ASCE)BE.1943-5592.0000369
[6]	WANG S C, LIU K Y, CHEN C H, et al. Experimental investigation on seismic behavior of scoured bridge pier with pile foundation[J]. Earthquake Engineering & Structural Dynamics, 2015, 44(6): 849-864.
[7]	梁发云, 陈海兵, 黄茂松, 等. 结构-群桩基础地震响应离心振动台模型试验[J]. 建筑结构学报, 2016, 37(9): 134-141. https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201609017.htm LIANG Fa-yun, CHEN Hai-bing, HUANG Mao-song, et al. Model test on seismic response of superstructure and pile group[J]. Journal of Building Structures, 2016, 37(9): 134-141. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZJB201609017.htm
[8]	WANG X W, YE A J, SHANG Y, et al. Shake-table investigation of scoured pile-group-supported bridges in liquefiable and nonliquefiable soils[J]. Earthquake Engineering & Structural Dynamics, 2019, 48(11): 1217-1237.
[9]	GANESH PRASAD G, BANERJEE S. The impact of flood-induced scour on seismic fragility characteristics of bridges[J]. Journal of Earthquake Engineering, 2013, 17(6): 803-828. doi: 10.1080/13632469.2013.771593
[10]	WANG Z, DUEÑAS-OSORIO L, PADGETT J E. Influence of scour effects on the seismic response of reinforced concrete bridges[J]. Engineering Structures, 2014, 76: 202-214. doi: 10.1016/j.engstruct.2014.06.026
[11]	KLINGA J V, ALIPOUR A. Assessment of structural integrity of bridges under extreme scour conditions[J]. Engineering Structures, 2015, 82: 55-71. doi: 10.1016/j.engstruct.2014.07.021
[12]	叶爱君, 刘伟岸, 王斌斌. 高桩承台基础与桥梁结构的动力相互作用[J]. 同济大学学报(自然科学版), 2007, 35(9): 1163-1168. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ200709002.htm YE Ai-jun, LIU Wei-an, WANG Bin-bin. Dynamic interaction between high-rise pile cap foundation and bridge structure[J]. Journal of Tongji University (Natural Science), 2007, 35(9): 1163-1168. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ200709002.htm
[13]	XU Y, SHANG Y, YE A. Dynamic interaction between bridge pier and its large pile foundation considering earthquake and scour depths[J]. Advances in Structural Engineering, 2016, 19(9): 1390-1402. doi: 10.1177/1369433216642077
[14]	SONG S T, WANG C Y, HUANG W H. Earthquake damage potential and critical scour depth of bridges exposed to flood and seismic hazards under lateral seismic loads[J]. Earthquake Engineering and Engineering Vibration, 2015, 14(4): 579-594. doi: 10.1007/s11803-015-0047-9
[15]	陆雪骏. 长江感潮河段桥墩冲刷研究[D]. 上海: 华东师范大学, 2016. LU Xue-jun. Research on the Local Scour at Bridge Piers in the Tidal Reach of the Changjiang River[D]. Shanghai: East China Normal University, 2016. (in Chinese)
[16]	何泓男, 戴国亮, 杨炎华, 等. 局部冲刷下群桩水平承载试验研究[J]. 岩土力学, 2015, 36(10): 2939-2945. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201510027.htm HE Hong-liang, DAI Guo-liang, YANG Yan-hua, et al. Experimental study of lateral bearing behavior of pile group foundation under local scour condition[J]. Rock and Soil Mechanics, 2015, 36(10): 2939-2945. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201510027.htm
[17]	LIN C, HAN J, BENNETT C, et al. Analysis of laterally loaded piles in sand considering scour hole dimensions[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2014, 140(6): 04014024. doi: 10.1061/(ASCE)GT.1943-5606.0001111
[18]	ZHANG H, CHEN S L, LIANG F Y. Effects of scour-hole dimensions and soil stress history on the behavior of laterally loaded piles in soft clay under scour conditions[J]. Computers and Geotechnics, 2017, 84: 198-209. doi: 10.1016/j.compgeo.2016.12.008
[19]	AMINI A, MELVILLE B W, ALI T M, et al. clear-water local scour around pile groups in shallow-water flow[J]. Journal of Hydraulic Engineering, 2012, 138(2): 177-185.
[20]	刘晶波, 王振宇, 杜修力, 等.波动问题中的三维时域黏弹性人工边界[J]. 工程力学, 2005, 22(6): 46-51. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200506007.htm LIU Jing-bo, WANG Zhen-yu, DU Xiu-li, et al. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems[J]. Engineering Mechanics, 2005, 22(6): 46-51. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX200506007.htm
[21]	LEE S J, KOMATITSCH D, HUANG B S, et al. Effects of topography on seismic-wave propagation: an example from Northern Taiwan[J]. Bulletin of the Seismological Society of America, 2009, 99(1): 314-325.
[22]	KHANBABAZADEH H, IYISAN R. A numerical study on the 2d behavior of clayey basins[J]. Soil Dynamics and Earthquake Engineering, 2014, 66: 31-41
[23]	LIN C. Evaluation of Lateral Behavior of Pile-Supported Bridges Under Scour Conditions[D]. Kansas: University of Kansas, 2012
[24]	MAKRIS N, GAZETAS G. Dynamic pile-soil-pile interaction. Part II: Lateral and seismic response[J]. Earthquake Engineering & Structural Dynamics, 1992, 21(2): 145-162.
[25]	PRIESTLEY M J N, SEIBLE F, CALVI G M. Seismic Design and Retrofit of Bridges[M]. New York: John Wiley & Sons, 1996.
[26]	HWANG J S, SHENG L H, GATES J H. Practical analysis of bridges on isolation bearings with Bi-linear hysteresis characteristics[J]. Earthquake Spectra, 1994, 10(4): 705-727.
[27]	SONG S T, CHAI Y H. Performance assessment of multi-column bents with extended pile-shafts under lateral earthquake loads[J]. The IES Journal Part A: Civil & Structural Engineering, 2008, 1(1): 39-54.

施引文献(15)

期刊类型引用(10)

1.	江杰，余云东，欧孝夺，柴文成，罗豪豪. 非对称局部冲刷条件下组合受荷桩水平承载力分析. 工程力学. 2025(03): 191-202 . 百度学术
2.	王磊，吕忠达，王飞，赵卓. 深水大直径桥墩水下振动台试验研究. 桥梁建设. 2025(01): 110-116 . 百度学术
3.	李雨润，刘毅，梁旭华. 液化场地-群桩-上部结构动力特性研究综述. 河北工业大学学报. 2024(01): 74-80 . 百度学术
4.	戴隆强. 基于GA-WNN的桥梁基础结构局部冲刷风险模糊评估方法. 粉煤灰综合利用. 2024(01): 145-149 . 百度学术
5.	张聪，冯忠居，林路宇，周桂梅，陈露. 震陷场地变截面单桩动力特性与损伤评价. 岩土力学. 2024(10): 3037-3046+3057 . 百度学术
6.	李忠献，郑庆涛，苏俊省，赵博. 地震-波浪联合作用下考虑冲刷效应的跨海斜拉桥振动台试验研究. 土木工程学报. 2024(10): 71-81 . 百度学术
7.	张浩. 桩基振动对安置房建筑基坑斜桩的影响. 四川建材. 2024(12): 107-109 . 百度学术
8.	李哲，刘彤，郭家，冯忠居，刘路路，王富春. 铺前大桥群桩基础冲刷特性分析. 东南大学学报(自然科学版). 2023(04): 617-627 . 百度学术
9.	沙仁智. 长期冲刷下跨海桥梁桩基动力特性及地震响应研究. 铁道建筑技术. 2023(09): 90-93+118 . 百度学术
10.	杜程，范一娜. 不同桩基加固参数对既有桥梁抗震性能的影响. 山东交通科技. 2022(04): 54-56+115 . 百度学术