0.   引言

由于降雨和蒸发交替作用,自然界的地表土普遍为非饱和土。地表污染物污染地下水的过程,实际上是污染物在非饱和土中向下迁移的过程,研究非饱和土中的污染物迁移规律,对于土和地下水污染防治具有积极的现实意义。当前对饱和土中污染物迁移的研究较多,而对非饱和土的相关研究还不够深入,试验研究非饱和土中污染物迁移机理具有重要科学意义。

当前国内外学者对非饱和土中污染物迁移开展了一些试验研究。Sharma等^[1]研究了杀菌剂在非饱和土中的吸附及迁移情况；Stanislaw^[2]研究了非饱和土中溶质迁移的水动力弥散问题,研究了碘在非饱和土中的迁移、衰减及吸附规律；杨金忠等^[3]用氯化钠作为示踪剂研究非饱和土中污染物运移,得到土中污染物浓度剖面的空间变异性；王超等^[4]等进行惰性污染物在非饱和土中迁移的土柱试验,建立了描述污染物迁移的可动水和不可动水数学模型；李旭^[5]进行土柱试验研究了不同降雨量条件下非饱和黏土中重金属镉、锌的运移；周念清等^[6]通过CT扫描技术研究了污染物在非饱和砂土中的运移规律；Cooke^[7]、Knight等^[8]、张建红等^[9]采用土工离心机进行了溶质在非饱和土中迁移的离心模型试验,验证了离心模拟污染物迁移的可行性,并得出非饱和土中污染物迁移的一些定性规律。上述试验研究多针对影响污染物迁移的对流或弥散作用,实际上,机械弥散对污染物迁移的作用随流速降低而减小,如Rowe^[10]指出,当达西流速小于3×10^-7 cm/s时,分子扩散就开始占主导；而非饱和土中流速往往较低,通常也属于扩散作用占主导的情况^[11]。另外,由于非饱和土含水率控制的技术瓶颈,上述研究多采用含水率变化的瞬态试验方法,多为定性研究,目前针对非饱和土中扩散系数随含水率变化的试验研究尚不多见。

本文设计了能够控制非饱和土样含水率在对流–扩散试验过程中保持不变的试验装置,进行了不同含水率土样的土柱试验,通过解析解拟合浓度分布剖面,求得水动力弥散系数和有效扩散系数,研究了有效扩散系数随含水率的变化规律。

1.   试验装置

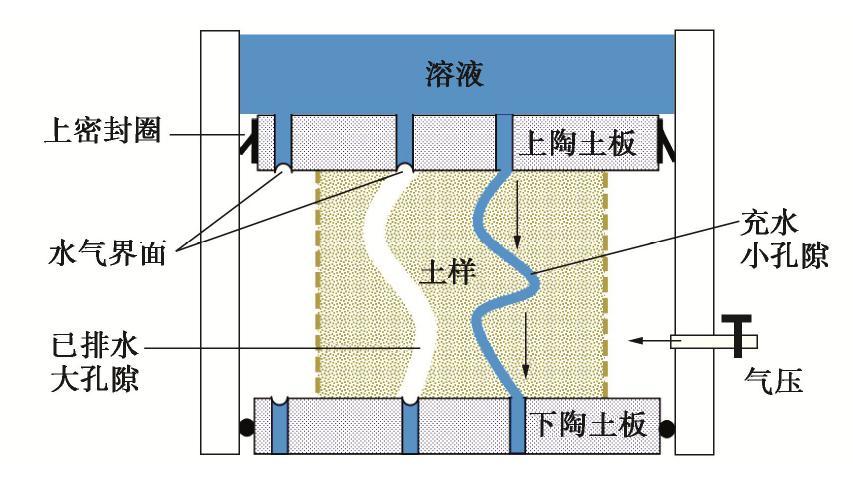
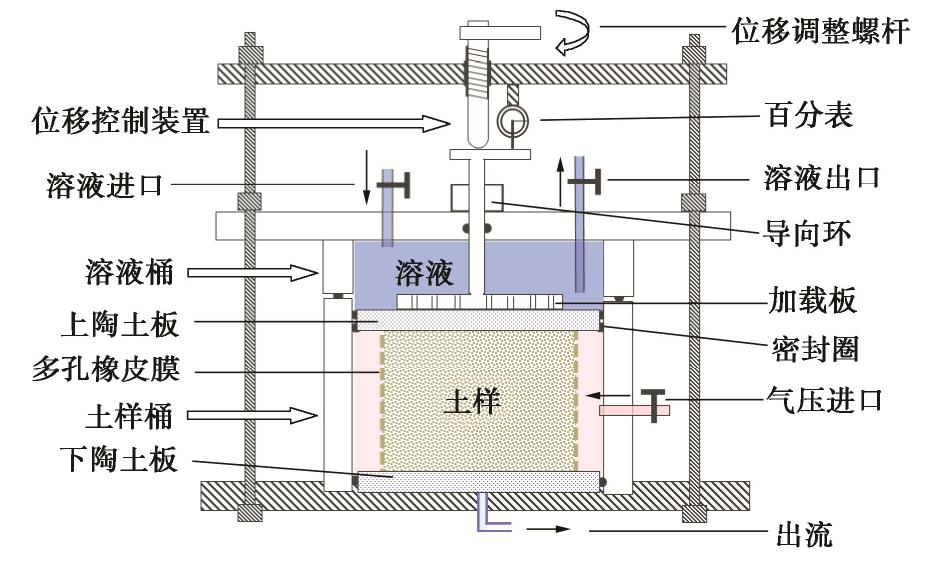
自制非饱和对流–扩散试验装置（发明专利：ZL201510224714.5）如图1所示,装置（自下而上）由土样桶、溶液桶和变形控制装置3部分组成。土样桶内径9 cm,底部和顶部各有一块多孔陶土板（Soilmoisture Ltd.,2Bar,厚度1 cm,饱和渗透系数1.73×10^-7 cm/s）,中间放置直径7 cm,高度5 cm的圆柱形土样,土样外包裹多孔橡皮膜（孔径5 mm,孔距5 mm）,陶土板与桶壁间设密封圈,通过土样桶壁上的进气孔施加指定气压,通过土样与桶壁间1 cm的间隙和多孔橡皮膜,气压可均匀施加于土样,类似于压力板仪测试土–水特征曲线（SWCC）时控制含水率的原理,通过气压也即基质吸力,可以控制土样含水率。

图  1  试验装置示意图

Figure  1.  Sketch diagram of test apparatus

下载: 全尺寸图片 幻灯片

上陶土板在对流–扩散试验过程中的工作原理如图2所示,在用目标溶液饱和上陶土板后,陶土板中所有微孔隙充满溶液,其中部分微孔隙与空气接触（包括土样和桶间隙处以及与已排水大孔隙接触的微孔隙）,试验中控制土样桶内气压大于上部溶液桶水头压力,则这些微孔隙水气界面处的弯液面将阻止孔隙内的溶液向下流动,同时阻止土样桶内气体通过,从而起到密闭作用；另一部分微孔隙直接与土样中充水小孔隙接触,微孔隙中没有水气界面,溶液桶中溶液可通过这些孔隙向下流动,逐渐驱替土样原孔隙中的去离子水,即实现溶质的对流–扩散,在这一过程中,气压保持不变,则土样含水率不变（与浓度差相关的渗透吸力的影响,将在后面讨论）。

图  2  非饱和渗透控制原理

Figure  2.  Principle of unsaturated flow

下载: 全尺寸图片 幻灯片

在土样由饱和到非饱和的过程中,基质吸力增大将导致一定量体缩,土样将与上陶土板脱离,此时,上陶土板所有微孔隙中都将产生弯液面,阻止溶液下渗到土样中,因此,本装置通过位移控制将上陶土板下移,保持土样与陶土板密切接触。控制的位移量由事先进行的SWCC试验中每级气压对应的土样高度改变量确定,并稍加保守控制。为保证陶土板移动过程中的密封性,上陶土板采用倒“V”型密封圈（图2）,一侧用胶粘于陶土板侧壁,一侧靠弹性与桶壁贴紧,当土样桶施加气压后,贴合更加紧密。某一级气压下的具体试验操作步骤如下：①用去离子水饱和土样和下陶土板,用目标溶液饱和上陶土板,将土样放置在下陶土板中央位置,按图1组装装置。②向土样桶施加指定气压,平衡后土样达到目标含水率,平衡标准参照压力板仪试验,此时土样干缩已完成。③根据事先标定的该气压对应的干缩量,控制上陶土板向下位移。④向溶液桶注入溶液,通过马氏瓶保持水头恒定（本文各试验中均为50 cm）,通过蠕动泵外接溶液瓶实现进口和出口溶液循环（1 mL/h）,保持浓度恒定,开始对流–扩散试验,从底部定时收集出流溶液测浓度。⑤当底部溶质出流达到源浓度10%～20%时,终止试验,撤掉气压,将土样取出切片,测孔隙溶液浓度,得到沿土样深度的溶质浓度分布。

2.   对流-扩散试验

2.1   饱和土样制备

试验最初选择使用天然的砂质壤土,大于0.075 mm颗粒含量为75%,试验过程中遇到的问题包括：由于大颗粒含量较多,其SWCC和渗透系数曲线较陡,在较高的气压下出水特别缓慢,给出流浓度测量造成困难,因此只能选择5,10和20 kPa的气压；土样的渗透系数明显大于陶土板渗透系数,使得最终计算的非饱和渗透系数误差较大；并且含水率降低时土样明显发生干缩变形。后来改用粉土,取自钱塘江边,含有15%砂粒、80%粉粒、5%黏粒,因其中黏粒含量不多,失水时体缩较小；为了增加其持水能力以使SWCC更平缓,掺入了3%的钙基膨润土,膨润土中蒙脱石含量71.4%,液限332%、塑限25%。这两种土曾被用于土–膨润土防渗墙的试验研究,具体性质指标可参见文献[12]。

首先将膨润土混入去离子水中,搅拌制成5%的膨润土泥浆,将泥浆与粉土混合搅拌,得到膨润土含量为3%的混合土。将混合土放入内径7 cm的模具中,在10 kPa压力下固结制样,同时从试样底部进水饱和,维持80 cm水头,固结和饱和过程持续120 h,得到的试样高度为5 cm、干密度1.41 g/cm³、孔隙率0.477、液限34%、塑限22.5%。

2.2   压力板仪试验

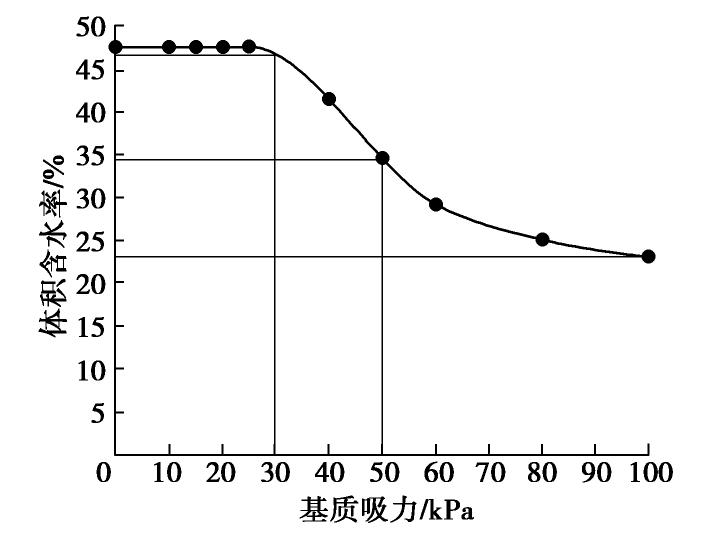
使用压力板仪（Model 1250,Soilmoisture Ltd.）测得上述土样的SWCC,为后面对流–扩散试验中含水率和位移控制提供基本参数。图3中SWCC上的含水率为按试样实测高度计算的含水率,即已经考虑了体缩的影响。

图  3  土样的土水特征曲线

Figure  3.  SWCC of soil sample

下载: 全尺寸图片 幻灯片

SWCC试验时使用无气水（由去离子水制备）,后续对流–扩散试验中使用氯化钠溶液,关于渗透吸力的影响讨论如下：渗透吸力主要与土粒外围双电层有关,而基质吸力主要与水气界面有关,盐浓度对渗透吸力影响很大,但对基质吸力（或含水率）的影响因土而异,Miller等^[13]的研究表明,离子浓度对低塑性粉质黏土基质吸力的影响不大,孙德安等^[14]也发现氯盐含量对粉土SWCC的影响不大。本文试验混合土样中粉土含量为97%,混合土塑性指数小于17,与上述研究的土类接近。且试验结束后将试样烘干测得的含水率（表1）,与图3相应气压下（试验拟控制的）的含水率完全一致,因此试样含水率基本没有受到溶液浓度的影响,对流–扩散试验中使用气压控制含水率是精准的。

表  1  对流-扩散试验数据及拟合

Table  1.  Parameters of advection-diffusion tests

气压/kPa	t/d	θ/%	v/(cm·s-1)	α/cm	D/(cm2·s-1)	R2	D*/(cm2·s-1)	τ
0	3	47.73	1.13×10-5	0.04	5.71×10-6	0.998	5.22×10-6	0.26
30	3.6	45.95	7.41×10-6	0.04	5.26×10-6	0.999	4.99×10-6	0.25
50	13.5	33.32	5.74×10-7	0.29	3.28×10-6	0.998	3.11×10-6	0.15
100	25	22.82	1.70×10-7	0.59	1.69×10-6	0.998	1.59×10-6	0.08

下载: 导出CSV 

| 显示表格

按SWCC选择后续对流–扩散试验的控制气压（即土样中基质吸力）,考虑两方面,一是不同基质吸力对应的含水率要明显不同,这样测得的非饱和渗透、扩散参数才会明显不同；二是试样含水率不能太低,否则出流溶液浓度测量难度较大。综合考虑,取试验气压为0,30,50和100 kPa,对应含水率分别为47.70%,46.05%,34.69%和23.21%,对应上陶土板需调整位移量为0,0.1,0.3和0.5 cm。

2.3   对流-扩散试验

目标溶质选用惰性离子氯离子,在土中基本不发生吸附,故溶质迁移过程中仅有对流和扩散起作用,试验使用浓度为0.1 mol/L的氯化钠溶液。先按溶液池法^[15]测得饱和土样中氯离子的有效扩散系数为D^*= 5.22×10^-6 cm²/s,结合氯离子的水相自由扩散系数D₀=20.3×10^-6 cm²/s,可知弯曲因子τ=D^*/ D₀=0.26。

溶质对流-扩散迁移过程中,机械弥散和分子扩散同时发生,这两个作用合起来被称为水动力弥散：

式中,D为水动力弥散系数,α为弥散度,v为孔隙水流速。通过土柱试验测定水动力弥散系数时,可采用切片法或累积浓度法^[15],若采用累积浓度法,就需要计入下陶土板对溶质的迁移的影响,所以这里采用切片法,只需分析土样孔隙中的溶质浓度。为获得理想的浓度剖面,当出流浓度达到源浓度10%～20%时,终止入渗试验,取出土样切片。

将切片烘干,烘干前后的质量差记为Δm,烘干后的切片碾碎,放入150 mL去离子水中制成悬浊液,震荡24 h,然后在3500 rpm/s转速下离心30 min,取上清液测得浓度C_sup,则可得到土中孔隙水浓度C：

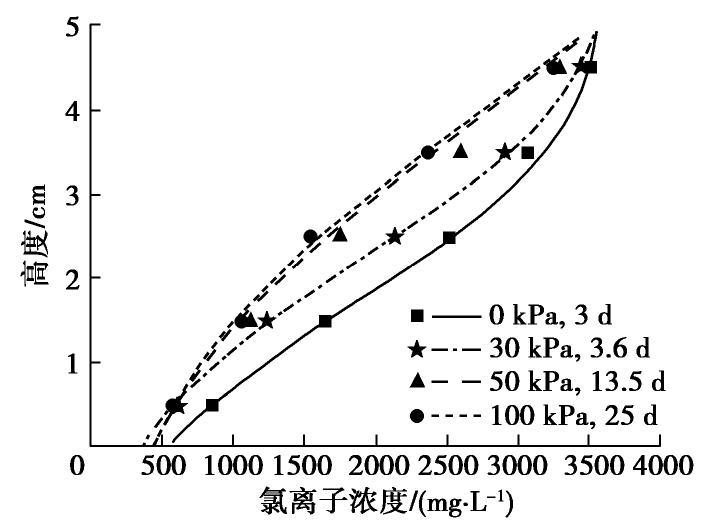
式中,${\rho }_{\text{w}}$为试验温度下水的密度,V_dl为制备悬浊液的去离子水体积。

气压0,30,50和100 kPa下试验分别进行3,3.6,13.5和25 d,得到的浓度剖面如图4所示。

图  4  土样中氯离子浓度实测值及拟合

Figure  4.  Pore-water concentration of chloride ion and fitting curves

下载: 全尺寸图片 幻灯片

3.   结果拟合与分析

使用一维对流–弥散方程解析解拟合试验结果,求水动力弥散系数D。本文试验中,控制含水率不变,因此污染物在非饱和土中运移的控制方程与饱和土中的方程具有相同形式,仅需将孔隙率n改写为体积含水率θ,方程如下：

式中,x为坐标,t为时间,V为实测出流量对应的达西流速,θ为试样体积含水率。试验开始时土样孔隙中为去离子水,氯化钠浓度为0,初始条件：

试验时上陶土板用盐溶液饱和,溶液桶中浓度恒定,可认为土样上表面入渗浓度不变：

对于底部定期收集溶液的土柱试验,常使用半无限边界^[15]：

拟合时流速v已知,且使用的是土柱高度范围内的浓度值,因此虽然式（6）定义无限远处的边界,但与土柱是有限长度并不矛盾^[15-17]。

式（3）～（6）的解为^[15]

式中,erfc为残差函数,ξ₁,ξ₂,ξ₃和ξ₄为无量纲的简写参数,具体可参文献[15]。

各级气压下的试验和拟合参数列入表1,表中含水率是试验后烘干法实测,流速按实际出流量计算。表中拟合D值时的确定系数R²均接近1,说明试验数据离散性较小,拟合精确。对于气压0 kPa（即饱和）的情况,因为已通过溶液池法测得了有效扩散系数,根据式（1）可计算得到$\alpha$=0.04 cm,对于非饱和的情形,D^*和$\alpha$均未知,试算步骤如下：

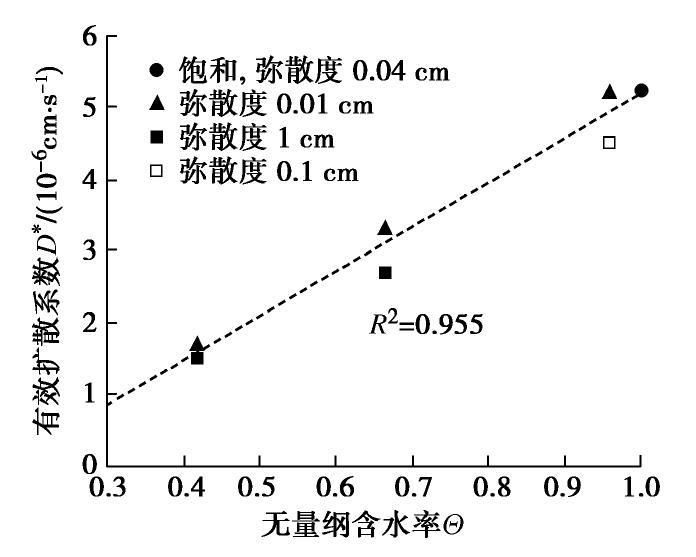
实验室内土柱试验的弥散度$\alpha$的范围一般在0.01～1 cm^[18],对于气压50和100 kPa,取此界限值依据前面拟合出的D计算D^*,对于气压30 kPa的情形,$\alpha$=1 cm会导致D^*值为负,考虑到此时含水率（45.95%）与饱和状态（47.73%）接近,因此$\alpha$应与饱和时的0.04 cm接近,故取其范围为0.01～0.1 cm计算。定义无量纲含水率Θ=(θ-θ_r)/(θ_s-θ_r),其中θ_r和θ_s分别为残余和饱和体积含水率,得到D^*与Θ的关系如图5所示,可见在试验的气压范围内,D^*与Θ之间基本呈线性关系。因此,下面按拟合得到的线性关系计算D^*和$\alpha$,30,50和100 kPa下D^*分别为4.99×10^-6,3.11×10^-6和1.59×10^-6 cm²/s,$\alpha$分别为0.04,0.29和0.59 cm,$\alpha$值都在前述假定范围之内,随含水率降低而增大,这是因为$\alpha$值与特征流程长度有关^[19],随饱和度降低,流动绕曲度增加,特征流程长度增加。

图  5  土样无量纲体积含水率与有效扩散系数的关系

Figure  5.  Relationship between Θ and D^*

下载: 全尺寸图片 幻灯片

试验过程中,两块陶土板也参与了溶质迁移,使用解析解拟合求D的过程中,使用了土样内的浓度分布,而不是下陶土板底部的出流浓度,避免了下陶土板的干扰,而上陶土板预先使用目标溶液饱和,其影响也很大程度减小。然而,在计算土样非饱和渗透系数时,因为实测的是下陶土板底部的出流量,所以必须考虑陶土板对渗流的影响,这里将陶土板也视为土层,采用3层土中渗流模型计算土样非饱和渗透系数：

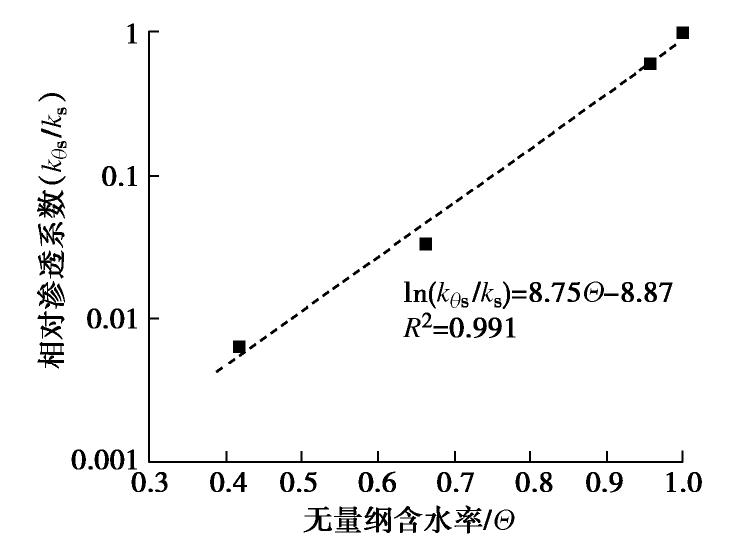
式中,$\overline{k}$为3层土的平均渗透系数,按实际出流量计算,H为3层土总厚度,H_c为单块陶土板厚度,H_s为土样高度,k_θs为土样非饱和渗透系数,k_θc为陶土板非饱和渗透系数,可根据陶土板饱和渗透系数计算如下：试验中陶土板处于非饱和状态时,只有与土样充水孔隙接触的陶土板微孔隙透水,陶土板中微孔隙分布是均匀的,假定土中孔隙分布也均匀,那么陶土板与土样接触面上充水孔隙比例与土样中一致,即等于土样体积含水率,$k_{\theta \text{c}}$可近似为

式中,n为土样孔隙率,θ/n为透水微孔隙比例,k_c为陶土板饱和渗透系数。根据式（8）可计算得到k_θs,将相对渗透系数k_θs/k_s与无量纲含水率Θ的关系示于图6。可见在本文试验范围内（Θ=0.417～1）,对数的渗透系数与Θ近似呈线性关系。

图  6  相对渗透系数与无量纲含水率的关系

Figure  6.  Relationship between relative unsaturated hydraulic conductivity and Θ

下载: 全尺寸图片 幻灯片

扩散系数、渗透系数和弥散度都是污染物迁移模拟分析中的基本参数,饱和土中上述参数尚且容易测定,而相应非饱和参数的测试费时费力,上述线性关系为基于饱和参数预测非饱和参数提供了依据,为涉及非饱和土中污染物迁移模拟时的参数选取提供了便利。本文试验方法也可为非饱和土中其它污染物迁移参数测试提供借鉴。因采用的试验装置所限,本文无法在很低的含水率下进行试验,而Hu等^[11]指出,在低含水率下,土中水以薄膜水形式存在,此时溶质扩散变得极其缓慢,有效扩散系数与含水率之间将不再是线性关系；同样,对数的非饱和渗透系数与含水率也将偏离线性关系。因此在运用相关线性规律时尚需注意土的含水率范围。

4.   结论

本文自制试验装置,以氯离子为示踪剂,旨在研究非饱和土中的溶质扩散规律,主要结论如下：

（1）自制的非饱和对流–扩散试验装置通过两块陶土板间的气压控制土样含水率,通过变形控制装置补偿干缩变形保证对流和扩散连续,试验过程中渗透吸力的影响可以忽略不计,含水率控制精确可靠。

（2）根据切片法测得土中氯离子浓度剖面,使用解析解拟合得到水动力弥散系数,进一步分析得到有效扩散系数,基质吸力由0增至100 kPa,土中氯离子有效扩散系数由5.22×10^-6降至1.59×10^-6 cm²/s,随无量纲含水率线性减小。

（3）溶质迁移的弥散度随含水率降低而增大,本文试验范围内,对数的非饱和渗透系数随含水率线性减小。