基于微震监测的应力场反演方法及其工程应用研究

唐超; 李庶林; 周梦婧; 刘胤池

doi:10.11779/CJGE202109019

基于微震监测的应力场反演方法及其工程应用研究 English Version

厦门大学建筑与土木工程学院,福建　厦门　360015

基金项目:

国家自然科学基金项目 51674218

详细信息

作者简介:
唐超(1997— ),男,硕士研究生,主要从事微震震源机制及应力场反演方面的研究。E-mail：25320181152879@stu.xmu.edu.cn

通讯作者:
李庶林, E-mail：shulin.li@163.com

中图分类号: TU435
计量
- 文章访问数: 284
- HTML全文浏览量: 48
- PDF下载量: 274
出版历程
- 收稿日期: 2020-11-11
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-08-31

Stress inversion based on microseismic monitoring and its engineering application

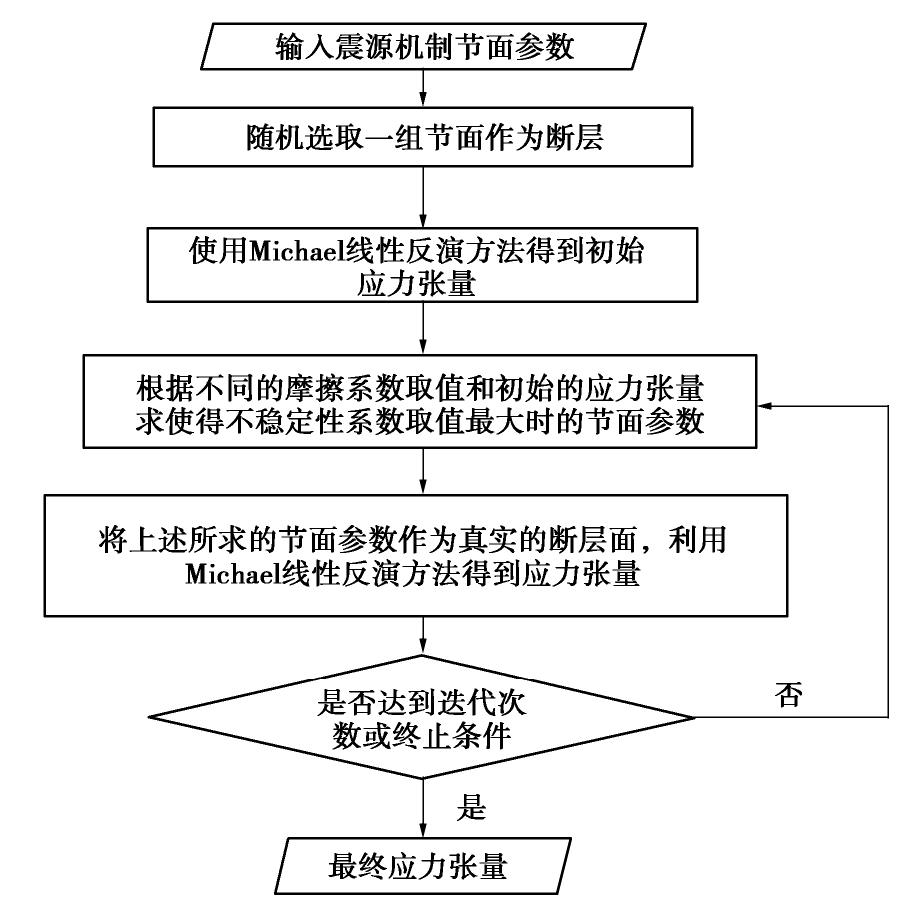
School of Architecture and Civil Engineering, Xiamen University, Xiamen 361005, China

摘要

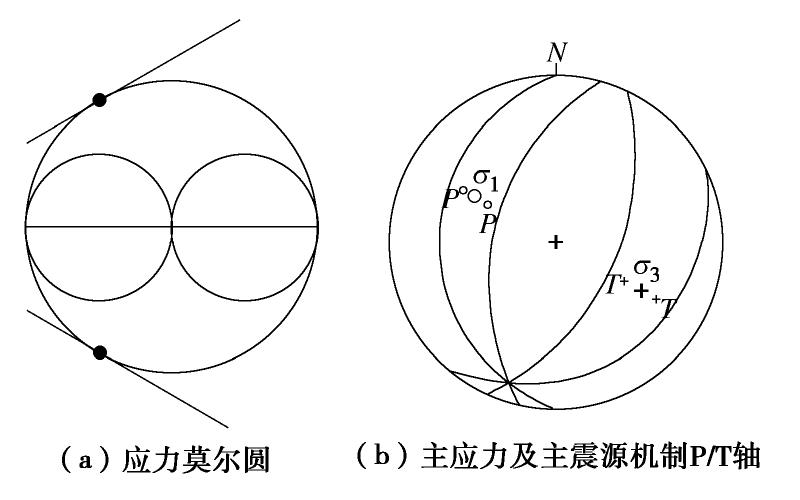
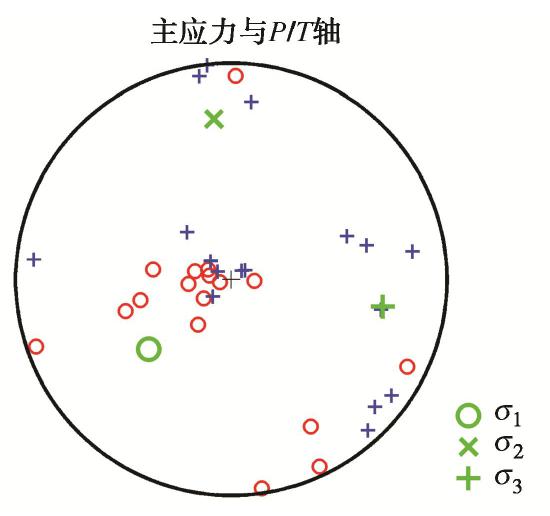
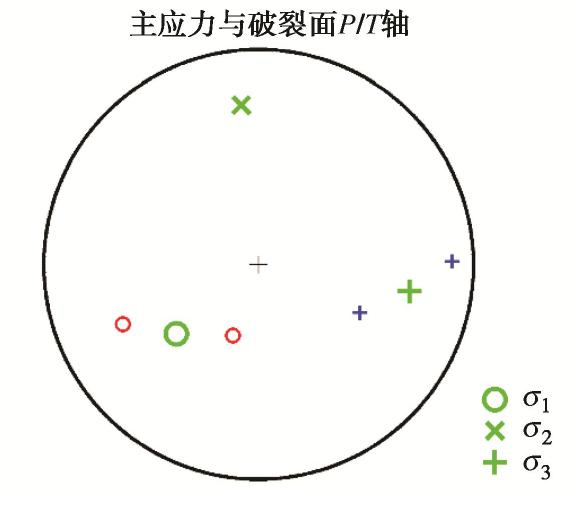
摘要: 确定工程中岩体所处的应力场环境是灾害监测预警与应用的基础,在微震震源机制解的基础上探索采用联合迭代反演方法反演应力场,该方法采用不稳定性系数I作为约束结合经典的线性反演方法反演应力场,有效避免了两个断层面的模糊性对反演结果的不利影响,提高了反演精度。通过多次反演选取能够产生最大不稳定性系数的摩擦系数 $μ$ 作为岩体的摩擦系数,并通过应力与摩擦系数定义了主破裂面。对一起典型的岩体破裂微震定位事件案例,首先分析了破裂类型以及破裂面方位,并对破裂的时间演化进行了推测；其次分析了加入不同程度噪声对应力反演结果的影响,并给出了分析结果；最后对应力场分布进行了分析,结果表明最大主应力轴的方位角与倾角为229.86°/48.57°；中间主应力轴的方位角与倾角为353.89°/26.28°；最小主应力轴的方位角与倾角为100.08°/29.44°,应力的分布与震源机制解P/T轴分布具有一致性；主破裂面的方位较好地符合了此次微震事件实际监测结果。
- 微震监测 /
- 应力场反演 /
- 震源机制 /
- 矩张量 /
- 岩体破裂
Abstract: Determining the stress field environment of rock mass in engineering is the basis of disaster monitoring, disaster warning and its application. A joint iterative inversion method is used to retrieve the stress field based on the focal mechanism. The method uses instability coefficient I as a constraint and combines it with the classical linear inversion method to retrieve the stress field, which can effectively avoid the negative influences of the fuzziness of the two fault planes on the inversion results and improve the accuracy of the results. To determine the optimal friction coefficient of rock mass, the friction coefficient which can produce the maximum instability coefficient is selected as that of rock mass through multiple inversion. The concept of the main fault plane is defined by the friction coefficient and stress. A typical case of rock fracture microseismic location event is presented and analyzed. Firstly, the source mechanism is analyzed, the type of fracture and the orientation of the fracture surface are obtained, and the time evolution of the fracture is predicted. Secondly, the error of the stress inversion results with different levels of noise is analyzed, and the results are presented. Finally, the distributions of stress filed are analyzed, and the results show that the azimuth angle and inclination angle of the maximum principal stress axis are 229.86º and 48.57º. The azimuth angle and inclination angle of the intermediate principal stress axis are 353.89º and 26.28º. The azimuth angle and inclination angle of the minimum principal stress axis are 100.08ºand 29.44º. The distribution of stress axes is consistent with the P/T axes of the focal mechanism. The orientation of the main fault plane is in great agreement with the actual monitoring results.
- microseismic monitoring /
- stress field inversion /
- focal mechanism /
- moment tensor /
- rock mass fracture

HTML全文

0. 引言

随着地球资源被大规模开发利用,移步有大量可利用资源的外星球成为了当前科学界的永恒的研究热点话题。目前,中国的“探月三期”工程走到了最为关键的一步——“绕、落、回”三步走的最后一步。中国计划于2020年实施“嫦娥五号”探月任务。借鉴美、苏等探月大国的采样方式,中国在采样阶段也将采用钻进取芯方式对月球次表层月壤进行采样^[1-3]。钻取过程中,月球次表层广泛分布的临界尺度颗粒由于其无法被取芯孔采集也无法被螺旋槽排出的特性,增加了采样的风险。目前,为了提高钻进可靠性,大多数研究着重于优化取芯钻具的结构设计方面^[4-5],忽略了临界尺度颗粒在钻进过程中的动力学特性与钻进参数之间的关系。

李宁等^[6]根据切削、静压及钻压作用过程建立旋进式触探试验推导出岩石的内摩擦角及黏聚力等的计算公式。刘泉声等^[7]研究岩石脆性指标对滚刀破岩功率的影响,结果表明滚刀更难贯入硬质岩石。Siavash等^[8]针对弧形切削刃对岩石切削负载影响研究,结果表明影响切削力的主要因素为切削刃与岩石相互作用面积、切削刃包络形状。Li等^[9]通过直尺切削试验,获得模拟月岩破碎行为及其负载特性,设计了一种高效能钻头,大大提高钻进可靠性。根据切削土壤的破坏形式,Che等^[10]开展了岩石切削性能和失效行为研究,试验结果表明,切削力随切削深度、前角以及岩石单轴抗压强度的增加而增大,但是受切削速度的影响程度较弱。Dagrain等^[11]将岩石切削过程中的负载特性分成几个主要阶段进行分析,结果表明随着切削深度的增加切削具的负载表现形式不同,随着钻进深度的增加钻进负载明显增加。刘天喜等^[12]和庞勇等^[13]通过钻取试验监测月壤大颗粒在不同位置时的运移特性及对钻具钻进力载的影响,试验结果表明,影响月壤大颗粒的典型力载特征及影响大颗粒运移特性的关键因素是表面形态。

本文针对在月球钻进取芯过程中,月壤临界尺度工况中的临界尺度颗粒受钻削作用时的孔底置出与孔壁置入运移特性与钻采阻力之间的对应关系进行探究,建立月壤临界尺度颗粒切削模型,通过离散元仿真方法及直尺切削试验验证方式,探究切削阻力时域曲线不同特征与临界尺度颗粒运移特性之间的关系。

1. 临界尺度颗粒运移特性

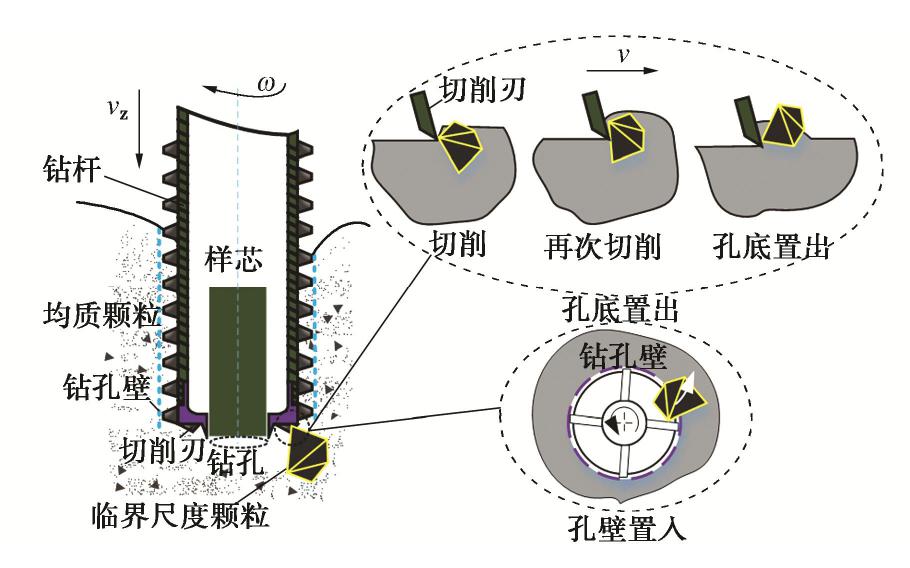
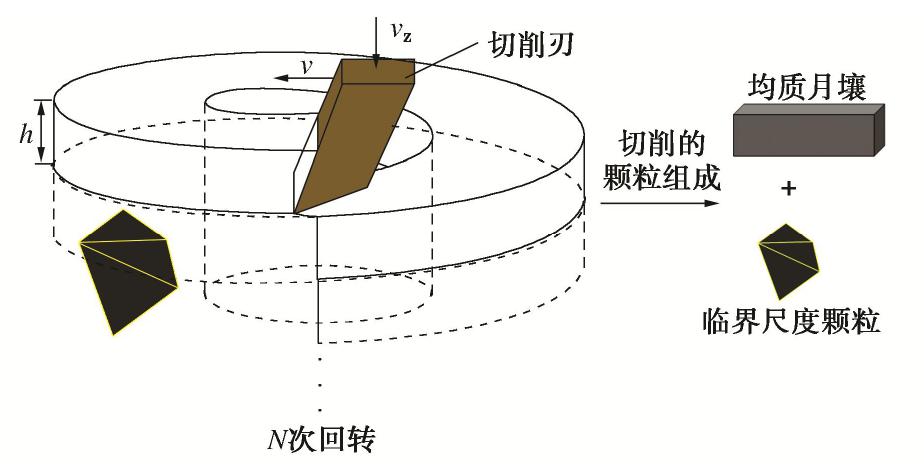
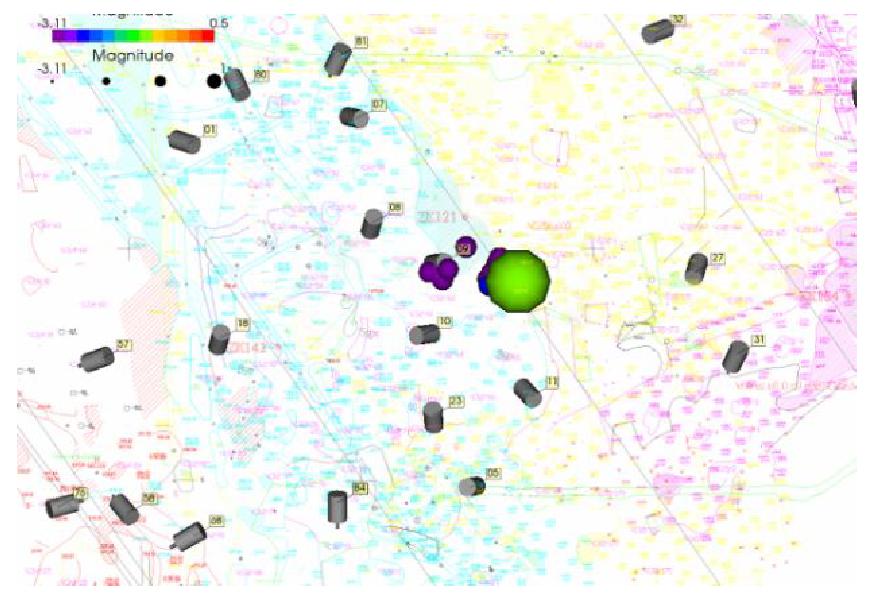
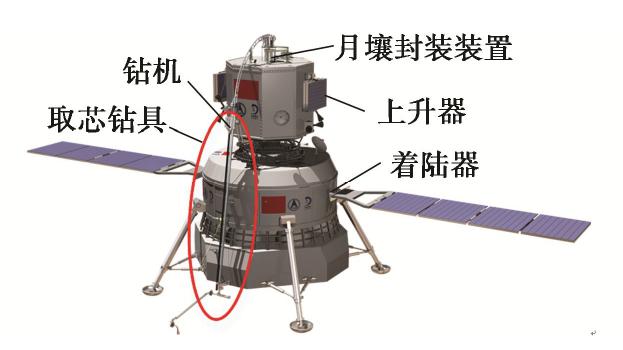
中国“嫦娥五号”探测器于2020年底在月球正面软着陆,首次完成了地外天体无人自动采样并返回地球,预计带回2 kg月壤样品^[14]。如图1所示,取芯钻具安装在无人着陆器上,其在钻机的驱动下钻进月球次表层,做回转和进尺运动,钻头对原位月壤进行破碎,钻杆排出破碎月壤,取芯机构进行月壤样品回收,软袋包裹月壤样品进入月壤封装装置。广泛分布的月壤临界尺度颗粒对采样任务影响极大,可直接影响取芯效果。探测器的着陆位置即为选定的钻取位置,其内月壤颗粒分布情况未知,无法自主识别并避免恶劣工况。

图 1 取芯钻具在着陆器上的安装位置

Figure 1. Mounting position of coring drill on lander

下载: 全尺寸图片幻灯片

如图2所示,为临界尺度颗粒的孔底置出与孔壁置入运移特性示意图。临界尺度颗粒无法进入采样孔也不能被钻杆螺旋槽排出,一部分直接嵌入孔壁；另一部分则位于钻头下方与切削具一同切削月壤,当其受到的切削阻力大于切削刃之间的夹紧力时,其中的一部分临界尺度颗粒脱离钻头嵌入孔壁,另一部分未被破碎的临界尺度颗粒被切削刃从孔底置出,剩余的存在于钻头下方。在临界尺度颗粒运移效果不良时,极易形成聚积区^[15],加剧钻头的磨损速度,甚至出现卡钻、跳钻等机械故障,导致钻进失败。

图 2 临界尺度颗粒的运移特性示意图

Figure 2. Migration characteristics of critical fragments

下载: 全尺寸图片幻灯片

图2中：v_z为进给速度,v为钻具线速度,ω为钻具旋转速度。

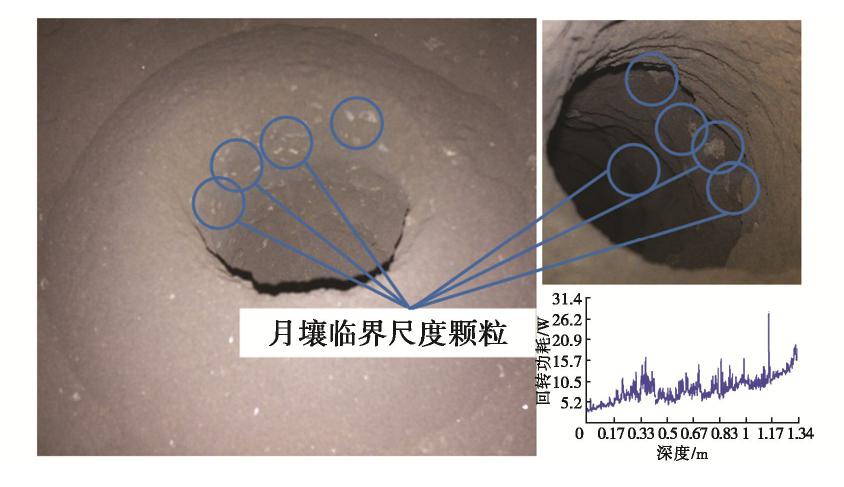
图3为月壤临界尺度颗粒钻取工况的地面模拟试验,当钻杆退出钻孔后,观察钻孔内壁可发现部分临界尺度颗粒内嵌在孔壁上,对钻进过程中的钻具的功耗和进给力数据进行监测,发现不平稳。

图 3 临界尺度工况地面钻取试验

Figure 3. Surface drilling tests on critical fragments

下载: 全尺寸图片幻灯片

2. 月壤临界尺度颗粒切削模型

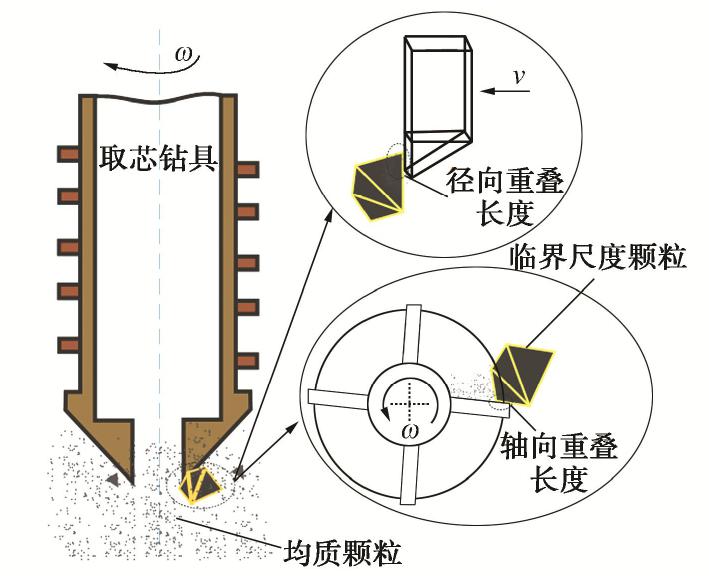
钻杆的阻力矩可用于判别月面钻进的可靠性。当钻进深度变化范围较小时,阻力矩波动程度可用来表示被钻对象的物理特性。因此,在钻削作用下,建立月壤临界尺度颗粒切削模型,可以通过二者相互作用过程中的钻具钻采阻力的变化趋势与临界尺度颗粒的运移特性之间建立联系。临界尺度颗粒与切削刃的轴向、径向重叠长度如图4所示。

图 4 临界尺度颗粒与切削刃作用示意图

Figure 4. Schematic diagram of overlap of critical fragments and cutter

下载: 全尺寸图片幻灯片

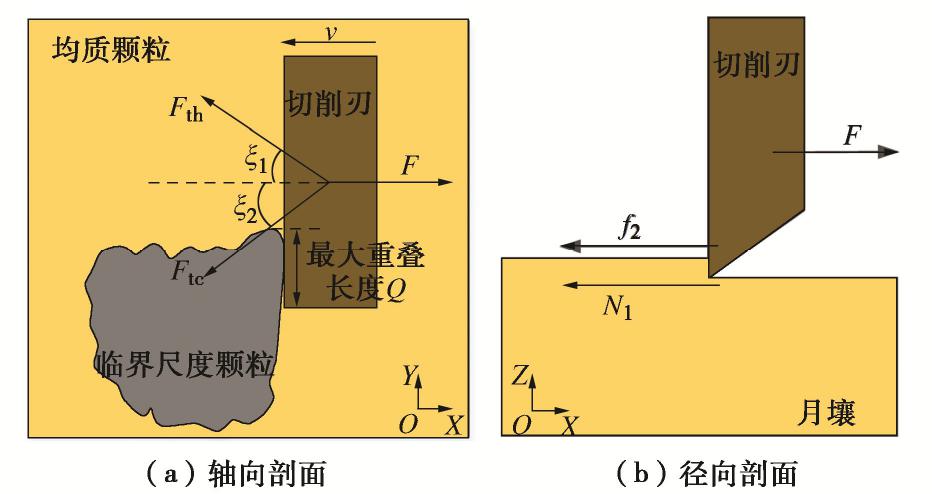
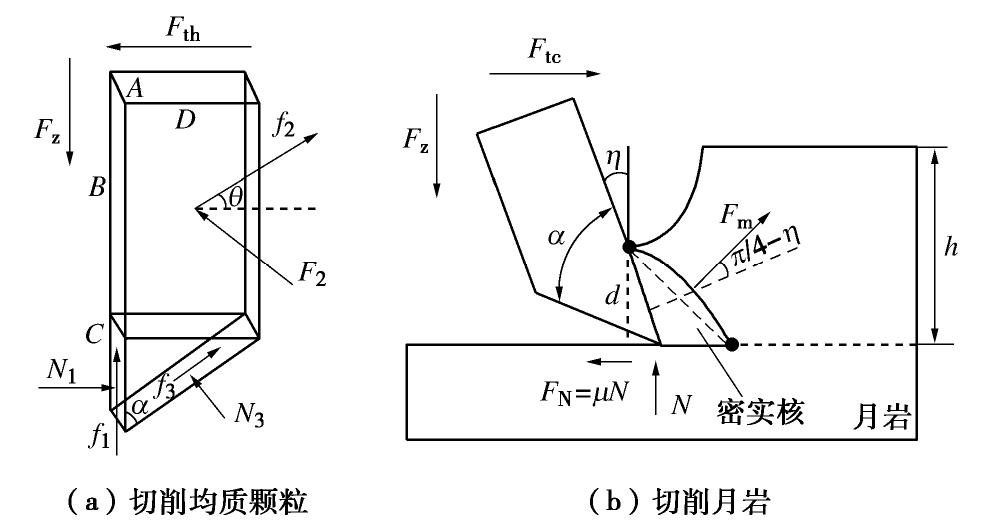
当钻头部分切削月壤时,将切削刃前方的月壤均质颗粒、月壤临界尺度颗粒进行独立分析,力学示意图如5所示。根据土壤切削失效准则,在切削方向上会形成失效月壤,本模型不考虑失效月壤的形成（后续试验采用吸力装置进行处理）。

图 5 切削刃与月壤作用受力示意图

Figure 5. Schematic diagram of axial section forces on cutter and lunar soil interaction

下载: 全尺寸图片幻灯片

切削刃水平方向的切削阻力

$F = \cos ξ_{1} F_{t h} + \cos ξ_{2} F_{t c}$ ,

(1)

式中,F为切削刃的总切削阻力,F_tc为切削刃对临界尺度颗粒的作用力,F_th为切削刃对均质颗粒的作用力,ξ₁及ξ₂分别为均质颗粒及临界尺度颗粒对切削刃产生的阻力与水平方向的夹角。

切削深度固定时,不计前端失效月壤及临界尺度颗粒碎屑的影响,根据切削刃前刀面与模拟月壤总的接触面积不变,所以有

$Δ s = Δ s_{1} + Δ s_{2}$ ,

(2)

式中,Δs₁,Δs₂分别为切削过程中接触临界尺度颗粒的面积、接触均质月壤的面积,Δs为切削刃切削模拟月壤的总面积。

费雷特直径定义为颗粒在某一平面投影轮廓上的最远两点的距离,当切削刃与临界尺度颗粒轴向重叠长度大于切削深度时,费雷特直径可等效为本文所述的切削刃与临界尺度颗粒径向重叠部分长度。根据林呈祥等^[16]对TJ-1模拟月壤颗粒的形貌参数统计,得出

${\begin{cases} Δ s_{3} = 0.545 Q^{2} - 0.207 Q + 0.707 \begin{matrix} \end{matrix} (Q ＞ 0), \\ Δ s_{3} = 0 \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \end{matrix} \end{matrix} \end{matrix} \end{matrix} \end{matrix} \end{matrix} (Q = 0), \end{cases}$

(3)

式中,Δs₃为临界尺度颗粒的投影轮廓面积,Q为临界尺度颗粒的费雷特直径。

根据已有研究及对原位月壤的研究数据拟合^[17],月壤自然堆积密度 $ρ_{z}$ 和下钻深度z呈一定线性关系：

$ρ_{z} = 1.92 \frac{z + 12.2}{z + 18}$ 。

(4)

孔隙率n,孔隙比e与月壤自然堆积密度满足

$e = \frac{n}{1 - n},$

(5)

$n = 1 - \frac{ρ_{z}}{ρ_{0}},$

(6)

式中, $ρ_{0}$ 为月壤相对密度,探月工程中一般取3.1 g/cm³。

内聚力c与内摩擦角φ如下式

$\tan φ = \frac{1.3779}{e} - 0.3925$ ,

(7)

$c = 60959 e^{- 22.552 n}$ 。

(8)

根据被动土压力系数K_p与内摩擦角φ之间的关系得

$K_{p} = \tan^{2} (\frac{π}{4} + \frac{φ}{2})$ 。

(9)

当切削刃前刀面上全部为均质颗粒时,切削刃在回转过程中受到的阻力主要为出露刃对均质月壤的切削作用,而孔壁的月壤会有向钻头运动的趋势,孔壁月壤会对该切削刃的侧壁有压力作用。根据朗肯土压力理论,当切削刃前刀面侧壁的月壤达到极限抗剪强度时,作用于切削刃上的作用力为主动或被动土压力^[18]。对切削刃力学分析如图6（a）所示。

图 6 切削月壤力学示意图

Figure 6. Diagram of mechanics of lunar soil cutting

下载: 全尺寸图片幻灯片

在切削方向上建立力学平衡方程式：

$F_{t h} - N_{1} - f_{2} \cos θ - f_{3} \sin α + N_{3} \cos α = 0$ ,

(10)

$N_{1} = \frac{1}{2} Δ s_{2} (ρ_{z} g C K_{p} + 2 c \sqrt{K_{p}})$ ,

(11)

$\begin{matrix} f_{2} = [ρ_{z} g z K_{p} + 2 c \sqrt{K_{p}} - ρ_{z} g (B + C) K_{p}] \cdot \\ \frac{1}{2} D (B + C) \end{matrix}$ 。

(12)

式中 N₁为被动土压力；F₂为孔壁对切削刃侧壁的土压力；f₂为F₂作用面产生的摩阻力；α为切削刃前角；C为切削刃出露刃长度；B=切削刃刃长-C；D为切削刃侧面长度；N₃为侧向土滑落对切削刃的支持力；f₃为N₃作用面产生的摩阻力；θ为钻进规程角。

由于切削刃做恒速螺旋下切运动,N₃及f₃可忽略,将式（11）,（12）代入式（10）得

$\begin{matrix} F_{t h} = \frac{1}{2} {Δ s_{2} (ρ_{z} g C K_{p} + 2 c \sqrt{K_{p}}) + f D (B + C) \cdot \\ [ρ_{z} g z K_{p} + 2 c \sqrt{K_{p}} - ρ_{z} g K_{p} (B + C)]} \end{matrix}$ ,

(13)

式中,f为切削刃与土体接触摩擦系数。

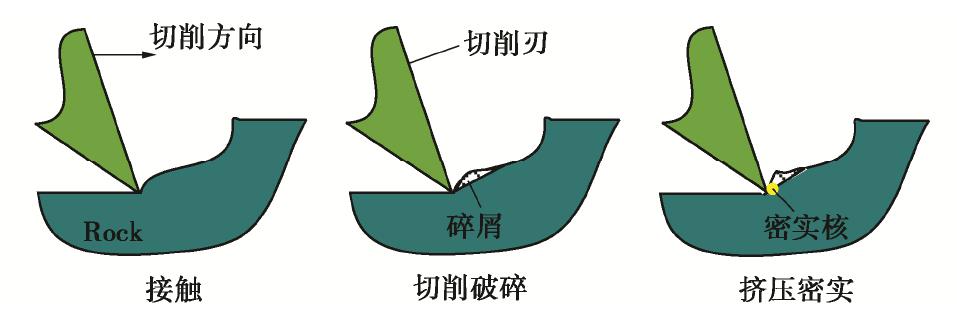
在切削过程中,切削刃切削月岩产生月岩碎屑,并被切削刃持续切削,切削刃与月岩之间的相互作用力不断增加,碎屑部分被挤压,形成密实核,因此需要在宏观上对密实核处进行描述^[20]。切削具回转,月岩表现为即抗压又抗剪。当切削刃仅接触月岩时,岩石回转切削力学模型如图6（b）所示,在切削刃与月岩相互接触的极小区域内,由于应力集中,密实核传递给母岩的合力为F_m,密实核的成型描述如图7所示。

图 7 密实核成型描述

Figure 7. Description of dense nucleation

下载: 全尺寸图片幻灯片

作用于母岩的合力

$F_{m} = 2 \sqrt{2} d Q σ_{s}$ ,

(14)

式中,d为密实核半径, $σ_{s}$ 为月岩抗压强度。

在切削方向上建立力学平衡方程式：

$\begin{matrix} F_{t c} - μ N - F_{m} \cos (\frac{π}{4} - η) \sin η + \\ F_{m} \sin (\frac{π}{4} - η) \cos η = 0 \end{matrix}$ ,

(15)

式中,μ为月岩与切削刃之间的滑动摩擦系数,N为月岩对切削刃支持力,η为切削刃前刀角,h为切削深度

整理式（14）,（15）得

$F_{t c} = 2 μ A h σ_{s} \tan \frac{α}{2} + δ Δ s_{1} σ_{s}$ ,

(16)

式中,δ为常量,与岩石破碎角（岩石剪切面与切削方向的夹角）有关,A为切削刃的底刃长度。

将式（8）,（9）,（13）和（16）代入式（1）中,即可得到在钻削作用下不同重叠率时切削刃的切削阻力：

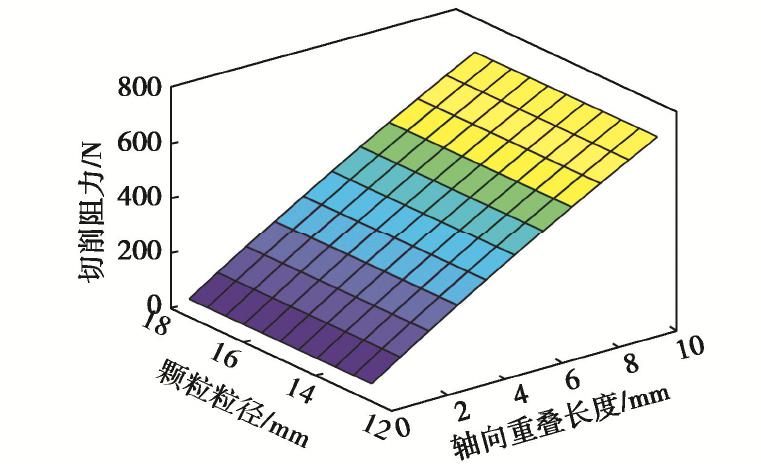
$\begin{matrix} F = \frac{1}{2} {Δ s_{2} [\frac{1.92 g C (z + 12) \tan^{2} (\frac{π + 2 φ}{4})}{z + 18} + \\ 2 c \tan (\frac{π + 2 φ}{4})] + \\ f D (B + C) \frac{1.92 g (z - B - C) (z + 12) \tan^{2} (\frac{π + 2 φ}{4})}{z + 18} + \\ 2 c \tan (\frac{π + 2 φ}{4})} + 2 μ A h σ_{s} \tan \frac{α}{2} + δ Δ s_{1} σ_{s} \end{matrix}$ 。

(17)

根据式（17）得到切削阻力受切削刃与临界尺度颗粒的不同作用位置及颗粒粒径影响下的变化曲线,如图8所示。可知,固定钻深时,切削阻力受到二者相互作用位置的影响最大。

图 8 固定钻进深度下的单刃切削阻力

Figure 8. Cutting resistances of fixed single edge at depth of drilling

下载: 全尺寸图片幻灯片

取芯钻具在恒进尺、回转运动的条件下,不同的下钻角度、预钻区临界尺度颗粒分布情况及在钻进过程中月壤颗粒的差速扰动均会对二者的相互作用位置产生影响,因此,定义归一化参数法向重叠率γ_D：

$γ_{D} = \frac{Q Δ s_{1}}{A Δ s_{3}}$ 。

(18)

3. 孔底置出与孔壁置入仿真模拟

3.1 切削轨迹等效分析

取芯钻具的一个钻进规程包括恒定的回转和进给运动,Wheeler等^[19]建立了惯性力与准静态切削模型叠加的模型,认为切削具线速度在低于4.36 km/h范围内,惯性力受到切削速度的影响不显著。中国探月任务中所使用的取芯钻具的回转速度为60～120 rpm,钻具最大径为30 mm,转速换算成线速度如表1所示,属于慢速切削速度范围内。因此,在惯性力不受影响的情况下,可将等距的螺旋线型的切削轨迹等效为直线型的切削轨迹。等效成直线运动之后切削轨迹上包含的颗粒类型,如图9所示。

表 1 钻具回转速度与线速度换算表

Table 1. Conversion of rotary speed and linear speed of drilling tool

回转速度/rpm	60	80	100	120
线速度/(mm·s^-1)	47.1	61.2	78.7	94.2

下载: 导出CSV

| 显示表格

图 9 回转轨迹等效示意图

Figure 9. Schematic diagram of equivalent rotation trajectory

下载: 全尺寸图片幻灯片

3.2 参数设置

本文采用离散元方法DEM进行仿真模拟。在对模拟月壤进行参数标定时,假设均质颗粒与临界尺度颗粒均为Molerus I型土体,各向同性。参考相关文献[20～22],仿真环境参数标定如表2所示。切削模拟月壤颗粒运动分析与应力分布对比,测定大范围稳定的仿真边界,并且可以完整的显示临界尺度颗粒的运移特性,本文设置仿真边界为x×y×z=100 mm×50 mm×40 mm。

表 2 仿真环境参数标定

Table 2. Parameter calibration of simulation environment

参数	数值
颗粒泊松比	0.35
均质颗粒半径/mm	1.0
临界尺度颗粒粒径/mm	15
颗粒密度/(kg·m^-3)	2900
颗粒剪切模量/Pa	1×10⁸
切削刃泊松比	0.3
切削刃密度/(kg·m^-3)	7800
切削刃杨氏模量/Pa	7×10⁷
切削深度/mm重力加速度/(m·s^-2)	41.6
切削速度/(mm·s^-1)	94.2
颗粒-颗粒恢复系数	0.1
颗粒-颗粒静摩擦系数	0.514
颗粒-颗粒动摩擦系数	0.1
颗粒-几何体恢复系数	0.2
颗粒-几何体静摩擦系数	0.3
颗粒-几何体动摩擦系数	0.1

下载: 导出CSV

| 显示表格

图10为在切削过程中,某瞬时临界尺度颗粒速度云图。从图10（a）可以看出,切削刃不断切削临界尺度颗粒,在切削方向上失效模拟月壤不断堆积,临界尺度颗粒质心上升,产生孔底置出现象；从图10（b）可以看出,受切削作用后,嵌入孔壁的临界尺度颗粒的运移速度接近于0,受到切削刃的差速扰动后没有回落现象,产生孔壁置入现象。

图 10 仿真切削过程速度云图

Figure 10. Simulation of cutting process speed nephogram

下载: 全尺寸图片幻灯片

3.3 仿真结果分析

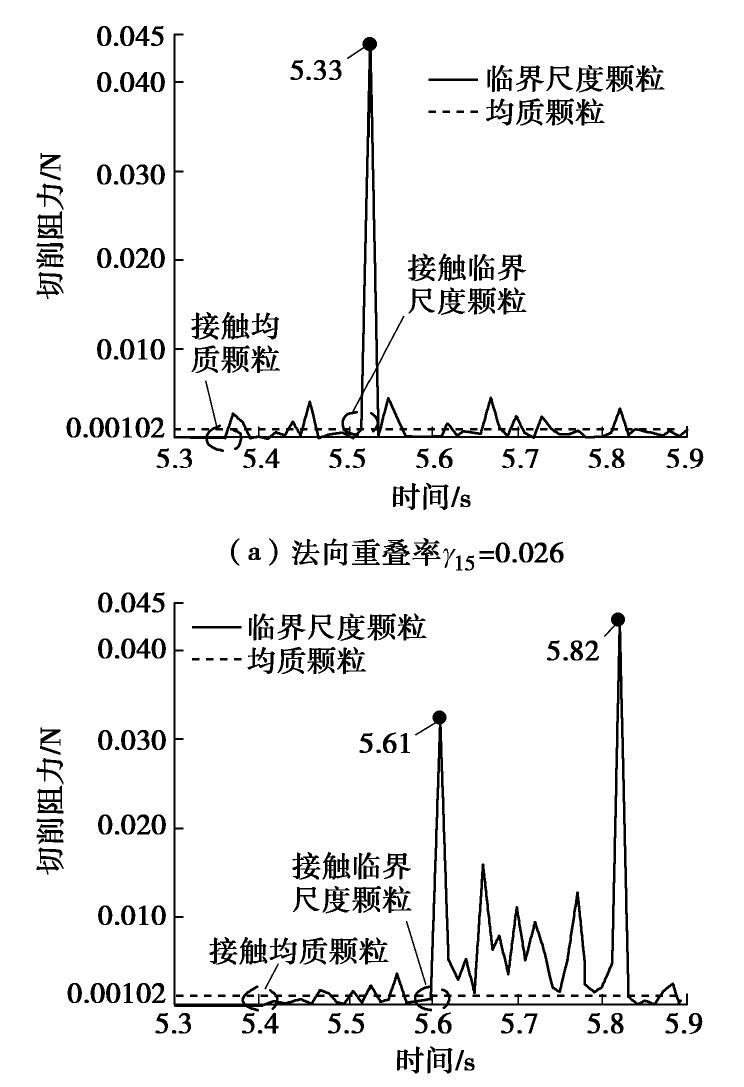
设置切削速度为94.2 mm/s切削深度为4 mm,仿真模拟结果分别如图11（a）,（b）所示。当法向重叠率 $γ_{15}$ =0.026时,临界尺度颗粒被切削刃有效拨开,产生孔壁置入现象,当法向重叠率 $γ_{15}$ =0.439,且切削刃底刃中点与颗粒质心重合时,临界尺度颗粒随动于切削刃,质心不断上升,产生孔底置出现象。

图 11 切削阻力时域变化曲线

Figure 11. Time-domain variation curves of cutting resistance

下载: 全尺寸图片幻灯片

临界尺度颗粒的孔底置出与孔壁置入现象,对应切削阻力时域曲线特征为连续峰值和仅有一个峰值点。通过仿真结果验证,可以根据切削阻力时域曲线特征判断临界尺度颗粒的运移特性。

4. 临界尺度颗粒的运移特性模拟试验

4.1 试验方法及原理

试验采用哈尔滨工业大学宇航空间机构及控制研究中心研制的直尺切削试验台SLC-1,如图12所示,试验台采用伺服电动缸作为直线运动的驱动装置,进尺调整机构调整切削深度,通过六维力传感器实现对切削阻力的测量,利用高速摄像机对临界尺度颗粒的运移特性进行记录。切削过程中,切削方向及侧向会产生失效模拟月壤[23],影响六维力传感器精度,因此,利用吸力装置来处理失效部分。

图 12 SLC-1试验台结构图

Figure 12. Structure drawing of SLC-1 testing bench

下载: 全尺寸图片幻灯片

经过筛选,选取小粒径、中粒径、大粒径的月壤临界尺度颗粒如图13（a）所示,粒径范围分别为3～14,14～16,16～30 mm。根据月壤粒径范围,月壤均质颗粒选用粒径范围在0.025～0.05 mm的天然玄武岩粉末,月壤临界尺度颗粒选用粒径为10～30 mm的天然玄武岩颗粒。通过液压机加载压实,使制备的模拟月壤的密度、内聚力、内摩擦角、孔隙比更接近真实月壤,制备的待切削的模拟月壤样本如图13（b）所示,压实之后的均质月壤物理力学参数如表3所示。

图 13 模拟月壤样品

Figure 13. Simulated lunar soil samples

下载: 全尺寸图片幻灯片

表 3 试验制备均质月壤物理力学参数

Table 3. Physical and mechanical parameters of prepared homogeneous lunar soil

参数	密度/(g·cm^-3)	泊松比	孔隙比	内摩擦角/(°)
数值	2.1	0.35	0.31	34.96

下载: 导出CSV

| 显示表格

4.2 试验结果分析

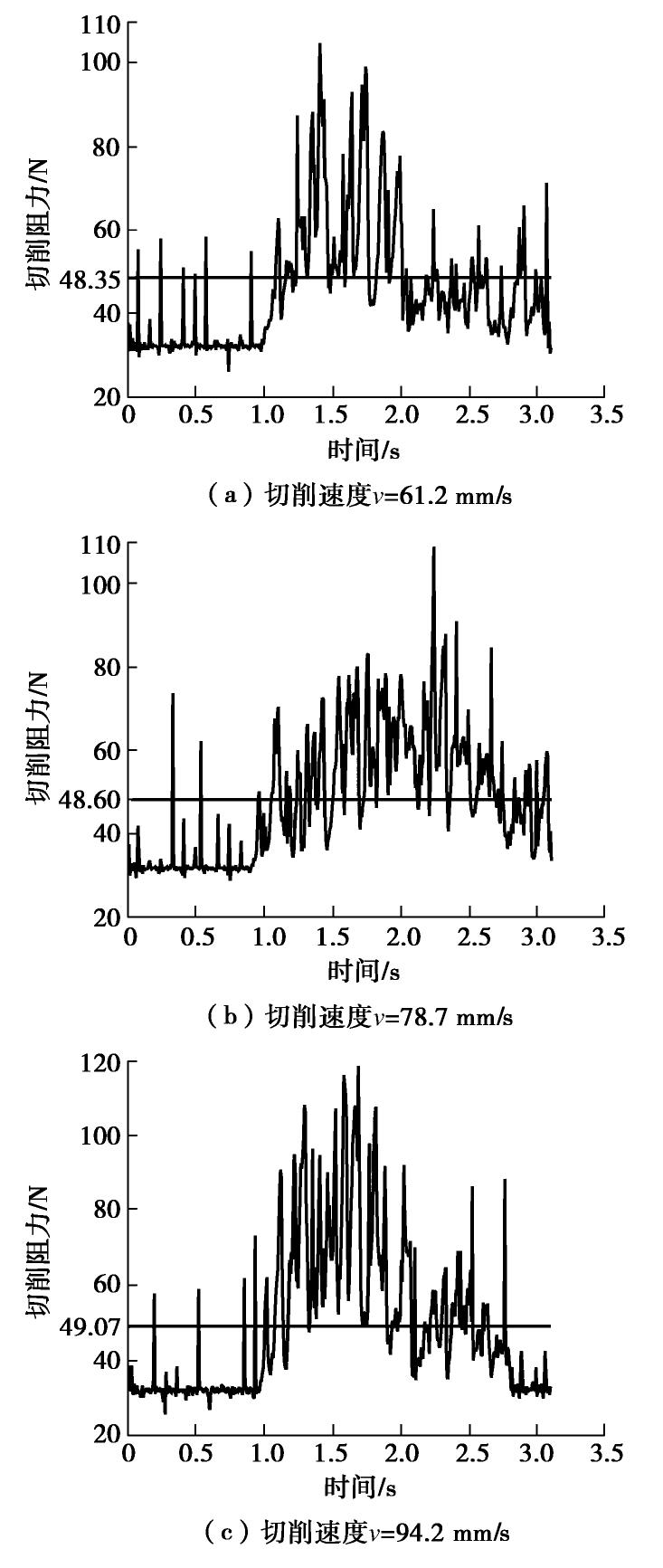
（1）切削速度对切削阻力的影响分析

对全部由月壤均质颗粒制备的模拟月壤进行直尺切削试验,通过控制切削刃的切削速度,得出切削刃的切削阻力时域变化曲线,如图14（a）～（c）所示,得出平均切削阻力,可以明显看出,切削速度的变化对切削阻力影响可以忽略。

图 14 平均切削阻力变化曲线

Figure 14. Average cutting resistance curves

下载: 全尺寸图片幻灯片

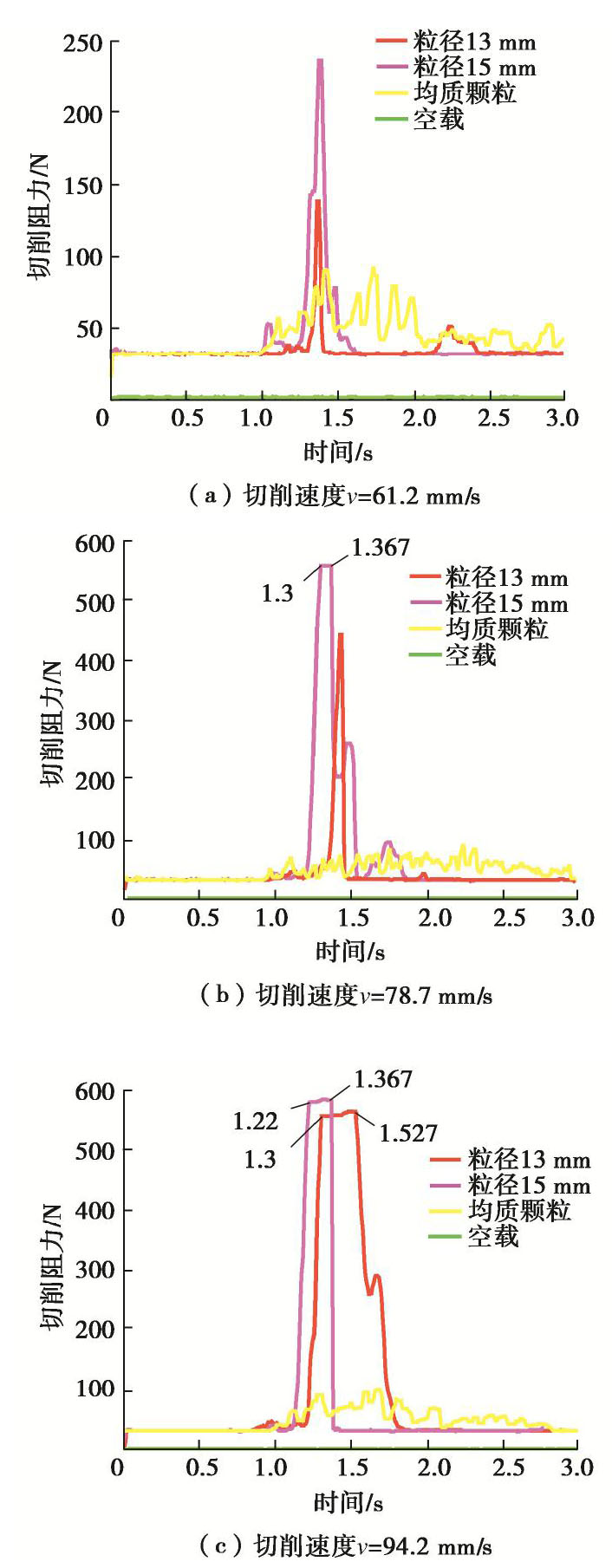
（2）孔壁置入与孔底置出现象分析

切削速度分别为61.2,78.7和94.2 mm/s的情况下,切削模拟月壤产生的切削阻力时域变化曲线分别如图15（a）～（c）所示。各曲线均经过滤波处理,空载时的切削阻力时域变化曲线均为在0 N附近波动的曲线。切削均质颗粒时,为在平均切削阻力附近波动的曲线。如图15（a）所示,当法向重叠率分别为 $γ_{13}$ =0.035及 $γ_{15}$ =0.026时,所产生的切削阻力时域变化曲线特征为均产生单峰值点,临界尺度颗粒产生孔壁置入现象,且此时法向重叠率较低,临界尺度颗粒更容易产生孔壁置入现象,与其粒径大小无关。如图15（b）所示,当法向重叠率分别为γ₁₃=0.198及γ₁₅=0.148时,切削阻力时域变化曲线特征分别为仅有一个单峰值点和连续峰值。如图15（c）所示,当法向重叠率分别为γ₁₃=0.587及γ₁₅=0.439,且切削刃质心与临界尺度颗粒质心的连线平行于切削方向时,切削阻力时域变化曲线特征均为含有连续峰值。

图 15 切削阻力时域变化曲线

Figure 15. Time-domain variation curves of cutting resistance

下载: 全尺寸图片幻灯片

如图16（a）所示,临界尺度颗粒-1被切削刃有效拨开,其质心偏移一侧均质颗粒产生松动,临界尺度颗粒嵌入孔壁,产生孔壁置入现象。如图16（b）所示,在切削轨迹上,临界尺度颗粒-2被切削刃持续切削,直至切削过程结束未脱离切削刃,从临界尺度颗粒初始位置可以看出,临界尺度颗粒最终上升至模拟月壤表面,产生孔底置出现象。

图 16 切削过程结束

Figure 16. Completion of cutting process

下载: 全尺寸图片幻灯片

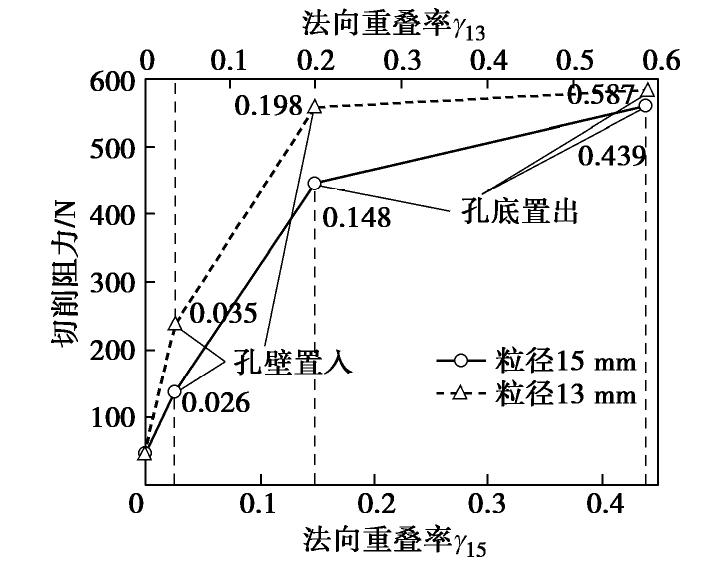
（3）法向重叠率对切削阻力的影响分析

由图17可以看出,在下钻深度变化范围较小的情况下,相同粒径的临界尺度颗粒,随着法向重叠率增加,切削刃的切削阻力呈逐渐增大趋势。

图 17 切削阻力–法向重叠率试验曲线

Figure 17. Curves of cutting resistance-normal overlap rate tests

下载: 全尺寸图片幻灯片

5. 结论

（1）法向重叠率的增加,会导致切削刃的切削阻力增加,并且临界尺度颗粒粒径因素对切削阻力影响较小。

（2）当法向重叠率越小时,临界尺度颗粒越容易产生孔壁置入现象。当法向重叠率越大时,临界尺度颗粒越容易产生孔底置出现象。

（3）钻具的切削阻力时域变化曲线可作为判别临界尺度颗粒运移特性的依据。当切削阻力时域变化曲线中含有连续峰值和仅有一个峰值点时,临界尺度颗粒分别产生孔底置出和孔壁置入现象,临界尺度颗粒粒径因素对其运移特性影响较小。

致谢：: 感谢捷克科学院地球物理研究所Václav Vavryčuk教授在应力场反演方面提供的帮助。

图 1 莫尔-库仑破坏准则

Figure 1. Mohr-Coulomb failure criterion

下载: 全尺寸图片幻灯片

图 2 断层不稳定系数I在莫尔圆中的定义

Figure 2. Definition of fault instability in Mohr circle

下载: 全尺寸图片幻灯片

图 3 联合迭代反演法流程图

Figure 3. Flow chart of joint iterative method

下载: 全尺寸图片幻灯片

图 4 主震源机制

Figure 4. Principal focal mechanism

下载: 全尺寸图片幻灯片

图 5 微震定位事件分布图

Figure 5. Diagram of microseismic event location

下载: 全尺寸图片幻灯片

图 6 典型微震定位事件波形图

Figure 6. Signals of typical microseismic event location

下载: 全尺寸图片幻灯片

图 7 震源机制的节平面

Figure 7. Nodal plane of focal mechanism

下载: 全尺寸图片幻灯片

图 8 震源机制解的应力莫尔圆

Figure 8. Stress Mohr circles

下载: 全尺寸图片幻灯片

图 9 震源类型图

Figure 9. Diagram of source type

下载: 全尺寸图片幻灯片

图 10 不同噪声水平下主应力轴的置信度

Figure 10. Confidence levels of principal stress axis with different levels of noise

下载: 全尺寸图片幻灯片

图 11 主应力和P/T轴分布图

Figure 11. Diagram of principal stress and focal mechanism P/T axes

下载: 全尺寸图片幻灯片

图 12 两个节面的断层面解玫瑰花图

Figure 12. Rose diagram of two nodal planes

下载: 全尺寸图片幻灯片

图 13 主应力与主破裂面P/T轴

Figure 13. Principal nodal lines and P/T axes

下载: 全尺寸图片幻灯片

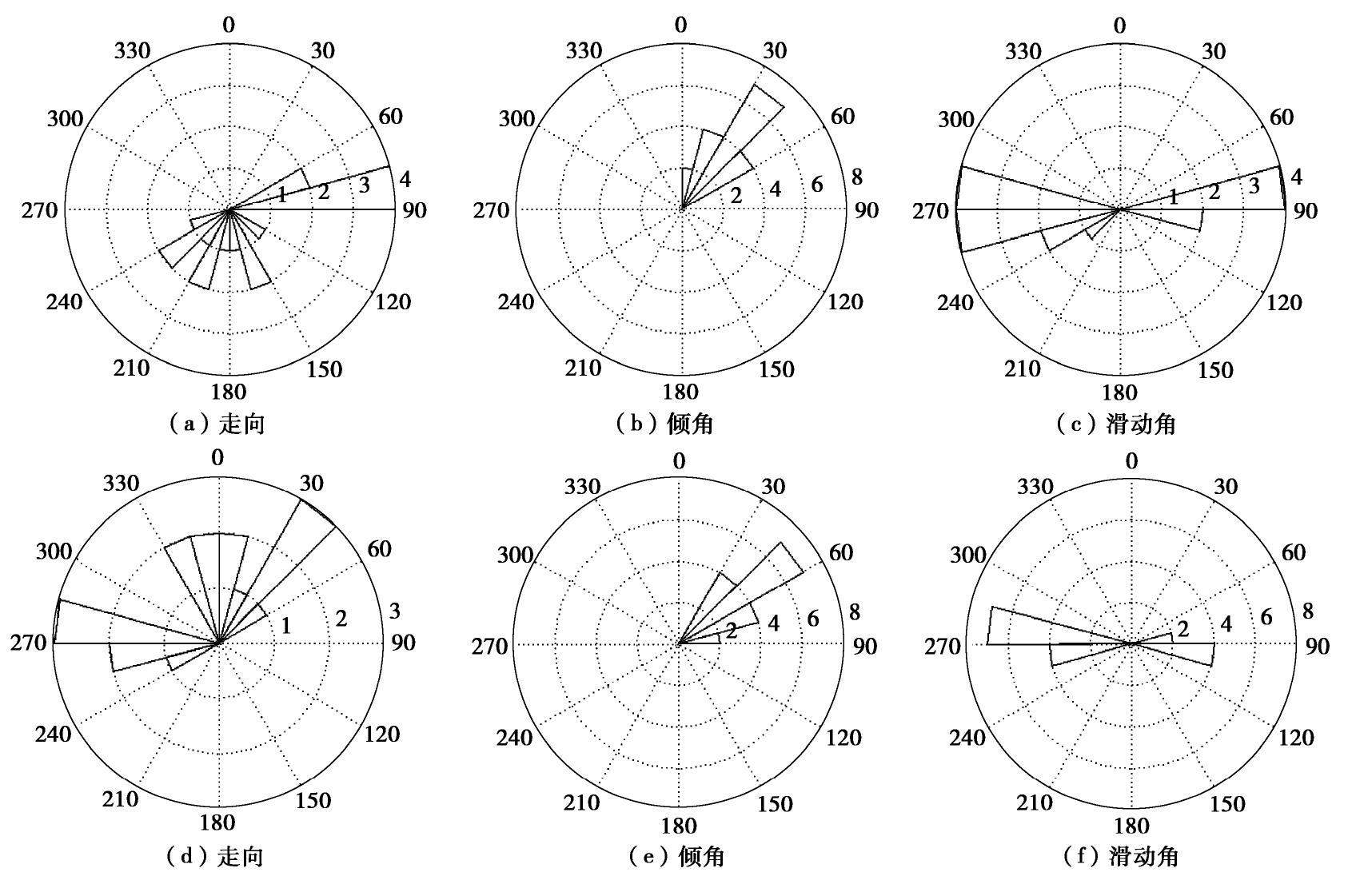
表 1 震源机制节面1及其节面2参数

Table 1 Fault parameters of nodal planes No. 1 and No. 2

事件编号	走向1/(°)	倾角1/(°)	滑动角1/(°)	走向2/(°)	倾角2/(°)	滑动角2/(°)
1	159.38	49.90	87.55	343.16	40.16	92.89
2	79.30	44.67	-96.12	267.87	45.65	-83.98
3	229.37	33.20	-78.19	35.92	57.58	-97.62
4	87.17	47.93	97.81	255.60	42.65	81.43
5	80.87	27.90	-111.29	284.66	64.15	-79.11
6	252.71	21.71	104.51	57.14	69.01	84.30
7	161.45	9.55	-94.78	346.30	80.47	-89.19
8	196.60	15.20	-83.52	9.89	74.89	-91.75
9	83.77	38.89	79.43	277.25	51.88	98.41
10	123.77	3.39	-127.33	341.15	87.29	-87.93
11	185.47	53.79	-90.46	6.24	36.21	-89.37
12	68.93	40.64	-107.31	271.25	51.55	-75.67
13	233.41	38.63	-82.05	43.28	51.80	-96.29
14	61.81	49.93	85.76	248.37	40.25	95.02
15	169.87	28.82	-91.70	351.81	61.19	-89.06
16	218.12	35.77	-86.69	34.04	54.29	-92.38
17	202.89	35.15	85.17	28.79	54.99	93.39

下载: 导出CSV

表 2 不同噪声水平平均应力误差

Table 2 Average errors of stress direction with different levels of noise

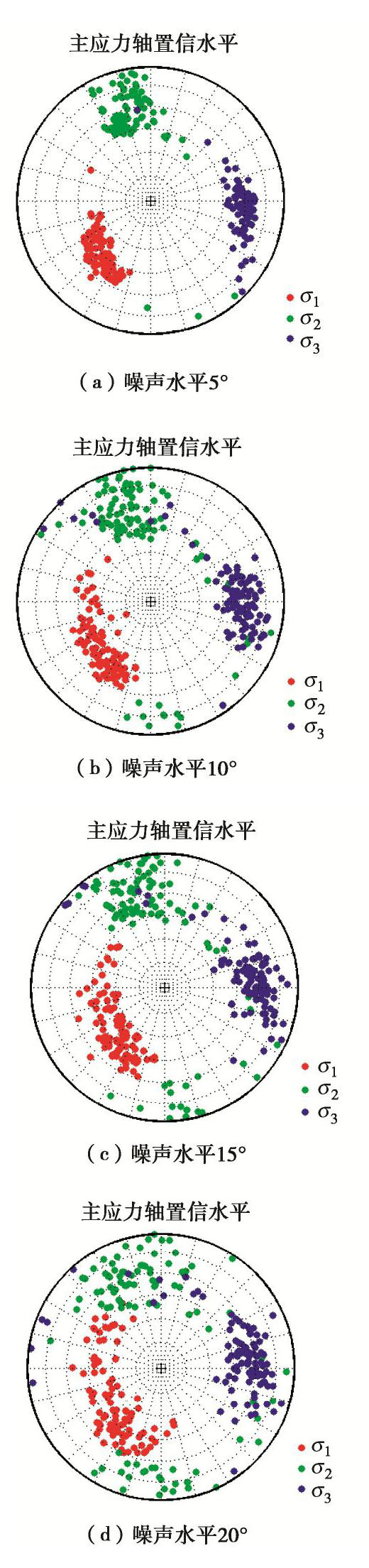
噪声水平/(°)	应力轴误差
噪声水平/(°)	$σ_{1}$	$σ_{2}$	$σ_{3}$
5	12	16	10
10	15	20	15
15	17	26	21
20	22	31	23

下载: 导出CSV

表 3 应力反演结果

Table 3 Results of stress inversion

应力主轴	$σ_{1}$	$σ_{2}$	$σ_{3}$	R
应力主轴	方位角/倾角	方位角/倾角	方位角/倾角	R
迭代反演	229.86°/48.57°	353.89°/26.28°	100.08°/29.44°	$0. 9$

下载: 导出CSV

表 4 主破裂面的参数

Table 4 Parameters of principal faults

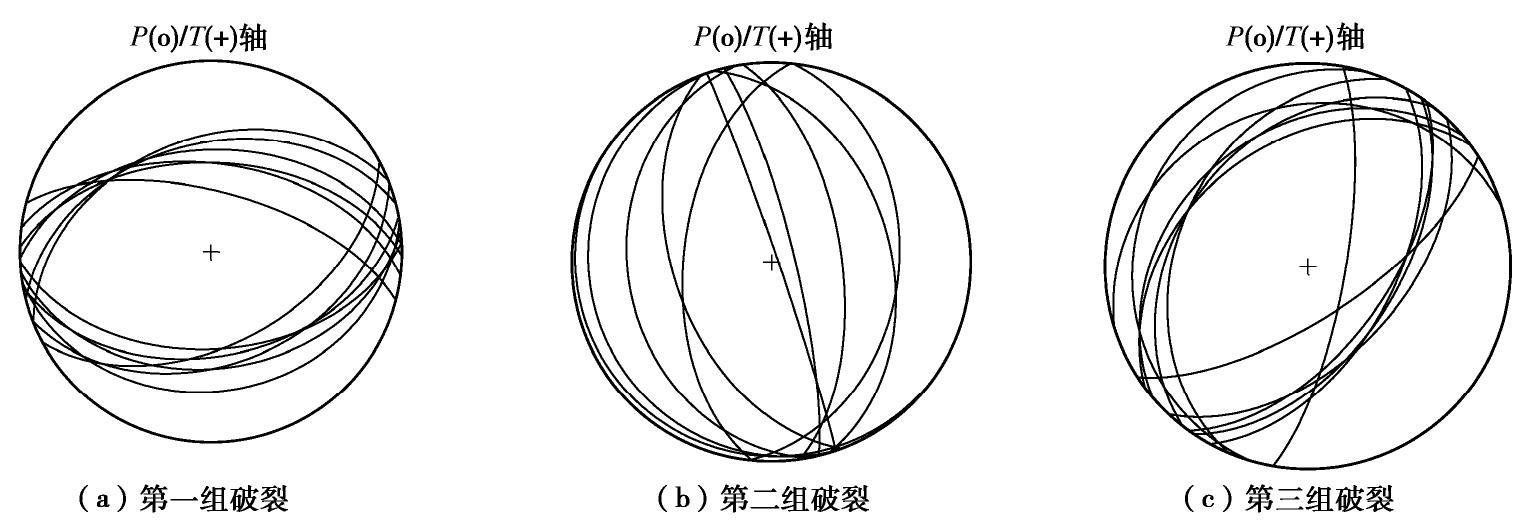
主破裂面	走向/(°)	倾角/(°)	滑动角/(°)
破裂面1	178.01	81.72	116.58
破裂面2	208.17	41.05	-47.60

下载: 导出CSV

参考文献(21)

[1]	彭府华, 李庶林, 程建勇, 等. 中尺度复杂岩体应力波传播特性的微震试验研究[J]. 岩土工程学报, 2014, 36(2): 312-319. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201402010.htm PENG Fu-hua, LI Shu-lin, CHENG Jian-yong, et al. Experimental study on characteristics of stress wave propagation in mesoscale and complex rock mass by micro-seismic monitoring[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(2): 312-319. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201402010.htm
[2]	钱波, 杨莹, 徐奴文, 等. 白鹤滩水电站左岸边坡岩石损伤变形反馈分析[J]. 岩土工程学报, 2019, 41(8): 1464-1471. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201908013.htm QIAN Bo, YANG Ying, XU Nu-wen, et al. Feedback analysis of rock damage deformation of slope at left bank of Baihetan Hydropower Station[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(8): 1464-147. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201908013.htm
[3]	于洋, 冯夏庭, 陈炳瑞, 等. 深部岩体隧洞即时型岩爆微震震源体积的分形特征研究[J]. 岩土工程学报, 2017, 39(12): 2173-2179. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201712005.htm YU Yang, FENG Xia-ting, CHENG Bin-rui, et al. Fractal characteristics of micro-seismic volume for different types of immediate rock-bursts in deep tunnels[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(12): 2173-2179. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201712005.htm
[4]	陆菜平, 窦林名, 吴兴荣, 等. 岩体微震监测的频谱分析与信号识别[J]. 岩土工程学报, 2005, 27(7): 772-775. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200507009.htm LU Cai-ping, DOU Lin-ming, WU Xing-rong, et al. Frequency spectrum analysis on microseismic monitoring and signal differentiation of rock material[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(7): 772-775. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200507009.htm
[5]	吴顺川, 黄小庆, 陈钒, 等. 岩体破裂矩张量反演方法及其应用[J]. 岩土力学, 2016, 37(增刊1): 1-18. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S1001.htm WU Shun-chuan, HUANG Xiao-qing, CHEN Fan, et al. Moment tensor inversion of rock failure and its application[J]. Rock and Soil Mechanics, 2016, 37(S1): 1-18. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S1001.htm
[6]	李庶林, 林恺帆, 周梦婧, 等. 基于矩张量分析的特大山体破坏前兆孕震机制研究[J]. 岩石力学与工程学报, 2019, 38(10): 2000-2009. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201910007.htm LI Shu-lin, LIN Kai-fan, ZHOU Meng-jing, et al. Study on failure precursors and seismogenic mechanisms of a large landslidebased on moment tensor analysis[J]. Chinese Journal of Rock Mechanic and Engineering, 2019, 38(10): 2000-2009. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201910007.htm
[7]	MCGARR A. Some applications of seismic sourcemechanism studies to assessing underground hazard[C]//Proceedings of First International Symposium on Rockbrust and Seismicity in Mines, 1984, Johannesburg.
[8]	WALLACE R E. Geometry of shearing stress and relation to faulting[J]. The Journal of Geology, 1951, 59(2): 118-130.
[9]	BOTT M H P. The mechanics of oblique slip faulting[J]. Geological Magazine, 1959, 96(2): 109-117.
[10]	ANGELIER J. Determination of the mean principal directions of stresses for a given fault population[J]. Tectonophysics, 1979, 56(3/4): T17-T26.
[11]	ETCHECOPAR A, VASSEUR G, DAIGNIERES M. An inverse problem in microtectonics for the determination of stress tensors from fault striation analysis[J]. Journal of Structural Geology, 1981, 3(1): 51-65.
[12]	GEPHART J W, FORSYTH D W. An improved method for determining the regional stress tensor using earthquake focal mechanism data: application to the San Fernando earthquake sequence[J]. Journal of Geophysical Research: Solid Earth, 1984, 89(B11): 9305-9320.
[13]	MICHAEL A J. Determination of stress from slip data: faults and folds[J]. Journal of Geophysical Research, 1984, 89(B13): 11517-11526.
[14]	MICHAEL A J. Use of focal mechanisms to determine stress: a control study[J]. Journal of Geophysical Research: Solid Earth, 1987, 92(B1): 357-368.
[15]	HARDEBECK J L, MICHAEL A J. Damped regional‐scale stress inversions: methodology and examples for southern California and the Coalinga aftershock sequence[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B11): 1-11.
[16]	VAVRYČUK V. Iterative joint inversion for stress and fault orientations from focal mechanisms[J]. Geophysical Journal International, 2014, 199(1): 69-77.
[17]	LAY T, WALLACE T C. Modern Global Seismology[M]. New York: Academic Press, 1995.
[18]	LUND B, SLUNGA R. Stress tensor inversion using detailed microearthquake information and stability constraints: Application to Ölfus in southwest Iceland[J]. Journal of Geophysical Research: Solid Earth, 1999, 104(B7): 14947-14964.
[19]	VAVRYČUK V, BOUCHAALA F, FISCHER T. High- resolution fault image from accurate locations and focal mechanisms of the 2008 swarm earthquakes in West Bohemia, Czech Republic[J]. Tectonophysics, 2013, 590: 189-195.
[20]	VAVRYČUK V. Principal earthquakes: theory and observations from the 2008 west bohemia swarm[C]//AGU Fall Meeting Abstracts, 2011, San Francisco.
[21]	VAVRYČUK V. Moment tensor decompositions revisited[J]. Journal of Seismology, 2015, 19(1): 231-252.

施引文献(16)

期刊类型引用(7)

1.	刘婷婷，阳润超，丁鹿阳，李新平，曾乐乐. 含非贯通节理花岗岩的力学特性与细观起裂机制研究. 岩石力学与工程学报. 2023(05): 1070-1082 . 百度学术
2.	罗亚琼，张超，李洁，卢霖，任中俊. 土石混合体大型三轴剪切变形特性及模拟方法. 水利水电技术(中英文). 2023(05): 168-176 . 百度学术
3.	蒋培林，丁书学，南华，乔静，刘江，田永超，李佳赛，李树杰. 中间主应力影响下加锚试样应力-应变曲线特征参数分析. 科学技术与工程. 2023(18): 7725-7733 . 百度学术
4.	戴俊，杨清清，张敏，蒋昊轩，王林涛，任一平. 微波照射下花岗岩单轴压缩损伤本构模型. 科学技术与工程. 2023(19): 8350-8357 . 百度学术
5.	刘兆阳，于开治，熊文彬. 围压作用下的泡沫铝特性研究. 科技与创新. 2023(15): 105-107+111 . 百度学术
6.	辛子朋，柴肇云，孙浩程，李天宇，刘新雨，段碧英. 砂质泥岩峰后破裂承载特征与块体分布规律研究. 岩土力学. 2023(08): 2369-2380 . 百度学术
7.	宋清蔚，朱万成，徐晓冬，张鹏海，陈承桢，刘溪鸽. 岩石破坏过程实时监测预警软件系统——搭建与初步应用. 金属矿山. 2022(10): 155-164 . 百度学术