Influences of critical fragment migration characteristics of lunar soil on drilling resistance
-
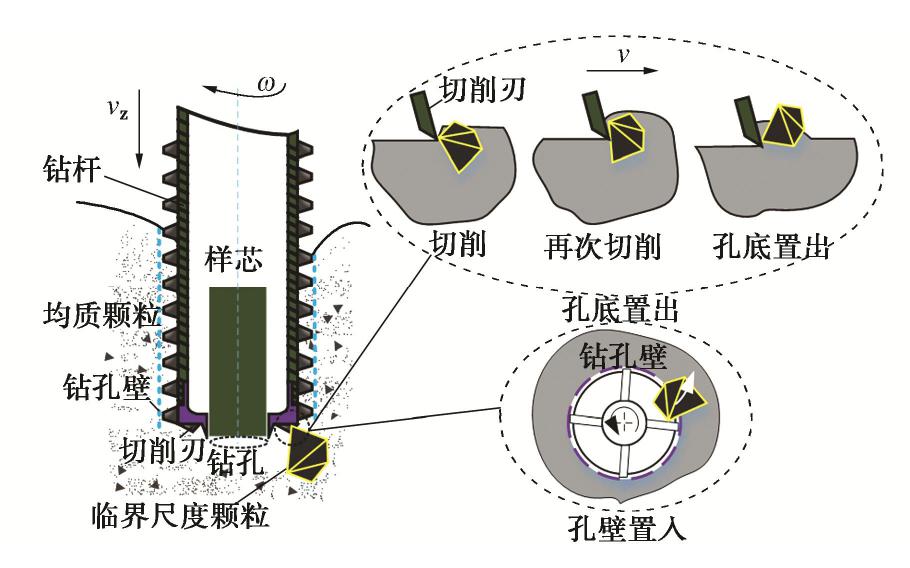
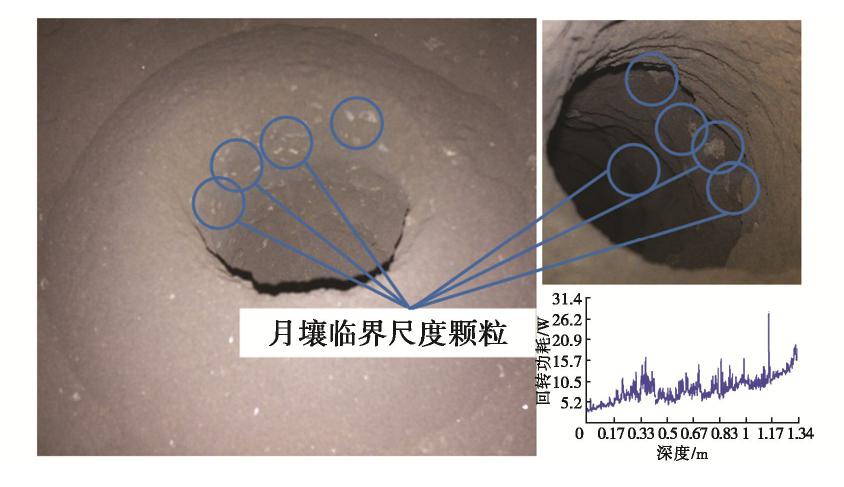
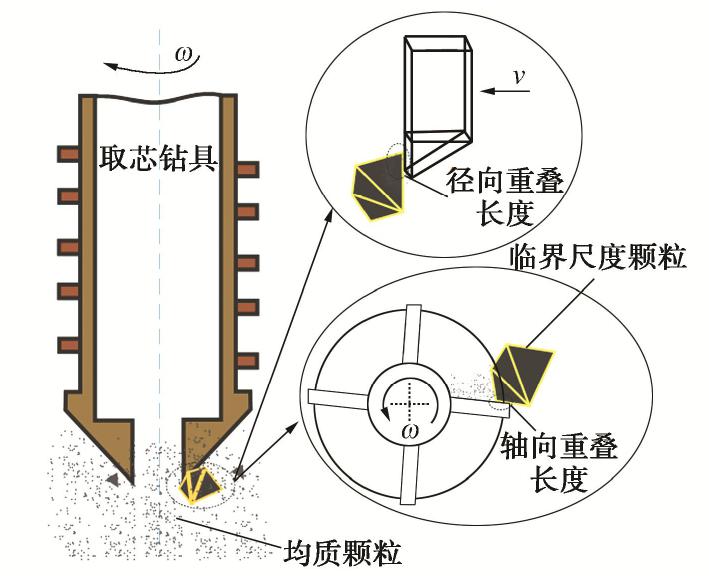
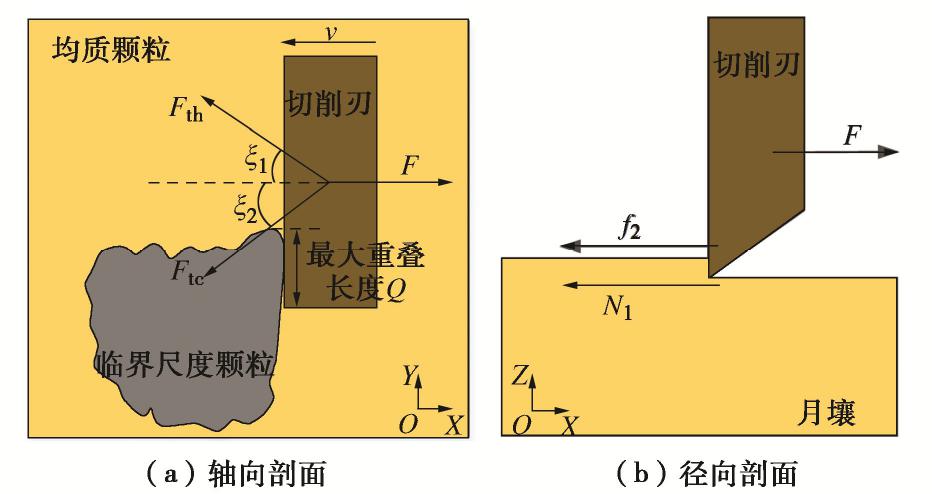
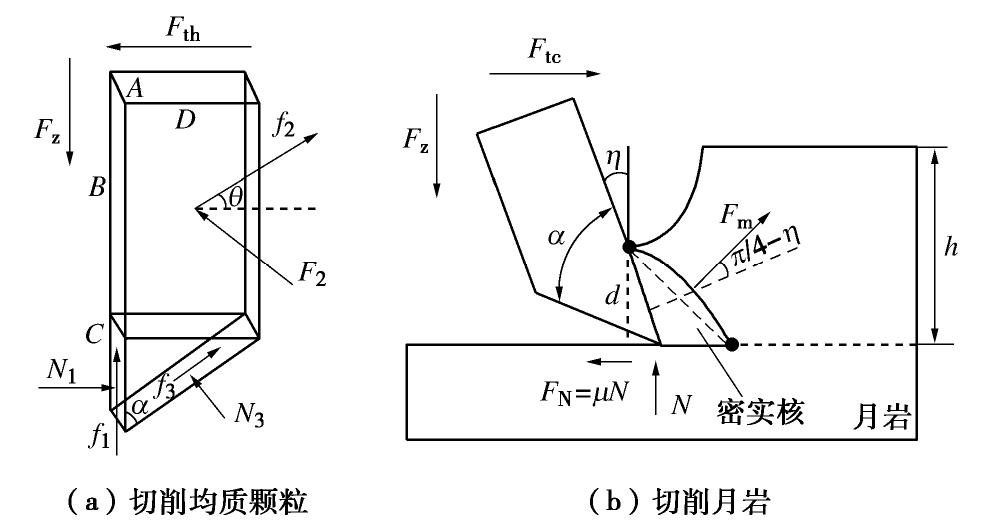
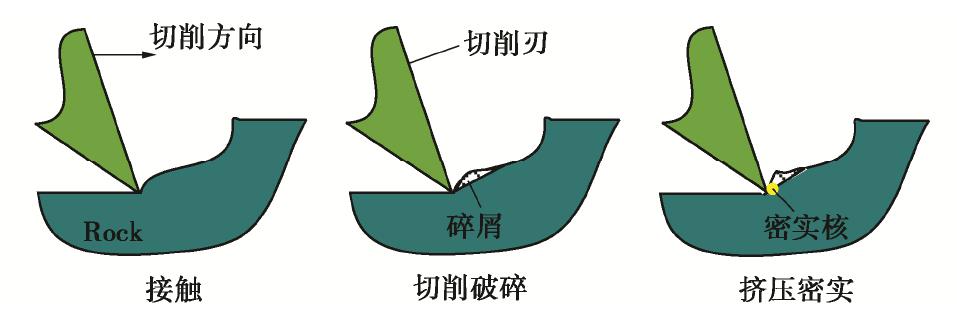
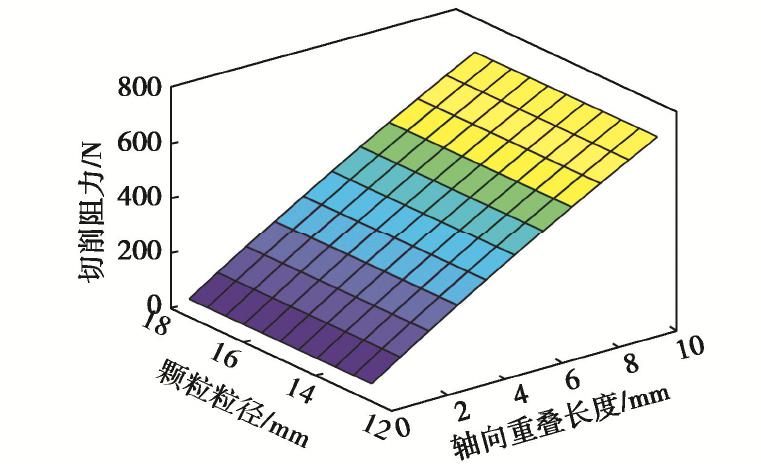
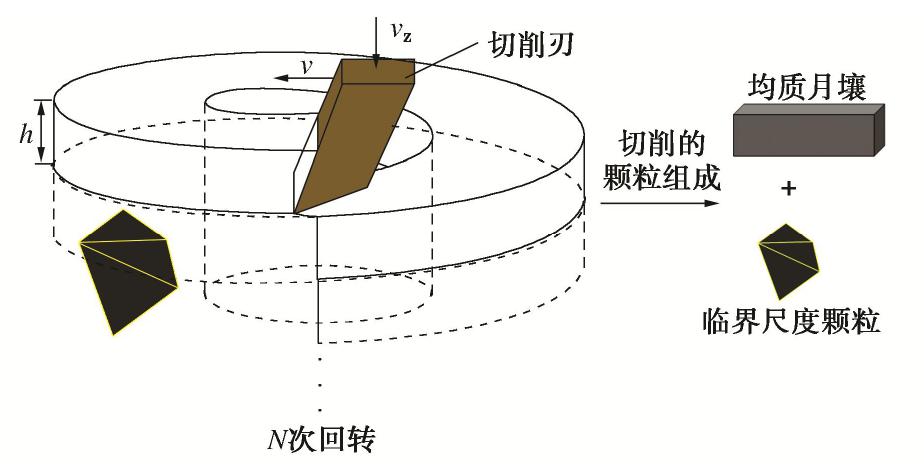
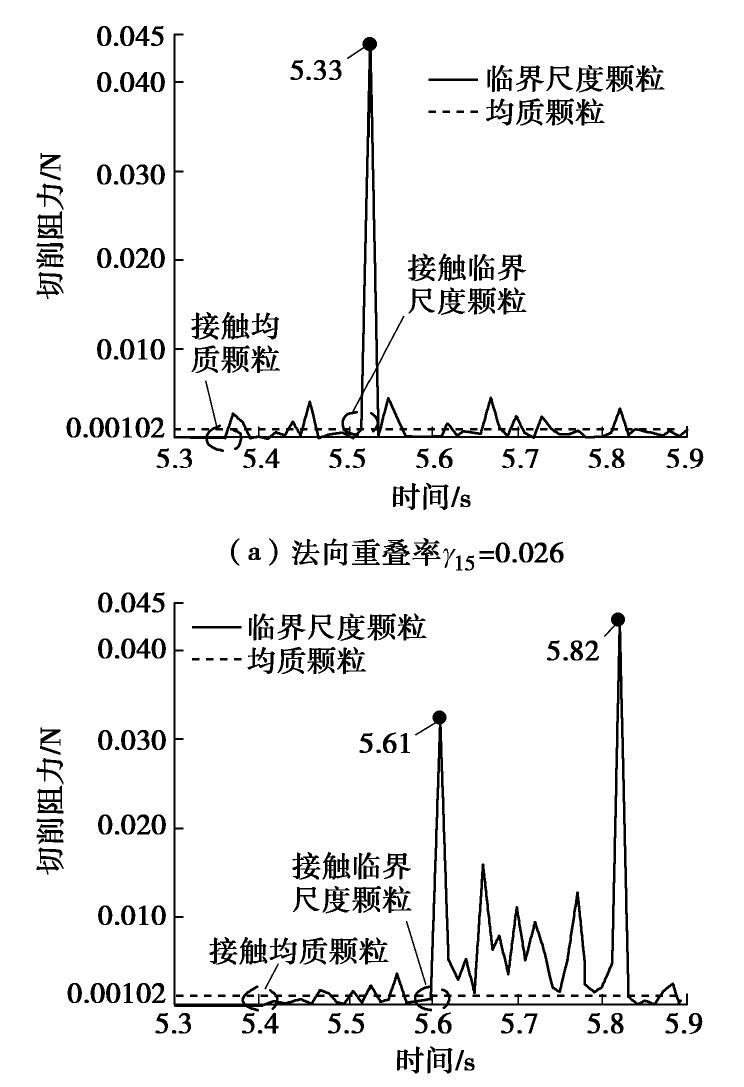
摘要: 临界尺度颗粒是指平均直径大于或等于钻头取芯孔直径的月球土壤颗粒,其广泛分布于月球次表层土壤中。在钻进过程中受到钻削作用,一部分临界尺度颗粒被从孔底置出,并被嵌入钻孔壁产生孔壁置入现象,从而增大了切削负载功耗；另一部分跟随钻具回转无法被取芯孔采集,从而增加了钻进失败的风险。通过建立月壤临界尺度颗粒切削模型,考虑临界尺度颗粒粒径及其与切削刃相互作用位置,对切削阻力的影响进行敏感度分析,得到位置的变化对切削阻力影响最明显。提出法向重叠率的概念,用以研究位置变化对临界尺度颗粒运移特性及切削阻力的影响关系。将切削刃的回转运动等效为直线运动,采用离散元方法验证法向重叠率对切削阻力的影响,得到法向重叠率与临界尺度颗粒孔底置出和孔壁置入现象之间的关系,以及对应的切削阻力时域变化曲线的特征。通过临界尺度颗粒运移特性模拟试验,得到法向重叠率与切削阻力呈同方向的线性关系,当临界尺度颗粒分别产生孔底置出和孔壁置入现象时,对应的切削阻力时域曲线特征分别为连续峰值和仅有一个峰值点。研究可为月球采样任务中的钻进工况参数识别提供理论依据。Abstract: The critical fragment refers to the lunar soil particles with average diameter greater than or equal to the diameter of coring bit hole, which is widely distributed in lunar subsurface soil. On one hand, due to the drilling effect in the drilling process, some of the critical fragments are placed from the bottom of the hole and embedded into the borehole wall to produce the hole wall insertion phenomenon, thus increasing consumption of the cutting load power. On the other hand, the others cannot be collected by the coring hole following the rotation of the drilling tool, thus increasing the risk of drilling failure. Firstly, the critical fragment cutting model for lunar soil is established, the particle size of the critical fragment and its interaction position with cutting edge are considered, the sensitivity of cutting resistance is analyzed, and it is obtained that the change of position has the most obvious influences on cutting resistance. Then, the concept of normal overlap ratio is put forward to study the influences of position change on the migration characteristics and cutting resistance of the critical fragment. The rotary motion of cutting edge is equivalent to the linear one, and the influences of normal overlap ratio on the cutting resistance are verified by the discrete element method, so as to obtain the relationship between the normal overlap ratio and the phenomenon of being placed from the bottom of the hole and embedded into the borehole wall to produce the hole wall insertion, as well as the characteristics of the corresponding time-domain change curve of cutting resistance. Finally, through the simulation tests on the migration characteristics of the critical fragment, it is found that the normal overlap ratio and cutting resistance have a linear relationship in the same direction. When the critical fragment produces the process of being placed from the bottom of the hole and embedded into the wall, the time-domain curve features of the corresponding cutting resistances are continuous peak points and only one peak point respectively. The above results may provide the theoretical basis for the parameter identification of drilling conditions in lunar sampling mission.
-
-
![]()
图 4 临界尺度颗粒与切削刃作用示意图
Figure 4. Schematic diagram of overlap of critical fragments and cutter
![]()
图 5 切削刃与月壤作用受力示意图
Figure 5. Schematic diagram of axial section forces on cutter and lunar soil interaction
![]()
图 8 固定钻进深度下的单刃切削阻力
Figure 8. Cutting resistances of fixed single edge at depth of drilling
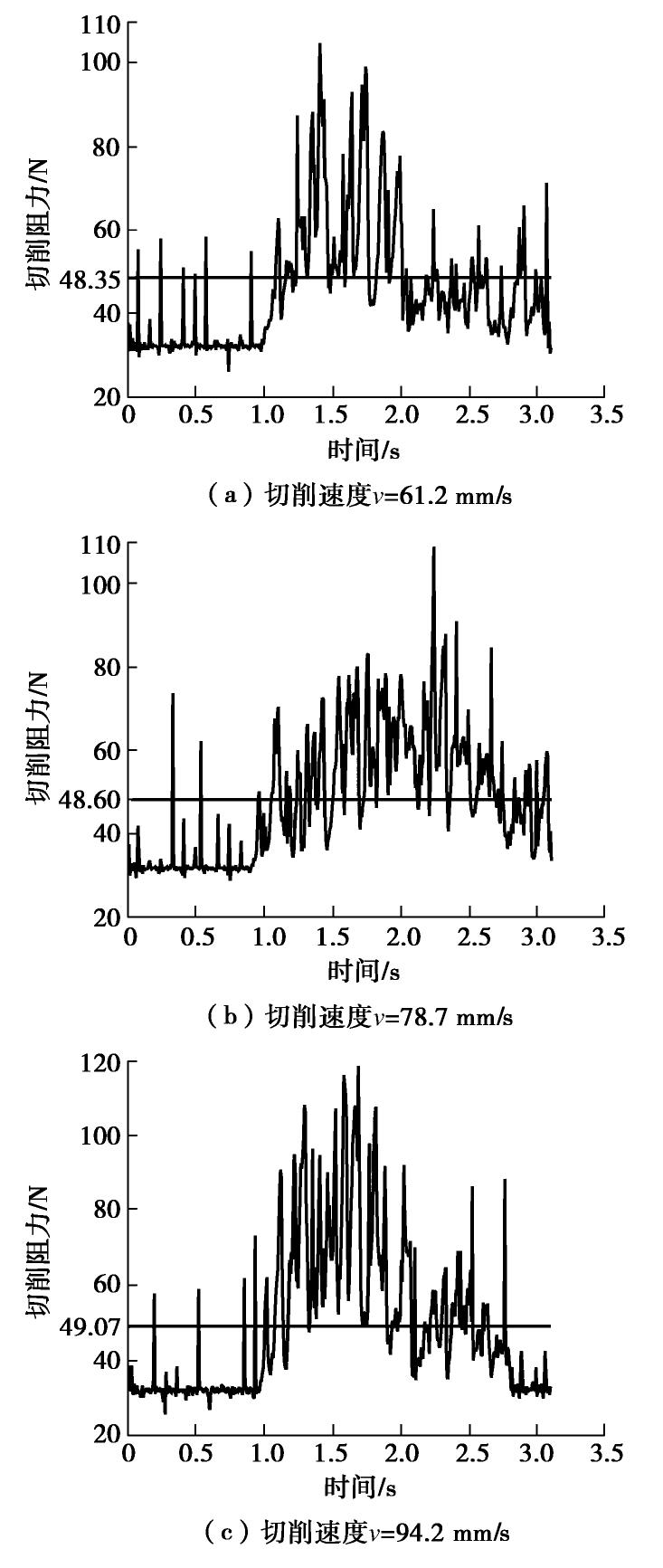
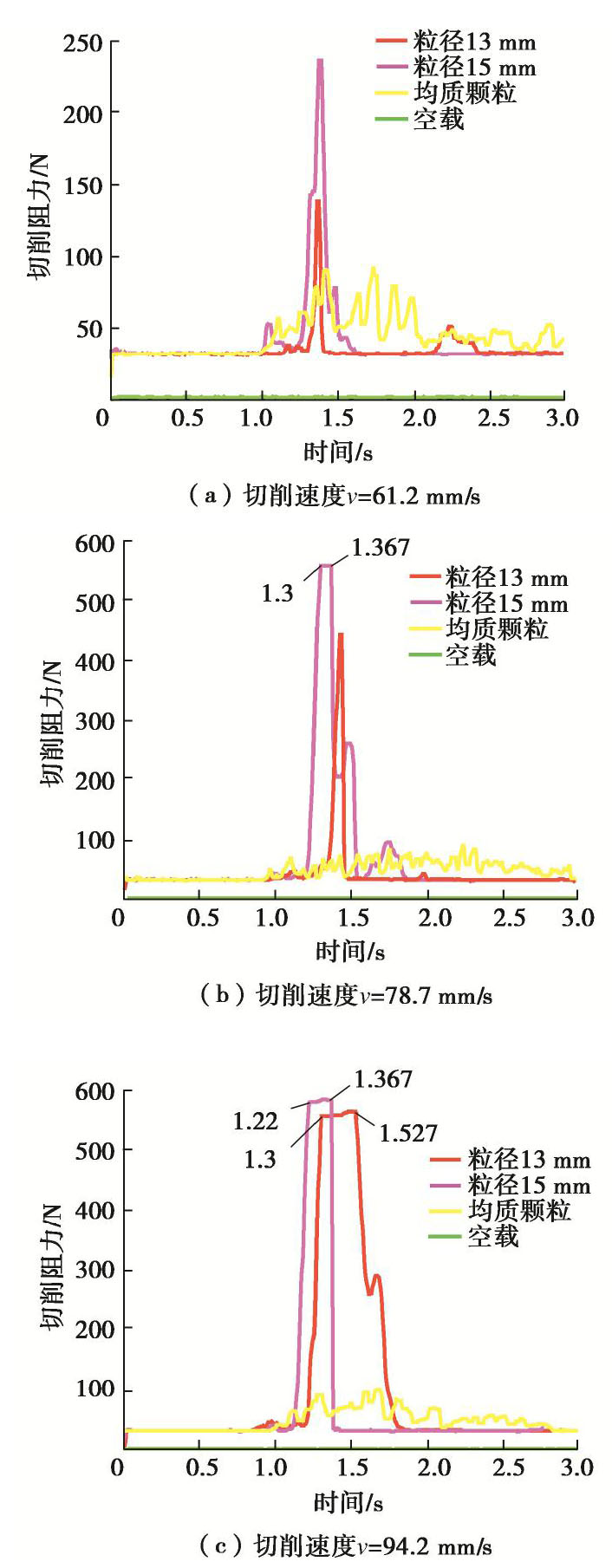
表 1 钻具回转速度与线速度换算表
Table 1 Conversion of rotary speed and linear speed of drilling tool
回转速度/rpm 60 80 100 120 线速度/(mm·s-1) 47.1 61.2 78.7 94.2 
下载: 导出CSV
表 2 仿真环境参数标定
Table 2 Parameter calibration of simulation environment
参数 数值 颗粒泊松比 0.35 均质颗粒半径/mm 1.0 临界尺度颗粒粒径/mm 15 颗粒密度/(kg·m-3) 2900 颗粒剪切模量/Pa 1×108 切削刃泊松比 0.3 切削刃密度/(kg·m-3) 7800 切削刃杨氏模量/Pa 7×107 切削深度/mm重力加速度/(m·s-2) 41.6 切削速度/(mm·s-1) 94.2 颗粒-颗粒恢复系数 0.1 颗粒-颗粒静摩擦系数 0.514 颗粒-颗粒动摩擦系数 0.1 颗粒-几何体恢复系数 0.2 颗粒-几何体静摩擦系数 0.3 颗粒-几何体动摩擦系数 0.1
下载: 导出CSV
表 3 试验制备均质月壤物理力学参数
Table 3 Physical and mechanical parameters of prepared homogeneous lunar soil
参数 密度/(g·cm-3) 泊松比 孔隙比 内摩擦角/(°) 数值 2.1 0.35 0.31 34.96
下载: 导出CSV
-
[1] 蒋明镜. 现代土力学研究的新视野——宏微观土力学[J]. 岩土工程学报, 2019, 41(2): 195-254. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm JIANG Ming-jing. New paradigm for modern soil mechanics: Geomechanics from micro to macro[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 195-254. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902002.htm
[2] 尹振宇, 许强, 胡伟. 考虑颗粒破碎效应的粒状材料本构研究：进展及发展[J]. 岩土工程学报, 2012, 34(12): 2170-2180. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201212006.htm YIN Zhen-yu, XU Qiang, HU Wei. Research on the constitutive properties of granular materials considering the effect of particle breakage: Progress and development[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(12): 2170-2180. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201212006.htm
[3] 唐钧跃, 全齐全, 姜生元, 等. 模拟月壤钻进力载建模及试验验证[J]. 机械工程学报, 2017, 53(7): 85-93. https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201707013.htm TANG Jun-yue, QUAN Qi-quan, JIANG Sheng-yuan, et al. Mechanics modeling and experimental validation for lunar regolith simulant drilling[J]. Journal of Mechanical Engineering, 2017, 53(7): 85-93. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXXB201707013.htm
[4] 郭汝坤, 冯春, 李战军, 等. 牙轮钻工作参数与岩体强度对应关系的理论分析与实验研究[J]. 岩土工程学报, 2016, 38(7): 1221-1229. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201607008.htm GUO Ru-kun, FENG Chun, LI Zhanjun, et al. Theoretical and experimental studies on relationship between working parameters of cone drill and rock strengths[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1221-1229. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201607008.htm
[5] 张宇, 陈善雄, 余飞, 等. 低应力水平下CAS-1模拟月壤力学特性试验研究[J]. 岩石力学与工程学报, 2015, 34(1): 174-181. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201501019.htm ZHANG Yu, CHEN Shan-xiong, YU Fei, et al. Esperimental study of mechanocal properties of lunar soil simulant CAS-1 under low stress[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(1): 174-181. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201501019.htm
[6] 李宁, 李骞, 宋玲. 基于回转切削的岩石力学参数获取新思路[J]. 岩石力学与工程学报, 2015, 34(2): 323-329. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201502013.htm LI Ning, LI Qian, SONG Ling. Acquiring mechanical parameters of rock basd on rotational cutting[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 323-329. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201502013.htm
[7] 刘泉声, 刘建平, 时凯, 等. 评价岩石脆性指标对滚刀破岩效率的影响[J]. 岩石力学与工程学报, 2016, 35(3): 498-510. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201603007.htm LIU Quan-sheng, LIU Jian-ping, SHI Kai, et al. Evaluation of rock brittleness indexes on rock fragmentation efficiency by disc cutter[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(3): 498-510. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201603007.htm
[8] DOSHVARPASSAND S, RICHARD T, MOSTOFI M. Effect of groove geometry and cutter in rock cutting[J]. Journal of Petroleum Science and Engineering, 2017, 151(10): 1-1.
[9] LI P, JIANG S Y, TANG D W, et al. Design and testing of coring bits on drilling lunar rock simulant[J]. Advances in Space Research, 2017, 59(4): 1057-1076.
[10] CHE D, ZHANG W Z, EHMANN K. Chip Formation and force responses in linear rock cutting: an experimental study[J]. Journal of Manufacturing Science and Engineering, 2017, 139(8): 1-12.
[11] DAGRAIN F, QUICKELBERGHE F V, TSHIBANGU J P. A new procedure to analyse the wear of cutting elements[C]//Eurock 2006, 2006, Belgium.
[12] 刘天喜, 魏承, 马亮, 等. 大颗粒岩块对月壤钻取过程的影响分析[J]. 岩土工程学报, 2014, 36(11): 2118-2126. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201411024.htm LIU Tian-xi, WEI Cheng, MA Liang, et al. Effect of large granular rocks on drilling process of lunar soils[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(11): 2118-2126. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201411024.htm
[13] 庞勇, 冯亚杰, 孙启臣, 等. 月壤大颗粒对钻进力载影响的仿真及试验研究[J]. 北京大学学报(自然科学版), 2019, 55(3): 397-404. https://www.cnki.com.cn/Article/CJFDTOTAL-BJDZ201903001.htm PANG Yong, FENG Ya-jie, SUN Qi-chen, et al. Simulation and experimental study on the effect of large granular rocks in lunar soil on drilling load[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2019, 55(3): 397-404. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BJDZ201903001.htm
[14] QIAN Y Q, XIAO L, YIN S, et al. The regolith properties of the Chang'e-5 landing region and the ground drilling experiments using lunar regolith simulants[J]. Elsevier Inc, 2020, 337(5): 113508-113521.
[15] TIAN Y, TANG B, YANG F, et al. Lunar critical fragment layer simulant identification using an impact method[J]. Acta Astronautica, 2020, 173(6): 294-302.
[16] 林呈祥, 凌道盛, 钟世英, 等. TJ-1模拟月壤颗粒几何特性[J]. 东北大学学报(自然科学版), 2016, 37(3): 451-456. https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX201603031.htm LIN Cheng-xiang, LING Dao-sheng, ZHONG Shi-ying, et al. Geometric characteristics of TJ-1 lunar soil simulant particles[J]. Journal of Northeastern University (Natural Science), 2016, 37(3): 451-456. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX201603031.htm
[17] 郑永春, 欧阳自远, 王世杰, 等. 月壤的物理和机械性质[J]. 矿物岩石, 2004, 24(4): 14-19. https://www.cnki.com.cn/Article/CJFDTOTAL-KWYS200404003.htm ZHENG Yong-chun, OUYANG Zi-yuan, WANG Shi-jie, et al. Physical and mechanical properties of lunar regolith[J]. Journal of Mineralogy and Petrology, 2004, 24(4): 14-19. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KWYS200404003.htm
[18] 胡伟, 孟建伟, 刘顺凯, 等. 单螺旋锚桩水平承载机理试验与理论研究[J]. 岩土工程学报, 2020, 42(1): 158-167. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202001025.htm HU Wei, MENG Jian-wei, LIU Shun-kai, et al. Experimental and theoretical researches on horizontal bearing mechansim of single screw anchor pile[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(1): 158-167. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202001025.htm
[19] WHEELER P, GODWIN R. Soil dynamics of single and multiple tines at speeds up to 20km/h[J]. Journal of Agricultural Engineering Research, 1996, 63(3): 243-249.
[20] LI P, JIANG S Y, TANG D W, et al. A PFC3D-based numerical simulation of cutting load for lunar rock simulant and experimental validation[J]. Advances in Space Research, 2017, 59(10): 2583-2599.
[21] 戴北冰, 杨峻, 刘锋涛, 等. 散粒土自然堆积的宏细观特征与形成机制[J]. 岩土工程学报, 2019, 41(增刊2): 57-60. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S2016.htm DAI Bei-bing, YANG Jun, LIU Feng-tao, et al. Macro- and micro-properties and formation mechanisms of granular piles[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S2): 57-60. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S2016.htm
[22] CARRIER W. Geotechnical Properties of Lunar Soil[R]. Lake Land: Lunar Geotechnical Institute, 2005.
[23] 田野, 陈萌萌, 杨飞, 等. 用于砂土层连续采样的柔性软袋式钻取采样技术研究[J]. 农业机械学报, 2018, 49(12): 246-252. https://www.cnki.com.cn/Article/CJFDTOTAL-NYJX201812030.htm TIAN Ye, CHEN Meng-meng, YANG Fei, et al. Technology of coring drill with flexible tube for sand layers continuous sampling[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(12): 246-252. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-NYJX201812030.htm
-
期刊类型引用(19)
1. 洪嘉伟，张彬，潘道明. 隧道注浆圈渗透系数对邻侧隧道的影响. 交通科技与管理. 2025(01): 147-151 . 
百度学术
2. 袁立刚，冷伍明，姜涌，朱铁环，安永林，岳健. 降雨对江底凹形纵坡隧道排水池区段的影响及排水报警方法. 铁道科学与工程学报. 2025(03): 1369-1382 . 百度学术
3. 陈云娟，王乐宁，周宗青，贾润枝，杨卓，罗平利，刘梦悦. 基于海底隧道衬砌孔隙水压力的涌水量预测方法及工程应用. 应用基础与工程科学学报. 2024(01): 288-300 . 百度学术
4. 韩智铭，闫科宇，王雪，朱正国，崔会敏. 有限地层三孔并行海底隧道渗流场解析研究. 铁道工程学报. 2024(01): 45-52 . 百度学术
5. 汤钰，王华宁，宋飞. 渗透各向异性地层中隧洞稳态渗流场的半解析预测模型. 力学季刊. 2024(02): 473-482 . 百度学术
6. 韩智铭，闫科宇，崔会敏，刘庆宽. 基于等效面积法的三孔并行海底隧道渗流场解析研究. 工程力学. 2024(S1): 112-116+149 . 百度学术
7. 高启程，姜启武，陈志杰，赖鹏安. 考虑损伤效应的隧道二维渗流场解析及涌水量预测. 人民长江. 2024(10): 197-204+211 . 百度学术
8. 李航达，杨广鹏，韩智铭. 多洞并行海底隧道最佳覆岩厚度变化规律研究. 石家庄铁道大学学报(自然科学版). 2024(03): 40-46 . 百度学术
9. 卢玉东，国金琦，程大伟，毛兴隆. 考虑固液二相互态特性的流固耦合模型. 中国公路学报. 2023(01): 58-69 . 百度学术
10. 张兵海，崔炜，张石磊，杜三林，邓检强，刘毅，朱银邦. 临近水库的隧洞二维渗流场解析解及工程应用研究. 水利水电技术(中英文). 2023(03): 126-134 . 百度学术
11. 马少坤，陈彩洁，段智博，刘莹. 基于镜像法的有限含水层内隧道渗流场解析解及其验证. 工程力学. 2023(05): 172-181 . 百度学术
12. 胡红星. 富水破碎带地层TBM隧道围岩稳定性研究. 科技与创新. 2023(17): 39-44 . 百度学术
13. 乔彤，周建，张天骄，蒋熠诚. 考虑渗透各向异性的水下非圆形隧道渗流场解析. 工程科学与技术. 2023(05): 109-117 . 百度学术
14. 徐锋. 隧道穿越富水断层多场耦合特征分析及施工控制技术. 铁道建筑技术. 2022(05): 148-152 . 百度学术
15. 金波，胡明，方棋洪. 考虑渗流效应的深埋海底隧道围岩与衬砌结构应力场研究. 力学学报. 2022(05): 1322-1330 . 百度学术
16. 郑培超，闫科宇，王雪，韩智铭. 海底隧道三孔并行渗流场泄压规律研究. 现代隧道技术. 2022(S1): 353-362 . 百度学术
17. 王昊，刘广，王静峰，张兴其，浦玉炳，严中，丁兆东. 少荃湖湖底隧道工程渗流场特性分析. 人民珠江. 2021(10): 63-67 . 百度学术
18. 李沣展，岳健，安永林，孙超杰，谭仁华. 河底浅埋小净距隧道施工期渗流性状分析. 湖南科技大学学报(自然科学版). 2021(04): 47-54 . 百度学术
19. 叶亮，丁文其，张清照. 地下水对岩石隧道衬砌作用计算方法的探讨. 现代隧道技术. 2021(S1): 326-335 . 百度学术
其他类型引用(13)
计量
- 文章访问数: 351
- HTML全文浏览量: 28
- PDF下载量: 114
- 被引次数: 32
