施工期同步注浆影响下盾构隧道管片纵向上浮特征分析与应用

黄旭民; 黄林冲; 梁禹

doi:10.11779/CJGE202109015

施工期同步注浆影响下盾构隧道管片纵向上浮特征分析与应用 English Version

中山大学航空航天学院,广东　深圳　518107

基金项目:

国家自然科学基金项目 51708564

深圳市自然科学基金可持续发展科技专项项目 KCXFZ20200121151603895

深圳市自然科学基金可持续发展科技专项项目 KCXFZ20201221173207020

深圳市自然科学基金面上项目 JCYJ20190807162401662

详细信息

作者简介:
黄旭民(1996— ),男,硕士,主要从事地下工程与隧道结构安全控制的科研工作。E-mail：huangxm67@mail2.sysu.edu.cn

通讯作者:
梁禹, E-mail：liangyu25@mail.sysu.edu.cn

中图分类号: TU431
计量
- 文章访问数: 308
- HTML全文浏览量: 35
- PDF下载量: 159
出版历程
- 收稿日期: 2021-01-14
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-08-31

Analysis and application of longitudinal uplift characteristics of segments of shield tunnels affected by synchronous grouting during construction period

School of Aeronautics and Astronautics, Sun Yat-sen University, Shenzhen 518107, China

摘要

摘要: 同步注浆是盾构施工中的关键工序,浆液压力产生的上浮力是导致施工期管片上浮的重要因素。在未凝固区长度范围内,上浮力逐渐衰减,上覆土体基床系数逐渐增加。针对该类复杂力学问题,基于弹性地基梁矩阵传递法理论,综合考虑了浆液黏度时变性、上覆土体基床系数各异性以及施工荷载步叠加效应的影响,提出了一种施工期盾构隧道管片上浮预测方法。将现场实测数据和模型计算结果进行比较,验证了计算模型的合理性。研究表明：在施工过程中,同步注浆引起的隧道上浮量最大处一般在距盾尾6～7环附近,远离盾构机40环以后影响较小；浆液黏度随时间增加使浆液流动性和周围土体渗透性降低,浆液压力衰减幅值减小,导致浆液未凝固区更长和上浮力更大。主要解决了复杂变基床系数条件下两类弹性地基梁计算方法耦合和考虑多因素影响下上浮量精细化预测的问题,其研究成果可为后续类似盾构隧道上浮量的控制提供参考。
- 管片上浮 /
- 基床系数 /
- 弹性地基梁 /
- 矩阵传递法 /
- 浆液黏度时变性
Abstract: The synchronous grouting is a key procedure during the construction of shield tunnels, and the uplift pressure generated by the grout is an important factor leading to the uplift of segments. Within the length of unconsolidated zone, the uplift pressure decreases and the foundation coefficient of the overlying soil increases gradually. Aiming at this kind of complex mechanical problem, a method for predicting the uplift of segments of shield tunnels during the construction period is proposed based on the theory of the matrix transfer method for elastic foundation beams. The influences of the time-varying property of grout viscosity, the variety of the foundation coefficient and the superimposed effect of construction load step are considered. The proposed model is well verified by the comparison between the theoretical results and the field test data. The results show that the maximum uplift of segments caused by the synchronous grouting is generally 6~7 rings away from the shield tail, and the influences are small beyond 40 rings. The time-varying property of grout viscosity affects the longitudinal distribution of unconsolidated zone and the uplift pressure. The grout viscosity increasing with time will decrease the grout fluidity and the permeability of surrounding soil. Therefore, it leads to the decrease of grout pressure which causes a larger uplift pressure and a longer length of unconsolidated zone. The coupling calculation of two kinds of elastic foundation beams under the complex variable foundation coefficient and the fine prediction for uplift of segments under the influences of multiple factors are solved. The research results can provide a reference for the subsequent control for the uplift of segments of the similar shield tunnels.
- segment uplift /
- foundation coefficient /
- elastic foundation beam /
- matrix transfer method /
- time-varying property of grout viscosity

HTML全文

0. 引言

近年来,盾构法应用越来越广泛,尤其在跨江隧道和城市地铁建设中。但是随着大直径盾构隧道的广泛应用,施工期管片上浮问题普遍而突出,过大的上浮量会导致管片错台、环缝张开、环间螺栓剪断和渗漏水等安全事故的发生,严重影响隧道成型质量。因此为了保证隧道施工与运营的安全,有必要对盾构隧道施工期管片的上浮机理进行研究,以及时采取科学合理的应对性措施。

盾构隧道的上浮问题是一个复杂的三维力学问题^[1],对于其上浮的原因,已有研究^[2]表明一般需要具备两大必要条件：①管片上浮变形发生的空间,②引起管片上浮的力。国内外学者从横向和纵向上分别对施工期盾构隧道的上浮问题进行研究,且已取得一定的成果。盾构隧道横向（局部）上浮机理的理论研究日益趋向成熟,主要包括均质圆环法^[3]、修正惯用法^[4-5]、多铰圆环法^[6]、梁-弹簧模型法^[7]、梁–接头模型法^[8]等。近年来盾构隧道纵向性能的研究受到越来越多的关注,但其研究目前尚处于起步阶段,主要有小泉淳^[7]提出的纵向梁–弹簧模型和志波尤纪夫^[9]提出的纵向等效连续化梁模型,之后的学者基于这两种理论做了大量的工作,叶飞等^[10]基于等效连续梁理论,将隧道和土体的相互作用等效为土弹簧,研究了同步注浆产生的不同形式上浮力作用下隧道结构的纵向变形特性。但是该模型没有考虑同步注浆过程中浆液硬化的时变性和上覆土体基床系数的各异性。朱令等^[11]、杨方勤^[12]、舒瑶等^[13]等考虑了同步注浆过程中浆液黏度时变性及上覆土体基床系数各异性的影响,但需要通过有限元数值模拟实现,难以被施工和设计人员接受及应用。

在前人研究的基础上,考虑浆液黏度时变性、上覆土体基床系数各异性以及施工步荷载叠加效应的影响,基于弹性地基梁的矩阵传递法理论,建立施工期盾构隧道纵向上浮分析模型,并进行了试验验证。

1. 隧道纵向上浮模型的构建

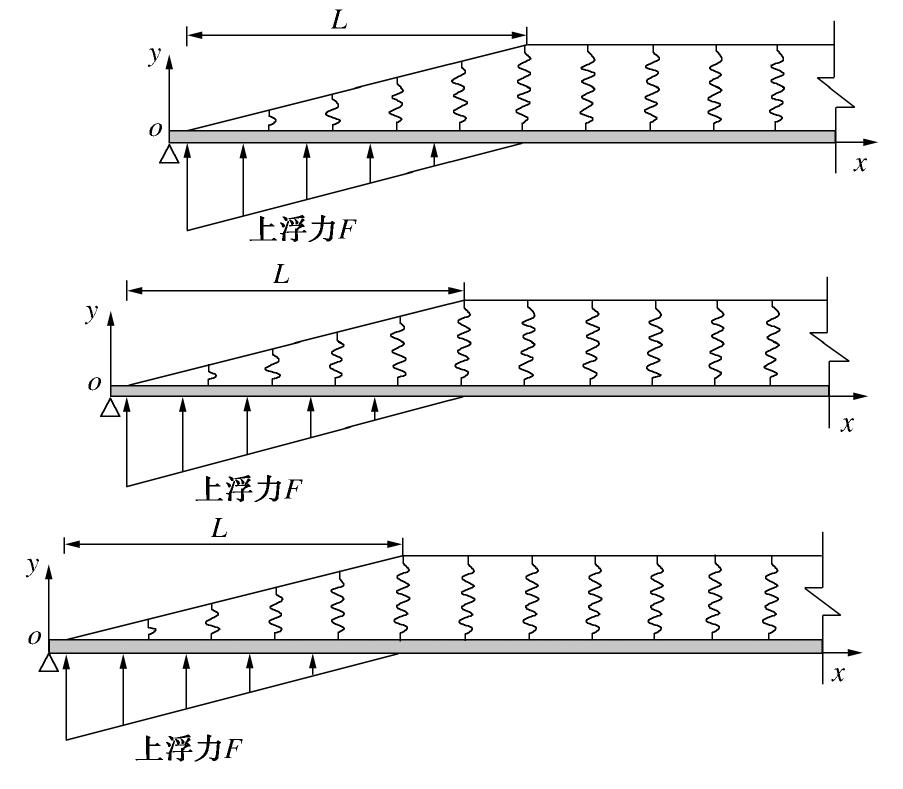
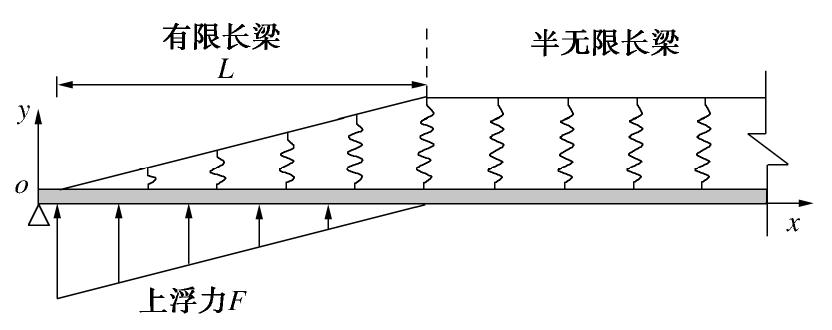
在盾尾进行同步注浆时,盾构隧道管片的受力为一个复杂的三维问题,涉及到地层-浆液-管片的相互作用,但是目前大多数的纵向分析都不考虑横向变形的影响,将隧道的三维受力简化为纵向的一维问题进行求解,最为经典的是日本学者志波由纪夫提出的纵向等效连续梁模型,由于该模型概念清楚、计算简单,近年来被广泛应用,本文的隧道纵向上浮模型的也是在等效连续梁模型的基础上构建,如图1所示。该模型可以分成两部分,第一部分为弹性地基上长度为L的有限长梁,在该段长度范围内,鉴于浆液压力的耗散和浆液黏度的时变特性^[14],假定上浮力呈现出三角形线性变化。随着浆液的逐渐硬化,上覆土体基床系数也从零逐渐增大,最后在距盾尾约为L处趋于一个稳定的值K,一般认为在该段范围内,基床系数近似于三角形线性变化。浆液未凝固区长度L根据隧道受到上浮力作用范围来确定。第二部分为离盾尾更远的弹性地基上的半无限长梁^[15-16],该段起点为距盾尾为L处,从该处起认为浆液固结硬化完成,因此基床系数不再发生变化,此外浆液压力已耗散至零,半无限长梁不受上浮力的作用。弹性地基有限长梁的左端认为是铰接以模拟盾尾处对管片的约束^[12],半无限长梁右端无穷远处变形、内力为零。有限长梁和半无限长梁在x=L处内力、变形连续,基于上述边界条件和矩阵传递法理论,求解上述耦合梁模型的内力和变形。

图 1 盾构隧道纵向上浮分析模型

Figure 1. Longitudinal uplift analysis model for shield tunnel

下载: 全尺寸图片幻灯片

盾构隧道的施工为一个动态的过程,随着盾构机的向前掘进一环,则同步注浆产生的上浮力向前移动一环,地基基床系数变化区间也向前移动一环。如此循环往复可模拟盾构机不断向前开挖的过程。施工步示意图如图2所示。

图 2 施工动态示意图

Figure 2. Diagram of dynamic construction

下载: 全尺寸图片幻灯片

2. 模型参数确定

2.1 等效地层抗力系数

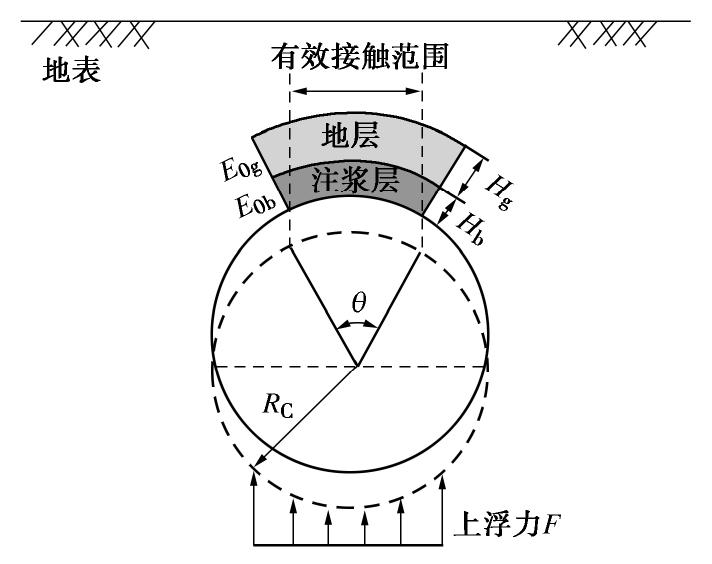
假定盾构隧道同步注浆材料及地层为弹性体,半无限长梁区域中的等效地层抗力系数示意图如图3所示。

图 3 等效地层抗力系数示意图

Figure 3. Stiffness coefficient of equivalent stratigraphic spring

下载: 全尺寸图片幻灯片

利用Muir Wood理论解^[17],计算注浆层与地层共同作用下的等效地层抗力系数：

$k = \frac{3 E_{0}}{(1 + ν) (5 - 6 v) R c}$ ,

(1)

$\begin{matrix} E_{0} = | - \frac{1}{D_{c} + 2 H \tan θ} + \frac{1}{D_{c}} | / [\frac{1}{E_{0b}} (- \frac{1}{D_{c} + 2 H_{b} \tan θ} + \frac{1}{D_{c}}) + \\ \frac{1}{E_{0g}} (- \frac{1}{D_{c} + 2 H_{g} \tan θ} + \frac{1}{D_{c} + 2 H_{b} \tan θ})] \end{matrix}$ ,

(2)

式中, $ν$ 为泊松比, $R_{c}$ 为管片形心线的半径, $D_{c}$ 为管片形心线的直径, $D_{0}$ 为管片外径, $E_{0}$ 为考虑同步注浆影响的等效地层变形模量, $E_{ob}$ 为壁后注浆层的变形模量, $E_{og}$ 为靠近注浆层的地层变形模量, $H$ 为注浆影响范围, $H_{b}$ 为同步注浆层的厚度, $H_{g}$ 为影响范围内地层的厚度, $θ$ 为荷载的分布宽度（一般取值30°）。

2.2 等效抗弯刚度

等效刚度法将每环衬砌环视为均质圆环,在纵向上基于刚度等效的思想把由管片和接头构成的盾构等效为具有相同结构刚度和特性的均质连续梁,其等效刚度大小^[18-19]]为

$E I_{eq} = \frac{\cos^{3} φ}{\cos φ + (\frac{π}{2} + φ) \sin φ} E_{c} I_{c}$ ,

(3)

$φ + \cot φ = π (\frac{1}{2} + \frac{n K_{b} l}{E_{c} A_{c}})$ 。

(4)

式中 $φ$ 为弯曲后中性轴的位置角； $K_{b}$ 为连接螺栓的线刚度, $K_{b} = E_{b} A_{b} / l_{b}$ , $E_{b}$ 为螺栓弹性模量, $A_{b}$ 为螺栓横截面积, $l_{b}$ 为螺栓计算长度, $n$ 为环间连接螺栓个数； $I_{c}$ 为隧道纵向惯性矩； $E_{c}$ 为管片弹性模量； $A_{c}$ 为隧道横截面面积； $l_{c}$ 为相邻两管片环中心线间的距离,其大小近似于管片环宽 $B$ 。

2.3 浆液未凝固区长度

同步注浆中浆液的凝固硬化为浆液压力逐渐耗散的复杂物理—化学过程,等效连续梁模型中浆液未凝固区长度主要和同步注浆工艺、浆液性质、地层特性以及注浆压力等因素有关。以往的研究^[11-12,15]中,浆液未凝固区的长度取值多基于现场的经验,并未给出合理的取值依据。梁禹等^[14]考虑浆液压力耗散、黏度时变性和地层特性等的影响,得到盾构隧道纵向浆液压力分布规律。浆液纵向扩散的最远距离可表征为浆液未凝固区长度,可表示为

$L = \frac{P_{G 0}}{B}$ ,

(5)

$P_{G 0} (t) = P_{0} - \frac{2 G}{r} \frac{1}{1 - ν} \frac{n_{i} - n_{e}}{1 - n_{i}} x (t)$ 。

(6)

式中 $G$ 为围岩土体剪切模量； $r$ 为围岩扰动层厚度； $ν$ 为扰动层泊松比； $n_{i}$ 为浆液孔隙比； $n_{e}$ 为浆液凝固硬化后浆饼孔隙率；通过室内试验获得, $P_{0}$ 为初始注浆压力, $P_{G0}$ 为考虑浆液压力耗散效应的初始浆液压力。 $x (t)$ 为浆饼的厚度,浆饼的厚度通过以下浆液固结方程求得

$(\frac{x}{k} + \frac{F}{k_{s} (t)}) \frac{d x}{d t} + C x = D h_{0}$ ,

(7)

式中, $x$ 为浆饼厚度, $F$ , $C$ , $D$ 为与隧道和浆液特性相关的系数, $k$ 为浆饼的渗透系数, $k_{s} (t)$ 为浆液向地层的渗透系数。考虑浆液黏度时变性影响时, $k_{s} (t)$ 可表示为

$k_{s} (t) = \frac{k_{w}}{β_{0}} e^{- ξ t}$ ,

(8)

式中, $β_{0}$ 为浆液初始黏度与水的黏度比, $β_{0} = u_{0} / u_{w}$ 。 $k_{w}$ 为水在地层中的渗透系数, $ξ$ 为跟浆液孔隙率相关的参数,通过室内试验获得。

2.4 浆液最大上浮力

最大上浮力取值为浆液压力及管片自重等荷载的合力,叶飞等^[10]提出了上浮力的分布形式近似为扇形分布。衬砌环受压密注浆作用,注浆浆液由于重力作用在管片下方聚集,形成较大的集中力或分布力,压密阶段注浆压力形成的向上的合力：

$F = \int_{- θ}^{θ} B P R_{0} \cos α d α = 2 B P R_{0} \sin θ (0 \leq θ \leq \frac{π}{2})$ 。

(9)

式中 $B$ 为浆液压力作用宽度,一般取1 m； $P$ 为该处管片所受浆液压力平均值； $R_{0}$ 为管片外径； $θ$ 为注浆浆液泡分布区域边界与竖向的夹角,一般取 $π / 2$ 。

3. 基于矩阵传递法的模型求解

将施工期的盾构隧道纵向上浮模型在x=L处分成两部分,左边为基床系数线性变化的有限长梁,梁的左端视为铰接,受线性荷载作用。右边为不受上浮力作用、基床系数固定的半无限长梁。对于这类复杂变基床系数的耦合弹性地基梁问题,目前的研究多基于有限元数值模拟手段对其进行求解,还没有形成更具体的理论对其进行分析。本章基于矩阵传递法理论^[20]对变基床系数条件下的弹性地基梁问题求解,克服了这两类地基梁计算方法不相同的困难,力学概念清晰、明确。

刘庆潭等^[20]通过拉普拉斯变换得到初参数解的形式：

(10)

式中, $v$ 为挠度, $θ$ 为转角, $M$ 为弯矩, $Q$ 为剪力, $K$ 为基床系数, $q$ 为线性荷载初值, $Δ q / Δ L$ 为线性荷载斜率。 $φ_{1}$ , $φ_{2}$ , $φ_{3}$ , $φ_{4}$ 为双曲函数和三角函数的组合形式,表示以下形式：

$\begin{array}{l} φ_{1} = c o h (β x) \cos (β x), \\ φ_{2} = c o h (β x) \sin (β x) + \sinh (β x) \cos (β x), \\ φ_{3} = c o h (β x) \cos (β x), \\ φ_{4} = c o h (β x) \sin (β x) - \sinh (β x) \cos (β x), \end{array}}$

(11)

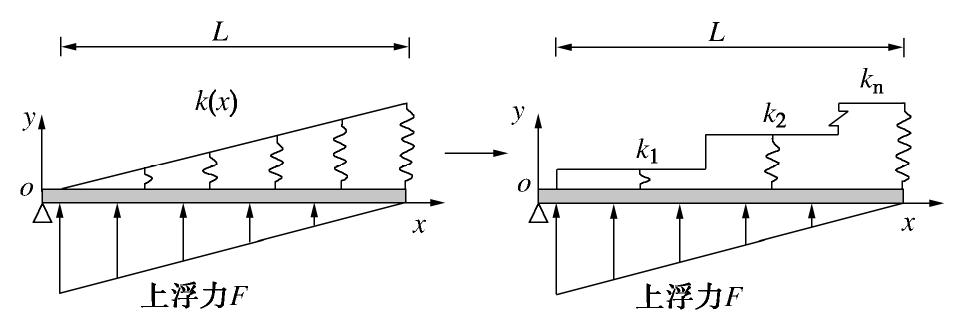
式中, $β$ 为地基梁特征系数,与地基梁抗弯刚度和基床系数有关。这种初参数解的形式也称为矩阵传递法,该方法对处理弹性地基上有限长梁的问题具有十分明显的优势。为了接下来方便计算,令式（11）的传递矩阵为 $T$ ,荷载影响项矩阵为 $F q$ 。

分析左半段弹性地基梁有限长梁变基床系数问题时,基于面积等效的思想将线性变化的三角形地基等效成若干段如图4所示,有限长梁左端的约束视为铰接,因此4个初参数的 $w_{0}$ , $M_{0}$ 被指定,剩下两个初参数 $θ_{0}$ , $Q_{0}$ 待求,参数的传递从左边铰接端开始,矩阵传递的过程可表示为

图 4 三角形基床转化为阶梯形基床

Figure 4. Conversion of triangular subgrade bed into stepped one

下载: 全尺寸图片幻灯片

$\begin{array}{l} S_{1} = T_{0} S_{0} + F q_{0}, \\ S_{2} = T_{1} S_{1} + F q_{1}, \\ S_{3} = T_{2} S_{2} + F q_{2}, \\ ... \\ S_{L} = T_{L - 1} S_{L - 1} + F q_{L - 1}, \end{array}}$

(12)

式中,S_n为第n段梁右端的内力矩阵,T_n-1为第n段梁的传递矩阵,Fq_n-1为第n段梁的荷载附加项矩阵。

从式（12）可以看出, $x = L$ 处的变形及内力可以表示为 $θ (0)$ , $Q (0)$ 的线性表达,再结合半无限长梁的无穷远端的边界条件就可以求解出 $θ (0)$ , $Q (0)$ 。结合式（11）,半无限长梁任意处的竖向位移可表示为

$\begin{array}{l} v = φ_{1} w_{L} - \frac{1}{2 β} φ_{2} θ_{L} - \frac{2 β^{2}}{K} φ_{3} M_{L} - \frac{β}{K} φ_{4} Q_{L} + \\ \frac{q}{K} (1 - φ_{1}) + \frac{Δ q}{K Δ L} (x - \frac{φ_{2}}{2 β}) \end{array}$ 。

(13)

引入4个衰减函数：

$\begin{array}{l} W_{1} = e^{- β x} \cos (β x), \\ W_{2} = e^{- β x} (\sin (β x) - \cos (β x)), \\ W_{3} = e^{- β x} \sin (β x), \\ W_{4} = e^{- β x} (\sin (β x) + \cos (β x)), \end{array}}$

(14)

4个增长函数：

$\begin{array}{l} U_{1} = e^{β x} \cos (β x), \\ U_{2} = e^{β x} (\sin (β x) - \cos (β x)), \\ U_{3} = e^{β x} \sin (β x), \\ U_{4} = e^{β x} (\sin (β x) + \cos (β x)), \end{array}}$

(15)

衰减函数、增长函数具有以下特性：

$\begin{array}{l} W (x = + \infty) = 0, \\ U (x = + \infty) = \infty 。 \end{array}}$

(16)

同时 $φ_{1}$ , $φ_{2}$ , $φ_{3}$ , $φ_{4}$ 和衰减函数、增长函数之间有着如下的关系：

$\begin{array}{l} φ_{1} = \frac{U_{1}}{2} + \frac{W_{1}}{2}, \\ φ_{2} = \frac{U_{4}}{2} + \frac{W_{2}}{2}, \\ φ_{3} = \frac{U_{3}}{2} - \frac{W_{3}}{2}, \\ φ_{4} = \frac{W_{4}}{2} + \frac{U_{2}}{2} 。 \end{array}}$

(17)

将式（17）代入式（13）并且结合无穷远处衰减函数的性质可以得到

$\begin{array}{l} v = \frac{U_{1}}{2} v_{L} - \frac{U_{4}}{4 β} θ_{L} - \frac{β^{2} U_{3}}{K} M_{L} - \frac{β U_{2}}{2 K} Q_{L} + \\ \frac{q}{K} (1 - \frac{U_{1}}{2}) + \frac{Δ q}{Δ L K} (x - \frac{U_{4}}{4 β}) \end{array}$ 。

(18)

将 $U_{1}$ , $U_{2}$ , $U_{3}$ , $U_{4}$ 按式（11）的形式代入式（18）可以得

$\begin{array}{l} v = e^{β x} (S_{1} \cos β x + S_{2} \sin β x) + \frac{q}{K} + \frac{Δ q}{Δ L K} x, \\ S_{1} = \frac{v_{L}}{2} - \frac{θ_{L}}{4 β} + \frac{β}{2 K} Q_{L} - \frac{q}{2 K} - \frac{Δ q}{4 K β Δ L}, \\ S_{2} = - \frac{θ_{L}}{4 β} - \frac{β^{2} M_{L}}{K} - \frac{β Q_{L}}{2 K} - \frac{Δ q}{4 K β Δ L} 。 \end{array}}$

(19)

由于半无限长弹性地基梁段不受上浮力作用,因此式（19）的 $q$ , $Δ q / Δ L$ 的值为0。根据半无限长梁的性质可知无穷远处的挠度 $v$ 等于0,由于 $x \to + \infty$ , $\sin α x$ 和 $\cos α x$ 不恒为0,所以要使式（19）中 $v$ 的收敛为0,必须使 $\sin α x$ 和 $\cos α x$ 的系数为零。因此可以得到 $S_{1}$ 和 $S_{2}$ ,可表示为

$\begin{matrix} \frac{v_{L}}{2} - \frac{θ_{L}}{4 β} + \frac{β}{2 K} Q_{L} = \frac{q}{2 K} + \frac{Δ q}{4 K β Δ L} - \\ \frac{θ_{L}}{4 β} - \frac{β^{2} M_{L}}{K} - \frac{β Q_{L}}{2 K} = \frac{Δ q}{4 K β Δ L} \end{matrix}$ 。

(20)

式（20）为半无限长梁的边界条件,从式（10）知 $v_{L}$ , $θ_{L}$ , $M_{L}$ , $Q_{L}$ 为 $θ_{0}$ , $Q_{0}$ 的线性表达,所以求解上述二元一次方程组即可求解出 $θ_{0}$ , $Q_{0}$ ,从而可以得到各段梁的变形和内力理论解。

4. 工程验证

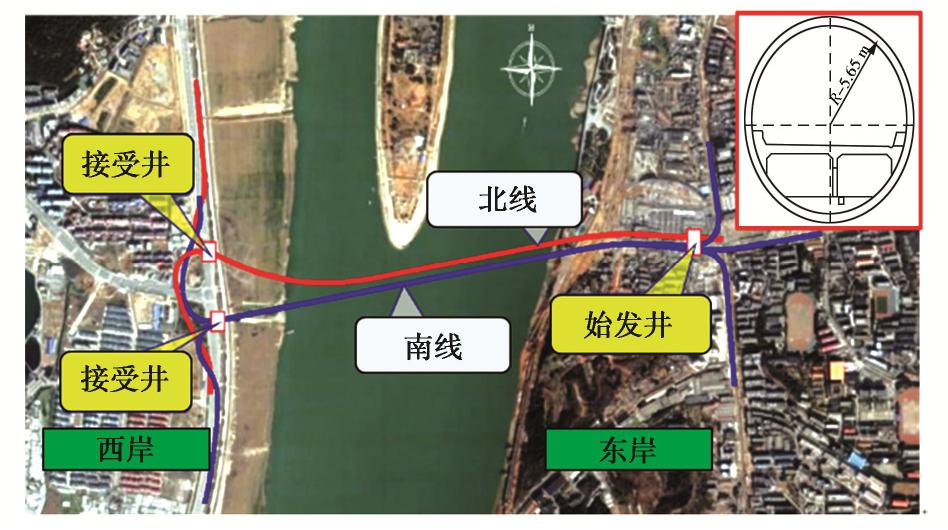
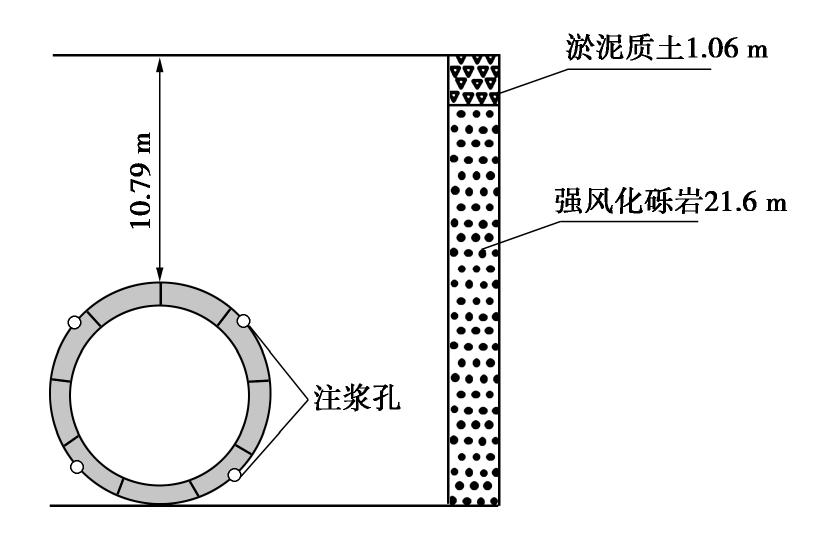
长沙市南湖路隧道采用盾构法施工,盾构隧道埋深为10.79 m,采用双管单层形式,分为南北两线穿越湘江,工程位置示意图如图5所示。选取的典型横断面如图6所示,地层从上到下依次为淤泥质土、强风化砾岩。

图 5 越江隧道工程位置图

Figure 5. Schematic diagram of tunnel across Xiangjiang River

下载: 全尺寸图片幻灯片

图 6 典型断面示意图

Figure 6. Schematic diagram of typical section

下载: 全尺寸图片幻灯片

4.1 参数选取

隧道管片外径5.65 m,管片内径5.15 m,管片厚度0.5 m,管片幅宽2 m,环向分块9块（即由6个标准块、2个邻接块和1个封顶块组成）,衬砌环采用错缝的方式拼接,每环选用12根M24螺栓,环缝选用10根M24螺栓。盾构机外径5.815 m,盾构注浆层厚度0.165 m,初始注浆压力为0.18 MPa,采用典型4孔注浆。模型的主要参数见表1,2所示。

表 1 浆液主要参数

Table 1. Key parameters of grout

初始注浆压力/MPa	注浆层厚度/m	浆饼渗透系数/(m·s^-1)	浆液孔隙率	浆饼孔隙率	浆体变形模量/MPa
0.18	0.165	4.7×10^-8	0.425	0.417	15

下载: 导出CSV

| 显示表格

表 2 地基土及混凝土部分参数

Table 2. Partial parameters of foundation soil and concrete

地层	混凝土密度/(kg·m^-3)	土体变形模量/MPa	土体泊松比	土体渗透系数/(m·d^-1)
强风化砾岩	2500	18.5	0.3	1.85×10^-6

下载: 导出CSV

| 显示表格

4.2 模型计算结果

（1）浆液纵向压力分布规律

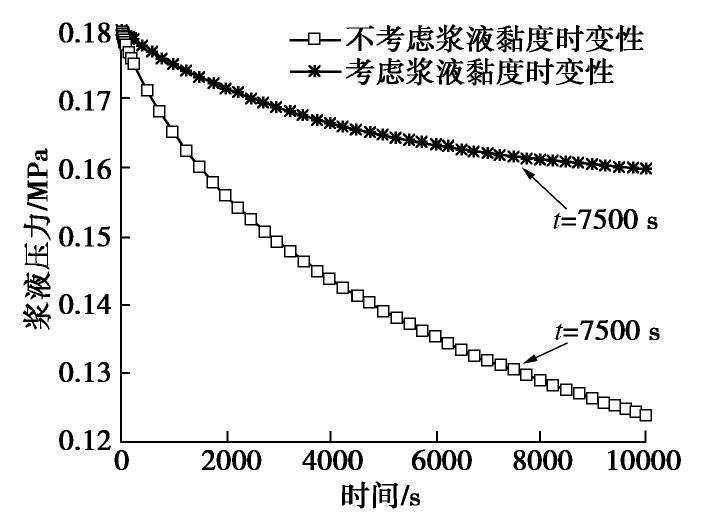
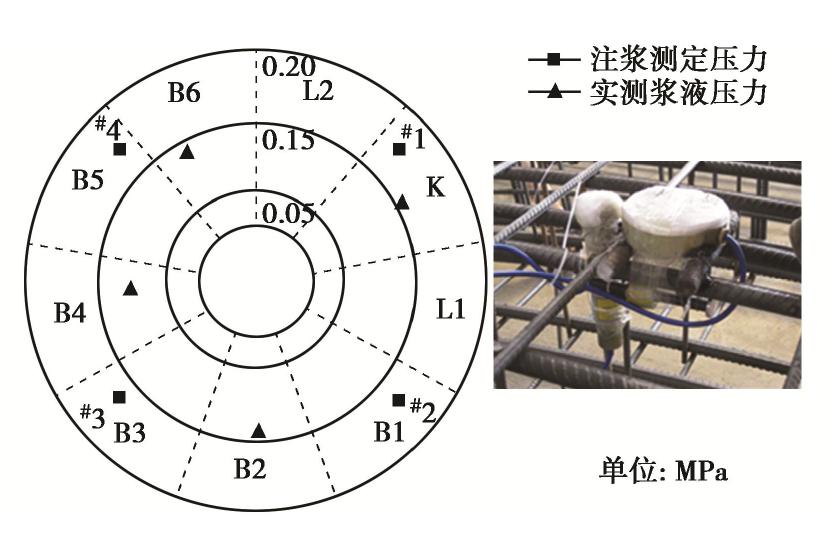
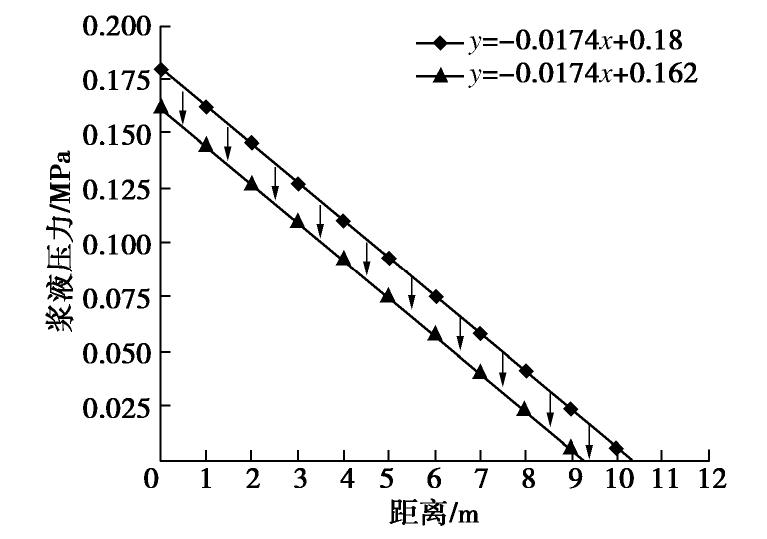
基于式（6）可以得到同步注浆作用下浆液压力耗散规律,如图7所示,注浆一般持续2～3 h,选择 $t$ =7500 s与 $t$ =0 s时浆液压力进行对比。从图7可知,考虑浆液黏度变化时 $t$ =7500 s的浆液压力相对于 $t$ =0 s的浆液压力衰减10%,不考虑浆液黏度变化时 $t$ =7500 s的浆液压力相对于 $t$ =0 s时的浆液压力衰减27.2%,因此考虑浆液黏度时变性的影响时,最终的衰减幅度更小。浆液黏度增大,其流动性和地层的渗透性变小,进而会影响浆液压力耗散。

图 7 浆液压力耗散曲线

Figure 7. Dissipation curves of grout pressure

下载: 全尺寸图片幻灯片

现场对注浆口附近浆液压力变化进行了监测,结果如图8所示,通过对比浆液设定压力和实测浆液压力的数据可知,注浆口处浆液压力存在一定的衰减,衰减幅度大致在16.6%～24.5%。现场的实测结果表明了纵向浆液扩散衰减理论的合理性,因此在分析同步注浆下盾构隧道纵向的力学行为时,应考虑浆液耗散效应带来的影响。

图 8 浆液压力现场实测

Figure 8. Field measurement of groug pressure

下载: 全尺寸图片幻灯片

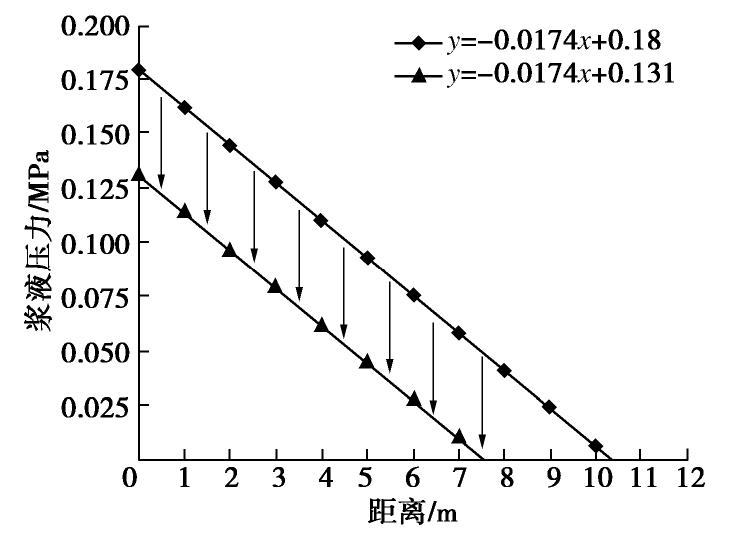
基于浆液压力耗散曲线计算结果,可以得到同步注浆过程中浆液压力沿纵向的扩散规律及浆液未凝固区长度,如图9,10所示,浆液压力沿纵向的分布呈线性衰减趋势,若不考虑浆液黏度时变性的影响,同步注浆过程中浆液压力的耗散幅度为0.049 MPa,占初始预设浆液压力的27.7%,浆液未凝固区长度为7.53 m。若考虑浆液黏度时变性的影响,浆液压力耗散幅度为0.018 MPa,占初始预设浆液压力的10%,浆液未凝固区长度为9.32 m,相对于不考虑浆液黏度时变性影响时,其长度增加1.79 m。

图 9 不考虑浆液黏度时变性的纵向浆液压力分布

Figure 9. Distribution of longitudinal pressure without consideration of time-varying property of grout viscosity

下载: 全尺寸图片幻灯片

图 10 考虑浆液黏度时变性的纵向浆液压力分布

Figure 10. Distribution of longitudinal pressure with consideration of time-varying property of grout viscosity

下载: 全尺寸图片幻灯片

（2）典型断面预测值

基于式（1）可以计算得到壁后注浆与地层共同作用下的等效地层抗力系数 $k$ =3.64×10² kN/m³,地层抗力系数乘以隧道宽度为基床系数K=4.11×10³ kN/m²,基于式（2）可以计算得到弹性地基上等效连续梁的等效抗弯刚度(EI)_eq=9.08×10⁸kN·m²。

根据前文得出的纵向浆液压力分布规律和式（9）,再减去管片自重可以得到纵向上浮力分布形式：

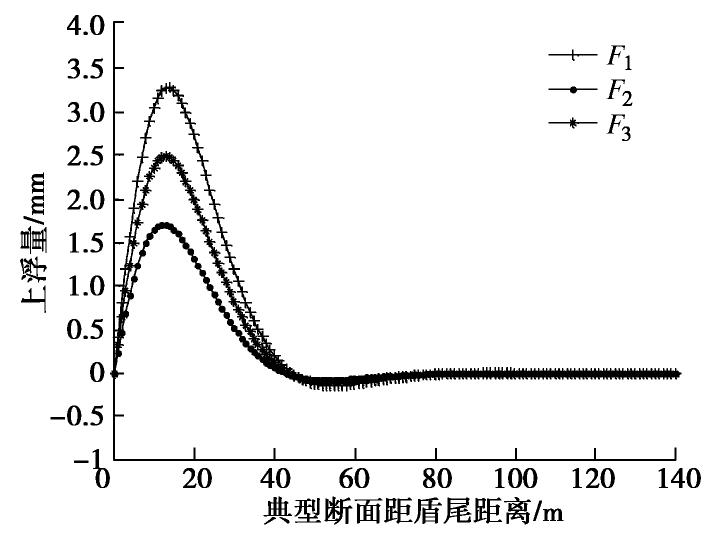
$\begin{array}{l} F_{1} (x) = 3643.94 - 393.24 x, \\ F_{2} (x) = 2536.51 - 393.24 x, \\ F_{3} (x) = 3227.18 - 393.24 x 。 \end{array}}$

(21)

式（21）分别为不考虑浆液压力耗散（下文简称为工况F₁）、考虑浆液压力耗散但不考虑浆液黏度时变性（工况F₂）、考虑浆液压力耗散和浆液黏度时变性（工况F₃）的3种盾构隧道纵向上浮力分布形式。将上述3种形式的上浮力作为盾构隧道纵向上浮分析模型的输入荷载,代入盾构隧道纵向上浮分析模型,可以得到一个施工步下的上浮量如图11所示,从盾构铰接端到无穷远处,上浮量先增大后减少,在6～7环（约12 m）达到最大,后迅速下降,约在20环（40 m）处降为零,随后出现一段数值较小的负位移,最后约40环（80 m）左右管片的位移重新为0,之后一直保持不变。工况F₁的上浮量最大,为3.3 mm；工况F₃的上浮量次之,为2.4 mm；工况F₂的上浮量最小,为1.7 mm。这是因为不考虑浆液压力耗散效应时,初始注浆压力最大,浆液未凝固区最长,同步注浆上浮力作用的范围最长；而工况F₃和F₂相比,浆液未凝固区长度更长,上浮力作用范围更长。

图 11 隧道纵向上浮量

Figure 11. Longitudinal uplift amount of tunnel

下载: 全尺寸图片幻灯片

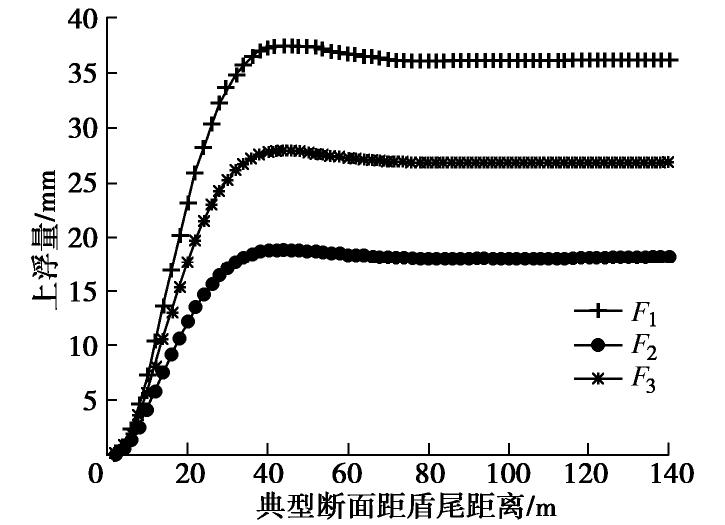
盾构机实际施工时不断向前掘进,还应考虑施工步的影响时,将典型断面对应的不同施工步下的上浮曲线进行叠加,得到目标环的上浮量变化规律,如图12所示,典型断面对应的目标环脱出盾构后,上浮量持续增加,约向前掘进40环（80 m）后目标环的上浮量趋于稳定,不再变化。工况F₁的最终上浮量最大,为36.1 mm；工况F₃次之,最终上浮量为25.3 mm；工况F₂最终上浮量最小,为17.6 mm。

图 12 典型断面累计上浮量

Figure 12. Cumulative uplift amount of a typical section

下载: 全尺寸图片幻灯片

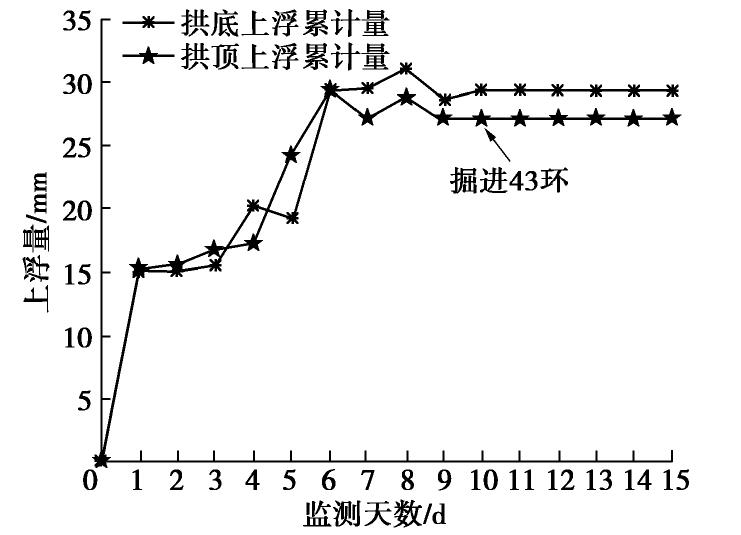
现场对典型断面的目标环拱顶和拱底的上浮量进行了监测,现场实测数据如图13所示,目标环脱出盾尾以后,第一天上浮量达15 mm。随后上浮量增长速率下降,最终约10 d后保持不变,拱顶的最终上浮量为28.7 mm,拱底的最终上浮量为26.8 mm,取两者的平均值（27.75 mm）作为目标环的最终上浮量。通过和前面3种情况下的对比可以发现,同时考浆液压力耗散效应和浆液黏度时变性影响的最终上浮量和现场实测数据最为接近,误差为8.8%,其他两种工况下的上浮量预测值误差较大,分别为30%和36.6%。

图 13 典型断面现场实测上浮量

Figure 13. Measured uplift amount of a typical section

下载: 全尺寸图片幻灯片

5. 结论与展望

基于弹性地基梁的矩阵传递法理论,综合考虑了浆液压力耗散效应、浆液黏度时变性、上覆土体基床系数各异性和施工步叠加效应的影响,建立施工期盾构隧道纵向上浮分析模型,并基于工程案例实测结果进行了验证,可得出以下结论：

（1）模型将施工期的盾构隧道视为变基床系数的有限长弹性地基梁和基床系数不变的半无限弹性地基长梁组成,通过初参数矩阵传递的形式,实现了这两类地基梁计算方法的耦合,同时解决了考虑浆液压力耗散效应、浆液黏度时变特性、基床系数各异性和施工步叠加效应等多因素影响下对上浮量精细化预测的问题。

（2）以长沙市南湖路隧道工程为案例,进行了实测数据与计算值的对比,发现计算结果和现场实测较为吻合,同时在盾构隧道施工过程中,同步注浆作用下引起的管片上浮量从盾尾处到无穷远先增大后减小,距盾尾约6～7环处上浮量最大,之后上浮量下降,远离盾尾超40环的管片不再上浮。研究成果可为后续类似盾构隧道上浮量的控制提供参考。

（3）建立的施工期盾构隧道纵向上浮分析模型没有考虑管片接头的弯曲非线性特性,始终认为纵向等效抗弯刚度为固定值,而纵向等效抗弯刚随弯矩、轴力变化呈现非线性动态变化的特性,因此为了能反映隧道纵向更为精确的内力和变形分布,还需建立更为精细化的上浮分析模型。

图 1 盾构隧道纵向上浮分析模型

Figure 1. Longitudinal uplift analysis model for shield tunnel

下载: 全尺寸图片幻灯片

图 2 施工动态示意图

Figure 2. Diagram of dynamic construction

下载: 全尺寸图片幻灯片

图 3 等效地层抗力系数示意图

Figure 3. Stiffness coefficient of equivalent stratigraphic spring

下载: 全尺寸图片幻灯片

图 4 三角形基床转化为阶梯形基床

Figure 4. Conversion of triangular subgrade bed into stepped one

下载: 全尺寸图片幻灯片

图 5 越江隧道工程位置图

Figure 5. Schematic diagram of tunnel across Xiangjiang River

下载: 全尺寸图片幻灯片

图 6 典型断面示意图

Figure 6. Schematic diagram of typical section

下载: 全尺寸图片幻灯片

图 7 浆液压力耗散曲线

Figure 7. Dissipation curves of grout pressure

下载: 全尺寸图片幻灯片

图 8 浆液压力现场实测

Figure 8. Field measurement of groug pressure

下载: 全尺寸图片幻灯片

图 9 不考虑浆液黏度时变性的纵向浆液压力分布

Figure 9. Distribution of longitudinal pressure without consideration of time-varying property of grout viscosity

下载: 全尺寸图片幻灯片

图 10 考虑浆液黏度时变性的纵向浆液压力分布

Figure 10. Distribution of longitudinal pressure with consideration of time-varying property of grout viscosity

下载: 全尺寸图片幻灯片

图 11 隧道纵向上浮量

Figure 11. Longitudinal uplift amount of tunnel

下载: 全尺寸图片幻灯片

图 12 典型断面累计上浮量

Figure 12. Cumulative uplift amount of a typical section

下载: 全尺寸图片幻灯片

图 13 典型断面现场实测上浮量

Figure 13. Measured uplift amount of a typical section

下载: 全尺寸图片幻灯片

表 1 浆液主要参数

Table 1 Key parameters of grout

初始注浆压力/MPa 注浆层厚度/m 浆饼渗透系数/(m·s^-1) 浆液孔隙率浆饼孔隙率浆体变形模量/MPa

0.18 0.165 4.7×10^-8 0.425 0.417 15

下载: 导出CSV

表 2 地基土及混凝土部分参数

Table 2 Partial parameters of foundation soil and concrete

地层混凝土密度/(kg·m^-3) 土体变形模量/MPa 土体泊松比土体渗透系数/(m·d^-1)

强风化砾岩 2500 18.5 0.3 1.85×10^-6

下载: 导出CSV

参考文献(20)

[1]	陈仁朋, 刘源, 刘声向. 盾构隧道管片施工期上浮特性[J]. 浙江大学学报：工学版, 2014, 48: 1068-1074. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201406014.htm CHEN Ren-peng, LIU Yuan, LIU Sheng-xiang. Characteristics of upward moving for lining during shield tunneling construction[J]. Journal of Zhejiang University: Engineering Science, 2014, 48: 1068-1074. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC201406014.htm
[2]	肖明清, 孙文昊, 韩向阳. 盾构隧道管片上浮问题研究[J]. 岩土力学, 2009, 30(4): 1041-1045. doi: 10.3969/j.issn.1000-7598.2009.04.031 XIAO Ming-qing, SUN Wen-hao, HAN Xiang-yang. Research on upward moving of segments of shield tunnel[J]. Rock and Soil Mechanics, 2009, 30(4): 1041-1045. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.04.031
[3]	侯公羽, 杨悦, 刘波. 盾构管片接头模型的改进及管片内力的数值计算[J]. 岩石力学与工程学报, 2007, 26(增刊1): 4284-4291. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2007S2103.htm HOU Gong-yu, YANG Yue, LIU Bo. Improved joint model of shield tunnel segments and numerical calculation of inner forces[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(S1): 4284-4291. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2007S2103.htm
[4]	魏纲, 张鑫海, 林心蓓. 基坑开挖引起的旁侧盾构隧道横向受力变化研究[J]. 岩土力学, 2020, 41(2): 636-644. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202002035.htm WEI Gang, ZHANG Xin-hai, LIN Xin-bei. Variations of transverse forces on nearby shield tunnel caused by foundation pits excavation[J]. Rock and Soil Mechanics, 2020, 41(2): 636-644. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202002035.htm
[5]	彭益成, 丁文其, 闫治国. 修正惯用法中弯曲刚度有效率的影响因素分析及计算方法[J]. 岩土工程学报, 2013, 31(增刊1): 495-500. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S1085.htm PENG Yi-cheng, DING Wen-qi, YAN Zhi-guo. Analysis and calculation method of effective bending rigidity ratio in modified routine method[J]. Chinese Journal of Geotechnical Engineering, 2013, 31(S1): 495-500. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S1085.htm
[6]	LEE K M, HOU X Y, GE X W, et al. An analytical solution for a jointed shield-driven tunnel lining[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(4): 365-390. doi: 10.1002/nag.134
[7]	KOIZUMI A, MURAKAMI H, ISHIDA T. Design method of segments at a sharply curved section[J]. Journal of Japanese Society of Civil Engineers, 1992(448): 111-120. (in Japanese)
[8]	朱合华, 周龙, 朱建文. 管片衬砌梁-弹簧广义模型及接头转动非线性模拟[J]. 岩土工程学报, 2019, 41(9): 1581-1590. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909002.htm ZHU He-hua, ZHOU Long, JU Jiann-wen. Beam-spring generalized model for segmental lining and simulation of its nonlinear rotation[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1581-1590. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909002.htm
[9]	SHIBA Y, KAWASHIMA K, OBINATA N. Seismic design method of shield tunnel using response displacement method[J]. Journal of Japanese Society of Civil Engineers, 1986, 5: 113.
[10]	叶飞, 朱合华, 丁文其. 基于弹性地基梁的盾构隧道纵向上浮分析[J]. 中国铁道科学, 2008, 29(4): 65-69. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200804011.htm YE Fei, ZHU He-hua, DING wen-qi. Longitudinal upward movement analysis of shield tunnel based on elastic foundation beam[J]. China Railway Science, 2008, 29(4): 65-69. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200804011.htm
[11]	朱令, 丁文其, 杨波. 壁后注浆引起盾构隧道上浮对结构的影响[J]. 岩石力学与工程学报, 2012, 31(增刊2): 3378-3382. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2012S1103.htm ZHU ling, DING Wen-qi, YANG Bo. Effect of shield tunnel uplift caused by back-filled grouting on structure[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(S2): 3378-3382. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2012S1103.htm
[12]	杨方勤. 超大直径泥水盾构隧道抗浮实验与理论研究[D]. 上海: 同济大学, 2010. YANG Fang-qin. Large Diameter Slurry Shield Tunnel Tests and Theoretical Studies of Anti-Floating[D]. Shanghai: Tongji University, 2010. (in Chinese)
[13]	舒瑶, 季昌, 周华顺. 考虑地层渗透性的盾构隧道施工期管片上浮预测[J]. 岩石力学与工程学报, 2017, 36(增刊1): 3516-3524. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2017S1046.htm SHU Yao, JI Chang, ZHOU Shun-hua. Prediction for shield tunnel segment uplift considering the effect of stratum permeability[J]. Chinese Journal of Rock Mechanic and Engineering, 2017, 36(S1): 3516-3524. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2017S1046.htm
[14]	梁禹, 黄林冲. 盾构隧道同步注浆压力时空分布规律[J]. 哈尔滨工业大学学报, 2018, 50(3): 165-170. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX201803023.htm LIANG Yu, HUANG Lin-chong. Grout pressure distribution characteristics in space-time domain of shield tunnels during synchronous grouting[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 165-170. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX201803023.htm
[15]	TALMON A M, BEZUIJEN A. Analytical model for beam action of a tunnel lining during construction[J]. International Journal of Numerical and Analytical Methods in GeoMechanics, 2013, 37(2): 181-200.
[16]	TALMON A M, BEZUIJEN A. Calculation of longitudinal bending moment and shear force for Shanghai Yangtze River Tunnel: application of lessons from Dutch research[J]. Tunneling and Underground Space Technology, 2013, 35(3): 161-171.
[17]	小泉淳. 盾构隧道管片设计-从容许应力设计法到极限状态设计法[M]. 北京: 中国建筑工业出版社, 2012: 187-189. Atsushi KOIZUMI. The Segment Design of Shield Tunneling[M]. Beijing: China Architecture and Building Press, 2012: 187-189. (in Chinese)
[18]	叶飞, 杨鹏博, 毛家骅. 基于模型试验的盾构隧道纵向刚度分析[J]. 岩土工程学报, 2015, 37(1): 83-90. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201501011.htm YE Fei, YANG Peng-bo, MAO Jia-hua. Longitudinal rigidity of shield tunnels based on model tests[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(1): 83-90. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201501011.htm
[19]	田敬学, 张庆贺. 盾构法隧道的纵向刚度计算方法[J]. 中国市政工程, 2001(3): 35-37. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGSZ200103011.htm TIAN Jing-xue, ZHANG Qing-he. Calculation of longitudinal rigidity of shield tunnels[J]. China Municipal Engineering, 2001(3): 35-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGSZ200103011.htm
[20]	刘庆潭, 倪国荣. 结构分析中的传递矩阵法[M]. 北京: 中国铁道出版社, 1997: 40-55. LIU Qing-tan, NI Guo-rong. Matrix Transfer Method for Structural Analysis[M]. Beijing: China Railway Publishing House, 1997: 40-55. (in Chinese)

施引文献(41)

期刊类型引用(29)

1.	李明宇，王越，陈健，高始军，田应飞，靳军伟，杨钊. 同步注浆上浮力作用下大盾构管片瞬时变形特征模型试验研究. 铁道学报. 2025(01): 171-182 . 百度学术
2.	唐辉. 盾构隧道壁后注浆浆液性能研究. 低温建筑技术. 2025(01): 96-99 . 百度学术
3.	王海涛，王悦，孙九春. 管片上浮模型试验平台研制. 隧道建设(中英文). 2025(01): 132-138 . 百度学术
4.	王超，邹金锋. 盾构注浆荷载作用下带榫管片水平轴线偏移量计算方法研究. 工程力学. 2024(01): 39-55 . 百度学术
5.	曾红波，石州，涂金光，徐金峰，肖中林. 临海富水地层大直径盾构隧道管片上浮机制及控制措施. 公路交通科技. 2024(01): 138-151 . 百度学术
6.	李明宇，朱康康，陈健，蔺云宏，吴龙骥，靳军伟，杨潇. 考虑土体剪切与接头剪切效应的盾构隧道纵向变形计算模型. 中国铁道科学. 2024(01): 142-154 . 百度学术
7.	苏恩杰，任超，叶飞，温小宝，韩兴博，胡瑞青. 泥质砂岩地层盾构隧道管片连续上浮规律与分析. 中南大学学报(自然科学版). 2024(02): 706-714 . 百度学术
8.	崔庆龙，张晟斌，许啸鹏，刘继国，李金，李铮. 超大盾构隧道施工期管片受力特征分析. 施工技术(中英文). 2024(03): 21-27+53 . 百度学术
9.	李明宇，王越，李庆民，陈健，王承震，蔺云宏，田应飞. 大盾构管片最不利上浮状态下三维形变特征模型试验方案设计. 中国铁道科学. 2024(02): 101-112 . 百度学术
10.	高俊华，杨光，赵森森，黄忠凯，张吾渝，张冬梅. 软土地区浅埋大直径盾构隧道管片上浮规律及预测：以上海机场联络线工程为例. 科学技术与工程. 2024(11): 4759-4768 . 百度学术
11.	包小华，李浚弘，陈湘生，沈俊，刘自明，姚义. 水下盾构隧道管片拼装质量控制方法研究现状与展望. 隧道建设(中英文). 2024(04): 643-662 . 百度学术
12.	夏明，张慧鹏，张志强，曾云嵘，徐腾飞. 泥质粉砂岩地层盾构隧道管片上浮影响因素. 城市轨道交通研究. 2024(07): 120-126 . 百度学术
13.	荆永波，武敖杰，孙星亮，韩小冬. 富水粉细砂层盾构同步注浆复合浆液配比试验. 粉煤灰综合利用. 2024(04): 53-58 . 百度学术
14.	黎程，马林东，李国栋，牟星宇，胡克. 穿江盾构隧道管片变形特性分析. 上海公路. 2024(03): 58-62+67+205 . 百度学术
15.	郭建磊，吉冰冰，陈雪峰，李博，吴联棒. 宁波地区复合地层盾构管片上浮影响参数研究. 安徽建筑. 2024(11): 150-152 . 百度学术
16.	李海滨，余刘成，李明宇，陈健，王越. 浅覆土大直径盾构管片上浮规律及控制分析. 地下空间与工程学报. 2024(06): 2000-2009 . 百度学术
17.	胡如成，钟小春，易斌斌，刘哲，刘程. 风化岩层盾尾同步双液浆控制管片上浮研究. 地下空间与工程学报. 2024(06): 2010-2019+2033 . 百度学术
18.	焦建林，傅鹤林. 曲线段大直径盾构掘进引发管片上浮影响. 湖南理工学院学报(自然科学版). 2023(01): 49-55 . 百度学术
19.	朱仰凯，张可能，胡达，肖超，张云毅，王玺. 考虑注浆结石体影响的隧道管片上浮理论解析. 中国安全生产科学技术. 2023(03): 93-100 . 百度学术
20.	张建勇，李明宇，陈健，余刘成，李义翔，杨公标，王越. 基于双面弹性地基梁的大直径盾构隧道管片上浮预测方法. 现代隧道技术. 2023(02): 159-167 . 百度学术
21.	竺维彬，刘昶，钟小春，游智，朱能文. 基于压缩及油脂逃逸试验的盾尾刷性能评价研究. 岩土工程学报. 2023(05): 1086-1093 . 本站查看
22.	钟浩嘉，晏启祥，魏源成，孟祥林，曹军军，邓林. 盾构隧道管片上浮力学特性精细化模拟分析. 铁道建筑. 2023(05): 105-109 . 百度学术
23.	钟小春，黄思远，槐荣国，朱诚，胡一康，陈旭泉. 基于浆液浮力试验的盾尾管片纵向上浮特征研究. 岩土力学. 2023(06): 1615-1624 . 百度学术
24.	李文，杨凡，吴圣智，刘越. 岩溶地层运营期地下水上涨引起管片上浮规律研究. 科学技术与工程. 2023(20): 8863-8872 . 百度学术
25.	苏恩杰，叶飞，何乔，任超，李思翰，张宏权. 基于卷积神经网络-长短期记忆的施工期盾构管片上浮过程预测模型. 同济大学学报(自然科学版). 2023(09): 1352-1361 . 百度学术
26.	吴林，王维，封坤，陶伟明，孟庆辉，甄文战. 盾构隧道纵向上浮分析模型中地基抗力系数研究. 现代隧道技术. 2022(03): 128-135 . 百度学术
27.	田小聪，张孟喜，卢康明，柯宁静. 浆液参数时变性对软土地区深埋盾构隧道开挖的影响. 铁道建筑. 2022(10): 112-116 . 百度学术
28.	洪成雨，周子平，陈伟斌，付艳斌，沈翔. 基于光频域反射技术的破碎带盾构隧道管片监测研究. 隧道建设(中英文). 2022(10): 1729-1737 . 百度学术
29.	谭毅俊，彭元栋，刘爽，苏栋，雷国平. 加固厚度对软土地层大直径盾构隧道抗浮的影响. 建筑科学与工程学报. 2021(06): 163-169 . 百度学术