粗粒土颗粒强度和弹性力学参数的试验研究

郭宇; 迟世春; 米晓飞

doi:10.11779/CJGE202109012

粗粒土颗粒强度和弹性力学参数的试验研究 English Version

郭宇^{1, 2,},
迟世春^{1, 2, ,},
米晓飞³

1.
大连理工大学海岸与近海工程国家重点实验室,辽宁　大连　116024
2.
大连理工大学建设工程学部水利工程学院工程抗震研究所,辽宁　大连　116024
3.
龙湖集团控股有限公司,北京　100029

基金项目:

国家重点研发计划项目 2016YFB0201001

详细信息

作者简介:
郭宇(1993— ),男,河北保定人,博士研究生,主要从事粗粒土颗粒破碎特性的研究。E-mail：jiangongguoyu@mail.dlut.edu.cn

通讯作者:
迟世春, E-mail：schchi@dlut.edu.cn

中图分类号: TU431
计量
- 文章访问数: 292
- HTML全文浏览量: 31
- PDF下载量: 134
出版历程
- 收稿日期: 2020-12-22
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-08-31

Experimental study on particle strength and elastic mechanical parameters of coarse-grained soil

GUO Yu^{1, 2,},
CHI Shi-chun^{1, 2, ,},
MI Xiao-fei³

1.
State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China
2.
Institute of Earthquake Engineering, School of Hydraulic Engineering, Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China
3.
Longfor Group Holdings Limited, Beijing 100029, China

摘要

摘要: 粗粒土的强度和变形特性直接影响堆石坝的变形规律,为从细观层面研究粗粒土的变形机理,离散元法作为一种有效手段被广泛用于粗粒土力学特性的模拟中。而颗粒强度和弹性力学参数对于离散元模型的构建至关重要,如何获取这些参数的分布规律是当前一项十分必要的工作。对一系列不同尺寸的大连石灰岩颗粒进行了单轴压缩试验,利用荷载—位移曲线的特征,确定了石灰岩颗粒强度和弹性模量的分布规律。统计结果表明：相较于Weibull分布和Logistic分布,Lognormal分布对于颗粒强度和弹性模量的统计效果最好；颗粒强度和弹性模量的均值都随着颗粒尺寸的增大而减小。然后基于参数的尺寸相关性特点建立了适合石灰岩的尺寸效应经验模型。最后对颗粒刚度进行了初步讨论,试验结果表明石灰岩颗粒的刚度具有明显的非线性特点。这些结果为粗粒土离散元数值模拟的细观参数标定提供了规律性方面的参考和支撑。
- 粗粒土 /
- 颗粒强度 /
- 弹性模量 /
- 刚度 /
- 概率分布 /
- 尺寸效应
Abstract: The strength and deformation characteristics of coarse-grained soil directly affect the deformation law of rockfill dams. In order to study the deformation mechanism of coarse-grained soil from the microscopic level, the discrete element method is widely used as an effective means to simulate the mechanical properties of coarse-grained soil. The particle strength and elastic mechanics are very important for the establishment of the discrete element method model. How to obtain the distribution law of these parameters is a very necessary work at present. The uniaxial compression tests are carried out on a series of Dalian limestone particles with different sizes, and the distribution law of mechanical parameters including the strength and elastic modulus is determined by characterizing the force-displacement experimental curves. The statistical results show that compared with the Weibull distribution and Logistic distribution, the Lognormal distribution has the best statistical effect on particle strength and elastic modulus, and the mean values of both two parameters decrease with the increase of particle size. Then, based on the size correlation of parameters, empirical models for size effect suitable for limestone are established. Finally, the stiffness of limestone particles is discussed preliminarily. The experimental results show that the stiffness of limestone particles has obvious nonlinear characteristics. These results may provide a reference and support for the calibration of microscopic parameters in the numerical simulation of the discrete element method for coarse-grained soil.
- coarse-grained soil /
- particle strength /
- elastic modulus /
- stiffness /
- probability distribution /
- size effect

HTML全文

0. 引言

粗粒土是一种常见的筑坝材料。粗粒土剪切过程中的颗粒破碎现象明显^[1],这是引起堆石坝发生变形的重要原因之一。随着中国超高坝的建设,越来越多的学者开始关注高应力作用下粗粒土颗粒的破碎特性^[2-5]。但是,由于试验条件的限制,宏观试验只能根据破碎前后的级配曲线演化来推断颗粒破碎程度。与宏观试验相比,近年来日益成熟的离散元法（discrete element method,简称DEM）数值模拟为从细观层面对粗粒土颗粒破碎进行研究提供了新途径^[6-10]。

在DEM数值模拟中,颗粒强度和弹性力学参数是模拟颗粒破碎以及颗粒—颗粒、颗粒—边界相互作用的重要材料特性,是影响数值模拟结果的关键因素之一。目前主流的细观参数标定方法,通常是先假定一组细观参数,通过对参数及其组合的调整使数值试样的宏观力学表现不断逼近土体的真实行为,直到数值试验与室内试验得到的宏观力学性质曲线基本接近时,认为该组细观参数已具备一定合理性,可以用于后续的数值计算中。这种依托于使用者经验的“试错法”需进行多次尝试并有一定的盲目性。考虑到DEM数值模拟建立在细观颗粒间相互作用的基础上,通过物理力学试验获得颗粒强度和弹性力学参数的真实分布规律,可以为DEM数值模拟的细观参数标定提供规律性方面的参考和支撑。

粗粒土的DEM数值模拟中需要考虑的细观参数主要是颗粒强度和弹性模量,关于它们的研究主要集中在两个方面。一是颗粒参数的离散性。以颗粒强度为例,比如McDowell等^[11-12]提出用Weibull分布来描述颗粒强度的分布特点,但是迟世春等^[13]对石灰岩颗粒进行相同试验之后却发现用该分布拟合颗粒强度离散性的效果不佳；另外还有张明等^[14]提出用对数正态分布来描述颗粒强度的随机性在实际应用上更为合理,米晓飞等^[15]用Logistic函数对颗粒强度的随机分布特点进行了描述。上述关于颗粒参数离散性分布特征的研究都是在确定某一特定分布函数后对试验结果进行拟合,对于结果缺少在不同分布类型之间的对比选优。二是颗粒参数的尺寸效应。目前对于颗粒强度的尺寸效应研究很多,结果表明粗粒土颗粒强度与颗粒尺寸之间存在着较强的相关性,这种相关性通常用幂函数关系来表示^[12-13,16]；而对于颗粒弹性模量的尺寸效应研究不多。总体来说,国内外学者对于粗粒土颗粒强度的研究已取得较为丰富的成果；虽然关于粒状材料的弹性力学参数的研究案例并不少^[17-21],但是对于粗粒土颗粒的弹性力学参数进行研究的先例却不多；目前,对于粗粒土颗粒的研究主要集中在粒径60 mm以下的小尺寸范围,得到的尺寸效应模型能否适用于更大的粒径范围也值得探究。

本文基于20～120 mm的粗粒土颗粒单轴压缩试验结果,确定颗粒强度和弹性模量,用统计学中的K-S检验法从Weibull分布、Lognormal分布和Logistic分布中分别比选出它们的最优分布类型,给出它们各自的尺寸效应经验模型。然后采用240 mm粗粒土颗粒的试验结果对提出的尺寸效应经验模型进行验证。最后对颗粒刚度的特点进行了初步讨论。

1. 试验材料和方法

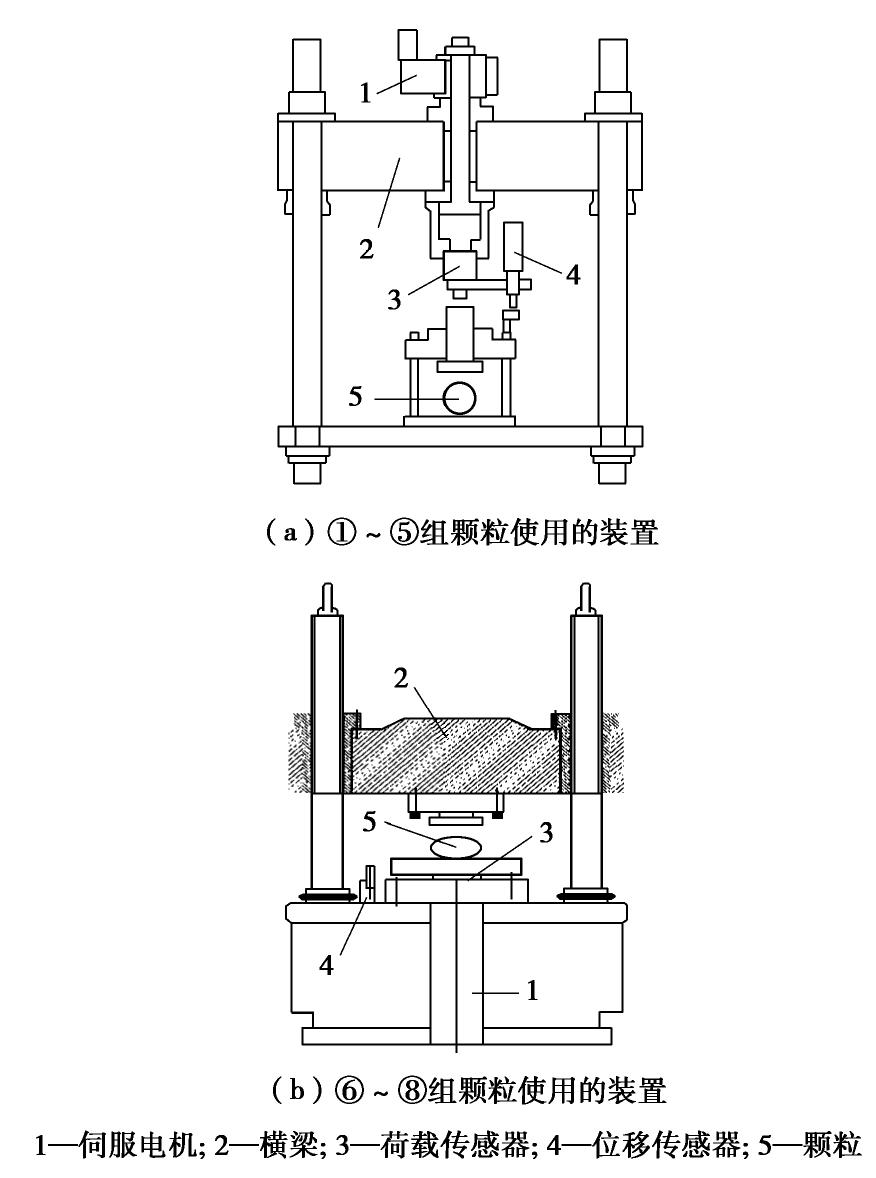
本试验采用爆破开采得到的大连石灰岩颗粒,按照粒径大小依次记为①～⑧组,粒径分别为20～24 mm、24～28 mm、28～32 mm、32～36 mm、36～40 mm以及60 mm、120 mm和240 mm。其中,①～⑤组颗粒由常规筛分得到,⑥～⑧组颗粒用特制的圆孔筛（直径分别为60±5,120±5,240±5 mm）挑选得到。为了减少颗粒形状对参数的影响,选取的颗粒几何形状相似,并剔除针状、扁平状等特殊颗粒。

由于石灰岩颗粒不是完全规则的球形,其尺寸仅用筛孔大小难以准确描述。试验时是将颗粒稳定放置在下刚性板上,并且进行多次试放,找到竖直高度最短的稳定放置状态,定义此时的高度为短轴H,并以此稳定状态进行轴向加载；在与H垂直的横截面中,取最大径为长轴L,与L垂直方向上的最大径为中轴W。此处的L、W和H互相垂直,并且满足 $L \geq W \geq H$ $L \geq W \geq H$ 。颗粒尺寸用算术平均径 $d_{a}$ $d_{a}$ 来衡量,各组颗粒的特征粒径用该组颗粒的算术平均径的均值表示,颗粒形状用球度S_p来描述：

d_{a} = (L + W + H) / 3

$d_{a} = (L + W + H) / 3$ ,

(1)

S_{p} = {(L \cdot W \cdot H)}^{1 / 3} / L \times 100 %

$S_{p} = {(L \cdot W \cdot H)}^{1 / 3} / L \times 100 %$ 。

(2)

本文选择的石灰岩颗粒样本的各项基本物理参数详见表1。由于本文试验中各组颗粒样本的球度接近,可以认为形状对各组的影响是相同的。

表 1 石灰岩颗粒的基本物理参数

Table 1. Basic physical parameters of limestone particles

编号	粒组/mm	个数	算数平均径d_a/mm	球度S_p/%	质量m/g
①	20~24	82	22.13±1.97	74.07±7.53	11.24±2.90
②	24~28	78	25.83±2.03	76.54±7.49	18.10±3.72
③	28~32	76	30.17±2.25	74.34±6.99	26.50±5.99
④	32~36	77	33.81±2.43	75.70±7.49	37.26±7.89
⑤	36~40	76	37.32±2.88	75.99±7.13	48.57±9.81
⑥	60	35	53.89±4.48	77.98±6.68	183.52±31.40
⑦	120	38	120.99±8.31	77.30±6.25	2532.56±2928.13
⑧	240	20	225.35±16.42	78.80±5.07	13357.50±1884.72
注：表中格式为“均值±标准差”。

下载: 导出CSV

| 显示表格

由于本文试验所用石灰岩颗粒的粒径范围大,为保证试验顺利进行,①～⑤组颗粒使用图1（a）所示装置进行单轴压缩试验,⑥～⑧组颗粒使用图1（b）所示装置进行单轴压缩试验。上述两种装置的试验原理相同,加载方式可以采用位移控制或力控制,试验过程相当于上、下两个平行的刚性平面挤压颗粒直至破碎。这两种装置只有最大加载能力和刚性平面最大间距存在区别。

图 1 试验装置示意图

Figure 1. Schematic diagram of test instrument

下载: 全尺寸图片幻灯片

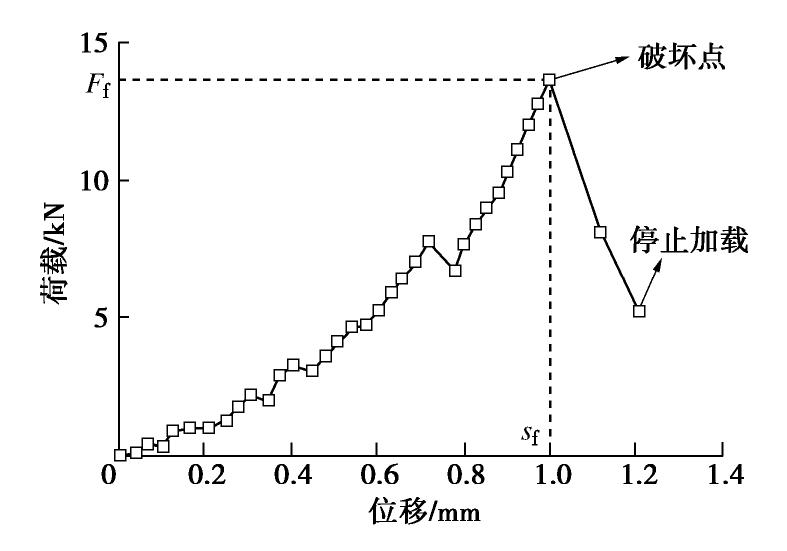
试验前将颗粒在烘箱内连续干燥6 h以上。将颗粒置于两刚性板间,通过控制位移施加轴向荷载,加载速率取0.5 mm/min,试验过程中自动记录荷载和位移。当观察到颗粒发生主体破坏后便停止加载,主体破坏是指颗粒产生贯穿型裂缝或分裂为几块。颗粒破碎前后的情况如图2所示,其荷载–位移曲线如图3所示。由于颗粒形状的不规则性会引起颗粒与刚性板之间的接触点附近产生应力集中,造成颗粒的局部压裂或者棱角破碎,反映在荷载–位移曲线上为荷载突然跌落,曲线呈现锯齿状。

图 2 颗粒破碎前后的照片

Figure 2. Photos of a particle before and after breakage

下载: 全尺寸图片幻灯片

图 3 石灰岩颗粒的荷载–位移曲线

Figure 3. Force-displacement curve of limestone particles

下载: 全尺寸图片幻灯片

2. 颗粒强度和弹性模量的确定

2.1 颗粒强度指标的确定

石灰岩颗粒强度指标由下式计算^[22]：

σ_{c} = \frac{F_{f}}{d^{2}}

$σ_{c} = \frac{F_{f}}{d^{2}}$ ,

(3)

式中, $σ_{c}$ $σ_{c}$ 为颗粒强度指标, $F_{f}$ $F_{f}$ 为颗粒破坏荷载,d为颗粒粒径,此处取每个颗粒的实际受力长度,即两刚性板之间的距离。

2.2 颗粒弹性模量的确定

文献[23]介绍了一种建立在固体力学中计算接触应力的赫兹理论的基础之上,用于计算质地相对坚硬且均匀的粒状材料弹性模量的方法。该方法所使用的试验手段和材料变形过程都与本文的试验研究极为相似,两刚性板的挤压是导致颗粒材料发生变形直至最后破坏的驱动力,所以本文采用该方法对石灰岩颗粒的弹性模量进行了计算。

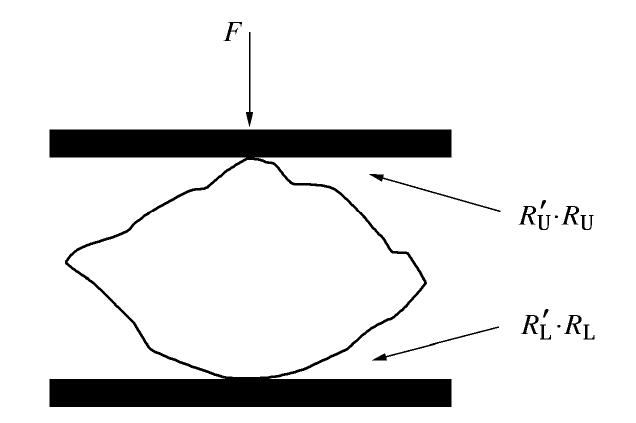
上述方法将受到两刚性板挤压的不规则颗粒（如图4所示）的荷载–位移关系用下式表示：

图 4 不规则颗粒受压示意

Figure 4. Diagram of compression on an irregular particle

下载: 全尺寸图片幻灯片

F = \frac{E}{0.338 K (1 - ν^{2})} \cdot s^{3 / 2}

$F = \frac{E}{0.338 K (1 - ν^{2})} \cdot s^{3 / 2}$ 。

(4)

式中 $F$ $F$ 为轴向荷载； $s$ $s$ 为轴向荷载 $F$ $F$ 作用下的变形量； $ν$ $ν$ 为泊松比,本文根据文献[24]中对各类岩石泊松比的汇总,假设石灰岩的泊松比 $ν = 0.25$ $ν = 0.25$ ； $E$ $E$ 为颗粒弹性模量；K为和颗粒接触点曲率有关的参数,引入该参数是因为颗粒表面粗糙导致接触点附近并非绝对光滑且连续,

K = {[K_{U} {(\frac{1}{R_{U}} + \frac{1}{{R^{'}}_{U}})}^{1 / 3} + K_{L} {(\frac{1}{R_{L}} + \frac{1}{{R^{'}}_{L}})}^{1 / 3}]}^{3 / 2}

$K = {[K_{U} {(\frac{1}{R_{U}} + \frac{1}{{R^{'}}_{U}})}^{1 / 3} + K_{L} {(\frac{1}{R_{L}} + \frac{1}{{R^{'}}_{L}})}^{1 / 3}]}^{3 / 2}$ 。

(5)

式中 ${R^{'}}_{U}$ ${R^{'}}_{U}$ , $R_{U}$ $R_{U}$ 分别为颗粒与上刚性板接触点处的最大和最小曲率半径； ${R^{'}}_{L}$ ${R^{'}}_{L}$ , $R_{L}$ $R_{L}$ 分别为颗粒与下刚性板接触点处的最大和最小曲率半径； $K_{U}$ $K_{U}$ , $K_{L}$ $K_{L}$ 为主曲率半径决定的常数,通过计算 $\cos θ$ $\cos θ$ ,可以从表2中对应查取, $θ$ $θ$ 为颗粒表面与刚性板接触点处接触主平面的夹角（°）,根据赫兹接触理论有 $K_{U}$ $K_{U}$ 和 $K_{L}$ $K_{L}$ 分别对应的 $\cos θ$ $\cos θ$ 表达式为

表 2 不同的θ对应的K_U（K_L）值（节选）^[23]

Table 2. Values of K_U (K_L) for various values of θ (excerpts)^[23]

θ/(°)	50	55	60	…	80	85	90
cos θ	0.6428	0.5736	0.5000	…	0.1736	0.0872	0.0
K_U(K_L)	1.198	1.235	1.267	…	1.342	1.349	1.351

下载: 导出CSV

| 显示表格

\begin{array}{l} K_{U} ： & \cos θ = (1 / R_{U} - 1 / {R^{'}}_{U}) / (1 / R_{U} + 1 / {R^{'}}_{U}) & , \\ K_{L} ： & \cos θ = (1 / R_{L} - 1 / {R^{'}}_{L}) / (1 / R_{L} + 1 / {R^{'}}_{L}) & 。 \end{array}}

$\begin{array}{l} K_{U} ： & \cos θ = (1 / R_{U} - 1 / {R^{'}}_{U}) / (1 / R_{U} + 1 / {R^{'}}_{U}) & , \\ K_{L} ： & \cos θ = (1 / R_{L} - 1 / {R^{'}}_{L}) / (1 / R_{L} + 1 / {R^{'}}_{L}) & 。 \end{array}}$

(6)

具体结合本文试验,石灰岩颗粒在自重下处于自稳定状态。可以认为颗粒与下刚性板之间近似面面接触,与上刚性板之间近似点面接触。这种情况下,颗粒与下刚性板接触点处的曲率 ${R^{'}}_{L} = R_{L} = \infty$ ${R^{'}}_{L} = R_{L} = \infty$ 。此时可以将式（4）具体写成

F = \frac{E}{0.338 (1 - ν^{2}) {[K_{U} {(1 / R_{U} + 1 / {R^{'}}_{U})}^{1 / 3}]}^{3 / 2}} \cdot s^{3 / 2}

$F = \frac{E}{0.338 (1 - ν^{2}) {[K_{U} {(1 / R_{U} + 1 / {R^{'}}_{U})}^{1 / 3}]}^{3 / 2}} \cdot s^{3 / 2}$ ,

(7)

式中, ${R^{'}}_{U}$ ${R^{'}}_{U}$ , $R_{U}$ $R_{U}$ 由颗粒的L,W和H计算^[18]：

{R^{'}}_{U} = (L^{2} / 4 + H^{2}) / (2 H)

${R^{'}}_{U} = (L^{2} / 4 + H^{2}) / (2 H)$ ,

(8)

R_{U} = (W^{2} / 4 + H^{2}) / (2 H)

$R_{U} = (W^{2} / 4 + H^{2}) / (2 H)$ ,

(9)

继续将式（7）简写为

F = C_{H} \cdot s^{3 / 2}

$F = C_{H} \cdot s^{3 / 2}$ ,

(10)

式中, $C_{H}$ $C_{H}$ 可以由颗粒破坏前的荷载–位移曲线拟合得到。因而,颗粒弹性模量E如下所示：

E = 0.338 C_{H} (1 - ν^{2}) {[K_{U} {(\frac{1}{R_{U}} + \frac{1}{{R^{'}}_{U}})}^{1 / 3}]}^{3 / 2}

$E = 0.338 C_{H} (1 - ν^{2}) {[K_{U} {(\frac{1}{R_{U}} + \frac{1}{{R^{'}}_{U}})}^{1 / 3}]}^{3 / 2}$ 。

(11)

3. 数理统计和分析

3.1 参数的数理统计方法

本文首先采用格布拉斯准则^[25]检测样本中的异常值。设 $X = (X_{1}, X_{2}, \dots, X_{n})$ $X = (X_{1}, X_{2}, \dots, X_{n})$ 是待检测数据,如果最值 $X_{i}$ $X_{i}$ 满足下式则为异常值,应予剔除。

\frac{| X_{i} - \bar{X} |}{S} \geq G (N, α)

$\frac{| X_{i} - \bar{X} |}{S} \geq G (N, α)$ 。

(12)

式中 $\bar{X}$ $\bar{X}$ 和 $S$ $S$ 分别为样本均值和标准差； $G$ $G$ 为格拉布斯临界值,根据样本容量 $N$ $N$ 和显著性水平 $α$ $α$ 查表^[25]得到。在剔除某一异常值后,应继续对余下的样本点进行检测,直到没有异常值为止。

然后根据已有研究经验^[11-17],本文尝试用Weibull分布、Lognormal分布和Logistic分布对颗粒强度 $σ_{c}$ $σ_{c}$ 和弹性模量E分别进行统计。

最后对于每个参数,使用K-S检验法^[26]定量地判断假设的概率分布类型是否合适,并从中确定最优分布形式。该方法通过将选定的分布类型的理论累积概率与观察到的经验累积概率进行比较,找出它们之间最大的差值,并参照抽样分布,给出这一差异是否处于偶然。如果两者较为接近,则表明实际样本的分布类型与假设的理论分布类型拟合程度很高。所有的统计分析均在显著性水平 $α = 0.05$ $α = 0.05$ 的条件下进行,即置信度为95%。

3.2 参数的最优分布类型

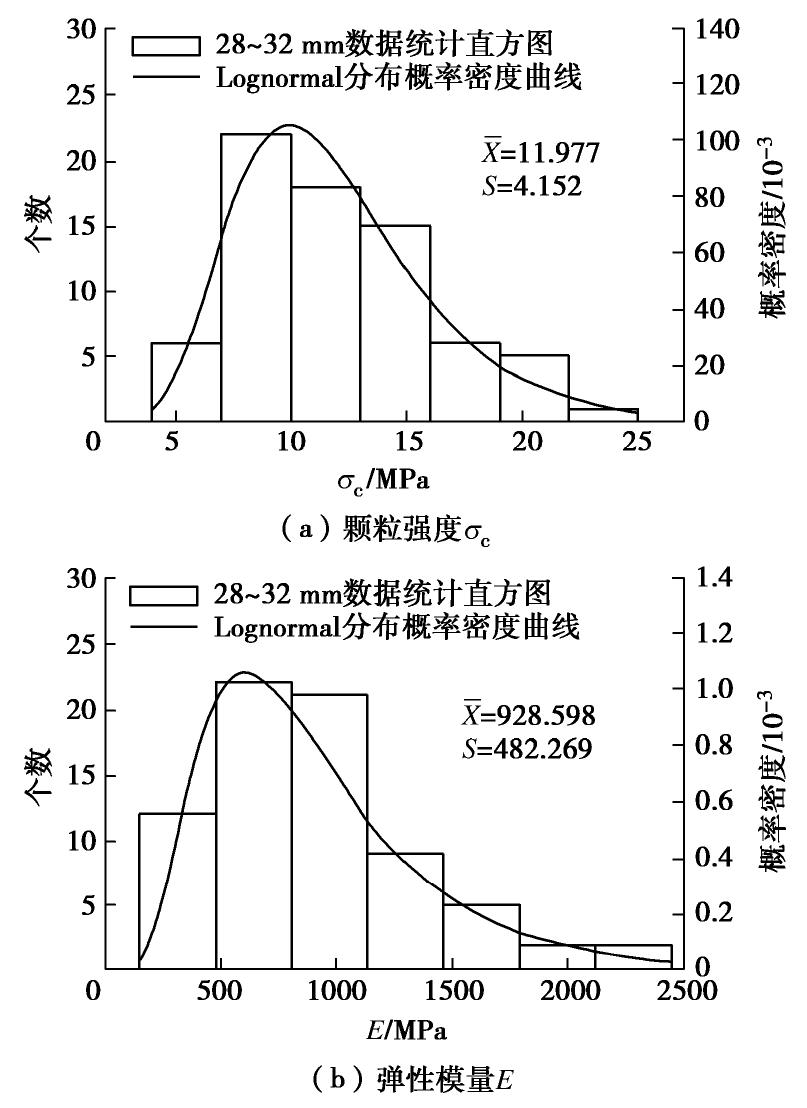
采用式（3）,（11）对各粒组的颗粒强度 $σ_{c}$ $σ_{c}$ 和弹性模量E进行整理,绘制参数统计直方图,并采用K-S检验法分别对3种假设分布类型进行了检验。其中,28～32 mm粒组的参数统计直方图和最优概率密度曲线如图5所示,限于篇幅,其他粒组略。各粒组的K-S检验结果详见表3,结果表明：①参数 $σ_{c}$ $σ_{c}$ 和E对于Weibull分布、Lognormal分布和Logistic分布都可接受；②对参数 $σ_{c}$ $σ_{c}$ 和E可以直接判定最优分布类型是Lognormal分布。

图 5 石灰岩颗粒参数统计直方图和最优概率密度曲线

Figure 5. Statistical histograms and optimal probability density functions of parameters for limestone particles

下载: 全尺寸图片幻灯片

表 3 石灰岩颗粒强度和弹性模量分布类型的K-S检验

Table 3. K-S test results of distribution types for strength and elastic modulus of limestone particles

编号	粒组/mm	颗粒强度					弹性模量
编号	粒组/mm	均值/MPa	分布形式	K-S值	判断	最优分布	均值/MPa	分布形式	K-S值	判断	最优分布
①	20~24	13.108	Weibull	0.085	满足	Lognormal	1005.193	Weibull	0.097	满足	Lognormal
			Lognormal	0.055	满足			Lognormal	0.073	满足
			Logistic	0.068	满足			Logistic	0.103	满足
②	24~28	12.389	Weibull	0.092	满足	Lognormal	1113.994	Weibull	0.095	满足	Lognormal
			Lognormal	0.062	满足			Lognormal	0.089	满足
			Logistic	0.096	满足			Logistic	0.092	满足
③	28~32	11.977	Weibull	0.078	满足	Lognormal	928.598	Weibull	0.073	满足	Lognormal
			Lognormal	0.056	满足			Lognormal	0.072	满足
			Logistic	0.089	满足			Logistic	0.085	满足
④	32~36	11.673	Weibull	0.128	满足	Lognormal	839.674	Weibull	0.100	满足	Lognormal
			Lognormal	0.112	满足			Lognormal	0.067	满足
			Logistic	0.126	满足			Logistic	0.084	满足
⑤	36~40	10.438	Weibull	0.084	满足	Lognormal	801.380	Weibull	0.102	满足	Lognormal
			Lognormal	0.040	满足			Lognormal	0.084	满足
			Logistic	0.077	满足			Logistic	0.126	满足
⑥	60	6.442	Weibull	0.113	满足	Lognormal	544.306	Weibull	0.135	满足	Lognormal
			Lognormal	0.079	满足			Lognormal	0.096	满足
			Logistic	0.089	满足			Logistic	0.138	满足
⑦	120	5.242	Weibull	0.103	满足	Lognormal	422.451	Weibull	0.169	满足	Lognormal
			Lognormal	0.048	满足			Lognormal	0.107	满足
			Logistic	0.076	满足			Logistic	0.143	满足
⑧	240	3.394	Weibull	0.117	满足	Lognormal	281.528	Weibull	0.125	满足	Lognormal
			Lognormal	0.084	满足			Lognormal	0.119	满足
			Logistic	0.126	满足			Logistic	0.121	满足

下载: 导出CSV

| 显示表格

3.3 参数的尺寸效应模型

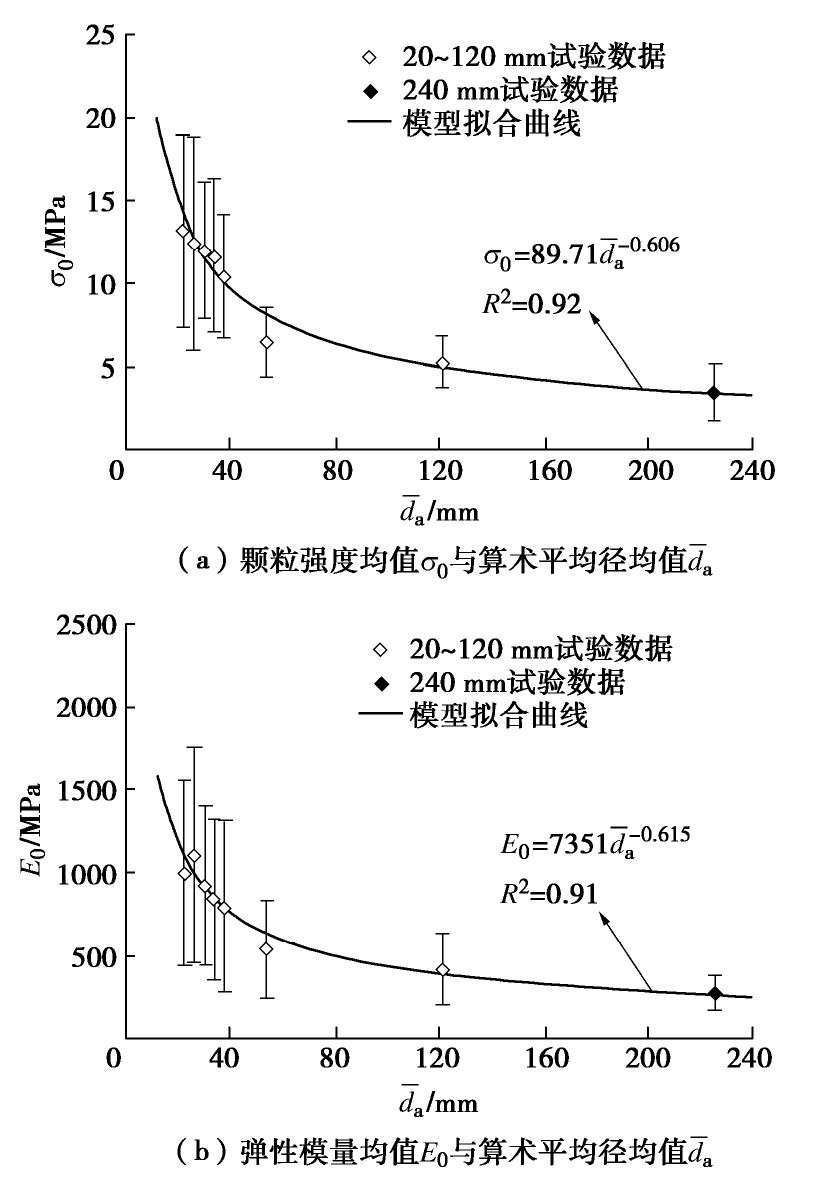
为进一步研究颗粒强度和弹性模量与粒径的相关性,选择参数均值作为其代表值绘制于图6中。由图6可知这两个参数与颗粒尺寸之间存在着明显的非线性相关性。为了能够简单明了地描述这一关系,采用式（13）的幂函数表达式对这一关系进行了拟合,并且将拟合结果作为参数的尺寸效应经验模型,拟合结果详见表4。

图 6 石灰岩颗粒参数的尺寸效应曲线

Figure 6. Curves of size effect of parameters for limestone particles

下载: 全尺寸图片幻灯片

表 4 参数的尺寸效应模型

Table 4. Models for size effect of parameters

参数名称	代表值含义及符号	尺寸效应模型	r²	预测误差/%
颗粒强度	均值 $σ_{0}$ $σ_{0}$	$σ_{0} =89 .71 {\bar{d}}_{a}^{- 0.606}$ $σ_{0} =89 .71 {\bar{d}}_{a}^{- 0.606}$	0.92	0.58
弹性模量	均值 $E_{0}$ $E_{0}$	$E_{0} = 7351 {\bar{d}}_{a}^{- 0.615}$ $E_{0} = 7351 {\bar{d}}_{a}^{- 0.615}$	0.91	6.61

下载: 导出CSV

| 显示表格

y = λ {\bar{d}}_{a}^{n}

$y = λ {\bar{d}}_{a}^{n}$ 。

(13)

式中 $y$ $y$ 为待研究参数代表值； ${\bar{d}}_{a}$ ${\bar{d}}_{a}$ 为颗粒算数平均径的均值； $λ$ $λ$ 和 $n$ $n$ 为拟合参数。为了验证本文所给的参数尺寸效应经验模型是否准确,对240 mm的颗粒试验结果进行了预测,颗粒强度 $σ_{c}$ $σ_{c}$ 、弹性模量E的预测值和试验值之间的相对误差分别为0.58%,6.61%,在可接受范围内。这表明,本文所给出的参数尺寸效应经验模型能够适用于更大的颗粒尺寸范围。尺寸效应经验模型的n值小于0说明大连石灰岩的颗粒强度和弹性模量的均值和颗粒尺寸之间呈负相关。该结果和前人统计结果一致^[12-13,17],同时弥补了对大尺寸不规则颗粒单轴压缩试验结果进行统计分析的空白。

4. 讨论

前文讨论了颗粒强度和弹性模量的随机分布规律和尺寸效应模型,除了上述两个参数外,颗粒刚度也是DEM数值模拟中需要考虑的重要参数之一。对于刚度的认识有两种：①认为刚度是线性的；②认为刚度是非线性的。而目前多把颗粒刚度看作是线性的。为了分析线性刚度和非线性刚度哪个更加符合实际情况,这里对石灰岩颗粒在破坏点之前的荷载—位移曲线进行了线性拟合（ $F = k s$ $F = k s$ ）和非线性拟合（ $F = C_{H} s^{3 / 2}$ $F = C_{H} s^{3 / 2}$ ）结果的对比,如图7所示。通过对每个颗粒线性拟合和非线性拟合结果的 $r^{2}$ $r^{2}$ 进行比较,发现本文试验有81.74%的颗粒用非线性拟合比线性拟合效果更好。这说明,在石灰岩颗粒受单轴压缩过程中,颗粒刚度用非线性来描述更加符合实际。

图 7 石灰岩颗粒荷载–位移曲线的线性拟合和非线性拟合结果对比

Figure 7. Comparison between linear fitting and nonlinear fitting results of load-displacement curves for limestone particles

下载: 全尺寸图片幻灯片

5. 结论

本文通过大量大连石灰岩颗粒单轴压缩试验,获得了颗粒强度和弹性模量的随机分布特征和尺寸效应经验模型,并对颗粒刚度的特点进行了初步讨论。这些统计结果反映了粗粒土颗粒在受力变形过程中的力学规律。建议在进行粗粒土DEM数值模拟时,对这些规律加以考虑。

（1）不仅粗粒土颗粒强度具有离散性,而且颗粒弹性模量同样具有离散性,该情况说明粗粒土颗粒在力学特性上表现出固有的离散性。

（2）大连石灰岩颗粒强度和弹性模量的最优概率分布类型是Lognormal分布。

（3）大连石灰岩颗粒强度和弹性模量的均值均与颗粒尺寸之间呈负相关,用幂函数拟合效果较好。可见,粗粒土颗粒强度和弹性模量都具有明显的尺寸效应。

（4）在石灰岩颗粒单轴压缩过程中,颗粒刚度用非线性来描述更加符合实际。

图 1 试验装置示意图

Figure 1. Schematic diagram of test instrument

下载: 全尺寸图片幻灯片

图 2 颗粒破碎前后的照片

Figure 2. Photos of a particle before and after breakage

下载: 全尺寸图片幻灯片

图 3 石灰岩颗粒的荷载–位移曲线

Figure 3. Force-displacement curve of limestone particles

下载: 全尺寸图片幻灯片

图 4 不规则颗粒受压示意

Figure 4. Diagram of compression on an irregular particle

下载: 全尺寸图片幻灯片

图 5 石灰岩颗粒参数统计直方图和最优概率密度曲线

Figure 5. Statistical histograms and optimal probability density functions of parameters for limestone particles

下载: 全尺寸图片幻灯片

图 6 石灰岩颗粒参数的尺寸效应曲线

Figure 6. Curves of size effect of parameters for limestone particles

下载: 全尺寸图片幻灯片

图 7 石灰岩颗粒荷载–位移曲线的线性拟合和非线性拟合结果对比

Figure 7. Comparison between linear fitting and nonlinear fitting results of load-displacement curves for limestone particles

下载: 全尺寸图片幻灯片

表 1 石灰岩颗粒的基本物理参数

Table 1 Basic physical parameters of limestone particles

编号	粒组/mm	个数	算数平均径d_a/mm	球度S_p/%	质量m/g
①	20~24	82	22.13±1.97	74.07±7.53	11.24±2.90
②	24~28	78	25.83±2.03	76.54±7.49	18.10±3.72
③	28~32	76	30.17±2.25	74.34±6.99	26.50±5.99
④	32~36	77	33.81±2.43	75.70±7.49	37.26±7.89
⑤	36~40	76	37.32±2.88	75.99±7.13	48.57±9.81
⑥	60	35	53.89±4.48	77.98±6.68	183.52±31.40
⑦	120	38	120.99±8.31	77.30±6.25	2532.56±2928.13
⑧	240	20	225.35±16.42	78.80±5.07	13357.50±1884.72
注：表中格式为“均值±标准差”。

下载: 导出CSV

表 2 不同的θ对应的K_U（K_L）值（节选）^[23]

Table 2 Values of K_U (K_L) for various values of θ (excerpts)^[23]

θ/(°)	50	55	60	…	80	85	90
cos θ	0.6428	0.5736	0.5000	…	0.1736	0.0872	0.0
K_U(K_L)	1.198	1.235	1.267	…	1.342	1.349	1.351

下载: 导出CSV

表 3 石灰岩颗粒强度和弹性模量分布类型的K-S检验

Table 3 K-S test results of distribution types for strength and elastic modulus of limestone particles

编号	粒组/mm	颗粒强度					弹性模量
编号	粒组/mm	均值/MPa	分布形式	K-S值	判断	最优分布	均值/MPa	分布形式	K-S值	判断	最优分布
①	20~24	13.108	Weibull	0.085	满足	Lognormal	1005.193	Weibull	0.097	满足	Lognormal
			Lognormal	0.055	满足			Lognormal	0.073	满足
			Logistic	0.068	满足			Logistic	0.103	满足
②	24~28	12.389	Weibull	0.092	满足	Lognormal	1113.994	Weibull	0.095	满足	Lognormal
			Lognormal	0.062	满足			Lognormal	0.089	满足
			Logistic	0.096	满足			Logistic	0.092	满足
③	28~32	11.977	Weibull	0.078	满足	Lognormal	928.598	Weibull	0.073	满足	Lognormal
			Lognormal	0.056	满足			Lognormal	0.072	满足
			Logistic	0.089	满足			Logistic	0.085	满足
④	32~36	11.673	Weibull	0.128	满足	Lognormal	839.674	Weibull	0.100	满足	Lognormal
			Lognormal	0.112	满足			Lognormal	0.067	满足
			Logistic	0.126	满足			Logistic	0.084	满足
⑤	36~40	10.438	Weibull	0.084	满足	Lognormal	801.380	Weibull	0.102	满足	Lognormal
			Lognormal	0.040	满足			Lognormal	0.084	满足
			Logistic	0.077	满足			Logistic	0.126	满足
⑥	60	6.442	Weibull	0.113	满足	Lognormal	544.306	Weibull	0.135	满足	Lognormal
			Lognormal	0.079	满足			Lognormal	0.096	满足
			Logistic	0.089	满足			Logistic	0.138	满足
⑦	120	5.242	Weibull	0.103	满足	Lognormal	422.451	Weibull	0.169	满足	Lognormal
			Lognormal	0.048	满足			Lognormal	0.107	满足
			Logistic	0.076	满足			Logistic	0.143	满足
⑧	240	3.394	Weibull	0.117	满足	Lognormal	281.528	Weibull	0.125	满足	Lognormal
			Lognormal	0.084	满足			Lognormal	0.119	满足
			Logistic	0.126	满足			Logistic	0.121	满足

下载: 导出CSV

表 4 参数的尺寸效应模型

Table 4 Models for size effect of parameters

参数名称	代表值含义及符号	尺寸效应模型	r²	预测误差/%
颗粒强度	均值 $σ_{0}$ $σ_{0}$	$σ_{0} =89 .71 {\bar{d}}_{a}^{- 0.606}$ $σ_{0} =89 .71 {\bar{d}}_{a}^{- 0.606}$	0.92	0.58
弹性模量	均值 $E_{0}$ $E_{0}$	$E_{0} = 7351 {\bar{d}}_{a}^{- 0.615}$ $E_{0} = 7351 {\bar{d}}_{a}^{- 0.615}$	0.91	6.61

下载: 导出CSV

参考文献(26)

[1]	贾宇峰, 王丙申, 迟世春. 堆石料剪切过程中的颗粒破碎研究[J]. 岩土工程学报, 2015, 37(9): 1692-1697. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201509024.htm JIA Yu-feng, WANG Bing-shen, CHI Shi-chun. Particle breakage of rockfill during triaxial tests[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1692-1697. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201509024.htm
[2]	刘汉龙, 秦红玉, 高玉峰, 等. 堆石粗粒料颗粒破碎试验研究[J]. 岩土力学, 2005, 26(4): 562-566. doi: 10.3969/j.issn.1000-7598.2005.04.011 LIU Han-long, QIN Hong-yu, GAO Yu-feng, et al. Experimental study on particle breakage of rockfill and coarse aggregates[J]. Rock and Soil Mechanics, 2005, 26(4): 562-566. (in Chinese) doi: 10.3969/j.issn.1000-7598.2005.04.011
[3]	张季如, 祝杰, 黄文竞. 侧限压缩下石英砂砾的颗粒破碎特性及其分形描述[J]. 岩土工程学报, 2008, 30(6): 783-789. doi: 10.3321/j.issn:1000-4548.2008.06.001 ZHANG Ji-ru, ZHU Jie, HUANG Wen-jing. Crushing and fractal behaviors of quartz sand-gravel particles under confined compression[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(6): 783-789. (in Chinese) doi: 10.3321/j.issn:1000-4548.2008.06.001
[4]	孔宪京, 刘京茂, 邹德高, 等. 紫坪铺面板坝堆石料颗粒破碎试验研究[J]. 岩土力学, 2014, 35(1): 35-40. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201401004.htm KONG Xian-jing, LIU Jing-mao, ZOU De-gao, et al. Experimental study of particle breakage of Zipingpu rockfill material[J]. Rock and Soil Mechanics, 2014, 35(1): 35-40. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201401004.htm
[5]	蔡正银, 李小梅, 关云飞, 等. 堆石料的颗粒破碎规律研究[J]. 岩土工程学报, 2016, 38(5): 923-929. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201605019.htm CAI Zheng-yin, LI Xiao-mei, GUAN Yun-fei, et al. Particle breakage rules of rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 923-929. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201605019.htm
[6]	CHENG Y P, NAKATA Y, BOLTON M D. Discrete element simulation of crushable soil[J]. Géotechnique, 2003, 53(7): 633-641. doi: 10.1680/geot.2003.53.7.633
[7]	DELUZARCHE R, CAMBOU B. Discrete numerical modelling of rockfill dams[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(11): 1075-1096. doi: 10.1002/nag.514
[8]	ALAEI E, MAHBOUBI A. A discrete model for simulating shear strength and deformation behaviour of rockfill material, considering the particle breakage phenomenon[J]. Granular Matter, 2012, 14(6): 707-717. doi: 10.1007/s10035-012-0367-7
[9]	CIANTIA M O, ARROYO M, BUTLANSKA J, et al. DEM modelling of cone penetration tests in a double-porosity crushable granular material[J]. Computers and Geotechnics, 2016, 73(1): 109-127.
[10]	邵晓泉, 迟世春, 陶勇. 堆石料剪切强度与变形的尺寸效应模拟[J]. 岩土工程学报, 2018, 40(10): 1766-1772. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201810003.htm SHAO Xiao-quan, CHI Shi-chun, TAO Yong. Numerical simulation of size effect on shear strength and deformation behavior of rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(10): 1766-1772. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201810003.htm
[11]	MCDOWELL G R, BOLTON M D, ROBERTSON D. The fractal crushing of granular materials[J]. Journal of the Mechanics and Physics of Solids, 1996, 44(12): 2079-2102.
[12]	MCDOWELL G R, BOLTON M D. On the micromechanics of crushable aggregates[J]. Géotechnique, 1998, 48(5): 667-679.
[13]	迟世春, 王峰, 贾宇峰, 等. 考虑细观单粒强度的堆石料破碎特性研究[J]. 岩土工程学报, 2015, 37(10): 1780-1785. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201510007.htm CHI Shi-chun, WANG Feng, JIA Yu-feng, et al. Modeling particle breakage of rockfill materials based on sigle particle strength[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(10): 1780-1785. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201510007.htm
[14]	张明, 卢裕杰, 杨强. 准脆性材料的破坏概率与强度尺寸效应[J]. 岩石力学与工程学报, 2010, 29(9): 1782-1789. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201009007.htm ZHANG Ming, LU Yu-jie, YANG Qiang. Failure probability and strength size effect of quasi-brittle materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(9): 1782-1789. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201009007.htm
[15]	米晓飞, 迟世春. 堆石颗粒强度的尺寸效应研究[J]. 水利与建筑工程学报, 2019, 17(4): 182-187, 197. https://www.cnki.com.cn/Article/CJFDTOTAL-FSJS201904032.htm MI Xiao-fei, CHI Shi-chun. Size effects of rockfill particle strength[J]. Journal of Water Resources and Architectural Engineering, 2019, 17(4): 182-187, 197. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-FSJS201904032.htm
[16]	MCDOWELL G R. Discussion: a probabilistic approach to sand particle crushing in the triaxial test[J]. Géotechnique, 2001, 51(3): 285-287.
[17]	PORTNIKOV D, KALMAN H. Determination of elastic properties of particles using single particle compression test[J]. Powder Technology, 2014, 268(8): 244-252.
[18]	杨作梅, 孙静鑫, 郭玉明. 不同含水率对谷子籽粒压缩力学性质与摩擦特性的影响[J]. 农业工程学报, 2015, 31(23): 253-260. https://www.cnki.com.cn/Article/CJFDTOTAL-NYGU201523034.htm YANG Zuo-mei, SUN Jing-xin, GUO Yu-ming. Effect of moisture content on compression mechanical properties and frictional characteristics of millet grain[J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(23): 253-260. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-NYGU201523034.htm
[19]	MADER-ARNDT K, AMAN S, FUCHS R, et al. Contact properties determination of macroscopic fine disperse glass particles via compression tests in normal direction[J]. Advanced Powder Technology, 2017, 28(1): 101-114.
[20]	YAP S F, ADAMS M J, SEVILLE J P K, et al. Single and bulk compression of pharmaceutical excipients: evaluation of mechanical properties[J]. Powder Technology, 2008, 185(1): 1-10.
[21]	ANTONYUK S, TOMAS J, HEINRICH S, et al. Breakage behaviour of spherical granulates by compression[J]. Chemical Engineering Science, 2005, 60(14): 4031-4044.
[22]	JAEGER J C. Failure of rocks under tensile condition[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1967, 4(2): 219-227.
[23]	Compression Test of Food Materials of Convex Shape: ASAE S368.4 DEC2000 (R2017)[S]. 2017.
[24]	蔡美峰. 岩石力学与工程[M]. 北京: 科学出版社, 2002. CAI Mei-feng. Rock Mechanics and Engineering[M]. Beijing: Science Press, 2002. (in Chinese)
[25]	魏治文, 程琳, 来记桃, 等. 几种异常值判别准则在安全监测数据处理中的应用[J]. 大坝与安全, 2009, 23(1): 67-69, 84. WEI Zhi-wen, CHENG Lin, LAI Ji-tao, et al. Application of some statistical criteria in safety monitoring data processing[J]. DAM & Safety, 2009, 23(1): 67-69, 84. (in Chinese)
[26]	马建全, 李广杰, 徐佩华, 等. 基于拉丁方抽样及K-S检验的边坡可靠性分析[J]. 岩土力学, 2011, 32(7): 2153-2156. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201107042.htm MA Jian-quan, LI Guang-jie, XU Pei-hua, et al. Reliability analysis of slope with Latin hypercube sampling and K-S test[J]. Rock and Soil Mechanics, 2011, 32(7): 2153-2156. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201107042.htm

施引文献(12)

期刊类型引用(4)

1.	罗仁宇，李奇志，祖公博，黄云进，杨耿超，姚清河. 基于卷积神经网络的超分辨率格子Boltzmann方法研究. 力学学报. 2024(12): 3612-3624 . 百度学术
2.	侯娟，滕宇阳，李昊，刘磊. 多孔介质曲折度对膨润土衬垫渗透性能的影响. 湖南大学学报(自然科学版). 2022(01): 155-164 . 百度学术
3.	陈经明，周泽超，陈茜茜，李寻，罗跃. 酸法地浸采铀多井系统中渗透系数时空演化模拟. 有色金属科学与工程. 2022(03): 106-116 . 百度学术
4.	吴志平，刘波平，王康，李石滨，胡毕炜，胡必伟，游杰. 基于高性能计算的离散介质冲击过程. 计算机与现代化. 2022(10): 41-46 . 百度学术