松散堆积体隧道压力拱效应试验与数值模拟

昝文博; 赖金星; 邱军领; 曹校勇; 冯志华; 宋飞庭

doi:10.11779/CJGE202109011

松散堆积体隧道压力拱效应试验与数值模拟 English Version

昝文博^{1, 2,},
赖金星¹,
邱军领^1, ,,
曹校勇³,
冯志华^{1, 4},
宋飞庭^{1, 5}

1.
长安大学公路学院,陕西　西安　710064
2.
陕西工业职业技术学院土木工程学院,陕西　咸阳　712000
3.
中交第一公路勘察设计研究院,陕西　西安　710075
4.
河北省交通规划设计研究院,河北　石家庄　050011
5.
武警第二机动总队交通某部,西藏　林芝　860000

基金项目:

陕西省重点研发计划项目 2020SF-428

中交股份科技项目 2016-ZJGJ-ZX-1201

详细信息

作者简介:
昝文博(1994— ),男,讲师,博士研究生,主要从事隧道及地下工程方面的教学和科研。E-mail：zanwb@chd.edu.cn

通讯作者:
邱军领, E-mail：junlingqiu@chd.edu.cn

中图分类号: U451
计量
- 文章访问数: 315
- HTML全文浏览量: 19
- PDF下载量: 154
出版历程
- 收稿日期: 2021-02-05
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-08-31

Experiments and numerical simulations on pressure-arch effect for a tunnel in loose deposits

1.
School of Highway, Chang’an University, Xi'an 710064, China
2.
School of Civil Engineering, Shaanxi Polytechnic Institute, Xianyang 712000, China
3.
CCCC First Highway Consultants Co., Ltd., Xi'an 710075, China
4.
Hebei Provincial Communications Planning and Design Institute, Shijiazhuang 050011, China
5.
A Traffic Department of the Second Mobile Brigade of the Armed Police, Nyingchi 860000, China

摘要

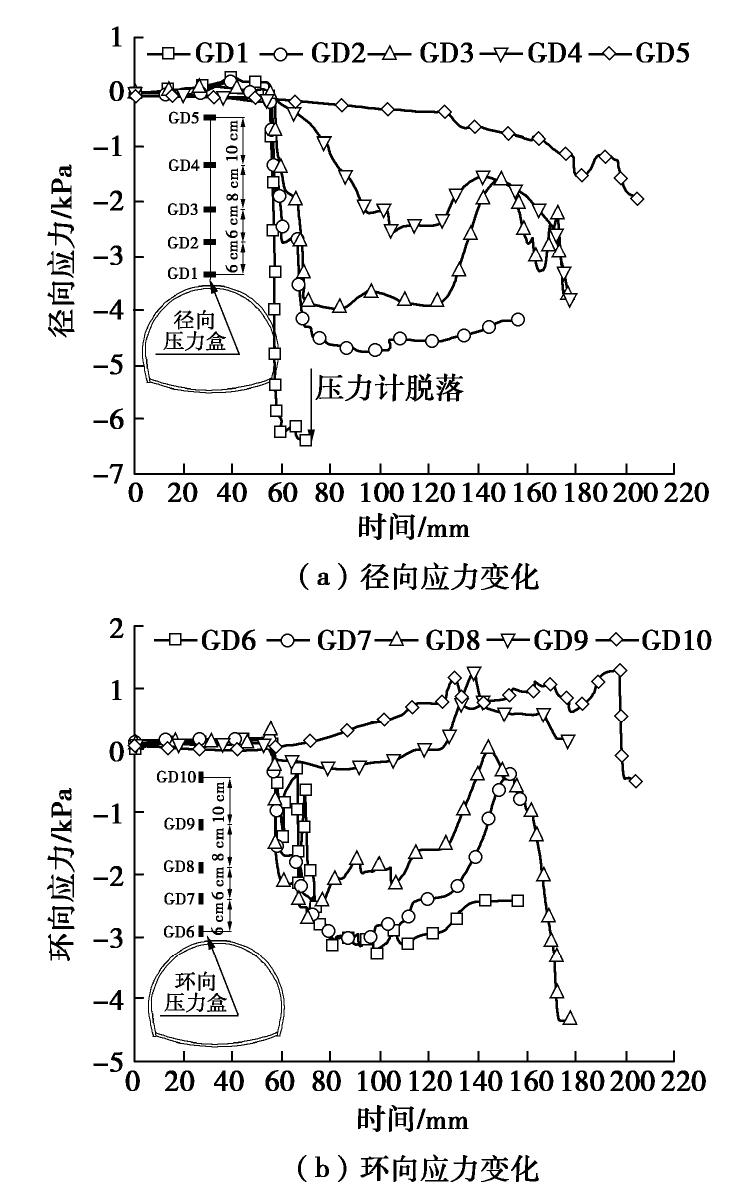
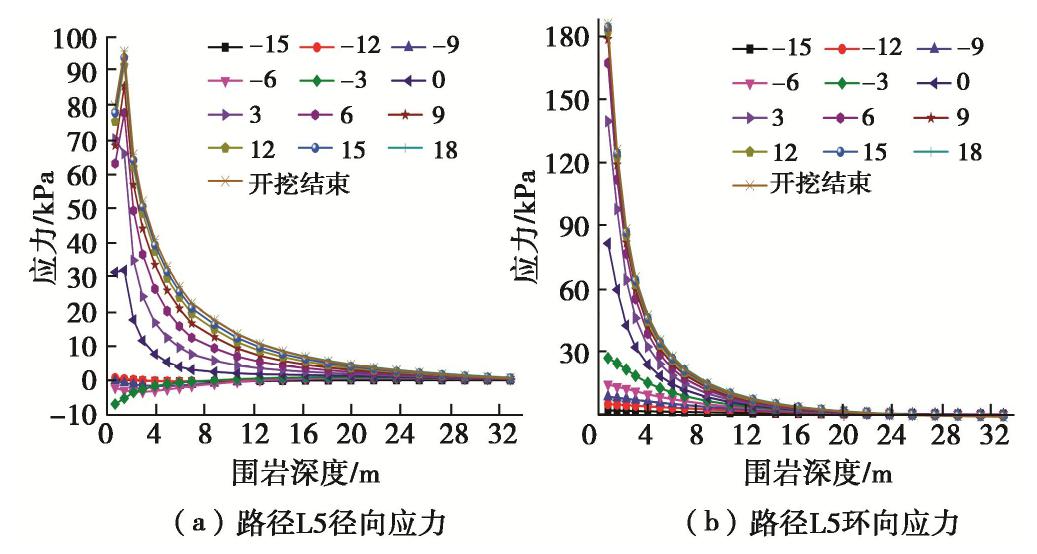
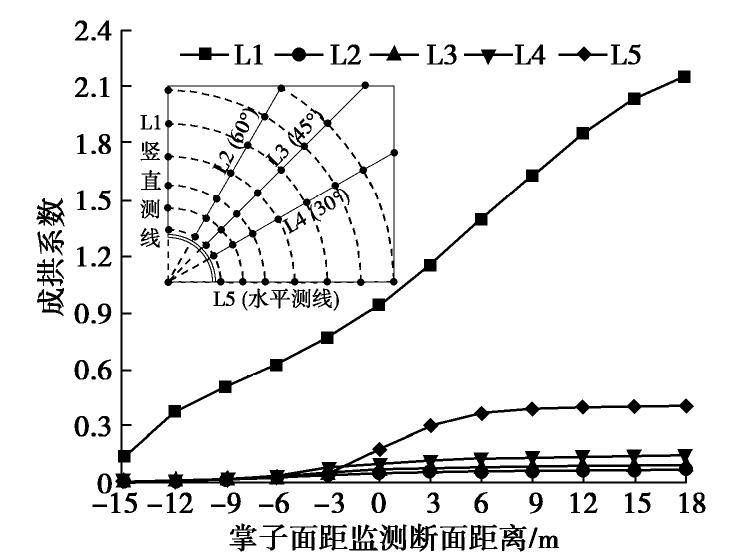
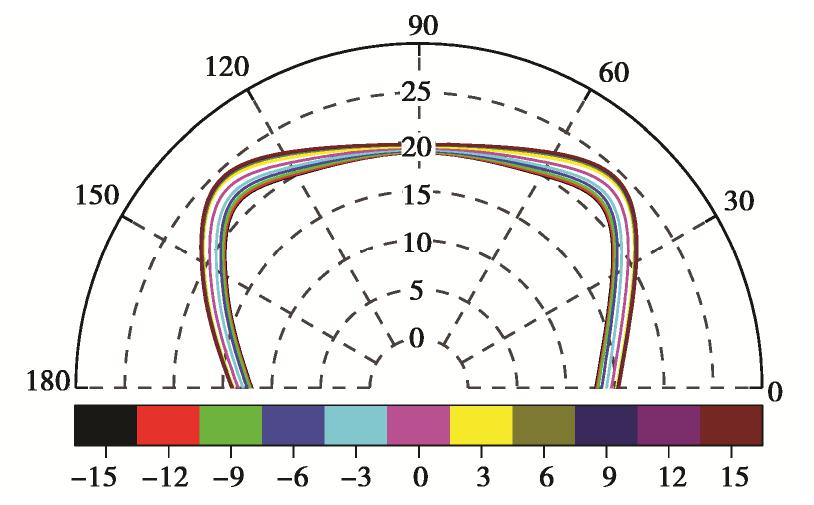
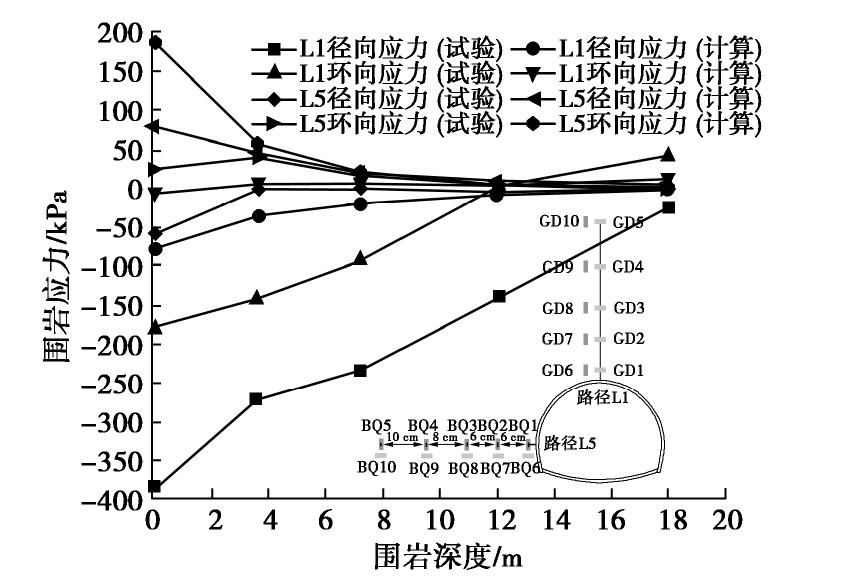
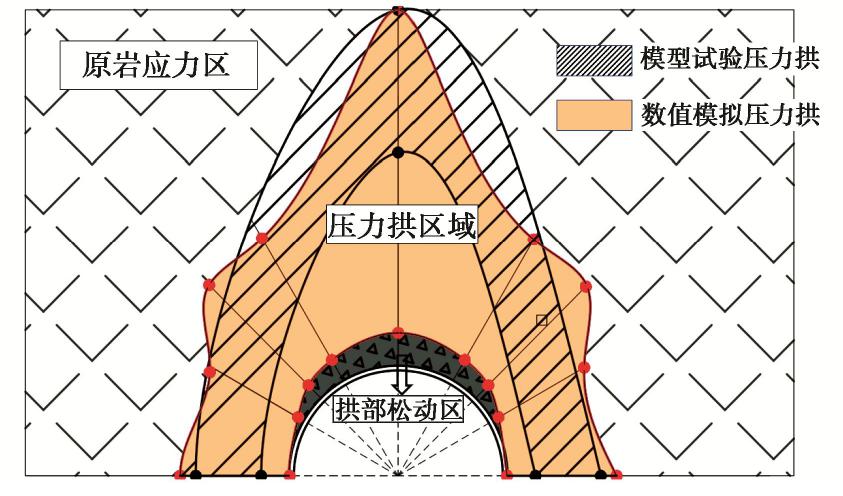
摘要: 以国道318线某堆积体隧道工程为背景,采用相似模型试验和有限元数值仿真相结合的方法研究松散堆积体隧道开挖引起的围岩应力扰动特征与压力拱形成机理,详细分析围岩径、环向应力变化及其压力拱的形成与稳定机制。结果表明：拱部围岩松动范围和松弛幅度均较大且已经延伸至地表,而边墙部位扰动深度较小但松弛幅度较大；拱部120°范围内围岩表现出明显的径向松动和环向成拱效应,边墙部位0～0.55倍开挖跨度范围内的围岩径向和环向应力显著增大形成高度应力集中区,承担着压力拱及其上的围岩荷重。围岩成拱系数具有显著的空间变化规律,其中拱顶成拱系数最大且随掌子面开挖近似呈线性增大,边墙成拱系数次之但受开挖空间效应的影响范围很小,30°～60°范围的成拱系数只在掌子面前后6 m范围内开挖时增长较大但很快便趋于稳定；试验和计算压力拱形状均呈尖拱形,它的形成对于维持洞室的稳定和减小支护结构的受力具有十分重要的意义。
- 隧道工程 /
- 松散堆积体 /
- 围岩应力 /
- 压力拱 /
- 数值模拟
Abstract: A tunnel in loose deposits, located in the National Highway No. 318, is referenced to investigate the stress disturbance characteristics and mechanism of pressure arch through a combination of physical tests and numerical simulations. The radial and circumferential stresses, formation and stability mechanism of the pressure arch are analyzed. The results show that the loose zone and extent of rock mass are larger and extend to the surface at tunnel arch, whereas a smaller zone and a larger extent are observed at tunnel sidewall. The rock mass within 120° at the arch shows an obvious radial loosing and circumferential arching effect. The rock mass within the range of 0~0.55 times the excavation span is identified to be the pressure-arch zone at the sidewall where the radial and circumferential stresses obviously increase, resulting in a high-stress concentration zone to bear the load of pressure arch and its surrounding rock. The arching coefficient has a significant spatial variation, meanwhile, it increases linearly with tunnel excavation and has the largest value at the vault, followed by that at the sidewall, in which the excavation space effect shows a marginal influence. The arching coefficient within the range of 30°~60° increases greatly when excavating within the range of 6 m before and behind the tunnel face, but it tends to be stable sooner. Both the experimental and calculated pressure arches exhibit pointed-arch shapes. Their formation is of great significance to maintaining the tunnel stability and reducing the stress of support structure.
- tunnel engineering /
- loose deposit /
- stress of rock mass /
- pressure arch /
- numerical simulation

HTML全文

0. 引言

中国水资源时空分布与社会经济发展不协调问题日益突出^[1]，为此“十四五”规划中重点强调：“要加强水利基础设施建设，提升水资源优化配置和水旱灾害防御能力”^[2]。水资源配置工程中，引调水管线的应用较为普遍，通常具有流量大、线路长、跨越的地形地质条件复杂等特点，管线的长期安全稳定运行，对整个工程至关重要。埋地钢管（也称回填钢管）特别适用于大直径、高内压和复杂外部环境的管线工程，在引调水及水电工程中得到了极大的关注，其未来发展潜力巨大。鉴于目前工程中的需求，新修编的《水利水电工程压力钢管设计规范》SL/T 281规范在参考国内外相关规范的基础上，着重增补了埋地钢管的相关设计内容^[3-4]。

埋地钢管为柔性管道，管土间存在复杂的相互作用，由钢管和土体共同承担外部荷载。覆土产生的土压力是钢管主要的外部荷载，故管顶土压力（以下简称土压力）的确定是埋地钢管结构设计的基础。土压力计算公式最早由Marston于1913年提出，假定沟槽内土体沿着沟槽侧壁滑移，管道承担全部回填土荷载，但对柔性管道适用性差^[5]。Spangler修正了该理论，假定沟槽内的土压力在管道和回填土上均匀分布，使其适用于柔性管道^[6]。由于Marston荷载仅考虑了直壁沟槽，Li等^[7]对其进行了改进，提出了梯形槽下的土压力计算公式。Shmulevich等^[8]对管径0.87~1.3 m的柔性管道的试验结果表明，土压力并非均匀分布，径向和切向土压力近似呈抛物线分布。周正峰等^[9-10]对管径0.61 m的埋地钢管开展有限元研究、李永刚^[11]对管径0.1 m和0.2 m钢管开展土箱试验，均得出土压力在管中心位置最大，从管中心向管侧大致呈抛物线分布。Tian等^[12]认为土压力在管中心存在波谷，将管中心到两侧土压力简化为抛物线分布，并对0.5 m及1 m管径的埋地钢管进行数值验证。Kawabata等^[13-14]分析了高埋深下管径0.9 m的柔性管道土压力情况，土压力呈“凹”形分布。伍鹤皋等^[15-16]以管径3 m的埋地钢管为研究对象，发现土压力分布与管径大小有关，并随着管道运行工况的变化而改变。周敏等^[17]采用室内试验，研究了地层沉陷下埋地柔性管道变形及土压力变化情况。

针对埋地钢管的研究，以往主要集中在给排水及油气行业，研究对象多为小直径管道，对于大直径管道（管径不小于1.2 m）的研究相对较少。随着国内引调水工程及水电工程的发展，水利行业大直径埋地钢管的应用逐渐增多，传统的土压力计算方法不能完全适用。为此，本文采用有限元法，分析了埋地钢管在不同管径、径厚比及埋深下的土压力情况，考虑到土压力的影响因素较为复杂，探讨了回填土参数、沟槽侧壁土-土摩擦系数及沟槽宽度的影响，对比分析了传统的棱柱荷载及Marston荷载的优劣，进而提出了较为适用于大直径埋地钢管的土压力模型。

1. 计算模型

1.1 模型介绍

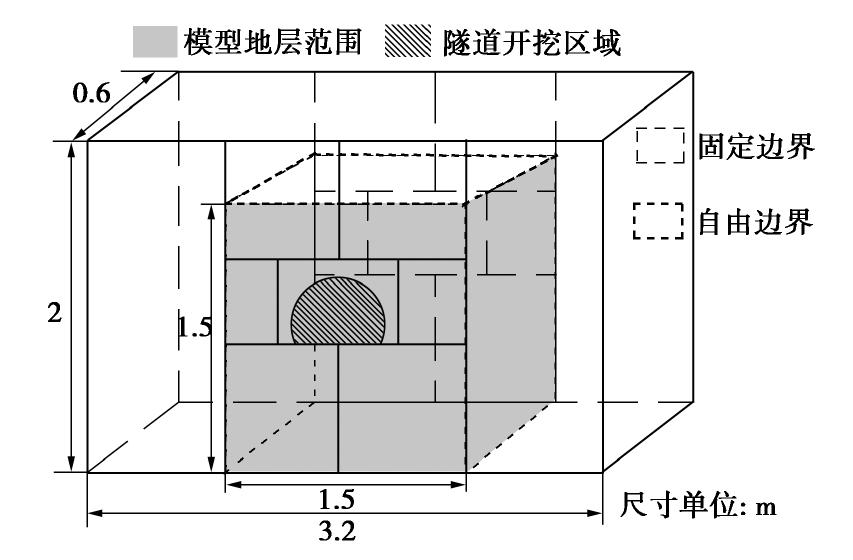
埋地钢管ANSYS有限元计算模型如图 1所示。采用直壁沟槽，假定管径为D，管顶覆土为H，沟槽宽度B为2D，沟槽深为H₁，管底垫层厚度0.3 m，垫层包角90°。模型底部、前后及左右端面施加沿法向的位移约束，顶面自由，整个模型宽为7B，高为4H₁，以消除边界条件的影响。钢管采用4节点壳单元SHELL 181模拟，土体采用8节点实体单元SOLID 45模拟。钢管采用的弹性模量、泊松比和密度分别为2.06×10⁵ MPa，0.3和7850 kg/m³。计算采用典型的土体参数进行分析见表 1。根据规范SL/T 281或CECS 141^[18]以及GB 50268^[19]，可确定典型土体种类及变形模量；根据规范及工程经验，土的密度通常为1600~2200 kg/m³；黏性土的泊松比为0.25~0.42，黏聚力为2~65 kPa，内摩擦角为15°~30°；砂土的泊松比为0.25~0.3，内摩擦角为28°~42°^[20-21]。

图 1 有限元计算模型

Figure 1. Finite element model

下载: 全尺寸图片幻灯片

表 1 土体种类及其材料参数

Table 1. Soil types and material parameters

名称	土体种类	变形模量/MPa	泊松比	黏聚力/kPa	内摩擦角/(°)	密度/(kg·m^-3)
原状土	黏性土；标准锤击数N_63.5 > 50	10	0.35	10	30	1800
回填土	黏性土；压实系数95%	5	0.35	10	30	1800
砂垫层	砂砾，细粒土含量不大于12%；压实系数95%	7	0.25	0	30	1800

下载: 导出CSV

| 显示表格

为满足美国土木工程师协会手册ASCE No.119^[22]对埋地钢管有限元模型可靠性的要求，土体本构关系采用经典的Drucker-Prager屈服准则^[23]；钢管与土体及沟槽侧壁土-土间设置面-面接触单元（TARGE 170和CONTA 174），并采用库仑摩擦模型模拟接触面间的相互关系，管-土及土-土间摩擦系数分别取0.25和0.577(tan30°)^{[9, 18]}。鉴于大直径埋地钢管施工时通常内部设置支撑，变形主要发生在施工完毕、撤去支撑阶段。为简化分析，模拟时通过直接调整土体模量及施加重力荷载的方式来实现土体碾压密实后管道所受土压力的效果。

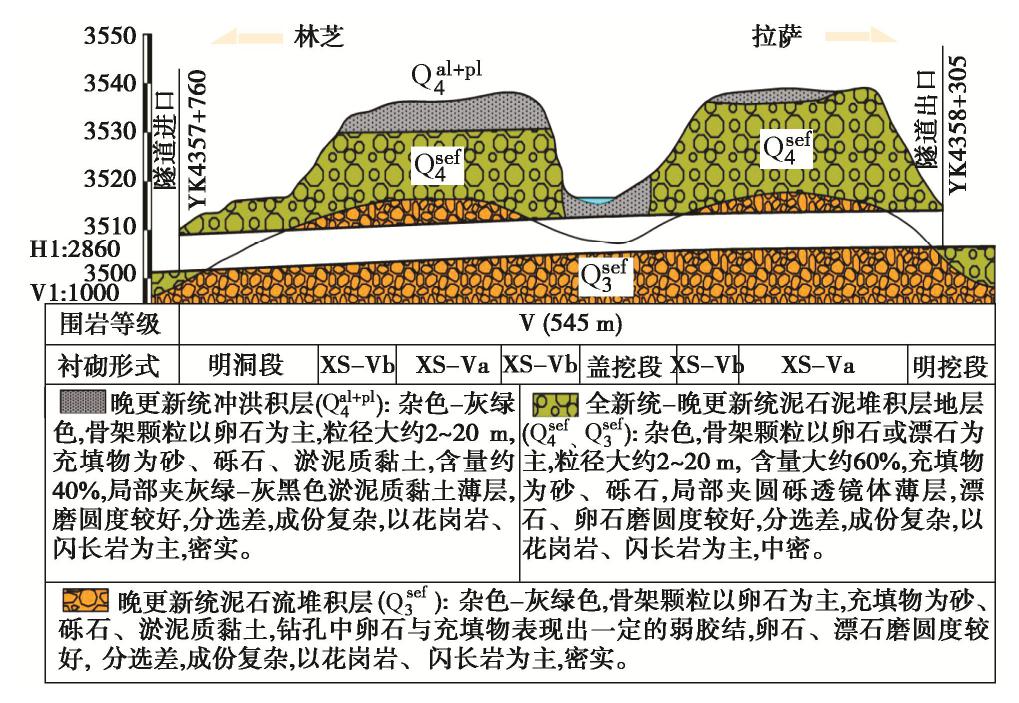
1.2 模型验证

为进一步说明本文有限元模拟技术的可靠性，结合试验结果，进行对比验证。文献[24]对埋地聚氯乙烯（PVC）塑料管道（管径150 mm，壁厚10 mm）进行土箱试验，获取了管周接触压力数据。建立相应的有限元模型，管材的弹性模量、泊松比和密度分别取3000 MPa，0.4，1400 kg/m³^[25]，土体参数采用试验给出的实测值。试验时土体上方施加50 kPa的均布压力。

图 2给出了有限元与试验的接触压力比较结果。可以看到，两种方法得出的管周接触压力从管顶到管底的分布趋势均为先减少、后增大，存在管顶/底大、管腰小特征；接触压力大小虽然有细微差别，但总体上较为接近。考虑到试验误差及模型简化等情况，故认为本文采用的有限元模拟技术具有较高的可靠性，可用于后续分析。

图 2 有限元与试验结果的管周接触压力比较

Figure 2. Comparison of contact pressures around pipes between finite element and test results

下载: 全尺寸图片幻灯片

2. 计算结果及分析

传统的土压力计算通常采用棱柱荷载 ${\sigma _{\text{p}}}$ 或Marston荷载 ${\sigma _{\text{M}}}$ ，均假定为均匀分布，但大小不同，计算见式（1），（2）。水利行业规范SL/T 281及给排水行业CECS系列规程均采用棱柱荷载。日本规范以2 m埋深为界，两种方法都有采用^[26]；美国水工协会手册AWWA M11中说明Marston荷载可用于窄槽下，棱柱荷载可作为保守设计^[6]。

${\sigma _{\text{M}}} = (1 - {{\text{e}}^{ - \frac{{2fK}}{B} \cdot H}})\gamma B/(2fK) = {C_{\text{d}}}\gamma B \text{, }$

(1)

${\sigma _{\text{p}}} = \gamma H。$

(2)

式中 $\gamma$ 为回填土的重度；B为沟槽宽度；f为沟槽侧壁土-土滑动摩擦系数；K为朗肯主动土压力系数；H为管顶埋深。

以管径D=3 m的埋地钢管为例，深入分析径厚比（管径D与壁厚t之比）及埋深对土压力的影响。土压力可从有限元计算获取的管周接触压力、切向力沿竖向方向分解得出。大直径埋地钢管的径厚比D/t通常在100~300范围内；为考虑埋深影响，在2~8 m范围内间隔2 m取值。

2.1 土压力分析

图 3为不同径厚比及埋深下的土压力分布。可以看出，埋深2 m、径厚比100时，土压力近似呈“倒盆形”分布，即土压力在管中心区域分布平坦，在距离管中心约（0.25~0.4）D处开始呈抛物线式急剧降低。随着径厚比的增加，土压力峰值逐步降低并从管中心区域移向管侧胸腔。这是由于径厚比增大后，管道竖向收缩变形加剧，胸腔管壁趋向平坦，承担了更多的土压力。此外，径厚比在100~150范围变动时，土压力降幅明显，大于200后，变化很小。埋深增加后，可明显加大土压力，对管道受力变形不利。埋深越深，土压力分布在管中心区域内凹越严重、管侧胸腔越突出，越易趋向“M形”。埋深越深，不同径厚比下，土压力峰值差也相应增加，如径厚比100与200下的峰值差，埋深4 m为埋深2 m的2.62倍。

图 3 不同径厚比D/t及埋深H下的土压力

Figure 3. Soil pressures under different diameter-thickness ratios D/t and cover depths H

下载: 全尺寸图片幻灯片

2.2 大小比较

将棱柱荷载 ${\sigma _{\text{p}}}$ 、Marston荷载 ${\sigma _{\text{M}}}$ 分别与数值计算得出的峰值土压力 ${\sigma _{{\text{max}}}}$ 、均值土压力 ${\sigma _{{\text{avg}}}}$ （土压力沿管径积分后除以管径）进行比较如图 4所示。可以看出，埋深2 m时，两种荷载与峰值土压力吻合良好，偏差均在10%以内，且径厚比越小，比较结果越低，甚至会低于1。由于土压力并不是均匀分布，其均值较峰值会有所降低，相较于均值土压力，两种荷载显著偏大，增幅在20%以内。埋深增加后，棱柱荷载和Marston荷载的准确性均显著降低，如埋深6 m时，较峰值土压力最大增幅分别为58%和31%，与均值土压力的相差则更大。

图 4 棱柱荷载

${\sigma _{\text{p}}}$ 、Marston荷载

${\sigma _{\text{M}}}$ 与有限元结果的比较

Figure 4. Comparison of prism load

${\sigma _{\text{p}}}$ and Marston load

${\sigma _{\text{M}}}$ with finite element results

下载: 全尺寸图片幻灯片

可见，棱柱荷载和Marston荷载存在两处问题，首先其假定的土压力均匀分布虽计算简便，但与实际差别较大；其次是当管道埋深高、径厚比大时，其大小偏差较大。此外，相较于棱柱荷载，Marston荷载在高埋深时，误差相对较小，但低埋深时，其结果偏小。

3. 敏感性分析

3.1 管径的影响

以管径D=1.5 m和0.5 m的钢管为研究对象，分别按照径厚比D/t=100~300和50~250（小直径管道的径厚比通常较小），埋深H=2 m和4 m进行参数分析，对比分析管顶土压力的分布情况及大小。

（1）土压力分析

各管径、径厚比及埋深下的土压力计算结果如图 5所示。可以看出，管径为1.5 m时，随着径厚比的增加，土压力分布逐步由抛物线向“倒盆形”过渡。当埋深较深、径厚比大即管道变形大时，管侧胸腔出现峰值，这与管径3 m的变化规律较为类似，不同之处在于，管径越小，土压力越倾向抛物线分布。与大直径管道不同，管径为0.5 m时，土压力均呈抛物线分布，这与以往小直径管道的研究结论基本相同。径厚比增加后，土压力峰值有所降低，特别是当径厚比从50变为100时，降幅最为显著，这是由于当径厚比为50时，钢管为刚性管道，承受了更多的覆土重，与柔性管道存在明显不同。

图 5 不同管径D、径厚比D/t及埋深H下的土压力

Figure 5. Soil pressures under different pipe diameters D, diameter-thickness ratios D/t and cover depths H

下载: 全尺寸图片幻灯片

基于上述分析可知，大/小直径管道土压力分布基本形式分别为“倒盆形”和抛物线。这是由于管径大后，土拱效应减弱，胸腔管壁分担的土压力增加，且胸腔土体体积会明显变大，加深了其影响程度。

（2）大小比较

图 6为不同管径下棱柱荷载、Marston荷载与有限元结果的比较。管径1.5 m与3 m的管道，土压力大小比较规律总体较为类似，但1.5 m管径下的偏差显著扩大，如埋深2 m时，棱柱荷载和Marston荷载分别最大为峰值/均值土压力的1.4/1.59和1.24/1.4倍。管径0.5 m的小直径管道，由于其土压力分布变化幅度较大，使得峰值与均值土压力存在较大差异。棱柱荷载除在埋深浅、径厚比特别小时，可能稍低于峰值土压力，其余情况下均远大于峰值/均值土压力，且埋深越深，径厚比越大，越显著。而Marston荷载在径厚比小时，远低于峰值土压力，但与均值土压力较为接近。

图 6 棱柱荷载

${\sigma _{\text{p}}}$ 、Marston荷载

${\sigma _{\text{M}}}$ 与有限元结果的比较

Figure 6. Comparison of prism load

${\sigma _{\text{p}}}$ and Marston load

${\sigma _{\text{M}}}$ with finite element results

下载: 全尺寸图片幻灯片

国内外研究多以小直径管道为研究对象，其径厚比及埋深通常较小，此时Marston荷载结果远小于土压力峰值，而棱柱荷载的安全性较高且计算简便，故多推荐采用棱柱荷载进行埋地钢管的结构设计。但对大直径管道而言，高埋深下Marston荷载大小与实际较为接近且总体偏大，而棱柱荷载明显过大，故对大直径、高埋深的管道，土压力计算可考虑采用Marston荷载。

3.2 相关参数的敏感性分析

以管径3 m的埋地钢管为例，埋深取2 m、径厚比取200，对回填土变形模量、泊松比、沟槽侧壁土–土摩擦系数及沟槽宽度进行敏感性分析。基于规范及工程经验，计算时回填土变形模量取3~9 MPa；回填土泊松比取0.25~0.42；土–土摩擦系数取0.2~0.8^{[18, 20]}。基于ASCE No.119的建议，上述分析采用的沟槽宽度B均为2倍管径，但工程中沟槽宽度的确定多基于施工条件，如按GB50268确定的最小沟槽宽度B/D约为1.5，分析时适当扩大B/D范围取1.5~3。

各参数下的土压力分布如图 7所示。可以看出，回填土模量的增加使得土压力减小，这是由于土体模量越大，填土越紧密，从而更易形成整体，起到一定的拱效应。泊松比、土–土摩擦系数与变形模量的土压力变化规律较为类似，在此不再赘述。对比第2节模型结果，回填土变形模量、泊松比和土–土摩擦系数的改变，分别使峰值土压力在原模型的基础上变化-7.6%~5.5%、-5.2%~6.1%、-6.1%~10%，均在10%以内。沟槽越宽，沟槽侧壁的影响越小，管道所受的土压力逐渐增大，但峰值土压力波动范围仅为-12.1%~14.2%。此外，对于埋深4 m的情况同样进行了参数敏感性分析，结果与上述分析类似。因此，工程实践中，为改善管道受力条件，应尽可能的提高回填土的材料性能、增加回填土与原状土的接触面粗糙程度及采用较窄的沟槽，以减轻土压力。

图 7 相关参数的敏感性分析

Figure 7. Sensitivity analysis of related parameters

下载: 全尺寸图片幻灯片

4. 盆式土压力模型

以往的土压力分布多假定为均匀或抛物线形式，而大直径管道的基本形式为“倒盆形”，与传统假定存在较大区别。为此，本文提出一种新型的土压力计算模型-盆式模型，来模拟大直径管道的土压力分布，计算图式如图 8所示。

图 8 盆式模型计算图式

Figure 8. Calculation diagram of basin model

下载: 全尺寸图片幻灯片

4.1 “直线+抛物线”土压力分布形式

上述分析中土压力分布的界限大体在距离管中心（0.25~0.4）D处，后经多次试算并考虑计算方便性，在盆式模型中假定以距离管中心D/3为界限，在[0，D/3]范围内为均匀分布即土压力 $\sigma$ 为一定值，[D/3，D/2]为抛物线分布，即采用“直线+抛物线”的盆形来描述大直径管道顶部的土压力分布形式。由于盆式土压力分布关于轴线对称，以图 8的右半侧为例进行土压力分布公式推导，过程如下。

当 $0 \leqslant x \leqslant D/3$ 时，

$y{\text{(}}x{\text{)}} = \sigma \text{, }$

(3)

当 $D/3 \leqslant x \leqslant D/2$ 时，在x₁-y₁坐标系内，假定抛物线方程为

${x_1}^2 = - 2p{y_1} \text{, }$

(4)

代入边界条件： ${x}_{1}=D/6，{y}_{1}=-\sigma$ ，得 $p = {{{D^2}} / {{\text{72}}\sigma }}$ ，故在x₁-y₁坐标系内，抛物线方程为

${x_1}^2 = - \frac{{{D^2}}}{{{\text{36}}\sigma }}{y_1} \text{, }$

(5)

经坐标变换，

${\left( {x - \frac{D}{{\text{3}}}} \right)^2} = - \frac{{{D^2}}}{{{\text{36}}\sigma }}{\kern 1pt} (y - \sigma ) \text{, }$

(6)

在x-y坐标系内，抛物线方程变为

$y(x) = - \frac{{{\text{36}}\sigma }}{{{D^2}}}{\left( {x - \frac{D}{{\text{3}}}} \right)^2}{\text{ + }}\sigma = - \frac{{{\text{36}}\sigma }}{{{D^2}}}{x^2}{\text{ + }}\frac{{{\text{24}}\sigma }}{D}x - {\text{3}}\sigma \text{, }$

(7)

故“直线+抛物线”土压力分布形式的公式表达为

$y(x) = \left\{ \begin{gathered} \sigma \hfill \\ - \frac{{{\text{36}}\sigma }}{{{D^2}}}{x^2}{\text{ + }}\frac{{{\text{24}}\sigma }}{D}x - {\text{3}}\sigma \hfill \\ \end{gathered} \right.\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {(0 \leqslant x \leqslant D/3)} \\ {(D/3 \leqslant x \leqslant D/2)} \end{array}} \end{array} 。$

(8)

4.2 “Marston+胸腔”荷载计算方法

相较于棱柱荷载，Marston荷载大小总体上较为接近实际土压力，高埋深时优势明显，但低埋深时结果偏小，这是由于以往埋地管道的管径较小，胸腔土体的影响很小，故传统的计算方法并未考虑其影响，但对大直径管道而言，浅埋时胸腔土体的影响很大。假定胸腔土体完全作用于管道，其产生的土压力沿管径均匀分布，计算公式为

$\sigma = {{\gamma \left( {\frac{{{D^2}}}{2} - \frac{1}{2}{\rm{ \mathsf{ π} }}\frac{{{D^2}}}{4}} \right)} \mathord{\left/ {\vphantom {{\gamma \left( {\frac{{{D^2}}}{2} - \frac{1}{2}{\rm{ \mathsf{ π} }}\frac{{{D^2}}}{4}} \right)} D}} \right. } D} = 0.107\gamma D 。$

(9)

为探究胸腔土体的影响程度，将胸腔土体产生的土压力与棱柱荷载进行比较，定义胸腔土压力影响因子 $\lambda$ 为

$\lambda = 0.107\gamma D/(\gamma H) \times 100{{\% }} = 0.107D/H \times 100{{\% }} 。$

(10)

可见，D/H越大，胸腔土体的影响越显著，如管径3 m、埋深2 m时，胸腔土体可在原有棱柱荷载的基础上增加16.1%的土压力；但当D/H < 1即管径小于埋深时，其影响低于10.7%。

工程实践中，小直径管道的管径通常远小于埋深，基本可以忽略胸腔土体的影响，但大直径管道的管径大于埋深的情况较为常见，胸腔土体应予以考虑。因此，针对大直径埋地钢管的特点，以Marston荷载为基础，考虑胸腔土体的影响，提出了“Marston+胸腔”荷载计算方法见图 9，计算公式为

$\sigma = \left\{ \begin{array}{l} {C_{\text{d}}}\gamma B{\text{ + }}0.107\gamma D\begin{array}{*{20}{l}} {}&{} \end{array} \hfill \\ {C_{\text{d}}}\gamma B \hfill \end{array} \right.\begin{array}{*{20}{l}} {{\text{(}}D > H{\text{)}}} \\ {(D \leqslant H{\text{)}}} \end{array} 。$

(11)

图 9 “Marston+胸腔”荷载计算示意

Figure 9. Calculation diagram of "Marston + pleura" load

下载: 全尺寸图片幻灯片

4.3 盆式模型适用性研究

为了研究本文提出的盆式模型的适用性，从管径、埋深及径厚比等方面，将盆式土压力模型的结果与有限元分析计算结果的土压力分布进行对比，比较结果如图 10所示。可以看出，当径厚比为100时，管道承受的土压力最大，受力最为不利，此时模型的吻合程度最高。直线段分布形式能够反应管中心区域土压力平缓变化特性，抛物线段分布形式可体现管腰附近土压力急剧变化情况。总体来看，该模型土压力分布范围基本上能够覆盖管道浅埋、深埋及各种径厚比情况，与有限元结果有较好的贴合度。径厚比越低，贴合程度越好，且对径厚比高、安全风险大的管道，存有较高的安全裕度。

图 10 各管径D、径厚比D/t及埋深H下的土压力

Figure 10. Soil pressures under different pipe diameters D, diameter-thickness ratios D/t, and cover depths H

下载: 全尺寸图片幻灯片

表 2为各土压力模型与有限元结果（径厚比为100）的比较。从峰值比较来看，盆式模型为有限元结果的0.93~1.11倍，相应的棱柱荷载及Marston荷载分别为有限元结果的0.66~1.57倍和0.64~1.04倍。3种模型比较而言，传统的棱柱和Marston荷载模型在管道埋深很浅时，土压力计算结果明显偏小，而盆式模型精确度有了显著的提升，尤其是在管径特别大的情况下。从均值比较来看，盆式模型为有限元结果的0.97~1.18倍，相应的棱柱荷载及Marston荷载分别为0.78~1.94倍和0.76~1.31倍，可见传统模型的土压力均匀分布形式有利有弊，虽能缩小浅埋时计算结果过小的误差，但同时也显著放大了高埋深下计算结果过大的缺陷，相较而言，盆式模型的分布形式更为优越。故无论是峰值比较还是均值比较，盆式模型的总体精确度均远高于传统模型，且适用范围更广。

表 2 各土压力模型与有限元结果（径厚比为100）的比较

Table 2. Comparison of soil pressure models and finite element results (diameter-thickness ratio of 100)

比较类型	埋深/m	峰值土压力比较				均值土压力比较
比较类型	埋深/m	管径1.2 m	管径2 m	管径3 m	管径4 m	管径1.2 m	管径2 m	管径3 m	管径4 m
盆式模型/有限元结果	1	1.01	1.00	0.99	0.93	1.18	1.07	1.00	0.97
	3	0.99	1.11	1.01	1.08	1.16	1.11	1.02	1.09
	7	0.94	1.01	1.03	1.04	1.03	1.09	1.11	1.10
棱柱荷载/有限元结果	1	0.96	0.86	0.77	0.66	1.26	1.03	0.87	0.78
	3	1.25	1.18	1.11	1.00	1.65	1.43	1.26	1.15
	7	1.57	1.39	1.28	1.23	1.94	1.69	1.55	1.46
Marston荷载/有限元结果	1	0.88	0.82	0.75	0.64	1.17	0.98	0.85	0.76
	3	0.99	1.02	1.01	0.93	1.31	1.24	1.15	1.07
	7	0.94	1.01	1.03	1.04	1.17	1.23	1.25	1.24

下载: 导出CSV

| 显示表格

总体而言，对于管径不小于1.2 m，径厚比在100~300范围内常见的大直径埋地钢管，该模型土压力分布形式较传统模型有了明显的提升，其计算方法较传统模型精确程度更高，适应性更强。其中对于径厚比为100的管道，误差控制在20%以内且总体偏大，对于径厚比更高的管道，该模型更为安全。此外，该模型对于小于1.2 m或径厚比低于100的埋地钢管以及其他埋地柔性管道是否适用，仍值得后续深入探讨。

5. 结论

（1）大/小直径管道的土压力分布基本形式分别为“倒盆形”和抛物线形，两者存在明显不同。径厚比及埋深对土压力影响显著，随着径厚比或埋深的增加，管道竖向收缩变形加剧，加大了胸腔管壁分担的荷载，土压力峰值逐步由管中心位置移向管侧胸腔，但径厚比大于200后，土压力变化很小。此外，土压力大小随着回填土变形模量及泊松比、沟槽侧壁土-土摩擦系数的增加而降低，影响程度均在10%以内；沟槽宽度的影响也较为有限，沟槽越宽，土压力越大。

（2）棱柱荷载和Marston荷载假定的均匀分布虽计算简便，但与大直径管道实际明显不符。棱柱荷载在高埋深时结果过大，而Marston荷载在低埋深时结果偏小，两种荷载的计算精度及适应性较差。大直径管道浅埋时，胸腔土体的影响需予以考虑。

（3）对于管径不小于1.2 m且径厚比不小于100的大直径埋地钢管提出了一种新型的管顶土压力计算模型-盆式模型，其荷载分布采用“直线+抛物线”形式，荷载大小按照“Marston+胸腔”荷载计算。该模型能够消减传统模型的缺陷，其土压力分布及大小基本能够覆盖管道浅埋、深埋及多种径厚比情况，计算精度及适应性较好，可为大直径埋地钢管的结构设计及规范制定提供借鉴和参考。

图 1 隧道地质纵断面图

Figure 1. Geological profile of tunnel

下载: 全尺寸图片幻灯片

图 2 模型箱尺寸示意图

Figure 2. Sketch map of model box

下载: 全尺寸图片幻灯片

图 3 量测断面测点布置图

Figure 3. Layout of measuring points for measurement section

下载: 全尺寸图片幻灯片

图 4 隧道开挖模型试验过程

Figure 4. Process of model tests on tunnel excavation

下载: 全尺寸图片幻灯片

图 5 拱顶路径围岩应力变化

Figure 5. Variation of stress of surrounding rock above vault

下载: 全尺寸图片幻灯片

图 6 边墙路径围岩应力变化

Figure 6. Variation of stress of surrounding rock at sidewall

下载: 全尺寸图片幻灯片

图 7 数值计算模型及应力提取路径

Figure 7. Numerical models and stress extraction paths

下载: 全尺寸图片幻灯片

图 8 路径L1应力变化

Figure 8. Variation of stress of path L1

下载: 全尺寸图片幻灯片

图 9 路径L2~L4应力变化

Figure 9. Variation of stress of path L2~L4

下载: 全尺寸图片幻灯片

图 10 路径L5应力变化

Figure 10. Variation of stress of path L5

下载: 全尺寸图片幻灯片

图 11 成拱系数随开挖步骤的变化

Figure 11. Variation of arching coefficient with tunnel excavation

下载: 全尺寸图片幻灯片

图 12 围岩压力拱形态变化

Figure 12. Variation of shape of pressure arch of surrounding rock

下载: 全尺寸图片幻灯片

图 13 计算与试验应力对比

Figure 13. Comparison between calculated and measured stresses

下载: 全尺寸图片幻灯片

图 14 松散堆积体隧道压力拱形态

Figure 14. Shape of pressure arch for tunnel in loose deposits

下载: 全尺寸图片幻灯片

表 1 相似材料配比

Table 1 Proportion of similar materials (%)

组成成分	2-4目石英砂	10-20目石英砂	20-40目石英砂	150目重晶石粉	600目重晶石粉
占比	35.7	34.8	9.7	10.5	9.3

下载: 导出CSV

表 2 原型及模型材料参数

Table 2 Parameters of materials of prototype and model

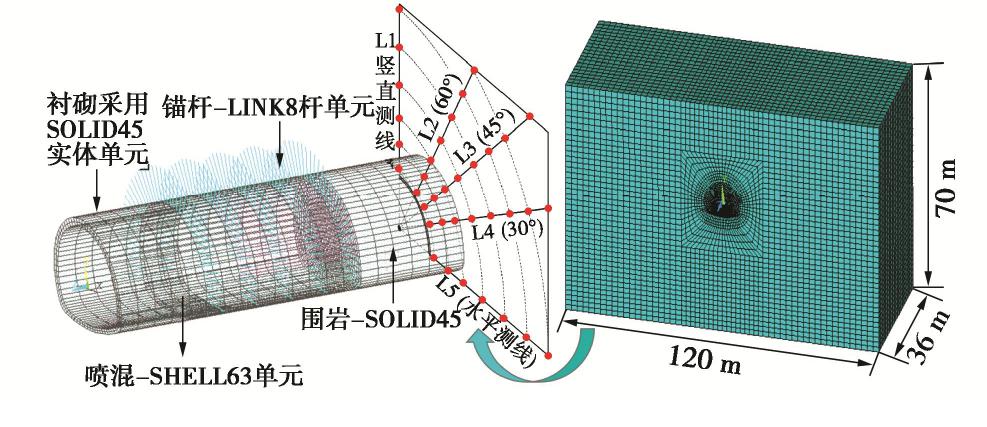
材料参数	内摩擦角φ/(°)	黏聚力c/kPa	泊松比μ	密度ρ/(g·cm^-3)	弹性模量E/MPa
原型	42.0	10.02	0.38	2.01	25
模型	41.6	13.71	0.38	1.98	0.40

下载: 导出CSV

表 3 围岩及支护计算参数

Table 3 Parameters of surrounding rock and support

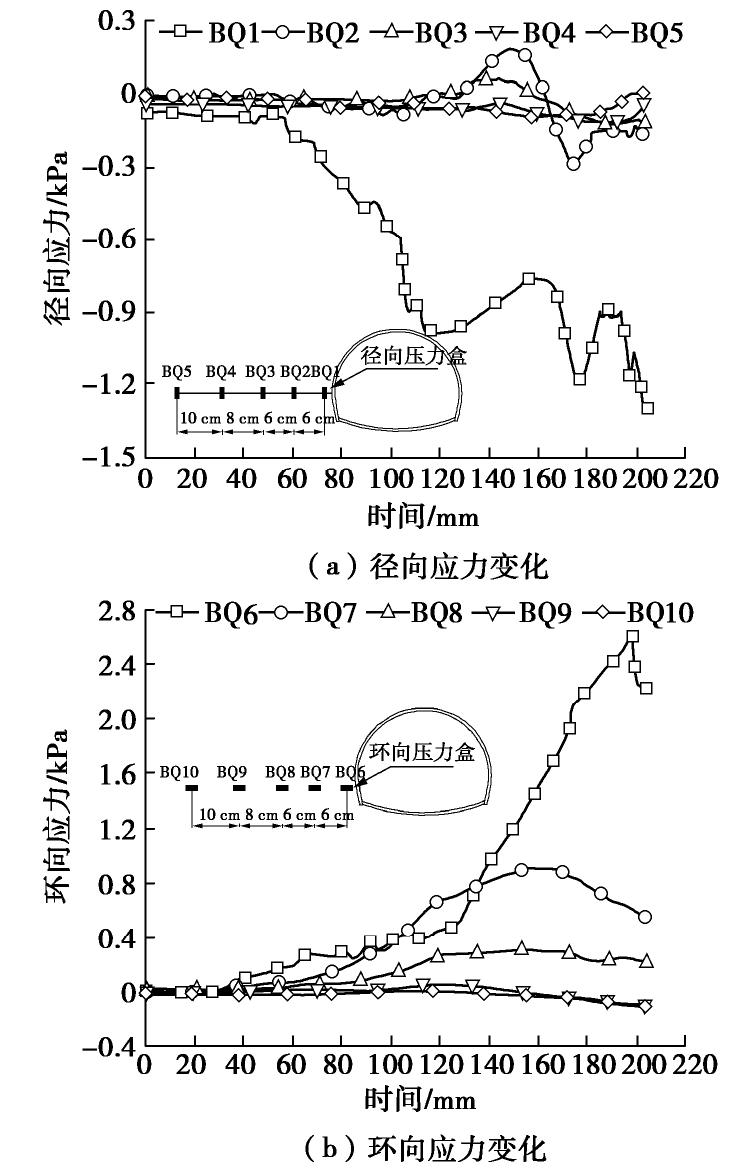
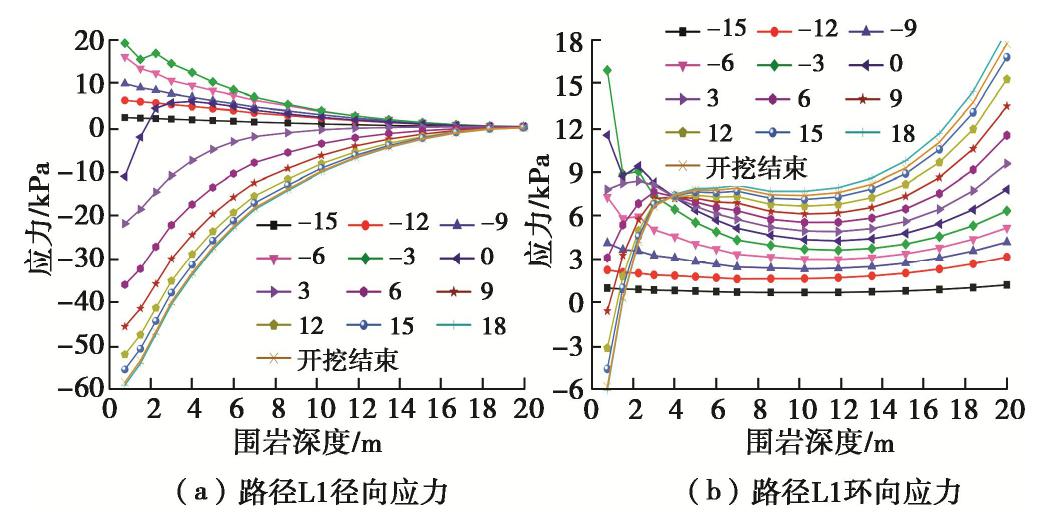
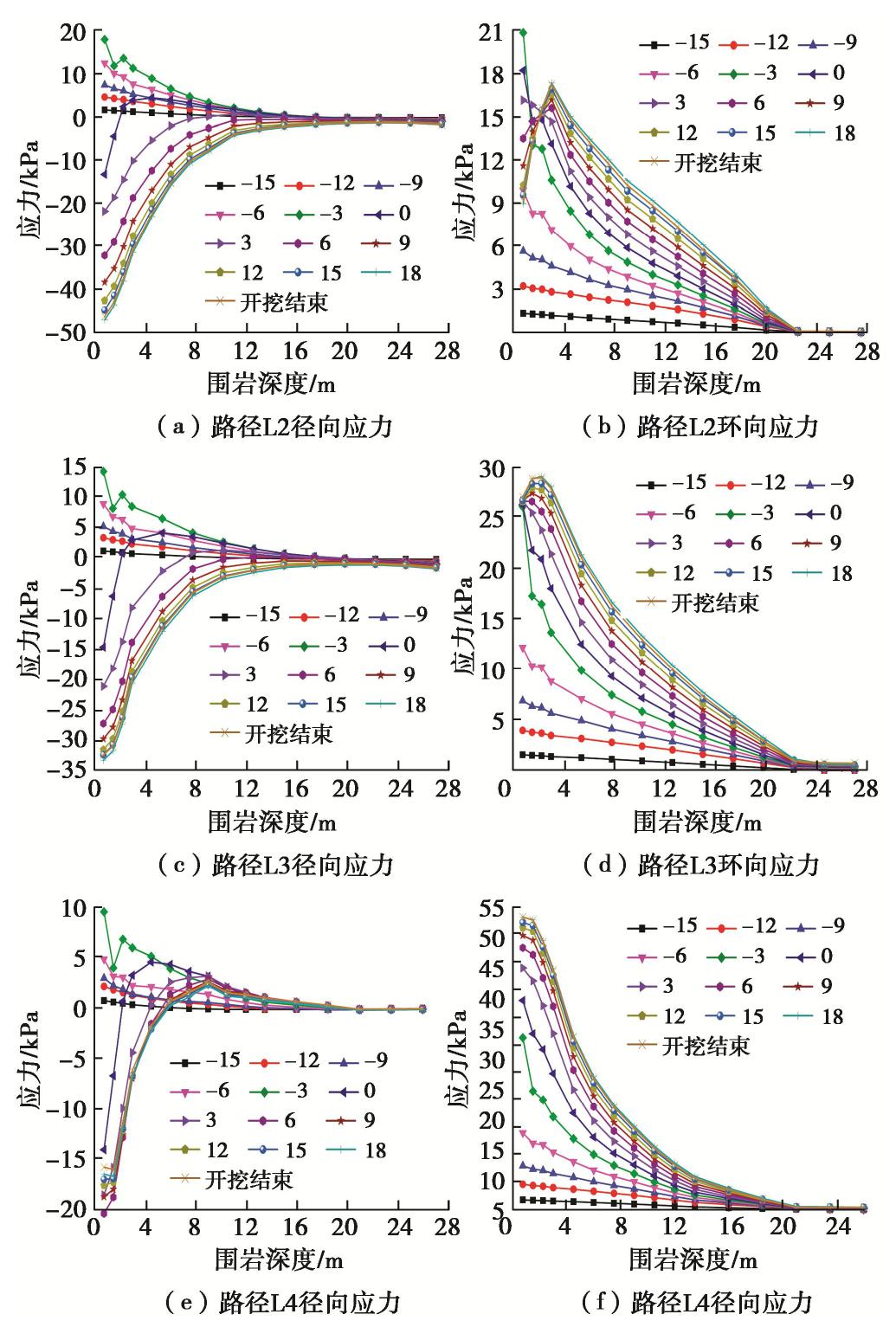
材料	弹性模量E/MPa	泊松比 $ν$	密度ρ/(g·cm^-3)	黏聚力c/kPa	内摩擦角φ/(°)
围岩	25	0.38	2.01	10.02	42.0
锚杆	200×10³	0.30	7.80	—	—
初期支护	25.2×10³	0.25	2.20	—	—
二次衬砌	29.5×10³	0.20	2.30	—	—

下载: 导出CSV

表 4 压力拱内外边界比较

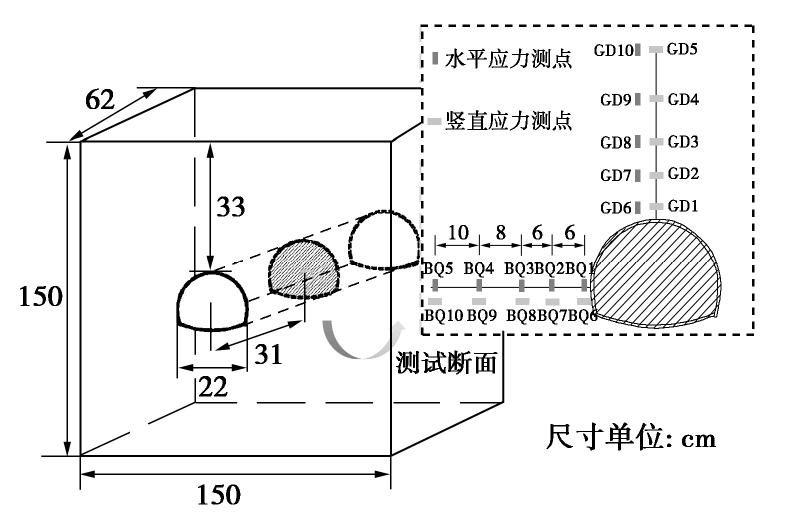
Table 4 Inner and outer boundaries of pressure arch

工况	拱顶路径		边墙路径
工况	内边界	外边界	内边界	外边界
数值模拟	2 m	20 m	0	14 m
模型试验	20 cm	33 cm	6 cm	20 cm
换算原型	12 m	20 m	3.6 m	12 m

下载: 导出CSV

表 5 计算与实测变形对比

Table 5 Comparison between calculated and measured deformations

名称	拱部沉降/mm			水平收敛/mm
名称	拱顶	左(右)拱肩	均值	上台阶	下台阶	均值
计算	19.2	14.8（14.8）	16.3	10.3	12.1	11.20
实测	14.7	10.2（12.8）	12.6	8.5	9.2	8.85

下载: 导出CSV

参考文献(21)

[1]	谢亦朋, 杨秀竹, 阳军生, 等. 松散堆积体隧道围岩变形破坏细观特征研究[J]. 岩土力学, 2019, 40(12): 4925-4934. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912043.htm XIE Yi-peng, YANG Xiu-zhu, YANG Jun-sheng, et al. Mesoscopic characteristics of deformation and failure on surrounding rocks of tunnel through loose deposits[J]. Rock and Soil Mechanics, 2019, 40(12): 4925-4934. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912043.htm
[2]	杨建周. 穿越松散堆积体围岩加固与隧道施工技术[J]. 铁道科学与工程学报, 2019, 16(5): 1266-1273. https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD201905021.htm YANG Jian-zhou. Reinforcement of surrounding rock and tunnel construction through loose deposits[J]. Journal of Railway Science and Engineering, 2019, 16(5): 1266-1273. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD201905021.htm
[3]	XIAO J Z, DAI F C, WEI Y Q, et al. Cracking mechanism of secondary lining for a shallow and asymmetrically-loaded tunnel in loose deposits[J]. Tunnelling and Underground Space Technology, 2014, 43: 232-240 doi: 10.1016/j.tust.2014.05.013
[4]	钟祖良, 别聪颖, 范一飞, 等. 土石混合体注浆扩散机制及影响因素试验研究[J]. 岩土力学, 2019, 40(11): 4194-4202. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201911009.htm ZHONG Zu-liang, BIE Cong-ying, FAN Yi-fei1, et al. Experimental study on grouting diffusion mechanism and influencing factors of soil-rock mixture[J]. Rock and Soil Mechanics, 2019, 40(11): 4194-4202. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201911009.htm
[5]	杨继红, 董金玉, 黄志全, 等. 不同含石量条件下堆积体抗剪强度特性的大型直剪试验研究[J]. 岩土工程学报, 2016, 38(增刊2): 161-166. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2016S2026.htm YANG Ji-hong, DONG Jin-yu, HUANG Zhi-quan, et al. Large-scale direct shear tests on accumulation body with different stone contents[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(S2): 161-166. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2016S2026.htm
[6]	WANG S R, LI C L, WANG Y G, et al. Evolution characteristics analysis of pressure-arch in a double-arch tunnel[J]. Tehnicki Vjesnik-Technical Gazette, 2016, 23: 181-189.
[7]	KONG X X, LIU Q S, ZHANG Q B, et al. A method to estimate the pressure arch formation above underground excavation in rock mass[J]. Tunnelling and Underground Space Technology, 2018, 71: 382-390.
[8]	WANG X Q, KANG H P, GAO F Q. Numerical study on the formation of pressure arch in bolted gravel plate[J]. Computers and Geotechnics, 2021, 130: 1-10.
[9]	朱合华, 黄锋, 徐前卫. 变埋深下软弱破碎隧道围岩渐进性破坏试验与数值模拟[J]. 岩石力学与工程学报, 2010, 29(6): 1113-1122. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201006006.htm ZHU He-hua, HUANG Feng, XU Qian-wei. Model test and numerical simulation for progressive failure of weak and fractured tunnel surrounding rock under different overburden depths[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(6): 1113-1122. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201006006.htm
[10]	黄锋, 朱合华, 徐前卫. 含软弱夹层隧道围岩松动破坏模型试验与分析[J]. 岩石力学与工程学报, 2016, 35(增刊1): 2915-2924. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2016S1037.htm HUANG Feng, ZHU He-hua, XU Qian-wei. Model test and analysis about loose failure of tunnel surrounding rock mass containing weak interlayer[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(S1): 2915-2924. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2016S1037.htm
[11]	房倩, 张顶立, 王毅远, 等. 圆形洞室围岩破坏模式模型试验研究[J]. 岩石力学与工程学报, 2011, 30(3): 564-571. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201103016.htm FANG Qian, ZHANG Ding-li, WANG Yi-yuan, et al. Model test study of failure modes surrounding rock for circular caverns[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(3): 564-571. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201103016.htm
[12]	李英杰, 张顶立, 宋义敏, 等. 软弱破碎深埋隧道围岩渐进性破坏试验研究[J]. 岩石力学与工程学报, 2012, 31(6): 1138-1147. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201206008.htm LI Ying-jie, ZHANG Ding-li, SONG Yi-min, et al. Experimental research of progressive damage of surrounding rock for soft fractured deep tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(6): 1138-1147. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201206008.htm
[13]	汪成兵. 均质岩体中隧道围岩破坏过程的试验与数值模拟[J]. 岩土力学, 2012, 33(1): 103-108. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201201017.htm WANG Cheng-bing. Laboratory and numerical investigation on failure process of tunnel constructed in homogeneous rock[J]. Rock and Soil Mechanics, 2012, 33(1): 103-108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201201017.htm
[14]	叶飞, 毛家骅, 刘燕鹏, 等. 软弱破碎隧道围岩动态压力拱效应模型试验[J]. 中国公路学报, 2015, 28(10): 76-82. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201510012.htm YE Fei, MAO Jia-hua, LIU Yan-peno, et al. Model test on effect of dynamic pressure arch of tunnel in soft broken surrounding rock[J]. China Journal of Highway and Transport, 2015, 28(10): 76-82. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201510012.htm
[15]	郑康成, 丁文其, 金威, 等. 特大断面隧道分步施工动态压力拱分析研究[J]. 岩土工程学报, 2015, 37(增刊1): 72-77. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2015S1016.htm ZHENG Kang-cheng, DING Wen-ai, JIN Wei, et al. Experimental and numerical study on staged construction pressure arch of super large section tunnel[J]. China Journal of Geotechnical Engineering, 2015, 37(S1): 72-77. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2015S1016.htm
[16]	崔蓬勃, 朱永全, 刘勇, 等. 考虑土拱发挥过程的非饱和砂土盾构隧道极限支护力计算方法研究[J]. 岩土工程学报, 2020, 42(5): 873-881. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202005013.htm CUI Peng-bo, ZHU Yong-quan, LIU Yong, et al. Calculation of ultimate supporting forces of shield tunnels in unsaturated sandy soils considering soil arching effects[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(5): 873-881. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202005013.htm
[17]	曲世韡. 深埋城市地铁隧道对地层变形的影响及压力拱形成规律研究[D]. 北京: 北京交通大学, 2013. QU Shi-fu. Study on Influence of Deep-buried Urban Subway Tunnel on Strata Deformation and Formation rule of Pressure Arch[D]. Beijng: Bejjing Jiaotong University, 2009. (in Chinese)
[18]	潘皇宋, 杜广印, 王坤, 等. 无衬砌黄土隧道压力拱模型试验及数值模拟[J]. 东南大学学报(自然科学版), 2019, 49(5): 949-955. https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX201905019.htm PAN Huang-song, DU Guang-yin, WANG Kun, et al. Model test and numerical simulation on pressure arch of unlined loess tunnel[J]. Journal of Southeast University (Natural Science Edition), 2019, 49(5): 949-955. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX201905019.htm
[19]	中交第一勘察设计研究院有限公司. 国道318林芝到拉萨段公路改造工程(二期)[R]. 西安, 2015. CCCC First Highway Consultants Co., Ltd., Reconstruction of Nyingchi-Lasa Section of National Highway 318 (Phase II)[R]. Xi'an, 2015. (in Chinese)
[20]	何珺, 张成平, 杨公标. 砂卵石地层小净距隧道渐进性破坏过程试验研究[J]. 土木工程学报, 2015, 48(增刊1): 362-367. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2015S1064.htm HE Jun, ZHANG Cheng-ping, YANG Gong-biao. Test study on progressive failure of closely spaced tunnel in sandy cobble ground[J]. China Civil Engineering Journal, 2015, 48(S1): 362-367. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2015S1064.htm
[21]	江权, 冯夏庭, 李邵军, 等. 高应力下大型硬岩地下洞室群稳定性设计优化的裂化-抑制法及其应用[J]. 岩石力学与工程学报, 2019, 38(6): 1081-1101. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201906002.htm JIANG Quan, FENG Xia-ting, LI Shao-jun. Cracking-restraint design method for large underground caverns with hard rock under high geostress condition and its practical application[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(6): 1081-1101. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201906002.htm

施引文献(5)

期刊类型引用(4)

1.	唐小平，邓良平，汪建海，梁榆峰，江杰，叶耿昌. 排水管道土压力数值分析及非开挖修复内衬管壁厚优化. 给水排水. 2024(02): 139-145 . 百度学术
2.	张常光，吴凯，孟祥忠，王晓轮. 稳态渗流下非饱和土涵洞竖向土压力的迭代解与简化. 哈尔滨工业大学学报. 2024(03): 68-77 . 百度学术
3.	于金弘，伍鹤皋，石长征，孙海清，汪碧飞，李娇娜. 考虑管道自重荷载的埋地钢管结构计算方法. 长江科学院院报. 2024(05): 155-161 . 百度学术
4.	朱珍锋，韩高孝. 沟埋式管道垂直土压力模拟试验研究. 水利与建筑工程学报. 2024(03): 99-106 . 百度学术