裂缝边坡三维极限上限拓展分析

饶平平; 吴健; 崔纪飞; 赵琳学

doi:10.11779/CJGE202109005

裂缝边坡三维极限上限拓展分析 English Version

1.
上海理工大学土木工程系,上海　200093
2.
悉尼大学土木工程学院,澳大利亚　悉尼　2008

基金项目:

国家自然科学基金项目 42077435

详细信息

作者简介:
饶平平(1984— ),男,博士,副教授,主要从事岩土力学教学与科研工作。E-mail：raopingping@usst.edu.cn

中图分类号: TU431
计量
- 文章访问数: 343
- HTML全文浏览量: 72
- PDF下载量: 206
出版历程
- 收稿日期: 2020-12-14
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-08-31

Extended three-dimensional analysis of cracked slopes using upper-bound limit method

1.
Department of Civil Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China
2.
School of Civil Engineering, The University of Sydney, Sydney 2008, Australia

摘要

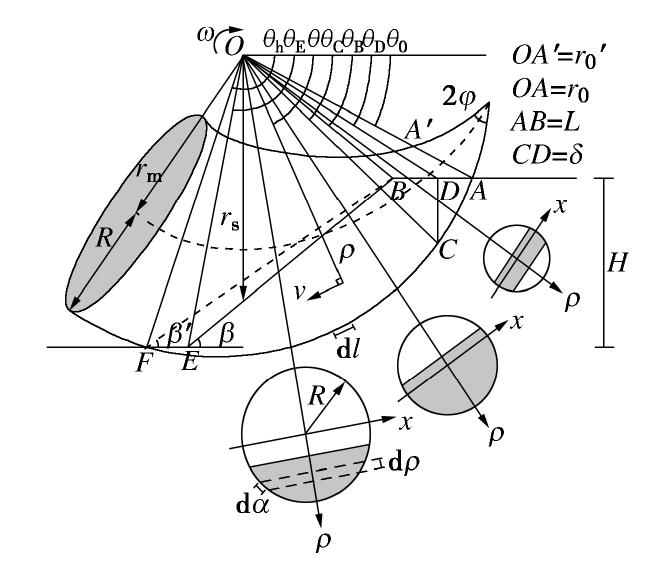
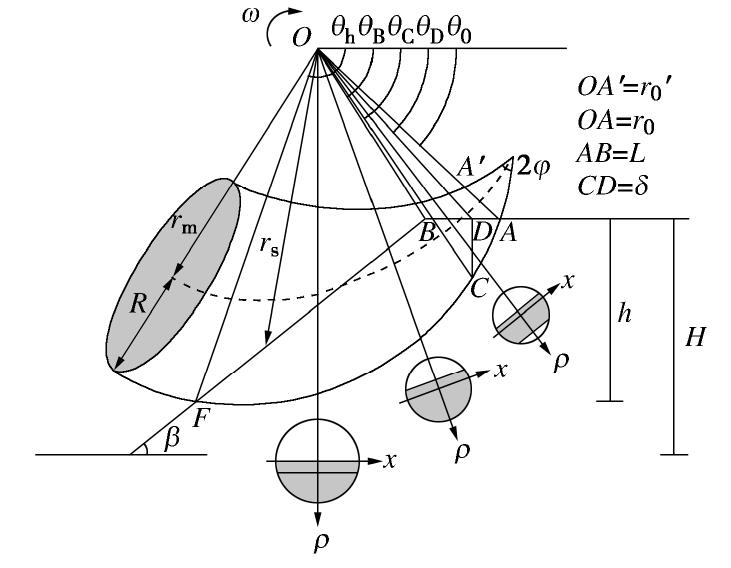
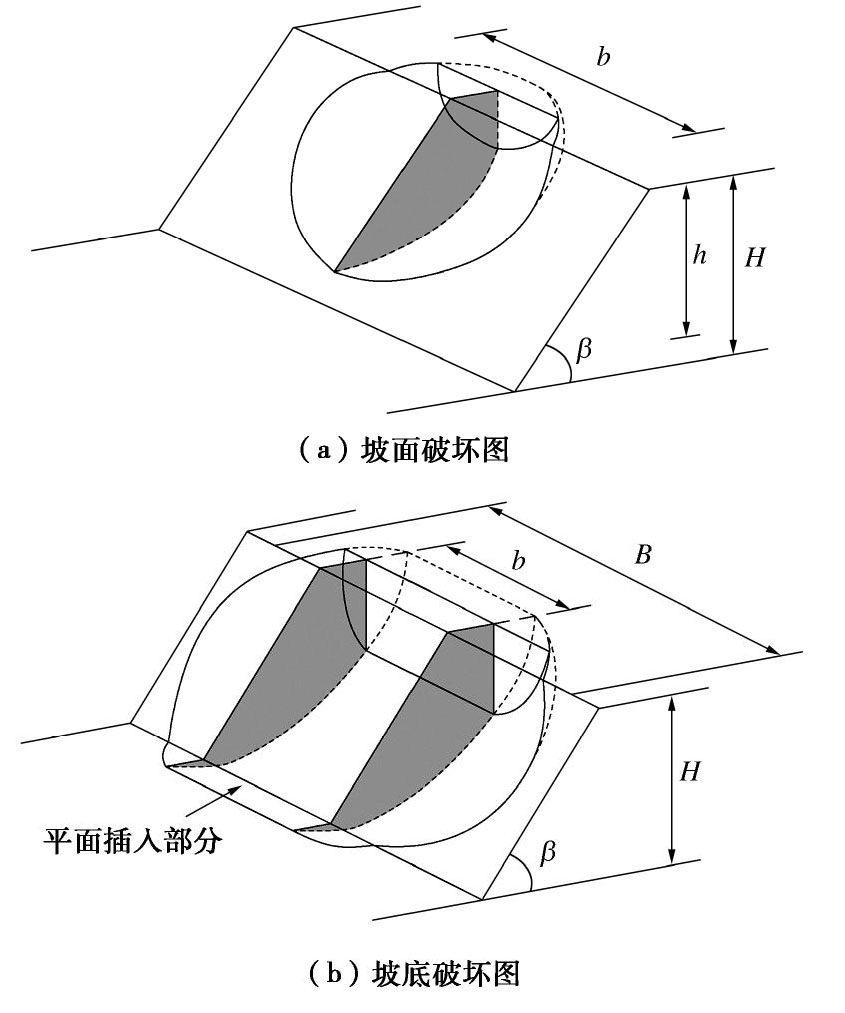
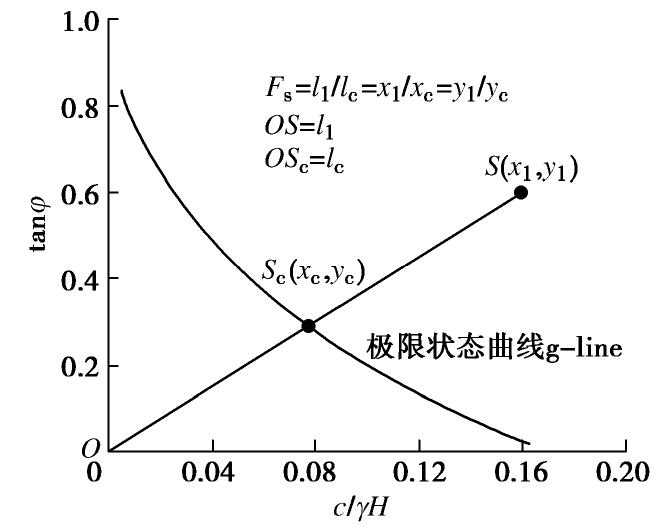
摘要: 裂缝的存在会降低边坡稳定性,而在边坡宽度受到限制时三维效应更加显著,因此有必要对裂缝边坡稳定性进行评估。针对裂缝边坡三维稳定性研究,基于极限分析上限定理,在三维破坏机构中引入一条垂直张拉裂缝,并引进机构参数拓展裂缝边坡三维破坏模式,包括坡面破坏和坡底破坏,建立能量平衡方程并通过优化算法求解裂缝边坡稳定系数上限解。根据g-line图像法绘制裂缝边坡稳定性图表以便读取安全系数。分析了边坡宽高比、坡角以及土体内摩擦角对裂缝边坡破坏模式和裂缝深度及位置的影响规律。结果表明：对于确定的边坡几何形态以及土体参数,存在最小边坡宽高比B/H^*,当边坡宽高比小于B/H^*,边坡发生坡面破坏且坡顶裂缝的影响可以忽略；内摩擦角φ小于5°时,边坡发生坡底破坏,而对于裂缝边坡,仅在φ=1°左右发生坡底破坏；随着边坡宽高比的增大,裂缝深度逐渐增加,裂缝位置逐渐远离坡肩,但对于坡角为75°的边坡裂缝深度先增大后减小。
- 边坡稳定性 /
- 极限分析 /
- 裂缝 /
- 安全系数 /
- 图表法
Abstract: The existence of cracks will reduce the stability of a slope and the three-dimensional effect is more significant when its width is limited. Therefore, it is necessary to evaluate the stability of cracked slopes. In order to study the three-dimensional stability of cracked slopes, based on the upper-bound theorem of limit analysis, a vertical tensile crack is introduced into the three-dimensional failure mechanism, and the mechanism parameters are introduced to extend the three-dimensional failure mode of slopes, including face failure and base failure. The energy balance equation is established, and the upper bounds of stability number of cracked slopes are obtained by the optimization algorithm. The stability charts of cracked slopes are established based on the g-line graphical method to read the factor of safety conveniently. The influences of slope width-to-height ratio, slope angle and internal friction angle of soils on the failure mechanism of cracked slopes and the crack depth and location are analyzed. The results show that for the specific slope geometry and soil parameters, there is a minimum slope width B/H^*. When the slope width is less than B/H^*, the failure surface passes above the slope toe, and the influences of the crack on the upper surface of the slope can be ignored. When the internal friction angle φ is less than 5°, the failure surface passes below the slope toe; for the cracked slope, only when φ=1°, failure surface passes below the slope. As the width of the slope increases, the crack depth gradually increases, and the crack location gradually moves away from the slope crest, while the crack depth of the slope with inclination 75° increases first and then decreases.
- slope stability /
- limit analysis /
- crack /
- factor of safety /
- graphical method

HTML全文

0. 引言

沉积盆地对其内部的地震动有显著的放大效应,这已被多次的震害及观测记录所证实。盆地地震效应的主要表现之一是盆地边缘附近产生的次生面波（Rayleigh波和Love波）,其周期长、衰减速度慢,且在传播过程中与体波可能发生多次干涉效应。次生面波对于盆地内密集的长大周期结构的地震破坏有重要影响^[1]。典型实例如1985年墨西哥地震中的墨西哥盆地^[2]、1996年日本神户地震中的大阪盆地^[3]、2008年汶川地震中的渭河盆地^[4]等的震害。Kawase^[3]的研究表明次生面波在盆地边缘产生并向盆地内部传播,面波与直达体波的相长干涉导致盆地边缘区域的地震动被显著放大,又称盆地的“边缘效应”。这一现象在1995年日本神户地震中大阪盆地^[3]、2001年云南施甸地震中施甸盆地^[5]等均被观测到。此外,对中小型盆地,波长较大的面波或体波间的干涉还会导致盆地共振现象的发生^[6-7]。

对盆地地震效应的研究而言,其热点之一是研究盆地内面波的产生与传播过程,以及面波与体波的相互作用对盆地地震动的影响,而从观测或模拟时程中识别和提取面波震相,并开展定量研究则是以上研究的基础之一。对于均匀场地条件下的远场台站或大型盆地,由于体波和面波传播速度的差异,二者在时域内已相互分离,因此可直接在时域内通过质点运动轨迹、传播视速度等方法识别面波震相。如Liu等^[8]利用Rayleigh面波的运动轨迹为逆进椭圆的特征对汶川地震中靠近渭河盆地的远场台站的面波震相进行了识别；Frankel等^[9]利用互相关技术对Santa Clara 谷地台阵记录的面波震相及其传播速度和方向进行了识别,但应用该方法的前提是面波与体波记录分离,对于二者相互叠加的情况则难以奏效。

对于盆地场地来说,其深度和宽度一般都不大,同时盆地内外介质阻抗差异大,这些都导致盆地内传播的面波和体波之间常常发生叠加干涉,往往在盆地台站记录的同一段时程中体波和面波成分同时存在,在时域中不易从中直接分离出面波震相。传统方法是将时域中的记录转换到频率域、频率–波数（f-k）域或时–频（t-f）域中进行处理。频域中识别面波主要是基于面波和体波的主频率差别较大的假定,如Abraham等^[10]认为面波的频率比体波明显要低,在傅氏谱上二者分属于不同的频段,通过设计适当的频率上下限并对原始记录进行带通滤波可以分离出面波震相。但对于体波和面波在频域中重叠严重的情况,频域滤波方法不易找出明显的滤波上下限。把某一测线上的观测点时程从时间–空间（t-x）域变换到f-k域,然后利用体波和面波在频率或视速度上的差异进行f-k滤波,进而将滤波后的结果逆变换到t-x域中压制或得到面波时程的方法在油气勘探的地震资料处理中应用较广泛^[11-12]。但对于盆地边缘的折射体波等具有和面波相近频率或视速度的情况,这一方法的效果并不理想。此外,频域方法和频率–波数域方法均是将暂态的地震记录信号进行无限的周期延拓后做傅氏变换,即认为信号是“静态”的,这与实际情况并不完全相符。因此,近年来,基于时–频变换的面波震相识别技术不断涌现,最典型的如时频极化分析技术等^[13-16],它通过将记录转换到t-f域,可只将满足面波/体波极化特征的部分保留,进而逆变换到时域获得所需的面波（包括Rayleigh波和Love波）及体波时程。目前,该技术已应用于台湾集集地震中台北盆地^[15]、新西兰Darfield地震中的Canterbury盆地^[16],以及意大利某沉积河谷^[17]的面波震相识别之中。但由于数值误差等原因,极化分析技术在实际应用中有时不能将模拟时程中的体波成分完全清除。在时频极化分析技术的基础上,近年来有研究者提出时间–频率–波数（t-f-k）域中的面波时程极化分析方法^[18-19],但该方法只适用于直线测线上的批量台站记录,无法处理单台记录或盆地内台站任意分布的情况,且对于采样点数量较大的地震波数据,由于需对每个时间点进行处理,导致该方法计算时间相对过长。因此,需求一种高效、有效的面波时程提取方法很有必要。

既有研究表明,盆地特征参数对盆地地震动放大特征或盆地次生面波特性有显著影响。Narayan^[20]利用有限差分方法研究了SH波斜入射时盆地倾角对盆地边缘产生的Love波强度及地震动放大系数的影响。发现相同的入射角度下,盆地边缘越陡地表位移峰值越大。Narayan^[21]研究了盆地内外介质的P和S波阻抗比对盆地转换Rayleigh面波（文中实际为差分地震动,即地表相邻观测点的时程之差除以二者的距离）的影响,表明盆地转换Rayleigh波的水平分量的最大和平均谱放大系数随两种阻抗的增加均增大,而垂直分量随P波阻抗的增加而增大,随S波阻抗的变化无一致规律。需要指出的是,以上差分地震动与面波并不等同,尤其是对于盆地斜边区域附近,面波和盆地斜边折射体波同时存在,导致差分运动时程中包含折射体波。Liu等^[22]研究了施甸盆地内外介质的阻抗比对盆地效应的影响,结果显示盆地内介质波速降低时,高阶模态面波会被激发,盆地内的共振现象也更易发生。Moczo等^[23]详细研究了盆地的阻抗比、品质因子、速度梯度及盆地形状等参数对盆地地面运动的影响,结果表明盆地放大效应的主要控制参数为盆地深宽比、介质阻抗比及土层衰减作用。李一琼^[24]探讨了盆地介质波速及覆盖层深度对规则二维盆地地表及差分地震动（DGM）的影响,发现盆地与基底波速差异越大,盆地斜边区域峰值变化越剧烈,DGM峰值越大,且DGM最大值靠近盆地中央区域。刘中宪等^[25]考察了盆地内外介质波速沿深度的变化对盆地地表地震动的影响。以上研究多集中在盆地特征参数对盆地内地震动强度的总体分布特征,以及频谱/反应谱特性的影响之上,而对于盆地观测点时程（地震记录或模拟时程）中面波震相的识别、盆地次生面波的形成与传播特征,以及盆地特征参数对次生面波强度/频谱特性的影响方面的研究相对较少。考虑到体波和面波两种特性迥异的震相在盆地内传播过程的确定对盆地地震效应研究的作用,以及面波对盆地内长大周期结构震害的重要影响,有必要开展盆地内面波传播特征及其影响因素的研究。

基于以上考虑,本文首先给出一种结合f-k滤波和时频极化分析技术的Rayleigh面波震相识别和提取方法,并通过实际算例验证了方法的合理性。然后基于理想化的二维盆地模型、显式有限元法和多次透射边界技术,数值模拟平面SV波垂直入射下盆地的地震响应。采用本文方法从盆地地表观测点时程中提取面波震相,进而详细研究了盆地内外介质的阻抗比对盆地放大系数（定义为盆地模型和水平成层模型对应观测点的位移峰值之比）、盆地次生Rayleigh面波的传播特征和强度分布的影响。

1. Rayleigh面波震相识别方法及验证

1.1 基于f-k变换及极化分析法的Rayleigh面波震相识别方法

本节给出一种综合f-k滤波和极化分析技术的Rayleigh面波震相识别和提取方法。其主要步骤为：①利用f-k滤波法将剖面时程中从盆地基底直达或多次反射的体波震相（其对应的水平视速度大）滤去,但可能会保留盆地边缘的折射波、盆地角点的衍射波等体波震相；②利用极化分析技术^[13,15]在时频域内对f-k滤波后的时程进行极化分析,仅保留符合Rayleigh面波极化特征（如质点运动轨迹为椭圆,垂直分量和水平分量相位相差 $π/ 2$ ）的部分；③将极化分析后的结果逆变换到时域得到提取的面波震相。由于f-k滤波已较成熟,以下主要对Meza-Fajardo et al.提出的时频域极化分析技术^[15]进行简单介绍。

Meza-Fajardo等^[15]提出一种基于S变换和归一化内积（normalized inner product,以下简称NIP）的面波震相识别方法。主要原理如下：

对于体波,其径向分量和垂直向分量始终同相位；对于Rayleigh面波,其径向分量和垂直向分量的相位相差 $π/ 2$ 。因此,若径向分量与相位改变 $π/ 2$ 后的垂直分量相位相同,则该震相即为Rayleigh波,这一过程可基于S变换技术在时频域中实现。以下对其步骤作简要叙述。

对于某三分量（EW,NS,UD）的地震记录,将其S变换后的结果分别标记为 $S_{l} (τ, f)$ （l=E,N,V）,其中 $τ$ 和f分别对应时间和频率轴。面波的传播方向 $θ$ 可根据Rayleigh面波的切向分量和相位改变后的垂直分量之间的相关系数为0的条件按下式计算：

$θ (τ, f) = \tan^{- 1} [\frac{E (τ, f) \cdot \hat{V} (τ, f)}{N (τ, f) \cdot \hat{V} (τ, f)}]$ ,

(1)

式中, $E (τ, f) = (\begin{array}{l} Re [S_{E} (τ, f)] \\ I M [S_{E} (τ, f)] \end{array})$ , $\hat{V} (τ, f)$ 表示垂直分量在时频域中相位改变 $π / 2$ 后的结果。

任意分量的S变换可表示为

$\begin{matrix} S_{l} (τ, f) = R e (S_{l} (τ, f)) + i I M (S_{l} (τ, f)) \\ = A_{l} (τ, f) e^{i Φ_{l} (τ, f)} \end{matrix}$ ,

(2)

式中, $Re [S_{l} (τ, f)]$ 和 $I M [S_{l} (τ, f)]$ 分别表示任意分量S变换后的实部和虚部, $A_{l} (τ, f)$ 表示其幅值。

根据式（2）,径向和垂直分量的时频域内积可表示为

$\begin{array}{l} R (τ, f) \cdot V (τ, f) \\ = A_{R} (τ, f) A_{V} (τ, f) \cos [Φ_{R} (τ, f) - Φ_{V} (τ, f)] \\ = Re [S_{R} (τ, f)] Re [S_{V} (τ, f)] + I M [S_{R} (τ, f)] I M [S_{V} (τ, f)] 。 \end{array}$

(3)

根据上述Rayleigh面波径向和垂直分量间的相位差特征,若垂直分量的相位改变 $π/2$ ,则

$\begin{matrix} Φ_{R} (τ, f) = Φ_{\hat{V}} (τ, f) & , & \cos [Φ_{R} (τ, f) - Φ_{\hat{V}} (τ, f)] = 1 \end{matrix}$

。

定义径向和相位改变后的垂直分量的归一化内积（NIP）为

$\begin{array}{l} N I P (R, \hat{V}) = \cos [Φ_{R} (τ, f) - Φ_{\hat{V}} (τ, f)] \\ = \frac{Re [S_{R} (τ, f)] Re [S_{\hat{V}} (τ, f)] + I M [S_{R} (τ, f)] I M [S_{\hat{V}} (τ, f)]}{A_{R} (τ, f) A_{\hat{V}} (τ, f)} 。 \end{array}$

(4)

因此,对于记录中的Rayleigh面波震相,其对应的 $N I P \approx 1$ ,即式（4）中等号最右侧的值约等于1。据此可设计简单的滤波器,将 $(τ, f)$ 空间中 $N I P$ 大于某值的各分量数据保留,其余赋值为零,进而得到只包含Rayleigh面波的各分量 $(τ, f)$ 空间值,最后对其进行S逆变换即得Rayleigh面波时程,从而实现时频域中对Rayleigh面波震相的识别和提取。面波传播的方位角根据提取的面波时程按式（1）的时域形式计算得到。若要提取体波震相,只需将 $(τ, f)$ 空间中NIP接近于0的各分量数据点保留,其余的赋值为零。

以上方法可同时识别顺进和逆进的Rayleigh面波、Love面波及体波,只需根据各自的极化特征做相应修改即可。

1.2 方法验证

Meza-Fajardo等^[15]已对时频极化分析技术提取单台记录中的面波时程的适用性进行了验证,以下主要验证本文方法用于识别和提取剖面等距分布台站时程中的面波的正确性。采用第2节中的盆地模型（盆地波速500 m/s）,模拟得到的盆地地表x分量的位移时程如图1（a）所示。可以看出,时程中存在次生面波、直达体波、多次反射/折射波、角点衍射体波等诸多震相。盆地边缘附近产生的次生面波与直达体波、折射体波或盆地基底反射波（每次反射时相位均改变 $π$ ）发生多次叠加干涉,从时域中很难直接分离出面波。此外,剖面时程f-k变换的结果（图2（a））也显示体波和面波在频域中存在多处重叠,尤其是在盆地的一维自振频率附近。采用本文方法提取得到的面波时程如图1（b）所示,图2（b）为其f-k变换的结果。可以看出,时程中体波的成分已基本被清除,这点从f-k域中能更清楚地看出（分布域通过原点,分布域上各点对应的相速度相等的区域对应体波成分）,基本仅有面波成分被保留。同时,时域时程也显示面波以恒定的速度向盆地内传播,在传播过程中出现一定程度的频散,且盆地角点附近产生的面波强度很弱,可能是由于此处面波与盆地斜边折射SV波或折射P波（图1（a）中红色虚线所示）的干涉所致,从x=700 m开始才有较明显的面波出现,并在传播过程中有增强的趋势。

图 1 盆地地表观测点的模拟时程及提取Rayleigh波时程

Figure 1. Simulated seismograms and extracted Rayleigh waves for observation points

下载: 全尺寸图片幻灯片

图 2 模拟及提取面波时程的f-k谱

Figure 2. f-k spectra for simulated seismograms and extracted Rayleigh waves

下载: 全尺寸图片幻灯片

上述结果表明本文方法在剖面时程的Rayleigh面波震相提取中效果良好,可以用于下一步的模拟时程中的Rayleigh面波震相和体波震相的识别。此外,本文方法综合了f-k滤波和时频极化分析技术的优点,且具有较高的计算效率。

2. 盆地模型及计算方法

采用理想化的二维盆地模型如图3所示。为简化分析,取半边盆地模型,盆地顶部宽2100 m,底部宽1900 m,盆地倾角 $θ$ =45°,深度h=200 m,盆地左侧基岩地表宽度500 m。介质参数见于表1。从模型底部垂直输入脉冲波（SV波）,输入波时程及频谱如图4所示,模拟最高频率约为8 Hz。观测点取在地表,盆地外侧5个观测点（x=100～500 m,观测点间距100 m）,盆地内部50个观测点（x=540～2500 m,各点间距40 m）,共计55个观测点（编号为1-55）,其中盆地与基岩交界处观测点编号为5。采用显式有限元与透射边界相结合的方法^[26]计算盆地的地震动响应,其中在模型的两侧边界和底边界设置二阶透射边界,以减少人工边界处反射波的影响。为满足有限元模拟的精度要求,模型最小网格尺寸5 m,计算时间步距0.001 s。

图 3 二维盆地计算模型（黑色圆点表示代表性的台站位置）

Figure 3. 2D basin model for investigations (solid circles-representative stations)

下载: 全尺寸图片幻灯片

表 1 计算模型介质参数

Table 1. Physical parameters of model

类型	剪切波速V_s/(m·s^-1)	压缩波速V_p/(m·s^-1)	密度/(kg·m^-3)
盆地	200~1500	2V_s	1700
基岩	3000	5196	2600

下载: 导出CSV

| 显示表格

图 4 输入波时程及其傅里叶谱

Figure 4. Time histories of input waves and their Fourier spectra

下载: 全尺寸图片幻灯片

3. 模拟结果

基于以上盆地模型,取盆地内沉积层为均一介质,保持其余参数不变,盆地覆盖层介质剪切波速分别取200,350,500,750,1000和1500 m/s,压缩波速等于剪切波速的两倍,密度参数保持不变,对应的盆地内外介质的阻抗比（IC $= ρ_{盆地} c_{盆地} / ρ_{基岩} c_{基岩}$ , $ρ$ 和c分别表示介质密度和波速,以下记为IC）分别为0.044,0.076,0.109,0.164,0.218,0.327,然后分别模拟得到地表观测点的地震动响应。采用第1节中的方法从模拟时程中提取Rayleigh面波震相,进而分析盆地内外介质阻抗比对盆地地震动及面波传播特征的影响。

3.1 阻抗比对盆地地表地震动的影响

不同阻抗比模型模拟得到的观测点水平、垂直分量的位移时程如图5所示。图中红色线为盆地与基岩交界点处时程,绿色线为地震动最大值处对应的时程曲线。可以看出,随盆地内外介质阻抗比（IC）的增加,次生面波的传播速度逐渐增大,但面波强度有递减的趋势（定量分析见下节）。水平分量的时程中包含直达体波、基底多次反射体波、盆地边缘折射的体波以及盆地边缘转换的次生面波等,而垂直分量的时程中主要为盆地边缘的折射体波及次生面波。直达体波和基底多次反射体波均导致盆地边缘附近面波的形成,且相对而言,IC越小,盆地内波场越复杂。

图 5 不同阻抗比模型对应的盆地地表观测点水平（左）和垂直(右)分量的模拟位移时程

Figure 5. Time histories of horizontal (left) and vertical (right) components for ground points of different IC models

下载: 全尺寸图片幻灯片

图6（a）,（b）所示为不同阻抗比模型下盆地地表观测点的位移峰值（PGD）分布。对水平分量（图6（a））,靠近盆地角点区域（大约5到13号观测点的范围）存在地震动被抑制的现象,其幅值甚至小于盆地外基岩场地的地震动峰值,且随盆地土层剪切波速的降低（盆地内外介质阻抗比减小）,这种抑制的程度趋于提高,如IC=0.044时盆地斜边区域最小的位移峰值仅为外部基岩场地的60%左右。从13号测点到20号测点左右,存在明显的盆地边缘效应的区域,该区域地震动峰值明显大于盆地内部区域。值得注意的是IC=0.044,0.076,0.109三个模型,其在盆地中间区域（24～29号测点范围）存在局部的地震动放大,且该区域的地震动幅值为地表观测点地震响应的最大值。另外值得注意的是并非盆地土层波速越小,其地震动最大值越大,如IC=0.076和0.109模型的地震响应最大值均大于IC=0.044模型,其原因可能与不同覆盖层波速时次生面波、直达体波、盆地斜边折射体波等震相之间的干涉过程和程度有关。结合图5、图8可以看出,IC=0.044时面波的传播速度最小,导致以上三震相同时叠加干涉的程度相比IC=0.076和0.109时小,因此相应的地震动峰值也降低。但IC大于0.076后,盆地内地震响应的最大值随土层波速的增加单调降低。同时,盆地中央区域的位移峰值也随土层波速的增加而单调降低,但基本不受盆地边缘效应的影响,其位移峰值与按水平成层模型计算的结果基本相同。

图 6 不同阻抗比模型对应的盆地地表观测点的位移峰值分布

Figure 6. PGD distributions for ground points of different IC models

下载: 全尺寸图片幻灯片

图 7 不同阻抗比模型对应的盆地地表观测点的放大系数分布

Figure 7. Amplification factor distributions for ground points of different IC models

下载: 全尺寸图片幻灯片

图 8 不同阻抗比模型对应的盆地地表观测点Rayleigh面波水平（左）和垂直（右）分量的位移时程

Figure 8. Time histories of Raleigh wave of horizontal (left) and vertical (right) components for ground points of changed IR models

下载: 全尺寸图片幻灯片

对垂直分量（图6（b））,位移峰值整体表现出在盆地边缘区域（6到11号观测点,200 m的范围）最大,向盆地内部逐渐递减的趋势。但较小阻抗比模型的位移峰值分布曲线在盆地边缘及内部区域出现强烈振荡,随阻抗比的增加,振荡现象基本消失,曲线趋于平缓。值得注意的是,尽管低阻抗比模型的峰值曲线振荡明显,但较大和较小峰值的分布区域对不同模型来说却较为相近,而盆地边缘最大峰值的位置有随土层波速的增加而右移的趋势。在盆地内部区域,地震反应峰值随阻抗比的增加而降低,而在盆地边缘,和水平分量类似,最小阻抗比模型的PGD小于次小阻抗比模型,但IC大于0.076之后,PGD最大值随阻抗比增加而降低。此外,若不考虑盆地效应,即按水平成层模型计算SV波垂直入射下的地震响应,则垂直分量的位移峰值应为0,而按盆地模型得到的位移峰值却相当大,基本为水平分量位移峰值的26%～75%（表2）,这部分垂直分量的地震动对于盆地内结构的地震反应分析而言不可忽略。

表 2 不同阻抗比模型模拟得到的盆地地表水平和垂直分量的PGD最大值及二者的比值

Table 2. Maximum values and ratios of PGDs of horizontal to vertical components of changed IC models

IC	水平分量位移最大值dx/m	垂直分量位移最大值dy/m	dy/dx
0.044	4.02	2.99	0.74
0.076	4.23	3.18	0.75
0.109	4.11	3.05	0.74
0.164	3.79	2.22	0.59
0.218	3.62	1.54	0.43
0.327	3.19	0.83	0.26

下载: 导出CSV

| 显示表格

图7给出了不同阻抗比的盆地模型相比不考虑盆地的一维水平成层模型模拟得到的地表位移峰值的比值（将其定义为盆地地震动的“放大系数”）。其总体分布特征与图6类似。相比水平成层模型,水平分量的地震动在盆地边缘附近放大1.1～1.2倍,而盆地斜边区域的最小PGD仅为水平成层模型的1/3左右；最大放大系数与阻抗比之间无一致规律性,随阻抗比的增大,除盆地中间27号点外,盆地边缘区域的放大系数也逐渐增大,但IC=0.327时的最大放大系数小于IC=0.218的结果。此外,最大放大系数（1.14）出现在IC=0.109模型的盆地中间区域,且整体而言IC=0.004模型的放大系数最小。

如前所述,垂直分量的地震动是由盆地特殊的几何形状引起。从图7（b）中可见,对该盆地模型,其垂直分量PGD可达水平成层模型的0.85倍,且整体来看,其放大系数（定义为盆地模型地表观测点垂直分量的PGD与水平成层模型对应观测点水平分量PGD的比值）最大值随阻抗比的增加而降低,这与水平分量的特征基本相反。对不同阻抗比模型,最大放大系数均出现在盆地边缘8号测点附近。在盆地内部,低阻抗比模型同样存在多个放大系数较大的区域。同时,水平和垂直分量的放大作用表明在盆地场地区域采用一维土层模型简化计算时,对结果应慎重考虑。

3.2 阻抗比对盆地次生面波的影响

采用第2节的方法从模拟的水平和垂直分量的位移时程中提取Rayleigh面波震相,其时程如图8所示。为对比方便,图8（a）,（b）中部分观测点的面波时程未完全展示,而只统一给出t=0～5 s的结果。可以看出,对不同阻抗比模型,面波的传播速度随盆地覆盖层剪切波速的增加而增大。对于小阻抗比模型,模拟时程显示有不同阶模态的面波存在（图8（a）中虚线所示）,而大阻抗比模型中则基本只有基阶面波存在。随阻抗比的增大,Rayleigh面波垂直分量的幅值明显大于水平分量,且面波的强度逐渐减弱,IC=0.327时盆地次生面波的幅值已非常微弱。此外,随盆地土层波速的增加,体波在盆地基底产生多次反射,每次反射回盆地的体波均引起新的次生面波产生,形成“平行”的多个面波波列（图8（c）～（e））,使得面波的持续时间显著增长。此外,阻抗比较小时,盆地角点处即可见有明显的面波产生,而阻抗比较大时距离盆地角点一定距离才可观察到清晰面波。

图9所示为盆地地表观测点Rayleigh面波幅值的分布。总体来看,无论水平还是垂直分量,面波幅值均随阻抗比的增大而降低。盆地内外介质波速差异较大时,水平和垂直分量的面波幅值在盆地内均存在明显的振荡,大值和小值的区域交替出现,且这些区域的位置基本相同。面波强度的交替变化可能与面波和体波间的相长或相消干涉有关。随阻抗比的增大,面波强度的分布趋于稳定,在盆地内部基本维持在某一定值附近。对小阻抗比模型,面波最大幅值并非出现在盆地边缘,而是位于盆地中间的某一位置；而对大阻抗比模型,面波最大值基本位于盆地边缘附近,水平分量在10号观测点附近达到最大值,向内部逐渐衰减到某一定值附近,垂直分量在13号测点附近达到最大值后向内部基本维持不变。

图 9 不同阻抗比模型的盆地内地表观测点次生Rayleigh面波的位移峰值分布

Figure 9. Amplitude distributions of basin-induced Rayleigh waves for ground points of different IC models

下载: 全尺寸图片幻灯片

面波幅值沿盆地内的振荡也可从波场快照中定性观察到。图10给出了IC=0.044模型对应的t=0.8 s～5 s每隔0.6 s的波传播快照,图中白色箭头所示为Rayleigh面波震相。可以看出,面波在传播过程中和直达体波（1.4 s）、折射体波（确切为盆地边缘折射的P和S波,以及二者在地表的反射波,2.0 s,2.6 s）、多次反射体波（3.2 s,3.8 s）及其它散射体波（4.4 s,5.0 s）之间发生多次相长或相消干涉,导致面波的幅值在传播过程中不断变化。同时,除面波和体波的干涉外,盆地内复杂的体波震相之间的干涉同样导致局部的地震动被放大,这可能是小阻抗比模型的最大位移峰值出现在盆地中间区域的原因。此外,波场快照还显示面波基本以恒定的速度传播,按图中虚线计算的传播速度与图8（a）中估计的面波传播速度较为接近,再次表明该震相为面波。

图 10 IC=0.044模型对应的不同时刻水平分量的位移波场快照（黑色实线之内为盆地）

Figure 10. Snapshots of horizontal component displacement wavefield for IC=0.044 model (black line-basin boundary)

下载: 全尺寸图片幻灯片

图11所示为盆地地表各点面波幅值与地震动峰值之比（以下简记为R）。可以看出,对水平分量,盆地内外介质的阻抗比越小,即盆地土层剪切波速越小,地震动时程中面波幅值与实际地震动峰值的比值越大,最大比值达0.85左右。

图 11 不同阻抗比模型的盆地内地表观测点次生Rayleigh面波的幅值与地震动峰值的比值

Figure 11. Distributions of ratio of amplitudes of basin-induced Rayleigh waves to PGDs of ground points for different IC models

下载: 全尺寸图片幻灯片

比较而言,盆地边缘区域的地震动峰值相比盆地内部区域受面波传播的影响更大,后者对应的R值在0.05～0.4之间,表明盆地中央区域的地震动峰值主要受被放大的体波控制。对垂直分量,从盆地边缘到盆地中央,面波幅值占地震动峰值的比例整体表现出逐渐增大的趋势,盆地中央区域的平均R值在0.7左右,表明其地震动峰值主要受面波的峰值控制。其中IC=0.076模型对应的47号测点的R值为1.05（>1）,即面波幅值大于真实位移峰值,考虑到真实时程为面波与体波的叠加,同时,提取该点的面波与体波时程显示二者在最大位移峰值时刻震相相反,即发生相消干涉,这可能是导致R大于1的主要原因。

4. 结论

本文首先基于f-k域滤波及质点运动时频极化分析技术,给出了一种识别和提取剖面时程中Rayleigh面波震相的方法,通过实际算例验证了方法的正确性。采用显式有限元结合多次透射边界方法模拟了二维盆地内外介质阻抗比变化时的地表地震动响应,利用前述方法从模拟位移时程中提取面波震相,进而定量研究了基底两侧阻抗比（IC）对盆地放大效应及盆地次生面波强度的影响。主要结论如下：

（1）相比传统方法,本文提取面波的方法综合考虑了面波与体波在传播速度、极化特征等方面的差异,实施效果良好。

（2）IC越小,盆地内波传播特征越复杂。对水平分量,盆地边缘效应的区域发生在距角点300～600 m的范围；IC较小时,PGD最大值出现于盆地内部而非边缘区域,盆地中央区域地震动峰值基本维持不变。对垂直分量,其位移峰值可达水平分量的75%；盆地边缘区域PGD最大,整体随远离盆地角点而递减,但IC较小时盆地地表PGD振荡明显。无论水平还是垂直分量,盆地最大位移峰值随IC的增加而降低,但IC过小时,最大PGD反而降低。

（3）相比一维水平成层模型,盆地斜边上方区域水平分量的地震动被抑制,放大系数（AF）小于1,盆地边缘及IC较小时的中间局部区域放大系数大于1,最大AF为1.14左右,出现于盆地中间区域；随IC的增大,水平分量最大放大系数也逐渐增大,但IC过大时最大AF反而降低。垂直分量AF随IC的增大而降低,最大放大系数位于盆地边缘,IC较小时盆地内AF分布有明显振荡。

（4）随IC的增大,两分量的面波强度均逐渐减弱,基底多次反射体波导致多次次生面波形成,使面波持时增长。IC较小时,面波幅值在盆地内振荡明显,最大值位于盆地中间某一位置；IC较大时,水平分量面波幅值在盆地边缘处最大,向盆地内部衰减趋于某定值；垂直分量面波幅值在盆地边缘区域最大,向内部基本不变。

此外,需要指出的是,本文结果是基于特定盆地倾角及盆地深度下得出的,而这些因素对盆地地震效应的影响不可忽略,有关各因素的影响将另文给出。

图 1 裂缝边坡三维旋转破坏机构

Figure 1. Three-dimensional failure mechanism of cracked slopes

下载: 全尺寸图片幻灯片

图 2 裂缝边坡三维旋转破坏拓展机构

Figure 2. Extended three-dimensional failure mechanism of cracked slopes

下载: 全尺寸图片幻灯片

图 3 平面应变机制插入示意图

Figure 3. Schematic diagram of insert portion of plane-strain mechanism

下载: 全尺寸图片幻灯片

图 4 读取安全系数示意图

Figure 4. Schematic diagram of reading factor of safety

下载: 全尺寸图片幻灯片

图 5 几何约束对三维破坏机构的影响

Figure 5. Influences of geometric constraints on 3D failure mechanism

下载: 全尺寸图片幻灯片

图 6 不考虑坡顶裂缝情况下边坡三维稳定性图表

Figure 6. Stability charts of 3D slopes without cracks on upper surface

下载: 全尺寸图片幻灯片

图 7 考虑坡顶裂缝情况下边坡三维稳定性图表

Figure 7. Stability charts of 3D slopes with cracks on upper surface

下载: 全尺寸图片幻灯片

图 8 边坡宽度对三维破坏机构的影响

Figure 8. Influences of slope width on 3D failure mechanism

下载: 全尺寸图片幻灯片

图 9 三维效应下边坡坡角对裂缝深度的影响

Figure 9. Influences of slope inclination on crack depth under 3D condition

下载: 全尺寸图片幻灯片

图 10 三维效应对裂缝深度的影响

Figure 10. Influences of three-dimensional effects on crack depth

下载: 全尺寸图片幻灯片

表 1 不考虑坡顶裂缝情况下三维边坡稳定系数对比

Table 1 Comparison of 3D stability factors of slopes without cracks

β/(°)	φ/(°)	B/H	θ ₀/(°)	θ _h/(°)	r ₀′/r₀	γH/c
β/(°)	φ/(°)	B/H	θ ₀/(°)	θ _h/(°)	r ₀′/r₀	本文解答	文献[19]解答	文献[20]解答
30	15	0.5	53.69	97.25	0.941	73.106^a	73.156^a	73.120^a
45	15	0.5	30.39	89.54	0.888	32.184^a	32.371^a	32.198^a
	30	0.8	57.27	95.34	0.856	62.121	62.213	62.121
60	15	0.5	14.43	80.14	0.843	20.889^a	21.512^a	20.805^a
	30	0.8	42.14	87.18	0.739	26.464	26.486	26.464
注：^a坡面破坏。

下载: 导出CSV

表 2 考虑坡顶裂缝情况下三维边坡稳定系数对比

Table 2 Comparison of 3D stability factors of slopes with cracks

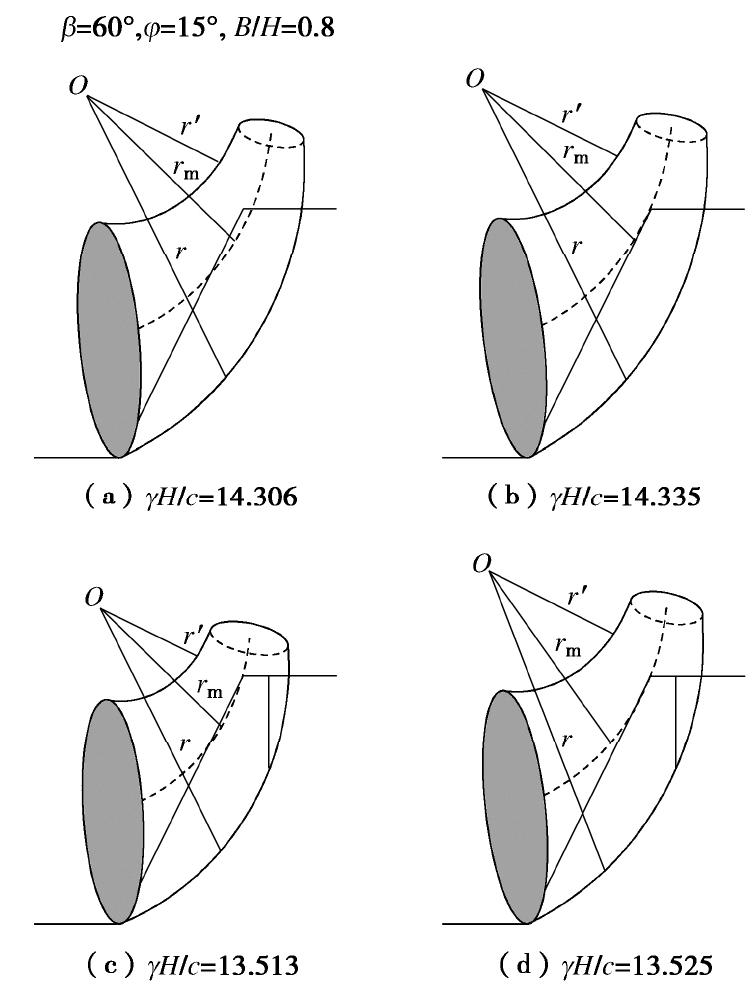
β/(°)	φ/(°)	B/H	γH/c
β/(°)	φ/(°)	B/H	本文解答	文献[17]解答
30	10	0.8	28.00	27.74
	20	3.0	47.81	47.75
45	10	0.8	15.82	15.68
	20	3.0	17.54	17.53
60	10	0.8	11.15	11.07
	20	3.0	10.60	10.59
70	10	0.8	8.33	8.26
	20	3.0	7.02	7.01

下载: 导出CSV

表 3 边坡稳定系数(φ=15°)

Table 3 Stability factors of slopes (φ=15°)

B/H		β/(°)
		30			45			60			75
		γH/c	δ/H	x/H	γH/c	δ/H	x/H	γH/c	δ/H	x/H	γH/c	δ/H	x/H
0.5	PC	73.155^a	0.003	0.043	31.978^a	0.126	0.041	19.903^a	0.331	0.041	14.085^a	0.477	0.070
0.5	IN	73.106^a	—	—	32.184^a	—	—	20.889^a	—	—	15.834^a	—	—
0.6	PC	61.199^a	0.015	0.075	26.685	0.145	0.043	16.670	0.389	0.057	11.713	0.599	0.082
0.6	IN	61.002^a	—	—	26.725	—	—	17.482	—	—	13.322	—	—
0.8	PC	46.051	0.021	0.107	20.913	0.186	0.111	13.524	0.392	0.117	9.598	0.587	0.126
0.8	IN	46.071	—	—	21.220	—	—	14.306	—	—	10.936	—	—
1.0	PC	38.698	0.046	0.123	18.230	0.211	0.136	11.965	0.386	0.148	8.505	0.571	0.150
1.0	IN	38.795	—	—	18.648	—	—	12.786	—	—	9.797	—	—
1.5	PC	30.874	0.084	0.145	15.298	0.234	0.173	10.190	0.382	0.186	7.217	0.553	0.182
1.5	IN	31.126	—	—	15.855	—	—	11.087	—	—	8.503	—	—
3.0	PC	25.124	0.114	0.170	12.994	0.248	0.207	8.722	0.379	0.220	6.111	0.539	0.211
3.0	IN	25.540	—	—	13.686	—	—	9.714	—	—	7.433	—	—
注：^a坡面破坏；PC考虑坡顶存在裂缝情况；IN考虑坡顶无裂缝情况；x/H裂缝位置与坡肩B的距离。

下载: 导出CSV

表 4 边坡稳定系数(φ=30°)

Table 4 Stability factors of slopes (φ=30°)

B/H		β/(°)
		45			60			75
		γH/c	δ/H	x/H	γH/c	δ/H	x/H	γH/c	δ/H	x/H
0.5	PC	96.560^a	0.001	0.040	40.219^a	0.125	0.041	23.673^a	0.389	0.029
0.5	IN	96.417^a	—	—	40.590^a	—	—	25.446^a	—	—
0.6	PC	80.718^a	0.021	0.061	33.511^a	0.187	0.042	19.361^a	0.552	0.016
0.6	IN	80.287^a	—	—	33.935^a	—	—	21.226^a	—	—
0.8	PC	61.978	0.045	0.067	25.882	0.263	0.061	15.137	0.523	0.081
0.8	IN	62.121	—	—	26.464	—	—	16.534	—	—
1.0	PC	53.724	0.068	0.069	22.644	0.250	0.092	13.261	0.491	0.107
1.0	IN	54.066	—	—	23.398	—	—	14.647	—	—
1.5	PC	45.243	0.088	0.076	19.260	0.251	0.115	11.186	0.466	0.134
1.5	IN	45.836	—	—	20.216	—	—	12.652	—	—
3.0	PC	39.061	0.098	0.084	16.677	0.252	0.132	9.516	0.452	0.156
3.0	IN	39.864	—	—	17.830	—	—	11.120	—	—
注：^a坡面破坏；PC考虑坡顶存在裂缝情况；IN考虑坡顶无裂缝情况；x/H裂缝位置与坡肩B的距离。

下载: 导出CSV

参考文献(28)

[1]	陈祖煜. 土质边坡稳定分析：原理·方法·程序[M]. 北京: 中国水利水电出版社, 2003. CHEN Zu-yu. Soil Slope Stability Analysis[M]. Beijing: China Water Power Press, 2003. (in Chinese)
[2]	陈曦, 刘春杰. 有限元强度折减法中安全系数的搜索算法[J]. 岩土工程学报, 2010, 32(9): 1443-1447. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201009028.htm CHEN Xi, LIU Chun-jie. Search algorithms for safety factor in finite element shear strength reduction method[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(9): 1443-1447. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201009028.htm
[3]	DRUCKER D C, PRAGER W. Soil mechanics and plastic analysis or limit design[J]. Quarterly of Applied Mathematics, 1952, 10(2): 157-165. doi: 10.1090/qam/48291
[4]	刘锋, 芮勇勤, 张春. 坡顶张拉裂缝对边坡稳定性影响[J]. 辽宁工程技术大学学报(自然科学版), 2016, 35(9): 949-954. https://www.cnki.com.cn/Article/CJFDTOTAL-FXKY201609010.htm LIU Feng, RUI Yong-qin, ZHANG Chun. Influence of tension cracks of slope crest on the stability of slope[J]. Journal of Liaoning Technical University (Natural Science), 2016, 35(9): 945-954. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-FXKY201609010.htm
[5]	秦会来, 周予启, 黄茂松, 等. 基于上限理论的预留土支护基坑极限抗力分析[J]. 岩土工程学报, 2020, 42(6): 1101-1107. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202006017.htm QIN Hui-lai, ZHOU Yu-qi, HUANG Mao-song, et al. Passive earth pressure analysis of berm-retained excavation by upper bound method[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(6): 1101-1107. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202006017.htm
[6]	吴梦喜, 杨家修, 湛正刚. 边坡稳定分析的虚功率法[J]. 力学学报, 2020, 52(3): 663-672. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202003007.htm WU Meng-xi, YANG Jia-xiu, ZHAN Zheng-gang. A virtual power slope stability analysis method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(3): 663-672. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB202003007.htm
[7]	CHEN W F. Limit Analysis and Soil Plasticity[M]. Amsterdam: Elsevier Science, 1975.
[8]	TERZAGHI K. Theoretical Soil Mechanics[M]. New York: Wiley, 1943.
[9]	SPENCER E. A method of analysis of the stability of embankments assuming parallel inter-slice forces[J]. Géotechnique, 1967, 17(1): 11-26. doi: 10.1680/geot.1967.17.1.11
[10]	COUSINS B F. Stability charts for simple earth slopes allowing for tension cracks[C]//Proceedings of the Third Australia-New Zealand Conference on Geomechanics, 1980, Wellington.
[11]	MICHALOWSKI R L. Stability assessment of slopes with cracks using limit analysis[J]. Canadian Geotechnical Journal, 2013, 50(10): 1011-1021. doi: 10.1139/cgj-2012-0448
[12]	UTILI S. Investigation by limit analysis on the stability of slopes with cracks[J]. Géotechnique, 2013, 63(2): 140-154. doi: 10.1680/geot.11.P.068
[13]	ZHAO L H, CHENG X, ZHANG Y, et al. Stability analysis of seismic slopes with cracks[J]. Computers and Geotechnics, 2016, 77: 77-90. doi: 10.1016/j.compgeo.2016.04.007
[14]	何毅, 余军炎, 袁冉, 等. 考虑坡顶倾角的土质裂隙边坡稳定性分析[J]. 中国公路学报, 2021, 34(5): 45-54. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202105005.htm HE Yi, YU Jun-yan, YUAN Ran, et al. Stability analysis of soil slope with cracks considering upper slope inclination angle[J]. China Jouranl of Highway and Transport, 2021, 34(5): 45-54. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202105005.htm
[15]	周志军, 朱林楦, 陈磊. 倾斜坡顶黄土边坡垂直裂隙深度计算方法[J]. 中国公路学报, 2021, 34(5): 37-44. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202105004.htm ZHOU Zhi-jun, ZHU Lin-xuan, CHEN Lei. Calculation method of vertical crack depth of loess slope with inclined crest[J]. China Journal of Highway and Transport, 2021, 34(5): 37-44. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202105004.htm
[16]	MICHALOWSKI R L, DRESCHER A. Three-dimensional stability of slopes and excavations[J]. Géotechnique, 2009, 59(10): 839-850.
[17]	HE Y, LIU Y, ZHANG Y, et al. Stability assessment of three-dimensional slopes with cracks[J]. Engineering Geology, 2019, 252: 136-144.
[18]	LI Z W, YANG X L, LI T Z. Static and seismic stability assessment of 3D slopes with cracks[J]. Engineering Geology, 2019, 265: 105450.
[19]	GAO Y F, ZHANG F, LEI G H, et al. An extended limit analysis of three-dimensional slope stability[J]. Géotechnique, 2013, 63(6): 518.
[20]	DOWON P, MICHALOWSKI R L. Intricacies in three-dimensional limit analysis of earth slopes[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2018, 42(17): 2109-2129.
[21]	SUN J, ZHAO Z. Stability charts for homogenous soil slopes[J]. Journal of Geotechnical & Geoenvironmental Engineering, 2013, 139(12): 2212-2218.
[22]	孙超伟, 柴军瑞, 许增光, 等. 求解三维均质边坡安全系数的稳定性图表法研究[J]. 岩土工程学报, 2018, 40(11): 2068-2077. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201811015.htm SUN Chao-wei, CHAI Jun-rui, XU Zeng-guang, et al. Stability charts for determining safety factors of 3D homogeneous slopes[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(11): 2068-2077. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201811015.htm
[23]	GAO Y F, ZHANG F, LEI G H, et al. Stability charts for 3D failures of homogeneous slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(9): 1528-1538.
[24]	LI A J, MERIFIELD R S, LYAMIN A V. Three-dimensional stability charts for slopes based on limit analysis methods[J]. Canadian Geotechnical Journal, 2010, 47(12): 1316-1334.
[25]	RAO P P, ZHAO L X, CHEN Q S, et al. Three-dimensional limit analysis of slopes reinforced with piles in soils exhibiting heterogeneity and anisotropy[J]. Soil Dynamics and Earthquake Engineering, 2019, 121: 194-199.
[26]	MICHALOWSKI R L. Stability charts for uniform slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(4): 351-355.
[27]	QIN C, CHIAN S C. New perspective on seismic slope stability analysis[J]. International Journal of Geomechanics, 2018, 18(7): 1-8.
[28]	CHEN Z Y. Random trials used in determining global minimum factors of safety of slopes[J]. Canadian Geotechnical Journal, 1992, 29(2): 225-233.

施引文献(13)

期刊类型引用(7)

1.	陈凌宇. 考虑子盆地影响的二维盆地非线性地震反应研究. 江苏建筑. 2024(05): 23-25+50 . 百度学术
2.	周青帅，刘启方. 不均匀软弱夹层对沉积盆地地震动放大的影响研究. 地震工程与工程振动. 2023(06): 183-193 . 百度学术
3.	魏成前. 入射波的卓越频率对盆地地震动响应的影响. 四川建材. 2022(01): 249-250 . 百度学术
4.	邵祖鹏，刘启方. 震源深度对二维盆地放大的影响研究. 地震研究. 2022(03): 489-497 . 百度学术
5.	刘启方. 2014年鲁甸地震龙头山镇盆地共振效应研究. 地震工程与工程振动. 2021(02): 43-52 . 百度学术
6.	于彦彦，丁海平. 盆地深度对盆地地表地震动及次生面波的影响. 地震工程与工程振动. 2021(03): 147-156 . 百度学术
7.	强生银，刘启方，温瑞智，王宏伟. 基于二维数值模拟的盆地地震动放大系数. 地震工程与工程振动. 2021(04): 131-144 . 百度学术