EPS颗粒混合轻量土的动变形特性及修正Hardin-Drnevich模型研究

侯天顺; 崔奕翔

doi:10.11779/CJGE202109004

EPS颗粒混合轻量土的动变形特性及修正Hardin-Drnevich模型研究 English Version

西北农林科技大学水利与建筑工程学院,陕西　杨凌　712100

基金项目:

国家自然科学基金项目 51509211

中国博士后基金项目 2016M602863

陕西省留学人员科技活动择优资助项目 2018031

陕西省社会发展科技攻关项目 2015SF260

陕西省博士后基金项目 2017BSHYDZZ50

杨凌示范区科技计划项目 2016GY-01

中央高校基本科研业务费专项资金项目 2452020169

详细信息

作者简介:
侯天顺(1981— ),男,湖北省郧西县人,博士,副教授,主要从事岩土力学、地基基础工程与地质灾害防治方面的教学与科研工作。E-mail：houtianshunyx@sina.com

中图分类号: TU435
计量
- 文章访问数: 259
- HTML全文浏览量: 35
- PDF下载量: 142
出版历程
- 收稿日期: 2020-10-24
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-08-31

Dynamic deformation characteristics and modified Hardin-Drnevich model for light weight soil mixed with EPS particles

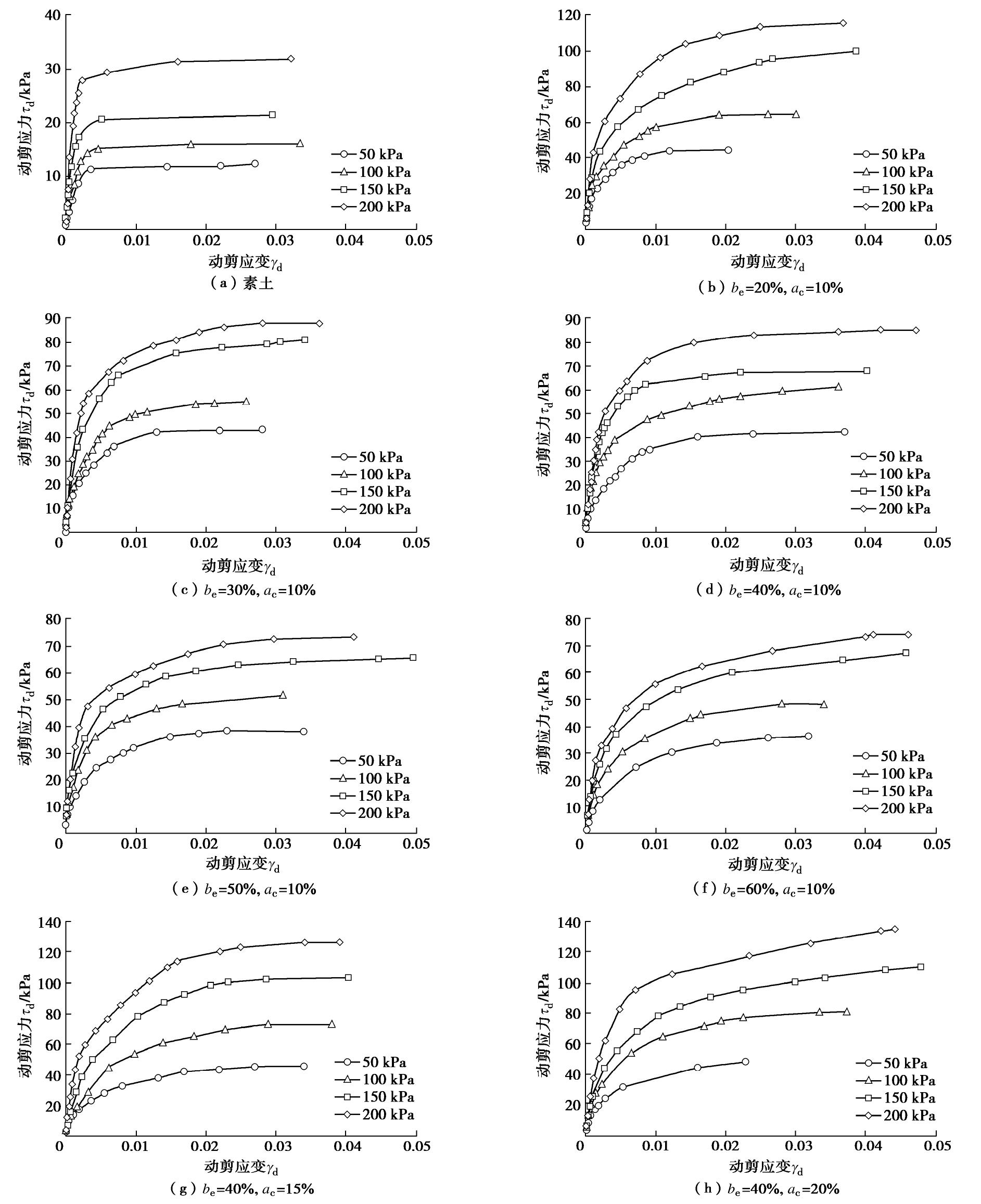
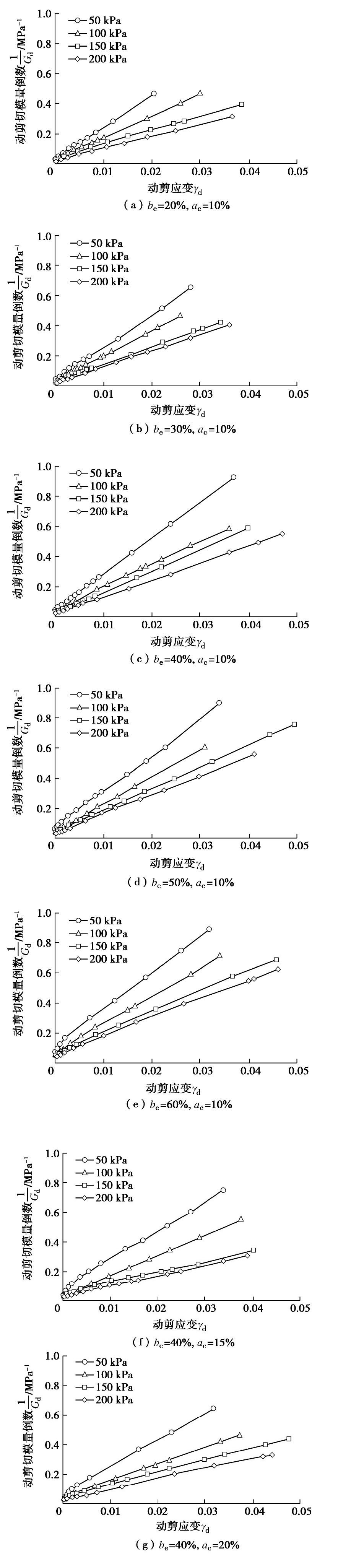
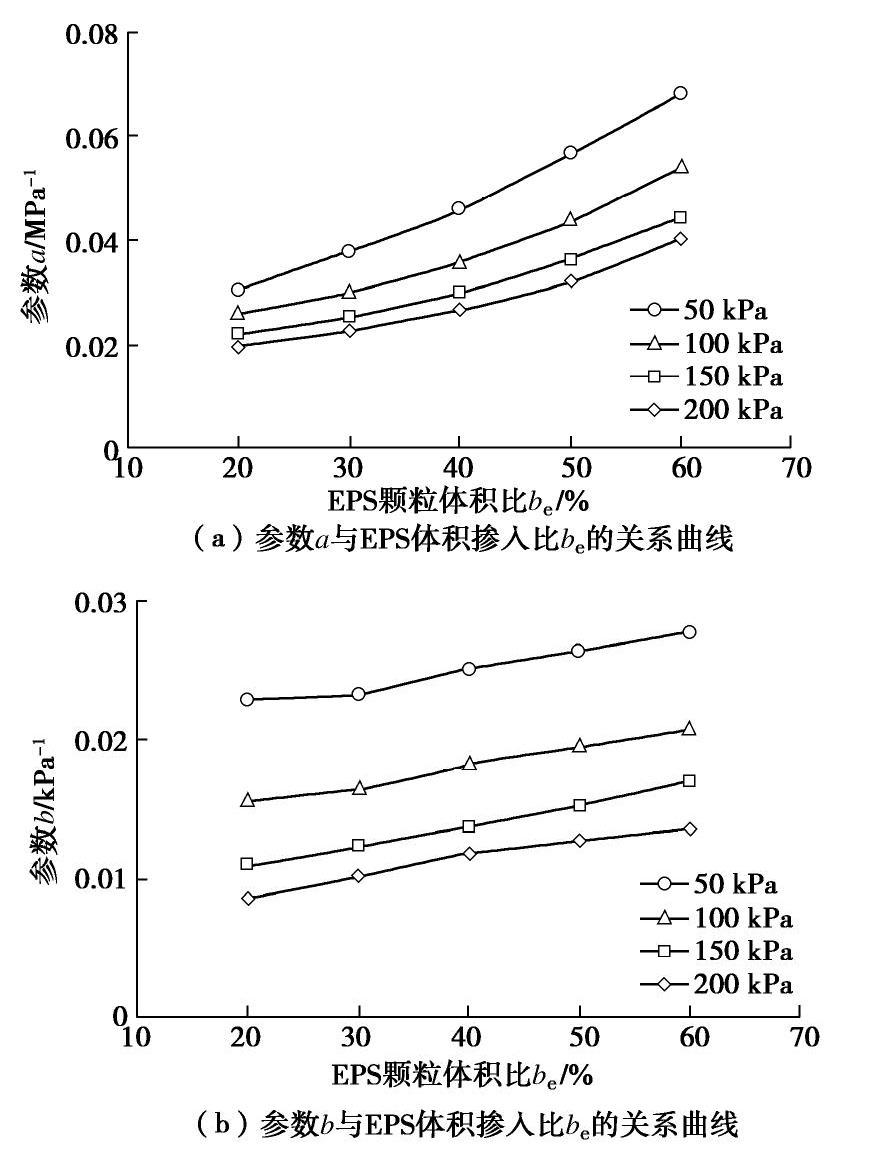
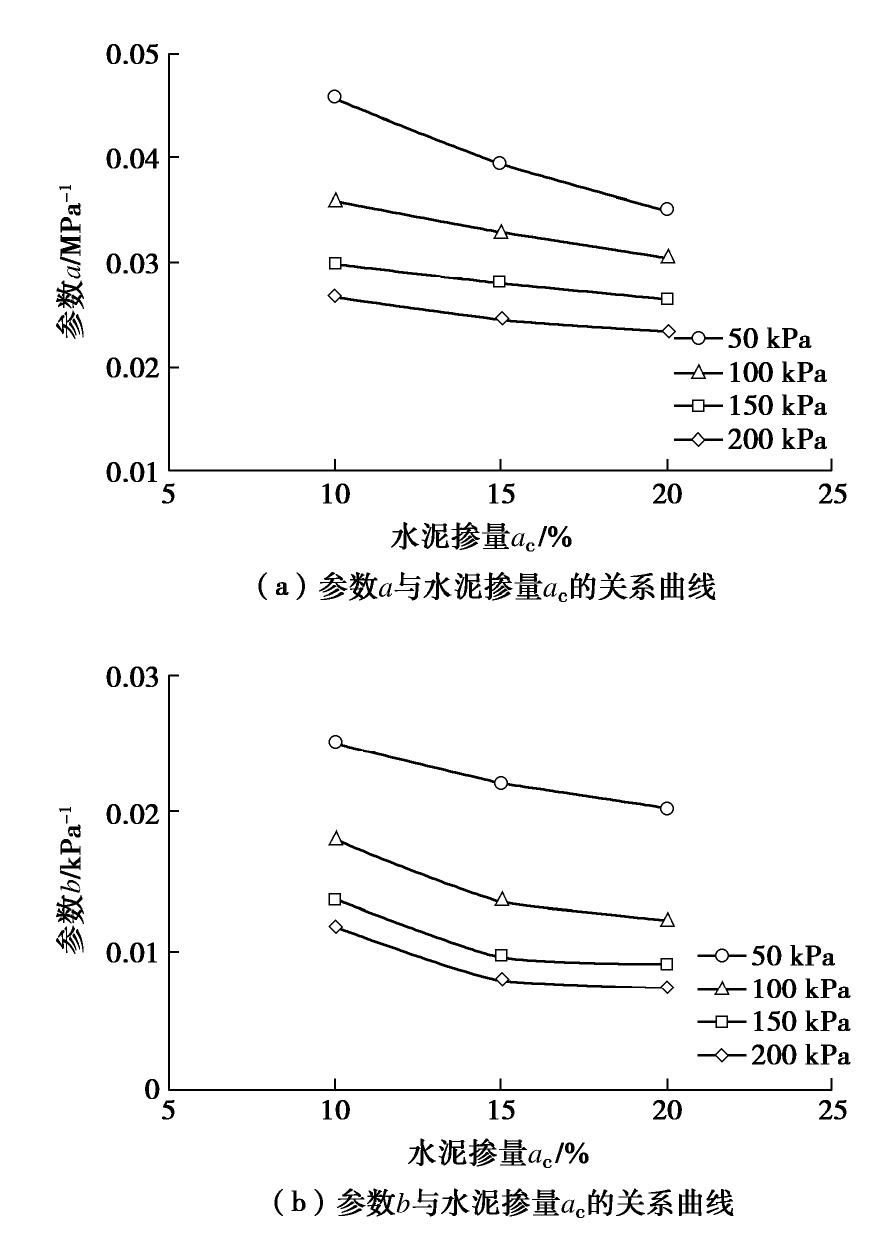
College of Water Resources and Architectural Engineering, Northwest A&F University, Yangling 712100, China

摘要

摘要: 为探究EPS颗粒混合轻量土的动变形特性,通过动三轴试验研究了不同配比、围压对轻量土骨干曲线、Hardin-Drnevich模型参数的影响规律,建立了修正Hardin-Drnevich模型,并对修正模型进行了验证。结果表明：轻量土的骨干曲线呈现出明显的非线性特性与应变硬化特征。轻量土动剪切模量的倒数与剪应变关系曲线符合线性递增的变化规律,其动变形特性可以由Hardin-Drnevich模型描述。最大动剪切模量的倒数和最大动剪应力的倒数随着围压和水泥掺量的增大而减小,随EPS颗粒体积比的增大而增大。在Hardin公式的基础上,引入相对结构度k和广义孔隙比 $e^{'}$ ,提出了模型参数的表达式,建立了修正Hardin-Drnevich模型。通过改变应力状态和应力路径对轻量土进行动三轴验证试验,发现模型计算值与试验值间的相对误差均小于11%,修正Hardin-Drnevich模型对轻量土骨干曲线的预测结果良好,这表明修正Hardin-Drnevich模型可以描述轻量土特殊结构性在复杂受力条件下的动力响应。
- 轻量土 /
- 动变形特性 /
- 修正Hardin-Drnevich模型 /
- 相对结构度 /
- 广义孔隙比 /
- 动三轴试验
Abstract: To investigate the dynamic deformation characteristics of light weight soil mixed with EPS particles, the influences of different mixed ratios and confining pressures on the backbone curve and the parameters of Hardin-Drnevich model for light weight soil are studied through the dynamic triaxial tests, and the modified Hardin-Drnevich model is established and verified. The results show that the backbone curve of light weight soil exhibits obvious nonlinear and strain-hardening characteristics. The relationship between reciprocal of dynamic shear modulus and shear strain of light weight soil increases linearly, indicating that the dynamic deformation characteristics of light weight soil can be described by the Hardin-Drnevich model. The reciprocal of the maximum dynamic shear modulus and that of the maximum dynamic shear stress decrease with the increase of confining pressure and cement content, and increase with the increase of volume ratio of EPS particles. On the basis of the Hardin formula, the expression for model parameters is proposed by introducing the relative structure k and the generalized pore ratio e', and the modified Hardin-Drnevich model is established. By changing the stress state and stress path, the relative error between the calculated value and the test value is less than 11%. The predicted results by the modified Hardin-Drnevich model for the backbone curves of light weight soil are good, which shows that the modified Hardin-Drnevich model can describe the dynamic response of the special structure of light weight soil under complex stress conditions.
- light weight soil /
- dynamic deformation characteristic /
- modified Hardin-Drnevich model /
- relative structural degree /
- generalized void ratio /
- dynamic triaxial test

HTML全文

0. 引言

中国水资源时空分布与社会经济发展不协调问题日益突出^[1]，为此“十四五”规划中重点强调：“要加强水利基础设施建设，提升水资源优化配置和水旱灾害防御能力”^[2]。水资源配置工程中，引调水管线的应用较为普遍，通常具有流量大、线路长、跨越的地形地质条件复杂等特点，管线的长期安全稳定运行，对整个工程至关重要。埋地钢管（也称回填钢管）特别适用于大直径、高内压和复杂外部环境的管线工程，在引调水及水电工程中得到了极大的关注，其未来发展潜力巨大。鉴于目前工程中的需求，新修编的《水利水电工程压力钢管设计规范》SL/T 281规范在参考国内外相关规范的基础上，着重增补了埋地钢管的相关设计内容^[3-4]。

埋地钢管为柔性管道，管土间存在复杂的相互作用，由钢管和土体共同承担外部荷载。覆土产生的土压力是钢管主要的外部荷载，故管顶土压力（以下简称土压力）的确定是埋地钢管结构设计的基础。土压力计算公式最早由Marston于1913年提出，假定沟槽内土体沿着沟槽侧壁滑移，管道承担全部回填土荷载，但对柔性管道适用性差^[5]。Spangler修正了该理论，假定沟槽内的土压力在管道和回填土上均匀分布，使其适用于柔性管道^[6]。由于Marston荷载仅考虑了直壁沟槽，Li等^[7]对其进行了改进，提出了梯形槽下的土压力计算公式。Shmulevich等^[8]对管径0.87~1.3 m的柔性管道的试验结果表明，土压力并非均匀分布，径向和切向土压力近似呈抛物线分布。周正峰等^[9-10]对管径0.61 m的埋地钢管开展有限元研究、李永刚^[11]对管径0.1 m和0.2 m钢管开展土箱试验，均得出土压力在管中心位置最大，从管中心向管侧大致呈抛物线分布。Tian等^[12]认为土压力在管中心存在波谷，将管中心到两侧土压力简化为抛物线分布，并对0.5 m及1 m管径的埋地钢管进行数值验证。Kawabata等^[13-14]分析了高埋深下管径0.9 m的柔性管道土压力情况，土压力呈“凹”形分布。伍鹤皋等^[15-16]以管径3 m的埋地钢管为研究对象，发现土压力分布与管径大小有关，并随着管道运行工况的变化而改变。周敏等^[17]采用室内试验，研究了地层沉陷下埋地柔性管道变形及土压力变化情况。

针对埋地钢管的研究，以往主要集中在给排水及油气行业，研究对象多为小直径管道，对于大直径管道（管径不小于1.2 m）的研究相对较少。随着国内引调水工程及水电工程的发展，水利行业大直径埋地钢管的应用逐渐增多，传统的土压力计算方法不能完全适用。为此，本文采用有限元法，分析了埋地钢管在不同管径、径厚比及埋深下的土压力情况，考虑到土压力的影响因素较为复杂，探讨了回填土参数、沟槽侧壁土-土摩擦系数及沟槽宽度的影响，对比分析了传统的棱柱荷载及Marston荷载的优劣，进而提出了较为适用于大直径埋地钢管的土压力模型。

1. 计算模型

1.1 模型介绍

埋地钢管ANSYS有限元计算模型如图 1所示。采用直壁沟槽，假定管径为D，管顶覆土为H，沟槽宽度B为2D，沟槽深为H₁，管底垫层厚度0.3 m，垫层包角90°。模型底部、前后及左右端面施加沿法向的位移约束，顶面自由，整个模型宽为7B，高为4H₁，以消除边界条件的影响。钢管采用4节点壳单元SHELL 181模拟，土体采用8节点实体单元SOLID 45模拟。钢管采用的弹性模量、泊松比和密度分别为2.06×10⁵ MPa，0.3和7850 kg/m³。计算采用典型的土体参数进行分析见表 1。根据规范SL/T 281或CECS 141^[18]以及GB 50268^[19]，可确定典型土体种类及变形模量；根据规范及工程经验，土的密度通常为1600~2200 kg/m³；黏性土的泊松比为0.25~0.42，黏聚力为2~65 kPa，内摩擦角为15°~30°；砂土的泊松比为0.25~0.3，内摩擦角为28°~42°^[20-21]。

图 1 有限元计算模型

Figure 1. Finite element model

下载: 全尺寸图片幻灯片

表 1 土体种类及其材料参数

Table 1. Soil types and material parameters

名称	土体种类	变形模量/MPa	泊松比	黏聚力/kPa	内摩擦角/(°)	密度/(kg·m^-3)
原状土	黏性土；标准锤击数N_63.5 > 50	10	0.35	10	30	1800
回填土	黏性土；压实系数95%	5	0.35	10	30	1800
砂垫层	砂砾，细粒土含量不大于12%；压实系数95%	7	0.25	0	30	1800

下载: 导出CSV

| 显示表格

为满足美国土木工程师协会手册ASCE No.119^[22]对埋地钢管有限元模型可靠性的要求，土体本构关系采用经典的Drucker-Prager屈服准则^[23]；钢管与土体及沟槽侧壁土-土间设置面-面接触单元（TARGE 170和CONTA 174），并采用库仑摩擦模型模拟接触面间的相互关系，管-土及土-土间摩擦系数分别取0.25和0.577(tan30°)^{[9, 18]}。鉴于大直径埋地钢管施工时通常内部设置支撑，变形主要发生在施工完毕、撤去支撑阶段。为简化分析，模拟时通过直接调整土体模量及施加重力荷载的方式来实现土体碾压密实后管道所受土压力的效果。

1.2 模型验证

为进一步说明本文有限元模拟技术的可靠性，结合试验结果，进行对比验证。文献[24]对埋地聚氯乙烯（PVC）塑料管道（管径150 mm，壁厚10 mm）进行土箱试验，获取了管周接触压力数据。建立相应的有限元模型，管材的弹性模量、泊松比和密度分别取3000 MPa，0.4，1400 kg/m³^[25]，土体参数采用试验给出的实测值。试验时土体上方施加50 kPa的均布压力。

图 2给出了有限元与试验的接触压力比较结果。可以看到，两种方法得出的管周接触压力从管顶到管底的分布趋势均为先减少、后增大，存在管顶/底大、管腰小特征；接触压力大小虽然有细微差别，但总体上较为接近。考虑到试验误差及模型简化等情况，故认为本文采用的有限元模拟技术具有较高的可靠性，可用于后续分析。

图 2 有限元与试验结果的管周接触压力比较

Figure 2. Comparison of contact pressures around pipes between finite element and test results

下载: 全尺寸图片幻灯片

2. 计算结果及分析

传统的土压力计算通常采用棱柱荷载 ${\sigma _{\text{p}}}$ 或Marston荷载 ${\sigma _{\text{M}}}$ ，均假定为均匀分布，但大小不同，计算见式（1），（2）。水利行业规范SL/T 281及给排水行业CECS系列规程均采用棱柱荷载。日本规范以2 m埋深为界，两种方法都有采用^[26]；美国水工协会手册AWWA M11中说明Marston荷载可用于窄槽下，棱柱荷载可作为保守设计^[6]。

${\sigma _{\text{M}}} = (1 - {{\text{e}}^{ - \frac{{2fK}}{B} \cdot H}})\gamma B/(2fK) = {C_{\text{d}}}\gamma B \text{, }$

(1)

${\sigma _{\text{p}}} = \gamma H。$

(2)

式中 $\gamma$ 为回填土的重度；B为沟槽宽度；f为沟槽侧壁土-土滑动摩擦系数；K为朗肯主动土压力系数；H为管顶埋深。

以管径D=3 m的埋地钢管为例，深入分析径厚比（管径D与壁厚t之比）及埋深对土压力的影响。土压力可从有限元计算获取的管周接触压力、切向力沿竖向方向分解得出。大直径埋地钢管的径厚比D/t通常在100~300范围内；为考虑埋深影响，在2~8 m范围内间隔2 m取值。

2.1 土压力分析

图 3为不同径厚比及埋深下的土压力分布。可以看出，埋深2 m、径厚比100时，土压力近似呈“倒盆形”分布，即土压力在管中心区域分布平坦，在距离管中心约（0.25~0.4）D处开始呈抛物线式急剧降低。随着径厚比的增加，土压力峰值逐步降低并从管中心区域移向管侧胸腔。这是由于径厚比增大后，管道竖向收缩变形加剧，胸腔管壁趋向平坦，承担了更多的土压力。此外，径厚比在100~150范围变动时，土压力降幅明显，大于200后，变化很小。埋深增加后，可明显加大土压力，对管道受力变形不利。埋深越深，土压力分布在管中心区域内凹越严重、管侧胸腔越突出，越易趋向“M形”。埋深越深，不同径厚比下，土压力峰值差也相应增加，如径厚比100与200下的峰值差，埋深4 m为埋深2 m的2.62倍。

图 3 不同径厚比D/t及埋深H下的土压力

Figure 3. Soil pressures under different diameter-thickness ratios D/t and cover depths H

下载: 全尺寸图片幻灯片

2.2 大小比较

将棱柱荷载 ${\sigma _{\text{p}}}$ 、Marston荷载 ${\sigma _{\text{M}}}$ 分别与数值计算得出的峰值土压力 ${\sigma _{{\text{max}}}}$ 、均值土压力 ${\sigma _{{\text{avg}}}}$ （土压力沿管径积分后除以管径）进行比较如图 4所示。可以看出，埋深2 m时，两种荷载与峰值土压力吻合良好，偏差均在10%以内，且径厚比越小，比较结果越低，甚至会低于1。由于土压力并不是均匀分布，其均值较峰值会有所降低，相较于均值土压力，两种荷载显著偏大，增幅在20%以内。埋深增加后，棱柱荷载和Marston荷载的准确性均显著降低，如埋深6 m时，较峰值土压力最大增幅分别为58%和31%，与均值土压力的相差则更大。

图 4 棱柱荷载

${\sigma _{\text{p}}}$ 、Marston荷载

${\sigma _{\text{M}}}$ 与有限元结果的比较

Figure 4. Comparison of prism load

${\sigma _{\text{p}}}$ and Marston load

${\sigma _{\text{M}}}$ with finite element results

下载: 全尺寸图片幻灯片

可见，棱柱荷载和Marston荷载存在两处问题，首先其假定的土压力均匀分布虽计算简便，但与实际差别较大；其次是当管道埋深高、径厚比大时，其大小偏差较大。此外，相较于棱柱荷载，Marston荷载在高埋深时，误差相对较小，但低埋深时，其结果偏小。

3. 敏感性分析

3.1 管径的影响

以管径D=1.5 m和0.5 m的钢管为研究对象，分别按照径厚比D/t=100~300和50~250（小直径管道的径厚比通常较小），埋深H=2 m和4 m进行参数分析，对比分析管顶土压力的分布情况及大小。

（1）土压力分析

各管径、径厚比及埋深下的土压力计算结果如图 5所示。可以看出，管径为1.5 m时，随着径厚比的增加，土压力分布逐步由抛物线向“倒盆形”过渡。当埋深较深、径厚比大即管道变形大时，管侧胸腔出现峰值，这与管径3 m的变化规律较为类似，不同之处在于，管径越小，土压力越倾向抛物线分布。与大直径管道不同，管径为0.5 m时，土压力均呈抛物线分布，这与以往小直径管道的研究结论基本相同。径厚比增加后，土压力峰值有所降低，特别是当径厚比从50变为100时，降幅最为显著，这是由于当径厚比为50时，钢管为刚性管道，承受了更多的覆土重，与柔性管道存在明显不同。

图 5 不同管径D、径厚比D/t及埋深H下的土压力

Figure 5. Soil pressures under different pipe diameters D, diameter-thickness ratios D/t and cover depths H

下载: 全尺寸图片幻灯片

基于上述分析可知，大/小直径管道土压力分布基本形式分别为“倒盆形”和抛物线。这是由于管径大后，土拱效应减弱，胸腔管壁分担的土压力增加，且胸腔土体体积会明显变大，加深了其影响程度。

（2）大小比较

图 6为不同管径下棱柱荷载、Marston荷载与有限元结果的比较。管径1.5 m与3 m的管道，土压力大小比较规律总体较为类似，但1.5 m管径下的偏差显著扩大，如埋深2 m时，棱柱荷载和Marston荷载分别最大为峰值/均值土压力的1.4/1.59和1.24/1.4倍。管径0.5 m的小直径管道，由于其土压力分布变化幅度较大，使得峰值与均值土压力存在较大差异。棱柱荷载除在埋深浅、径厚比特别小时，可能稍低于峰值土压力，其余情况下均远大于峰值/均值土压力，且埋深越深，径厚比越大，越显著。而Marston荷载在径厚比小时，远低于峰值土压力，但与均值土压力较为接近。

图 6 棱柱荷载

${\sigma _{\text{p}}}$ 、Marston荷载

${\sigma _{\text{M}}}$ 与有限元结果的比较

Figure 6. Comparison of prism load

${\sigma _{\text{p}}}$ and Marston load

${\sigma _{\text{M}}}$ with finite element results

下载: 全尺寸图片幻灯片

国内外研究多以小直径管道为研究对象，其径厚比及埋深通常较小，此时Marston荷载结果远小于土压力峰值，而棱柱荷载的安全性较高且计算简便，故多推荐采用棱柱荷载进行埋地钢管的结构设计。但对大直径管道而言，高埋深下Marston荷载大小与实际较为接近且总体偏大，而棱柱荷载明显过大，故对大直径、高埋深的管道，土压力计算可考虑采用Marston荷载。

3.2 相关参数的敏感性分析

以管径3 m的埋地钢管为例，埋深取2 m、径厚比取200，对回填土变形模量、泊松比、沟槽侧壁土–土摩擦系数及沟槽宽度进行敏感性分析。基于规范及工程经验，计算时回填土变形模量取3~9 MPa；回填土泊松比取0.25~0.42；土–土摩擦系数取0.2~0.8^{[18, 20]}。基于ASCE No.119的建议，上述分析采用的沟槽宽度B均为2倍管径，但工程中沟槽宽度的确定多基于施工条件，如按GB50268确定的最小沟槽宽度B/D约为1.5，分析时适当扩大B/D范围取1.5~3。

各参数下的土压力分布如图 7所示。可以看出，回填土模量的增加使得土压力减小，这是由于土体模量越大，填土越紧密，从而更易形成整体，起到一定的拱效应。泊松比、土–土摩擦系数与变形模量的土压力变化规律较为类似，在此不再赘述。对比第2节模型结果，回填土变形模量、泊松比和土–土摩擦系数的改变，分别使峰值土压力在原模型的基础上变化-7.6%~5.5%、-5.2%~6.1%、-6.1%~10%，均在10%以内。沟槽越宽，沟槽侧壁的影响越小，管道所受的土压力逐渐增大，但峰值土压力波动范围仅为-12.1%~14.2%。此外，对于埋深4 m的情况同样进行了参数敏感性分析，结果与上述分析类似。因此，工程实践中，为改善管道受力条件，应尽可能的提高回填土的材料性能、增加回填土与原状土的接触面粗糙程度及采用较窄的沟槽，以减轻土压力。

图 7 相关参数的敏感性分析

Figure 7. Sensitivity analysis of related parameters

下载: 全尺寸图片幻灯片

4. 盆式土压力模型

以往的土压力分布多假定为均匀或抛物线形式，而大直径管道的基本形式为“倒盆形”，与传统假定存在较大区别。为此，本文提出一种新型的土压力计算模型-盆式模型，来模拟大直径管道的土压力分布，计算图式如图 8所示。

图 8 盆式模型计算图式

Figure 8. Calculation diagram of basin model

下载: 全尺寸图片幻灯片

4.1 “直线+抛物线”土压力分布形式

上述分析中土压力分布的界限大体在距离管中心（0.25~0.4）D处，后经多次试算并考虑计算方便性，在盆式模型中假定以距离管中心D/3为界限，在[0，D/3]范围内为均匀分布即土压力 $\sigma$ 为一定值，[D/3，D/2]为抛物线分布，即采用“直线+抛物线”的盆形来描述大直径管道顶部的土压力分布形式。由于盆式土压力分布关于轴线对称，以图 8的右半侧为例进行土压力分布公式推导，过程如下。

当 $0 \leqslant x \leqslant D/3$ 时，

$y{\text{(}}x{\text{)}} = \sigma \text{, }$

(3)

当 $D/3 \leqslant x \leqslant D/2$ 时，在x₁-y₁坐标系内，假定抛物线方程为

${x_1}^2 = - 2p{y_1} \text{, }$

(4)

代入边界条件： ${x}_{1}=D/6，{y}_{1}=-\sigma$ ，得 $p = {{{D^2}} / {{\text{72}}\sigma }}$ ，故在x₁-y₁坐标系内，抛物线方程为

${x_1}^2 = - \frac{{{D^2}}}{{{\text{36}}\sigma }}{y_1} \text{, }$

(5)

经坐标变换，

${\left( {x - \frac{D}{{\text{3}}}} \right)^2} = - \frac{{{D^2}}}{{{\text{36}}\sigma }}{\kern 1pt} (y - \sigma ) \text{, }$

(6)

在x-y坐标系内，抛物线方程变为

$y(x) = - \frac{{{\text{36}}\sigma }}{{{D^2}}}{\left( {x - \frac{D}{{\text{3}}}} \right)^2}{\text{ + }}\sigma = - \frac{{{\text{36}}\sigma }}{{{D^2}}}{x^2}{\text{ + }}\frac{{{\text{24}}\sigma }}{D}x - {\text{3}}\sigma \text{, }$

(7)

故“直线+抛物线”土压力分布形式的公式表达为

$y(x) = \left\{ \begin{gathered} \sigma \hfill \\ - \frac{{{\text{36}}\sigma }}{{{D^2}}}{x^2}{\text{ + }}\frac{{{\text{24}}\sigma }}{D}x - {\text{3}}\sigma \hfill \\ \end{gathered} \right.\begin{array}{*{20}{c}} {}&{\begin{array}{*{20}{c}} {(0 \leqslant x \leqslant D/3)} \\ {(D/3 \leqslant x \leqslant D/2)} \end{array}} \end{array} 。$

(8)

4.2 “Marston+胸腔”荷载计算方法

相较于棱柱荷载，Marston荷载大小总体上较为接近实际土压力，高埋深时优势明显，但低埋深时结果偏小，这是由于以往埋地管道的管径较小，胸腔土体的影响很小，故传统的计算方法并未考虑其影响，但对大直径管道而言，浅埋时胸腔土体的影响很大。假定胸腔土体完全作用于管道，其产生的土压力沿管径均匀分布，计算公式为

$\sigma = {{\gamma \left( {\frac{{{D^2}}}{2} - \frac{1}{2}{\rm{ \mathsf{ π} }}\frac{{{D^2}}}{4}} \right)} \mathord{\left/ {\vphantom {{\gamma \left( {\frac{{{D^2}}}{2} - \frac{1}{2}{\rm{ \mathsf{ π} }}\frac{{{D^2}}}{4}} \right)} D}} \right. } D} = 0.107\gamma D 。$

(9)

为探究胸腔土体的影响程度，将胸腔土体产生的土压力与棱柱荷载进行比较，定义胸腔土压力影响因子 $\lambda$ 为

$\lambda = 0.107\gamma D/(\gamma H) \times 100{{\% }} = 0.107D/H \times 100{{\% }} 。$

(10)

可见，D/H越大，胸腔土体的影响越显著，如管径3 m、埋深2 m时，胸腔土体可在原有棱柱荷载的基础上增加16.1%的土压力；但当D/H < 1即管径小于埋深时，其影响低于10.7%。

工程实践中，小直径管道的管径通常远小于埋深，基本可以忽略胸腔土体的影响，但大直径管道的管径大于埋深的情况较为常见，胸腔土体应予以考虑。因此，针对大直径埋地钢管的特点，以Marston荷载为基础，考虑胸腔土体的影响，提出了“Marston+胸腔”荷载计算方法见图 9，计算公式为

$\sigma = \left\{ \begin{array}{l} {C_{\text{d}}}\gamma B{\text{ + }}0.107\gamma D\begin{array}{*{20}{l}} {}&{} \end{array} \hfill \\ {C_{\text{d}}}\gamma B \hfill \end{array} \right.\begin{array}{*{20}{l}} {{\text{(}}D > H{\text{)}}} \\ {(D \leqslant H{\text{)}}} \end{array} 。$

(11)

图 9 “Marston+胸腔”荷载计算示意

Figure 9. Calculation diagram of "Marston + pleura" load

下载: 全尺寸图片幻灯片

4.3 盆式模型适用性研究

为了研究本文提出的盆式模型的适用性，从管径、埋深及径厚比等方面，将盆式土压力模型的结果与有限元分析计算结果的土压力分布进行对比，比较结果如图 10所示。可以看出，当径厚比为100时，管道承受的土压力最大，受力最为不利，此时模型的吻合程度最高。直线段分布形式能够反应管中心区域土压力平缓变化特性，抛物线段分布形式可体现管腰附近土压力急剧变化情况。总体来看，该模型土压力分布范围基本上能够覆盖管道浅埋、深埋及各种径厚比情况，与有限元结果有较好的贴合度。径厚比越低，贴合程度越好，且对径厚比高、安全风险大的管道，存有较高的安全裕度。

图 10 各管径D、径厚比D/t及埋深H下的土压力

Figure 10. Soil pressures under different pipe diameters D, diameter-thickness ratios D/t, and cover depths H

下载: 全尺寸图片幻灯片

表 2为各土压力模型与有限元结果（径厚比为100）的比较。从峰值比较来看，盆式模型为有限元结果的0.93~1.11倍，相应的棱柱荷载及Marston荷载分别为有限元结果的0.66~1.57倍和0.64~1.04倍。3种模型比较而言，传统的棱柱和Marston荷载模型在管道埋深很浅时，土压力计算结果明显偏小，而盆式模型精确度有了显著的提升，尤其是在管径特别大的情况下。从均值比较来看，盆式模型为有限元结果的0.97~1.18倍，相应的棱柱荷载及Marston荷载分别为0.78~1.94倍和0.76~1.31倍，可见传统模型的土压力均匀分布形式有利有弊，虽能缩小浅埋时计算结果过小的误差，但同时也显著放大了高埋深下计算结果过大的缺陷，相较而言，盆式模型的分布形式更为优越。故无论是峰值比较还是均值比较，盆式模型的总体精确度均远高于传统模型，且适用范围更广。

表 2 各土压力模型与有限元结果（径厚比为100）的比较

Table 2. Comparison of soil pressure models and finite element results (diameter-thickness ratio of 100)

比较类型	埋深/m	峰值土压力比较				均值土压力比较
比较类型	埋深/m	管径1.2 m	管径2 m	管径3 m	管径4 m	管径1.2 m	管径2 m	管径3 m	管径4 m
盆式模型/有限元结果	1	1.01	1.00	0.99	0.93	1.18	1.07	1.00	0.97
	3	0.99	1.11	1.01	1.08	1.16	1.11	1.02	1.09
	7	0.94	1.01	1.03	1.04	1.03	1.09	1.11	1.10
棱柱荷载/有限元结果	1	0.96	0.86	0.77	0.66	1.26	1.03	0.87	0.78
	3	1.25	1.18	1.11	1.00	1.65	1.43	1.26	1.15
	7	1.57	1.39	1.28	1.23	1.94	1.69	1.55	1.46
Marston荷载/有限元结果	1	0.88	0.82	0.75	0.64	1.17	0.98	0.85	0.76
	3	0.99	1.02	1.01	0.93	1.31	1.24	1.15	1.07
	7	0.94	1.01	1.03	1.04	1.17	1.23	1.25	1.24

下载: 导出CSV

| 显示表格

总体而言，对于管径不小于1.2 m，径厚比在100~300范围内常见的大直径埋地钢管，该模型土压力分布形式较传统模型有了明显的提升，其计算方法较传统模型精确程度更高，适应性更强。其中对于径厚比为100的管道，误差控制在20%以内且总体偏大，对于径厚比更高的管道，该模型更为安全。此外，该模型对于小于1.2 m或径厚比低于100的埋地钢管以及其他埋地柔性管道是否适用，仍值得后续深入探讨。

5. 结论

（1）大/小直径管道的土压力分布基本形式分别为“倒盆形”和抛物线形，两者存在明显不同。径厚比及埋深对土压力影响显著，随着径厚比或埋深的增加，管道竖向收缩变形加剧，加大了胸腔管壁分担的荷载，土压力峰值逐步由管中心位置移向管侧胸腔，但径厚比大于200后，土压力变化很小。此外，土压力大小随着回填土变形模量及泊松比、沟槽侧壁土-土摩擦系数的增加而降低，影响程度均在10%以内；沟槽宽度的影响也较为有限，沟槽越宽，土压力越大。

（2）棱柱荷载和Marston荷载假定的均匀分布虽计算简便，但与大直径管道实际明显不符。棱柱荷载在高埋深时结果过大，而Marston荷载在低埋深时结果偏小，两种荷载的计算精度及适应性较差。大直径管道浅埋时，胸腔土体的影响需予以考虑。

（3）对于管径不小于1.2 m且径厚比不小于100的大直径埋地钢管提出了一种新型的管顶土压力计算模型-盆式模型，其荷载分布采用“直线+抛物线”形式，荷载大小按照“Marston+胸腔”荷载计算。该模型能够消减传统模型的缺陷，其土压力分布及大小基本能够覆盖管道浅埋、深埋及多种径厚比情况，计算精度及适应性较好，可为大直径埋地钢管的结构设计及规范制定提供借鉴和参考。

图 1 不同围压条件下轻量土的骨干曲线

Figure 1. Backbone curves of light weight soil under different confining pressures

下载: 全尺寸图片幻灯片

图 2 不同围压条件下动剪切模量倒数1/G_d与动剪应变γ_d的关系曲线

Figure 2. Relationship curves between reciprocal of dynamic shear modulus and dynamic shear strain under different confining pressures

下载: 全尺寸图片幻灯片

图 3 模型参数与EPS颗粒体积掺入比b_e的关系曲线

Figure 3. Relationship curves between model parameters and particles content of EPS

下载: 全尺寸图片幻灯片

图 4 模型参数与水泥掺量a_c的关系曲线

Figure 4. Relationship curves between model parameters and cement content

下载: 全尺寸图片幻灯片

图 5 不同应力状态下模型计算值与试验值的对比

Figure 5. Comparison between calculated and test values under different stress states

下载: 全尺寸图片幻灯片

图 6 不同应力路径下模型计算值与试验值的对比

Figure 6. Comparison between calculated and test values under different stress paths

下载: 全尺寸图片幻灯片

表 1 土的物理性质指标

Table 1 Physical properties of soil

天然含水率w/%	相对质量密度G_s	天然密度ρ/(g·cm^-3)	塑限w_P/%	液限w_L/%	塑性指数I_P	液性指数I_L	孔隙比e	有机质/%
19.75	2.72	1.702	21.27	33.62	12.35	-0.123	0.91	<5

下载: 导出CSV

表 2 轻量土动三轴试验方案

Table 2 Dynamic triaxial test schemes of light weight soil

影响因素	方案一	方案二	方案三
EPS颗粒体积掺入比b_e/%	20,30,40,50,60	40	0
水泥掺入比a_c/%	10	10,15,20	0
含水率w/%	50	50	21.3
龄期T/d	28	28	0
固结压力σ_c /kPa	50,100,150,200	50,100,150,200	50,100,150,200
固结应力比/K_c	1.0	1.0	1.0
振动频率f/Hz	1	1	1
动剪应力比/s	0.075	0.075	0.075

下载: 导出CSV

表 3 轻量土的相对结构度k的计算结果

Table 3 Calculated results of structural parameter k of light weight soil

配比	素土	b_e=20%a_c=10%	b_e=30%a_c=10%	b_e=40%a_c=10%	b_e=50%a_c=10%	b_e=60%a_c=10%	b_e=40%a_c=15%	b_e=40%a_c=20%
相对结构度k	1	8.952	8.488	7.401	5.303	4.027	8.248	8.709

下载: 导出CSV

表 4 轻量土广义孔隙比 $e^{'}$ 的计算结果

Table 4 Calculated results of generalized void ratio $e^{'}$ of light weight soil

水泥掺量a_c/%	EPS颗粒体积掺入比b_e/%
水泥掺量a_c/%	0	20	30	40	50	60
0	0.619	—	—	—	—	—
10	—	1.307	1.612	2.018	2.590	3.439
15	—	1.251	1.547	1.938	2.489	3.310
20	—	1.199	1.485	1.865	2.396	3.194

下载: 导出CSV

表 5 最大动剪切模量公式的回归参数值

Table 5 Values of regression parameters of formula for maximum dynamic shear modulus

A	n₁	η₁
0.103	-0.305	14.135

下载: 导出CSV

表 6 参数b经验公式回归参数值

Table 6 Values of regression parameters of empirical formula for parameter b

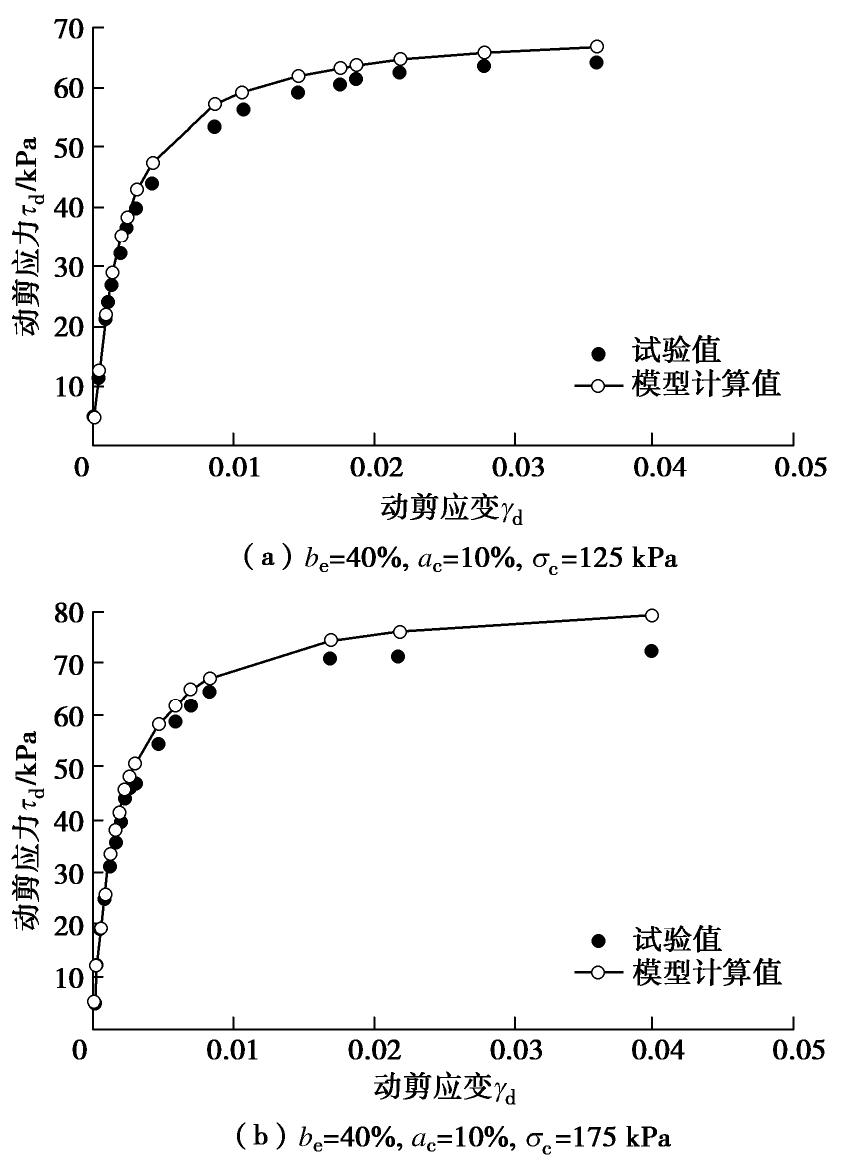
η₂	n₂	B	n₃	C	n₄
0.0834	1.18	0.037	-12.3	0.437	-0.8

下载: 导出CSV

表 7 改变应力状态的轻量土动三轴验证试验方案

Table 7 Dynamic triaxial validation test schemes of light weight soil by changing stress state

EPS颗粒体积掺入比b_e/%	水泥掺入比a_c/%	含水率w/%	龄期T/d	固结压力σ_c/kPa	固结应力比K_c	振动频率f/Hz	每级循环周数
40	10	50	28	125,175	1	1	10

下载: 导出CSV

表 8 改变应力路径的轻量土动三轴验证试验方案

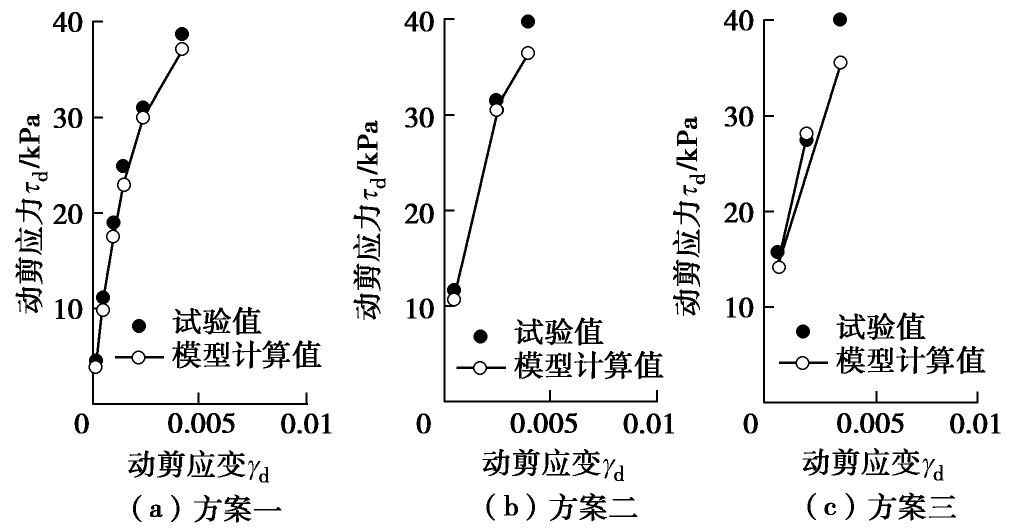
Table 8 Dynamic triaxial validation test schemes of light weight soil by changing stress path

方案一	方案二	方案三
正弦波	正弦波	正弦波
加载	加载	加载
共6级	共3级	共3级
1/10 τ_max	2/10 τ_max	4/10 τ_max
2/10 τ_max	4/10 τ_max	2/10 τ_max
……	6/10 τ_max	6/10 τ_max
6/10 τ_max

下载: 导出CSV

参考文献(26)

[1]	侯天顺, 徐光黎. 发泡颗粒混合轻量土三轴应力-应变-孔压特性试验[J]. 中国公路学报, 2009, 22(6): 10-17. doi: 10.3321/j.issn:1001-7372.2009.06.002 HOU Tian-shun, XU Guang-li. Experiment on triaxial pore water pressure-stress-strain characteristics of foamed particle light weight soil[J]. China Journal of Highway and Transport, 2009, 22(6): 10-17. (in Chinese) doi: 10.3321/j.issn:1001-7372.2009.06.002
[2]	侯天顺, 徐光黎. 发泡颗粒混合轻量土抗剪强度特性试验研究[J]. 中国矿业大学学报, 2010, 39(4): 534-540. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD201004011.htm HOU Tian-shun, XU Guang-li. Experimental study on the shear strength characteristics of foamed particle light weight soil[J]. Journal of China University of Mining & Technology, 2010, 39(4): 534-540. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD201004011.htm
[3]	HOU T S. Influence of expanded polystyrene size on deformation characteristics of light weight soil[J]. Journal of Central South University, 2012, 19(11): 3320-3328. doi: 10.1007/s11771-012-1410-x
[4]	HOU T S. Model for compaction density and engineering properties of light weight soil[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(11): 2127-2135. doi: 10.11779/CJGE201411020
[5]	谢定义. 土动力学[M]. 西安: 西安交通大学出版社, 2011. XIE Ding-yi. Soil Dynamics[M]. Xi'an: Xi'an Jiaotong University Press, 2011. (in Chinese)
[6]	HARDIN B O, BLACK W L. Vibration modulus of normally consolidated clay[J]. Journal of the Soil Mechanics and Foundations Division, 1968, 94(2): 353-369. doi: 10.1061/JSFEAQ.0001100
[7]	SEED H B, IDRISS I M. Soil Modulus and Damping Factors for Dynamic Response Analysis[R]. California: Earthquake Engineering Research Center, University of California, EERC70-10, 1970.
[8]	HARDIN B O, DRNEVICH V P. Shear modulus and damping in soils: design equations and curves[J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1972, 98(7): 667-692. doi: 10.1061/JSFEAQ.0001760
[9]	HARDIN B O, DRNEVICH V P. Shear modulus and damping in soils: measurement and parameter effects[J]. ASCE, J Soil Mech Found Div, 1972, 98(SM6): 603-624.
[10]	胡文尧, 王天龙. 关于黏性土剪切模量和阻尼比与剪应变关系模型中的参数[J]. 同济大学学报(自然科学版), 1982(2): 53-61. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ198202005.htm HU Wen-yao, WANG Tian-long. Parameters of dynamic stress-strain models for cohesive soil[J]. Journal of Tongji University (Natural Science), 1982(2): 53-61. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ198202005.htm
[11]	郑大同, 王惠昌. 循环荷载作用下土的非线性应力应变模型[J]. 岩土工程学报, 1983, 5(1): 65-76. doi: 10.3321/j.issn:1000-4548.1983.01.006 ZHENG Da-tong, WANG Hui-chang. Nonlinear stress-strain model of soil under cyclic loading[J]. Chinese Journal of Geotechnical Engineering, 1983, 5(1): 65-76. (in Chinese) doi: 10.3321/j.issn:1000-4548.1983.01.006
[12]	陈国兴, 谢君斐, 张克绪. 土的动模量和阻尼比的经验估计[J]. 地震工程与工程振动, 1995, 15(1): 73-84. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC199501008.htm CHEN Guo-xing, XIE Jun-fei, ZHANG Ke-xu. Empirical estimation of dynamic modulus and damping ratio of soil[J]. Earthquake Engineering and Engineering Vibration, 1995, 15(1): 73-84. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC199501008.htm
[13]	刘雪珠, 陈国兴, 胡庆兴. 南京地区新近沉积土的动剪切模量和阻尼比的初步研究[J]. 地震工程与工程振动, 2002, 22(5): 127-132. doi: 10.3969/j.issn.1000-1301.2002.05.023 LIU Xue-zhu, CHEN Guo-xing, HU Qing-xing. Primary study on dynamic shear modulus and damping ratio of recently deposited soil in area of Nanjing[J]. Earthquake Engineering and Engineering Vibration, 2002, 22(5): 127-132. (in Chinese) doi: 10.3969/j.issn.1000-1301.2002.05.023
[14]	陈国兴, 刘雪珠. 南京及邻近地区新近沉积土的动剪切模量和阻尼比的试验研究[J]. 岩石力学与工程学报, 2004, 23(8): 1403-1410. doi: 10.3321/j.issn:1000-6915.2004.08.033 CHEN Guo-xing, LIU Xue-zhu. Testing study on ratio of dynamic shear moduli and ratio of damping for recently deposited soils in Nanjing and its neighboring areas[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1403-1410. (in Chinese) doi: 10.3321/j.issn:1000-6915.2004.08.033
[15]	YUAN X M, SUN J, SUN R. Effect of consolidation ratios on maximum dynamic shear modulus of sands[J]. Earthquake Engineering and Engineering Vibration, 2005, 4(1): 59-68. doi: 10.1007/s11803-005-0024-9
[16]	袁晓铭, 孙静. 非等向固结下砂土最大动剪切模量增长模式及Hardin公式修正[J]. 岩土工程学报, 2005, 27(3): 264-269. doi: 10.3321/j.issn:1000-4548.2005.03.004 YUAN Xiao-ming, SUN Jing. Model of maximum dynamic shear modulus of sand under anisotropic consolidation and revision of Hardin’s formula[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(3): 264-269. (in Chinese) doi: 10.3321/j.issn:1000-4548.2005.03.004
[17]	雷华阳, 姜岩, 陆培毅, 等. 交通荷载作用下结构性软土动本构关系的试验研究[J]. 岩土力学, 2009, 30(12): 3788-3792. doi: 10.3969/j.issn.1000-7598.2009.12.039 LEI Hua-yang, JIANG Yan, LU Pei-yi, et al. Experimental study of dynamic constitutive relation of structural soft soils under traffic loading[J]. Rock and Soil Mechanics, 2009, 30(12): 3788-3792. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.12.039
[18]	孙锐, 于啸波, 袁晓铭, 等. 季冻区典型土类动剪切模量阻尼比计算方法[J]. 岩土工程学报, 2017, 39(1): 116-128. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201701012.htm SUN Rui, YU Xiao-bo, YUAN Xiao-ming, et al. Method for dynamic shear moduli and damping ratio of typical soils in seasonal frozen region[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(1): 116-128. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201701012.htm
[19]	姬凤玲, 吕擎峰, 李明东. 疏浚淤泥EPS颗粒轻质混合土本构模型研究[J]. 深圳大学学报, 2006, 23(3): 195-200. https://www.cnki.com.cn/Article/CJFDTOTAL-SZDL200603001.htm JI Feng-ling, LÜ Qing-feng, LI Ming-dong. Study on the constitutive model of lightweight EPS-bead-treated soil made from silt[J]. Journal of Shenzhen University (Science and Engineering), 2006, 23(3): 195-200. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SZDL200603001.htm
[20]	黎冰. 动荷载下黏土与EPS颗粒混合轻质土的变形和强度特性试验研究[D]. 南京: 河海大学, 2007. LI Bing. Experimental Study on the Deformation and Strength Properties of Light Weight Clay-EPS Beads Soil Under Cyclic Loading[D]. Nanjing: Hohai University, 2007. (in Chinese)
[21]	GAO Y F, WANG S M, CHEN C B. A united deformation- strength framework for light weight sand-EPS beads soil (LSES) under cyclic loading[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(8): 1144-1153. doi: 10.1016/j.soildyn.2011.04.002
[22]	GAO H M, BU C Y, WANG Z H, et al. Dynamic characteristics of expanded polystyrene composite soil under traffic loadings considering initial consolidation state[J]. Soil Dynamics and Earthquake Engineering, 2017, 102: 86-98.
[23]	HU Y, GAO H M, WANG Z H, et al. Dynamic modulus and damping ratio of EPS composite soil under small strain condition[C]//Proceedings of the 6th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, 2017, Rhodes Island.
[24]	HOU T S, PEI Z W, LUO Y S, et al. Study on the dynamic constitutive relationship of EPS particles light weight soil based on hardin-drnevich model[J]. Geotechnical and Geological Engineering, 2020, 38(2): 1785-1798.
[25]	土工试验方法标准：GB/T50123—2019[S]. 2019. Standard for Geotechnical Testing Method: GB/T50123—2019[S]. 2019. (in Chinese)
[26]	KONDNER R L. Hyperbolic stress-strain responses: Cohesive soils[J]. Journal of soil Mechanics and Foundation Division, ASCE, 1964, 89(1): 126-127.

施引文献(5)

期刊类型引用(4)

1.	唐小平，邓良平，汪建海，梁榆峰，江杰，叶耿昌. 排水管道土压力数值分析及非开挖修复内衬管壁厚优化. 给水排水. 2024(02): 139-145 . 百度学术
2.	张常光，吴凯，孟祥忠，王晓轮. 稳态渗流下非饱和土涵洞竖向土压力的迭代解与简化. 哈尔滨工业大学学报. 2024(03): 68-77 . 百度学术
3.	于金弘，伍鹤皋，石长征，孙海清，汪碧飞，李娇娜. 考虑管道自重荷载的埋地钢管结构计算方法. 长江科学院院报. 2024(05): 155-161 . 百度学术
4.	朱珍锋，韩高孝. 沟埋式管道垂直土压力模拟试验研究. 水利与建筑工程学报. 2024(03): 99-106 . 百度学术