膨胀土–EPS缓冲层–挡墙体系侧压力的模拟和计算

丁鲁强; 韩仲; 邹维列; 万梁龙; 匡文壮

doi:10.11779/CJGE202108022

膨胀土–EPS缓冲层–挡墙体系侧压力的模拟和计算 English Version

1.
武汉大学土木建筑工程学院,湖北　武汉　430072
2.
深圳市住宅工程管理站,广东　深圳　518000
3.
武汉理工大学土木工程与建筑学院,湖北　武汉　430070

基金项目:

国家重点研发计划项目 2019YFC1509800

国家自然科学基金项目 51979206

国家自然科学基金项目 51809199

详细信息

作者简介:
丁鲁强(1991— ),男,博士,主要从事非饱和土特性和道路岩土工程等方面的科研工作。E-mail：luqiang.ding@whu.edu.cn

通讯作者:
韩仲, E-mail：zhong.han@whu.edu.cn

中图分类号: TU432
计量
- 文章访问数: 244
- HTML全文浏览量: 23
- PDF下载量: 151
出版历程
- 收稿日期: 2020-09-04
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-07-31

Modelling and calculating lateral pressure of expansive soil-EPS inclusion-retaining wall system

1.
School of Civil Engineering, Wuhan University, Wuhan 430072, China
2.
Residence Engineering Management Station of Shenzhen Municipality, Shenzhen 518000, China
3.
School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan 430072, China

摘要

摘要: 采用ABAQUS有限元热力耦合模块,以热膨胀类比膨胀土增湿膨胀,对膨胀土–EPS缓冲层–挡墙体系进行了数值模拟,研究了EPS缓冲层与墙体和膨胀土间的界面摩擦、墙后膨胀土的宽度、EPS块体间隙等因素对EPS缓冲层减压性能的影响。结果表明：①膨胀土–EPS缓冲层之间、挡墙–EPS缓冲层之间的界面摩擦力使作用在挡墙上的侧压力产生重分布,进而显著影响挡墙的倾覆力矩,但对水平推力影响很小；②墙后膨胀土宽度越宽,作用在膨胀土–EPS缓冲层–挡墙上的侧压力越大。当膨胀土宽度超过挡墙高度的2倍时,墙后侧压力不再明显增加；③组成EPS缓冲层的EPS块体间的间隙不影响挡墙上的侧压力分布。结合数值模拟结果,对膨胀土–EPS缓冲层–挡墙体系的工作机理进行了分析,提出了挡墙侧压力的计算模型。以重力式挡墙为例,说明了该计算模型在膨胀土–EPS缓冲层–挡墙体系设计中的应用,为EPS用于膨胀土挡墙缓冲减压的工程设计提供参考。
- 膨胀土 /
- EPS /
- 挡墙 /
- 侧压力 /
- 数值模拟
Abstract: The thermal fields and thermal expansion are used to simulate the moisture fields and swelling of expansive soils upon wetting in this study. The thermal-mechanical coupled finite element analysis is employed to simulate the "expansive soil-EPS inclusion-retaining wall" system using ABAQUS. The following influences are analyzed: (1) the interface friction among the EPS, the wall and the expansive soil; (2) the width of the expansive soil, and (3) the gap between the EPS blocks. The numerical results indicate that the lateral pressure on the retaining wall increases as the width of the expansive soil increases until the width exceeds two times the height of the retaining wall. The interface friction induces redistribution of the lateral pressure on the wall and affects of the overturning moment on the wall. The gaps between the EPS blocks do not affect the lateral pressure on the wall. The interaction mechanisms between expansive soil, EPS inclusion and retaining wall are explored based on the numerical results, and a model for calculating the lateral pressure on the "expansive soil-EPS inclusion-retaining wall" is proposed. The design method for the "expansive soil-EPS inclusion-retaining wall" is illustrated by taking the gravity retaining wall as an example.
- expansive soil /
- EPS /
- retaining wall /
- lateral pressure /
- numerical analysis

HTML全文

0. 引言

重力式抗滑挡墙是防治膨胀土边坡浅层滑动的主要措施之一。膨胀土吸水膨胀后,作用在挡墙上的侧压力显著增大,其增幅甚至超过静止土压力^[1],造成挡墙出现失稳、断裂等破坏现象^[2]。试验研究表明,在挡墙后设置一定厚度的粒料层,不仅可以起到滤水的作用,还可以减小作用在挡墙上的侧压力。但即使设置粒料层,竣工后挡墙仍可能滑动甚至被推倒^[3]。

聚苯乙烯泡沫（expanded polystyrene,即EPS）是聚苯乙烯颗粒经预发泡、塑模制造等步骤得到的材料,具有密度小、压缩性大等特点。EPS被广泛应用于道路、建筑、水利、市政等领域的工程建设中。在膨胀土与挡墙之间设置一定厚度的EPS作为缓冲层,形成“膨胀土–EPS缓冲层–挡墙”体系,能有效减小作用在挡墙上的侧压力^[4-6]。然而,目前对EPS缓冲层与膨胀土、挡墙之间相互作用机理的认识还不深入,限制了EPS在膨胀土挡墙等支挡结构中的应用。因此,有必要对膨胀土–EPS缓冲层–挡墙体系开展进一步研究,探明墙后侧压力分布的特点和计算方法,为EPS在膨胀土地区的边坡挡墙、建筑物地下室侧墙、隧（涵）洞边墙等支挡结构中的应用提供设计依据。

本文首先通过数值模拟手段,探明EPS缓冲层与膨胀土、挡墙之间的相互作用机理以及影响EPS缓冲层减压性能的因素。在此基础上,对膨胀土–EPS缓冲层–挡墙体系进行受力分析,提出挡墙上侧压力的计算方法,为相关工程设计提供参考。

1. 数值模拟

1.1 理论基础

在热力学中,材料吸热膨胀产生的应变ε_T与温度增量∆T之间的关系可表示为

$ε_{T} = α_{T} Δ T$ ,

(1)

式中, $α_{T}$ 为材料热膨胀系数。

大量试验结果表明^[7-9],膨胀土的含水率增量∆w与膨胀应变ε_w之间的关系也可由线性函数表示：

$ε_{w} = α_{w} Δ w$ ,

(2)

式中,α_w为膨胀土的增湿膨胀系数。

可见,膨胀土的增湿膨胀与材料的热膨胀在数学关系上是一致的。因此,可以将∆T等同于∆w,将 $α_{T}$ 等同于 $α_{w}$ ,进而通过模拟土体的热膨胀过程等效模拟土体的吸湿膨胀过程。

热传导微分方程与非饱和土的渗流微分方程类似^[10]。不考虑材料自身发热时,热传导微分方程为

$\frac{\partial}{\partial x} (λ_{x} \frac{\partial T}{\partial x}) + \frac{\partial}{\partial y} (λ_{y} \frac{\partial T}{\partial y}) + \frac{\partial}{\partial z} (λ_{z} \frac{\partial T}{\partial z}) = C_{T} \frac{\partial T}{\partial t}$ 。

(3)

式中 $λ_{x}$ , $λ_{y}$ , $λ_{z}$ 分别为x,y,z方向的导热系数；T为温度；t为时间；C_T为体积比热容。

不考虑重力水头时,非饱和渗流微分方程为

$\frac{\partial}{\partial x} (k_{x} \frac{\partial h_{s}}{\partial x}) + \frac{\partial}{\partial y} (k_{y} \frac{\partial h_{s}}{\partial y}) + \frac{\partial}{\partial z} (k_{z} \frac{\partial h_{s}}{\partial z}) = C_{w} \frac{\partial h_{s}}{\partial t}$ ,

(4)

式中,k_x,k_y,k_z分别为x,y,z方向的渗透系数,C_w为比水容量,h_s为基质吸力水头。

膨胀土在吸湿膨胀过程中,含水率w与基质吸力之间存在一一对应关系（即土–水特征曲线）,故式（4）也可表示为

$\frac{\partial}{\partial x} (k_{x} \frac{\partial w}{\partial x}) + \frac{\partial}{\partial y} (k_{y} \frac{\partial w}{\partial y}) + \frac{\partial}{\partial z} (k_{z} \frac{\partial w}{\partial z}) = C_{w} \frac{\partial w}{\partial t}$ 。

(5)

比较式（3）,（5）可知,T与w对应, $λ$ 与k对应,C_T与C_w对应。因此,材料热传导本构关系可用来模拟非饱和渗流本构关系。

1.2 膨胀土–EPS缓冲层–挡墙体系基本模型及其参数

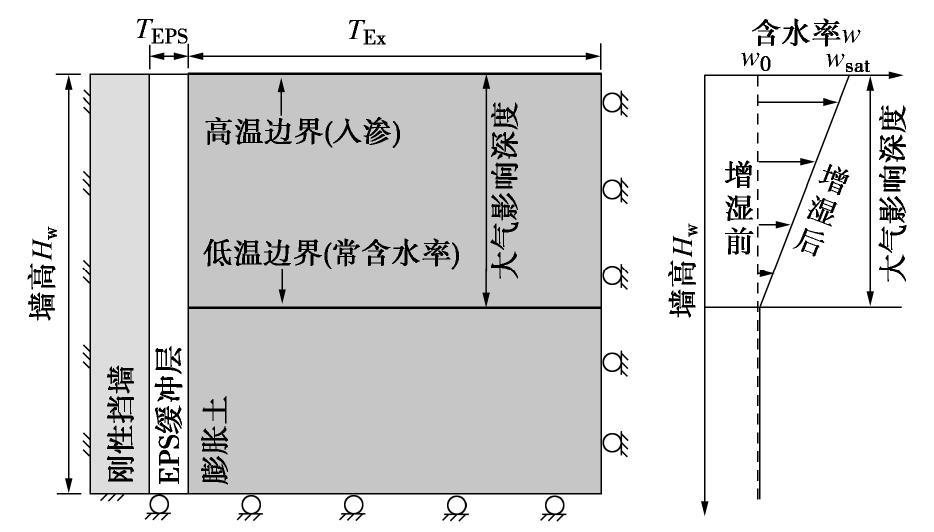
本文采用ABAQUS有限元软件中的热–力耦合分析模块对膨胀土的入渗过程以及增湿膨胀过程进行模拟,建立了如图1所示的基本模型。不考虑挡墙本身的变形,将其设为刚体,即刚性挡墙。模型中,挡墙高度H_w设为6 m；挡墙后的EPS缓冲层沿墙背均匀分布,厚度T_EPS设为0.3 m；墙后膨胀土的计算宽度T_Ex设为12 m。模型右侧水平约束,挡墙固定端约束,膨胀土和EPS缓冲层底部竖向约束。

图 1 基本模型及其增湿模式

Figure 1. Basic model and wetting process

下载: 全尺寸图片幻灯片

假设膨胀土体内初始含水率w₀为均匀分布。大气影响深度H_E为3 m,即3 m以下的膨胀土的含水率为定值,不受降雨入渗影响。土体表面在降雨入渗后达到饱和含水率w_sat,入渗后土体含水率自地表的w_sat逐渐减小至H_E = 3 m处的w₀后变为常数（见图1）。

数值模拟采用稳态分析,不考虑时间因素,即只研究温度（即等效的含水率）分布达到平衡后的情况。因此,式（3）中等式的右边为0,此时比热容C_T对温度分布无影响,可取任意值。土体各深度处初始温度相同。土体表面为高温边界（表征入渗边界）,大气影响深度处为低温边界（表征常含水率）,此时土体中出现稳定的热传导（即等效的渗流）,只要导热系数λ为常数,温度在均质土体中总是线性分布的。因此λ可取任意值,本文取1。

经上述模拟,在模型土体大气影响深度范围内形成线性分布的温度场,以模拟图1所示土体增湿后线性分布的含水率。根据增湿后各深度处的∆T（即等效的∆w）,按照式（1）计算相应的热膨胀量（即等效的增湿膨胀量）以及在不同侧限条件下对挡墙的侧压力。

EPS的密度为14.9 kg/m³（记为EPS15）,采用线弹性模型进行模拟弹性模量为2.37 MPa^[11]；由于EPS的泊松比较小,甚至为负数^[12],因此在数值模拟中取一个较小的值0.01。在基本模型中,不考虑EPS缓冲层与膨胀土、EPS缓冲层与挡墙之间的摩擦,摩擦的影响在2.2节中讨论。EPS缓冲层选用四边形平面应变单元进行模拟。

本文膨胀土采用万梁龙^[13]所测南阳膨胀土的相关参数通过莫尔-库仑弹塑性本构模型进行模拟。假设膨胀土均质且各向同性,其弹性模量、内摩擦角和黏聚力随含水率的增加而线性减小,而泊松比、增湿膨胀系数为常数,如表1所示。为简化分析,膨胀土的湿密度取定值1850 kg/m³。由于含水率在大气影响深度内由地表向下线性减小,膨胀土的内摩擦角、黏聚力和弹性模量均随埋深的增加而线性减小。膨胀土选用四边形平面应变热–位移耦合计算单元进行模拟。

表 1 数值模拟中采用的参数

Table 1. Parameters used in numerical simulation

含水率	弹性模量/MPa	黏聚力/kPa	内摩擦角/(°)	泊松比	增湿膨胀系数
w₀=17%	22.8	117	28.5	0.19	0.024
w_sat=30%	8.1	20	9.7	0.19	0.024

下载: 导出CSV

| 显示表格

数值模拟中设置土体初始温度为17℃（数值上等于膨胀土初始状态下的含水率w₀）并施加重力（重力加速度取9.8 m/s²）,其后激活温度边界条件,膨胀土顶面温度为30℃,大气影响深度处温度为17℃,分别与w_sat和w₀数值相等。

1.3 数值模拟方法的验证

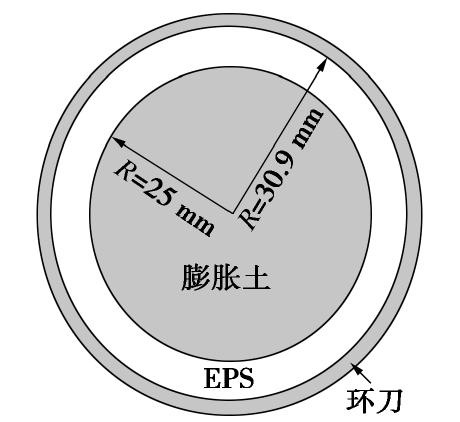
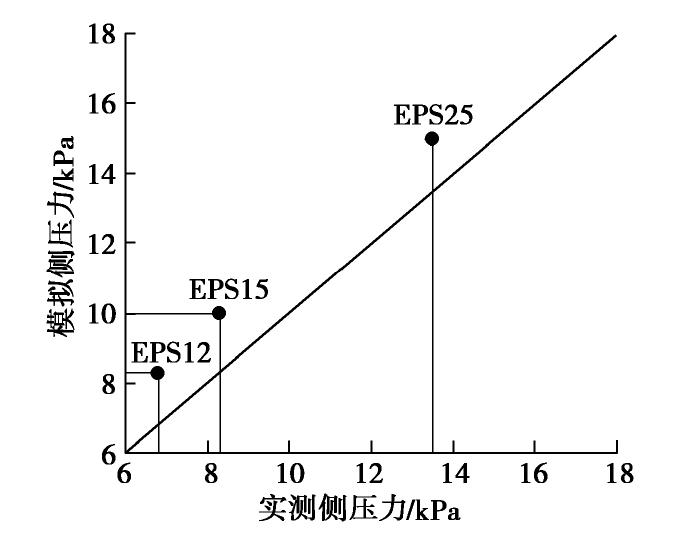
为验证数值模拟方法的可靠性,对万梁龙^[13]所测南阳膨胀土–EPS缓冲层模型试验结果进行了模拟。万梁龙^[13]制作了图2所示单元体模型,运用可测侧向压力的K₀固结仪,测得57 kPa竖向荷载下膨胀土完全饱和时EPS缓冲层作用于环刀的侧压力。模型中膨胀土参数见表1,采用了3种密度的EPS缓冲层（11.9,14.9,24.2 kg/m³,相应弹性模量为1.7,2.4,5.6 MPa,分别记为EPS12,EPS15,EPS25）。

图 2 膨胀土-EPS缓冲层单元体模型

Figure 2. Elemental specimen of expansive soil-EPS inclusion system

下载: 全尺寸图片幻灯片

用ABAQUS建立图2所示模型进行模拟。模拟结果与实测结果大体一致（见图3）,进而证明了数值方法的可靠性。模拟结果较试验结果稍大,这和EPS缓冲层的尺寸效应有关。EPS尺寸越小,其弹性模量越小,能进一步减小侧压力^[13]。

图 3 试验与模拟结果对比

Figure 3. Comparison between measured and modelled results

下载: 全尺寸图片幻灯片

1.4 基本模型模拟结果

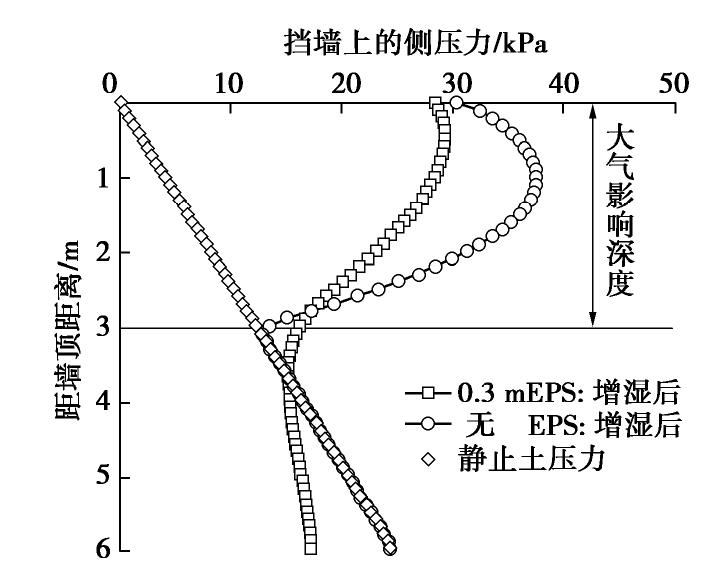
图4为增湿膨胀后作用在墙背上的侧压力分布,以及无EPS缓冲层时饱和土作用于挡墙的静止土压力。在大气影响深度范围内,当墙背后无EPS缓冲层时,作用在墙背上的侧压力随着距墙顶距离的增加,出现先增大后减小的趋势,这与其他学者^[1-2,14-17]的实测结果一致。当设置0.3 m厚的EPS缓冲层时,作用在墙背上的侧压力随着埋深同样呈现先增大后减小的特点,但侧压力的值较无EPS时明显降低。侧压力的峰值由37.5 kPa降低22%至29.2 kPa。单位宽度内侧压力的合力在无EPS时为94 kN,设置EPS后降为74 kN,对合力的减压效果达21 %。

图 4 作用在墙背上的侧压力

Figure 4. Lateral pressures on retaining wall

下载: 全尺寸图片幻灯片

无EPS缓冲层时,挡墙侧压力在大气影响深度处回归到静止土压力,形成一个明显的拐点。当有EPS缓冲层时,侧压力在大气影响深度处的过渡变得更为平缓。这是因为EPS缓冲层允许膨胀土发生侧向变形,通过协调侧向变形,使侧压力产生了重新分布。不设EPS缓冲层时土压力大于设有EPS缓冲层时的墙背侧压力,同样体现了EPS缓冲层的减压效果。

总体上,在6 m的墙高范围内,单位宽度内侧压力的合力在无EPS时为149 kN,设置EPS后降为122 kN,对合力的减压效果达18%；侧压力对墙踵的合力矩在无EPS时为524 kN·m,设置EPS后降为441 kN·m,对合力矩的减压效果达16%。

大气影响深度范围内墙背上侧压力先增大后减小的分布是以下因素共同作用的结果：①地表膨胀土吸水多,膨胀显著,但由于其竖向膨胀变形不被限制,因此刚性挡墙对其侧向变形限制作用以及相应产生的侧压力有限；②随着深度的增加,膨胀土竖向应力增大,自身膨胀变形所受约束相应增大,因此侧压力也随之增大；③含水率的增量随深度减小,膨胀变形和膨胀力,以及因此产生的侧压力也相应减小。

2. 参数分析

现有试验和数值模拟结果表明,EPS缓冲层的弹性模量越小,厚度越大,作用在挡墙上的侧压力越小,减压效果越好^[6]。除此之外,EPS缓冲层与墙和土之间的界面摩擦、墙后膨胀土的计算宽度、EPS缓冲层的连续性也是设计中需考虑的关键因素。本文基于基本模型,就这些因素进行参数分析研究。

2.1 膨胀土的计算宽度

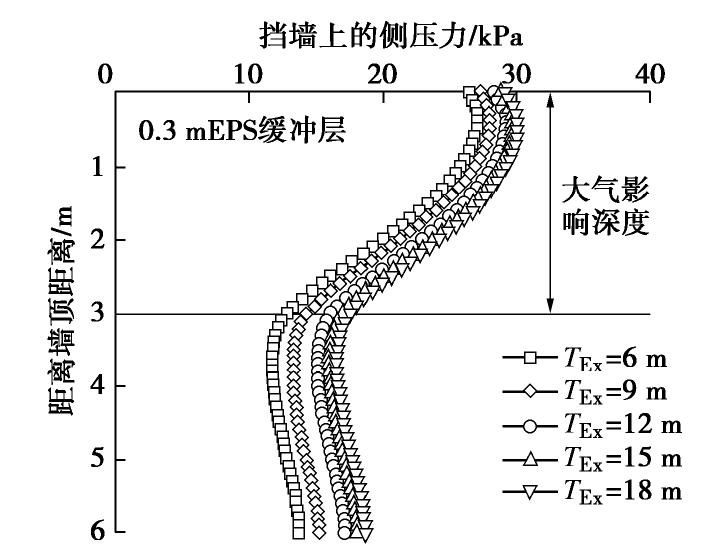
为探究墙后膨胀土计算宽度对挡墙侧压力的影响,取挡墙后膨胀土的宽度T_Ex为6,9,12,15,18 m,其他条件与基本模型相同。图5为挡墙上的侧压力分布。随着膨胀土计算宽度的增加,挡墙上的侧压力逐渐增加,当膨胀土的计算宽度超过墙高的2倍,即12 m时,作用在墙背上的侧压力不再显著变化。因此,膨胀土–EPS缓冲层–挡墙体系的计算模型中,墙后膨胀土宜取至少2倍墙高以计算最大侧压力。

图 5 膨胀土计算宽度对挡墙上的侧压力的影响

Figure 5. Influences of width of expansive soil on lateral pressure

下载: 全尺寸图片幻灯片

2.2 膨胀土-EPS缓冲层-挡墙材料的界面摩擦

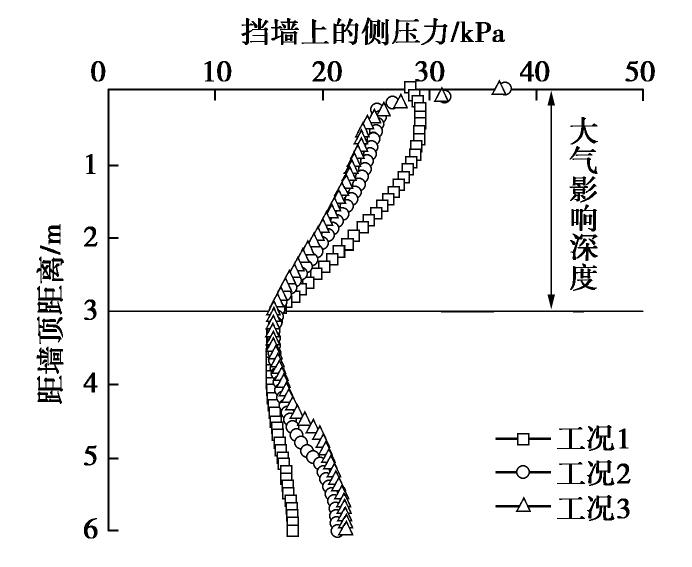
假设EPS缓冲层与膨胀土以及与挡墙的摩擦系数相同。考虑3种工况,即EPS缓冲层–膨胀土、EPS缓冲层–挡墙界面的摩擦系数为0（工况1）,0.5（工况2）和0.8（工况3）。

图6为不同界面摩擦情况下挡墙上的侧压力分布。随着摩擦系数的增大,挡墙上部的侧压力有减小趋势,挡墙下部的侧压力有增大趋势。3种工况下作用在挡墙上的水平推力以及水平推力的倾覆力矩如表2所示。3种工况下挡墙上的水平推力差别不大,但倾覆力矩随摩擦系数的增大而明显减小,由无摩擦时（工况1）的441 kN·m降低至摩擦系数为0.8时（工况3）的376 kN·m,降低了15%。

图 6 界面摩擦对挡墙侧压力的影响

Figure 6. Influences of interface friction on lateral pressure

下载: 全尺寸图片幻灯片

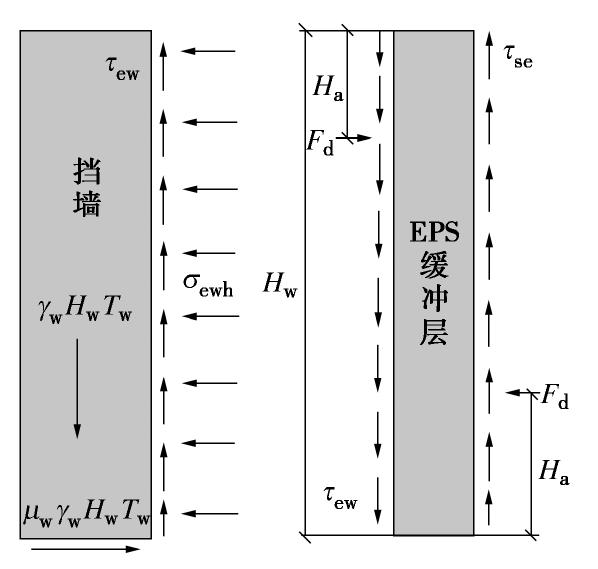
表 2 不同界面摩擦工况下挡墙的受力情况

Table 2. Influences of interface friction

工况	界面摩擦系数	水平推力/kN	倾覆力矩/(kN·m)
1	0	122	441
2	0.5	121	380
3	0.8	120	376

下载: 导出CSV

| 显示表格

EPS缓冲层受力状态如图7所示。当有界面摩擦时,大气影响深度范围内的膨胀土产生向上的膨胀变形,在与EPS的接触面上形成向上的摩擦力 $τ_{1}$ ,相应地,大气影响深度以下膨胀土与EPS的接触面上以及EPS与墙的接触面上分别形成向下的摩擦力 $τ_{2}$ 和 $τ_{3}$ ,以与 $τ_{1}$ 平衡。因此, $τ_{1}$ 的合力应大于 $τ_{2}$ 的合力。

图 7 界面摩擦对EPS受力的影响

Figure 7. Influences of interface friction on stress on EPS

下载: 全尺寸图片幻灯片

若选择墙踵,即EPS缓冲层的左下角为基准点,则 $τ_{1}$ 与 $τ_{2}$ 的合力形成逆时针作用的力矩。此时,EPS缓冲层两侧的正应力合力F_d也会形成顺时针作用的力矩与之平衡,造成F_d作用位置较没有摩擦力时改变。同时,剪应力引起的EPS缓冲层压缩量的变化。两者共同作用下,EPS缓冲层两侧的正应力,以及作用域挡墙上的侧压力产生重分布。

2.3 EPS挡墙的连续性

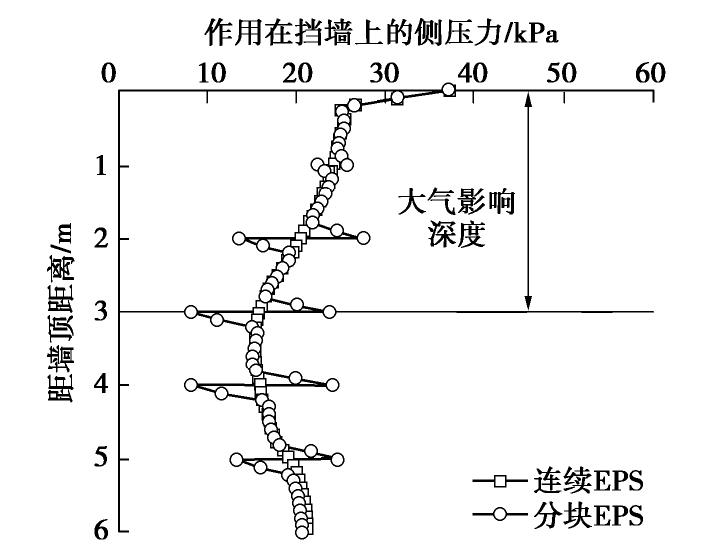
EPS在制造、运输和使用中多为尺寸固定的块体,实际建造的EPS缓冲层为块体组合而成,而不是连续的整体。因此,在基本模型的基础上,将EPS缓冲层由一个整体变为由6个EPS块体组成的结构。相邻EPS块体之间建立接触面,每个EPS块体高1 m。设EPS缓冲层–膨胀土、EPS缓冲层–挡墙以及EPS-EPS界面上的摩擦系数为0.5。

图8为连续EPS缓冲层（即基本模型）和不连续EPS缓冲层情况下挡墙上侧压力的分布。墙背上的侧压力则在EPS块体界面处表现出突变的现象,但总体上侧压力的分布与基本模型一致,因此EPS块体间的间隙对挡墙侧压力的分布的影响可以忽略。

图 8 EPS缓冲层的连续性对挡墙侧压力的影响

Figure 8. Influences of continuity of EPS on lateral pressure

下载: 全尺寸图片幻灯片

3. 膨胀土-EPS缓冲层-挡墙体系作用机理及侧压力计算方法

3.1 EPS缓冲层与膨胀土、挡墙相互作用机理

EPS缓冲层与膨胀土和挡墙间的作用机理包括：①EPS缓冲层的高压缩性为膨胀土提供一定的侧向膨胀空间,从而使膨胀土对挡墙的侧向挤压作用减弱,侧压力减小；②膨胀土的侧向位移使其自身的抗剪强度得到一定程度的发挥,使作用在挡墙上的侧压力减小；③EPS缓冲层与挡墙及膨胀土间的界面摩擦使得作用在挡墙上的侧压力产生重分布,增加了挡墙承受的倾覆力矩,但对挡墙上的水平推力无明显影响。

3.2 侧压力计算方法

计算模型中取膨胀土的计算宽度T_Ex= 2H_w且仅考虑大气影响深度范围内的膨胀土。不考虑膨胀土和EPS的流变特性,将膨胀土和EPS缓冲层视为线弹性材料。可用两个连接的弹簧S_Ex和S_EPS分别替代膨胀土和EPS缓冲层,其刚度分别为K_Ex和K_EPS：

$K_{Ex} = E_{sat} / T_{Ex}$ ,

(6)

$K_{EPS} = E_{EPS} / T_{EPS}$ 。

(7)

本文第2部分的数值模拟结果表明,作用在膨胀土–EPS缓冲层–挡墙体系上的侧压力沿埋深方向呈非线性分布。假设无EPS缓冲层时,作用在挡墙上侧压力的最大值为P_LAS。当膨胀土吸水膨胀后与EPS缓冲层达到平衡时,EPS缓冲层的压缩变形为D,建立如下平衡方程：

$P_{LAS} - D K_{Ex} = D K_{EPS}$ 。

(8)

此时,作用在挡墙上的侧压力 $σ_{ewh}$ = DK_EPS。将式（6）,（7）代入式（8）并整理,可得

$σ_{ewh} = \frac{P_{LAS}}{1 + \frac{T_{EPS} E_{sat}}{T_{Ex} E_{EPS}}}$ 。

(9)

为简化分析,假设σ_ewh沿墙高均匀分布。 $σ_{ewh}$ 为经EPS缓冲层减压后的侧压力最大值。因此,依据本方法进行的挡墙设计是偏于保守和安全的。

当膨胀土膨胀时,挡墙和EPS缓冲层均受到剪应力,如图9所示。作用在挡墙上的剪应力τ_ew和EPS缓冲层上的剪应力τ_se为

$τ_{ew} = c_{ew} + \tan φ_{ew} σ_{ewh}$ ,

(10)

$τ_{se} = c_{se} + \tan φ_{se} σ_{ewh}$ 。

(11)

图 9 大气影响深度范围内挡墙和EPS缓冲层的受力分析

Figure 9. Stresses on retaining wall and EPS inclusion

下载: 全尺寸图片幻灯片

式中 $φ_{ew}$ 为EPS缓冲层–挡墙界面的摩擦角；φ_se为EPS缓冲层–膨胀土界面的摩擦角；c_ew为EPS缓冲层–挡墙界面的黏聚力；c_se为膨胀土–EPS缓冲层界面的黏聚力。根据力的平衡原理,τ_se与τ_ew在数值上应相等,都等于两者绝对值：

$τ_{se} = τ_{ew} = \min {| τ_{se} |, | τ_{ew} |}$ 。

(12)

本文第2节的分析表明,EPS缓冲层两侧的摩擦力会使作用在挡墙上部的侧压力产生重分布。假设侧压力以单位宽度上集中力F_d的形式作用在EPS挡墙上形成力偶,F_d离EPS上下边缘的距离为H_a,如图9所示。F_d可由下式确定：

$F_{d} = H_{w} σ_{ewh}$ 。

(13)

根据相对墙踵的力矩平衡可确定H_a,表达式为

$F_{d} (H_{w} - 2 H_{a}) = H_{w} τ_{se} T_{EPS}$ ,

(14)

$H_{a} = \frac{1}{2} (H_{w} - \frac{τ_{se} T_{EPS}}{σ_{ewh}})$ 。

(15)

3.3 侧压力计算方法的验证

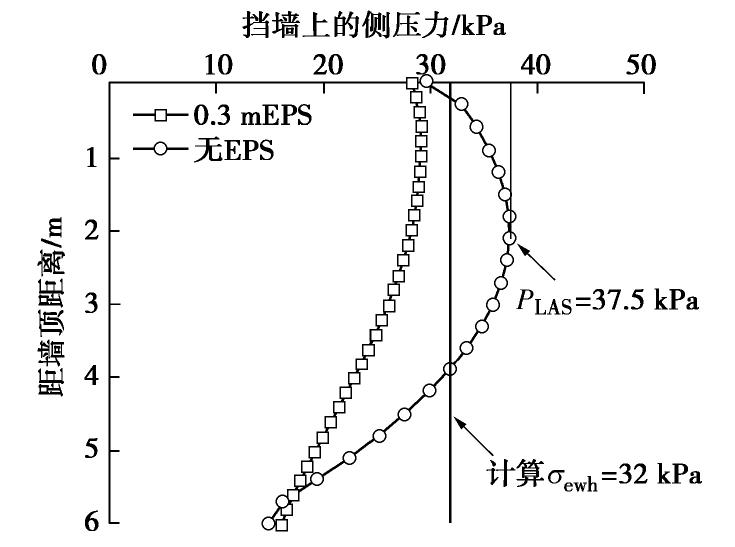
采用本文所提侧压力计算方法计算基本模型中大气影响深度范围内（即3 m墙高范围内）EPS缓冲层的减压效果。取P_LAS= 37.5 kPa,即无EPS缓冲层时挡墙上的最大侧压力。其他参数与基本模型相同,根据式（9）计算得到有EPS缓冲层时挡墙上的最大侧压力 $σ_{ewh}$ = 32 kPa,计算结果如图10所示。可见,计算所得 $σ_{ewh}$ 与数值模拟结果相近,说明本文侧压力计算方法具有合理性。

图 10 模拟和计算所得挡墙上的侧压力

Figure 10. Modelled and calculated stresses on retaining wall

下载: 全尺寸图片幻灯片

4. 设计应用算例

EPS缓冲层密度越小,减压效果越好。但EPS密度过小时,其稳定性和强度较低,不便施工。因此,宜使用密度不小于12 kg/m³的EPS,即EPS12。需要注意的是,密度较小的EPS弹性模量也小,受力时产生较大压缩,可能造成临近膨胀土较大的位移。所以,EPS密度的选择应考虑临近膨胀土对位移和变形的限制条件。EPS的压缩应变宜控制在3%～5%。

本文以常见的重力式挡墙为例,通过一个算例说明侧压力计算模型在设计膨胀土–EPS缓冲层–挡墙体系中的应用,并与无缓冲层的重力式挡墙进行对比。

设挡墙材料为素混凝土,墙高H_w = 3 m,挡墙重度 $γ_{wall}$ =24 kN/m³,挡墙与底部垫层之间的摩擦系数μ_wall = 0.8（见图9）；饱和膨胀土弹性模量为10 MPa,P_LAS = 37.5 kPa；EPS缓冲层选取EPS12,其弹性模量为1.7 MPa；φ_ew = 26°,c_ew = 7 kPa；φ_se =7°,c_se = 13 kPa。抗滑移安全系数F_s=1.3,抗倾覆安全系数F_t= 1.5。为简化分析,设挡墙横截面为矩形,不考虑挡墙埋深的影响。

通过抗滑移验算,可得挡墙宽度T_w：

$\begin{array}{l} \frac{(γ_{wall} H_{w} T_{w} - τ_{ew} H_{w}) μ_{wall}}{σ_{ewh} H_{w}} \geq F_{s} \\ \Rightarrow T_{w} \geq \frac{σ_{ewh} F_{s}}{γ_{wall} μ_{wall}} + \frac{τ_{ew}}{γ_{wall}} \end{array}$ 。

(16)

取T_EPS = 0.3 m,结合式（9）可得 $σ_{ewh}$ = 29 kPa；由式（10）～（12）可得τ_se = 16.6 kPa；由式（14）可得T_w ≥ 2 m。由式（13）,（15）可得F_d = 87 kN,H_a=1.41 m；将不同T_w代入

$\frac{0.5 γ_{wall} H_{w} T_{w}^{2}}{T_{w} H_{w} τ ew+(H_{w} - H_{a}) F_{d}} \geq F_{t}$

(17)

进行抗倾覆验算试算,可得T_w = 3.7 m满足抗倾覆验算要求。对于不设置EPS缓冲层的重力式挡墙,令 $σ_{ewh}$ = P_LAS = 37.5 kPa,按照上述步骤可以得出挡墙的最小厚度为4.2 m,对比可见,0.3 m厚的EPS缓冲层可以有效减小重力式挡墙的设计厚度。

5. 结论

本文用温度场类比湿度场,采用热膨胀模拟了膨胀土–EPS缓冲层–挡墙体系在膨胀土增湿膨胀后的性状,并对不同情况下EPS缓冲层的减压性能进行了参数分析。基于数值模拟结果,通过理论分析,提出了膨胀土挡墙侧压力的计算方法,并通过一个算例对侧压力计算方法在设计中的应用进行了详细说明。得到以下3点结论。

（1）EPS缓冲层的连续性对其减压效果影响不大,可将EPS缓冲层视为连续的整体。EPS缓冲层–膨胀土、EPS缓冲层–挡墙之间的摩擦不会明显影响挡墙上的水平推力,但会使侧压力发生重分布,使倾覆力矩减小。

（2）挡墙后膨胀土计算宽度的增加会使作用在挡墙上的侧压力增大,但当膨胀土宽度超过墙高的2倍时,膨胀土宽度对作用在膨胀土–EPS缓冲层–挡墙上的侧压力影响不大。计算中宜取两倍墙高作为墙后膨胀土的计算宽度。

（3）总结了EPS缓冲层与膨胀土、挡墙相互作用机理。在此基础上,提出了膨胀土–EPS缓冲层–挡墙体系中挡墙上侧压力计算模型。该模型能够合理计算EPS缓冲层的减压效果,基于该模型的设计偏于保守和安全。

图 1 基本模型及其增湿模式

Figure 1. Basic model and wetting process

下载: 全尺寸图片幻灯片

图 2 膨胀土-EPS缓冲层单元体模型

Figure 2. Elemental specimen of expansive soil-EPS inclusion system

下载: 全尺寸图片幻灯片

图 3 试验与模拟结果对比

Figure 3. Comparison between measured and modelled results

下载: 全尺寸图片幻灯片

图 4 作用在墙背上的侧压力

Figure 4. Lateral pressures on retaining wall

下载: 全尺寸图片幻灯片

图 5 膨胀土计算宽度对挡墙上的侧压力的影响

Figure 5. Influences of width of expansive soil on lateral pressure

下载: 全尺寸图片幻灯片

图 6 界面摩擦对挡墙侧压力的影响

Figure 6. Influences of interface friction on lateral pressure

下载: 全尺寸图片幻灯片

图 7 界面摩擦对EPS受力的影响

Figure 7. Influences of interface friction on stress on EPS

下载: 全尺寸图片幻灯片

图 8 EPS缓冲层的连续性对挡墙侧压力的影响

Figure 8. Influences of continuity of EPS on lateral pressure

下载: 全尺寸图片幻灯片

图 9 大气影响深度范围内挡墙和EPS缓冲层的受力分析

Figure 9. Stresses on retaining wall and EPS inclusion

下载: 全尺寸图片幻灯片

图 10 模拟和计算所得挡墙上的侧压力

Figure 10. Modelled and calculated stresses on retaining wall

下载: 全尺寸图片幻灯片

表 1 数值模拟中采用的参数

Table 1 Parameters used in numerical simulation

含水率弹性模量/MPa 黏聚力/kPa 内摩擦角/(°) 泊松比增湿膨胀系数

w₀=17% 22.8 117 28.5 0.19 0.024
w_sat=30% 8.1 20 9.7 0.19 0.024

下载: 导出CSV

表 2 不同界面摩擦工况下挡墙的受力情况

Table 2 Influences of interface friction

工况界面摩擦系数水平推力/kN 倾覆力矩/(kN·m)

1 0 122 441
2 0.5 121 380
3 0.8 120 376

下载: 导出CSV

参考文献(17)

[1]	MOHAMED O Z, TAHA Y K, EL-AZIZ E-S M A. Field study of the distribution of lateral swelling pressure of expansive soil on retaining structure[J]. Journal of Engineering Sciences, 2014, 42(2): 289-302.
[2]	王秉勇. 裂土地区挡土墙上承受的膨胀力分析[J]. 路基工程, 1993, 9(4): 5-11. https://www.cnki.com.cn/Article/CJFDTOTAL-LJGC199304001.htm WANG Bing-yong. Expansive force analysis of retaining wall in earth retaining wall[J]. Subgrade Engineering, 1993, 9(4): 8-14. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LJGC199304001.htm
[3]	蒋忠信, 李敏, 牛怀俊, 等. 南昆铁路膨胀泥岩路堑边坡工程试验[J]. 路基工程, 1999(5): 34-42. https://www.cnki.com.cn/Article/CJFDTOTAL-LJGC199905010.htm JIANG Zhong-xin, LI Min, NIU Huai-jun, et al. Experiment of expansive mudstone cutting slope in Nan-Kun railway[J]. Subgrade Engineering, 1999(5): 34-42. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LJGC199905010.htm
[4]	AYTEKIN M. Numerical modeling of EPS geofoam used with swelling soil[J]. Geotextiles and Geomembranes, 1997, 15(1/2/3): 133-146.
[5]	IKIZLER S B, AYTEKIN M, VEKLI M. Reductions in swelling pressure of expansive soil stabilized using EPS geofoam and sand[J]. Geosynthetics International, 2009, 16(3): 216-221. doi: 10.1680/gein.2009.16.3.216
[6]	IKIZLER S B, AYTEKIN M, NAS E. Laboratory study of expanded polystyrene (EPS) geofoam used with expansive soils[J]. Geotextiles and Geomembranes, 2008, 26(2): 189-195. doi: 10.1016/j.geotexmem.2007.05.005
[7]	ZHENG J L, ZHANG R, YANG H P. Highway subgrade construction in expansive soil areas[J]. Journal of Materials in Civil Engineering, 2009, 21(4): 154-162. doi: 10.1061/(ASCE)0899-1561(2009)21:4(154)
[8]	曾仲毅, 徐帮树, 胡世权, 等. 增湿条件下膨胀土隧道衬砌破坏数值分析[J]. 岩土力学, 2014, 35(3): 871-880. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201403044.htm ZENG Zhong-yi, XU Bang-shu, HU Shi-quan, et al. Numerical analysis of tunnel liner failure mechanism in expansive soil considering water-increased state[J]. Rock and Soil Mechanics, 2014, 35(3): 871-880. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201403044.htm
[9]	ZOU W L, HAN Z, YE J B. Influence of external stress and initial density on the volumetric behavior of an expansive clay during wetting[J]. Environmental Earth Sciences, 2020, 79(10): 211. doi: 10.1007/s12665-020-08960-1
[10]	晁峰, 王明年, 舒东利, 等. 膨胀土附加应力场对深基坑土压力的影响[J]. 中南大学学报(自然科学版), 2016, 47(9): 3177-3182. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201609036.htm CHAO Feng, WANG Ming-nian, SHU Dong-li, et al. Earth pressure of deep foundation pit effected by additional stress field of expansive soil[J]. Journal of Central South University (Science and Technology), 2016, 47(9): 3177-3182. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201609036.htm
[11]	WAN L L, ZOU W L, WANG X Q, et al. Comparison of three inclusions in reducing lateral swelling pressure of expansive soils[J]. Geosynthetics International, 2018, 25(5): 481-493.
[12]	ABDELRAHMAN G E, KAWABE S, TSUKAMOTO Y, et al. Small-strain stress-strain properties of expanded polystyrene geofoam[J]. Soils and Foundations, 2008, 48(1): 61-71.
[13]	万梁龙. 聚苯乙烯泡沫(EPS)减小膨胀土挡墙侧压力的研究[D]. 武汉: 武汉大学, 2019. WAN Liang-long. Reduction of Lateral Pressure on Retaining Walls Backfilling with Expansive Soil Using Expanded Polystyrene (EPS) Geofoam[D]. Wuhan: Wuhan University, 2019. (in Chinese)
[14]	张颖钧. 挡墙后裂土膨胀压力分布与设计计算方法[J]. 铁道学报, 1995, 17(1): 93-102. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB501.012.htm ZHANG Ying-jun. Distribution of lateral swelling pressure and the method of design and computation of retaining wall[J]. Journal of the China Railway Society, 1995, 17(1): 93-102. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB501.012.htm
[15]	谢兰芳. 云桂铁路膨胀土地段桩板墙及柔性挡墙试验研究[D]. 长沙: 中南大学, 2012. XIE Lan-fang. Experimental Study on Pile-Sheet Retaining Wall and Flexible Retaining Wall Applied in Yun-Gui Railway[D]. Changsha: Central South University, 2012. (in Chinese)
[16]	汪鹏福. 云桂铁路膨胀土路堑边坡桩板墙现场监测与理论研究[D]. 长沙: 中南大学, 2014. WANG Peng-fu. Field test and Theoretical Study of Pile-Plank Wall on Expansive Soil Cutting Slope in Yun-Gui Railway[D]. Changsha: Central South University, 2014. (in Chinese)
[17]	BRACKLEY I J A, SANDERS P J. In situ measurement of total natural horizontal stresses in an expansive clay[J]. Géotechnique, 1992, 42(3): 443-451.

施引文献(14)

期刊类型引用(5)

1.	杨果林，李文生，段君义，杨啸，李兴瑷，夏晓鹏. 缓冲层-桩板墙组合支护膨胀土边坡现场试验研究. 湖南大学学报(自然科学版). 2025(01): 24-33 . 百度学术
2.	段君义，曹鹏远，粟雨，林宇亮，杨果林. 膨胀土地基膨胀特性对无砟轨道路基变形性能的影响. 中南大学学报(自然科学版). 2024(09): 3530-3542 . 百度学术
3.	邹维列，樊科伟，张攀，韩仲. 土工泡沫减压膨胀土挡墙侧向压力及影响因素分析. 岩土力学. 2023(09): 2537-2544+2554 . 百度学术
4.	李恒达，贺亮亮，张宇飞，刘思维，雷超雯. 格构式双排桩板墙台地支护体系变形与受力特性分析. 结构工程师. 2023(06): 179-188 . 百度学术
5.	王欢，杨惠如，曹义康，邱翱博，凡超文. 粉砂土改良弱膨胀土路基沉降特性研究. 河南大学学报(自然科学版). 2021(06): 719-727 . 百度学术