一种改进的盾构隧道双层衬砌计算模型及其工程应用

王俊; 徐国文; 蔚艳庆; 何佳; 何川; 王士民

doi:10.11779/CJGE202108015

一种改进的盾构隧道双层衬砌计算模型及其工程应用 English Version

王俊^1,,
徐国文^2, ,,
蔚艳庆¹,
何佳¹,
何川²,
王士民²

1.
四川省公路规划勘察设计研究院有限公司,四川　成都　610041
2.
西南交通大学交通隧道工程教育部重点实验室,四川　成都　610031

详细信息

作者简介:
王俊(1987— ),男,四川绵阳人,博士,主要从事隧道设计与科研方面的工作。E-mail：luckywangjun@126.com

通讯作者:
徐国文, E-mail：xgw80033@163.com

中图分类号: TU311;U455.43
计量
- 文章访问数: 232
- HTML全文浏览量: 27
- PDF下载量: 149
出版历程
- 收稿日期: 2020-05-29
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-07-31

An improved model for shield tunnels with double-layer linings and its application in engineering

1.
Sichuan Highway Planning, Survey, Design and Research Institute Ltd., Chengdu 610041, China
2.
Key Laboratory of Transportation Tunnel Engineering, Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China

摘要

摘要: 提出一种改进的盾构隧道双层衬砌计算模型,该模型可以反映接头抗弯刚度的非线性以及管片与二次衬砌接触面压剪弹簧失效机理。采用该模型对狮子洋隧道衬砌的力学行为进行了分析,结果表明：①管片结构最大正负弯矩随接头抗弯刚度增大而增大,而二次衬砌内力及管片结构最大轴力受接头抗弯刚度影响较小；②若不考虑管片与二次衬砌接触面的接触弹簧失效,将会使得计算结果量值偏大；③当盾构隧道所处岩层均匀时（t/D=0或1,t为结构范围内软弱层的厚度,D为隧道直径）,全环各个位置处接头刚度值差别不大,当岩层不均匀时,接头抗弯刚度的取值差异分布显著；④径向弹簧、切向弹簧受力的最大值与平均值随着t/D的增加呈增大的趋势。
- 盾构隧道 /
- 双层衬砌 /
- 抗弯刚度 /
- 接触面 /
- 弹簧
Abstract: An improved model for shield tunnels with double-layer linings is proposed. It can reflect the nonlinear characteristic of bending stiffness of segment joints and the failure mechanism of compression and shear springs between segments and secondary linings. The internal force of linings of Shiziyang tunnel is analyzed using this model. The results show that: (1) The increment of bending stiffness of the segment joints can increase the values of the maximum positive and negative bending moments of the segments, while it has slight effect on the internal force of the secondary linings and the maximum axial force of the segments. (2) The internal force is larger than that in reality if the failure mechanism of springs between segments and secondary linings is not considered in the model. (3) The bending stiffness of joints varies slightly if the structure is situated in uniform strata (t/D=0 or 1, t is the distance from the tunnel top to the stratum interface, D is the diameter of tunnel), while its value varies sharply if the structure is situated in nonuniform strata. (4) The maximum and average forces of compression and shear springs will increase with the increment of t/D.
- shield tunnel /
- double-layer lining /
- bending stiffness /
- interface /
- spring

HTML全文

0. 引言

柱状节理常见于玄武岩岩体,节理面独特的空间结构分布使得岩体强度表现出强各向异性。已有学者针对柱状节理岩体开展了现场原位试验和大量的相似材料室内试验^[1-5],验证了柱状节理岩体的强度各向异性并总结了材料强度参数的各向异性分布规律。但目前对于柱状节理岩体各向异性本构研究的报道还不多,而已有的一些各向同性模型则不能很好的描述柱状节理岩体的强度各向异性特性。

柱状节理岩体为岩块和结构面的综合体,其表征单元体较室内试验可研究的尺度要大许多,很难通过室内试验来研究柱状节理岩体的变形和强度特征。而原位试验虽然可以在一定程度上反映节理岩体的工程力学特性,但受限于场地、设备、成本等因素,一些物理力学参数难以获取。由于柱状节理岩体具有结构周期性,可以应用数值均匀化方法开展多尺度分析计算,如多重有限元（FE²）或跨尺度有限元离散元耦合（FEM/DEM）。该类方法避免了复杂本构方程的建立,适用于满足均匀化条件的复杂细观结构材料。但多尺度方法计算量巨大,难以直接应用于大型水电工程的计算。因此建立可以准确描述柱状节理岩体力学特性的本构模型具有重要意义。柱状节理岩体显著的各向异性是本构的建模的难点。微结构张量作为材料微观结构的一种度量,可用来描述岩体介质中孔隙或裂纹的空间分布。本文在传统力学模型的基础上引入微结构张量,建立柱状节理岩体各向异性本构模型。

Kanatani^[6-7]最早系统研究了材料空间分布与微结构张量的关系,初步建立了空间分布函数的表达式。Pietruszczak等^[8]通过组合强度参数的空间分布,把经典各向同性准则拓展为各向异性,建立了基于微结构张量的各向异性屈服准则。Gao等^[9]将微结构张量参数引入屈服函数,提出了一种具有交叉各向异性的岩土材料的广义破坏准则,该准则在描述大范围材料的强度随加载方向的变化时具有通用性和鲁棒性。钟世英等^[10]采用多组节理面局部坐标系与整体坐标系的投影关系定义了材料空间的微结构张量表达,将其引入莫尔库仑强度准则,得到了多组节理岩体的各向异性强度准则。

然而现阶段基于微结构张量的各向异性本构模型尚存在不足,或以页岩等层状岩石为研究对象^[8-9],模型不能较好反映柱状节理岩体物理力学试验特性,或模型较为复杂,参数不易确定^[10],实际应用较为困难。

为此,本文提出了一种既保留了数学的严谨性又具有一定实用性的方法。首先,结合微结构张量理论推导了柱状节理岩体各向异性弹塑性本构积分公式,然后基于FLAC^3D对自定义本构进行了二次开发,并结合柱状节理相似结构材料三轴岩石力学试验对本文提出的自定义本构模型进行了验证。应用所开发各向异性弹塑性本构模型对白鹤滩水电站坝基开挖工程进行了数值模拟分析,数值模拟结果与坝基岩体开挖工程监测结果基本相符。研究结果对白鹤滩水电工程建设具有一定应用价值。

1. 各向异性弹塑性本构

1.1 弹性刚度矩阵及空间旋转变换

理想弹性体的本构关系可表示为

$ε = C σ$ 。

(1)

柱状节理岩体（如图1）可简化为横观各向同性材料,由广义胡克定律,在材料空间的局部坐标系下其柔度矩阵可表示为

图 1 全局坐标系中的柱状节理材料

Figure 1. Cylindrical joint materials in global coordinate system

下载: 全尺寸图片幻灯片

$\begin{matrix} C = [\begin{matrix} \frac{1}{E_{1}} & - \frac{ν_{12}}{E_{1}} & - \frac{ν_{13}}{E_{3}} & 0 & 0 & 0 \\ - \frac{ν_{12}}{E_{1}} & \frac{1}{E_{1}} & - \frac{ν_{13}}{E_{3}} & 0 & 0 & 0 \\ - \frac{ν_{13}}{E_{3}} & - \frac{ν_{13}}{E_{3}} & \frac{1}{E_{3}} & 0 & 0 & 0 \\ 0 & 0 & 0 & \frac{1}{G_{13}} & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{G_{13}} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{2 (1 + ν_{12})}{E_{1}} \end{matrix}] \\ = {[D^{e}]}^{- 1} \end{matrix}$ ,

(2)

式中, $E_{1}$ 为平行于各向同性面的弹性模量, $E_{3}$ 为垂直于各向同性面的弹性模量, $G_{13}$ 为垂直平面的剪切模量, $ν_{12}$ 为平行面内的泊松比, $ν_{13}$ 为垂直方向的泊松比, $D^{e}$ 为弹性刚度矩阵。

全局坐标系下的柔度矩阵 $C^{'}$ 可由局部坐标系下的柔度矩阵 $C$ 旋转得到

$C^{'} = Q^{T} C Q$ ,

(3)

式中, $Q$ 为一个包含局部坐标轴与全局坐标轴夹角 $α$ 的二阶张量,可表示为

$Q = [\begin{matrix} \cos^{2} α & \sin^{2} α & 0 & \frac{\sin 2 α}{- 2} & 0 & 0 \\ \sin^{2} α & \cos^{2} α & 0 & \frac{\sin 2 α}{2} & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ \sin 2 α & - \sin 2 α & 0 & \cos 2 α & 0 & 0 \\ 0 & 0 & 0 & 0 & \cos α & - \sin α \\ 0 & 0 & 0 & 0 & \sin α & \cos α \end{matrix}]$ 。

(4)

对于横观各向同性材料,需要给出两个夹角,分别为材料的倾向 $α$ 和倾角 $β$ 。后续推导若不加说明,默认在材料空间中的局部坐标系展开。

1.2 各向异性屈服函数及塑性势函数

定义微结构张量 $a_{i j}$ 主轴与材料空间的局部坐标系同轴,三维空间中微结构张量 $a_{i j}$ 可由单位向量 $e_{i}$ 表示为

$\begin{matrix} a_{i j} = a_{1} e_{i}^{(1)} e_{j}^{(1)} + a_{2} e_{i}^{(2)} e_{j}^{(2)} + e_{i}^{(3)} e_{j}^{(3)} \\ = a_{1} m_{i j}^{(1)} + a_{2} m_{i j}^{(2)} + a_{3} m_{i j}^{(3)} \end{matrix}$ ,.

(5)

式中, $a_{i}$ 为微结构张量的主值, $m_{i j}$ 为结构取向张量。

定义广义加载单位向量 $l_{i}$ 为

$l_{i} = \frac{L_{i}}{\sqrt{L_{k} L_{k}}} = \frac{L_{i}}{\sqrt{σ_{i j} σ_{i j}}} = \frac{L_{i}}{\sqrt{tr σ^{2}}}$ ,

(6)

$L_{i} = \sum_{x = 1}^{3} L_{x} e_{i}^{(x)}$ ,

(7)

$L_{x} = \sqrt{σ_{1 x}^{2} + σ_{2 x}^{2} + σ_{3 x}^{2}}$ 。

(8)

考虑微结构张量 $a_{i j}$ 在 $l_{i}$ 方向上的投影,即

$\begin{matrix} η = a_{i j} l_{i} l_{j} = a_{1} \frac{tr(m^{(1)} σ^{2})}{tr σ^{2}} + a_{2} \frac{tr(m^{(2)} σ^{2})}{tr σ^{2}} + \\ a_{3} \frac{tr(m^{(3)} σ^{2})}{tr σ^{2}} \end{matrix}$ 。

(9)

式（9）所定义参数 $η$ 是一个无量纲的标量,综合考虑了材料结构面取向对加载空间的影响,反映了材料强度的方向依赖性,因此可用来描述材料强度的各向异性空间分布。式（9）也可表示为偏量的形式：

$η = \hat{η} (1 + A_{i j} l_{i} l_{j})$ ,

(10)

$\hat{η} = a_{k k} / 3, A_{i j} = (a_{i j} - \hat{η} δ_{i j}) / \hat{η}$ 。

(11)

式（10）最早由Kanatani^[6-7]提出。更一般的,该式可表示为

$\begin{matrix} η = \hat{η} (1 + A_{i j} l_{i} l_{j} + A_{i j k l} l_{i} l_{j} l_{k} l_{l} + \dots) \\ = \hat{η} (1 + A_{i j} l_{i} l_{j} + b_{1} {(A_{i j} l_{i} l_{j})}^{2} + \dots) \end{matrix}$ 。

(12)

本文采用一种修正的莫尔库仑准则^[11]来描述岩石柱体的塑性行为,并考虑各向异性和塑性硬化：

$\begin{matrix} f = \sqrt{{(q K (θ))}^{2} + {(e_{f} c \cos ϕ)}^{2}} + \\ η_{f} h (ξ) (p \sin ϕ - c \cos ϕ) \end{matrix}$ ,

(13)

$\begin{matrix} p = \frac{σ_{k k}}{3},_{}^{} {_{}^{}}_{}^{}_{}^{} q = \sqrt{\frac{3}{2} J_{2}}, \\ J_{2} = s_{i j} s_{i j},_{}^{} {_{}^{}}_{}^{}_{}^{} s_{i j} = σ_{i j} - \frac{σ_{k k}}{3} δ_{i j} \end{matrix}$ 。

(14)

式中 $c$ 为材料黏聚力, $ϕ$ 为材料内摩擦角,可通过试验确定； $e_{f}$ 为子午面上拟合屈服线的双曲偏心率,可通过调整 $e_{f}$ 来调整抗拉强度大小； $η_{f}$ 为微结构张量参数, $h (ξ)$ 为塑性硬化函数, $ξ$ 为塑性内变量； $p$ 为平均应力, $q$ 为偏应力, $J_{2}$ 为应力偏量第二不变量, $θ$ 为Lode角, $K (θ)$ 为关于Lode角的函数。

Lode角函数采用分段形式对屈服面角点进行平滑修正：

$K (θ) = {\begin{matrix} \cos θ - \frac{\sin θ \cos ϕ}{\sqrt{3}} & | θ | \leq θ_{t} \\ K_{1} - K_{2} \sin 3 θ & | θ | > θ_{t} \end{matrix}$ ,

(15)

$\begin{matrix} K_{1} = \frac{1}{3} \cos θ_{t} (3 + \tan θ_{t} \tan 3 θ_{t} + \\ \frac{1}{\sqrt{3}} (\tan 3 θ_{t} - 3 \tan θ_{t}) sign(θ) \sin ϕ) \end{matrix}$ ,

(16)

$K_{2} = \frac{1}{3 \cos 3 θ_{t}} (sign(θ) \sin θ_{t} + \frac{1}{\sqrt{3}} \sin θ_{t} \sin ϕ)$ ,

(17)

式中, $θ_{t}$ 为容许Lode角,当 $| θ | \leq θ_{t}$ 时,与经典Mohr–Coulomb准则一致,当 $| θ | > θ_{t}$ 时,对屈服函数迹线进行平滑处理。

取等效塑性剪应变 ${\bar{γ}}^{p}$ 作为塑性内变量,定义塑性硬化函数为^[12]

$h (ξ) = h_{0} - (h_{1} - h_{0}) \frac{ξ}{B + ξ}$ ,

(18)

$ξ = {\bar{γ}}^{p} = \int d {\bar{γ}}^{p},_{}^{} {_{}^{}}_{}^{} d {\bar{γ}}^{p} = \sqrt{\frac{2}{3} d e_{i j}^{p} d e_{i j}^{p}}$ ,

(19)

式中, $h_{0}$ 为初始屈服阈值, $h_{1}$ 为峰值屈服阈值, $B$ 为描述塑性硬化率大小的参数。

塑性势函数与屈服函数形式一致,即

$g = \sqrt{q^{2} K^{2} (θ) + {(e_{f} c \cos ψ)}^{2}} + η_{f} p \sin ψ$ ,

(20)

式中, $ψ$ 为膨胀角,当 $ψ \neq ϕ$ 时即为非关联流动。

1.3 屈服函数及塑性势函数求导

由于本构数值积分中将涉及到屈服函数及塑性势函数的偏导数,故先行给出偏导数的求解。首先计算屈服函数对应力张量的偏导数,根据式（13）有

$\frac{\partial f}{\partial σ_{i j}} = (\frac{\partial f}{\partial I_{1}} \frac{\partial I_{1}}{\partial σ_{i j}} + \frac{\partial f}{\partial J_{2}} \frac{\partial J_{2}}{\partial σ_{i j}} + \frac{\partial f}{\partial θ} \frac{\partial θ}{\partial σ_{i j}}) + (\frac{\partial f}{\partial η_{f}} \frac{\partial η_{f}}{\partial σ_{i j}})$ ,

(21)

式中,

$\begin{matrix} \frac{\partial I_{1}}{\partial σ_{i j}} = δ_{i j},_{}^{} {_{}^{}}_{}^{} \frac{\partial J_{2}}{\partial σ_{i j}} = s_{i j}, \\ \frac{\partial θ}{\partial σ_{i j}} = \frac{\sqrt{3}}{2 \sqrt{J_{2}^{3}} \cos 3 θ} (\frac{3 J_{3}}{2 J_{2}} s_{i j} - s_{i k} s_{k j} + \frac{2}{3} J_{2} s_{i j}) \end{matrix}$ ,

(22)

$\frac{\partial η_{f}}{\partial σ_{i j}} = \frac{2 η_{0} (A_{k i} σ_{k j} σ_{p q} σ_{p q} - A_{p k} σ_{p q} σ_{k q} σ_{i j})}{{(σ_{m n} σ_{m n})}^{2}}$ ,

(23)

$\frac{\partial f}{\partial I_{1}} = \frac{1}{3} η_{f} h \sin ϕ, \frac{\partial f}{\partial J_{2}} = \frac{1}{2} α_{f} K, \frac{\partial f}{\partial θ} = α_{f} J_{2} \frac{d K}{d θ}$ ,

(24)

$\frac{\partial f}{\partial η_{f}} = h (ξ) (p \sin ϕ - c \cos ϕ)$ ,

(25)

$α_{f} = 3 K / \sqrt{3 J_{2} K^{2} + {(e_{f} c \cos ϕ)}^{2}}$ ,

(26)

$\frac{d K}{d θ} = {\begin{matrix} - \sin θ - \frac{\cos θ \sin ϕ}{\sqrt{3}} & | θ | \leq θ_{t} \\ - 3 K_{2} \cos 3 θ & | θ | > θ_{t} \end{matrix}$ 。

(27)

然后计算塑性势函数对应力张量的偏导数。由于式（20）采取了与屈服函数相一致的形式,因此塑性势函数对应力张量的一阶偏导数只需将内摩擦角 $ϕ$ 替换为膨胀角 $ψ$ ,即

$\frac{\partial g}{\partial σ_{i j}} = (\frac{\partial g}{\partial I_{1}} \frac{\partial I_{1}}{\partial σ_{i j}} + \frac{\partial g}{\partial J_{2}} \frac{\partial J_{2}}{\partial σ_{i j}} + \frac{\partial g}{\partial θ} \frac{\partial θ}{\partial σ_{i j}}) + (\frac{\partial g}{\partial η_{f}} \frac{\partial η_{f}}{\partial σ_{i j}})$ 。

(28)

式中,

$\frac{\partial g}{\partial I_{1}} = \frac{1}{3} η_{f} h \sin ψ, \frac{\partial g}{\partial J_{2}} = \frac{1}{2} α_{g} K, \frac{\partial g}{\partial θ} = α_{g} J_{2} \frac{d K}{d θ}$ ,

(29)

$\frac{\partial g}{\partial η_{f}} = h (ξ) p \sin ψ$ ,

(30)

$α_{g} = 3 K / \sqrt{3 J_{2} K^{2} + {(e_{f} c \cos ψ)}^{2}}$ 。

(31)

1.4 弹塑性刚度矩阵

根据塑性一致性条件,对于式（13）中的屈服函数,其增量形式满足：

$d f = \frac{\partial f}{\partial σ_{i j}} d σ_{i j} + \frac{\partial f}{\partial h} \frac{\partial h}{\partial ξ} d ξ = 0$ 。

(32)

此外,考虑到应力增量和应变增量满足

$d σ_{i j} = D_{i j k l}^{e} d ε_{k l}^{e} = D_{i j k l}^{e} (d ε_{k l} - d ε_{k l}^{p})$ 。

(33)

根据塑性力学,塑性应变增量可由塑性因子 $λ$ 以流动法则表示为

$d ε_{k l}^{p} = d λ \frac{\partial g}{\partial σ_{i j}}$ 。

(34)

等效塑性剪应变 ${\bar{γ}}^{p}$ 也可以流动法则表示为

$d ξ = d {\bar{γ}}^{p} = d λ \sqrt{\frac{2}{3} dev (\frac{\partial g}{\partial σ_{i j}}) dev (\frac{\partial g}{\partial σ_{i j}})}$ 。

(35)

将式（32）～（35）联立,可解得

$d λ = H^{- 1} \frac{\partial f}{\partial σ_{i j}} D_{i j k l}^{e} d ε_{k l}^{p}$ ,

(36)

$\begin{matrix} H = \frac{\partial f}{\partial σ_{i j}} D_{i j k l}^{e} \frac{\partial g}{\partial σ_{k l}} - \\ \frac{\partial f}{\partial h} \frac{\partial h}{\partial ξ} \sqrt{\frac{2}{3} dev (\frac{\partial g}{\partial σ_{i j}}) dev (\frac{\partial g}{\partial σ_{i j}})} \end{matrix}$ ,

(37)

式中,H为塑性硬化模量。

将式（36）回代入式（33）,可得应变增量与应力增量的一致性表达：

$d σ_{i j} = D_{i j k l}^{e} (d ε_{k l} - d λ \frac{\partial g}{\partial σ_{i j}}) = D_{i j k l}^{ep} d ε_{k l}$ ,

(38)

$D_{i j k l}^{ep} = D_{i j k l}^{e} - H^{- 1} D_{i j p q}^{e} \frac{\partial f}{\partial σ_{p q}} \frac{\partial g}{\partial σ_{m n}} D_{m n k l}^{e}$ ,

(39)

式中, $D_{i j k l}^{ep}$ 即为一致性弹塑性刚度矩阵。

2. 数值算例

基于建立的柱状节理岩体的各向异性弹塑性本构模型,结合FLAC^3D软件对该模型进行了二次开发,并对柱状节理相似结构材料三轴岩石力学试验成果进行了模拟。根据国际岩石力学学会（ISRM）推荐标准,圆柱样直径为50 mm,柱体高度为100 mm,网格数量10000个,底面固定,顶面控制加载速度为5×10^-7 m/s,柱体四周施加固定围压4 MPa。

可由不同空间方向的柱状节理岩体的峰值强度进行拟合确定微结构张量系数。图2给出了强度参数关于方向角的微结构张量参数拟合曲线。

图 2 不同拟合阶数下单轴抗压强度随柱体倾角变化规律

Figure 2. Variation of uniaxial compressive strength under different fitting orders with column inclination

下载: 全尺寸图片幻灯片

为了解释固有的各向异性,假设单轴抗压强度 $f_{c}$ 受样本方向的影响,并结合与式（12）相似的分布函数来描述其变化。为了能反映材料各向异性屈服强度,并防止欠拟合和过拟合,本文采用二阶微结构张量来描述柱状节理岩体强度参数的空间分布屈服函数：

$f_{c} = \hat{f} {1 + A (1 - 3 \cos^{2} β) + b {[A (1 - 3 \cos^{2} β)]}^{2}}$ ,

(40)

式中,

$\hat{f} = 12.76 MPa, A = 1.894, b = 0.3526$ 。

(41)

其余计算参数可根据室内试验曲线^[1]数据,应用单纯形最优化方法在MATLAB中构造寻优函数编程计算得到。模型计算参数如表1所示。

表 1 柱状节理岩体基本力学参数表

Table 1. Mechanical parameters of columnar joints

编号	^#1	^#2	^#3	^#4	^#5	^#6	^#7	^#8	^#9	^#10	^#11	^#12	^#13	^#14	^#15	^#16
参数	E₁/MPa	E₂/MPa	G₁₃/MPa	$v_{12}$	$v_{13}$	c/MPa	$φ$ /(°)	$e_{f}$	$\overset{⌢}{η}$	A	b	$h_{0}$	$h_{1}$	$e_{f}$	B	$θ_{t}$
数值	9.81	22.1	4.69	0.22	0.06	0.72	35.2	0.75	0.23	1.89	0.35	0.77	1.21	0.53	0.0018	25°

下载: 导出CSV

| 显示表格

应用表1给出的力学参数,在FLAC^3D中可以调用自定义本构模型来模拟柱状节理岩体的弹塑性变形行为。数值模拟结果如图3和图4所示。

图 3 三轴数值模拟位移云图（倾角75°,围压4 MPa）

Figure 3. Displacement nephogram by triaxial numerical simulation (angle of 75° and confining pressure of 4 MPa)

下载: 全尺寸图片幻灯片

图 4 三轴试验与模拟结果对比（倾角75°,围压4 MPa）^[13]

Figure 4. Comparison between triaxial test and simulated results (angle of 75°and confining pressure of 4 MPa)

下载: 全尺寸图片幻灯片

本文将柱状节理岩体概化为横观各向同性连续体,建立描述岩体力学特性的宏观本构模型。该模型采用了一种考虑抗拉强度和屈服面角点平滑的修正Mohr–Coulomb准则,将其扩展到了空间各向异性,包含一个各向异性标量参数,该参数用应力和结构取向张量的混合不变量表示。

结果表明,柱体倾角为75°时节理岩体的变形具有明显的方向性,模拟所得应力–应变曲线与试验数据^[13]基本吻合。

应该强调的是,在对问题进行分析时,式（18）中硬化特性仅通过调用一个标量参数B来描述,由于式（18）仅限于硬化状态,不包括应变软化分支。当然也可以采用一种更复杂的方法,并假设这些特征受到围压的影响,然而这样将不可避免地生成一组额外的参数及公式。此外,该方法目的在于研究工程尺度柱状节理岩体的物理力学特性,应用了一种折中的处理策略,当研究尺度较小时,则需要进一步考虑对岩体内部的结构面开展精细模拟。

3. 白鹤滩高坝坝基开挖工程数值分析

3.1 白鹤滩坝区工程地质特征及网格建模

白鹤滩水电站坐落于金沙江下游云南巧家县镜内,是金沙江下游干流河段梯级开发的第二个梯级电站。主坝为混凝土双曲拱坝,最大坝高289 m,计划2022年建设完工。白鹤滩水电站坝区属中山峡谷地貌,坝址为单斜地层,主要为二叠系上统峨眉山组玄武岩,如图5,可分为11个岩流层,岩层走向N30～50°E,倾向SE,倾角15°～25°。岩层岩性主要分为斜斑玄武岩、隐晶玄武岩、柱状节理玄武岩、杏仁状玄武岩、角砾熔岩和凝灰岩等。右岸坡顶顶部出露三叠系下统飞仙关组泥质粉砂岩、粉砂质泥岩及少量砂岩^[2]。其中出露 $P_{2} β_{3}$ 层为柱状节理玄武岩,柱体长度为2～3 m,柱体倾角70°～85°,柱体截面主要为不规则五边形和四边形,截面边长为10～20 cm。柱体内部隐节理发育,开挖前节理闭合紧密^[14]。

图 5 拱坝轴线地质剖面示意图

Figure 5. Illustration of engineering geological section of arch axis

下载: 全尺寸图片幻灯片

图6（a）为开挖模拟所用网格模型,坐标原点位于拱坝轴线,建模范围为1300 m×1500 m×1296 m。在模型局部区域,对单元进行了细化剖分,网格平均边长约为1.5 m。采用Hypermesh剖分三维实体,并形成网格文件,然后将数据转换为相应的软件格式,建立了数值计算网格模型,单元总数145万个,节点26万个。坝基开挖边坡及柱状节理玄武岩体为计算分析重点关注的部位。除了层间错动带,该网格模型还考虑了断层F16、F17,以及柱状节理玄武岩层 $P_{2} β_{3}$ 中的层内错动带LS3319、LS3319-1、RS3315和RS336,如图6（b）所示。

图 6 白鹤滩坝基开挖计算网格模型

Figure 6. Calculation grid model for excavation of foundation of …Baihetan Dam

下载: 全尺寸图片幻灯片

3.2 模型参数及工况设置

对模型前后左右4个侧面施加法向约束,对底面施加x,y,z三向约束作为边界条件。模型自下而上共划分有8个地层,模型计算参数根据工程地质条件和岩石力学参数试验等确定,主要岩体力学参数如表2所示。

表 2 主要岩体基本物理力学参数

Table 2. Basic mechanical parameters of main rock mass

岩层分类	$ρ$ /(kg·m^-3)	E/GPa	$ν$	c/MPa	$φ$ /(°)
C₄层面以上	2700	11.0	0.23	1.10	47.7
C₄~C₃层面	2700	13.2	0.23	1.37	51.8
C_3-1~柱状节理顶面	2600	10.2	0.24	1.07	48.0
柱状节理层	2700	10.0	0.25	0.90	47.7
角砾熔岩层	2600	9.0	0.24	1.08	47.2
微新岩岩层	2850	22.0	0.22	2.10	57.2
C₄	2130	0.4	0.35	0.10	28.0
C₃	2130	0.4	0.34	0.10	28.0
C_3-1	2050	0.7	0.35	0.04	28.0
F₁₆	2130	1.5	0.35	0.20	29.2
F₁₇风化上段	2000	0.7	0.35	0.04	15.6
F₁₇风化下段	2130	1.2	0.35	0.05	20.8
F₁₇微新岩体	2130	2.0	0.35	0.20	29.2
LS₃₃₁	2150	1.5	0.35	0.30	30.0
LS₃₃₁₉	2110	0.3	0.35	0.10	26.0
LS_3319-1	2000	0.3	0.35	0.15	27.0
RS₃₃₆	2000	0.3	0.35	0.15	27.0
RS₃₃₁₅	2000	0.3	0.35	0.15	26.0

下载: 导出CSV

| 显示表格

考虑左右岸坝基岩石工程现场实际施工工序,依照表3对边坡开挖过程设置了10个开挖步。

表 3 模型开挖工况设置

Table 3. Setting of model excavation conditions

开挖步编号	开挖台阶高程	现场开挖完成时间
^#1	左岸800 m	2013.10.24
^#2	左岸700 m	2014.08.19
^#3	右岸800 m	2014.11.10
^#4	左岸650 m	2014.12.03
^#5	右岸700 m	2015.03.30
^#6	右岸650 m	2015.06.24
^#7	右岸600 m	2016.01.27
^#8	左岸600 m	2016.06.03
^#9	600 m高程以下	2016.07.26
^#10	保护层	2016.08.14

下载: 导出CSV

| 显示表格

3.3 计算结果分析

图7为白鹤滩开挖模型左岸坝基不同高程处测点位移变化曲线图。左岸坝基建基面岩体位移随开挖进程逐渐增大；开挖完成时,岩体位移随岩体所在高程减小而先增大后减小,坝基底部柱状节理岩体位移大于上部非柱状节理岩体。

图 7 左岸坝基不同高程处测点位移变化曲线图

Figure 7. Curves of displacement change at measurement points at different elevations of dam foundation at left bank

下载: 全尺寸图片幻灯片

图8为考虑柱状节理岩体各向异性时白鹤滩坝基边坡开挖过程位移变化云图。

图 8 考虑柱状节理岩体各向异性模型开挖过程位移变化云图

Figure 8. Cloud charts of displacement change in excavation process considering anisotropic model of columnar jointed rock mass

下载: 全尺寸图片幻灯片

开挖完成时,建基面最大位移超过50 mm,平均位移为25～40 mm；坝基开挖全过程中,最大位移出现在各开挖步开挖梯段的边坡坡脚及开挖台阶面上；岩体变形范围和变形程度随开挖进程逐渐增大；表层岩体的变形较大,变形程度随岩体深度增加而逐渐减小；岩体变形围绕断层和错动带发展,断层和错动带周围的岩体变形显著大于不含断层和错动带的岩体（实际现场开挖中对坝基出露断层采取了置换处理）。

图9为左岸坝基658 m高程处多点变位计Mzjc-2监测所得位移时程曲线,以及分别采用各向异性模型和各向同性模型计算所得的变形曲线。从图中可以看到,相比于只采用各向同性模型,采用各向异性模型的位移计算结果与现场监测结果更为接近。

图 9 左岸坝基多点变位计Mzjc-2监测结果与计算结果对比

Figure 9. Comparison between monitoring and calculated results of Mzjc-2 multi-point displacement meter

下载: 全尺寸图片幻灯片

表4为坝基开挖完成时刻左岸坝基柱状节理试验区及左岸坝肩下游边坡处多点变位计变形监测结果与数值模型计算结果的对比。

表 4 坝基开挖结束时监测变形与计算位移对比

Table 4. Comparison of monitored deformations and calculated displacements at completion end of excavation of dam foundation

测点编号	监测结果/mm	各向异性模型		各向同性模型
测点编号	监测结果/mm	计算值/mm	误差/%	计算值/mm	误差/%
Mzjc-2	25.4	23.7	6.7	19.2	24.4
Mzjc-3	24.9	21.8	12.4	18.0	27.7
M_ZBJ-3	6.6	5.6	15.2	4.9	25.8

下载: 导出CSV

| 显示表格

结果表明：各向异性模型位移计算误差明显小于各向同性模型,这在柱状节理区域表现更为显著。

为生成质量较高的三维网格模型,本文所用开挖模型中开挖梯段高差（50～100 m）与实际工程施工台阶（5～10 m）存在较大差距,这在模拟计算结果中主要体现在变形的时间节点与实际监测结果存在一定出入。另一方面,本文计算所采用的各向异性弹塑性本构模型不能完整体现节理岩体卸荷松弛的时效性。在后续的工作中,考虑引入各向异性时效损伤以本文的相关工作进一步深化完善。

4. 结论

（1）结合微结构张量理论扩展了经典莫尔库仑模型,完整推导了柱状节理岩体的各向异性弹塑性本构模型。考虑各向异性的本构模型可以直观反映岩体强度的各向异性空间分布,计算所需参数均可由试验结果计算得到。

（2）结合FLAC^3D二次开发接口对自定义本构模型进行了开发。对所开发模型进行了数值验证,数值计算结果与柱状节理相似材料室内三轴压缩试验结果基本一致,表明该模型可以体现柱状节理材料的空间各向异性特性。

（3）应用所开发本构模型对白鹤滩水电站坝基边坡开挖过程进行了模拟。计算结果表明,与未考虑各向异性相比,考虑柱状节理岩体强度各向异性时坝基边坡位移更接近于现场多点位移计监测结果,本文研究工作对白鹤滩水电工程建设有一定参考价值。

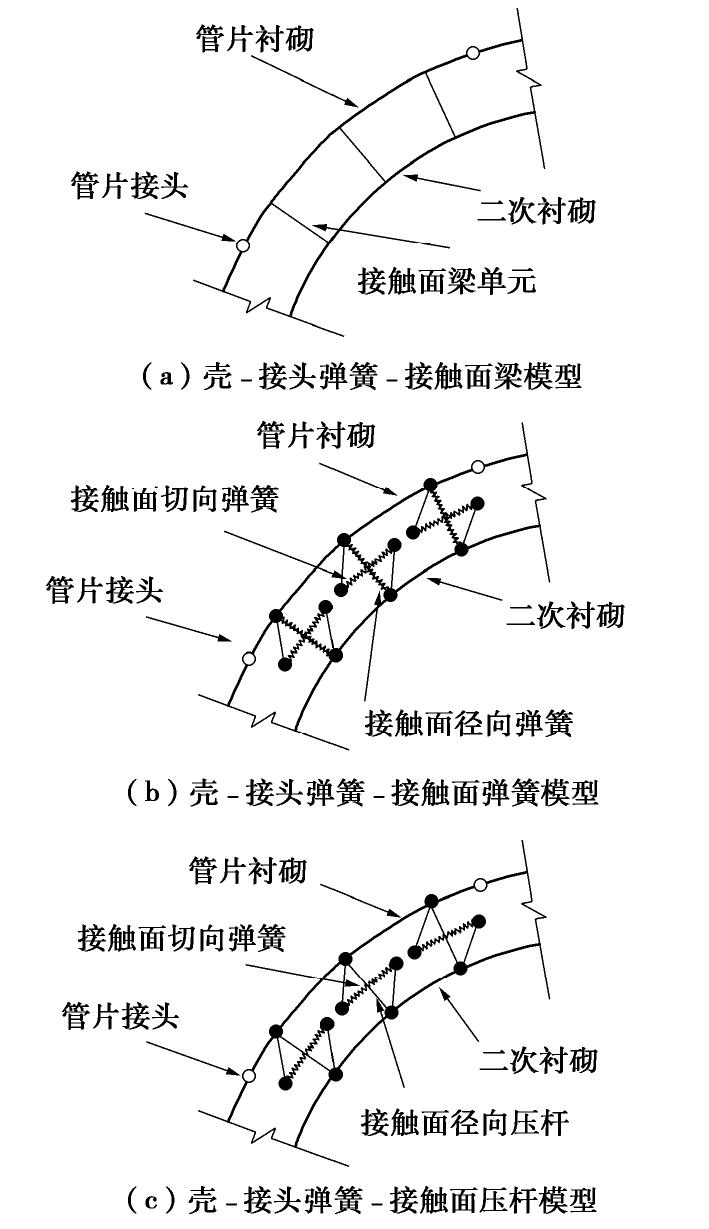
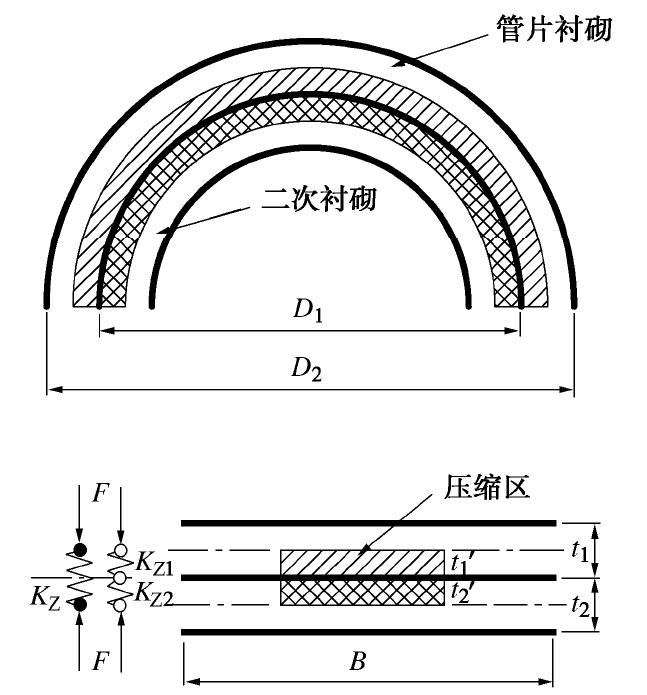
图 1 常用计算模型^[12]

Figure 1. Existing models

下载: 全尺寸图片幻灯片

图 2 狮子洋隧道管片衬砌分块图

Figure 2. Diagram of segment linings of Shiziyang tunnel

下载: 全尺寸图片幻灯片

图 3 双层衬砌模型

Figure 3. Model for double-layer linings

下载: 全尺寸图片幻灯片

图 4 接头处连接弹簧的设置

Figure 4. Setting of springs at joints

下载: 全尺寸图片幻灯片

图 5 两种模型计算结果比较

Figure 5. Comparison of calculated results between two models

下载: 全尺寸图片幻灯片

图 6 衬砌内力取值随k_R0变化规律

Figure 6. Inner forces of structure vs. k_R0

下载: 全尺寸图片幻灯片

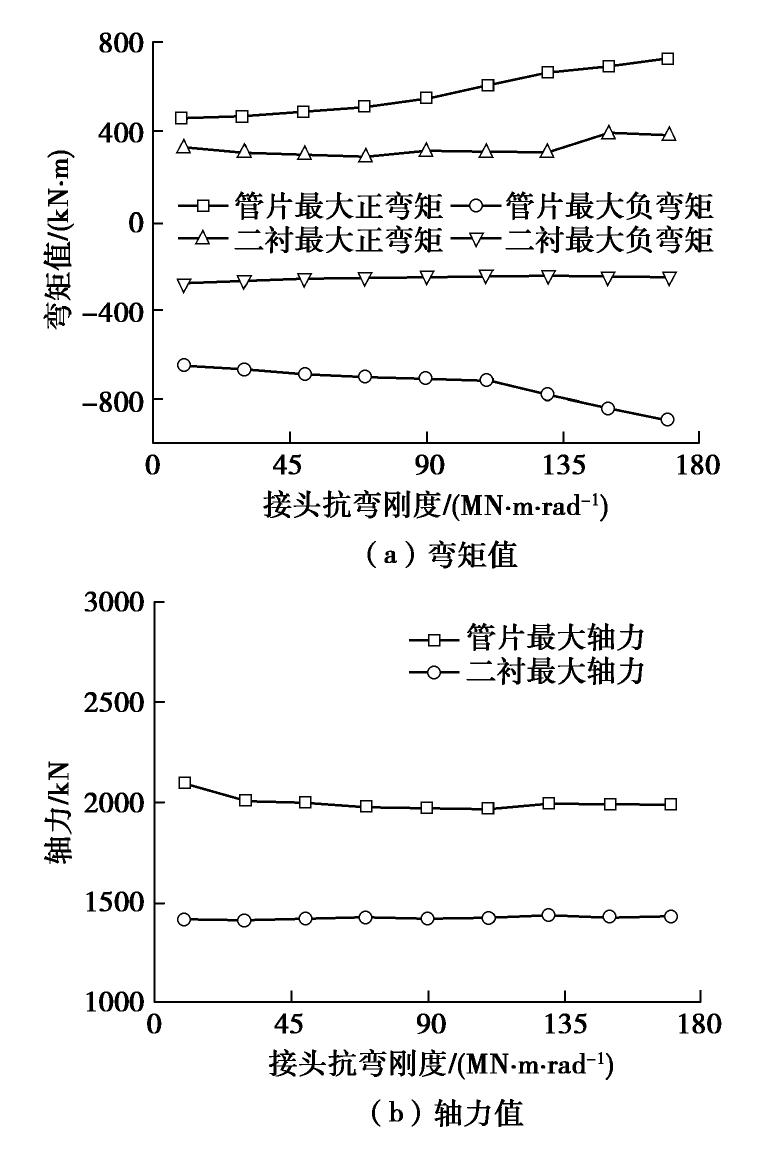
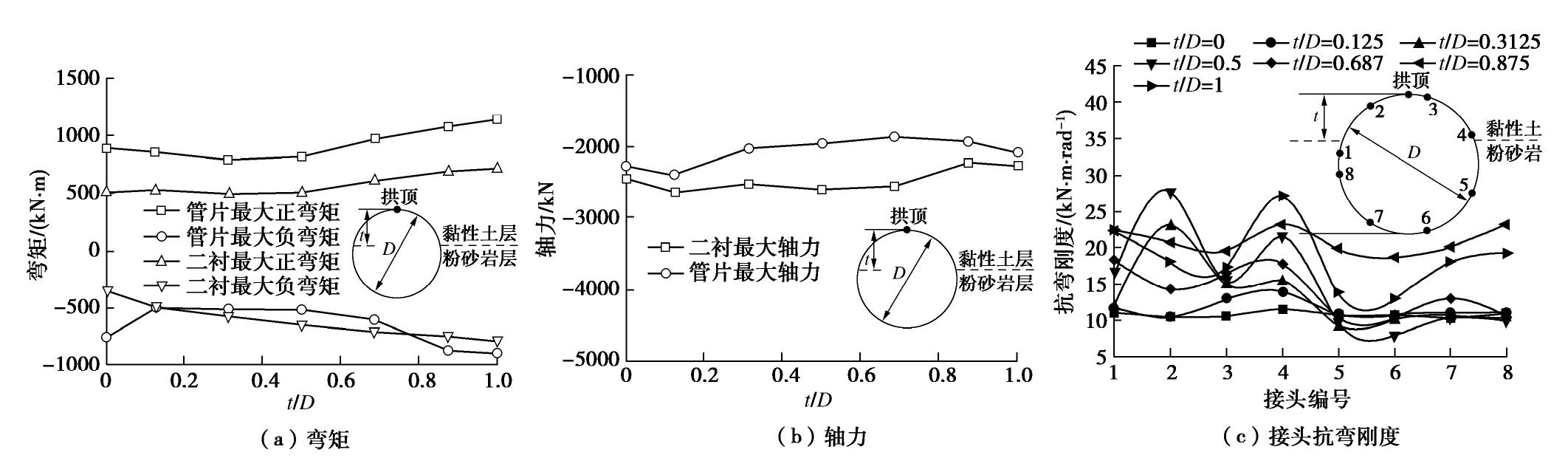
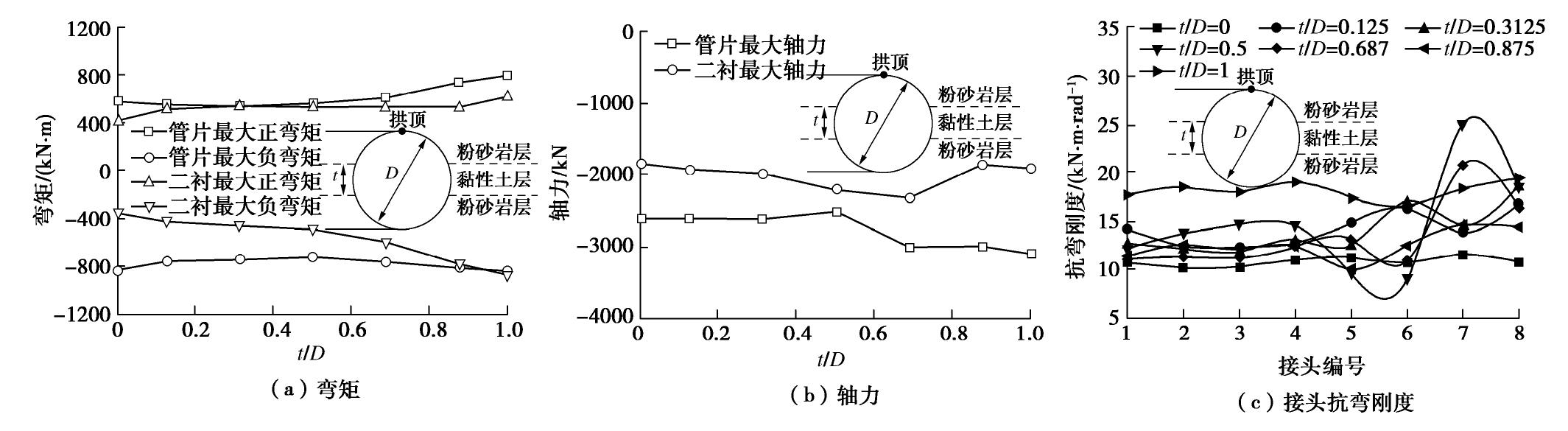
图 7 接头抗弯刚度与内力关系^[16]

Figure 7. Relationship between bending stiffness of joints and internal force

下载: 全尺寸图片幻灯片

图 8 接触面压缩刚度计算示意图

Figure 8. Compression stiffnesses of contact surface

下载: 全尺寸图片幻灯片

图 9 计算流程图

Figure 9. Flow chart of calculation

下载: 全尺寸图片幻灯片

图 10 岩层I计算结果

Figure 10. Calculated results of layer I

下载: 全尺寸图片幻灯片

图 11 岩层II计算结果

Figure 11. Calculated results of layer II

下载: 全尺寸图片幻灯片

图 12 接触面弹簧受力（单位：kN,从左至右为t/D=0,0.5,1）

Figure 12. Forces of springs on interface

下载: 全尺寸图片幻灯片

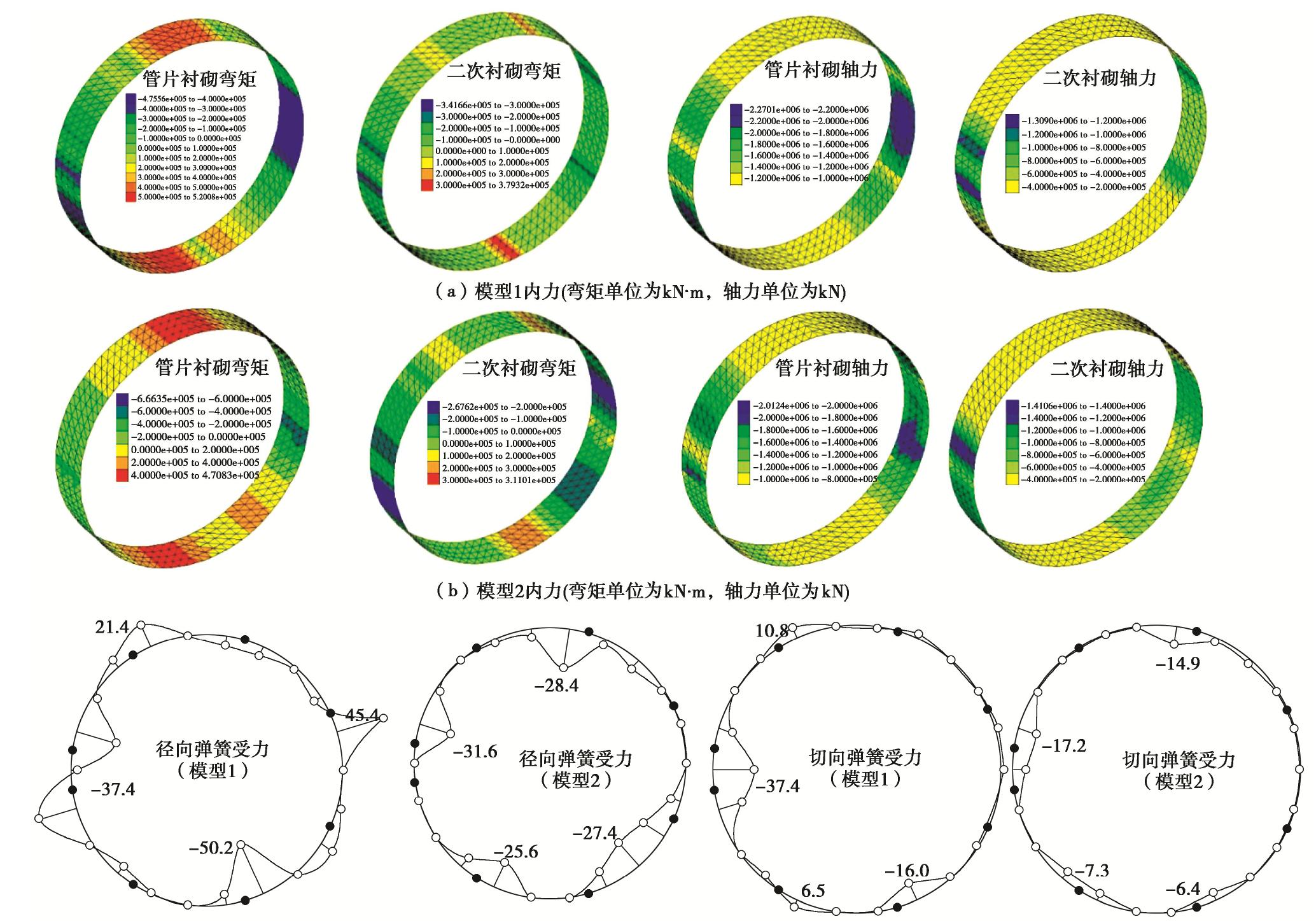
表 1 两种模型内力值

Table 1 Internal forces of two models

项目管片衬砌内力二次衬砌内力
M_max/(kN·m) M_min/(kN·m) N_max /kN M_max/(kN·m) M_min/(kN·m) N_max/kN

模型1 520.08 -475.56 2270.1 379.32 -341.66 1309.0
模型2 470.83 -666.35 2012.4 311.01 -267.02 1410.6

下载: 导出CSV

表 2 地层力学参数

Table 2 Mechanical parameters of strata

类别变形模量E₀/MPa 天然重度γ/(kN·m^-3) 黏聚力c/kPa 内摩擦角φ/(°)

黏性土层 4.6 19.2 17 10.0
泥质粉砂岩层 8820.0 26.5 6270 35.0

下载: 导出CSV

表 3 双层衬砌材料参数

Table 3 Material parameters of two-layer linings

类型混凝土强度等级弹性模量/GPa 密度/(kg·m^-3) 泊松比

管片衬砌 C50 34.5 2450 0.2
二次衬砌 C30 30.0 2450 0.2

下载: 导出CSV

参考文献(22)

[1]	张凤祥, 朱合华, 傅德明. 盾构隧道[M]. 北京: 人民交通出版社, 2004: 1-20. ZHANG Feng-xiang, ZHU He-hua, FU De-ming. Shiled Tunnlling Method[M]. Beijing: China Communications Press, 2004: 1-20. (in Chinese)
[2]	李宇杰, 何平, 秦东平. 盾构隧道管片纵缝错台的影响分析[J]. 工程力学, 2012, 29(11): 277-282. doi: 10.6052/j.issn.1000-4750.2011.04.0239 LI Yu-jie, HE Ping, QIN Dong-ping. Influence analysis on longitudinal dislocation for shield tunnel segment[J]. Engineering Mechanics, 2012, 29(11): 277-282. (in Chinese) doi: 10.6052/j.issn.1000-4750.2011.04.0239
[3]	刘印, 张冬梅, 黄宏伟. 盾构隧道局部长期渗水对隧道变形及地表沉降的影响分析[J]. 岩土力学, 2013, 34(1): 291-304. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201301042.htm LIU Yin, ZHANG Dong-mei, HUANG Hong-wei. Influence of long-term partial drainage of shield tunnel on tunnel deformation and surface settlement[J]. Rock and Soil Mechanics, 2013, 34(1): 291-304. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201301042.htm
[4]	刘曙光. 盾构隧道混凝土管片的承载力退化模型及其试验研究[D]. 南京: 南京航空航天大学, 2012. LIU Shu-guang. Study on Carrying Capacity Deteriorating Model and Experimental Research on Shield Tunnel Concrete[D]. Nangjing: Nanjing University of Aeronautics and Astronautics, 2012. (in Chinese)
[5]	周济民. 水下盾构法隧道双层衬砌结构力学特性[D]. 成都: 西南交通大学, 2012. ZHOU Ji-min. Research on Mechanical Behavior of Double-Layer Lining Strunture for Underwater Shield Tunnel[D]. Chengdu: Southwest Jiaotong University, 2012. (in Chinese)
[6]	晏启祥, 姚超凡, 何川, 等. 水下盾构隧道双层衬砌分析模型的比较研究[J]. 铁道学报, 2015, 37(12): 114-120. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201512021.htm YAN Qi-xiang, YAO Chao-fang, HE Chuan, et al. Comparative study of analysis models for underwater shield tunnel with double linings[J]. Journal of the China Railway Society, 2015, 37(12): 114-120. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201512021.htm
[7]	王国富, 路林海, 唐卓华. 济南地铁盾构隧道管片选型研究[M]//第八届中日盾构隧道交流会论文集. 南京: 河海大学出版社, 2015: 6-15. WANG Guo-fu, LU Lin-hai, TANG Zhuo-hua. Segment selection research on Ji'nan metro shield tunnel[M]//The Eighth China Japan Symposium on Shield Tunnel. Nanjing: Hohai University Press, 2015, 6-15. (in Chinese)
[8]	Working Group No.2, International Tunneling Association. Guidelines for the design of shield tunnel lining[J]. Tunneling and Underground Space Technology, 2000, 15(3): 303-331. doi: 10.1016/S0886-7798(00)00058-4
[9]	地铁设计规范：GB50157—2003[S]. 2003. Code for Design of Metro: GB50157—2003[S]. 2003. (in Chinese)
[10]	赵德安, 雷晓燕, SWOBODA G. 单、双层衬砌隧道的非线性有限元分析[J]. 中国公路学报, 2003, 16(1): 62-67. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200301015.htm ZHAO De-an, LEI Xiao-yan, SWOBODA G. Nonlinear FEM analysis for single and double lining tunnels[J]. China Journal of Highway and Transport, 2003, 16(1): 62-67. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200301015.htm
[11]	晏启祥, 程曦, 何川, 等. 水压条件下盾构隧道双层衬砌力学特性分析[J]. 铁道工程学报, 2010(9): 55-59. https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201009012.htm YAN Qi-xiang, CHENG Xi, HE Chuan, et al. Analysis of mechanical properties of double-layered lining of shield tunnel under water pressure[J]. Journal of Railway Engineering Society, 2010(9): 55-59. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201009012.htm
[12]	姚超凡, 晏启祥, 何川, 等. 一种改进的盾构隧道双层衬砌分析模型及其应用研究[J]. 岩石力学与工程学报, 2014, 33(1): 80-89. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201401009.htm YAO Chao-fan, YAN Qi-xiang, HE Chuan, et al. An improved analysis model for shield tunnel with double-layer lining and its applications[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(1): 80-89. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201401009.htm
[13]	吴全立, 王梦恕, 董新平. 盾构管片接头非线性转动刚度研究[J]. 土木工程学报, 2014, 47(4): 109-114. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201404016.htm WU Quan-li, WANG Meng-shu, DONG Xin-ping. Study on nonlinear rotational stiffness of shield segment joint[J]. China Civil Engineering Journal, 2014, 47(4): 109-114. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201404016.htm
[14]	张冬梅, 樊振宇, 黄宏伟. 考虑接头力学特性的盾构隧道衬砌结构计算方法研究[J]. 岩土力学, 2010, 31(8): 2546-2552. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201008033.htm ZHANG Dong-mei, FAN Zhen-yu, HUANG Hong-wei. Calculation method of shield tunnel lining considering mechanical characteristics of joints[J]. Rock and Soil Mechanics, 2010, 31(8): 2546-2552. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201008033.htm
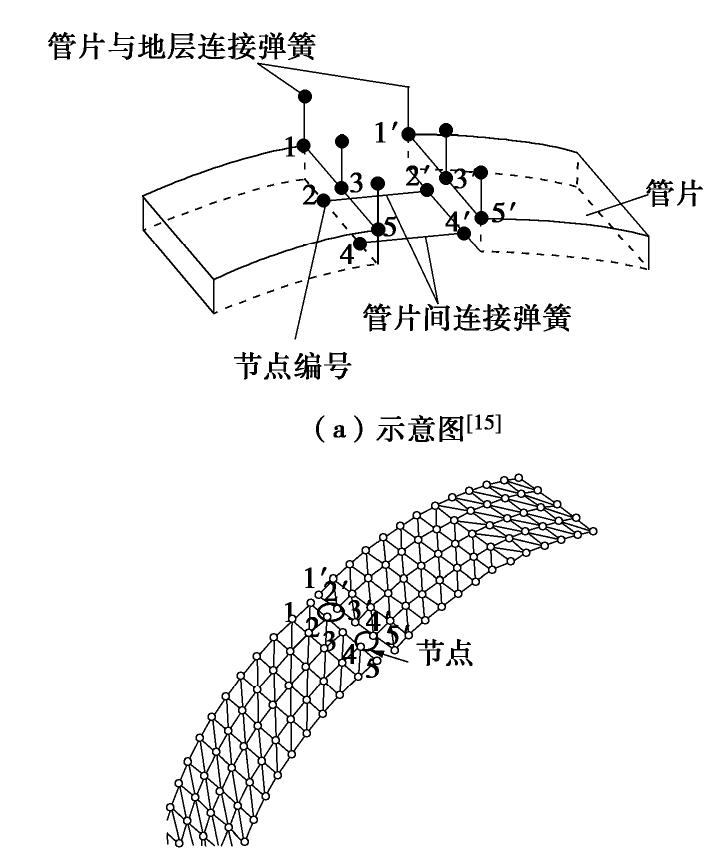
[15]	徐国文, 王士民, 汪冬兵. 基于接头抗弯刚度非线性的壳-弹簧-接触-地层模型的建立[J]. 工程力学, 2016, 33(12): 158-166. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201612020.htm XU Guo-wen, WANG Shi-min, WANG Dong-bing. Shell-spring-contact-ground model based on segment joint stiffness nonlinearity[J]. Engineering Mechanics, 2016, 33(12): 158-166. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201612020.htm
[16]	Itasca Consulting Group. Inc FLAC3D User’s Manual, Version3.0[R]. Itasca Consulting Group, 2004.
[17]	封坤. 大断面水下盾构隧道管片衬砌结构的力学行为研究[D]. 成都: 西南交通大学, 2012: 45-78. FENG Kun. Research on Mechanical Behavior of Segmental Lining Structure of Underwater Shield Tunnel with Large Cross-section[D]. Chengdu: Southwest Jiaotong University, 2012: 45-78. (in Chinese)
[18]	张厚美, 过迟, 吕国梁. 盾构压力隧洞双层衬砌的力学模型研究[J]. 水利学报, 2001, 32(4): 28-33. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200104004.htm ZHANG Hou-mei, GUO Chi, LU Guo-liang. Mechanical model for shield pressure tunnel with secondary linings[J]. Journal of Hydraulic Engineering, 2001, 32(4): 28-33. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200104004.htm
[19]	曾东洋, 何川. 地铁盾构隧道管片接头抗弯刚度的数值计算[J]. 西南交通大学学报, 2004, 39(6): 744-748. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT200406010.htm ZENG Dong-yang, HE Chuan. Numerical simulation of segment joint bending stiffness of metro shield tunnel[J]. Journal of Southwest Jiaotong University, 2004, 39(6): 744-748. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT200406010.htm
[20]	CAVALARO S H P, AGUADO A. Packer behavior under simple and coupled stresses[J]. Tunnelling and Underground Space Technology, 2012, 28: 159-173.
[21]	DO N A, DIAS D, ORESTE P, et al. 2D numerical investigation of segmental tunnel lining behavior[J]. Tunnelling and Underground Space Technology, 2013, 37: 115-127.
[22]	佐久门彰三, 石田智郎. 一次覆工、二次覆工门のせん断特性を考虑したシ一ルドトンネルの轴刚性评价[C]//土木学会论文集, 1990(424): 251-259. SHOZO Saku, Ishida TOMORO. The hgidity of the shield tunnel considering the shear characteristics of the primary lining and the secondary lining[C]//Proceeding of Civil Society, 1990(424): 251-259. (in Japanese)

施引文献(35)

期刊类型引用(24)

1.	夏晶晶，贺姣姣. 基于直剪试验土石混合体路基的稳定性问题研究. 山西建筑. 2025(01): 125-128+172 . 百度学术
2.	郜力君，郝捷. 含石率及坡度对土石混合路堑边坡稳定性的影响分析. 交通世界. 2025(Z2): 154-156 . 百度学术
3.	邹弈，朱碧堂，吴颖彪，周宇航. 断层破碎带黏性夹泥岩体与基岩接触界面大型直剪试验研究. 华东交通大学学报. 2025(01): 45-51 . 百度学术
4.	李利萍，余泓浩，李秋雨，潘一山. 砂岩不同含水特性对超低摩擦效应影响试验研究. 力学学报. 2025(03): 687-700 . 百度学术
5.	程虎，李重情，穆朝民. 冻结温度对不同粒径冻土石混合体劈裂特性的影响. 煤矿安全. 2024(01): 160-166 . 百度学术
6.	代兴先，宋杨，张志彬，齐子怡，刘棋瑞. 土石混合料力学特性和颗粒破碎研究. 河北水利电力学院学报. 2024(01): 1-8 . 百度学术
7.	李慎刚，石云方，刘晋宁，蒋琛. 碎石土路基填料压实及渗透特性. 工程科学学报. 2024(05): 918-926 . 百度学术
8.	SHI Yunfang，LI Shengang，JIANG Chen，LIU Jinning. Gravel hardness effect on compaction characteristics of gravelly soil. Journal of Mountain Science. 2024(04): 1432-1443 . 必应学术
9.	谢周州，赵炼恒，李亮，黄栋梁，张子健，周靖. 基于振动台试验的不同含石率土-石混合体边坡地震动响应差异性研究. 岩土力学. 2024(08): 2324-2337 . 百度学术
10.	王楠楠，高霞，张吉哲，张保勇，吴强. 基于平行黏结模型的含瓦斯水合物煤体宏细观力学性质研究. 煤炭学报. 2024(S1): 314-326 . 百度学术
11.	魏东旭，彭雄志，张佳，范帅，冯瑨. 石灰岩碎石土大型直剪试验研究. 勘察科学技术. 2024(04): 1-5+43 . 百度学术
12.	李刚，尹小涛. 基于数字化施工的山区公路土石混合弃渣工程尺度参数测定方法研究. 水利与建筑工程学报. 2024(06): 76-82 . 百度学术
13.	陈小翔. 碎石土路基填料压实及渗透特性研究. 江西建材. 2024(10): 52-54 . 百度学术
14.	杨忠平，李进，刘浩宇，张益铭，刘新荣. 土石混合体-基岩界面剪切力学特性块石尺寸效应. 岩土力学. 2023(04): 965-974 . 百度学术
15.	刘建平，周花玉，何天奎，余镜南，张坤，潘玉丛，刘泉声. 含根量对根–土石复合体的抗剪强度影响试验初探——以垂丝海棠为例. 岩石力学与工程学报. 2023(S1): 3618-3628 . 百度学术
16.	刘飞禹，孔剑捷，姚嘉敏. 含石量和压实度对格栅-土石混合体界面剪切特性的影响. 岩土工程学报. 2023(05): 903-911 . 本站查看
17.	韩志洋，曹志翔，黄开放. 基于离散元模拟的土石混合体剪切与变形特性研究. 中国农村水利水电. 2023(05): 238-244 . 百度学术
18.	唐丽云，黄涛，汪卫兵，金龙，孙强，李国玉，罗滔. 冻融循环下土石混合体-混凝土界面剪切特性及孔隙结构演化特征试验研究. 中南大学学报(自然科学版). 2023(05): 1954-1969 . 百度学术
19.	张俊云，张乐，高福洲，唐永吉，何卓岭，王鹰. 干湿循环下红层土石混合料强度及变形特性的试验研究. 西南交通大学学报. 2023(06): 1394-1404 . 百度学术
20.	程晓颖，乔婷，秦建敏，季顺迎. 复杂形态碎石颗粒的三维离散元模拟及试验验证. 计算机辅助工程. 2023(04): 40-47 . 百度学术
21.	YANG Zhong-ping，LI Shi-qi，TIAN Xin，HU Yuan-xin，LI Wan-kun. Cumulative damage effect on debris slopes under frequent microseisms. Journal of Mountain Science. 2022(03): 781-797 . 必应学术
22.	崔熙灿，张凌凯，王建祥. 高堆石坝砂砾石料的细观参数反演及三轴试验模拟. 农业工程学报. 2022(04): 113-122 . 百度学术
23.	宋颖能. 朱家涧水库大坝土石方及渗控工程实施探讨. 内蒙古煤炭经济. 2022(08): 160-162 . 百度学术
24.	覃国强. 不同含石率及坡度条件下土石混合体路堑高边坡失稳机制分析. 福建交通科技. 2022(06): 21-25 . 百度学术

其他类型引用(11)

资源附件(0)

图(12) / 表(3)

计量

文章访问数: 232
HTML全文浏览量: 27
PDF下载量: 149
被引次数: 35

0. 引言
1. 各向异性弹塑性本构
1.1 弹性刚度矩阵及空间旋转变换
1.2 各向异性屈服函数及塑性势函数
1.3 屈服函数及塑性势函数求导
1.4 弹塑性刚度矩阵
2. 数值算例
3. 白鹤滩高坝坝基开挖工程数值分析
3.1 白鹤滩坝区工程地质特征及网格建模
3.2 模型参数及工况设置
3.3 计算结果分析
4. 结论

0. 引言
1. 各向异性弹塑性本构
1.1 弹性刚度矩阵及空间旋转变换
1.2 各向异性屈服函数及塑性势函数
1.3 屈服函数及塑性势函数求导
1.4 弹塑性刚度矩阵
2. 数值算例
3. 白鹤滩高坝坝基开挖工程数值分析
3.1 白鹤滩坝区工程地质特征及网格建模
3.2 模型参数及工况设置
3.3 计算结果分析
4. 结论

参考文献(22)

施引文献

资源附件(0)

项目	管片衬砌内力			二次衬砌内力
项目	M_max/(kN·m)	M_min/(kN·m)	N_max /kN	M_max/(kN·m)	M_min/(kN·m)	N_max/kN
模型1	520.08	-475.56	2270.1	379.32	-341.66	1309.0
模型2	470.83	-666.35	2012.4	311.01	-267.02	1410.6

类别	变形模量E₀/MPa	天然重度γ/(kN·m^-3)	黏聚力c/kPa	内摩擦角φ/(°)
类别	黏性土层	4.6	19.2	17	10.0
泥质粉砂岩层	8820.0	26.5	6270	35.0

一种改进的盾构隧道双层衬砌计算模型及其工程应用 English Version

作者简介: 王俊(1987— ),男,四川绵阳人,博士,主要从事隧道设计与科研方面的工作。E-mail：luckywangjun@126.com

通讯作者: 徐国文, E-mail：xgw80033@163.com

计量

出版历程

An improved model for shield tunnels with double-layer linings and its application in engineering

0. 引言

1. 各向异性弹塑性本构

1.1 弹性刚度矩阵及空间旋转变换

1.2 各向异性屈服函数及塑性势函数

1.3 屈服函数及塑性势函数求导

1.4 弹塑性刚度矩阵

2. 数值算例

3. 白鹤滩高坝坝基开挖工程数值分析

3.1 白鹤滩坝区工程地质特征及网格建模

3.2 模型参数及工况设置

3.3 计算结果分析

4. 结论

期刊类型引用(24)

其他类型引用(11)

计量

出版历程

目录

0. 引言

1. 各向异性弹塑性本构

1.1 弹性刚度矩阵及空间旋转变换

1.2 各向异性屈服函数及塑性势函数

1.3 屈服函数及塑性势函数求导

1.4 弹塑性刚度矩阵

2. 数值算例

3. 白鹤滩高坝坝基开挖工程数值分析

3.1 白鹤滩坝区工程地质特征及网格建模

3.2 模型参数及工况设置

3.3 计算结果分析

4. 结论

作者简介:
王俊(1987— ),男,四川绵阳人,博士,主要从事隧道设计与科研方面的工作。E-mail：luckywangjun@126.com

通讯作者:
徐国文, E-mail：xgw80033@163.com