考虑土拱渐进发展的松动土压力研究

雷华阳; 刘旭; 加瑞; 施福硕; 许英刚

doi:10.11779/CJGE202108008

考虑土拱渐进发展的松动土压力研究 English Version

雷华阳^{1, 2,},
刘旭¹,
加瑞¹,
施福硕¹,
许英刚¹

1.
天津大学建筑工程学院,天津　300350
2.
天津大学滨海土木工程结构与安全教育部重点实验室,天津　300350

基金项目:

国家重点研发计划项目课题 2017YFC0805402

土木工程防灾国家重点实验室开放基金项目 SLDRCE17-01

详细信息

作者简介:
雷华阳(1974— ),女,博士,教授,博士生导师,主要从事岩土工程等方面的教学和科研工作。E-mail：leihuayang74@163.com

中图分类号: TU432
计量
- 文章访问数: 493
- HTML全文浏览量: 43
- PDF下载量: 371
出版历程
- 收稿日期: 2020-09-13
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-07-31

Loosening earth pressure considering progressive development of soil arching

1.
School of Civil Engineering, Tianjin University, Tianjin 300350, China
2.
Key Laboratory of Coast Civil Structure and Safety of the Ministry of Education, Tianjin University, Tianjin 300350, China

摘要

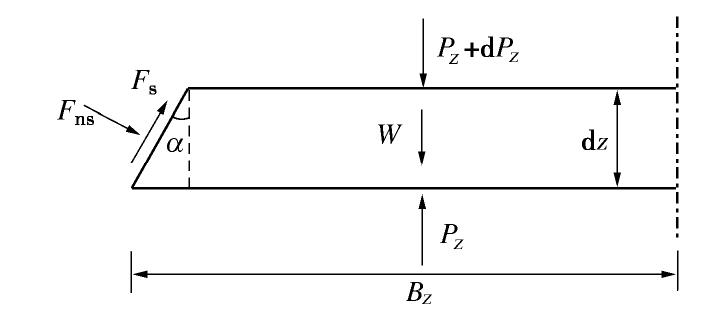
摘要: 结构上方土压力的确定是顶管工程设计和施工中的重要环节,施工中地层损失所引起的上方土体相对滑动使得竖向土压力减小,即形成土拱效应。在Terzaghi松动土压力模型的基础之上,通过水平微分土条的主应力轴偏转角的分析构建了平衡方程,考虑了施工深度以及地层损失对滑移破坏面形态的影响,并利用土拱形成的初始状态和稳定状态的边界条件分别进行了求解计算,分析了土拱效应的渐进发展趋势。经过对比分析,验证了计算模型的合理性,结合顶管施工的实际情况,探究了土体剪胀角和摩擦角对土拱效应的影响,为顶管施工中的土压力计算提供参考依据。
- 松动土压力 /
- 土拱效应 /
- 应力偏转 /
- 渐进发展 /
- 等沉面高度
Abstract: The calculation of the earth pressure on the structure is important for the design and construction of pipe jacking. Due to the ground loss, the arching effect caused by the relative slip between interfaces can relieve the vertical earth pressure. Based on the Terzaghi model, the equilibrium differential equation is established through the principal stress rotation analysis, and the influences of depth and ground loss on the shape of failure plane are studied. The equation is solved under the boundary condition of the initial state and the steady state. Compared with the previous studies, the proposed method is reasonable. According to the actual situation in pipe jacking construction, the effects of the dilatancy angle and friction angle on the arching effect are explored. The results show that the dilatancy angle of the soil has an important influence on the initial shape of the failure surface, and the friction angle affects the stress state and shear strength of the soil, which may provide a reference for the calculation of loosening earth pressure in pipe jacking construction.
- loosening earth pressure /
- soil arching effect /
- principal stress rotation /
- progressive development /
- equal settlement section height

HTML全文

0. 引言

对于饱和砂土地震液化触发判别问题,应用最广泛的Seed简化判别方法主要建立在包含液化宏观震害现象、地震动加速度记录和场地原位测试指标三要素的地震液化实例数据和液化分界线的基础上^[1-3]。以基于原位剪切波速测试指标的液化实例为例,图1给出了地震液化和非液化实例,以及区分液化与否的分界线^[4]。由于强震液化事件彻底破坏易液化土体原有结构性,导致了消除液化土层既往沉积作用的“时钟重置”效应,使得震后获得的场地原位测试指标与真正控制场地抗液化性能的震前土体工程力学特性不对应。考虑到针对地震液化场地的原位测试一般发生在震后数天或数月甚至更长的时间里,图1中地震液化实例数据的剪切波速和相应的液化分界线可能存在与测试时间相关的系统误差。因此,研究震后易液化场地饱和砂土土层的剪切波速（或其它原位测试指标）随时间的变化规律,对正确认识现有基于原位测试指标的液化判别简化方法的可靠性并对震后测试指标进行合理修正具有重要的科学意义。

图 1 基于剪切波速的地震液化实例数据与分界线

Figure 1. v_s-based field case histories and liquefaction boundary curves

下载: 全尺寸图片幻灯片

土体在自然沉积过程中或者经受外荷载剧烈扰动后,其刚度和强度等工程力学参数在恒定应力状态下随时间变化的现象被称为“时间效应”,且该变化可以通过原位测试指标（例如,SPT、CPT和V_s）体现^[5-7]。例如,Andrus等^[8]通过静力触探与剪切波速的经验关系获得了原位砂土剪切波速和完全扰动后剪切波速的比值MEVR,初步揭示了地质时间尺度上的砂土时间效应（见图2）；周燕国等^[9]结合剪切波速（剪切模量）的Hardin公式^[10]和静力触探测试,提出了砂土时间效应的表征指标A_I,并利用不同地质年代砂土实测数据对其表征能力进行了检验。然而,上述研究主要面向地质沉积年代和土性测试指标的经验关系,关注数万年到数十万年甚至更长的地质时间尺度,并没有考虑地质沉积年代中可能受到的各种扰动（如强震事件）对土体工程力学特性的影响。以图2为例,深色椭圆圈内的数据并不符合图中拟合斜线的趋势,而这个时间范围（10^-1～10² a）正是实际工程服役寿命或者高烈度区强震重现周期的范围。Pavlenko等^[11]研究1995年神户地震中场地刚度演化问题,发现液化使得场地刚度急剧降低,但在震后较长一段时间内无法恢复到地震液化前的值。可见,对于实际工程,震后较短的时间尺度内场地土体的时间效应更具有工程意义,是影响易液化场地在余震中的地震响应和再液化可能性的重要因素。

图 2 土体测量与估算剪切波速比的时变趋势

Figure 2. Time variation of measured to estimated velocity ratio

下载: 全尺寸图片幻灯片

针对上述问题,本文对新西兰基督城的REHS强震台站在2010—2011年间的若干强震记录的尾波进行水平与竖向谱比（HVSR）分析,获得了该台站所在的易液化场地在地震前后小应变剪切刚度随时间的发展规律。在此基础上,提出了综合考虑主固结和次固结作用的震后饱和砂土小应变刚度计算模型,并合理预测了REHS台站场地震后刚度恢复变化过程。

1. 场地条件与强震台站记录分析

HVSR方法通过对强震台站的三向加速度记录进行分析得到场地卓越频率以及场地土层结构分布,相比于其它场地频率分析方法,HVSR方法相对简单,能够基本消除震源和传播路径的影响,得到的场地卓越频率更可靠^[12-13]。场地的卓越频率与场地平均剪切波速的关系可表示为^[14]

$v_{savg} = 4 H f$ 。

(1)

式中, $v_{savg}$ 为场地平均剪切波速,H为场地土层厚度,f为场地卓越频率。

根据弹性理论,土体小应变剪切模量表达为

$G_{\max} = ρ \cdot v_{s}^{2}$ 。

(2)

本文针对新西兰基督城CBD区的REHS台站（见图3）,通过触发液化的强震本身和之后发生余震的加速度记录的尾波信号,获得场地卓越频率,根据式（1）,（2）分析从2010年以来3次强震事件之后场地刚度随时间变化规律。REHS台站所处场地的上覆软弱土层厚度约为20 m,存在较厚的饱和粉质砂土层和洁净砂土层,下卧刚度较大的砂卵石层（见图4）,是较典型的易液化场地^[15]。

图 3 基督城REHS强震台站位置（来源：www.nzgd.org.nz）

Figure 3. REHS strong motion station at Christchurch (source: www.nzgd.org.nz)

下载: 全尺寸图片幻灯片

图 4 REHS台站场地土层信息

Figure 4. Soil profile at REHS station site

下载: 全尺寸图片幻灯片

本文采用Geopsy软件进行HVSR分析,该软件能够多窗口同时计算H/V谱比和上覆土层的卓越频率f,并计算它们的平均值和方差。H/V谱比曲线的峰值对应的频率即为该尾波窗口时间对应的卓越频率。图5是尾波窗口选取和计算结果示意图,其中黑色实线代表所有窗口的平均值,两条虚线分别代表它的上、下限,竖向灰色条状区域代表了平均峰值所在的频率段。采用地震动记录的尾波进行HVSR分析获得场地卓越频率需满足一定的条件,即首先要保证主震后的选取的余震强度足够小,一是为了避免该余震事件对场地刚度恢复过程产生额外的显著影响,二是为了尾波段对应场地土体处于小应变弹性应变响应状态；其次,为保证数据处理结果的可靠性,均要求H/V谱比值大于2.0,而且卓越频率的误差在±0.3 Hz以内。

图 5 地震尾波HVSR谱比分析

Figure 5. HVSR analysis of seismic coda wave

下载: 全尺寸图片幻灯片

2. 震后场地小应变刚度演化规律

图6给出了REHS台站场地2010年至2011年间3次强震后场地卓越频率随时间的发展情况。考虑到每次强震事件之后大部分余震在台站的地震动强度都很小,可以忽略其对震后场地的进一步扰动作用。每张图上方的黑色虚线代表2010年9月3日M_w7.2地震事件之前场地的卓越频率（f_i=2.20 Hz）,由2010年大震之前的小震记录进行HVSR分析得到；右上角红色虚线表示强震事件后场地的稳定值,可视为下次强震前的场地卓越频率初始值。由图6可见,每次强震后场地刚度恢复至相对稳定的状态所需要的时间基本一致（为数天到数十天）,而且场地稳定后的卓越频率均值接近但低于最初的水平（即2.20 Hz）。

图 6 震后场地卓越频率时变规律

Figure 6. Evolution of fundamental frequency of earthquake site

下载: 全尺寸图片幻灯片

由图6（b）可见,20110221 M_w6.2地震事件中场地卓越频率受到强余震地震历史的影响,因此图7仅将图6（a）和（c）的归一化场地卓越频率（f/f_i）随时间发展规律归纳在一起。由图7可见,震后场地刚度恢复速率基本一致,呈现对数形式的增长,这与PENG等^[16-17]的研究发现类似。而基督城场地小应变刚度在震后10～100 d会有显著的恢复。根据Downes等^[18]的研究,2010年距上次基督城发生强震液化的时间间隔接近100 a,可以认为基督城典型易液化场地的新近沉积时间（或液化的重现周期）为100 a左右,所以尽管REHS台站场地的砂土层刚度在液化后的数月内会有较大的恢复,但仍小于震前水平。需要指出的是,在基督城的其它强震台站（如CBGS和CCCC台站）场地也观测到了类似规律^[19]。另外,注意到图7中同一时间对应的频率数据存在一定离散性,原因包括：首先,HVSR方法不能完全消除震源及传播路径的影响；其次,地震动加速度信号（尤其是小震事件）信噪比水平不同；再次,地下水位的季节性升降等环境变化带来的可能影响。

图 7 震后场地归一化卓越频率变化规律

Figure 7. Evolution of normalized fundamental frequency of earthquake site

下载: 全尺寸图片幻灯片

3. 饱和砂土震后小应变刚度计算模型

需要注意,Andrus等^[8]将砂土的MEVR参数用于剪切模量的时间效应修正,这种修正主要反映数十万年甚至更久的由于颗粒胶结引起的时间效应,不能合理反映砂土液化后短期内刚度的变化规律（即孔压消散与次固结引起的时间效应）,而大部分震后实例调查的原位测试均是在这一时间段获得的；其次,这种修正对特定地震和场地数据的依赖性较大,数据十分有限,规律的一般性不强。本节基于饱和砂土的主固结与次固结过程,提出了考虑有效应力变化和砂土颗粒间接触力均质化（包括孔隙比变化）这两个主要因素的震后饱和砂土小应变刚度计算模型。

3.1 主固结影响函数

首先考虑由孔压消散和孔隙变化引起的剪切模量增量,可采用Hardin公式表示土体小应变剪切模量与土体孔隙比及有效应力的关系：

$G_{\max} = A \cdot F (e) {({σ^{'}}_{m})}^{n}$ ,

(3)

式中,G_max为砂土小应变剪切模量,A为结构性参数,F(e)为孔隙比方程, ${σ^{'}}_{m}$ 为平均有效应力,n约等于0.5。

平均固结度U通常定义为

$U = \frac{S_{ct}}{S_{c \infty}}$ ,

(4)

式中,S_ct为地基某时刻的主固结变形,S_c∞为地基的最终主固结变形。

根据太沙基一维固结理论,平均固结度U为

$U = 1 - \sum_{m = 1}^{\infty} \frac{2}{M^{2}} e^{- M^{2} T_{v}}$ 。

(5)

式中,竖向固结时间因子T_v为

$T_{v} = \frac{k_{v} t}{H^{2} γ_{w} m_{v}}$ ,

(6)

式中,k_v为土的竖向渗透系数,t为固结时间,H为土层厚度, $γ_{w}$ 为水的重度,m_v为土体体积压缩模量。

设砂土震后初始孔隙比为e₀,主固结完成后孔隙比为e_c∞,固结中土体孔隙比为e_ct,则由式（4）可以得到土体平均固结度：

$U = \frac{e_{0} - e_{ct}}{e_{0} - e_{c \infty}}$ 。

(7)

超静孔压比与砂土有效应力的关系如下：

$1 - r_{u} (t) = {[\frac{{σ^{'}}_{m, t}}{{σ^{'}}_{m,i}}]}^{2}$ ,

(8)

式中, $r_{u} (t)$ 为t时刻砂土的超静孔压比, ${σ^{'}}_{m, t}$ 为t时刻砂土的有效应力, ${σ^{'}}_{m,i}$ 为砂土的初始最大有效应力。

考虑到在主固结阶段砂土剪切模量增长主要由有效应力增加和孔隙比减小引起的,而结构性变化的影响很小。因此本文假设砂土主固结过程中结构性参数A不变,结合式（3）,（7）,（8）得到砂土震后剪切模量随时间的变化函数如下：

$\frac{G_{pc} (t)}{G_{R}} = \frac{F (e_{0} - U e_{0} + U e_{c \infty})}{F (e_{c \infty})} {[1 - \frac{p_{0}}{σ^{'}} (1 - U)]}^{0.5}$ ,

(9)

式中,G_pc(t)为任意固结时刻的砂土小应变剪切模量,G_R为砂土在参考时间时的小应变剪切模量,一般参考时间t_R大于主固结时间t_p。

3.2 次固结影响函数

砂土次固结过程中,颗粒间接触力均质化（包括孔隙比减小）也是引起砂土刚度随时间增长的一个重要因素^[20-21]。本文采用Howie等^[22]基于室内试验提出的经验公式加以描述：

$\frac{G_{sc} (t)}{G_{R}} = 1 + \frac{Δ G}{G_{R}} \cdot \lg (\frac{t}{t_{R}})$ ,

(10)

式中,t为固结时间,t_R为参考时间,G_sc(t)为任意固结时刻的小应变剪切模量,G_sc,R为在参考时间的小应变剪切模量, $Δ G$ /G_sc,R为剪切模量增长速率,对于特定的土体需根据室内固结试验确定。

3.3 饱和砂土震后小应变刚度计算模型

在震后一定的时间段,砂土剪切模量变化受上述两个因素共同影响,本文假设这两种机理相互独立,结合式（9）,（10）得

$\frac{G (t)}{G_{R}} = 1 + \frac{Δ G_{pc} (t)}{G_{R}} + \frac{Δ G_{sc} (t)}{G_{R}}$ 。

(11)

式（11）结合 $G = ρ v_{s}^{2}$ 和 $v_{s} = 4 H f$ 可得到场地卓越频率随随时间发展的函数：

$\frac{f (t)}{f_{R}} = \sqrt{\frac{G (t)}{G_{R}}}$ 。

(12)

根据现有围绕基督城场地的研究成果,式（12）的参数取值如下：该场地上覆软弱土层厚20 m,主要由砂土和粉土组成,排水条件良好^[15]；根据CPT测试的I_c和渗透系数的经验关系^[23]取土层平均渗透系数k_v=2.5×10^-5 m/s；土层的平均压缩模量由动力触探锤击数与压缩模量的经验关系^[24]得到,取E_s=15.0 MPa；土层初始平均超静孔压比取p₀=0.8。另外,假设震后场地刚度需要经历震前同样的沉积时间才能恢复至2010年9月3日强震液化事件之前的震前值,则参考时间取为t_R=100 a。

根据式（12）计算得到基督城REHS台站场地液化后基频随时间的发展规律如图8中的曲线所示,图中上、下两条边界线代表由于参数取值带来的标准差。由图8可见,该计算模型对图6（a）,（c）中的两次强震数据的预测效果较好,能够考虑震后一定时间内饱和砂土刚度的恢复规律。

图 8 震后刚度发展函数预测效果

Figure 8. Prediction of post-earthquake stiffness function

下载: 全尺寸图片幻灯片

4. 结论

为研究震后饱和砂土场地原位测试指标变化规律及其与震前值的差异,本文针对新西兰基督城的典型易液化场地,开展了从实际场地卓越频率监测分析到砂土小应变刚度计算模型的研究。主要结论如下：

（1）针对基督城系列强震,对REHS强震台站记录信号进行HVSR分析,揭示了震后场地刚度整体呈现指数形式的增长规律。场地小应变刚度会在震后经过数天的快速恢复后进入相对稳定的缓慢上升期。对于震前沉积时间较久的场地,场地刚度在震后短时间内难以恢复到震前水平,现有基于震后原位调查获得的液化实例数据应当根据震后原位测试时间进行适当的修正。

（2）假设震后场地刚度需要经历震前同样的沉积时间才能恢复至震前值,基于主固结与次固结过程提出了具有物理意义的饱和砂土震后小应变刚度计算模型,可估算基督城典型易液化场地在强震后平均小应变刚度随时间的发展规律。该计算模型为将特定场地的震后原位测试指标（如剪切波速）修正到对应的震前值提供了一种有效手段。

注意到本文所揭示的震后场地小应变刚度演化规律和所建议的计算模型及参数主要针对新西兰基督城场地,有必要进一步研究更多的其它地震和场地刚度演化规律,并获取各类易液化场地和土体参数,才能为将液化实例中的震后原位测试指标修正到震前原状土的对应值提供定量依据,提高当前基于液化实例调查的地震液化简化判别方法的准确性。

图 1 浅埋条件下滑移破坏面发展示意图

Figure 1. Development of failure surface with shallow burial depth

下载: 全尺寸图片幻灯片

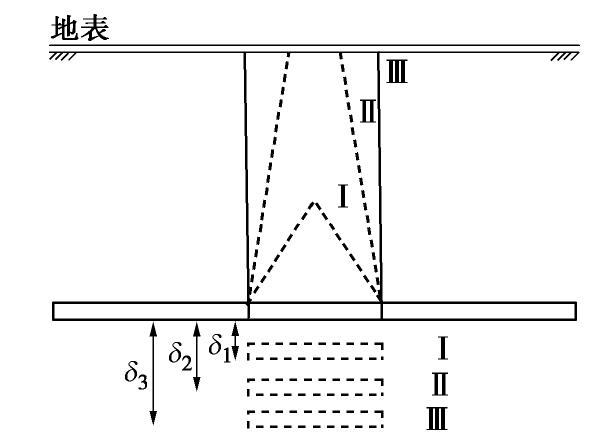
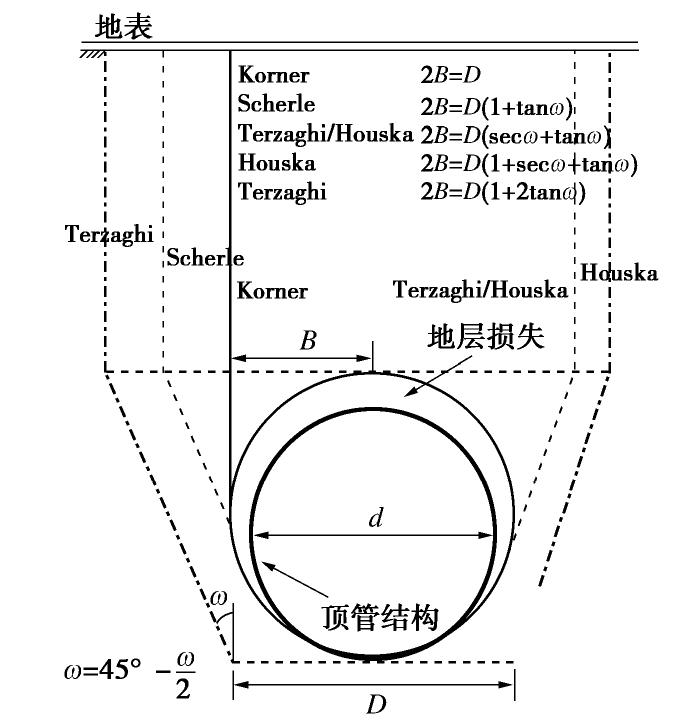
图 2 滑移面的宽度范围（改自文献[28]）

Figure 2. Widths of failure surface in different theories

下载: 全尺寸图片幻灯片

图 3 水平微分土条应力分布图

Figure 3. Distribution of stresses on horizontal soil element

下载: 全尺寸图片幻灯片

图 4 水平微分土条滑移面应力状态

Figure 4. Stresses on failure surface of horizontal soil element

下载: 全尺寸图片幻灯片

图 5 水平微分土条受力分析图

Figure 5. Forces applied to horizontal soil element

下载: 全尺寸图片幻灯片

图 6 滑移破坏面与竖直方向夹角随变形发展关系

Figure 6. Normalized displacement versus angle between failure surface and vertical plane

下载: 全尺寸图片幻灯片

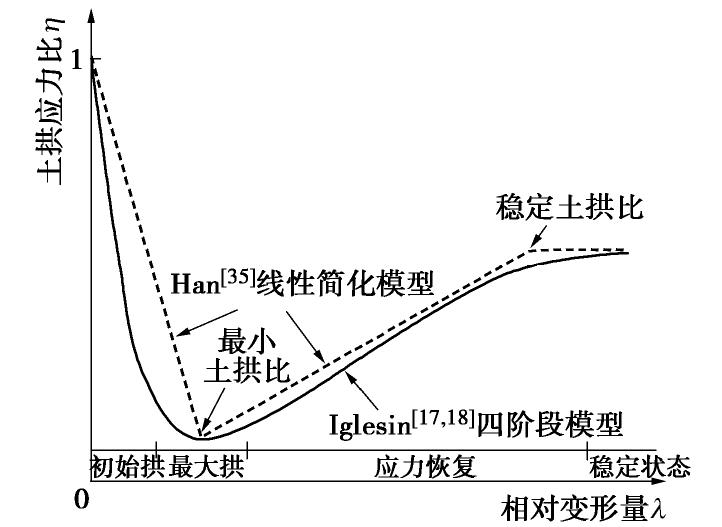
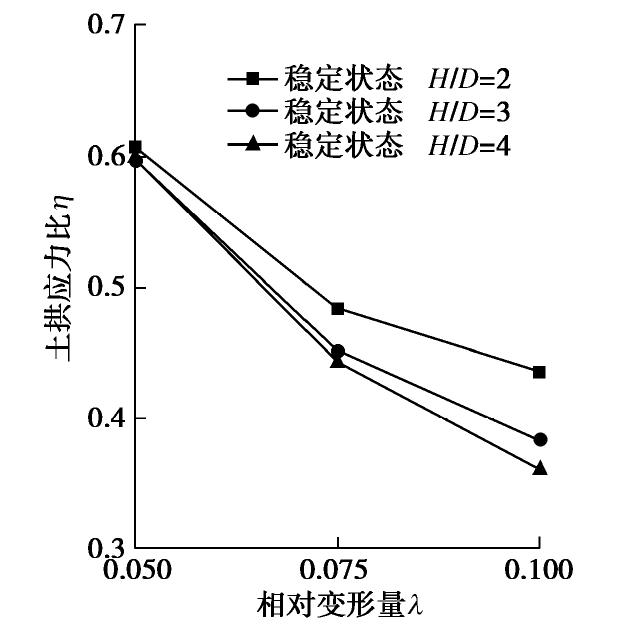
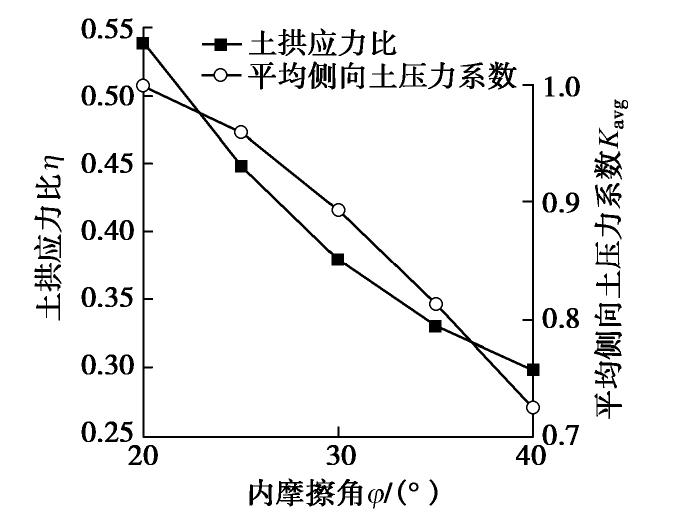
图 7 土拱应力比变化示意图(改自文献[35])

Figure 7. Soil-arching ratio versus normalized displacement

下载: 全尺寸图片幻灯片

图 8 滑移破坏面高度关系示意图

Figure 8. Sketch of failure surface height

下载: 全尺寸图片幻灯片

图 9 干砂试验结果与解析解计算结果对比

Figure 9. Comparison between trapdoor test and calculated results

下载: 全尺寸图片幻灯片

图 10 侧向土压力系数对比

Figure 10. Comparison of coefficients of lateral earth pressure under different internal friction angle

下载: 全尺寸图片幻灯片

图 11 土拱应力比随相对变形量发展

Figure 11. Soil-arching ratio versus normalized displacement

下载: 全尺寸图片幻灯片

图 12 顶管上方平均竖向应力沿深度方向分布

Figure 12. Distribution of mean vertical stress along depth

下载: 全尺寸图片幻灯片

图 13 剪胀角与土拱应力比及平均侧向土压力系数的关系

Figure 13. Influences of dilatancy angle on soil-arching ratio and coefficient of lateral earth pressure

下载: 全尺寸图片幻灯片

图 14 内摩擦角与土拱应力比及平均侧向土压力系数的关系

Figure 14. Influences of internal friction angle on soil-arching ratio and coefficient of lateral earth pressure

下载: 全尺寸图片幻灯片

参考文献(38)

[1]	何君佐, 廖少明, 陈立生, 等. 软土地层管幕群顶进的相互作用及闭合姿态的实测分析[J]. 岩土工程学报, 2020, 42(2): 279-288. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202002012.htm HE Jun-zuo, LIAO Shao-ming, CHEN Li-sheng, et al. Field investigations on interaction between jacking pipes and closure of pipe roofs in soft ground[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(2): 279-288. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202002012.htm
[2]	刘波, 章定文, 刘松玉, 等. 大断面顶管通道近接穿越下覆既有地铁隧道数值模拟与现场试验[J]. 岩石力学与工程学报, 2017, 36(11): 2850-2860. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201711024.htm LIU Bo, ZHANG Ding-wen, LIU Song-yu, et al. Numerical simulation and field monitoring on a large cross-section pipe-jacking underpass traversing existing metro tunnels[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(11): 2850-2860. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201711024.htm
[3]	CUI Q L, XU Y S, SHEN S L, et al. Field performance of concrete pipes during jacking in cemented sandy silt[J]. Tunnelling and Underground Space Technology, 2015, 49: 336-344. doi: 10.1016/j.tust.2015.05.005
[4]	MA B S, NAJAFI M. Development and applications of trenchless technology in China[J]. Tunnelling and Underground Space Technology, 2008, 23(4): 476-480. doi: 10.1016/j.tust.2007.08.003
[5]	杨仙, 张可能, 黎永索, 等. 深埋顶管顶力理论计算与实测分析[J]. 岩土力学, 2013, 34(3): 757-761. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201303024.htm YANG Xian, ZHANG Ke-neng, LI Yong-song, et al. Theoretical and experimental analyses of jacking force during deep-buried pipe jacking[J]. Rock and Soil Mechanics, 2013, 34(3): 757-761. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201303024.htm
[6]	ZHANG H F, ZHANG P, ZHOU W, et al. A new model to predict soil pressure acting on deep burial jacked pipes[J]. Tunnelling and Underground Space Technology, 2016, 60: 183-196. doi: 10.1016/j.tust.2016.09.005
[7]	JANSSEN H A. Versuche uber getreidedruck in silozellen[J]. Zeitschrift des Vereines Deutscher Ingenieure, 1895, 39(35): 1045-1049. (in Deutsch)
[8]	MARSTON A, ANDERSON A O. The Theory of Loads on Pipe in Ditches and Tests of Cement and Clay Drain Tile and Sewer Pipe[R]. Ames: Iowa Engineering Experiment Station, Iowa State College, 1913.
[9]	周敏, 杜延军, 王非, 等. 地层沉陷中埋地HDPE管道力学状态及模型试验分析[J]. 岩土工程学报, 2016, 38(2): 253-262. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201602011.htm ZHOU Min, DU Yan-jun, WANG Fei, et al. Physical modeling of mechanical responses of HDPE pipes and subsurface settlement caused by land subsidence[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(2): 253-262. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201602011.htm
[10]	周敏, 杜延军, 张亚军, 等. 埋地HDPE管道施工过程中土拱效应变化特征研究[J]. 岩石力学与工程学报, 2015, 34(2): 414-424. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201502023.htm ZHOU Min, DU Yan-jun, ZHANG Ya-jun, et al. Variation of soil arching effect during burying process of HDPE pipes[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 414-424. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201502023.htm
[11]	TERZAGHI K T. Theoretical Soil Mechanics[M]. New York: John Wiley & Sons Inc, 1943.
[12]	陈若曦, 朱斌, 陈云敏, 等. 基于主应力轴旋转理论的修正Terzaghi松动土压力[J]. 岩土力学, 2010, 31(5): 1402-1406. doi: 10.3969/j.issn.1000-7598.2010.05.009 CHEN Ruo-xi, ZHU Bin, CHEN Yun-min, et al. Modified Terzaghi loozening earth pressure based on theory of main stress axes rotation[J]. Rock and Soil Mechanics, 2010, 31(5): 1402-1406. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.05.009
[13]	徐超, 张兴亚, 韩杰, 等. 加载条件对土拱效应影响的Trapdoor模型试验研究[J]. 岩土工程学报, 2019, 41(4): 726-732. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201904021.htm XU Chao, ZHANG Xing-ya, HAN Jie, et al. Trapdoor model tests on impact of loading conditions on soil arching effect[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(4): 726-732. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201904021.htm
[14]	朱斌, 陈若曦, 陈云敏, 等. Trapdoor位移相关土压力及抗沉陷加筋设计新方法[J]. 岩土工程学报, 2009, 31(12): 1895-1901. doi: 10.3321/j.issn:1000-4548.2009.12.014 ZHU Bin, CHEN Ruo-xi, CHEN Yun-min, et al. Trapdoor deflection-related earth pressure and new design method of reinforcements to resist local subsidence[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(12): 1895-1901. (in Chinese) doi: 10.3321/j.issn:1000-4548.2009.12.014
[15]	给水排水工程管道结构设计规范：GB50332—2002[S]. 北京: 中国建筑工业出版社, 2002. Structural Design Code for Pipeline Water Supply and Waste Water Engineering: GB50332—2002[S]. Beijing: China Architecture & Building Press, 2009. (in Chinese)
[16]	给水排水工程顶管技术规程：CECS246: 2008[S]. 北京: 中国计划出版社, 2008. Technical Specification for Pipe Jacking of Water Supply and Sewerage Engineering: CECS246: 2008[S]. Beijing: China Planning Press, 2008.(in Chinese)
[17]	IGLESIA G R, EINSTEIN H H, WHITMAN R V. Validation of centrifuge model scaling for soil systems via trapdoor tests[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(11): 1075-1089. doi: 10.1061/(ASCE)GT.1943-5606.0000517
[18]	IGLESIA G R, EINSTEIN H H, WHITMAN R V. Investigation of soil arching with centrifuge tests[J]. Journal of Geotechnical and Geoenvironmental engineering, 2014, 140(2): 04013005. doi: 10.1061/(ASCE)GT.1943-5606.0000998
[19]	EVANS C H. An Examination of Arching in Granular Soils[D]. Massachusetts: Massachusetts Institute of Technology, 1983.
[20]	STONE K J, WOOD D M. Effects of dilatancy and particle size observed in model tests on sand[J]. Soils and Foundations, 1992, 32(4): 43-57. doi: 10.3208/sandf1972.32.4_43
[21]	RUI R, VAN TOL A, XIA Y, et al. Investigation of soil-arching development in dense sand by 2D model tests[J]. Geotechnical Testing Journal, 2016, 39(3): 415-430.
[22]	RUI R, VAN TOL F, XIA X-L, et al. Evolution of soil arching; 2D DEM simulations[J]. Computers and Geotechnics, 2016, 73: 199-209. doi: 10.1016/j.compgeo.2015.12.006
[23]	RUI R, VAN TOL F, XIA Y-Y, et al. Evolution of soil arching: 2D analytical models[J]. International Journal of Geomechanics, 2018, 18(6): 04018056. doi: 10.1061/(ASCE)GM.1943-5622.0001169
[24]	COSTA Y D, ZORNBERG J G, BUENO B S, et al. Failure mechanisms in sand over a deep active trapdoor[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(11): 1741-1753. doi: 10.1061/(ASCE)GT.1943-5606.0000134
[25]	汪成兵, 朱合华. 埋深对软弱隧道围岩破坏影响机制试验研究[J]. 岩石力学与工程学报, 2010, 29(12): 2442-2448. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201012011.htm WANG Cheng-bing, ZHU He-hua. Experimental study of influence mechanism of buried depth on surrounding rock failure of tunnel constructed in soft rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(12): 2442-2448. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201012011.htm
[26]	PAIK K H, SALGADO R. Estimation of active earth pressure against rigid retaining walls considering arching effects[J]. Géotechnique, 2003, 53(7): 643-653. doi: 10.1680/geot.2003.53.7.643
[27]	汪大海, 贺少辉, 刘夏冰, 等. 基于主应力旋转特征的浅埋隧道上覆土压力计算及不完全拱效应分析[J]. 岩石力学与工程学报, 2019, 38(6): 1284-1296. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201906019.htm WANG Da-hai, HE Shao-hui, LIU Xia-bing, et al. A modified method for determining the overburden pressure above shallow tunnels considering the distribution of the principal stress rotation and the partially mobilized arching effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(6): 1284-1296. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201906019.htm
[28]	STEIN D, MÖLLERS K, BIELECKI R. Microtunnelling[M]. Berlin, Germany: Ernest & Sohn, 1989.
[29]	HANDY R L. The arch in soil arching[J]. Journal of Geotechnical Engineering, 1985, 111(3): 302-318. doi: 10.1061/(ASCE)0733-9410(1985)111:3(302)
[30]	徐长节, 梁禄钜, 陈其志, 等. 考虑松动区内应力分布形式的松动土压力研究[J]. 岩土力学, 2018, 39(6): 1927-1934. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201806002.htm XU Chang-jie, LIANG Lu-ju, CHEN Qi-zhi, et al. Research on loosening earth pressure considering the patterns of stress distribution in loosening zone[J]. Rock and Soil Mechanics, 2018, 39(6): 1927-1934. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201806002.htm
[31]	汪大海, 贺少辉, 刘夏冰, 等. 地层渐进成拱对浅埋隧道上覆土压力影响研究[J]. 岩土力学, 2019, 40(6): 2311-2322. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201906031.htm WANG Da-hai, HE Shao-hui, LIU Xia-bing, et al. Studies of the progressive ground arching on the loosening pressure above shallow tunnels[J]. Rock and Soil Mechanics, 2019, 40(6): 2311-2322. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201906031.htm
[32]	赖丰文, 陈福全, 万梁龙. 考虑不完全土拱效应的浅层地基竖向应力计算[J]. 岩土力学, 2018, 39(7): 2546-2554. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201807027.htm LAI Feng-wen, CHEN Fu-quan, WAN Liang-long. Vertical stress calculation of shallow foundations based on partially developed soil arching effect[J]. Rock and Soil Mechanics, 2018, 39(7): 2546-2554. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201807027.htm
[33]	黎春林. 盾构隧道施工松动土压力计算方法研究[J]. 岩土工程学报, 2014, 36(9): 1714-1720. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201409024.htm LI Chun-lin. Method for calculating loosening earth pressure during construction of shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(9): 1714-1720. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201409024.htm
[34]	叶飞, 樊康佳, 宋京, 等. 基于不完全拱效应的隧道预处理机制与计算方法[J]. 岩石力学与工程学报, 2017, 36(6): 1469-1478. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201706018.htm YE Fei, FAN Kang-jia, SONG Jing, et al. The pretreatment mechanism of tunnels and its calculation method based on the incomplete arch effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(6): 1469-1478. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201706018.htm
[35]	HAN J, WANG F, AL-NADDAF M, et al. Progressive development of two-dimensional soil arching with displacement[J]. International Journal of Geomechanics, 2017, 17(12): 04017112.
[36]	SPANGLER M G, HANDY R L. Soil Engineering[M]. New York: Harper & Row, 1982.
[37]	加瑞. 盾构隧道垂直土压力松动效应的研究[D]. 南京: 河海大学, 2007. JIA Rui. Study on Relaxation Effect of Vertical Soil Pressure for Shield Tunnel[D]. Nanjing: Hohai University, 2007. (in Chinese)
[38]	朱伟, 钟小春, 加瑞. 盾构隧道垂直土压力松动效应的颗粒流模拟[J]. 岩土工程学报, 2008, 30(5): 750-754. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200805025.htm ZHU Wei, ZHONG Xiao-chun, JIA Rui. Simulation on relaxation effect of vertical earth pressure for shield tunnels by particle flow code[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(5): 750-754. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200805025.htm

施引文献(2)

期刊类型引用(2)

1.	刘志文，王媛，董琪，高山. 不连续界面渗流的堤防防渗膜防渗效果模拟研究. 人民黄河. 2024(06): 48-53+67 . 百度学术
2.	张升，兰鹏，苏晶晶，熊海斌. 基于PINNs算法的地下水渗流模型求解及参数反演. 岩土工程学报. 2023(02): 376-383+443-444 . 本站查看