Exact integral solutions for one-dimensional thermal consolidation of semi-infinite saturated soils
-
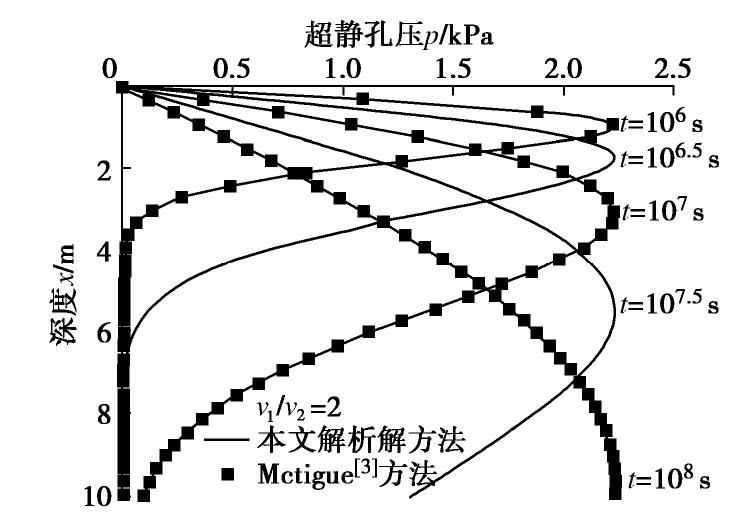
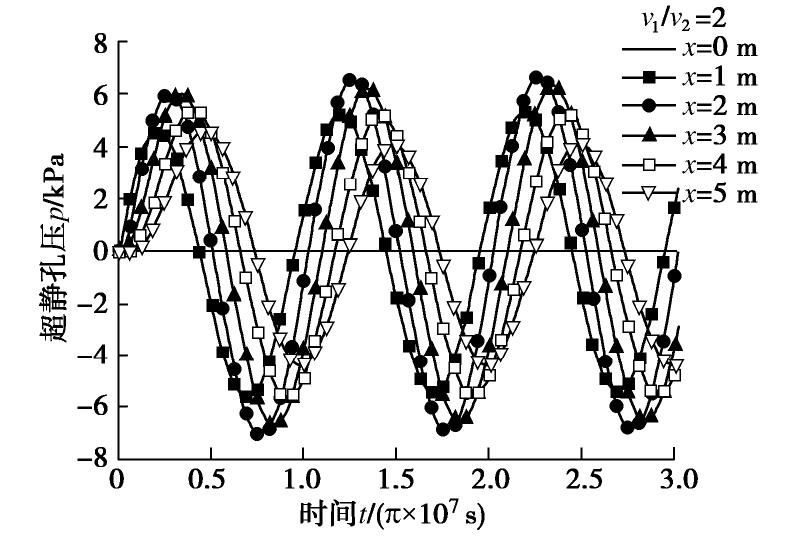
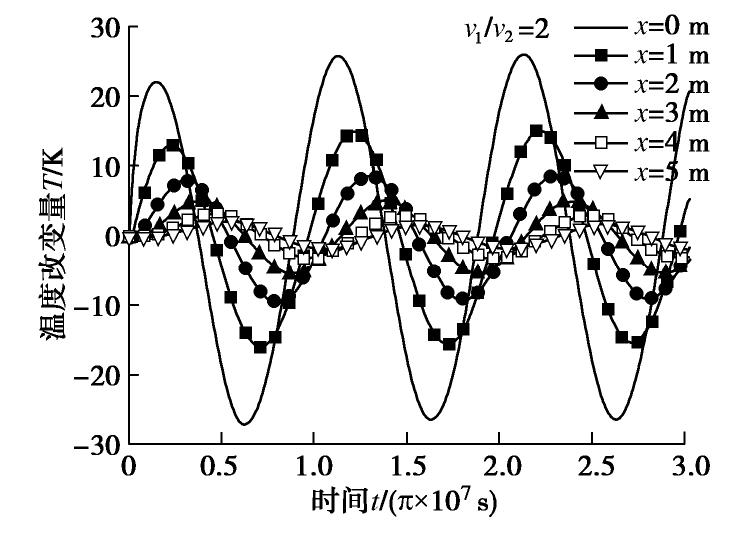
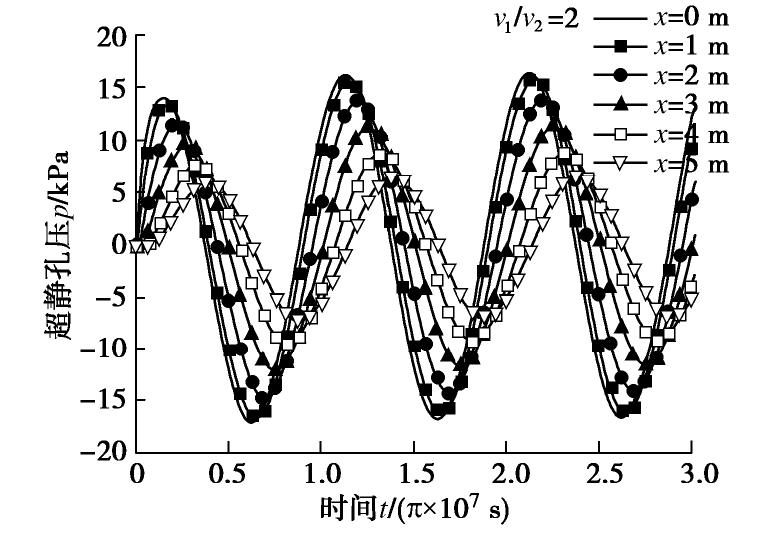
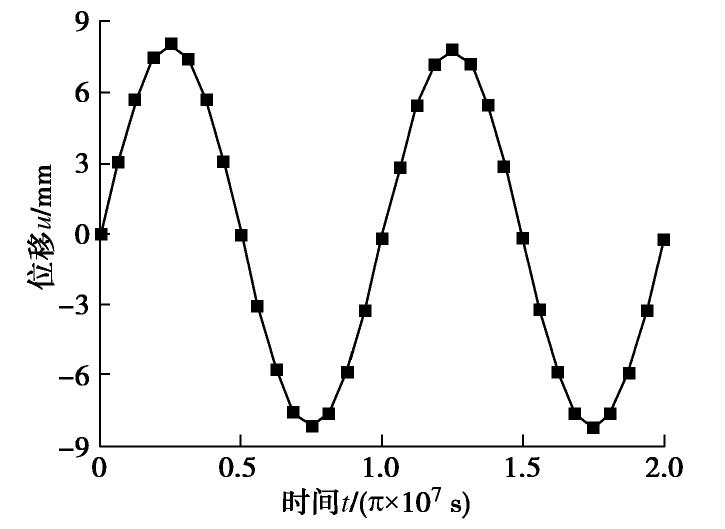
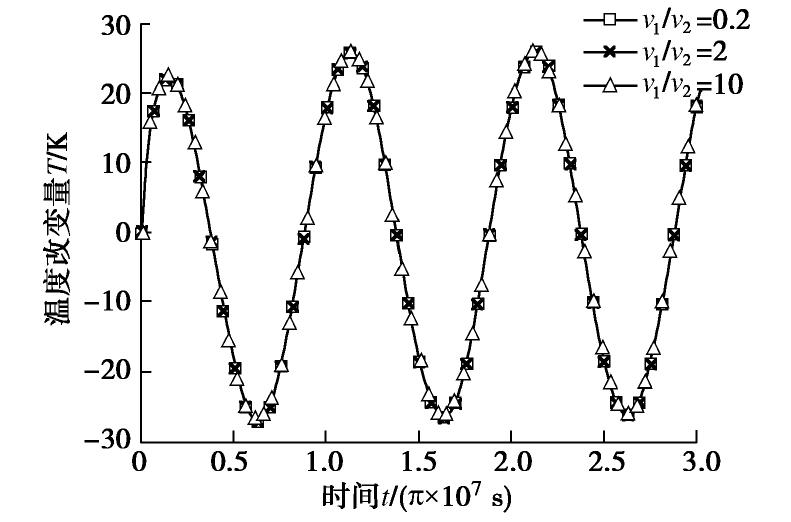
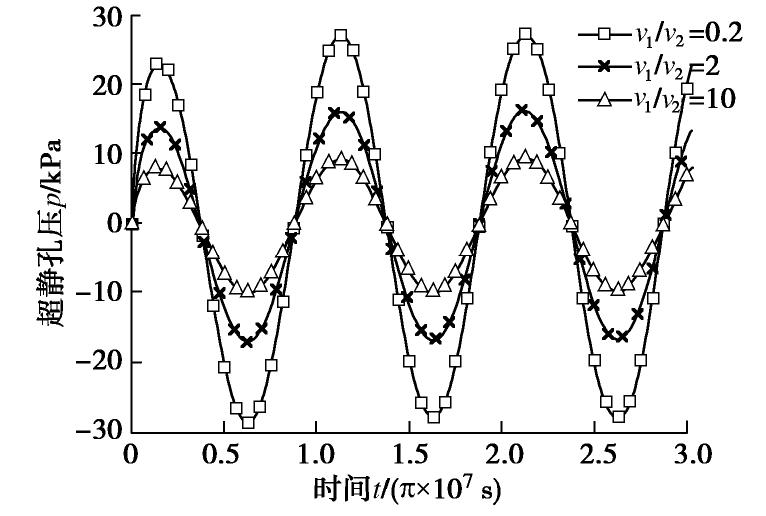
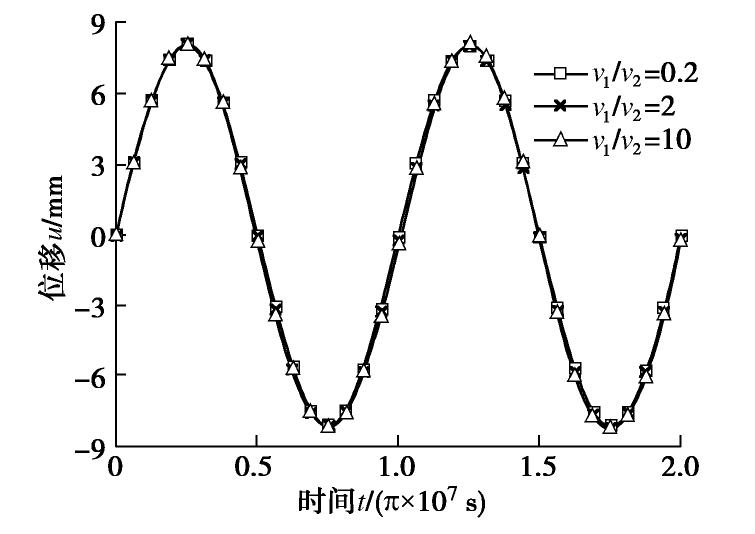
摘要: 基于Coussy提出的饱和多孔介质热–水–力耦合理论,给出考虑热渗效应和等温热流效应的饱和土热固结耦合控制方程,然后通过正弦和余弦变换方法,结合Hamilton-Cayley定理,给出了两类任意非齐次边界条件下,半无限空间饱和土一维热固结精确积分解的求解方法,避免了Laplace变换处理复杂边界问题时的数值反演。最后,通过算例验证了本文解析解的正确性,并分析了半无限空间表面透水或不透水时,饱和土体在季节性温度荷载作用下的温度、超静孔压和位移响应特性。结果表明：温度、超静孔压和位移受季节性温度荷载影响而呈现周期性波动,表面不透水情形的土体超静孔压和位移响应明显高于相应的表面透水情形的土体响应。Abstract: Based on the thermo-hydro-mechanical coupled theory for saturated porous media proposed by Coussy, two coupled governing equations for thermal consolidation of saturated soils are presented, taking thermo-osmosis and thermo- filtration into account. The sine and cosine transforms as well as the Hamilton-Cayley law are used to obtain exact integral solutions for one-dimensional thermal consolidation of semi-infinite saturated soils with two types of arbitrary nonhomogeneous boundary conditions. It helps avoid the errors of numerical inverse Laplace transform when dealing with complex boundary conditions. Finally, case studies are provided to validate the proposed analytical solutions and to investigate the thermal responses of saturated soils with seasonal thermal loads on the permeable or impermeable surface. The results show that temperature change, excess pore water pressure and displacement all fluctuate periodically due to seasonal thermal loads. The responses of the excess pore water pressure and displacement of the saturated soils with an impermeable surface are much higher than those with a permeable surface.
-
0. 引言
随着基坑工程建设不断发展,基坑设计理论和施工技术也在不断完善。然而目前的基坑设计仍然存在着基于二维剖面进行设计,而未考虑空间效应,未考虑实际施工中不利因素等问题。
在深基坑工程不断发展的同时,基坑垮塌事故也时有发生,其中不乏由于施工中超挖而导致基坑大范围垮塌的案例。如某基坑护坡桩由于在施工过程中开挖到坑底时未施工锚杆导致基坑发生倾覆失稳破坏[1]；2001年上海市静安区某复合土钉支护基坑由于连续的两次严重超挖导致连续两次的事故,最终导致周边建筑物大面积开裂,造成严重的经济损失[2]；2008年杭州地铁湘湖站北2基坑由于超挖导致连续垮塌事故[3-4]；2009年上海宝山区某基坑由于贴边局部超挖导致围护结构发生“踢脚”破坏[5]。
从上述事故中可以看出,超挖可能会导致基坑发生多种形式的失稳破坏,为此,众多学者展开了一系列研究。Itoh等[6]通过离心机试验表明超挖会使桩锚支护体系锚杆受力过大导致锚头断裂进而产生倾覆破坏。Tan等[7]通过统计基坑监测数据指出正常开挖阶段,一旦超过正常开挖深度,超挖区地连墙最大水平变形将会骤增。黄天明[8]通过试验及数值模拟研究了悬臂排桩支护基坑中,超挖对支护桩连续破坏的作用机理。
基坑连续破坏方面,Choosrithong等[9]研究表明减小地连墙的嵌固深度会导致连续破坏发生前允许内支撑失效的数量减小,即降低了支护结构的冗余度。程雪松等[10-11]通过模型试验及数值模拟对悬臂排桩由局部少数支护桩破坏引发邻近支护桩依次连续出现受弯破坏（弯曲型连续破坏）的机理进行了研究。郑刚等[12-13]对内支撑支护结构及锚杆支护结构由于结构强度不足引发的连续破坏机理进行了研究。
纵观出现的事故垮塌案例及已有研究,对于基坑局部超挖引发局部倾覆破坏进而导致倾覆型连续破坏的过程及机理尚缺乏研究。为此本文以杭州某工程事故为背景展开研究,首先基于实际工程建立三维有限差分模型,对局部超挖引发大范围倾覆的机理进行了分析,提出了倾覆型连续破坏的评价指标,同时对冠梁对连续破坏的影响进行了讨论,进而探究了坑外超载和土体扰动等因素对倾覆型连续破坏的影响。
1. 某倾覆型连续破坏事故介绍
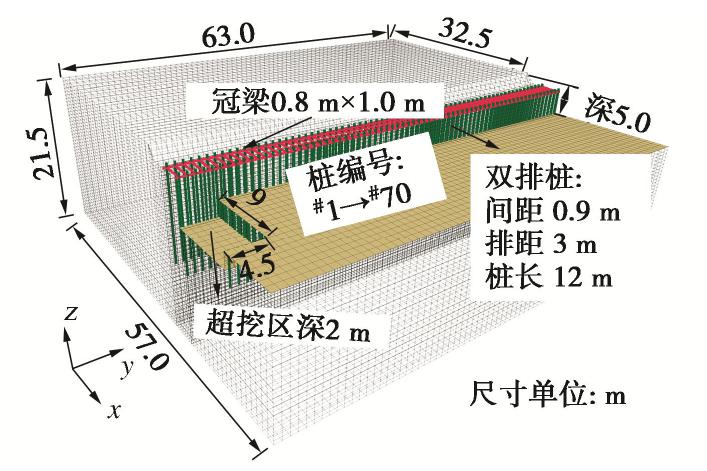
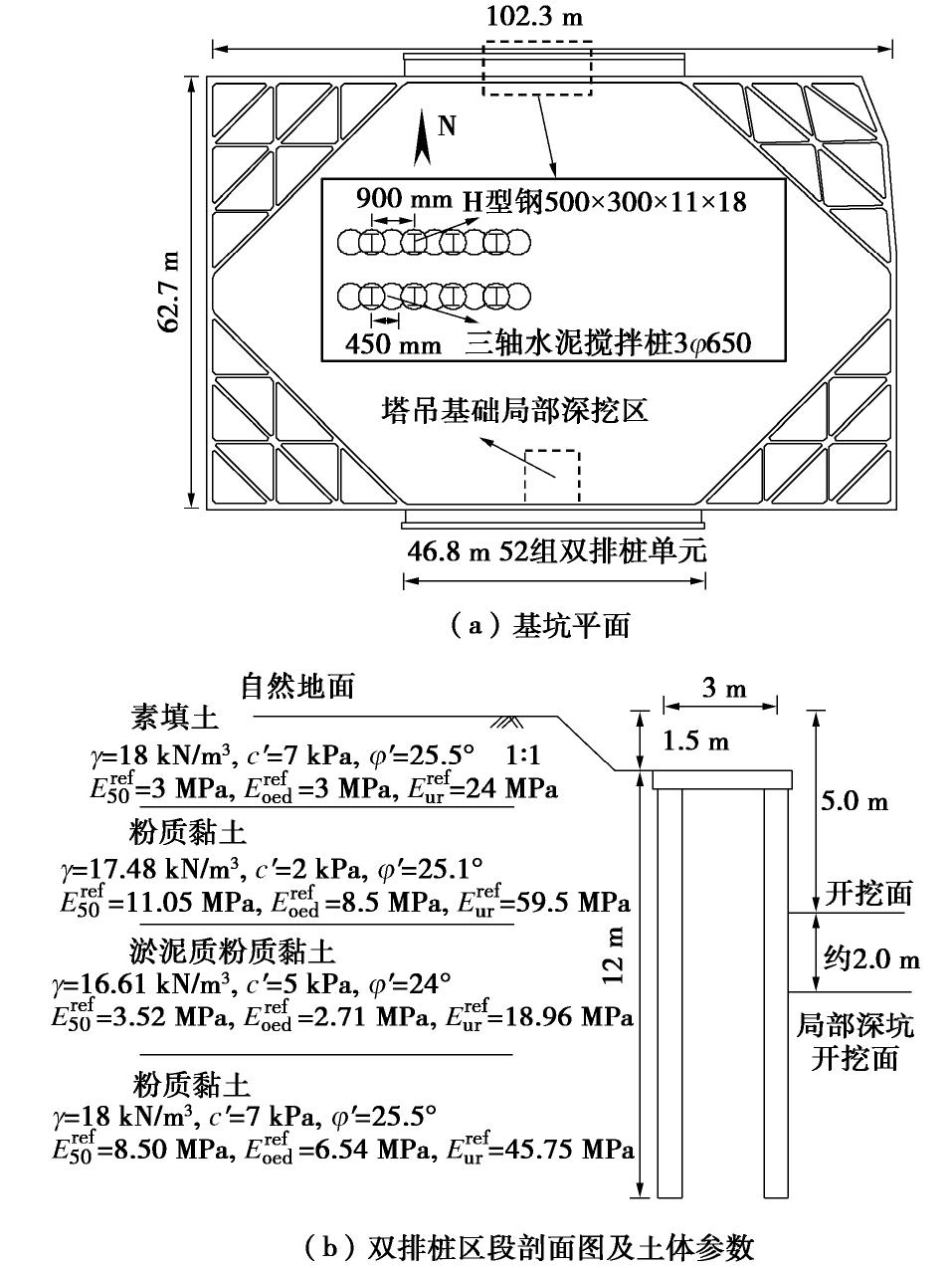
某工程基坑采用SMW工法单排桩和双排桩结合的方式进行支护,其中基坑长边中部采用双排桩,长边角部附近采用单排桩联合角撑的支护形式。基坑平面图及双排桩区段剖面图如图1所示。
![]()
图 1 基坑平面、双排桩剖面及土体参数[14]Figure 1. Plan view of excavation, section of double-row pile retaining structure and soil properties事故发生时,如图2所示,基坑南侧中部局部超挖处及临近较大范围双排桩向坑内倾覆,产生较大变形,桩后地表土体下沉,地面出现多处裂缝。事故调查发现,坑外有大量钢筋堆放及运行的车辆会形成超载并且车辆行驶会对坑外土体造成扰动；紧邻坑边有一塔吊井,形成“坑中坑”,而此深约2 m的塔吊基础基坑位置的支护结构并未进行专门设计,形成“超挖”,此外塔吊运行可能对坑内坑底以下土体产生扰动。调查组针对以上现象并结合当地土质条件,初步判断基坑事故形式为倾覆失稳破坏。
2. 有限差分数值模型
2.1 数值模型建立
为研究此双排桩基坑在沿基坑长度方向上支护结构产生倾覆型连续破坏机理,以上述案例基坑南侧双排桩支护结构为原型,以局部塔吊深坑中部为对称面,根据对称性建立如图3所示的模型,模型尺寸为57 m×63 m×21.5 m。模型在4个竖直边界约束法向位移,在模型底部边界约束水平和竖向位移,设置地下水位位于自然地面下2 m深度处。双排桩中,定义靠近坑内侧的桩为前排桩,坑外侧桩为后排桩,前后排桩均设置70根桩,根据距离对称面的远近,设编号为#1～#70。
如图1所示,实际工程中,基坑南侧双排桩部分一半模型仅有26组双排桩单元,然而此处为研究双排桩连续破坏,对模型进行了扩大,设置70组双排桩单元。同一排桩桩顶设有冠梁,工程中前后排桩采用0.2 m厚的混凝土盖板连接,根据绕y方向抗弯刚度等效原则,将双排桩之间的连接等效为0.9 m×0.2 m的连梁。基坑大面积开挖深度为5.0 m,塔吊基础位置局部深坑平面尺寸假定为9 m×9 m,深度假定为2 m,即总深度7.0 m,此“坑中坑”采用拉森钢板桩支护。
2.2 土体及结构参数
本文模型中土体采用Plastic-hardening硬化模型,支护桩深度范围内的土层分布及土体参数见图1。土体参数依据勘察报告结合已有参考文献[14]综合选取。
在模型中,支护桩、冠梁和连梁分别采用Pile、Beam单元进行模拟。支护桩为SMW工法桩,工字钢为主要受力构件,弹性模量取为200 GPa,泊松比为0.3；冠梁和连梁单元材料均为钢筋混凝土,弹性模量为30 GPa,泊松比为0.2。由于支护桩为SMW工法桩,因此模型中对前、后排桩桩后部分土体强度进行加固,以模拟SMW工法中的水泥搅拌桩。
2.3 模拟方法
模拟采用将Zone单元删除的方式模拟土体开挖过程,开挖分为大面积开挖5.0 m和局部超挖2.0 m两步进行,其中大面积开挖即对整个基坑进行开挖,局部超挖仅对超挖区内土体进行开挖。
大面积开挖采用静力计算模式,重点关注开挖完成后基坑位移与桩身内力,局部超挖采用显式动力模拟方法,重点研究在超挖过程中桩身受力及变形的变化情况。显式动力计算时模型采用局部阻尼,阻尼比近似取为10%[11],局部阻尼系数为0.314。由于此动力计算不涉及动力加载,在边界不会发生动力波的反射,因此可保持静力边界条件。
3. 超挖引发的变形及内力分析
3.1 基坑位移分析
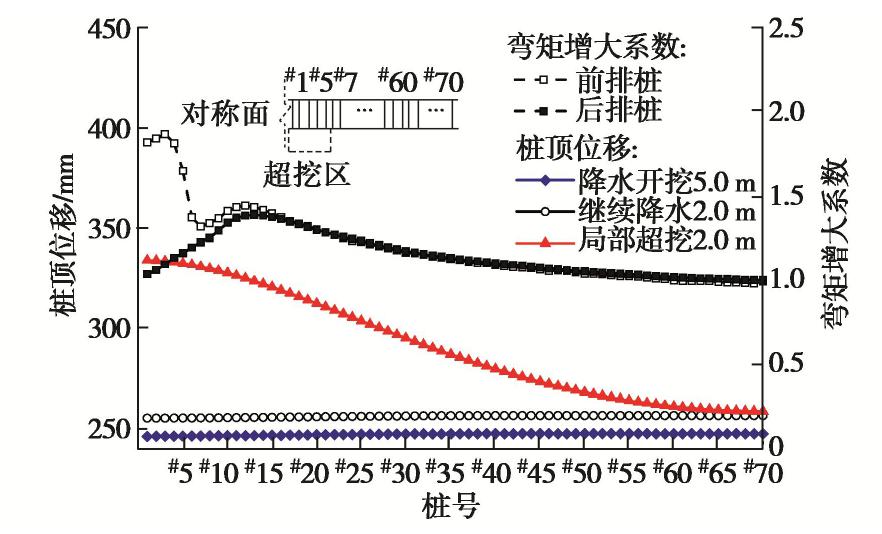
图4为模型中前排桩桩顶位移沿桩号变化规律曲线,可以看出超挖区中心#1桩桩顶位移增加最大,距离超挖区越远,支护桩位移增加越小,与实际垮塌案例中类似。超挖使超挖区内及超挖区外一定范围内支护桩位移显著增加,形成倾覆破坏。可见,支护桩倾覆并非局限于超挖范围内,而是会对邻近支护桩产生影响,形成倾覆型连续破坏。在此模拟中,局部超挖引起支护桩位移增大的影响范围约为60组双排桩单元,影响范围较大。实际工程案例中由于有坑角处水平角撑的支护作用,使单排桩区段受到超挖的影响相对较小,而双排桩区段均出现一定程度倾覆。
![]()
图 4 桩顶位移与弯矩增大系数随桩号变化曲线Figure 4. Curves of displacement at pile top and load transfer coefficient3.2 支护结构内力分析
参考文献[11],将局部超挖产生的弯矩（荷载）增大系数Im定义为局部超挖后桩身最大弯矩与大面积开挖后桩身最大弯矩的比值。图4为本工程中局部超挖导致的桩身弯矩增大系数随桩号变化曲线。局部超挖使前后排桩最大弯矩上升,对于前排桩的影响大于后排桩,且越靠近超挖区域中心,前排桩弯矩增大系数越大。在超挖区外,前后排桩弯矩增大系数先上升后下降。在模型边缘弯矩增大系数约为1,表明桩身最大弯矩在此处几乎不受影响。
由于前后排桩均使用500×300×11×18的H型钢,由钢结构设计规范[15]进行钢梁抗弯承载力计算,设计值为545 kN·m,数值模拟计算出的超挖后支护结构弯矩最大值为366 kN·m,远小于极限承载力,因此支护桩理论上不会发生弯曲破坏。事故中出现的大面积垮塌不是由于超挖产生的支护桩弯曲型连续破坏,因此与案例调查结论一致,此基坑垮塌中支护结构发生了倾覆型连续破坏。
根据本案例的冠梁配筋图及混凝土设计规范[16]可以得到冠梁受弯承载力及受剪承载力设计值分别为651 kN·m和841.5kN。在超挖过程中冠梁的弯矩及剪力的最大计算值分别为424 kN·m和551 kN,因此本案例超挖中不会发生冠梁的受弯及受剪破坏。
4. 不考虑冠梁荷载传递作用时超挖引发的倾覆连续破坏分析
4.1 不考虑冠梁荷载传递作用的抗倾覆稳定状态值
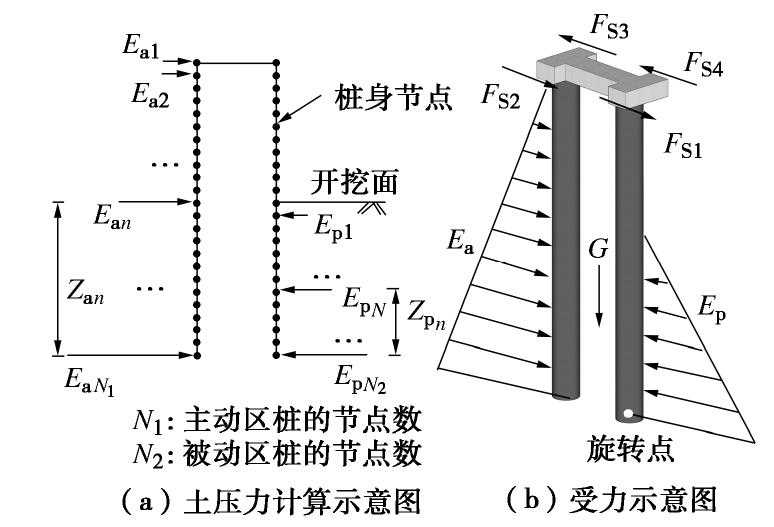
建筑基坑支护技术规程[17]规定双排桩支护结构抗倾覆安全系数KQ的表达式为
, (1) 式中,Epk,Eak,G分别为被动土压力和主动土压力的合力、双排桩间土体重力合力,Zp,Za分别为被动土压力的合力和主动土压力的合力到桩底的垂直距离,ZG为重力合力到前排桩底的水平距离。
规程所定义的抗倾覆安全系数代表的是支护结构在主被动区土压力均达到极限状态时发生倾覆破坏的判断指标。实际工程中,基坑开挖即导致桩身发生向坑内的微小倾覆变形,但主被动土压力并非同时达到,达到被动土压力的变形要远大于主动土压力[18]。事实上,在基坑开挖后的任一时刻,主被动区土压力对桩产生的力矩不断调整直至稳定,可见,支护结构的倾覆稳定指标应是动态变化的,因而抗倾覆安全系数无法对支护结构的实时倾覆稳定状态做出判断。
参考式（1）定义支护结构随时间变化的抗倾覆稳定状态值KO(t)（以下简称稳定状态值）,如图5和下式所示：
, (2) 式中,
, 分别为t时刻作用在节点n上的主被动区土压力的合力。由式（2）计算得到稳定状态值小于1则代表此时支护桩趋于向坑内的倾覆转动,等于1则表示支护桩保持稳定。 4.2 超挖前后支护桩主被动区土压力变化
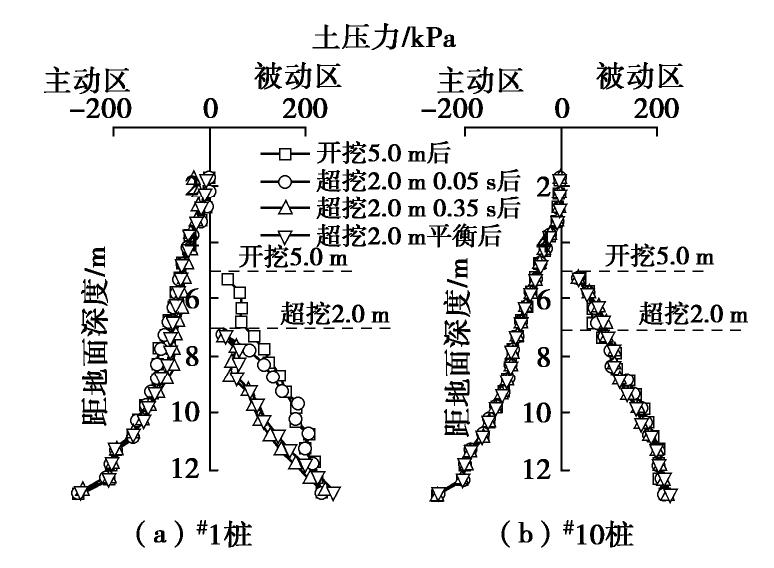
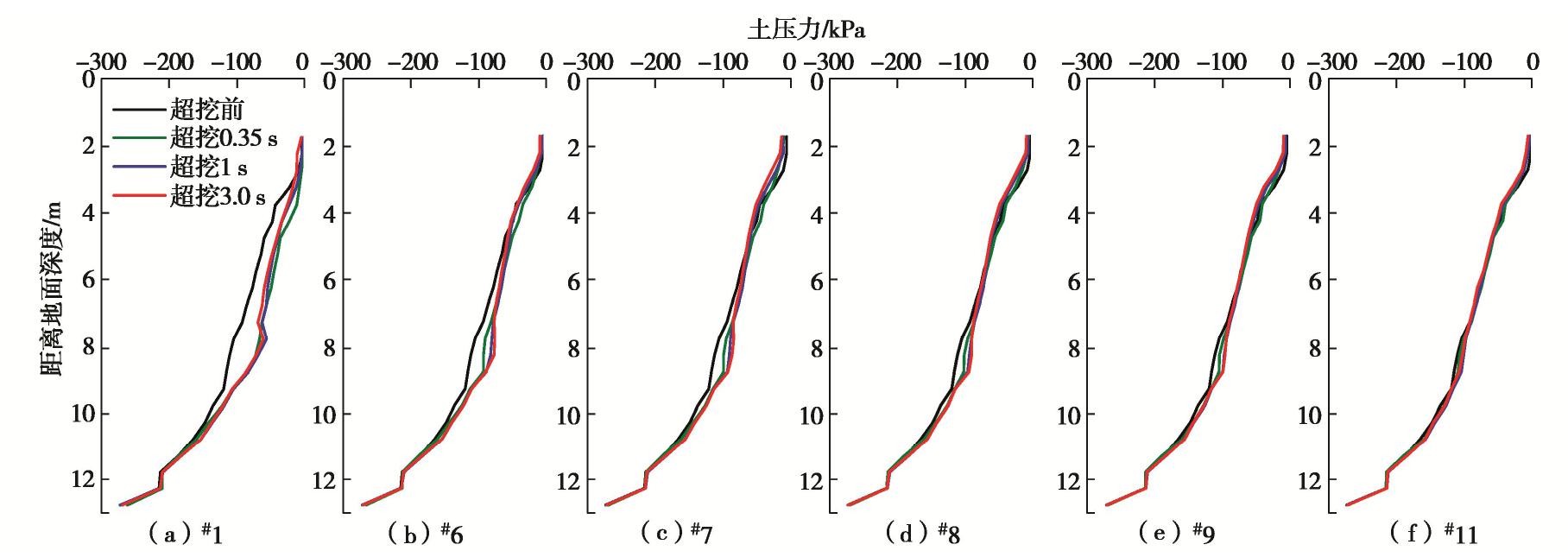
图6为#1桩和#10桩开挖5.0 m及超挖2.0 m后过程中主动区和被动区土压力随深度分布图。#1桩主动区大部分土压力在超挖过程中,由于桩身向坑内倾覆而减小,随后上升,但稳定后较超挖前略有减小；被动区土压力由于上覆土层开挖,在开挖面附近逐渐减小至接近0,在超挖0.05 s时被动区上部土压力降低,下部土压力与超挖前相近；超挖0.35 s时,被动区土压力达到最小值。超挖达到平衡后,被动区土压力整体升高,且由于桩身上部位移更大,因此上部土压力上升更多,并逐渐向被动土压力靠近。
在超挖0.35 s时#1桩主动区桩身中部土压力降低,而桩顶土压力上升。出现这个现象主要原因在于超挖后桩身发生向坑内的水平变形,使得桩身中部土压力减小,与此同时,在此剖面内产生土拱效应,土拱拱脚作用在桩顶附近,使桩顶附近土压力增大。
由于#10桩不在超挖范围内,在超挖0.05 s后,其被动区相当于“坑中坑”的主动区,因此也可以观察到其被动区土压力在超挖后略微降低。在超挖达到平衡后,由于超挖区内支护桩向坑内变形大,与超挖区外产生了不协调变形,引发超挖区外支护桩变形增大,被动区土压力相对超挖前略有增加,其产生的力矩也随之小幅度增大。
4.3 超挖后支护桩受力及稳定状态值变化
式（2）不考虑冠梁的作用,桩身稳定状态值由主被动区土压力绕前排桩底的力矩决定,由于式（2）定义的值随时间变化,因此超挖过程计算采用动力计算记录每个时刻的土压力变化。
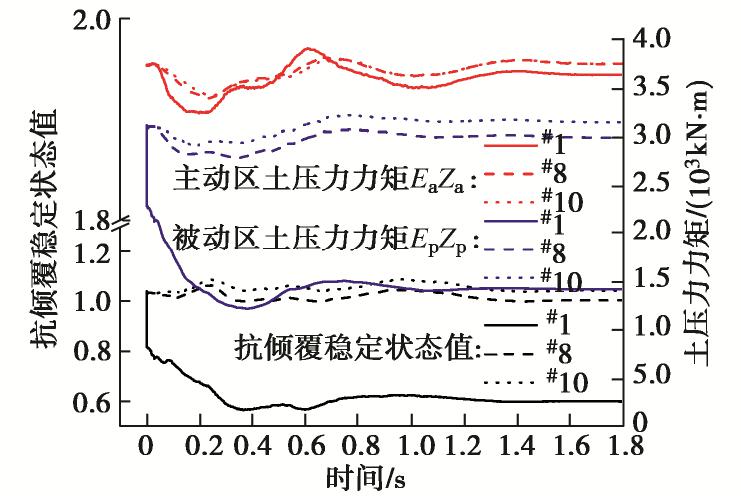
图7为超挖区内#1、#8、#10桩身稳定状态值及超挖后主被动区土压力产生的力矩时程曲线。对#1桩而言,在超挖后主动区力矩由于支护桩向坑内产生一定位移,土与后排桩产生桩土相互作用而处于波动中,并最终比超挖前略小。被动区力矩由于被动区土层的开挖迅速大幅减小,随后由于桩身位移的增加,被动区土压力略有增加,并逐渐趋于稳定,最终被动区土压力力矩较超挖前大幅下降。基于主被动区土压力力矩变化,依式（2）计算的稳定状态值在超挖后首先迅速大幅减小后略有增大,然后逐渐趋于稳定,这也与#1桩发生了倾覆破坏的现象相吻合。
![]()
图 7 #1、#8、#10桩身抗倾覆稳定状态值及力矩时程曲线Figure 7. Time history curves of anti-overturning status value and moments of pile No. #1, #8, #10#8及#10桩位于超挖区外,因此被动区力矩不会产生类似#1桩中大幅度降低,然而由于其被动区相当于“坑中坑”的主动区,因此也可以观察到其被动区力矩在超挖后略微降低,且越远离超挖区,被动区力矩降低越少,随后由于桩身向坑内位移而上升的现象。由于超挖,超挖区以内桩后土体向坑内运动,产生土拱作用于超挖区以外的支护桩上,因此#8及#10桩主动区力矩小幅升高,随后由于桩身向坑内位移而降低,最终与初始状态基本持平。基于主被动区土压力力矩变化,依式（2）计算的稳定状态值在超挖后有所波动,但并未出现大幅降低,与#8及#10桩发生了倾覆破坏的现象不太相符。
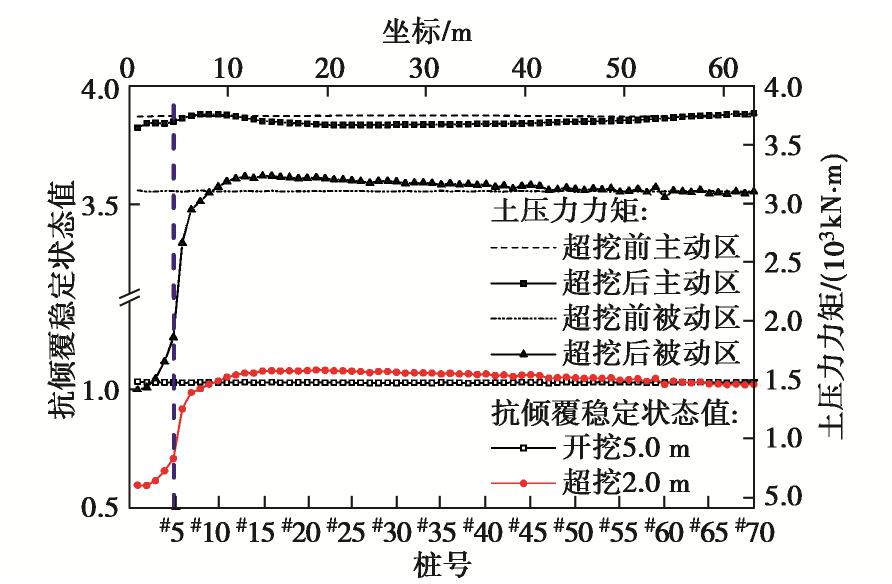
图8为超挖稳定后稳定状态值及主被动区土压力对旋转点力矩沿基坑长度方向上的变化曲线。由前述分析可知,在超挖区内,即对于#1～#5桩,超挖使主动区力矩降低小于被动区力矩降低,稳定状态值降低至小于1,即超挖区内支护桩发生倾覆失稳破坏。
![]()
图 8 超挖稳定后桩身稳定状态值及力矩随桩号变化曲线Figure 8. Anti-overturning status values and moment curves of piles after over-excavation在超挖区外#6～#9桩,主动区力矩几乎不变,而被动区力矩略有降低,主要是由于此处相当于局部超挖坑的主动区,土压力产生的力矩降低部分大于双排桩向坑内变形引起的力矩升高部分,因此稳定状态值降低,这与#6～#9桩出现了倾覆破坏的现象相吻合。
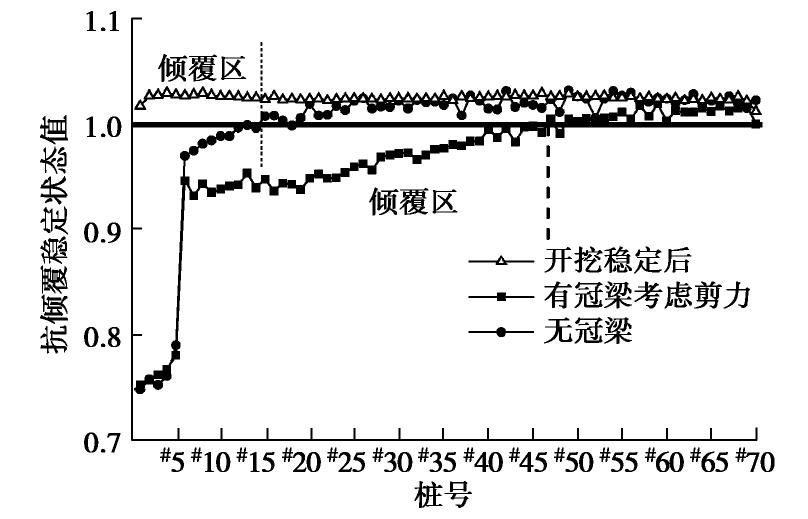
#10～#50桩由于支护桩向坑内转动,被动区土压力增大,稳定状态值在超挖后的整个过程中始终没有显著降低,甚至较超挖前有小幅上升。然而观察事故现场图2及计算结果图4,#10桩及远离超挖区的支护桩,也有较多桩发生了倾覆破坏。这说明式（2）中的稳定状态值不适用于此范围支护桩倾覆稳定的判断,不能很好地用于分析倾覆型连续破坏的机理及范围。
5. 考虑冠梁荷载传递作用时超挖引发的倾覆连续破坏分析
5.1 考虑冠梁荷载传递作用的抗倾覆稳定状态值
冠梁能够起到协调超挖区内外桩身变形及受力的作用,忽略冠梁荷载传递作用的式（2）无法很好地用于分析倾覆型连续破坏。对于基坑超挖这种三维问题,需要考虑冠梁的荷载传递对双排桩单元产生力矩,如图5（b）所示,定义三维双排桩单元稳定状态值计算：
, (3) 。 (4) 式中 Fs=Fs1+Fs2+Fs3+Fs4,为邻近双排桩通过冠梁传递给本组双排桩单元的水平剪力的合力,并规定合力指向坑内即产生倾覆力矩为正,指向坑外即产生抗倾覆力矩为负；H为支护桩长度。
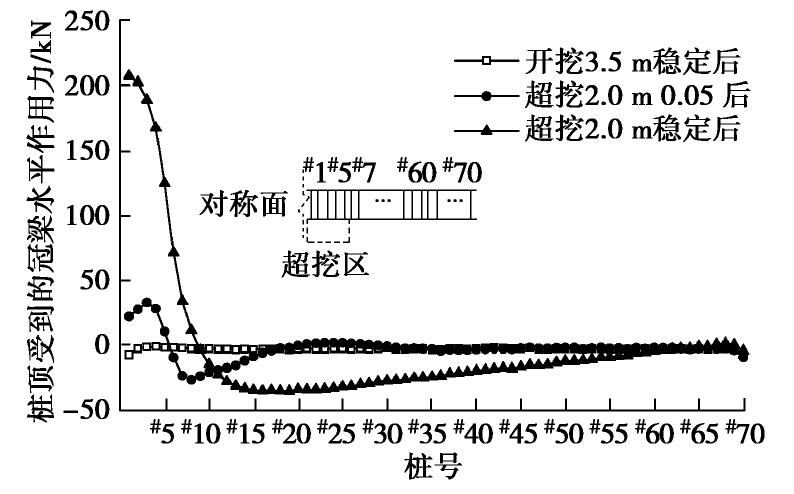
图9为冠梁作用在支护桩顶的水平合力Fs沿基坑长度方向的分布曲线。在开挖5.0 m后剪力几乎为0；在超挖0.05 s后,冠梁剪力作用在#1～#5桩顶的合力指向坑外,冠梁剪力作用在#6～#62桩顶的合力指向坑内；随时间增长剪力变化增大,最终在稳定状态下,冠梁剪力作用在#1～#8桩顶的合力均指坑外,表明此8根支护桩受到了冠梁向坑外的水平作用力,#9及更远的支护桩受到冠梁向坑内的水平作用力。
5.2 超挖后支护桩稳定状态值变化
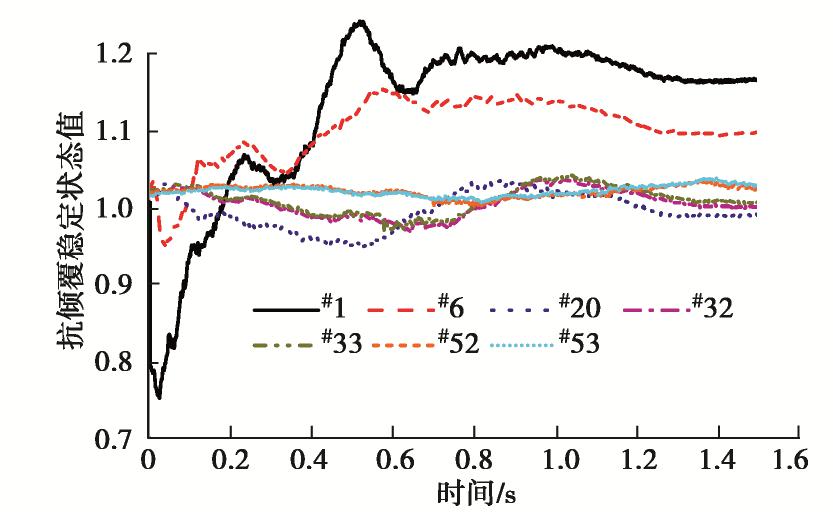
提取在计算过程中每一时刻的稳定状态值KO(t),并绘制超挖过程中稳定状态值变化的时程曲线（图10）。在超挖2.0 m后,超挖区内#1桩稳定状态值显著降低,说明支护桩会倾覆,并产生向坑内的变形。超挖区外的#6、#20、#32、#33支护桩稳定状态值也会相继降低至小于1,即也会出现向坑内的倾覆变形。受到超挖影响的区域内的支护桩稳定状态值均呈现先减小后增大的趋势,增大是由于支护桩位移增大,被动区土压力增大。在远离超挖区的#50桩附近,稳定状态值虽有小幅波动,但其始终大于1,因此,远离超挖区的支护桩较难发生倾覆变形。
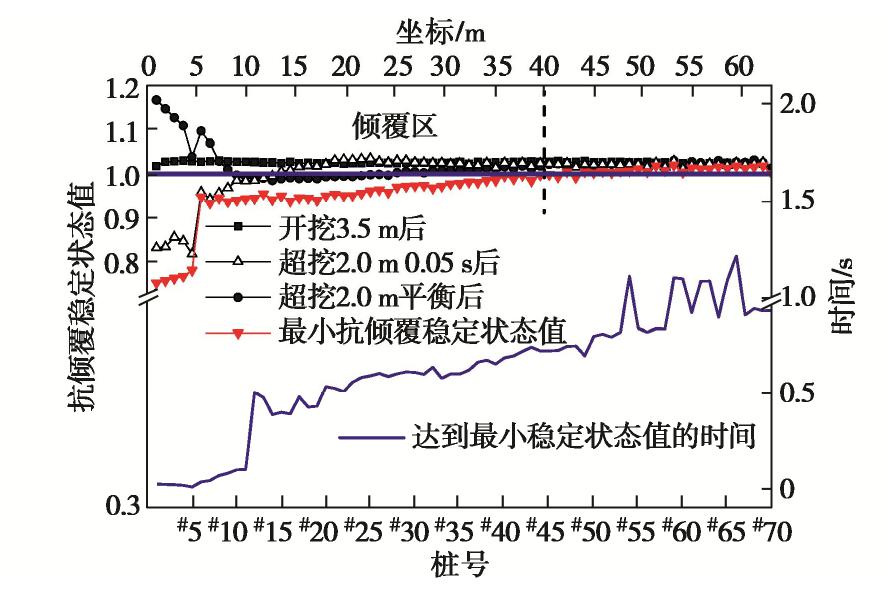
图11中红线为提取每组双排桩单元的稳定状态值时程曲线的最小值。将支护桩稳定状态值最小值小于1的区域定义为局部超挖倾覆影响区,此区域内支护桩均有发生倾覆破坏的趋势,均会产生向坑内的变形。局部超挖倾覆影响区区域的桩数约为45根桩（约40 m）,约是超挖范围的9倍。可见,由于冠梁的荷载传递作用,局部超挖引发的倾覆影响区远大于局部超挖区。而计算出的倾覆影响区大于如图2实际观察到的倾覆范围主要是由于实际案例中远离超挖区的支护桩有坑角角撑支撑,支护刚度较大,阻止了倾覆型连续破坏的传递。
![]()
图 11 桩身稳定状态值及达到最小值所需时间Figure 11. Minimum anti-overturning status values and time of reaching minimum value图11中下方蓝色曲线亦可表示每根支护桩达到稳定状态值的最小值所需时间,随桩号增加即距离局部超挖区越远,稳定状态值达到最小的时间越长。在超挖后的0.05 s内,超挖区以内的支护桩稳定状态值即达到最小,随后在0.2 s内超挖区以外的#6～#12支护桩稳定状态值也达到最小,此时经历0.3 s的稳定阶段,随后开始出现大面积的倾覆现象。整体呈现出越远离超挖区,达到最小值所需的时间越长,说明超挖使支护桩发生的连续倾覆破坏是随时间增长而逐步向远处传递的,体现了连续破坏的过程。
6. 冠梁对倾覆型连续破坏的影响
由前述分析可知,当抗倾覆稳定状态值不考虑冠梁荷载传递作用时,局部超挖导致稳定状态值在超挖区内降低,在超挖区外仅有少数几根支护桩降低,大部分支护桩略有升高；在考虑冠梁荷载传递作用时,基坑局部超挖导致超挖区域外较大范围支护桩稳定状态值均降低,能够更真实反映基坑实际的倾覆破坏情况。由此可见,冠梁在倾覆连续破坏分析中起到了重要的作用,为探究冠梁在倾覆型连续破坏中的传递作用机理,本节将原有工程中的冠梁删除,依前述方法重新研究。
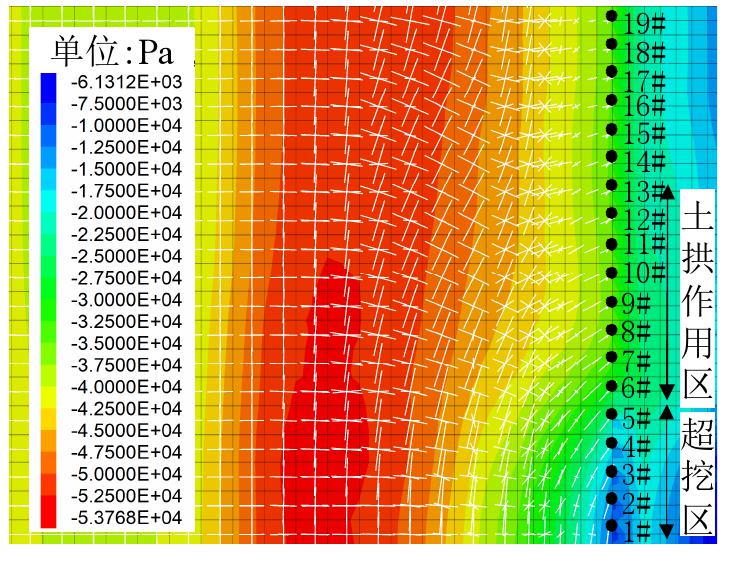
在没有冠梁的情况下,局部超挖后,支护桩之间的荷载传递作用将主要通过土体实现。图12为桩后主动区土压力随深度的分布曲线。可以发现超挖区内#1桩在超挖后,由于支护桩向坑内大幅变形,使主动区土压力降低。由于超挖区内外支护桩产生了不协调的位移差,并且支护桩上半部分变形较大,因而在主动区形成土拱效应作用在超挖区外支护桩上半部分,使此部分土压力增大,支护桩向坑内变形。图13为基坑3.5 m深度处水平向土压力云图及主应力矢量方向,可以看出主应力矢量发生旋转形成土拱,大主应力在超挖区内平行于基坑长度方向,在超挖区外逐渐接近于垂直作用在支护桩上,增大了超挖区外支护桩倾覆力矩。
![]()
图 13 土压力云图与主应力方向分布Figure 13. Contour plot of earth pressure and direction of principal stress tensor超挖区外支护桩向坑内的位移使得桩身中下部区域产生卸荷,土压力有一定程度的减小,如图12中的#6～#9所示。在远离超挖区的#11桩,土拱作用及卸荷作用均较小,土压力变化不明显。
由前述分析可见,当不存在连续冠梁时,超挖区外支护桩上的主动区土压力变化是由超挖区支护桩大幅变形引发的土拱效应及支护桩自身位移引发的卸荷作用共同决定。而当存在连续冠梁时,支护桩桩顶还将受到冠梁传递的荷载作用,局部超挖引发的荷载传递机理更加复杂,如图5（b）所示。
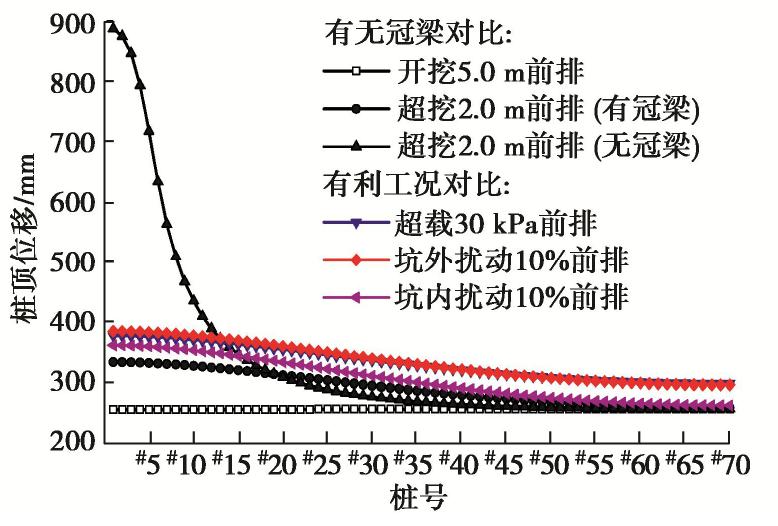
图14为局部超挖前后桩顶最大位移随桩号的变化曲线图,在正常开挖结束后,冠梁有无对桩顶位移无影响；在超挖2.0 m时,超挖区内#1桩桩顶位移相比超挖前增加约2.5倍,远大于前述有冠梁的情况。删除冠梁减弱了支护桩之间的联系,随远离超挖区,桩顶位移迅速减小。因此删除冠梁使局部桩顶位移增大,但影响范围减小。
图15为有无冠梁稳定状态值的最小值对比。可以发现删除冠梁后,超挖区内稳定状态值最小值略微降低,但超挖区外的倾覆影响区范围（#1～#14桩）明显减小,远小于有冠梁的情况（#1～#45桩）。
对于弯曲型连续破坏,冠梁能够起到降低局部破坏区以外支护桩的弯矩传递系数,并增加传递范围的作用,对抵抗连续破坏总体有利[11]。而对于本文研究的倾覆型连续破坏,冠梁加重超挖区以外的倾覆程度,扩大倾覆垮塌范围,对基坑安全相对不利。
7. 施工不利因素分析
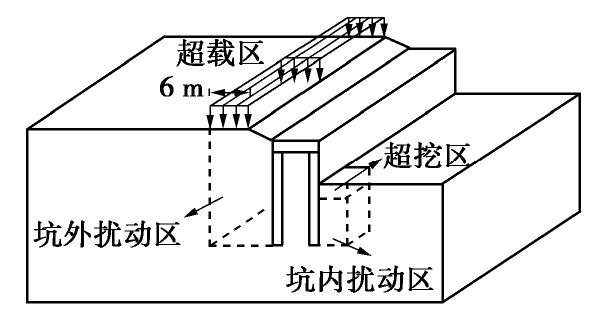
由前所述,坑外超载可能是导致支护结构发生倾覆型连续破坏的原因之一。坑外车辆经过和坑内塔吊运行均会对土体产生循环荷载,使土体强度降低。由于工程位于杭州软土地区,土体灵敏度较高,扰动对土体强度影响很大,能够使土产生结构性破坏并发生软化[4]。为此,本节以坑外超载及土体扰动两种不利工况进行分析。
如图16所示,坑外超载和扰动作用在坑外6 m范围内,深度方向上,坑外扰动作用在桩长范围内。考虑到本工程开挖前基坑外已有施工车辆通道及钢筋堆载等,因此数值模拟中坑外超载和扰动施加于大面积开挖前；坑内扰动发生在局部超挖后塔吊运行时,因此将局部超挖和塔吊运行导致的坑内扰动合并为一步计算,以此综合考虑局部超挖和其坑内扰动的不利影响。不利工况下的支护桩顶位移如图14所示,坑外超载及扰动均使支护桩位移增加,其中坑外扰动和超载所造成的影响程度和影响范围均大于坑内扰动。
7.1 坑外超载
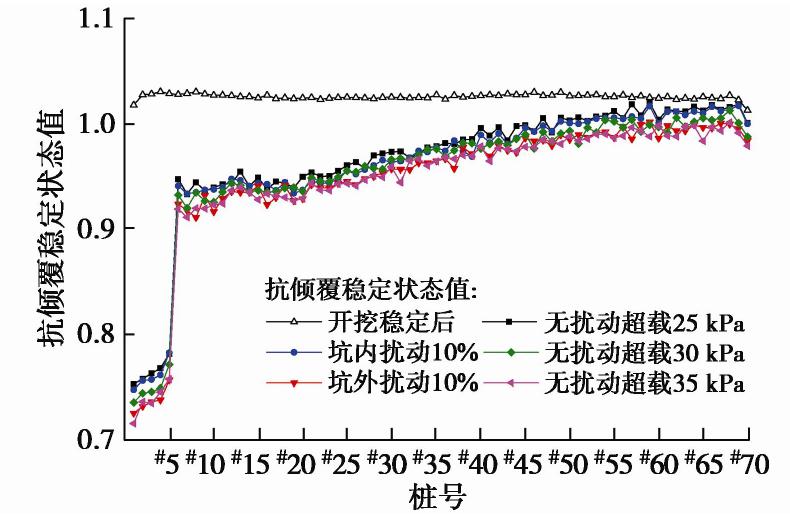
在原始工况坑外超载25 kPa的基础上,分别增加至30,35 kPa,研究超载对倾覆型连续破坏的影响。由图14可知,由于超载的增加,支护桩位移进一步增加,在超挖情况下,超载30 kPa时支护桩最大位移达到近0.4 m。
图17由不同超载情况下,最小稳定状态值沿基坑长度方向的变化曲线,可见超载增大使稳定状态值降低,对超挖区内外有相同的作用。因此超载增大,将同时增大超挖区内外产生倾覆的风险,并增大倾覆型连续破坏的范围。
7.2 土体扰动
根据文献[4],基坑事故导致土体强度降低约10%～20%。因此本节分别将扰动区内的土体强度及模量折减10%来研究土体扰动对支护结构的影响,扰动区范围如图16所示,其中对于黏聚力及土体模量采用直接折减的办法,对于内摩擦角采用正切值折减。由图14可知,土体扰动后,支护桩位移大幅增加。
图17由土体扰动情况下,超挖后最小稳定状态值变化曲线可见,由于坑外扰动沿基坑全长,坑内扰动仅局限于超挖区以内,因而相比无扰动的情况,坑外扰动引发的稳定状态值降低的范围大于坑内扰动。此外坑内扰动情况下,稳定状态值降低也不局限于坑内,而使坑外稳定状态值同样减小,也印证了局部扰动增加支护结构发生倾覆型连续破坏的风险。
8. 结论
本文依托某实际双排桩基坑倾覆事故进行有限差分建模分析,建立模型模拟局部超挖,提出判断倾覆型连续破坏发生和发展范围的抗倾覆稳定状态值,并对事故中的不利因素进行分析,揭示了倾覆型连续破坏的机理,得到以下6点结论。
（1）本文案例中,局部超挖使前后排桩最大弯矩增大,前排桩弯矩增大达2.5倍,然而局部超挖后支护桩的弯矩仍在安全储备范围内,不会使支护桩或冠梁结构发生强度破坏,因而局部超挖仅引发了支护结构倾覆破坏。
（2）当局部超挖引发超挖区内支护桩倾覆破坏时,其同样会对超挖区外支护桩产生影响,引发大范围的倾覆型连续破坏。局部超挖发生后,倾覆破坏主要通过主动区土拱效应及冠梁的荷载传递作用向超挖区外传递。
（3）本文提出抗倾覆稳定状态值（简称稳定状态值）作为实时判断支护桩倾覆稳定状态的指标。局部超挖后,局部超挖区和邻近支护结构稳定状态值瞬间减小,趋于倾覆,各支护桩稳定状态值最小值决定了支护结构是否发生倾覆型连续破坏及其扩展范围。支护桩抗倾覆稳定状态值由主被动区土压力及其桩顶冠梁剪力变化共同决定,当其小于1时,支护结构出现倾覆破坏趋势。且计算时应考虑冠梁的荷载传递作用,否则倾覆范围在超挖区外将被低估。
（4）在局部超挖情况下,随着远离超挖区,支护桩稳定状态值最小值增大,达到最小值所用的时间加长,呈现出远离超挖区,支护桩依次连续倾覆,但倾覆程度逐渐减小的特点。
（5）在无冠梁的支护体系中,倾覆型连续破坏主要由土拱效应传递。对于悬臂支护结构,连续破坏可主要分为弯曲型和倾覆型。对于弯曲型连续破坏,冠梁能够显著降低局部破坏区以外支护桩的荷载传递系数,从而起到降低连续破坏发生风险的作用；而冠梁不能降低倾覆型连续破坏发生风险,反而会加重超挖区以外的倾覆程度,进而扩大倾覆垮塌范围。
（6）坑外的超载及坑内外的扰动会使稳定状态值降低,增大倾覆型连续破坏的传递范围及倾覆程度。
-
![]()
图 1 半无限空间饱和土一维热固结计算模型
Figure 1. Model for one-dimensional thermal consolidation of semi-infinite saturated soils
![]()
图 2 表面温度突增时不同时刻温度分布图
Figure 2. Distribution of temperature change along depth at different moments subjected to step temperature increase
![]()
图 3 表面温度突增时不同时刻超静孔压分布图
Figure 3. Distribution of excess pore pressure along depth at different moments subjected to step temperature increase
![]()
图 4 边界条件(A)不同深度处温度变化过程
Figure 4. Evolution of temperature change with time at different depths under boundary condition A
![]()
图 5 边界条件(A)不同深度处超静孔压变化过程
Figure 5. Evolution of excess pore pressure with time at different depths under boundary condition A
![]()
图 6 边界条件(A)表面位移变化过程
Figure 6. Evolution of surface displacement of soils with time under boundary condition A
![]()
图 7 边界条件(B)不同深度处温度变化过程
Figure 7. Evolution of temperature change with time at different depths under boundary condition B
![]()
图 8 边界条件(B)不同深度处超静孔压变化过程
Figure 8. Evolution of excess pore pressure with time at different depths under boundary condition B
![]()
图 9 边界条件(B)表面位移变化过程
Figure 9. Evolution of surface displacement of soils with time under boundary condition B
![]()
图 10 边界条件(B)不同扩散数表面温度随时间变化
Figure 10. Evolution of temperature of surface with time with different coefficients under boundary condition B
![]()
图 11 边界条件(B)不同扩散数表面超静孔压随时间变化
Figure 11. Evolution of excess pore pressure of surface with time with different coefficients under boundary condition B
![]()
图 12 边界条件(B)不同扩散数表面位移随时间变化
Figure 12. Evolution of displacement of surface with time with different coefficients under boundary condition B
![]()
图 13 边界条件(B)不同扩散数超静孔压随深度变化
Figure 13. Distribution of excess pore pressure along depth with different coefficients under boundary condition B
表 1 饱和土体的材料参数
Table 1 Material parameters of saturated soils
孔隙率n 泊松比μ 土体弹性模量E/MPa 土颗粒体积模量Ks/GPa 土颗粒密度ρs/(kg·m-3) 土颗粒比热容cs/(J·kg-1·K-1) 土颗粒热膨胀系数αs/K-1 孔隙流体体积模量Kw/GPa 孔隙流体密度ρw/(kg·m-3) 孔隙流体比热容cw/(J·kg-1·K-1) 孔隙流体热膨胀系数αw/K-1 土体热传导系数KT/(J·s-1·m-1·K-1) 热渗系数Sw/(m2·s-1·K-1) 0.4 0.3 5 20 2600 800 1.5×10-5 5 1000 4200 2×10-5 1 5×10-11 
下载: 导出CSV
-
[1] BOOKER J R, SAVVIDOU C. Consolidation around a spherical heat source[J]. International Journal of Solids and Structures, 1984, 20(11/12): 1079-1090.
[2] BOOKER J R, SAVVIDOU C. Consolidation around a point heat source[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1985, 9(2): 173-184. doi: 10.1002/nag.1610090206
[3] MCTIGUE D F. Thermoelastic response of fluid-saturated porous rock[J]. Journal of Geophysical Research, 1986, 91(B9): 9533-9542. doi: 10.1029/JB091iB09p09533
[4] GIRAUD A, ROUSSET G. Thermoelastic and thermoplastic response of a porous space submitted to a decaying heat source[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1995, 19(7): 475-495. doi: 10.1002/nag.1610190703
[5] SMITH D W, BOOKER J R. Green’s functions for a fully coupled thermoporoelastic material[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1993, 17(3): 139-163. doi: 10.1002/nag.1610170302
[6] SMITH D W, BOOKER J R. Boundary element analysis of linear thermoelastic consolidation[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1996, 20(7): 457-488. doi: 10.1002/(SICI)1096-9853(199607)20:7<457::AID-NAG805>3.0.CO;2-H
[7] BAI M, ABOUSLEIMAN Y. Thermoporoelastic coupling with application to consolidation[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1997, 21(2): 121-132. doi: 10.1002/(SICI)1096-9853(199702)21:2<121::AID-NAG861>3.0.CO;2-W
[8] ZHOU Y, RAJAPAKSE R K N D, GRAHAM J. A coupled thermoporoelastic model with thermo-osmosis and thermal filtration[J]. International Journal of Solids and Structures, 1998, 35(34/35): 4659-4683.
[9] ZHOU Y, RAJAPAKSE R K N D, GRAHAM J. Coupled consolidation of a porous medium with a cylindrical or a spherical cavity[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1998, 22(6): 449-475. doi: 10.1002/(SICI)1096-9853(199806)22:6<449::AID-NAG930>3.0.CO;2-H
[10] BLOND E, SCHMITT N, HILD F. Response of saturated porous media to cyclic thermal loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(11): 883-904. doi: 10.1002/nag.301
[11] 白冰. 循环温度荷载作用下饱和多孔介质热-水-力耦合响应[J]. 工程力学, 2007, 24(5): 87-92. doi: 10.3969/j.issn.1000-4750.2007.05.015 BAI Bing. Thermo-hydro-mechanical responses of saturated porous media under cyclic thermal loading[J]. Engineering Mechanics, 2007, 24(5): 87-92. (in Chinese) doi: 10.3969/j.issn.1000-4750.2007.05.015
[12] BAI B. Fluctuation responses of saturated porous media subjected to cyclic thermal loading[J]. Computers and Geotechnics, 2006, 33(8): 396-403. doi: 10.1016/j.compgeo.2006.08.005
[13] BAI B. Thermal consolidation of layered porous half-space to variable thermal loading[J]. Applied Mathematics and Mechanics, 2006, 27(11): 1531-1539. doi: 10.1007/s10483-006-1111-1
[14] LIU G B, XIE K H, ZHENG R Y. Model of nonlinear coupled thermo-hydro-elastodynamics response for a saturated poroelastic medium[J]. Science in China Series E: Technological Sciences, 2009, 52(8): 2373-2383. doi: 10.1007/s11431-008-0220-8
[15] LIU G B, XIE K H, ZHENG R Y. Thermo-elastodynamic response of a spherical cavity in saturated poroelastic medium[J]. Applied Mathematical Modelling, 2010, 34(8): 2203-2222. doi: 10.1016/j.apm.2009.10.031
[16] HE L W, JIN Z H. A local thermal nonequilibrium poroelastic theory for fluid saturated porous media[J]. Journal of Thermal Stresses, 2010, 33(8): 799-813. doi: 10.1080/01495739.2010.482358
[17] YANG Y, GUERLEBECK K, SCHANZ T. Thermo-osmosis effect in saturated porous medium[J]. Transport in Porous Media, 2014, 104(2): 253-271. doi: 10.1007/s11242-014-0332-5
[18] AI Z Y, YE Z, ZHAO Z, et al. Time-dependent behavior of axisymmetric thermal consolidation for multilayered transversely isotropic poroelastic material[J]. Applied Mathematical Modelling, 2018, 61: 216-236. doi: 10.1016/j.apm.2018.04.012
[19] AI Z Y, YE Z, LI Y. Quasti-static response of a multilayered transversely isotropic porothermoelastic material subjected to a cylindrical heat source[J]. Computers and Geotechnics, 2019, 107: 201-213. doi: 10.1016/j.compgeo.2018.11.024
[20] AI Z Y, WANG L J. Precise solution to 3D coupled thermohydromechanical problems of layered transversely isotropic saturated porous media[J]. International Journal of Geomechanics, 2018, 18(1): 4017121. doi: 10.1061/(ASCE)GM.1943-5622.0001027
[21] WANG L J, ZHU B, CHEN Y M, CHEN R P, SHI X S. Precise model for predicting excess pore-water pressure of layered soils induced by thermal-mechanical loads[J]. Journal of Engineering Mechanics, 2019, 145(1): 4018114. doi: 10.1061/(ASCE)EM.1943-7889.0001544
[22] 王路君, 艾智勇. 衰变热源作用下饱和多孔介质热固结问题的扩展精细积分法[J]. 力学学报, 2017, 49(2): 324-334. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201702009.htm WANG Lu-jun, AI Zhi-yong. EPIM for thermal consolidation problems of saturated porous media subjected to a decaying heat source[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(2): 324-334. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201702009.htm
[23] 钮家军, 凌道盛, 王秀凯, 等. 饱和单层土体一维热固结精确解[J]. 岩土工程学报, 2019, 41(9): 1715-1723. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909018.htm NIU Jia-jun, LING Dao-sheng, WANG Xiu-kai, et al. Exact solutions for one-dimensional thermal consolidation of single-layer saturated soil[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1715-1723. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909018.htm
[24] COUSSY O. Poromechanics[M]. Chichester: John Wiley & Sons Ltd, 2004.
[25] BAI B. Thermal response of saturated porous spherical body containing a cavity under several boundary conditions[J]. Journal of Thermal stresses, 2013, 36(11): 1217-1232. doi: 10.1080/01495739.2013.788389
[26] BAI B, LI T. Irreversible consolidation problem of a saturated porothermoelastic spherical body with a spherical cavity[J]. Applied Mathematical Modelling, 2013, 37(4): 1973-1982. doi: 10.1016/j.apm.2012.05.003
[27] CARNAHAN C L. Thermodynamic coupling of heat and matter flows in near-field regions of nuclear waste repositories[J]. MRS Proceedings, 1983, 26(1): 1023-1030.
[28] HORSEMAN S T, MCEWEN T J. Thermal constraints on disposal of heat-emitting waste in argillaceous rocks[J]. Engineering Geology, 1996, 41(1/2/3/4): 5-16.
-
期刊类型引用(19)
1. 沈书拯，江巍，欧阳晔，谭亿虹，吴剑，陈勇. 基于三维连续-离散耦合模型的门架式双排抗滑桩受力分析. 防灾减灾工程学报. 2025(01): 84-94 . 
百度学术
2. 王洪涛，李建华，殷允腾，张红军，宣兆腾，赵明珠. 承压水作用下岩质地层基坑抗突涌安全厚度研究. 建筑结构学报. 2024(06): 213-223 . 百度学术
3. 马勤. 超挖对软土基坑工程稳定性的影响分析. 现代矿业. 2024(04): 121-123 . 百度学术
4. 张瑞程. 新型斜撑-排桩基坑支护体系工程应用分析. 施工技术(中英文). 2024(12): 162-166 . 百度学术
5. 王强，宋歌，廖利，刘国伟，蔡崇德. 全地下空间枢纽深基坑支护结构变形特征控制. 铁路技术创新. 2024(03): 178-185 . 百度学术
6. 赵升峰，汪敏营，邬喜春，李明东. 不同深度基坑中桩加支撑支护特性研究. 江苏建筑. 2024(06): 112-115+129 . 百度学术
7. 赵玉成，代兆宇，夏瑞萌，娄海成. 雄安新区深基坑双排桩支护的实践与探讨. 粉煤灰综合利用. 2024(06): 79-83+95 . 百度学术
8. 蔡红岩. 供水泵站基坑排桩支护局部失效引发连续破坏机理研究. 陕西水利. 2023(01): 100-102 . 百度学术
9. 曾诚. 基坑局部设置双排桩桩长桩径对连续变形控制效果影响研究. 中国新技术新产品. 2023(07): 81-85 . 百度学术
10. 梁文辉. 深基坑双排桩式围护结构支护施工技术研究. 江西建材. 2023(09): 244-245+248 . 百度学术
11. 黄礼明. 某邻近既有建筑的异形软土基坑变形控制. 福建建筑. 2023(11): 84-88 . 百度学术
12. 徐琳，黄程翔，邵根才，杨璞，李宝山. 软土地区基坑超挖对围护结构变形的影响. 建筑安全. 2023(12): 33-36 . 百度学术
13. 魏焕卫，李传斌，种记鑫，郑晓. 局部超挖对内支撑结构的施工效应. 计算机辅助工程. 2023(04): 56-65 . 百度学术
14. 常强. 双排桩治理边坡的数值模拟研究. 黑龙江水利科技. 2022(04): 37-39+179 . 百度学术
15. 郑刚，程雪松，周海祚，张天奇，于晓旋，刁钰，王若展，衣凡，张文彬，郭伟. 岩土与地下工程结构韧性评价与控制. 土木工程学报. 2022(07): 1-38 . 百度学术
16. 唐小军，袁仕贵. 铁路桥台基坑开挖支护方案及稳定性计算. 中国水运. 2022(08): 146-148 . 百度学术
17. 唐小军，袁仕贵. 铁路桥台基坑开挖支护方案及稳定性计算. 中国水运. 2022(15): 146-148 . 百度学术
18. 孙永梅，程海涛，米春荣，孙贝. 土体超挖对深基坑变形影响分析. 山西建筑. 2021(19): 61-63 . 百度学术
19. 曾锦秀. 基于上限法的边坡双排抗滑桩变形计算方法. 福建工程学院学报. 2021(06): 538-544 . 百度学术
其他类型引用(10)
计量
- 文章访问数: 238
- HTML全文浏览量: 52
- PDF下载量: 127
- 被引次数: 29
