气态水迁移诱发非饱和粗粒土冻胀的试验研究

刘建龙; 滕继东; 张升; 盛岱超

doi:10.11779/CJGE202107015

气态水迁移诱发非饱和粗粒土冻胀的试验研究 English Version

刘建龙^1,,
滕继东^{1, 2, ,},
张升^{1, 2},
盛岱超^{1, 2, 3}

1.
中南大学土木工程学院,湖南　长沙　410075
2.
中南大学高速铁路建造技术国家工程实验室,湖南　长沙　410075
3.
悉尼科技大学土木与环境工程学院,悉尼　2007

基金项目:

国家自然科学基金项目 51878665

国家自然科学基金项目 U1834206

中南大学创新驱动项目 2020CX034

湖南省自然科学基金项目 2020JJ5748

湖湘青年英才项目 2020RC3008

湖南省研究生科研创新项目 CX20200110

中南大学研究生自主探索创新项目 2020zzts146

详细信息

作者简介:
刘建龙(1989— ),男,博士研究生,主要从事非饱和土与冻土等方面的科研工作。E-mail：jianlong8903@163.com

通讯作者:
滕继东, E-mail：jdteng@csu.edu.cn

中图分类号: TU445
计量
- 文章访问数: 365
- HTML全文浏览量: 36
- PDF下载量: 182
出版历程
- 收稿日期: 2020-10-23
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-06-30

Experimental study on frost heave in unsaturated coarse-grained soil caused by vapour transfer

LIU Jian-long^1,,
TENG Ji-dong^{1, 2, ,},
ZHANG Sheng^{1, 2},
SHENG Dai-chao^{1, 2, 3}

1.
Department of Geotechnical Engineering, Central South University, Changsha 410075, China
2.
National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China
3.
School of Civil and Environmental Engineering, University of Technology Sydney, Sydney 2007, Australia

摘要

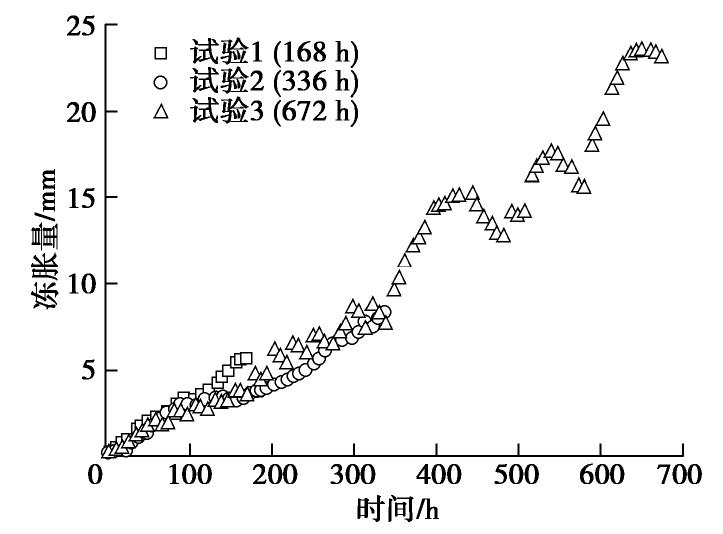
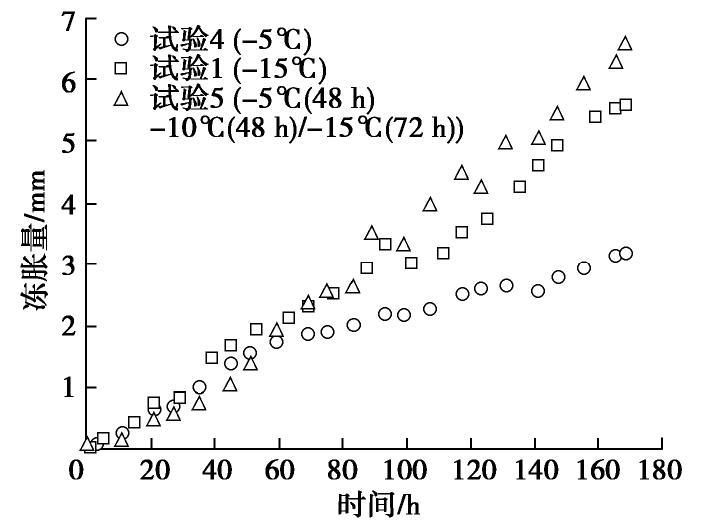
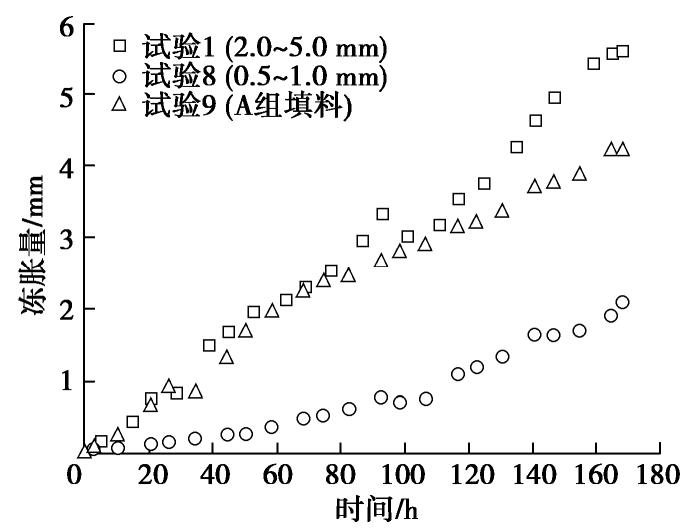
摘要: 寒区高铁粗粒土路基冻胀机理问题一直困扰科研和工程技术人员,气态水迁移诱发冻胀是目前广被关注的解释之一,但在直接试验证据方面研究较少。为证明气态水迁移可以诱发非饱和粗粒土冻胀,并进一步阐释非饱和粗粒土的冻胀机制,基于新开发的粗粒土冻胀试验仪,开展了系列的室内试验。结果表明,仅有气态水补给条件下,无细粒含量的粗粒土发生了明显冻胀,试验测得6 cm高的土柱336 h的冻胀量可达8.30 mm,672 h的冻胀量达到23.46 mm。基于X-CT扫描试验观察了气态水补给下冻胀粗粒土中冰的分布特征,发现在恒定温度梯度下冻土中无层状分布的冰透镜体,仅存在一条包含分凝冰和饱和孔隙冰的水平冻结带。冻胀试验发现土柱的冻胀量随温度梯度的增大而增大；梯度降温更有利于气态水的迁移补给,并导致更大的冻胀；土柱的初始含水率越高,越不利于气态水在土中的迁移,冻胀量越小。气态水补给诱发冻胀的试验现象,对传统液态水在细颗粒中成冰冻胀的冻土理论形成了较好补充,同时对揭示寒区高速铁路路基的冻胀机制有重要价值。
- 冻胀 /
- 非饱和粗粒土 /
- 气态水迁移 /
- 试验研究
Abstract: The frost heave caused by vapour transfer has recently attracted much attention, but there is little experimental evidence so far. A series of laboratory experiments are carried out by using the newly developed frost heave apparatus. The results show that considerable frost heave occurs in coarse-grained soil with zero fine content (<0.075 mm) while the specimen is subjected to only vapour supply. The observed frost heave in the 6 cm-high specimen reaches 8.30 mm and 23.46 mm after freezing 336 h and 672 h, respectively. The characteristics of ice lens is observed by the X-TC tests, and the distinct ice lens formation is not observed in the specimen. Under the constant temperature gradient, only one horizontal freezing zone containing segregated ice and saturated pore ice rather than layered ice lens in the frozen soil is observed. The results also show that the frost heave increases with the increasing temperature gradient. Ramped freezing is more conducive to vapour transfer, and leads to greater frost heave than step freezing. A higher initial water content of the soil specimen results in a smaller frost heave in coarse-grained soil. This study has important implications to reveal the mechanism of frost heave in high-speed railways in cold regions.
- frost heave /
- unsaturated coarse-grained soil /
- vapour transfer /
- experimental study

HTML全文

0. 引言

对于饱和砂土地震液化触发判别问题,应用最广泛的Seed简化判别方法主要建立在包含液化宏观震害现象、地震动加速度记录和场地原位测试指标三要素的地震液化实例数据和液化分界线的基础上^[1-3]。以基于原位剪切波速测试指标的液化实例为例,图1给出了地震液化和非液化实例,以及区分液化与否的分界线^[4]。由于强震液化事件彻底破坏易液化土体原有结构性,导致了消除液化土层既往沉积作用的“时钟重置”效应,使得震后获得的场地原位测试指标与真正控制场地抗液化性能的震前土体工程力学特性不对应。考虑到针对地震液化场地的原位测试一般发生在震后数天或数月甚至更长的时间里,图1中地震液化实例数据的剪切波速和相应的液化分界线可能存在与测试时间相关的系统误差。因此,研究震后易液化场地饱和砂土土层的剪切波速（或其它原位测试指标）随时间的变化规律,对正确认识现有基于原位测试指标的液化判别简化方法的可靠性并对震后测试指标进行合理修正具有重要的科学意义。

图 1 基于剪切波速的地震液化实例数据与分界线

Figure 1. v_s-based field case histories and liquefaction boundary curves

下载: 全尺寸图片幻灯片

土体在自然沉积过程中或者经受外荷载剧烈扰动后,其刚度和强度等工程力学参数在恒定应力状态下随时间变化的现象被称为“时间效应”,且该变化可以通过原位测试指标（例如,SPT、CPT和V_s）体现^[5-7]。例如,Andrus等^[8]通过静力触探与剪切波速的经验关系获得了原位砂土剪切波速和完全扰动后剪切波速的比值MEVR,初步揭示了地质时间尺度上的砂土时间效应（见图2）；周燕国等^[9]结合剪切波速（剪切模量）的Hardin公式^[10]和静力触探测试,提出了砂土时间效应的表征指标A_I,并利用不同地质年代砂土实测数据对其表征能力进行了检验。然而,上述研究主要面向地质沉积年代和土性测试指标的经验关系,关注数万年到数十万年甚至更长的地质时间尺度,并没有考虑地质沉积年代中可能受到的各种扰动（如强震事件）对土体工程力学特性的影响。以图2为例,深色椭圆圈内的数据并不符合图中拟合斜线的趋势,而这个时间范围（10^-1～10² a）正是实际工程服役寿命或者高烈度区强震重现周期的范围。Pavlenko等^[11]研究1995年神户地震中场地刚度演化问题,发现液化使得场地刚度急剧降低,但在震后较长一段时间内无法恢复到地震液化前的值。可见,对于实际工程,震后较短的时间尺度内场地土体的时间效应更具有工程意义,是影响易液化场地在余震中的地震响应和再液化可能性的重要因素。

图 2 土体测量与估算剪切波速比的时变趋势

Figure 2. Time variation of measured to estimated velocity ratio

下载: 全尺寸图片幻灯片

针对上述问题,本文对新西兰基督城的REHS强震台站在2010—2011年间的若干强震记录的尾波进行水平与竖向谱比（HVSR）分析,获得了该台站所在的易液化场地在地震前后小应变剪切刚度随时间的发展规律。在此基础上,提出了综合考虑主固结和次固结作用的震后饱和砂土小应变刚度计算模型,并合理预测了REHS台站场地震后刚度恢复变化过程。

1. 场地条件与强震台站记录分析

HVSR方法通过对强震台站的三向加速度记录进行分析得到场地卓越频率以及场地土层结构分布,相比于其它场地频率分析方法,HVSR方法相对简单,能够基本消除震源和传播路径的影响,得到的场地卓越频率更可靠^[12-13]。场地的卓越频率与场地平均剪切波速的关系可表示为^[14]

$v_{savg} = 4 H f$ 。

(1)

式中, $v_{savg}$ 为场地平均剪切波速,H为场地土层厚度,f为场地卓越频率。

根据弹性理论,土体小应变剪切模量表达为

$G_{\max} = ρ \cdot v_{s}^{2}$ 。

(2)

本文针对新西兰基督城CBD区的REHS台站（见图3）,通过触发液化的强震本身和之后发生余震的加速度记录的尾波信号,获得场地卓越频率,根据式（1）,（2）分析从2010年以来3次强震事件之后场地刚度随时间变化规律。REHS台站所处场地的上覆软弱土层厚度约为20 m,存在较厚的饱和粉质砂土层和洁净砂土层,下卧刚度较大的砂卵石层（见图4）,是较典型的易液化场地^[15]。

图 3 基督城REHS强震台站位置（来源：www.nzgd.org.nz）

Figure 3. REHS strong motion station at Christchurch (source: www.nzgd.org.nz)

下载: 全尺寸图片幻灯片

图 4 REHS台站场地土层信息

Figure 4. Soil profile at REHS station site

下载: 全尺寸图片幻灯片

本文采用Geopsy软件进行HVSR分析,该软件能够多窗口同时计算H/V谱比和上覆土层的卓越频率f,并计算它们的平均值和方差。H/V谱比曲线的峰值对应的频率即为该尾波窗口时间对应的卓越频率。图5是尾波窗口选取和计算结果示意图,其中黑色实线代表所有窗口的平均值,两条虚线分别代表它的上、下限,竖向灰色条状区域代表了平均峰值所在的频率段。采用地震动记录的尾波进行HVSR分析获得场地卓越频率需满足一定的条件,即首先要保证主震后的选取的余震强度足够小,一是为了避免该余震事件对场地刚度恢复过程产生额外的显著影响,二是为了尾波段对应场地土体处于小应变弹性应变响应状态；其次,为保证数据处理结果的可靠性,均要求H/V谱比值大于2.0,而且卓越频率的误差在±0.3 Hz以内。

图 5 地震尾波HVSR谱比分析

Figure 5. HVSR analysis of seismic coda wave

下载: 全尺寸图片幻灯片

2. 震后场地小应变刚度演化规律

图6给出了REHS台站场地2010年至2011年间3次强震后场地卓越频率随时间的发展情况。考虑到每次强震事件之后大部分余震在台站的地震动强度都很小,可以忽略其对震后场地的进一步扰动作用。每张图上方的黑色虚线代表2010年9月3日M_w7.2地震事件之前场地的卓越频率（f_i=2.20 Hz）,由2010年大震之前的小震记录进行HVSR分析得到；右上角红色虚线表示强震事件后场地的稳定值,可视为下次强震前的场地卓越频率初始值。由图6可见,每次强震后场地刚度恢复至相对稳定的状态所需要的时间基本一致（为数天到数十天）,而且场地稳定后的卓越频率均值接近但低于最初的水平（即2.20 Hz）。

图 6 震后场地卓越频率时变规律

Figure 6. Evolution of fundamental frequency of earthquake site

下载: 全尺寸图片幻灯片

由图6（b）可见,20110221 M_w6.2地震事件中场地卓越频率受到强余震地震历史的影响,因此图7仅将图6（a）和（c）的归一化场地卓越频率（f/f_i）随时间发展规律归纳在一起。由图7可见,震后场地刚度恢复速率基本一致,呈现对数形式的增长,这与PENG等^[16-17]的研究发现类似。而基督城场地小应变刚度在震后10～100 d会有显著的恢复。根据Downes等^[18]的研究,2010年距上次基督城发生强震液化的时间间隔接近100 a,可以认为基督城典型易液化场地的新近沉积时间（或液化的重现周期）为100 a左右,所以尽管REHS台站场地的砂土层刚度在液化后的数月内会有较大的恢复,但仍小于震前水平。需要指出的是,在基督城的其它强震台站（如CBGS和CCCC台站）场地也观测到了类似规律^[19]。另外,注意到图7中同一时间对应的频率数据存在一定离散性,原因包括：首先,HVSR方法不能完全消除震源及传播路径的影响；其次,地震动加速度信号（尤其是小震事件）信噪比水平不同；再次,地下水位的季节性升降等环境变化带来的可能影响。

图 7 震后场地归一化卓越频率变化规律

Figure 7. Evolution of normalized fundamental frequency of earthquake site

下载: 全尺寸图片幻灯片

3. 饱和砂土震后小应变刚度计算模型

需要注意,Andrus等^[8]将砂土的MEVR参数用于剪切模量的时间效应修正,这种修正主要反映数十万年甚至更久的由于颗粒胶结引起的时间效应,不能合理反映砂土液化后短期内刚度的变化规律（即孔压消散与次固结引起的时间效应）,而大部分震后实例调查的原位测试均是在这一时间段获得的；其次,这种修正对特定地震和场地数据的依赖性较大,数据十分有限,规律的一般性不强。本节基于饱和砂土的主固结与次固结过程,提出了考虑有效应力变化和砂土颗粒间接触力均质化（包括孔隙比变化）这两个主要因素的震后饱和砂土小应变刚度计算模型。

3.1 主固结影响函数

首先考虑由孔压消散和孔隙变化引起的剪切模量增量,可采用Hardin公式表示土体小应变剪切模量与土体孔隙比及有效应力的关系：

$G_{\max} = A \cdot F (e) {({σ^{'}}_{m})}^{n}$ ,

(3)

式中,G_max为砂土小应变剪切模量,A为结构性参数,F(e)为孔隙比方程, ${σ^{'}}_{m}$ 为平均有效应力,n约等于0.5。

平均固结度U通常定义为

$U = \frac{S_{ct}}{S_{c \infty}}$ ,

(4)

式中,S_ct为地基某时刻的主固结变形,S_c∞为地基的最终主固结变形。

根据太沙基一维固结理论,平均固结度U为

$U = 1 - \sum_{m = 1}^{\infty} \frac{2}{M^{2}} e^{- M^{2} T_{v}}$ 。

(5)

式中,竖向固结时间因子T_v为

$T_{v} = \frac{k_{v} t}{H^{2} γ_{w} m_{v}}$ ,

(6)

式中,k_v为土的竖向渗透系数,t为固结时间,H为土层厚度, $γ_{w}$ 为水的重度,m_v为土体体积压缩模量。

设砂土震后初始孔隙比为e₀,主固结完成后孔隙比为e_c∞,固结中土体孔隙比为e_ct,则由式（4）可以得到土体平均固结度：

$U = \frac{e_{0} - e_{ct}}{e_{0} - e_{c \infty}}$ 。

(7)

超静孔压比与砂土有效应力的关系如下：

$1 - r_{u} (t) = {[\frac{{σ^{'}}_{m, t}}{{σ^{'}}_{m,i}}]}^{2}$ ,

(8)

式中, $r_{u} (t)$ 为t时刻砂土的超静孔压比, ${σ^{'}}_{m, t}$ 为t时刻砂土的有效应力, ${σ^{'}}_{m,i}$ 为砂土的初始最大有效应力。

考虑到在主固结阶段砂土剪切模量增长主要由有效应力增加和孔隙比减小引起的,而结构性变化的影响很小。因此本文假设砂土主固结过程中结构性参数A不变,结合式（3）,（7）,（8）得到砂土震后剪切模量随时间的变化函数如下：

$\frac{G_{pc} (t)}{G_{R}} = \frac{F (e_{0} - U e_{0} + U e_{c \infty})}{F (e_{c \infty})} {[1 - \frac{p_{0}}{σ^{'}} (1 - U)]}^{0.5}$ ,

(9)

式中,G_pc(t)为任意固结时刻的砂土小应变剪切模量,G_R为砂土在参考时间时的小应变剪切模量,一般参考时间t_R大于主固结时间t_p。

3.2 次固结影响函数

砂土次固结过程中,颗粒间接触力均质化（包括孔隙比减小）也是引起砂土刚度随时间增长的一个重要因素^[20-21]。本文采用Howie等^[22]基于室内试验提出的经验公式加以描述：

$\frac{G_{sc} (t)}{G_{R}} = 1 + \frac{Δ G}{G_{R}} \cdot \lg (\frac{t}{t_{R}})$ ,

(10)

式中,t为固结时间,t_R为参考时间,G_sc(t)为任意固结时刻的小应变剪切模量,G_sc,R为在参考时间的小应变剪切模量, $Δ G$ /G_sc,R为剪切模量增长速率,对于特定的土体需根据室内固结试验确定。

3.3 饱和砂土震后小应变刚度计算模型

在震后一定的时间段,砂土剪切模量变化受上述两个因素共同影响,本文假设这两种机理相互独立,结合式（9）,（10）得

$\frac{G (t)}{G_{R}} = 1 + \frac{Δ G_{pc} (t)}{G_{R}} + \frac{Δ G_{sc} (t)}{G_{R}}$ 。

(11)

式（11）结合 $G = ρ v_{s}^{2}$ 和 $v_{s} = 4 H f$ 可得到场地卓越频率随随时间发展的函数：

$\frac{f (t)}{f_{R}} = \sqrt{\frac{G (t)}{G_{R}}}$ 。

(12)

根据现有围绕基督城场地的研究成果,式（12）的参数取值如下：该场地上覆软弱土层厚20 m,主要由砂土和粉土组成,排水条件良好^[15]；根据CPT测试的I_c和渗透系数的经验关系^[23]取土层平均渗透系数k_v=2.5×10^-5 m/s；土层的平均压缩模量由动力触探锤击数与压缩模量的经验关系^[24]得到,取E_s=15.0 MPa；土层初始平均超静孔压比取p₀=0.8。另外,假设震后场地刚度需要经历震前同样的沉积时间才能恢复至2010年9月3日强震液化事件之前的震前值,则参考时间取为t_R=100 a。

根据式（12）计算得到基督城REHS台站场地液化后基频随时间的发展规律如图8中的曲线所示,图中上、下两条边界线代表由于参数取值带来的标准差。由图8可见,该计算模型对图6（a）,（c）中的两次强震数据的预测效果较好,能够考虑震后一定时间内饱和砂土刚度的恢复规律。

图 8 震后刚度发展函数预测效果

Figure 8. Prediction of post-earthquake stiffness function

下载: 全尺寸图片幻灯片

4. 结论

为研究震后饱和砂土场地原位测试指标变化规律及其与震前值的差异,本文针对新西兰基督城的典型易液化场地,开展了从实际场地卓越频率监测分析到砂土小应变刚度计算模型的研究。主要结论如下：

（1）针对基督城系列强震,对REHS强震台站记录信号进行HVSR分析,揭示了震后场地刚度整体呈现指数形式的增长规律。场地小应变刚度会在震后经过数天的快速恢复后进入相对稳定的缓慢上升期。对于震前沉积时间较久的场地,场地刚度在震后短时间内难以恢复到震前水平,现有基于震后原位调查获得的液化实例数据应当根据震后原位测试时间进行适当的修正。

（2）假设震后场地刚度需要经历震前同样的沉积时间才能恢复至震前值,基于主固结与次固结过程提出了具有物理意义的饱和砂土震后小应变刚度计算模型,可估算基督城典型易液化场地在强震后平均小应变刚度随时间的发展规律。该计算模型为将特定场地的震后原位测试指标（如剪切波速）修正到对应的震前值提供了一种有效手段。

注意到本文所揭示的震后场地小应变刚度演化规律和所建议的计算模型及参数主要针对新西兰基督城场地,有必要进一步研究更多的其它地震和场地刚度演化规律,并获取各类易液化场地和土体参数,才能为将液化实例中的震后原位测试指标修正到震前原状土的对应值提供定量依据,提高当前基于液化实例调查的地震液化简化判别方法的准确性。

图 1 试验装置图

Figure 1. Schematic of testing apparatus

下载: 全尺寸图片幻灯片

图 2 颗粒级配曲线

Figure 2. Grain-size distribution curves

下载: 全尺寸图片幻灯片

图 3 试样顶部的温度和相对湿度（试验1）

Figure 3. Temperatures and humidities at top of specimen (Case 1)

下载: 全尺寸图片幻灯片

图 4 土体温度随时间的变化（试验5）

Figure 4. Temperature vs. time (case 5)

下载: 全尺寸图片幻灯片

图 5 土柱的温度分布

Figure 5. Temperature profiles in steady state

下载: 全尺寸图片幻灯片

图 6 不同时间条件下的冻胀量

Figure 6. Frost heaves at different time

下载: 全尺寸图片幻灯片

图 7 冻胀后试样1的xz剖面CT扫描图

Figure 7. Sectional images of frozen specimen 1 tested by X-CT

下载: 全尺寸图片幻灯片

图 8 液态水诱发冻胀的分凝冰

Figure 8. Ice lenses in fine-graded soils caused by liquid water

下载: 全尺寸图片幻灯片

图 9 不同边界温度条件下的冻胀量

Figure 9. Frost heaves under different boundary temperatures

下载: 全尺寸图片幻灯片

图 10 冻胀后试样5的xz剖面CT扫描图

Figure 10. Sectional images of frozen specimen 5 tested by X-CT

下载: 全尺寸图片幻灯片

图 11 不同初始含水率条件下的冻胀量

Figure 11. Frost heaves in soils with different initial water contents

下载: 全尺寸图片幻灯片

图 12 不同粒径分布的试样的冻胀量

Figure 12. Frost heaves in different soils

下载: 全尺寸图片幻灯片

图 13 冻胀后试样8的xz剖面CT扫描图

Figure 13. Section images of frozen specimen 8 tested by X-CT

下载: 全尺寸图片幻灯片

图 14 冻胀后试样9的xz剖面CT扫描图

Figure 14. Sectional images of frozen specimen 9 tested by X-CT

下载: 全尺寸图片幻灯片

表 1 试样的基本物理参数

Table 1 Physical properties of experiment materials

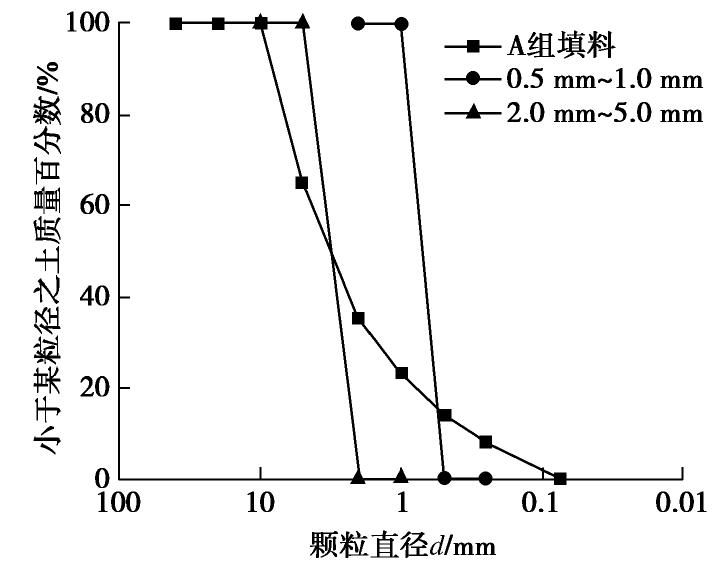
材料	相对质量密度	最大干密度/(g·cm^-3)	最小干密度/(g·cm^-3)
粗砂(0.5~1.0 mm)	2.63	1.64	1.37
细砾(2.0~5.0 mm)	2.64	1.67	1.45
A组填料(0.075~10 mm)	2.64	1.68	1.47

下载: 导出CSV

表 2 试验条件

Table 2 Test conditions

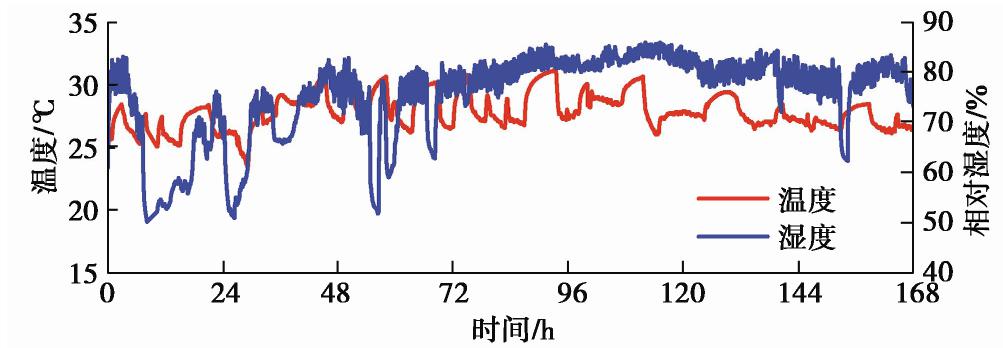
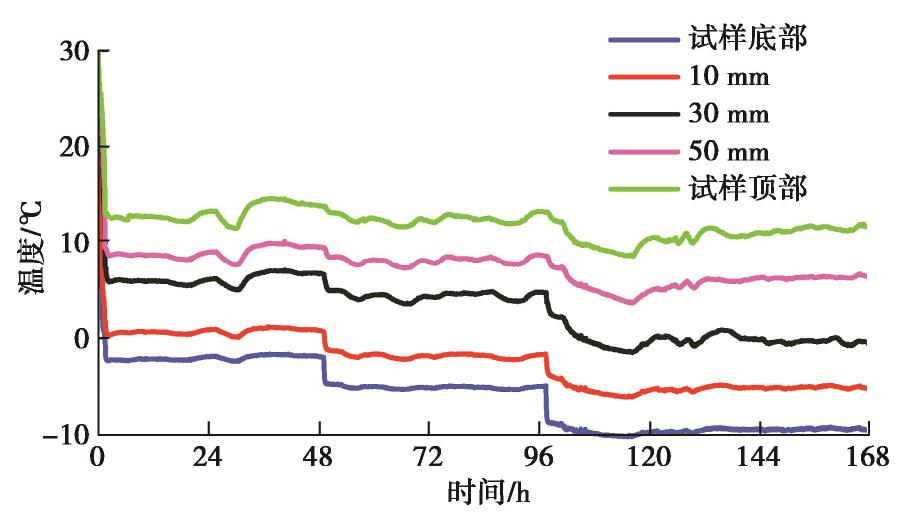
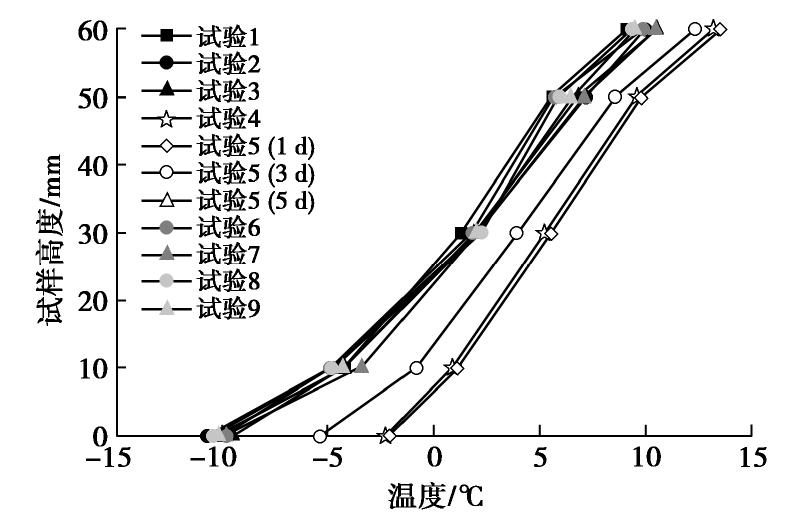
编号	粒径/mm	初始含水率/%	冷温盘设定温度/℃	试样底部实际温度/℃	试样顶部实际温度/℃	冻结时间/h
1	2.0~5.0	3	-15	-10.01	9.69	168
2	2.0~5.0	3	-15	-10.46	10.1	336
3	2.0~5.0	3	-15	-10.20	10.21	672
4	2.0~5.0	3	-5	-2.37	13.89	168
5	2.0~5.0	3	-5 (48 h) / -10 (48 h) /-15 (72 h)	-1.68 / -5.26 / -9.98	13.61 / 12.28 / 10.06	168
6	2.0~5.0	0	-15	-9.84	9.38	168
7	2.0~5.0	5	-15	-9.83	10.49	168
8	0.5~1.0	3	-15	-10.39	10.67	168
9	A组填料	3	-15	-10.20	9.50	168

下载: 导出CSV

表 3 环境温度和相对湿度的平均值

Table 3 Mean values of air temperature and humidity

试验编号	1,4,5	2	3	6,7	8	9
温度/℃	27.27	25.31	25.87	29.51	27.66	27.35
相对湿度/%	72.62	69.45	69.25	74.96	70.81	74.39

下载: 导出CSV

参考文献(29)

[1]	赵国堂, 蒋金洋, 崔颖辉, 等. 高速铁路路基填料中细颗粒分布特征及其对冻胀的影响[J]. 铁道学报, 2017, 39(10): 1-9. doi: 10.3969/j.issn.1001-8360.2017.10.001 ZHAO Guo-tang, JIANG Jin-yang, CUI Ying-hui, et al. Distribution features of fine-grain in filling materials of high-speed railway subgrade and its impact on frost heaving[J]. Journal of the China Railway Society, 2017, 39(10): 1-9. (in Chinese) doi: 10.3969/j.issn.1001-8360.2017.10.001
[2]	蔡德钩. 高速铁路季节性冻土路基冻胀时空分布规律试验[J]. 中国铁道科学, 2016, 37(3): 16-21. doi: 10.3969/j.issn.1001-4632.2016.03.003 CAI De-gou. Test on frost heaving spatial-temporal distribution of high speed railway subgrade in seasonal frozen soil region[J]. China Railway Science, 2016, 37(3): 16-21. (in Chinese) doi: 10.3969/j.issn.1001-4632.2016.03.003
[3]	铁路路基设计规范：TB 10001—2016[S]. 2017. Code for Design of Railway Earth Structure: TB 10001—2016[S]. 2017. (in Chinese)
[4]	叶阳升, 王仲锦, 程爱君, 等. 路基的填料冻胀分类及防冻层设置[J]. 中国铁道科学, 2007, 28(1): 1-7. doi: 10.3321/j.issn:1001-4632.2007.01.001 YE Yang-sheng, WANG Zhong-jin, CHENG Ai-jun, et al. Frost heave classification of railway subgrade filling material and the design of anti-freezing layer[J]. China Railway Science, 2007, 28(1): 1-7. (in Chinese) doi: 10.3321/j.issn:1001-4632.2007.01.001
[5]	NIU F J, LI A Y, LUO J, et al. Soil moisture, ground temperatures, and deformation of a high-speed railway embankment in Northeast China[J]. Cold Regions Science and Technology, 2017, 133: 7-14. doi: 10.1016/j.coldregions.2016.10.007
[6]	盛岱超, 张升, 李希. 高速列车与路基冻胀相互作用机理[J]. 岩土工程学报, 2013, 35(12): 2186-2191. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201312008.htm SHENG Dai-chao, ZHANG Sheng, LI Xi. Effects of train loads on frost heave of embankments[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(12): 2186-2191. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201312008.htm
[7]	BESKOW G. Soil freezing and frost heaving with special application to roads and railroads[J]. Swedish Geology Survey Yearbook (Series C), 1935, 26(3): 375.
[8]	SHE W, WEI L S, ZHAO G T, et al. New insights into the frost heave behavior of coarse grained soils for high-speed railway roadbed: Clustering effect of fines[J]. Cold Regions Science and Technology, 2019, 167: 102863. doi: 10.1016/j.coldregions.2019.102863
[9]	NIU F J, ZHENG H, LI A Y. The study of frost heave mechanism of high-speed railway foundation by field-monitored data and indoor verification experiment[J]. Acta Geotechnica, 2020, 15(3): 581-593. doi: 10.1007/s11440-018-0740-8
[10]	EIGENBROD K D, KENNEPOHL G J A. Moisture accumulation and pore water pressures at base of pavements[J]. Transportation Research Record, 1996, 1546: 151-161. doi: 10.1177/0361198196154600117
[11]	张中琼. 多年冻土区沥青路面热效应机理研究[D]. 兰州: 中国科学院寒区旱区环境与工程研究所, 2012. ZHANG Zhong-qiong. Study on the Mechanism of Asphalt Pavement's Thermal Effects in Permafrost Regions[D]. Lanzhou: Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences, 2012, Lanzhou. (in Chinese)
[12]	张升, 贺佐跃, 滕继东, 等. 非饱和土水汽迁移与相变：两类“锅盖效应”的试验研究[J]. 岩土工程学报, 2017, 39(5): 961-968. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201705029.htm ZHANG Sheng, HE Zuo-yue, TENG Ji-dong, et al. Water vapor transfer and phase change in unsaturated soils: experimental study on two types of canopy effect[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(5): 961-968. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201705029.htm
[13]	TENG J, SHAN F, HE Z, et al. Experimental study of ice accumulation in unsaturated clean sand[J]. Géotechnique, 2019, 69(3): 251-259. doi: 10.1680/jgeot.17.P.208
[14]	GAO J Q, LAI Y M, ZHANG M Y, et al. Experimental study on the water-heat-vapor behavior in a freezing coarse-grained soil[J]. Applied Thermal Engineering, 2018, 128: 956-965. doi: 10.1016/j.applthermaleng.2017.09.080
[15]	ZHANG S, TENG J D, HE Z Y, et al. Importance of vapor flow in unsaturated freezing soil: a numerical study[J]. Cold Regions Science and Technology, 2016, 126: 1-9. doi: 10.1016/j.coldregions.2016.02.011
[16]	TENG J D, LIU J L, ZHANG S, et al. Modelling frost heave in unsaturated coarse-grained soils[J]. Acta Geotechnica. 2020, 15(11): 3307-3320. doi: 10.1007/s11440-020-00956-2
[17]	PENNER E. Heaving pressure in soils during unidirectional freezing[J]. Canadian Geotechnical Journal, 1967, 4(4): 398-408. doi: 10.1139/t67-067
[18]	O'NEILL K, MILLER R D. Exploration of a rigid ice model of frost heave[J]. Water Resources Research, 1985, 21(3): 281-296. doi: 10.1029/WR021i003p00281
[19]	SHENG D, AXELSSON K, KNUTSSON S. Frost heave due to ice lens formation in freezing soils[J]. Hydrology Research, 1995, 26(2): 125-146. doi: 10.2166/nh.1995.0008
[20]	THOMAS H R, CLEALL P, LI Y C, et al. Modelling of cryogenic processes in permafrost and seasonally frozen soils[J]. Géotechnique, 2009, 59(3): 173-184. doi: 10.1680/geot.2009.59.3.173
[21]	LAI Y M, PEI W S, ZHANG M Y, et al. Study on theory model of hydro-thermal-mechanical interaction process in saturated freezing silty soil[J]. International Journal of Heat and Mass Transfer, 2014, 78: 805-819. doi: 10.1016/j.ijheatmasstransfer.2014.07.035
[22]	KONRAD J M, MORGENSTERN N R. A mechanistic theory of ice lens formation in fine-grained soils[J]. Canadian Geotechnical Journal, 1980, 17(4): 473-486. doi: 10.1139/t80-056
[23]	KONRAD J M. Estimation of the segregation potential of fine-grained soils using the frost heave response of two reference soils[J]. Canadian Geotechnical Journal, 2005, 42(1): 38-50. doi: 10.1139/t04-080
[24]	DASH J G, REMPEL A W, WETTLAUFER J S. The physics of premelted ice and its geophysical consequences[J]. Reviews of Modern Physics, 2006, 78(3): 695-741. doi: 10.1103/RevModPhys.78.695
[25]	SARUYA T, KURITA K, REMPEL A W. Experimental constraints on the kinetics of ice lens initiation and growth[J]. Physical Review E, 2013, 87(3): 032404. doi: 10.1103/PhysRevE.87.032404
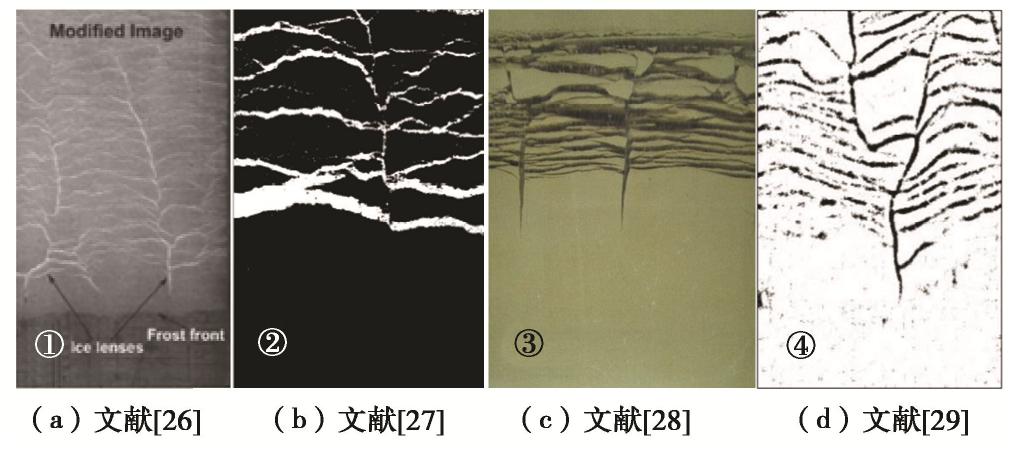
[26]	XIA D. Frost Heave Studies Using Digital Photographic Technique[D]. Edmonton: University of Alberta, 2006.
[27]	ARENSON L, SEGO D, TAKE W. Measurement of ice lens growth and soil consolidation during frost penetration using particle image velocimetry (PIV)[C]//60th Canadian Geotechnical Conference, 2007, Ottawa.
[28]	ZHENG H, SASAKI Y, KANIE S. Image processing method for observing ice lenses produced by the frost heave process[J]. Cold Regions Science and Technology, 2020, 171: 102977. doi: 10.1016/j.coldregions.2019.102977
[29]	周永毅, 张建经. 一种新型冻土可视化试验系统及其在冻融试验中的应用[J]. 岩石力学与工程学报, 2020, 39(8): 1671-1681. doi: 10.13722/j.cnki.jrme.2020.0036 ZHOU Yong-yi, ZHANG Jian-jing. A novel visualization apparatus for freezing soils and its application in freezing-thawing test[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(8): 1671-1681. (in Chinese) doi: 10.13722/j.cnki.jrme.2020.0036

施引文献(2)

期刊类型引用(2)

1.	刘志文，王媛，董琪，高山. 不连续界面渗流的堤防防渗膜防渗效果模拟研究. 人民黄河. 2024(06): 48-53+67 . 百度学术
2.	张升，兰鹏，苏晶晶，熊海斌. 基于PINNs算法的地下水渗流模型求解及参数反演. 岩土工程学报. 2023(02): 376-383+443-444 . 本站查看