求解非均质渗流场的改进数值流形方法

周凌峰; 王媛; 冯迪

doi:10.11779/CJGE202107014

求解非均质渗流场的改进数值流形方法 English Version

周凌峰^1,,
王媛^{1, 2, ,},
冯迪¹

1.
河海大学土木与交通学院,江苏　南京　210024
2.
河海大学水利水电学院,江苏　南京　210024

基金项目:

国家自然科学基金项目 U1765204

国家自然科学基金项目 41772340

国家重点研发计划项目 2016YFC0401804

详细信息

作者简介:
周凌峰(1991— ),男,博士研究生,主要从事岩土数值分析方面的研究工作。E-mail：zhoulf618@126.com

通讯作者:
王媛, E-mail：wangyuanhhu@163.com

中图分类号: TU43
计量
- 文章访问数: 295
- HTML全文浏览量: 36
- PDF下载量: 268
出版历程
- 收稿日期: 2020-09-16
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-06-30

An improved numerical manifold method for solving heterogeneous seepage problem

ZHOU Ling-feng^1,,
WANG Yuan^{1, 2, ,},
FENG Di¹

1.
College of Civil and Transportation Engineering, Hohai University, Nanjing 210024, China
2.
College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210024, China

摘要

摘要: 精确的流速场计算是模拟非均质多孔介质渗流、溶质运移以及污染物迁移等过程的基础。常规方法计算得到流速场精度低、连续性差。高阶流形方法可以显著提高流速场计算精度,但对于高水力梯度问题,流速场依然是不连续的,且常常伴随着线性相关问题,导致求解精度降低,甚至求解失败。针对这一问题,采用两种改进的权函数构造流形单元上的总体近似函数,编制相应的程序,消除高阶覆盖函数带来的线性相关问题,且分别得到节点连续和全局连续的流速/梯度解。通过若干算例对改进权函数程序的收敛性和精度进行分析。
- 数值流形方法 /
- 非均质 /
- 达西流速 /
- 权函数 /
- 高阶
Abstract: An accurate velocity filed is important for simulating Darcy flow, solution transport and contaminant migration in heterogeneous porous media. Generally, the velocity results calculated by the conventional numerical methods have low precision and poor continuity. To overcome this defect, two improved weight functions are used to construct the global approximation on manifold elements and two improved NMM codes are developed to eliminate the linear dependence problems caused by the higher-order overburden functions, and the velocity/gradient solutions of node continuity and global continuity are obtained, respectively. Furthermore, the convergence and accuracy of the improved weight function NMM codes are analyzed through several examples.
- numerical manifold method /
- heterogeneity /
- Darcy velocity /
- weight function /
- high order

HTML全文

0. 引言

由于地质构造等因素,断层、裂隙以及空洞等广泛存在于自然界中,水流在非均质材料体中流动时受非均质性影响很大。特别是随着各类大型水电工程的开发建设,各类工程施工措施如人工防渗墙、防渗帷幕、土工膜等的应用,使得工程渗流计算更加困难,流速场的分布也变得异常复杂。而精确求解达西流速场是模拟非均质多孔介质渗流、溶质运移以及污染物运移等过程的基础^[1]。因此,如何提高非均质渗流的达西流速场计算精度具有重要的研究意义。

由于试验尺寸和观测手段的局限,采用物理试验的方法研究非均质渗流具有较大的局限性。因此,数值方法被广泛应用于非均质渗流的模拟研究。目前最主要的方法是使用有限元方法,存在的主要问题是计算流速场精度较低,且往往是不连续的。因为常规有限元方法采用水头为求解变量,而流速是根据达西定律对水头结果求导得到的,因此精度比水头低一阶。为了提高流速场的计算精度,国内外学者提出各种后处理技术,如双重网格法^[2]、Yeh方法^[3]。比较有代表性的双重网格法将直接法求解的有限元网格进行一个微小的偏移形成新网格,利用双重网格之间的水头差计算流速解,提高了流速场的精度。有学者采用混合有限元方法,同时求解水头和流速,计算精度高但是其计算代价较大^[4]。因此,亟需发展一种能够准确求解达西流速的数值方法。

数值流形方法（NMM）是最近比较热门的数值方法,可以统一求解连续-非连续问题,因而广泛应用于岩石力学等领域^[5-6]。NMM采用数学和物理两套独立的覆盖系统,因而前处理过程比有限元等传统的网格类方法更有优势,不需要复杂的网格划分技术,只需使用规则的网格覆盖整个计算区域。同时,NMM的自由度定义在物理覆盖上,覆盖函数可以根据求解问题的类型自由选择,因而在实际应用中十分灵活高效,是一种十分具有潜力的数值方法。目前NMM主要应用于固体力学领域,对于流体力学方面也有一些探索。Zhang等^[7]使用NMM直接求解NS方程,模拟了非定常不可压缩黏性流问题。陈远强等^[8]研究了饱和-非饱和渗流数值流形方法的应用。李伟等^[9]采用MLS-NMM技术模拟稳定渗流问题。Wang等^[10]使用NMM模拟自由面渗流。Wang等^[11]采用高阶NMM进行非均质渗流模拟,可以显著提高流速场计算精度,但是存在线性相关问题,且对于高水力梯度问题,局部流速场依然是不连续的。

综上所述,目前对于如何在非均质渗流模拟中提高达西流速场的计算精度和连续性的研究较少。本文将简要介绍数值流形方法计算渗流问题的基本理论,并探讨梯度场不连续的原因。在此基础上,分别采用节点梯度连续和全局梯度连续的权函数,构造流形单元上的全局逼近,消除了高阶NMM的线性相关性,并计算得到精确且连续的流速场。最后结合若干算例说明了新方法计算结果的精度和收敛性。

1. 数值流形方法基本理论

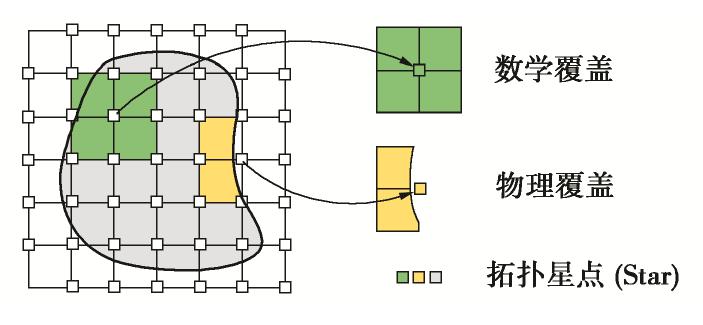
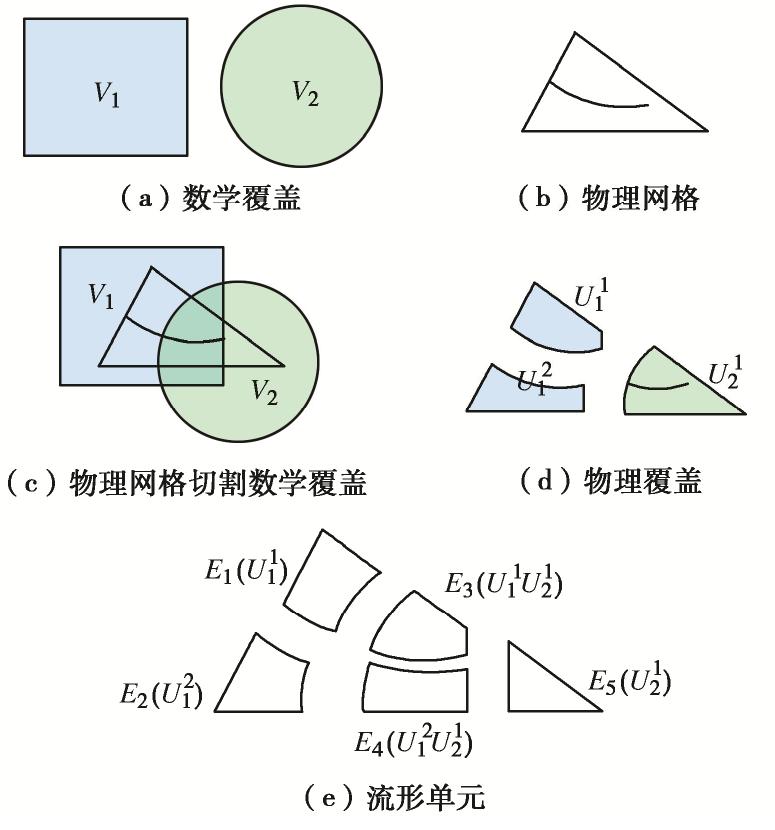
关于NMM的详细理论可参考文献[12],本文不过多展开介绍,仅以一个简单的例子说明NMM的基本概念和流形单元的生成过程。如图1（a）所示,本例中的数学覆盖为一个矩形和一个圆形,分别定义为V₁和V₂。物理网格（即实际计算域,图1（b））为一带裂纹的三角形。NMM覆盖系统的优势在于无需按照计算域划分计算网格,只需使用数学覆盖完全覆盖物理网格,便可相互切割形成物理覆盖和流形单元（图1（c））。值得注意的是,除了边界,内部的裂纹也可切割数学覆盖,因而NMM可以方便地表征裂纹两侧的不连续。如图1（d）中数学覆盖V₁被裂纹完全切割后形成两个独立的物理覆盖U₁¹和U₁²,而数学覆盖V₂仅被部分切割后形成物理覆盖U₂¹。本例最终形成5个流形单元（图1（e））,分别为E₁(U₁¹),E₂(U₁²),E₃(U₁¹U₂¹),E₄(U₁²U₂¹),E₅(U₂¹)。

图 1 流形单元的生成过程

Figure 1. Formation process of manifold elements

下载: 全尺寸图片幻灯片

2. 非均质渗流问题的NMM计算格式

2.1 NMM近似格式

按照单位分解法的理论,NMM的局部近似定义在物理覆盖上,称为覆盖函数。覆盖函数可以是常数、多项式,甚至一般级数,即

$h_{i} (x) = p^{T} (x) \cdot a$ ,

(1)

式中,i为覆盖编号, $x$ 为坐标, $p^{T} (x)$ 为覆盖函数级数表达式的基函数向量, $a$ 为计算自由度向量。

NMM的总体近似定义在流形单元上,因为流形单元是物理覆盖的重叠部分,需要通过权函数将流形单元上的所有覆盖函数连接起来得到,即

$h (x) = \sum_{i = 1}^{n^{PC}} w_{i} (x) \cdot h_{i} (x) = N a$ ,

(2)

式中, $n^{PC}$ 为流形单元上的物理覆盖数量, $w_{i} (x)$ 为第i个覆盖上的权函数,为方便与有限元对比,定义N为形函数,可表示为

$N = \sum_{i = 1}^{n^{PC}} w_{i} (x) \cdot p^{T} (x)$ 。

(3)

NMM权函数具有以下特点：

（1）非负性

$\begin{array}{l} w_{i} (x) \geq 0, x \in U_{i}, \\ w_{i} (x) = 0, x \notin U_{i}, \end{array}}$

(4)

（2）单位分解性

$\sum_{x \in U_{j}} w_{j} (x) = 1$ 。

(5)

本文采用规则的矩形网格作为数学网格,如图2所示,数学网格节点（NMM中也称为拓扑星点）周围的4个矩形单元共同形成一个数学覆盖。因而每个流形单元上有4层覆盖。NMM局部近似定义在物理覆盖上,采用拓扑星点处的一阶泰勒展开式作为覆盖函数,即

$h_{i} (x, y) = h_{i 1} + h_{i 2} (x - x_{i}) + h_{i 3} (y - y_{i})$ ,

(6)

图 2 矩形数学网格的覆盖系统示意图

Figure 2. Cover system of rectangular mathematical meshes

下载: 全尺寸图片幻灯片

式中, $(x_{i}, y_{i})$ 为覆盖i的拓扑星点坐标, $h_{i 1} ~ h_{i 3}$ 为覆盖i上的自由度。

权函数默认采用四节点等参元的双线性形函数（本文称为W₀,相应的程序称为NMM-W₀）：

$\begin{array}{l} w_{1} = (1 - ξ) (1 - η) / 4, \\ w_{2} = (1 + ξ) (1 - η) / 4, \\ w_{3} = (1 + ξ) (1 + η) / 4, \\ w_{4} = (1 - ξ) (1 + η) / 4 。 \end{array}}$

(7)

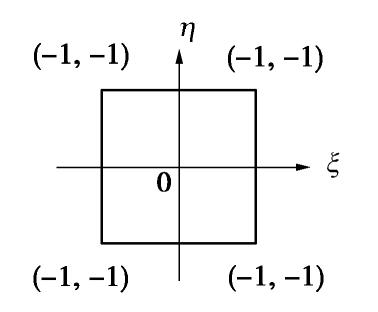
其中, $ξ$ 和 $η$ 分别为数学覆盖变换到[-1,1]×[-1,1]等参元上的局部坐标,如图3所示。

图 3 局部坐标系

Figure 3. Local coordinate system

下载: 全尺寸图片幻灯片

综上所述,流形单元上水头的总体近似函数可以表示为

$h (x, y) = \sum_{i = 1}^{4} w_{i} (x, y) \cdot h_{i} (x, y) = N a$ 。

(8)

2.2 渗流控制方程

对于稳定渗流问题,将达西定律代入水流连续性方程可得到渗流控制方程：

$- \nabla^{T} (K \nabla h) + Q = 0$ 。

(9)

其中, $\nabla$ 为梯度算子, $K$ 为渗透张量（对于非均质渗流一般可表示为坐标的函数）,Q为源汇项。

如图4所示,相关边界条件可表示为

$\begin{array}{l} h = \bar{h} (Γ_{D}), \\ q_{n} = \bar{q} (Γ_{N}) 。 \end{array}}$

(10)

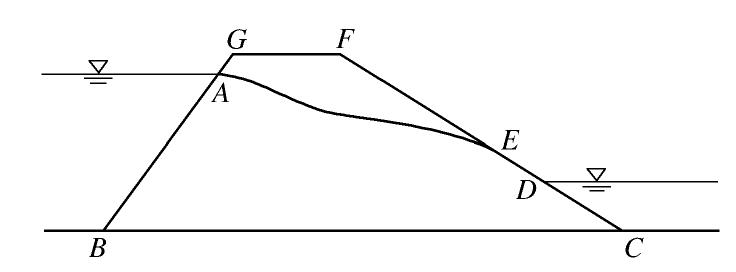
其中, $\bar{h}$ 是水头边界 $Γ_{D}$ （如图4中AB与CD）上的给定水头值, $\bar{q}$ 是流量边界 $Γ_{N}$ （如图4中BC）上的给定法向流量值。当涉及无压渗流时,还需考虑自由面边界条件 $Γ_{f}$ （如图4中AE）,以及溢出面 $Γ_{s}$ （如图4中DE）需满足

$\begin{array}{l} h = y, q_{n} = 0 (Γ_{f}), \\ h = y, q_{n} < 0 (Γ_{s}) 。 \end{array}}$

(11)

图 4 渗流问题几何示意图

Figure 4. Geometric diagram of seepage problem

下载: 全尺寸图片幻灯片

由于自由面的位置是未知的,需要通过迭代求解,本文使用的自由面迭代算法可参考文献[10]。对于非均质问题,自由面的迭代求解过程与均质问题类似,但在自由面插值时需要考虑单元的实际渗透系数以及相应的高阶插值格式。

根据式（8）可知,水头表示为

$h = N a$ 。

(12)

水力梯度表示为

$j = \nabla h = \nabla N a = B a$ ,

(13)

式中, $B = \nabla N$ 。

根据达西定律,达西流速表示为

$v = - K j = - K B a$ 。

(14)

式中, $K = K (x, y)$ 为非均质渗透系数张量。

根据变分原理可以建立泛函表达式,将原偏微分方程定解问题转化为泛函求极值问题。与有限元类似,计算域 $Ω$ 内的泛函可表示为

$\begin{matrix} Π (h) = \int_{Ω} [\frac{1}{2} {(\nabla h)}^{T} (K \nabla h) - h Q] d Ω - \\ \int_{Γ_{N}} h \bar{q} d Γ + \frac{α}{2} \int_{Γ_{D}} {(h - \bar{h})}^{2} d Γ \end{matrix}$ ,

(15)

式中, $α$ 为施加本质边界条件使用的罚函数。

将式（12）代入式（15）后,对所有求解未知量 $a_{1}$ ~ $a_{m}$ （m为总自由度）求偏导,即

$\frac{\partial Π}{\partial a} = {\begin{matrix} \frac{\partial Π}{\partial a_{1}} \\ ⋮ \\ \frac{\partial Π}{\partial a_{m}} \end{matrix}} = 0$ ,

(16)

可得线性代数方程组：

$C a = F$ ,

(17)

式中,C为渗透系数矩阵项,F为右端流量项,表达式分别为

$C = \int_{Ω} B^{T} K B d Ω + α \int_{Γ_{D}} N^{T} N d Γ$ ,

(18)

$F = \int_{Ω} N^{T} Q d Ω + \int_{Γ_{N}} N^{T} \bar{q} d Γ + α \int_{Γ_{D}} N^{T} \bar{h} d Γ$ 。

(19)

NMM程序中通常使用单纯形积分求解式（18）,（19）的积分表达式。由于本文考虑非均质渗流场,渗透系数矩阵项的被积函数表达式可能很复杂,因此本文采用高斯积分求解C和F。

3. NMM权函数的改进

3.1 梯度场不连续的原因

从NMM总体近似函数的角度来分析梯度场（流速场）不连续的原因。对水头的总体近似函数（8）求偏导,得到水力梯度,以x方向水力梯度为例,有

$\begin{matrix} j_{x} = \frac{\partial h (x, y)}{\partial x} \\ = \sum_{i = 1}^{4} (\frac{\partial w_{i} (x, y)}{\partial x} h_{i} (x, y) + w_{i} (x, y) \frac{\partial h_{i} (x, y)}{\partial x}) \end{matrix}$ 。

(20)

观察式（20）不难发现,括号内后一项的权函数仍然保留,因为其单位分解性,这部分仍然是连续的；但是前一项中,权函数的偏导数无法保证其单位分解性,故而无法保证连续性。

分析下列情形：①当覆盖函数选取为常数时,式（20）括号内后一项为0,只剩下前一项不连续项,显然得到的梯度场是不连续的。②当覆盖函数选取为一阶或更高阶多项式时,梯度表达式中的两项同时存在,由于后一项的存在,连续性会提高,但是仍然没有完全消除不连续项的影响。

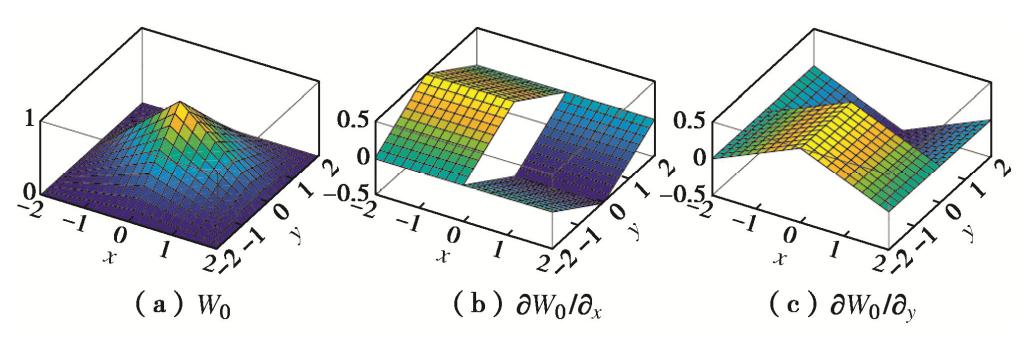
图5分别给出了W₀及其偏导数的图像（为简便起见,此处忽略了等参元局部坐标系转换,直接绘制于总体坐标系中）。从图5中可以看出,权函数W₀的偏导数只在一个方向连续,另一个方向存在跳跃。因此可知,即使采用了高阶覆盖函数,NMM-W₀的梯度场也是不连续的。

图 5 双线性权函数及其偏导数

Figure 5. Bilinear weight function and its partial derivatives

下载: 全尺寸图片幻灯片

根据上面的分析可以得出两种解决的思路：①构造偏导数具有单位分解性的权函数,②构造覆盖边界上偏导数为零的权函数。显然,方法①的构造难度较大。本文采用方法②,能够使不连续项恒为零,从而彻底消除梯度表达式中不连续的因素。

3.2 权函数改进形式A：节点连续

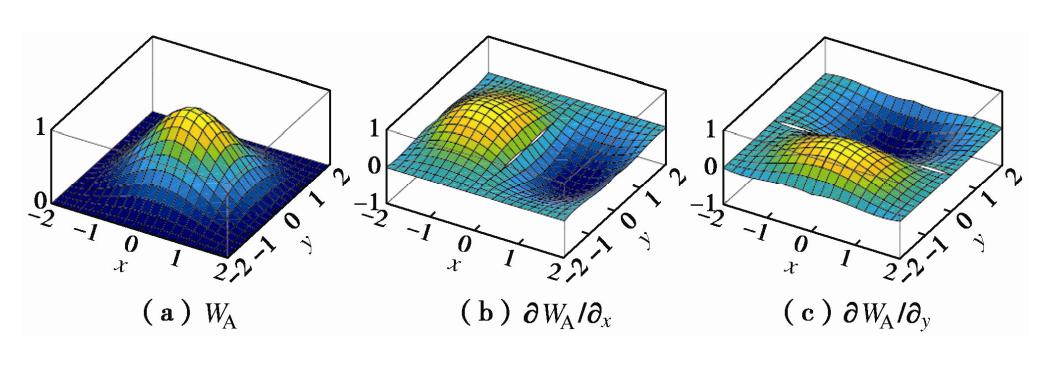
第一种改进的权函数（本文称为W_A,相应的程序称为NMM-W_A）,是常用于力学分析中的节点应力连续单元使用的权函数^[13]。权函数W_A在图3局部坐标系中的表达式为

$\begin{array}{l} w_{1} = (1 - ξ) (1 - η) (2 - ξ - η - ξ^{2} - η^{2}) / 8, \\ w_{2} = (1 + ξ) (1 - η) (2 + ξ - η - ξ^{2} - η^{2}) / 8, \\ w_{3} = (1 + ξ) (1 + η) (2 + ξ + η - ξ^{2} - η^{2}) / 8, \\ w_{4} = (1 - ξ) (1 + η) (2 - ξ + η - ξ^{2} - η^{2}) / 8 。 \end{array}}$

(21)

图6为改进权函数W_A及其偏导数的图像。从图中可以看出,权函数偏导数的连续性大为改善,但是边界处的偏导数不是严格为零,只能保证节点导数为零。因此NMM-W_A的梯度场结果满足在拓扑星点处连续。当流形单元节点不是拓扑星点时,梯度场的连续性将无法保证。Yang等^[14]使用类似的权函数进行裂纹分析,取得不错的效果。

图 6 改进权函数W_A及其偏导数

Figure 6. Improved weight function W_A and its partial derivatives

下载: 全尺寸图片幻灯片

3.3 权函数改进形式B：全局连续

第二种改进的权函数（本文称为W_B,相应的程序称为NMM-W_B）,选自有限元中二维Hermite单元的节点场量对应的形函数^[15]。权函数W_B在图3局部坐标系中的表达式为

$\begin{array}{l} w_{1} = (2 - 3 ξ + ξ^{3}) (2 - 3 η + η^{3}) / 16, \\ w_{2} = (2 + 3 ξ - ξ^{3}) (2 - 3 η + η^{3}) / 16, \\ w_{3} = (2 + 3 ξ - ξ^{3}) (2 + 3 η - η^{3}) / 16, \\ w_{4} = (2 - 3 ξ + ξ^{3}) (2 - 3 η + η^{3}) / 16 。 \end{array}}$

(22)

图7为改进权函数W_B及其偏导数的图像。从图中可以看出,权函数W_B的偏导数满足连续且边界处恒为零。因此NMM-W_B可以保证梯度场的全局连续性。Yang等^[16]使用该形函数进行力学分析,得到连续的应力/应变场结果。

图 7 改进权函数W_B及其偏导数

Figure 7. Improved weight function W_B and its partial derivatives

下载: 全尺寸图片幻灯片

4. 算例验证

在矩形网格渗流分析程序NMM-W₀基础上,分别编制了基于两种改进权函数的NMM计算程序NMM-W_A和NMM-W_B。使用改进后的NMM程序计算了4个非均质渗流算例,验证了计算结果的精度和收敛性。

4.1 算例1：渗透系数连续变化的弱非均质渗流

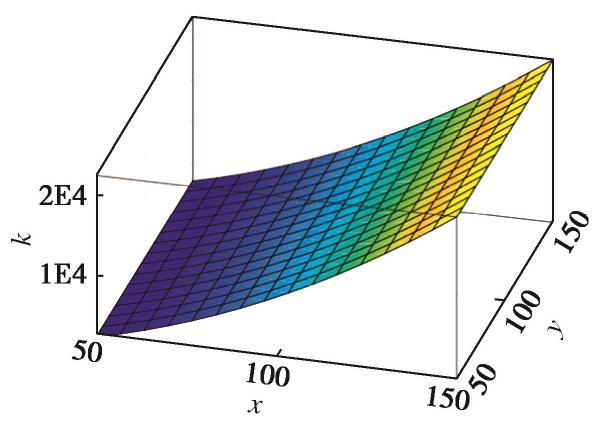
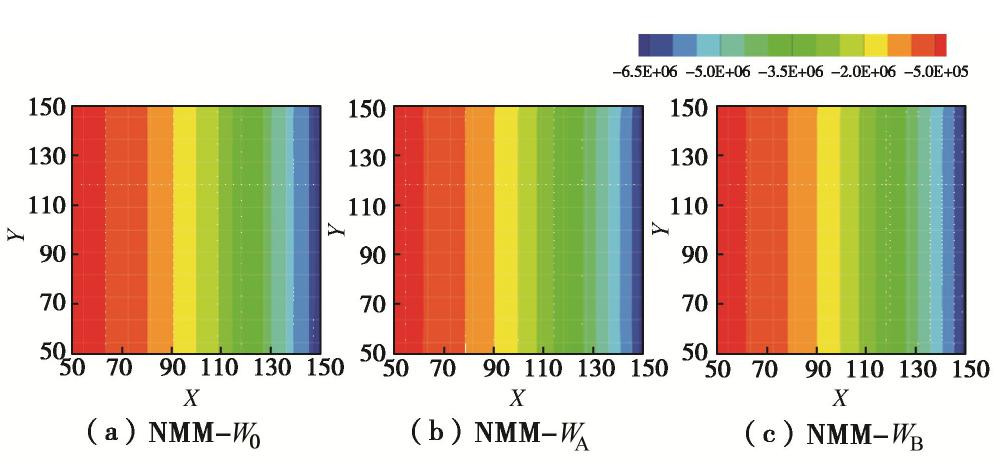
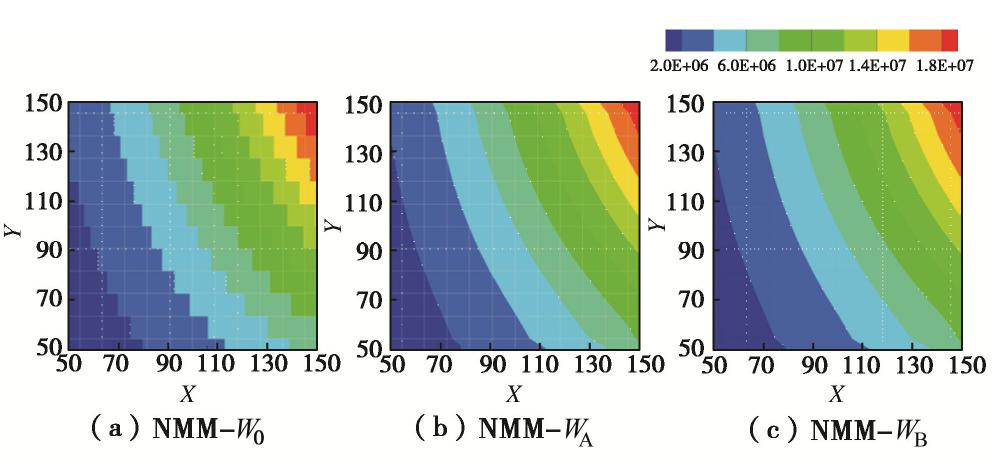
如图8所示,在[50,150]×[50,150]的矩形计算域内,渗透系数 $K (x, y) = x^{2}$ ,沿x方向连续变化^[17]。构造如下解析解为 $H (x, y) = x^{2} - 3 y^{2}$ ,边界条件由解析解反推得到。根据式（14）可知,达西流速解析解分别为 $v_{x} (x, y) = - 2 x^{3}$ 和 $v_{y} (x, y) = 6 x^{2} y$ 。本例为无量纲模型,故所有参数量纲均为1。

图 8 渗透系数分布示意图

Figure 8. Distribution of permeability coefficient

下载: 全尺寸图片幻灯片

分别使用NMM-W₀、NMM-W_A和NMM-W_B程序模拟本算例,图9,10分别为x和y方向流速的等值线结果。从图中可以看出,3个程序的流速场计算结果是一致的,但是NMM-W0的计算结果连续性差,单元间流速是不连续的,而NMM-W_A和NMM-W_B计算的流速均是连续的。

图 9 x方向流速等值线图

Figure 9. Contour maps of Darcy velocity in x direction

下载: 全尺寸图片幻灯片

图 10 y方向流速等值线图

Figure 10. Contour maps of Darcy velocity in y direction

下载: 全尺寸图片幻灯片

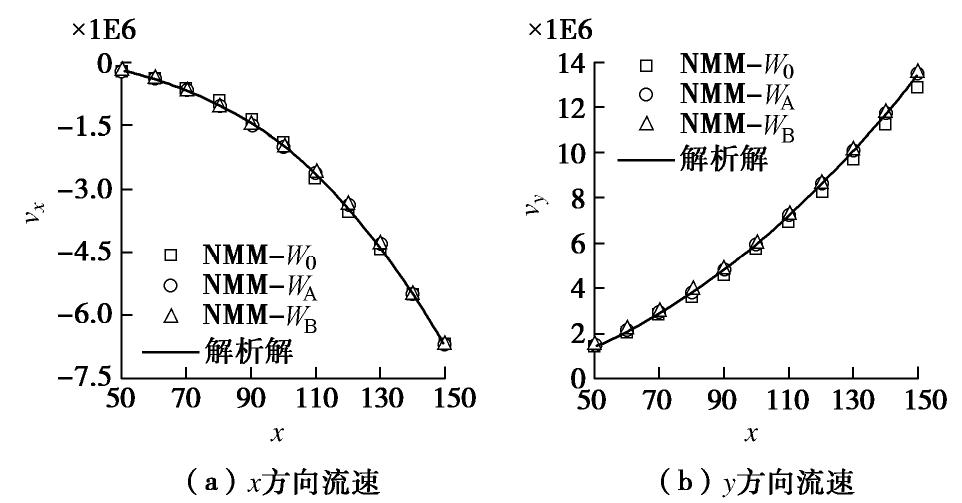
选取y=100处的数值结果与本例解析解对比,结果如图11所示。从图中可以看出流速计算结果均接近解析解,且改进后程序的结果更精确。

图 11 y=100处流速计算结果与解析解的对比图

Figure 11. Comparison between numerical and analytical solutions

下载: 全尺寸图片幻灯片

为进一步分析计算结果的精度与收敛性,分别定义水头与流速的误差范数为

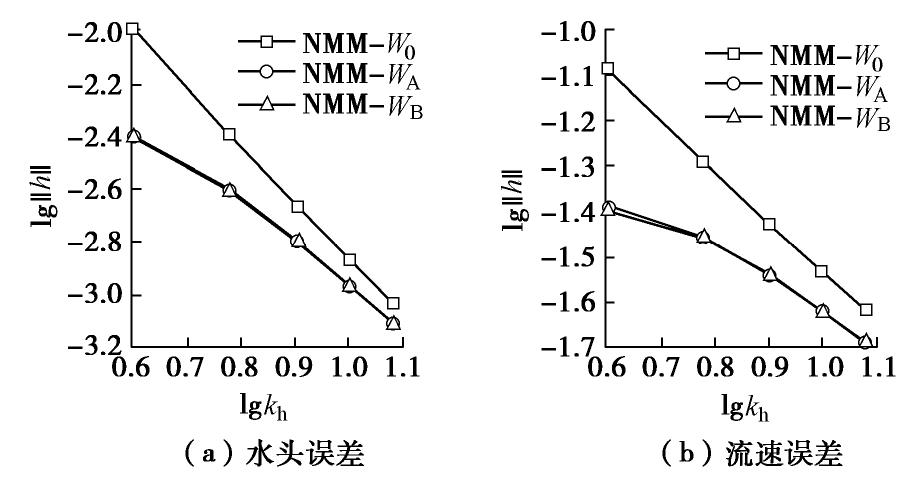
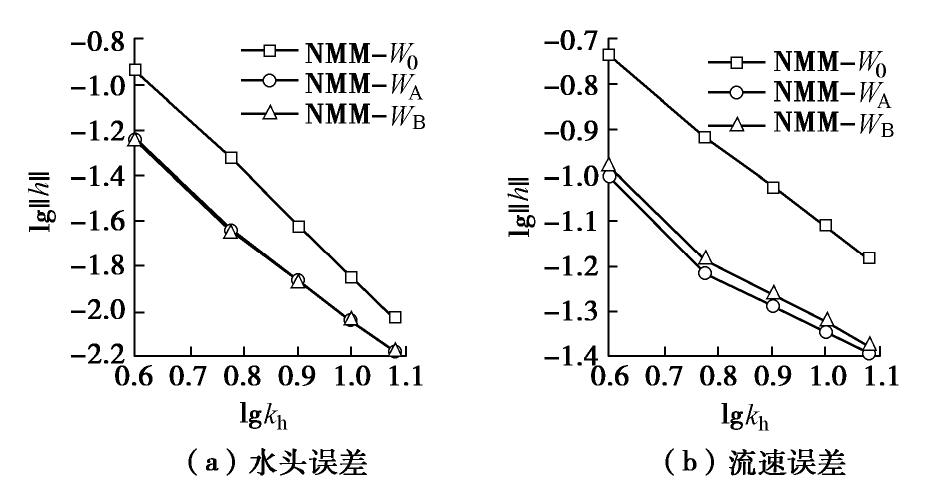
$‖ h ‖ = \sqrt{\frac{\int_{Ω} {(h^{ex} - h^{num})}^{2} d Ω}{\int_{Ω} {(h^{ex})}^{2} d Ω}}$ ,

(23)

$‖ v ‖ = \sqrt{\frac{\int_{Ω} {(j^{ex} - j^{num})}^{T} K (j^{ex} - j^{num}) d Ω}{\int_{Ω} {(j^{ex})}^{T} K (j^{ex}) d Ω}}$ 。

(24)

式中,上标ex表示解析解,上标num表示数值解。在对水头和流速的误差统计后,分别绘制算例一中水头与流速的收敛性曲线如图12所示（k_h为数学网格层数）,可以看出使用改进程序NMM-W_A和NMM-W_B的计算结果是收敛的,且精度比NMM-W₀更高。

图 12 水头与流速的收敛性曲线

Figure 12. Convergence curves of hydraulic head and velocity

下载: 全尺寸图片幻灯片

为了验证改进程序对线性相关问题的改善,表1记录了不同权函数与覆盖函数组合的总体系数矩阵亏秩数。当亏秩数不为零时即说明该线性方程组存在线性相关问题,计算结果将不可靠^[18]。从表1中可以看出,采用双线性权函数W₀时直接升高覆盖函数的阶次会带来线性相关问题,而采用改进权函数W_A和W_B的NMM程序均不出现线性相关问题。

表 1 不同NMM程序总体系数矩阵的亏秩数与总计算自由度

Table 1. Number of nullity and total degrees of freedom

k_h	P₀-W₀	P₁-W₀	P₁-W_A	P₁-W_B
4	0/25	10/75	0/75	0/75
6	0/49	14/147	0/147	0/147
8	0/81	18/243	0/243	0/243
10	0/121	22/363	0/363	0/363
12	0/169	26/507	0/507	0/507
注：P为覆盖函数的阶次,其中P₀为常数,P₁为一阶泰勒展开多项式。

下载: 导出CSV

| 显示表格

4.2 算例2：渗透系数局部剧烈变化的强非均质渗流

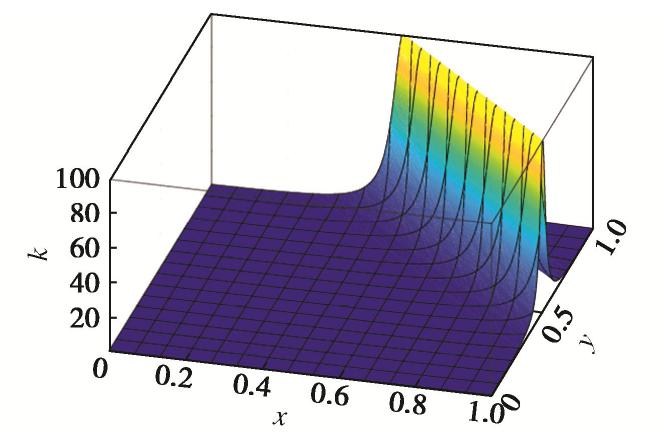
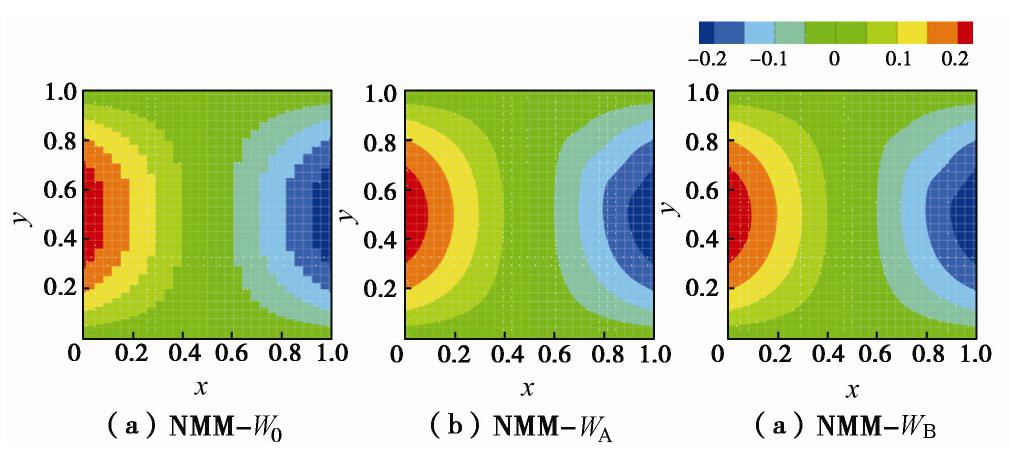
如图13所示,在[0, 1]×[0, 1]的矩形计算域内,渗透系数 $K (x, y) = 1 / {2 + 1.99 \sin [π (x + y)]}$ ,在局部存在剧烈变化^[19]。参照文献[19]构造如下解析解为 $H (x, y) =$ $x y (1 - x) (1 - y)$ ,边界条件和源汇项由解析解反推得到。根据式（13）,（14）可分别求出本例水力梯度和达西流速的解析解。本例为无量纲模型,故所有参数量纲均为1。

图 13 渗透系数分布示意图

Figure 13. Distribution of permeability coefficient

下载: 全尺寸图片幻灯片

分别使用NMM-W₀、NMM-W_A和NMM-W_B模拟本算例。图14为x方向水力梯度的计算结果,可见改进后程序的梯度场计算结果是连续的。

图 14 x方向水力梯度等值线图

Figure 14. Contour maps of hydraulic gradient in x direction

下载: 全尺寸图片幻灯片

图15为x方向流速的计算结果,可以看出在渗透系数突变处的流速的变化最剧烈。图16给出了局部放大的流速场结果,可见改进后程序的流速场计算结果也是连续的。

图 15 x方向流速等值线图

Figure 15. Contour maps of Darcy velocity in x direction

下载: 全尺寸图片幻灯片

图 16 x方向流速等值线图局部放大示意图

Figure 16. Partial enlargement view of Darcy velocity in x direction

下载: 全尺寸图片幻灯片

分别绘制算例二中水头和流速的收敛性曲线如图17所示。同样可以看出使用改进程序NMM-W_A和NMM-W_B的计算结果是收敛的,且精度比NMM-W₀更高。

图 17 水头和流速收敛性曲线

Figure 17. Convergence curves of hydraulic head and velocity

下载: 全尺寸图片幻灯片

4.3 算例3：渗透系数随机分布的非均质坝基渗流

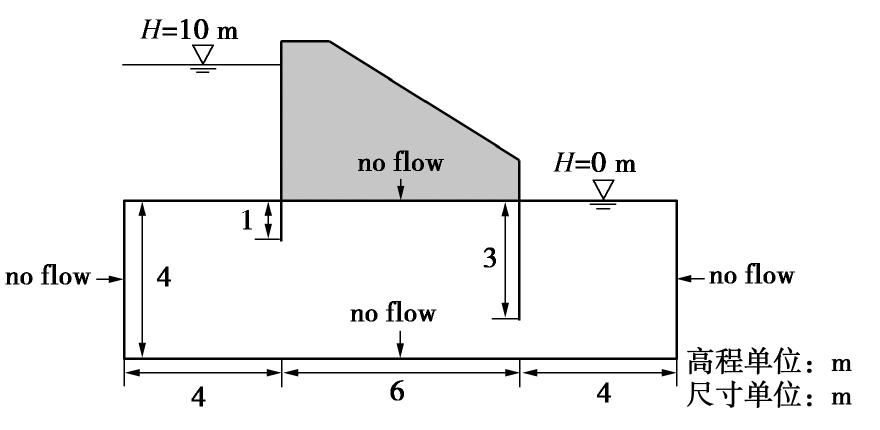
本例对渗透系数随机分布的非均质坝基有压渗流进行模拟,坝前后分别有防渗墙/防渗膜^[20]。考虑到防渗墙/膜厚度很薄,且渗透性很低,可以认为不透水,在NMM建模中可以不用实体建模,而直接使用不透水线切割模型模拟防渗墙/膜的效果。

模型尺寸以及边界条件如图18所示,坝基土层渗透系数使用Weibull分布表征,满足Weibull分布的随机变量x的概率密度函数表示为

$f (x) = \frac{b}{a} {(\frac{x}{a})}^{b - 1} e^{- {(x / a)}^{b}}$ ,

(25)

图 18 计算模型尺寸及边界条件示意图

Figure 18. Model sizes and boundary conditions

下载: 全尺寸图片幻灯片

式中,a为比例参数,b为形状参数,可以表征非均匀性（b值越小非均匀性越强）。本例中取a=1×10^-4 m/s,形状参数b分别设置为1,5,10来模拟不同程度的非均质坝基土层。

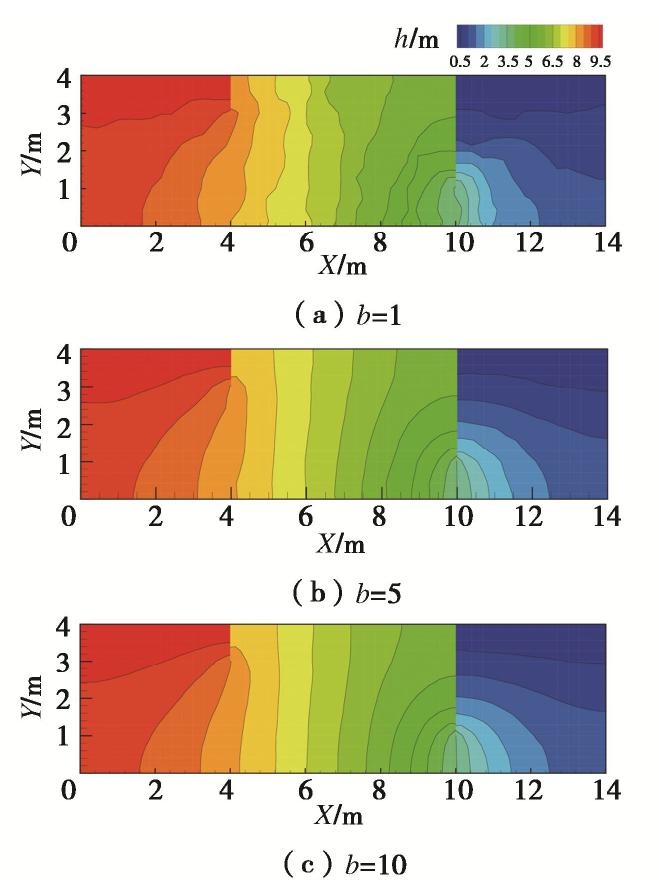
采用NMM-W₀分别进行b=1,5,10三种不同程度的非均质坝基渗流模拟,水头等值线分布如图19所示。从图19中可以看出,非均质性越高,水头分布线越曲折。改进程序NMM-W_A和NMM-W_B的水头计算结果也是类似的,这里不作赘述。

图 19 不同均匀程度对水头等值线的影响

Figure 19. Contour maps of hydraulic head under different heterogeneities

下载: 全尺寸图片幻灯片

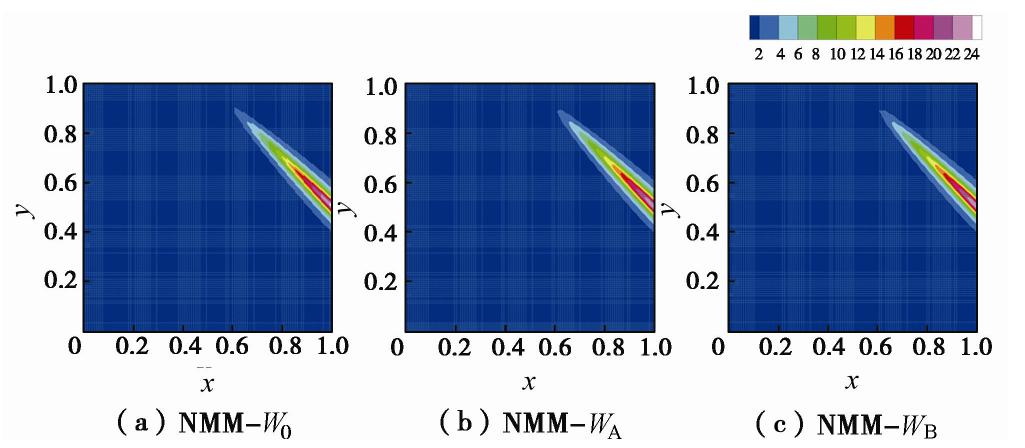
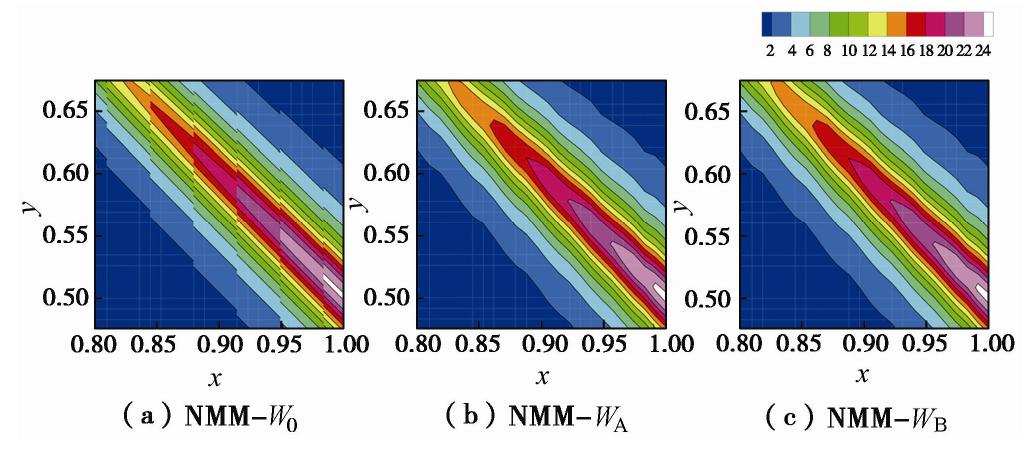
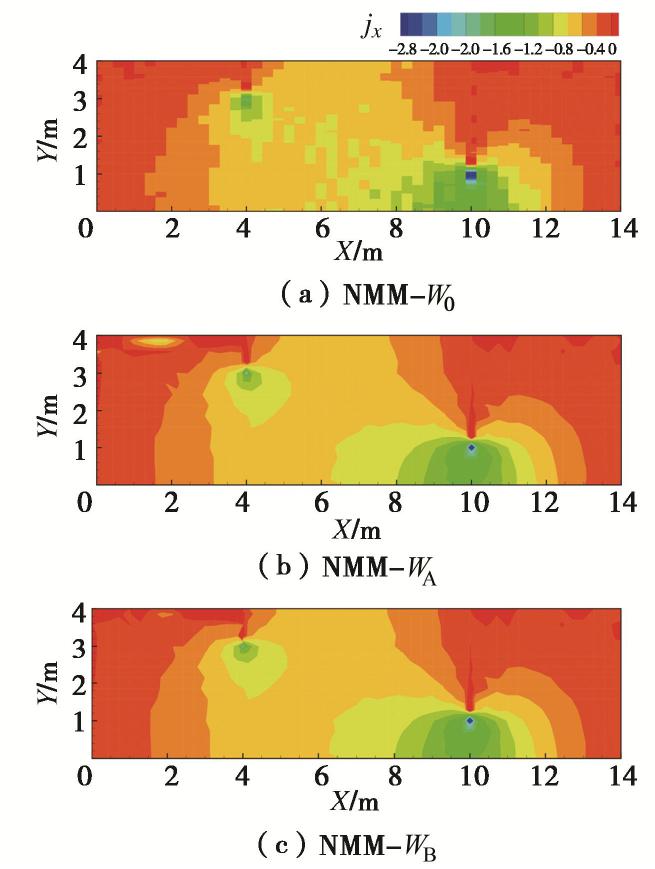
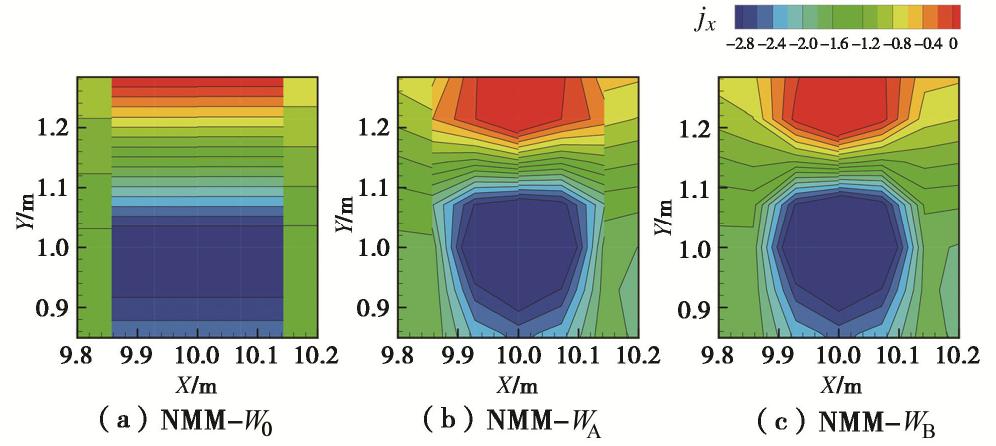
由于本例中单元的渗透系数是随机分布的,每个单元边界的渗透系数都不连续,因而达西流速的计算结果在单元之间必然也是不连续的。所以考察水力梯度结果,选取b=10的某一组随机渗透系数分布,将NMM-W₀、NMM-W_A和NMM-W_B的x方向水力梯度计算结果进行对比,如图20所示。对下游防渗墙/膜底部高水力梯度区的计算结果局部放大（见图21）,可以看出NMM-W_A的梯度场计算结果仅保证在节点处连续,而在单元边界处不连续,而NMM-W_B的梯度场计算结果满足全局连续。

图 20 x方向水力梯度等值线图

Figure 20. Contour maps of hydraulic gradient in x direction

下载: 全尺寸图片幻灯片

图 21 局部高水力梯度放大图

Figure 21. Partial enlargement view of hydraulic gradient

下载: 全尺寸图片幻灯片

4.4 算例4：渗透系数随机分布的非均质自由面渗流

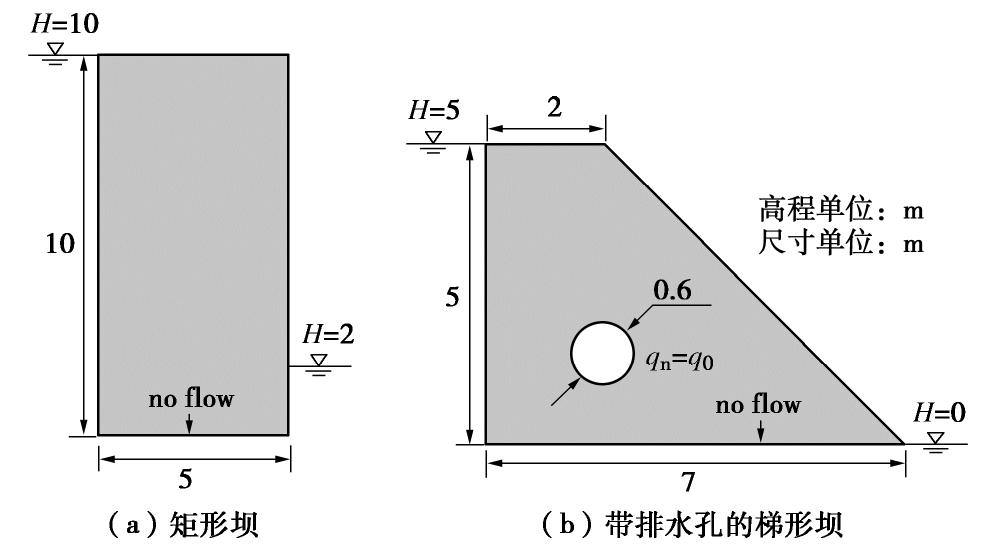
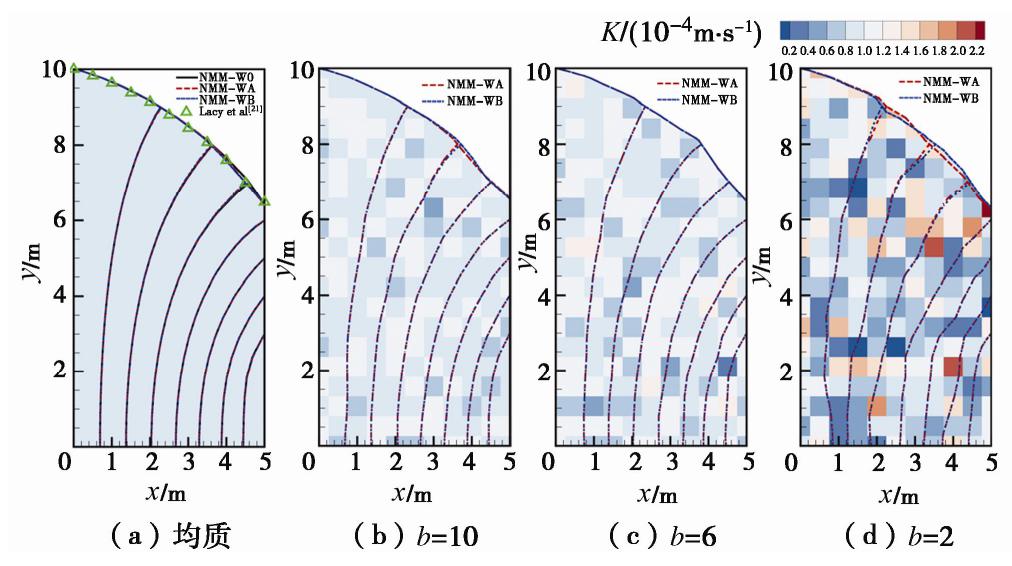
前3个算例均属于有压渗流问题,而实际工程中的渗流分析多以无压渗流为主。为验证改进NMM程序对无压渗流的适用性,构造了两个非均质自由面渗流的算例（见图22）。其中,第一个是简化的矩形坝,其计算模型尺寸及边界条件如图22（a）所示。本例的非均质渗透系数仍采用式（25）的Weibull分布表征,取a=1×10^-4 m/s,调整形状参数b来模拟不同程度的非均质坝体。

图 22 计算模型尺寸及边界条件示意图

Figure 22. Model sizes and boundary conditions

下载: 全尺寸图片幻灯片

图23（a）为考虑均质材料的矩形坝计算结果,可以看出不同NMM程序计算得到的自由面光滑且位置与文献结果^[21]保持一致,验证了改进NMM程序对无压渗流问题的适用性。图23（b）～（d）分别为不同非均质材料（b=10,6,2）的自由面与水头等值线计算结果。图中单元的颜色表示渗透系数,可以看出NMM-W_A与NMM-W_B计算得到的自由面结果具有很好的一致性,且非均质性越强,自由面与水头等值线越曲折。

图 23 矩形坝自由面渗流计算结果

Figure 23. Computed results of a rectangular dam

下载: 全尺寸图片幻灯片

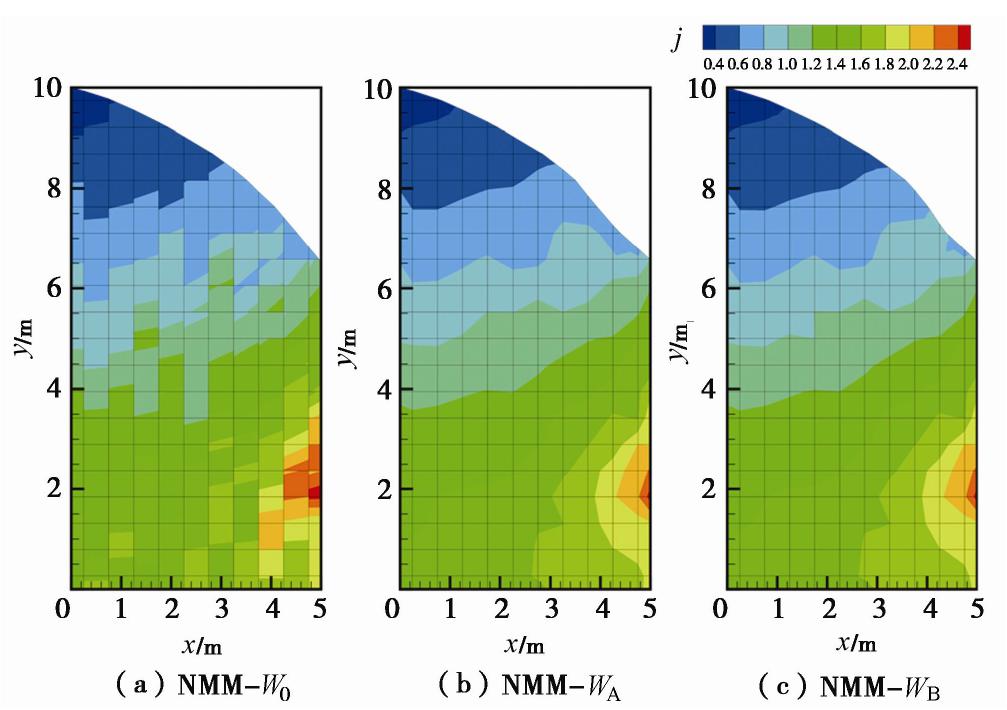
考察b=10这一组的水力梯度计算结果（见图24）,可知改进后的程序对于非均质无压渗流问题同样可以得到连续的梯度场结果。

图 24 水力梯度等值线图（b=10）

Figure 24. Contour maps of hydraulic gradient

下载: 全尺寸图片幻灯片

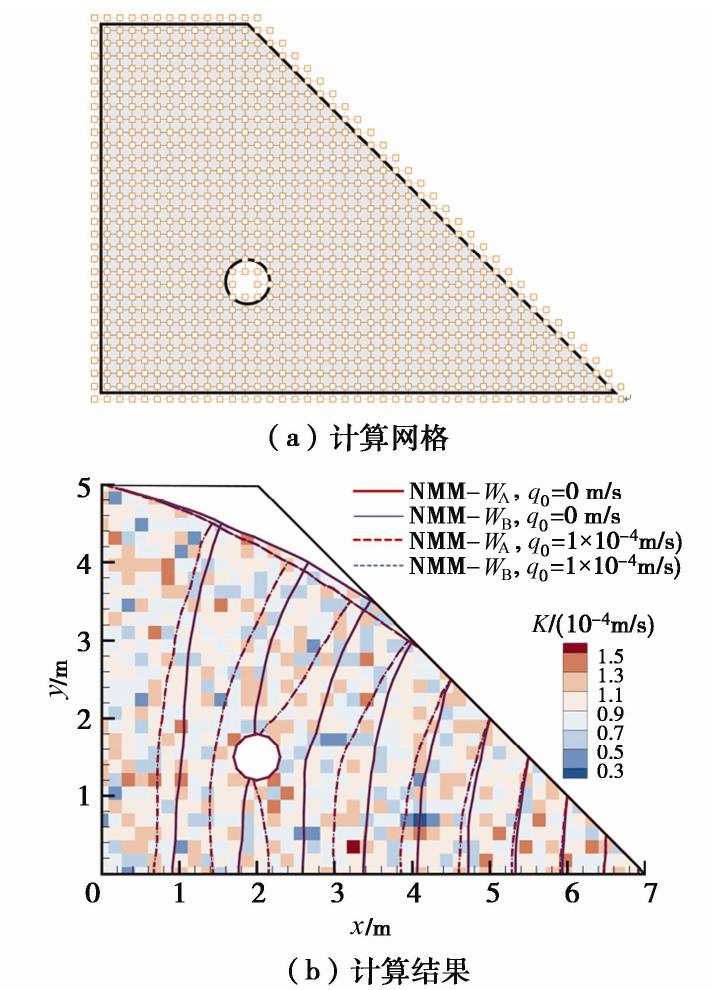
为进一步验证本文改进NMM程序对复杂无压渗流的适用性,最后模拟了一个考虑排水孔的梯形坝自由面渗流问题,其模型尺寸与边界条件见图22（b）。基于NMM双重覆盖系统的优势,不论边界形状是否规则,均可使用规则的数学网格去覆盖生成流形单元。这使得NMM的前处理工作大为简化,本例的计算网格如图25（a）所示。非均质渗透系数同矩形坝算例（取b=5）,图25（b）给出了排水孔流量q₀分别为0,1×10^-4 m/s时改进NMM程序的计算结果,成功地模拟了排水孔降低渗流自由面的现象。

图 25 考虑排水孔梯形坝的计算网格与结果

Figure 25. Computed meshes and results of a dam with drain hole

下载: 全尺寸图片幻灯片

5. 结论

本文分析了渗流计算程序NMM-W₀计算流速场精度低且不连续的原因,在此基础上使用两种改进权函数分别编制了新的渗流计算程序。使用改进后的程序进行非均质渗流算例验证。主要得出以下4点结论。

（1）改进后的程序NMM-W_A和NMM-W_B均没有线性相关问题。

（2）误差分析表明,改进后的程序NMM-W_A和NMM-W_B对水头和流速的计算是收敛的,且精度高于NMM-W₀。

（3）改进权函数后可以获得连续性更好的流速/梯度解,其中NMM-W_A保持流速/梯度场在拓扑星点处连续,但在局部高水力梯度位置单元边界上的流速/梯度场是不连续的,而NMM-W_B可以获得全局连续的流速/梯度场。

（4）算例表明,本文改进NMM程序同样适用于非均质的无压渗流问题,且可获得连续的流速/梯度场。

图 1 流形单元的生成过程

Figure 1. Formation process of manifold elements

下载: 全尺寸图片幻灯片

图 2 矩形数学网格的覆盖系统示意图

Figure 2. Cover system of rectangular mathematical meshes

下载: 全尺寸图片幻灯片

图 3 局部坐标系

Figure 3. Local coordinate system

下载: 全尺寸图片幻灯片

图 4 渗流问题几何示意图

Figure 4. Geometric diagram of seepage problem

下载: 全尺寸图片幻灯片

图 5 双线性权函数及其偏导数

Figure 5. Bilinear weight function and its partial derivatives

下载: 全尺寸图片幻灯片

图 6 改进权函数W_A及其偏导数

Figure 6. Improved weight function W_A and its partial derivatives

下载: 全尺寸图片幻灯片

图 7 改进权函数W_B及其偏导数

Figure 7. Improved weight function W_B and its partial derivatives

下载: 全尺寸图片幻灯片

图 8 渗透系数分布示意图

Figure 8. Distribution of permeability coefficient

下载: 全尺寸图片幻灯片

图 9 x方向流速等值线图

Figure 9. Contour maps of Darcy velocity in x direction

下载: 全尺寸图片幻灯片

图 10 y方向流速等值线图

Figure 10. Contour maps of Darcy velocity in y direction

下载: 全尺寸图片幻灯片

图 11 y=100处流速计算结果与解析解的对比图

Figure 11. Comparison between numerical and analytical solutions

下载: 全尺寸图片幻灯片

图 12 水头与流速的收敛性曲线

Figure 12. Convergence curves of hydraulic head and velocity

下载: 全尺寸图片幻灯片

图 13 渗透系数分布示意图

Figure 13. Distribution of permeability coefficient

下载: 全尺寸图片幻灯片

图 14 x方向水力梯度等值线图

Figure 14. Contour maps of hydraulic gradient in x direction

下载: 全尺寸图片幻灯片

图 15 x方向流速等值线图

Figure 15. Contour maps of Darcy velocity in x direction

下载: 全尺寸图片幻灯片

图 16 x方向流速等值线图局部放大示意图

Figure 16. Partial enlargement view of Darcy velocity in x direction

下载: 全尺寸图片幻灯片

图 17 水头和流速收敛性曲线

Figure 17. Convergence curves of hydraulic head and velocity

下载: 全尺寸图片幻灯片

图 18 计算模型尺寸及边界条件示意图

Figure 18. Model sizes and boundary conditions

下载: 全尺寸图片幻灯片

图 19 不同均匀程度对水头等值线的影响

Figure 19. Contour maps of hydraulic head under different heterogeneities

下载: 全尺寸图片幻灯片

图 20 x方向水力梯度等值线图

Figure 20. Contour maps of hydraulic gradient in x direction

下载: 全尺寸图片幻灯片

图 21 局部高水力梯度放大图

Figure 21. Partial enlargement view of hydraulic gradient

下载: 全尺寸图片幻灯片

图 22 计算模型尺寸及边界条件示意图

Figure 22. Model sizes and boundary conditions

下载: 全尺寸图片幻灯片

图 23 矩形坝自由面渗流计算结果

Figure 23. Computed results of a rectangular dam

下载: 全尺寸图片幻灯片

图 24 水力梯度等值线图（b=10）

Figure 24. Contour maps of hydraulic gradient

下载: 全尺寸图片幻灯片

图 25 考虑排水孔梯形坝的计算网格与结果

Figure 25. Computed meshes and results of a dam with drain hole

下载: 全尺寸图片幻灯片

表 1 不同NMM程序总体系数矩阵的亏秩数与总计算自由度

Table 1 Number of nullity and total degrees of freedom

k_h	P₀-W₀	P₁-W₀	P₁-W_A	P₁-W_B
4	0/25	10/75	0/75	0/75
6	0/49	14/147	0/147	0/147
8	0/81	18/243	0/243	0/243
10	0/121	22/363	0/363	0/363
12	0/169	26/507	0/507	0/507
注：P为覆盖函数的阶次,其中P₀为常数,P₁为一阶泰勒展开多项式。

下载: 导出CSV

参考文献(21)

[1]	薛禹群, 谢春红. 地下水数值模拟[M]. 北京: 科学出版社, 2007: 175-178. XUE Yu-qun, XIE Chun-hong. Numerical Simulation for Groundwater[M]. Beijing: Science Press, 2007: 175-178. (in Chinese)
[2]	BATU V. A finite element dual mesh method to calculate Nodal Darcy velocities in nonhomogeneous and anisotropic aquifers[J]. Water Resources Research, 1984, 20(11): 1705-1717. doi: 10.1029/WR020i011p01705
[3]	YEH G T. On the computation of Darcian velocity and mass balance in the finite element modeling of groundwater flow[J]. Water Resources Research, 1981, 17(5): 1529-1534. doi: 10.1029/WR017i005p01529
[4]	谢春红, 赵文良, 张天岭, 等. 地下水不稳定渗流达西速度计算新方法[J]. 岩土工程学报, 1996, 18(1): 68-74. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC601.009.htm XIE Chun-hong, ZHAO Wen-liang, ZHANG Tian-ling, et al. A new method for calculating the Darcy velocity of unstable groundwater seepage[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(1): 68-74. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC601.009.htm
[5]	张湘伟, 章争荣, 吕文阁, 等. 数值流形方法研究及应用进展[J]. 力学进展, 2010, 40(1): 1-12. https://www.cnki.com.cn/Article/CJFDTOTAL-LXJZ201001003.htm ZHANG Xiang-wei, ZHANG Zheng-rong, LÜ Wen-ge, et al. Advances and perspectives in numerical manifold method and its applications[J]. Advances in Mechanics, 2010, 40(1): 1-12. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXJZ201001003.htm
[6]	MA G W, AN X M, HE L. The numerical manifold method: a review[J]. International Journal of Computational Methods, 2010, 7(1): 1-32. doi: 10.1142/S0219876210002040
[7]	ZHANG Z R, ZHANG X W, YAN J H. Manifold method coupled velocity and pressure for Navier-Stokes equations and direct numerical solution of unsteady incompressible viscous flow[J]. Computers and Fluids, 2010, 39(8): 1353-1365. doi: 10.1016/j.compfluid.2010.04.005
[8]	陈远强, 杨永涛, 郑宏, 等. 饱和-非饱和渗流的数值流形法研究与应用[J]. 岩土工程学报, 2019, 41(2): 338-347. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902014.htm CHEN Yuan-qiang, YANG Yong-tao, ZHENG Hong, et al. Saturated-unsaturated seepage by numerical manifold method[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 338-347. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201902014.htm
[9]	李伟, 郑宏. 基于数值流形法的渗流问题边界处理新方法[J]. 岩土工程学报, 2017, 39(10): 1867-1873. doi: 10.11779/CJGE201710015 LI Wei, ZHENG Hong. New boundary treatment for seepage flow problem based on numerical manifold method[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(10): 1867-1873. (in Chinese) doi: 10.11779/CJGE201710015
[10]	WANG Y, HU M S, ZHOU Q L, et al. Energy-work-based numerical manifold seepage analysis with an efficient scheme to locate the phreatic surface[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(15): 1633-1650. doi: 10.1002/nag.2280
[11]	WANG Y, HU M S, ZHOU Q L, et al. A new second-order numerical manifold method model with an efficient scheme for analyzing free surface flow with inner drains[J]. Applied Mathematical Modelling, 2016, 40(2): 1427-1445. doi: 10.1016/j.apm.2015.08.002
[12]	SHI G H. Manifold methods of material analysis[C]//Transactions of the 9th Army Conference on Applied Mathematics and Computing. Minneapolis, 1991.
[13]	唐旭海, 郑超, 吴圣川, 等. 节点应力连续的四边形单元[J]. 应用数学和力学, 2009, 30(12): 1427-1439. doi: 10.3879/j.issn.1000-0887.2009.12.004 TANG Xu-hai, ZHENG Chao, WU Sheng-chuan, et al. A novel four -node quadrilateral element with continuous nodal stress[J]. Applied Mathematics and Mechanics, 2009, 30(12): 1427-1439. (in Chinese) doi: 10.3879/j.issn.1000-0887.2009.12.004
[14]	YANG Y T, SUN G H, ZHENG H, et al. A four-node quadrilateral element fitted to numerical manifold method with continuous nodal stress for crack analysis[J]. Computers & Structures, 2016, 177: 69-82.
[15]	王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003: 112-113. WANG Xu-cheng. Finite Element Method[M]. Beijing: Tsinghua University Press, 2003: 112-113. (in Chinese)
[16]	YANG Y T, SUN G H, ZHENG H. A high-order numerical manifold method with continuous stress/strain field[J]. Applied Mathematical Modelling, 2020, 78: 576-600. doi: 10.1016/j.apm.2019.09.034
[17]	谢一凡. 改进多尺度有限单元法求解二维地下水流问题[D]. 南京: 南京大学, 2015: 45-46. XIE Yi-fan. Modified Multiscale Finite Element Method for 2-D Groundwater Flow Problems[D]. Nanjing: Nanjing University, 2015: 45-46. (in Chinese)
[18]	AN X M, LI L X, MA G W, et al. Prediction of rank deficiency in partition of unity-based methods with plane triangular or quadrilateral meshes[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(5/6/7/8): 665-674.
[19]	赵文凤, 谢一凡, 吴吉春. 一种模拟节点达西渗透流速的双重网格多尺度有限单元法[J]. 岩土工程学报, 2020, 42(8): 1474-1481. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202008018.htm ZHAO Wen-feng, XIE Yi-fan, WU Ji-chun. A dual-mesh multiscale finite element method for simulating nodal Darcy velocities in aquifers[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(8): 1474-1481. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202008018.htm
[20]	GRIFFITHS D V, FENTONT G A. The Random Finite Element Method (RFEM) in Steady Seepage Analysis[M]//CISM Courses and Lectures. Vienna: Springer, 2007: 225-241.
[21]	LACY S J, PREVOST J H. Flow through porous media: a procedure for locating the free surface[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1987, 11(6): 585-601.

施引文献(2)

期刊类型引用(2)

1.	刘志文，王媛，董琪，高山. 不连续界面渗流的堤防防渗膜防渗效果模拟研究. 人民黄河. 2024(06): 48-53+67 . 百度学术
2.	张升，兰鹏，苏晶晶，熊海斌. 基于PINNs算法的地下水渗流模型求解及参数反演. 岩土工程学报. 2023(02): 376-383+443-444 . 本站查看