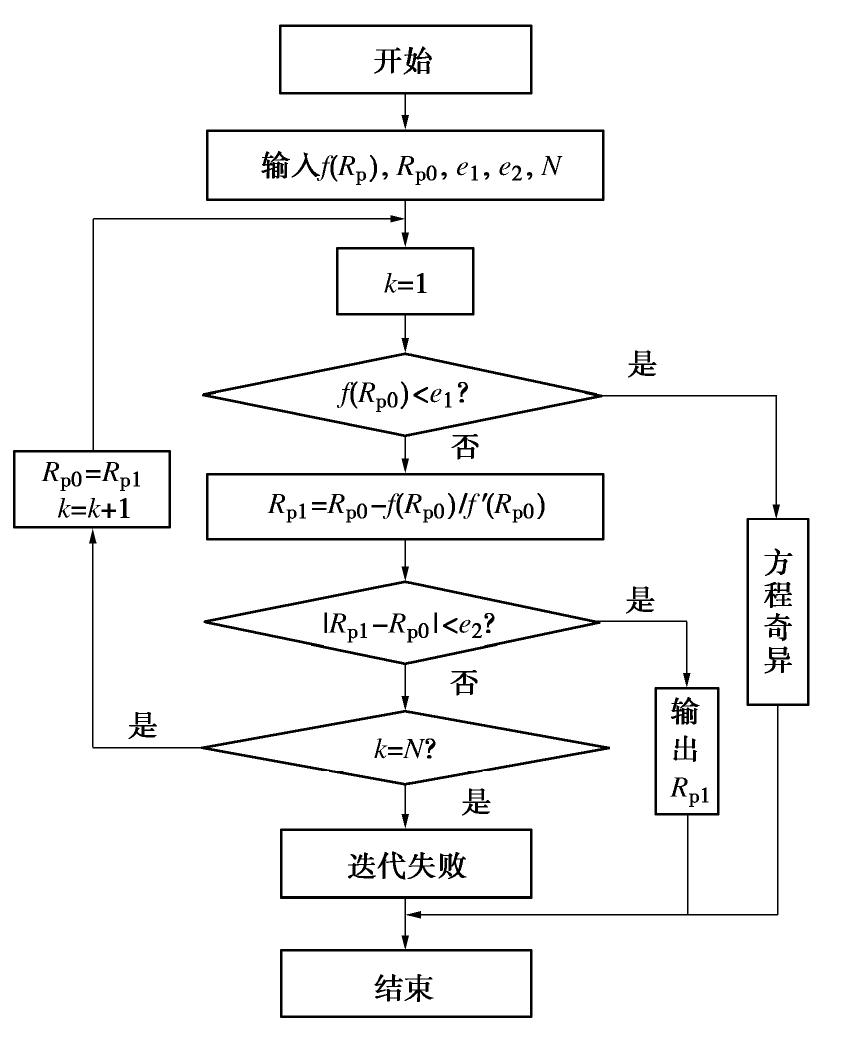
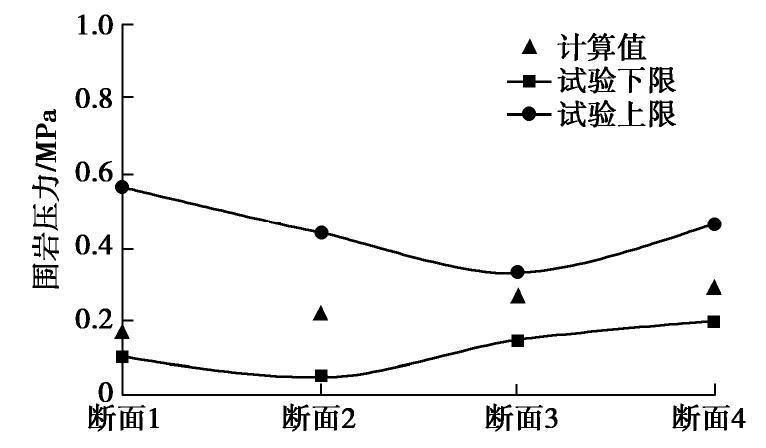
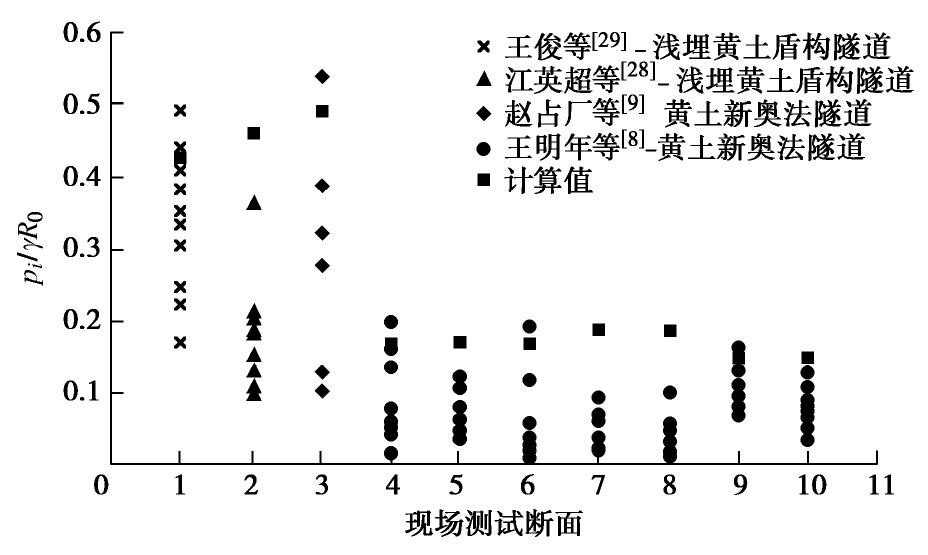
Pressure of surrounding rock of deep-buried loess shield tunnel
-
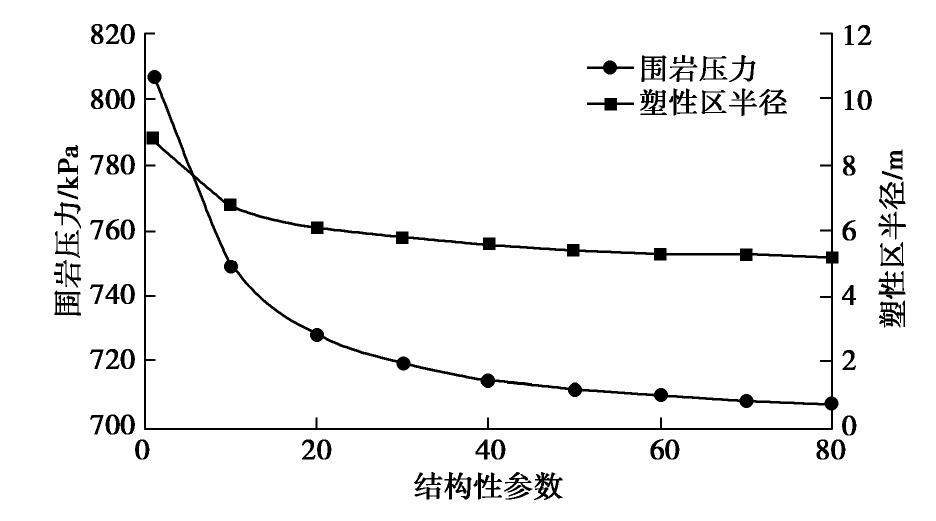
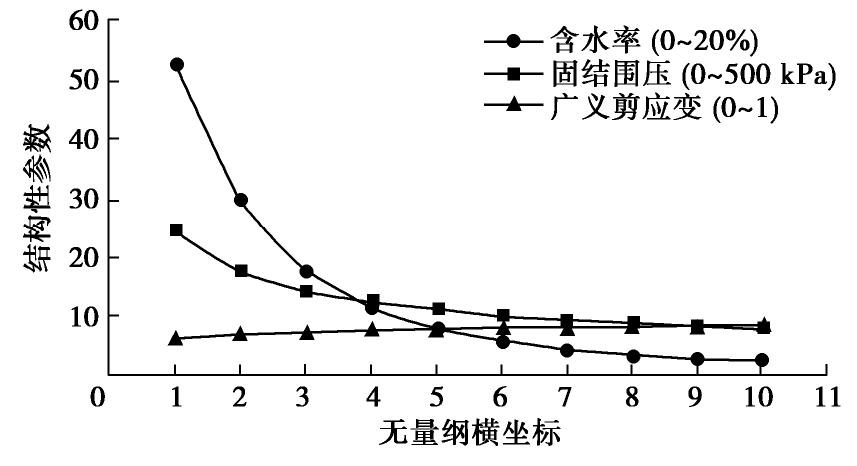
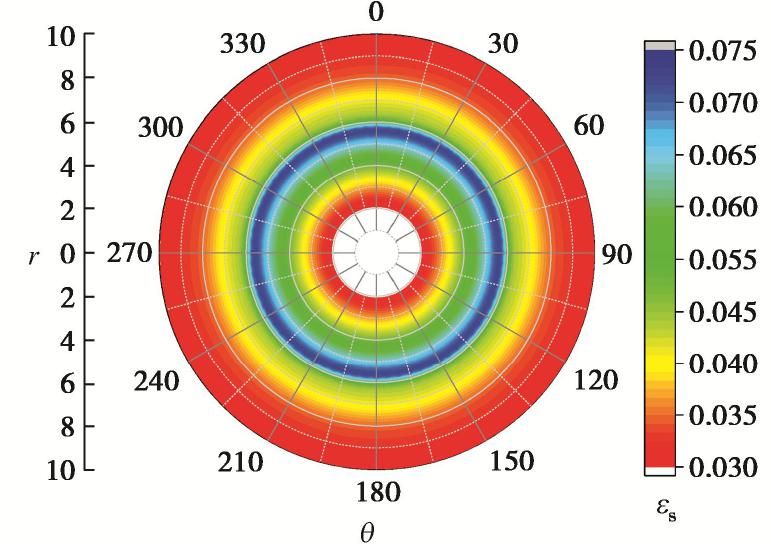
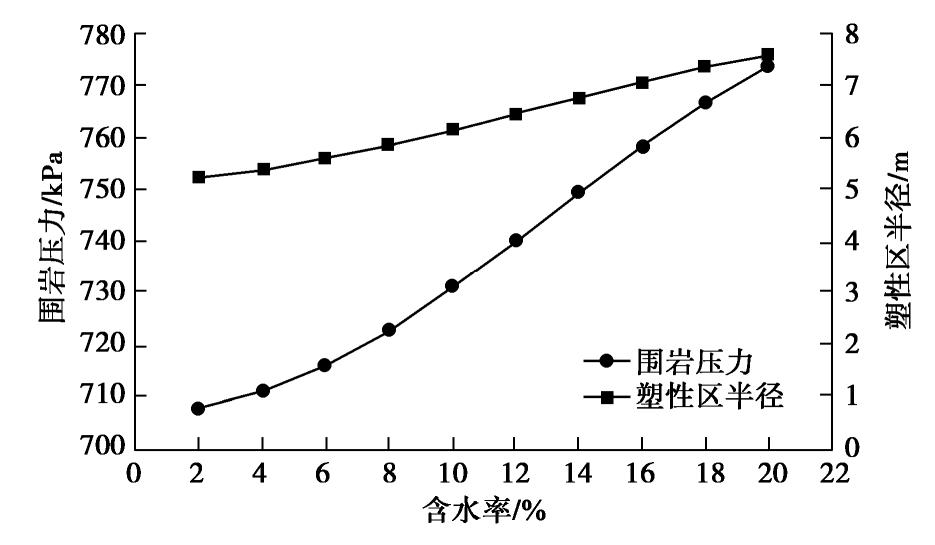
摘要: 随着盾构隧道工程的发展,越来越多的深埋黄土盾构隧道逐步出现。对其围岩压力进行准确计算对衬砌设计及服役期的安全评价具有重要意义。围绕深埋黄土盾构隧道围岩压力的计算,考虑盾构隧道衬砌与围岩的径向变形连续条件,基于芬纳公式,推导了盾构隧道衬砌内力、围岩应力及围岩变形的解析解;引入黄土结构性参数,给出了适用黄土盾构隧道的围岩压力解析解;结合隧道开挖后围岩的广义剪应变,构建了黄土隧道围岩结构性参数的求解方法;结合黄土结构性参数,讨论了围岩增湿对黄土结构性参数及围岩压力的影响。研究发现:广义剪应变在塑性区内沿径向增大,在弹性区内逐渐减小,2倍塑性区半径外基本稳定;围岩的黄土结构性参数在塑性区内可认为均匀分布;围岩含水率由2%增加至20%时,塑性区的扩大幅度约为33%,围岩压力的增幅约为10%。研究成果以期对深埋黄土盾构隧道的围岩压力计算提供思路。Abstract: With the development of shield tunnel engineering, more and more deep-buried loess shield projects have gradually appeared. The calculation of pressure of the surrounding rock is of great significance to the design of linings and safety evaluation during the service period. The aim of this study is to establish a theoretical solution for pressure of the surrounding rock of deep-buried loess shield tunnel. With the consideration of the continuous conditions of the radial deformation at the interface between the linings and the surrounding rock, the analytical solutions for forces and displacements of the linings and surrounding rock are derived based on the Fenner formula. Then, the analytical solution of pressure of the surrounding rock applicable to loess shield tunnel is given by introducing the structural parameters of loess. Considering the generalized shear strain of the surrounding rock after tunnel excavation, a solving method for the structural parameters of surrounding rock of loess tunnel is given. The influences of humidification on the structural parameters of loess and the pressure of surrounding rock are then discussed by introducing the surrounding rock structural parameters of loess. It is found that the generalized shear strain increases radially in the plastic zone and gradually decreases in the elastic zone. It is basically stable outside the twice the radius of the plastic zone. The structural parameters of loess of the surrounding rock can be recognized as evenly distributed in the plastic zone. When the water content of rock increases from 2% to 20%, the expansion of the plastic zone is about 33%, and the increase of the pressure of the surrounding rock is about 10%. The research results are expected to provide ideas for the calculation of pressure of the surrounding rock of deep-buried loess shield tunnels.
-
Keywords:
- shield tunnel /
- loess /
- surrounding rock pressure /
- Fenner formula /
- structural parameter
-
0. 引言
中国正积极推进海洋强国战略,海洋资源开发产业发展十分迅速,高桩码头、跨海桥梁、海洋平台、风电机组、输电塔等海上构筑物不断涌现,各种大直径管桩也因各自的优点和特点广泛应用于上述大型海洋工程中。海上构筑物存在复杂的荷载条件,海上构筑物的桩基础不仅需要承受上部结构的自重荷载,同时需要承受风荷载、波浪力、水流力、地震作用等水平动荷载,在极端环境工况下,巨大的水平向荷载会引起桩基础发生较大的水平变形,使得风机停机、油气平台倾斜失效。此外,当桩基础和上部结构一阶自振频率与这些动荷载的激振频率接近时,容易发生共振,在基础和结构中引起更大的内力从而导致其产生崩塌破坏。研究水平动荷载作用下海洋工程中大直径管桩的受荷机理,对于中国科技兴海的战略发展具有重要的科学意义和工程实用价值。
近几十年,广大学者对水平动荷载下桩的动力响应问题开展了深入的研究。早期应用最广泛的计算模型是Winkler模型[1-2],其将桩周土和桩底土对桩的作用简化为弹簧和阻尼器的形式,但Winkler模型的缺点是不能真正的考虑桩–土耦合振动,且在实际工程中难以精确的确定模型参数取值。后来Novak等[3]提出平面应变假定建立了简化桩土耦合振动理论,并基于这一理论展开了各种桩基振动特性的基础性研究,得到了许多重要结论。Novak平面应变理论的缺陷是忽略了土体内部纵向应力梯度的变化,应用到实际工程中时难免带来误差。与之相比,将土体视为三维连续介质,严格考虑桩土耦合作用及桩侧土竖向应力梯度变化的桩振动解析理论,在理论上更为精确。Novak等[4]将土体考虑为一个有限厚度的土层并考虑土体纵向应力梯度变化,得到了水平动载作用下刚性支承桩振动响应解析解。余俊等[5]将土体考虑为饱和两相介质,通过引入势函数对Biot动力固结方程解耦,研究了饱和土中端承桩的水平振动响应。章敏等[6]则研究了非饱和土中端承桩的水平振动特性。
以上这些研究均假定桩完全埋入土体中,然而海洋桩基多采用高桩的形式[7-8],其变形机理与完全埋入式桩基有明显的差异。许多学者曾对动荷载下高桩基础水平动力响应问题进行了研究。马宏旺等[9]采用数值模拟的方法研究了循环荷载作用下海上风电单桩基础水平动力特性。任青等[10]基于动力Winkler模型,提出了考虑桩顶竖向荷载的海洋群桩基础水平振动模型。Hu等[11]研究了考虑桩身轴力的饱和土地基中高桩基础的水平动力响应。
上述研究都是将高桩基础未埋入土中部分桩体考虑为自由段,而海洋桩基础其上部桩身是埋入海水中,桩身水平振动引起海水动水压力会对桩的水平振动特性产生影响。付鹏等[12-13]在徐汉忠[14]针对水中圆柱梁水平振动响应研究的基础上系统研究了海洋高桩基础水平振动响应问题,得到了一些有益的结论。但其研究是针对实心桩,而海洋工程中得到广泛应用的大直径管桩由于其薄壁中空的特性及桩芯土的存在与实心桩振动特性存在显著差异[15]。本文假设海水为无黏性不可压缩流体,考虑海洋大直径管桩与土体及流体的相互作用,求解得到了海洋大直径管桩基础水平振动响应解析解,并分析了其水平振动响应特性,本文研究成果可为海洋大直径管桩基础的工程设计提供参考。
1. 定解问题的建立
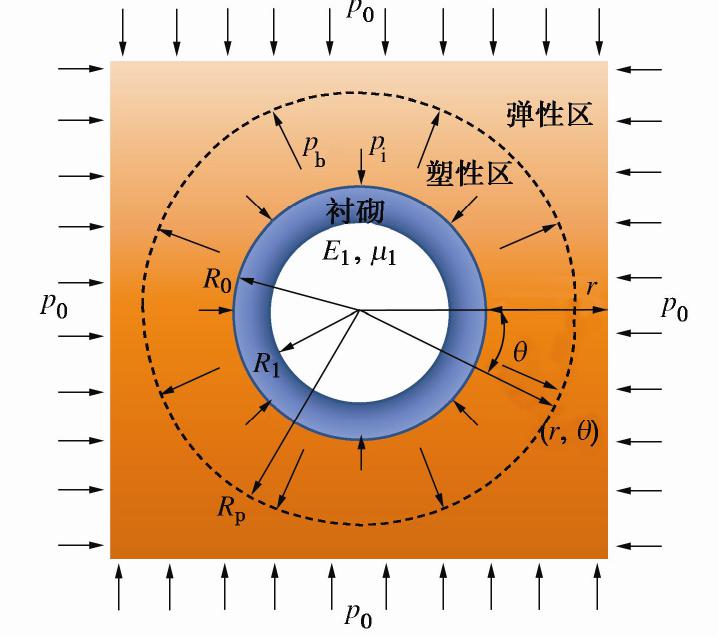
本文计算模型如图 1所示,桩长为H,外半径为r1,内半径为r2的大直径管桩埋入上覆海水下卧刚性基岩的黏弹性土层中。海水深度和土层厚度分别为H1,H2。管桩桩顶受到谐和激振水平荷载Peiωt作用,其中P为水平荷载幅值,ω为荷载频率,t为时间。
(1)流体运动控制方程
将海水假定为无黏性不可压缩流体,其控制方程为拉普拉斯方程,在柱坐标系下可表示为
∂2ϕj∂r2+1r∂ϕj∂r+1r2∂2ϕj∂θ2+∂2ϕj∂z2=0, (1) 式中,ϕj为海水速度势函数,j = 1,2。当j = 1时,上述方程和参数对应桩周海水,当j=2时,其对应管桩内壁腔内海水。
(2)土体运动控制方程
根据弹性动力学理论,忽略土体竖向位移,建立桩周土和桩芯土在柱坐标系上的运动控制方程为
G∗∇2urj+(λ∗+G∗)∂ej∂r−G∗r2(2∂uθj∂θ+urj)+ G∗∂2urj∂z2=−ρsω2urj, (2) G∗∇2uθj+(λ∗+G∗)∂ejr∂θ−G∗r2(uθj−2∂urj∂θ)+ G∗∂2uθj∂z2=−ρsω2uθj, (3) 式中,∇2=∂2∂r2+1r∂∂r+1r2∂2∂θ2为拉普拉斯算子,urj(r,θ,z),uθj(r,θ,z)为土体径向和切向位移;λ∗=λ(1+2iβs),G∗=G(1+2iβs)为土体复拉梅常数,其中i=√−1,βs为土体阻尼比,ρs为土体密度,ej=∂urj∂r+urjr+∂uθjr∂θ为土体体应变,同理,j = 1,2。当j = 1时,上述方程和参数对应桩周土,当j = 2时,其对应管桩内壁桩芯土。
(3)管桩水平振动方程
埋入海水和土层段的管桩控制方程分别为
E∗pIp∂4upw∂z4−ρpApω2upw+fw1+fw2=0(−H1⩽z⩽0), (4) E∗pIp∂4ups∂z4−ρpApω2ups+fs1 + fs2=0(0⩽z⩽H2), (5) 式中,upw,ups为埋入海水段和埋入土层段的管桩水平位移,fw1,fw2为作用于单位长度桩身的海水动水压力,fs1,fs2为作用于单位长度桩身的土体抗力,E*p=Ep(1+2iβp)为管桩复弹性模量,其中EP为桩弹性模量,βp为桩身材料阻尼比,Ip为管桩截面惯性矩,Ap为管桩截面面积,ρp为桩身材料密度。
2. 方程求解
2.1 海水运动方程求解
(1)桩周海水运动方程求解
基于分离变量法,海水速度势函数可表示为
ϕ1=R1(r)Φ1(θ)Z1(z)iωeiωt。 (6) 为简便起见,下文表达式中省略时间因子eiωt项。式(1)的通解为
ϕ1=[Aw1Im(hr)+Bw1Km(hr)]⋅[Cw1sin(mθ)+Dw1cos(mθ)]⋅ [Ew1cos(hz)+Fw1sin(hz)]iω , (7) 式中,Im(hr),Km(hr)分别为第一类和第二类m阶修正贝塞尔函数,Aw1,Bw1,Cw1,Dw1,Ew1,Fw1为待定系数。
海水边界条件假定为
ϕ1|z=−H1=0, (8) ∂ϕ1∂z|z=0=0, (9) ϕ1|r→∞<∞。 (10) 将式(7)代入上述边界条件可得
ϕ1=∞∑n=1Aw1nK1(hnr)cos(hnz)iωcosθ, (11) 式中,hn=(2n−1)π2H1,n=1,2,3,⋯。
海水中的动水压力为
q1=−ρw∂ϕ1∂t=ρwω2∞∑n=1Aw1nK1(hnr)cos(hnz)cosθ, (12) 式中,ρw为海水密度。
作用于单位长度桩身的海水动水压力为
fw1=∫2π0q1|r=r1r1cosθdθ=πr1ρwω2∞∑n=1Aw1nK1(hnr1)cos(hnz)。 (13) (2)桩芯海水运动方程求解
与桩周海水方程求解过程类似,可求得桩芯海水速度势函数通解为
ϕ2=[Aw2I1(hr)+Bw2K1(hr)]⋅[Cw2sin(mθ)+Dw2cos(mθ)]⋅ [Ew2cos(hz)+Fw2sin(hz)]iω , (14) 式中,Aw2,Bw2,Cw2,Dw2,Ew2,Fw2为待定系数。
桩芯海水边界条件假定为
ϕ2|z=−H1=0, (15) ∂ϕ2∂z|z=0=0, (16) ϕ2|r=0<∞, (17) 将式(14)代入以上边界条件,可得
ϕ2=∞∑n=1Aw2nI1(hnr)cos(hnz)iωcosθ。 (18) 桩芯海水动水压力为
q2=ρw∂ϕ2∂t=−ρwω2∞∑n=1Aw2nI1(hnr)cos(hnz)cosθ。 (19) 作用于单位长度桩身的海水动水压力为
fw2=∫2π0q2|r=r2r2cosθdθ=−πr2ρwω2∞∑n=1Aw2nI1(hnr2)cos(hnz)。 (20) 2.2 土体运动方程求解
(1)桩周土体运动方程求解
对方程(2)、(3)进行微分变换∂(2)∂r+(2)r+∂(3)r∂θ,可得
(λ∗+2G∗)∇2e1+G∗∂2e1∂z2+ρω2e1=0。 (21) 通过分离变量法容易得到方程(21)的通解为
e1=[As11Km(q1r)+Bs11Im(q1r)]⋅[Cs11sin(mθ)+ Ds11cos(mθ)]⋅[Es11sin(gz)+Fs11cos(gz)] , (22) 式中,q21=G∗g2−ρω2λ∗+2G∗,As11,Bs11,Cs11,Ds11,Es11,Fs11为待定系数。
桩周土边界条件假定为
∂ur1∂z|z=0=∂uθ1∂z|z=0=0, (23) ur1|z=H2=uθ1|z=H2=0, (24) ur1|r→∞=uθ1|r→∞=0。 (25) 将式(22)代入边界条件可得
e1=∞∑n=1As11nK1(q1nr)cos(gnz)cosθ, (26) 式中,gn=(2n−1)π2H2,n=1,2,3,⋯。
ur1,uθ1可表示为
ur1(r,θ,z)=¯ur1(r,z)cosθ ,uθ1(r,θ,z)=¯uθ1(r,z)sinθ 。} (27) 将式(26),(27)代入式(2),(3)并分别相加和相减得到
G∗(∂2∂r2+∂r∂r−4r2+∂2∂z2)U1+ρω2U1 =∞∑n=1(λ∗+G∗)As11nq1nK2(q1nr)cos(gnz) , (28) G∗(∂2∂r2+∂r∂r+∂2∂z2)V1+ρω2V1 =∞∑n=1(λ∗+G∗)As11nq1nK0(q1nr)cos(gnz) , (29) 式中,U1=ˉur1+ˉuθ1,V1=ˉur1−ˉuθ1。
基于分离变量法并考虑上文土体边界条件,可得
U1=∞∑n=1[γnAs11nK2(q1nr)+As12nK2(q2nr)]cos(gnz), (30) V1=∞∑n=1[γnAs11nK0(q1nr)+As13nK0(q2nr)]cos(gnz) , (31) 式中,q22n=G∗g2n−ρω2G∗,γn=(λ∗+G∗)q1nG∗(q21n−g2n)+ρω2,As12n,As13n为待定系数。
考虑土体体应变定义,可得
As13n=−As12n。 (32) 因此桩周土位移ur1,uθ1可表示为
ur1=∞∑n=1[γnAs11nK2(q1nr)+K0(q1nr)2+ As12nK2(q2nr)−K0(q2nr)2]cos(gnz)cosθ, (33) uθ1=∞∑n=1[γnAs11nK2(q1nr)−K0(q1nr)2+ As12nK2(q2nr)+K0(q2nr)2]cos(gnz)sinθ。 (34) 桩周土与管桩交界面处的连续条件可表示为
ur1|r=r1=upcosθ ,uθ1|r=r1=−upsinθ 。} (35) 将式(33),(34)代入式(35),可得
As12n=δ1nAs11n, (36) 式中,δ1n=−γnK2(q1nr1)K2(q2nr1)。
根据式(33),(34)可求得桩周土应力为
σr1=∞∑n=1As1n{[(λ∗+2G∗)K1(q1nr)−2G∗γnK2(q1nr)r]− 2G∗δ1nK2(q2nr)r}cos(gnz)cosθ , (37) τrθ1=−G∗∑As1n{2γnK2(q1nr)r+ δ1n[q2nK1(q2nr)+2K2(q2nr)r]}cos(gnz)sinθ 。 (38) 进而可求得单位长度桩身受到的桩周土体抗力为
fs1=−∫2π0(σr1cosθ−τrθ1sinθ)|r=r1r1dθ =−πr1∞∑n=1As1n[(λ∗+2G∗)K1(q1nr1)+ G∗δ1nq2nK1(q2nr1)]cos(gnz)。 (39) (2)桩芯土体运动方程求解
与求解桩周土方程过程类似,容易求得桩芯土体应变通解为
e2=[As21Km(q1r)+Bs21Im(q1r)]⋅[Cs21sin(mθ)+Ds21cos(mθ)]⋅ [Es21sin(gz)+Fs21cos(gz)] , (40) 桩芯土边界条件假定为
∂ur2∂z|z=0=∂uθ2∂z|z=0=0, (41) ur2|z=H2=uθ2|z=H2=0, (42) ur2|r→∞=uθ2|r→∞=0。 (43) 将式(40)代入边界条件可得
e2=∞∑n=1As21nI1(q1nr)cos(gnz)cosθ。 (44) ur2,uθ2可表示为
ur2(r,θ,z)=¯ur2(r,z)cosθ ,uθ2(r,θ,z)=¯uθ2(r,z)sinθ 。} (45) 类似桩周土求解过程,可得
G∗(∂2∂r2+∂r∂r−4r2+∂2∂z2)U2+ρω2U2 =−∞∑n=1(λ∗+G∗)As21nq1nI2(q1nr)cos(gnz) , (46) G∗(∂2∂r2+∂r∂r+∂2∂z2)V2+ρω2V2 =−∞∑n=1(λ∗+G∗)As21nq1nI0(q1nr)cos(gnz) , (47) 式中,U2=ˉur2+ˉuθ2,V2=ˉur2−ˉuθ2。
方程(46),(47)的解为
U2=∞∑n=1[−γnAs21nI2(q1nr)+As22nI2(q2nr)]cos(gnz), (48) V2=∞∑n=1[−γnAs21nI0(q1nr)−As22nI0(q2nr)]cos(gnz), (49) 因此桩芯土位移ur2,uθ2可表示为
ur2=∞∑n=1[−γnAs21nI2(q1nr)+I0(q1nr)2+ As22nI2(q2nr)−I0(q2nr)2]cos(gnz)cosθ , (50) uθ2=∞∑n=1[−γnAs21nI2(q1nr)−I0(q1nr)2+As22nI2(q2nr)+I0(q2nr)2]⋅ cos(gnz)sinθ 。 (51) 类似地,基于桩芯土与管桩交界面处的连续条件可求得
As22n=δ2nAs21n , (52) 式中,δ2n=γnI2(q1nr0)I2(q2nr0)。
单位长度桩身受到的桩芯土体抗力为
fs2=∫2π0(σr2cosθ−τrθ2sinθ)|r=r2r2dθ =πr2∞∑n=1As2n[(λ∗+2G∗)I1(q1nr2)− G∗δ2nq2nI1(q2nr2)]cos(gnz)。 (53) 2.3 管桩水平振动方程求解
将上文求得的桩周和桩芯海水动水压力和土体抗力代入管桩控制方程(4),(5)中,可得
E*pIp∂4upw∂z4−ρpApω2upw+πr1ρwω2∞∑n=1Aw1nK1(hnr1)cos(hnz)+ πr2ρwω2∞∑n=1Aw2nI1(hnr2)cos(hnz)=0 , (54) E*pIp∂4ups∂z4−ρpApω2ups−πr1∞∑n=1As1n[(λ∗+2G∗)K1(q1nr1)+G∗δ1nq2nK1(q2nr1)]cos(gnz)πr2∞∑n=1As2n[(λ∗+2G∗)I1(q1nr2)− G∗δ2nq2nI1(q2nr2)]cos(gnz)=0。 (55) 式(54),(55)解的形式为
upw=Nw1sin(kz)+Nw2cos(kz)+Nw3sinh(kz)+Nw4cosh(kz)− ∞∑n=1ζw1nAw1ncos(hnz)−∞∑n=1ζw2nAw2ncos(hnz) , (56) ups=Ns1sin(kz)+Ns2cos(kz)+Ns3sinh(kz)+Ns4cosh(kz)− ∞∑n=1ζs1nAs1ncos(gnz)−∞∑n=1ζs2nAs2ncos(gnz) , (57) 式中,k4=ρpApω2E*pIp,ζw1n=πr1ρwω2K1(hnr1)E∗pIp(h4n−k4),ζw2n=πr2ρwω2I1(hnr2)E*pIp(h4n−k4),ζs1n=−πr1[(λ∗+2G∗)K1(q1nr1)+G∗δ1nq2nK1(q2nr1)]E∗pIp(g4n−k4),ζs2n=πr2[(λ∗+2G∗)I1(q1nr2)−G∗δ2nq2nI1(q2nr2)]E∗pIp(g4n−k4)。
由管桩与海水流体交界面处速度连续条件及与土体交界面处位移连续条件:
∂ϕ1∂r|r=r1=∂ϕ2∂r|r=r2=∂upw∂tcosθ, (58) ur1|r=r1=ur2|r=r2=upscosθ。 (59) 将桩周、桩芯海水速度势和土体位移表达式以及管桩位移表达式代入,可得
∞∑n=1Aw1nηw1ncos(hnz)=∞∑n=1Aw2nηw1ncos(hnz)=Nw1sin(kz)+Nw2cos(kz)+Nw3sinh(kz)+Nw4cosh(kz)− ∞∑n=1ζw1nAw1ncos(hnz)−∞∑n=1ζw2nAw2ncos(hnz) , (60) ∞∑n=1As1nηs1ncos(gnz)=∞∑n=1As2nηs2ncos(gnz)=Ns1sin(kz)+Ns2cos(kz)+Ns3sinh(kz)+Ns4cosh(kz)− ∞∑n=1ζs1nAs1ncos(gnz)−∞∑n=1ζs2nAs2ncos(gnz) , (61) 式中,ηw1n=−hn2[K0(hnr1)+K2(hnr1)],ηw2n=hn2[I0(hnr2)+I2(hnr2)],ηs1n=γnK2(q1nr1)+K0(q1nr1)2+δ1nK2(q2nr1)−K0(q2nr1)2,ηs2n=−γnI2(q1nr2)+I0(q1nr2)2+δ2nI2(q2nr2)−I0(q2nr2)2。
由式(60),(61)容易得到
Aw2n=ηw1nηw2nAw1n, (62) As2n=ηs1nηs2nAs1n。 (63) 将式(62)代入式(60),式(63)代入式(61),可得
Nw1sin(kz)+Nw2cos(kz)+Nw3sinh(kz)+Nw4cosh(kz)−∞∑n=1ζw1nηw2n+ζw2nηw1nηw2nAw1ncos(hnz)=∞∑n=1ηw1nAw1ncos(hnz) , (64) Ns1sin(kz)+Ns2cos(kz)+Ns3sinh(kz)+Ns4cosh(kz)−∞∑n=1ζs1nηs2n+ζs2nηs1nηs2nAs1ncos(gnz)=∞∑n=1ηs1nAs1ncos(gnz) 。 (65) 将式(64)两边同时乘以cos(hnz)并在区间[-H1, 0]上积分,式(65)同时乘以cos(gnz)并在区间[0, H2]上积分,可得
Aw1n=ηw2n(χw1nNw1+χw2nNw2+χw3nNw3+χw4nNw4), (66) As1n=ηs2n(χs1nNs1+χs2nNs2+χs3nNs3+χs4nNs4), (67) 式中
χw1n=2∫0−H1sin(kz)cos(hnz)dzH1(ηw1nηw2n+ζw1nηw2n+ζw2nηw1n), χw2n=2∫0−H1cos(kz)cos(hnz)dzH1(ηw1nηw2n+ζw1nηw2n+ζw2nηw1n),χw3n=2∫0−H1sinh(kz)cos(hnz)dzH1(ηw1nηw2n+ζw1nηw2n+ζw2nηw1n),χw4n=2∫0−H1cosh(kz)cos(hnz)dzH1(ηw1nηw2n+ζw1nηw2n+ζw2nηw1n),χs1n=2∫H20sin(kz)cos(gnz)dzH2(ηs1nηs2n+ζs1nηs2n+ζs2nηs1n),χs2n=2∫H20cos(kz)cos(gnz)dzH2(ηs1nηs2n+ζs1nηs2n+ζs2nηs1n),χs3n=2∫H20sinh(kz)cos(gnz)dzH2(ηs1nηs2n+ζs1nηs2n+ζs2nηs1n),χs4n=2∫H20cosh(kz)cos(gnz)dzH2(ηs1nηs2n+ζs1nηs2n+ζs2nηs1n)。 继而可得到:
Aw2n=ηw1n(χw1nNw1+χw2nNw2+χw3nNw3+χw4nNw4), (68) As2n=ηs1n(χs1nNs1+χs2nNs2+χs3nNs3+χs4nNs4)。 (69) 至此可得到埋入海水段和埋入土层段的管桩桩身位移、转角、弯矩和剪力的表达式为
upw=Nw1[sin(kz)−∞∑n=1κw1ncos(hnz)]+Nw2[cos(kz)−∞∑n=1κw2ncos(hnz)]+Nw3[sinh(kz)−∞∑n=1κw3ncos(hnz)]+ Nw4[cosh(kz)−∞∑n=1κw4ncos(hnz)] , (70) ϕpw=Nw1[kcos(kz)+∞∑n=1κw1nhnsin(hnz)]+Nw2[−ksin(kz)+∞∑n=1κw2nhnsin(hnz)]+Nw3[kcosh(kz)+∞∑n=1κw3nhnsin(hnz)]+ Nw4[ksinh(kz)+∞∑n=1κw4nhnsin(hnz)] , (71) MpwE∗pIp=Nw1[−k2sin(kz)+∞∑n=1κw1nh2ncos(hnz)]+Nw2[−k2cos(kz)+∞∑n=1κw2nh2ncos(hnz)]+Nw3[k2sinh(kz)+∞∑n=1κw3nh2ncos(hnz)]+ Nw4[k2cosh(kz)+∞∑n=1κw4nh2ncos(hnz)] , (72) QpwE*pIp=Nw1[−k3cos(kz)−∞∑n=1κw1nh3nsin(hnz)]+Nw2[k3sin(kz)−∞∑n=1κw2nh3nsin(hnz)]+Nw3[k3cosh(kz)−∞∑n=1κw3nh3nsin(hnz)]+ N4[k3sinh(kz)−∞∑n=1κw4nh3nsin(hnz)] , (73) ups=Ns1[sin(kz)−∞∑n=1κs1ncos(gnz)]+Ns2[cos(kz)−∞∑n=1κs2ncos(gnz)]+Ns3[sinh(kz)−∞∑n=1κs3ncos(gnz)]+ Ns4[cosh(kz)−∞∑n=1κs4ncos(gnz)] , (74) ϕps=Ns1[kcos(kz)+∞∑n=1κs1ngnsin(gnz)]+Ns2[−ksin(kz)+∞∑n=1κs2ngnsin(gnz)]+Ns3[kcosh(kz)+∞∑n=1κs3ngnsin(gnz)]+ Ns4[ksinh(kz)+∞∑n=1κs4ngnsin(gnz)] , (75) MpsE∗pIp=Ns1[−k2sin(kz)+∞∑n=1κs1ng2ncos(gnz)]+Ns2[−k2cos(kz)+∞∑n=1κs2ng2ncos(gnz)]+Ns3[k2sinh(kz)+∞∑n=1κs3ng2ncos(gnz)]+ Ns4[k2cosh(kz)+∞∑n=1κs4ng2ncos(gnz)] , (76) QpsE∗pIp=Ns1[−k3cos(kz)−∞∑n=1κs1ng3nsin(gnz)]+Ns2[k3sin(kz)−∞∑n=1κs2ng3nsin(gnz)]+Ns3[k3cosh(kz)−∞∑n=1κs3ng3nsin(gnz)]+ N4[k3sinh(kz)−∞∑n=1κs4ng3nsin(gnz)] , (77) 式中,κw1n=(ζw1nηw2n+ζw2nηw1n)χw1n,κw2n=(ζw1nηw2n+ζw2nηw1n)χw2n,κw3n=(ζw1nηw2n+ζw2nηw1n)χw3n,κw4n=(ζw1nηw2n+ζw2nηw1n)χw4n,κs1n=(ζs1nηs2n+ζs2nηs1n)χs1n,κs2n=(ζs1nηs2n+ζs2nηs1n)χs2n,κs3n=(ζs1nηs2n+ζs2nηs1n)χs3n,κs4n=(ζs1nηs2n+ζs2nηs1n)χs4n。
桩顶边界条件为
Mpw|z=−H1=0Qpw|z=−H1=Peiωt, (78) 桩底边界条件为
ups|z=H2=0ϕps|z=H2=0。 (79) 同时管桩满足如下连续条件:
upw|z=0=ups|z=0 ,φpw|z=0=φps|z=0 ,Mpw|z=0=Mps|z=0 ,Qpw|z=0=Qps|z=0 。} (80) 将式(70)~(77)确定的桩身位移、转角、弯矩和剪力表达式代入边界条件和连续条件式(78)~(80)得到一个八元一次线性方程组,求解这一线性方程组可得到待定系数Nw1,Nw2,Nw3,Nw4,Ns1,Ns2,Ns3,Ns4,将得到的系数带回原方程即可得到桩身位移和应力解析解。
3. 对比验证与参数分析
3.1 对比验证
为了验证本文解的正确性,将本文理论解与有限元模拟结果对比,图 2为利用ABAQUS软件建立的桩–土–海水系统数值分析模型,桩–土–海水参数按照3.2节所列数据进行赋值,为避免边界反射效应的影响,桩周土和海水径向距离设置为桩半径的20倍,并在土体外侧采用无限元边界,海水外侧采用非反射边界。有限元模型中桩采用B31梁单元,土体采用C3D8R单元,海水采用AC3D8声单元,桩–土和桩–海水界面设置Embedded接触,土–海水界面设置Tie接触,而后建立稳态动力分析步对其频域响应特性进行分析。图 3所示为本文理论解与有限元计算结果得到的桩顶柔度因子实部对比情况,从图中可以看出,本文理论解与有限元模拟计算结果较为吻合,从而进一步验证了本文解的正确性。
3.2 桩顶水平动力柔度因子特性分析
根据式(70)可得在桩顶作用谐振荷载Peiωt下的桩顶水平位移,定义桩顶水平动力柔度因子Chh:
Chh=upw|z=−H1P, (81) 式中,Chh为单位水平荷载作用下桩顶产生的水平位移幅值,即是表征桩顶柔度的参数。下文对海洋大直径管桩基础桩顶柔度因子特性进行分析,主要分析动水压力、海水深度、桩内外半径、桩土模量、桩土阻尼比等参数对桩顶柔度因子的影响。参数分析中,如何其他特殊说明,计算参数取值为H2 = 20 m,H1/H2 = 0.3,r1 = 0.5 m,r2 = 0.8 r1,Ep = 30 GPa,G = 50 MPa,ρp= 2400 kg/m3,ρs= 1600 kg/m3,ρw= 1000 kg/m3,βp= 0.025,βs= 0.05,νs=0.3。
图 4给出了考虑海水动水压力及不考虑动水压力时海洋管桩桩顶水平动力柔度因子随频率的变化情况。
与完全埋入式桩基础不同,海洋高桩基础的桩顶水平动力柔度因子存在共振现象,在低于共振频率时,桩顶柔度因子一直随频率增大而逐渐增大,实部表示真实的柔度,虚部表示吸收振动能量的阻尼,在达到共振频率时其实部和虚部数值极大,这对海洋桩基础上部结构的水平承载性能是极其不利的,需要在其动力设计中考虑这一现象。从图 4可以看出,考虑海水动水压力计算的得到的桩顶水平动力柔度因子的共振频率比不考虑动水压力时小,即海水动水压力作用使得桩更容易在较低频率时发生共振。同时可以发现,海水动水压力对桩顶水平动力柔度因子共振幅值影响不大。
图 5给出了埋入海水段桩身长度对桩顶水平动力柔度因子的影响,可以看出,当埋入海水段桩身很短(H1/H2 = 0.1)时,桩顶柔度因子基本没有发生共振,此时更接近于完全埋入式桩的柔度因子特性,随着埋入海水段桩身长度逐渐增大,低频段桩顶柔度幅值显著增大,同时桩顶柔度因子共振现象变得显著,同时其共振频率显著减小且共振幅值显著增大。图 6,7给出了管桩外半径和内半径对桩顶水平动柔度因子的影响,可以发现,随着外半径增大,低频段桩顶柔度幅值显著减小,桩顶柔度因子的共振频率增大,共振幅值减小,而随着内半径与外半径比值的减小,低频段桩顶柔度幅值减小,同时桩顶柔度因子共振频率和共振幅值也减小,这种减小趋势随着内外半径比值继续减小逐渐减弱,管桩的桩顶柔度因子共振频率和共振幅值显著大于实心桩。
图 8,9给出了桩身弹性模量和土体剪切模量对桩顶水平动力柔度因子的影响,随着桩身弹性模量的增大,低频段桩顶柔度幅值显著减小,桩顶柔度因子的共振频率增大,共振幅值显著减小,而随着土体剪切模量的增大,低频段桩顶柔度幅值减小,桩顶柔度因子的共振频率增大,其共振幅值略有增大,但当土体剪切模量增大到较大值时,其对低频段桩顶柔度幅值和桩顶柔度因子共振幅值的影响不再明显。
4. 结论
本文考虑海水动水压力作用和桩–土–流体耦合振动,求解得到了黏弹性地基中海洋大直径管桩水平动力响应解析解,基于所得解对大直径管桩桩顶动力柔度因子进行了参数分析,得出3点结论。
(1)海水动水压力作用使得桩更容易在较低频率时发生共振,但对桩顶水平动力柔度因子共振幅值影响不大。
(2)埋入海水段桩身长度增大,低频段桩顶柔度幅值显著增大,同时桩顶柔度因子共振频率显著减小且共振幅值显著增大。管桩外半径增大,桩顶柔度因子的共振频率减小,共振幅值增大,内半径与外半径比值减小,桩顶柔度因子共振频率和共振幅值也减小。
(3)桩身弹性模量增大,桩顶柔度因子的共振频率增大,共振幅值显著减小,土体剪切模量增大,低频段桩顶柔度幅值减小,桩顶柔度因子的共振频率增大。
-
表 1 计算参数取值表
Table 1 Values of calculation parameters
材料 弹性模量E/GPa 泊松比μ 重度 /(kN·m-3) 黏聚力c/kPa 内摩擦角φ/(°) 围岩 2 0.37 22 20 11.5 衬砌 17 0.20 25 — — -
[1] TERZAGHI K. Theoretical Soil Mechanics[M]. Hoboken: John Wiley and Sons, 1943.
[2] LI S, JIANIE Y C, HO I H, et al. Experimental and numerical analyses for earth pressure distribution on high-filled cut-and-cover tunnels[J]. KSCE Journal of Civil Engineering, 2020, 24(6): 1903-1913. doi: 10.1007/s12205-020-1693-7
[3] HAN L, YE G L, CHEN J J, et al. Pressures on the lining of a large shield tunnel with a small overburden: a case study[J]. Tunnelling and Underground Space Technology, 2017, 64(8): 1-9.
[4] 何川, 张景, 封坤. 盾构隧道结构计算分析方法研究[J]. 中国公路学报, 2017, 30(8): 1-14. doi: 10.3969/j.issn.1001-7372.2017.08.001 HE Chuan, ZHANG Jing, FENG Kun. Research on structural analysis method of shield tunnels[J]. China Journal of Highway and Transport, 2017, 30(8): 1-14. (in Chinese) doi: 10.3969/j.issn.1001-7372.2017.08.001
[5] TAKANO Y H, WORKING GRP NO.2 I T A. Guidelines for the design of shield tunnel lining[J]. Tunnelling and Underground Space Technology, 2000, 15(3): 303-331. doi: 10.1016/S0886-7798(00)00058-4
[6] CHEN K H, PENG F L. An improved method to calculate the vertical earth pressure for deep shield tunnel in Shanghai soil layers[J]. Tunnelling and Underground Space Technology, 2018, 75(5): 43-66.
[7] 卢钦武, 邓涛, 关振长. 水平地震作用下浅埋隧道围岩压力的计算方法研究[J]. 岩土工程学报, 2020, 42(6): 1093-1100. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202006016.htm LU Qin-wu, DENG Tao, GUAN Zhen-chang. Ground loading of shallow tunnels under seismic scenario[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(6): 1093-1100. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202006016.htm
[8] 王明年, 王志龙, 桂登斌, 等. 考虑开挖方法影响的深埋隧道围岩形变压力计算方法研究[J/OL]. 西南交通大学学报, 1-10. WANG Ming-nian, WANG Zhi-long, GUI Deng-bin, et al. Study on deformation load calculation method of surrounding rock in deep-buried tunnel considering the influence of excavation method[J/OL]. Journal of Southwest Jiaotong University, 1-10. (in Chinese)
[9] 赵占厂, 谢永利, 杨晓华, 等. 黄土公路隧道围岩压力测试分析[J]. 现代隧道技术, 2003, 40(2): 58-61. doi: 10.3969/j.issn.1009-6582.2003.02.014 ZHAO Zhan-chang, XIE Yong-li, YANG Xiao-hua, et al. Ground pressure measurement and analysis for highway tunnels located in loess[J]. Modern Tunnelling Technology, 2003, 40(2): 58-61. (in Chinese) doi: 10.3969/j.issn.1009-6582.2003.02.014
[10] 赵占厂, 谢永利. 黄土公路隧道结构设计与施工中的若干问题[J]. 现代隧道技术, 2008, 45(6): 56-60, 81. https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD200806013.htm ZHAO Zhan-chang, XIE Yong-li. Some problems about structural design and construction for highway loess tunnels[J]. Modern Tunnelling Technology, 2008, 45(6): 56-60, 81. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD200806013.htm
[11] 王建宇. 对形变压力的认识——隧道围岩挤压性变形问题探讨[J]. 现代隧道技术, 2020, 57(4): 1-11. https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD202004001.htm WANG Jian-yu. The key way is to release the genuine rock pressure—discussion on problems of tunnelling in squeezing ground[J]. Modern Tunnelling Technology, 2020, 57(4): 1-11. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD202004001.htm
[12] 王明年, 王志龙, 张霄, 等. 深埋隧道围岩形变压力计算方法研究[J]. 岩土工程学报, 2020, 42(1): 81-90. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202001015.htm WANG Ming-nian, WANG Zhi-long, ZHANG Xiao, et al. Method for calculating deformation pressure of surrounding rock of deep-buried tunnels[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(1): 81-90. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202001015.htm
[13] WANG M N, DONG Y C, YU L. Analytical solution for a loess tunnel based on a bilinear strength criterion[J]. Soil Mechanics and Foundation Engineering, 2020, 57(4): 296-304.
[14] 王明年, 董宇苍, 于丽. 基于双线性强度准则的黄土隧道围岩弹塑性解析解[J]. 中国铁道科学, 2019, 40(6): 68-77. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201906010.htm WANG Ming-nian, DONG Yu-cang, YU Li. Elastoplastic analytical solution to surrounding rock of loess tunnel based on bilinear strength criterion[J]. China Railway Science, 2019, 40(6): 68-77. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201906010.htm
[15] LUO Y B, CHEN J X, GAO S T, et al. Stability analysis of super-large-section tunnel in loess ground considering water infiltration caused by irrigation[J]. Environmental Earth Sciences, 2017, 76(22).
[16] 李国良, 邵生俊, 靳宝成, 等. 黄土隧道地基的湿陷性问题研究[J]. 铁道工程学报, 2015, 32(12): 12-16, 50. https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201512003.htm LI Guo-liang, SHAO Sheng-jun, JIN Bao-cheng, et al. Research on the problems of collapsibility of loess tunnel foundation[J]. Journal of Railway Engineering Society, 2015, 32(12): 12-16, 50. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDGC201512003.htm
[17] WENG X L, SUN Y F, YAN B H, et al. Centrifuge testing and numerical modeling of tunnel face stability considering longitudinal slope angle and steady state seepage in soft clay[J]. Tunnelling and Underground Space Technology, 2020, 101(7): 1-14.
[18] WENG X L, SUN Y F, ZHANG Y W, et al. Physical modeling of wetting-induced collapse of shield tunneling in loess strata[J]. Tunnelling and Underground Space Technology, 2019, 90(8): 208-219.
[19] 谢定义, 齐吉琳. 土结构性及其定量化参数研究的新途径[J]. 岩土工程学报, 1999, 21(6): 651-656. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC199906000.htm XIE Ding-yi, QI Ji-lin. Soil structure characteristics and new approach in research on its quantitative parameter[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(6): 651-656. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC199906000.htm
[20] 谢定义, 齐吉琳, 张振中. 考虑土结构性的本构关系[J]. 土木工程学报, 2000, 33(4): 35-41. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200004007.htm XIE Ding-yi, QI Ji-lin, ZHANG Zhen-zhong. A constitutive laws considering soil structural properties[J]. China Civil Engineering Journal, 2000, 33(4): 35-41. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200004007.htm
[21] 陈昌禄, 邵生俊, 邓国华. 土的结构性参数与强度的关系及其在边坡稳定分析中的应用[J]. 中南大学学报(自然科学版), 2010, 41(1): 328-334. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201001056.htm CHEN Chang-lu, SHAO Sheng-jun, DENG Guo-hua. Relationship between soil structural parameters and strength and its application in slope stability analysis[J]. Journal of Central South University (Science and Technology), 2010, 41(1): 328-334. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201001056.htm
[22] 邵生俊, 龙吉勇, 于清高, 等. 湿陷性黄土的结构性参数本构模型[J]. 水利学报, 2006, 37(11): 1315-1322. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200611005.htm SHAO Sheng-jun, LONG Ji-yong, YU Qing-gao, et al. A constitutive model of collapsible loess with structural parameter[J]. Journal of Hydraulic Engineering, 2006, 37(11): 1315-1322. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200611005.htm
[23] 邓国华, 邵生俊. 黄土隧道围岩的结构性变化特征分析[J]. 岩土工程学报, 2008, 30(2): 219-224. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200802011.htm DENG Guo-hua, SHAO Sheng-jun. Variation characteristic analysis of a structural parameter for surrounding soils in loess tunnels[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(2): 219-224. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200802011.htm
[24] 邓国华, 邵生俊, 陈昌禄, 等. 一个可考虑球应力和剪应力共同作用的结构性参数[J]. 岩土力学, 2012, 33(8): 2310-2314. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201208014.htm DENG Guo-hua, SHAO Sheng-jun, CHEN Chang-lu, et al. A structural parameter reflecting coupling action between shear stress and spherical stress[J]. Rock and Soil Mechanics, 2012, 33(8): 2310-2314. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201208014.htm
[25] 邓国华. 真三轴条件下黄土的结构性参数及结构性本构关系研究[D]. 西安: 西安理工大学, 2009. DENG Guo-hua. Research on Structure Parameter of Loess and Structure Constitutive Relations under Ture Tri-Axial Condition[D]. Xi'an: Xi'an University of Technology, 2009. (in Chinese)
[26] 邓国华, 邵生俊, 佘芳涛. 结构性黄土的修正剑桥模型[J]. 岩土工程学报, 2012, 34(5): 834-841. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201205010.htm DENG Guo-hua, SHAO Sheng-jun, SHE Fang-tao. Modified Cam-clay model of structured loess[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(5): 834-841. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201205010.htm
[27] 邹志林. 海底取水盾构隧道双层衬砌结构受力特性研究[D]. 长沙: 中南大学, 2013. ZOU Zhi-lin. Study of Mechanical Characters of Subsea Water-Intaken Shield Tunnel with Double Lining[D]. Changsha: Central South University, 2013. (in Chinese)
[28] 江英超, 何川, 方勇, 等. 盾构施工对黄土地层的扰动及管片衬砌受荷特征[J]. 中南大学学报(自然科学版), 2013, 44(7): 2934-2941. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201307043.htm JIANG Ying-chao, HE Chuan, FANG Yong, et al. Soil disturbance caused by shield tunneling and segment lining loading characteristics in loess strata[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 2934-2941. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201307043.htm
[29] 王俊, 方勇, 何川, 等. 盾构隧道施工对砂性地层的扰动及管片受荷特征[J]. 地下空间与工程学报, 2015, 11(1): 156-162, 170. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201501024.htm WANG Jun, FANG Yong, HE Chuan, et al. Disturbance of shield tunnel construction to sandy stratum and load bearing characteristics of segment lining[J]. Chinese Journal of Underground Space and Engineering, 2015, 11(1): 156-162, 170. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201501024.htm
[30] 王明年, 郭军, 罗禄森, 等. 高速铁路大断面深埋黄土隧道围岩压力计算方法[J]. 中国铁道科学, 2009, 30(5): 53-58. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200905010.htm WANG Ming-nian, GUO Jun, LUO Lu-sen, et al. Calculation method for the surrounding rock pressure of deep buried large sectional loess tunnel of high-speed railway[J]. China Railway Science, 2009, 30(5): 53-58. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200905010.htm
-
期刊类型引用(3)
1. 吴彩虹,茅嘉炜,翁锴亮. 考虑桩端土影响的桩土界面摩擦特性离散元模拟分析. 结构工程师. 2024(06): 181-186 .  百度学术
百度学术
2. 韦全余,石军,冯哲源,李洪亚,华瑞平. 搅拌桩复合地基沉降因素及计算方法研究进展. 土工基础. 2023(01): 118-123 .  百度学术
百度学术
3. 时昆鹏,丁肇伟,宋春雨,陈龙珠. 考虑桩土局部分离的饱和土体中桩基水平动力响应分析. 结构工程师. 2022(04): 141-150 .  百度学术
百度学术
其他类型引用(5)




 下载:
下载: