振动台试验中地下结构地震响应预测方法

江志伟; 刘晶波; 许成顺

doi:10.11779/CJGE202107006

振动台试验中地下结构地震响应预测方法 English Version

江志伟^{1, 2,},
刘晶波¹,
许成顺²

1.
清华大学土木工程系,北京　100084
2.
北京工业大学城市与工程安全减灾教育部重点实验室,北京　100124

基金项目:

国家自然科学基金项目 52008233

国家自然科学基金项目 U1839201

国家重点研发计划课题 2018YFC1504305

详细信息

作者简介:
江志伟(1988— ),男,博士后,主要从事地下结构抗震方面的科研工作。E-mail：zhiweijiang163@163.com

中图分类号: TU43
计量
- 文章访问数: 285
- HTML全文浏览量: 35
- PDF下载量: 168
出版历程
- 收稿日期: 2020-04-01
- 网络出版日期: 2022-12-02
- 刊出日期: 2021-06-30

Prediction method for seismic responses of underground structures in shaking table tests

1.
Department of Civil Engineering, Tsinghua University, Beijing 100084, China
2.
The Key Laboratory of Urban Security and Disaster Engineering of the Ministry of Education, Beijing University of Technology, Beijing 100124, China

摘要

摘要: 考虑土–结构相互作用的地下结构大型振动台试验成本极高,周期长,通常难以在短期内多次重复开展,为保证试验顺利开展,在试验前对其响应开展预测工作具有重要意义。采用完全数值模拟进行预测的方法在模型试验中已得到广泛的使用,但这种方法有时会产生较大误差,特别是对于强非线性的地下结构振动台模型试验。为提高预测方法的准确性,提出了一种整体式反应位移法数值模拟与自由场试验相结合的方法来预测地下模型结构在振动台试验中的地震响应。首先,介绍采用自由场振动台试验获取整体式反应位移法计算参数的方法,基于此,分别采用所提出方法和传统全数值方法预测某地铁车站结构模型在振动台试验中的地震响应,并将预测结果与后续试验结果进行对比。结果表明：所提出方法预测结果准确性较传统全数值方法预测结果准确性有大幅提升,方法可用以定性地预测后续试验结果,并可在一定程度上指导和完善后续试验方案。
- 地下结构 /
- 地震响应 /
- 振动台试验 /
- 试验预测 /
- 整体式反应位移法 /
- 抗震
Abstract: The large-scale shaking table tests on an underground structure embedded in soil need extremely high cost and long test period, and usually they can hardly be frequently conducted in a short time. In order to successfully conduct the tests, predicting their responses before the tests is meaningful. The fully-numerical prediction method has been widely applied in model tests, but sometimes the results may have a great error, especially under the strong non-linear condition. To improve the accuracy of the prediction, the method combining both the numerical analysis and the free-field shaking table tests is proposed to predict the seismic responses of underground model structures in shaking table tests. The method using the data of the free-field tests to estimate the parameters for the Integral Responses Displacement Method is firstly introduced. The seismic responses of underground model structures in shaking table tests are predicted using the proposed method and the traditional fully-numerical prediction method. The predicted results are then compared with those by the subsequent tests. It is shown that the accuracy of the predicted results by the proposed method is greatly improved compared with that by the traditional fully numerical method. The proposed method can be used to qualitatively predict the seismic responses of underground structures in shaking table tests and further improve the design of the subsequent tests.
- underground structure /
- seismic response /
- shaking table test /
- experimental prediction /
- integral response displacement method /
- seismic resistance

HTML全文

0. 引言

微生物岩土加固技术是利用微生物作用生成的有机、无机物材料填充孔隙和胶结岩土颗粒，以改善岩土体的工程性能的技术方法^[1-2]。相较传统的Portland水泥或高聚物加固方法，该技术具有对土体环境影响小、可持续性强的优点。微生物加固技术中研究最多、应用最广的为微生物诱导碳酸钙沉淀(microbially induced calcite precipitation, MICP)技术。MICP技术中高产脲酶芽孢杆菌使用最为普遍，其基本原理是利用自然界中广泛存在的无毒害的高产脲酶芽孢杆菌将尿素水解成铵根离子和碳酸根离子，然后碳酸根离子与环境中的钙离子结合生成碳酸钙沉淀^[1-2]。目前，MICP技术能够增大土体强度和刚度，封堵裂隙等，因而可广泛应用于提高砂土抗液化能力^[3-4]，降低土体渗透性以改善其抗渗透变形能力^[5-6]，冻土地区残积土加固^[7]，三合土表面耐水性处理^[8]，尾矿黏土处理^[9]，泥炭土和有机质黏土改良^[10-11]，沙丘固化与沙漠治理^[12]以及岩体裂隙加固^[13]等。

针对MICP加固砂土的力学性能，目前已有学者做了大量相关试验研究。Feng等^[14]通过三轴排水试验研究了围压和胶结程度对MICP加固石英砂力学特性的影响。结果表明，MICP加固砂的强度、剪胀性和初始弹性模量与胶结程度呈正相关。Liu等^[15]对MICP加固钙质砂进行了相关试验研究，表明碳酸钙含量增加并不会引起被加固土体的峰值内摩擦角改变，但是黏聚力会显著提高，这与MICP加固石英砂^[16-17]的试验结果不同。目前，针对MICP加固砂土的本构理论研究较试验研究少。方祥位等^[18]基于损伤力学理论建立了MICP加固珊瑚砂的损伤本构模型。Gai等^[19]基于次加载面理论建立了微生物加固砂土的本构模型，但其未考虑MICP胶结作用对土体黏聚力的影响。

本文基于临界状态土力学理论框架，采用非关联流动法则，建立状态相关的MICP加固砂土弹塑性本构模型。随后，将建立的模型分别模拟MICP加固石英砂和钙质砂的三轴排水剪切试验。计算结果表明，该模型可以较好地模拟不同加固程度和不同固结围压下试样的应力–应变关系和剪胀特性。

1. MICP加固砂土的力学特性分析

1.1 MICP加固与破坏机理

MICP加固砂土时，生成的碳酸钙晶体一般有3种沉积形式：①碳酸钙晶体附着在砂颗粒表面，使砂颗粒表面变粗糙，示意图和SEM(scanning electron microscopy)图^[20]如图 1(a)和图 1(b)所示；②碳酸钙晶体在砂颗粒间逐渐沉积生长成较大的晶簇，并将砂颗粒连接起来，形成桥接作用，示意图和SEM图^[20]如图 1(c)和图 1(d)所示；③碳酸钙晶体附着在相邻的砂颗粒接触处，将其胶结起来，示意图和SEM图^[20]如图 1(e)和图 1(f)所示。

图 1 MICP加固砂土机理示意图与SEM图^[20]

Figure 1. Schematic diagrams and SEM images^[20] of MICP-treated sands

下载: 全尺寸图片幻灯片

碳酸钙晶体的沉积形式会对MICP加固砂土的力学行为产生显著影响：第一种沉积形式可以填充砂颗粒间孔隙并增加其表面粗糙度，使土体内摩擦角增大，剪胀增加；第二种和第三种碳酸钙沉积形式主要是对砂土颗粒起到胶结作用，可以显著提高土体强度和剪胀性。对MICP加固Ottawa20/30砂进行三轴剪切后重塑装样再剪切试验，发现试样经过多次剪切之后强度与未加固砂基本相同，但是剪胀和刚度较未加固砂仍有提高^[21]。MICP加固砂土的破坏机理可以假设为：剪切过程中碳酸钙的胶结作用逐渐破坏但附着在砂颗粒表面的碳酸钙未被完全磨损掉，同时胶结破坏后的碳酸钙转化为第一种沉积形式。胶结作用退化造成强度降低，出现应变软化现象和剪胀。当胶结作用完全丧失后，附着在砂颗粒表面的碳酸钙仍会使其表面粗糙度增加，刚度和剪胀增加，但是对强度贡献较小。

1.2 破坏包络线

胶结土体的破坏包络线一般通过对同一胶结程度，不同围压下三轴剪切试样的峰值强度进行拟合得到，通过破坏包络线可以确定MICP加固砂土的初始黏聚力和峰值摩擦角。图 2分别给出了MICP加固Ottawa20/30砂^[22]，MICP加固石英砂^[23]和MICP加固钙质砂^[24]在 $p' - q$ 空间中的峰值应力点和破坏包络线。

图 2 试验峰值应力点和破坏包络线

Figure 2. Test peak stress points and failure envelopes

下载: 全尺寸图片幻灯片

中的 ${B_{{\text{ca}}}}$ 和 ${\text{CCC}}$ 分别为MICP加固石英砂和MICP加固钙质砂中生成的碳酸钙的质量分数。对于MICP加固石英砂，采用酸洗法去除生成的碳酸钙并根据质量差值计算得到碳酸钙的质量分数^[23]：

${B_{{\text{ca}}}} = ({m_{\text{i}}} - {m_{\text{a}}})/{m_{\text{i}}} \times 100\% \text{，}$

(1)

式中， ${m_{\text{i}}}$ 为MICP加固后的试样干重， ${m_{\text{a}}}$ 为酸洗后的试样干重。

对于MICP加固钙质砂，由于钙质砂主要成分为碳酸钙，所以不能采用酸洗法计算生成的碳酸钙质量，一般直接用MICP加固试样和未加固试样的干重差值计算得到碳酸钙质量分数^[24]：

${\text{CCC}} = ({m_{{\text{MICP}}}} - {m_{{\text{un}}}})/{m_{{\text{un}}}} \times 100\% \text{，}$

(2)

式中， ${m_{{\text{MICP}}}}$ 为MICP加固后的试样干重， ${m_{{\text{un}}}}$ 为未加固试样干重。

从可以看出，由于碳酸钙的胶结作用，MICP加固之后的Ottawa20/30砂，石英砂和钙质砂的黏聚力均增加。MICP加固钙质砂在 $p' - q$ 空间破坏包络线的斜率减小，峰值摩擦角相较未加固钙质砂明显减小，可能原因为钙质砂颗粒表面存在很多孔隙，且砂颗粒形状多棱角状，MICP加固过程中生成的碳酸钙将钙质砂颗粒表面的内孔隙填充，使其表面更加规整导致摩擦角减小^[24]。

1.3 临界状态线

分别给出了在 $e$ – $\ln p'$ 和 $p'$ – $q$ 空间中MICP加固石英砂^[23]和MICP加固钙质砂^[24]的临界状态线。可以看出，在 $e$ – $\ln p'$ 空间中MICP加固石英砂和MICP加固钙质砂的临界状态线随加固程度增加向上移动，且近似平行。造成这种现象的原因可能是由于剪切过程中试样达到临界状态时砂颗粒间仍然存在一定的胶结作用碳酸钙，同时附着在砂颗粒表面的碳酸钙也会产生影响。从可以看出， $p'$ – $q$ 空间中MICP加固石英砂的临界状态线随加固程度增加，斜率逐渐增大，表明被加固砂土的临界状态摩擦角增加，主要是由于加固程度较高时有更多的碳酸钙附着在砂颗粒表面，导致其表面粗糙度增加。同时，加固程度的提高也会使剪切过程中胶结砂颗粒的碳酸钙破碎之后转化为增加砂颗粒表面粗糙度的碳酸钙更多。从图 3(d)可以看出，MICP加固钙质砂的临界状态线与未加固钙质砂的临界状态线的斜率相差不大，表明MICP加固钙质砂的临界状态摩擦角增加程度有限，主要是因为钙质砂的颗粒表面存在内孔隙，生成的碳酸钙将这些内孔隙填充。胶结作用破坏后仍有部分碳酸钙附着在砂颗粒表面，但是其对临界状态摩擦角的贡献并不如MICP加固石英砂明显。

图 3 MICP加固石英砂和MICP加固钙质砂的临界状态线

Figure 3. Critical state lines of MICP-treated silica sand and MICP-treated calcareous sand

下载: 全尺寸图片幻灯片

2. MICP加固砂土本构模型

2.1 屈服面方程

Yao等^[25]基于UH模型中的椭圆屈服面，引入临界状态参数 $\chi$ ，提出了适用于砂土的屈服面形式，如。在 $p'$ – $q$ 平面内屈服面方程表示为

$f = \frac{{({\text{1 + }}\chi ){q^2}}}{{M_{{\text{cs}}}^2{{p'}^2} - \chi {q^2}}} - \frac{{{p_0}}}{{p'}} + 1 = 0 。$

(3)

图 4 砂土与MICP加固砂土的屈服面

Figure 4. Yield surfaces of sands and MICP-treated sands

下载: 全尺寸图片幻灯片

式中 $p'$ 为平均有效应力； $q$ 为剪应力； ${p_0}$ 为屈服面尺寸； ${M_{{\text{cs}}}}$ 为临界状态应力比； $\chi$ 为临界状态参数，可以控制屈服面形状。当 $\chi {\text{ = 0}}$ 时，屈服面形状退化为修正剑桥模型的椭圆，当 ${\text{0 < }}\chi {\text{ < 1}}$ 时，屈服面形状为水滴型，其对屈服面形状的影响可参考Yao等^[25]。

对于MICP加固砂土，其屈服面由于胶结作用相较于未加固砂土的屈服面向 $p'$ 轴的负半轴扩大，表示胶结作用使土体具有一定程度的抗拉强度。MICP加固砂土的屈服面形状如图 4所示。

对式(3)修正之后可得MICP加固砂土的屈服面方程为

$F = \frac{{({\text{1 + }}\chi ){q^2}}}{{M_{{cs} }^2{{(p' + {p_{\text{t}}})}^2} - \chi {q^2}}} - \frac{{{p_0} + {p_{\text{t}}}}}{{p' + {p_{\text{t}}}}} + 1 = 0 \text{，}$

(4)

式中， ${p_{\text{t}}}$ 为胶结作用引起的抗拉强度。

Baudet等^[26]在研究结构性土的本构模型时，认为结构性的丧失同时受塑性体积应变和塑性剪应变的影响，但是两者的影响比例目前还不能通过试验得到，可假设两者的影响相同。Chen等^[27]通过定义塑性损伤应变来表示塑性体积应变和塑性剪应变对胶结作用退化的综合影响：

$\varepsilon _{\text{d}}^{\text{p}} = \sqrt {{{(\varepsilon _{\text{v}}^{\text{p}})}^2} + {{(\varepsilon _{\text{q}}^{\text{p}})}^2}} 。$

(5)

本文采用式(5)的形式并认为抗拉强度 ${p_{\text{t}}}$ 随塑性损伤应变的累计逐渐减小，可以表示为

${p_{\text{t}}} = {p_{{\text{t0}}}}\exp \left( { - \xi \frac{{{\text{1 + }}{e_0}}}{{\lambda - \kappa }}\varepsilon _{\text{d}}^{\text{p}}} \right) \text{，}$

(6)

式中， ${p_{{\text{t0}}}}$ 为初始抗拉强度，可以由 $p'$ – $q$ 空间中的破坏包络线与 $p'$ 轴截距得到， $\xi$ 为胶结退化速率参数， $\lambda$ 和 $\kappa$ 分别为 $e$ – $\ln p'$ 空间中的临界状态线斜率和回弹线斜率。

Chen等^[27]将剪切过程中胶结退化速率与塑性损伤应变建立指数函数关系，表征胶结退化速率随塑性损伤应变的累计逐渐增加。对MICP加固砂土的试验结果表明，胶结作用退化速率与围压也有关。胶结退化速率 $\xi$ 需要综合考虑塑性应变与围压的影响，采用如下表达式：

$\xi = {\xi _0}\exp (\alpha {p_{{\text{ic}}}} + \beta \varepsilon _{\text{d}}^{\text{p}})\text{，}$

(7)

式中， ${\xi _0}$ 为初始胶结退化速率， $\alpha$ 和 $\beta$ 为材料参数， ${p_{{\text{ic}}}}$ 为固结围压。

加载方向的单位向量 $n = {\left[ {{n_{\text{p}}}, {n_{\text{q}}}} \right]^{\text{T}}}$ 的两个分量为

${n_{\text{p}}} = {\text{(}}\partial F/\partial p'{\text{)}}/{L_{\text{F}}} \text{，} {n_{\text{q}}} = {\text{(}}\partial F/\partial q{\text{)}}/{L_{\text{F}}} \text{，}$

(8)

式中， ${L_{\text{F}}}$ 为加载方向向量的模：

${L_{\text{F}}} = \sqrt {{{(\partial F/\partial p')}^2} + {{(\partial F/\partial q)}^2}} 。$

(9)

$\partial F/\partial p'$ 和 $\partial F/\partial q$ 分别为屈服面方程对 $p'$ 和 $q$ 的偏导：

$\frac{{\partial F}}{{\partial p'}} = - \frac{{2M_{{\rm{cs}}}^2(1 + \chi )(p' + {p_{\text{t}}}){q^2}}}{{{{\left[ {M_{{\rm{cs}}}^2{{(p' + {p_t})}^2} - \chi {q^2}} \right]}^2}}} + \frac{{{p_0} + {p_{\text{t}}}}}{{p' + {p_{\text{t}}}}} \text{，}$

(10)

$\frac{{\partial F}}{{\partial q}} = \frac{{2M_{{\rm{cs}}}^2(1 + \chi ){{(p' + {p_{\text{t}}})}^2}q}}{{{{\left[ {M_{{\rm{cs}}}^2{{(p' + {p_{\text{t}}})}^2} - \chi {q^2}} \right]}^2}}} 。$

(11)

2.2 塑性势函数与流动法则

砂土等散粒状土体的力学行为与土体所处的状态有关^[28]，胶结砂土的本构模型研究中同样也可以引入状态参数^[29-31]。Been等^[32]所提出的状态参数应用较为广泛，其可以表示为当前孔隙比 $e$ 与相同平均有效应力下对应的临界状态空隙比 ${e_{{\text{cs}}}}$ 之间的差值：

$\psi = e - {e_{{\text{cs}}}} \text{，}$

(12)

式中，临界状态线CSL上的孔隙比 ${e_{{\text{cs}}}}$ 可表示为

${e_{{\text{cs}}}} = {e_{{\text{cs0}}}} - \lambda \ln p' \text{，}$

(13)

式中， ${e_{{\text{cs0}}}}$ 为 $p' = 1$ kPa时的临界状态孔隙比。

采用非关联流动法则，塑性势函数为

$g = \frac{{({\text{1 + }}\chi ){q^2}}}{{{M_{\text{d}}}^{\text{2}}{{(p' + {p_{\text{t}}})}^2} - \chi {q^2}}} - \frac{{{p_0} + {p_{\text{t}}}}}{{p' + {p_{\text{t}}}}} + 1 = 0 \text{，}$

(14)

式中， ${M_{\text{d}}}$ 为剪胀应力比，其与状态参数有关，采用Li等^[33]提出的指数函数表达式：

${M_{\text{d}}} = {M_{{\text{cs}}}}\exp ({k_{\text{d}}}\psi ) \text{，}$

(15)

式中， ${k_{\text{d}}}$ 为剪胀相关的材料常数。

塑性流动方向单位向量 $m = {[{m_{\text{p}}}, {m_{\text{q}}}]^{\text{T}}}$ 的两个分量可分别表示为

${m_{\text{p}}} = (\partial g/\partial p')/{L_{\text{g}}} \text{，} {m_{\text{q}}} = (\partial g/\partial q)/{L_{\text{g}}} \text{，}$

(16)

式中， ${L_{\text{g}}}$ 为加载方向向量的模：

${L_{\text{g}}} = \sqrt {{{(\partial g/\partial p')}^2} + {{(\partial g/\partial q)}^2}} 。$

(17)

$\partial g/\partial p'$ 和 $\partial g/\partial q$ 分别为塑性势函数对 $p'$ 和 $q$ 的偏导：

$\frac{{\partial g}}{{\partial p'}} = - \frac{{2{M_{\text{d}}}^2(1 + \chi )(p' + {p_t}){q^2}}}{{{{\left[ {{M_{\text{d}}}^{\text{2}}{{(p' + {p_t})}^2} - \chi {q^2}} \right]}^2}}} + \frac{{{p_0} + {p_t}}}{{p' + {p_t}}} \text{，}$

(18)

$\frac{{\partial g}}{{\partial q}} = \frac{{2{M_{\text{d}}}^{\text{2}}(1 + \chi ){{(p' + {p_t})}^2}q}}{{{{\left[ {{M_{\text{d}}}^{\text{2}}{{(p' + {p_{\text{t}}})}^2} - \chi {q^2}} \right]}^2}}} 。$

(19)

2.3 弹塑性增量关系

弹性体积应变分量和剪应变分量为

${\text{d}}\varepsilon _{\text{v}}^{\text{e}} = {\text{d}}p'/K \text{，} {\text{d}}\varepsilon _{\text{q}}^{\text{e}} = {\text{d}}q/(3G) \text{，}$

(20)

式中， $K$ 为体积模量， $G$ 为剪切模量。表达式分别如下：

$K = (1 + {e_0})p/\kappa \text{，} G = 1.5K(1 - 2\nu )/(1 + \nu ) \text{，}$

(21)

式中， ${e_0}$ 为固结完成时的初始孔隙比， $\nu$ 为泊松比。

塑性体积应变分量和剪应变分量为

${\text{d}}\varepsilon _{\text{v}}^{\text{p}} = \left\langle {({n_{\text{p}}}{\text{d}}p' + {n_{\text{q}}}{\text{d}}q)/H} \right\rangle {m_{\text{p}}} \text{，}$

(22)

${\text{d}}\varepsilon _q^p = \left\langle {({n_{\text{p}}}{\text{d}}p' + {n_{\text{q}}}{\text{d}}q)/H} \right\rangle {m_{\text{q}}} \text{，}$

(23)

式中， $H$ 为塑性模量， $\left\langle {} \right\rangle$ 为Macaulay括号：当 $a \leqslant 0$ 时， $\left\langle a \right\rangle = 0$ ；当 $a > 0$ 时， $\left\langle a \right\rangle = a$ 。

2.4 塑性模量

塑性模量一般可以通过屈服面方程的一致性条件求得，但是为了描述土体塑性变形的状态相关性，需要将状态参数引入塑性模量中。本文塑性模量采用如下形式：

$H = {h_0}G{M_{{\text{cs}}}}({M_{\text{b}}} - {\eta ^*})/({M_{\text{b}}}{\eta ^*}) \text{，}$

(24)

式中， ${h_0}$ 为塑性模量参数， ${M_{\text{b}}}$ 为峰值应力比， ${\eta ^*}$ 为修正应力比。

峰值应力比 ${M_{\text{b}}}$ 表达式为^[33]

${M_{\text{b}}} = {M_{{\text{cs}}}}\exp ( - {k_{\text{b}}}\psi ) \text{，}$

(25)

式中， ${k_{\text{b}}}$ 为峰值应力比相关的材料常数。

修正应力比 ${\eta ^*}$ 可以表示为

${\eta ^*} = q/(p' + {p_{\text{t}}}) 。$

(26)

3. 模型预测

3.1 模型参数分析

引入状态参数的MICP胶结砂土边界面本构模型共有13个参数，其中 $\kappa$ 和 $\mu$ 为弹性相关的参数， $\lambda$ ， $\chi$ ， ${M_{{\text{cs}}}}$ 和 ${e_{{\text{cs0}}}}$ 为临界状态参数， ${p_{{\text{t0}}}}$ ， ${\xi _0}$ ， $\alpha$ 和 $\beta$ 为胶结作用及胶结退化有关的参数， ${k_{\text{d}}}$ 为剪胀相关的参数， ${k_{\text{b}}}$ 为峰值状态参数， ${h_0}$ 为塑性模量参数。

参数 $\lambda$ ， $\kappa$ ， $\mu$ ， ${M_{{\text{cs}}}}$ 为修正剑桥模型中的参数，可通过三轴试验和等向压缩试验获得。 ${e_{{\text{cs0}}}}$ 可以通过不同围压三轴试验的临界状态孔隙比在 $e$ – $\ln p'$ 空间中拟合得到^[27]。参数 $\chi$ 通过Yao等^[25]介绍的方法确定，但是由于缺乏MICP加固砂土正常固结线NCL的试验数据，该参数通过拟合试验数据的应力–应变关系得到。 ${p_{{\text{t0}}}}$ 的确定方法前文已经叙述。 ${\xi _0}$ ， $\alpha$ 和 $\beta$ 可以通过拟合三轴排水剪切试验的应力–应变关系得到。 ${k_{\text{d}}}$ 和 ${k_{\text{b}}}$ 的确定方法可以参考Li等^[33]、Xiao等^[34]和孙增春等^[35]。塑性模量参数 ${h_0}$ 可以通过拟合三轴剪切试验的应力–应变曲线得到^[34]。采用中的基准分析参数，分析临界状态参数 $\chi$ ，胶结作用退化速率参数 ${\xi _0}$ ， $\alpha$ 和 $\beta$ 对应力–应变关系，剪胀规律和胶结作用演化的影响。

表 1 模型分析参数

Table 1. Model analysis parameters

初始状态	弹性参数	临界状态参数	胶结作用参数	其他参数
${e_0} = 0.8$ ${p_{{\text{ic}}}} = 100$ kPa	$\mu$ =0.25 $\kappa = 0.005$	$\lambda = 0.08$	${p_{t0}} = 80$ kPa	${k_{\text{d}}} = 1.5$ ${k_{\text{b}}} = 1.0$ ${h_0} = 2.0$
		${M_{{\text{cs}}}} = 1.5$	${\xi _0} = 0.2$
		${e_{{\text{cs0}}}} = 1.2$	$\alpha = 0.01$
		$\chi = 0.1$	$\beta = 1.0$

下载: 导出CSV

| 显示表格

为参数 $\chi$ ， ${\xi _0}$ ， $\alpha$ ， $\beta$ 的变化对应力–应变关系、体变规律和胶结退化的影响。从可知，参数 $\chi$ 对体积应变的变化影响明显，随着 $\chi$ 的增大，体变由剪缩过渡到剪胀。同时，随着 $\chi$ 的增大，胶结退化速率增加，应变软化更加明显，但是峰值偏应力不变，说明 $\chi$ 的变化主要影响峰值强度后的胶结破坏速率，且 $\chi$ 增大会使到达峰值强度的应变减小。可以看出，参数 ${\xi _0}$ 和 $\alpha$ 对模拟结果的影响相似，即随着参数取值增加，胶结退化加快，且峰值强度降低，应变软化和剪胀更加明显，说明上述两个参数影响不仅影响峰值强度后的胶结破坏速率，同时影响峰值强度前的胶结破坏速率，即随着参数取值增大，在达到峰值强度前已有大量胶结作用破坏，使被加固土体整体强度降低。从可以看出，随着参数 $\beta$ 的增大，胶结作用破坏速率增加，同时应变软化和剪胀更加明显，但是峰值强度和剪缩部分的体变几乎不受影响。从式(5)可以看出，参数 $\beta$ 主要控制塑性损伤应变对胶结作用退化速率的影响，随着塑性应变的累计，参数 $\beta$ 对退化速率的影响增大。

图 5 参数对模型预测的影响

Figure 5. Influences of parameters on model performance

下载: 全尺寸图片幻灯片

3.2 模型描述与试验对比

为了验证模型的适用性，选取MICP加固Ottawa 20/30砂、石英砂和钙质砂的三轴排水试验结果与模型计算结果进行对比分析。其中，Lin等^[22]分别对未加固和MICP加固的Ottawa 20/30砂开展了三轴排水剪切试验，试样的初始孔隙比为0.65，初始有效固结围压分别为25，50，100 kPa。Xiao等^[23]分别对未加固和3种MICP加固程度(B_ca=1.8%，B_ca =3.5%和B_ca=5.1%)的石英砂开展了4种有效固结围压(20，50，100，200 kPa)三轴排水剪切试验，试样的初始孔隙比为0.65。Cui等^[24]对不同MICP加固程度的钙质砂进行三轴排水剪切试验，固结围压分别为100，200，300 kPa，试样的初始孔隙比为0.92。模型参数均通过试验数据进行校准，不同材料的模型计算参数取值见表 2。

表 2 模型计算参数

Table 2. Model parameters

参数	Ottawa 20/30砂	MICP 加固Ottawa 20/30砂	MICP 加固石英砂B_ca=1.8%	MICP 加固石英砂B_ca=3.5%	MICP加固钙质砂
$\mu$	0.32	0.30	0.30	0.30	0.25
$\lambda$	0.009	0.001	0.049	0.051	0.047
$\kappa$	0.001	0.015	0.005	0.005	0.002
${M_{{\text{cs}}}}$	1.29	1.43	1.23	1.42	1.43
${e_{{\text{cs0}}}}$	0.714	0.736	1.024	1.054	1.349
$\chi$	0.02	0.1	0.1	0.1	0.1
${k_{\text{d}}}$	2.5	1.5	1.5	1.2	1.5
${k_{\text{b}}}$	1.0	1.5	2.0	0.8	0.1
${h_0}$	0.8	5.0	1.5	2.5	3.5
${p_{{\text{t0}}}}$ /kPa	—	92.5	32.21	36.29	434.5
${\xi _0}$	—	0.28	0.21	0.15	0.27
$\alpha$	—	0.013	-0.016	0.01	-0.005
$\beta$	—	5.0	1.0	2.0	5.0

下载: 导出CSV

| 显示表格

图 6为Ottawa 20/30砂和MICP加固Ottawa 20/30砂^[22]在不同围压下的试验结果与本构模型模拟结果对比。可以看出，模型可以较好地模拟Ottawa 20/30砂在各围压下的应力–应变发展规律和剪胀现象。对于MICP加固Ottawa 20/30砂，本文建立的本构模型计算得到各围压下的应力–应变曲线的峰值应力点对应的轴向应变大于试验结果，模拟的剪胀整体大于试验结果。但是，本文模型可以较好地模拟出MICP加固Ottawa 20/30砂在达到峰值强度后，由于塑性应变的累计，碳酸钙对土体的胶结大量破坏而出现强度陡降的脆性破坏。

图 6 Ottawa 20/30砂和MICP加固Ottawa 20/30砂三轴排水试验结果与模型预测对比

Figure 6. Comparison between test results and model predictions on Ottawa 20/30 sand and MICP-treated Ottawa 20/30 sand under drained triaxial compression

下载: 全尺寸图片幻灯片

图 7为两种加固程度(B_ca=1.8%，B_ca =3.5%)的MICP加固石英砂^[23]在不同初始有效围压下的试验结果与数值模拟结果对比，从图中可以看出模型能够较好地反映MICP加固石英砂的软化特性和体积变化规律。图 8给出了本文模型计算结果与Cui等^[24]对MICP加固钙质砂(CCC=25.5%)的三轴排水剪切试验结果的对比，可以看出本文所建立的本构模型可以较好地模拟出MICP加固钙质砂的应变软化特性，且其胶结退化速率随围压改变而不同，具体为低围压时胶结退化速率较快，软化更加明显；高围压时胶结退化速率较慢。同时，上述结果也验证了本文将胶结退化速率与围压建立关系的正确性。对MICP加固钙质砂体变的变化规律的模拟结果较差，表现为低围压时剪胀较小，且剪胀增长速率较慢，高围压时剪胀过大。

图 7 B_ca=1.8%和B_ca=3.5% MICP加固石英砂三轴排水试验结果与模型预测对比

Figure 7. Comparison between test results and model predictions on MICP-treated silica sand for B_ca=1.8% and B_ca=3.5% under drained triaxial compression

下载: 全尺寸图片幻灯片

图 8 CCC =25.5% MICP加固钙质砂三轴排水试验结果与模型预测对比

Figure 8. Comparison between test results and model predictions on MICP-treated calcareous sand for CCC =25.5% under drained triaxial compression

下载: 全尺寸图片幻灯片

4. 结论

本文针对MICP加固砂土的强度和变形特征，在分析加固和破坏机理的基础上，基于临界状态土力学理论框架，将胶结退化速率与围压和塑性应变建立关系，采用非关联流动法则，引入状态参数和剪胀应力比及峰值应力比，建立了MICP加固砂土状态相关的弹塑性本构模型。将模型计算结果分别与MICP加固Ottawa 20/30砂、MICP加固石英砂和MICP加固钙质砂的三轴试验结果进行对比，得到以下结论：

(1) 通过对MICP加固砂土的破坏包络线进行分析，发现石英砂和钙质砂经MICP加固后土体黏聚力都有所增加，但是MICP加固石英砂的峰值摩擦角增加，MICP加固钙质砂的峰值摩擦角减小。主要是两种砂土颗粒本身的形状、表面粗糙度及钙质砂存在的内孔隙使碳酸钙沉积方式及对力学性能的贡献存在差异导致。

(2) 对MICP加固石英砂和MICP加固钙质砂的临界状态线进行分析，发现临界状态线在 $e$ – $\ln p'$ 空间中随加固程度增加而向上移动，可能是由于被加固土体中的胶结作用未完全破坏或碳酸钙附着在砂颗粒表面的影响。在 $p'$ – $q$ 空间中随加固程度增加MICP加固石英砂的临界状态线的斜率逐渐增大，但是MICP加固钙质砂的斜率增加不明显，主要是由于钙质砂的颗粒表面存在内孔隙。

(3) 通过对不同MICP加固程度的3种砂土的三轴排水剪切试验的模拟，表明本文建立的本构模型能够较好地模拟MICP加固砂土随胶结退化出现的应变软化行为及体积变化规律。

图 1 砂土的级配曲线

Figure 1. Grain-size distribution curve of sand

下载: 全尺寸图片幻灯片

图 2 振动台和模型箱

Figure 2. Shaking table and model box

下载: 全尺寸图片幻灯片

图 3 传感器布置方案

Figure 3. Schematic diagram of arrangement of sensors

下载: 全尺寸图片幻灯片

图 4 0.4g阶段台面地震记录及其正则化傅里叶频谱(A_mpk为傅里叶幅值)

Figure 4. Input seismic motions and normalized Fourier amplitudes with peak amplitude A_mpk

下载: 全尺寸图片幻灯片

图 5 土体的相对位移与加速度

Figure 5. Relative displacements and accelerations of soil at structural region

下载: 全尺寸图片幻灯片

图 6 地震荷载作用下土体的剪应力–剪应变关系(IM-12)

Figure 6. Shear stress vs. shear strain hysteresis of sand under seismic motion at IM-12

下载: 全尺寸图片幻灯片

图 7 自由场试验中土体的动剪应变–动剪切模量比估算结果(CH08, 0.4g阶段)

Figure 7. Estimated shear modulus degradation relationships obtained from shaking table tests (CH08, 0.4g stage)

下载: 全尺寸图片幻灯片

图 8 整体式反应位移法有限元计算模型

Figure 8. Finite element model of integral response deformation method

下载: 全尺寸图片幻灯片

图 9 后续试验中的模型车站结构

Figure 9. Model structure in subsequent tests

下载: 全尺寸图片幻灯片

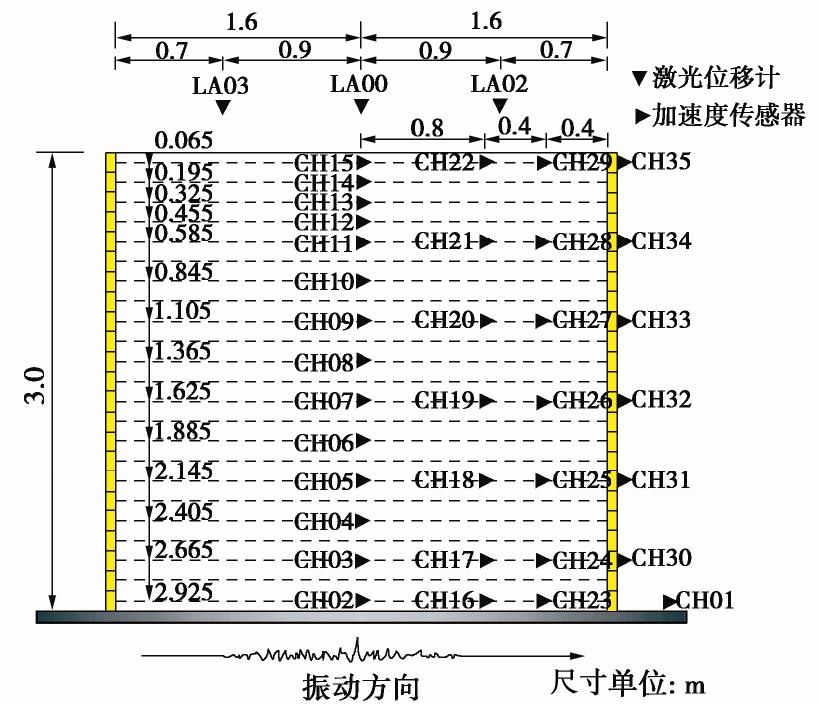
表 1 动力荷载的输入顺序

Table 1 Sequence of input motions

工况序号	动力荷载	峰值加速度/g	试验阶段/g
IM-1	第一次白噪声	0.05
IM-2	第一次脉冲	0.05
IM-3	Loma Prieta (LP)	0.20	0.20
IM-4	Kobe	0.20
IM-5	汶川	0.20
IM-6	北京人工记录	0.20
IM-7	第二次白噪声	0.05
IM-8	第二次脉冲	0.05
IM-9	Loma Prieta (LP)	0.40	0.40
IM-10	Kobe	0.40
IM-11	汶川	0.40
IM-12	北京人工记录	0.40
IM-13	第三次白噪声	0.05
IM-14	第三次脉冲	0.05

下载: 导出CSV

表 2 土层的最大剪切模量G_max估算结果

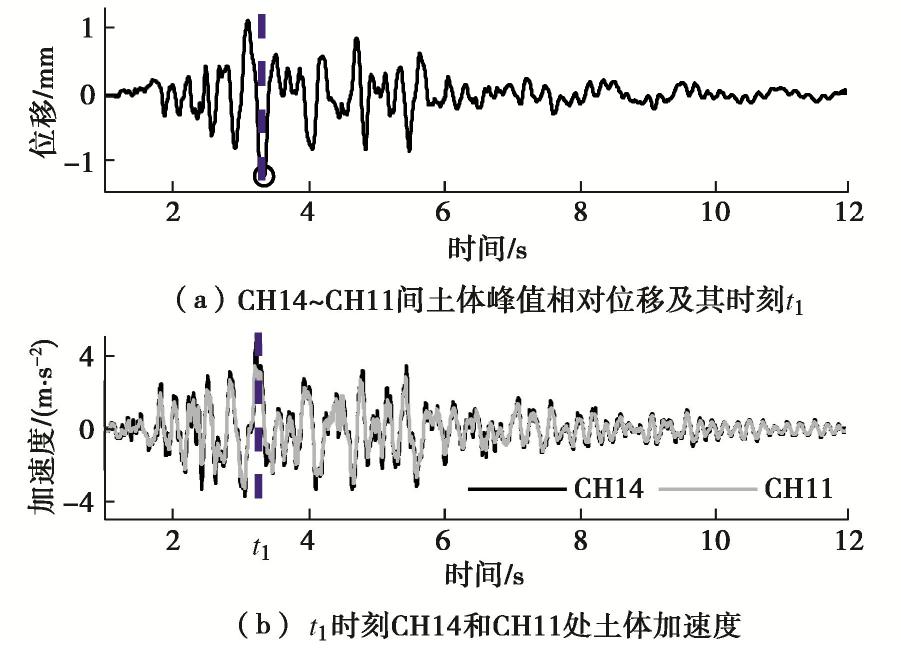
Table 2 Maximum shear moduli of soil layers (MPa)

工况	土层1	土层2	土层3
第一次脉冲	5.0	21.7	55.4
第二次脉冲	4.0	12.0	32.4

下载: 导出CSV

表 3 整体式反应位移法计算中所使用的荷载参数

Table 3 Loads for integral response displacement method

工况	土体相对位移/mm	加速度/(m·s^-2)		结构周围剪应力/kPa
工况	土体相对位移/mm	顶板	底板	顶板	底板	左墙	右墙
IM-6	0.47	3.00	2.73	-0.70	-2.63	-0.97	0.97
IM-12	-1.23	-3.46	-3.14	0.81	3.08	1.14	-1.14

下载: 导出CSV

表 4 土层的材料属性G

Table 4 Estimated dynamic shear moduli G of soil (MPa)

工况	土层1(G₁)	土层2(G₂)	土层3(G₃)
IM-6	1.8	7.9	25.9
IM-12	1.5	2.7	9.2

下载: 导出CSV

表 5 结构的材料与截面属性

Table 5 Properties of material and section

密度/(kg·m^-3)	弹性模量/GPa	截面厚度/cm
密度/(kg·m^-3)	弹性模量/GPa	底板	中板	顶板	墙	柱
2400	13.8	2.7	1.3	2.3	2.3	0.259

下载: 导出CSV

表 6 预测与后续试验结果对比

Table 6 Comparison between predicted and subsequent test results

工况		后续试验结果	本文方法预测结果	全数值方法预测结果
IM-6	顶一底板水平相对位移/mm	0.35	0.45	0.15
	顶板右端竖向位移/mm	0.05	0.09	0.02
	地下一层右侧柱底应变/με	2.15	5.54	7.32
	地下一层右侧柱顶应变/με	1.95	6.10	7.24
	地下一层左侧墙底应变/με	0.27	0.70	1.96
	地下一层左侧墙顶应变/με	0.86	0.46	1.35
	地下一层右侧墙底应变/με	0.44	0.75	1.96
	地下二层右侧柱底应变/με	3.02	3.43	6.41
	地下二层左侧柱底应变/με	1.48	3.45	6.39
	地下二层左侧墙顶应变/με	0.81	0.79	2.47
	地下二层右侧墙顶应变/με	0.76	0.80	2.47
	地下二层右侧墙底应变/με	1.21	1.22	3.08
IM-12	顶-底板水平相对位移/mm	0.88	0.75	0.35
	顶板右端竖向位移/mm	1.10	0.15	0.10
	地下一层右侧柱底应变/με	5.01	7.93	13.33
	地下一层右侧柱顶应变/με	7.80	7.94	14.32
	地下一层左侧墙底应变/με	1.06	0.93	2.61
	地下一层左侧墙顶应变/με	2.59	0.51	1.20
	地下一层右侧墙底应变/με	1.63	0.93	2.44
	地下二层右侧柱底应变/με	2.82	3.62	10.32
	地下二层左侧柱底应变/με	3.36	3.59	10.28
	地下二层左侧墙顶应变/με	2.79	0.93	3.28
	地下二层右侧墙顶应变/με	1.82	0.92	3.39
	地下二层右侧墙底应变/με	1.38	1.44	4.27
注：表中的位移和应变均为相应地震工况作用下的峰值大小。

下载: 导出CSV

参考文献(28)

[1]	TANG B Z, LI X J, CHEN S, et al. Investigations of seismic response to an irregular-section subway station structure located in a soft clay site[J]. Engineering Structures, 2020, 217: 110799. doi: 10.1016/j.engstruct.2020.110799
[2]	WU W F, GE S P, YUAN Y, et al. Seismic response of subway station in soft soil: Shaking table testing versus numerical analysis[J]. Tunnelling and Underground Space Technology, 2020, 100: 103389. doi: 10.1016/j.tust.2020.103389
[3]	禹海涛, 陈希卓, 李攀. 基于双台阵模拟地震空间差动效应的模型箱参数解析[J]. 岩土工程学报, 2020, 42(8): 1428-1434. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202008011.htm YU Hai-tao, CHEN Xi-zhuo, LI Pan. Analytical solution for design parameters of model box to simulate seismic spatial variability effect using double-array shaking tables[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(8): 1428-1434. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202008011.htm
[4]	刘必灯, 郭迅. 西南交通大学8 m×10 m地震模拟振动台运行对场地振动的影响分析[J]. 中国地震, 2019, 35(2): 226-237. doi: 10.3969/j.issn.1001-4683.2019.02.002 LIU Bi-deng, GUO Xun. Experimental study of field vibration influence induced by the 8 m×10 m shake table of Southwest Jiaotong University[J]. Earthquake Research in China, 2019, 35(2): 226-237. (in Chinese) doi: 10.3969/j.issn.1001-4683.2019.02.002
[5]	陈学伟, 季静, 吴培烽, 等. E-Defense振动台试验预测性分析比赛的研究综述[J]. 世界地震工程, 2010, 26(3): 175-181. https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC201003029.htm CHEN Xue-wei, JI Jing, WU Pei-feng, et al. Summary on research of blind analysis contest of E-Defense shaking table test[J]. World Earthquake Engineering, 2010, 26(3): 175-181. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC201003029.htm
[6]	孙严. 基于框架结构盲测试验OpenSEES建模参数敏感性分析[D]. 哈尔滨: 黑龙江科技大学, 2016. SUN Yan. Sensitivity Analysis of Modeling Parameters for OpenSees Based on Frame Blind Test[D]. Harbin: Heilongjiang University of Science and Technology, 2016. (in Chinese)
[7]	张震. 场地地震反应一维数值分析方法对比分析[D]. 廊坊: 防灾科技学院, 2020. ZHANG Zhen. Comparison on One Dimension Numerical Methods of Site Seismic Response Analysis[D]. Langfang: Institute of Disaster Prevention, 2020. (in Chinese)
[8]	GRIFFITHS S C, COX B R, RATHJE E M. Challenges associated with site response analyses for soft soils subjected to high-intensity input ground motions[J]. Soil Dynamics and Earthquake Engineering, 2016, 85: 1-10. doi: 10.1016/j.soildyn.2016.03.008
[9]	杨林德, 季倩倩, 郑永来, 等. 软土地铁车站结构的振动台模型试验[J]. 现代隧道技术, 2003, 40(1): 7-11. doi: 10.3969/j.issn.1009-6582.2003.01.002 YANG Lin-de, JI Qian-qian, ZHENG Yong-lai, et al. Shaking table test on metro station structures in soft soil[J]. Modern Tunnelling Technology, 2003, 40(1): 7-11. (in Chinese) doi: 10.3969/j.issn.1009-6582.2003.01.002
[10]	李杰, 岳庆霞, 陈隽. 地下综合管廊结构振动台模型试验与有限元分析研究[J]. 地震工程与工程振动, 2009, 29(4): 41-45. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200904005.htm LI Jie, YUE Qing-xia, CHEN Jun. Research on shaking-table test and finite element numerical simulation of utility tunnel[J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(4): 41-45. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200904005.htm
[11]	WANG Z Z, JIANG Y J, ZHU C A, et al. Shaking table tests of tunnel linings in progressive states of damage[J]. Tunnelling and Underground Space Technology, 2015, 50: 109-117. doi: 10.1016/j.tust.2015.07.004
[12]	MOGHADAM M R, BAZIAR M H. Seismic ground motion amplification pattern induced by a subway tunnel: shaking table testing and numerical simulation[J]. Soil Dynamics and Earthquake Engineering, 2016, 83: 81-97. doi: 10.1016/j.soildyn.2016.01.002
[13]	陈国兴, 王炳辉, 孙田. 饱和南京细砂动剪切模量特性的大型振动台试验研究[J]. 岩土工程学报, 2012, 34(4): 582-590. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201204004.htm CHEN Guo-xing, WANG Bing-hui, SUN Tian. Dynamic shear modulus of saturated Nanjing fine sand in large scale shaking table tests[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(4): 582-590. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201204004.htm
[14]	DIHORU L, BHATTACHARYA S, MOCCIA F, et al. Dynamic testing of free field response in stratified granular deposits[J]. Soil Dynamics and Earthquake Engineering, 2016, 84: 157-168. doi: 10.1016/j.soildyn.2016.02.014
[15]	TSAI C C, LIN W C, CHIOU J S. Identification of dynamic soil properties through shaking table tests on a large saturated sand specimen in a laminar shear box[J]. Soil Dynamics and Earthquake Engineering, 2016, 83: 59-68. doi: 10.1016/j.soildyn.2016.01.007
[16]	刘晶波, 王文晖, 赵冬冬, 等. 地下结构抗震分析的整体式反应位移法[J]. 岩石力学与工程学报, 2013, 32(8): 1618-1624. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201308015.htm LIU Jing-bo, WANG Wen-hui, ZHAO Dong-dong, et al. Integral response deformation method for seismic analysis of underground structure[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(8): 1618-1624. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201308015.htm
[17]	刘晶波, 王文晖, 赵冬冬, 等. 复杂断面地下结构地震反应分析的整体式反应位移法[J]. 土木工程学报, 2014, 47(1): 134-142. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201401018.htm LIU Jing-bo, WANG Wen-hui, ZHAO Dong-dong, et al. Integral response deformation method in seismic analysis of complex section underground structures[J]. China Civil Engineering Journal, 2014, 47(1): 134-142. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201401018.htm
[18]	刘晶波, 王东洋, 谭辉, 等. 整体式反应位移法的理论推导及一致性证明[J]. 土木工程学报, 2019, 52(8): 18-23. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201908003.htm LIU Jing-bo, WANG Dong-yang, TAN Hui, et al. Theorectical derivation and consistency proof of the integral response deformation method[J]. China Civil Engineering Journal, 2019, 52(8): 18-23. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201908003.htm
[19]	ZENG X, SCHOFIELD A N. Design and performance of an equivalent-shear-beam container for earthquake centrifuge modelling[J]. Géotechnique, 1996, 46(1): 83-102.
[20]	倪克闯. 成层土中桩基与复合地基地震作用下工作性状振动台试验研究[D]. 北京: 中国建筑科学研究院, 2013. NI Ke-chuang. Shaking Table Test of Pile and Composite Foundations' Dynamic Behavior in Layered Soils Subjected to Earthquake Excitation[D]. Beijing: China Academy of Building Research, 2013. (in Chinese)
[21]	SEED H B, IDRISS I M. Soil Moduli and Damping Factors for Dynamic Response Analyses[R]. Berkeley: Earthquake Engineering Research Center, University of California, 1970.
[22]	SADREKARIMI A. Dynamic behavior of granular soils at shallow depths from 1g shaking table tests[J]. Journal of Earthquake Engineering, 2013, 17: 227-252.
[23]	ANJALI M, VIVEK B, RAYCHOWDHURY P. Seismic response analysis of Ganga sand deposits using shake table tests[J]. International Journal of Geo-Engineering, 2015, 6(1): 11.
[24]	ZEGHAL M, ELGAMAL A W. Analysis of site liquefaction using earthquake records[J]. Journal of Geotechnical Engineering, 1994, 120(6): 996-1017.
[25]	LI Z, ESCOFFIER S, KOTRONIS P. Using centrifuge tests data to identify the dynamic soil properties: application to Fontainebleau sand[J]. Soil Dynamics and Earthquake Engineering, 2013, 52: 77-87.
[26]	地下结构抗震设计标准：GB/T 51336—2018[S]. 2018. Standard for Seismic Design of Underground Structures: GB/T 51336—2018[S]. 2018. (in Chinese)
[27]	江志伟. 装配式地铁隧道和车站结构抗震研究[D]. 北京: 北京工业大学, 2019. JIANG Zhi-wei. Aseismic Investigations on Precast Subway Tunnel and Station[D]. Beijing: Beijing University of Technology, 2019. (in Chinese)
[28]	刘洪涛, 许紫刚, 杜修力. 基于不同计算方法下的装配整体式地铁车站抗震性能研究[J]. 特种结构, 2019, 36(5): 71-76. https://www.cnki.com.cn/Article/CJFDTOTAL-TZJG201905013.htm LIU Hong-tao, XU Zi-gang, DU Xiu-li. Analysis of seismic performance of assembled monolithic subway station based on different calculation methods[J]. Special Structures, 2019, 36(5): 71-76. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TZJG201905013.htm

施引文献(23)

期刊类型引用(8)

1.	刘雪莹，俞缙，周先齐，姚玮，任崇鸿，蔡燕燕. 一种新的岩石各向异性蠕变-渗透率模型. 岩土工程学报. 2025(02): 275-283 . 本站查看
2.	郭建春，张涛，武玺，赵志红，李宗源，曾杰. 煤层气压裂水平井生产动态分析及其渗透率协同演化机制. 煤炭学报. 2025(01): 516-531 . 百度学术
3.	张磊丽，蔡婷婷，石磊，姜玉龙，夏瑾. 不同温度-围压-气体压力下煤体蠕变-渗流演化规律. 煤矿安全. 2024(03): 36-45 . 百度学术
4.	赵一博. 计算多孔介质流线迂曲度及其分形维数的新几何模型. 材料导报. 2024(S2): 282-286 . 百度学术
5.	李钊，倪冠华，杨威，温永瓒，王刚，刘震，王振洋. 不同冲击倾向性煤体孔隙结构及瓦斯吸附特征研究. 煤炭科学技术. 2024(S2): 56-70 . 百度学术
6.	张学博，王豪，杨明，王攀，韩林秀. 抽采钻孔失稳坍塌对瓦斯抽采的影响机制研究及应用. 煤炭学报. 2023(08): 3102-3115 . 百度学术
7.	王科文. 瓦斯抽采钻孔新型封孔工艺试验研究. 山东煤炭科技. 2023(09): 128-130 . 百度学术
8.	许江，饶豪魁，彭守建，陈奕安，陈灿灿，马天宇. 三轴应力条件下凝灰岩广义应力松弛流变模型的构建. 采矿与安全工程学报. 2023(06): 1264-1272 . 百度学术