Creep characteristics and model study of composite geomembrane with different film thicknesses
-
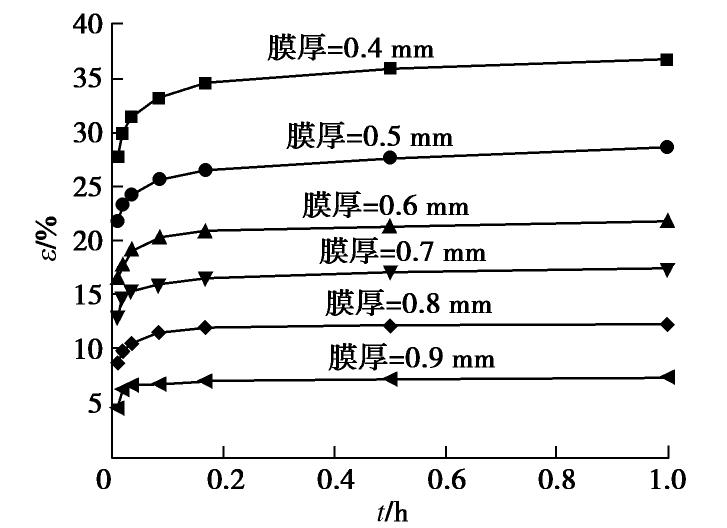
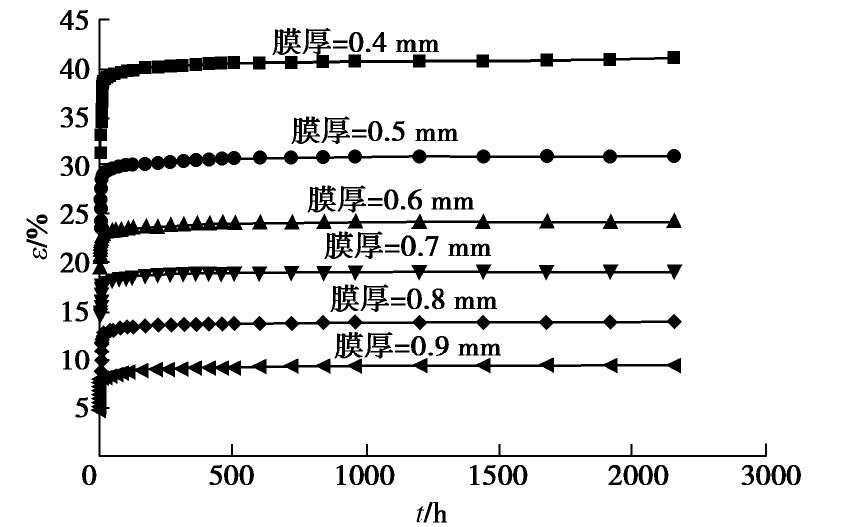
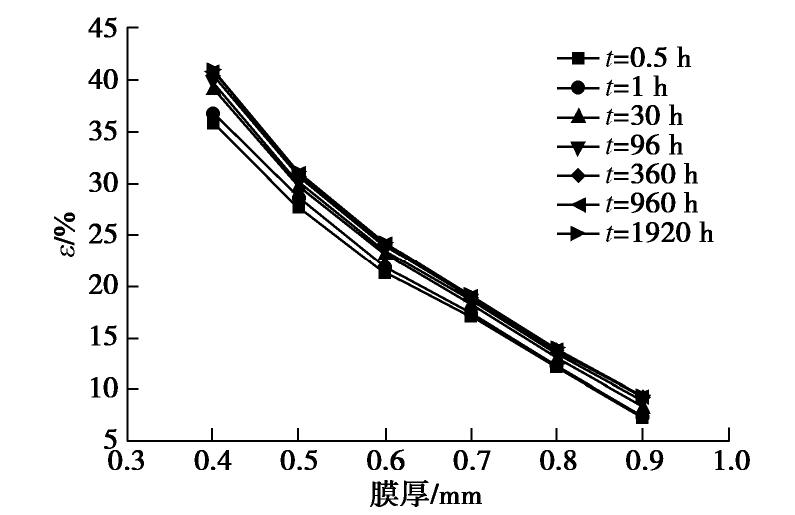
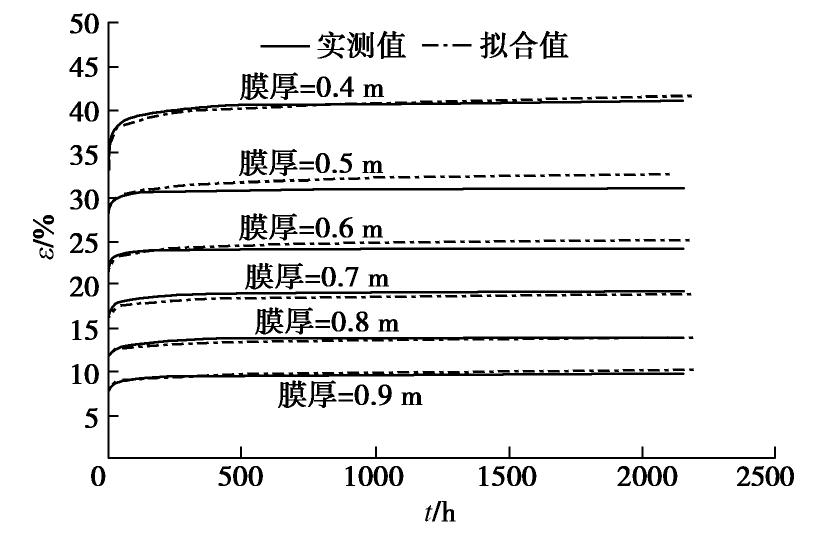
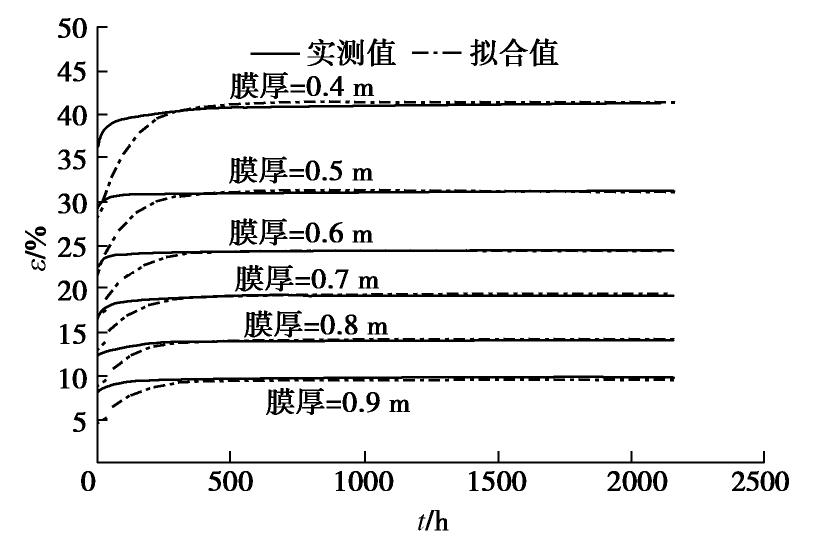
摘要: 复合土工膜被广泛使用于土石坝中,其长期变形性能对结构安全及稳定性至关重要。通过长达90 d的蠕变试验,对比分析了复合土工膜在不同厚度下的蠕变规律,对典型的经验蠕变模型进行了归纳分类,综合蠕变试验结果,提出了基于厚度水平的经验蠕变模型,验证了其适用性与可靠性;通过理论分析,提出了三参数黏弹性本构模型,应用Marquardt优化迭代算法及全局最优化求解模型参数,论证其合理性。结果表明:荷载施加瞬时位移量迅速增加,并随时间的增加应变增量逐渐减小,最后趋于稳定;当荷载为膜厚0.4 mm最大拉伸荷载的60%时,膜厚每增加0.1 mm,长期稳定时应变降低约6%;提出基于厚度的经验蠕变模型可有效反映应变与时间的关系,初始阶段的拟合效果更好;黏弹性本构模型中,厚度较薄时kelvin体对变形的影响更大,厚度较厚时弹性系数E1对变形的发展发挥着主要作用,本构模型能够较准确的反映材料蠕变的最终应变量。经验蠕变模型与本构模型结合可较好的预测不同厚度水平下复合土工膜的整体变形。Abstract: Through 90 days of creep tests, the creep laws of composite geomembrane at different thickness levels are compared and analyzed. The previous typical creep models are classified and compared with the creep test results. An empirical creep model based on thickness level is proposed to verify its applicability and reliability. Based on the analysis of materials and creep data, a three-parameter viscoelastic constitutive model is proposed, and its rationality is demonstrated by using the Marquardt optimization iterative algorithm and the global optimization to solve model parameters. The results show that the composite geomembrane exhibits strong lateral contraction under the long-term tensile action of the load. The instantaneous displacement of the load increases rapidly, and the strain increment decreases with the increase of time, and finally tends to be stable. The strain of different film thicknesses is little affected by time. When the load level is 60%, every 0.1 mm increase in film thickness from 0.4 mm to 0.9 mm reduces the strain by about 6% in long-term stability. The empirical creep model based on thickness can effectively reflect the relationship between creep strain and time of two films, and the initial stage has better fitting effect. The three-parameter viscoelastic constitutive model is suitable for the attenuation creep curve and can accurately reflect the final strain of the materials in the creep stage.
-
Keywords:
- composite geomembrane /
- creep behavior /
- constitutive model /
- long-term deformation
-
0. 引言
作为文明起源最早、延续时间最长的国家之一,中国的广阔疆域上遍布土遗址,其中属于全国重点文物保护单位的就有近400个,涵盖了上至石器时代下至明清的各个时期。它们是人类活动的产物,更是特定历史阶段的科学技术、社会经济及精神文化信息的重要载体,极具保护价值和意义。然而,由于土遗址常与大地直接相连且暴露在开放环境中,自然外营力的长期作用导致多种病害综合发育,加速了文物本体的劣化与消亡。
土遗址表层的结皮龟裂及剥离病害尤为普遍和典型[1-2]。通常认为结皮的出现与雨蚀有关,即表层土体在雨滴打击作用下局部饱和、崩解而形成蠕流泥浆,随后逐渐干燥收缩变为硬壳,甚至开裂起翘(图 1)。张虎元等[3]统计结皮层的表观特征发现,其厚度与墙体建筑工艺有关,一般在1~15 mm之间,分布形态包括连续状、片状和斑点状。崔凯等[4]指出干旱区夯土遗址的表面剥离具有二元结构,壳层与下伏粉层在颗粒组成、孔隙率及易溶盐含量等方面均存在差异。为模拟表层结皮的形成发育过程,前人开展了一系列室内试验,初步揭示了遗址土泥浆在蒸发过程中的体积收缩规律[5]以及裂隙网络形态演化和扩展机制[6-7]。
土体的干缩开裂现象本质上是应力作用的结果,即当干燥过程中产生的基质吸力所引起的张拉应力超过土体自身抗拉强度时,便会出现裂隙。土水特征曲线可用于预测土体变形、强度等力学特性,开展考虑体变的非饱和土持水特性研究,对于揭示土遗址劣化机理、制定合理的科学防治措施具有重要的理论与工程实践意义。针对遗址土持水特性,有文献测定了脱湿条件下土体含水率随基质吸力变化规律,并讨论了矿物成分[8-9]、含盐量[10]以及化学加固材料[11]等因素对曲线的影响。然而需要强调的是,即使基质吸力相同,饱和度差异也会造成土体力学特性的显著不同[12-13]。尤其对于高塑性土而言,其干燥收缩不可忽略,持水和体变特性之间存在强烈的水力耦合效应,含水率与孔隙比往往随吸力同时改变并相互作用[14-15]。张雪东等[16]、邹维列等[17]修正了土体变形对饱和度的影响,并基于此建立了孔隙率与经典土水特征曲线模型参数之间的函数关系。
实际上,土的宏观变形和持水能力都与其颗粒排布、孔隙尺寸等密切相关,因此土体微观结构演变在近些年也越来越受到关注[18-19]。在干燥收缩的过程中,不同土样在各孔径范围的孔隙体积变化规律比较复杂。压实样宏观体积收缩包括团聚体间孔隙收缩和团聚体内孔隙收缩两部分,但以前者为主,即大孔中的自由水更容易被优先蒸发[20]。Sun等[21]发现重塑泥浆样的孔径分布曲线为单峰形态,曲线峰值的高度及其移动规律最终决定了持水特性。牛庚等[22]对比了单、双峰孔隙结构土样在脱湿阶段的微观特征和持水能力差异,并基于各自的孔径分布曲线确定了相应的进气值和残余吸力。
目前,土遗址表层结皮病害的相关机理仍不明晰,迫切需要更加系统、深入的研究,以便为治理和预防保护提供科学依据。本文以新疆交河故城为对象,利用当地黄土配制成泥浆后在室内开展自然风干条件下的自由收缩试验,获取试样宏观体积随含水率的发展规律,并借助压汞法探究微观孔隙结构的演变进程。在此基础上,结合交河遗址土的质量含水率与基质吸力关系,建立考虑体变的土水特征曲面模型,综合分析基质吸力和孔隙比对饱和度的影响机制。
1. 试验概况
1.1 试验材料与试样制备
本试验用土取自新疆交河故城遗址,属于低塑性黏土,其基本物理性质指标如表 1所示。X射线衍射分析表明,主要矿物成分为石英(35%)、长石(37%)和方解石(14%),黏土矿物以伊利石–蒙脱石互层型为主。原状样中易溶盐总量为3663.2 mg/kg,因此需对其进行脱盐处理[10],以消除固有盐分可能产生的影响。
表 1 遗址土的基本物理性质指标Table 1. Basic physical parameters of earthen heritage soil天然含水率
/%天然密度
/(g·cm-3)颗粒
相对质量密度液限
/%塑限
/%塑性
指数颗粒粒径分布/% 0.075~2 mm 0.002~0.075 mm < 0.002 mm 1.74 1.65 2.7 30 19 11 4.4 79.4 16.2 为配制初始含水率45%(1.5倍液限)的泥浆,先将烘干的脱盐土与去离子水充分混合、搅拌,利用机械振动的方式使试样内部气泡完全排出后,密封保存48 h以保证水分分布均匀且不存在团聚体。
1.2 试验方法与步骤
首先,准备25个圆形塑料培养皿(D=6.5 cm,H=2 cm),并在其内表面涂抹凡士林,以降低内壁摩阻力对试样变形的影响;再依次将平衡好的泥浆等量缓慢注入培养皿中,防止大量气泡混入;在室温(20±1)℃条件下开展自由收缩试验,即通过蒸发3 h、密封1 h交替的方式使试样缓慢风干至各自预设的目标含水率。然后,将达到目标含水率的饼状试样密封静置24 h以消除动态蒸发造成的局部水分差异,再用刀片将其切分成数个约1 cm3的方块并削去突出棱角备用。随机选择3个方块,采用烘箱法获取准确含水率;另取4个方块由蜡封法[23]测定密度并换算得到相应的孔隙比。分别求取2组方块样测试结果的平均值,作为该饼状试样实际的含水率和孔隙比。
同时,选取8个不同含水率试样开展压汞试验。将切好的目标土块放入液氮快速冷冻,再采用冷冻干燥机在气压2 Pa、温度-63.8℃的条件下连续抽真空48 h使其达到完全干燥状态,以降低脱湿过程对试样原有孔隙结构的破坏。利用压汞仪完成试样微观孔隙结构测试,仪器包括两个低压仓和一个高压仓,低压由氮气提供,探测孔径范围为3.6~360 μm,高压由高压油提供,可探测最小孔径为0.003 μm。
2. 试验结果与分析
2.1 收缩特征曲线
实测的遗址土泥浆收缩特征曲线如图 2所示,该曲线反映了试样孔隙比随体积含水比的变化关系。其中,体积含水比的定义是孔隙水与土颗粒两者体积之比,可由质量含水率与土颗粒相对质量密度相乘得到(即ew=wGs)。
结果表明,伴随着蒸发的进行,泥浆样发生显著的体积收缩,孔隙比也相应减小。按照从饱和到干燥的顺序,收缩特征曲线可依次划分为正常收缩段、残余收缩段和零收缩段3部分,未出现结构收缩段。这是由于试样初始含水率较高,混合搅拌过程使得土颗粒均匀分散,不存在团聚体,且相互之间黏聚力弱,试样各向同性好。
在正常收缩段,e与ew之间满足1∶1的线性关系,说明孔隙体积收缩量与蒸发的水分体积完全相等,此时试样始终处于饱和状态。当ew降低至0.6左右时,收缩进入残余段,即e减小速率变慢,曲线呈下凹形。这一阶段内的蒸发水量大于孔隙体积收缩量,表明空气开始逐渐进入试样。正常收缩段与残余收缩段的分界点对应含水率为22%,该值是表征土体由饱和向非饱和状态转变的关键参数。随着风干持续进行,ew降低到约0.43后,e几乎不再随之变化,曲线由此进入零收缩段。这一拐点对应的临界含水率为16%,即土体缩限,该值是评价黏性土收缩开裂特性的重要指标之一。
总体而言,交河遗址土泥浆的残余收缩段较短,绝大部分体积变化都发生在其处于饱和状态时的正常收缩段,这与其他学者[5, 24]得到的结论类似。
为定量描述土体e和ew之间的关系,前人建立了一系列收缩特征曲线模型[25]。针对类似于本文的不包括结构收缩段的双拐点、三段式曲线形态,Leong等[26]曾提出下列表达式:
e(ew)=emin+12S0⟨ew+1kln{cosh[k(ew−e′w)]cosh(k⋅e′w)}⟩。 (1) 式中emin为试样收缩稳定后的最小孔隙比,又称残余孔隙比;S0为试样初始饱和度,取1;k为残余收缩段的曲率;e′w为正常收缩段和零收缩段直线部分的延长线交点所对应的体积含水比。由于此处的正常收缩段斜率为1,故e′w与emin在数值上相等。
结果表明,该模型很好地描述了交河遗址土泥浆的完整收缩过程(图 2),其中emin,k的拟合值分别为0.545和7.671,拟合相关系数为0.997。
2.2 微观孔隙结构
实测的不同含水率试样的汞累计注入曲线如图 3所示。可以看出,随着风干程度的增加,最终的汞累计注入量不断减小,且这种变化趋势在高含水率段更为明显。当含水率降至21.64%以下时,土体孔隙体积收缩则逐渐停止并达到稳定。
将各试样最终的汞累计注入量与土颗粒相对质量密度相乘,可计算得到其压汞孔隙比eMIP。该值与自由收缩试验实测的孔隙比e相比始终偏小,但差值通常在10%以内(表 2)。这一偏差应与土体中存在的几种水银难以进入的特殊孔隙有关[27],包括被土颗粒完全包围的孤立封闭孔隙、截面半径显著变化的瓶颈式孔隙以及超过仪器测量界限的过大或过小孔隙。
表 2 不同含水率试样的eMIP与e对比Table 2. Comparison between eMIP and e of specimens with different water contents含水率/% eMIP e eMIP/e 30.51 0.784 0.826 0.949 27.14 0.720 0.734 0.981 23.48 0.604 0.664 0.910 21.64 0.555 0.609 0.911 17.68 0.524 0.565 0.927 13.54 0.512 0.547 0.936 9.76 0.511 0.546 0.936 2.74 0.502 0.547 0.918 孔径分布曲线反映了不同直径的孔隙各自所占有的体积。如图 4(a)所示,交河遗址土泥浆在干燥收缩过程中的孔径分布曲线形态呈典型的单峰结构。当含水率从30.51%降至27.14%时,曲线主峰对应孔径保持在1 μm左右且高度不变,3~11 μm孔径范围内的大孔数量有所减少。当含水率降至23.48%,曲线主峰向左移动且高度略有降低,对应孔径减小为约0.6 μm。这3条曲线在孔径5 μm附近均出现陡降,对应汞注入增量为0。这一现象与压汞试验的操作步骤有关,即试样在低压仓内测试结束后,需要经历卸除外压、取出并转移至高压仓以及再次加压的过程[28]。这会导致局部孔径范围内的注汞体积测量误差,但由于该部分孔隙在交河遗址土泥浆中所占比例很小,因此对微观孔隙结构演变规律的整体分析没有太大影响。随着含水率继续降低至17.68%,曲线主峰位置和高度几乎都不再变化,仅有孔径在1~3 μm的孔隙体积略微减少。
值得注意的是,当含水率低于缩限时,试样的孔径分布曲线形态经历了从单峰变为双峰并最终再次回归单峰结构的过程(图 4(b))。具体而言,含水率降至13.54%后,除了原有主峰外,曲线在更小的0.1~0.5 μm孔径范围出现新的隆起。随着蒸发继续进行,该隆起逐渐减小至消失,而主峰的高度及其对应孔径反而略有增加。
一般来说,压实黏土的孔径分布曲线形态呈双峰结构,其大、小孔分别指由黏土层叠体聚集形成的颗粒集合体之间及其内部的孔隙。小孔主要集中在0.01~0.1 μm范围内,且基本不受吸力和应力影响[19, 29]。因此,遗址土泥浆试样在低含水率段表现出的双峰结构与传统大、小孔的成因并不相同。Fiès等[30]和孙文静等[31]指出,粉土风干过程中的孔径分布曲线形态演变机制与土颗粒的几何重分布有关。当试样由饱和状态变为非饱和时,黏粒收缩更加剧烈,从而在其与粉土颗粒的交界面处会形成微观裂隙,即对应着在孔径分布曲线小孔径范围出现的新的隆起。后续干燥时该隆起逐渐消失而曲线主峰略微右移,这实际代表了裂隙由小到大不断发育、连通的过程。
3. 考虑体变的土水特征
3.1 基于孔隙比
根据已有的交河遗址土泥浆在脱湿过程中的质量含水率w与基质吸力ψm关系[10]:
w=1.47+28.53[1+(ψm/449.91)0.72]1.09, (2) 可求取自由收缩试验中各试样的吸力值,并得到相应的ew–ψm关系,如图 5所示。为丰富高吸力段数据,图中补充了张悦等[10]的盐溶液蒸气平衡试验实测结果。
Tarantino[32]系统研究多种土性的重塑样和压实样后发现,ew随ψm的变化规律不受孔隙比影响,且两者在双对数坐标中的高吸力段呈线性减小趋势,符合幂函数表达式:
ew=Aψ−Bm, (3) 式中,A,B为拟合参数。本文选择ψm > 1000 kPa的数据点进行拟合,得到A,B分别为3.9335和0.3850,拟合相关系数为0.971。
根据各试样的实际w和e计算其饱和度Sr,得到相应的Sr–ψm关系,如图 6所示。由于盐溶液蒸气平衡试验中试样的含水率远小于缩限,故认为其已达到收缩稳定,孔隙比均取残余值0.545。采用经典van Genuchten(vG)模型[33]进行描述,即
Sr=[1+(aψm)n]−m, (4) 式中,a,n,m为拟合参数。结果表明,a,n,m对应取值为0.0046,2.2942和0.1815,拟合相关系数0.998。
结合式(4),ew–ψm关系还可写为
ew=eSr=e[1+(aψm)n]−m。 (5) 显然在lgew–lgψm平面内,随着基质吸力不断增大,式(5)对应曲线应向式(3)对应曲线逐渐逼近且最终重合,即满足ψm→∞时两者相交且斜率相等。基于该条件推导得出各参数之间关系如下:
m=Bn, (6) a=(eA)1/1BB。 (7) 将式(6),(7)及拟合参数A,B和n的值综合代入式(4),最终得到考虑体变的修正vG模型的土水特征曲面模型:
Sr={1+[(e3.9335)2.5974ψm]2.2942}−0.1678 。 (8) 至此可获得交河遗址土脱湿条件下的Sr–e–ψm曲面,如图 7所示,反映了基质吸力和孔隙比对饱和度的综合影响。可以看出,对于经历自由干缩的泥浆试样而言,其饱和度沿着曲面移动、发展,最终形成的是一条连续穿过一系列恒体积土水特征曲线的空间曲线。
干燥初期,ψm增大导致含水率降低,但由于试样体积同步发生收缩,e相应减小,因此Sr在低吸力范围内仍然维持在1附近。一旦含水率达到缩限试样变形则很快停止,此后Sr随着ψm的增大完全沿着某特定e对应的土水特征曲线快速降低。
3.2 基于孔隙分布
压汞试验过程与土体蒸发干燥类似,本质上都是孔隙介质内部非润湿相流体入侵润湿相流体的过程,因此可基于实测的微观结构特征对持水特性进行预测[21, 34-35]。
假设孔隙均为理想圆柱体,则基质吸力ψm满足Young-Laplace方程[36]:
ψm=ua−uw=4σcosθD, (9) 式中,ua,uw分别为水-气界面两侧的孔隙气压力和孔隙水压力(Pa),D为孔隙直径(m),σ为水的表面张力,取0.0728 N/m,θ为水与土颗粒的接触角,取0°。
将汞累计注入曲线中,最小孔径对应的最终累计注入量记为Vmt,任意孔径D对应的累计注入量记为Vm。假设土体吸力达到孔径D的相应值时,所有小于该孔径的孔隙维持饱和而大于该孔径的孔隙完全干燥,此时的有效饱和度Se可按下式计算:
Se=Vmt−VmVmt×100%。 (10) 对于土中始终存在的那一部分水银难以进入的特殊孔隙,将其体积Vn占实际总孔隙体积V0之比定义为残余饱和度Sres:
Sres=VnV0×100%, (11) 实际饱和度Sr,有效饱和度Se和残余饱和度Sres三者满足以下关系:
Se=Sr−Sres1−Sres。 (12) 综上,结合土的汞累计注入曲线(图 3)和式(9)~(12)可分析实际饱和度在全吸力范围内的变化规律。
如图 8所示,根据不同含水率试样微观结构推算得到的Sr–ψm关系曲线形态大体相似,各曲线在较低和较高吸力段变化平缓且基本趋于一致,但中间段则随着试样含水率降低而不断向右平移。对于交河遗址土而言,利用含水率13.54%(低于缩限)试样的压汞数据计算的饱和度在ψm<1000 kPa时与试验实测值较为接近,但之后随着吸力增加两者间的偏差则先增大后减小。
基于某特定含水率试样的孔隙分布推算全吸力范围内的饱和度时,实际上并未考虑到吸力改变引起的孔径变化,即整条土水特征曲线上的土体微观结构始终保持不变。图 8中虚线是利用式(8)的修正土水特征曲面模型所预测的恒体积土水特征曲线,其孔隙比分别与3个试样对应相同,并从左向右依次减小。虽然其与基于孔隙分布方法获得的曲线不完全重合,但变化规律大体相似。很明显,对于交河遗址土而言,试样含水率越低孔隙比越小,根据其孔隙分布预测的饱和度结果越接近泥浆的实测曲线。
土体的真实孔隙并非完全理想的圆柱状毛细管,大多具有不规则截面,且其形状、尺寸和连通度等极为复杂。Liu等[19]指出,泥浆干燥收缩时,孔隙入口及主体尺寸各自的变化对微观结构演变规律的影响程度显著不同。然而,压汞试验测得的仅是孔隙入口处(孔喉)的尺寸分布,无法反映通道整体的几何情况。除此之外,测试过程中的加压作用不但使水银进入孔隙,还可能引起高含水率试样的等向压缩,即导致某种程度的额外变形[37]。因此,基于孔隙分布对土体的持水特性开展预测时,试样选择及试验操作等因素对结果的影响不可忽略。
4. 结论
本文针对交河遗址土泥浆开展脱湿试验,从宏观和微观角度重点探究了其在干燥过程中的体积变化规律,在此基础上建立考虑体变的土水特征曲面模型,综合分析了基质吸力和孔隙比对土体饱和度的影响机制。主要结论如下:
(1) 根据孔隙比变化规律,泥浆收缩特征曲线可分为正常收缩段、残余收缩段以及零收缩段3部分,其临界点分别对应土体进气时的含水率(22%)和缩限(16%);绝大部分体积变化发生在饱和状态下的正常收缩段;
(2) 泥浆的总孔隙体积在干燥过程中不断减小,随后逐渐稳定不变,孔径分布曲线形态主要呈单峰结构,但由于土体内部细微裂隙的形成与发展,曲线形态在含水率低于缩限的阶段经历了单峰与双峰的相互转换;
(3) 基于vG模型建立的脱湿土水特征曲面有效反映了基质吸力和孔隙比对饱和度的综合影响,干缩泥浆的土水特征曲线实质是一条连续穿过一系列恒体积土水特征曲线的空间曲线。
-
表 1 复合土工膜的基本力学性能
Table 1 Technical indices of composite geomembrane
膜厚/mm 拉伸强度/(kN·m-1) 伸长率/% 圆柱顶破强力/kN 撕裂强力/kN 纵向 横向 纵向 横向 纵向 横向 0.4 14.4 14.6 51 51 2.7 0.50 0.51 0.5 16.3 16.9 56 53 3.1 0.57 0.59 0.6 18.1 18.4 66 66 3.6 0.64 0.64 0.7 21.3 21.6 69 67 4.4 0.71 0.74 0.8 23.9 24.2 73 69 5.2 0.79 0.80 0.9 26.8 27.3 88 92 6.9 0.91 0.92 表 2 典型的经验蠕变模型
Table 2 Typical empirical creep models
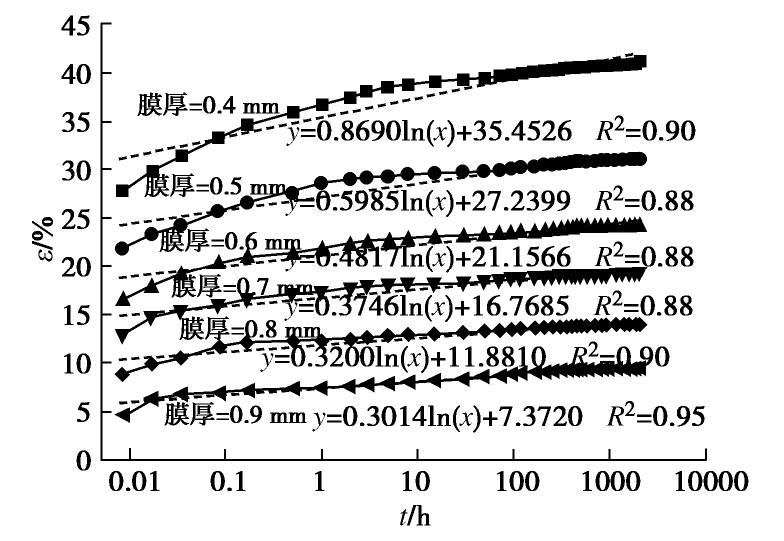
类型 表达形式 备注 幂函数型 ε=a+btn a, b, n为材料的相关系数 对数函数型 ε=ε0+mlgt m为蠕变曲线斜率, ε0 为初始应变双曲线函数型 ε=εi+ta+bt εi 为加载瞬时蠕变,a, b为材料参数蠕变速率型 ˙ε=c1εc2ˉT(t1t)m c1, c2, m为材料相关参数, ˉT 为应力水平。其它经验型 εt=ε0+A1−meaL(t1−m−1) L为应力水平,a, A, m为常数 表 3 蠕变模型的过程参数
Table 3 Progress data of creep models
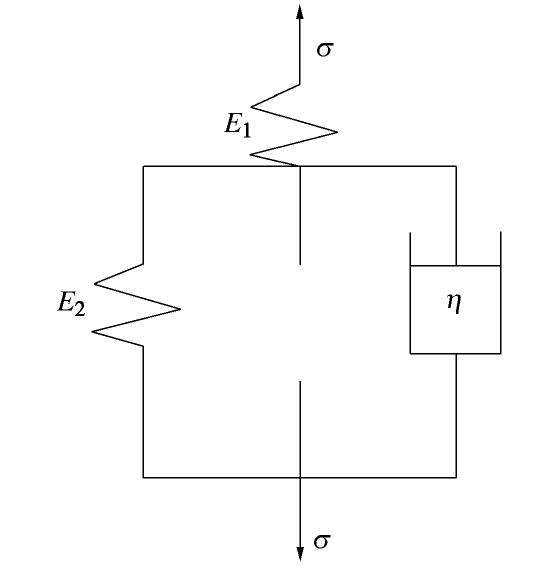
厚度D 厚度水平Di ε0 m 0.4 1.00 35.4526 0.8690 0.5 1.25 27.2399 0.5985 0.6 1.50 21.1566 0.4817 0.7 1.75 16.7658 0.3746 0.8 2.00 11.8810 0.3200 0.9 2.25 7.3720 0.3014 表 4 复合土工膜三参数黏弹性模型参数值
Table 4 Values of parameters of three-parameter viscoelastic model for composite geomembrane
厚度D E1/MPa E2/MPa η /(MPa·s-1)0.4 3.103 0.204 24.271 0.5 3.952 0.170 19.346 0.6 5.230 0.127 14.668 0.7 6.724 0.098 11.387 0.8 9.852 0.063 7.344 0.9 18.701 0.026 3.229 -
[1] 顾淦臣. 土工膜用于水库防渗工程的经验[J]. 水利水电科技进展, 2009, 29(6): 34-38, 48. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD200906012.htm GU Gan-cheng. Experience of applying geomembrane in reservoir seepage control[J]. Advances in Science and Technology of Water Resources, 2009, 29(6): 34-38, 48. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD200906012.htm
[2] 岑威钧, 温朗昇, 和浩楠. 水库工程防渗土工膜的强度、渗漏与稳定若干关键问题[J]. 应用基础与工程科学学报, 2017, 25(6): 1183-1192. doi: 10.16058/j.issn.1005-0930.2017.06.011 CEN Wei-jun, WEN Lang-sheng, HE Hao-nan. Strength, leakage and stability problems of impermeable geomembrane for reservior project[J]. Journal of Basic Science and Engineering, 2017, 25(6): 1183-1192. (in Chinese) doi: 10.16058/j.issn.1005-0930.2017.06.011
[3] 束一鸣, 吴海民, 姜晓桢. 中国水库大坝土工膜防渗技术进展[J]. 岩土工程学报, 2016, 38(增刊1): 1-9. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2016S1003.htm SHU Yi-ming, WU Hai-min, JIANG Xiao-zhen. The development of anti-seepage technology with geomembrane on reservoirs and dams in China[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(S1): 1-9. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2016S1003.htm
[4] BLACK P J, HOLTZ R D. Performance of geotextile separators five years after installation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(5): 404-412. doi: 10.1061/(ASCE)1090-0241(1999)125:5(404)
[5] PETROV R J, ROWE R K. Geosynthetic clay liner (GCL)-chemical compatibility by hydraulic conductivity testing and factors impacting its performance[J]. Canadian Geotechnical Journal, 1997, 34(6): 863-885. doi: 10.1139/t97-055
[6] 李倩. 土工膜蠕变机理及其长期预测研究[D]. 济南: 山东大学, 2009. LI Qian. Research on Mechanism and Long-Term Prediction of Geomembrances Creep[D]. Jinan: Shandong University, 2009. (in Chinese)
[7] 李艳琴. 复合土工膜蠕变性能的研究[D]. 济南: 山东大学, 2006. LI Yan-qin. Study on Creep Properties of Composite Geomembrances[D]. Jinan: Shandong University, 2009. (in Chinese)
[8] 王钊. 土工合成材料的蠕变试验[J]. 岩土工程学报, 1994, 16(6): 96-102. doi: 10.3321/j.issn:1000-4548.1994.06.011 WANG Zhao. Creep test for geosynthetics[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(6): 96-102. (in Chinese) doi: 10.3321/j.issn:1000-4548.1994.06.011
[9] 王钊, 李丽华, 王协群. 土工合成材料的蠕变特性和试验方法[J]. 岩土力学, 2004, 25(5): 723-727. doi: 10.3969/j.issn.1000-7598.2004.05.011 WANG Zhao, LI Li-hua, WANG Xie-qun. Creep properties and testing methods of geosynthetics[J]. Rock and Soil Mechanics, 2004, 25(5): 723-727. (in Chinese) doi: 10.3969/j.issn.1000-7598.2004.05.011
[10] 王广月, 李华銮, 李艳琴. 复合土工膜蠕变性能的试验研究[J]. 岩土力学, 2009, 30(6): 1599-1603. doi: 10.3969/j.issn.1000-7598.2009.06.011 WANG Guang-yue, LI Hua-luan, LI Yan-qin. Experimental research on creep properties of composite geomembrane[J]. Rock and Soil Mechanics, 2009, 30(6): 1599-1603. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.06.011
[11] JEON Y H, KIM S H, YOO H K. Assessment of long-term performances of polyester geogrids by accelerated creep test[J]. Polymer Testing, 2002, 21(5): 489-495. doi: 10.1016/S0142-9418(01)00097-6
[12] MAHDAVI R, GOODARZI V, ALI KHONAKDAR H, et al. Experimental analysis and prediction of viscoelastic creep properties of PP/EVA/LDH nanocomposites using master curves based on time-temperature superposition[J]. Journal of Applied Polymer Science, 2018, 135(38): 46725-46736. doi: 10.1002/app.46725
[13] YANG T C, CHIEN Y C, WU T L, et al. Effects of heat-treated wood particles on the physico-mechanical properties and extended creep behavior of wood/recycled-hdpe composites using the Time-temperature superposition principle[J]. Materials, 2017, 10(4): 365-377. doi: 10.3390/ma10040365
[14] DIAS M H, JANSEN K M B, LUINGE J W, et al. Effect of fiber-matrix adhesion on the creep behavior of CF/PPS composites: temperature and physical aging characterization[J]. Mechanics of Time-Dependent Materials, 2016, 20(2): 245-262. doi: 10.1007/s11043-016-9294-z
[15] MARTIN P, ROBERT K, LLJA K, et al. Determination of the long-term properties in laminate-thickness direction of textile-reinforced thermoplastic composites under compression using time-temperature superposition[J]. Advanced Engineering Materials, 2016, 18(3): 369-375. doi: 10.1002/adem.201500475
[16] WINESETT D A, ZHU S, SOKOLOV J, et al. Time-temperature superposition of phase separating polymer blend films[J]. High Performance Polymers, 2000, 12(4): 599-602. doi: 10.1088/0954-0083/12/4/315
[17] 刘华北. 土工合成材料循环受载、蠕变和应力松弛特性的统一本构模拟[J]. 岩土工程学报, 2006, 28(7): 823-828. doi: 10.3321/j.issn:1000-4548.2006.07.004 LIU Hua-bei. Unified constitutive modeling of the cyclic, creep and stress relaxation behavior of geosynthetics[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(7): 823-828. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.07.004
[18] MURPHY G P. The influence of geoform creep on performance of a compressible inclusion[J]. Geotextiles and Geomembranes, 1997, 15(1): 121-130.
[19] 李丽华, 王钊, 陈轮. 加速土工合成材料蠕变试验的荷载叠加法[J]. 岩土工程学报, 2007, 29(3): 410-413. doi: 10.3321/j.issn:1000-4548.2007.03.016 LI Li-hua, WANG Zhao, CHEN Lun. Load superposition for accelerating creep test of geosynthetics[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(3): 410-413. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.03.016
[20] 姜海波. 土石坝坝体、坝基和水库库区土工膜防渗体力学特性及渗透系数研究[D]. 乌鲁木齐: 新疆农业大学, 2011. JIANG Hai-bo. Study on Mechanical Properties and Permeability Coefficient of Impervious Body with Geomembrane for Earth Rockfill Dam and Reservoir Area[D]. Wulumuqi: Xinjiang Agricultural University, 2011. (in Chinese)
[21] 土工合成材料测试规程:SL235—2012[S]. 2012. Test Procedure for Geosynthetics: SL235—2012[S]. 2012. (in Chinese)
[22] 周志刚, 李雨舟. 土工格栅蠕变特性及其黏弹塑性损伤本构模型研究[J]. 岩土工程学报, 2011, 33(12): 1943-1949. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201112022.htm ZHOU Zhi-gang, LI Yu-zhou. Creep properties and viscoelastic-plastic-damaged constitutive model of geogrid[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(12): 1943-1949. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201112022.htm
[23] 包承纲, 童军, 丁金华. 土工合成材料流变参数合理选择的研究[J]. 岩土工程学报, 2015, 37(3): 410-418. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201503004.htm BAO Cheng-gang, TONG Jun, DING Jin-hua. Reasonable selection of rheological parameters of geosynthetics[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(3): 410-418. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201503004.htm
[24] SIRIWARDANE H, GONDLE R, KUTUK B. Analysis of flexible pavements reinforced with geogrids[J]. Geotechnical and Geological Engineering. 2010, 28(3): 287-297. http://www.researchgate.net/profile/Raj_Gondle/publication/226265774_Analysis_of_Flexible_Pavements_Reinforced_with_Geogrids/links/00b49531885b7ae9f7000000




 下载:
下载: