岩土工程安全系数法稳定分析中的荷载与抗力

李广信

doi:10.11779/CJGE202105016

岩土工程安全系数法稳定分析中的荷载与抗力 English Version

李广信

清华大学水沙科学与水利水电工程国家重点实验室,北京　100084

基金项目:

十三五国家重点研发计划 2017YFC0404803

国家自然科学基金项目 41790434

详细信息

作者简介:
李广信(1941—),男,黑龙江宾县人,教授,博士生导师,长期从事土力学教学和土的本构关系、土工合成材料工程、高土石坝以及地基基础工程的科研工作。E-mail: ligx@tsinghua.edu.cn

中图分类号: TU43
计量
- 文章访问数: 354
- HTML全文浏览量: 22
- PDF下载量: 401
出版历程
- 收稿日期: 2020-11-15
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-04-30

Load and resistance in stability analysis of geotechnical engineering with safety factor method

LI Guang-xin

State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing100084, China

摘要

摘要: 讨论了在岩土工程的稳定分析中安全系数的定义及其不同的表示方式,指出了荷载与抗力的区分与界定的一些原则。提出在分析稳定问题时,静水下的岩土体与结构物的浮力应当与其重力具有相同身份；如用水压力计算应当与用浮力计算应得到相同的结果；对于在渗透场中的饱和土体,用其表面的水压力计算,应当与土骨架用浮力及渗透力计算得到相同的结果。指出在抗滑稳定分析中的力或力矩,作为荷载具有更大的权重,所以一些不确定性很小的反向力与力矩常常被当成负的荷载,因而用岩土材料的强度折减系数表示其安全系数可以正确地界定岩土抗滑稳定分析中的荷载与抗力。
- 安全系数 /
- 荷载 /
- 抗力 /
- 强度折减系数 /
- 水的作用
Abstract: The definition and different expressions of safety factor in stability analysis of geotechnical engineering are discussed, and the regulation of distinction between load and resistance in the stability analysis are pointed out. In the stability analysis in geotechnical engineering, the buoyancy of rock mass and structures under static water level shall have the same status of their gravity. The calculated results by use of water pressures on their surfaces have to be equal to those by use of deducting buoyancy. For the saturated soil mass in seepage field, the calculated results by use of the water pressures have to be equal to those by use of considering buoyancy and seepage force on soil skeleton. In the stability analysis, the forces or moments as the loads should have greater weight, thus some reverse forces and moments with little uncertainty will be treated as negative loads rather than the positive resistances. Accordingly, the load and resistance can be defined well provided that safety factor is expressed as the strength reduction factor in the analysis of stability against sliding.
- safety factor /
- load /
- resistance /
- strength reduction factor /
- action of water

HTML全文

0. 引言

岩土工程中的稳定分析问题包括边坡、土压力引起的支挡结构、地基承载力等主要是抗滑稳定问题,也有渗透稳定、倾覆与塌陷、抗浮、流滑与液化等问题。由于作为天然材料的岩土的复杂性与多样性,很难完全采用可靠性理论进行其稳定分析,到目前为止,考虑极限平衡的安全系数法仍然是岩土工程中承载能力极限状态的设计中的主要方法。在这些问题中,所谓的安全系数包括对具体对象计算分析得到的现实的安全系数和有关规范中主要根据经验规定的设计容许（最小）安全系数。安全系数法是一种经验的方法,亦称“单一安全系数法”。它是将工程中包含的一切不确定性因素,都放入单一的容许安全系数之中,这些不确定性包括作用（荷载）的各种代表值、材料的性质及参数、设计、计算与施工的可靠性与精确性；也包括要满足经济、政治、社会和环境等要求,就是说用单一安全系数涵盖了所有不可预估的因素与风险,可以说,“安全系数是个筐,一切不确定因素往里装”,因而在此法中就无需再引入其他系数了,例如重要性系数^[1]、工作条件系数^[2]、荷载放大系数^[3]、分项系数^[4]等。

安全系数的被普遍接受的定义就是抗力与荷载之比,在分析处于极限平衡的对象上可能有多项力或力矩要素时,安全系数的最基本的定义为

抗 力 荷 载

$K = \frac{抗力}{荷载} = \frac{\sum_{i = 1}^{n} R_{i}}{\sum_{j = 1}^{m} S_{i}}$ ,

(1)

式中, $S_{i}$ 为作用的标准值, $R_{i}$ 为极限抗力,而哪些要素属于抗力 $R_{i}$ ,哪些要素属于荷载 $S_{i}$ ,在各类稳定分析及不同的规范中,对其认识和规定还很不一致,是一个亟待进行讨论与统一认识的问题。

如何界定荷载与抗力是有其规则的,不能随意处理,例如不能简单地认为作用于对象上与滑动方向一致的力和或转动方向一致的力矩都是荷载,反之就是抗力。关于这种界定,目前大体上有以下3种情况。

（1）公认的,约定俗成的荷载与抗力

在挡土结构的滑移与倾覆稳定分析中,主动土压力总是荷载,而被动土压力则是抗力。在一些类型的挡土墙中（如重力式挡墙）,墙体的重力产生主要的抗力。

在地基承载力问题中,上部结构与基础自重是主要的荷载；而由地基土的抗剪强度所决定的地基承载力则是抗力。在边坡稳定问题中,由自重引起的滑动力（矩） $W_{i} \sin θ_{i}$ 是最基本的荷载,由于 $θ_{i}$ 可正可负,所以这个“滑动力”可能与滑动方向相反,成为“负荷载”；而由土体抗剪强度产生的抗滑力 $W_{i} \cos θ_{i} \cdot$ $\tan φ_{i} +$ $c_{i} l_{i}$ 则是主要的抗力。

在有些情况判断下,敌我的区分似乎是约定俗成的习惯。比如葛优的老爹葛存壮,陈佩斯的老爹陈强,一直都扮演反面角色,于是人们在影视中见到就他们自然把他们归入了敌方,在土体的极限平衡分析中似乎也有这种情况。

（2）有争议的,见仁见智的情况

在这种情况中,不同的人会有不同的意见,特别是不同的标准、规范也有不同的规定。其中水压力身份的判断常常会出现不一致；而某些与滑动方向反向的力,属于负的荷载,还是正的抗力也往往争论不休,难以定案,似乎属于双面间谍。

（3）错误的、不被容许的作法

这类作法违背岩土工程的基本概念和原理,违背同行的共识,认敌为友或以友为敌,会工程带来极大的危害。岩土工程安全系数法中的荷载与抗力是一个很复杂和宽广的课题,在中国的有关规范中,出现了各种不同的表示与规定；不同的工程技术人员也会有不同的理解与主张。本人对此发表以下一些看法,以期引起关注和讨论。

1. 安全系数的不同表示

1.1 荷载放大系数与强度折减系数

对于式（1）的K=R/S可以表示为S=R/K,或者R=KS。前者的安全系数K可称为“抗力折减系数”或“强度折减系数”；后者K可称为“荷载放大系数”。安全系数为折减系数最早为Bishop在边坡抗滑稳定分析中所提出,目前在绝多数边坡抗滑稳定分析中都在使用它；近年来在有限元边坡稳定分析中也被广泛地应用,即c_e=c/K,tanφ_e=tanφ/K。

如果工况极为简单或者计算高度简化,例如用瑞典圆弧法边坡稳定分析,由于不计一切条间力,以滑动力矩与抗滑力矩间的关系计算安全系数,两种表示法都可以得到相同的安全系数的显式表达式：

$K = \frac{\sum c_{i} l_{i} + W_{i} \cos θ_{i}^{} \tan φ_{i}}{\sum W_{i} \sin θ_{i}}$ 。

(2)

但是在一些考虑条间力的相对复杂的边坡稳定分析中,很难得到式（2）这样的显式解,例如简化毕肖甫法采用强度折减系数为安全系数为

$K = \frac{\sum_{i = 1}^{n} \frac{1}{m_{α i}} (W_{i} \tan φ_{i} + c_{i}^{} b_{i})}{\sum_{i = 1}^{n} W_{i} \sin α_{i}}$ ,

(3)

式中, $m_{α i} = \cos θ_{i} + \frac{\sin θ_{i} \tan φ_{i}}{K}$ , $W_{i}$ 为第i土条的重力, $θ_{i}$ 为第i土条的圆心角。

将安全系数表示为强度折减系数,成为隐式解,需要通过迭代计算到安全系数。

传递系数法亦称不平衡推力法,它适用于任意形状滑动面的情况。如果用荷载放大系数表示安全系数,则可得到显式解；用强度折减系数表示安全系数就要用隐式解。但是在一些条件下显式解会出现失真的情况^[5]。

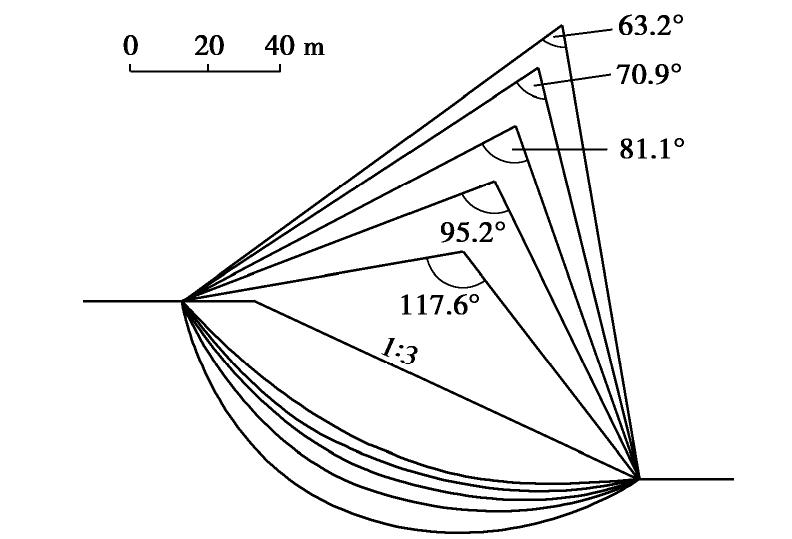
图1为一滑动土坡的例题,对几个始点与终点相同,圆弧的圆心角不同的滑弧分别用传递系数法的显式法和隐式法进行计算,土坡的 $γ$ =17 kN/m³, $φ$ =35°,c=50 kPa。表1为其计算结果。

图 1 用传递系数法计算的边坡

Figure 1. Calculation of slope with transfer coefficient method

下载: 全尺寸图片幻灯片

表 1 不同方法计算的结果

Table 1. Results by different methods

圆心角/(°)	毕肖甫法K_b	显式传递系数法		隐式传递系数法
圆心角/(°)	毕肖甫法K_b	K_t1	$\frac{K_{t 1} - K_{b}}{K_{b}} /%$	K_t2	$\frac{K_{t1} - K_{b}}{K_{b}} /%$
117.6	3.020	4.421	46.4	3.025	0.2
95.6	2.614	3.199	22.4	2.620	0.2
81.1	2.451	2.800	14.2	2.456	0.2
70.9	2.371	2.613	10.2	2.375	0.2
63.2	2.332	2.514	7.9	2.335	0.1

下载: 导出CSV

| 显示表格

其中以毕肖甫法为基准,可见隐式法的结果与毕肖甫法足够近似,而显式法则偏差很大,尤其是在圆心角较大,出现滑动面反翘时。

1.2 安全系数的其他表示方法

近年来用有限元法进行边坡稳定分析也有较快的发展,与条分法不同,有限元法考虑了变形协调,因而不需要为满足全部力的静力平衡而作出假设。强度折减系数使用较为普遍,也还有其他安全系数的表达形式。

（1）材料强度安全系数

这种定义最早用于材料力学以及结构构件,即以材料的强度与其实际的最大应力之比定义安全系数,对于岩土材料即以其滑动面上的抗剪强度与实际剪应力之比,即

$K = \frac{τ_{f}}{τ}$ 。

(4)

但这只是滑动面上局部的安全系数,滑动面上各处的安全系数都不同；在用于有限元法时,常常沿滑动面平均,得到的平均值作为边坡在在此滑动面的安全系数。另外,滑动面在每一点的滑动方向不同,其中的剪应力τ也难以合理确定。

（2）矢量和法安全系数

葛修润院士在2008年的黄文熙讲座中介绍了他所提出的“矢量和法安全系数”的概念^[6]。他指出了在有限元边坡稳定分析中,通常潜在滑动面非圆弧,可能为折线形,也可能为任意曲线,对于岩质边坡更是如此。他提出的矢量和法安全系数的表达式为

$K = \frac{\sum R {(θ)}_{i}}{\sum S {(θ)}_{i}}$ ,

(5)

式中,θ为滑坡的计算方向,是滑坡整体潜在的滑动趋势方向,可表达为

$\tan θ = \frac{\sum τ_{i} Δ l_{i} \sin α_{i}}{\sum τ_{i} Δ l_{i} \cos α_{i}}$ ,

(6)

式中, $τ_{i}$ 为用有限元法计算的潜在滑动面在i点的滑动剪应力, $Δ l_{i}$ 为所取的滑动面i点处微线段, $α_{i}$ 为滑动面在该点的倾角。

可见这种安全系数的定义,就是在滑动面上把作用在各小分段的滑动力矢量按矢量和合成导致可能发生滑动的力矢,称为滑动力矢；把作用于潜在滑动面上各小分段的抗滑力矢量,通过矢量和形成总的抗滑力矢,总抗滑力矢与总滑动力矢之比就是计算的安全系数。

2. 稳定分析中水的作用

在稳定分析的很多情况下,水起到了极为重要的作用。以土骨架为隔离体,则在骨架上作用的体积力有浮力和渗透力；以饱和土体为隔离体,在其水下各边界上作用有水压力,水也会在岩体和结构物的各表面上作用着水压力,这些水压力不应随意作为荷载或抗力。静止的水位以下部分的饱和土体、岩体和结构物各边界上的水压力,其总水平分力的代数和为零；竖直分力的代数和就是浮力。在渗流场中的饱和土体,作用于其各面上的水压力的矢量和应等于作用于其土骨架的浮力与渗透力的矢量和。

2.1 浮力应跟着重力

浮力与重力都是体积力,如果要计算水下饱和土或土骨架的重力需要使用浮重度 $γ^{'} = γ_{\max} - γ_{w}$ 。其中γ_w就是单位体积饱和土的浮力。所以在边坡抗滑稳定分析中,地下水位以下土的滑动力与抗滑力,通常都取其浮重度计算。

在验算地基承载力时,需要满足下式^{[3, 7]}：

$p_{k} \leq f_{a}$ ,

(7)

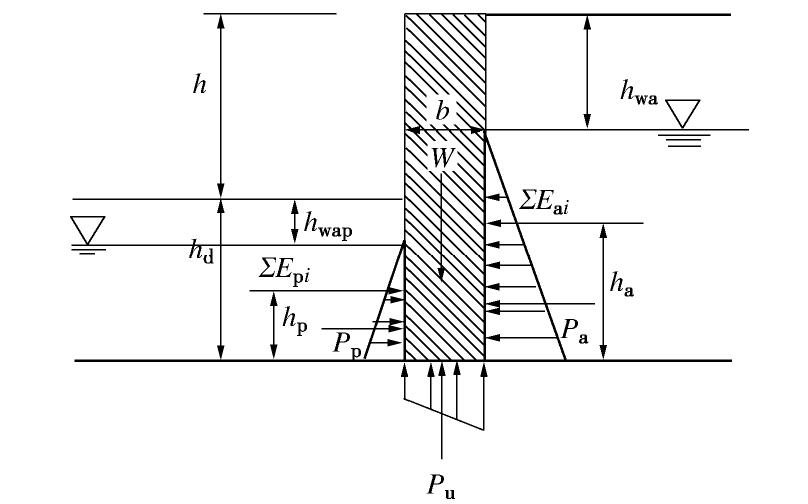
式中, $p_{k}$ 为基底平均压力标准值,p_k=(F_k+G_k)/A,其中G_k为基础自重和基础上土重,对稳定地下水以下部分应扣除水的浮力。地基持力层承载力特征值f_a= $m_{b} γ_{b}$ + $m_{d} γ_{m} d$ +M_cc_k,其中 $γ$ 为基础底面以下土的重度, $γ_{m}$ 基础底面以上土的加权平均重度,地下水位以下都取浮重度。可见在这种情况下,重力无论是作为荷载还是抗力,浮力总是紧跟着重力。

广义上作用于岩土体及结构物下部的扬压力也应属于浮力,例如重力式挡土墙底部的扬压力。在文献[3]中,在抗倾覆稳定验算中,错误地认为所有逆时针力矩均是荷载,同时也将两侧的水压力分别与同侧的土压力一起成为荷载与抗力,见图2。最后给出的计算墙厚b的公式就是按照墙体抗倾覆得出来的：

图 2 水泥土墙的抗倾覆稳定

Figure 2. Anti-overturning stability of gravity cement-soil wall

下载: 全尺寸图片幻灯片

$b \geq \sqrt{\frac{10 \times (1.2 γ_{0} h_{a} \sum E_{a i} - h_{p} \sum E_{p i})}{5 γ_{cs} (h + h_{d}) - 2 γ_{0} γ_{w} (2 h + 3 h_{d}^{} - h_{wp} - 2 h_{wa})}}$ ,

(8)

式中含有安全系数K=1.2,可同时又引进了重要性系数 $γ_{0}$ ,可知这个公式至少包含有4个错误：=①不应以扬压力 $p_{u}$ 为荷载；=②不应在E_p与E_a中包括土压力和水压力,使主动侧水平水压力为荷载,被动侧的水压力为抗力；=③使用了单一安全系数就不应再计入重要性系数；④对于图示的均匀的“砂土或碎石土”,两侧水压力不应按静水压力计算,使墙底两侧出现很大的水头差,发生无始无终的渗流。

2.2 水压力和浮力与渗透力

对于静水下的岩土体和结构物,我们可以计算其浮力,并在稳定分析中从其重力里扣除；也可计算其表面上的水压力,但两种计算方法的结果应当相等。

图3是一位于水体岸边的有节理缝的危岩,它被水体淹没高度的一半。如果节理缝处的摩擦系数为μ,可以先从其重力里扣除1/4其体积的浮力,计算其滑动的安全系数；也可用其两表面的水压力计算,二者计算的安全系数必须相等。这样后者的安全系数应为

图 3 部分在水下的危岩的稳定

Figure 3. Stability of partly underwater dangerous rock

下载: 全尺寸图片幻灯片

$K = \frac{(W \cos θ - P_{w1} + P_{w 2 n}) μ}{W \sin θ - P_{w2t}}$ ,

(9)

亦即必须把 $μ P_{w1}$ 当成负的抗力, $μ P_{w2n}$ 当成正的的抗力, $P_{w2t}$ 当成负的荷载。

《建筑基坑支护技术规程》^[8]对于水土分算情况给出的支挡结构上水平主动与被动土压力表达式：

$p_{ak} = (σ_{ak} - u_{a}) K_{a, i} - 2 c_{i} \sqrt{K_{a, i}} + u_{a}$ ,

(10)

$p_{pk} = (σ_{pk} - u_{p}) K_{p, i} + 2 c_{i} \sqrt{K_{p, i}} + u_{p}$ ,

(11)

式中,u_a,u_p为支护结构外（主动）侧、内（被动）侧计算点的孔隙水压力。

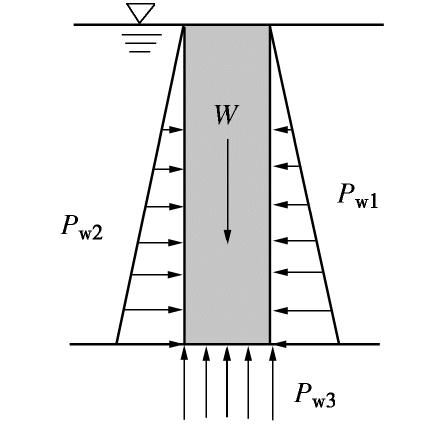
可能是为了与水土合算的主、被动土压力表达一致,这里将两侧的水压力计入土压力之中,分别当成了荷载与抗力,这种做法是错误的。在图4表示处于静水中的墙,如果从自重中扣除浮力,它既没有抗滑稳定问题,也不存在抗滑及抗倾覆稳定问题。如果认为存在三面的水压力与其总自重,则应两侧的水压力抵消；从自重力扣除扬压力。

图 4 静水下的墙

Figure 4. Stable wall under static water

下载: 全尺寸图片幻灯片

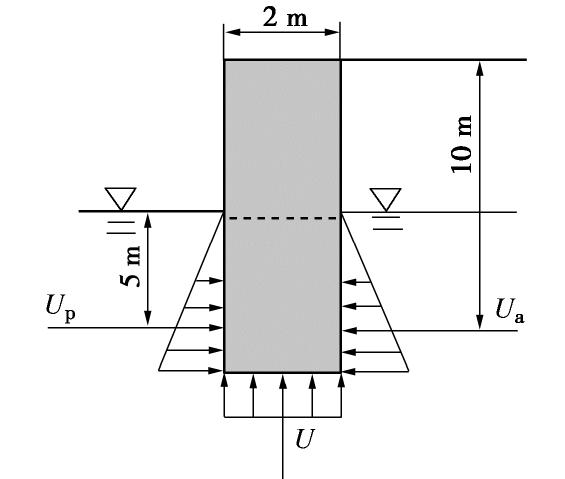
图5是一个部分处于静止的地下水位以下的水泥土墙,水泥土重度为 $γ_{cs}$ =20 kN/m³,所在土层c=0,φ=30°,γ=18 kN/m³（水上下相同）,两侧地下水位与坑底齐平。按照不同方法处理水压力,计算其抗倾覆稳定安全系数K_ov,计算结果见表2。

图 5 重力式挡土墙上的倾覆稳定

Figure 5. Anti-overturning stability of gravity retaining wall

下载: 全尺寸图片幻灯片

表 2 水压力不同计算方法的结果

Table 2. Results of water pressure by different methods

编号	计算方法	K_ov
①	水下水泥土用浮重度计算,不计任何水压力	2.55
②	水泥土用饱和重度计算,侧向水压力抵消,从自重中扣除扬压力U	2.55
③	主动侧水压力为荷载,被动侧水压力为抗力,墙自重中扣除扬压力U	2.27
④	主动侧水压力为荷载,被动侧水压力为抗力,扬压力U为荷载	1.82

下载: 导出CSV

| 显示表格

可见,水下部分的水泥土按浮重度计算,得到的安全系数为2.55（方法①）；第二种算法是两侧水压力相等互相抵消,从墙的自重中扣除扬压力,结果也是K_ov=2.55（方法②）；若如果按照文献[8]的算法,将右侧水压力当成荷载,左侧水压力当成抗力,那么K_ov为2.27；如果按照文献[1]计算,将扬压力U也当成荷载,则安全系数变为1.82。

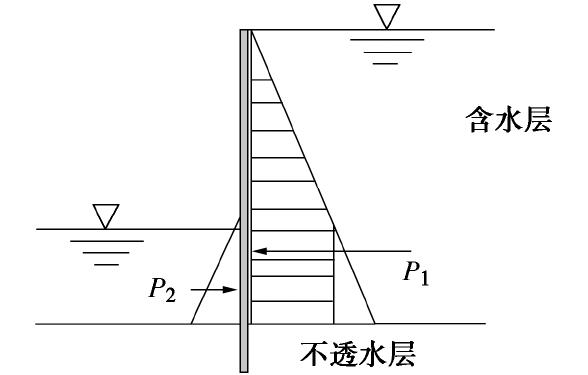
对于这个问题,《上海基坑规范》^[9]与冶金部的《建筑基坑技术规范》^[10]是正确的,亦即以两侧水压力差的“净水压力”作为荷载,在图6中,当下部为不透水层,上部为含水层时,两侧都作用有静水压力P₁与P₂,其荷载是净水压力P₁-P₂（见阴影部分）。

图 6 支护结构上的净水压力

Figure 6. Net water pressures on retaining and protection structures

下载: 全尺寸图片幻灯片

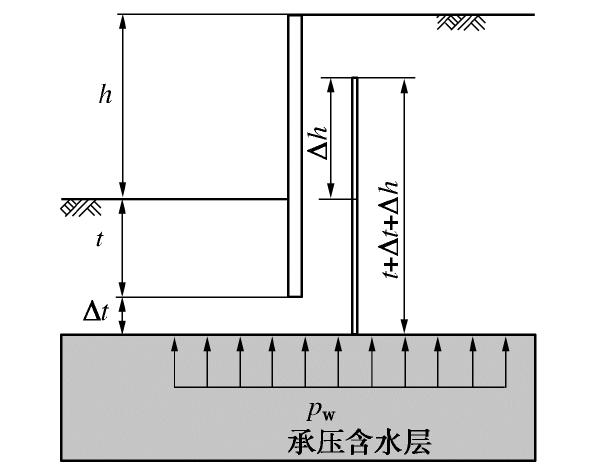
在文献[3]中,对于基坑坑底承压水的渗透稳定中规定如图7与下式所示：

图 7 坑底抗渗流稳定验算示意图

Figure 7. Diagram for checking seepage stability at bottom of foundation pit

下载: 全尺寸图片幻灯片

$K = \frac{γ_{sat} （ t + Δ t)}{p_{w}} = \frac{(γ^{'} + γ_{w}) (t + Δ t)}{γ_{w} (t + Δ t + Δ h)} 。$

(12)

如果坑底土中发生向上的稳定渗流,它就是流土问题,用土骨架为隔离体的静力平衡,用土骨架自重与渗透力表示,流土安全系数为^[11]

$K^{'} = \frac{γ^{'}}{j} = \frac{i_{c r}}{i}$ 。

(13)

如果 $γ^{'}$ = $γ_{w}$ =10 kN/m³,t+Δt=5 m,Δh=2 m,按照式（13）,用土骨架的有效应力表示,则安全系为系数为2.5；按照式（12）的饱和土极限平衡计算,安全系数为1.43。可见用饱和土体与土骨架为隔离体会得到了完全不同的安全系数值。为了使二者一致,应当从式（12）的自重和水压力中均扣除浮力 $γ_{w}$ (t+Δt),则与式（13）相同。可见在极限分析中,荷载与抗力出现同质同量的（水压）力,它们应当相互抵消。

2.3 滑动面上的水压力

如上所述,在岩土滑动稳定分析中,如果以饱和土体为隔离体,则在其界面上作用有水压力。它与滑动面上重力的法向分力方向相反,使抗滑力（矩）减少。所以在各种抗滑稳定分析中,都是从法向力中扣除滑动面上的水压力。

在土坡滑动分析的各种条分法中,条底在水下时要从法向力中扣除孔隙水压力。

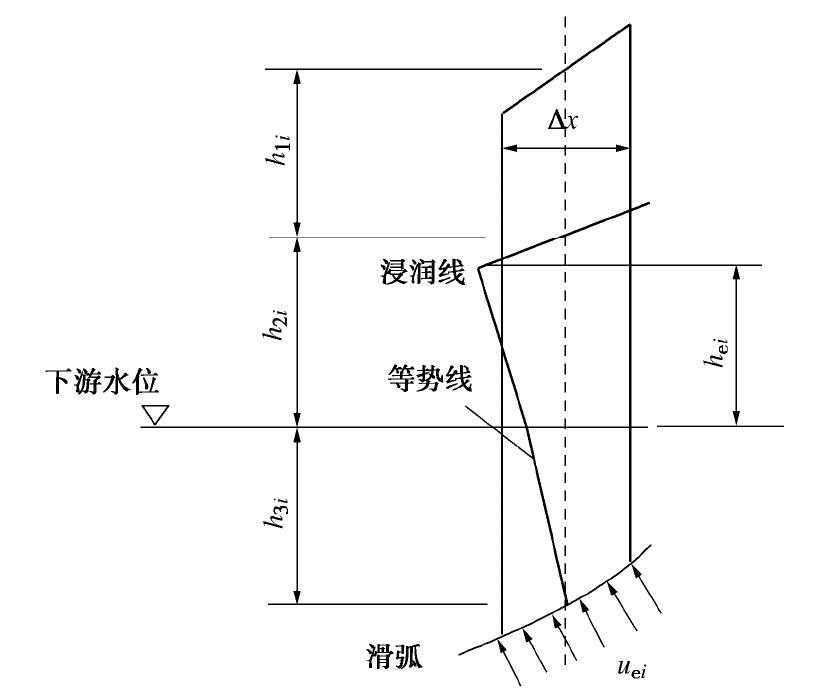
$K = \frac{\sum {c_{i} l_{i} + [(γ h_{i 1} + γ_{sat} h_{i 2} + γ^{'} h_{i 3}) b \cos α_{i} - u_{e i} l_{i}] \tan φ_{i}}}{\sum (γ h_{i 1} + γ_{sat} h_{i 2} + γ^{'} h_{i 3}) b \sin φ_{i}} 。$

(14)

在图8和式（14）中,该土条分为3段,h_1i,h_2i,和h_3i,其中h_3i位于下游水位以下,按浮重度计算就已经等于扣除了浮力；h_2i部分按饱和重度计算自重,对应的压力水头为h_ei、孔隙水压力u_ei=h_ei× $γ_{w}$ ,从法向力中扣除。h_1i部分在浸润线水位以上,取天然重度。

图 8 滑弧面上的孔隙水压力

Figure 8. Pore water pressures on sliding surface

下载: 全尺寸图片幻灯片

可见浸润线与下游静水位之间的土体按饱和重度计算,同时在法向力中扣除孔隙水压力u_eil_i。在岩坡和岩体的抗滑稳定分析中,也会遇到裂缝水的压力问题需要从滑动面上的法向压力中扣除水压力；在挡土墙和基础的抗滑稳定分析中,底面在地下水位以下时,法向压力也必须扣除水压力后计算抗滑力。

3. 滑动面上的反向切向力

在岩土工程的抗滑稳定分析中,滑动岩土体、结构物的重力、作用于土骨架上的渗透力及外部作用（如锚杆）在岩土体上的力等,都会在其滑动面上分解为法向分力与切向分力。相对于滑动方向,这些切向分力有正有负,在不同的规范标准中有不同的规定,这就存在着歧义与混乱。

在岩土稳定分析中的两个要素中,荷载通常具有更大的权重,抗力需要除以安全系数才可以与其平等。所以在具体工程中,减少荷载比增加同样数量的抗力更加有效,即所谓“扬汤止沸,不如锅底抽薪”。譬如自重滑动力w_isinθ_i只涉及滑动体的尺寸、重度和倾角,而抗滑力则要用岩土强度指标这样的不确定性很大的参数,因而反向的滑动力（矩）往往是作为负的荷载。

3.1 岩土体自重的反向切向分力

在边坡稳定分析的各种计算方法中,岩土体在滑动面上的切向分力总是被归入滑动力。

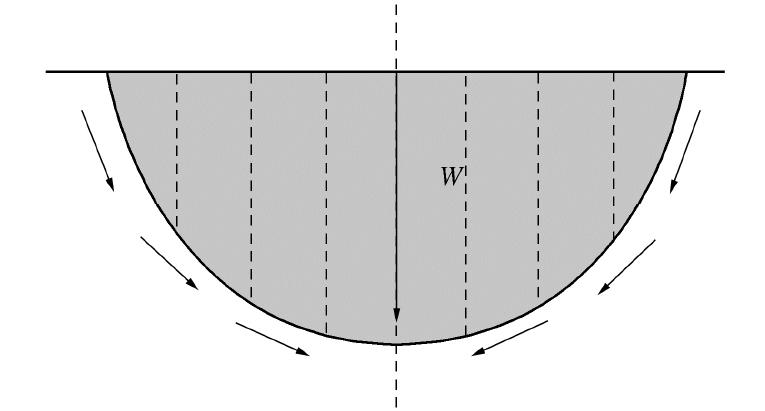
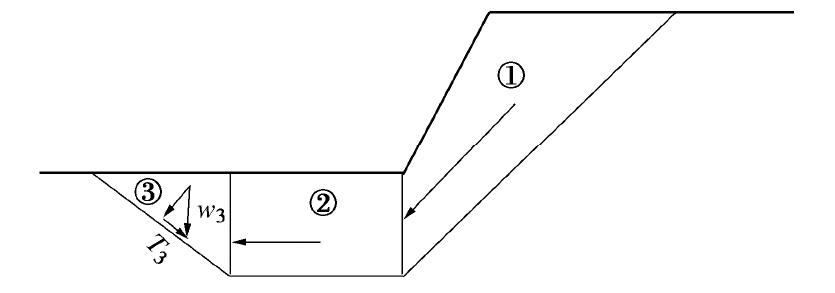
图9表示一卧于平地下的半圆柱形岩土体,用条分法进行抗滑问题分析,各条的法向分力与切向分力分别为N_i和T_i,由于其结构与力系都是对称的,总滑动力矩 $R \sum T_{i} = 0$ ,不存在滑动稳定的问题。如果以反向的T_i为抗力,则它向左、向右滑动都可以算出相等的安全系数,如果c=φ=0,则K=1.0,岂不是庸人自扰。

图 9 平地内的半圆岩土体

Figure 9. Semicircular rock mass under ground

下载: 全尺寸图片幻灯片

图10为用传递系数法分析的一个折线滑动面问题,3块岩土体自重的切向分力分别为T₁>0,T₂=0,T₃<0。但它们应一律被当成滑动力。

图 10 一个传递系数法的例子

Figure 10. Example of transfer coefficient method

下载: 全尺寸图片幻灯片

如前所述,在传递系数法中,当安全系数表示为“荷载放大系数”时,可得到显式解。在具有上翘的滑动面时,可能出现剩余下滑力为P_n-1≤0,根据最后一块岩土体的剩余下滑力等于0°的条件,由于T₃为负的滑动力,可计算出该块的总滑动力为零或负值,安全系数无限大或者为为负值,即出现Duncan所谓的“数值分析问题”^[12]。而安全系数定义为“强度折减系数”则没没有这个问题,总可计算得到较合理的安全系数。

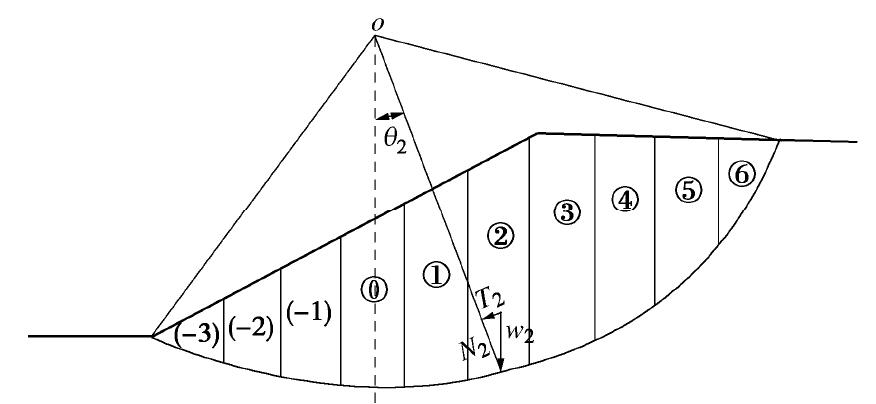
图11表示圆弧条分法边坡稳定分析,由于θ_i可以大于、等于或小于0°,则各土条自重的切向分力W_isinθ_i可能与滑动方向相同或相反。那么就有两种选择,一是令所有与滑动方向相反的力都产生抗滑力矩；另一种是所有在滑动面上的切向分力都产生滑动力矩。

图 11 圆弧条分法的边坡稳定分析

Figure 11. Analysis of slope stability by circular slicing method

下载: 全尺寸图片幻灯片

以瑞典条分法为例,

（1）如果按照前者,则安全系数表示为

$K = \frac{\sum_{i = - 3}^{6} [W_{i} \cos θ_{i} \tan φ_{i} + c_{i} l_{i}] + （ - \sum_{j = - 3}^{0} W_{j} \sin θ_{j} ）}{\sum_{k = 1}^{6} W_{k} \sin θ_{k}}$ 。

(15)

（2）如果定义安全系数为“强度折减系数”,则

$\begin{array}{l} c_{e} = \frac{1}{K} c, \\ \tan φ_{e} = \frac{1}{K} \tan φ 。 \end{array}}$

(16)

安全系数的表达式为（其中分母有一部分为负值）

$K = \frac{\sum_{i = - 3}^{6} (W_{i} \cos θ_{i} \tan φ_{i} + c_{i} l_{i})}{\sum_{i = - 3}^{6} W_{i} \sin θ_{i}}$ 。

(17)

式（17）就是各种条分法及安全系数的一般表达式。在这种情况下,分母部分切向分力（矩）的不确定性较小,而主要的不确定性和风险都在于岩土的强度指标c与φ,所以几乎所有的条分法都是用基于强度折减系数定义安全系数,这样,安全系数就合理地反映了岩土强度参数的不确定性。

3.2 结构物滑动面上的反向切向力

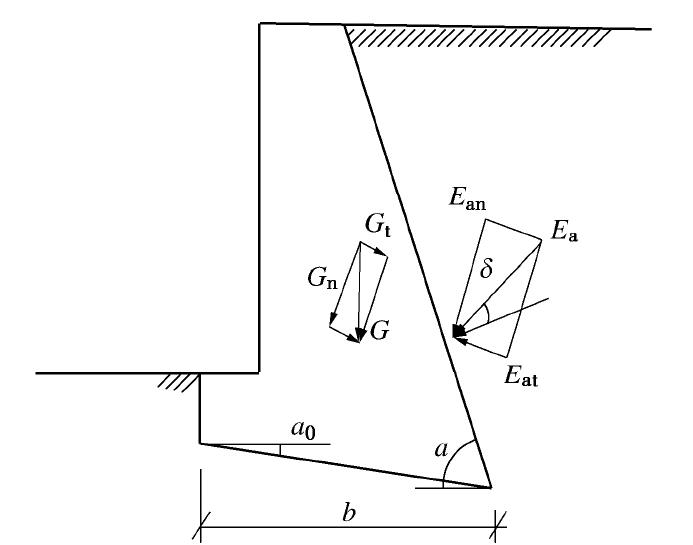
图12为文献[3]的图6.7.5-1,表示的为一后倾式的重力挡土墙。

图 12 挡土墙的抗滑稳定分析

Figure 12. Analysis of sliding stability of retaining wall

下载: 全尺寸图片幻灯片

这个挡土墙底部和背部都是倾斜的,其主动土压力E_a和挡土墙的重力G都可以沿着墙底滑动面分解为法向和切向的两个分力,而它们的切向分力可能是与滑动方向一致与相反的。

如果用强度折减定义安全系数,设折减后的摩擦系数为 $μ_{e} = \tan δ_{e} = \frac{1}{K} \tan δ$ ,则挡土墙沿墙底滑动的安全系数为

$K = \frac{(G_{n} + E_{an}) μ}{E_{at} - G_{t}}$ 。

(18)

亦即将挡土墙自重在基底的反向切向力 $G_{t}$ 从主动土压力的滑动分力E_at中减去,成为负的滑动力,而不作为抗力,这也就是文献[3]中的式（6.7.5-1）,是合理的。

3.3 锚杆土钉的切向力

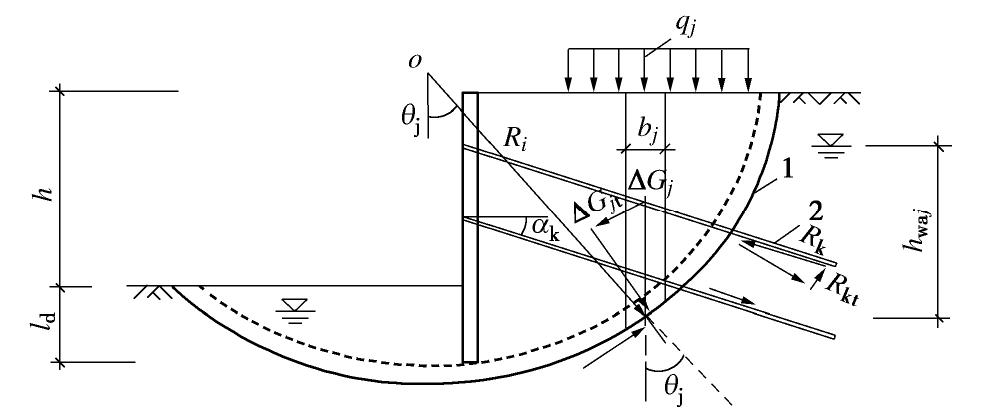
这种情况就比较复杂,图13表示的文献[8]中的复合土钉墙的稳定分析,R_k是土钉或者锚杆的轴向拉力（等于施加在滑动土体滑动面处在轴向的压力）,它作用于在滑动面上的两个分力为R_kn=R_ksin(θ_j+ $α_{k}$ )和

$\begin{array}{l} R_{kt} = R_{k} \cos (θ_{j} + α_{k}), \\ K = \frac{\sum c_{j} l_{j} + (q_{j} b_{j} + Δ G_{j}) \cos θ_{j} \tan φ_{j} + \sum (R_{kt,k} + ψ_{v k} R_{k,k}) / s_{x, k}}{\sum (q_{j} b_{j} + Δ G_{j}) \sin θ_{j}}, \end{array}}$

(19)

图 13 复合土钉墙的稳定分析

Figure 13. Stability analysis of composite soil-nailing wall

下载: 全尺寸图片幻灯片

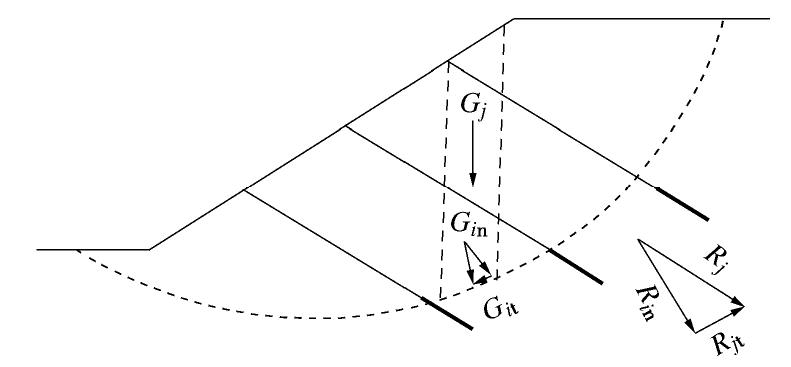
式中, $ψ_{v}$ 为锚杆的法向力R_kn引起的摩阻力,这里锚杆的切向分力R_kt被当成了抗力。

而在《岩土锚杆与喷射混凝土支护工程技术规范》GB 50086—2015中^[13],这个切向力则被当成负的滑动力,见图14和下式：

图 14 文献[13]中的锚杆加固土坡稳定分析

Figure 14. Stability analysis of soil slope reinforced by anchor bolt in Reference [13]

下载: 全尺寸图片幻灯片

$K = \frac{\sum_{i = 1}^{n} (G_{i n} \tan φ_{i} + c_{i} l_{i}) + \sum_{j = i}^{m} R_{j n} \tan φ_{j}}{\sum_{i = 1}^{n} G_{i t} - \sum_{j = 1}^{m} R_{j t}}$ 。

(20)

这样,两本用于支护结构的规范,其规定却相反,计算的安全系数值也不等。这种情况已是屡见不鲜了。这十分不利于中国岩土工程中稳定性的设计与评估,使工程技术人员没有了共同的语言与共同的标准。按照强度折减系数定义安全系数,则没有人为任意规定的余地,式（20）就是唯一的。

文献[4]中关于用局部锚杆加固危岩的式(10.2.4),得

$K_{b} (G_{t} - f G_{n} - c A) \leq \sum N_{akt i} + f \sum N_{akn i}$ ,

(21)

式中,A为滑动面面积,c为土的黏聚力,f为滑动面上的摩擦系数,G_t,G_n分别为不稳定块体自重在平行和垂直于滑面方向的分力,N_akti,N_akni分别为第i根锚杆轴向拉力在抗滑方向和垂直于滑动面方向上的分力； $K_{b}$ 为锚杆钢筋抗拉安全系数。

这个公式看起来很别扭,像μG_n与cA这里的老牌的抗滑力也被划归了敌军阵营,似乎是认为左侧括弧内是“危岩”的剩余下滑力,当做加固前的滑动力,而锚杆的反向切向力与摩阻力都被视为抗滑力。

如果危岩在没加固时的安全系数为K₀,K_r是加固后容许的最小安全系数。则应当用式（22）计算钢筋的极限抗拉拔强度标准值强度R_k。α+θ为锚杆与滑动面切线间的夹角。

$K_{r} = \frac{K_{0} G_{t} + μ R_{k} \sin (α + θ)}{G_{t} - R_{k} \cos (α + θ)}$ 。

(22)

4. 饱和软黏土的荷载与承载力

建筑行业地基承载力确定方法通常包括：

（1）地基极限承载力的普遍表达式为

$p_{u} = \frac{1}{2} γ b N_{γ} + γ_{m} d N_{q} + c N_{c}$ 。

(23a)

（2）文献[3]中的地基承载力特征值公式：

$f_{a} = M_{b} γ_{b} + M_{d} γ_{m} d + M_{c} c_{k}$ 。

(24a)

在两个公式中, $γ_{m}$ 为基底以上土的加权平均重度。

饱和黏土地基是按不排水强度指标计算其承载力^[3],就会发现在两式中,当φ_u=0°时,N_γ=0,M_b=0；N_q= M_d=1.0；对于普朗德尔公式N_c=5.14,对于太沙基公式N_c=5.70,式（24a）中的M_c=3.14。

这时有一个非常有趣的现象,φ_u=0°时的两个公式可写为

$p_{k} = \frac{F_{k} + G_{k}}{A} \leq f_{a} = \frac{1}{K} (γ_{m} d + N_{c} c)$ ,

(23b)

$p_{k} = \frac{F_{k} + G_{k}}{A} \leq f_{a} = γ_{m} d + M_{c} c$ 。

(24b)

也可写为

$p_{k} \leq N_{c} c / K + γ_{m} d / K$ ,

(23c)

$p_{k} - γ_{m} d \leq M_{c} c$ 。

(24c)

可见式（24c）中 $γ_{m} d$ 这一项可直接从荷载中扣除,亦即在 $φ_{u}$ =0°情况下,它可以像浮力一样从基础自重中扣除,而式（23c）中, $γ_{m} d$ 则被当做承载力一部分而被除以安全系数K。

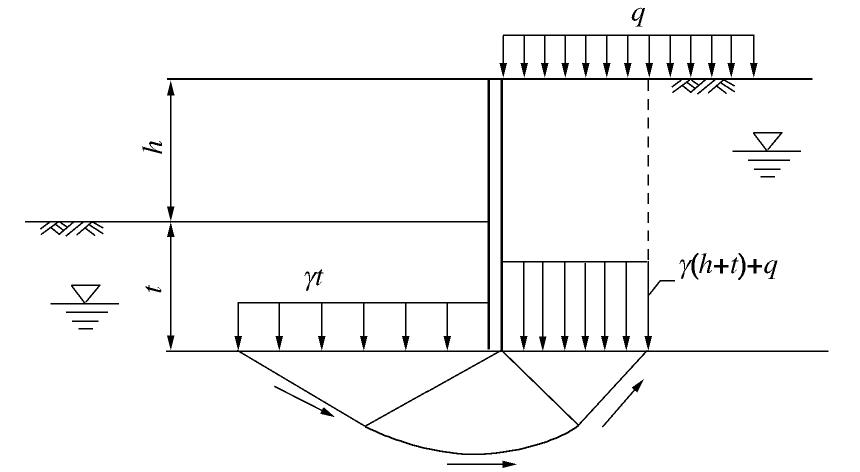
文献[3]中关于饱和软黏土（ $φ_{u}$ =0°）基坑的抗隆起稳定公式,见图15与下式：

图 15 软土基坑的坑底隆起

Figure 15. Uplift of bottom of soft soil foundation pit

下载: 全尺寸图片幻灯片

$K = \frac{极限承载力}{基底荷载} = \frac{5.14 c_{u} + γ t}{γ (t + H) + q}$ 。

(25)

此式存在着一个悖论,如果认为土层的不排水强度 $c_{u}$ 为常数,则支护墙底插入深t越大,其计算的安全系数就越小,这也是由于同质同量 $γ t$ 既当做荷载,也当做抗力。

《铁路桥涵地基和基础设计规范（TB 10002—2005）》^[14]就正确地认识到这一点,对于浅基础的容许承载[σ]力公式为

$[σ] = \frac{5.14 c_{u}}{m^{'}} + γ h$ ,

(26)

式中, $c_{u}$ 为软黏土的不排水强度的黏聚力,m′为安全系数, $γ$ 为基底以上的土重度,h为基础埋深。由于 $γ h$ 这部分极限承载力没有被安全系数除,这就可以从荷载中扣除 $γ h$ ,亦即将 $γ h$ 当成负的荷载。p为基底压力,上式就可写成 $p - γ h \leq \frac{5.14 c_{u}}{m^{'}}$ 。

5. 结论

在用安全系数法分析岩土稳定问题时,区分荷载与抗力是很重要的问题,目前还存在一些歧义与混乱。

当研究的岩土体或结构体全部或部分位于静水下时,最简单的方法就是从自重力扣除这部分浮力,当用其各表面上的水压力计算时,则水压力的身份的选择,应使计算结果与扣除浮力的计算结果相同。

在渗流场中的饱和土体可取土骨架为隔离体,对于土骨架,水的作用表现为浮力与渗透力两个体积力；而取饱和土体为隔离体时,作用于其表面的水压力身份的确定,应与以土骨架为隔离体的计算结果相同。

在各种稳定分析中,荷载的权重更大,岩土工程的不确定性与风险主要在于抗力项,由于岩土材料是天然材料,其性质的复杂性、分布的不可确知性与影响因素的多样性,使其强度指标是其不确定性与风险的主要部分,因而抗滑稳定分析中普遍使用强度折减系数表示安全系数,以使不确定性集中于抗力项,这样就合理地界定了各力的要素的身份,避免了荷载与抗力混淆的问题。

由于荷载的权重更大,一些具有很少不确定性的反向力或力矩,并不作为抗力,而是被当成负的荷载。如图2,4～6中左侧的水平水压力,图3中的水压力切向分力P_w2t,图7中的浮力 $γ_{w}$ (t+Δt),图9～12中自重的反向切向分力,图14中锚杆的反向切向力R_jt,式（25）中的 $γ h$ 等都被当成负的荷载,而不是抗力。

图 1 用传递系数法计算的边坡

Figure 1. Calculation of slope with transfer coefficient method

下载: 全尺寸图片幻灯片

图 2 水泥土墙的抗倾覆稳定

Figure 2. Anti-overturning stability of gravity cement-soil wall

下载: 全尺寸图片幻灯片

图 3 部分在水下的危岩的稳定

Figure 3. Stability of partly underwater dangerous rock

下载: 全尺寸图片幻灯片

图 4 静水下的墙

Figure 4. Stable wall under static water

下载: 全尺寸图片幻灯片

图 5 重力式挡土墙上的倾覆稳定

Figure 5. Anti-overturning stability of gravity retaining wall

下载: 全尺寸图片幻灯片

图 6 支护结构上的净水压力

Figure 6. Net water pressures on retaining and protection structures

下载: 全尺寸图片幻灯片

图 7 坑底抗渗流稳定验算示意图

Figure 7. Diagram for checking seepage stability at bottom of foundation pit

下载: 全尺寸图片幻灯片

图 8 滑弧面上的孔隙水压力

Figure 8. Pore water pressures on sliding surface

下载: 全尺寸图片幻灯片

图 9 平地内的半圆岩土体

Figure 9. Semicircular rock mass under ground

下载: 全尺寸图片幻灯片

图 10 一个传递系数法的例子

Figure 10. Example of transfer coefficient method

下载: 全尺寸图片幻灯片

图 11 圆弧条分法的边坡稳定分析

Figure 11. Analysis of slope stability by circular slicing method

下载: 全尺寸图片幻灯片

图 12 挡土墙的抗滑稳定分析

Figure 12. Analysis of sliding stability of retaining wall

下载: 全尺寸图片幻灯片

图 13 复合土钉墙的稳定分析

Figure 13. Stability analysis of composite soil-nailing wall

下载: 全尺寸图片幻灯片

图 14 文献[13]中的锚杆加固土坡稳定分析

Figure 14. Stability analysis of soil slope reinforced by anchor bolt in Reference [13]

下载: 全尺寸图片幻灯片

图 15 软土基坑的坑底隆起

Figure 15. Uplift of bottom of soft soil foundation pit

下载: 全尺寸图片幻灯片

表 1 不同方法计算的结果

Table 1 Results by different methods

圆心角/(°)	毕肖甫法K_b	显式传递系数法		隐式传递系数法
圆心角/(°)	毕肖甫法K_b	K_t1	$\frac{K_{t 1} - K_{b}}{K_{b}} /%$ $\frac{K_{t 1} - K_{b}}{K_{b}} /%$	K_t2	$\frac{K_{t1} - K_{b}}{K_{b}} /%$ $\frac{K_{t1} - K_{b}}{K_{b}} /%$
117.6	3.020	4.421	46.4	3.025	0.2
95.6	2.614	3.199	22.4	2.620	0.2
81.1	2.451	2.800	14.2	2.456	0.2
70.9	2.371	2.613	10.2	2.375	0.2
63.2	2.332	2.514	7.9	2.335	0.1

下载: 导出CSV

表 2 水压力不同计算方法的结果

Table 2 Results of water pressure by different methods

编号	计算方法	K_ov
①	水下水泥土用浮重度计算,不计任何水压力	2.55
②	水泥土用饱和重度计算,侧向水压力抵消,从自重中扣除扬压力U	2.55
③	主动侧水压力为荷载,被动侧水压力为抗力,墙自重中扣除扬压力U	2.27
④	主动侧水压力为荷载,被动侧水压力为抗力,扬压力U为荷载	1.82

下载: 导出CSV

参考文献(14)

[1]	建筑基坑支护技术规程：JGJ 120—99[S]. 1999. Technical Specification for Retaining and Protection of Building Excavation: JGJ 120—99[S]. 1999. (in Chinese)
[2]	建筑边坡工程技术规范：GB 50330—2002[S]. 2002. Technical Code for Building Slope Engineering: GB 50330—2002[S]. 2002. (in Chinese)
[3]	建筑地基基础设计规范：GB 50007—2011[S]. 2011. Code for Design Building Foundation: GB 50007—2011[S]. 2011. (in Chinese)
[4]	建筑边坡工程技术规范：GB 50330—2013[S]. 2013. Technical Code for Building Slope Engineering” Second Edition: GB 50330—2013[S]. 2013. (in Chinese)
[5]	陈祖煜. 土质边坡稳定分析[M]. 北京: 中国水利水电出版社, 2003. CHEN Zu-yu. Soil Slope Stability Analysis[M]. Beijing: China Water Conservancy and Hydropower Press, 2003. (in Chinese)
[6]	葛修润. 岩石疲劳破坏的变形控制率、岩石力学试验的实时X射线CT扫描和边坡坝基坑稳定分析的新方法[J]. 岩土工程学报2008, 30(1): 1-20. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200801003.htm GE Xiu-run. Deformation control law of rock failure, real-time X-ray CT scan of geotechnical testing, and new method of stability analysis of slopes and dam foundations[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(1): 1-20.(in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200801003.htm
[7]	建筑桩基技术规范：JGJ 94—2008[S]. 2008. Technical Code for Building Pile Foundation: JGJ 94—2008[S]. 2008. (in Chinese)
[8]	建筑基坑支护技术规程：JGJ 120—2012[S]. 2012. Technical Specification for Retaining and Protection of Building Excavation: JGJ 120—2012[S]. 2012. (in Chinese)
[9]	上海市标准：基坑工程技术规范：DG/TJ8—61—2010[S]. 2010. Shanghai Stand Code for Design of Excavation Engineering: DG/TJ8—61—2010[S]. 2000. (in Chinese)
[10]	建筑基坑工程技术规范：YB 9258—97[S]. 1997. Code for Technique of Building Foundation Pit Engineering: YB 9258—97[S]. 1997. (in Chinese)
[11]	水利水电工程地质勘察规范：GB 50487—2008[S]. 2008. Code for Engineering Geological Investigation of Water Resources and Hydropower: GB 50487—2008[S]. 2008. (in Chinese)
[12]	DUNCAN J M. State of the art. Limit equilibrium and finite element analysis of slopes[J]. Journal of Geotechnical Engineering, ASCE, 1996, 122(7): 577-596.
[13]	岩土锚杆与喷射混凝土支护工程技术规范：GB 50086—2015[S]. 2015. Technical Code for Engineering of Ground Anchorages and Shotcrete Support: GB 50086—2015[S]. 2015. (in Chinese)
[14]	铁路桥涵地基和基础设计规范：TB 10002—2005[S]. 2005. Code for Design on Subsuil and Foundation of Railway Bridge and Culvert: TB 10002—2005[S]. 2005. (in Chinese)