0.   引言

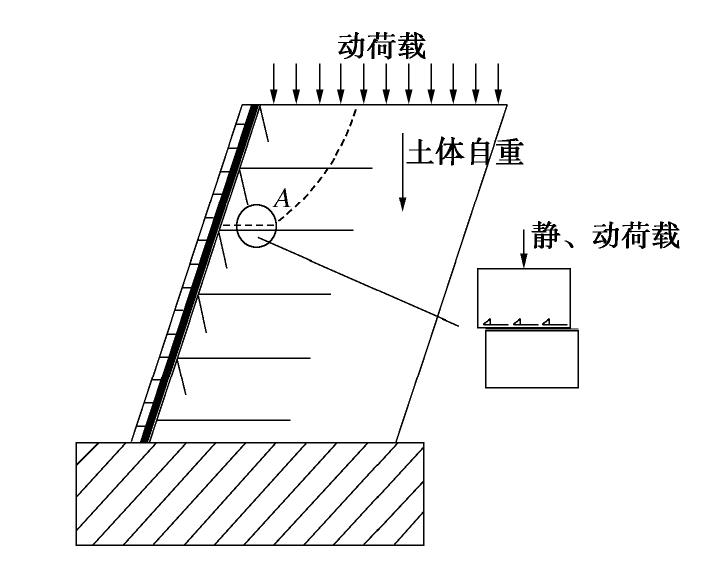
作为一种高效、经济的地基处理手段,柔性土工合成材料（土工织物、土工格栅等）在道路工程中得到了广泛的应用^[1]。道路的加筋土路基承受填土自重及车辆等静动力载荷的综合作用,所引起的筋-土界面剪切响应（图1）对路基稳定及行车安全具有重要影响。为设计更优化和安全的加筋土结构,需要对筋土界面相互作用进行清晰理解和准确定量^[3]。

图  1  加筋挡墙的相互作用剪切机制(引自Palmeira^[2])

Figure  1.  Interaction shear mechanism in a geogrid reinforced soil wall (modified from Palmeira^[2])

下载: 全尺寸图片 幻灯片

常规的直剪试验是基于法向静荷载作用,研究不同因素（填料性质、格栅孔径等）对筋土界面剪切应力和体积响应的影响^[4]。已有研究分析剪切速率对界面剪切行为的影响：徐超等^[5]认为当剪切速率不超过一定界限时,其对筋-土接触面剪切强度的影响可以忽略；刘飞禹等^[6]进行了一系列不同剪切速率的筋土界面剪切试验,提出剪切速率对单调直剪下的界面特性影响较小；Sweta等^[7]评估了不同剪切速率下加筋道砟的界面特性,试验表明,随着剪切速率的增加,摩擦角和剪胀角在减小,而破碎率在增加。

交通等动荷载会对加筋土层产生不同方向的动态应力。其中,对界面剪切方向的影响已有一些研究,如：Alaie等^[8]研究了EPS颗粒含量对EPS-砂混合料与土工格栅的界面循环剪切特性的影响,结果表明,当EPS含量增加时,剪切刚度减小而阻尼比增大；刘飞禹等^[9]通过循环剪切试验发现,筋-土界面峰值剪切应力随粒孔比的增大,表现出先增大后减小的趋势。实际工程中,垂直于界面剪切方向亦存在动力作用,且频率是影响结构动力响应的重要参数^[10]。仅少部分学者探究了法向动荷载对筋土界面剪切特性的影响：徐超等^[11]初步探索了0.01～0.5 Hz的法向循环荷载频率对土工格栅与石英砂的界面剪切应力、体积改变的影响,并指出动荷载作用下界面剪切特性较复杂；王家全等^[12]对法向循环荷载下的筋土界面直剪试验进行了颗粒流模拟,并分析了剪切过程的应力场、位移场、孔隙率、滑动比的变化。

综上所述,法向循环应力作用下的筋土界面剪切特性及频率影响仍缺乏相关的试验数据,需要更深入的探究^[13],且法向动力下剪切速率对筋土界面摩擦特性的影响还未见有报道。本文应用动态直剪仪在不同法向初始应力下开展了一系列法向循环荷载的砾石-土工格栅界面剪切试验。水平剪切速率设定为0.1,1,5,10 mm/min,法向循环频率分别为0.1,0.5,1,2 Hz,并分析这两者对筋土界面剪切行为的影响,探究了这类动力试验的相位特性和拟静力剪切强度参数,为加筋土结构的应用和设计提供参考依据。

1.   试验材料与方法

1.1   试验材料与仪器

本文采用公路路基常用的角状砾石作为试验填料（图2（a））,其物理性质指标见表1。加筋材料为聚丙烯塑料土工格栅（图2（b））,其技术指标见表2。

图  2  试验材料实物图

Figure  2.  Testing materials

下载: 全尺寸图片 幻灯片

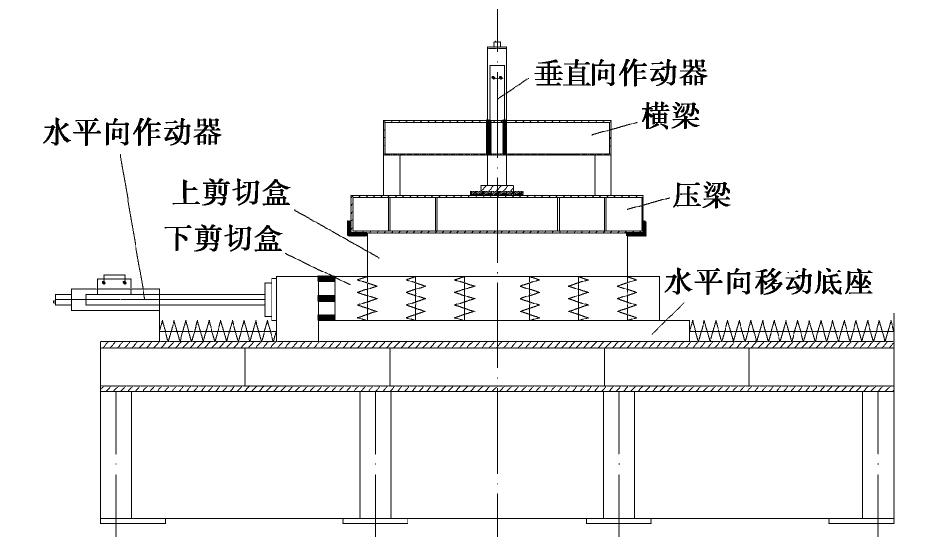
表  1  砾石物理性质指标

Table  1.  Physical properties of gravelly soil

填料	相对质量密度Gs	最大孔隙比emax	最小孔隙比emin	颗粒粒径/mm			不均匀系数Cu	曲率参数Cc
				有效粒径D10	连续粒径D30	限制粒径D60
砾石	2.62	0.66	0.47	3.19	4.30	5.41	1.70	1.07

下载: 导出CSV 

| 显示表格

表  2  格栅技术指标

Table  2.  Techncal indices of geogrid

土工合成材料	单位面积质量/(g·m-2)	网孔尺寸/mm	纵横肋尺寸/mm		极限延伸率/%		极限抗拉强度/(kN·m-1)
			纵向	横向	纵向	横向	纵向	横向
聚丙烯塑料土工格栅	400	30×30	5	5	13	15	30	30

下载: 导出CSV 

| 显示表格

试验采用RAW-60/2微机控制电液伺服动态直剪仪,如图3所示。上、下剪切盒尺寸分别为600 mm× 200 mm×50 mm和800 mm×200 mm×50 mm,其它参数见文献[14]。

图  3  室内动态直剪仪示意图

Figure  3.  Dynamic direct shear apparatus

下载: 全尺寸图片 幻灯片

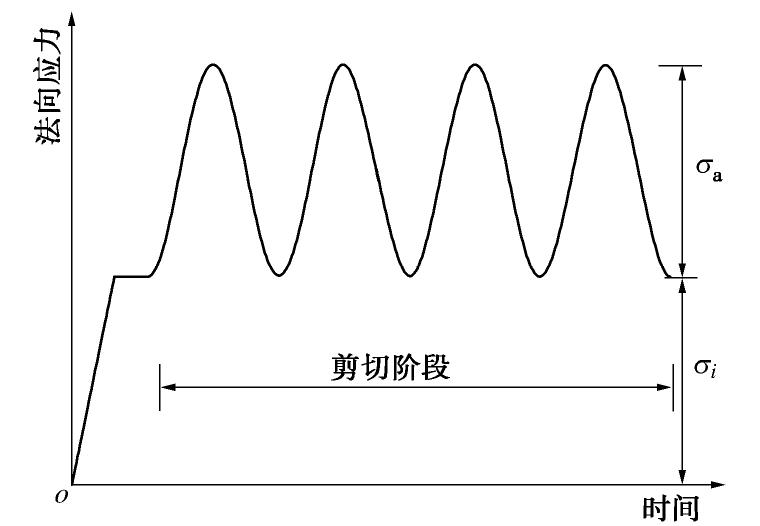
砾石经筛分搅拌,分层填满剪切盒并压实,在下盒上表面铺设土工格栅,并在边缘固定格栅^[15]。每层砾石的压实厚度均为25 mm,通过控制每层填料相同的质量,保证每次试验试样达到相同的75%相对密实度。试验阶段,控制仪器对试样匀速加载法向初始应力,并静置一段时间使位移达到稳定,之后在法向继续加载循环荷载,并同时在水平向进行剪切,直至达到设定的剪切位移,如图4所示。

图  4  法向循环加载示意图

Figure  4.  Set-up of normal cyclic loads

下载: 全尺寸图片 幻灯片

1.2   试验方案

交通荷载作用下产生的竖向附加应力受车型、深度等因素的影响^[16],本文选取具有代表性的循环幅值${\sigma }_{\text{a}}$为20 kPa。初始应力${\sigma }_i$有20,40,60 kPa 3种工况,大致代表界面受到的1～4 m的土层静态应力状态。法向循环荷载采用正弦波形,加载频率为0.1～2 Hz,能够代表交通荷载的作用^[17]。水平向最大剪切位移为90 mm,剪切速率分别取0.1,1,5,10 mm/min。试验方案如表3所示。

表  3  法向循环荷载下的直剪试验方案

Table  3.  Summary of direct tests under normal cyclic loading

组号	初始应力/kPa	频率f/Hz	剪切速率ν/(mm·min-1)
T1	40	0.1,0.5,1,2	0.1,1,5,10
T2	20,40,60	0.5	1
T3	20,60	0.1,0.5,1,2	1
T4	20,60	0.5	0.1,1,5,10

下载: 导出CSV 

| 显示表格

2.   结果分析

2.1   筋–土界面剪切行为

图5为不同试验条件下法向循环荷载的砾石-格栅界面直剪行为曲线。法向循环荷载下的剪切应力与法向应力类似,表现出循环动态变化的特征；法向位移亦是压缩和膨胀交替循环变化。从整体上看,剪切应力先增大至峰值,随后降低至稳定的残余状态,表现出显著的软化特征；在剪切初期,试验经历了剪缩过程,到达最大压缩量后剪胀至试验停止。图5（b）为剪切位移为50 mm处应力和位移随时间变化的关系曲线。法向应力在40～60 kPa循环变化,而剪切应力与法向位移亦随时间动态变化,剪切应力与法向应力的峰值存在约0.8 s的时间差。法向位移与应力协同变化,这是因为较大的法向应力更能限制位移的改变,对应着较小的剪胀位移。

图  5  T1：不同频率和剪切速率下界面剪切试验结果

Figure  5.  T1: results of interface shear tests at different frequencies and shear rates

下载: 全尺寸图片 幻灯片

由图5（a）～（e）可知,随着法向加载频率的增大,应力曲线呈下移趋势,且应力波动范围在减小。这说明较大的循环频率下更频繁的颗粒调整,可能导致界面嵌锁机制不稳定,颗粒与颗粒、颗粒与格栅的接触作用力更小。同时可以发现,随频率的增大,最大剪缩量增大,分别为0.54,0.57,0.63,0.64 mm；而最大剪胀量在减小,分别为5.59,5.09,4.48,4.44 mm。根据图5（c）和（f）～（h）,随着水平剪切速率的增加,应力曲线呈上升趋势,且应力波动范围在增加,可见较大剪切速率下的剪切应力更难以克服界面相互作用阻力。此外,竖向最大剪缩量随剪切速率的增加而减小,分别为0.87,0.57,0.41,0.33 mm；最大剪胀量则反之,分别为4.76,5.09,5.59,6.00 mm。当剪切速率较大时,更剧烈的颗粒重新排列导致界面剪胀更加明显^[18]。

2.2   特征应力与剪切幅值

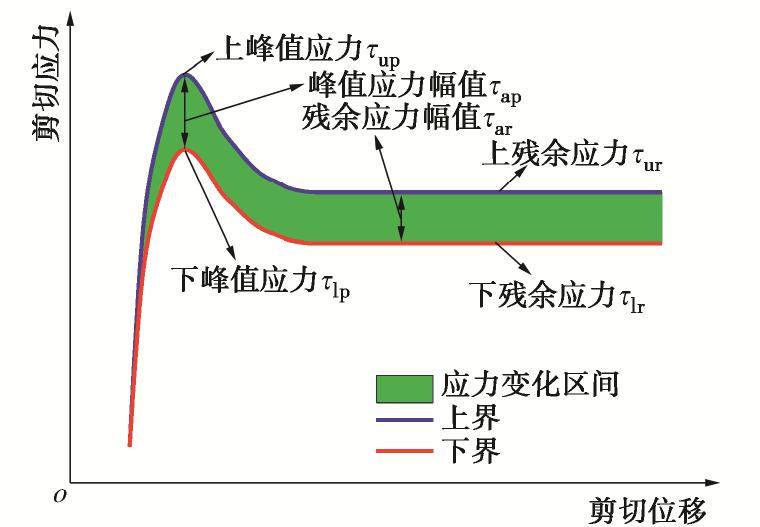
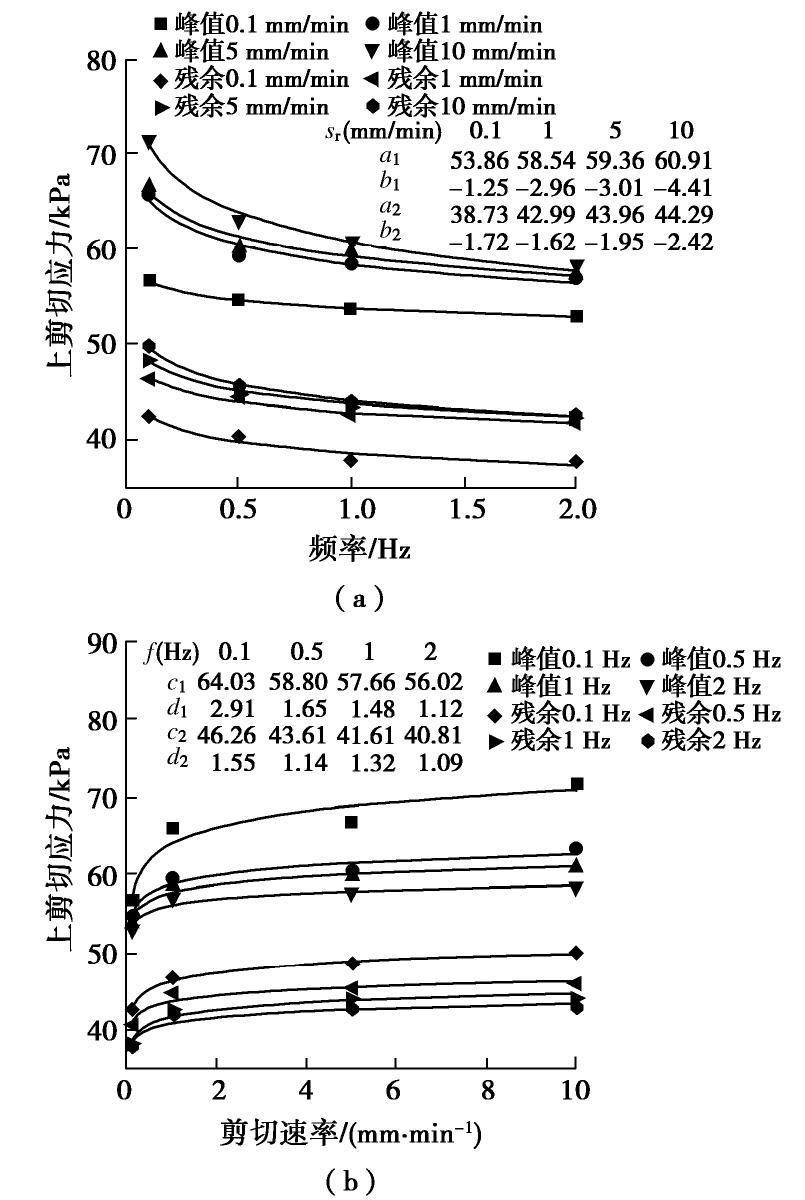
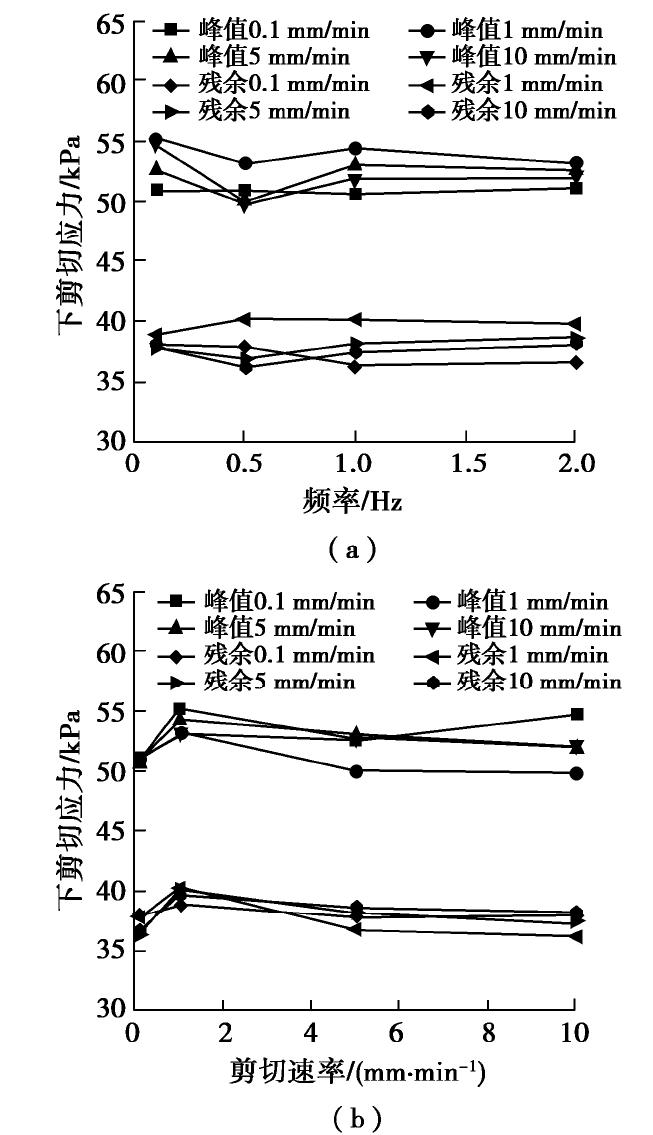
根据上述对界面剪切行为的分析,绘制剪切应力–位移的模型简图,见图6。本文选取4个特征应力和2个幅值参数进行分析：上峰值应力${\tau }_{\text{up}}$和上残余应力${\tau }_{\text{ur}}$分别为曲线上界的峰值和残余值；下峰值应力${\tau }_{\text{lp}}$和下残余应力${\tau }_{\text{lr}}$分别为曲线下界的峰值和残余值；而相应的变化区间则为峰值应力幅值${\tau }_{\text{ap}}$和残余应力幅值${\tau }_{\text{ar}}$。

图  6  剪切应力–位移模型简图

Figure  6.  Schematic diagram of shear stress-displacement curve

下载: 全尺寸图片 幻灯片

图7描述了筋土界面剪切应力–位移曲线上界的剪切应力与频率、剪切速率的关系曲线。从图7（a）可知,上峰值应力、上残余应力与频率均呈负相关变化趋势。在剪切速率为0.1 mm/min时,当频率从0.1 Hz增加到2 Hz,上峰值应力从56.72 kPa减小到52.99 kPa,上残余应力从42.60 kPa降低到37.80 kPa,其他剪切速率下也具有相同的变化规律。在法向循环频率较小时,应力受频率的改变影响较大,而当频率超过1 Hz时,应力改变较小并趋向于稳定。鉴于上述的变化特点,用对数关系表达上剪切应力与频率的变化关系,

式中,f为法向循环荷载的频率,$a_1$,$b_1$和$a_2$,$b_2$为相应的经验参数,具体数值见图7（a）。

图  7  上剪切应力与频率、剪切速率关系曲线

Figure  7.  Relationship between upper shear stress and frequency/shear rate

下载: 全尺寸图片 幻灯片

从图7（b）可知,上峰值应力、上残余应力均与剪切速率呈正相关变化趋势。而Sweta等开展的静荷载下的单调直剪试验结果表明^[9],峰值剪切应力与剪切速率呈负相关变化,可见在不同的法向加载条件,界面剪切特性的差异性。在频率为0.1 Hz时,当剪切速率从0.1 mm/min增加到10 mm/min,上峰值应力从56.72 kPa增加到71.53 kPa,上残余应力从42.6 kPa增加到49.93 kPa,其他频率下亦具有相同的变化规律。在剪切速率较小时,应力增加显著,而当剪切速率大于5 mm/min后,应力变化幅度较小,也即受剪切速率的影响较小。根据上述特点,建立上峰值、上残余应力与剪切速率的经验公式,

式中,$s_{\text{r}}$为水平向剪切速率,$c_1$,$d_1$和$c_2$,$d_2$为相应的经验参数,拟合结果见图7（b）。

图8描述了筋土界面剪切应力–位移曲线下界的剪切应力与频率、剪切速率的关系曲线。相较于上界的剪切应力,下剪切应力受频率和剪切速率的影响较小。例如,剪切速率为1 mm/min时,下峰值应力随频率的改变在50.58～51.14 kPa,下残余应力在36.28～37.91 kPa变化。频率为2 Hz时,下峰值应力随剪切速率的改变在51.14～53.15 kPa,下残余应力在36.57～39.69 kPa变化。与上应力相同的是,当频率大于1 Hz、剪切速率大于5 mm/min,应力变化不明显,接近恒定。

图  8  下剪切应力与频率、剪切速率关系曲线

Figure  8.  Relationship between lower shear stress and frequency/shear rate

下载: 全尺寸图片 幻灯片

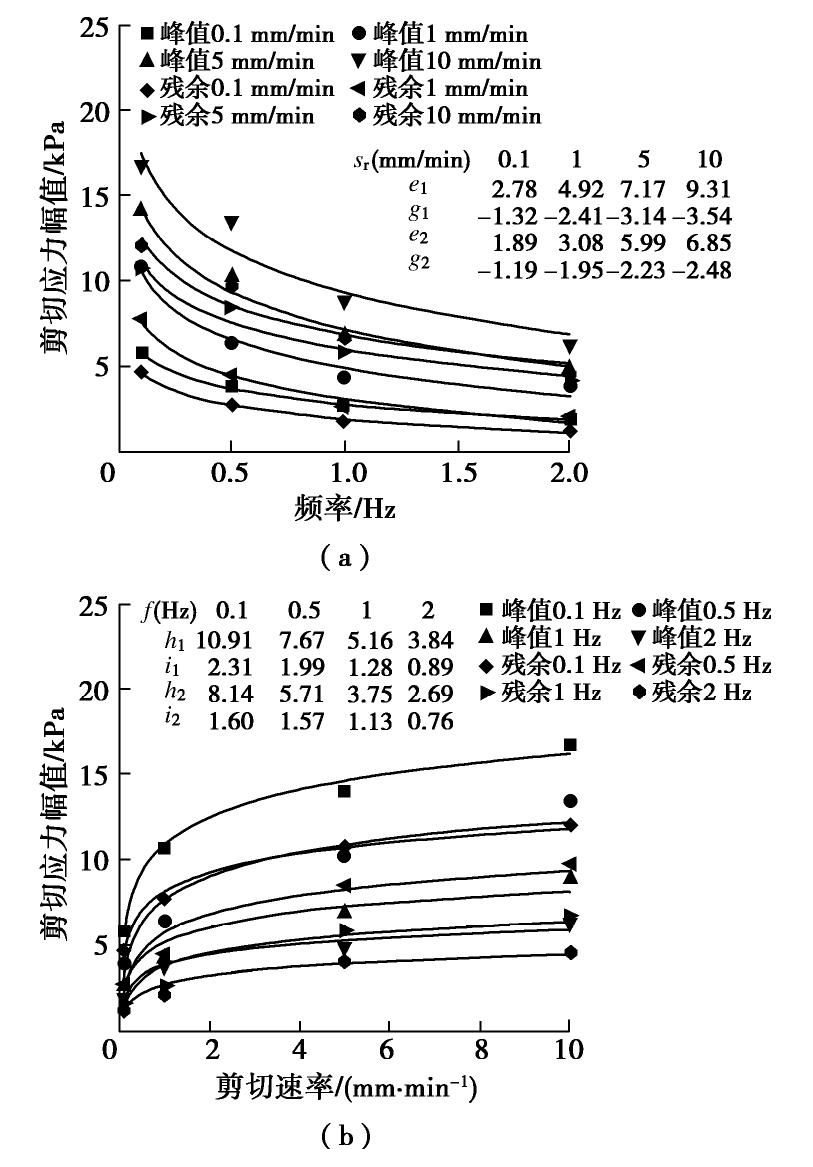
剪切应力幅值代表剪切应力波动的剧烈程度。在相同的法向应力幅值下,由于频率和剪切速率的差异,界面剪切应力幅值亦有显著区别。根据图9（a）的试验数据可知,无论是在峰值还是残余状态,当频率增加时,剪切应力幅值随之降低,且频率越大,改变的程度越小。因此,可用对数函数建立剪切应力幅值与频率的经验表达式,

式中,$e_1$,$g_1$,$e_2$,$g_2$分别为相应的经验参数,具体值见图9（a）。

图  9  剪切应力幅值与频率、剪切速率关系曲线

Figure  9.  Relationship between shear stress amplitude and frequency/ shear rate

下载: 全尺寸图片 幻灯片

根据图9（b）,当剪切速率增大时,剪切应力幅值随之增加,同样的,剪切速率越大,改变的程度越小,可建立剪切应力幅值与频率的经验表达式：

式中,$h_1$,$i_1$,$h_2$,$i_2$分别为相应的经验参数,具体值见图9（b）。

2.3   时间差

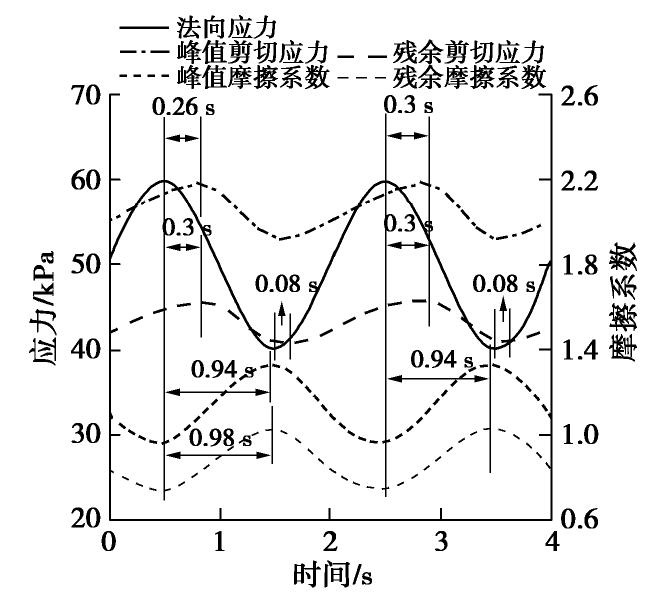
图10为选取的频率为0.5 Hz和剪切速率为1 mm/min的界面峰值和残余阶段剪切应力、摩擦系数（剪切应力/法向应力）与法向应力随时间变化曲线图。法向循环荷载作用下的剪切应力、摩擦系数、法向位移随时间以接近正弦波的形态循环变化,且这几种波形并不完全同步改变,而是存在着一定的时间差（图5（b）,图10）。由图10可知,无论是峰值还是残余状态,法向应力与剪切应力的峰值时间差约为0.3 s,这一现象可能是由于颗粒调整滞后性导致的剪切应力滞后性,剪切应力在法向应力达到峰值后的一定位移达到峰值。而谷值时间差为0.08 s,低于峰值的时间差,这可能是由于颗粒在低应力水平下调整更加容易。摩擦系数与法向应力的时间差约在0.94～0.98 s,接近半个周期。为了探究法向循环荷载作用下砾石-格栅界面的剪切滞后特性,采用相对时间差^[19]参数,其计算式见式（9）。作为一种动力测试手段,法向动荷载下的直剪试验的相位滞后特征是重要的剪切行为之一,下文探究了频率和剪切速率对时间差的影响。

图  10  峰值和残余阶段应力、摩擦系数随时间的变化曲线

Figure  10.  Development of stress and friction coefficient with time during peak and residual stages

下载: 全尺寸图片 幻灯片

式中,$T_{\text{R}}$为两种循环波的相对时间差,$\Delta t$为峰值（谷值）之间的时间差,T为周期,f为频率。

（1）剪切应力–法向应力

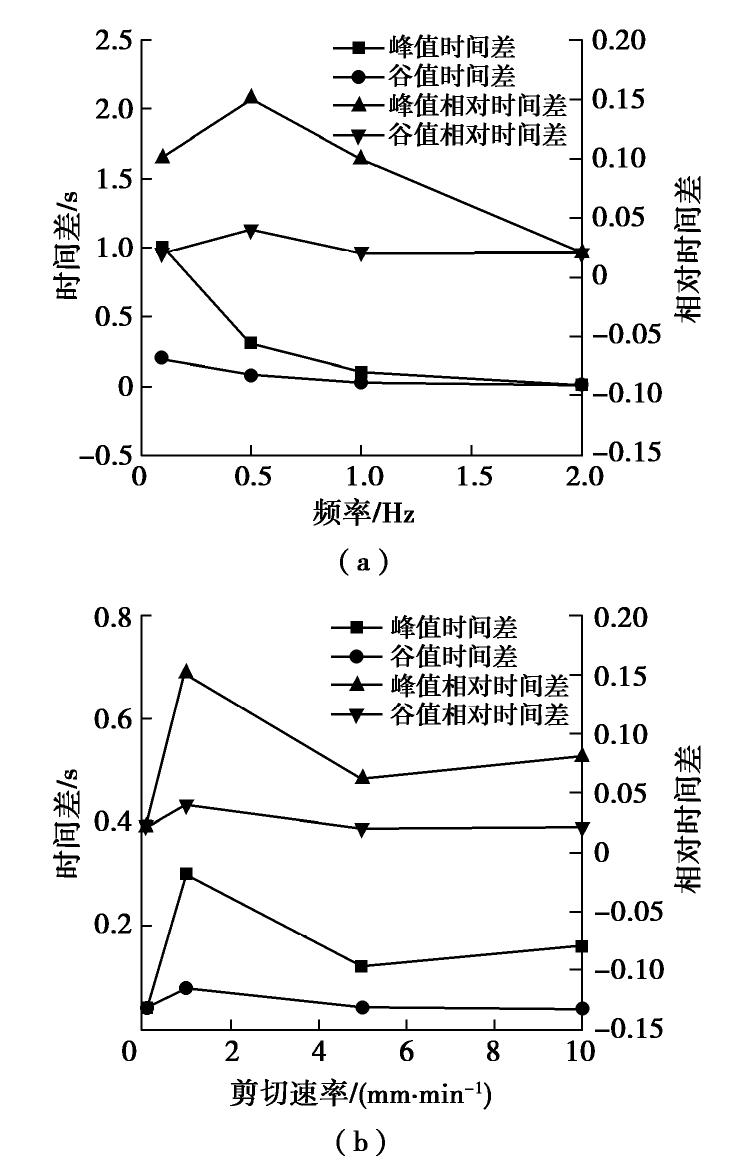
选取峰值剪切应力阶段,分析不同频率、剪切速率下筋土界面剪切应力与法向应力的时间差。图11（a）绘制了剪切速率为1 mm/min时,峰、谷值时间差和相对时间差随频率的变化曲线。当频率增大时,峰、谷值时间差均随之减小,且减小的幅度越来越小。峰值相对时间差分别为0.10,0.15,0.10,0.02,在频率为0.5 Hz时最大。当频率较大时,相对时间差趋向于0,也即剪切应力循环变化与法向应力接近一致。谷值相对时间差分别为0.02,0.04,0.02,0.02,即在这4种循环频率下剪切应力谷值的滞后程度均较小。

图  11  界面剪切与法向应力的时间差与频率、剪切速率的关系曲线

Figure  11.  Relationship between time shift of interface shear stress-normal stress and frequency/shear rate

下载: 全尺寸图片 幻灯片

在频率为0.5 Hz时（图11（b））,剪切应力与法向应力间的时间差与相对时间差具有相同变化趋势,在剪切速率为1 mm/min时相对时间差最大,即此时界面剪切应力的滞后性最显著,而当剪切速率较大时,时间差更加稳定,受剪切速率的影响较小。

（2）摩擦系数-法向应力

表4列出了砾石-格栅界面峰、谷值法向应力与摩擦系数的时间差。根据试验结果可知,在频率为0.1 Hz时,峰值和谷值时间差约为5 s,相对时间差接近0.5。其他频率下的相对时间差通过式（9）计算可知亦约0.5,也即受频率和剪切速率的影响较小。同时,高剪切速率下摩擦系数-法向应力相对时间差略低于低剪切速率的情况。

表  4  T1：摩擦系数与法向应力的峰、谷值时间差

Table  4.  T1: peak and valley time shift of friction coefficient-normal stress

频率/Hz	剪切速率/(mm·min-1)
	0.1	1	5	10
0.1	5/5	4.5/5	4.5/4.8	4.4/4.5
0.5	1.04/1	0.94/0.96	0.92/0.88	0.88/0.88
1.0	0.51/0.51	0.47/0.49	0.47/0.47	0.47/0.45
2.0	0.28/0.25	0.26/0.23	0.26/0.24	0.25/0.22
注：峰值时间差（s）/谷值时间差（s）。

下载: 导出CSV 

| 显示表格

2.4   拟静力强度参数

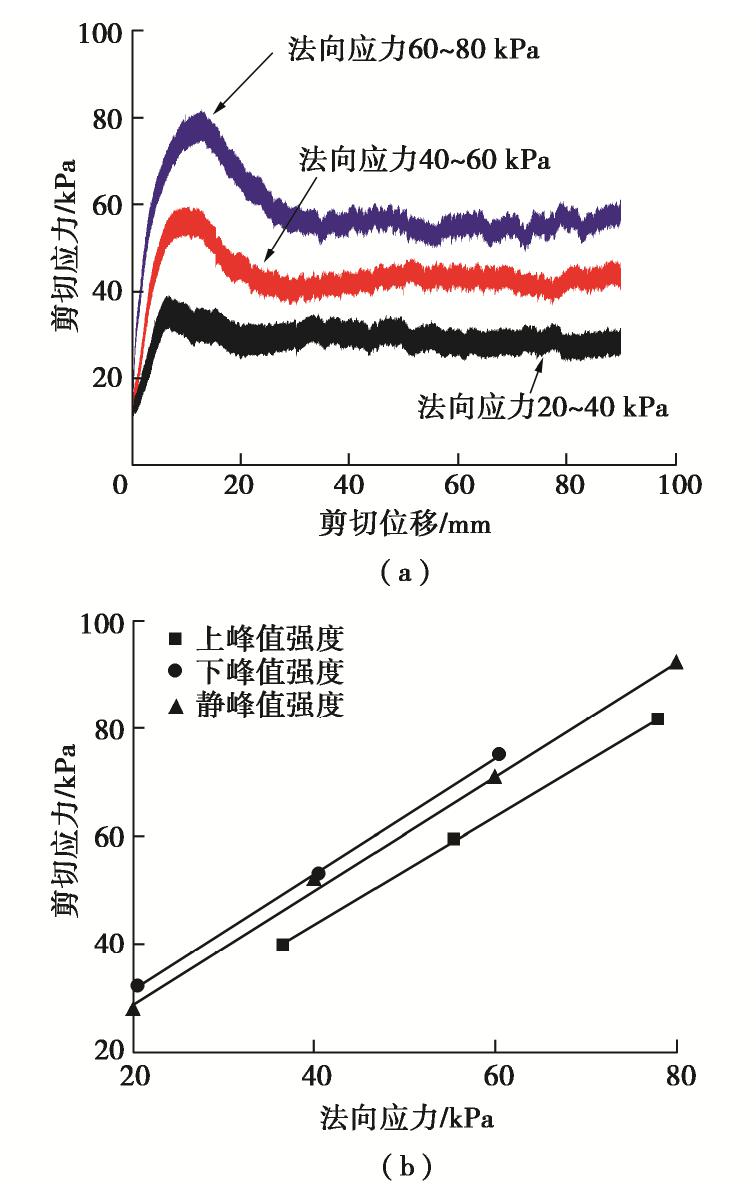
图12（a）为频率0.5 Hz和剪切速率1 mm/min时3种初始应力水平作用下的筋土界面剪切应力–位移曲线。法向应力水平的提高,意味着试验过程中试样被压密,界面孔隙率减小,颗粒间咬合力增强,故而界面相互作用阻力更大^[20],相应的应力–位移曲线也随之上移。法向循环应力作用下,峰值阶段存在着多组对应的法向应力与剪切应力,且二者存在一定的时间差,这就存在如何确定强度参数的问题。本文选取上峰值应力和下峰值应力作为峰值阶段的两个代表应力,通过Mohr-Coulomb准则得到上、下界的拟静力峰值强度参数,见图12（b）。上峰值的摩擦角和似黏聚力分别是45.16°和3.37 kPa,下峰值分别为46.98°和10.29 kPa,而静荷载作用下的峰值参数为46.50°和7.94 kPa,处于上、下峰值参数之间,线性拟合的相关系数均达到0.99。上峰值具有更小的摩擦角和似黏聚力。

图  12  T2：不同法向应力下剪切应力曲线

Figure  12.  T2: shear stress curves under different normal stress conditions

下载: 全尺寸图片 幻灯片

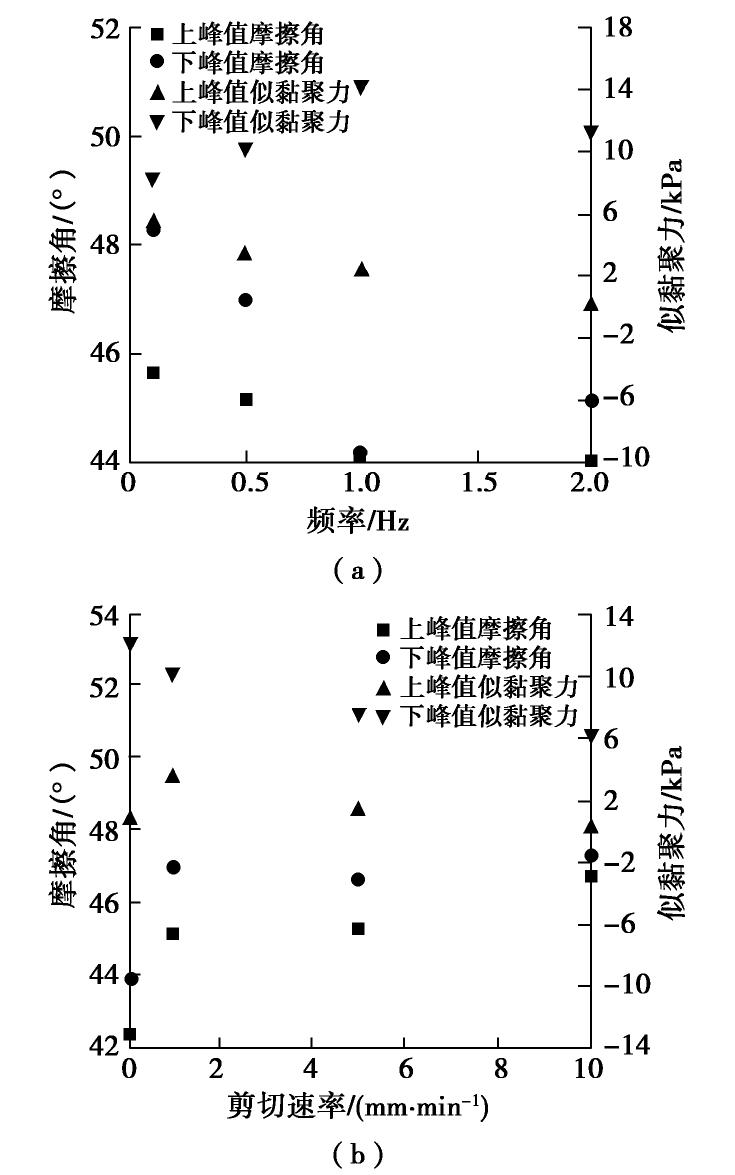
图13为拟静力峰值强度参数（摩擦角、似黏聚力）与频率、剪切速率的关系曲线。在这8组试验中,下峰值摩擦角和似黏聚力均大于上峰值的参数。为了保证足够的安全储备,应取上峰值参数作为抗剪强度。随着频率的增加,上峰值摩擦角从45.66°减小至44.04°；上峰值似黏聚力从5.51 kPa减小至0.12 kPa；而下峰值参数有增有减。随剪切速率的增加,上峰值摩擦角从42.38°增加至46.76°；上峰值似黏聚力变化较小,分别为0.69,3.37,1.19,0.16 kPa；下峰值摩擦角总体呈增加趋势,而峰值似黏聚力则是随之减小。由上述分析可知,上峰值摩擦角与剪切应力随频率和剪切速率的变化趋势基本一致。实际应用中无法按真实的动力荷载来进行设计和参数选取,常需要进行拟静力处理,而法向动荷载作用下的剪切强度的参数选取受诸多条件影响,需要结合工程实际,作进一步深入分析。

图  13  T2—T4：不同频率、剪切速率的拟静力强度参数

Figure  13.  T2-T4: quasi-static strength parameters at different frequencies and shear rates

下载: 全尺寸图片 幻灯片

3.   讨论

本文基于循环荷载下的直剪试验,模拟了车辆等动荷载与土层静荷载共同作用下筋-土界面剪切行为。常规的界面直剪试验不考虑法向动荷载影响,这与实际的路基工程存在差异,本文的试验方式更接近真实的界面受力状态,所得的关于剪切应力、法向位移等的结论能更好指导工程建设。剪切速率作为直剪试验中的一个重要因素,是实际工程中界面滑移、剪应力加载的体现,而法向加载频率则是反映交通荷载的重要特征,两者对筋-土界面剪切特性的影响对相互作用机理研究和工程应用是有意义的。

法向动荷载作用下,筋土界面存在“时间差”现象,其反映的是界面剪切应力、摩擦系数相较于法向应力的相位特征和滞后性。这一概念的意义主要在：首先,这一现象的产生与颗粒运动密切相关,故而可为后续更深入的微观颗粒运动、机理分析等提供依据；其次,剪切应力不同的时间差,使得剪切应力与法向应力的波形无法对应,这对强度参数的选取有较大影响,对实际工程有一定的意义；最后,由于摩擦系数与法向应力存在稳定的时间差,可应用于分析摩擦系数、剪切应力与法向应力的相互动力关系。对剪切应力的拟静力处理,则为动力下的筋土界面剪切强度参数选取提供了一定参考。

4.   结论

本文进行了一系列室内大型直剪试验,探究了法向循环荷载下土工格栅与砾石的界面剪切行为,包括峰值和残余剪切应力、体变响应、剪切应力幅值、时间差、拟静力强度参数等,分析了水平向剪切速率和法向加载频率的影响,得到3点主要结论。

（1）法向循环应力的作用下,界面剪切应力表现出循环动态变化的特征。上峰值、上残余剪切应力及剪切应力幅值均随频率的增大而减小,随剪切速率的增大而增大,可用对数函数建立经验表达式。

（2）在峰值剪切状态,剪切应力与法向应力的峰值时间差大于谷值,且当频率为0.5 Hz或剪切速率为1 mm/min时峰值相对时间差最大。摩擦系数与法向应力的相对时间差接近恒定的0.5个周期。

（3）下峰值摩擦角和似黏聚力大于上峰值的参数,上峰值摩擦角随频率的增加而减小,随剪切速率的增加而增大。