多形态贯通型岩体结构面宏细观剪切力学行为研究

刘新荣; 许彬; 黄俊辉; 蔺广义; 周小涵; 王继文; 熊飞

doi:10.11779/CJGE202103002

多形态贯通型岩体结构面宏细观剪切力学行为研究 English Version

刘新荣^{1, 2, 3,},
许彬^{1, 2, 3, ,},
黄俊辉¹,
蔺广义¹,
周小涵^{1, 2},
王继文¹,
熊飞¹

1.
重庆大学土木工程学院,重庆　400045
2.
库区环境地质灾害防治国家地方联合工程研究中心,重庆　400045
3.
山地城镇建设与新技术教育部重点实验室（重庆大学）,重庆　400045

基金项目:

国家自然科学基金项目 41972266

国家自然科学基金项目 41772319

国家重点研发计划项目 2018YFC1504802

重庆市博士后科研基金项目 cstc2019jcyj-bshX0072

重庆市研究生科研创新项目 CYS19005

详细信息

作者简介:
刘新荣（1969— ）,男,教授,博士生导师,主要从事岩土工程的教学与科研工作。E-mail：liuxrong@126.com

通讯作者:
许彬, E-mail: geotechnicale2016@163.com

中图分类号: TU45
计量
- 文章访问数: 340
- HTML全文浏览量: 23
- PDF下载量: 217
出版历程
- 收稿日期: 2020-06-14
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-02-28

Macro-meso shear mechanical behaviors of coalescent rock joints with different morphologies

LIU Xin-rong^{1, 2, 3,},
XU Bin^{1, 2, 3, ,},
HUANG Jun-hui¹,
LIN Guang-yi¹,
ZHOU Xiao-han^{1, 2},
WANG Ji-wen¹,
XIONG Fei¹

1.
School of Civil Engineering, Chongqing University, Chongqing 400045, China
2.
National Joint Engineering Research Center for Prevention and Control of Environmental Geological Hazards in the TGR Area, Chongqing 400045, China
3.
Key Laboratory of New Technology for Construction of Cities in Mountain Area (Chongqing University), Ministry of Education, Chongqing 400045, China

摘要

摘要: 采用室内直剪试验和PFC^2D离散元程序,系统地研究了考虑一阶（二阶）起伏体影响的贯通型锯齿状（波浪状）岩体结构面宏细观剪切力学行为。研究表明：①相同法向压力下,结构面宏观损伤质量、峰值剪应力（位移）及应力降随一阶起伏角变大而分别增大、近似线性增大（减小）及先增大后减小；相同一阶起伏角下,其则随法向压力变大而分别增大、均近似线性增大及增大（锯齿状）或先增大后减小（波浪状）。②结构面宏细观损伤演化过程经历初始压密非线性变形（压密效应）、近似线弹性压剪变形（爬坡效应）、缓慢压剪断裂非线性变形（爬坡-啃断效应）、应力脆性跌落塑性变形（啃断效应）及理想塑性流动变形（滑移效应）5个发展阶段。③结构面宏细观剪切破坏模式可概化为压密-爬坡破坏、爬坡-啃断破坏及啃断-滑移破坏3种基本类型；结构面细观损伤裂纹数量（能量）演化曲线均呈初期微增、中期陡增及后期缓增的阶段性变化特征,且细观损伤颗粒近似呈“梯形面状”分布于结构面附近。④根据极限平衡法和强度折减法,通过岩质边坡算例稳定性分析验证了结构面剪切强度估算公式的合理性。
- 岩体结构面形态 /
- 直剪试验 /
- PFC^2D /
- 宏细观剪切力学行为 /
- 剪切强度估算公式
Abstract: To investigate the macro-meso shear mechanical behaviors of coalescent saw-tooth (wavy) rock joints considering the impact of the first-order (second-order) asperities, the laboratory direct shear tests and PFC^2D numerical simulations are conducted. The results indicate that: (1) The macro-damage mass increases, the peak shear stress (displacement) approximately linearly increases (decreases) and the stress drop increases first then decreases as the first-order undulant angle increases under the same normal stress. The macro-damage increases, the peak shear stress (displacement) approximately linearly increases, and the stress drop increases (saw-tooth) or increases first then decreases (wavy) as the normal stress increases under the same first-order undulant angle. (2) There are five stages in the macro-meso damage evolution process, i.e., initial nonlinear deformation (compacting effect), approximately linear-elastic deformation (climbing effect), nonlinear deformation due to compression-shear fracture (climbing-gnawing effect), plastic deformation due to a drop in the brittle stress (gnawing effect) and ideal plastic flow deformation (sliding effect). (3) The macro-meso shear failure modes include compacting-climbing failure, climbing-gnawing failure and gnawing-sliding failure. The curves of the meso-damage crack quantity (energy) include three stages, i.e., a slight, steep and slow increase in the initial, middle and later stages, respectively, and the meso-damage particles are distributed near the rock joints in an approximately "trapezoidal-shape". (4) According to the limit equilibrium and strength reduction methods, the rationality of shear strength estimation formulas for the rock joints is verified through the stability analysis of rock slope examples.
- morphology of rock joints /
- direct shear test /
- PFC^2D /
- macro-meso shear mechanical behavior /
- shear strength estimation formula

HTML全文

0. 引言

中国幅员辽阔,地质条件复杂多样,在复杂地层条件下,隧道支护体系的可靠设计是保证隧道安全施工的重要前提。目前对于支护结构的设计多依赖于工程经验,缺乏必要的理论支撑,而工程案例数量的有限性、工程条件的局限性以及工程经验的可靠性都将使得经验设计方法受到极大限制^[1]。因此,对支护设计理论的研究极为必要,不仅能为隧道安全施工提供指导,也为隧道运营期间支护结构的有效运作提供科学依据。

目前工程中常用的隧道支护设计方法包括经验设计法、理论分析法以及现场监测法等3种^[2]。经验设计法即根据以往工程经验,提供一套系统的设计建议和干预方案,该方法往往基于对岩土体的地质力学特性进行分级,因此围岩分级方法得以广泛使用^[3-5]。理论分析法是指通过解析或数值方法,获取围岩和支护结构的应力应变状态,进而对隧道安全性进行评价,并设计必要的支护结构来维持隧道稳定^[6-8]。现场监测法即通过在项目规划、设计和施工中的监测数据及时反馈修正设计方案^[9]。以上3种设计方法均能为隧道设计提供有利信息,并在一定程度上支撑了隧道支护设计理论的发展。但当前研究表明^[10],隧道支护结构体系各子构件之间存在相互作用关系,当其协同工作时可使得支护效率最高,而目前的隧道设计方法均未考虑支护体系之间的协同效应。

在隧道设计中,工程安全性和经济性往往相互矛盾,而支护体系的协同设计目标在于以最小的支护代价实现最佳的围岩稳定性控制效果,本质上为多目标优化问题。但目前对于隧道支护体系的协同效应尚无系统完整的认识,对于支护结构体系的多目标优化方法亦处于探索阶段,因此也给支护设计的定量化带来困难。

本文首先构建隧道围岩协同支护系统,阐明隧道支护体系协同作用构成、研究层次及其表征参数,建立基于加权表征的多目标问题隶属度转化方法,由此提出隧道支护体系协同设计原则与方法,并将该方法应用于新建京张高铁八达岭长城站大跨过渡段,可为隧道支护结构体系的协同优化提供一种思路。

1. 隧道围岩协同支护系统

1.1 协同支护系统的构成与层次

所谓协同,指的是多个不同的资源或个体,协调一致地完成某一目标的过程或能力^[11]。就隧道围岩安全性而言,协同支护的目标在于以最小的支护代价实现最佳的围岩稳定性控制效果。因此,隧道围岩协同支护是以围岩工程响应和支护作用机理为基础,以协同学的基本原理和方法为指导,研究隧道围岩稳定性控制过程中支护—围岩系统的协同作用及其演化机制。在此过程中以围岩变形控制为核心,通过支护系统的合理设计和优化实现隧道支护—围岩系统的协同作用,充分发挥支护和围岩的力学性能,使系统功能在宏观整体上大于各子系统之和,即产生“1+1>2”的协同支护效应,从而降低隧道围岩失稳和结构失效概率,保证隧道全寿命周期的正常使用功能。这是协同支护与组合支护或联合支护的本质区别所在^[12]。

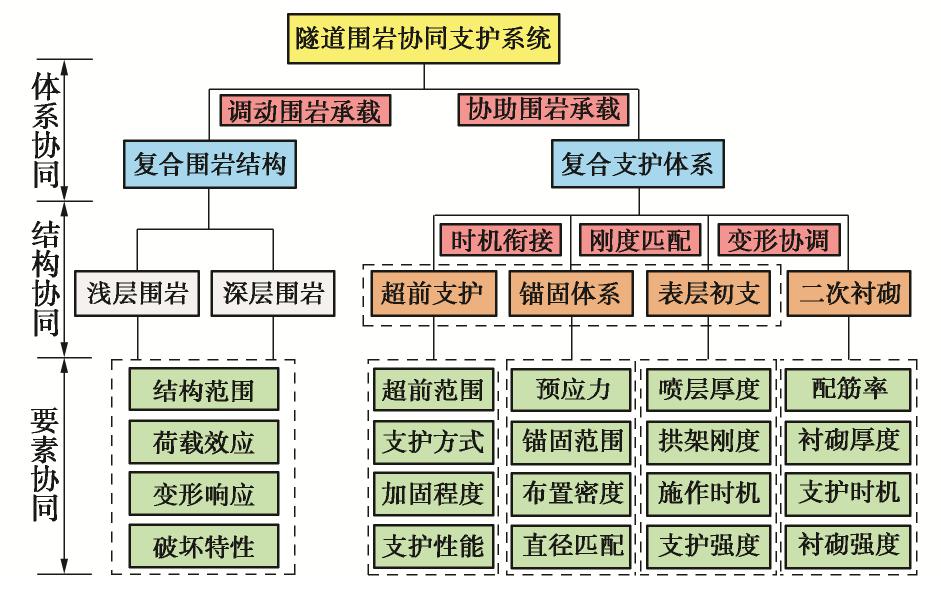
隧道支护体系的协同作用包括支护结构与围岩的协同、不同支护形式之间的协同以及支护结构各要素的协同等3个层面,如图1所示。

图 1 隧道围岩协同支护系统的基本组成

Figure 1. Basic composition of synergistic support system in surrounding rock of tunnels

下载: 全尺寸图片幻灯片

隧道围岩协同支护系统由支护系统与围岩系统两大子系统组成,二者之间的体系协同即隧道支护—围岩动态作用关系,由此可确定隧道围岩变形控制标准,是隧道支护设计的基本前提。超前支护和初期支护为支护系统的下一级子系统,其中初期支护按其承载机制又划分为锚固体系和表层初支^[10],通过各自目标的实现促使围岩尽快达到稳定,而二次衬砌则保障围岩长期安全。不同支护之间的结构协同使得子系统的功能发挥至最佳,是支护设计的重要依据。各支护构件的承载性能由多个要素决定,不同要素之间存在着必然的内在联系,而要素协同则能最大程度地发挥构件性能,是隧道支护体系协同优化的核心内容。

1.2 协同支护研究内容与表征参数

根据隧道施工过程原理,不同支护构件先后施作并与围岩相互作用,最终形成隧道支护体系。当协同支护得以实现时,整个支护系统内部形成一种分工明确、协调配合、联动互补的动态平衡状态。因此,结合隧道支护的本质作用特性,协同支护系统特征表现为支护时机衔接、刚度匹配以及变形协调,其中前两者为协同支护的工作方式,后者为工作状态。即以支护时机的衔接和支护刚度的匹配为基础,以现场施工质量为保障,从而达到支护—围岩系统的变形协调,实现协同支护效应。

在协同支护系统中,围岩条件客观存在,支护体系为工作方法,可供选择的空间较大,是协同支护的控制性因素,也是本文研究的重点内容。从隧道支护—围岩作用机制出发,协同支护主要研究3个方面的内容：一是以围岩为主体研究对象,研究围岩系统在支护作用下的力学响应；二是以支护体系为研究对象,研究各支护构件之间的相互作用对于支护体系工作性能的影响机制；三是以支护—围岩系统为研究对象,研究系统的协同作用机理、状态及其影响因素。

隧道支护—围岩作用过程中,围岩稳定性的表征参数为“围岩变形”^[1],而促使围岩由开挖后的不稳定结构迅速变成整体稳定结构的内驱力则是“支护阻力”。可见,“围岩变形”和“支护阻力”贯穿于隧道工程活动的始终,是研究协同支护的标志性参数。

2. 协同优化基本原理

隧道支护体系协同优化的本质上是非线性多目标优化问题。在最优化问题中,对于具有m个目标、n个设计变量的多目标优化问题可表示为如下数学模型：

$\begin{array}{l} \min f (x) = [f_{1} (x), f_{2} (x), \dots, f_{m} (x)] \\ s .t . g_{j} (x) \leq 0, j = 1, 2, \dots f \\ h_{k} (x) = 0, k = 1, 2, \dots g \end{array}$ ,

(1)

式中, $x = (x_{1}, x_{2}, \dots x_{n}) \in R^{n}$ , $x$ 为设计变量, $R^{n}$ 为设计变量 $x$ 所张成的决策空间, $f_{i} (x)$ : $R^{n} \to R$ 表示第k个目标函数, $f (x)$ 为目标函数所张成的准则空间； $g_{j} (x)$ 和 $h_{k} (x)$ 分别表示第j个不等式约束条件和第k个等式约束条件,f和g为两种约束条件个数,这两种约束条件即构成了可行域。

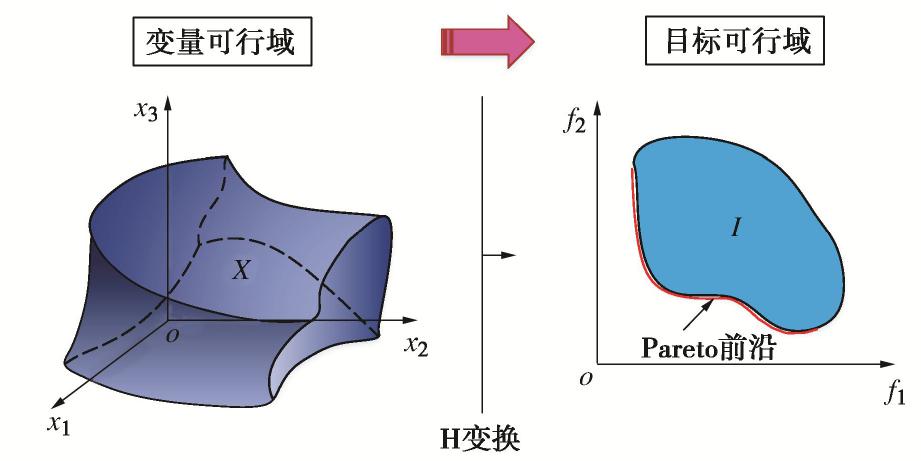
定义 $Ω = {x \in R^{n} | g (x) \leq 0, h (x) = 0}$ 为变量可行域, $I = {z \in R^{m} | z = f (x), x \in Ω}$ 为目标可行域,则根据目标函数的概念, $I$ 为 $Ω$ 通过空间变换H： $R^{n} \to R^{m}$ 所成的像,如图2所示。

图 2 多目标优化基本原理

Figure 2. Basic principle of multi-objective optimization

下载: 全尺寸图片幻灯片

在多目标优化设计中,对其中某一目标进行优化时必将牺牲其他目标为代价,对于总体目标存在多个最优折中解,又称为Pareto最优解。判断向量 $x^{*} \in Ω$ 为Pareto最优解的依据为不存在 $x \in Ω$ 使得 $f (x) <$ $f (x^{*})$ 。

由于准则空间I是部分有序的,若想从所有可行解中找出最满意的解答,则需补充额外的判定条件。一般采用l_p度量方法（又称明氏距离）来衡量不同空间点及其与参考点 $f^{id}$ 之间的距离,其表达式为^[13]

$d_{p} (z, y) = {\begin{cases} {(\sum_{i = 1}^{m} {| z_{i} - y_{i} |}^{p})}^{1 / p} (1 \leq p < \infty) \\ \max_{i = 1, 2, \dots m} | z_{i} - y_{i} | (p = \infty) \end{cases}$ ,

(2)

式中, $z$ 和 $y$ 为准则空间内两个不同的点, $z_{i}$ 和 $y_{i}$ 分别为不同设计变量取值。

参考点 $f^{id}$ 此处取为绝对最优解,即

$z^{id} = {\begin{matrix} \min_{x \in Ω} f_{1} (x) & \min_{x \in Ω} f_{2} (x) & \dots & \min_{x \in Ω} f_{m} (x) \end{matrix}}$ 。

(3)

显然, $f^{id}$ 可通过对m个单目标问题进行求解得到,如此则可将最优化问题转化为寻找准则空间内与参考点距离最小的可行解,即

$\min_{z \in I} d_{p} (f, f^{id})$ 。

(4)

3. 基于分组加权的目标函数隶属度转化方法

3.1 目标函数的分组加权法

在传统的多目标优化过程中,往往会事先对各目标进行重要性评估,进而对各目标赋予相应权重,采用线性加权法简化计算,则多目标优化问题可写为^[14]

$\min_{z \in I} ρ_{p} (f, ω, v) = {\begin{cases} \min_{f \in I} {[\sum_{i = 1}^{m} {(ω_{i} | f_{i} - f_{i}^{i d} |)}^{p}]}^{1 / p} (1 \leq p < \infty), \\ \min_{f \in I} \max_{i = 1, 2, \dots m} ω_{i} | f_{i} - v_{i} | (p = \infty), \end{cases}$

(5)

式中, $v$ 为设计者自主决定的限值, $ω$ 为权重向量, $ω = {\begin{matrix} ω_{1} & ω_{2} & \dots & ω_{m} \end{matrix}}$ 且 $\sum_{i = 1}^{m} ω_{i} = 1$ 。

对于高维度多目标优化方法,传统Pareto支配关系对最优解的选择压力衰减严重,计算结果的收敛性和多样性亦难以同时保证,从而给决策方案的制定带来困难^[15-16]。在工程中一般需要采取目标降维方法再行计算。为此,本文将传统线性加权方法进一步拓展,提出分组加权法的思路,即将原始目标按照主要矛盾进行分组,从而使得组内目标重要性程度基本相当,而组间目标矛盾突出,进一步将各组重要性进行排序并依次求解。据此可将m维多目标问题降为k维,即

$\min_{x \in Ω} f_{k} (x) = \min_{x \in Ω} {\begin{matrix} \sum_{i = r_{0} + 1}^{r_{1}} λ_{i} f_{i} (x) & \sum_{i = r_{1} + 1}^{r_{2}} λ_{i} f_{i} (x) & \dots & \sum_{i = r_{k - 1} + 1}^{r_{k}} λ_{i} f_{i} (x) \end{matrix}},$

(6)

式中,显然有 $r_{0} = 0$ 且 $r_{k} = m$ 。对于多目标系统决策,要求目标权向量满足 $\sum_{i = r_{α - 1} + 1}^{r_{α}} λ_{i} = 1, α = 1, 2, \dots, k$ 。

现说明降维前后多目标问题解的关系,以 $P_{m}$ 和 $P_{k} (λ^{k})$ 分别表示降维前后多目标问题 $P_{m}$ 和 $P_{k}$ 的解, $λ^{k} = {\begin{array}{l} \begin{matrix} λ_{1} & λ_{2} & \dots & λ_{r_{1}} \end{matrix} & ⋮ & \begin{matrix} λ_{r_{1} + 1} & \dots & λ_{r_{2}} \end{matrix} & ⋮ & \begin{matrix} λ_{r_{k - 1} + 1} & \dots & λ_{r_{k}} \end{matrix} \end{array}}$ ,令 $x^{*} \in P_{k} (λ^{k})$ ,则有

$\sum_{i = r_{α - 1} + 1}^{r_{α}} λ_{i} f_{i} (x^{*}) \leq \sum_{i = r_{α - 1} + 1}^{r_{α}} λ_{i} f_{i} (x) (α = 1, 2, \dots k)$ 。

(7)

若存在 $x \in Ω$ 使得

$f_{i} (x) \leq f_{i} (x^{*}) (i = 1, 2, \dots m)$ 。

(8)

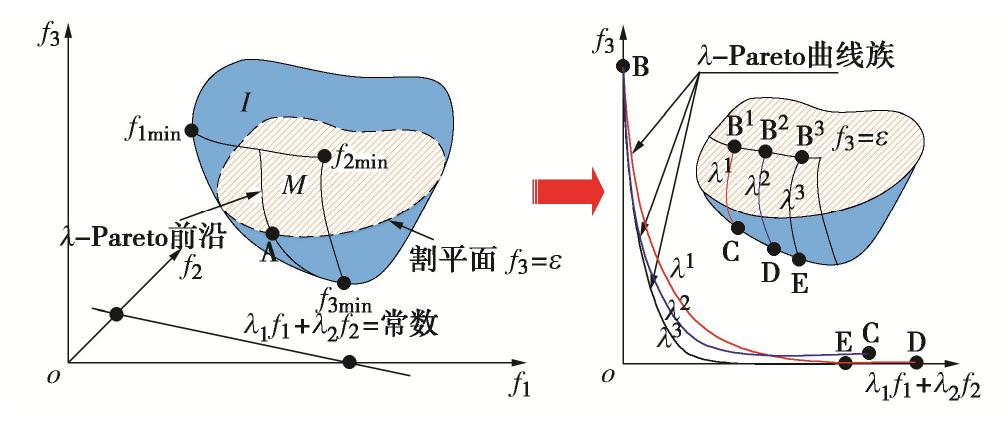
则式（8）中不等式必然取等号,否则将与式（7）矛盾,这便意味着 $x^{*} \in P_{m}$ ,如此则有 $P_{k} (λ_{k}) \subset P_{m}$ ,即问题 $P_{k}$ 的解必然是 $P_{m}$ 的解。但由于降维后的问题得到了仅是原始问题的子集,为了得到满足决策者需求的最优解,权重向量 $λ^{k}$ 的确定就显得尤为重要。事实上,对于多目标凸规划问题,存在 $\cup_{λ^{k}} P_{k} (λ^{k}) = P_{m}$ ,这与传统线性加权法的结论是一致的。以三目标规划问题为例,图解说明本文分组加权法的优势,如图3所示。假定可行解集形状规则,图中M表示该问题的Pareto前沿,其角点对应于各目标达到最小值。

图 3 三目标分组加权法的几何解释

Figure 3. Geometric interpretation of three-objective grouping weighting method

下载: 全尺寸图片幻灯片

将前两个目标进行线性组合,并定义半空间 $S_{H} = {f \in R^{3} | f_{3} \leq ε}$ ,则可将该问题简化为

$\min_{f \in I} {λ_{1} f_{1} + λ_{2} f_{2} f_{3}} = \min_{f \in I \cap ε} {λ_{1} f_{1} + λ_{2} f_{2}}$ 。

(9)

式（9）为线性函数,其最小值即为该问题解答。若以约束值 $ε$ 为变量可得到完整的 $λ$ -Pareto前沿曲线,而对于确定的权重向量则可得到最优解,即图3中点A。相应地,改变权重向量即可得到 $λ$ -Pareto曲线族,从而覆盖整个M区域。可见,经过降维处理后计算过程得到极大简化,且计算结果更为简洁,决策者可通过直观图解法来寻求最优解,决策过程更为清晰。

3.2 目标可行域的隶属度转化

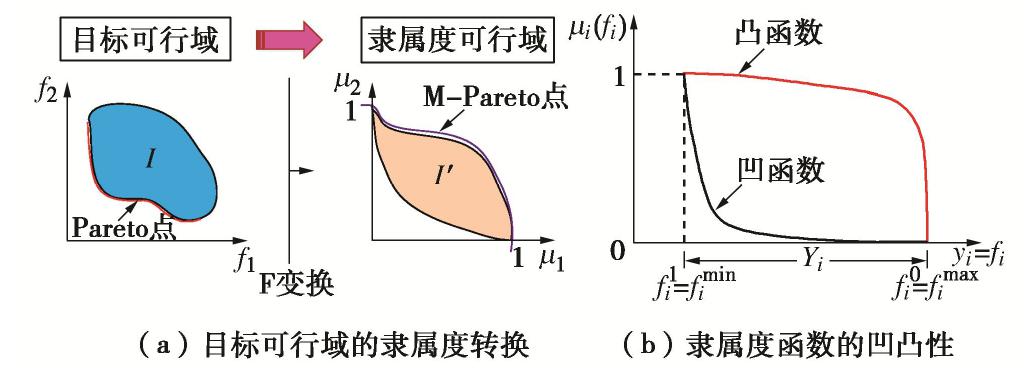
考虑到决策者其对于各目标函数往往存在一定期望值,为此,本节提出基于目标函数分组加权的隶属度转化方法。令 $μ_{i} (f_{i})$ 为第i个降维后目标函数的隶属度值,其取值区间为[0,1]且越趋近于1表明该目标对应解满意程度越高。当降维后的k个隶属度关系确定时,目标可行域可通过空间变换F： $I \subset R^{k} \to R^{k}$ 映射至隶属度可行域,如图4所示,则I通过F形成的像为 $I^{'} = {[μ_{1} (f_{1}), μ_{2} (f_{2}), \dots, μ_{i} (f_{i})] | f \in I}$ 。隶属度关系的确定原则为,若对某一目标函数严格要求,则相应的隶属关系为凸函数,而对于相对宽松的目标则对应凹形隶属度函数,见图4（b）。

图 4 多目标优化问题的隶属度表征方式

Figure 4. Membership representation of multi-objective optimization problem

下载: 全尺寸图片幻灯片

显然,根据决策者的偏好要求,隶属度关系的选取也势必导致最终决策方案的差异。当某一目标函数的最小值 $f_{i}^{\min}$ 和最大值 $f_{i}^{\max}$ 确定时,通过隶属度关系即可得到相应的隶属度值,进而通过明氏距离可对最优解的优劣性进行判断,即

$d_{p} (μ, \bar{μ}) = {\begin{cases} {(\sum_{i = 1}^{m} {| μ_{i} - \bar{μ_{i}} |}^{p})}^{1 / p} (1 \leq p < \infty) \\ \max_{i = 1, 2, \dots m} | μ_{i} - \bar{μ_{i}} | (p = \infty) \end{cases}$ 。

(10)

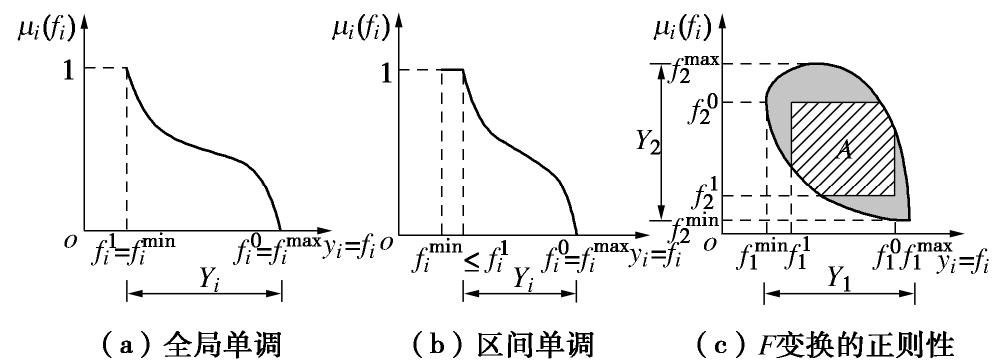
将通过隶属度转换后的最优解称为M-Pareto解,为了明确M-Pareto解与Pareto解的关系,以双目标优化问题为例,考虑如下两种情况：①各隶属度函数在区间 $Y_{i} = [f_{i}^{\min}, f_{i}^{\max}]$ 严格单调递减；②至少有一个隶属度函数仅在子区间 $[f_{i}^{1}, f_{i}^{0}]$ 内单调递减,而在其他区间内为常数,如图5所示。

图 5 隶属度函数的单调性及其影响

Figure 5. Monotonicity of membership function and its influence

下载: 全尺寸图片幻灯片

对于第一类问题,各隶属度函数在整个区间内均可逆,变换F的雅克比行列式处处不为零,因而F及其逆F^-1均为正则变换,此时位于可行域I前沿上的点通过F变换形成的像也位于 $I^{'}$ 前沿上,即各Pareto点必然是M-Pareto点。同理,由隶属度函数的单调性可知,若某点 $P = [f_{1} (x_{1}), f_{2} (x_{1})]$ 位于I的边界上但非Pareto解,则 $x_{1}$ 也不是M-Pareto解。由于F与F^-1均为正则变换,因此I与 $I^{'}$ 为同构空间,可见目标函数的隶属度变换将不会影响最优解的搜索范围。而对于第二类问题,各隶属度函数仅在子区间 $[f_{i}^{1}, f_{i}^{0}] \subset Y_{i}$ 内可逆,因此F仅在子集 $A \subset I$ 内为正则变换,而F的以上属性也仅在子空间A内成立,见图5（c）。

3.3 决策唯一性及其影响因素

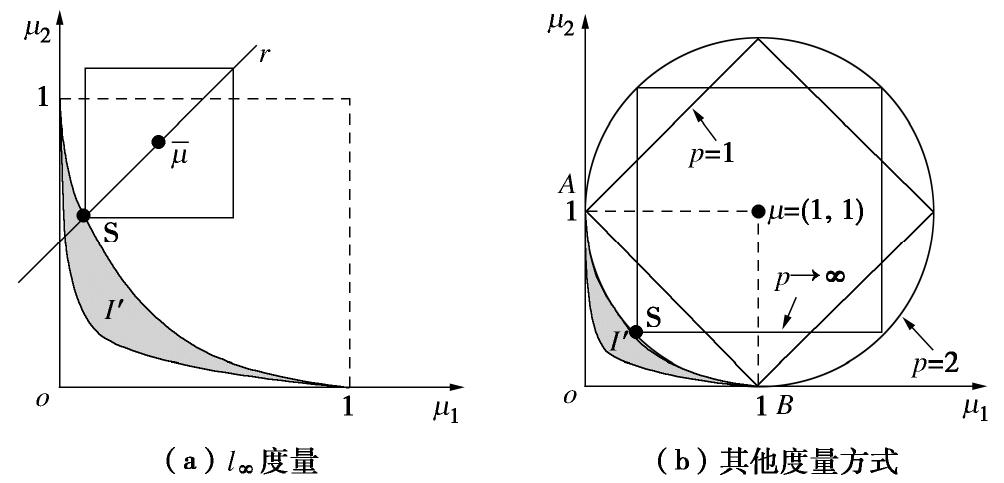
由于隶属度函数的引入,优化过程无疑将增加一个环节,决策结果的唯一性也将受到度量方式、参考点、目标函数以及隶属度函数等四个因素的综合影响^[17],以下将分别进行分析。

（1）度量方法的影响

假定各目标均为单叶函数,则采用 $l_{\infty}$ 度量方式时总能找到唯一的最优解,如图6（a）所示。事实上,无论参考点 $\bar{μ}$ 取何值,过参考点且倾角为45°的直线r与M-Pareto前沿总存在唯一交点S即为最优解。而采取其他度量方式时解的唯一性将无法保证,见图6（b）,当 $p = 1$ 时点A和点B距参考点距离相同,但均非折中解答,而当 $p = 2$ 时各M-Pareto点均有可能为最优解。由此可见,度量方法的选取应与目标函数相适应,否则将无法得到满意的最优解。

图 6 采用不同度量方式时M-Pareto解的唯一性特点

Figure 6. Uniqueness of M-Pareto solution with different measures

下载: 全尺寸图片幻灯片

（2）参考点的影响

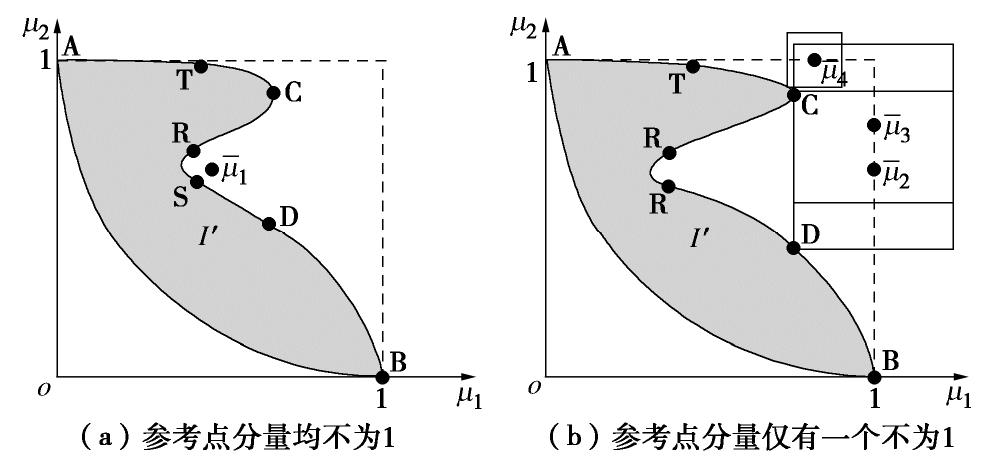
当目标函数存在局部极小值时,若 $\bar{μ}$ 取值较为随意,则可能出现局部M-Pareto最优解被其他可行解占优的情况,如图7（a）所示。

图 7 参考点的选取对最优解唯一性的影响

Figure 7. Influences of selection of reference points on uniqueness of optimal solution

下载: 全尺寸图片幻灯片

当参考点为 ${\bar{μ}}_{1}$ 时,点S为局部M-Pareto点,但无论从哪个目标函数看,点R和点T都占优于点S。而当参考点中仅有一个分量不为1时,至多仅有两个点C和D同时满足要求,且C为M-Pareto点,而一般而言仅能找到一个距其最近的点且必然为M-Pareto解,如图7（b）所示。因此,当至少有一个目标函数出现局部极小值时,为了保证M-Pareto解的满意度,参考点 $\bar{μ}$ 应至多仅有一个分量 ${\bar{μ}}_{i}$ 不为1。

（3）目标函数的影响

当目标函数在某个区间内 $[x_{1}, x_{2})$ 为常数时,由于F的正则性,该区间在隶属度空间内的像也为常数,则该段不存在M-Pareto点,当M-Pareto前沿曲线关于某一目标函数为常数且参考点在该方向分量为1时,其他方向将存在无穷种可能使得 $l_{\infty}$ 度量与该段重合,而相应的解答也可取为 $[x_{1}, x_{2})$ 区间内的任一点。

（4）隶属度函数的影响

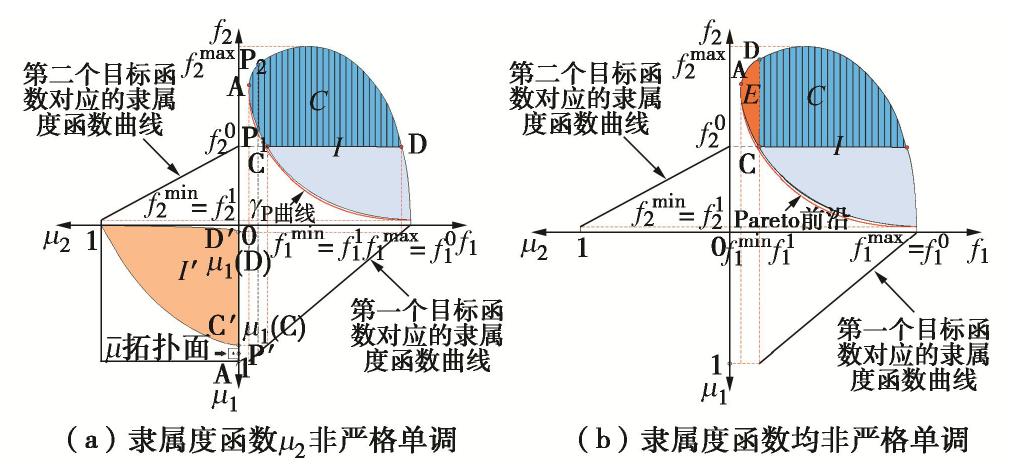
假定目标函数单叶,令 $f_{2}^{0} < f_{2}^{\max}$ ,则隶属度函数 $μ_{2}$ 非严格单调函数。集合C的各竖条微元映射至隶属度空间内的像为单一点,如图8所示,P₁P₂段通过F变换在隶属度空间内形成的像为点 $P^{'}$ , $(A^{'}, C^{'}]$ 段为I中各垂直段包含Pareto前沿的映射。

图 8 隶属度函数的选择对最优解唯一性的影响

Figure 8. Influences of choice of membership function on uniqueness of optimal solution

下载: 全尺寸图片幻灯片

当参考点 $\bar{μ}$ 确定时, $\bar{μ}$ 拓扑面与 $(A^{'}, C^{'}]$ 段将存在无数交点,则无法确定最优解。如 $f_{2}^{0} < f_{2}^{\max}$ 时解x的相关结果完全不满足决策需求,此时决策者倾向于得到其他目标函数的高满意度解答,如此则将以牺牲 $f_{2}$ 为代价。鉴于目标函数 $f_{2}$ 的上述判断结果,导致大量解答关于 $f_{2}$ 的满意度极低,且无法判定其优劣性。而当 $f_{1}^{1} > f_{1}^{\min}$ 时,二维子集E在隶属度空间内的像为同一点,如此则在存在无穷解,如图8（b）所示。

4. 隧道支护体系协同设计流程及原则

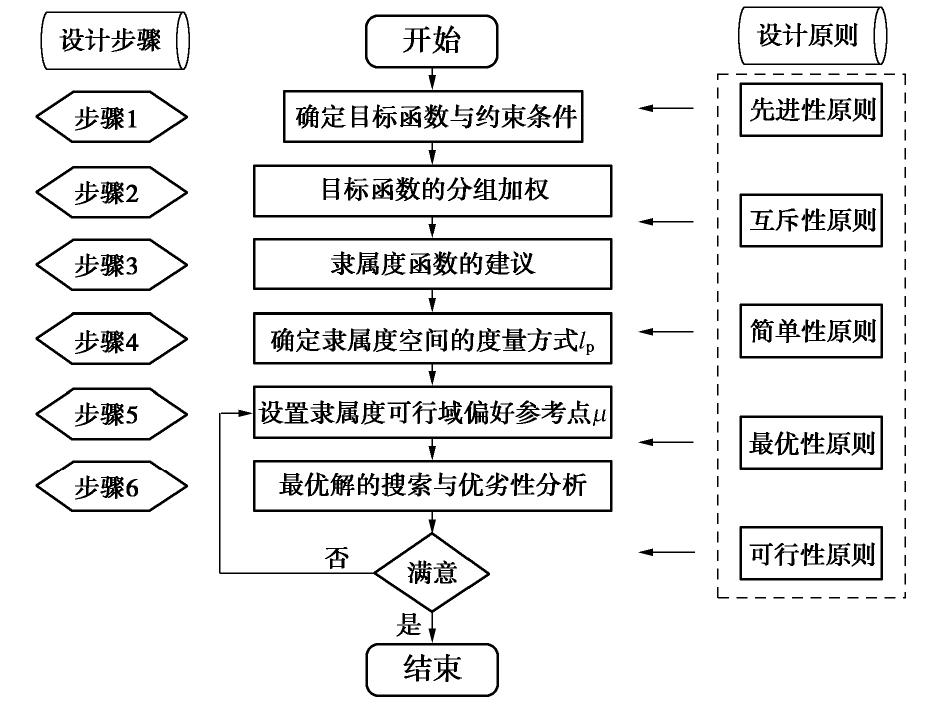
隧道支护体系基本功能为控制围岩稳定,故以围岩变形、支护受力以及支护成本为目标,建立支护体系优化设计方法,而支护受力又包括不同支护构件所承担荷载,因此为高维多目标优化问题。考虑到不同支护结构的受力具有目标一致性,可将其按一定规律组合后构建新的目标函数,由此实现目标降维。根据前文提出的基于分组加权的目标函数隶属度转化方法,确定隧道支护设计的最优化设计流程如图9所示。

图 9 多目标协同优化设计流程

Figure 9. Multi-objective synergistic optimization design process

下载: 全尺寸图片幻灯片

（1）多目标优化模型的建立。首先明确隧道设计多目标优化要素,构建多目标优化模型。在此阶段,应尽量保证所建立目标函数的先进性,这也是保证隧道最终设计方案科学性和合理性的关键。事实上,目前的工程实践往往落后于理论发展水平,如二次衬砌作为安全储备的设计理念已提出30余年,而具体如何正确实现则在近年才得到诠释^{[10, 18]}；无独有偶,岩爆防控理论也比其在矿山与隧道工程中的应用早10余年^[19]。因此,科学的设计方案应基于先进的设计理论,创建现有先进技术与工程实践的桥梁。

（2）目标函数的分组加权。基于主要矛盾对目标函数进行分组,根据组内各目标的重要程度及属性差异赋予相应权重,从而构建新的多目标问题 $P_{k}$ ,并将目标函数组按决策偏好进行排序。此外,在分组时可以单一准则（如工程成本）作为独立组别,而当 $k = 1$ 时则对应传统的线性加权法。此步骤为多目标优化问题降维处理的核心,需满足互斥性原则,而其关键则在于各目标权重的准确确定。

（3）隶属度函数的建立。以降维后的多目标问题 $P_{k}$ 为基础,根据设计者的需求选择相应的隶属度函数,构建隶属度空间,从而将目标函数转换为无量纲的隶属度值,便于决策者进行比较和判断。为保证计算过程的收敛性,隶属度函数的选取应遵循简单性原则,同时应结合前文中决策唯一性影响规律进行确定。

（4）确定度量方式 $l_{p}$ 。为了比较各可行解的优劣性,需采用相应的度量方式。工程中常用曼哈顿距离（ $p = 1$ ）、欧氏距离（ $p = 2$ ）或切比雪夫距离（ $p = \infty$ ）来进行衡量,合理的度量方式应根据隶属度空间的属性进行选取,不仅应保证M-Pareto解的多样性,也应便于决策者选择符合其偏好的满意解。

（5）设置参考点。参考点为决策者的确定偏好策略,表征k维目标的最理想状态,可使得算法所得解集有效收敛到偏好区域。一般地,各目标分量可取为1,而当各目标之间矛盾较为突出时应适当牺牲次要目标,如对于围岩条件极差的隧道工程,隧道安全性为首要目标,此时可适当降低经济性要求,即经济性指标分量取小于1值。

（6）最优解的搜索与优劣性分析。对式（10）进行求解,从而得到该多目标问题的最优解,若所得最优解满足决策者需求且切实可行,则将其作为最终决策方案,否则返回步骤（5）重新计算。需要指出,此处的最优性原则不仅指所得解的理论最优性,还应进一步考虑施工难度,基于目前施工水平选择最优方案。

5. 工程应用

5.1 工程概况

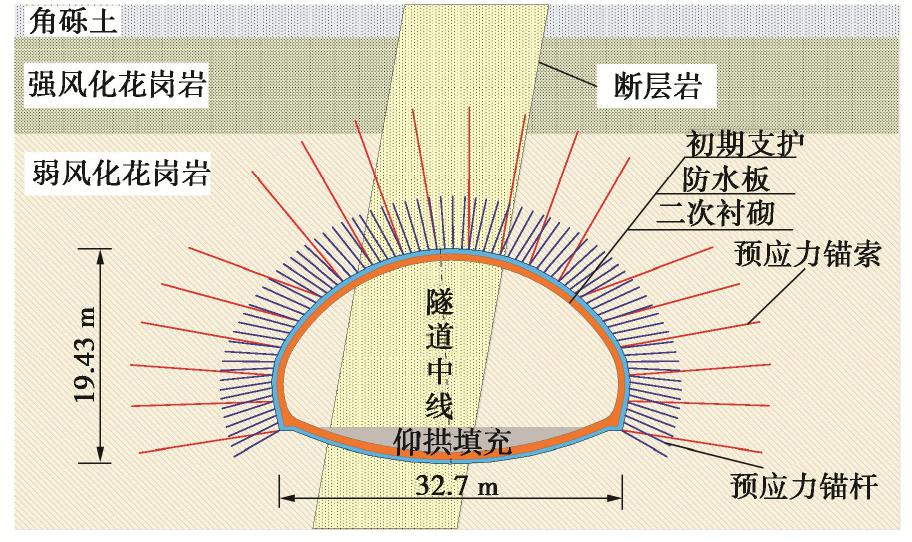
京张高铁是中国《中长期铁路网规划》中“八纵八横”高速铁路网“京兰通道”和“京昆通道”的重要组成部分,是世界上第一条智能化高速铁路。线路总体呈南东—北西走向,全长174 km,共设10个车站。其中八达岭长城站作为全线唯一的地下车站,最大埋深达102 m,是目前中国埋深最大的高速铁路地下车站。长城站两端通过163 m的大跨过渡段与正线隧道连通,其中张家口侧起讫里程为DK68+285— DK68+448,最大开挖跨度为32.7 m,开挖面积达494.4 m²,是目前世界上开挖跨度最大的高速铁路隧道,工程建设风险高,成为该项目的控制性工程。

本文选取DK68+285—DK68+305进行研究,隧道典型横断面如图10所示。隧道主要穿越3种典型地层,其中地表为角砾土；上部为强风化花岗岩,岩芯呈短柱状或块状,一般节长8～54 mm；其下部为弱风花岗岩,岩芯呈长柱状,一般节长11～27 cm。隧道穿越一条断层破碎带,其产状为236°∠80°,为一压扭性断裂,上盘为花岗岩,下盘为斑状二长花岗岩,断层带内为压碎岩。将地勘资料转化为Hoek-Brown准则参数,如表1所示。表中,m_b,s和a为岩体材料参数。

图 10 新八达岭隧道V级围岩段典型断面与地层分布

Figure 10. Typical section and stratigraphic distribution of section of grade V surrounding rock of new Badaling tunnel

下载: 全尺寸图片幻灯片

表 1 地层物理力学参数

Table 1. Physical and mechanical parameters of ground

地层名称	重度γ/(kN·m^-3)	泊松比μ	弹性模量E/GPa	单轴抗压强度σ_ci/MPa	m_b	s/10^-5	a
角砾土	20	0.30	0.447	20	0.175	1.20	0.561
强风化花岗岩	22	0.30	0.570	23	0.504	1.79	0.550
弱风化花岗岩	25	0.25	0.958	29	0.843	4.54	0.531
断层岩	20	0.30	0.447	20	0.437	1.20	0.561

下载: 导出CSV

| 显示表格

隧道拱顶埋深100 m,围岩级别为V级,围岩稳定性差,采用复合式衬砌结构进行设计。超前支护为掌子面玻璃纤维锚杆,由于其最终将被清除,故此处仅对初期支护和二次衬砌进行优化。根据现场施工资料,初期支护封闭成环时距掌子面距离约为10 m,而二次衬砌支护时机约为60 m,支护参数如表2所示。

表 2 新八达岭隧道支护体系设计参数

Table 2. Design parameters for support of new Badaling tunnel

支护形式	支护参数
锚杆	直径d_b=32 mm,长L_b=11 m,间距S_cb=1.2 m,排距S_lb=0.8 m,预应力F_sb=100 kN
锚索	7Φ15.2 mm钢绞线,长L_c=25 m,间距S_cc=排距S_lc=2.4 m,预应力F_sc=1000 kN
喷射混凝土	C30喷射混凝土,厚度t₁=35 cm,弹性模量E₁=25 GPa
钢架	4Φ22钢格栅,间距为S_s=0.8 m/榀,等效弹性模量E_s=2.66 GPa
二次衬砌	C35现场模筑混凝土,厚度t₂=60 cm,弹性模量E₂=30 GPa

下载: 导出CSV

| 显示表格

5.2 多目标优化要素

考虑到在对支护参数进行优化时隧道往往已开始施工,为使得本文计算结果更具有可操作性,对支护形式中的易变更参数进行优化,具体如表3所示。

表 3 待优化支护参数

Table 3. Parameters for support to be optimized

支护形式	锚杆	锚索	喷射混凝土	钢架	二次衬砌
协同优化参数	间距S_cb,排距S_lb	间距S_cc,排距S_lc	厚度t₁	间距S_s	厚度t₂

下载: 导出CSV

| 显示表格

假定锚固构件矩形布置且S_c=S_l,研究表明,当锚固构件间距小于0.5 m时将会破坏岩体完整性,且工程施工难度较大。此外,Hoek和Brown指出锚杆间距最大值与锚杆长度、节理间距J_s等因素有关^[20]。因此,锚杆间距的约束条件为

$\begin{array}{l} 0.5 m \leq S_{c} \leq S_{m}, \\ S_{c} = 0.5 + 0.1 n, n = 0, 1, 2, \dots, \\ S_{m} = \min {L / 2, (1.5 J_{s}, J_{s} \geq 0.5 m), 2 m} 。 \end{array}}$

(11)

对于锚索间距约束条件仍采取上式,而区别在于式（11）第3式中无2 m的限制。根据规范^[21],喷射混凝土厚度的约束条件为

$5 cm \leq t_{1} \leq 35 cm$ 。

(12)

钢架间距的约束条件为

$\begin{array}{l} 0.5 m \leq S_{c} \leq 1.5 m, \\ S_{c} = 0.5 + 0.25 n (n = 0, 1, 2, \dots) 。 \end{array}}$

(13)

二次衬砌通常为现场模筑混凝土,此处考虑为素混凝土,为了施工方便,其约束条件应满足：

$\begin{array}{l} 25 cm \leq t_{2} \leq 100 cm, \\ t_{2} = 25 + 5 n, n = 0, 1, 2, \dots 。 \end{array}}$

(14)

各支护构件成本可表示为

$\begin{array}{l} 锚固构件 \to c_{b,c} = 2 π r_{0} P_{b,c} L_{b,c} / (S_{cb,c} S_{lb,c}), \\ 喷射混凝土 \to c_{1} = 2 π r_{0} P_{1} t_{1}, \\ 钢架 \to c_{s} = 2 π r_{0} ρ P_{s} A, \\ 二次衬砌 \to c_{2} = 2 π r_{0} P_{2} t_{2} 。 \end{array}}$

(15)

式中 $P_{b,c}$ 为锚固构件每延米的钻孔和支护成本,下标b和c分别代表锚杆和锚索； $P_{1}$ 为喷射混凝土每方支护成本； $P_{s}$ 为钢架每延米支护成本, $ρ$ 为钢筋密度, $A$ 为钢架横截面积； $P_{2}$ 为每方混凝土结构的造价, $t_{2}$ 为二次衬砌厚度。

因此,隧道支护成本目标函数可表示为

$c = c_{b} + c_{c} + c_{1} + c_{s} + c_{2}$ 。

(16)

5.3 基于分组加权的目标函数隶属度转化

隧道支护体系多目标优化问题为

$\min_{x \in Ω} f (x) = \min_{x \in Ω} {\begin{matrix} u_{r} & p_{1} & p_{2} & p_{3} & p_{4} & p_{5} & c \end{matrix}}$ 。

(17)

式中, $p_{i}$ （ $i = 1, 2, \dots, 5$ ）分别为锚杆、锚索、喷射混凝土、钢架和二次衬砌受力,可根据文献[22～24]确定。

显然,式（17）为七维多目标优化问题,为使得计算结果收敛需对其进行降维。由于各支护构件的受力本质矛盾不突出,可划分为同一目标,基于前文提出的分组加权思想可将式（17）写为

$\min_{x \in Ω} f (x) = \min_{x \in Ω} {\begin{matrix} u_{r} & \sum_{i = 1}^{5} λ_{i} p_{i} & c \end{matrix}}$ ,

(18)

式中, $u_{r}$ 为围岩最终变形, $λ_{i}$ 为各支护构件权重。

隧道支护体系权重可根据1～9标度确定^[25],结合既有研究成果^{[10, 26-27]},构造支护体系重要性评价因素5阶判断矩阵（n=5）：

$\bar{B} = [\begin{matrix} 1 & 2 & 1 / 2 & 1 / 2 & 1 \\ 1 / 2 & 1 & 1 / 4 & 1 / 3 & 1 / 2 \\ 2 & 4 & 1 & 2 & 3 \\ 2 & 3 & 1 / 2 & 1 & 3 \\ 1 & 2 & 1 / 3 & 1 / 3 & 1 \end{matrix}]$ 。

(19)

经计算, $\bar{B}$ 的最大特征值为 $ω_{\max} = 5.536$ ,进而可得隧道支护体系中锚杆、锚索、喷射混凝土、钢架和二次衬砌权向量分别为

$λ = [0.145, 0.110, 0.359, 0.260, 0.126]$ 。

(20)

为使得最终优化结果与一般可行解差异性更显著,定义隶属度表达形式如下：

$μ_{i} = \frac{1 - e^{\frac{a_{i} (f_{i}^{0} - f_{i})}{f_{i}^{0} - f_{i}^{1}}}}{1 - e^{a_{i}}} (i =1,2,3)$ ,

(21)

式中, $a_{i}$ 为隶属度函数形状控制参数,根据文献[17],取 $a_{i} = 0.1$ 。

5.4 优化结果分析

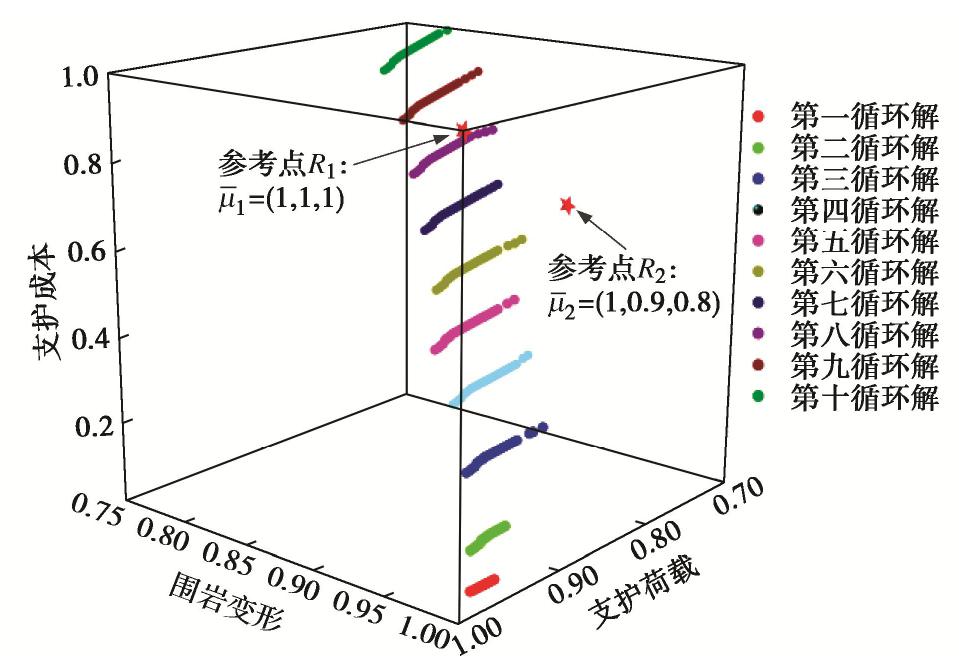
根据图9的思路建立数值计算模型对支护—围岩关系进行计算,采用Hoek-Brown准则,各支护结构的支护特性曲线计算方法参考文献[28],并基于前文思路对支护参数进行优化,采用Matlab数学软件进行编程,将计算结果绘制于隶属度空间内,如图11所示。图中,支护荷载为经分组加权后的隶属度函数。

图 11 支护体系多目标优化结果

Figure 11. Multi-objective optimization results of support system

下载: 全尺寸图片幻灯片

可见,满足要求的可行解共1004个,而M-Pareto点仅有10个,这表明在所有的设计方案中最优解仅占1%,若不对支护体系进行优化设计,则支护方案很大概率上是不合理的。此外,当参考点R₁取为常规值 ${\bar{μ}}_{1} = (1, 1, 1)$ 时,则距离最近的空间点坐标为 $μ_{1} = (0.77,$ $0.73, 0.96)$ ,围岩变形和支护受力的满意度较低。考虑到研究断面围岩条件较差,参考点应向隧道安全性方向偏好,因此将参考点R₂取 ${\bar{μ}}_{2} = (1,$ $0.9,$ $0.8)$ ,此时最优解在该隶属度空间内坐标为 $μ_{2} =$ $(0.85,$ $0.76, 0.79)$ 。显然调整后,隧道安全得以保证,更符合工程需求,此时支护优化方案如表4所示。

表 4 支护参数优化结果

Table 4. Optimization results of support parameters

支护参数	S_cb(S_lb)/m	S_cc(S_lc)/m	t₁/cm	S_s/m	t₂/cm
优化结果	1.2	2.8	30	1	45

下载: 导出CSV

| 显示表格

5.5 现场监测结果

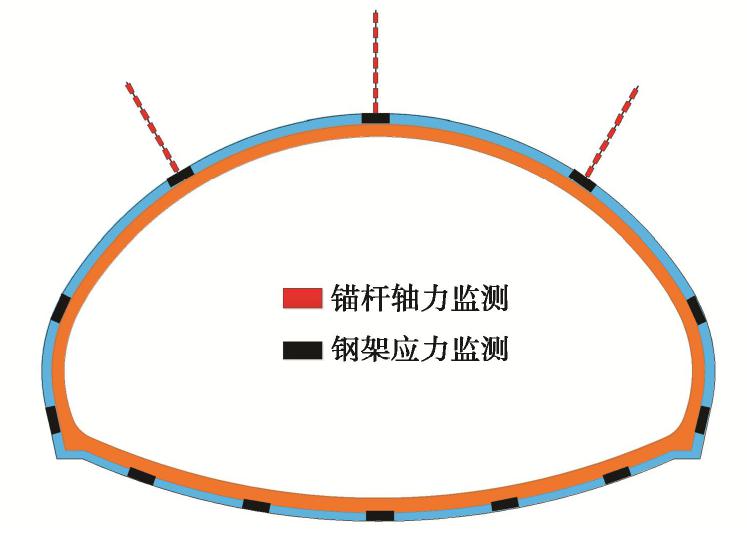
隧道施工中对围岩变形和支护力进行了监控量测,其中围岩变形采用全站仪测量。由于隧道基于初期支护承受全部荷载的理念进行设计,因此本文重点对锚杆和钢架受力进行分析,测点布置如图12所示。

图 12 支护受力测点布置示意图

Figure 12. Schematic diagram of arrangement of measuring points for supporting force

下载: 全尺寸图片幻灯片

锚杆沿全长轴力采用钢筋计进行测量,在锚杆自由段均匀布置7个钢筋计作为套筒安装于锚杆上,两端间距为1.4 m,中部间距为1.3 m,而对于格栅钢架受力采用钢筋计焊接在四肢支架上,现场仪器布置情况如图13所示。

图 13 现场仪器布置情况

Figure 13. Arrangement of field instruments

下载: 全尺寸图片幻灯片

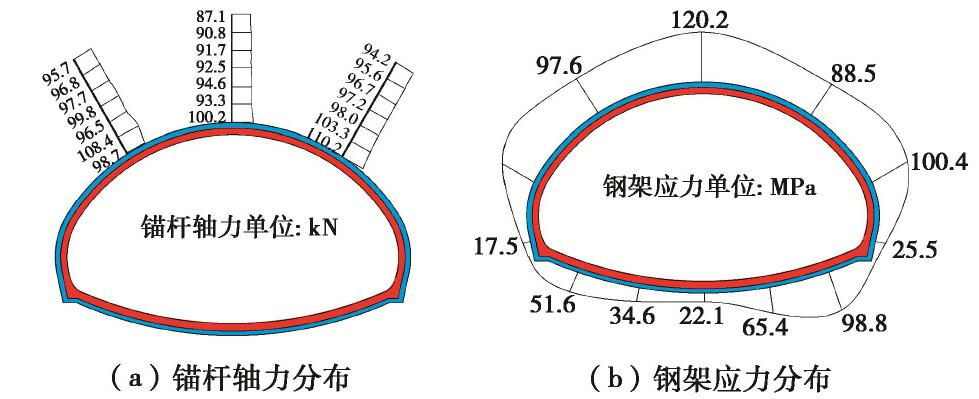
根据规范规定,当隧道围岩变形稳定后,所选监测断面支护结构受力结果如图14所示。

图 14 支护结构受力分布图

Figure 14. Stress distribution of support structure

下载: 全尺寸图片幻灯片

可见,由于测力计的布置影响了安装区域内锚杆与围岩的黏结程度,因此锚杆轴力沿全长波动性较小,但基本上呈现出由浅部到深部递减的趋势,而钢架受力最大值出现在拱顶。此外,在当前支护方案下锚杆轴力最大值为110.2 kN,而钢架应力最大值为110 MPa,远低于其结构设计强度；隧道拱顶围岩变形量仅为18 mm,这进一步表明当前基于经验的设计方法是偏于保守的。

6. 结论

本文构建了隧道围岩协同支护系统,阐明了隧道支护体系的协同作用原理,建立了支护体系设计的多目标优化模型,提出了协同优化设计原则与方法,并在新建京张高铁八达岭隧道中进行应用,获得如下主要结论：

（1）隧道协同支护以支护—围岩作用机制为基础,以协同学的基本原理为指导,研究隧道支护—围岩系统的协同增强效应。协同作用特点表现为时机衔接、刚度匹配与变形协调,前两者为协同工作方式,而后者则为协同工作状态。

（2）协同支护系统是由围岩系统与支护系统按一定工作方式组合在一起的复杂系统,包括支护与围岩的体系协同、不同支护之间的结构协同以及同一支护的要素协同等3个层次。系统稳定性的表征参数为围岩变形,而内驱力则是支护阻力,二者贯穿于隧道工程活动始终,是研究协同支护的标志性参数。

（3）隧道支护体系协同设计的本质为多目标优化问题,为此提出以围岩变形、支护受力和支护成本为目标,并考虑到不同支护结构受力的目标一致性,建立了基于目标函数分组加权表征的隶属度转化方法,提出了隧道支护体系协同优化设计原则和方法,实现了隧道支护设计理论的新突破。

（4）工程应用与分析表明,在所有可行解中最优解仅占1%,其他解答难以在经济性和安全性之间寻求平衡,这便意味着若不采用协同优化设计,则支护方案或因过度注重安全而增大工程造价,亦或因强调经济性而偏于危险,而目前工程中的经验设计方法往往是偏于保守的。

图 1 现场取样、试件加工及力学参数确定

Figure 1. On-site sampling, processing of specimens and determination of mechanical parameters

下载: 全尺寸图片幻灯片

图 2 试验模型概化设计示意图与实物图

Figure 2. Schematic diagrams of general design of the test models and the physical diagrams

下载: 全尺寸图片幻灯片

图 3 试验设备与加载示意图

Figure 3. Schematic diagrams of test facilities and loading

下载: 全尺寸图片幻灯片

图 4 结构面宏观损伤质量变化曲线

Figure 4. Variation curves of macro-damage mass of rock joints

下载: 全尺寸图片幻灯片

图 5 结构面剪切应力与剪切位移关系曲线

Figure 5. Relation curves between shear stress and shear displacement of rock joints

下载: 全尺寸图片幻灯片

图 6 各因素下结构面峰值剪切应力（位移）和应力降变化曲线

Figure 6. Variation curves of peak shear stress (displacement) and stress drop of rock joints under different factors

下载: 全尺寸图片幻灯片

图 7 结构面宏观损伤演化过程

Figure 7. Macro-damage evolution process of rock joints

下载: 全尺寸图片幻灯片

图 8 数值计算模型

Figure 8. Numerical models

下载: 全尺寸图片幻灯片

图 9 模拟结果与试验结果对比

Figure 9. Comparsion between simulated and test results

下载: 全尺寸图片幻灯片

图 10 结构面细观损伤裂纹数量和细观损伤能量变化曲线

Figure 10. Variation curves of meso-damage crack quantity and meso-damage energy of rock joints

下载: 全尺寸图片幻灯片

图 11 结构面细观损伤演化过程

Figure 11. Meso-damage evolution process of rock joints

下载: 全尺寸图片幻灯片

图 12 结构面宏细观退化机理概化描述示意图（工况^#3和^#5及工况^#8和^#14）

Figure 12. Schematic diagrams of general description for macro-meso degradation mechanisms of joints (conditions No. 3, 5, 8 and 14)

下载: 全尺寸图片幻灯片

图 13 结构面抗剪强度参数与一阶起伏角关系曲线

Figure 13. Relation curves between shear strength parameters and first-order undulant angle of rock joints

下载: 全尺寸图片幻灯片

图 14 边坡稳定性分析概化设计示意图和剪切应变增量云图

Figure 14. Schematic diagrams of general design for slope stability analysis and nephograms of shear strain increment

下载: 全尺寸图片幻灯片

表 1 室内试验工况

Table 1 Laboratory test conditions

工况编号	结构面形态	一阶起伏角/(°)	二阶起伏角/(°)	法向压力/MPa
^#1	锯齿状	30	45	3.0
^#2		45		1.5
^#3		45		3.0
^#4		45		4.5
^#5		60		3.0
^#6	波浪状	30	0	3.0
^#7		45		1.5
^#8		45		3.0
^#9		45		4.5
^#10		60		3.0

下载: 导出CSV

表 2 数值计算工况

Table 2 Numerical calculation conditions

工况编号	结构面形态	一阶起伏角/(°)	二阶起伏角/(°)	法向压力/MPa
^#1~^#3	锯齿状	30	45	1.5 3.0 4.5
^#4~^#6		45
^#7~^#9		60
^#10~^#12	波浪状	30	0
^#13~^#15		45
^#16~^#18		60

下载: 导出CSV

表 3 数值计算细观力学参数

Table 3 Meso-mechanical parameters of numerical calculations

圆形颗粒		光滑节理		平行键
摩擦系数	0.6	键合方式	1	半径乘子	1.0
最大半径/mm	0.54	摩擦系数	0.5	剪切强度/MPa	62.5
弹性模量/GPa	12	剪胀角/(°)	0	法向强度/MPa	48.5
法向切向刚度比	1.5	抗拉强度/MPa	0	弹性模量/GPa	25
最大最小半径比	1.42	剪切刚度/(GPa·m^-1)	80	法向切向刚度比	2.5
体积密度/(g·cm^-3)	2.75	法向刚度/(GPa·m^-1)	80	剪切法向强度标准差	±5

下载: 导出CSV

参考文献(18)

[1]	LIU X R, KOU M M, LU Y M, et al. An experimental investigation on the shear mechanism of fatigue damage in rock joints under pre-peak cyclic loading condition[J]. International Journal of Fatigue, 2018, 106: 175-184. doi: 10.1016/j.ijfatigue.2017.10.007
[2]	刘永权. 频发微震下库区顺层岩质边坡累积损伤演化机理及稳定性研究[D]. 重庆: 重庆大学, 2017. LIU Yong-quan. Study on Cumulative Damage Evolution Mechanism and Stability of Bedding Rock Slope in Reservoir Area Under Frequent Microseismic[D]. Chongqing: Chongqing University, 2017. (in Chinese)
[3]	黄润秋. 岩石高边坡稳定性工程地质分析[M]. 北京: 科学出版社, 2012. HUANG Run-qiu. Engineering Geology for High Rock Slopes[M]. Beijing: Science Press, 2012. (in Chinese)
[4]	PATTON F D. Multiple models of shear failure in rock[C]//Proceedings of the 1st Congress of the International Society of Rock Mechanics (ISRM), 1966, Portugal: 509-513.
[5]	BARTON N. Review of a new shear strength criterion for rock joints[J]. Engineering Geology, 1973, 7: 287-332. doi: 10.1016/0013-7952(73)90013-6
[6]	HOEK E, BRAY J. Rock Slope Engineering[M]. 3rd ed. London: Institution of Mining and Metallurgy, 1981.
[7]	BANDIS S C, LUMSDEN A C, BARTON N R. Fundamentals of rock joint deformation[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1983, 20(6): 249-268.
[8]	SEIDEL J P, HABERFIELD C M. The application of energy principles to the determination of the sliding resistance of rock joints[J]. Rock Mechannics and Rock Engineering, 1995, 28(4): 211-226. doi: 10.1007/BF01020227
[9]	朱小明, 李海波, 刘博, 等. 含一阶和二阶起伏体节理剪切强度的试验研究[J]. 岩石力学与工程学报, 2011, 30(9): 1810-1818. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201109011.htm ZHU Xiao-ming, LI Hai-bo, LIU Bo, et al. Experimental study of shear strength of joints with first-order and second-order asperities[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(9): 1810-1818. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201109011.htm
[10]	周辉, 程光坦, 朱勇, 等. 大理岩规则齿形结构面剪切特性试验研究[J]. 岩土力学, 2019, 40(3): 852-860. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201903004.htm ZHOU Hui, CHENG Guang-tan, ZHU Yong, et al. Experimental study of shear deformation characteristics of marble dentate joints[J]. Rock and Soil Mechanics, 2019, 40(3): 852-860. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201903004.htm
[11]	LIU X R, LIU Y Q, LU Y M, et al. Experimental and numerical study on pre-peak cyclic shear mechanism of artificial rock joints[J]. Structural Engineering and Mechanics, 2020, 74(3): 407-423.
[12]	黄达, 黄润秋, 雷鹏. 贯通型锯齿状岩体结构面剪切变形及强度特征[J]. 煤炭学报, 2014, 39(7): 1229-1237. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201407006.htm HUANG Da, HUANG Run-qiu, LEI Peng. Shear deformation and strength of through-going saw-tooth rock discontinuity[J]. Journal of China Coal Society, 2014, 39(7): 1229-1237. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201407006.htm
[13]	王刚, 张学朋, 蒋宇静, 等. 基于颗粒离散元法的岩石节理面剪切破坏细观机理[J]. 中南大学学报(自然科学版), 2015, 46(4): 1442-1453. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201504035.htm WANG Gang, ZHANG Xue-peng, JIANG Yu-jing, et al. Meso-mechanism research on shear failure of rock joint based on particle discrete element method[J]. Journal of Central South University (Science and Technology), 2015, 46(4): 1442-1453. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201504035.htm
[14]	刘新荣, 许彬, 刘永权, 等. 频发微小地震下顺层岩质边坡累积损伤及稳定性分析[J]. 岩土工程学报, 2020, 42(4): 632-641. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202004008.htm LIU Xin-rong, XU Bin, LIU Yong-quan, et al. Cumulative damage and stability analysis of bedding rock slope under frequent microseisms[J]. Chinese Journal of Geotechnicale Engineering, 2020, 42(4): 632-641. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202004008.htm
[15]	雷鹏. 硬性接触型岩体结构面剪切特性及边坡稳定性分析[D]. 重庆: 重庆大学, 2014. LEI Peng. Analysis on Shear Properties of Through Discontinuity and Stability of Slope with Through Discontinuity[D]. Chongqing: Chongqing University, 2014. (in Chinese)
[16]	MURALHA J, GRASSELLI G, TATONE B, et al. ISRM suggested method for laboratory determination of the shear strength of rock joints: revised version[J]. Rock Mechanics and Rock Engineering, 2014, 47(1): 291-302.
[17]	YOON J. Application of experimental design and optimization to PFC model calibration in uniaxial compression simulation[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(6): 871-889.
[18]	CHENG Y M, LANSIVAARA T, WEI W B. Two- dimensional slope stability analysis by limit equilibrium and strength reduction methods[J]. Computer and Geotechnics, 2007, 34(3): 137-150.

施引文献(40)

期刊类型引用(14)

1.	洪开荣，刘永胜，潘岳. 钻爆法山岭隧道修建技术发展与展望. 现代隧道技术. 2024(02): 67-79 . 百度学术
2.	赵建利，郝雪航，余洋，李鹏程，高华民. 苏基克纳里水电站调压竖井无锚支护研究. 河北水利电力学院学报. 2024(03): 38-44 . 百度学术
3.	侯艳娟，张顶立，李然，陈旭，齐伟伟. 深埋三连拱隧道围岩压力计算方法. 力学学报. 2024(11): 3213-3226 . 百度学术
4.	丁祥，刘勇，任玉鹏，韩智铭，马凯蒙. 以初期支护为主要承载结构的衬砌参数优化研究. 公路. 2024(12): 487-492 . 百度学术
5.	张顶立，孙振宇，陶伟明. 隧道围岩大变形灾害特点与主动控制方法. 铁道标准设计. 2023(01): 1-9 . 百度学术
6.	陈文博，张顶立，孙振宇，陈旭，孟令赞. 铁路隧道概率极限状态设计分项系数标定与讨论. 铁道标准设计. 2023(01): 17-24 . 百度学术
7.	姚志雄，刘梦飞，吴波，刘耀星，陈希茂，郑国文，罗芷祎. 基于承载特性的群洞稳定性及初期支护优化研究. 现代隧道技术. 2023(01): 119-129 . 百度学术
8.	刘鹤冰. 基于投资控制的高速公路PPP项目投资人对设计人的管理研究. 铁道建筑技术. 2023(09): 199-202 . 百度学术
9.	梁鹏，高永涛，周喻，邓代强. 隧道初支合理支护时机确定方法及其工程应用. 工程科学学报. 2022(02): 265-276 . 百度学术
10.	刘鹤冰. PPP模式下高速公路项目设计优化全过程管理探究. 铁道建筑技术. 2022(09): 131-135 . 百度学术
11.	王嘉琛，张顶立，孙振宇，方黄城，刘昌. 水平互层围岩隧道破坏机理及其范围预测模型. 力学学报. 2022(10): 2835-2849 . 百度学术
12.	刘耀儒，侯少康，程立，黄跃群. 水利工程智能建造进展及关键技术. 水利水电技术(中英文). 2022(10): 1-20 . 百度学术
13.	彭磊. 公路小净距隧道后行洞支护结构位移及受力特性分析. 产业科技创新. 2021(01): 105-107 . 百度学术
14.	焦战，肖洪天. 基于博弈赋权和综合灰色关联的围岩支护评价. 科学技术与工程. 2021(34): 14769-14774 . 百度学术