基于主动加热型FBG的土体干密度原位测量方法研究

刘洁; 孙梦雅; 施斌; 魏广庆; 郭君仪; 郑兴

doi:10.11779/CJGE202102020

基于主动加热型FBG的土体干密度原位测量方法研究 English Version

刘洁^1,,
孙梦雅¹,
施斌^1, ,,
魏广庆²,
郭君仪¹,
郑兴¹

1.
南京大学地球科学与工程学院,江苏　南京　210023
2.
苏州南智传感科技有限公司,江苏　苏州　215123

基金项目:

国家自然科学基金重点项目 41230636

国家重大科研仪器研制项目 41427801

详细信息

作者简介:
刘洁（1998—）,女,硕士研究生,主要从事地质监测方面的研究。E-mail：dz1929013@smail.nju.edu.cn

通讯作者:
施斌, E-mail: shibin@nju.edu.cn

中图分类号: TU411
计量
- 文章访问数: 289
- HTML全文浏览量: 23
- PDF下载量: 116
出版历程
- 收稿日期: 2020-04-12
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-01-31

Feasibility study on actively heated FBG methods for dry density measurement

1.
School of Earth Sciences and Engineering, Nanjing University, Nanjing 210023, China
2.
NanZee Sensing Technology, Ltd., Suzhou 215123, China

摘要

摘要: 针对现有干密度原位测量技术的局限性,提出了一种基于主动加热型FBG的土体干密度原位测量方法（简称H-FBG干密度法）,该法通过土体的导热系数,建立温度特征值（T_t）与干密度ρ_d之间的关系,进而对干密度进行原位测量；在室内试验的基础上,讨论了该方法的最优加热参数,研究了土类型与含水率对测量结果的影响,证明了该方法的可行性。试验结果表明：T_t随着ρ_d增加而降低,指数函数模型相较于幂函数模型和线性模型的T_t - ρ_d曲线拟合效果要好；H-FBG干密度法最优加热参数为15 W/m和5 min；高含水率土体受微观结构的影响,随着ρ_d增加T_t变化率减小。
- H-FBG干密度法 /
- 土体 /
- 原位测量 /
- 特征值 /
- 导热性
Abstract: An in-situ method based on the actively heated fiber Bragg grating for monitoring dry density is proposed (abbreviated to H-FBG) to make a progress in the existing technique. The relationship between the temperature characteristic value (T_t) and the dry density (ρ_d) is established through the thermal conductivity for the in-situ monitoring of the dry density. A series of indoor tests are carried to verify the feasibility of the method, the effects of moisture content and types of soils are discussed, and the heating parameters are determined. The results show that T_t decreases with the increasing ρ_d, and it is described well using the exponential function. 15 W/m and 5 min can be the best heating parameters applied for the measurement. The temperature of the soils with a higher water content decreases slowly owing to the effects of micro-structure of soils. The results may provide the theoretical and technical foundation for the further application of the proposed method.
- H-FBG method for dry density measurement /
- soil /
- in-situ monitoring /
- characteristic value /
- thermal conductivity

HTML全文

0. 引言

干密度是反映土体工程性质的一个基本物理量,是土力学计算和土质学分析中的一个重要参数^[1],因此土体干密度测量的准确性,对于土体工程性质的评价具有重要意义。

目前,土体干密度最常用的测量方法是环刀法,它是通过钻孔获取原状土样,再在实验室中用环刀从原状土样上切取试样烘干获得土体的干密度。这种方法存在两大不足：①取样和切样过程中易产生扰动,特别对于一些结构性软土,钻孔取样很难保证其原状性,而且对于一些砂性土很难保证环刀法切取试样时的完整性；②环刀法无法对土体干密度进行长期原位监测。除了环刀法,也有一些土体干密度原位测量方法,其中时域反射技术（TDR）、热探针法为点式测量,精度不高,地质雷达法、电阻率法等则适用于大范围的测量,精度很低,在实际工作中很少使用^[2-3]。因此,研发一种便捷的土体干密度原位测量方法具有重要意义。

布拉格光纤光栅（FBG）传感技术,因其灵敏度高、抗电磁干扰、抗腐蚀、对被测物体影响小且易于远程无线准分布监测等优点而在工程结构和岩土体监测中被广泛应用^[4]。Cao等^[5]采用主动加热型FBG技术,提出了一种土体含水率准分布式光纤监测方法,这一方法根据土体热传导原理,将FBG传感器作为土中线性热源,通过建立H-FBG测得的温度特征值与土中含水率之间的关系来测量土中的含水率。然而,在实际岩土工程中,也有这样的情况,即土中的含水率变化很小,而干密度变化很大。如在地基、路基和坝基的土料填筑过程中,土中的最优含水率或水分变化很小,其填筑质量取决于土的干密度是否达到要求。在这类工程情况下,工程建设部门需要掌握填筑土的干密度变化来保证工程建设质量,因此监测土体原位干密度的变化也是一种现实需求。

本文即是在课题组已有的土体含水率光纤监测研究成果的基础上,提出了一种基于主动加热型FBG的土体干密度原位测量方法（简称H-FBG干密度法）。在试验的基础上,建立了基于温度特征值的干密度计算模型,确定了最优加热参数,分析了含水率对干密度测量的影响,证明了这一技术方法的可行性,研究结果为该技术的研发和推广打下了理论和技术基础。

1. H-FBG干密度法的基本原理

1.1 测量原理

H-FBG干密度法的基本原理是：将H-FBG传感器作为线性热源埋入土中加热,将测得的加热过程中的温度升高值定义为温度特征值 $T_{t}$ ,再通过土体的导热系数 $λ$ ,建立干密度 $ρ_{d}$ 与 $T_{t}$ 的关系,从而由 $T_{t}$ 计算出 $ρ_{d}$ 。将FBG刚玉管作为线性热源,将该问题简化成二维热传导问题^[6], $T_{t}$ 的解析解为

$T_{t} = \frac{Q}{4 π λ} E i (\frac{r^{2}}{4 a t})$ ,

(1)

$E i (x) = \int \begin{array}{l} \infty \\ x \end{array} \exp (- u) \frac{d u}{u}$ 。

(2)

令 $u = \frac{r^{2}}{4 α t}$ ,当r取较小值,t取较大值的时候, $E i (u)$ 的值可以用它的级数展开式的前两项表示：

$T_{t} = \frac{Q}{4 π λ} [- γ - \ln (\frac{r^{2}}{4 a t})]$ 。

(3)

将常数项简化为h,则式（4）为

$\begin{array}{l} T_{t} = \frac{Q}{4 π λ} (\ln t + h), \\ h = - [γ + \ln (\frac{r^{2}}{4 α})] 。 \end{array}}$

(4)

式中, $T_{t}$ 为加热前后的温度升高值（K）,t为加热时间（s）, $λ$ 为土体的导热系数(W/(m∙k)), $r$ 为距离光纤的距离（m）, $Q$ 为单位长度加热功率（W/m）, $α$ 为热扩散系数（m²/s）, $γ$ 为欧拉常数,取0.57726。

在含水率和被测土质一定的情况下, $ρ_{d}$ 与 $λ$ 的关系为

$ρ_{d} = f (λ)$ ,

(5)

$ρ_{d}$ 与 $T_{t}$ 之间的关系为

$ρ_{d} = f (T_{t})$ 。

(6)

通过式（6）中的函数关系,由 FBG刚玉管的温度特征值可以求出土体干密度。

1.2 干密度计算模型

$ρ_{d}$ 与 $λ$ 的关系是建立 $T_{t}$ 与 $ρ_{d}$ 计算模型的关键,目前还没有完全成熟的理论公式,已经建立的导热系数模型多是以饱和度S_r、天然密度 $ρ_{b}$ 、孔隙率n等为直接参数^[7],以上这些参数都与 $ρ_{d}$ 有关：

$S_{r} = \frac{w G_{s} ρ_{d}}{G_{s} ρ_{w} - ρ_{d}}$ ,

(7)

$n = 1 - \frac{ρ_{d}}{G_{s} ρ_{w}}$ 。

(8)

式中, $S_{r}$ 为饱和度, $n$ 为孔隙率, $w$ 为含水率, $G_{s}$ 为固体颗粒的相对质量密度, $ρ_{w}$ 为水的密度。

结合已有的导热系数模型研究发现 $T_{t}$ - $ρ_{d}$ 模型有3种,分别是指数函数模型、幂函数模型和线性函数模型。

（1）指数函数模型

Singh等^[8]基于热探针法,在Kersten模型的基础上,通过经验回归,提出了与土体类型相关的指数函数模型^[9]：

$λ = \frac{1.07 \lg w + d}{10^{3 - 0.6243 ρ_{d}}}$ ,

(9)

式中,d为与土体类型相关的参数

联立式（4）,（9）,可得

$T_{t} = \frac{Q}{4 π} \frac{10^{3 - 0.6243 ρ_{d}}}{1.07 \lg w + d} (\ln t + h)$ 。

(10)

在相同的测量条件下,将各常数项简化为a,b后,可以得到

$T_{t} = 10^{a - b ρ_{d}}$ ,

(11)

式中, $a = 3 + \lg (\frac{Q}{4 π} \frac{\ln t + h}{1.07 \lg w + d})$ , $b = 0.6243$ 。

（2）幂函数模型

Chung等^[10]在研究砂土和黏土表面的热效应时提出了以体积含水率θ为自变量的经验模型,在砂土和黏土中都得到了较好的应用：

$λ = e_{1} + e_{2} θ + e_{3} θ^{\frac{1}{2}}$ ,

(12)

$θ = \frac{w ρ_{d}}{ρ_{w}}$ 。

(13)

联立式（4）,（12）,（13）可得

$λ = e_{1} + e_{2} \frac{ρ_{d} w}{ρ_{w}} + e_{3} {(\frac{ρ_{d} w}{ρ_{w}})}^{\frac{1}{2}}$ ,

(14)

$T_{t} = \frac{Q}{4 π} \frac{1}{e_{1} + e_{2} \frac{ρ_{d} w}{ρ_{w}} + e_{3} {(\frac{ρ_{d} w}{ρ_{w}})}^{\frac{1}{2}}} (\ln t + h)$ 。

(15)

式中,e₁,e₂,e₃为与土体类型有关的系数。将各常数项简化为a,b,c后可以得到

$T_{t} = \frac{1}{a + b ρ_{d} + c \sqrt{ρ_{d}}}$ ,

(16)

式中, $a = \frac{4π e_{1}}{Q ρ_{w}}$ , $b = \frac{4π e_{2} w}{Q ρ_{w}}$ , $c = \frac{4π e_{3} \sqrt{w}}{Q ρ_{w}}$ 。

（3）线性模型

土体导热系数与各相的体积、分布和排列有关,将土体视为固体颗粒、水和空气组成的混合物,并联函数模型假设通过不同组分的热通量是相同的,是计算 $λ$ 的重要模型之一^[11]：

$\frac{1}{λ} = \frac{1 - n}{λ_{s}} + \frac{n S_{r}}{λ_{w}} + \frac{n - n S_{r}}{λ_{a}}$ 。

(17)

联立式（7）,（8）,（17）可得

$\frac{1}{λ} = \frac{ρ_{d}}{G_{s} ρ_{w} λ_{s}} + \frac{w ρ_{d}}{ρ_{w}} + \frac{1}{λ_{a}} [1 - \frac{ρ_{d} (1 + G_{s} w)}{G_{s} ρ_{w}}]$ 。

(18)

式中, $λ_{a}$ , $λ_{s}$ , $λ_{w}$ 分别为空气、固体颗粒和水的导热系数。

联立式（4）,（18）可得

$T_{t} = \frac{Q}{4 π} [(\frac{1}{G_{s} ρ_{w} λ_{s}} + \frac{w}{ρ_{w}} - \frac{1}{λ_{a}} \frac{(1 + G_{s} w)}{G_{s} ρ_{w}}) ρ_{d} + \frac{1}{λ_{a}}] (\ln t + h) 。$

(19)

将各常数项简化为a,b后可以得到

$T_{t} = a - b ρ_{d}$ ,

(20)

式中, $a = \frac{Q}{4 π} (\frac{1}{G_{s} ρ_{w} λ_{s}} + \frac{w}{ρ_{w}} - \frac{1}{λ_{a}} \frac{(1 + G_{s} w)}{G_{s} ρ_{w}}) (\ln t + h)$ , $b = \frac{Q}{4 π λ_{a}} (\ln t + h)$ 。

2. H-FBG干密度试验

为了验证H-FBG干密度原位测量方法的可行性,建立干密度计算模型,分析含水率和土类型对测量结果的影响,在室内开展了不同含水率的砂土和黄土试样的干密度测量试验。

2.1 试验装置

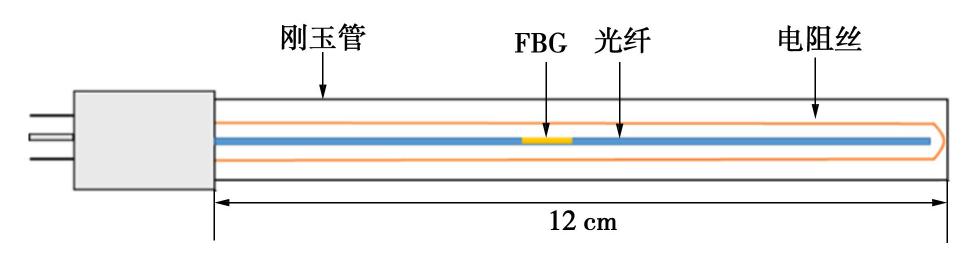
试验装置如图1,使用的H-FBG传感器由四孔刚玉管、U型电阻丝和测温光纤组成（图2）,刚玉管外径为6 mm,内部孔径为1 mm,有效加热电阻为8.2 Ω,感测长度为12 cm。试验所采用的土样为延安黄土试样与人工配比砂土试样,级配曲线见图3,基本物理参数见表1。试验选取尺寸为20 cm×20 cm×15 cm的有机玻璃透明盒作为容器,在20 cm×20 cm的面上中间部位开直径约为1 cm的孔用于放置H-FBG传感器。

图 1 室内试验装置图

Figure 1. Setup of experimental equipment in laboratory

下载: 全尺寸图片幻灯片

图 2 FBG刚玉管传感器结构图

Figure 2. Structure of FBG sensor

下载: 全尺寸图片幻灯片

图 3 土样颗粒级配曲线

Figure 3. Grain-size distribution curves of test soils

下载: 全尺寸图片幻灯片

表 1 土样的基本物理参数

Table 1. Basic physical parameters of test soils

初始含水率w/%	塑限w_p/%	液限w_L/%	塑性指数I_p
4.2	17	27	10

下载: 导出CSV

| 显示表格

2.2 试验方法

试样烘干后通过改变加水量分别配置含水率为8%,16%的黄土试样和含水率为8%的砂土试样,并且通过烘干法测量试样的真实含水率。试验干密度区间黄土试样设置为0.9～1.5 g/cm³,砂土试样设置为1.2～1.5 g/cm³,变化梯度为0.1 g/cm³,通过控制土颗粒质量来配置不同干密度的试样。

填土完成后将传感器分别连接可调节的直流电源和A-01型FBG解调仪,用于加热和采集传感器的中心波长数据,分别在35,30,25,20,15,10,5 W/m的功率下加热20 min,加热结束后改变干密度继续下一组试验。

3. 试验结果与分析

3.1 温度特征值与干密度的关系

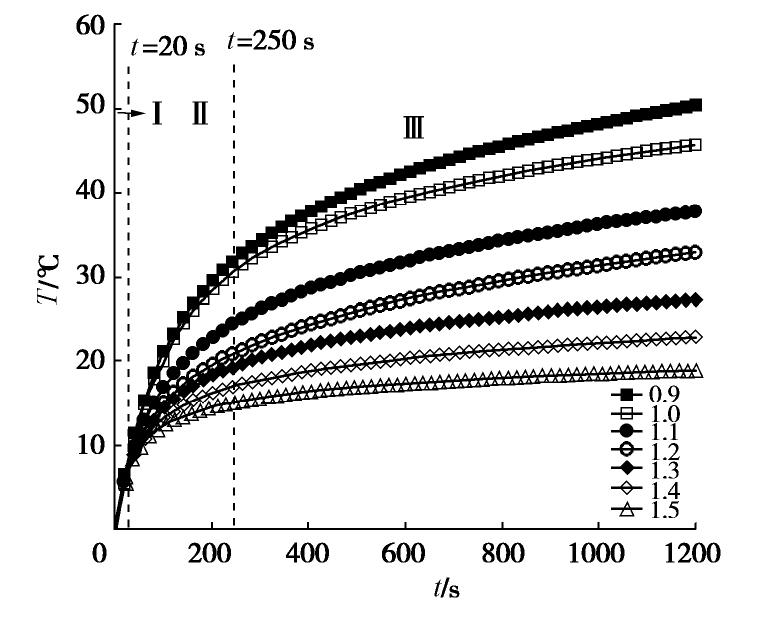
由FBG记录到的波长数据,可以得到不同干密度土样的温度时程曲线。在35 W/m功率下加热20 min,以8%含水率黄土试样的加热过程（图4）为例,可以看到升温过程分为3个阶段,第Ⅰ阶段（0～20 s）温度增长较快,反映管体吸收电阻丝的热量；第Ⅱ阶段（20～250 s）升温速率逐渐下降并趋于稳定,热量从管体传递到周围土体；第Ⅲ阶段（250～1200 s）热量传递达到相对的动态平衡,管体温度趋于稳定。

图 4 8%含水率黄土试样温度时程曲线

Figure 4. Curves of temperature rise of loess samples

下载: 全尺寸图片幻灯片

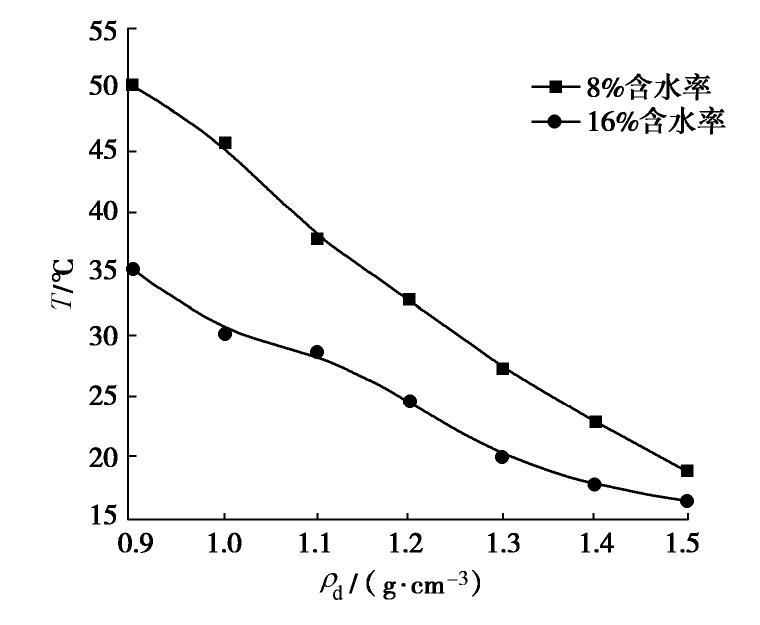
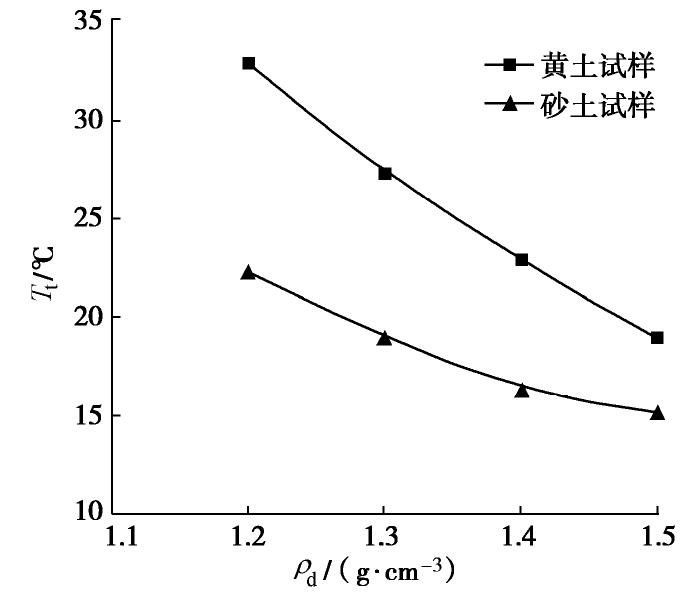
由升温曲线可以得到不同干密度试样的温度特征值,见图5,6,试样的 $T_{t}$ 均随 $ρ_{d}$ 增大而减小,出现这种结果的原因主要是：矿物颗粒导热系数平均值约为2.9 W/(m·K),而水和气体的导热系数分别0.6,0.024 W/(m·K)^[12],随着 $ρ_{d}$ 增大,单位体积内的土颗粒数量增加、孔隙减小、空气被压缩排出,颗粒接触面积增加,比热容增大,导热系数增大,导致 $T_{t}$ 减小。

图 5 不同含水率黄土试样T_t-ρ_d曲线

Figure 5. T_t - ρ_d curves of loess with different water contents

下载: 全尺寸图片幻灯片

图 6 8%含水率砂土与黄土试样T_t-ρ_d曲线

Figure 6. T_t - ρ_d curves of sand and loess with water content of 8%

下载: 全尺寸图片幻灯片

3.2 土类型与含水率对干密度测量的影响

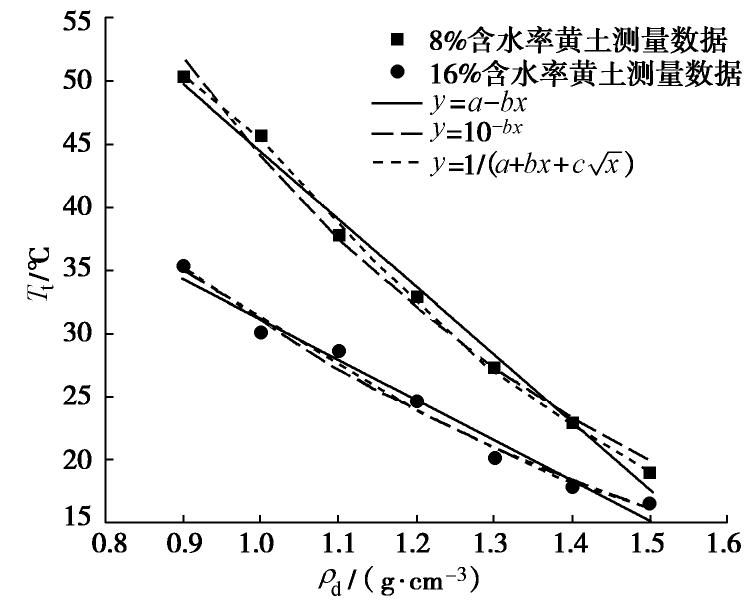
含水率、干密度和矿物组成都是影响土体导热性质的重要因素。从图5可以看出：相同干密度下黄土8%含水率试样的 $T_{t}$ 值较16%试样的高,原因是低含水率土体的孔隙中水所占的体积小,而低导热性气体所占的体积大。从图6中可以看出,相同含水率和相同干密度下黄土试样的 $T_{t}$ 较砂土试样的高,这是因为砂土试样中的石英矿物含量高,导热系数较黏土矿物大。

此外,16%的黄土试样的 $T_{t}$ 随 $ρ_{d}$ 的变化率要比8%的试样小,因为对于16%的高含水率试样,随着密实度增加,不仅单位体积矿物颗粒数量增加,同时还存在土中微观结构的变化。在外力和土压力等作用下,黏土等颗粒会趋于定向排列,颗粒间接触点增多,颗粒周围水化膜的赋存形态发生变化,粒间水桥通道加强,接触热阻减小^[13],孔隙中的自由水也可以形成连续分布孔隙水,在孔隙中产生导热通道^[14],因此 $T_{t}$ 变化率减小。

3.3 干密度计算模型的选择与验证

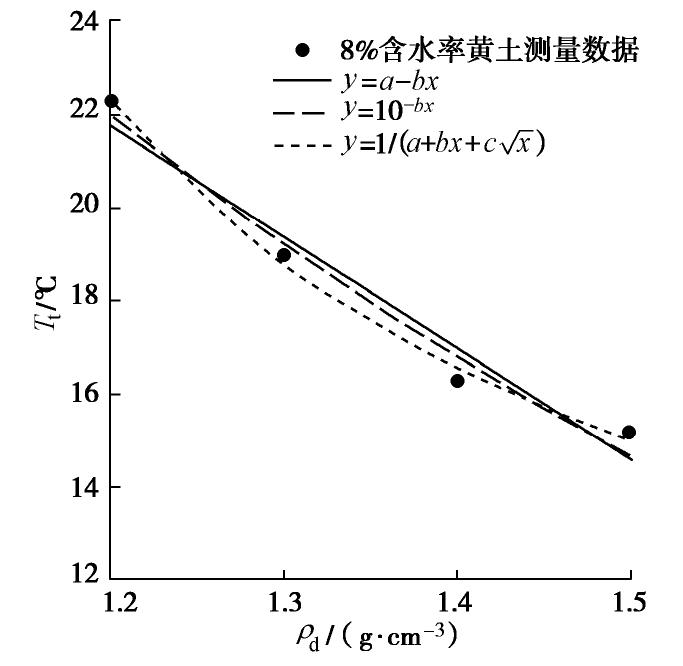
为了评价干密度计算模型的好坏,基于式（11）,（16）,（20）所得的指数函数模型、幂函数模型和线性函数模型,运用最小二乘法得到 $T_{t}$ 与 $ρ_{d}$ 之间的拟合曲线和函数关系式,见图7,8；表2为各模型拟合参数、相关系数R²和均方根误差RMSE,测量误差 $σ$ 为

图 7 黄土试样T_t-ρ_d拟合曲线

Figure 7. Fitting curves of T_t-ρ_d of loess

下载: 全尺寸图片幻灯片

图 8 8%含水率砂土试样T_t-ρ_d拟合曲线

Figure 8. Fitting curves of T_t-ρ_d of sand with water content of 8%

下载: 全尺寸图片幻灯片

表 2 不同函数模型相关系数平方与均方根误差

Table 2. Fitting parameters of function models

土类	含水率	函数模型	表达式	a	b	c	R²	RMSE/(g·cm^-3)	σ/%
黄土	8%	指数函数	$T_{t} = 10^{a - b ρ_{d}}$	2.31	0.67	—	0.989	0.021	1.4
		幂函数	$T_{t} = \frac{1}{a + b ρ_{d} + c \sqrt{ρ_{d}}}$	0.33	0.37	-0.68	0.993	0.047	3.4
		线性函数	$T_{t} = a - b ρ_{d}$	98.11	53.68	—	0.989	0.018	1.4
	16%	指数函数	$T_{t} = 10^{a - b ρ_{d}}$	2.04	0.55	—	0.980	0.027	1.9
		幂函数	$T_{t} = \frac{1}{a + b ρ_{d} + c \sqrt{ρ_{d}}}$	0.15	0.20	-0.32	0.978	0.055	4.3
		线性函数	$T_{t} = a - b ρ_{d}$	59.80	28.99	—	0.953	0.041	3.1
砂土	8%	指数函数	$T_{t} = 10^{a - b ρ_{d}}$	2.00	0.55	—	0.975	0.008	1.2
		幂函数	$T_{t} = \frac{1}{a + b ρ_{d} + c \sqrt{ρ_{d}}}$	-0.27	-0.09	0.39	0.992	0.030	4.7
		线性函数	$T_{t} = a - b ρ_{d}$	47.23	21.41	—	0.945	0.013	1.8

下载: 导出CSV

| 显示表格

$σ = \frac{| ρ_{dr} - ρ_{de} |}{ρ_{dr}}$ 。

(21)

式中, $ρ_{dr}$ 为真实值, $ρ_{de}$ 为测量值

不同含水率和不同土类型试样的 $T_{t}$ - $ρ_{d}$ 各拟合函数的相关系数R²均高于0.95。当黄土试样含水率为8%时,幂函数R²最高,RMSE最大为0.051 g/cm³；指数函数和线性函数的R²和σ相同,分别为0.989和1.4%,RMSE分别为0.021,0.017 g/cm³。当黄土试样含水率为16%时,指数函数R²最高,RMSE和 $σ$ 最小分别为0.027 g/cm³和1.9%；。砂土试样中幂函数R²最高,RMSE最大为0.03 g/cm³；指数函数R²为0.9751,RMSE和 $σ$ 最小,分别为0.008 g/cm³和1.2%；线性函数R²最低。8%含水率试样各模型拟合度和测量精度较16%含水率试样高,可能是因为高含水率试样易聚合成球状集合体,制作土样的均匀性更难控制。综合三组试验结果分析,线性模型在低含水率中拟合效果较好,在高含水率黄土及砂土中适用性较差；指数函数在两组含水率中均取得了较好的拟合结果,是最优的计算模型。

3.4 最优加热参数选择

H-FBG干密度法中加热功率过大或加热时间过长均可能会干扰原状土体的水分运移,同时对便携式测试设备来说,过多的能源消耗会影响电池的使用时间；而功率过小或加热时间过短会使热源影响范围过小,从而降低测量的准确性。因此,分别进行了不同功率和不同加热时间下的测试试验,对测试结果进行了指数函数拟合,依据拟合效果和测量误差选择最优加热参数。

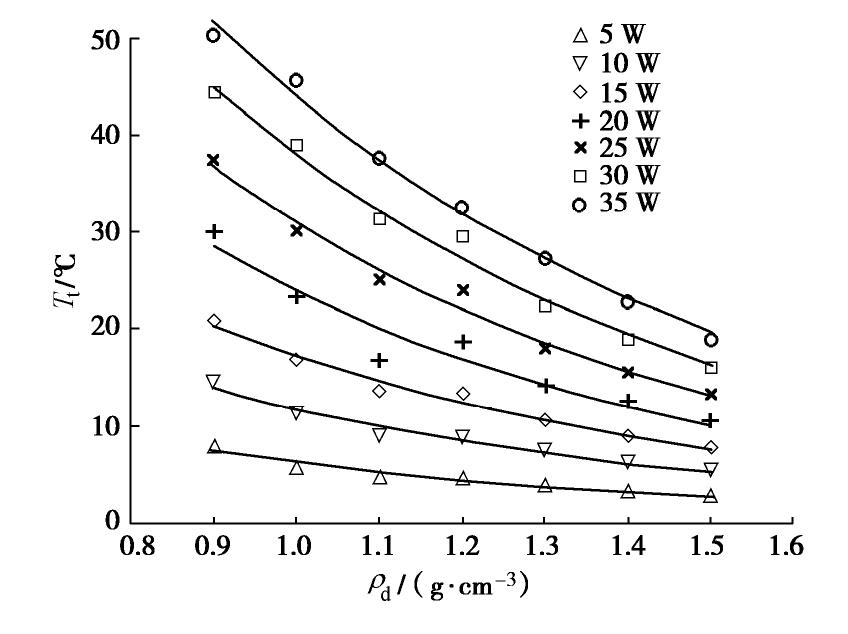
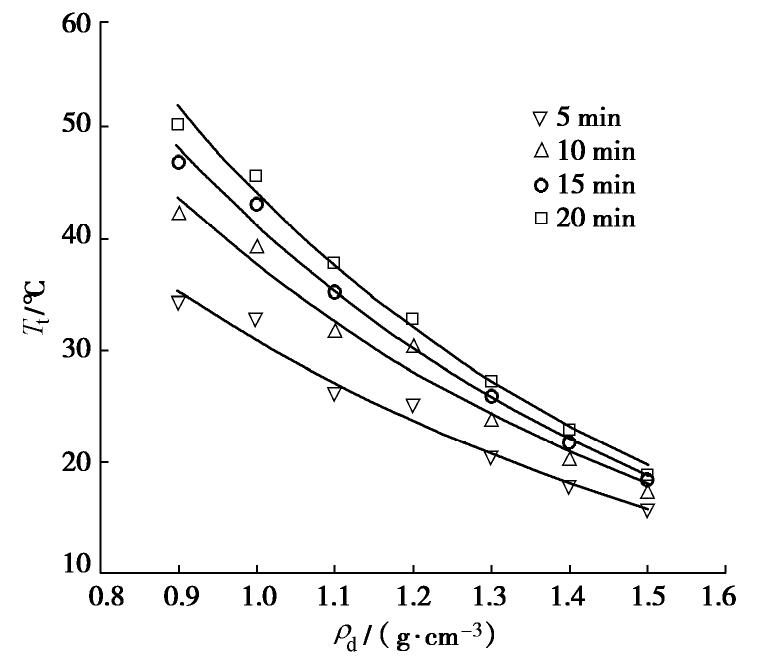
在加热时间为20 min的前提下,分别在5,10,15,20,25,30,35 W/m功率下对含水率为8%试样进行加热。由图9和表3可知,功率越大, $T_{t}$ 越高,不同功率下的 $T_{t}$ 均随 $ρ_{d}$ 增大而降低。35 W/m功率下 R²最大, $σ$ 最小,分别为0.989和1.4%；5 W/m的加热功率下R²最小, $σ$ 最大,分别为0.933和3.1%；在15 W/m加热功率下R²为0.975, $σ$ 为1.7%,与35 W/m功率下 $σ$ 相近,同时能源消耗较小,因此选择15 W/m为最优的加热功率。

图 9 不　同加热功率下的T_t-ρ_d拟合曲线

Figure 9. Fitting curves of T_t-ρ_d under different heating powers

下载: 全尺寸图片幻灯片

表 3 不同加热功率下的T_t-ρ_d曲线拟合参数

Table 3. Fitting parameters of T_t-ρ_d under different heating powers

功率/(W·m^-1)	a	b	R²	RMSE/(g·cm^-3)	σ/%
5	1.48	0.69	0.933	0.021	3.1
10	1.73	0.66	0.956	0.027	2.2
15	1.90	0.67	0.975	0.028	1.7
20	2.09	0.71	0.928	0.050	3.1
25	2.19	0.70	0.976	0.026	2.2
30	2.28	0.70	0.985	0.032	1.9
35	2.31	0.67	0.989	0.039	1.4

下载: 导出CSV

| 显示表格

在加热功率为15W/m的前提下,分别加热5,10,15,20 min,从图10和表4可以看出,加热时间越长T_t越高,不同加热时间的R²,RMSE和 $σ$ 相近,因此选择5 min为目前的最优加热时间。

图 10 不同加热时间下的T_t-ρ_d拟合曲线

Figure 10. Fitting curves of T_t-ρ_d under different heating time

下载: 全尺寸图片幻灯片

表 4 不同加热时间下的T_t-ρ_d曲线拟合参数

Table 4. Fitting parameters of T_t-ρ_d under different heating time

时间/min	a	b	R²	RMSE/(g·cm^-3)	σ/%
5	2.04	0.55	0.972	0.024	1.7
10	2.19	0.61	0.975	0.025	1.8
15	2.27	0.65	0.988	0.026	1.7
20	2.31	0.67	0.989	0.025	1.6

下载: 导出CSV

| 显示表格

4. 结论

本文通过土体导热系数与干密度之间的关系,建立了 $T_{t}$ - $ρ_{d}$ 计算模型,提出了H-FBG干密度原位测量方法；通过室内试验研究了该方法的可行性,分析了含水率和土类型对测量结果的影响和最优加热参数,结论如下：

（1） $T_{t}$ 随着 $ρ_{d}$ 的增加而降低,二者之间存在唯一对应关系,H-FBG干密度原位测量方法具有可行性。

（2）受颗粒间水桥通道等微观结构变化的影响,高含水率土体 $T_{t}$ 变化率随 $ρ_{d}$ 的增加而减小。

（3）相较于幂函数模型和线性函数模型,指数函数模型拟合度高,测量误差小,参数简单,是最佳的干密度计算模型。

（4）在节约能源的情况下,H-FBG法最优加热参数为15 W/m和5 min。

本文是土体原位H-FBG干密度法的可行性研究,但在现实应用中还需要从以下4个方面进行完善：①干密度测量精度的提高以及室外原位试验验证；②不同土类和含水率下的函数模型的适用性以及参数标定；③现场刚玉管的布设方式及其对土体的扰动问题；④准分布式原位测量的加热设备和无线数据传输功能的设计。

图 1 室内试验装置图

Figure 1. Setup of experimental equipment in laboratory

下载: 全尺寸图片幻灯片

图 2 FBG刚玉管传感器结构图

Figure 2. Structure of FBG sensor

下载: 全尺寸图片幻灯片

图 3 土样颗粒级配曲线

Figure 3. Grain-size distribution curves of test soils

下载: 全尺寸图片幻灯片

图 4 8%含水率黄土试样温度时程曲线

Figure 4. Curves of temperature rise of loess samples

下载: 全尺寸图片幻灯片

图 5 不同含水率黄土试样T_t-ρ_d曲线

Figure 5. T_t - ρ_d curves of loess with different water contents

下载: 全尺寸图片幻灯片

图 6 8%含水率砂土与黄土试样T_t-ρ_d曲线

Figure 6. T_t - ρ_d curves of sand and loess with water content of 8%

下载: 全尺寸图片幻灯片

图 7 黄土试样T_t-ρ_d拟合曲线

Figure 7. Fitting curves of T_t-ρ_d of loess

下载: 全尺寸图片幻灯片

图 8 8%含水率砂土试样T_t-ρ_d拟合曲线

Figure 8. Fitting curves of T_t-ρ_d of sand with water content of 8%

下载: 全尺寸图片幻灯片

图 9 不　同加热功率下的T_t-ρ_d拟合曲线

Figure 9. Fitting curves of T_t-ρ_d under different heating powers

下载: 全尺寸图片幻灯片

图 10 不同加热时间下的T_t-ρ_d拟合曲线

Figure 10. Fitting curves of T_t-ρ_d under different heating time

下载: 全尺寸图片幻灯片

表 1 土样的基本物理参数

Table 1 Basic physical parameters of test soils

初始含水率w/%	塑限w_p/%	液限w_L/%	塑性指数I_p
4.2	17	27	10

下载: 导出CSV

表 2 不同函数模型相关系数平方与均方根误差

Table 2 Fitting parameters of function models

土类	含水率	函数模型	表达式	a	b	c	R²	RMSE/(g·cm^-3)	σ/%
黄土	8%	指数函数	$T_{t} = 10^{a - b ρ_{d}}$ $T_{t} = 10^{a - b ρ_{d}}$	2.31	0.67	—	0.989	0.021	1.4
		幂函数	$T_{t} = \frac{1}{a + b ρ_{d} + c \sqrt{ρ_{d}}}$ $T_{t} = \frac{1}{a + b ρ_{d} + c \sqrt{ρ_{d}}}$	0.33	0.37	-0.68	0.993	0.047	3.4
		线性函数	$T_{t} = a - b ρ_{d}$ $T_{t} = a - b ρ_{d}$	98.11	53.68	—	0.989	0.018	1.4
	16%	指数函数	$T_{t} = 10^{a - b ρ_{d}}$ $T_{t} = 10^{a - b ρ_{d}}$	2.04	0.55	—	0.980	0.027	1.9
		幂函数	$T_{t} = \frac{1}{a + b ρ_{d} + c \sqrt{ρ_{d}}}$ $T_{t} = \frac{1}{a + b ρ_{d} + c \sqrt{ρ_{d}}}$	0.15	0.20	-0.32	0.978	0.055	4.3
		线性函数	$T_{t} = a - b ρ_{d}$ $T_{t} = a - b ρ_{d}$	59.80	28.99	—	0.953	0.041	3.1
砂土	8%	指数函数	$T_{t} = 10^{a - b ρ_{d}}$ $T_{t} = 10^{a - b ρ_{d}}$	2.00	0.55	—	0.975	0.008	1.2
		幂函数	$T_{t} = \frac{1}{a + b ρ_{d} + c \sqrt{ρ_{d}}}$ $T_{t} = \frac{1}{a + b ρ_{d} + c \sqrt{ρ_{d}}}$	-0.27	-0.09	0.39	0.992	0.030	4.7
		线性函数	$T_{t} = a - b ρ_{d}$ $T_{t} = a - b ρ_{d}$	47.23	21.41	—	0.945	0.013	1.8

下载: 导出CSV

表 3 不同加热功率下的T_t-ρ_d曲线拟合参数

Table 3 Fitting parameters of T_t-ρ_d under different heating powers

功率/(W·m^-1)	a	b	R²	RMSE/(g·cm^-3)	σ/%
5	1.48	0.69	0.933	0.021	3.1
10	1.73	0.66	0.956	0.027	2.2
15	1.90	0.67	0.975	0.028	1.7
20	2.09	0.71	0.928	0.050	3.1
25	2.19	0.70	0.976	0.026	2.2
30	2.28	0.70	0.985	0.032	1.9
35	2.31	0.67	0.989	0.039	1.4

下载: 导出CSV

表 4 不同加热时间下的T_t-ρ_d曲线拟合参数

Table 4 Fitting parameters of T_t-ρ_d under different heating time

时间/min	a	b	R²	RMSE/(g·cm^-3)	σ/%
5	2.04	0.55	0.972	0.024	1.7
10	2.19	0.61	0.975	0.025	1.8
15	2.27	0.65	0.988	0.026	1.7
20	2.31	0.67	0.989	0.025	1.6

下载: 导出CSV

参考文献(14)

[1]	高登辉, 陈正汉, 郭楠, 等. 干密度和基质吸力对重塑非饱和黄土变形与强度特性的影响[J]. 岩石力学与工程学报, 2017, 36(3): 736-744. GAO Deng-hui, CHEN Zheng-han, GUO Nan, et al. The influence of dry density and matrix suction on deformation and strength characteristics of the remolded unsaturated loess[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(3): 736-744. (in Chinese)
[2]	SAKAKI T, KHLER S, HERTRICH M, et al. FE/LUCOEX: Density measurement of granulated bentonite mixture in a full scale mockup test using dielectric tools[C]//LUCOEX Conference and Workshop: Full-scale Demonstration Tests in Technology Development of Repositories for Disposal of Radioactive Waste, 2015, Skarshamn.
[3]	SAKAKI T, FIRAT L B, VOGT T, et al. Heated fiber-optic cables for distributed dry density measurements of granulated bentonite mixtures: feasibility experiments[J]. Geomechanics for Energy and the Environment, 2019, 17: 57-65.
[4]	施斌, 张丹, 朱鸿鹄. 地质与岩土工程分布式光纤监测技术[M]. 北京: 科学出版社, 2019. SHI Bin, ZHANG Dan, ZHU Hong-hu. Distributed Fiber Optic Sensing for Geoengineering Monitoring[M]. Beijing: Science Press, 2019. (in Chinese)
[5]	CAO D F, SHI B, ZHU H H, et al. A soil moisture estimation method using actively heated fiber Bragg grating sensors[J]. Engineering Geology, 2018, 242: 142-149.
[6]	WEISS J D. Using fiber optics to detect moisture intrusion into a landfill cap consisting of a vegetative soil barrier[J]. Air Repair, 2003, 53(9): 1130-1148.
[7]	DONG Y, MCCARTNEY J S, LU N. Critical review of thermal conductivity models for unsaturated soils[J]. Geotechnical & Geological Engineering, 2014, 33(2): 207-221.
[8]	SINGH D, DEVID K. Generalized relationships for estimating soil thermal resistivity[J]. Experimental Thermal & Fluid ence, 2000, 22: 133-143.
[9]	KERSTEN M S. The thermal conductivity of soils[J]. Highway Research Board, 1949, 28: 391-409.
[10]	CHUNG S O, HORTON R. Soil heat and water flow with a partial surface mulch[J]. Water Resources Research, 1987, 23(12): 2175-2186.
[11]	许模, 王迪, 蒋良文, 等. 岩土体导热系数研究进展[J]. 地球科学与环境学报, 2011, 33(4): 421-427, 433. XU Mo, WANG Di, JIANG Liang-wen, et al. Review on thermal conductivity coefficient of rock and soil mass[J]. Journal of Earth Science and Environment, 2011, 33(4): 421-427, 433. (in Chinese)
[12]	谈云志, 喻波, 胡新江, 等. 非饱和土热导率预估模型研究[J]. 岩土工程学报, 2013, 35(增刊1): 129-133. TAN Yun-zhi, YU Bo, HU Xin-jiang, LIU Xiao-ling. Study of thermal conductivity for unsaturated unfrozen and frozen soils[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S1): 129-133. (in Chinese)
[13]	王铁行, 刘自成, 卢靖. 黄土导热系数和比热容的实验研究[J]. 岩土力学, 2007(4): 655-658. WANG Tie-xing, LIU Zi-cheng, LU Jing. Experimental study on the coefficient of thermal conductivity and specific volume heat of loess[J]. Rock and Soil Mechanics, 2007(4): 655-658. (in Chinese)
[14]	甄作林, 朱江鸿, 张虎元, 等. 砂土导热性能测试与预测研究[J]. 地下空间与工程学报, 2018, 14(6): 1577-1586. ZHEN Zuo-lin, ZHU Jiang-hong, ZHANG Hu-yuan, et al. Study on the measurement and prediction of thermal properties for sand[J]. Chinese Journal of Underground Space and Engineering, 2018, 14(6): 1577-1586. (in Chinese)

施引文献(3)

期刊类型引用(2)

1.	姚俊成，刘洁，王金路，孙梦雅，方可，施斌. 基于主动加热型分布式温度感测光缆的土体导热系数测量方法. 水文地质工程地质. 2023(01): 179-188 . 百度学术
2.	程伟，孙梦雅，徐洪兵，施斌，郭君仪，刘洁. 基于AHFO-FBG的黄土含水率不同率定方法对比分析. 工程地质学报. 2023(03): 1073-1083 . 百度学术