密排横向管幕理论分析研究

张宇; 陶连金; 董立朋; 赵旭; 边金; 安韶; 陈向红

doi:10.11779/CJGE202102017

密排横向管幕理论分析研究 English Version

张宇^1,,
陶连金^1, ,,
董立朋²,
赵旭¹,
边金³,
安韶¹,
陈向红⁴

1.
北京工业大学建筑与工程学院,北京　100124
2.
中铁隧道局集团有限公司,广东　广州　511458
3.
广东海洋大学,广东　湛江　524088
4.
中煤炭建工集团有限公司,北京　100161

基金项目:

国家重点研发计划项目 2017YFC0805403

国家自然科学基金项目 41877218

详细信息

作者简介:
张宇（1993— ）,男,博士研究生,主要从事地下工程施工风险方面的研究工作。E-mail：411101866@qq.com

通讯作者:
陶连金, E-mail: ljtao@bjut.edu.cn

中图分类号: TU43
计量
- 文章访问数: 224
- HTML全文浏览量: 37
- PDF下载量: 106
出版历程
- 收稿日期: 2020-04-01
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-01-31

Theoretical analysis of horizontal pipe curtains with tight rows

1.
Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education, Beijing University of Technology, Beijing 100124, China
2.
China Railway Tunnel Bureau Group Co., Ltd., Guangzhou 511458, China
3.
Guangdong Ocean University, Zhanjiang 524088, China
4.
China Coal Construction Group Co., Ltd., Beijing 100161, China

摘要

摘要: 大直径管幕超前预支护对暗挖工程中的变形控制具有积极作用,管幕的布置形式可分为纵向与横向两种。以北京平安里地铁车站工程及其实测数据为基础,探索性地将带有锁扣的横向管幕简化为弹性薄板,继而对比分析了采用弹性薄板理论和连续梁理论的计算结果；最后,针对导洞开挖跨度、上覆土层厚度、钢管壁厚以及钢管内浆体弹性模量等参数进行了影响分析。结果表明：①无论是在变形趋势,还是在最终变形量上,弹性薄板理论的挠度计算结果都与实测数据吻合性较好,而简支梁与弹性地基梁理论仅最终变形量与实测结果较为吻合；②在相同荷载条件下,弹性薄板理论计算得到的最大弯矩值稍大于简支梁的计算结果,但两者相差不超过10%；③钢管壁厚和浆体弹性模量对管幕变形的影响较小,而开挖导洞跨度和上覆土层厚度对管幕变形与弯矩的影响较大。
- 管幕结构 /
- 弹性薄板理论 /
- 连续梁理论 /
- 现场实测 /
- 对比分析
Abstract: The pre-support of large-diameter pipe curtains plays an active role in controlling the deformation of excavations, and the layout of the pipe curtains can be divided into vertical and horizontal types. Based on the measured data of Pinganli metro station in Beijing, the horizontal pipe curtains with lock are simplified into the elastic thin plates, and the results of the elastic plate theory and the continuous beam theory are compared and analyzed. Finally, the influences of excavation span, height of overburden, wall thickness of steel pipes and elastic modulus of grouting materials are analyzed. The results show: (1) The results of the settlement calculation of the elastic thin plate theory are in good agreement with the measured data both in the settlement trend and in the final settlement, while the calculated results of the simply supported beams and the elastic foundation beams are only in good agreement with the measured ones in the final settlement. (2) Under the same load conditions, the maximum bending moment calculated by the elastic thin plate theory is slightly larger than that of the simply supported beams, but this difference is not more than 10%. (3) The elastic modulus of slurry and the thickness of the steel pipe wall have small effects on the settlement and bending moment of the pipe curtains, while the excavation span and the height of overburden have great influences on the settlement and bending moment of the pipe curtains. The research results may provide a new way to simplify pipe curtains into homogeneous elastic thin plates for calculation, and provide the theoretical support for design of the pipe curtains.
- pipe curtain structure /
- theory of elastic thin plate /
- continuous beam theory /
- field measurement /
- comparative analysis

HTML全文

0. 引言

在地下结构施工中,管幕法是一种极为有效的超前支护工法。该法在结构上部的外围土层中,预先进行钢管顶进,并在各钢管两侧利用锁扣相连,在锁扣空隙内填充止水材料作为浆体,形成一个能抵御上部荷载的超前支护体系,并起到隔断周围水土的作用,从而减小对周围土体与既有建构筑物的扰动。由于该工法能够严格控制沉降,从而常用于超浅埋、超近距穿越等复杂工程,如北京地铁8号线木大区间正线下穿既有10号线盾构区间工程^[1],新机场线磁各庄站—草桥站洞桩法区间上穿既有10号线盾构区间工程^[2]以及19号线超浅埋平安里地铁车站工程^[3]。

已有国内外学者对管幕法的开挖力学行为进行了研究。Kotake等^[4]研究了注浆管幕的承载机理与加固效果,证明管幕可以很好地限制围岩的应力释放,保证掌子面的稳定性；Tan等^[5]利用FLAC软件对管幕法进行数值模拟分析,证明管幕施作可明显减少隧道的变形；Yamakawa等^[6]将钢管的转动效应考虑在内,推导了管幕受荷下的半解析半数值解；贾金青等^[7]将108 mm小管棚简化为梁,利用Pastner弹性地基梁理论对管棚的开挖力学行为进行了理论解析的推导,并通过现场监测数据进行了验证；周顺华等^[8]基于原位观测和室内土工离心模拟试验,阐述了管棚支护的“棚架机理”,并根据钢管直径将管棚分为小管棚体系、中管棚体系与大管棚体系；肖世国等^[9]将管幕简化为固定梁与弹性地基梁,对箱涵顶进管幕施工中管幕的承载机制进行了分析；孙旻等^[10]将纵向管幕简化为板,利用数值模拟手段研究了在施工过程中地表沉降与管幕周围土体位移的变化规律,数值结果与实测结果较为一致,然而该论文中并未对管幕结构在施工过程中的内力进行分析；杨光辉等^[11]通过室内足尺试验,对锁扣管幕的接头力学性能进行了研究；谭忠盛等^[12]依托首都机场T2—T3联络隧道下穿飞机跑道工程,研究了不同管幕布置形式、管径大小以及开挖方法对地表、管幕沉降的影响；赵文等^[13]、贾鹏蛟等^[14]、关永平等^[15]通过数值模拟,室内试验等手段,研究了STS新管幕结构的承载能力及其影响因素,并给出了翼缘板厚度与钢管壁厚之比的合理取值范围。

在现有研究成果中,为便于分析,学者们往往将构成管幕的钢管简化成梁,并忽略钢管之间的锁扣连接,从而可以利用连续梁理论求得开挖阶段管幕的变形与内力。然而,钢管之间的锁扣连接了相邻钢管,协调了各管的变形,使得管幕成为一个整体结构,其变形与受力在各个方向上都趋向于连续,力学机理更偏向于弹性薄板理论。所以,应在考虑锁扣连接条件下建立管幕的力学模型,这对管幕设计和正确预测沉降具有工程实践意义。

在本文中,首先介绍了纵向布置和横向布置的两种管幕布置形式,继而阐述了两种求解横向管幕开挖力学行为的理论方法：连续梁理论和弹性薄板理论；然后,以北京地铁19号线平安里地铁站为工程依托,将横向管幕在开挖过程的实测结果与两种理论的计算结果对比分析；最后,针对导洞开挖跨度、上覆土层厚度、钢管壁厚以及钢管内浆体弹性模量等参数进行了影响分析,并对比分析了两种理论的计算结果。

1. 管幕布置形式与简化方法

1.1 管幕布置形式

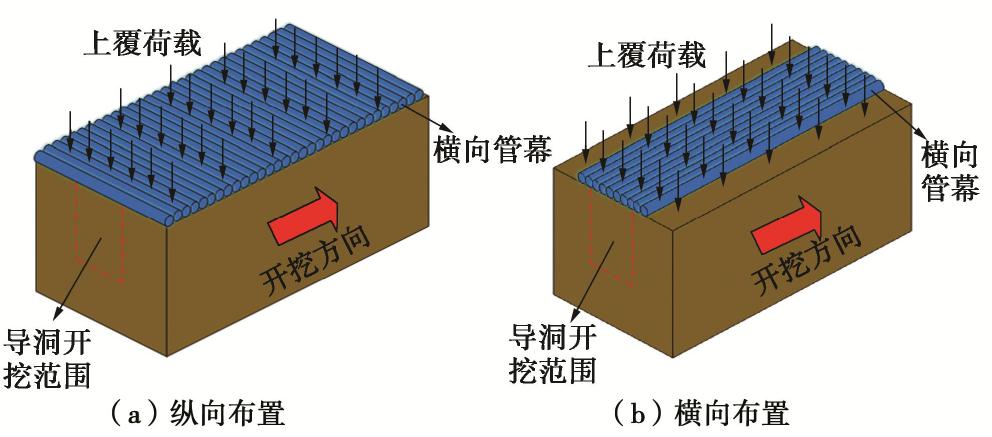
管幕由带锁扣的密排钢管构成,现有两种管幕布置形式：纵向布置和横向布置。管幕纵向布置是指钢管顶进方向与隧道纵向平行,而管幕横向布置是指钢管顶进方向与隧道纵向垂直,如图1所示。纵向管幕在地铁车站与隧道建设中较为常见,而横向管幕一般只用于地铁车站工程。地铁车站纵向长度可以达到200～300 m,而横向长度通常仅为纵向长度的1/10。在纵向管幕施工时,钢管顶进长度较长,较难控制钢管顶进精度,极易在顶进阶段对地表与周围管线造成不可恢复的破坏；并且随钢管顶进长度的增加,顶推力也随之增加,这需要顶管承载墙具有足够的承载力；同时,在开挖过程中,纵向管幕需要辅以较密的格栅/型钢拱架支撑,使得管幕和拱架形成完整的支护体系。相较于纵向管幕来说,横向管幕的钢管顶进长度小,顶进的精度控制较容易,在先行导洞内即可进行钢管的顶进,对承载墙的要求较低；在开挖阶段,管幕可充当开挖后的拱顶初期支护；但横向管幕在顶进前需要进行先行导洞的开挖,在先行导洞开挖过程中会对地表与周围管线造成一定的影响。

图 1 管幕的布置形式

Figure 1. Arrangement of pipe curtains

下载: 全尺寸图片幻灯片

1.2 管幕简化方法

（1）基于连续梁理论的简化

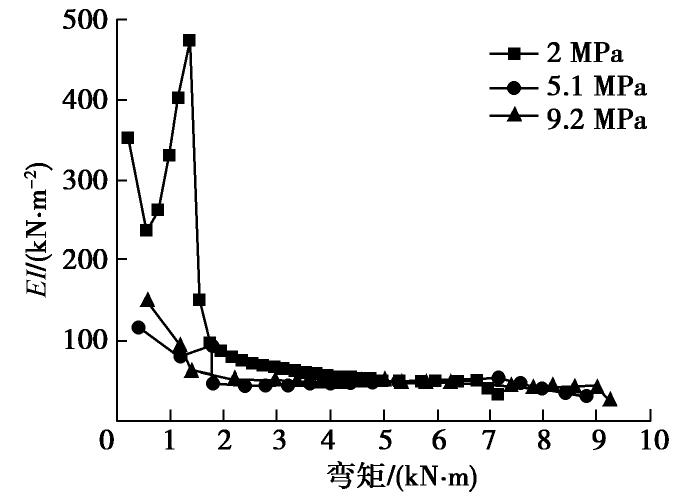
杨光辉等^[11]对注浆锁扣进行了节点纯弯曲足尺试验,得到了锁扣内部不同强度注浆材料下锁扣接头的抗弯刚度,如图2所示。试验中得到的接头抗弯刚度最大约为500 kN·m²。以直径402 mm,壁厚16 mm的钢管为例,注浆填充后,计算得到的弯曲刚度为7800 kN·m²,锁扣接头的弯曲刚度仅为注浆后钢管的1/15,认为锁扣传力能力有限,可不予考虑。所以,在对管幕进行分析时,可忽略接头处的影响,将管幕简化为各自独立的钢管。

图 2 管幕接头弯曲试验曲线^[11]

Figure 2. Curves of bending tests on joints of pipe curtains^[11]

下载: 全尺寸图片幻灯片

（2）基于弹性薄板理论的简化

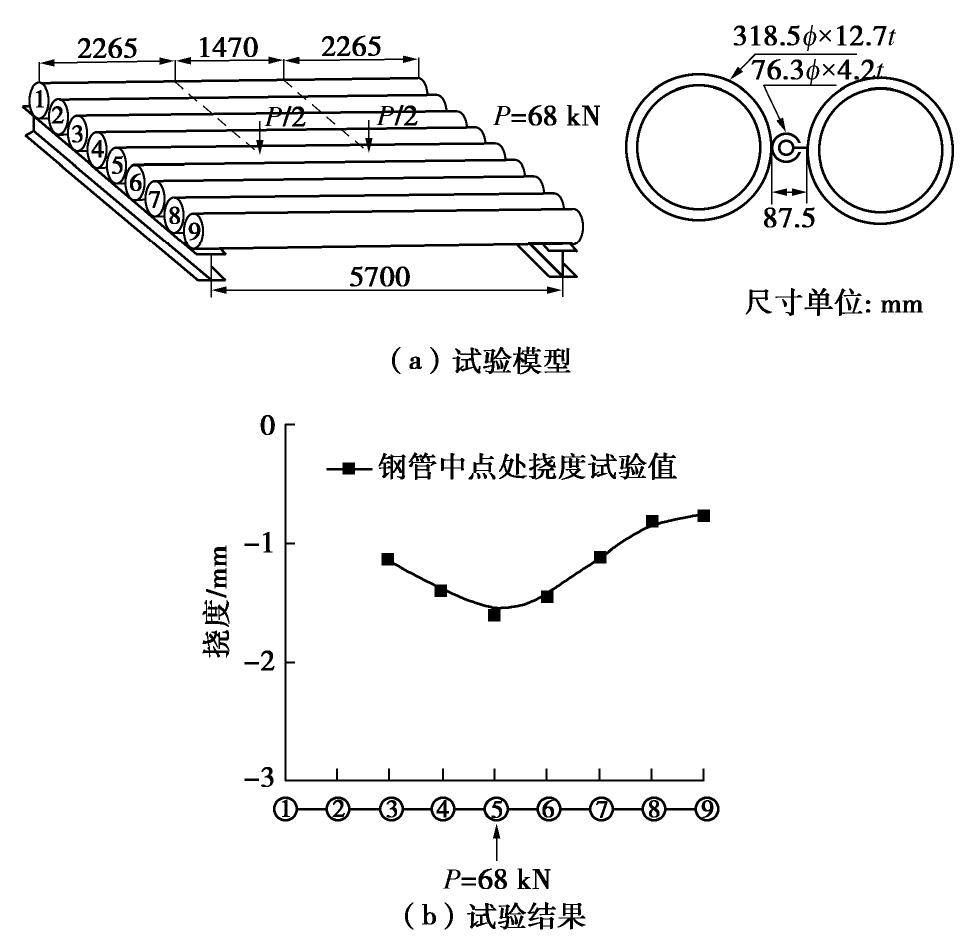
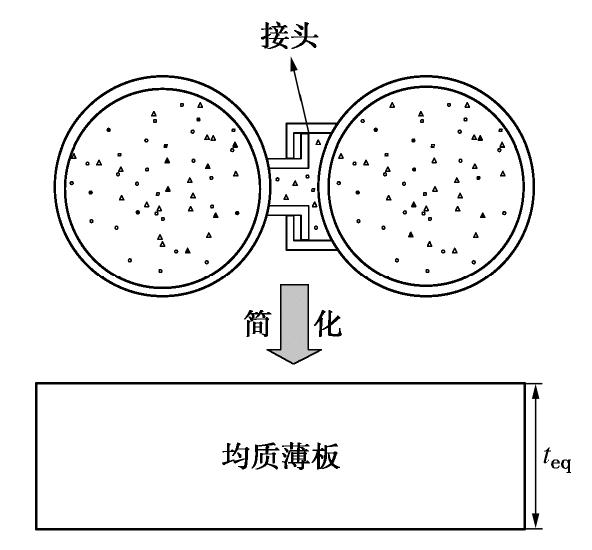
Yamakawa等^[6]通过半解析、半数值法推导了考虑钢管转动效应的管幕受荷下的解析式,并通过室内试验对该解析式进行了验证。然而,该解析式求解过程较为繁琐,难以直接应用于实际工程。图3给出了文献[6]中横向管幕室内试验模型与钢管跨中挠度结果,图3（b）中横坐标序号为钢管编号,与图3（a）相对应。可以看出,管幕变形呈现出一定的连续性。基于该试验,不考虑钢管的转动效应与接头对管幕弯曲刚度的贡献,可将管幕简化为弹性薄板,如图4所示。

图 3 日本管幕加载试验模型与结果^[6]

Figure 3. Model and results of loading tests on pipe curtains^[6]

下载: 全尺寸图片幻灯片

图 4 管幕简化示意图

Figure 4. Simplification of pipe curtains

下载: 全尺寸图片幻灯片

在利用弹性薄板理论对管幕进行解析时,需要对简化后等效弹性模量E_eq和等效厚度t_eq进行取值。采用文献^[16]中将抗弯刚度与抗压刚度同时等效的方法得到薄板的弹性模量E_eq和厚度t_eq。等效方法如下：

$t_{eq} = \sqrt{12 \frac{K_{g} + K_{j}}{R_{g} + R_{j}}}$ ,

(1)

$E_{eq} = \frac{R_{g} + R_{j}}{b_{1} t_{eq}}$ 。

(2)

式中 t_eq为薄板等效厚度,E_eq为薄板等效弹性模量, $R_{g}$ 为钢管抗压刚度, $R_{j}$ 为钢管内浆体抗压刚度, $K_{g}$ 为钢管抗弯刚度, $K_{j}$ 为钢管内浆体抗弯刚度,b₁为管幕的承载宽度,在这里取为钢管圆心距。

2. 连续梁计算理论

2.1 弹性地基梁计算方法^[17]

（1）弹性地基梁力学模型

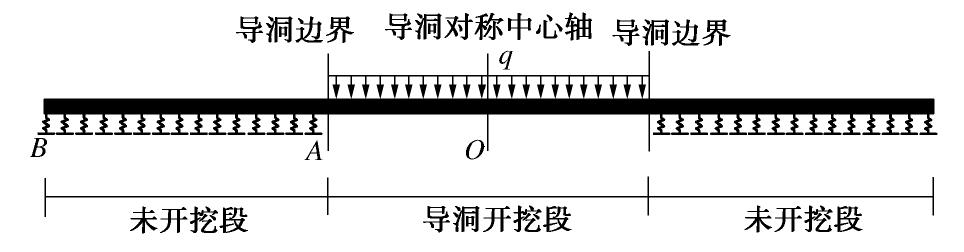
本节将钢管简化为梁,用弹簧模拟钢管与土体的相互作用。简化计算模型如图5所示。管幕承受上部均布荷载,O为开挖导洞中点,A为开挖导洞边界,AB为管幕在未开挖段的长度,且AB段符合Winkler计算假定的弹性围岩-钢管结构梁力学计算模型。现将OA段钢管划分为m个单元,将AB段钢管划分为n个单元,单元之间通过节点传递荷载。

图 5 管幕弹性地基梁简化模型

Figure 5. Simplified model for elastic foundation beams of pipe curtains

下载: 全尺寸图片幻灯片

（2）单元受力分析

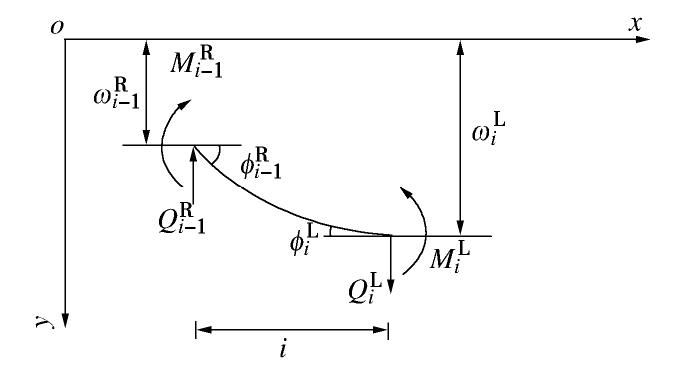
取钢管长度方向第 $i$ 个单元进行受力分析,如图6所示。图中, $ω_{i - 1}^{R}$ 为节点单元i-1右侧的挠度, $M_{i - 1}^{R}$ 为节点单元i-1右侧的弯矩, $ϕ_{i - 1}^{R}$ 为节点单元i-1右侧的转角, $Q_{i - 1}^{R}$ 为节点单元i-1右侧的剪力, $ω_{i}^{L}$ 为节点单元i左侧的挠度, $M_{i}^{L}$ 为节点单元i左侧的弯矩, $ϕ_{i}^{L}$ 为单元 $i$ 左侧的转角, $Q_{i}^{L}$ 为节点单元i左侧的剪力。

图 6 第i个单元受力分析

Figure 6. Force analysis for i-unit

下载: 全尺寸图片幻灯片

根据受力平衡条件,可以得到如下平衡方程：

$Q_{i}^{L} - Q_{i - 1}^{R} = 0$ ,

(3)

$M_{i}^{L} - M_{i - 1}^{R} - Q_{i - 1}^{R} L_{i} = 0$ ,

(4)

$ω_{i}^{L} = ω_{i - 1}^{R} - ϕ_{i - 1}^{R} L_{i} - M_{i}^{L} \frac{L_{i}^{2}}{2 E I_{i}} + Q_{i}^{L} \frac{L_{i}^{3}}{3 E I_{i}}$ ,

(5)

$ϕ_{i}^{L} = ϕ_{i - 1}^{R} + M_{i}^{L} \frac{L_{i}}{E I_{i}} - Q_{i}^{L} \frac{L_{i}^{3}}{2 E I_{i}}$ 。

(6)

式中 EI_i为钢管的抗弯刚度,L_i为钢管长度。

将上述方程整理成矩阵形式,可得

$\begin{matrix} [S_{i}^{L}] = [\begin{matrix} 1 \\ Q_{i}^{L} \\ M_{i}^{L} \\ ω_{i}^{L} \\ ϕ_{i}^{L} \end{matrix}] = [\begin{matrix} 1 & 0 & 0 & 0 0 \\ 0 & 1 & 0 & 0 0 \\ 0 & L_{i} & 1 & 0 0 \\ \begin{array}{l} 0 \\ 0 \end{array} & \begin{array}{l} - \frac{L_{i}^{3}}{6 E I_{i}} \\ \frac{L_{i}^{2}}{2 E I_{i}} \end{array} & \begin{array}{l} - \frac{L_{i}^{2}}{2 E I_{i}} \\ \frac{L_{i}^{}}{E I_{i}} \end{array} & \begin{array}{l} 1 - L_{i} \\ 01 \end{array} \end{matrix}] [\begin{matrix} 1 \\ Q_{i - 1}^{R} \\ M_{i - 1}^{R} \\ ω_{i - 1}^{R} \\ ϕ_{i - 1}^{R} \end{matrix}] \\ = [D_{i, j - 1}] [S_{i - 1}^{R}] 。 \end{matrix}$ .

(7)

式中 $[S_{i}^{L}]$ 为节点单元i左侧的内力矩阵； $[D_{i, i - 1}^{L}]$ 为梁单元的传递矩阵； $[S_{i - 1}^{R}]$ 为节点单元i-1右侧的内力矩阵。

（3）节点受力分析

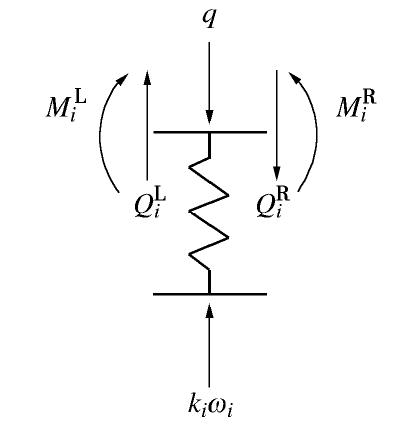
对第 $i$ 个节点单元的内力进行分析,如图7所示。图中, $Q_{i}^{R}$ , $M_{i}^{R}$ , $ω_{i}^{R}$ , $ϕ_{i}^{R}$ 分别为节点单元i右侧的剪力、弯矩、挠度、转角, $Q_{i}^{L}$ , $M_{i}^{L}$ , $ω_{i}^{L}$ , $ϕ_{i}^{L}$ 分别为单元i左侧的剪力、弯矩、挠度、转角。对于导洞内节点（OA段）,取k_i=0即可。

图 7 第i节点的内力传递

Figure 7. Internal force transfer of i-unit

下载: 全尺寸图片幻灯片

根据平衡条件可得矩阵方程：

$[S_{i}^{R}] = [\begin{matrix} 1 \\ Q_{i}^{R} \\ M_{i}^{R} \\ ω_{i}^{R} \\ ϕ_{i}^{R} \end{matrix}] = [\begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} \begin{matrix} 1 \\ - q_{i} \\ M_{i} \\ 0 \\ 0 \end{matrix} & \begin{matrix} 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{matrix} \end{matrix} & \begin{matrix} 0 \\ 0 \\ 1 \\ 0 \\ 0 \end{matrix} \end{matrix} & \begin{matrix} 0 \\ k_{i} \\ 0 \\ 1 \\ 0 \end{matrix} \end{matrix} & \begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{matrix} \end{matrix}] [\begin{matrix} 1 \\ Q_{i - 1}^{L} \\ M_{i - 1}^{L} \\ ω_{i - 1}^{L} \\ ϕ_{i - 1}^{L} \end{matrix}] = [G_{i}] [S_{i}^{L}],$

(8)

式中, $[S_{i}^{R}]$ 为节点单元i右侧的内力矩阵, $[G_{i}]$ 为节点单元i左右两侧内力的传递矩阵,k_i为地基系数^[18]：

$k_{i} = \frac{0.65 E_{s}}{B (1 - μ^{2})} \sqrt[12]{\frac{E_{s} B^{4}}{E I}}$ ,

(9)

式中, $E_{s}$ 为土体弹性模量,μ为土体泊松比,EI为梁抗弯刚度,B为梁宽度（本文为取钢管外径）。

由式（7）,（8）可得

$S_{n}^{L} = [D_{n, n - 1}] [G_{n - 1}] \dots \dots [G_{i}] [D_{i, i - 1}] \dots \dots [G_{1}] [D_{1, 0}] [S_{0}^{R}] 。$

(10)

结合边界条件即可求得式（10）。

对于图5所示的地基模型,边界条件为

${[\begin{matrix} Q_{o} & ϕ_{o} \end{matrix}]}^{T} = {[\begin{matrix} 0 & 0 \end{matrix}]}^{T}, {[\begin{matrix} Q_{B} & M_{B} \end{matrix}]}^{T} = {[\begin{matrix} 0 & 0 \end{matrix}]}^{T}$ 。

(11)

2.2 简支梁与固支梁计算方法

对于简支梁与固支梁的计算方法,只需要将图5中A点的约束条件改为简支梁与固支梁所对应的边界条件即可。计算方法已在2.1节中叙述,不再赘述。

其中,简支梁的边界条件为

${[\begin{matrix} Q_{o} & ϕ_{o} \end{matrix}]}^{T} = {[\begin{matrix} 0 & 0 \end{matrix}]}^{T}, {[\begin{matrix} ω_{A} & M_{A} \end{matrix}]}^{T} = {[\begin{matrix} 0 & 0 \end{matrix}]}^{T}$ 。

(12)

固支梁的边界条件为

${[\begin{matrix} Q_{o} & ϕ_{o} \end{matrix}]}^{T} = {[\begin{matrix} 0 & 0 \end{matrix}]}^{T}, {[\begin{matrix} ω_{A} & ϕ_{A} \end{matrix}]}^{T} = {[\begin{matrix} 0 & 0 \end{matrix}]}^{T}$ 。

(13)

2.3 连续梁理论模型验证

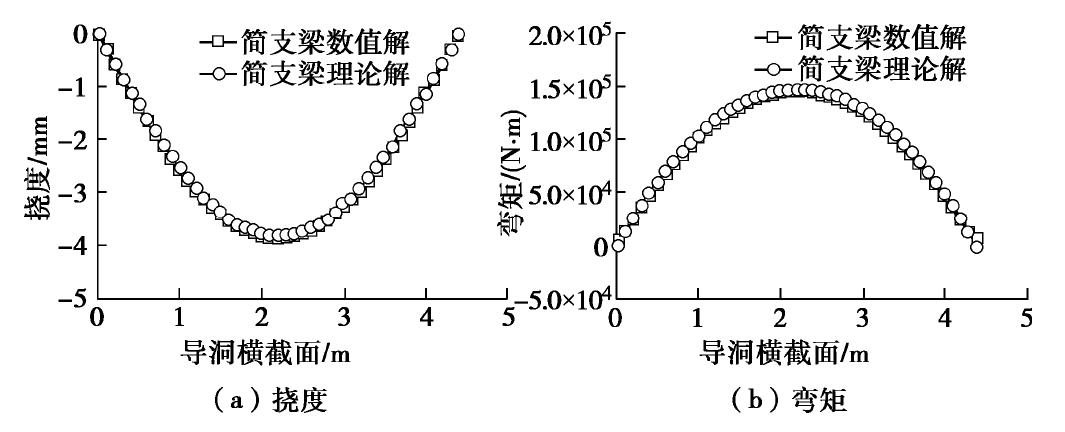
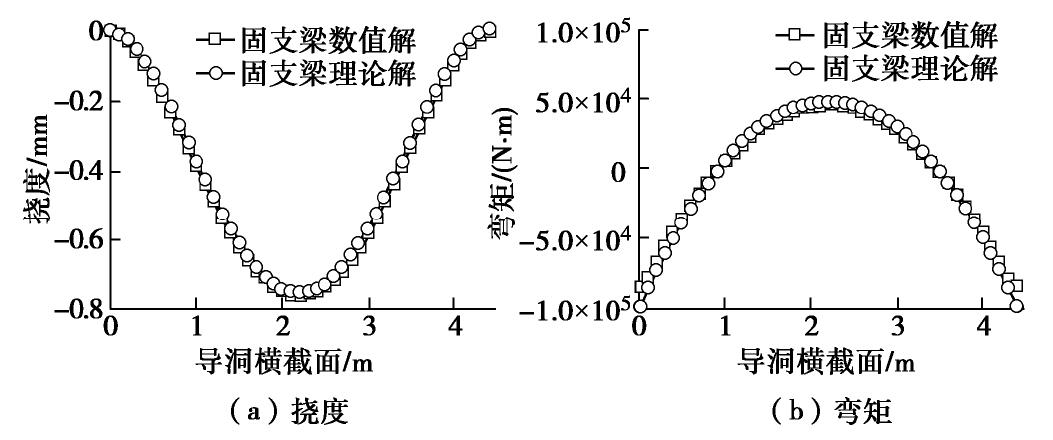
为验证本节连续梁计算理论的正确性,采用有限元数值方法分别对简支梁、固支梁和弹性地基梁进行计算,并将计算结果与理论模型计算结果进行对比分析。在有限元软件中,利用梁单元对等效后的管幕结构进行建模,梁单元的计算参数按4.1节取值。

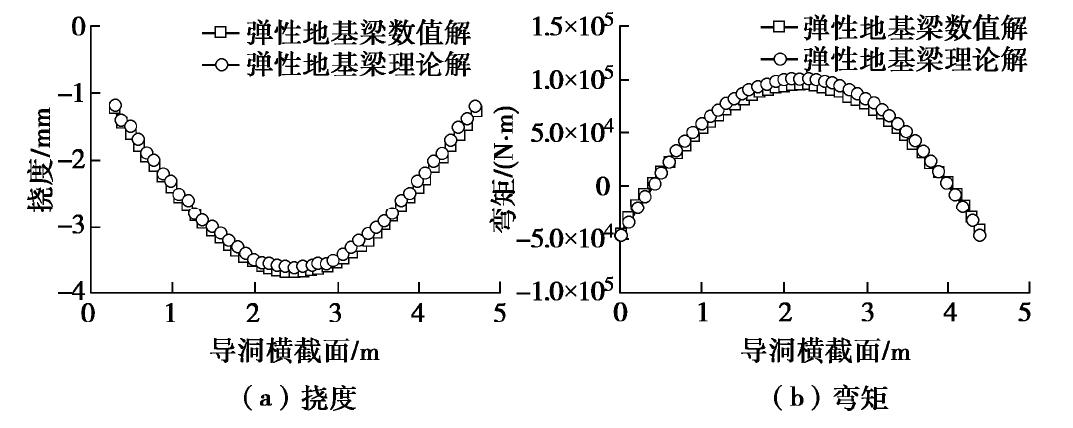
图8～10分别为简支梁、固支梁和弹性地基梁数值解与理论解的挠度和弯矩对比图。从图中可以看出,数值解与理论解趋势基本一致,且两者吻合度高,证明了本节连续梁理论的正确性。

图 8 简支梁数值解与理论解对比

Figure 8. Comparison between numerical and theoretical solutions of simply supported beams

下载: 全尺寸图片幻灯片

图 9 固支梁数值解与理论解对比

Figure 9. Comparison between numerical and theoretical solutions of fixed beams

下载: 全尺寸图片幻灯片

图 10 弹性地基梁数值解与理论解对比

Figure 10. Comparison between numerical and theoretical solutions of beams on elastic foundation

下载: 全尺寸图片幻灯片

3. 弹性薄板计算理论

3.1 边界条件的简化

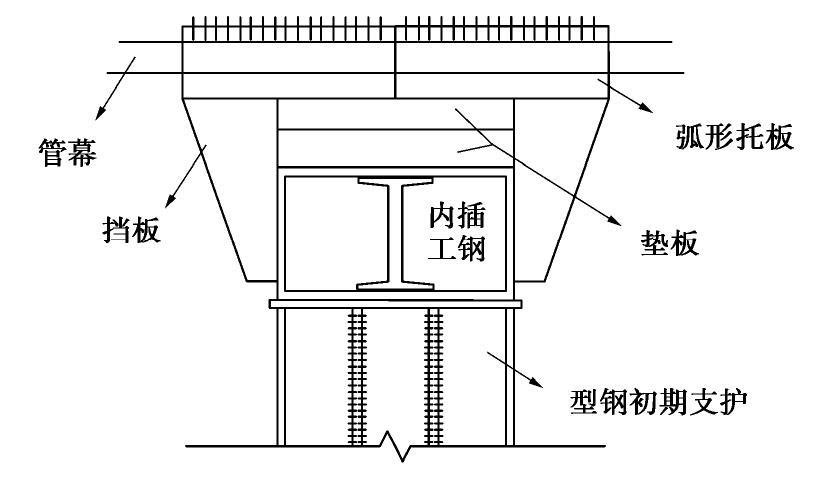
在管幕法施工中,横向管幕自身具有刚度高的优点,为充分发挥此特点,可取消传统封闭式导洞施工中拱顶的初支（顶部）,改由初支侧墙、初支底板以及管幕组成封闭结构,初支侧墙与管幕之间设置有专用连接节点,节点详图如图11所示,连接节点由弧形托板、挡板、垫板、调节件构成,管幕与弧形托板之间焊接,弧形托板与垫板之间搭接。管幕、弧形托板、垫板、调节件与初支侧墙共同构成竖向传力体系。由于管幕、初支侧墙以及初支底板已构成封闭体系,故在上覆荷载作用下,管幕与侧墙初支相连支座处沉降可以忽略不计,但管幕可以发生微小的转角,所以管幕与初支连接处可简化为铰接支座。对于掌子面处管幕边界条件,为简化分析,也可按铰接支座处理。综上所述,随着导洞的开挖,管幕可简化为“三边简支,一边自由”的弹性薄板进行分析。

图 11 管幕与初支侧墙连接节点图

Figure 11. Joints of pipe curtains and side wall with primary support

下载: 全尺寸图片幻灯片

3.2 力学模型的建立

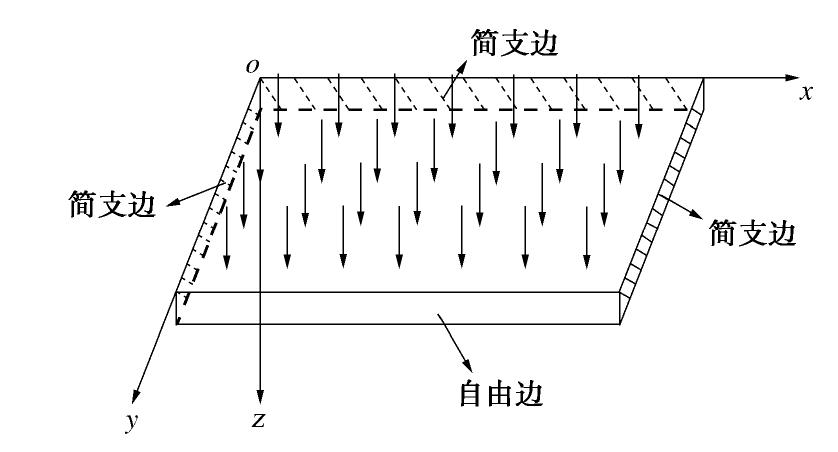
根据薄板的小挠度弯曲理论^[19],建立如图12所示的力学模型,其中,x方向为导洞开挖跨度,导洞沿y方向的负方向进行开挖,y=0处为导洞掌子面。

图 12 弹性薄板力学模型图

Figure 12. Mechanical model for elastic thin plates

下载: 全尺寸图片幻灯片

3.3 解析式的求解

矩形薄板弹性弯曲的基本方程为

$\frac{\partial^{4} ω}{\partial x^{4}} + 2 \frac{\partial^{4} ω}{\partial x^{2} \partial y^{2}} + \frac{\partial^{4} ω}{\partial y^{4}} = \frac{q}{D}$ ,

(14)

式中,q为作用在板上的荷载,D为薄板的弯曲刚度,ω为薄板挠度。

借鉴黄炎等^[20-21]的研究成果与弹性力学中关于莱维解^[19]的叙述：对于存在一对边（x=0,a）为简支的矩形薄板,薄板通解可写为如下形式：

$\begin{array}{l} ω = \sum_{m} [A_{m} sinh α (b - y) + B_{m} sinh α y + C_{m} α (b - y) \cdot \\ cosh α (b - y) + D_{m} α y cosh α y] \sin α x + ω_{0} \end{array}$ ,

(15)

式中,ω₀为式（15）的任一特解,可取为

$ω_{0} = \sum_{m} \sum_{n} A_{m n} \sin α x \sin β y$ ,

(16)

$A_{m n} = \frac{4 q (1 - \cos m π)(1 - \cos n π)}{π^{6} D m n {(\frac{m^{2}}{a^{2}} + \frac{n^{2}}{b^{2}})}^{2}}$ ,

(17)

$D = \frac{E h^{3}}{12 (1 - μ^{2})}$ ,

(18)

$α = \frac{m π}{a} (m = 1, 2, \dots, \infty), β = \frac{n π}{b} (n = 1, 2, \dots, \infty)$ 。

(19)

根据模型图12所示,式（15）在y=0和y=b分别满足边界条件：

$ω_{y = 0} = 0, {\frac{\partial^{2} ω}{\partial y^{2}}}_{y = 0} = 0$ ,

(20)

$\begin{array}{l} {(M_{y})}_{y = b} = {[- D (\frac{\partial^{2} ω}{\partial y^{2}} + μ \frac{\partial^{2} ω}{\partial x^{2}})]}_{y = b} = 0, \\ {(F_{S_{y}})}_{y = b} = {[\frac{\partial^{3} ω}{\partial y^{3}} + (2 - μ) \frac{\partial^{3} ω}{\partial x^{2} \partial y}]}_{y = b} = 0 。 \end{array}}$

(21)

联立式（15）～（21）可得

$A_{m} = C_{m} = 0$ ,

(22)

$\begin{array}{l} B_{m} = - {8 q (1 - \cos m π) (1 - \cos n π) β \cos β b [β^{2} + (2 - μ) α^{2}]} \cdot \\ {π^{6} D m n α^{3} {(\frac{m^{2}}{a^{2}} + \frac{n^{2}}{b^{2}})}^{2} (1 - μ) [(μ + 3) \cosh α b + \frac{(1 - μ) α b}{\sinh α b}]}^{- 1} - \\ {4 q (1 - \cos m π) (1 - \cos n π) b β \cos β b [β^{2} + (2 - μ) α^{2}] \cosh α b} \cdot \\ {π^{6} D m n α^{2} {(\frac{m^{2}}{a^{2}} + \frac{n^{2}}{b^{2}})}^{2} [(μ + 3) \cosh α b \sinh α b + (1 - μ) α b]}^{- 1}, \\ D_{m} = {4 q (1 - \cos m π) (1 - \cos n π) β \cos β b [β^{2} + (2 - μ) α^{2}]} \cdot \\ {π^{6} D m n α^{3} {(\frac{m^{2}}{a^{2}} + \frac{n^{2}}{b^{2}})}^{2} [(μ + 3) \cosh α b + \frac{(1 - μ) α b}{\sinh α b}]}^{- 1} 。 \end{array}$

(23)

将式（22）和（23）代入式（15）即可得到“三边简支,一边自由”在均布荷载下的挠度解析式,同时可得到薄板 $x$ 和 $y$ 方向弯矩解析式为

$\begin{array}{l} M_{x} = \sum_{m} [(μ - 1) B_{m} α^{2} \sinh α y \sin α x + 2 μ D_{m} α^{2} \sinh α y \sin α x + \\ (μ - 1) D_{m} α^{3} y \cosh α y \sin α x] - \sum_{m} \sum_{n} A_{m n} \sin α x \sin β y (α^{2} + μ β^{2}), \\ M_{y} = \sum_{m} [(1 - μ) B_{m} α^{2} \sinh α y \sin α x + 2 D_{m} α^{2} \sinh α y \sin α x + \\ (1 - μ) D_{m} α^{3} y \cosh α y \sin α x] - \sum_{m} \sum_{n} A_{m n} \sin α x \sin β y (β^{2} + μ α^{2}) 。 \end{array}}$

(24)

3.4 弹性薄板理论模型验证

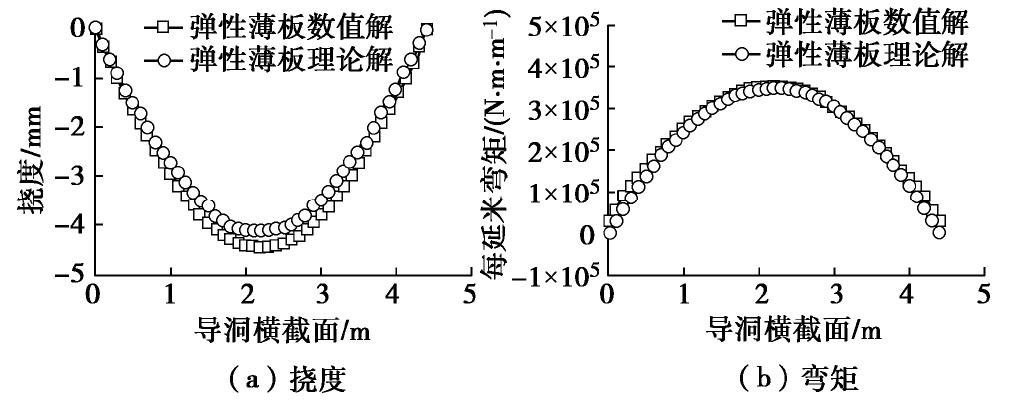
同样采用有限元数值方法对本节的理论解析式进行验证。利用有限元软件中壳单元对等效后的管幕结构进行建,薄板纵向长度取为10 m,横向长度取导洞开挖跨度4.4 m,其余计算参数仍按4.1节取值。

图13给出了薄板自由边数值解与理论解的挠度和x向弯矩对比图。从图中可以看出,在挠度计算结果方面,数值解略大于理论解,跨中挠度的数值解为-4.43 mm,而理论解为-4.11 mm,偏差率为7.8%,两者拟合度较好；而在弯矩计算结果方面,理论解与数值解基本吻合。因此,验证了本节弹性薄板理论解析式的正确性。

图 13 弹性薄板数值解与理论解对比

Figure 13. Comparison between numerical solution and theoretical solutions of elastic thin plates

下载: 全尺寸图片幻灯片

4. 计算结果及对比分析

4.1 依托工程及参数介绍

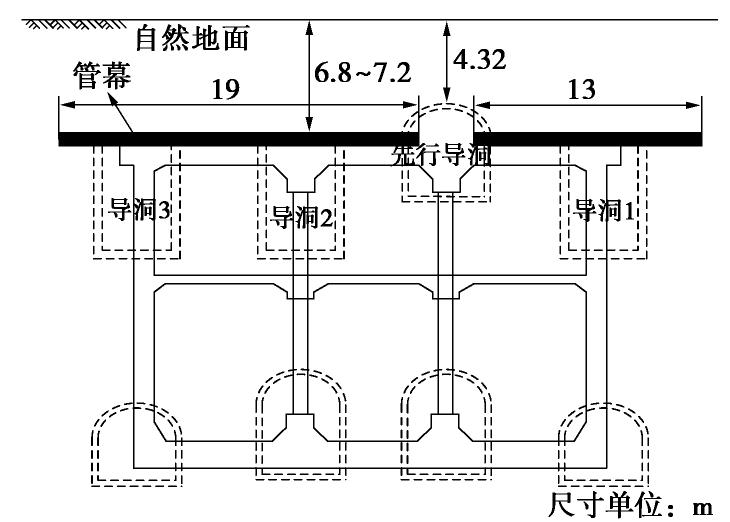
本文以北京地铁19号线平安里站为工程依托,将现场实测导洞拱顶数据与两种理论的计算结果对比分析。平安里地铁车站主体结构设计长度为225.45 m,标准段宽度为25.1 m。车站结构顶板的覆土厚度约为6.8～7.2 m,底板埋深为20.7～21.15 m,采用PBA工法进行开挖。主体结构施工时,首先对先行导洞进行开挖,然后在先行导洞内沿车站横向打设钢管形成管幕,先行导洞拱顶最小覆土约为4.32 m,车站标准段横断面如图14所示。管幕采用直径D_e=402 mm,壁厚t=16 mm的钢管,钢管之间采用锁扣连接,相邻钢管圆心距为450 mm。钢管内灌注水泥砂浆,钢管弹性模量E_g=210 GPa,水泥砂浆弹性模量E_j=2 GPa,管幕覆土厚度7 m,重度为20 kN/m³,导洞开挖跨度为4.4 m。

图 14 车站横断面图

Figure 14. Cross section of station

下载: 全尺寸图片幻灯片

连续梁理论的计算参数：取钢管总长14.4 m,其中导洞内长度为4.4 m,土体中长度为10 m,导洞两侧各5 m,管幕等效弹性模量E_q=60 GPa,惯性矩I=0.00126 m⁴,等效抗弯刚度E_qI=7800kN·m²,并将管幕分为144份（m为22,n为50）,即每0.1 m划分为一个单元,地基系数k_i=3.44×10⁴ kN/m³。

弹性薄板理论需要的计算参数为：根据式（1）,（2）计算得到管幕等效后的薄板厚度t_eq=0.47 m,薄板弯曲刚度D=190000 kN·m,取等效后薄板的泊松比μ=0.3。

4.2 管幕挠度对比分析

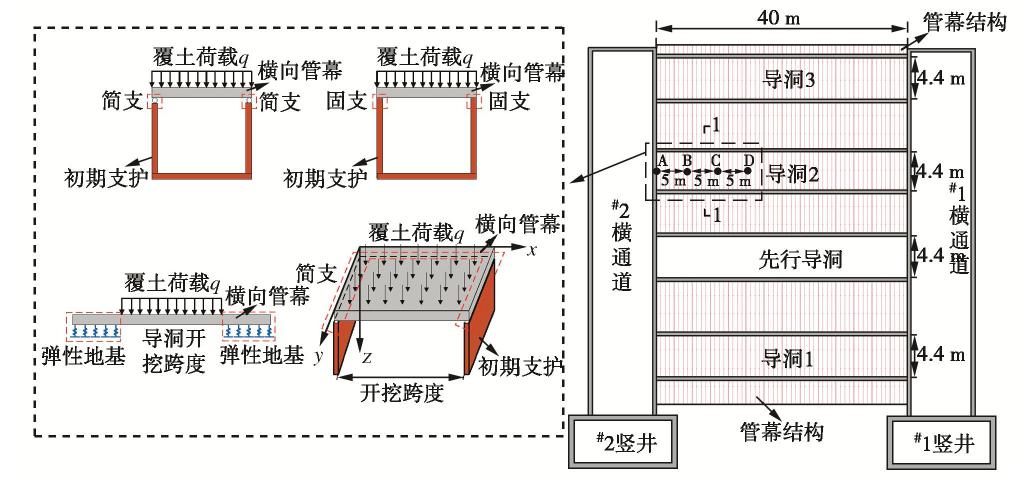
在施工过程中,对^#2导洞开挖过程中拱顶沉降进行了现场监测。监测点位置及不同模型计算简图如图15所示。

图 15 测点布置与不同模型计算简图

Figure 15. Layout of monitoring points and calculation diagram

下载: 全尺寸图片幻灯片

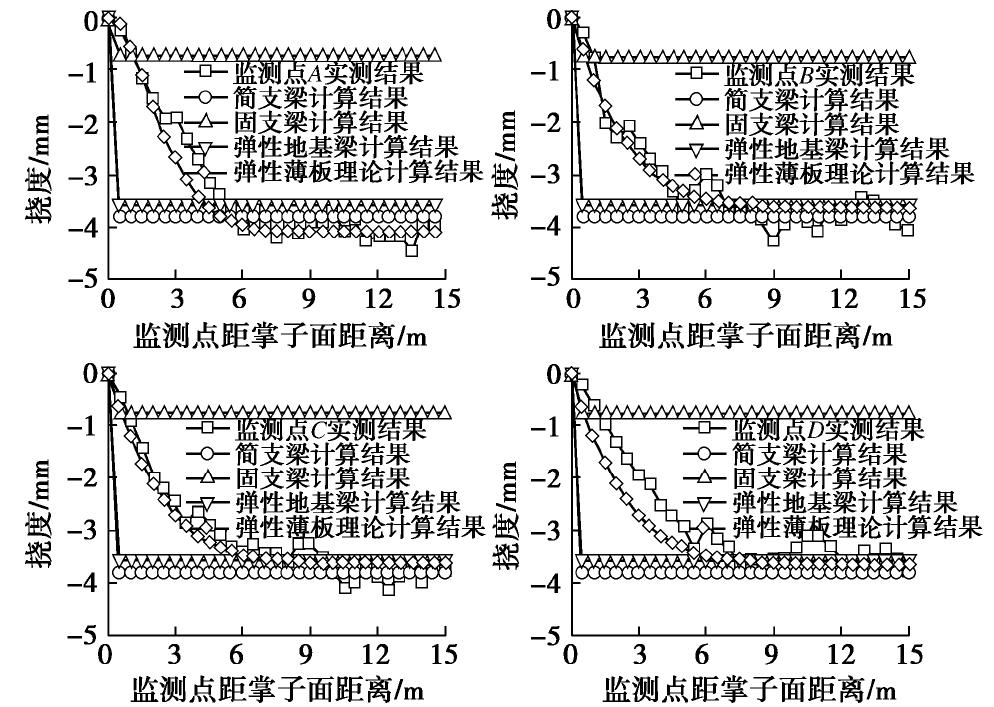
不同测点处实测数据与两种理论的计算结果如图16所示。由图16可知,在掌子面通过监测点后4 m范围内,管幕处于快速变形阶段；而掌子面通过监测点4～6 m范围内,管幕处于缓慢变形阶段；掌子面通过监测点6 m以后,管幕的沉降趋于稳定,在一定范围内波动。根据弹性薄板理论计算得到的不同测点最终挠度分别为：-4.1 mm（A点）和-3.6 mm（B,C,D点）；连续梁理论计算得到的不同测点的挠度均相同,分别为：-3.8 mm（简支梁）、-0.75 mm（固支梁）以及-3.6 mm（弹性地基梁）。通过将两种理论计算结果与实测数据对比分析,发现：弹性薄板理论计算结果无论是在变形趋势上,还是在最终变形量上都与实测数据吻合性较好；而简支梁与弹性地基梁理论的计算结果仅在最终变形量上与实测结果较为吻合,无法预测管幕的变形过程；而固支梁的计算结果仅为-0.75 mm,远远小于实测结果。产生该现象的原因：连续梁理论不考虑钢管之间的连接,当开挖掌子面超过钢管的承载范围后,钢管的变形即达到了稳定阶段,故连续梁理论的解近乎于一条直线；而弹性薄板理论考虑了锁扣的作用,管幕相当于横向长度不变,纵向长度随着掌子面开挖不断增长的弹性薄板,故弹性薄板理论计算结果可以有趋势的预测管幕的变形。以上现象说明了管幕的变形规律更符合弹性薄板理论,虽然弹性地基梁与简支梁理论也可以较好地预测管幕的最终变形量,但连续梁理论无法预测在开挖过程中管幕的变形。

图 16 导洞拱顶沉降曲线

Figure 16. Settlement curves of crown

下载: 全尺寸图片幻灯片

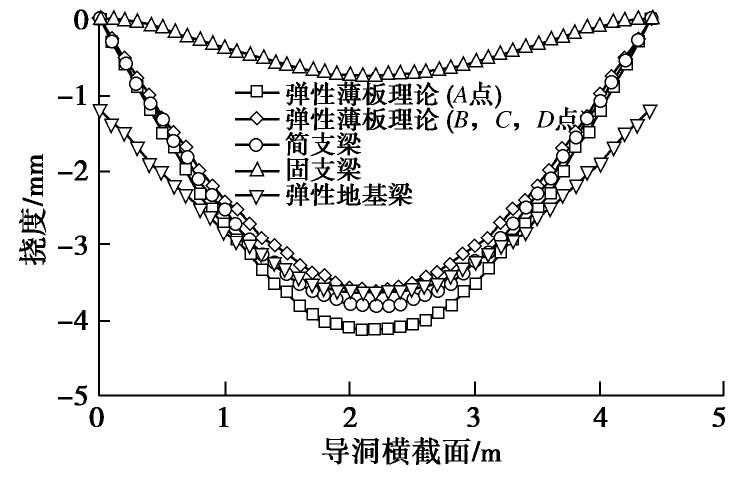
图17给出了不同理论下监测点A,B,C,D截面的最终变形结果。由图17可以看出,由于受自由边的影响,弹性薄板理论计算得到的自由边的最终变形结果要稍稍大于其他3个截面；简支梁与弹性薄板理论计算得到的最终变形结果较为一致；而弹性地基梁理论计算结果在跨中附近与简支梁、弹性薄板理论的计算结果较为接近,但该计算结果在边界处存在1.2 mm的沉降；固支梁理论计算得到的最终沉降量最小,远远小于其他理论的计算结果。

图 17 不同理论计算得到的管幕最终变形曲线

Figure 17. Curves of final settlement calculated by different theories

下载: 全尺寸图片幻灯片

4.3 管幕弯矩对比分析

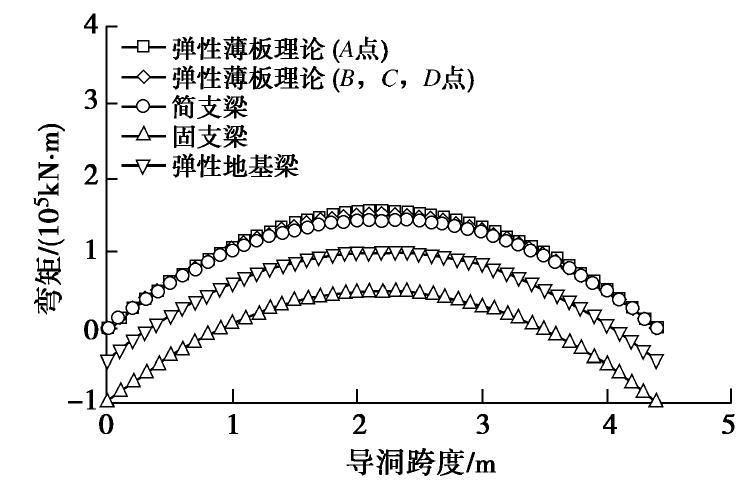
薄板弯矩分为x方向（导洞横向）与y方向（导洞纵向）,由于y方向自由边的存在,y方向弯矩远小于x方向弯矩。故在下文对薄板弯矩分析时,仅对薄板最大弯矩（x方向）进行分析,x和y方向如图12所示。图18给出了连续梁与弹性薄板理论计算得到的不同截面管幕的最终弯矩图。值得注意的是,通过理论解析得到的弯矩计算结果为薄板单位宽度的弯矩值,单位为N·m/m。因此,弹性薄板的x方向弯矩计算结果需乘以管幕间距（0.45 m）才可以得到作用在单根管幕结构上的弯矩值。可以看出,弹性薄板理论的弯矩计算结果为157.5 kN·m,不同截面的弯矩值较为接近；对于连续梁理论的计算结果,简支梁计算的弯矩计算结果最大,为146 kN·m,固支梁与弹性地基梁计算结果大小相同,固支梁为-100 kN·m,弹性地基梁为100 kN·m；固支梁弯矩最大值出现在支座处,而其余计算结果均出现在跨中。弹性薄板理论的弯矩计算结果稍大于简支梁理论的计算结果,但两者相差仅为7.9%。因此,在对管幕进行设计时,可利用弹性薄板理论的弯矩计算结果进行承载力包络设计或简支梁理论的弯矩计算结果乘以一定的安全系数进行设计,保证管幕的有效性以及施工的安全性。

图 18 不同理论计算得到的管幕x方向弯矩曲线

Figure 18. Bending moments calculated by different theories

下载: 全尺寸图片幻灯片

5. 影响参数分析

在本节中拟对钢管壁厚度、注浆材料弹性模量、导洞开挖跨度以及作用在管幕上荷载大小等参数进行管幕挠度与弯矩的影响分析。计算基本参数照5.1节选取。由于篇幅限制以及为便于分析,在后文中取不同参数下薄板挠度、x方向弯矩的最大值与连续梁理论的计算结果进行对比分析。

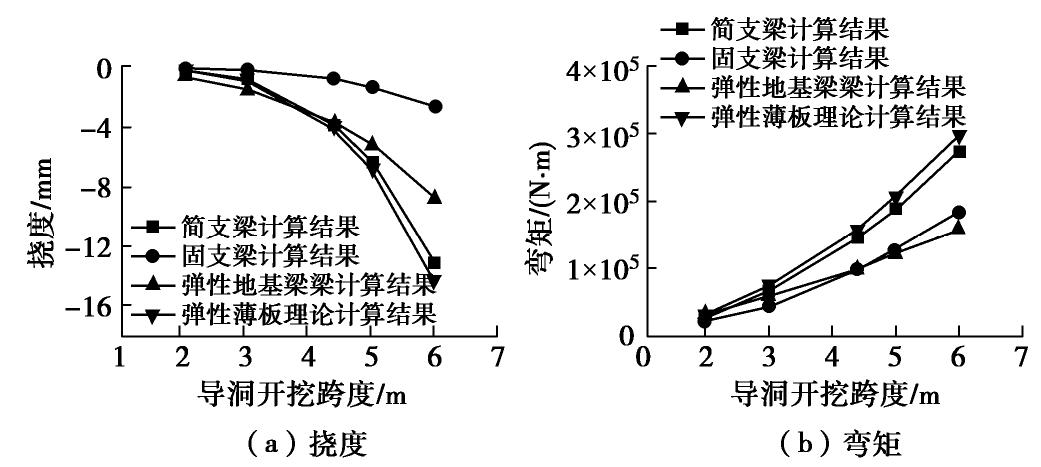
5.1 导洞开挖跨度的影响

分别取导洞跨度为2,3,4.4,5,6 m,得到不同理论计算的挠度和弯矩随导洞开挖跨度的变化规律,如图19所示。可以看出,不同理论挠度和弯矩的计算结果均随导洞开挖跨度的增大而非线性增大。弹性薄板理论与简支梁理论的挠度计算结果较为接近,且增长速度远远大于弹性地基梁和固支梁计算结果；弹性地基梁挠度增长速度次之,固支梁挠度增长速度最慢。当导洞跨度为6 m时,管幕挠度分别为：14.3 mm（弹性薄板）、13.2 mm（简支梁）、8.8 mm（弹性地基梁）和2.6 mm（固支梁）。

图 19 不同开挖跨度管幕对比曲线

Figure 19. Comparison curves of pipe curtains with different excavation spans

下载: 全尺寸图片幻灯片

弹性薄板理论和简支梁理论计算的弯矩增长速度最快,固支梁计算增长速度次之,弹性地基梁增长速度最慢。导洞跨度为6 m时,不同理论计算得到的弯矩分别为：298 kN·m（弹性薄板）、274 kN·m（简支梁）、184 kN·m（固支梁）、161.6 kN·m（固支梁）。弹性薄板理论的弯矩计算结果稍大于简支梁理论的计算结果。当导洞跨度为6 m时,弹性薄板和简支梁的挠度计算结果相差约为8.3%,而弯矩计算结果相差约为8.8%。综上所述,横向管幕结构的弯矩和挠度计算结果对导洞跨度参数的变化较为敏感,在进行设计时应对导洞跨度进行合理的设计。

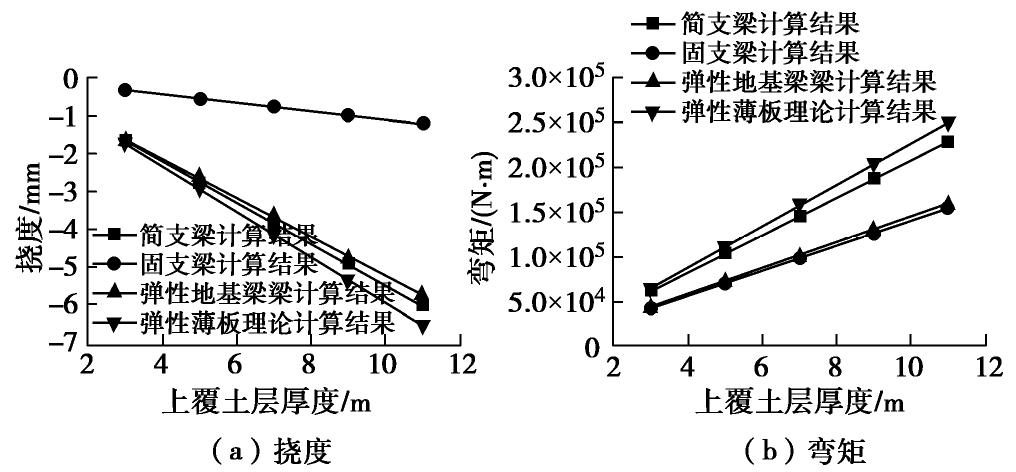
5.2 上覆土层厚度的影响

取上覆土层厚度分别为3,5,7,9,11 m,得到不同理论下挠度与弯矩随上覆土层厚度变化规律,如图20所示。不同理论的挠度和弯矩计算结果均随上覆土层厚度增长而线性增长。从图20（a）可以看出,弹性薄板、简支梁和弹性地基梁的挠度计算结果较为接近,且增长速度也较为一致；固支梁的计算结果最小,且增长速度最为缓慢。分析图20（b）,弹性薄板的弯矩计算结果最大,且增长速度最快,简支梁次之,固支梁与弹性地基梁弯矩计算结果最小,增长速度最慢。当上覆土层厚度达到11 m时,弹性薄板理论和简支梁理论的挠度计算结果分别为6.5,6 mm,两者相差为8.3%；而弯矩计算结果分别为249,228 kN·m,两者相差9.2%。结合5.1节分析结果,可以看出弹性薄板理论的挠度和弯矩计算结果均稍大于简支梁计算结果,但不超过10%。因此,宜采用弹性薄板理论和简支梁理论对横向管幕进行承载力设计,当使用简支梁理论进行管幕设计时,应乘以一定的安全系数保证管幕结构的有效性。

图 20 不同上覆土层厚度管幕对比曲线

Figure 20. Comparison curves of pipe curtains with different heights of overburden

下载: 全尺寸图片幻灯片

5.3 钢管壁厚的影响

图21为钢管壁厚分别为10,12,14,16 mm时,不同理论的挠度计算值随钢管壁厚的变化曲线。值得说明的是,钢管壁厚只影响梁与板的弯曲刚度,在外荷载与边界条件未改变的前提下,弯曲刚度的变化并不影响简支梁、固支梁与板的弯矩,虽然弯曲刚度的变化对弹性地基梁的弯矩结果有一定影响,但经过计算发现,弯矩值的变化率不超5%,故在这里并未给出弯矩计算结果。分析图21可知,随着钢管壁厚的增加,不同理论计算得到的挠度在减小,当壁厚从10 mm增加到16 mm,弹性薄板理论计算的挠度从6 mm减小到4.1 mm,简支梁从5.6 mm减小到3.8 mm,弹性地基梁从4.8 mm减小到3.6 mm,固支梁仅从1.1 mm减小到0.75 mm,可见弹性薄板与简支梁的减小幅度最大,弹性地基梁次之,固支梁最小。

图 21 不同钢管壁厚管幕最大挠度对比曲线

Figure 21. Comparison curves of maximum settlement under different wall thicknesses of steel pipe

下载: 全尺寸图片幻灯片

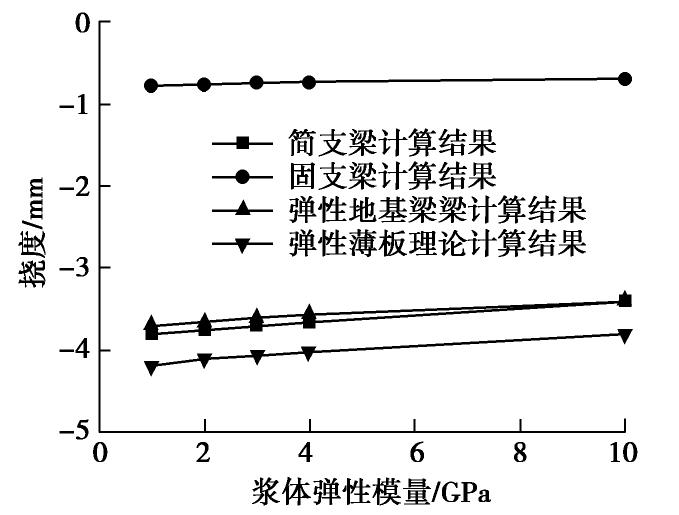
5.4 钢管内浆体弹性模量的影响

图22为在不同浆体弹性模量下,不同理论的挠度计算结果变化趋势图。同样的,浆体弹性模量对弹性薄板、简支梁和固支梁的弯矩计算结果无影响,并且对弹性地基梁的计算结果影响有限,所以本节中同样对弯矩不做叙述。由图22可以看出,随着浆体弹模的增加,管幕挠度近似于线性减小,但减小幅度较小；当浆体弹模从1 GPa增加到10 GPa时,弹性薄板计算挠度从4.2 mm降低到3.8 mm,简支梁从3.8 mm降低到3.4 mm,弹性地基梁从3.7 mm降低到3.4 mm,固支梁从0.76 mm降低到0.68 mm,可见浆体弹模对挠度的影响甚微。结合5.3节研究内容,相较于提高注浆弹模,增加钢管壁厚对减小管幕挠度更为有效。

图 22 不同浆体弹模管幕最大挠度对比曲线

Figure 22. Comparison curves of maximum settlement of pipe curtains with different elastic moduli of grouting materials

下载: 全尺寸图片幻灯片

6. 结论

本文利用弹性薄板理论与连续梁理论,对不同简化条件下的横向管幕进行了解析计算,并利用现场实测数据和有限元对两种理论的计算结果进行了验证,最后对不同参数下弹性薄板理论和连续梁理论的挠度和弯矩计算结果进行了对比分析,得出以下5点结论。

（1）无论是在变形趋势上,还是在最终变形量上,弹性薄板理论的计算结果都与实测数据吻合性较好；简支梁与弹性地基梁理论的计算结果仅在最终变形量上与实测结果较为吻合,而无法预测管幕的变形过程。

（2）在连续梁理论的计算结果中,简支梁的弯矩与挠度计算结果最大,而固支梁的弯矩与挠度计算值最小,故对管幕与初支侧墙连接时,应尽可能地保证管幕边界为固支端,如将管幕与初支侧墙之间焊接,保证管幕不会发生微小转角,这样可以在一定程度上降低管幕挠度与弯矩。

（3）在相同荷载条件下,弹性薄板理论的挠度和弯矩计算结果均稍大于简支梁的计算结果,但两者相差较小,不超过10%。可利用弹性薄板理论和简支梁理论对管幕进行承载力设计,但利用简支梁理论设计时,应乘以一定的安全系数保证管幕结构的有效性以及施工的安全性。

（4）通过参数影响分析发现,浆体弹性模量和钢管壁厚对管幕变形的影响较小,而开挖导洞跨度、上覆土层厚度和钢管壁厚对管幕变形与弯矩的影响较大；在受荷一定的情况下,应对开挖导洞合理的设计。

（5）弹性薄板解为管幕法提供了一种新的理论解,有利于对管幕在施工中的力学行为进行预测,并对设计进行进一步的精细化。

图 1 管幕的布置形式

Figure 1. Arrangement of pipe curtains

下载: 全尺寸图片幻灯片

图 2 管幕接头弯曲试验曲线^[11]

Figure 2. Curves of bending tests on joints of pipe curtains^[11]

下载: 全尺寸图片幻灯片

图 3 日本管幕加载试验模型与结果^[6]

Figure 3. Model and results of loading tests on pipe curtains^[6]

下载: 全尺寸图片幻灯片

图 4 管幕简化示意图

Figure 4. Simplification of pipe curtains

下载: 全尺寸图片幻灯片

图 5 管幕弹性地基梁简化模型

Figure 5. Simplified model for elastic foundation beams of pipe curtains

下载: 全尺寸图片幻灯片

图 6 第i个单元受力分析

Figure 6. Force analysis for i-unit

下载: 全尺寸图片幻灯片

图 7 第i节点的内力传递

Figure 7. Internal force transfer of i-unit

下载: 全尺寸图片幻灯片

图 8 简支梁数值解与理论解对比

Figure 8. Comparison between numerical and theoretical solutions of simply supported beams

下载: 全尺寸图片幻灯片

图 9 固支梁数值解与理论解对比

Figure 9. Comparison between numerical and theoretical solutions of fixed beams

下载: 全尺寸图片幻灯片

图 10 弹性地基梁数值解与理论解对比

Figure 10. Comparison between numerical and theoretical solutions of beams on elastic foundation

下载: 全尺寸图片幻灯片

图 11 管幕与初支侧墙连接节点图

Figure 11. Joints of pipe curtains and side wall with primary support

下载: 全尺寸图片幻灯片

图 12 弹性薄板力学模型图

Figure 12. Mechanical model for elastic thin plates

下载: 全尺寸图片幻灯片

图 13 弹性薄板数值解与理论解对比

Figure 13. Comparison between numerical solution and theoretical solutions of elastic thin plates

下载: 全尺寸图片幻灯片

图 14 车站横断面图

Figure 14. Cross section of station

下载: 全尺寸图片幻灯片

图 15 测点布置与不同模型计算简图

Figure 15. Layout of monitoring points and calculation diagram

下载: 全尺寸图片幻灯片

图 16 导洞拱顶沉降曲线

Figure 16. Settlement curves of crown

下载: 全尺寸图片幻灯片

图 17 不同理论计算得到的管幕最终变形曲线

Figure 17. Curves of final settlement calculated by different theories

下载: 全尺寸图片幻灯片

图 18 不同理论计算得到的管幕x方向弯矩曲线

Figure 18. Bending moments calculated by different theories

下载: 全尺寸图片幻灯片

图 19 不同开挖跨度管幕对比曲线

Figure 19. Comparison curves of pipe curtains with different excavation spans

下载: 全尺寸图片幻灯片

图 20 不同上覆土层厚度管幕对比曲线

Figure 20. Comparison curves of pipe curtains with different heights of overburden

下载: 全尺寸图片幻灯片

图 21 不同钢管壁厚管幕最大挠度对比曲线

Figure 21. Comparison curves of maximum settlement under different wall thicknesses of steel pipe

下载: 全尺寸图片幻灯片

图 22 不同浆体弹模管幕最大挠度对比曲线

Figure 22. Comparison curves of maximum settlement of pipe curtains with different elastic moduli of grouting materials

下载: 全尺寸图片幻灯片

参考文献(21)

[1]	张倍. 砂卵石地层中管幕施工适用性研究[D]. 北京: 北京工业大学, 2017. ZHANG Bei. Study on the Applicability of Pipe-Roof Pre-Support System in Gravel Stratum[D]. Beijing: Beijing University of Technology, 2017. (in Chinese)
[2]	王兆卿. 洞桩法隧道上穿既有地铁区间隧道变形机理及变形控制技术[D]. 北京: 北京工业大学, 2019. WANG Zhao-qin. Deformation Mechanism of Tunnels in Existing Metro Tunnels and Deformation Control Technology[D]. Beijing: Beijing University of Technology, 2019. (in Chinese)
[3]	高胜雷. 棚盖法平顶暗挖地铁车站施工力学行为研究[D]. 北京: 北京工业大学, 2018. GAO Sheng-lei. Study on the Construction Mechanics of Subway Station With Flat Roof[D]. Beijing: Beijing University of Technology, 2018. (in Chinese)
[4]	KOTAKE N, YAMAMOTO O. Design for umbrella method based on numerical analyses and field measurements[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1995, 32(3): A136.
[5]	TAN W L, RANJITH P G. Numerical analysis of pipe roof reinforcement in soft ground tunneling[C]//Proc of the 16th International Conference on Engineering Mechanics, ASCE, 2003, Seattle.
[6]	YAMAKAWA S, GOTO Y. Analysis of load distribution by joinnt in pipe beam roof[J]. Proceedings of the Japan Society of Civil Engineers, 1980(301): 1-12.
[7]	贾金青, 王海涛, 涂兵雄, 等. 管棚力学行为的解析分析与现场测试[J]. 岩土力学, 2010, 31(6): 1858-1864. doi: 10.3969/j.issn.1000-7598.2010.06.031 JIA Jin-qing, WANG Hai-tao, TU Bing-yong, et al. Analytical approach and field monitoring for mechanical behaviors of pipe roof reinforcement[J]. Rock and Soil Mechanics, 2010, 31(6): 1858-1864. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.06.031
[8]	周顺华. 软弱地层浅埋暗挖施工中管棚法的棚架原理[J]. 岩石力学与工程学报, 2005, 24(7): 2565-2570. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200514027.htm ZHOU Shun-hua. Principles of pipe roof applied to shallow-buried tunnels in soft ground[J]. Chinese Journal of Geotechnical Engineering, 2005, 24(7): 2565-2570. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200514027.htm
[9]	肖世国, 李向阳, 夏才初, 等. 管幕内顶进箱涵时顶部管幕力学作用的试验研究[J]. 现代隧道技术, 2006(2): 22-32. https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD200601003.htm XIAO Shi-guo, LI Xiang-yang, XIA Cai-chu, et al. Study on the behavior of the upper pipe-curtain during the advance of a box culvert within pipe-curtains by a model test[J]. Modern Tunnelling Technology, 2006(2): 22-32. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD200601003.htm
[10]	孙旻, 徐伟. 软土地层管幕法施工三维数值模拟[J]. 岩土工程学报, 2006, 28(11): 1497-1500. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2006S1041.htm SUN Min, XU Wei. 3D numerical simulation of pipe-curtain method in soft soils[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(11): 1497-1500. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2006S1041.htm
[11]	杨光辉, 朱合华, 李向阳. 钢管幕锁口接头力学特性试验研究[C]//第三届上海国际隧道工程研讨会, 2007, 上海: 695-700. YANG Guang-hui, ZHU He-hua, LI Xiang-yang. Experimental study on mechanics characteristics of interlock[C]//The third Shanghai International Tunnelling Seminar, 2007, Shanghai: 695-700. (in Chinese)
[12]	谭忠盛, 孙晓静, 马栋, 等. 浅埋大跨隧道管幕预试验研究[J]. 土木工程学报, 2015, 48(增刊1): 429-434. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2015S1077.htm TAN Zhong-sheng, SUN Xiao-jing, MA Dong, et al. Experimental research of pipe-roof pre-supporting technology for the shallow large-span tunnel[J]. China Civil Engineering Journal, 2015, 48(S1): 429-434. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2015S1077.htm
[13]	赵文, 贾鹏蛟, 王连广, 等. 地铁车站STS新管幕构件抗弯承载力试验研究[J]. 工程力学, 2016, 33(8): 167-176. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201608023.htm ZHAO Wen, JIA Peng-jiao, WANG Lian-guang. Experimental study on the flexural capacity of steel tube slab members of subway station[J]. Engineering Mechanics, 2016, 33(8): 167-176. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201608023.htm
[14]	贾鹏蛟, 赵文, 郝云超, 等. 不同结构参数下STS管幕构件力学性能的数值分析[J]. 东北大学学报(自然科学版), 2016, 37(8): 1177-1181. https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX201608023.htm JIA Peng-jiao, ZHAO Wen, HAO Yun-chao. Numerical analysis of the mechanical properties of steel tube slab component under different structural parameters[J]. Journal of Northeastern University (Natural Science), 2016, 37(8): 1177-1181. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX201608023.htm
[15]	关永平, 赵文, 王连广, 等. STS管幕结构抗弯性能试验研究及参数优化[J]. 工程力学, 2017, 34(9): 83-91. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201709011.htm GUAN Yong-ping, ZHAO Wen, WANG Lian-guang, et al. Study on parameter optimization and the flexural behavior of steel tube slab structures[J]. Engineering Mechanics, 2017, 34(9): 83-91. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201709011.htm
[16]	李树忱, 晏勤, 谢璨. 膨胀性黄土隧道钢拱架-格栅联合支护力学特性研究[J]. 岩石力学与工程学报, 2017, 36(2): 446-456. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201702016.htm LI Shu-chen, YAN Qin, XIE Can. The mechanical behavior of composite supports of steel-grid in loess tunnel[J]. Chinese Journal of Geotechnical Engineering, 2017, 36(2): 446-456. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201702016.htm
[17]	张治国, 马兵兵, 黄茂松, 等. 山区滑坡诱发既有隧道受力变形影响分析[J]. 岩土力学, 2018, 39(10): 3555-3564. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201810009.htm ZHANG Zhi-guo, MA Bing-bing, HUANG Mao-song, et al. Influence analyses on force and deformation of existing tunnels induced by landslide in mountain region[J]. Rock and Soil Mechanics, 2018, 39(10): 3555-3564. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201810009.htm
[18]	VESIC A S. Bending of beams resting on isotropic elastic solid[J]. Journal of Soil Mechanics and Foundation Engineering, ASCE, 1961, 87(2): 35-53.
[19]	徐芝纶. 弹性力学[M]. 5版. 北京: 高等教育出版社, 2016. XU Zhi-lun. Elasticity[M]. 5th ed. Beijing: Higher Education Press, 2016. (in Chinese)
[20]	黄炎. 矩形薄板弹性弯曲问题的一般解析解法[J]. 国防科技大学学报, 1983(3): 1-16. https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ198303000.htm HUANG Yan. A general analytical method for elastic bending of rectangular thin plates[J]. Journal of National Defense University of Defense Technology, 1983(3): 1-16. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ198303000.htm
[21]	黄炎. 矩形薄板弹性弯曲的精确解析解法[J]. 力学学报, 1987, 19(增刊): 230-235. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB1987S1028.htm HUANG Yan. Exact analytical method for elastic bending of rectangular thin plates[J]. Chinese Journal of Theoretical and Applied Mechanics, 1987, 19(S0): 230-235. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB1987S1028.htm

施引文献(11)

期刊类型引用(8)

1.	杨旭辉，柏谦，贾鹏蛟. 地铁车站小直径管幕-横梁支护参数优化分析. 沈阳工业大学学报. 2025(01): 114-123 . 百度学术
2.	邱建，赵文，路博，孙旭. 新型管幕工法修建地铁车站地层变形特性及参数优化. 东北大学学报(自然科学版). 2024(11): 1645-1655 . 百度学术
3.	崔光耀，宋博涵，何继华，田宇航. 超近接上跨既有隧道施工影响分区及加固措施效果. 长江科学院院报. 2023(06): 114-118+125 . 百度学术
4.	伍凯，毕延哲，杨鑫，储修琼. 超浅覆土小净距上跨运营线路盾构掘进超前管幕支护模拟分析. 路基工程. 2023(04): 130-136 . 百度学术
5.	陈凯. 基于变形控制的密排管幕顶管施工顺序优化分析. 铁道勘察. 2023(05): 149-157 . 百度学术
6.	王子君，赵文，程诚，柏谦. 地铁车站小直径管幕工法开挖变形规律. 东北大学学报(自然科学版). 2022(11): 1630-1637 . 百度学术
7.	袁庆利. 大直径密排管幕的力学分析及在地铁车站中的应用. 吉林水利. 2021(06): 1-10 . 百度学术
8.	张贺. 新型钢管幕力学变形特征及其在地铁车站中的应用. 工程建设. 2021(09): 1-6 . 百度学术