密排横向管幕理论分析研究

张宇; 陶连金; 董立朋; 赵旭; 边金; 安韶; 陈向红

doi:10.11779/CJGE202102017

密排横向管幕理论分析研究 English Version

张宇^1,,
陶连金^1, ,,
董立朋²,
赵旭¹,
边金³,
安韶¹,
陈向红⁴

1.
北京工业大学建筑与工程学院,北京　100124
2.
中铁隧道局集团有限公司,广东　广州　511458
3.
广东海洋大学,广东　湛江　524088
4.
中煤炭建工集团有限公司,北京　100161

基金项目:

国家重点研发计划项目 2017YFC0805403

国家自然科学基金项目 41877218

详细信息

作者简介:
张宇（1993— ）,男,博士研究生,主要从事地下工程施工风险方面的研究工作。E-mail：411101866@qq.com

通讯作者:
陶连金, E-mail: ljtao@bjut.edu.cn

中图分类号: TU43
计量
- 文章访问数: 223
- HTML全文浏览量: 37
- PDF下载量: 106
出版历程
- 收稿日期: 2020-04-01
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-01-31

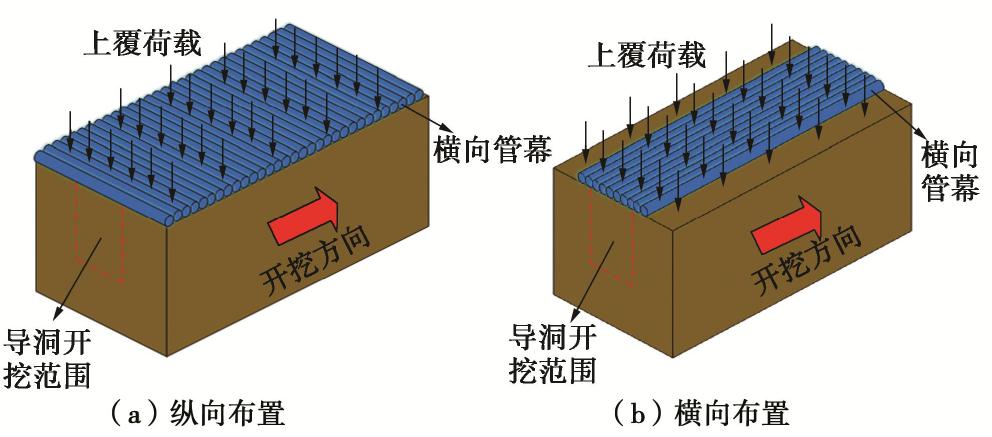
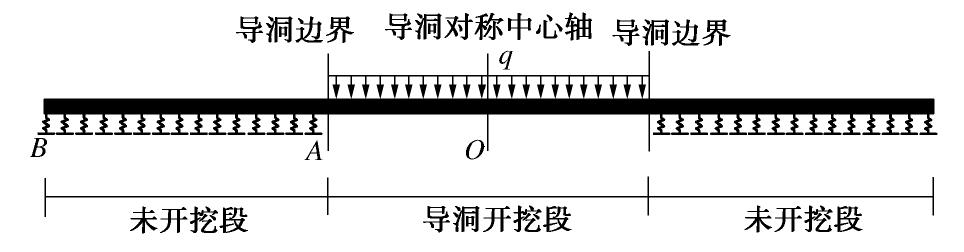
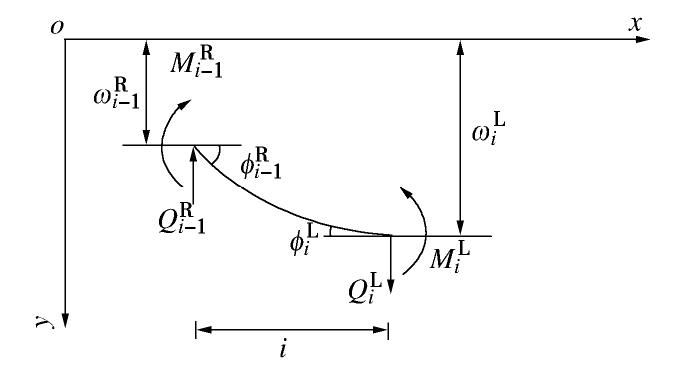
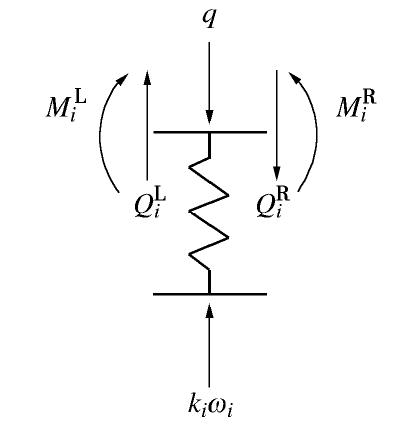
Theoretical analysis of horizontal pipe curtains with tight rows

1.
Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education, Beijing University of Technology, Beijing 100124, China
2.
China Railway Tunnel Bureau Group Co., Ltd., Guangzhou 511458, China
3.
Guangdong Ocean University, Zhanjiang 524088, China
4.
China Coal Construction Group Co., Ltd., Beijing 100161, China

摘要

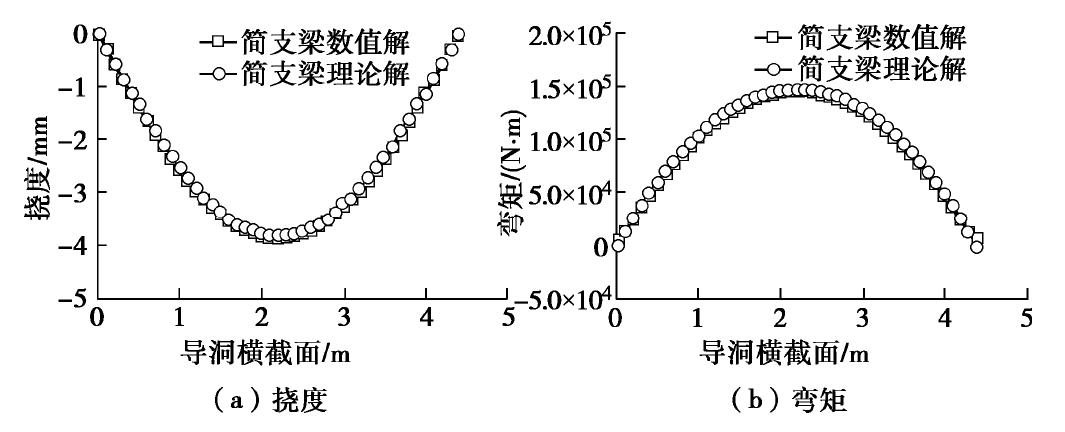
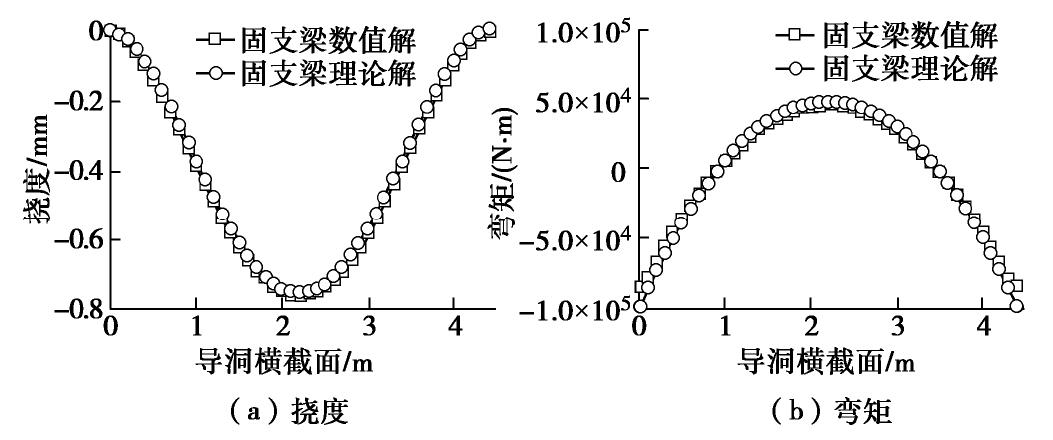
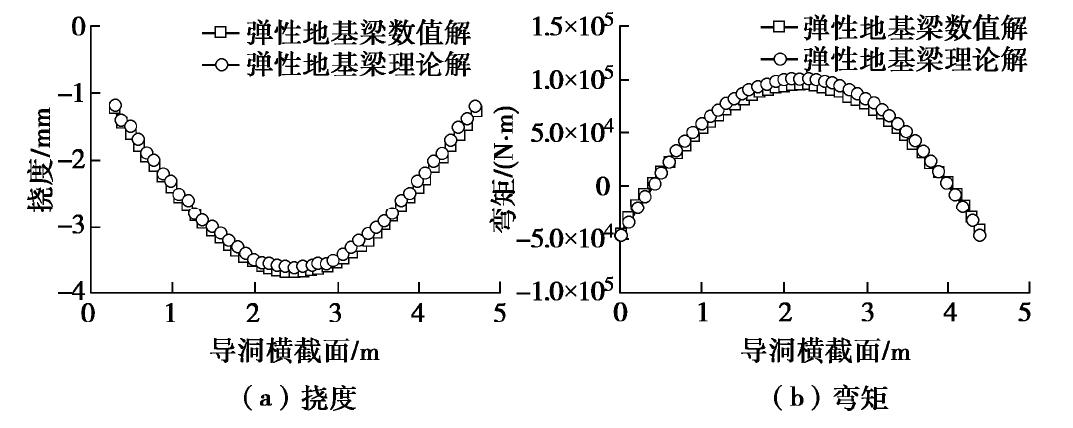
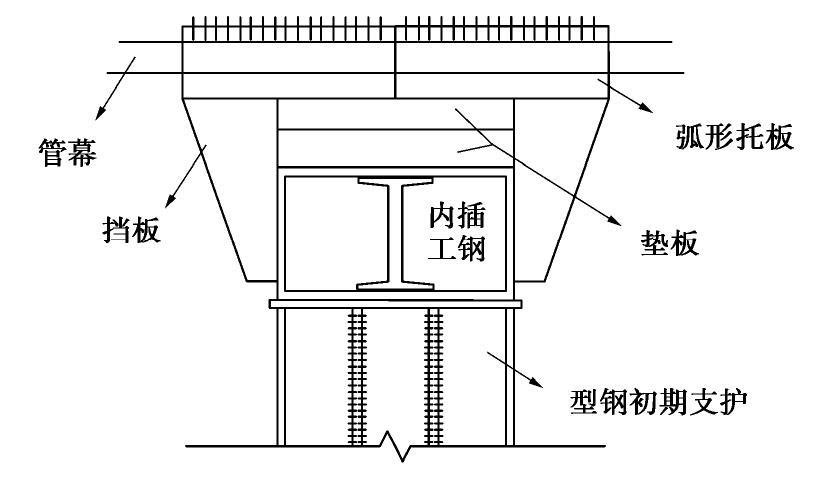
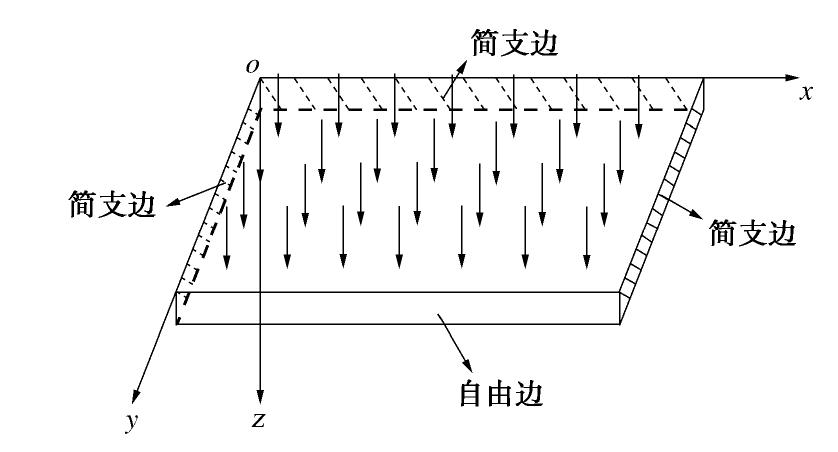
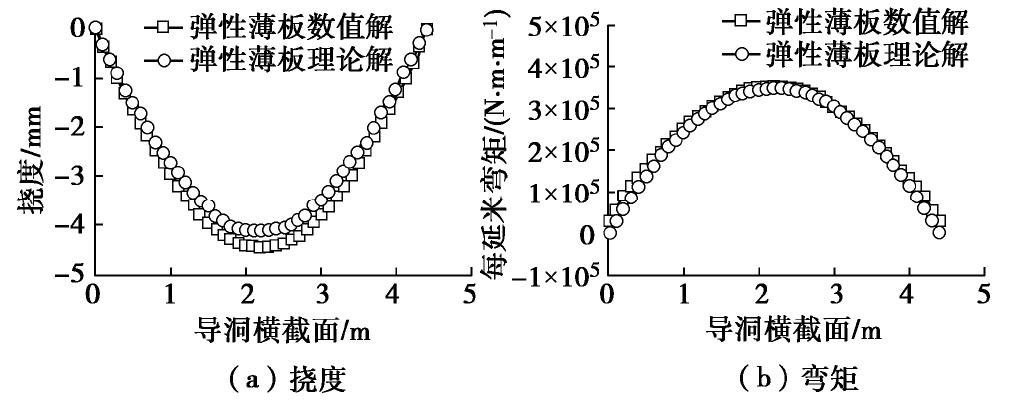
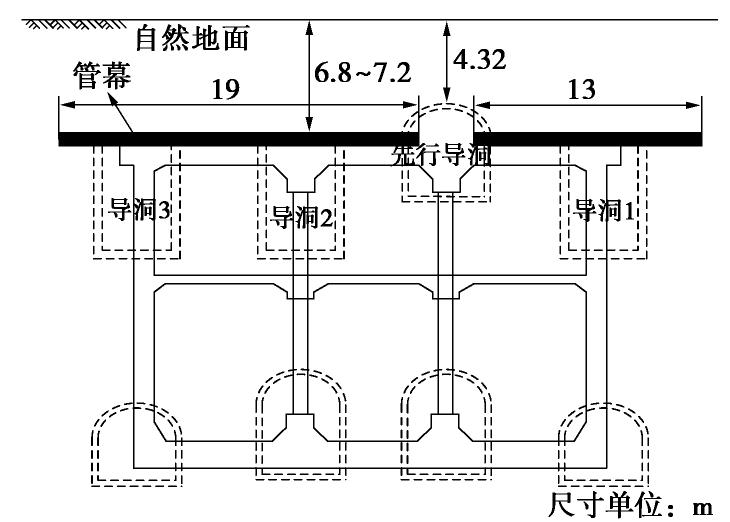
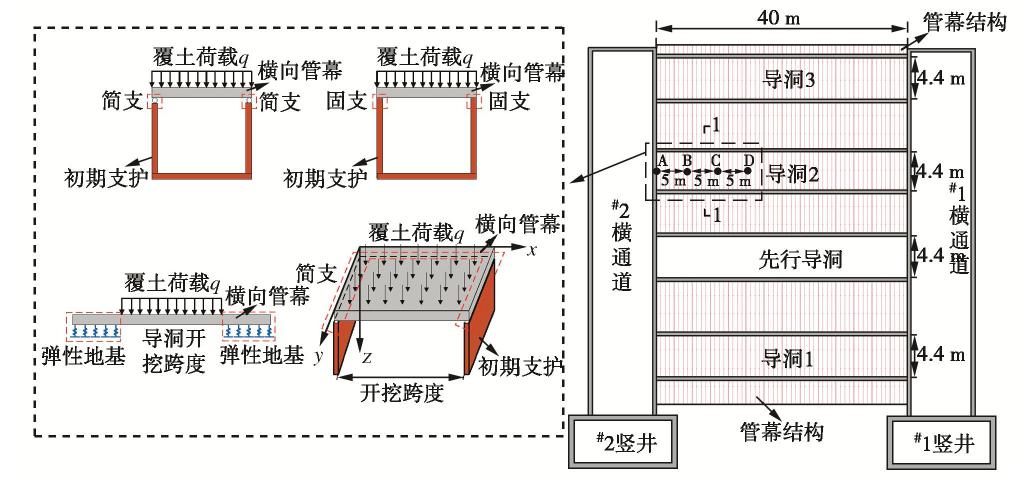
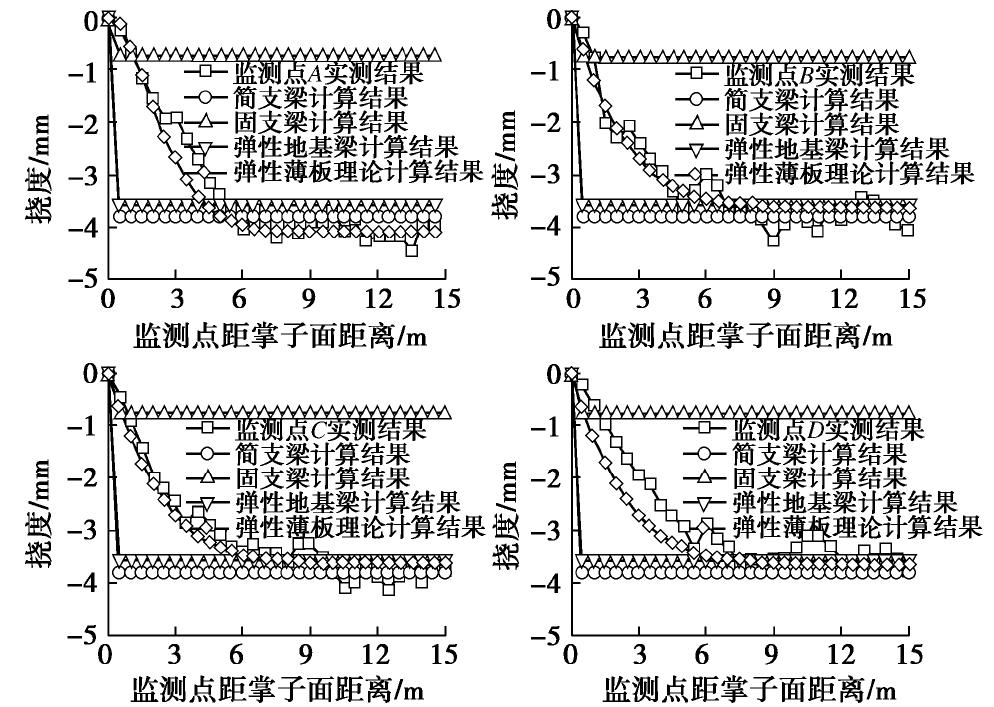
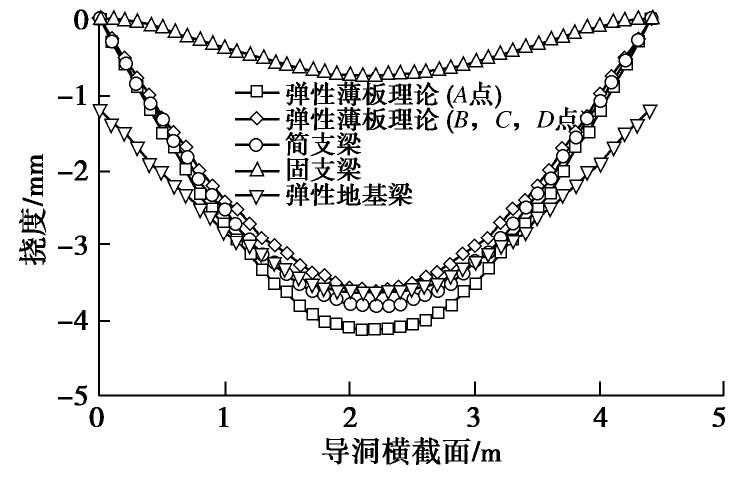
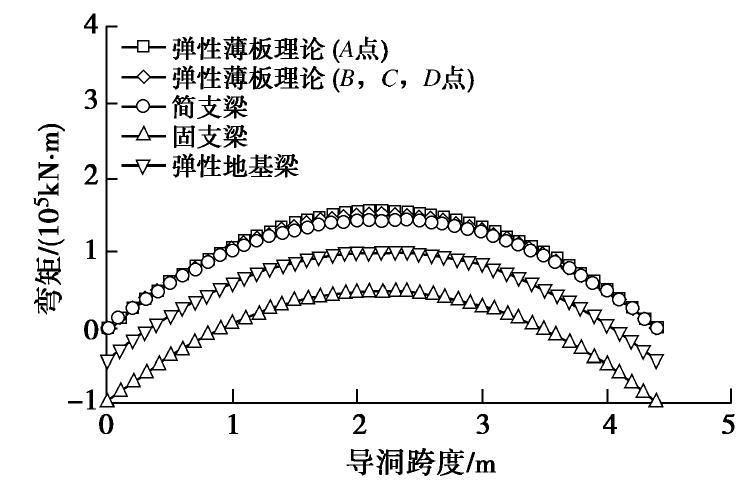
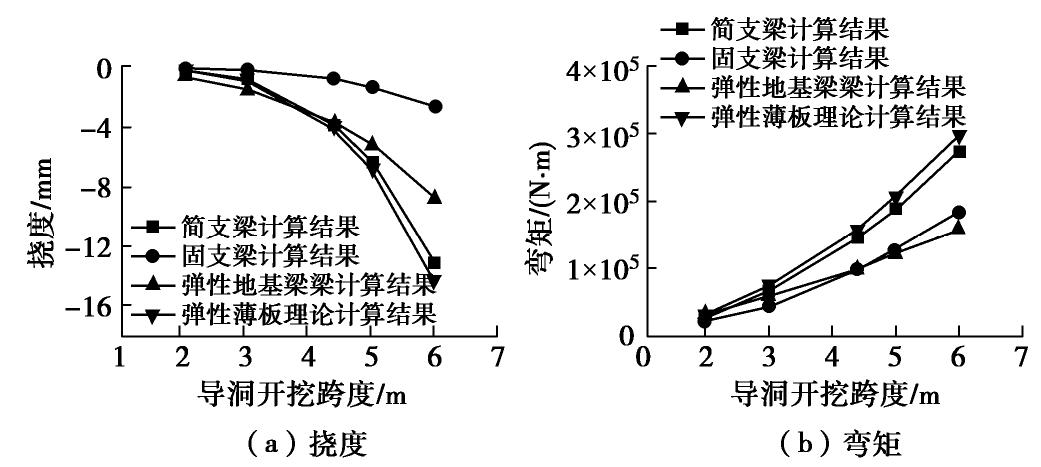
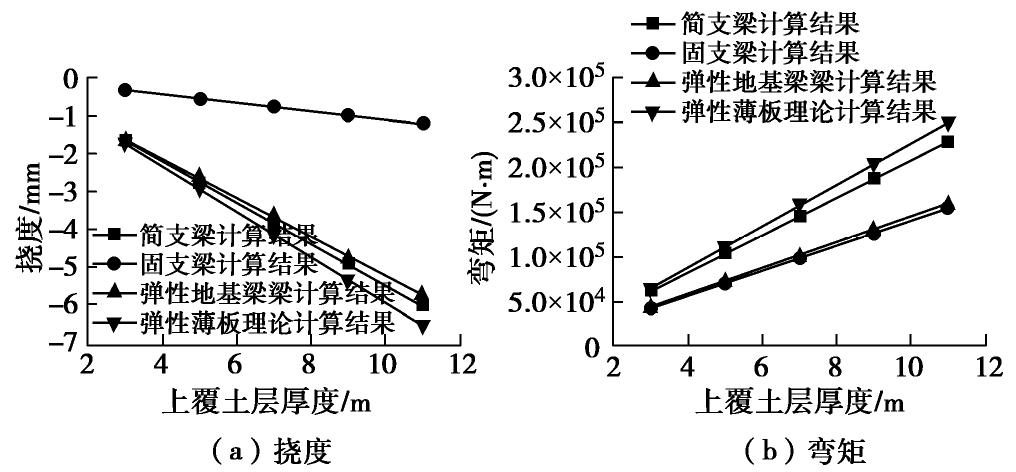
摘要: 大直径管幕超前预支护对暗挖工程中的变形控制具有积极作用,管幕的布置形式可分为纵向与横向两种。以北京平安里地铁车站工程及其实测数据为基础,探索性地将带有锁扣的横向管幕简化为弹性薄板,继而对比分析了采用弹性薄板理论和连续梁理论的计算结果；最后,针对导洞开挖跨度、上覆土层厚度、钢管壁厚以及钢管内浆体弹性模量等参数进行了影响分析。结果表明：①无论是在变形趋势,还是在最终变形量上,弹性薄板理论的挠度计算结果都与实测数据吻合性较好,而简支梁与弹性地基梁理论仅最终变形量与实测结果较为吻合；②在相同荷载条件下,弹性薄板理论计算得到的最大弯矩值稍大于简支梁的计算结果,但两者相差不超过10%；③钢管壁厚和浆体弹性模量对管幕变形的影响较小,而开挖导洞跨度和上覆土层厚度对管幕变形与弯矩的影响较大。
- 管幕结构 /
- 弹性薄板理论 /
- 连续梁理论 /
- 现场实测 /
- 对比分析
Abstract: The pre-support of large-diameter pipe curtains plays an active role in controlling the deformation of excavations, and the layout of the pipe curtains can be divided into vertical and horizontal types. Based on the measured data of Pinganli metro station in Beijing, the horizontal pipe curtains with lock are simplified into the elastic thin plates, and the results of the elastic plate theory and the continuous beam theory are compared and analyzed. Finally, the influences of excavation span, height of overburden, wall thickness of steel pipes and elastic modulus of grouting materials are analyzed. The results show: (1) The results of the settlement calculation of the elastic thin plate theory are in good agreement with the measured data both in the settlement trend and in the final settlement, while the calculated results of the simply supported beams and the elastic foundation beams are only in good agreement with the measured ones in the final settlement. (2) Under the same load conditions, the maximum bending moment calculated by the elastic thin plate theory is slightly larger than that of the simply supported beams, but this difference is not more than 10%. (3) The elastic modulus of slurry and the thickness of the steel pipe wall have small effects on the settlement and bending moment of the pipe curtains, while the excavation span and the height of overburden have great influences on the settlement and bending moment of the pipe curtains. The research results may provide a new way to simplify pipe curtains into homogeneous elastic thin plates for calculation, and provide the theoretical support for design of the pipe curtains.
- pipe curtain structure /
- theory of elastic thin plate /
- continuous beam theory /
- field measurement /
- comparative analysis

HTML全文

0. 引言

深层地质处置被认为是处置高放废物最合理的方法。膨润土具有低渗透性、较好的吸附性和较大的膨胀性等特点,被广泛认为是深层地质处置库理想的缓冲/回填材料^[1-3]。由压实膨润土构成的屏障的一个重要功能是填充建造或运行过程中可能产生的裂缝,形成封闭的环境,防止核素迁移。在过去几十年中,膨润土基缓冲/回填材料的膨胀特性得到了广泛的研究^[4-7]。研究结果表明,膨润土的膨胀受干密度、孔隙流体化学物质和温度等多种因素的影响^[8-10]。

相关研究表明,温度对不同膨润土膨胀的影响是不同的,即使在不同的试验条件下对同一膨润土的影响也不相同^[11-13]。Pusch等^[14]指出温度对膨润土膨胀力的影响与其主要的阳离子有一定关系,温度升高可提高高密实钠膨润土的膨胀力,但会降低二价膨润土膨胀力。蒙脱石类黏土的膨胀过程大致可分为晶层膨胀和渗透膨胀^[15]。在水分进入膨润土的初始阶段,膨胀是由存在于蒙脱石单元层之间的可交换阳离子的水化作用引起的（阳离子与水发生化合反应,在其周围形成一定的水分子层）,称之为晶层膨胀。随着水分进一步渗入并充填蒙脱石集合体内的孔隙,集合体膨胀并裂开成薄层叠体,甚至为单层晶层,形成渗透膨胀也称为双电层膨胀^[16]。扩散双电层（DDL）模型适用于渗透膨胀。根据DDL模型,DDL的厚度随温度的升高而增大。因此,如果DDL在粒间孔隙中发育良好,温度会促进黏土的膨胀。通常,扩散双电层在钠基膨润土中容易发展,但其间距随着阳离子价的增加而减小,导致二价膨润土中DDL的形成相对困难。因此,温度往往会促进钠基膨润土的膨胀,例如GMZ膨润土^[17-18]。此外,DDL的发展还取决于荷载或试样的干密度,在小荷载或低密度的试样中,扩散双电层可以得到很好的发展。在这种情况下,渗透膨胀仍是主要的膨胀形式。Romero等^[19]报告了FEBEX Ca/Mg-膨润土的自由膨胀率随温度升高而增加。Cho等^[4]发现加热可以促进干密度较低的Korea钙基膨润土的膨胀力。Bag等^[12]也发现温度升高使Bikane钙基膨润土的膨胀力有轻微的增加。然而,对于高压实膨润土,无论是钠基膨润土^[13,20]还是二价膨润土^[21],膨胀性能均随温度的增加而降低。这主要是因为晶层膨胀是高压下高压实膨润土主要的膨胀形式^[13]。在这种情况下,晶层间水分子的动能受到热量的促进,导致水分子不稳定,蒙脱石吸水能力降低^[13]。因此,根据目前的研究可以推断,在渗透膨胀为主的情况下,膨润土的膨胀特性随着温度的升高而增强,而在晶层膨胀的情况下则相反。

高庙子（GMZ）膨润土被认为是中国深层地质处置首选的缓冲/回填材料。不同条件下GMZ膨润土膨胀性能的研究已取得较丰富的成果^{[16-17, 22]}。但温度对GMZ膨润土膨胀性能的影响还不够明确。另外,目前比较缺乏膨胀性能随温度变化的定量评价模型。DDL模型是适用于压实膨润土渗透膨胀的计算方法^[23]。但目前也发现了DDL模型的一些局限性,如DDL模型不适用于晶层膨胀或浓盐溶液中的膨胀计算。此外,该模型所需参数较多且较难确定,不方便应用。Xu等^[24]发现蒙脱石孔隙率e_m与竖向压力p之间存在分形关系,可表示为e_m=Kp^D-3。这是一种定量评价膨润土膨胀性能的简便有效方法,模型得到了室温下不同膨胀性黏土试验数据的验证^{[3, 25]}。但该模型并没有考虑到温度变化对膨胀性能的影响。

本文开展不同温度下GMZ膨润土膨胀性能试验,分析了温度对膨胀性能的影响机理,基于DDL模型和分形模型,建立了一种温度作用下GMZ膨润土膨胀性能的简便计算方法。

1. 材料与试验方法

1.1 GMZ膨润土

GMZ膨润土来源于内蒙古自治区高庙子矿床。该膨润土被选用作为中国高放废物处置库的缓冲/回填主料。对GMZ膨润土进行研究可为处置库的设计提供科学依据。GMZ膨润土的物理化学指标见表1。

表 1 GMZ膨润土的物理化学指标^[22]

Table 1. Physicochemical indices of GMZ bentonite

土粒相对质量密度	液限w_L/%	塑限w_P/%	塑性指数I_P	蒙脱石含量C_m/%	阳离子交换量/(cmol·kg^-1)	主要交换性阳离子/(cmol·kg^-1)
土粒相对质量密度	液限w_L/%	塑限w_P/%	塑性指数I_P	蒙脱石含量C_m/%	阳离子交换量/(cmol·kg^-1)	Na⁺	Ca²⁺	Mg²⁺	K⁺
2.66	276	37	239	75	75.1	36.2	24.7	11.9	3.62

下载: 导出CSV

| 显示表格

1.2 试验装置

所用不同温度下膨胀试验的试验装置如图1所示,该装置其主要包括自制的固结室和电加热套,温度可以用温度控制器调节。电加热套和固结室可以安装于普通的三联中压固结仪。

图 1 温度作用下膨胀性能试验装置

Figure 1. Experimental apparatus for swelling tests under different temperatures

下载: 全尺寸图片幻灯片

1.3 膨胀试验

将GMZ膨润土配制成含水率约18.0 %的湿土,并在环刀中静压制成高度1.0 cm,直径6.18 cm的饼状试样。将压实试样放入自制的固结室中,连同外部加热套安装于三联固结仪中。设置目标温度,一次性施加所需荷载,加蒸馏水进行渗流饱和,外部容器中水面高度保持高于试样顶面的1.0 cm左右。采用百分表记录膨润土的膨胀率随时间的增加过程,膨胀率为高度变化量与原试样高度之比,当在24 h内百分表指针保持不动,认为试样膨胀饱和完成,此时的最终膨胀率称为最大膨胀率。

在膨胀力试验中,将压实试样安装在固结仪中并对其施加恒定温度后,记录指针的初始读数,向试样中注入蒸馏水。当样品开始膨胀时,迅速施加竖向荷载到样品上,让指针回到原来的位置,在试验过程中保持指针变化量小于0.01 mm。当百分表读数在某压力下保持24 h不变时,认为达到最大膨胀压力p_s,试验完成。

Pastina等^[26]发现高放废物储存库中的最高温度可接近于90℃,且距离核废料储藏罐距离越远温度越低。据此本文将膨胀变形和膨胀力试验的温度设定为25℃,40℃,60℃和90℃。膨胀变形试验中各试样的初始状态和试验条件见表2。

表 2 膨胀变形试验中试样的初始状态和试验条件

Table 2. Initial and experimental conditions of samples in swelling deformation tests

初始干密度/(g·cm^-3)	初始含水率/%	温度/℃	竖向荷载/kPa
1.70 ± 0.03	17.7~18.1	25,40,60,90	6.25,12.5,25,50,100,200,400,800
1.50 ± 0.03	17.5~17.9	25,40,60,90	100,400
1.60 ± 0.03	17.6~18.2	25,40,60,90	100,400

下载: 导出CSV

| 显示表格

1.4 氮吸附试验

在蒸馏水中膨胀后,卸载膨润土试样,在105℃的烘箱中干燥12 h,然后磨成粉末状,过200目筛。对原GMZ膨润土粉末和40℃,90℃水中膨胀后的试样进行了N₂吸附试验,分析了温度对GMZ膨润土表面性质的影响。

2. 膨胀试验结果

图2为不同温度下初始干密度为1.7 g/cm³的GMZ膨润土的最大膨胀率ε_max。可以发现,ε_max随竖向荷载的增大而减小,随温度的升高而增大。这是由于在本次试验条件下,渗透膨胀为主要膨胀形式,这种状况下,蒙脱石颗粒间扩散双电层厚度随温度的增加而增大,进而增强了膨胀变形。从图中也可发现,温度升高引起的膨胀率的增加随竖向压力的增大而减小。当竖向荷载较小时,试样的膨胀率随着温度的升高明显增大,而竖向荷载较大时,试样的膨胀率随温度升高轻微增加。

图 2 不同温度下的GMZ膨润土的最大膨胀率

Figure 2. ε_max of GMZ bentonite under different temperatures

下载: 全尺寸图片幻灯片

图3为初始干密度为1.7 g/cm³试样的最大膨胀率与温度之间的关系。可以看出在给定的压力下,试样的ε_max随温度增加线性增加,而随着竖向荷载的增加,线性ε_max-T_c关系的斜率逐渐减小。

图 3 不同荷载作用下GMZ膨润土的ε_max-T_c关系

Figure 3. Relationship between ε_max and T_c of GMZ bentonite under different stresses

下载: 全尺寸图片幻灯片

如图4所示,在相同的荷载和温度条件下,GMZ膨润土试样的ε_max随初始干密度ρ_d的增大线性增加,这与室温下不同膨润土的试验结果一致^{[1, 27]}。

图 4 25℃和60℃时GMZ膨润土的ε_max-ρ_d关系

Figure 4. Relationship between ε_max and ρ_d for GMZ bentonite at 25℃ and 60℃

下载: 全尺寸图片幻灯片

在膨胀力试验中,膨润土试样的干密度相对较低（ρ_d=1.35～1.55 g/cm³）。从图5中可以发现,在给定温度下,膨胀力随初始干密度呈指数增长,对于相同密度的样品,膨胀力随温度升高而增大。此外,相较于膨胀变形随温度增加轻微增加,温度对GMZ膨润土膨胀力的影响较大,且随初始干密度的增大而显著增大。这种差异主要是由于GMZ膨润土具有较高的膨胀性,需要较高的应力来防止膨胀变形；此外,根据Zhang等^[28]GMZ膨润土压缩曲线发现压实膨润土的压缩模量可达到30 MPa^-1。微小的变形变化需要较大的荷载维持,所以膨胀变形随温度略有增加,而膨胀力显著增加。

图 5 不同温度下GMZ膨润土的p_s-ρ_d关系

Figure 5. Relationship between p_s and ρ_d for GMZ bentonite under different temperatures

下载: 全尺寸图片幻灯片

3. 膨胀性能计算

3.1 e_m-p分形关系

GMZ膨润土的膨胀性能主要是由其中蒙脱石矿物所引起的^[29]。膨润土的膨胀性能可采用膨胀饱和时的蒙脱石孔隙比e_m表示^[29]：

$e_{m} = \frac{e}{α} = \frac{V_{w}}{V_{m}}$ 。

(1)

式中 e为膨润土试样膨胀饱和的孔隙比； $α$ 为膨润土中蒙脱石的含量；V_w为饱和试样中的水体积； $V_{m}$ 为蒙脱石的体积。

基于N₂等温吸附方程^[30],Xu等^[25]给出了蒙脱石吸附水的相应表达式：

$e_{m} = η {(\ln h_{r})}^{D - 3}$ ,

(2)

式中,η为吸水系数,h_r为相对湿度。

当含水率高于10%时,Kahr等给出膨润土的膨胀力计算公式为^[31]

$p = \frac{R T}{M υ} \ln h_{r}$ ,

(3)

式中,R为气体常数,T为热力学温度,M和 $υ$ 分别为水的分子质量和部分比体积。因此,将式（2）和（3）相结合,可以得出膨胀性能的e_m-p分形关系^[24]：

$e_{m} = {Kp}^{D - 3}$ ,

(4)

式中,D为膨润土表面分维,K为反映膨润土中蒙脱石矿物膨胀性能的系数,简称为蒙脱石膨胀系数,K越大蒙脱石的膨胀性能越大,在温度一定时只与蒙脱石交换性阳离子有关^[32]。

膨润土的分形维数可通过N₂吸附得到。图6绘制了不同蒸气压p/p₀下原始GMZ膨润土粉末和40℃和90℃下试样的N₂吸附量V_ads。可以发现3个试样的等温吸附线基本相同。采用Frenkel-Halsey-Hill方程计算了试样的表面分维^[33],各试样的D值约为2.75。表明膨润土的分形维数基本不受试验温度的影响,这主要是因为GMZ膨润土的矿物组成在25℃到90℃范围的蒸馏水中没有发生改变^[18],膨润土的表面结构在膨胀过程中没有受到化学反应的作用。

图 6 GMZ膨润土的N₂等温吸附线

Figure 6. N₂ adsorption isotherms of GMZ bentonite samples

下载: 全尺寸图片幻灯片

3.2 K-T_c关系

如上所述,当荷载一定时,膨润土的膨胀随温度的升高而增大,而分形维数为常数,所以可以认为温度对GMZ膨润土膨胀的影响主要表现在蒙脱石膨胀系数K的变化,该系数随温度的升高而增大。膨润土的膨胀性能随温度的升高而提高,也说明此时渗透膨胀为主,而DDL模型在这种情况下有很好的应用。因此,利用DDL模型可以计算GMZ膨润土在不同温度下的膨胀系数K。

Gouy-Chapman的DDL理论是基于两个蒙脱石层间的排斥力和吸引力提出的^[34]。完全饱和时的e_m表示为^[34]

$e_{m} = \frac{d - R_{ion}}{t + R_{ion}}$ 。

(5)

式中,t为蒙脱石层的厚度（0.96 nm）,d为两蒙脱石层之间距离的一半,R_ion为未水化的交换性阳离子的平均半径。

DDL模型表明膨胀力可以表示为^[34]

$p = f_{r} - f_{a}$ ,

(6)

式中,f_a为范德华力,表达式为^[34]

（ ） （ ）

$f_{a} = \frac{A_{h}}{24 π} [\frac{1}{d^{3}} + \frac{2}{（ d + t ）^{3}} - \frac{2}{（ d + t / 2 ）^{3}}]$ 。

(7)

式中,A_h为Hamaker常数（2.2×10^-20 J）。

蒙脱石间排斥力f_r计算式为^[34]

$f_{r} = 2 n b T (\cosh u - 1)$ ,

(8)

$u = 8 artanh [e^{- κ d} \tanh (Z / 4)]$ ,

(9)

$κ = \sqrt{\frac{2 n ν^{2} {e^{'}}^{2}}{ε k T}}$ ,

(10)

$Z = 2 arsinh (96.5 \times \frac{CEC}{S} \sqrt{\frac{1}{8 n ε k T}})$ 。

(11)

式中 u为平行蒙脱石层间中平面的静电势；1/κ为Debye长度（m）；b为Boltzmann常数（1.38×10^-23J/k）；ε为孔隙水的静态介电常数（6.95×10^-10C²/J/m）；n₀为孔隙水离子浓度（10×6.023×10²³个/m³）；CEC为阳离子交换量（75.1 cmol/kg）； $e^{'}$ 为电子电荷（1.602×10^-19C）；S为GMZ膨润土的总比表面积（0.75×810 m²/g）。

通常认为当膨润土在一定荷载作用下饱和时,渗透膨胀是在晶层膨胀完成之后才开始的^[15]。因此,半间距d应满足^[22]

$d > \frac{t + R_{i o n}}{t} d_{m} + R_{i o n}$ ,

(12)

其中,

$d_{m} = \frac{1}{CEC} \sum_{i}^{} {EXC}_{i} d_{i}$ ,

(13)

$R_{ion} = \frac{1}{CEC} \sum_{i}^{} {EXC}_{i} R_{i}$ 。

(14)

式中 EXC_i和R_i分别为第i个交换性阳离子的交换量和离子半径；Na⁺、K⁺、Mg²⁺和Ca²⁺的半径分别为0.098,0.133,0.082,0.1115 nm^[15]；d_i为仅存在第i个交换性阳离子蒙脱石晶层膨胀最大距离,对于K⁺、Ca²⁺、Mg²⁺和Na⁺,d_i分别为0.6,0.9,0.9,1.2 nm^[15]。因此,根据式（12）,常温时GMZ膨润土发生渗透膨胀d值应大于1.25 nm^[22]。将该值作为GMZ膨润土发生渗透膨胀和晶层膨胀的临界值,代入式（5）可以算出临界蒙脱石孔隙比约为1.086,并可估算出相应的荷载值为1820 kPa。所以对于GMZ膨润土而言,当荷载小于1820 kPa时,渗透膨胀为主要膨胀形态,反之,则以晶层膨胀为主。

由于渗透膨胀时蒙脱石层间间距随温度的升高而略有增加,在DDL模型的计算中,令GMZ膨润土在每个温度下的d等于1.3 nm,此时相应的蒙脱石孔隙比为1.13,对应于不同温度下保持体积不变的膨胀力试验。通过计算可以发现（表3）,DDL理论计算的膨胀力p随温度的增加而增大,得出的膨胀系数K随温度呈线性增加（图7）,K与温度T_c的关系式为

表 3 不同温度下膨胀系数K计算

Table 3. Calculated values of swelling coefficient K under different temperatures

T_c/℃	Z	κ/m^-1	u	p/kPa	K
25	19.172	691409134	3.456	1393.12	6.904
30	19.156	685683554	3.485	1465.08	6.992
40	19.123	674646562	3.542	1615.84	7.165
50	19.092	664125934	3.598	1775.94	7.336
60	19.061	654082622	3.652	1945.66	7.506
70	19.032	644481593	3.705	2125.26	7.673
80	19.003	635291309	3.756	2315.02	7.839
90	18.975	626483295	3.806	2515.22	8.003

下载: 导出CSV

| 显示表格

图 7 计算的GMZ膨润土K-T_c关系

Figure 7. Calculated relationship between K and T_c for GMZ bentonite

下载: 全尺寸图片幻灯片

$K = 0.017 T_{c} + 6.486$ ,

(15)

式中,T_c为摄氏温度（℃）。

3.3 验证与计算

结合K-T_c关系可得到不同温度下GMZ膨润土的e_m-p关系：

$e_{m} = (0.017 T_{c} + 6.486) p^{D - 3}$ 。

(16)

从式（16）可以看出,当荷载相同时,孔隙比与温度之间存在线性关系。采用式（16）估算了不同温度下GMZ膨润土e_m（图8）。室温条件下,Sun等^[35]GMZ膨润土试验数据也用于比较。结果表明,不同温度下GMZ膨润土的蒙脱石孔隙比的估算值与试验值吻合较好。

图 8 不同温度下GMZ膨润土的蒙脱石孔隙比估算值

Figure 8. Estimation of montmorillonite void ratio of GMZ bentonite under different temperatures

下载: 全尺寸图片幻灯片

根据Bag等^[12]对Bikaner膨润土开展的膨胀试验结果,发现相同荷载下,Bikaner膨润土试样的孔隙比也随温度呈线性增加,不同温度下的e-p关系式可表示为 $e = (0.033 T_{c} + 6.58) p^{D - 3}$ ,其中D= 2.785。Bikaner膨润土膨胀预测值与试验数据的比较如图9所示,孔隙比预测值与试验数据之间吻合较好。

图 9 不同温度下GMZ膨润土的蒙脱石孔隙比估算值^[13]

Figure 9. Estimation of void ratio for Bikaner bentonite under different temperatures

下载: 全尺寸图片幻灯片

根据土力学公式,饱和后试样的最大膨胀率与试样孔隙比之间的关系为

$ε_{max} = \frac{e - e_{0}}{1 + e_{0}} \times 100 %$ 。

(17)

式中,e为饱和后膨润土试样的孔隙比,e₀为初始孔隙比,可以表达为

$e_{0} = \frac{d_{s} ρ_{w}}{ρ_{d}} - 1$ 。

(18)

式中,d_s为GMZ膨润土土粒相对质量密度,ρ_w为水的密度,ρ_d为试样的干密度。

结合式（1）,（17）和（18）,膨润土的最大膨胀率 $ε_{\max}$ 与孔隙比e_m之间关系为

$ε_{\max} = (\frac{{αe}_{m} + 1}{d_{s} ρ_{w}} ρ_{d} - 1) × 100 %$ 。

(19)

将式（16）代入式（19）中,可以得出不同温度下GMZ膨润土的最大膨胀率。从式（19）也可以看出,当荷载和温度条件相同时, $ε_{\max}$ 随试样的初始干密度线性增加,这与试验数据一致（图4）。同样,如图10所示,在相同的荷载和密度条件下, $ε_{\max}$ 随温度线性增加。 $ε_{\max}$ -T_c关系的斜率随竖向荷载减小,但随初始干密度增大而增大,表明温度对膨胀变形的影响随压力的增大而减弱,随干密度的增大而增强。

图 10 不同温度下GMZ膨润土最大膨胀率的预测值

Figure 10. Prediction of maximum swelling strain of GMZ bentonite at different temperatures

下载: 全尺寸图片幻灯片

当式（19）中的膨胀率等于零时,可得出不同温度下GMZ膨润土的膨胀力：

$p_{s} = {[\frac{1}{K α} (\frac{G_{s}}{ρ_{d}} - 1)]}^{\frac{1}{D- 3}}$ 。

(20)

由式（20）可知,膨胀力应随温度或初始干密度呈指数增长。初始干密度显著促进了温度对膨胀力的影响。如图11所示,不同温度下膨胀压力的预测值与试验数据之间也具有较好的一致性。

图 11 不同干密度不同温度时GMZ膨润土的膨胀力

Figure 11. Prediction of swelling pressure of GMZ bentonite with different densities under different temperatures

下载: 全尺寸图片幻灯片

4. 结论

（1）由于在本次试验条件下,渗透膨胀占主导地位,温度增加了黏土颗粒间扩散双电层的厚度,进而提高了GMZ膨润土的膨胀性能。使得膨胀率和膨胀力均随温度的升高而增大。

（2）当其他条件相同时,GMZ膨润土的最大膨胀率随温度呈线性增加,膨胀力随温度和干密度呈指数增长。温度对膨胀性能的影响还与试样干密度有关,干密度越大,温度升高对膨胀性能的促进作用越明显。

（3）压实膨润土的膨胀性能可采用分形模型表达成e_m=Kp^D-3。试验结果表明,GMZ膨润土在在25℃～90℃范围内蒸馏水中膨胀时,其分形维数D不变。同时,采用DDL模型计算得出蒙脱石的膨胀系数K随温度呈线性增加,GMZ膨润土的K-T_c关系可表示为 $K = 0.017 T_{c} + 6.486$ 。利用e_m-p与温度的关系,可以估算出GMZ膨润土在不同温度下的膨胀变形和膨胀压力。

（4）本文中计算模型是建立在膨润土矿物在100 ℃以内基本不发生改变的基础上的。当温度更高时,膨润土中某些矿物可能会发生化学反应并对膨胀性能产生影响,这种条件下膨胀性能的变化仍有待进一步的研究。

图 1 管幕的布置形式

Figure 1. Arrangement of pipe curtains

下载: 全尺寸图片幻灯片

图 2 管幕接头弯曲试验曲线^[11]

Figure 2. Curves of bending tests on joints of pipe curtains^[11]

下载: 全尺寸图片幻灯片

图 3 日本管幕加载试验模型与结果^[6]

Figure 3. Model and results of loading tests on pipe curtains^[6]

下载: 全尺寸图片幻灯片

图 4 管幕简化示意图

Figure 4. Simplification of pipe curtains

下载: 全尺寸图片幻灯片

图 5 管幕弹性地基梁简化模型

Figure 5. Simplified model for elastic foundation beams of pipe curtains

下载: 全尺寸图片幻灯片

图 6 第i个单元受力分析

Figure 6. Force analysis for i-unit

下载: 全尺寸图片幻灯片

图 7 第i节点的内力传递

Figure 7. Internal force transfer of i-unit

下载: 全尺寸图片幻灯片

图 8 简支梁数值解与理论解对比

Figure 8. Comparison between numerical and theoretical solutions of simply supported beams

下载: 全尺寸图片幻灯片

图 9 固支梁数值解与理论解对比

Figure 9. Comparison between numerical and theoretical solutions of fixed beams

下载: 全尺寸图片幻灯片

图 10 弹性地基梁数值解与理论解对比

Figure 10. Comparison between numerical and theoretical solutions of beams on elastic foundation

下载: 全尺寸图片幻灯片

图 11 管幕与初支侧墙连接节点图

Figure 11. Joints of pipe curtains and side wall with primary support

下载: 全尺寸图片幻灯片

图 12 弹性薄板力学模型图

Figure 12. Mechanical model for elastic thin plates

下载: 全尺寸图片幻灯片

图 13 弹性薄板数值解与理论解对比

Figure 13. Comparison between numerical solution and theoretical solutions of elastic thin plates

下载: 全尺寸图片幻灯片

图 14 车站横断面图

Figure 14. Cross section of station

下载: 全尺寸图片幻灯片

图 15 测点布置与不同模型计算简图

Figure 15. Layout of monitoring points and calculation diagram

下载: 全尺寸图片幻灯片

图 16 导洞拱顶沉降曲线

Figure 16. Settlement curves of crown

下载: 全尺寸图片幻灯片

图 17 不同理论计算得到的管幕最终变形曲线

Figure 17. Curves of final settlement calculated by different theories

下载: 全尺寸图片幻灯片

图 18 不同理论计算得到的管幕x方向弯矩曲线

Figure 18. Bending moments calculated by different theories

下载: 全尺寸图片幻灯片

图 19 不同开挖跨度管幕对比曲线

Figure 19. Comparison curves of pipe curtains with different excavation spans

下载: 全尺寸图片幻灯片

图 20 不同上覆土层厚度管幕对比曲线

Figure 20. Comparison curves of pipe curtains with different heights of overburden

下载: 全尺寸图片幻灯片

图 21 不同钢管壁厚管幕最大挠度对比曲线

Figure 21. Comparison curves of maximum settlement under different wall thicknesses of steel pipe

下载: 全尺寸图片幻灯片

图 22 不同浆体弹模管幕最大挠度对比曲线

Figure 22. Comparison curves of maximum settlement of pipe curtains with different elastic moduli of grouting materials

下载: 全尺寸图片幻灯片

参考文献(21)

[1]	张倍. 砂卵石地层中管幕施工适用性研究[D]. 北京: 北京工业大学, 2017. ZHANG Bei. Study on the Applicability of Pipe-Roof Pre-Support System in Gravel Stratum[D]. Beijing: Beijing University of Technology, 2017. (in Chinese)
[2]	王兆卿. 洞桩法隧道上穿既有地铁区间隧道变形机理及变形控制技术[D]. 北京: 北京工业大学, 2019. WANG Zhao-qin. Deformation Mechanism of Tunnels in Existing Metro Tunnels and Deformation Control Technology[D]. Beijing: Beijing University of Technology, 2019. (in Chinese)
[3]	高胜雷. 棚盖法平顶暗挖地铁车站施工力学行为研究[D]. 北京: 北京工业大学, 2018. GAO Sheng-lei. Study on the Construction Mechanics of Subway Station With Flat Roof[D]. Beijing: Beijing University of Technology, 2018. (in Chinese)
[4]	KOTAKE N, YAMAMOTO O. Design for umbrella method based on numerical analyses and field measurements[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1995, 32(3): A136.
[5]	TAN W L, RANJITH P G. Numerical analysis of pipe roof reinforcement in soft ground tunneling[C]//Proc of the 16th International Conference on Engineering Mechanics, ASCE, 2003, Seattle.
[6]	YAMAKAWA S, GOTO Y. Analysis of load distribution by joinnt in pipe beam roof[J]. Proceedings of the Japan Society of Civil Engineers, 1980(301): 1-12.
[7]	贾金青, 王海涛, 涂兵雄, 等. 管棚力学行为的解析分析与现场测试[J]. 岩土力学, 2010, 31(6): 1858-1864. doi: 10.3969/j.issn.1000-7598.2010.06.031 JIA Jin-qing, WANG Hai-tao, TU Bing-yong, et al. Analytical approach and field monitoring for mechanical behaviors of pipe roof reinforcement[J]. Rock and Soil Mechanics, 2010, 31(6): 1858-1864. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.06.031
[8]	周顺华. 软弱地层浅埋暗挖施工中管棚法的棚架原理[J]. 岩石力学与工程学报, 2005, 24(7): 2565-2570. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200514027.htm ZHOU Shun-hua. Principles of pipe roof applied to shallow-buried tunnels in soft ground[J]. Chinese Journal of Geotechnical Engineering, 2005, 24(7): 2565-2570. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200514027.htm
[9]	肖世国, 李向阳, 夏才初, 等. 管幕内顶进箱涵时顶部管幕力学作用的试验研究[J]. 现代隧道技术, 2006(2): 22-32. https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD200601003.htm XIAO Shi-guo, LI Xiang-yang, XIA Cai-chu, et al. Study on the behavior of the upper pipe-curtain during the advance of a box culvert within pipe-curtains by a model test[J]. Modern Tunnelling Technology, 2006(2): 22-32. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD200601003.htm
[10]	孙旻, 徐伟. 软土地层管幕法施工三维数值模拟[J]. 岩土工程学报, 2006, 28(11): 1497-1500. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2006S1041.htm SUN Min, XU Wei. 3D numerical simulation of pipe-curtain method in soft soils[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(11): 1497-1500. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2006S1041.htm
[11]	杨光辉, 朱合华, 李向阳. 钢管幕锁口接头力学特性试验研究[C]//第三届上海国际隧道工程研讨会, 2007, 上海: 695-700. YANG Guang-hui, ZHU He-hua, LI Xiang-yang. Experimental study on mechanics characteristics of interlock[C]//The third Shanghai International Tunnelling Seminar, 2007, Shanghai: 695-700. (in Chinese)
[12]	谭忠盛, 孙晓静, 马栋, 等. 浅埋大跨隧道管幕预试验研究[J]. 土木工程学报, 2015, 48(增刊1): 429-434. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2015S1077.htm TAN Zhong-sheng, SUN Xiao-jing, MA Dong, et al. Experimental research of pipe-roof pre-supporting technology for the shallow large-span tunnel[J]. China Civil Engineering Journal, 2015, 48(S1): 429-434. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2015S1077.htm
[13]	赵文, 贾鹏蛟, 王连广, 等. 地铁车站STS新管幕构件抗弯承载力试验研究[J]. 工程力学, 2016, 33(8): 167-176. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201608023.htm ZHAO Wen, JIA Peng-jiao, WANG Lian-guang. Experimental study on the flexural capacity of steel tube slab members of subway station[J]. Engineering Mechanics, 2016, 33(8): 167-176. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201608023.htm
[14]	贾鹏蛟, 赵文, 郝云超, 等. 不同结构参数下STS管幕构件力学性能的数值分析[J]. 东北大学学报(自然科学版), 2016, 37(8): 1177-1181. https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX201608023.htm JIA Peng-jiao, ZHAO Wen, HAO Yun-chao. Numerical analysis of the mechanical properties of steel tube slab component under different structural parameters[J]. Journal of Northeastern University (Natural Science), 2016, 37(8): 1177-1181. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DBDX201608023.htm
[15]	关永平, 赵文, 王连广, 等. STS管幕结构抗弯性能试验研究及参数优化[J]. 工程力学, 2017, 34(9): 83-91. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201709011.htm GUAN Yong-ping, ZHAO Wen, WANG Lian-guang, et al. Study on parameter optimization and the flexural behavior of steel tube slab structures[J]. Engineering Mechanics, 2017, 34(9): 83-91. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201709011.htm
[16]	李树忱, 晏勤, 谢璨. 膨胀性黄土隧道钢拱架-格栅联合支护力学特性研究[J]. 岩石力学与工程学报, 2017, 36(2): 446-456. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201702016.htm LI Shu-chen, YAN Qin, XIE Can. The mechanical behavior of composite supports of steel-grid in loess tunnel[J]. Chinese Journal of Geotechnical Engineering, 2017, 36(2): 446-456. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201702016.htm
[17]	张治国, 马兵兵, 黄茂松, 等. 山区滑坡诱发既有隧道受力变形影响分析[J]. 岩土力学, 2018, 39(10): 3555-3564. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201810009.htm ZHANG Zhi-guo, MA Bing-bing, HUANG Mao-song, et al. Influence analyses on force and deformation of existing tunnels induced by landslide in mountain region[J]. Rock and Soil Mechanics, 2018, 39(10): 3555-3564. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201810009.htm
[18]	VESIC A S. Bending of beams resting on isotropic elastic solid[J]. Journal of Soil Mechanics and Foundation Engineering, ASCE, 1961, 87(2): 35-53.
[19]	徐芝纶. 弹性力学[M]. 5版. 北京: 高等教育出版社, 2016. XU Zhi-lun. Elasticity[M]. 5th ed. Beijing: Higher Education Press, 2016. (in Chinese)
[20]	黄炎. 矩形薄板弹性弯曲问题的一般解析解法[J]. 国防科技大学学报, 1983(3): 1-16. https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ198303000.htm HUANG Yan. A general analytical method for elastic bending of rectangular thin plates[J]. Journal of National Defense University of Defense Technology, 1983(3): 1-16. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GFKJ198303000.htm
[21]	黄炎. 矩形薄板弹性弯曲的精确解析解法[J]. 力学学报, 1987, 19(增刊): 230-235. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB1987S1028.htm HUANG Yan. Exact analytical method for elastic bending of rectangular thin plates[J]. Chinese Journal of Theoretical and Applied Mechanics, 1987, 19(S0): 230-235. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB1987S1028.htm

施引文献(15)

期刊类型引用(9)

1.	陈梦豪，付海，曹珊珊，林铭宇，陈良宇. 温度对MX-80膨润土物理性能的影响. 金陵科技学院学报. 2024(01): 46-53 . 百度学术
2.	李裕诚，陈永贵，刘丽，叶为民，王琼. 高压实膨润土多尺度膨胀力特性研究进展. 岩土工程学报. 2024(11): 2457-2464 . 本站查看
3.	薄纯悦，刘春红，冷佳欣，陈聪. 含水率和干密度对三峡库区紫色土膨胀特性的影响. 土壤. 2024(06): 1381-1389 . 百度学术
4.	项国圣，卞云飞，付文青，周殷康. 热-碱作用对压实膨润土抗剪性能的影响. 安徽建筑大学学报. 2024(06): 8-14 . 百度学术
5.	李彩霞，李俊，徐猛，刘敏，刘桂祺. 氯盐溶液对钠基膨润土垫层膨胀性能的影响. 土木与环境工程学报(中英文). 2023(01): 97-104 . 百度学术
6.	王琼，张佳南，高岑，苏薇，刘樟荣，叶为民. 基于梯度提升决策树算法的膨润土膨胀力预测. 世界核地质科学. 2023(03): 775-786 . 百度学术
7.	曾召田，张瀚彬，邵捷昇，车东泽，吕海波，梁珍. MX-80膨润土高温老化时间效应的细微观分析. 岩土力学. 2023(S1): 145-153 . 百度学术
8.	胡志杰，项国圣，付文青，王浩，李华健. 荷载-溶液作用下膨润土压缩渗透性能研究. 地下空间与工程学报. 2023(06): 1851-1858 . 百度学术
9.	项国圣，胡志杰，葛磊，王浩. 含盐水溶液作用下膨润土膨胀性能衰减机理. 华北水利水电大学学报(自然科学版). 2022(05): 85-91 . 百度学术