基于上限法分析椭圆形结构的极限承载力

瑜璐; 杨庆; 张金利

doi:10.11779/CJGE202102016

基于上限法分析椭圆形结构的极限承载力 English Version

大连理工大学海岸与近海工程国家重点实验室,辽宁　大连　116023

基金项目:

国家重点研发计划项目 2016YFE0200100

国家自然科学基金重点项目 51639002

详细信息

作者简介:
瑜璐（1983— ）,女,博士研究生,主要从事深海锚固系统方面的研究工作。E-mail：yulu@mail.dlut.edu.cn

通讯作者:
杨庆, E-mail: qyang@dlut.edu.cn

中图分类号: TU43
计量
- 文章访问数: 236
- HTML全文浏览量: 29
- PDF下载量: 140
出版历程
- 收稿日期: 2020-04-22
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-01-31

Ultimate bearing capacity of elliptical tip by upper bound analysis

State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116023, China

摘要

摘要: 基于塑性极限理论上限法分析锚桩椭圆形端部和椭圆T-bar的极限承载力及承载力系数,并考虑椭圆形端部的长径比（ξ≥1）和界面摩擦系数对承载力以及承载力系数的影响。分别详细介绍锚桩和T-bar的椭圆端部速度场以及相应速度矢端图的构建。速度场的总能量损耗率是速度间断面能量损耗率和塑性区变形损耗率之和,端部承载力系数等于速度场总能量损耗率与椭圆端部速度,直径和土体强度的比值。结果显示：①椭圆形端部的长径比是1的上限解与前人研究圆形端部结果具有很好的一致性,从而验证了锚桩和T-bar椭圆端部上限模型的合理性；②摩擦力对承载力系数的影响随着端部的长径比的增大而增大；③椭圆端部-土界面完全粗糙时,上限解与下限解和数值解具有较好一直性；随着摩擦系数的降低,承载力系数上限值逐渐大于下限值。
- 上限法 /
- 椭圆形端部 /
- 极限承载力 /
- T-bar /
- 锚桩
Abstract: For the anchor pile with elliptical tip and T-bar, the bearing capacity and factor are obtained based on the upper-bound limit analysis of plasticity considering the influences of the aspect ratio of the elliptical tip (ξ≥1) and the friction coefficient. The velocity fields and hodographs of the elliptical tip of the anchor pile and T-bar are introduced. The total energy dissipation is figured by summing up each part of the internal energy dissipation and the energy dissipation on the velocity discontinuous surface. The bearing factor is equal to the ratio of the total energy dissipation over the velocity and diameter of the elliptical tip and soil strength. It is found that for ξ=1, there is a good consistency between the upper bound solutions and the previous results. Therefore, the upper bound models for the elliptical tip are rational. The influences of friction force become more significant with the increasing ξ for the penetration resistance coefficient. The upper and lower-bound solutions maintain consistency. The upper bound solutions of the bearing capacity are generally larger than the lower ones as the decreasing friction factor.
- upper bound method /
- elliptical tip /
- ultimate bearing capacity /
- T-bar /
- anchor pile

HTML全文

0. 引言

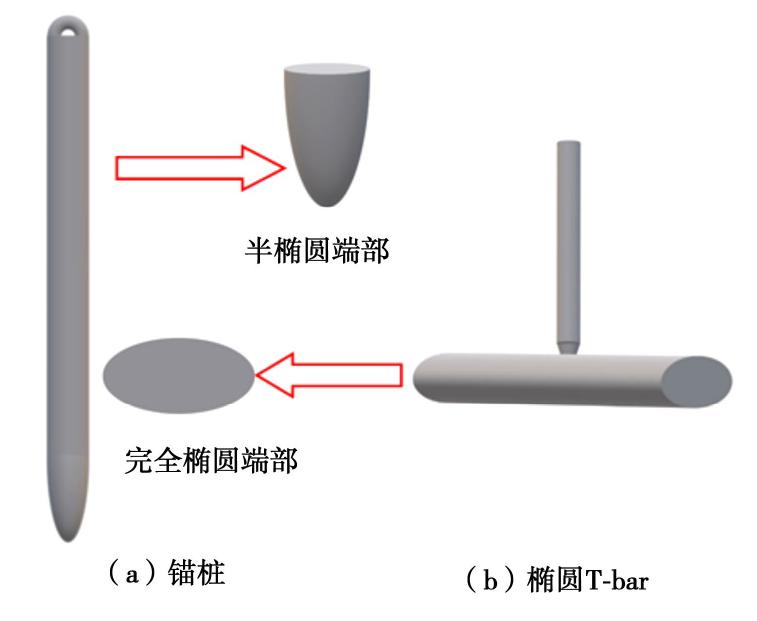
近年来随着海洋工业的发展,复杂的海底地貌对海洋结构物的端部承载力提出更高要求。越来越多的圆形,圆锥形或椭圆形端部取代传统平板形用于海洋结构物,例如,桩靴（spudcan）的圆锥形端部、鱼雷锚 (torpedo anchor, dynamical installation anchor)的椭圆形或圆锥形端部、海底管线的圆形端部、T-bar的圆形端部、重力贯入仪（free fall cone penetrometer,expendable bottom penetrometer）的圆锥形或类椭圆形端部等等（如图1所示）。众所周知,海洋结构物的端部形状影响结构物的安装深度和承载力,从而影响上部海洋平台的安全性和生产能力。海洋结构物承载力的研究主要基于离心机试验、现场试验、1g试验,数值计算和理论计算等方法。Martin等^[1]和Hu等^[2] 分别通过1g试验和离心机试验研究了桩靴的竖向（V）,水平（H）以及抗弯（M）承载力,并给出承载力V-H-M包络曲线。Houlsby等^[3]通过滑移线的有限差分法研究了不同夹角的圆锥形端部承载力,与此同时考虑了埋深,土体强度以及界面摩擦等因素对极限承载力的影响。Randoph^[4]详细介绍了圆形桩的水平极限承载力的上下限模型,该模型被Murff等^[5]和Aubeny等^[6]引入圆形海底管线承载力的研究。随后Randolph等^[7]、Martin等^[8]进一步改进圆形端部上限法的速度场,优化后上下限解的差值减小,因此更趋近于精确解。Gao 等^[9-10]也通过下限法研究了浅埋海底管线承载力与埋深的关系。Randolph等^[11]还将圆桩的上限模型用于T型全流动贯入仪（T-bar）承载力的研究。Richarson等^[12]通过离心机试验方法研究了鱼雷锚不同形状的端部承载力,试验结果显示：椭圆形端部的贯入阻力大于圆锥形或平板形,而平板形和圆锥形端部具有相似的端部承载力。O’ Loughlin等^[13]通过离心机试验确定长径比（锚尖长/锚杆半径）为3.8的椭圆形端部的承载力系数N_c为12。到目前为止,已有大量学者对平板形、圆形和圆锥形端部的承载力进行了研究,但对于椭圆形端部承载力的理论研究相对较少。椭圆形端部根据土体流动趋势、边界条件和形状等因素分为两类：用于锚桩,鱼雷锚和重力贯入仪（类似于静力触探）等海洋结构物的半椭圆端部（见图2（a））；以及用于椭圆形海底管线,椭圆形T-bar等结构物的完全椭圆端部（见图2（b））。刘朝安等^[14]研究了椭圆形T-bar的承载力,比较分析了完全光滑和完全粗糙时的上下限解,但并未详细介绍上限法速度场的构建以及摩擦系数的变化对承载力的影响。

图 1 海洋结构物

Figure 1. Ocean structures

下载: 全尺寸图片幻灯片

图 2 示意图

Figure 2. Schematic diagram of anchor pile and T-bar

下载: 全尺寸图片幻灯片

本文基于塑性极限分析上限法对深埋锚桩（半椭圆端部贯入土体达到完全回流）和椭圆形T-bar（完全椭圆端部贯入土体达到完全回流）的端部承载力进行研究,同时考虑椭圆端部的长径比（ξ≥1）和摩擦系数ω对承载力的影响。详细介绍椭圆结构速度场和速度矢量图的构建。并与前人研究结果和数值解进行比较分析进而验证椭圆结构上限模型的可行性。

1. 上限法及基本假设

岩土问题是非常复杂的,往往伴随着土体不连续、各向异性、体胀、体缩、软化和大变形等现象。Meyerhof^[15]、Chen^[16]将金属加工理论中的塑性极限分析法用以解决应力-应变关系复杂的岩土问题。将土体假设为理想弹塑性或刚塑性体,忽略土体弹塑性过渡阶段的应力应变响应,仅考虑土体达到屈服强度的应力应变关系,该方法在保证工程安全的前提下大大简化了计算过程。塑性极限分析法分为下限法和上限法。上限法从能量角度出发根据土体破坏机制构建满足几何方程,体积不变和速度边界条件的运动许可速度场。上限解总是大于等于真实载荷。下限法需构建满足静力平衡方程、应力边界条件、屈服准则、流动法则等条件的静力许可应力场,应力场对应的最大荷载小于等于真实荷载。当上下限解相等时施加荷载是精确解。

1.1 上限法原理

上限法也称为基于虚功原理和变分极值原理的能量法,用于寻求复杂塑性问题的近似解。上限法不仅可以解决二维的平面应变问题和轴对称问题,而且可以解决部分三维问题,此外还可求解高速变形的温度场^[17]。

外力做功的功率小于等于变形体内塑性变形的功率和一系列速度不连续面上的剪切应力耗散的功率：

$\int_{S} T_{i} v_{i} d S + \int_{V} f_{i} v_{i} d V \leq \int_{V} σ_{i j} {\dot{ε}}_{i j} d V + \int_{A} K Δ v_{t} d A$ 。

(1)

式中 T_i,f_i分别为体力和面力；v_i为虚拟许可速度场的速度；∆v_t为速度间断面上切向速度差； $σ_{i j}$ 为与 ${\dot{ε}}_{i j}$ 相对应的应力； ${\dot{ε}}_{i j}$ 为根据速度场确定的应变率。

塑性区屈服应力 $σ_{i j}$ 与 ${\dot{ε}}_{i j}$ 服从流动法则：

$d ε_{_{i j}}^{p} = d λ \frac{\partial F}{\partial σ_{i j}}$ ,

(2)

式中,F为屈服函数, $d λ$ 为塑性流动因子, $d ε_{_{i j}}^{p}$ 塑性应变增量。

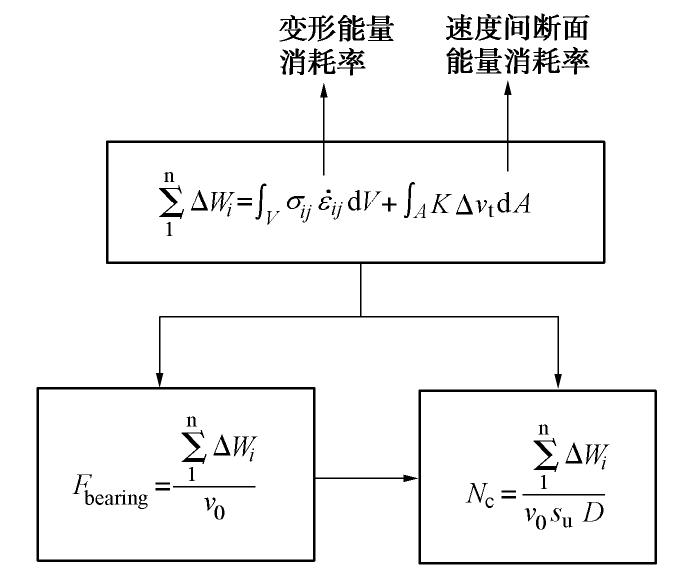
Tresca材料的屈服函数为 $F = σ_{1} - σ_{3} - 2 K = 0$ （其中K为剪切屈服强度）,则 ${\dot{ε}}_{1}^{p} / {\dot{ε}}_{3}^{p} = - 1$ 。Coulomb材料的屈服函数为： $F = σ_{1} (1 - \sin φ) -$ $σ_{3} (1 - \sin φ) -$ $2 c \cos φ = 0$ 或 $τ_{n} = c - σ_{n} \tan φ$ ,（其中c为黏聚力,φ为Coulomb土体内摩擦角,τ_n为破坏面上剪切应力, $σ_{n}$ 为破坏面上正应力） ${\dot{ε}}_{1}^{P} = - \tan^{2} (π / 4 -$ $φ / 2) {\dot{ε}}_{3}^{P}$ , ${\dot{γ}}^{P} = - {\dot{ε}}^{p} / \tan φ$ ,（式中, ${\dot{γ}}^{P}$ 为塑性剪应变, ${\dot{ε}}^{p}$ 为正应力 $σ_{n}$ 方向塑性应变率）。Tresca材料塑性状态体积应变率为0。Coulomb材料体积应变率不为0,出现剪胀的现象^[18-21],Chen^[16]指出摩擦材料符合非相关流动法则,按照理想塑性理论（满足相关流动法则）预测的上限解可能伴随着剪胀大于实际剪胀情况。

基于上限法计算承载力系数或承载力流程如图3所示,式中F_bearing为端部承载力,N_c为端部承载力系数, $\sum_{1}^{n} Δ W_{i}$ 为能量消耗率之和,v₀为椭圆端部的运动速度,s_u为土体不排水抗剪强度,D椭圆端部的直径。

图 3 承载力和承载力系数计算流程图

Figure 3. Flow chart of calculation of bearing capacity and factor

下载: 全尺寸图片幻灯片

1.2 模型假设

对于深埋的椭圆形结构,土体服从完全回流破坏机制。

（1）假设土体为各向同性的纯黏土（即土体内摩擦角φ=0）,破坏过程中无水排出且体积保持不变。土体假设为理想刚塑性材料,服从Tresca屈服准则。

（2）忽略土体重度的影响。根据Martin等^[22]和Meyerhof^[15]对吸力锚、桩和基础结构的研究表明土重不影响系数N_c仅影响土重承载力系数N_γ,因此对N_c研究可忽略土重因素。本文不考虑周围土体有上覆荷载工况,因此无N_q系数影响。

（3）假设椭圆端部的锚桩和T-bar均是刚体。

（4）椭圆端部和锚桩侧壁摩擦系数相同。

1.3 数值模型

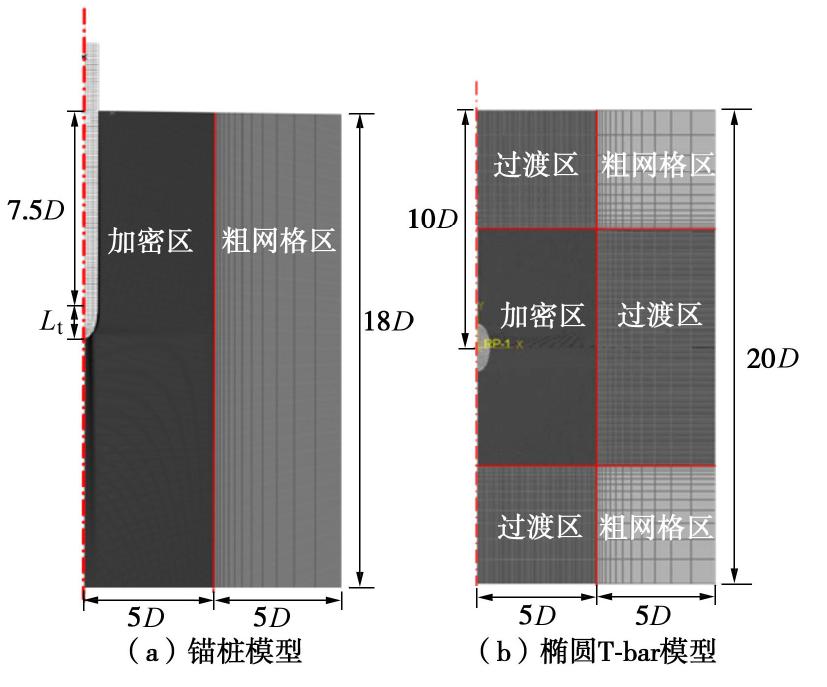
在ABAQUS软件中分别构建锚桩和椭圆形T-bar预埋在土中的平面应变模型（图4）。土体为各向同性的纯黏土,服从Tresca屈服准则。土体参数选取参考前人对深海锚、平板锚和海底管线研究（Kim等^[23]、O’Beirne等^[24]、Wang等^[25-26]）,土体浮重度 $γ^{'}$ = 6 kN/m³,不排水抗剪强度s_u =10 kPa,弹性模量E=500s_u,泊松比 $ν$ =0.49。网格单元类型为CPE4,经过网格密度对承载力影响验证确定加密区网单元尺寸为D/100,土体网格数量520000～540000。锚桩或T-bar与土界面采用完全光滑或完全粗糙的面-面接触,并且接触后不允许分离。锚桩椭圆端部末端预埋深为7.5D,椭圆形T-bar中心预埋深也为10D。

图 4 数值模型图

Figure 4. Numerical models

下载: 全尺寸图片幻灯片

2. 椭圆端部承载力分析

构建椭圆形端部特征线场根据椭圆参数方程： $X = L_{t} \cos δ, Y = \frac{D}{2} \sin δ,$ 其中, $δ =arctan [(\frac{2 L_{t}}{D}) \tan η]$ , $δ$ 为椭圆离心角其（η为椭圆圆心角,D为椭圆端部的直径,L_t为椭圆端部的长度）。椭圆上一点法线方向角为 $φ_{nj} = arctan [(D / 2 L_{t}) \tan δ_{i}]$ ,对应的椭圆某段弧长 $L_{arc} = (D / 2) \int \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ$ （式中 $ξ = 2 L_{t} /$ $D$ ）。土体服从Tresca屈服准则,椭圆端部与土体界面摩擦系数 $ω = \sin Δ = τ_{x y} / s_{u}$ （ $Δ$ 为界面摩擦角）^[27]。

2.1 锚桩椭圆端部承载力

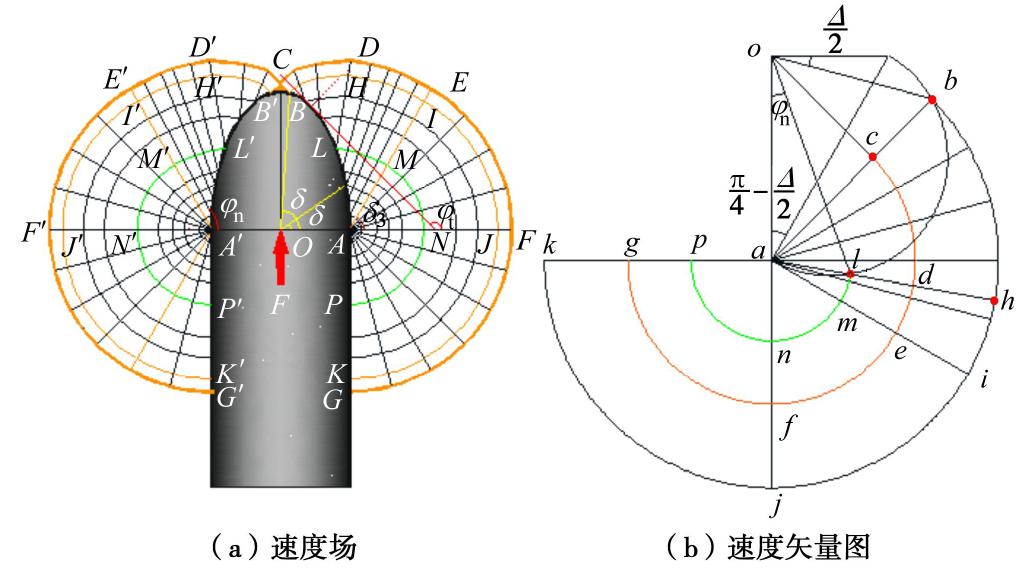
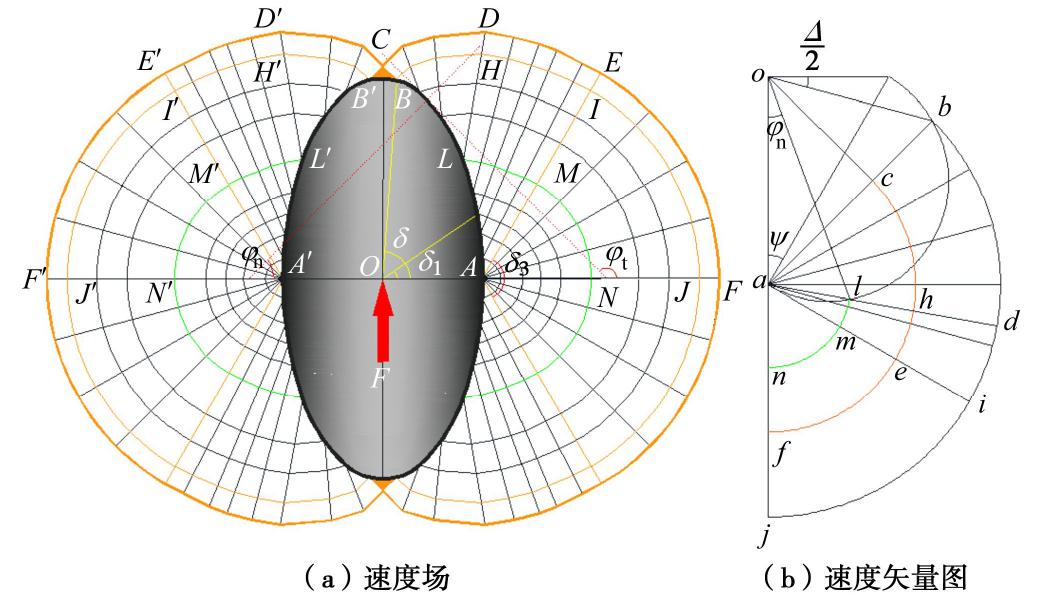
锚桩安装过程中土体围绕椭圆端部向桩侧流动,根据土体的回流破坏机制构建虚拟速度场。椭圆形端部速度场需满足相关流动法则,速度边界条件,几何方程以及体积不变等条件。速度场的主应变方向与下限法中应力场的主应力方向一致（如图5（a）所示）。由于锚桩椭圆端部速度场关于x=0平面对称,因此只需研究一半速度场,总能量损耗为一半速度场能量损耗的2倍。Randolph^[4]、Murff等^{[5, 8]}、Aubeny等^[6]在对圆形端部的研究中根据塑性区变形半径,间断速度,应变率等因素将虚拟速度场分为5部分：刚性区,异心扇形剪切区,同心扇形剪切区,弥散楔形剪切区和同心圆柱区。参考前人研究,本文也将半椭圆形端部速度场分为5部分。

图 5 锚桩椭圆端部速度场和速度矢量图

Figure 5. Velocity fields and hodographs of elliptical tip of anchor pile

下载: 全尺寸图片幻灯片

图5（b）是与速度场相对应的速度矢量图。速度场内（ABCDEFG区域内）土体进入塑性,场外土体为刚性区则速度为0。因为速度场的速度间断线法向速度必须是连续的,切向速度可以不连续,而椭圆端部速度场内直线特征线与场外刚性区相连,所以直线特征线的速度为0。速度矢量图中矢量a-c-b表示速度场B点和C点切向速度的大小和方向,矢量a-d-h表示速度场H点和D点切向速度大小和方向,同理矢量图中a-e-i和a-f-j也分别表示速度场E点、I点、F点和J点切向速度的大小和方向。矢量图中ob和ol的方向分别平行于椭圆形端部B点和L点的切线方向,速度场中LMNP速度间断线在L点的切向速度与椭圆形端部L点切线的交点就是矢量图中的l点,因此矢量ol的长度是L点土体在ALB弧线边界上的速度,椭圆端部ALB弧线边界上一系列点对应速度矢量图中弧线alb上的点。矢量图中∠aob和∠aol分别是速度场B点处和L点处的法向角。

（1）由于椭圆端部和土体界面存在摩擦,因此在椭圆端部前端形成一个刚性区（BCB´）,该区域土体与椭圆端部具有相同的运动速度v₀。如果椭圆端部与土体界面光滑,则刚性区面积为0。

（2）BCDEIH异心扇形剪切区,扇形中心在椭圆形端部边界上移动,扇形的切向虚拟速度为 $v_{t -out} =$ $v_{0} / \sqrt{2}$ ,扇形区半径为,

$L_{B C} = \frac{D \sqrt{2} \cos δ_{B}}{2}$ ,

(3)

式中, $δ_{B}$ 为圆心角π/2- $Δ$ /2所对的离心角,即刚性区边界B点所对应的离心角。

（3）EFGKJI为扇形剪切区,扇形中心均为A点,半径等于 $L_{B C}$ ,扇形区内圆弧速度间断线的切向虚拟速度为 $v_{t-out}$ 。

（4）ALBHIM是弥散楔形剪切变形区,该区域与BCDEIH异心扇形剪切区相似,中心沿着椭圆形边界逆时针移动,扇形区半径为

$\begin{matrix} R = \frac{D \sqrt{2} \cos δ_{B}}{2} + ρ_{\frac{π}{2}} \sin (δ_{B} - δ_{\frac{π}{2}}) + \\ \cos ψ \frac{D}{2} \int_{δ_{2}}^{δ_{1}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ \end{matrix}$ ,

(4)

式中, $ψ = \frac{π}{4} - \frac{Δ}{2}$ , $ρ_{\frac{π}{2}} = \frac{D}{2} \sqrt{{(ξ \sin θ_{\frac{π}{2}})}^{2} + {(\cos θ_{\frac{π}{2}})}^{2}}$ , $δ_{\frac{π}{2}}$ 为圆心角π/2所对的离心角, $δ_{1}$ 和 $δ_{2}$ 是椭圆上任意两个离心角且 $δ_{2}$ < $δ_{1}$ 。当 $ξ = 2 L_{t} / D = 1$ 时,椭圆形端部变成圆形端部,因此公式（4）就可以简化为

$R = \frac{D}{2} [\sqrt{2} \cos (\frac{π}{2} - \frac{Δ}{2}) + \sin ψ + \cos ψ (η_{1} - η_{2})]$ 。

(5)

式（5）与Randolph等^[4]给出的弥散楔形剪切区的半径相同。

沿着椭圆形端头土体界面ALB的速度 $v_{t-ALB} =$ $v_{0} (\cos φ_{n} +tan ψ \sin φ_{n})$ 。速度剪断线BHI内的速度为 $v_{t-in} = v_{0} \sin φ_{n} / cos ψ$ ,BHI速度曲线外BCDEIH剪切区的速度等于 $v_{t-out} = v_{0} / \sqrt{2}$ ,由此可知BHI速度曲线处出现切向不连续速度差 $Δ v_{t} = v_{0} [\sin φ_{n} sec ψ - 1 / \sqrt{2}]$ 。扇形剪切变形区内一系列特征曲线的速度梯度随着半径减小而逐渐降低。

（5）AMIJKP是同心圆柱区,圆弧线的半径为

$R^{'} = \frac{D \sqrt{2} \cos δ_{B}}{2} + \cos ψ \frac{D}{2} \int_{δ_{2}}^{δ_{1}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ 。$

(6)

速度剪断线IJK的速度类似于BHI速度剪断线 $Δ v_{t}$ ,同样同心圆柱区内特征曲线的速度梯度随着半径减小而逐渐降低,但是A点处的速度不为0。

（1）速度间断线的能量损耗率

a）刚性区BC边

$Δ {\dot{W}}_{B C} = \frac{1}{2} s_{u} v_{0} D \cos δ_{B}$ 。

(7)

b）间断面 $\overset{⌢}{C D E}$

$\overset{⌢}{C D E}$ 面的半径为

$\begin{matrix} R_{0} = \frac{D \sqrt{2} \cos δ_{B}}{2} + ρ_{\frac{π}{2}} \sin (δ_{B} - δ_{\frac{π}{2}}) + \\ \cos ψ \frac{D}{2} \int_{δ_{1}}^{δ_{B}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ \end{matrix}$ 。

Randolph等对圆形桩横向承载力研究中,异心扇形剪切区的弧长 $L_{arc} = \int_{0}^{\frac{π}{2} - \frac{Δ}{2}} R d η$ ,且 $η_{B} = \frac{π}{2} - \frac{Δ}{2}$ ,而 $ξ$ >1的椭圆形端部 $δ_{B} > \frac{π}{2} - \frac{Δ}{2}$ ( $L_{t}$ ≥ $\frac{D}{2}$ ),因此需对弧长 $L_{C D E} = \int_{0}^{δ_{B}} R_{0} d δ_{1}$ 进行修正,引入修正半径 ${R^{'}}_{0}$ ：

${R^{'}}_{0} = \frac{D \sqrt{2} \cos δ_{B}}{2} + \cos ψ \frac{D}{2} \sqrt{{(\sin δ_{B})}^{2} + {(ξ \cos δ_{B})}^{2}}$ ,

$\overset{⌢}{C D E}$ 弧线长为

$\begin{array}{l} L_{C D E} = \int_{0}^{δ_{B}} R_{0} d δ_{1} + {R^{'}}_{0} (\frac{π}{2} - \frac{Δ}{2} - δ_{B}), \\ Δ {\dot{W}}_{C D E} = \frac{s_{u} v_{0}}{\sqrt{2}} {{R^{'}}_{0} (\frac{π}{2} - \frac{Δ}{2} - δ_{B}) + \\ [\int_{0}^{δ_{B}} \frac{D \sqrt{2} \cos δ_{B}}{2} + ρ_{\frac{π}{2}} \sin (δ_{B} - δ_{\frac{π}{2}}) + \\ \cos (\frac{π}{4} - \frac{Δ}{2}) \frac{D}{2} \int_{δ_{1}}^{δ_{B}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ] d δ_{1}} \end{array}$ 。

(8)

c）间断面 $\overset{⌢}{E F G}$

$\overset{⌢}{E F G}$ 面的半径为

$R_{1} = \frac{D \sqrt{2} \cos δ_{B}}{2} + \cos ψ \frac{D}{2} \int_{0}^{δ_{B}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ$ 。

$\overset{⌢}{E F G}$ 弧线长为

$\begin{matrix} L_{E F G} = \int_{- \frac{π}{2}}^{\frac{π}{4} + \frac{Δ}{2}} R_{1} d δ_{3} \\ Δ {\dot{W}}_{E F G} = \frac{s_{u} v_{0}}{\sqrt{2}} \\ \int_{- \frac{π}{2}}^{\frac{π}{4} + \frac{Δ}{2}} [\frac{D \sqrt{2} \cos δ_{B}}{2} + \cos ψ \frac{D}{2} \cdot \\ \int_{0}^{δ_{B}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ] d δ_{3} \end{matrix}$ 。

(9)

d）间断面 $\overset{⌢}{B H I}$

$\overset{⌢}{B H I}$ 面的半径为 $R_{2} = ρ_{\frac{π}{2}} \sin (δ_{B} - δ_{\frac{π}{2}}) + \cos ψ \frac{D}{2} \cdot$ $\int_{δ_{1}}^{δ_{B}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ 。$ 同理于间断面 $\overset{⌢}{C D E}$ 的弧长计算, $\overset{⌢}{B H I}$ 弧线长也需要考虑修正半径 ${R^{'}}_{2}$ ： ${R^{'}}_{2} = \cos ψ \frac{D}{2} \sqrt{{(\sin δ_{B})}^{2} + {(ξ \cos δ_{B})}^{2}}$ 。 $\overset{⌢}{B H I}$ 弧线长为 $L_{B H I} = \int_{0}^{δ_{B}} R_{2} d δ_{1} + {R^{'}}_{2} (\frac{π}{2} - \frac{Δ}{2} - δ_{B})$ , $\overset{⌢}{B H I}$ 速度间断线：

$\begin{array}{l} Δ v_{t} = v_{0} (\sin φ_{n} \sec ψ - 1 / \sqrt{2}), \\ Δ {\dot{W}}_{B H I} = s_{u} v_{0} (\sin φ_{n} \sec ψ - 1 / \sqrt{2}) \cdot \\ {{R^{'}}_{2} (\frac{π}{2} - \frac{Δ}{2} - δ_{B}) + [\int_{0}^{δ_{B}} ρ_{\frac{π}{2}} \sin (δ_{B} - δ_{\frac{π}{2}}) + \cos ψ \frac{D}{2} \cdot \\ \int_{δ_{1}}^{δ_{B}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ] d δ_{1}} \end{array}$ 。

(10)

e）间断面 $\overset{⌢}{I J K}$

$\overset{⌢}{I J K}$ 面的半径为 $R_{3} = \cos ψ \frac{D}{2} \int_{0}^{δ_{B}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} \cdot$ $d δ$ , $\overset{⌢}{I J K}$ 弧线长为 $L_{I J K} = \int_{- \frac{π}{2}}^{\frac{π}{4} + \frac{Δ}{2}} R_{3} d δ_{3}$ , $\overset{⌢}{I J K}$ 速度间断线为

$\begin{array}{l} Δ v_{t} = (\sin φ_{n} \sec ψ - 1 / \sqrt{2}), Δ {\dot{W}}_{I J K} = s_{u} v_{0} (\sin φ_{n} \cdot \\ \sec ψ - 1 / \sqrt{2}) \cdot \\ \int_{- \frac{π}{2}}^{\frac{π}{4} + \frac{Δ}{2}} [\cos ψ \frac{D}{2} \int_{0}^{δ_{B}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ] d δ_{3} \end{array}$ ,

(11)

式中,δ₃为同心圆区的圆心角。

f）椭圆形端部间断面 $\overset{⌢}{A L B}$

$\overset{⌢}{A L B}$ 弧线长为 $L_{A L B} = \frac{D}{2} \int_{0}^{δ_{B}} \sqrt{{(\sin δ)}^{2} +(ξ \cos δ)^{2}} d δ,$ $\overset{⌢}{A L B}$ 速度为

$\begin{array}{l} v_{t - A L B} = v_{0} (\cos φ_{n} + \tan ψ \sin φ_{n}), \\ Δ {\dot{W}}_{A L B} = s_{u} v_{0} sin Δ \frac{D}{2} \cdot \\ \int_{0}^{δ_{B}} [(\cos φ_{n} + \tan ψ \sin φ_{n}) \cdot \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}}] d δ 。 \end{array}$

(12)

g）考虑锚桩侧面APKG与土体界面摩擦时需计算锚桩-土体界面摩擦所损耗能量,若不考虑桩侧摩擦可忽略此项。

边界APKG： $L_{A P K G} = R_{1}$ ,

$\begin{matrix} Δ {\dot{W}}_{A P K G} = s_{u} v_{0} \sin Δ (\frac{D \sqrt{2} \cos δ_{B}}{2} + \cos ψ \frac{D}{2} \cdot \\ \int_{0}^{δ_{B}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ) \end{matrix}$ 。

(13)

（2）塑形变形区内的内能损耗率

a）BCDEFGKJIH扇形剪切区的内能损耗,速度为 $v_{t-out} = v_{0} / \sqrt{2} d δ$ ,半径为 $L_{B C}$ ,则

$Δ {\dot{W}}_{B C D E F G K J I H} = s_{u} \int_{- \frac{π}{2}}^{\frac{3 π}{4}} \frac{v_{0}}{\sqrt{2}} L_{B C} d δ$ 。

(14)

b）ALBHIM是弥散楔形剪切变形区的内能损耗,变形区半径为

$R_{4} = ρ_{\frac{π}{2}} \sin (δ_{B} - δ_{\frac{π}{2}}) + \cos ψ \frac{D}{2} \int_{δ_{1}}^{δ_{2}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ,$

变形区速度为 $v_{t -in} = v_{0} \sin φ_{n} / \cos ψ$ ,变形区应变率为

$\begin{array}{l} {\dot{γ}}_{A L B H I M} = - ({\frac{\partial v_{t -in}}{\partial R_{4}} |}_{δ_{2}} - \frac{v_{t -in}}{R_{4}}), \\ Δ {\dot{W}}_{A L B H I M} = \dot{γ} s_{u} \int_{0}^{δ_{B}} \int_{0}^{δ_{2}} R_{4} \frac{\partial R_{4}}{\partial δ_{2}} d δ_{1} d δ_{2} 。 \end{array}}$

(15)

c）AMIJKP是同心圆柱区的内能损耗,圆柱区半径为 $R_{5} = \cos ψ \frac{D}{2} \int_{0}^{δ_{2}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ$ ,圆柱区应变率为

$\begin{array}{l} {\dot{γ}}_{A M I J K P} = - ({\frac{\partial v_{t -in}}{\partial R_{5}} |}_{δ_{2}} - \frac{v_{t -in}}{R_{5}}), \\ Δ {\dot{W}}_{A M I J K P} = {\dot{γ}}_{A M I J K P} s_{u} \int_{0}^{δ_{B}} \int_{- \frac{π}{2}}^{\frac{π}{4} + \frac{Δ}{2}} R_{5} \frac{\partial R_{5}}{\partial δ_{2}} d δ_{3} d δ_{2} 。 \end{array}}$

(16)

锚桩椭圆形端部的承载力系数等于速度间断面和塑性区变形能量损耗率之和与不排水抗剪强度、贯入速度以及桩径的比值。

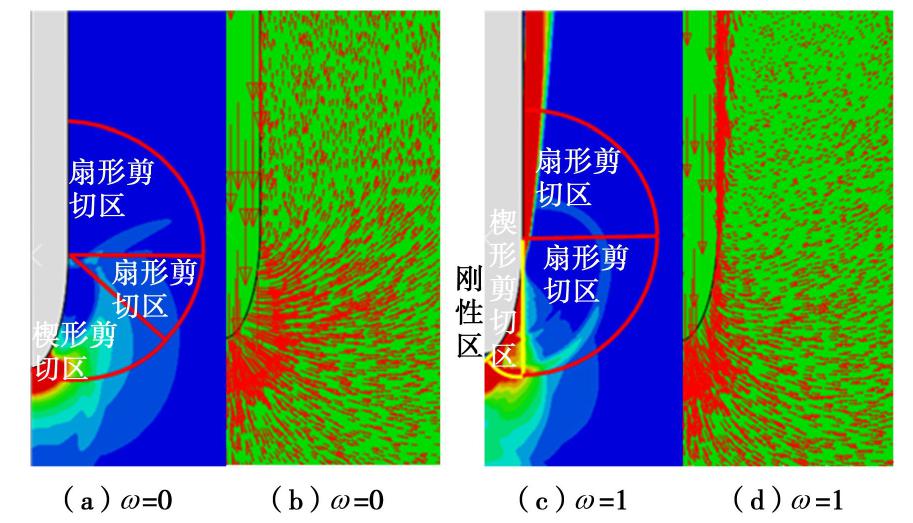
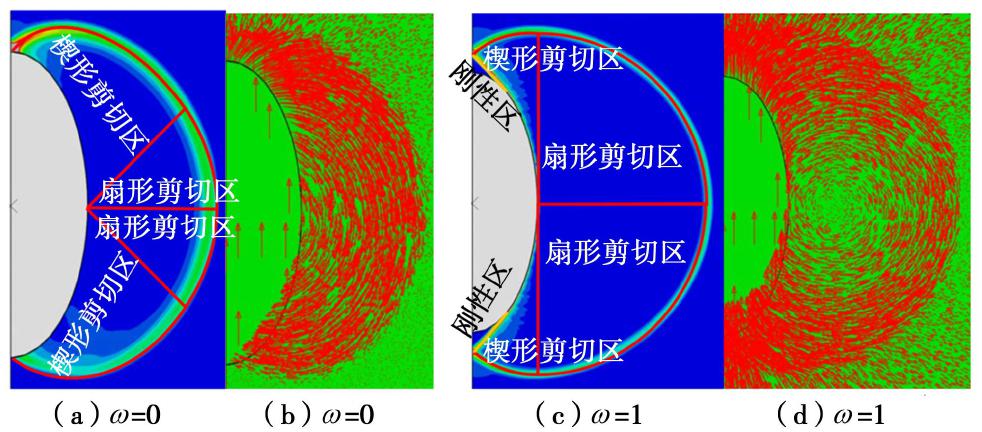
$\begin{matrix} N_{c} = 2 [\overset{速度间断面能量消耗率}{\overset{︷}{(Δ {\dot{W}}_{B C} + Δ {\dot{W}}_{C D E} + Δ {\dot{W}}_{E F G} + Δ {\dot{W}}_{B H I} + Δ {\dot{W}}_{I J K} + Δ {\dot{W}}_{A L B} + Δ {\dot{W}}_{A P K G})}} + \\ \overset{变形能量消耗率}{\overset{︷}{(Δ {\dot{W}}_{B C D E F G K J I H} + Δ {\dot{W}}_{A L B H I M} + Δ {\dot{W}}_{A M I J K P})}}] / s_{u} v_{0} D \end{matrix}$ 。

(17)

图6为数值分析中锚桩贯入土体达到完全回流后桩端土体的等效塑性应变云图和位移矢量图。其中图6（a）和（b）分别是光滑椭圆端部的等效塑性应变云图和位移矢量图,土体围绕着锚桩从桩尖向桩侧流动。图6（c）和（d）分别是粗糙椭圆端部的等效塑性应变云图和位移矢量图,因为桩-土界面摩擦桩尖出现一个刚性区,刚性区的面积随长径比的增大而逐渐减小,刚性区内的土体黏附在桩尖表面随着锚桩进行同向同速运动且不发生滑动,剪切区的土体仍然从桩尖向桩侧流动。根据图6（a）和（c）比较发现,ω=0楔形剪切区与扇形剪切区的分界在-45°,而ω增大到1时分界在-90°,等效塑性应变云图与上限法的虚拟速度场分区基本一致。由此可见,上限法中构造的椭圆形端部虚拟速度场是合理的。

图 6 椭圆形端部等效塑性应变云图和位移矢量图

Figure 6. Equivalent plastic strain nephograms and displacement vector graphs of elliptical tip

下载: 全尺寸图片幻灯片

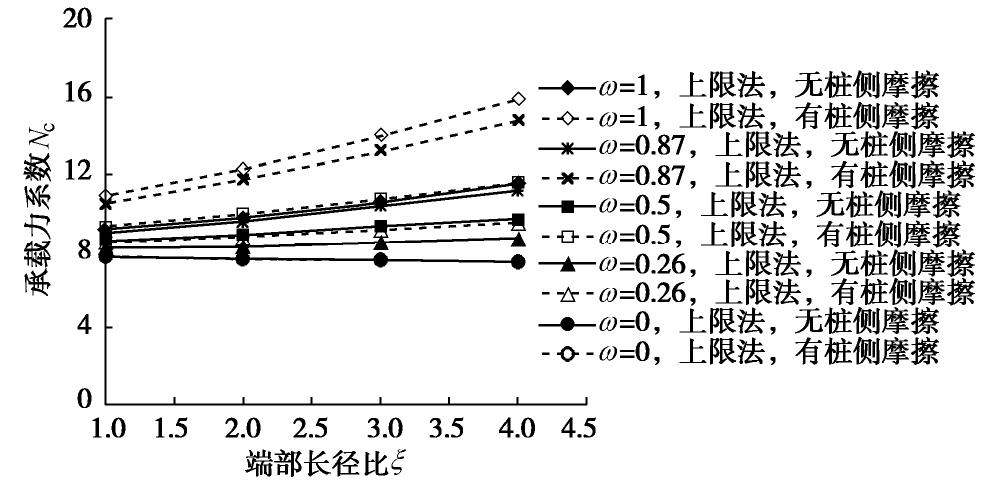
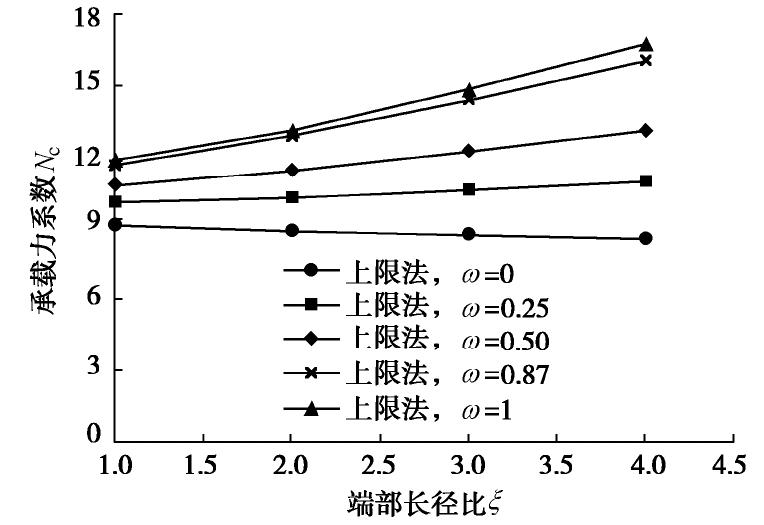
如图7所示,锚桩-土界面光滑（ω=0）时,承载力系数（N_c）随着桩尖长径比（ $ξ$ ）的增加而减小,因为 $ξ$ 越大,桩尖横断面的面积越小,在相同压强下压力越小即贯入阻力越小。当锚桩-土界面摩擦增大（0<ω≤1）,N_c随着 $ξ$ 的增加而增大；因为 $ξ$ 增加,端部面积增大,锚桩-土界面摩擦相应增大,因而端部承载力也增大。由此可见,随着 $ξ$ 逐渐增大将由压应力逐渐转向剪应力提供主要承载应力,即摩擦力对承载力的影响越显著。桩尖长径比越大贯入过程中端部对土体的影响范围越大,则锚桩侧面摩擦面积越大（此处考虑的桩侧摩擦面积是指受端部影响桩侧土体进入塑性区的面积）。当ω=0时桩侧摩擦能量损耗为0,有桩侧摩擦和无桩侧摩擦的承载力系数完全重合。当ω=1, $ξ$ =1时,考虑桩侧摩阻力的承载力系数比无桩侧摩阻力的N_c大2.04；而 $ξ$ 增大到4时,考虑桩侧摩阻力的承载力系数比无桩侧摩阻力的N_c大4.35,由此可见,椭圆锚尖长径比越大对周围土体扰动范围越大。

图 7 椭圆锚桩长径比与承载力系数关系

Figure 7. Relation curves between N_c and ξ of elliptical anchor pile

下载: 全尺寸图片幻灯片

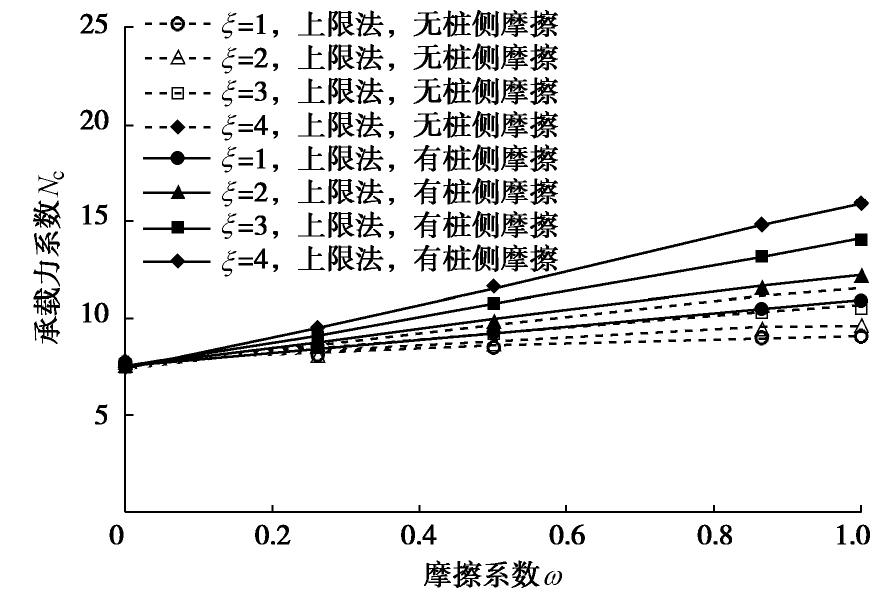
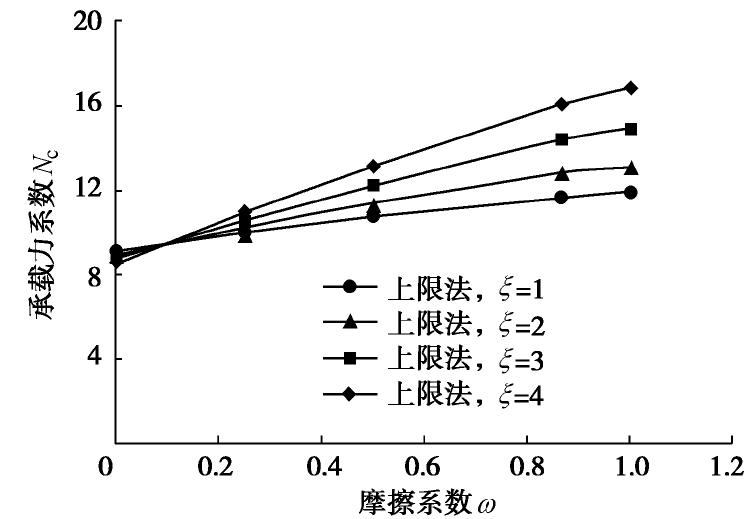
图8可见,当 $ξ$ =1时,完全粗糙的承载力系数是完全光滑的1.18倍,当 $ξ$ 增长到4时,完全粗糙与完全光滑的承载力系数比增长到1.56倍。当ω=0时,无桩侧摩擦力 $ξ$ =1与 $ξ$ =4的承载力系数最大差值分别是0.29；当ω=1时, $ξ$ =1与 $ξ$ =4 的N_c最大差值增大到2.45；然而ω=0.05～0.10时, $ξ$ =1与 $ξ$ =4的N_c差值仅有0.050～0.067,由此可见,当椭圆端部与土界面摩擦在0.05～0.10时,N_c上限解受端部长径比的影响最小。

图 8 椭圆锚桩承载力系数与摩擦系数关系

Figure 8. Relation curves between ω and N_c of elliptical anchor pile

下载: 全尺寸图片幻灯片

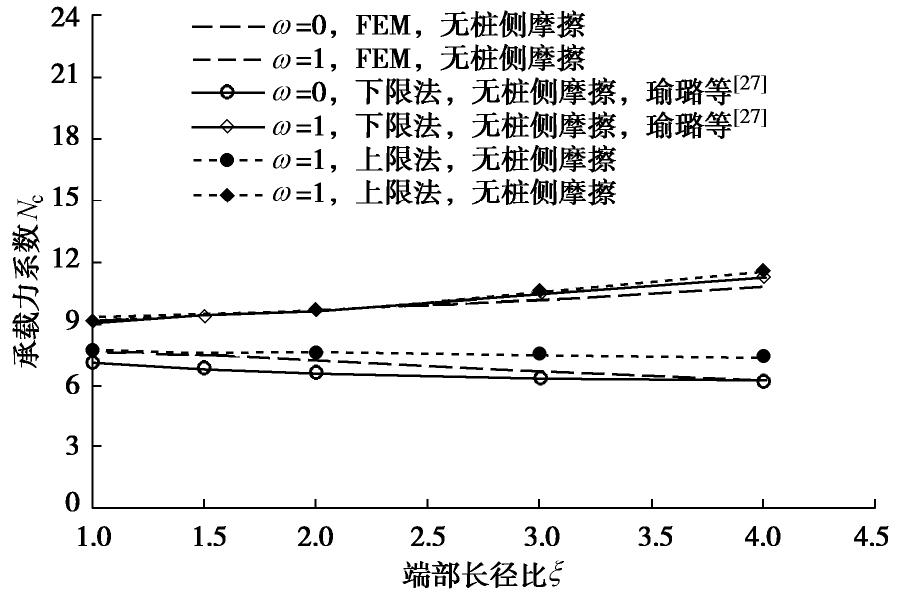
当 $ξ$ =1时椭圆形端部退化为圆形端部,完全粗糙的承载力系数上限解N_c=9.11约等于Aubeny等^[6]根据扩展Randolph-Houlsby速度场计算的上限解N_c=9.12,如果本文上限模型考虑桩侧摩擦力能量损耗,则承载力系数为10.9。Aubeny等的研究主要针对深海沟内圆形管线的极限承载力无侧摩擦力的影响。通过与Aubeny等研究结果比较分析验证了锚桩椭圆端部上限模型是可行性的。图9比较分析椭圆端部锚桩的N_c上限解,下限解与数值解,当ω=1时,椭圆端部承载力系数数值解与上下限解是基本一致；当ω=0时,1≤ $ξ$ <1.5的数值解与椭圆端部上限解一直, $ξ$ >1.5的数值解逐渐靠近椭圆端部下限解。

图 9 椭圆锚桩承载力系数的上、下限解和数值解

Figure 9. Comparison btween upper solutions and numerical results of N_c of elliptical anchor pile

下载: 全尺寸图片幻灯片

锚桩的椭圆端部是轴对称的椭球体,而本文上限模型是基于平面应变理论推导,因此需考虑形状修正。Terzaghi等^[28],Meryerhof等^[15]提出圆形基础和条形基础之间的承载力形状系数是1.2。椭球形端部可以视为无数圆形基础断面的集合,因此本文选用修正系数为1.2。O’Loughlin等^[13]通过离心机试验确定鱼雷锚锚尖 $ξ$ =3.8且锚-土界面摩擦系数是0.4时,锚端的承载力系数（N_c）是12。上限模型 $ξ$ =3.8且ω=0.4的N_c上限解是11.04（考虑形状系数修正N_c=9.2×1.2）,考虑桩侧摩擦能量损耗N_c上限解是12.72。

2.2 椭圆T-bar承载力

T-bar是基于全流动（full-flow）理论提出的一种新型贯入仪,因为贯入过程中土体围绕探头发生回流故称为全流贯入仪。T-bar的端部承载力是探头上下土压力差。椭圆形T-bar的虚拟速度场是关于x平面和y平面对称的四象限速度场（见图10（a））,速度场的总能量损耗率等于4倍第一象限速度场的能量损耗率。图10（b）为椭圆形T-bar虚拟速度场对应的速度矢量图,其构建原则与锚桩椭圆端部相同。椭圆形T-bar的虚拟速度场与仅关于y轴对称的锚桩速度场有所区别：刚性区（ $B C B^{'}$ ）,和弥散楔形剪切区（ALBHIM）的速度间断面能量损耗和变形能量损耗是相同的,下文将不再赘述；而异心扇形剪切区（BCDEIH）、同心扇形剪切区（IEFJ）和同心圆柱壳区（AMIJN）的能量损耗略有不同,具体如下：

图 10 椭圆形端部速度场和速度矢量图

Figure 10. Velocity fields and hodographs of tip of torpedo anchor deep embedment

下载: 全尺寸图片幻灯片

（1）速度间断线的能量损耗率

a）间断面 $\overset{⌢}{E F}$

$\begin{array}{l} Δ {\dot{W}}_{E F} = s_{u} \cdot \frac{v_{0}}{\sqrt{2}} \cdot \\ \int_{0}^{\frac{π}{4} + \frac{Δ}{2}} [\frac{D \sqrt{2} \cos δ_{B}}{2} + \cos ψ \frac{D}{2} \cdot \int_{0}^{δ_{B}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ] d δ_{3} 。 \end{array}$

(18)

b）间断面 $\overset{⌢}{I J}$

$\begin{array}{l} Δ {\dot{W}}_{I J} = s_{u} v_{0} (\sin φ_{n} \sec ψ - 1 / \sqrt{2}) \cdot \\ \int_{0}^{\frac{π}{4} + \frac{Δ}{2}} [\cos ψ \frac{D}{2} \int_{0}^{δ_{B}} \sqrt{{(\sin δ)}^{2} + {(ξ \cos δ)}^{2}} d δ] d δ_{3} \end{array}$ 。

(19)

（2）塑形变形区内的内能损耗率

a）BCDEFJIH扇形剪切区的内能损耗,速度为 $v_{t} = v_{0} / \sqrt{2} d δ$ ,半径为 $L_{B C}$ ,则

$Δ {\dot{W}}_{B C D E F G K J I H} = s_{u} \int_{0}^{\frac{3 π}{4}} \frac{v_{0}}{\sqrt{2}} L_{B C} d δ$ 。

(20)

b）AMIJN同心圆柱区的内能损耗

$Δ {\dot{W}}_{A M I J N} = \dot{γ} s_{u} A_{A F G} = \dot{γ} s_{u} \int_{0}^{δ_{B}} \int_{0}^{\frac{π}{4} + \frac{Δ}{2}} R_{5} \frac{\partial R_{5}}{\partial δ_{2}} d δ_{3} d δ_{2}$ 。

(21)

椭圆T-bar承载力系数计算如下：

$\begin{matrix} N_{c} = 4 [\overset{速度间断面的能量损耗}{\overset{︷}{(Δ {\dot{W}}_{B C} + Δ {\dot{W}}_{C D E} + Δ {\dot{W}}_{E F} + Δ {\dot{W}}_{B H I} + Δ {\dot{W}}_{I J} + Δ {\dot{W}}_{A L B})}} + \\ \overset{变形能的能量损耗}{\overset{︷}{(Δ {\dot{W}}_{B C D E F J I H} + Δ {\dot{W}}_{A L B H I M} + Δ {\dot{W}}_{A M I J N})}}] / s_{u} v_{0} D \end{matrix}$ 。

(22)

图11为数值分析中椭圆T-bar贯入土体的等效塑性应变云图和位移矢量图。其中,图11（a）和（b）分别是光滑T-bar的等效塑性应变云图和位移矢量图,土体围绕着T-bar从T头受压区流向受拉区,达到完全回流破坏机制。图11（c）和（d）分别是T-bar的等效塑性应变云图和位移矢量图,T-bar与土体界面摩擦导致T-bar前后两端出现刚性区,与锚桩相似刚性区面积随长径比的增大而逐渐减小,位移矢量图中显示刚性区土体黏附在T头并随T-bar同速运动不发生脱离。图11（a）和（c）的等效塑性应变云图与上限法的虚拟速度场形状基本一致。通过上述分析,上限法中构造的椭圆T-bar虚拟速度场是可行的。

图 11 椭圆T-bar的等效塑性应变云图和位移矢量图

Figure 11. Equivalent plastic strain nephograms and displacement vector graphs of elliptical T-bar

下载: 全尺寸图片幻灯片

由图12,13可知,当ξ=1时,椭圆T-bar简化为传统的圆形T-bar,ω=0的N_c=9.14；ω=1的N_c=11.94。上限解与1984年Randolph^[4]给出的上下限解相等,由此可见,椭圆T-bar上限模型是合理的。椭圆T-bar承载力系数受长径比和摩擦系数影响其规律与椭圆端部锚桩的规律相同,当ω=1时,N_c随着 $ξ$ 的增大而增大；当ω=0时,N_c随着 $ξ$ 的增大而减小。椭圆T-bar长径比越大受摩擦力影响越大, $ξ$ =2时,ω=1的承载力系数是ω=0的1.48倍,当 $ξ$ 增大到4时,ω=1的N_c增大为ω=0的1.97倍。刘朝安等^[14]对椭圆T-bar研究也得到一致的结论。

图 12 椭圆T-bar长径比与承载力系数关系

Figure 12. Relation curves between N_c and ξ of elliptical T-bar

下载: 全尺寸图片幻灯片

图 13 椭圆T-bar承载力系数与摩擦系数关系

Figure 13. Relation curves between ω and N_c of elliptical T-bar

下载: 全尺寸图片幻灯片

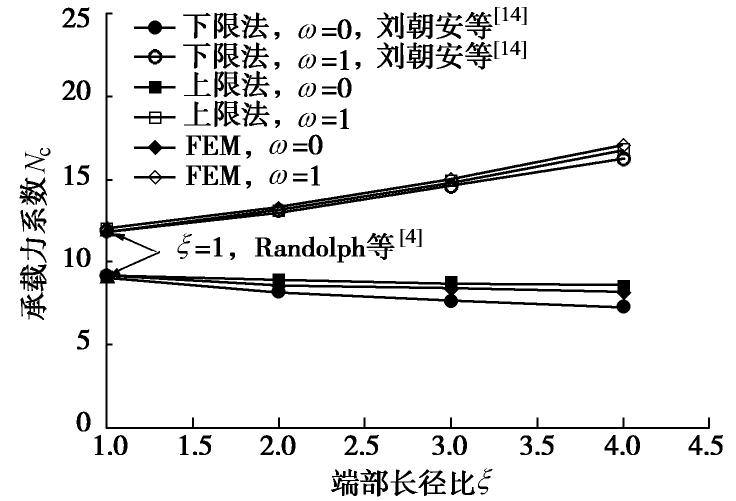
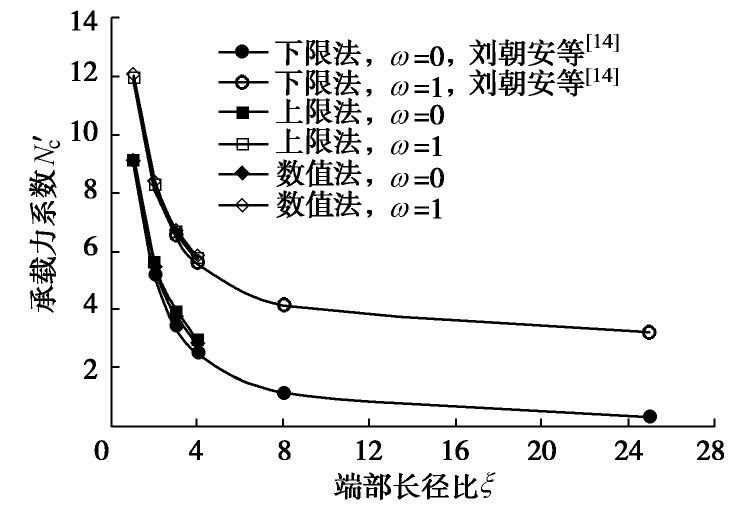
图14比较分析椭圆T-bar的上,下限解和数值解。当 $ξ$ =1时,数值解与上限解,刘朝安等^[14]下限解及Randolph的上下限解（界面光滑N_c=9.14,界面粗糙 N_c=11.94）^[4]的最大差值小于1.2%。当ω=0时,N_c的上限解大于数值解和刘朝安等^[14]的下限解并且随着 $ξ$ 增大差值逐渐增大,其最大差值是17.74%；当ω=1时,上限解与数值解,刘朝安等^[14]的下限解都具有较好的一致性。由此可见,椭圆T-bar的上限解是合理的。图15参考刘朝安等^[14]对椭圆形T-bar承载力的研究,其中 $N_{c}^{'} =$ $F_{t} / (s_{u} \sqrt{2 [{(L_{t})}^{2} + {(D / 2)}^{2}]})$ 。 $N_{c}^{'}$ 的上限解与数值解和刘朝安的下限解近乎重合。进一步验证 $ξ$ ≥1时椭圆T-bar上限法模型是可行的。椭圆T-bar的上限模型也适用于深埋椭圆形海底管线或椭圆形桩横向承载力的研究。

图 14 比较分析T-bar椭圆端部的上限解和数值解

Figure 14. Comparison between upper-bound solutions and numerical results of elliptical T-bar

下载: 全尺寸图片幻灯片

图 15 比较分析T-bar椭圆端部的上限解和下限解

Figure 15. Comparison between upper-bound solutions and lower-bound results of elliptical T-bar

下载: 全尺寸图片幻灯片

3. 结论

本文基于塑性极限分析上限法推导不同长径比（ $ξ$ ≥1）的锚桩和椭圆T-bar承载力系数,并考虑界面摩擦对承载力系数的影响。分别详细介绍锚桩椭圆端部速度场和椭圆T-bar速度场以及相应速度矢端图的构建。

（1）当 $ξ$ =1时椭圆形端部退化为圆形端部,上限解与前人研究结果展现出良好的一致性,验证了锚桩和T-bar椭圆端部上限模型的合理性。

（2）当ω=0时,椭圆端部承载力系数N_c随长径比 $ξ$ 的增大而减小；当ω=1时,N_c随着 $ξ$ 的增大而增大。

（3）摩擦力对承载力系数的影响随着 $ξ$ 增大而增大。

（4）当ω=1时,椭圆形端部的上限解与下限解和数值解具有较好一直性。随着摩擦系数的降低,承载力系数上限解逐渐大于下限解。

（5）椭圆T-bar上限法模型也适用于海底管线或椭圆形桩的承载力的研究。

图 1 海洋结构物

Figure 1. Ocean structures

下载: 全尺寸图片幻灯片

图 2 示意图

Figure 2. Schematic diagram of anchor pile and T-bar

下载: 全尺寸图片幻灯片

图 3 承载力和承载力系数计算流程图

Figure 3. Flow chart of calculation of bearing capacity and factor

下载: 全尺寸图片幻灯片

图 4 数值模型图

Figure 4. Numerical models

下载: 全尺寸图片幻灯片

图 5 锚桩椭圆端部速度场和速度矢量图

Figure 5. Velocity fields and hodographs of elliptical tip of anchor pile

下载: 全尺寸图片幻灯片

图 6 椭圆形端部等效塑性应变云图和位移矢量图

Figure 6. Equivalent plastic strain nephograms and displacement vector graphs of elliptical tip

下载: 全尺寸图片幻灯片

图 7 椭圆锚桩长径比与承载力系数关系

Figure 7. Relation curves between N_c and ξ of elliptical anchor pile

下载: 全尺寸图片幻灯片

图 8 椭圆锚桩承载力系数与摩擦系数关系

Figure 8. Relation curves between ω and N_c of elliptical anchor pile

下载: 全尺寸图片幻灯片

图 9 椭圆锚桩承载力系数的上、下限解和数值解

Figure 9. Comparison btween upper solutions and numerical results of N_c of elliptical anchor pile

下载: 全尺寸图片幻灯片

图 10 椭圆形端部速度场和速度矢量图

Figure 10. Velocity fields and hodographs of tip of torpedo anchor deep embedment

下载: 全尺寸图片幻灯片

图 11 椭圆T-bar的等效塑性应变云图和位移矢量图

Figure 11. Equivalent plastic strain nephograms and displacement vector graphs of elliptical T-bar

下载: 全尺寸图片幻灯片

图 12 椭圆T-bar长径比与承载力系数关系

Figure 12. Relation curves between N_c and ξ of elliptical T-bar

下载: 全尺寸图片幻灯片

图 13 椭圆T-bar承载力系数与摩擦系数关系

Figure 13. Relation curves between ω and N_c of elliptical T-bar

下载: 全尺寸图片幻灯片

图 14 比较分析T-bar椭圆端部的上限解和数值解

Figure 14. Comparison between upper-bound solutions and numerical results of elliptical T-bar

下载: 全尺寸图片幻灯片

图 15 比较分析T-bar椭圆端部的上限解和下限解

Figure 15. Comparison between upper-bound solutions and lower-bound results of elliptical T-bar

下载: 全尺寸图片幻灯片

参考文献(28)

[1]	MARTIN C M. Physical and Numerical Modelling of Offshore Foundations under Combined Loads[D]. Oxford: University of Oxford, 1994.
[2]	HU P, WANG D, CASSIDY M J, et al. Predicting the resistance profile of a spudcan penetrating sand overlying clay[J]. Canadian Geotechnical Journal, 2014, 51(10): 1151-1164. doi: 10.1139/cgj-2013-0374
[3]	MARTIN C M, HOULSBY G T. Undrained bearing capacity factors for conical footings on clay[J]. Géotechnique, 2003, 53(5): 513-520. doi: 10.1680/geot.2003.53.5.513
[4]	RANDOLPH M F, HOULSBY G T. The limiting pressure on a circular pile loaded laterally in cohesive soil[J]. Géotechnique, 1984, 34(3): 457-457.
[5]	MURFF J D, WAGNER D A, RANDOLPH M F. Pipe penetration in cohesive soil[J]. Géotechnique, 1989, 39(2): 213-229. doi: 10.1680/geot.1989.39.2.213
[6]	AUBENY C P, SHI H, MURFF J D. Collapse loads for a cylinder embedded in trench in cohesive soil[J]. International Journal of Geomechanics, 2005, 10: 320-325.
[7]	RANDOLPH M F, MARTIN C M, HU Y. Limiting resistance of a spherical penetrometer in cohesive material[J]. Géotechnique, 2000, 50(5): 573-582. doi: 10.1680/geot.2000.50.5.573
[8]	MARTIN C M, RANDOLPH M F. Upper-bound analysis of lateral pile capacity in cohesive soil[J]. Géotechnique, 2006, 56(2): 141-145. doi: 10.1680/geot.2006.56.2.141
[9]	GAO F P, ZHAO B. Slip-line field solution for ultimate bearing capacity of a pipeline on clayey soils[J]. Theoretical & Application Mechanics Letters, 2012, 2(5): 1-4
[10]	GAO F P, WANG N, ZHAO B. Ultimate bearing capacity of a pipeline on clayey soils: slip-line field solution and FEM simulation[J]. Ocean Engineering, 2013, 73(6): 159-167.
[11]	EINAV I, RANDOLPH M F. Combining upper bound and strain path methods for evaluating penetration resistance[J]. International Journal for Numerical Methods in Engineering, 2005, 63: 1991-2016. doi: 10.1002/nme.1350
[12]	RICHARDSON M D. Dynamically Installed Anchors for Floating Offshore Structures[D]. Perth: University of Western Australia, 2008.
[13]	O’LOUGHLIN C D, RICHARDSON M D, RANDOLPH M F. Centrifuge tests on dynamically installed anchors[C]//ASME 2009 28th International Conference on Ocean, Offshore and Arctic Engineering, 2009, Honolulu, Hawaii: 391-399.
[14]	刘朝安, 贾宁, 孟庆辉, 等. 椭圆形截面T型触探贯入阻力研究[J]. 工程地质学报, 2016, 24(增刊): 214-220. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-GCDZ201610001034.htm LIU Chao-an, JIA Ning, MENG Qing-hui, et al. Research on the resistance of T-bar test with oval cross section[J]. Journal of Engineering Geology, 2016, 24(S0): 214-220. (in Chinese) https://cpfd.cnki.com.cn/Article/CPFDTOTAL-GCDZ201610001034.htm
[15]	MEYERHOF G G. The ultimate bearing capacity of foundations[J]. Géotechnique, 1951, 2(4): 301-332. doi: 10.1680/geot.1951.2.4.301
[16]	CHEN W F. Limit Analysis and Soil Plasticity[M]. Amsterdam: Elsevier, 1975: 244-274.
[17]	闫洪. 塑性成形原理[M]. 北京: 清华大学出版社, 2006. YAN Hong. Fundamental of Plastic Forming[M]. Beijing: Tsinghua University Press, 2006. (in Chinese)
[18]	龚晓南. 土塑性力学[M]. 杭州: 浙江大学出版社, 1990. GONG Xiao-nan. Soil Plastic Mechanics[M]. Hangzhou: Zhejiang University Press, 1990. (in Chinese)
[19]	YAO Y P, HOU W, ZHOU A N. UH model: Three- dimensional unified hardening model for overconsolidated clays[J]. Géotechnique, 2009, 59(5): 451-469. doi: 10.1680/geot.2007.00029
[20]	YAO Y P, ZHOU A N. Non-isothermal unified hardening model: a thermo-elasto-plastic model for clays[J]. Géotechnique, 2013, 63(15): 1328-1345. doi: 10.1680/geot.13.P.035
[21]	YAO Y P, SUN D A, MATSUOKA H. A unified constitutive model for both clay and sand with hardening parameter independent on stress path[J]. Computers and Geotechnics, 2008, 35(2): 210-222. doi: 10.1016/j.compgeo.2007.04.003
[22]	MARTIN C M, RANDOLPH M F. Applications of the lower and upper bound theorems of plasticity to collapse of circular foundations[C]//Proc 10th IACMAG Conf, 2001, Tucson: 1417-1428.
[23]	KIM Y H, HOSSAIN M S, WANG D. Effect of strain rate and strain softening on embedment depth of a dynamically installing anchor in clay[J]. Ocean Engineering, 2015, 108: 704-715. doi: 10.1016/j.oceaneng.2015.07.067
[24]	O’BEIRNE C, O’LOUGHLIN C D, WANG D, et al. Capacity of dynamically installed anchors as assessed through field testing and three-dimensional large-deformation finite element analyses[J]. Canadian Geotechnical Journal, 2015, 52(5): 548-562. doi: 10.1139/cgj-2014-0209
[25]	WANG D, HU Y, RANDOLPH M F. Three-dimensional large deformation finite-element analysis of plate anchors in uniform clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(2): 355-365. doi: 10.1061/(ASCE)GT.1943-5606.0000210
[26]	WANG D, WHITE D J, RANDOLPH M F. Large- deformation finite element analysis of pipe penetration and large-amplitude lateral displacement[J]. Canadian Geotechnical Journal, 2010, 47(8): 842-856(15). doi: 10.1139/T09-147
[27]	瑜璐, 杨庆, 杨钢, 等. 塑性极限分析鱼雷锚锚尖贯入阻力[J]. 岩土力学, 2020, 41(6): 1-11. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202006019.htm YU Lu, YANG Qing, YANG Gang, et al. An analysis of the resistance of elliptical tip of torpedo anchor by plastic limit analysis[J]. Rock and Soil Mechanics, 2020, 41(6): 1-11. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202006019.htm
[28]	TERZAGHI K, PECK R B, MESRI G. Soil Mechanics in Engineering Practice[M]. 2nd ed. New York: John Wiley& Sons, 1967: 223-224.