软土中碎石桩模型试验的三维离散-连续介质耦合数值模拟

谭鑫; 胡政博; 冯龙健; 赵明华

doi:10.11779/CJGE202102015

软土中碎石桩模型试验的三维离散-连续介质耦合数值模拟 English Version

谭鑫^{1, 2,},
胡政博¹,
冯龙健¹,
赵明华^{1, 2}

1.
湖南大学土木工程学院,湖南　长沙　410082
2.
建筑安全与节能教育部重点实验室（湖南大学）,湖南　长沙　410082

基金项目:

湖南创新型省份建设专项经费项目 2019GK1011

国家自然科学基金青年基金项目 51508181

湖南省自然科学基金项目 2019JJ50056

详细信息

作者简介:
谭鑫（1983— ）,男,博士,副教授,主要从事岩土工程数值模拟方面的教学和科研工作。E-mail：xintan@hnu.edu.cn

中图分类号: TU43
计量
- 文章访问数: 306
- HTML全文浏览量: 28
- PDF下载量: 131
出版历程
- 收稿日期: 2020-04-08
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-01-31

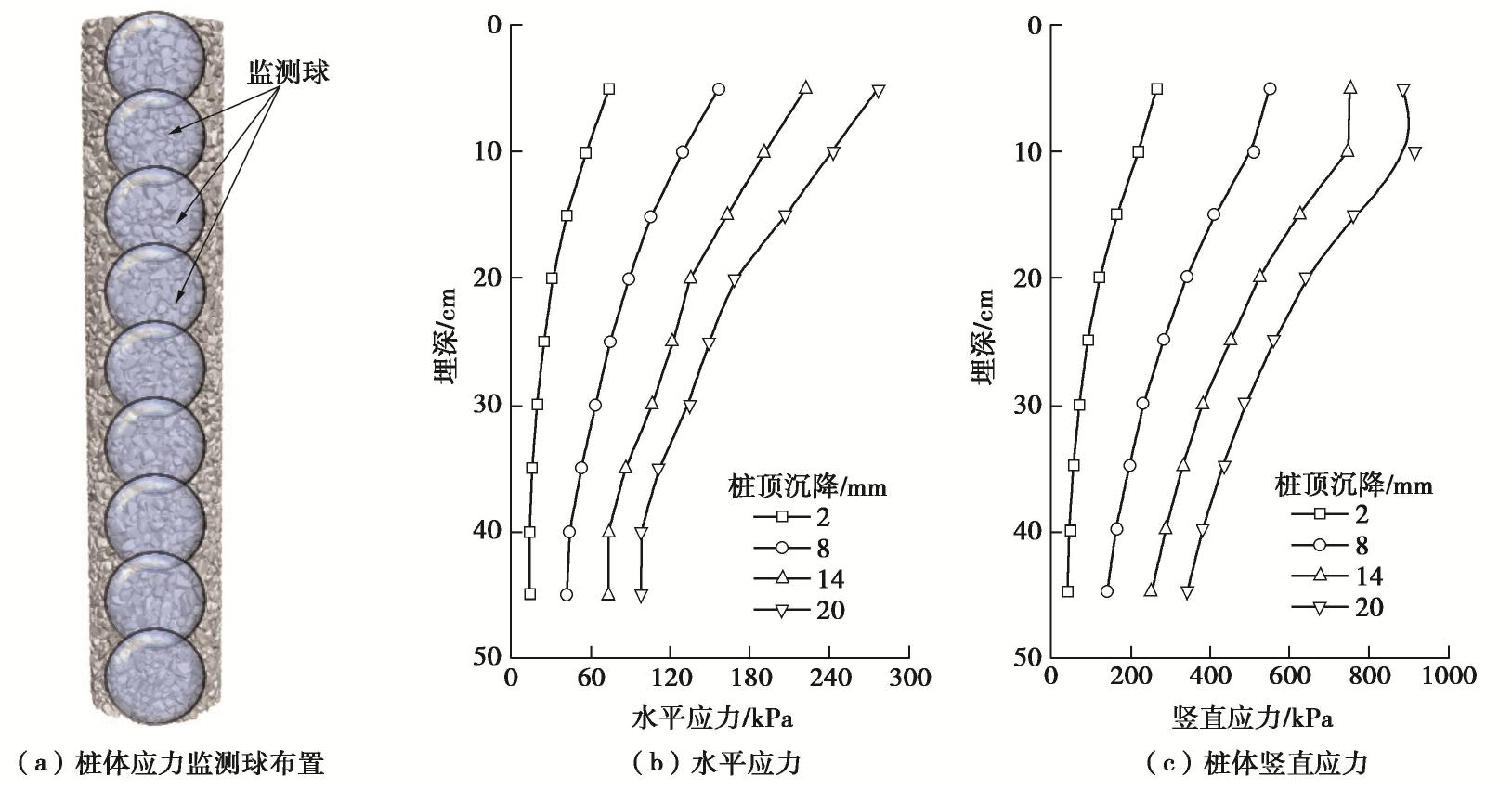
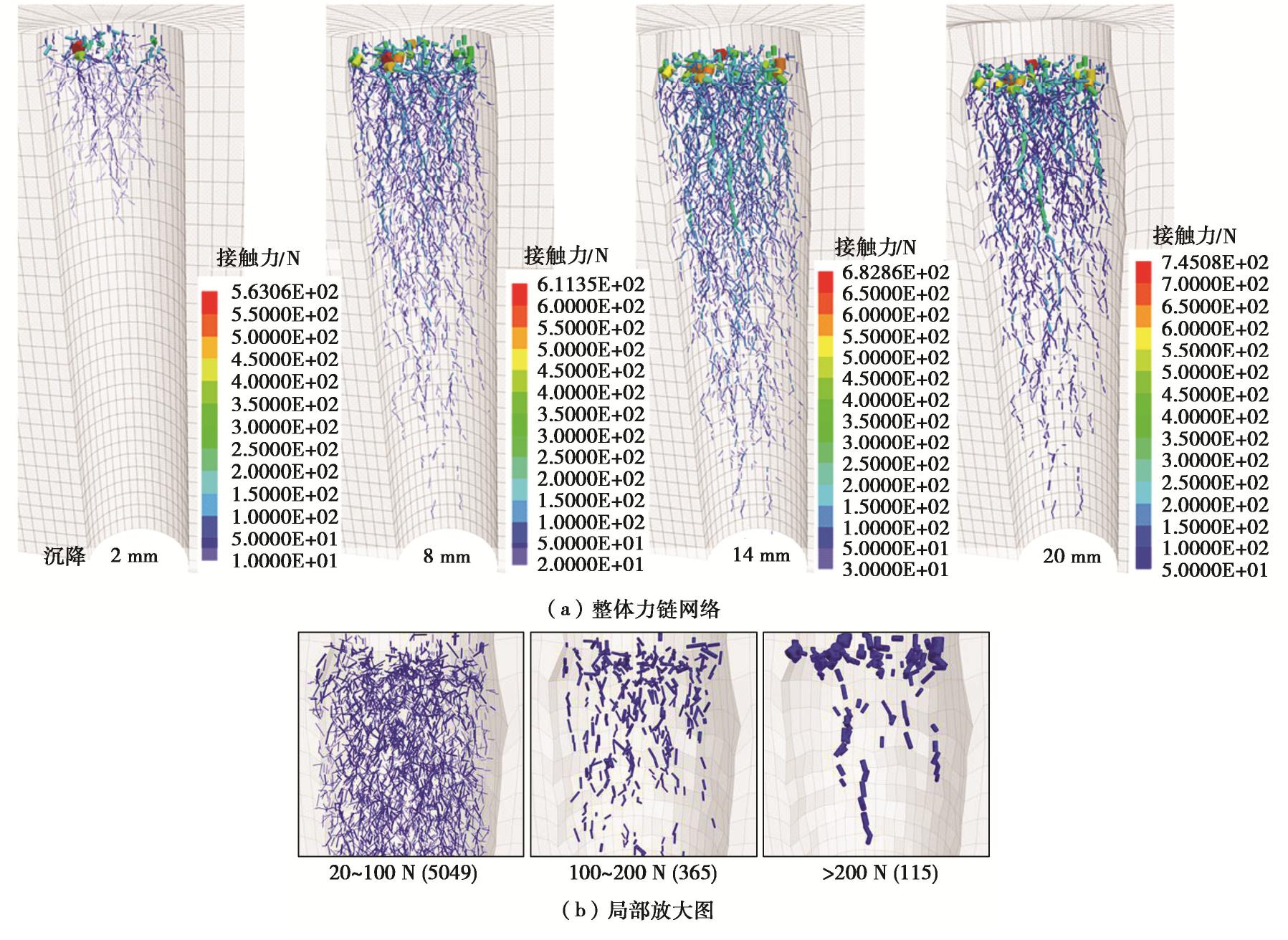
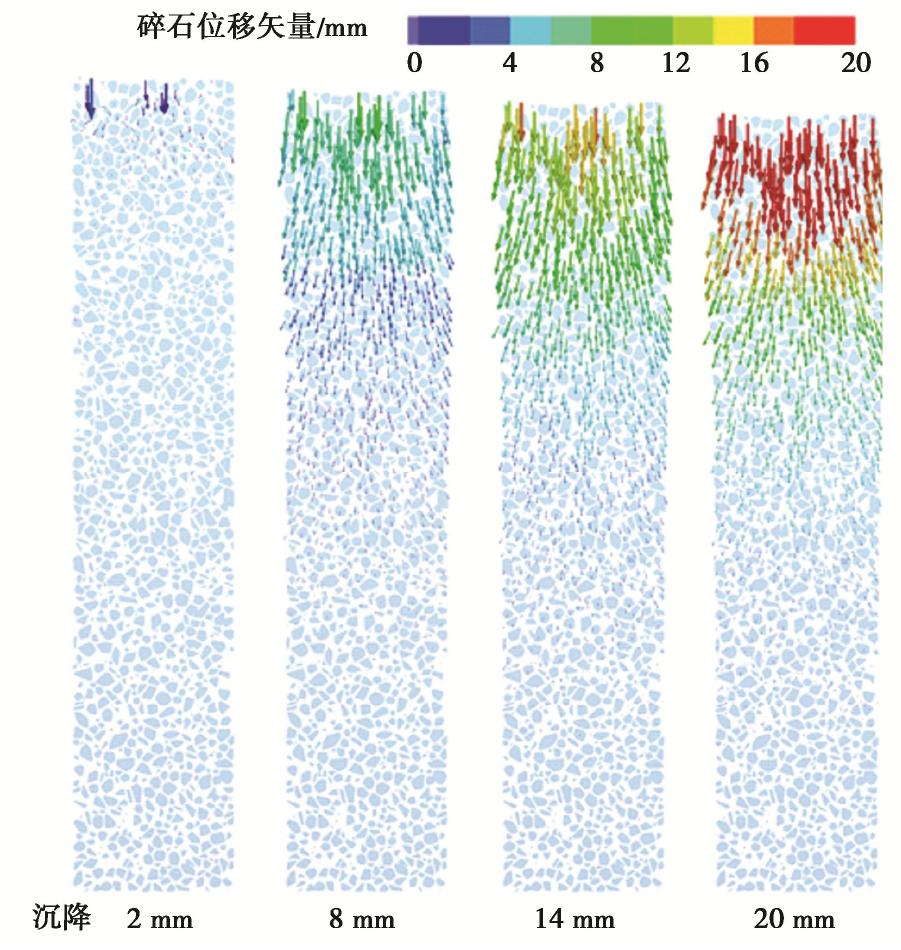
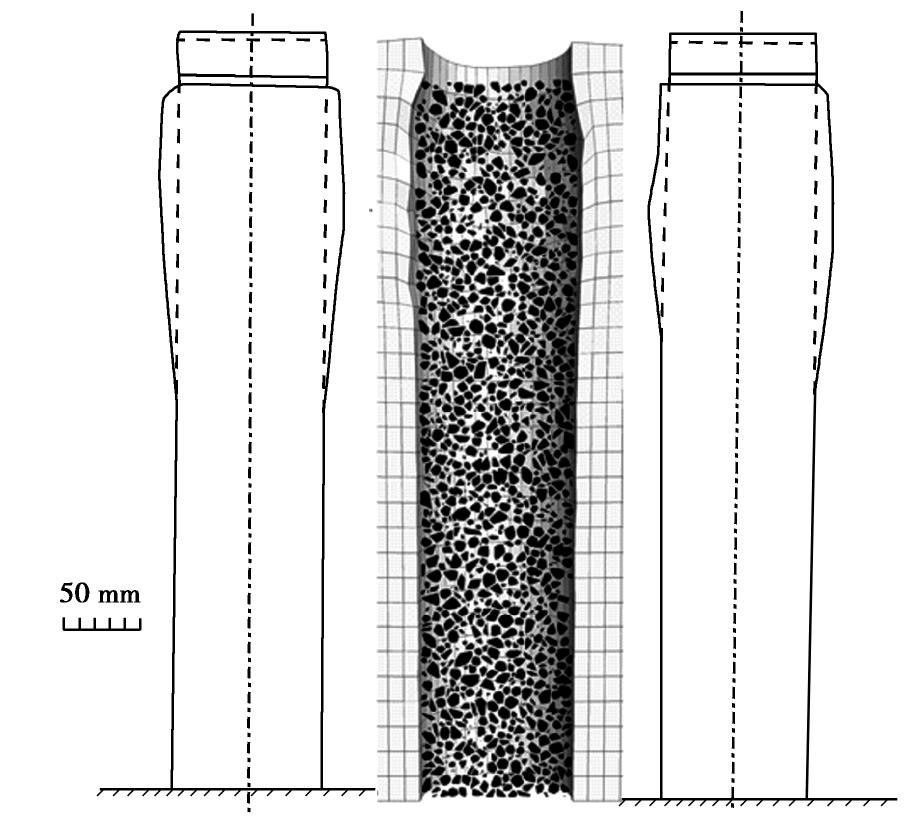
Three-dimensional discrete-continuous coupled numerical simulation of a single stone column in soft soils

1.
College of Civil Engineering, Hunan University, Changsha 410082, China
2.
Key Laboratory of Building Safety and Energy Efficiency of the Ministry of Education, Hunan University, Changsha 410082, China

摘要

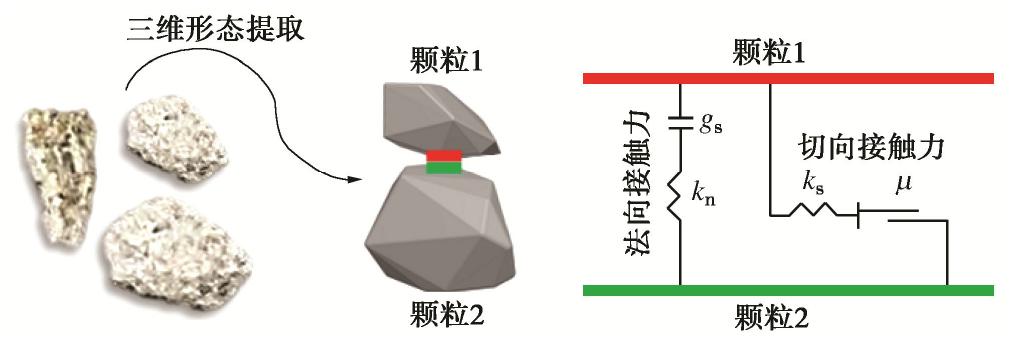
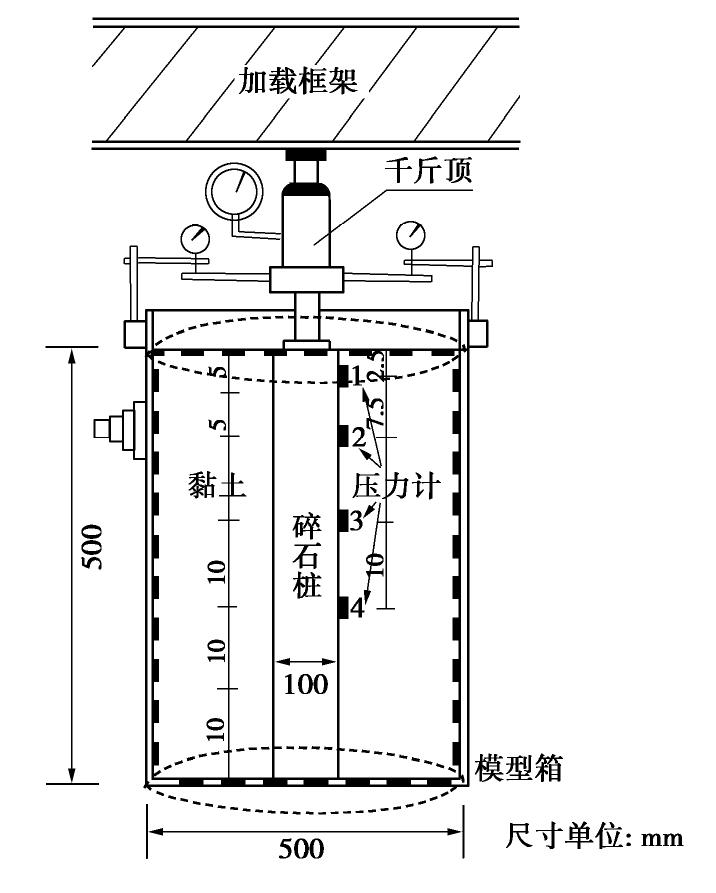
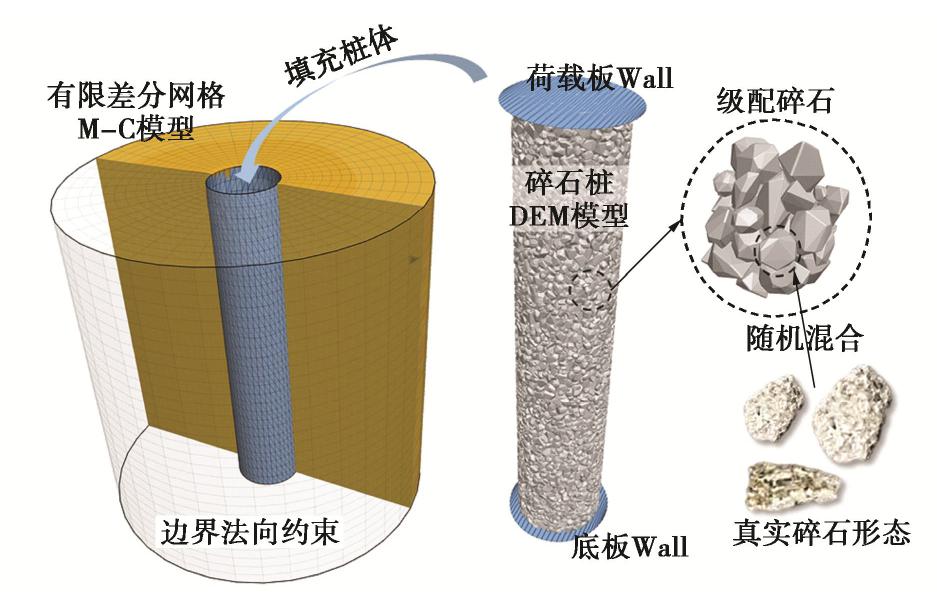
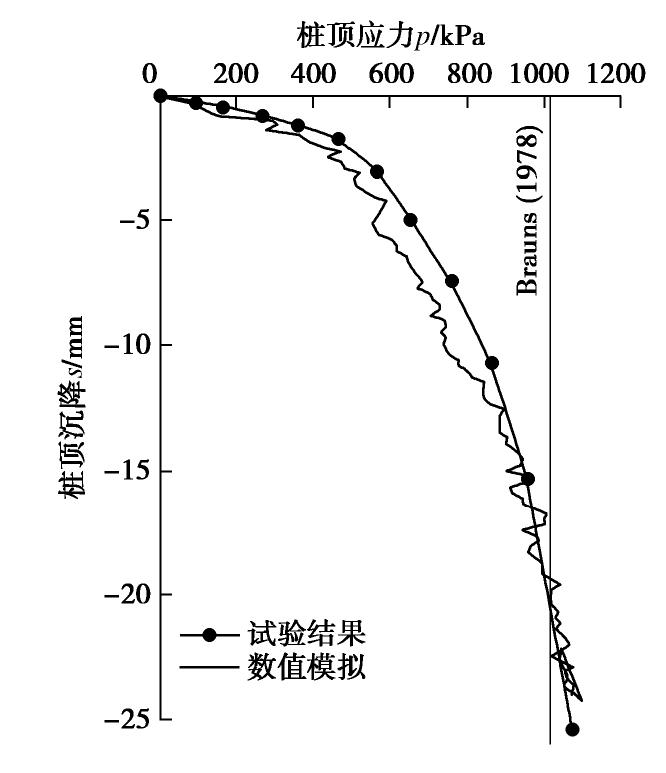
摘要: 采用连续-非连续介质耦合数值模型对碎石桩单桩受荷室内模型试验的变形及破坏全过程进行模拟。其中碎石桩体采用考虑碎石真实形态的三维刚性多面体进行模拟,软土采用有限差分网格模拟。数值模拟获得的单桩荷载-沉降曲线以及鼓胀变形曲线与模型试验结果显示出较好的吻合程度。基于离散单元方法建立的碎石桩模型无需复杂的本构模型便能有效反映其变形和失稳特性,耦合连续介质模型进行模拟则更好地揭示了桩土相互作用机理。通过荷载-沉降曲线、土体应力应变场以及桩体碎石接触力链网络讨论了碎石桩单桩承载的破坏过程；并总结了碎石桩宏观变形失效与其细观颗粒受力运动的联系,碎石桩体承载和传力的机制能够通过其内部力链网络结构与形态得到较好解释。
- 碎石桩 /
- 力链 /
- 颗粒 /
- 离散单元法 /
- 数值模拟
Abstract: The discrete-continuous coupled numerical model is used to simulate the complete bearing and failure process of a single stone column in soft soils. The three-dimensional polyhedron considering the actual gravel shape is used to simulate the stone column, and the finite difference grid is used to model the soft soils. The load-settlement curve and bulging deformation curves obtained by the numerical simulation are in good agreement with the model test results. The stone column modeled by the discrete element method can effectively reflect its deformation and failure characteristics, without using complex constitutive model. The column-soil interactions can be well revealed by the coupled simulation scheme. The bearing and failure process is summarized through the analysis on the load-settlement curve, the stress and strain field of the surrounding soils, and the contact force chains of the stone column. The relationship between the macroscopic deformation and failure behaviors of the stone column and the microscopic grain movement is summarized. The bearing mechanism of the stone column can be well explained according to the structure and shape of the force chain networks inside the column body.
- stone column /
- force chain /
- grain /
- discrete element method /
- numerical simulation

HTML全文

0. 引言

随着中国经济的高速发展以及城市化进程的加速推进,发达的交通网络成为城市发展必不可少的组成部分,其中,地铁隧道一直以高效、快捷、安全、环保、节能著称。现如今,盾构法施工也被广泛使用。然而,在复杂的城市施工环境中,由于基坑开挖卸荷土体,大范围建筑群施工,建筑材料临时堆放等地表堆载工况时有发生,这些既有荷载可以等效为分布在地表上的堆积荷载,将会在地层中引起附加应力,影响盾构隧道施工和地层沉降^[1]。同时,在实际工程中,地基土体会随时间变化而具有流变特性,可以近似为黏弹性材料。因此,有必要对黏弹性土体中考虑地表堆载作用下的盾构隧道施工影响行为进行研究,对其诱发的地层沉降及时域表达做出正确预测,同时对隧道的选址进行指导。

目前,国内外学者关于软土盾构隧道施工诱发地层响应问题进行了相关研究,主要方法有经验法、数值模拟法和理论解析法。在经验法方面,Celestino等^[2]通过分析大量的工程实测数据,提出了隧道施工诱发地层变形的经验解法。数值模拟法^[3-5]作为一种有效方法被广泛运用于研究隧道施工诱发地层变形问题,但需要进行复杂的前期建模,选取复杂土体本构关系用于拟合土体,同时需要选取专业的数值软件,计算结果一般需要耗费较长的时间。而理论解析法具有耗时短,精度高等特点,典型方法有：镜像法^[6-7]、复变函数法^[8-17]、弹性力学的Mindlin解法^[18-19]和随机介质理论^[20]。

在复变函数法研究方面,Verruijt^[9]给出了洞周均匀变形的圆形隧道弹性半平面问题的弹性解,王立忠等^[11]提出了洞周椭圆化变形的弹性解,然而其研究仅适用于无地表荷载下浅埋圆形隧道开挖问题,也无法考虑地基的黏弹性。蔚立元等^[14]采用Verruijt提供的解析解,得到了地表存在均匀水压作用下的隧道变形弹性解答。Kong等^[21]运用复变函数法对斜坡下浅埋偏压隧道开挖问题进行了研究,得到了斜坡下隧道开挖引发的地层响应的弹性解,但其研究仅适用于斜坡问题下的隧道开挖问题,且没有考虑土体流变效应。王华宁等^[22-23]针对黏弹性土体中浅埋隧道施工问题,采用复变函数理论和应力控制方法得到了隧道开挖位移和应力场的理论解答,对本文研究有重要启发,但其并未考虑地表荷载作用,也没有采用位移控制方法进行研究。

上述研究^{[9, 11, 14, 21-23]}针对复变函数理论在隧道工程上的应用做了积极探索,但大多未考虑地表堆载的作用,也没有体现在隧道施工中扰动土体的流变特性。而在实际工程中,隧道开挖引起土体变形具有明显的时间效应,特别是在软土地区,土体流变效应尤为显著。本文基于地表堆积荷载和隧道洞周椭圆化收敛变形模式的边界条件,并考虑了土体的黏弹性,提出了在任意地表堆积荷载作用下,盾构隧道施工诱发周围地层变形响应的时域解析解。其中,采用Boltzmann黏弹性流变模型^[24-25]来模拟土体的黏弹性,运用映射函数将半无限土体区域映射成单位圆环,并通过Laplace变换和逆变换,建立了可以表达土体区域内任意一点任意时刻的黏弹性位移和应力的解析函数,使得土体区域满足地表应力边界条件和洞周位移边界条件,以求解上述解析函数的各项系数,最后利用求解的解析函数得到盾构隧道开挖引起的土体位移,并与实测数据的结果作对比,从而验证其解析解的可靠性和实用性。

1. 黏弹性地层地表堆载作用下的隧道开挖引起土体变形时域解

1.1 任意堆载作用力学模型

黏弹性土体中考虑地表任意堆载作用的盾构隧道开挖问题的计算模型,可视为地表存在任意堆载作用下含圆形孔洞的均质半平面体的黏弹性问题,如图1所示,该模型主要针对土压平衡和泥水平衡盾构隧道。地表任意堆载为随x变化的函数,即 $F = q (x)$ ,其作用范围为 $x_{1} \leq x \leq x_{2}$ 。隧道半径为 $r_{0}$ ,隧道圆心埋深为 $h$ ,隧道洞周存在椭圆化收敛位移 $U_{r}$ ,A,B,C,D为平面上的点。建立一个平面直角坐标系,其中,A为坐标原点,B为无穷远处点,C和D分别为隧道拱顶与拱底位置,R区域为黏弹性土体区域。

图 1 受地表堆载影响的隧道开挖力学模型

Figure 1. Mechanical model for tunnel excavation affected by surcharge loading

下载: 全尺寸图片幻灯片

1.2 黏弹性本构模型解答

本文选取Boltzmann黏弹性地基模型,已有理论研究表明^[24-25],其可以较好地模拟土体在某一时刻的弹性变形以及土体随时间变化的黏性变形。Boltzmann三参量黏弹性地基模型是由两个元件串联组成,分别为弹性元件（H体）和黏性元件（K体）,如图2所示。其黏弹性体的本构关系为

图 2 Boltzmann黏弹性流变模型

Figure 2. Boltzmann viscoelastic rheological model

下载: 全尺寸图片幻灯片

$Γ^{″} \cdot σ_{k k} (t) = Ω^{″} \cdot ε_{k k} (t)$ ,

(1)

$Γ^{'} \cdot S_{i j} (t) = Ω^{'} \cdot e_{i j} (t)$ 。

(2)

式中 $σ_{k k} (t)$ 为应力球张量； $ε_{k k} (t)$ 为应变球张量； $S_{i j} (t)$ 为应力偏张量； $e_{i j} (t)$ 为应变偏张量； $Γ^{'}$ , $Γ^{″}$ , $Ω^{'}$ , $Ω^{″}$ 为线性微分算子,如下：

$Γ^{'} = \sum_{k = 0}^{m} {\hat{Γ^{'}}}_{k} \frac{d^{k}}{d^{k} t}$ ,

(3)

$Γ^{″} = \sum_{k = 0}^{m} {\hat{Γ^{″}}}_{k} \frac{d^{k}}{d^{k} t}$ ,

(4)

$Ω^{'} = \sum_{k = 0}^{n} {\hat{Ω^{'}}}_{k} \frac{d^{k}}{d^{k} t}$ ,

(5)

$Ω^{″} = \sum_{k = 0}^{n} {\hat{Ω^{″}}}_{k} \frac{d^{k}}{d^{k} t}$ ,

(6)

式中, ${\hat{Γ^{'}}}_{k}$ , ${\hat{Γ^{″}}}_{k}$ , $\hat{Ω^{'}}$ , ${\hat{Ω^{″}}}_{k}$ 为材料黏弹性质相关系数。

则根据其本构关系,偏张量部分的黏弹性本构关系为

$(G_{h} + G_{k}) S_{i j} (t) + η_{k} \frac{d S_{i j}}{d t} = 2 G_{h} G_{k} e_{i j} (t) + 2 G_{h} η_{k} \frac{d e_{i j}}{d t}$ 。

(7)

其球张量部分的弹性本构关系为

$σ_{kk} (t) = 3 K ε_{kk} (t)$ ,

(8)

式中, $G_{h}$ 和 $G_{k}$ 为剪切模量, $η_{k}$ 为黏性系数, $K$ 为体积模量。

将式（7）,（8）代入式（3）～（6）,可得各线性微分算子表达式：

$Γ^{'} = (G_{h} + G_{k}) + η_{k} \frac{d}{d t}$ ,

(9)

$Γ^{″} = 1$ ,

(10)

$Ω^{'} = 2 G_{h} G_{k} + 2 G_{h} η_{k} \frac{d}{d t}$ ,

(11)

$Ω^{″} = 3 K$ 。

(12)

对式（9）～（12）进行Laplace变换得

${\tilde{Γ}}^{'} (s) = (G_{h} + G_{k}) + η_{k} s$ ,

(13)

${\tilde{Γ}}^{″} (s) = 1$ ,

(14)

${\tilde{Ω}}^{'} (s) = 2 G_{h} G_{k} + 2 G_{h} η_{k} s$ ,

(15)

${\tilde{Ω}}^{″} (s) = 3 K$ 。

(16)

由弹性-黏弹性对应原理,对剪切模量 $G$ 和泊松比 $ν$ 进行Laplace变换,可得 $\tilde{G} (s)$ 和 $\tilde{ν} (s)$ 为

$\tilde{G} (s) = \frac{{\tilde{Ω}}^{'} (s)}{2 {\tilde{Γ}}^{'} (s)}$ ,

(17)

$\tilde{ν} (s) = \frac{{\tilde{Ω}}^{″} (s) {\tilde{Γ}}^{'} (s) - {\tilde{Ω}}^{'} (s) {\tilde{Γ}}^{″} (s)}{2 {\tilde{Ω}}^{″} (s) {\tilde{Γ}}^{'} (s) + {\tilde{Ω}}^{'} (s) {\tilde{Γ}}^{″} (s)}$ 。

(18)

将式（13）～（16）代入式（17）,（18）,可得

$\tilde{G} (s) = \frac{G_{h} G_{k} + G_{h} η_{k} s}{(G_{h} + G_{k}) + η_{k} s}$ ,

(19)

$\tilde{ν} (s) = \frac{3 K (G_{h} + G_{k} + η_{k} s) - 2 G_{h} G_{k} - 2 G_{h} G_{k} s}{6 K (G_{h} + G_{k} + η_{k} s) + 2 G_{h} G_{k} + 2 G_{h} G_{k} s}$ 。

(20)

根据弹性-黏弹性问题对应原理,对于黏弹性问题,只要得到弹性问题的解,然后将弹性问题里的土体弹性参数替换为黏弹性参数并进行Laplace变换,之后再进行逆变换便可得到黏弹性问题物理域的解。

1.3 一般黏弹性问题位移、应力表达

接下来采用复变函数理论,根据平面问题复变函数解法^[26]与弹性力学平面问题基本方程^[27],隧道开挖引起的土体位移分量以及土体内的应力可通过R区域内的解析函数 $ϕ (z)$ 和 $ψ (z)$ 表示：

$2 G (U_{x} + i U_{y}) = (3 - 4 ν) ϕ (z) - z \cdot \bar{ϕ^{'} (z)} - \bar{ψ (z)}$ ,

(21)

$σ_{x} + σ_{y} = 2 [ϕ^{'} (z) + \bar{ϕ^{'} (z)}]$ ,

(22)

$σ_{y} - σ_{x} + 2 i σ_{x y} = 2 e^{2 i θ} [\bar{z} ϕ^{″} (z) + ψ^{'} (z)]$ 。

(23)

式中, $\bar{ϕ^{'} (z)}$ 和 $\bar{ψ (z)}$ 分别为 $ϕ^{'} (z)$ 和 $ψ (z)$ 的共轭函数, $\bar{z}$ 为 $z$ 的共轭坐标。

将其通过Laplace变换得到

$\begin{matrix} U_{x}^{s} + i U_{y}^{s} = \frac{1}{2 s \tilde{G} (s)} [\begin{array}{l} \end{array} (3 - 4 \tilde{ν} (s)) ϕ (z, s) - \\ z \frac{\bar{\partial ϕ (z, s)}}{\partial z} - \bar{ψ (z, s)}], \end{matrix}$

(24)

$σ_{x}^{s} + σ_{y}^{s} = 2 [\frac{\partial ϕ (z, s)}{\partial z} + \frac{\bar{\partial ϕ (z, s)}}{\partial z}]$ ,

(25)

$σ_{y}^{s} - σ_{x}^{s} + 2 i σ_{x y}^{s} = 2 e^{2 i θ} [\bar{z} \frac{\partial^{2} ϕ (z, s)}{\partial z^{2}} + \frac{\partial ψ (z, s)}{\partial z}]$ 。

(26)

将式（24）,（25）通过Laplace逆变换,解得

$\begin{matrix} U_{x}^{t} + i U_{y}^{t} = \frac{1}{2 G (t)} [(3 - 4 v (t)) ϕ (z, t) - \\ z \frac{\bar{\partial ϕ (z, t)}}{\partial z} - \bar{ψ (z, t)}], \end{matrix}$

(27)

$σ_{x}^{t} + σ_{y}^{t} = 2 [\frac{\partial ϕ (z, t)}{\partial z} + \frac{\bar{\partial ϕ (z, t)}}{\partial z}]$ ,

(28)

$σ_{y}^{t} - σ_{x}^{t} + 2 i σ_{x y}^{t} = 2 e^{2 i θ} [\bar{z} \frac{\partial^{2} ϕ (z, t)}{\partial z^{2}} + \frac{\partial ψ (z, t)}{\partial z}]$ 。

(29)

式中 $U_{x}^{t}$ 和 $U_{y}^{t}$ 分别为x方向与y方向上黏弹性土体位移分量, $σ_{x}^{t}$ , $σ_{y}^{t}$ 分别为x方向与y方向上黏弹性土体正应力分量, $σ_{x y}^{t}$ 为黏弹性土体切应力。

将式（19）,（20）代入式（24）,展开整理可得

$U_{x}^{t} + i U_{y}^{t} = \frac{1}{2 G (t)} [H (t) ϕ (z, t) - z \frac{\bar{\partial ϕ (z, t)}}{\partial z} - \bar{ψ (z, t)}]$ ,

(30)

$式中, G (t) = \frac{G_{h} G_{k}}{G_{h} + G_{k} - G_{h} e^{- \frac{G_{k}}{η_{k}} t}},$

(31)

$\begin{matrix} H (t) = \frac{G_{k}}{G_{h} + G_{k} - G_{h} e^{- \frac{G_{k}}{η_{k}} t}} [- \frac{G_{h}}{G_{k} e^{\frac{G_{k}}{η_{k}} t}} + \\ \begin{matrix} \frac{(G_{h} + G_{k}) (7 G_{h} G_{k} + 3 G_{h} K + 3 G_{k} K)}{G_{h} G_{k}^{2} + 3 G_{k}^{2} K + 3 G_{h} G_{k} K} \end{matrix} - \\ \underset{}{\frac{6 G_{h}^{3} η_{k}}{(G_{h} η_{k} + 3 K η_{k}) (G_{h} G_{k} + 3 G_{h} K + 3 G_{k} K) N}}] \end{matrix}$ ,

(32)

$N = e^{\frac{G_{h} G_{k} + 3 G_{h} K + 3 G_{k} K}{G_{h} η_{k} + 3 K η_{k}} t}$ 。

(33)

对于具体问题,需要解出解析函数 $ϕ (z)$ 和 $ψ (z)$ ,代入式（27）～（29）,便可得到黏弹性问题的应力与位移解答。

1.4 时域解析函数解答

在地表有堆积荷载作用下,且在隧道洞周 $| z + i h | = r_{0}$ 处有已知的位移,则边界条件如下：

$z = \bar{z} : F_{0} (z, t)= ϕ (z, t) + z \cdot \frac{\bar{\partial ϕ (z, t)}}{\partial z} + \bar{ψ (z, t)}$ ,

(34)

$\begin{matrix} | z + i h | = r_{0} : T_{0} (z, t) = 2 G (t) (U_{x}^{s} + i U_{y}^{s}) \\ = H (t) ϕ (z, t) - z \cdot \frac{\bar{\partial ϕ (z, t)}}{\partial z} - \bar{ψ (z, t)} \end{matrix}$ 。

(35)

式中, $H (t)$ 由式（32）确定, $G (t)$ 为剪切模量。

对于半无限平面内的圆孔隧道问题的弹性解答已经由Verruijt^[9]给出,根据复变函数理论,应用保角映射将土体 $z$ 平面R区域,映射到 $ζ$ 平面 $Θ$ 圆环区域,如图3所示,原 $z$ 平面内A,B,C,D各点通过保角映射到 $ζ$ 平面为 $A^{'}$ , $B^{'}$ , $C^{'}$ , $D^{'}$ ,其映射函数如下：

图 3 共形映射区域

Figure 3. Conformal transformation

下载: 全尺寸图片幻灯片

$z = ω (ζ) = - i h \frac{1 - α^{2}}{1 + α^{2}} \frac{1 + ζ}{1 - ζ}$ ,

(36)

式中, $α = (h - \sqrt{h^{2} - r_{0}^{2}}) / r_{0}$ , $ω (ζ)$ 为解析函数。通过保角映射, $z$ 平面区域内的解析函数 $ϕ (z, t)$ 和 $ψ (z, t)$ 转化为

$ϕ (z, t) = ϕ (ω (ζ), t) = Φ (ζ, t)$ ,

(37)

$ψ (z, t) = Ψ (ω (ζ), t) = Ψ (ζ, t)$ 。

(38)

由于 $ϕ (z, t)$ 和 $ψ (z, t)$ 在 $z$ 平面是解析函数,则 $Φ (ζ, t)$ 和 $Ψ (ζ, t)$ 在 $ζ$ 平面圆环域里进行解析,可以将其展开为Laurent级数形式：

$Φ (ζ, t) = a_{0} (t) + \sum_{k = 1}^{\infty} a_{k} (t) ζ^{k} + \sum_{k = 1}^{\infty} b_{k} (t) ζ^{- k}$ ,

(39)

$Ψ (ζ, t) = c_{0} (t) + \sum_{k = 1}^{\infty} d_{k} (t) ζ^{k} + \sum_{k = 1}^{\infty} d_{k} (t) ζ^{- k}$ 。

(40)

式中,a₀, $a_{k}$ , $b_{k}$ , $c_{0}$ , $c_{k}$ , $d_{k}$ 均为待定系数,可以通过边界条件确定。

由于 $z \cdot \frac{\bar{\partial ϕ (z, t)}}{\partial z} = \frac{ω (ζ)}{\bar{ω' (ζ)}} \cdot \frac{\bar{\partial Φ (ζ, t)}}{\partial ζ}$ ,将 $ζ$ 用复平面极坐标表示,即 $ζ = ρ σ$ (ρ为 $ζ$ 平面半径, $σ = e^{i θ}$ ),则

$\frac{ω (ζ)}{\bar{ω' (ζ)}} = - \frac{1}{2} \frac{(1 + ρ σ) {(σ - ρ)}^{2}}{(1 - ρ σ) σ^{2}}$ ,

(41)

$z$ 平面内的边界条件由式（34）,（35）改写为

$| ζ | = 1 : F_{1} (ζ, t) = Φ (ζ, t) + \frac{ω (ζ)}{\bar{ω' (ζ)}} \frac{\bar{\partial Φ (ζ, t)}}{\partial ζ} + \bar{Ψ (ζ, t)},$

(42)

$\begin{array}{l} | ζ | = α : T_{1} (ζ, t) = 2 G (t) (U_{x}^{s} + i U_{y}^{s}) \\ \begin{matrix} = H (t) Φ (ζ, t) \end{matrix} - \frac{ω (ζ)}{\bar{ω^{'} (ζ)}} \cdot \frac{\bar{\partial Φ (ζ, t)}}{\partial ζ} - \bar{Φ (ζ, t)} \end{array}$ 。

(43)

将 $F_{1} (ζ, t)$ 按照Fourier级数展开：

$F_{1} (σ, t) = \sum_{- \infty}^{+ \infty} B_{k} (t) σ^{k}$ ,

(44)

其中,系数 $B_{k}$ 可由下式确定：

$\begin{array}{l} B_{0} = - \frac{1}{2 π} \int_{x_{1}}^{x_{2}} i q (x) θ d x, \\ B_{k} = \frac{1}{2 k π} \int_{x_{1}}^{x_{2}} q (x) (\exp (- i k θ) - 1) d x, \\ B_{- k} = \bar{B_{k}} = \frac{1}{2 k π} \int_{x_{1}}^{x_{2}} q (x) (\exp (i k θ) - 1) d x \\ (k = 1, 2, 3, \dots), \end{array}}$

(45)

式中, $θ$ 为其复平面上的辐角,

$θ = Arg [\frac{(1 + α^{2}) x i - h (1 - α^{2})}{h (1 - α^{2}) + (1 + α^{2}) x i}]$ 。

(46)

将式（39）～（41）,（44）和（45）代入式（42）,可得

$\begin{array}{l} c_{0} = \bar{B_{0}} - \bar{a_{0}} - \frac{1}{2} a_{1} - \frac{1}{2} b_{1}, \\ c_{k} = B_{k} - \bar{b_{k}} + \frac{1}{2} (k - 1) a_{k - 1} - \frac{1}{2} (k + 1) a_{k + 1}, \\ d_{k} = \bar{B_{k}} - \bar{a_{k}} + \frac{1}{2} (k - 1) b_{k - 1} - \frac{1}{2} (k + 1) b_{k + 1} \\ (k = 1, 2, 3, \cdot \cdot \cdot) 。 \end{array}}$

(47)

将式（43）两边同乘 $(1 - α σ)$ ,得到

$\begin{array}{l} T_{1} (ζ, t) (1 - α σ) \\ = (1 - α σ) [H (t) Φ (ζ, t) - \frac{ω (ζ)}{\bar{ω' (ζ)}} \cdot \frac{\bar{\partial Φ (ζ, t)}}{\partial ζ} - \bar{Φ (ζ, t)}] \end{array}$ 。

(48)

令 $Y (ζ, t) = T_{1} (ζ, t) (1 - α σ)$ ,将 $Y (ζ, t)$ 按照Laurent级数展开：

$\begin{array}{l} Y (α σ, t) = \sum_{- \infty}^{+ \infty} A_{k} (t) σ^{k} = A_{0} (t) + A_{1} (t) σ + \\ \begin{matrix} \begin{matrix} \end{matrix} & \begin{matrix} \sum_{k = 2}^{\infty} A_{k} (t) σ^{k} + \sum_{k = 1}^{\infty} A_{- k} (t) σ^{- k} \end{matrix} \end{matrix} \end{array}$ 。

(49)

将式（39）～（41）,（47）和（48）代入式（49）,可得

(50)

本文针对盾构开挖的土工影响采用位移控制手段体现。既有研究表明,盾构隧道开挖面土体变形由均匀径向收缩、椭圆化变形以及整体下沉组成^[28-30],如图4所示。

图 4 隧道边界椭圆化收敛变形模式

Figure 4. Elliptical convergence deformation mode of tunnel boundary

下载: 全尺寸图片幻灯片

在z平面内,以隧道圆心为原点的极坐标系下,隧道径向初始位移边界条件为^[30]

$U_{r} = - \frac{1}{4} u_{0} (5 + 3 \sin θ - 3 \cos^{2} θ)$ ,

(51)

式中, $u_{0}$ 为盾构与拼装衬砌的半径差,体现了衬砌的几何效应。Lee等^[31]认为：盾构引起的土地损失变形主要是由间隙参数GAP决定,其主要由物理间隙U₀、隧道掌子面上等效三维弹塑性变形U_3D和盾构施工的工艺质量w等三部分组成。由于本文考虑的是平面应变问题,不考虑三维变形效应U_3D,w是由盾构机操作水平决定的,为使本文提出的时域解简洁有效,笔者做了一些简化,假定盾构机操作正常且盾构隧道施工影响满足平面应变条件,故而不计入U_3D和w影响。

同时, $u_{0}$ 与已知地层损失率有如下关系：

$u_{0} = \frac{8}{7} r_{0} (1 - \sqrt{1 - V_{L}})$ ,

(52)

式中, $V_{L}$ 为地层损失率。

将式（51）通过坐标变换转换至到xoy直角坐标系下,再通过共形映射式（36）转换至 $ζ$ 平面内,即可得到 $| ζ | = α$ 时的位移边界条件：

$\begin{array}{l} U |_{ρ = α} = - \frac{1}{4} u_{0} {5 + 3 \cdot [\frac{1 + α^{2}}{2 α} - \frac{{(1 - α^{2})}^{2}}{2 α} \frac{1}{(1 - α σ) (1 - α σ^{- 1})}] + \\ \begin{matrix} \end{matrix} \frac{3}{4} \frac{{(1 - α^{2})}^{2} {(σ^{- 1} - σ)}^{2}}{{(1 - α σ)}^{2} {(1 - α σ^{- 1})}^{2}}} \cdot i \cdot \frac{α - σ}{1 - α σ} \end{array}$ 。

(53)

将式（53）代入式（49）,可得

$\begin{array}{l} 2 G (t) \cdot U |_{ρ = α} (1 - α σ) = T_{1} (α σ) (1 - α σ) \\ \begin{matrix} \end{matrix} = A_{0} + A_{1} σ + \sum_{k = 2}^{\infty} A_{k} σ^{k} + \sum_{k = 1}^{\infty} A_{- k} σ^{- k} \end{array}$ 。

(54)

式中, $A_{0} = - (\frac{3}{4} α^{2} + \frac{5}{2} α + \frac{3}{4}) u_{0} i G (t)$ , $A_{1} = (\frac{7}{4} + \frac{9}{4} α +$ $(\frac{3}{2} α^{2} - \frac{3}{4} α^{3} - \frac{3}{4} α^{4}) u_{0} i G (t), A_{k} = - \frac{3}{8} {(1 - α^{2})}^{2} α^{k - 3} \cdot$ $[(k + 1) α^{2} + (2 - k) + 2 α] u_{0} i G (t), A_{- k} = \frac{3}{8} {(1 - α^{2})}^{2} α^{k - 1} u_{0} i G (t) 。$

至此,通过系数 $A_{0}$ , $A_{1}$ , $A_{k}$ , $A_{- k}$ 可以得到待定系数 $a_{0}$ , $a_{k}$ , $b_{k}$ , $c_{0}$ , $c_{k}$ , $d_{k}$ ,从而解出 $ζ$ 平面内的解析函数 $Φ (ζ, t)$ 与 $Ψ (ζ, t)$ ,将其通过映射函数逆变换即可得到z平面内的解析函数 $ϕ (z, t)$ 和 $ψ (z, t)$ ,随后将其代入式（27）～（29）,可以求得本文黏弹性扰

动土体位移场和应力场,即

位移场：

$U_{x}^{t} + i U_{y}^{t} = \frac{1}{2 G (t)} [(3 - 4 v (t)) ϕ (z, t) - z \frac{\bar{\partial ϕ (z, t)}}{\partial z} - \bar{ψ (z, t)}] ；$

(55)

应力场：

$σ_{x}^{t} + σ_{y}^{t} = 2 [\frac{\partial ϕ (z, t)}{\partial z} + \frac{\bar{\partial ϕ (z, t)}}{\partial z}]$ ,

(56)

$σ_{y}^{t} - σ_{x}^{t} + 2 i σ_{x y}^{t} = 2 e^{2 i θ} [\bar{z} \frac{\partial^{2} ϕ (z, t)}{\partial z^{2}} + \frac{\partial ψ (z, t)}{\partial z}]$ 。

(57)

2. 本文时域解析解答与工程实测数据对比分析

2.1 无堆载影响下的地层变形时效分析对比

为验证本文时域解析解答的准确性,选取Chou等^[32]、Bobet^[33]中的两条实测隧道数据与解析解答进行对比。两条隧道分别为Regent Park隧道南线和Regent Park隧道北线,其土质皆为伦敦黏土,其中Regent Park隧道南线具体参数为：外半径2.07 m,埋深34.1 m,土体杨氏模量56 MPa,土体重度19 kN/m³,地层损失率1.4%。黏弹性参数： $G_{h}$ 取20.72 MPa, $G_{k}$ 取33.6 MPa,体积模量K取61.6 MPa,黏性系数 $η_{k}$ 取224 MPa∙d；Regent Park隧道北线具体参数为：外半径2.07 m,埋深20.1 m,土体杨氏模量32 MPa,土体重度19 kN/m³,地层损失率1.3 %。黏弹性参数： $G_{h}$ 取11.84 MPa, $G_{k}$ 取19.2 MPa,体积模量K取35.2 MPa,黏性系数 $η_{k}$ 取128 MPa∙day。

为了使得对比结果更为全面,体现理论解析的可靠性,选取计算两条隧道开挖两个月后的地表沉降与隧道竖向中轴线处的地层沉降,并与实测数据进行对比验证。

图5,6分别为Regent Park隧道南线和北线在地表和隧道竖向中轴线的长期沉降对比结果。由图5（a）所示,在地表x=0 m处,解析解与实测数据的沉降值分别为6.84,5.46 mm,相差1.38 mm,而在地表x=12 m处,解析解与实测数据的沉降值分别为5.26,1.84 mm,相差3.42 mm。由图5（b）所示,在地表隧道竖向中轴线处,解析解与实测数据的沉降值分别为6.84,5.46 mm,相差1.38 mm,而在地下20 m隧道竖向中轴线处,解析解与实测数据的沉降值分别为8.23,6.41 mm,相差1.82 mm。由图6（a）所示,在地表x=0 m处,解析解与实测数据的沉降值分别为8.56,7.03 mm,相差1.53 mm,而在地表x=10 m处,解析解与实测数据的沉降值分别为5.45,3.08 mm,相差2.37 mm。由图6（b）所示,在地表隧道竖向中轴线处,解析解与实测数据的沉降值分别为8.56,7.03 mm,相差1.53 mm,而在地下16 m隧道竖向中轴线处,解析解与实测数据的沉降值分别为15.13,13.89 mm,相差1.24 mm。综上所述,可以发现本文解析解得到的地表长期沉降值与实测值相比,在地表距离隧道开挖区较远处一般表现为偏大,而在计算隧道竖向中轴线处地层沉降时,本文解析解和实测数据较为吻合,且总体上解析结果较实测数据偏大。

图 5 Regent Park南线长期沉降对比

Figure 5. Comparison of long-term settlement of Regent Park southbound tunnel

下载: 全尺寸图片幻灯片

图 6 Regent Park北线长期沉降对比

Figure 6. Comparison of long-term settlement of Regent Park northbound tunnel

下载: 全尺寸图片幻灯片

通过上述算例分析表明,本算法具有较好程序扩展性,可以屏蔽地表荷载影响部分,即 $z$ 平面内边界条件（42）考虑为地表自由边界,从而验证了黏弹性地层土质带来的单一影响。

2.2 受堆载影响下的地层变形时效分析对比

文献[34]针对滨海软土地区盾构隧道穿越新建海堤工程做了大量的现场监测,其可简化为本文地面堆载作用下的黏弹性地层盾构施工模型。为验证本文解析解的可靠性,选取文献中实测数据进行对比分析。

该工程位于浙江沿海乐清电厂,输水隧道自循环水泵房始,向东南方向海域延伸,单长约1500 m,采用盾构法施工,隧道直径4.84 m。图7为海堤与盾构隧道位置示意图,其中图7（a）为监测段隧道纵向剖面图,其隧道埋深为11 m,平均海堤高度约6.2 m,其填筑荷载约240 kPa。图7（b）为监测处隧道截面图,本文在计算中海堤作用范围取40 m,取监测点D2和D3,其位置如图7（b）所示。根据现场监测数据,当隧道开挖52 d时,其海堤增加至8 m,其填筑荷载达到298 kPa。相关黏弹性土体参数为： $G_{h}$ 取2.4 MPa, $G_{k}$ 取6.8 MPa,体积模量K取10.5 MPa,黏性系数 $η_{k}$ 取125 MPa∙d。

图 7 海堤盾构隧道示意图

Figure 7. Schematic diagram of shield tunnel under seawall

下载: 全尺寸图片幻灯片

图8为观测点沉降值随时间变化对比结果,图9为沉降速率值随时间变化的对比结果。由图8（a）所示,在D2点处解析结果与实测结果最大相差高达8.78 mm；由图8（b）所示,在D3点处解析解与实测结果最大相差仅为3.79 mm。同时在图8中也可发现D3点相较D2点处的解析结果,与实测结果相差较小。综上所述,可以发现本文解析解得到的沉降值与实测值相比,在距离隧道开挖区较远处一般表现为偏大,而在计算隧道竖向中轴线处时,本文解析解和实测数据较为吻合,且总体上解析结果较实测数据偏大。同时可以发现开挖至52天时,随着海堤荷载增加,地表沉降值与沉降速率显著增加（尤其沉降速率曲线存在明显阶跃,本算法可以对其进行精准模拟）,但沉降变化速率逐渐衰弱直至为零。

图 8 沉降值随时间变化图

Figure 8. Change of settlement value with time

下载: 全尺寸图片幻灯片

图 9 沉降速率值随时间变化图

Figure 9. Change of settlement rate value with time

下载: 全尺寸图片幻灯片

通过上述算例分析表明,本算法可以较好体现地表荷载的影响,对于荷载量值突变完整模拟,而改变式（44）所示的荷载表达形式,可以进一步扩展本算法有关地表荷载的适用范围（如动载等）。

3. 结语

本文在考虑地表堆载作用下,引入隧道洞周的椭圆化收敛变形位移控制模式,采用复变函数法理论并运用Laplace变换技术,提出了地表堆载作用下盾构隧道开挖引起的周围地层位移场和应力场的时域解。研究表明,地表堆载及土体黏弹特性对隧道开挖影响显著,不容忽略。在地表堆载影响下,随着隧道开挖后时间的推移,开挖引起的地层变形不断增加,沉降速率则呈现出逐渐衰弱直至为零规律,而堆载突变导致其地表沉降值尤其沉降速率变化显著。本文成果可为地表存在堆积荷载作用下的隧道工程施工引起的地层位移场和应力场作初期预估。

本文方法适用于土压平衡和泥水平衡盾构下的浅埋隧道,对其他形式开挖如气压平衡盾构还需进一步确认其适用性。同时在计算地层变形的时效性时仅考虑了土体的黏弹特性,没有考虑固结耦合效应,这将在接下来的工作中加以研究。

图 1 三维碎石颗粒及其接触模型

Figure 1. 3D gravel particles and contact model

下载: 全尺寸图片幻灯片

图 2 模型试验设置

Figure 2. Setup of model tests

下载: 全尺寸图片幻灯片

图 3 数值模型设置

Figure 3. Numerical model

下载: 全尺寸图片幻灯片

图 4 单桩载荷试验的p-s曲线

Figure 4. p-s curves of loading tests on a single stone column

下载: 全尺寸图片幻灯片

图 5 不同沉降下桩体鼓胀变形及桩周土体应力分布曲线

Figure 5. Distribution of column bulging deformation and soil stresses under varying settlements

下载: 全尺寸图片幻灯片

图 6 不同沉降下土体水平位移及应力分布

Figure 6. Horizontal displacement and stress contours of surrounding soils under varying settlements

下载: 全尺寸图片幻灯片

图 7 不同沉降下土体竖直位移及应力分布

Figure 7. Vertical displacement and stress contours of surrounding soils under varying settlements

下载: 全尺寸图片幻灯片

图 8 不同沉降下桩周土体剪应变分布

Figure 8. Shear strain contours of surrounding soil under varying settlements

下载: 全尺寸图片幻灯片

图 9 不同沉降下桩土平均应力分布

Figure 9. Average stresses of stone column under varying settlements

下载: 全尺寸图片幻灯片

图 10 桩体内部力链网络

Figure 10. Force chain networks inside stone column

下载: 全尺寸图片幻灯片

图 11 不同沉降下碎石位移矢量

Figure 11. Displacement vectors of gravels under varying settlements

下载: 全尺寸图片幻灯片

图 12 最终破坏桩体轮廓

Figure 12. Failure stone column at final loading stage

下载: 全尺寸图片幻灯片

表 1 碎石桩体的材料参数

Table 1 Material parameters of stone column

块体及微观接触参数（输入）							宏观表象参数（计算）
接触杨氏模量E_c/Pa	接触刚度比k_s/k_s	接触摩擦系数μ	碎石粒径d/mm	相对密实度	碎石数量	块体重度γ/(kN·m^-3)	压缩模量E_o/MPa	弹性模量E_c/MPa	泊松比 $ν$ $ν$	表观摩擦角φ/(°)
2.0×10⁹	2.0	0.55	3~12	0.8	8130	25	75	45	0.35	42

下载: 导出CSV

表 2 软土的材料参数

Table 2 Material parameters of soils

c_u/kPa	φ/(°)	E/MPa	$ν$ $ν$	$ρ$ $ρ$ /(g·cm^-3)
48	0	6.0	0.4	1700

下载: 导出CSV

参考文献(20)

[1]	刘汉龙, 赵明华. 地基处理研究进展[J]. 土木工程学报, 2016, 49(1): 103-122. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201601013.htm LIU Han-long, ZHAO Ming-hua. Review of ground improvement technical and its application in China[J]. China Civil Engineering Journal, 2016, 49(1): 103-122. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201601013.htm
[2]	郭尤林, 赵明华, 彭文哲. 基于改进应变楔模型的固体-散体串联组合桩鼓胀变形及沉降分析[J]. 岩土工程学报, 2019, 41(11): 2149-2155. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201911025.htm GUO You-lin, ZHAO Ming-hua, PENG Wen-zhe. Lateral bulgings and settlements of solid-bulk tandem compound piles based on modified strain wedge model[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(11): 2149-2155. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201911025.htm
[3]	陈建峰, 顾子昂, 王兴涛, 等. 冻融条件下加筋碎石桩复合地基路堤性状研究[J]. 岩土工程学报, 2020, 42(8): 1394-1400. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202008005.htm CHEN Jian-feng, GU Zi-ang, WANG Xin-tao, et al. Behaviour of embankment on composite foundation with geosynthetic-encased stone columns under freeze-thaw condition[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(8): 1394-1400. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202008005.htm
[4]	谭鑫, 冯龙健, 赵明华, 等. 刚性基础下筋箍碎石桩复合地基桩土应力比计算模型[J]. 中国公路学报, 2019, 32(9): 42-50. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201909005.htm TAN Xin, FENG Long-jian, ZHAO Ming-hua, et al. Calculation model for stress concentration ratio of composite foundation reinforced by geosynthetic-encased stone columns[J]. China Journal of Highway and Transport, 2019, 32(9): 42-50. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL201909005.htm
[5]	陈建峰, 韩杰. 夯扩碎石桩群桩承载性状研究[J]. 中国公路学报, 2010, 23(1): 26-31. doi: 10.3969/j.issn.1001-7372.2010.01.005 CHEN Jian-feng, HAN Jie. Research on bearing behavior of rammed aggregate pier group[J]. China Journal of Highway and Transport, 2010, 23(1): 26-31. (in Chinese) doi: 10.3969/j.issn.1001-7372.2010.01.005
[6]	赵明华, 顾美湘, 张玲, 等. 竖向土工加筋体对碎石桩承载变形影响的模型试验研究[J]. 岩土工程学报, 2014, 36(9): 1587-1593. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201409006.htm ZHAO Ming-hua, GU Mei-xiang, ZHANG Ling, et al. Model tests on influence of vertical geosynthetic-encasement on performance of stone columns[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(9): 1587-1593. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201409006.htm
[7]	陈建峰, 韩杰. 夯扩碎石桩单桩载荷试验数值模拟[J]. 岩土工程学报, 2009, 31(9): 1366-1370. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200909011.htm CHEN Jian-feng, HAN Jie. Numerical modeling of loading tests on a rammed aggregate pier[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(9): 1366-1370. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200909011.htm
[8]	蒋敏敏, 肖昭然, 蔡正银. 高速公路碎石桩复合地基加固数值模拟[J]. 公路, 2012, 31(1): 8-12. https://www.cnki.com.cn/Article/CJFDTOTAL-GLGL201201004.htm JIANG Min-min, XIAO Zhao-ran, CAI Zheng-yin. Numerical simulation of stone columns reinforced foundation of expressway[J]. Highway, 2012, 31(1): 8-12. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GLGL201201004.htm
[9]	王复明, 方宏远, 曹凯, 等. 高聚物碎石桩模型试验及数值分析[J]. 岩土工程学报, 2018, 40(增刊2): 1-5. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2018S2003.htm WANG Fu-ming, FANG Hong-yuan, CAO Kai, et al. Model tests and numerical analyses of polymer gravel piles[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(S2): 1-5. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2018S2003.htm
[10]	蒋明镜, 肖俞, 陈双林, 等. 砂土中单桩竖向抗压承载机制的离散元分析[J]. 岩土力学, 2010, 31(增刊2): 366-372. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2010S2066.htm JIANG Ming-jin, XIAO Yu, CHEN Shuang-lin, et al. Discrete element analysis of bearing mechanism of single pile in sand under vertical load[J]. Rock and Soil Mechanics, 2010, 31(S2): 366-372. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2010S2066.htm
[11]	谭鑫, 赵明华, 金宇轩, 等. 碎石桩单桩受荷模型试验的离散单元法数值模拟[J]. 湖南大学学报(自然科学版). 2019(1): 101-108. https://www.cnki.com.cn/Article/CJFDTOTAL-HNDX201903014.htm TAN Xin, ZHAO Ming-hua, JIN Yu-xuan, et al. Numerical simulation of loading test on a single stone column using discrete element method[J]. Journal of Hunan University (Natural Sciences), 2019(1): 101-108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HNDX201903014.htm
[12]	INDRARATNA B, NGO N T, RUJIKIATKAMJORN C, et al. Coupled discrete element-finite difference method for analyzing the load deformation behavior of a single stone column in soft soil[J]. Computers and Geotechnics, 2015, 63: 267-278.
[13]	TAN X, ZHAO M H, ZHU Z. Elastic properties calibration approach for discrete element method model based on Voronoi tessellation method[J]. Geotechnical and Geological Engineering. 2019, 37(3): 2227-2236.
[14]	TAN X, ZHAO M H, CHEN W. Numerical simulation of a single stone column in soft clay using the discrete-element method[J]. International Journal of Geomechanics, 2018, 18(12): 0418176.
[15]	TAN X, FENG L J, HU Z B, et al. A DEM-FDM coupled numerical study on the deformation and failure process of the isolated stone column in soft soil[J/OL]. Bulletin of Engineering Geology and the Environment, 2019. doi: 10.1007/s10064-019-01671-3.
[16]	GU M X, HAN J, ZHAO M H. Three-dimensional discrete-element method analysis of stresses and deformations of a single geogrid-encased stone column[J]. International Journal of Geomechanics, 2017, 9(17): 1-14.
[17]	GU M X, HAN J, ZHAO M H. Three-dimensional DEM analysis of single geogrid-encased stone columns under unconfined compression: a parametric study[J]. Acta Geotech, 2017, 12(3): 559-572.
[18]	STAHL M, KONIETZKY H. Discrete element simulation of ballast and gravel under special consideration of grain-shape, grain-size and relative density[J]. Granular Matter, 2011, 13(4): 417-428.
[19]	STAHL M, KONIETZKY H, KAMP L. Discrete element simulation of geogrid-stabilised soil[J]. Acta Geotechnica, 2014, 9(6): 1073-1084.
[20]	GE G, MEGUID M A. Effect of particle shape on the response of geogrid-reinforced systems: insights from 3D discrete element analysis[J]. Geotextiles and Geomembranes, 2018, 46(6): 685-698.

施引文献(10)

期刊类型引用(5)

1.	孙立军，付金伟，刘美，汪德才，郭长龙. 地表堆载对盾构隧道稳定性影响的三维试验研究. 工程勘察. 2024(11): 1-6+20 . 百度学术
2.	张明飞，王凯文，李广慧，杨延栋，薛茹. 基于Flamant解的堆载对隧道影响解析方法. 地下空间与工程学报. 2023(S1): 131-138 . 百度学术
3.	李少华. 跨海大直径盾构隧道堤防稳定性分析. 铁道建筑技术. 2023(10): 171-174 . 百度学术
4.	葛存源，席培胜，穆琳，胡彩云. 盾构法隧道施工地层变形管控分析. 兰州工业学院学报. 2022(03): 44-47+68 . 百度学术
5.	王祖贤，施成华，刘建文. 非对称推力作用下盾构隧道附加响应的解析解. 岩土力学. 2021(09): 2449-2460 . 百度学术