基于改进角点理论的砂土非共轴模型及其应用

王兴; 孔亮; 李学丰

doi:10.11779/CJGE202102005

基于改进角点理论的砂土非共轴模型及其应用 English Version

王兴^{1, 2,},
孔亮^{1, 2, ,},
李学丰³

1.
青岛理工大学理学院,山东　青岛　266033
2.
青岛理工大学土木工程学院,山东　青岛　266033
3.
宁夏大学固体力学研究所,宁夏　银川　750021

基金项目:

国家自然科学基金项目 51778311

国家自然科学基金项目 11572165

详细信息

作者简介:
王兴（1988— ）,男,博士研究生,主要从事岩土本构关系方面的研究工作。E-mail：1306825892@qq.com

通讯作者:
孔亮, E-mail: qdkongliang@163.com

中图分类号: TU43
计量
- 文章访问数: 282
- HTML全文浏览量: 16
- PDF下载量: 163
出版历程
- 收稿日期: 2020-04-21
- 网络出版日期: 2022-12-04
- 刊出日期: 2021-01-31

Non-coaxial sand model based on improved vertex theory and its application

WANG Xing^{1, 2,},
KONG Liang^{1, 2, ,},
LI Xue-feng³

1.
School of Civil Engineering, Qingdao University of Technology, Qingdao 266033, China
2.
School of Sciences, Qingdao University of Technology, Qingdao 266033, China;
3.
Solid Mechanics Institute, Ningxia University, Yinchuan 750021, China

摘要

摘要: 基于传统角点理论建立的非共轴模型虽然能够描述砂土的非共轴行为,但却具有一定的理论缺陷。提出了一种改进的角点理论并将其应用到了砂土状态相关剪胀模型中,从而建立了一个新的砂土非共轴模型。该模型仅在主应力方向改变的加载条件下给出非共轴塑性变形,克服了传统角点模型的不足。构建了模型的隐式积分算法和相应的一致性切线刚度张量,并通过Toyoura砂的单剪试验对算法进行了验证,证明了算法的正确性。最后,利用建立的模型分析了条形基础的承载力,预测结果表明：非共轴塑性的引入使得地基模型整体刚度下降,导致力学响应表现出一些软化特征,忽略非共轴塑性的影响可能导致工程设计偏于危险。
- 非共轴 /
- 改进的角点理论 /
- 隐式积分算法 /
- 条形基础的承载力
Abstract: Although the non-coaxial models based on the traditional vertex theory can capture the non-coaxial behavior of sand, they contain some theoretical defects. An improved vertex theory is proposed and added to the state-dependent dilatancy model for sand, thus a new non-coaxial sand constitutive model is established. In this model, the non-coaxial plastic deformation is given only under loading conditions involving the change of the principal stress direction, which overcomes the shortcomings of the traditional vertex non-coaxial models. The implicit stress integration algorithm and consistent stiffness tensor of the model are given, and then the algorithm is verified by the simple shear experiment on Toyoura sand. Finally, the bearing capacity of strip foundation is analyzed by using the established model. The predicted results show that the introduction of the non-coaxial plasticity reduces the overall stiffness of the foundation model and results in a softer mechanical response, and neglecting the non-coaxial influences may lead to unsafe design.
- non-coaxiality /
- improved vertex theory /
- implicit integration algorithm /
- bearing capacity of strip foundation

HTML全文

0. 引言

非共轴性是指在弹塑性加载过程中塑性应变率主方向与应力主方向之间的非一致性。传统弹塑性模型由于隐含了塑性应变率与应力共轴的假设,因此在描述岩土材料的变形特性方面存在一定的局限性^[1-8]。早在1975年,Rudnicki等^[4]就已经指出,若采用传统的塑性位势理论计算,将高估裂隙岩体的刚度。为更加精确地描述裂隙岩体的塑性变形,Rudnicki等^[4]提出了所谓的角点理论。在这一理论中,引入了一个额外的塑性模量控制裂隙岩体对切线应力率的响应。后来,Hshiguchi等^[5-7]发展了广义形式的角点理论。钱建固等^[9-10]应用Gram-Schimidt张量正交化理论,建立了三维化的角点理论。通过在传统模型中引入角点理论可以明显地改善无法描述非共轴行为这一缺陷。目前,借助于角点理论,研究者们已经建立了多种形式的非共轴模型。Yang等^[11-13]通过将Rudnicki等^[4]提出原始的角点理论引入Drucker-Prager模型和临界状态土力学模型CASM对单剪试验中的砂土非共轴行为进行了模拟。李学丰等^[14]参考钱建固等^[9-10]的研究成果,建立了一个砂土的非共轴模型并对Matsuoka的铝棒堆积体试验进行了模拟,得到了与试验数据较为一致的结果。王兴等^[2]利用非共轴模型分析了砂土地基的承载力,探讨了非共轴因素对预测结果的影响。扈萍等^[15]、陈洲泉等^[16-17]也分别采用非共轴模型模拟了砂土的空心圆柱扭剪试验。结果表明,角点理论能够再现砂土在单剪试验与空心圆柱试验中的非共轴现象。

尽管上述研究已经证明传统角点理论（本文将前述提及的角点理论统称为传统的角点理论）在描述砂土非共轴行为方面的合理性,但仍然存在一些值得商榷的问题。例如在平面应变试验条件下,若从单元体角度考虑,砂土试样内部仅存在3个同向的主应力与主应变,并不存在真正意义上的非共轴塑性变形,至少在土体单元产生应变局部化行为之前是成立的。但按照已有的角点理论,在加载开始阶段便会产生附加的塑性变形,将其称为非共轴塑性显然并不恰当。究其原因是由于在上述的角点理论中,非共轴塑性的产生不仅受主应力方向变化的影响也受到主应力大小变化的影响。另一个值得关注的问题是,虽然已经发展了一些角点型的非共轴模型,但相关模型的有限元应用研究仍然比较少见。尽管目前已有一些相关的研究,例如Yang等^[18-19]利用角点型的Drucker-Prager模型分析了条形基础的承载力问题；Yuan等^[20-21]分析了非共轴因素对于隧道开挖引起的地面沉降的影响。但由于上述研究以理想塑性模型为平台,不能充分反映砂土的变形特性,例如剪胀性、状态相关特性等^[22-23]。此外,在模型的数值积分方面,已有研究都采用了控制误差的显式积分格式^{[18-21, 24]}。相比较而言,隐式积分格式^[25]在迭代结束时能够自动满足屈服面的一致性条件,具有二次收敛速度,具备一些独特的优势,但关于角点类模型的隐式积分算法研究却还未见报道。

在本文中,笔者尝试重新定义角点理论中的一些基本概念,使得非共轴塑性的产生仅与主应力方向的改变有关,进而建立一个改进角点理论,然后结合Li等^[26]提出的砂土状态相关剪胀模型建立一个新的砂土非共轴模型。进一步地,为方便模型在有限元仿真分析中的应用,尝试发展适用于该模型的隐式积分方案。利用ABAQUS软件的用户材料子程序接口,将模型嵌入到ABAQUS软件材料库中并对Toyoura砂的单剪试验进行模拟,以检验积分方案的精确性和稳定性。最后,通过模拟砂土地基上条形基础的承载力问题,简要分析非共轴因素对计算结果的影响。

1. 改进的角点理论

1.1 切线方向与切线应力空间

假设非共轴塑性是由于主应力方向的改变所引发。为了建立二者之间的关系,需将应力率张量 $\dot{σ}$ 分解成两部分,一部分仅改变主应力的方向,另一部分仅改变主应力的大小。为此,假设 $Q$ 是某一单位正交张量,将其作用于应力张量 $σ$ 可得转换应力张量 $\bar{σ} = Q σ Q^{T}$ 。根据单位正交张量的性质可知, $\bar{σ}$ 和 $σ$ 的主值相同,但主方向不同。基于上述认识,定义一个二阶张量：

$n = \lim_{\bar{σ} \to σ} \frac{\bar{σ} - σ}{‖ \bar{σ} - σ ‖}$ ,

(1)

式中, $n$ 为切线方向张量。

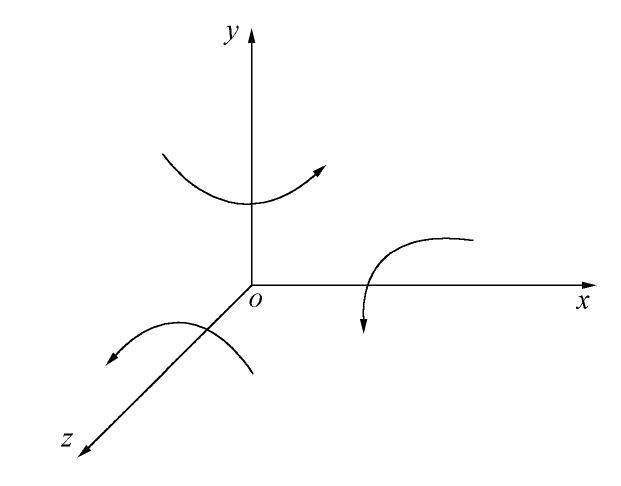
按照式（1）,假如应力率张量 $\dot{σ}$ 与 $n$ 同向,即 $\dot{σ} = (\dot{σ} : n) n$ ,那么 $\dot{σ}$ 仅改变应力的主方向而不改变应力的主值。进一步地,建立一个如图1所示的笛卡尔坐标系。

图 1 笛卡尔坐标系示意图

Figure 1. Diagram of Cartesian coordinate system

下载: 全尺寸图片幻灯片

应力张量 $σ$ 在这一坐标系下的分量形式可表示为

$σ_{i j} = [\begin{matrix} σ_{x} & τ_{x y} & τ_{x z} \\ τ_{x y} & σ_{y} & τ_{y z} \\ τ_{x z} & τ_{y z} & σ_{z} \end{matrix}]$ 。

(2)

假设应力张量 $σ$ 仅绕z轴旋转,则单位正交张量 $Q^{z}$ 可以表示为

$Q_{i j}^{z} = [\begin{matrix} \cos α_{z} & \sin α_{z} & 0 \\ - \sin α_{z} & \cos α_{z} & 0 \\ 0 & 0 & 1 \end{matrix}]$ ,

(3)

式中, $α_{z}$ 表示绕Z轴的旋转角。将式（3）代入式（1）,则可得切线方向张量 $n^{z}$ ：

$n_{i j}^{z} = \frac{[\begin{matrix} 2 τ_{x y} & σ_{y} - σ_{x} & τ_{y z} \\ σ_{y} - σ_{x} & - 2 τ_{x y} & - τ_{x z} \\ τ_{y z} & - τ_{x z} & 0 \end{matrix}]}{\sqrt{8 τ_{x y}^{2} + 2 τ_{y z}^{2} + 2 τ_{x z}^{2} + 2 {(σ_{x} - σ_{y})}^{2}}}$ 。

(4)

同理可知,当应力张量 $σ$ 仅绕x轴、y轴旋转时,相应的单位正交张量 $Q^{x}$ 和 $Q^{y}$ 分别为

$Q_{i j}^{x} = [\begin{matrix} 1 & 0 & 0 \\ 0 & \cos α_{x} & \sin α_{x} \\ 0 & - \sin α_{x} & \cos α_{x} \end{matrix}]$ ,

(5)

$Q_{i j}^{y} = [\begin{matrix} \cos α_{y} & 0 & \sin α_{y} \\ 0 & 1 & 0 \\ - \sin α_{y} & 0 & \cos α_{y} \end{matrix}]$ ,

(6)

式中, $α_{x}$ 和 $α_{y}$ 分别表示绕x轴和y轴的旋转角。相应的切线方向张量 $n^{x}$ 和 $n^{y}$ 分别为

$n_{i j}^{x} = \frac{[\begin{matrix} 0 & τ_{x z} & - τ_{x y} \\ τ_{x z} & 2 τ_{y z} & σ_{z} - σ_{y} \\ - τ_{x y} & σ_{z} - σ_{y} & - 2 τ_{y z} \end{matrix}]}{\sqrt{8 τ_{y z}^{2} + 2 τ_{x y}^{2} + 2 τ_{x z}^{2} + 2 {(σ_{z} - σ_{y})}^{2}}}$ ,

(7)

$n_{i j}^{y} = \frac{[\begin{matrix} 2 τ_{x z} & τ_{y z} & σ_{z} - σ_{x} \\ τ_{y z} & 0 & - τ_{x y} \\ σ_{z} - σ_{x} & - τ_{x y} & - 2 τ_{x z} \end{matrix}]}{\sqrt{2 τ_{y z}^{2} + 2 τ_{x y}^{2} + 8 τ_{x z}^{2} + 2 {(σ_{x} - σ_{z})}^{2}}}$ 。

(8)

由于表示旋转变化的任意一个单位正交张量 $Q$ 可以表示为3个张量 $Q^{z}$ , $Q^{x}$ 和 $Q^{y}$ 的组合,因此任意的切线方向张量 $n$ 可以表示为

$\begin{matrix} n = \lim_{σ^{z x y} \to σ} \frac{σ^{z x y} - σ}{‖ σ^{z x y} - σ ‖} \\ = \lim_{\begin{array}{l} α_{z} \to 0 \\ α_{x} \to 0 \\ α_{y} \to 0 \end{array}} {\frac{σ^{z x y} - σ^{z x} + σ^{z x} - σ^{z} + σ^{z} - σ}{‖ σ^{z x y} - σ ‖}} \\ = \lim_{\begin{array}{l} α_{z} \to 0 \\ α_{x} \to 0 \\ α_{y} \to 0 \end{array}} {\begin{cases} \frac{σ^{z x y} - σ^{z x}}{‖ σ^{z x y} - σ^{z x} ‖} \frac{‖ σ^{z x y} - σ^{z x} ‖}{‖ σ^{z x y} - σ ‖} \\ + \frac{σ^{z x} - σ^{z}}{‖ σ^{z x} - σ^{z} ‖} \frac{‖ σ^{z x} - σ^{z} ‖}{‖ σ^{z x y} - σ ‖} \\ + \frac{σ^{z} - σ}{‖ σ^{z} - σ ‖} \frac{‖ σ^{z} - σ ‖}{‖ σ^{z x y} - σ ‖} \end{cases}} \\ = λ_{y} n^{y} + λ_{x} n^{x} + λ_{z} n^{z} \end{matrix}$ 。

(9)

式中 $λ_{y}$ , $λ_{x}$ 和 $λ_{z}$ 分别表示3个非负的系数； $σ^{z x y}$ 代表应力张量 $σ$ 绕z轴、x轴和y轴旋转后的结果；相应地, $σ^{z x}$ 和 $σ^{z}$ 分别代表绕z轴、x轴和仅绕z轴旋转的结果。三者可分别表示为

$σ^{z x y} = Q^{y} \cdot Q^{x} \cdot Q^{z} \cdot σ \cdot {(Q^{z})}^{T} \cdot {(Q^{x})}^{T} \cdot {(Q^{y})}^{T}$ ,

(10a)

$σ^{z x} = Q^{x} \cdot Q^{z} \cdot σ \cdot {(Q^{z})}^{T} \cdot {(Q^{x})}^{T}$ ,

(10b)

$σ^{z} = Q^{z} \cdot σ \cdot {(Q^{z})}^{T}$ 。

(10c)

式（9）表明,任意的切线方向张量 $n$ 可以表示为 $n^{y}$ , $n^{x}$ 和 $n^{z}$ 的线性组合。另外,由于 $n^{y}$ , $n^{x}$ 和 $n^{z}$ 三者线性无关,因此可以认为 $n^{y}$ , $n^{x}$ 和 $n^{z}$ 构成了一个切线应力空间。进一步地,基于 $n^{y}$ , $n^{x}$ 和 $n^{z}$ 构建三个新的切线方向张量：

$n_{1} = n^{z}$ ,

(11a)

$n_{2} = \frac{n^{x} - (n^{x} : n_{1}) n_{1}}{‖ n^{x} - (n^{x} : n_{1}) n_{1} ‖}$ ,

(11b)

$n_{3} = \frac{n^{y} - (n_{2} : n^{y}) n_{2} - (n_{1} : n^{y}) n_{1}}{‖ n^{y} - (n_{2} : n^{y}) n_{2} - (n_{1} : n^{y}) n_{1} ‖}$ 。

(11c)

容易证明, $n_{1}$ , $n_{2}$ 和 $n_{3}$ 三者之间存在关系：

$n_{i} : n_{j} = δ_{i j}$ ,

(12)

式中, $δ_{i j}$ 为Kronecker符号。式（12）表明, $n_{1}$ , $n_{2}$ 和 $n_{3}$ 可视为切线应力空间的3个正交规范化的单位基张量。

1.2 切线应力率与切线投影算子

任意的应力率张量 $\dot{σ}$ 在切线应力空间的分量可以表示为

$\begin{matrix} {\dot{σ}}_{t} = (\dot{σ} : n_{1}) n_{1} + (\dot{σ} : n_{2}) n_{2} + (\dot{σ} : n_{3}) n_{3} \\ = (n_{1} \otimes n_{1} + n_{2} \otimes n_{2} + n_{3} \otimes n_{3}) : \dot{σ} \\ = Ι_{t} : \dot{σ} \end{matrix}$ 。

(13)

式中 ${\dot{σ}}_{t}$ 为切线应力率张量； $Ι_{t}$ 为切线投影算子,它将任意的二阶张量投射进入切线应力空间中,并且易证 $Ι_{t}$ 满足

$Ι_{t} : Ι_{t} = Ι_{t}$ ,

(14)

${\dot{σ}}_{t} = Ι_{t} : \dot{σ} = Ι_{t} : {\dot{σ}}_{t}$ 。

(15)

1.3 非共轴塑性应变率

参考Hashiguchi等^[5-7]的研究成果,在改进的角点理论中假设非共轴塑性应变率张量 ${\dot{ε}}^{pn}$ 与切线应力率张量 ${\dot{σ}}_{t}$ 之间为线性关系：

${\dot{ε}}^{pn} = T E^{- 1} : {\dot{σ}}_{t}$ ,

(16)

式中, $T$ 为非共轴系数, $E$ 为弹性刚度张量。由于新定义的切线应力率张量 ${\dot{σ}}_{t}$ 仅包含主应力方向变化的信息,而不包含主应力大小变化的信息,因此根据式（16）,仅当主应力方向发生改变时才会引发非共轴塑性变形。

2. 砂土的非共轴本构模型

Li等^[26]提出了一个可以在较大的密度和压力范围内模拟砂土变形的状态相关剪胀模型,但由于没有考虑主应力方向改变的影响,无法描述砂土的非共轴行为。由于主应力轴旋转加载条件下通常涉及到三维应力状态,因此首先利用插入角隅函数的方法将模型三维化^[27-28],在此基础上,通过引入改进的角点理论来构建一个砂土的非共轴模型。

2.1 状态变量

模型的状态变量 $ψ$ 定义为相同压力下当前孔隙比 $e$ 与临界孔隙比 $e_{c}$ 的差值,即

$ψ = e - e_{c}$ ,

(17)

$e_{c}$ 采用Li等^[26]提出的形式：

$e_{c} = e_{Γ} - λ_{c} {(p / p_{a})}^{ξ}$ 。

(18)

式中 $e_{Γ}$ , $λ_{c}$ 和 $ξ$ 为材料常数； $p_{a}$ 为标准大气压； $p = tr(σ)/3$ 为平均应力。

2.2 弹性部分

模型的剪切模量 $G$ 、体积模量 $K$ 都与砂土密度和平均应力 $p$ 有关,其表达式为

$G = G_{0} \frac{{(2.97 - e)}^{2}}{1 + e} \sqrt{p p_{a}}$ ,

(19)

$K = G \frac{2 (1 + ν)}{3 (1 - 2 ν)}$ 。

(20)

式中 $G_{0}$ 为材料常数； $ν$ 为泊松比。

2.3 屈服函数与塑性模量

模型中采用的屈服函数为

$f = q - M g (θ) p = 0$ ,

(21)

式中 $q = \sqrt{3 J_{2}}$ 为广义剪应力； $J_{2} = s : s / 2$ 为 $s$ 的第二不变量,其中 $s = σ - tr(σ) / 3$ 为偏应力张量； $M$ 为硬化内变量；应力罗德角 $θ = \sin^{- 1} (3 \sqrt{3} J_{3} / 2 J_{2}^{3}) / 3$ ； $J_{3} = tr(s^{3})/3$ 为 $s$ 的第三不变量； $g (θ)$ 为引入的角隅函数,这里采用Dafalias等^[29]建议的形式：

$g (θ) = \frac{\sqrt{{(1 + c^{2})}^{2} + 4 c (1 - c^{2}) \sin 3 θ} - (1 + c^{2})}{2 (1 - c) \sin 3 θ}$ ,

(22)

式中 $c = M_{e} / M_{c}$ 为形状系数； $M_{e}$ 和 $M_{c}$ 分别为三轴拉伸与压缩条件下极限应力比的比值。模型中塑性模量 $K_{p}$ 为

$K_{p} = h G e^{n ψ} [\frac{M_{c} g (θ) e^{- n ψ}}{η} - 1]$ ,

(23)

式中, $M_{c}$ 为临界状态应力比；应力比 $η = q / p$ ； $n$ 为材料常数；Li等^[26]建议 $h$ 取为孔隙比的函数 $h = h_{1} -$ $h_{2} e$ , $h_{1}$ 和 $h_{2}$ 为2个材料常数。

2.4 剪胀方程与塑性势

剪胀方程为塑性体应变率 ${\dot{ε}}_{v}^{p}$ 与广义塑性剪应变率 ${\dot{ε}}_{q}^{p}$ 之比,具体形式为

$d = \frac{{\dot{ε}}_{v}^{p}}{{\dot{ε}}_{q}^{p}} = \frac{d_{0}}{M_{c} g (θ)} [M_{c} g (θ) e^{m ψ} - η]$ ,

(24)

式中, $d_{0}$ 和 $m$ 为材料常数。积分可得势函数：

$g = q - \frac{d_{0} M_{c} g (θ) p}{d_{0} - M_{c} g (θ)} [1 - {(\frac{p}{p_{0}})}^{\frac{d_{0}}{M_{c} g (θ)} - 1}]$ ,

(25)

式中, $p_{0}$ 为塑性势面与 $p$ 轴的交点。

2.5 硬化模量

根据式（21）,由一致性条件可得

$\dot{f} = \frac{\partial f}{\partial σ} : \dot{σ} + \frac{\partial f}{\partial Μ} \frac{\partial Μ}{\partial ε_{q}^{p}} {\dot{ε}}_{q}^{p} = 0$ ,

(26)

根据塑性理论^[30]可知

$L = \frac{1}{K_{p}} \frac{\partial f}{\partial σ} : \dot{σ}$ ,

(27)

${\dot{ε}}_{q}^{p} = L \sqrt{\frac{2}{3} {(\frac{\partial g}{\partial σ})}^{'} : {(\frac{\partial g}{\partial σ})}^{'}}$ 。

(28)

式中 $L$ 为塑性指标； ${(\frac{\partial g}{\partial σ})}^{'} = \frac{\partial g}{\partial σ} - \frac{1}{3} tr (\frac{\partial g}{\partial σ})$ 。结合式（23）,（26）,（27）,可得硬化模量 $H_{p}$ 的表达式为

$H_{p} = \frac{\partial Μ}{\partial ε_{q}^{p}} = \frac{h G e^{n ψ} [\frac{M_{c} g (θ) e^{- n ψ}}{η} - 1]}{g (θ) p \sqrt{\frac{2}{3} {(\frac{\partial g}{\partial σ})}^{'} : {(\frac{\partial g}{\partial σ})}^{'}}}$ 。

(29)

2.6 非共轴切线刚度张量

基于小变形假设,总应变率张量 $\dot{ε}$ 可分解为弹性应变率张量 ${\dot{ε}}^{e}$ 、共轴塑性应变率张量 ${\dot{ε}}^{cp}$ 与非共轴塑性应变率张量 ${\dot{ε}}^{np}$ 三者之和：

$\dot{ε} = {\dot{ε}}^{e} + {\dot{ε}}^{cp} + {\dot{ε}}^{np}$ 。

(30)

式（30）中的共轴塑性应变率张量 ${\dot{ε}}^{cp}$ 由传统位势理论确定,而非共轴塑性应变率张量 ${\dot{ε}}^{np}$ 由式（16）确定。结合弹性本构关系可得

$\begin{matrix} \dot{σ} = E : {\dot{ε}}^{e} = E : (\dot{ε} - {\dot{ε}}^{cp} - {\dot{ε}}^{np}) \\ = E : \dot{ε} - L E : \frac{\partial g}{\partial σ} - T Ι_{t} : \dot{σ} \end{matrix}$ 。

(31)

对式（31）移项并利用式（14）可得

$\begin{matrix} \dot{σ} = {(I + T Ι_{t})}^{- 1} : (E : \dot{ε} - L E : \frac{\partial g}{\partial σ}) \\ = (I - \frac{T}{1 + T} Ι_{t}) : (E : \dot{ε} - L E : \frac{\partial g}{\partial σ}) \end{matrix}$ ,

(32)

式中, $I$ 为四阶单位张量。联合式（27）,（32）可得

$L = \frac{\frac{\partial f}{\partial σ} : (I - \frac{T}{1 + T} Ι_{t}) : E : \dot{ε}}{K_{p} + \frac{\partial f}{\partial σ} : (I - \frac{T}{1 + T} Ι_{t}) : E : \frac{\partial g}{\partial σ}}$ 。

(33)

此外,当屈服函数 $f$ 和势函数 $g$ 都可表示为应力不变量的函数时,即 $f = (p, J_{2}, J_{3})$ 和 $g = (p, J_{2}, J_{3})$ ,则经过一些简单的代数运算后可以证明：

$n_{i} : \frac{\partial f}{\partial σ} = n_{i} : \frac{\partial g}{\partial σ} = 0 (i = 1, 2, 3)$ 。

(34)

将式（33）代入式（32）中,并利用式（34）,最终可得非共轴本构关系式：

$\begin{matrix} \dot{σ} = D : \dot{ε} \\ = (E - \frac{E : \frac{\partial g}{\partial σ} \otimes \frac{\partial f}{\partial σ} : E}{K_{p} + \frac{\partial f}{\partial σ} : E : \frac{\partial g}{\partial σ}} - \frac{T}{1 + T} Ι_{t} : E) : \dot{ε} \end{matrix}$ ,

(35)

式中, $D$ 为非共轴模型的切线刚度张量。

根据前述的改进角点理论可知,本文建立的非共轴模型仅在主应力轴旋转加载条件下会计算出非共轴塑性变形,而在主应力方向固定的加载模式中,例如平面应变试验的情况,将不会给出附加的非共轴塑性变形。

3. 模型的数值实现与验证

目前,大多数研究者^[18-21]在非共轴模型的应力更新过程中采用了显式积分技术。与此不同,本文在这一环节采用了一种完全隐式的积分格式,这样不仅克服了显式算法中存在的应力飘逸问题,而且具有二次收敛性的优势,并且其编程实现也相对简单。隐式积分算法在时间步结束时强化屈服面的一致性条件并更新应力及塑性内变量,主要由两个步骤组成：弹性预测与塑性修正。其中塑性修正通常是指利用Newton-Raphson迭代法将超出弹性域的应力拉回至更新后的屈服面的过程。

3.1 弹性预测

在弹性预测步中,假设 $t_{n} ~ t_{n +1}$ 时间步内的应变增量 $Δ ε$ 全部为弹性应变,相关弹性模量与塑性变量保持不变,新的应力按照如下方式进行计算：

$^{tr} σ =^{n} σ + E : Δ ε =^{n} σ +^{tr} σ$ ,

(36)

式中上标“tr”代表试探值；上标“n”代表 $t_{n}$ 时刻的值。将试探应力带入屈服函数中,若 $f$ ≤ $0$ ,则试探应力即为最终应力；若 $f > 0$ ,则需进行塑性修正。

3.2 塑性修正

将式（31）改写为增量形式：

$Δ^{n + 1} σ = Δ^{tr} σ - L E : \frac{\partial g}{\partial^{n + 1} σ} - T^{n} I_{t} : Δ^{n + 1} σ$ ,

(37)

式中,上标“n+1”代表 $t_{n +1}$ 时刻的值。由式（37）可得

$^{n + 1} σ = {(I + T^{n} I_{t})}^{- 1} : (Δ^{tr} σ -^{n + 1} L E : \frac{\partial g}{\partial^{n + 1} σ}) +^{n} σ$ 。

(38)

结合屈服条件、流动法则和硬化规律,则塑性修正过程可以表示为求解如下的一组非线性方程（为便于表示,将 $t_{n +1}$ 时刻变量的上标“n+1”隐去）：

$R = {\begin{array}{l} σ - {(I + T^{n} I_{t})}^{- 1} : (Δ^{tr} σ - L E : \frac{\partial g}{\partial σ}) -^{n} σ = 0 \\ M -^{n} M -^{n} H_{p} Δ ε_{q}^{p} = 0 \\ Δ ε_{q}^{p} - L \sqrt{\frac{2}{3} {(\frac{\partial g}{\partial σ})}^{'} : {(\frac{\partial g}{\partial σ})}^{'}} = 0 \\ f = q - M g (θ) p = 0 \end{array}$ ,

(39)

式中, $R$ 为残余矢量。方程组式（39）中的未知量为 $σ$ , $M$ , $L$ , $Δ ε_{q}^{p}$ 。将应力与相关塑性变量的迭代初始值分别设为σ=(I+TⁿI_t)^-1:Δ^trσ+ⁿσ,M=ⁿM,L=0, $Δ ε_{q}^{p} = 0$ ,利用Newton-Raphson迭代法求解即可得到 $t_{n +1}$ 时刻的应力与塑性变量。

3.3 一致性刚度张量

在有限元仿真分析中,通常采用一致性刚度张量 $D^{con}$ 替代切线刚度张量 $D$ 。一致性刚度张量的定义式如下：

$D^{con} = \frac{\partial Δ σ}{\partial Δ ε}$ ,

(40)

注意到σ=Δσ+ⁿσ,因此式（40）又可表示为

$D^{con} = \frac{\partial Δ σ}{\partial Δ ε}$ 。

(（(41))

将式（39）对应变增量 $Δ ε$ 取微分可得

$\frac{\partial Δ σ}{\partial Δ ε} = \bar{E} - \bar{E} : \frac{\partial g}{\partial σ} \otimes \frac{\partial L}{\partial Δ ε} - L \bar{E} : \frac{\partial^{2} g}{\partial σ^{2}} : \frac{\partial σ}{\partial Δ ε}$ ,

(42a)

$\frac{\partial M}{\partial Δ ε} - H_{p} \frac{\partial Δ ε_{q}^{p}}{\partial Δ ε} = 0$ ,

(42b)

$\frac{\partial Δ ε_{q}^{p}}{\partial Δ ε} - \frac{\partial L}{\partial Δ ε} r - L \frac{\partial r}{\partial σ} : \frac{\partial σ}{\partial Δ ε} = 0$ ,

(42c)

$\frac{\partial f}{\partial σ} : \frac{\partial σ}{\partial Δ ε} + \frac{\partial f}{\partial M} \frac{\partial M}{\partial Δ ε} = 0$ 。

(42d)

式中 $\bar{E} = {(I + T Ι_{t})}^{- 1} : E$ ； $r = \sqrt{\frac{2}{3} {(\frac{\partial g}{\partial σ})}^{'} : {(\frac{\partial g}{\partial σ})}^{'}}$ 。需注意的是,在式（42a）～（42d）中, $\bar{E}$ 和 $H_{p}$ 使用 $t_{n}$ 时刻的值计算而其他变量使用 $t_{n +1}$ 时刻的收敛值计算。联立式（45a）～（45d）可得

$D^{con} = \frac{\partial Δ σ}{\partial Δ ε} = E^{*} - \frac{E^{*} : \frac{\partial g}{\partial σ} \otimes C : E^{*}}{K_{p} + C : E^{*} : \frac{\partial g}{\partial σ}}$ ,

(43a)

$E^{*} = {(I + L \bar{E} : \frac{\partial^{2} g}{\partial σ^{2}})}^{- 1} : \bar{E}$ ,

(43b)

$C = \frac{\partial f}{\partial σ} + H_{p} L \frac{\partial f}{\partial Μ} \frac{\partial r}{\partial σ}$ 。

(43c)

比较式（43a）,（35）可知, $D^{con}$ 与 $D$ 的表达式并不相同。原因是式（43a）表示的一致性刚度张量 $D^{con}$ 是在进行增量运算并更新应力及塑性变量后取微分所得,而常规的切线刚度张量 $D$ 则是首先进行微分运算所得,然后进行增量运算更新应力及塑性变量。

3.4 积分方案的验证

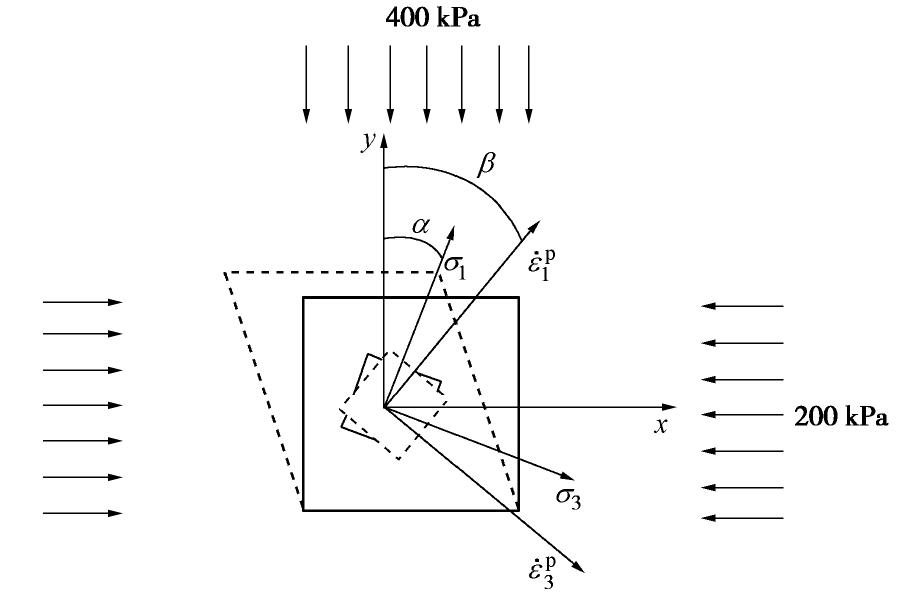
以ABAQUS软件为平台,利用Fortran语言编写了模型的UMAT子程,将模型嵌入进了ABAQUS材料库中。通过模拟砂的单剪试验来验证算法的精确性和稳定性。试验模型如图2所示,材料假设为Toyoura砂,其平均粒径为0.24 mm,颗粒相对质量密度为2.64,最大和最小孔隙比分别为 $e_{\max} = 0.97$ 和 $e_{\min} =$ $0.63$ 。有限元单元类型选择四边形等参单元,模型尺寸为10 cm×10 cm,竖向压力为 $σ_{y}$ =400 kPa,静止侧压力系数为 $K_{0}$ =0.5,假设初始孔隙比 $e_{0}$ =0.88。模型参数取自文献[26],弹性参数 $G_{0} = 125$ , $ν = 0.05$ ,临界状态参数 $c = 0.75$ , $M_{cs} = 1.25$ , $e_{Γ} = 0.934$ , $λ = 0.019$ , $ξ = 0.7$ ,硬化参数 $n = 1.1$ , $h_{1} = 3.15$ , $h_{2} = 3.05$ 。

图 2 单剪试验中的主应力方向和塑性应变率方向

Figure 2. Directions of principal stress and plastic strain rate in simple shear tests

下载: 全尺寸图片幻灯片

剪切过程中保持竖向压力不变,施加20%的剪应变,总的加载步数设为500。加载过程中研究主应力方向偏转角 $α$ ,主塑性应变率方向偏转角 $β$ ,如图2所示,其中 $α$ 与 $β$ 的定义分别为

$\tan 2 α = \frac{2 τ_{x y}}{σ_{y} - σ_{x}}$ ,

(44a)

$\tan 2 β = \frac{2 {\dot{ε}}_{x y}^{p}}{{\dot{ε}}_{y}^{p} - {\dot{ε}}_{x}^{p}}$ 。

(44b)

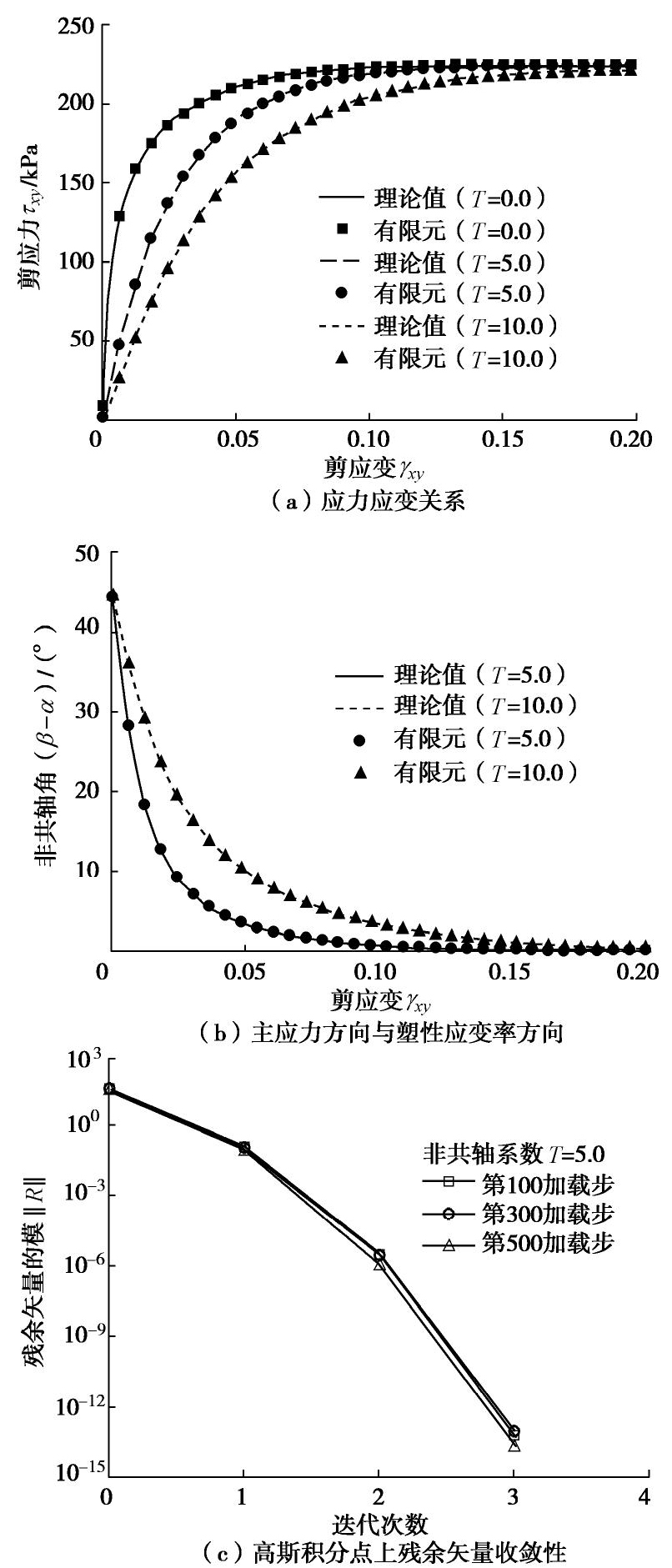
式中 $σ_{x}$ 为水平向应力； $τ_{x y}$ 为剪应力； ${\dot{ε}}_{x}^{p}$ 和 ${\dot{ε}}_{y}^{p}$ 分别为水平与竖直向塑性应变率； ${\dot{ε}}_{x y}^{p}$ 为塑性剪应变率。

图3展示了当非共轴系数取不同值时,采用有限元方法预测值与理论值的比较。图3（a）,（b）表明,当非共轴系数取不同值时,有限元方法预测的应力应变关系曲线和非共轴角的变化曲线都与点积分结果完全重合；图3（c）展示了单元高斯积分点处的残余矢量的收敛历史,可以清楚地发现发展的隐式积分算法具有二次收敛速度。因此,模拟结果证明构建的隐式积分方案具有良好的稳定性和精确性。

图 3 有限元预测值与理论值比较

Figure 3. Comparison between predicted values of finite element method and theoretical results

下载: 全尺寸图片幻灯片

4. 模型的工程应用

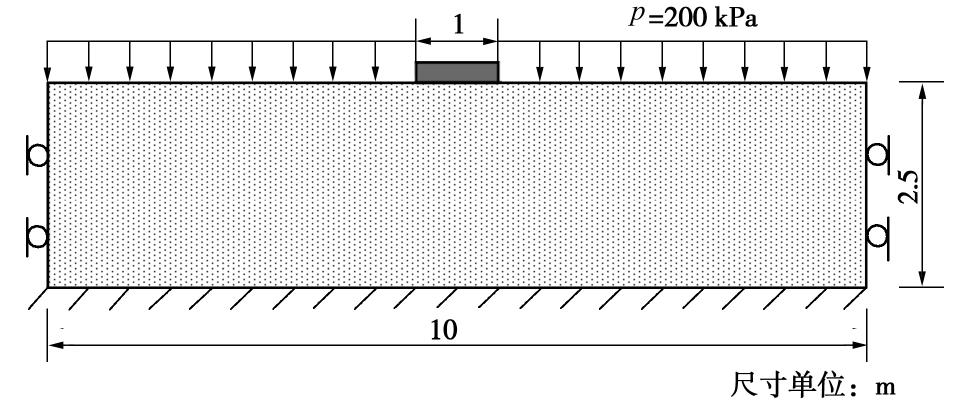
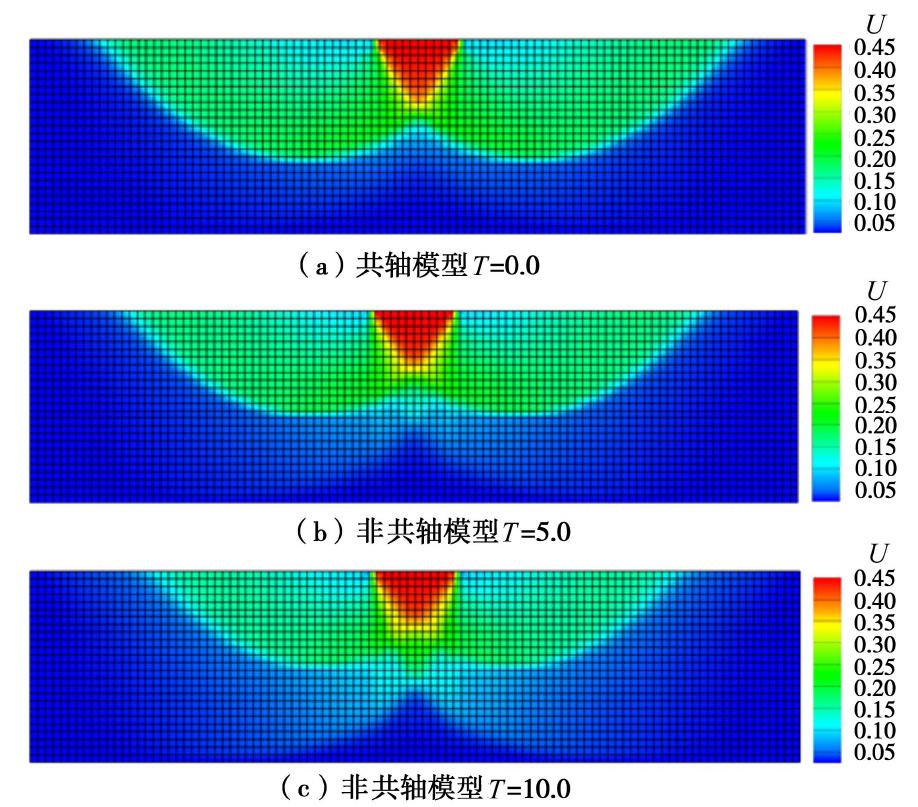
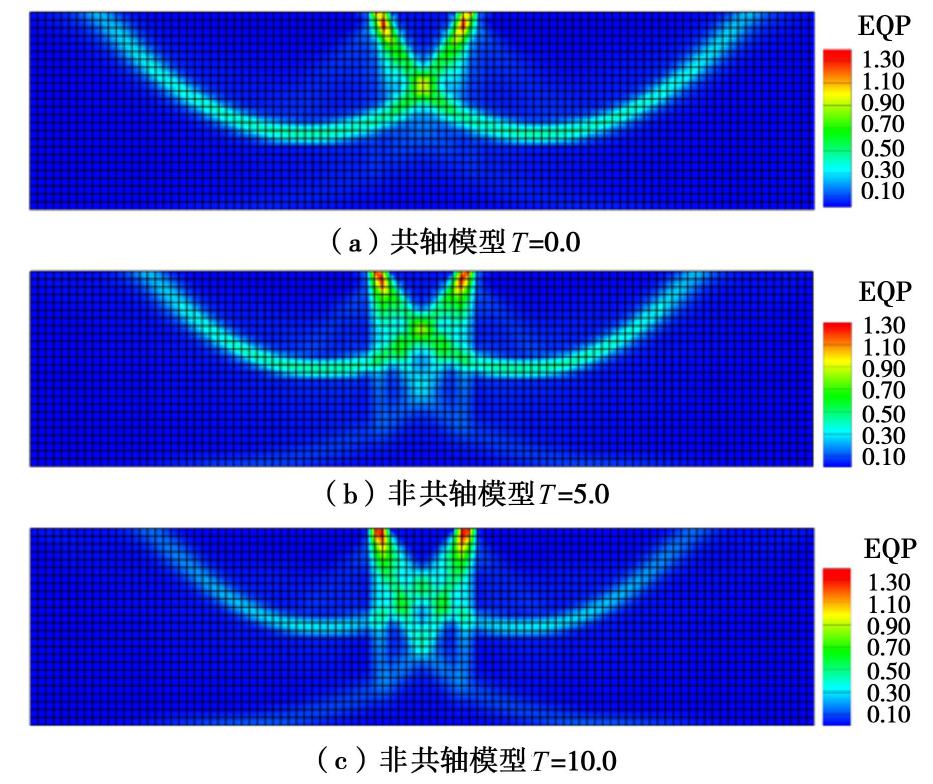
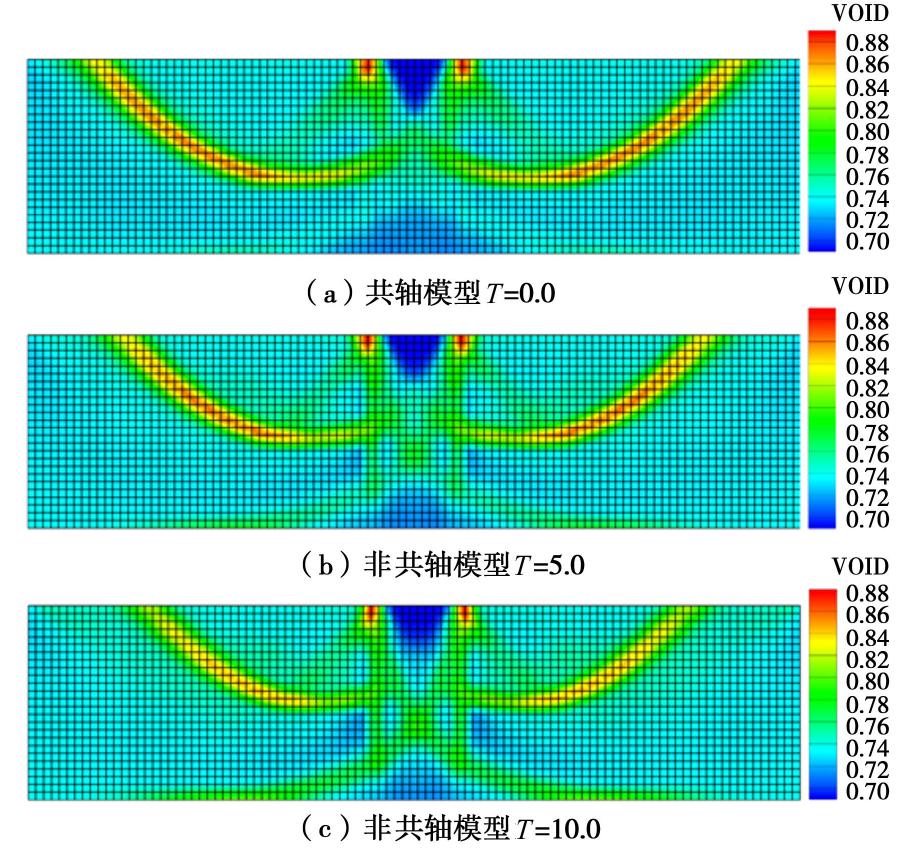
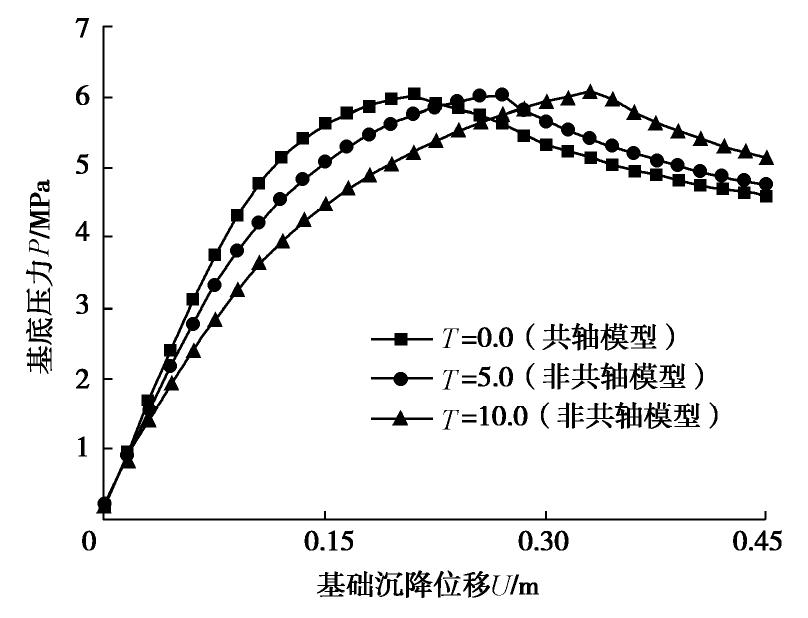
这里通过一个条形基础承载力问题的模拟来简要分析非共轴因素对预测结果的影响。地基模型如图4所示,地基宽为10 m,深为2.5 m,顶部条形基础宽为1 m,假设为完全粗糙的刚性基础。地基模型共划分为2500个单元,单元类型为四边形等参单元。加载开始前,在模型顶部施加一个200 kPa的均布压力,然后对刚性基础施加0.45 m向下的位移荷载。加载过程中固定底部边界的水平与竖直方向位移及两侧边界的水平方向位移。地基材料假设为标准Toyoura砂,并假设地基中的孔隙比 $e_{0} = 0.76$ 且均匀分布,为简化计算,忽略重力影响。非共轴系数 $T$ 分别取0.0,5.0,10.0三个值,以研究其大小对计算结果的影响。

图 4 地基承载力问题计算模型

Figure 4. Schematic diagram of bearing capacity of strip foundation

下载: 全尺寸图片幻灯片

图5给出了最终总位移云图。比较图5（a）～（c）可知,在不同非共轴系数的情况下,条形基础下方均形成了明显的刚性核（图中红色区域）和界限明显的滑动区（图中绿色区域）；随非共轴系数的增加,滑动区域的面积呈现出减小的趋势。图6显示了最终的广义塑性剪应变云图。对比图6（a）～6（c）可以发现,加载结束时,3种非共轴系数条件下均出现了明显的剪切带,其从基础下部向两侧延伸,表现出对数螺旋线的形式；随着非共轴系数增加,剪切带与地基表面的交点逐渐向中间靠拢。图7给出了不同非共轴系数下的孔隙比分布云图。比较图7,6可以看出,剪切带内部的砂土发生了明显的剪胀变形,而条形基础底部的砂土产生了显著剪缩；当非共轴系数逐渐增加时,条形基础下方逐渐显现出两条交叉的次生剪切带,向地基底部延伸。图8为预测的基底压力与沉降位移关系曲线。由图8可知,在加载前期阶段,非共轴模型预测的基底压力小于共轴模型的预测值,且随着非共轴系数的增加,差异也更加明显；不同非共轴系数下预测的峰值压力分别为6040 kPa（ $T = 0.0$ ）,6033 kPa（ $T = 5.0$ ）,6073 kPa（ $T = 10.0$ ）,与峰值压力相对应的沉降位移分别为0.21 m（ $T = 0.0$ ）,0.27 m（ $T = 5.0$ ）,0.33 m（ $T = 10.0$ ）。峰值压力大小基本一致,但峰值压力对应的沉降位移随非共轴系数增加而显著增加。因此考虑非共轴塑性因素基本不影响峰值基础压力的大小,但会延缓峰值基础压力的出现。

图 5 最终的总位移云图

Figure 5. Contours of final total displacement

下载: 全尺寸图片幻灯片

图 6 最终的广义塑性剪应变云图

Figure 6. Contours of final generalized plastic shear strain

下载: 全尺寸图片幻灯片

图 7 最终的孔隙比云图

Figure 7. Contours of final void ratio

下载: 全尺寸图片幻灯片

图 8 基底压力与基础沉降位移关系曲线

Figure 8. Curves of average pressure versus vertical displacement of strip foundation

下载: 全尺寸图片幻灯片

图5～8表明,非共轴塑性的引入会影响最终预测的滑动区范围、剪切带形态和孔隙比的分布,软化基础压力-基础沉降位移曲线,非共轴系数越大,对预测结果的影响也更加显著；整体上,考虑非共轴塑性将使得地基模型的整体刚度下降,进而表现出更加软化的力学响应。因此,在地基承载力问题的模拟中忽略了非共轴塑性的影响,有可能高估地基刚度,导致工程设计偏于危险。

5. 结论

（1）基于定义的切线方向张量重新定义了切线应力率的概念,进而提出了一种改进角点理论。进一步地将该理论加入到了砂土状态相关剪胀模型中,从而建立了一个新的砂土非共轴模型。模型仅在主应力方向改变的加载条件下会计算出非共轴塑性变形,克服了传统角点类模型的不足。

（2）首次将隐式积分算法应用到了角点类非共轴模型中。推导了与模型积分相关的公式并给出了相应的一致性切线刚度张量。单剪试验的有限元模拟表明了算法具有良好的精确性和稳定性。

（3）分析了条形基础的承载力问题,模型的预测结果表明,非共轴塑性的引入将导致地基模型的整体刚度下降,进而表现出更加软化的力学响应。假如忽略了非共轴塑性的影响,有可能导致工程设计偏于危险。

图 1 笛卡尔坐标系示意图

Figure 1. Diagram of Cartesian coordinate system

下载: 全尺寸图片幻灯片

图 2 单剪试验中的主应力方向和塑性应变率方向

Figure 2. Directions of principal stress and plastic strain rate in simple shear tests

下载: 全尺寸图片幻灯片

图 3 有限元预测值与理论值比较

Figure 3. Comparison between predicted values of finite element method and theoretical results

下载: 全尺寸图片幻灯片

图 4 地基承载力问题计算模型

Figure 4. Schematic diagram of bearing capacity of strip foundation

下载: 全尺寸图片幻灯片

图 5 最终的总位移云图

Figure 5. Contours of final total displacement

下载: 全尺寸图片幻灯片

图 6 最终的广义塑性剪应变云图

Figure 6. Contours of final generalized plastic shear strain

下载: 全尺寸图片幻灯片

图 7 最终的孔隙比云图

Figure 7. Contours of final void ratio

下载: 全尺寸图片幻灯片

图 8 基底压力与基础沉降位移关系曲线

Figure 8. Curves of average pressure versus vertical displacement of strip foundation

下载: 全尺寸图片幻灯片

参考文献(30)

[1]	郑颖人, 孔亮. 岩土塑性力学[M]. 2版. 北京: 中国建筑工业出版社, 2020. ZHENG Ying-ren, KONG Liang. Geotechnical Plastic Mechanics[M]. 2nd ed. Beijing: China Architecture and Building Press, 2020. (in Chinese)
[2]	王兴, 孔亮, 李学丰. 砂土非共轴本构模型及其在地基承载力方面的应用[J]. 岩土工程学报, 2020, 42(5): 893-899. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202005016.htm WANG Xing, KONG Liang, LI Xue-feng. Three-dimensional non-coaxial constitutive model for sand and its application in bearing capacity of foundation[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(5): 893-899. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202005016.htm
[3]	TIAN Y, YAO Y P. Constitutive modeling of principal stress rotation by considering inherent and induced anisotropy of soils[J]. Acta Geotechnica, 2018, 13(6): 1299-1311. doi: 10.1007/s11440-018-0680-3
[4]	RUDNICKI J W, RICE J R. Conditions for the localization of deformation in pressure-sensitive dilatant materials[J]. Journal of the Mechanics and Physics of Solids, 1975, 23(6): 371-394. doi: 10.1016/0022-5096(75)90001-0
[5]	HASHIGUCHI K. The tangential plasticity[J]. Metals and Materials, 1998, 4(4): 652-656. doi: 10.1007/BF03026374
[6]	HASHIGUCHI K, TSUTSUMI S. Elastoplastic constitutive equation with tangential stress rate effect[J]. International Journal of Plasticity, 2001, 17(1): 117-145. doi: 10.1016/S0749-6419(00)00021-8
[7]	HASHIGUCHI K, TSUTSUMI S. Shear band formation analysis in soils by the subloading surface model with tangential stress rate effect[J]. International Journal of Plasticity, 2003, 19(10): 1651-1677. doi: 10.1016/S0749-6419(02)00113-4
[8]	田雨, 姚仰平, 罗汀. 从各向异性的角度解释和模拟土的非共轴特性[J]. 岩土力学, 2018, 39(6): 2035-2042. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201806015.htm TIAN Yu, YAO Yang-ping, LUO Ting. Explanation and modeling of non-coaxiality of soils from anisotropy[J]. Rock and Soil Mechanics, 2018, 39(6): 2035-2042. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201806015.htm
[9]	钱建固, 黄茂松, 杨峻. 真三维应力状态下土体应变局部化的非共轴[J]. 岩土工程学报, 2006, 28(4): 511-515. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200604015.htm QIAN Jian-gu, HUANG Mao-song, YANG Jun. Effect of non-coaxial plasticity on onset strain localization in soils under 3D stress condition[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(4): 511-515. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200604015.htm
[10]	钱建固, 黄茂松. 复杂应力状态下岩土体的非共轴塑性流动理论[J]. 岩石力学与工程学报, 2006, 25(6): 1260-1264. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200606029.htm QIAN Jian-gu, HUANG Mao-song. Non-coaxial plastic flow theory in multi-dimensional stress state[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(6): 1260-1264. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200606029.htm
[11]	YANG Y, YU H S. Numerical aspects of non-coaxial model implementations[J]. Computers and Geotechnics, 2010, 37(1/2): 93-102.
[12]	YANG Y, YU H S. Application of a non-coaxial soil model in shallow foundations[J]. Geomechanics and Geoengineering: An International Journal, 2006, 1(2): 139-150. doi: 10.1080/17486020600777101
[13]	YANG Y, YU H S. A non-coaxial critical state soil model and its application to simple shear simulations[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(13): 1369-1390. doi: 10.1002/nag.531
[14]	李学丰, 黄茂松, 钱建固. 宏-细观结合的砂土单剪试验非共轴特性分析[J]. 岩土力学, 2013, 34(12): 3418-3424. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201312012.htm LI Xue-feng, HUANG Mao-song, QIAN Jian-gu. Analysis of non-coaxial characters of sand for simple shear test with the method of macro-meso-incorporation[J]. Rock and Soil Mechanics, 2013, 34(12): 3418-3424. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201312012.htm
[15]	扈萍, 黄茂松, 钱建固. 砂土非共轴特性的本构模拟[J]. 岩土工程学报, 2009, 31(5): 793-798. doi: 10.3321/j.issn:1000-4548.2009.05.025 HU Ping, HUANG Mao-song, QIAN Jian-gu. Non-coaxial plasticity constitutive modeling of sands[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(5): 793-798. (in Chinese) doi: 10.3321/j.issn:1000-4548.2009.05.025
[16]	陈洲泉, 黄茂松. 砂土各向异性与非共轴特性的本构模拟[J]. 岩土工程学报, 2018, 40(2): 243-251. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201802005.htm CHEN Zhou-quan, HUANG Mao-song. Constitutive modeling of anisotropic and non-coaxial behaviors of sand[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(2): 243-251. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201802005.htm
[17]	CHEN Z, HUANG M. Non-coaxial behavior modeling of sands subjected to principal stress rotation[J]. Acta Geotechnica, 2019: 15(3): 655-669.
[18]	YANG Y, OOI J, ROTTER M, et al. Numerical analysis of silo behavior using non-coaxial models[J]. Chemical Engineering Science, 2011, 66(8): 1715-1727. doi: 10.1016/j.ces.2011.01.012
[19]	YANG Y, YU H S, KONG L. Implicit and explicit procedures for the yield vertex non-coaxial theory[J]. Computers and Geotechnics, 2011, 38(5): 751-755.
[20]	YUAN R, YU H S, HU N, et al. Non-coaxial soil model with an anisotropic yield criterion and its application to the analysis of strip footing problems[J]. Computers and Geotechnics, 2018, 99: 80-92.
[21]	袁冉, 杨文波, 余海岁, 等. 土体非共轴各向异性对城市浅埋土质隧道诱发地表沉降的影响[J]. 岩土工程学报, 2018, 40(4): 673-680. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201804017.htm YUAN Ran, YANG Wen-bo, YU Hai-sui, et al. Effects of non-coaxiality and soil anisotropy on tunneling-induced subsurface settlements[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(4): 673-680. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201804017.htm
[22]	蔡正银, 李相菘. 砂土的剪胀理论及其本构模型的发展[J]. 岩土工程学报, 2007, 29(8): 13-19. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200708004.htm CAI Zheng-yin, LI Xiang-song. Development of dilatancy theory and constitutive model of sand[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(8): 13-19. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200708004.htm
[23]	姚仰平, 刘林, 罗汀. 砂土的UH模型[J]. 岩土工程学报[J]. 2016, 38(12): 2147-2153. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201612004.htm YAO Yang-ping, LIU Lin, LUO Ting. UH model for sands[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(12): 2147-2153. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201612004.htm
[24]	SLOAN S W. Substepping schemes for the numerical integration of elastoplastic stress-strain relations[J]. International Journal for Numerical Methods in Engineering, 1987, 24(5): 893-911.
[25]	SIMO J C, TAYLOR R L. Consistent tangent operators for rate-independent elastoplasticity[J]. Computer Methods in Applied Mechanics and Engineering, 1985, 48(1): 101-118.
[26]	LI X S, DAFALIAS Y F. Dilatancy for cohesionless soils[J]. Géotechnique, 2000, 50(4): 449-460.
[27]	姚仰平, 路德春, 周安楠. 岩土类材料的变换应力空间及其应用[J]. 岩土工程学报, 2005, 27(1): 24-29. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200501002.htm YAO Yang-ping, LU De-chun, ZHOU An-nan. Transformed stress space for geomaterials and its application[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(1): 24-29. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200501002.htm
[28]	孔亮, 李学丰, 赵占兵. 土体热力学本构模型的改进、验证及有限元分析[J]. 岩土工程学报, 2009, 31(10): 121-127. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200910026.htm KONG Liang, LI Xue-feng, ZHAO Zhan-bing. Improvement, verification and FEM analysis of thermomechanical model for soil[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(10): 24-29. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200910026.htm
[29]	LI X S, DAFALIAS Y F. Constitutive modeling of inherently anisotropic sand behavior[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(10): 868-880.
[30]	DAFALIAS Y F. An anisotropic critical state soil plasticity model[J]. Mechanics Research Communications, 1986, 13(6): 341-347.

施引文献(3)

期刊类型引用(3)

1.	常江芳，王伟，牛庆合，闻磊. 非共轴特性对岩土材料应变局部化行为影响的数值研究. 科学技术与工程. 2023(03): 1176-1184 . 百度学术
2.	孔亮，王兴，李学丰. 非共轴次加载面模型及其对地基承载特性的模拟. 岩石力学与工程学报. 2021(12): 2535-2544 . 百度学术
3.	王兴，孔亮，李学丰. 基于应力率正交分解的广义非共轴理论. 岩土工程学报. 2021(12): 2180-2189 . 本站查看