基于响应面法的盾构施工膨润土改良参数优化

徐征杰; 郭晓阳

doi:10.11779/CJGE202101023

基于响应面法的盾构施工膨润土改良参数优化 English Version

徐征杰,
郭晓阳^,

上海隧道工程有限公司,上海　200032

详细信息

作者简介:
徐征杰(1982— ),男,硕士,高级工程师,主要从事地下工程施工方面的技术研究工作。E-mail: bepatient@163.com

通讯作者:
郭晓阳, E-mail: 651402719@qq.com

中图分类号: TU411;U455
计量
- 文章访问数: 292
- HTML全文浏览量: 19
- PDF下载量: 123
出版历程
- 收稿日期: 2020-05-01
- 网络出版日期: 2022-12-04
- 刊出日期: 2020-12-31

Optimization of bentonite parameters for shield tunneling based on response surface method

XU Zheng-jie,
GUO Xiao-yang^,

Shanghai Tunnel Engineering Co., Ltd., Shanghai 200032, China

摘要

摘要: 为确定福州地铁4号线金牛山—工业路盾构区间强风化花岗岩地层中的膨润土改良最优参数,分别选择膨润土泥浆浓度、掺入比和盾构推进速度3个影响因素,以渣土塌落度、渗透系数和改良成本为响应值。采用中心复合试验设计方法进行了20组试验,分别构建了各响应值的响应面函数。试验结果表明,膨润土泥浆浓度、掺入比和盾构推进速度对渣土改良效果均有较大影响,且各因素之间存在显著交互作用。利用响应面-满意度函数,将渣土改良的3个响应值优化问题转化为单一响应值优化,获得强风化花岗岩地层在不同盾构推进速度下的最优改良参数。该方法科学合理,为金牛山—工业路盾构区间在强风化花岗岩内的高效施工提供了技术保障。
- 土压平衡盾构 /
- 渣土改良 /
- 膨润土 /
- 多目标优化 /
- 响应面
Abstract: In order to determine the optimal parameters of bentonite improvement in the strongly weathered granite strata in Jinniu Mountain-Gongye Road shield interval of Fuzhou metro line 4, the concentration and mixing ratio of bentonite slurry and advancing speed of shield are selected as the three factors, and the slump, permeability and improvement cost of soils are taken as the response values. The central composite design (CCD) method is used to carry out 20 groups of tests, and the response surface functions of each response value are constructed respectively. The results show the concentration and mixing ratio of bentonite slurry and advancing speed of shield all have great influences on the improvement effect of soils, and there is a significant interaction among these factors. By using the response surface-satisfaction function, the optimization problem of three response values for soil improvement is transformed into that of a single response value, and the optimal improvement parameters of the strongly weathered granite strata under different advancing speeds of shield tunneling are obtained. The proposed method is scientific and reasonable, which provides a technical guarantee for the efficient construction of Jinniu Mountain-Gongye Road shield interval in the strongly weathered granite strata.
- EPB shield /
- soil improvement /
- bentonite /
- multi-objective optimization /
- response surface

HTML全文

0. 引言

土压平衡式盾构通过密闭土仓内的渣土平衡开挖面,学者们普遍认为,土仓内渣土应该具有良好的流塑性、较低的渗透性和较小的内摩擦角等特征^[1]。渣土性能不良可能会带来刀具磨损、刀盘结泥饼、螺旋输送机口堵塞和喷涌等问题,给工程施工造成极大的困难^[2]。因此,必须要进行土体改良。

膨润土改良技术广泛应用于砂砾层、卵石层、砂层和风化岩层等地层。Tang等^[3]、Barzegari等^[4]、Huang等^[5]、姜厚停等^[6]针对砂砾石地层,利用RUB隧道掘进模拟试验、土壤磨损试验及剪切试验以及现场掘进试验等方法进行研究,认为膨润土泥浆能有效改变土的力学性能,降低刀具磨损,并针对该地层得到了合理的改良参数。张润来等^[7]针对砂卵石地层采用膨润土改良,进行室内塌落度试验、搅拌试验、泥浆黏度试验和剪切试验确定了适宜的改良参数。Ding等^[8]、Wang等^[9]针对高水压条件下的中粒砂层,通过塌落度试验和渗透试验分析了不同注入率时的膨润土改良效果,并将试验结果应用于盾构施工中。

现有文献中得到的膨润土方案是针对特定土层,适用于强风化花岗岩的研究还较少。其次,膨润土改良效果受盾构推进速度影响较大,但该方面尚缺少相应的研究方法和结论。

本文依托福州4号线金牛山—工业路盾构区间强风化花岗岩地层,将响应曲面法引入膨润土改良施工参数的优化分析。探讨了膨润土泥浆掺入比、浓度和盾构推进速度对渣土性能的影响规律,明确了不同盾构推进速度下的最优膨润土改良方案。

1. 工程背景

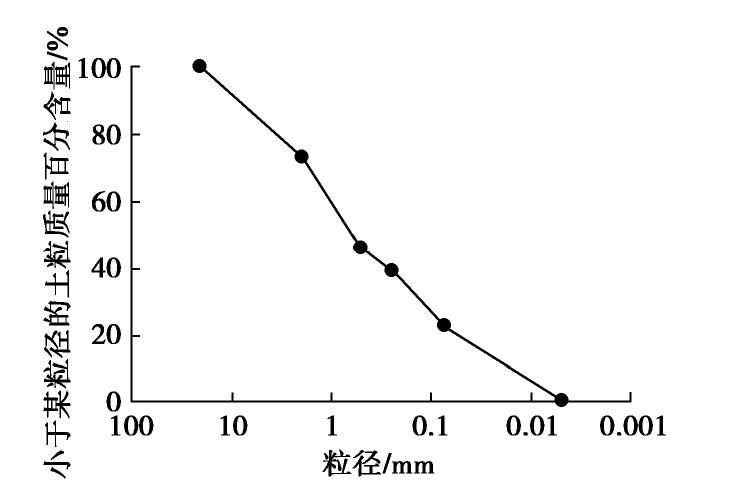
福州地铁4号线金牛山—工业路盾构区间全长约900 m,隧道埋深在14～25 m。区间主要穿越地层为<7-1>强风化花岗岩。天然的强风化花岗岩标准贯入试验锤击数为65,呈灰黄色,含大量中粗粒石英颗粒、白云母片及长石,风化强烈,岩芯多呈砂土状,平均石英砾粒33.22%,遇水易软化、崩解,粒径级配曲线见图1。

图 1 粒径级配曲线

Figure 1. Grain-size distribution curve

下载: 全尺寸图片幻灯片

由于区间隧道靠近闽江,地层含水率达30%,对改良渣土的抗渗性能要求较高。土压平衡盾构在富水岩层中掘进时常用气压辅助模式,这要求开挖渣土具有良好的稳定性和气密性。由于天然的强风化花岗岩地层表现出强烈的崩解性和离析性,难以满足气压辅助模式的要求,因此选择膨润土泥浆作为改良剂。

2. 试验方案

2.1 试验材料

试验土取自福州4号线金牛山站基坑底部强风化花岗岩地层,将所取土加水至与隧道区间地层含水率一致,取样过程及试验土样见图2。试验用钠基膨润土来自漳州华欣,基本性质如表1所示。

图 2 土样制备

Figure 2. Preparation of soil samples

下载: 全尺寸图片幻灯片

表 1 膨润土基本性质表

Table 1. Basic properties of bentonite

吸蓝量/(g·100g^-1)	胶质价/(mL·15g^-1)	膨胀倍数/(mL·g^-1)	pH值	细度（200目）
32	400	20	8.0~9.5	95

下载: 导出CSV

| 显示表格

2.2 盾构机土舱相似模型

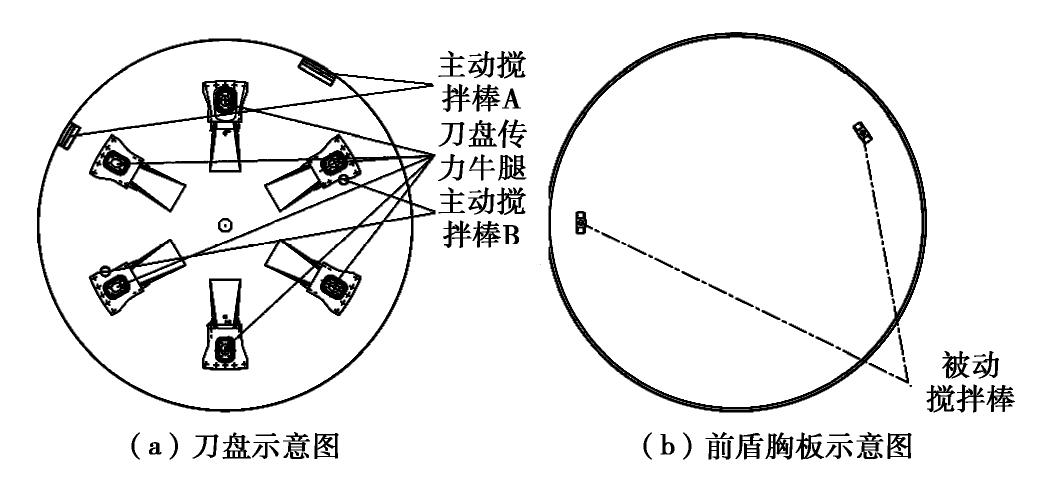
为探究推进速度对渣土性能的影响,以福州4号线金牛山—工业路区间盾构机土舱（见图3）为背景,按1∶15的缩尺比例制作盾构机土舱相似模型如图4所示。模型主要包括搅拌箱体、主动搅拌棒A、主动搅拌棒B和被动搅拌棒。

图 3 盾构机土舱示意图

Figure 3. Schematic diagram of earth chamber of shield machine

下载: 全尺寸图片幻灯片

图 4 盾构机土舱相似模型

Figure 4. Similar model for EPB shield chamber

下载: 全尺寸图片幻灯片

当盾构机推进速度变化时,由于土仓大小和刀盘转速固定,渣土从螺旋输送机排出前的刀盘转数也会受到影响：

$n = \frac{l r}{v}$ 。

(1)

式中 n为渣土从进入土舱到被螺旋输送机排出期间的刀盘搅拌转数；l为盾构机土舱长度（cm）；r为刀盘转速（rad/min）；v为推进速度（cm/min）。结合本工程的实际情况,盾构机土舱长度为100 cm,推进过程中刀盘转速为1.2 rad/min。由式（1）得到推进速度（cm/min）影响搅拌转数（rad）的实际关系：

$n = \frac{120}{v}$ 。

(2)

由于推进速度难以通过室内试验直接控制,实际试验通过调整土仓相似模型的刀盘转数模拟盾构机推进速度的变化。

图5为土仓相似模型在相同改良参数下模拟不同推进速度时的改良情况。

图 5 改良效果对比

Figure 5. Comparison of improvement effect

下载: 全尺寸图片幻灯片

显然,当推进速度较高时,搅拌转数较低,渣土与膨润土无法均匀混合,膨润土泥浆只存在于渣土的表面,改良效果因此受到较大影响。由此可得,推进速度是影响渣土改良效果的重要因素之一。

2.3 响应变量及评价指标

试验选取塌落度和渗透系数作为响应变量。采用标准塌落度桶测定渣土的塌落度值。根据Budach等^[10]的研究,渣土塌落度在100～200 mm以内为宜。由于改良后的渣土已不再属于砂质土,故选用《土工试验规程：SL237—1999》^[11]中的变水头渗透试验法测定渣土的渗透系数。根据瞬时达西定律计算得到水温为17℃时渣土的渗透系数：

$K_{17} = \frac{2.3 a l}{A Δ t} \times \lg \frac{h_{1}}{h_{2}}$ 。

(3)

式中 K₁₇为水温为17℃时试样的渗透系数（cm/s）；2.3为ln和lg的变换因数；a为变水头管的断面面积（cm²）；l为试样高度（cm）；A为试验截面积（cm²）；Δt为测读水头的起始到终止时间段（s）；h₁和h₂为起始和终止水头（cm）。由于强风化花岗岩中石英含量较高,刀盘切削过程中会产生大量热量,使土中水温度升高,利用式（4）将K₁₇转化为40℃时的渗透系数K₄₀：

$K_{40} = K_{17} \frac{η_{17}}{η_{40}}$ ,

(4)

式中,η₁₇,η₄₀为17℃和40℃时水的动力黏滞系数（KPa·s）,K₄₀为水温40℃时试样的渗透系数。

为控制喷涌的发生,朱伟等^[12]推导得到了渣土临界渗透系数的表达式：

$K = \frac{Q L_{1} A_{2} - Q L_{2} A_{1}}{A_{1} A_{2} (H_{1} - H_{2})}$ 。

(5)

式中 H₁,H₂分别为开挖面中心和螺旋输送机出口的水头；Q为螺旋输送机出口处渗流量；L₁,L₂分别为土舱和螺旋输送机长度；A₁,A₂分别为土舱和螺旋输送机的截面积；K为渣土临界渗透系数。工程取出螺旋输送机出口的水头为0,渗水量为0.3 cm³/s,开挖面中心水头为20.4 m,代入式（5）得到渗透系数的临界值lgK=-4.45。但由于地下工程的复杂性,可以认为渣土渗透系数处于10^-4.45～10^-5.45cm/s时仍存在喷涌的风险。

2.4 中心复合试验设计与试验结果

选取膨润土泥浆浓度（m_p/m_n）、掺入比（V_n/V_s）和盾构机推进速度3个对渣土性能影响比较大的因素,以三因素五水平（-1.682,-1.000,0,1.000,1.682）的中心复合试验表安排试验,所得结果汇总入表2中。试样的塌落度变化范围为8～231 mm,lgK₄₀变化范围为-4.57～-5.64。该结果可用于寻找膨润土改良施工参数的最优值。

表 2 中心复合试验结果表

Table 2. Results of central composite tests

运行序	浓度/%	掺入比/%	推进速度/(cm·min^-1)	塌落度/mm	lgK₄₀
1	5	15	3.5	35	-4.83
2	8	8	2.5	8	-5.11
3	5	15	1.5	113	-4.89
4	11	35	1.5	140	-5.64
5	8	25	2.5	122	-4.98
6	11	15	1.5	56	-5.41
7	5	35	1.5	231	-4.68
8	5	35	3.5	201	-4.72
9	8	25	4.2	153	-4.60
10	8	25	2.5	147	-4.96
11	3	25	2.5	183	-4.57
12	8	25	2.5	151	-4.93
13	8	42	2.5	191	-5.17
14	13	25	2.5	106	-5.42
15	8	25	2.5	138	-5.04
16	11	15	3.5	30	-5.14
17	8	25	0.8	171	-5.01
18	8	25	2.5	147	-5.00
19	11	35	3.5	155	-5.39
20	8	25	2.5	141	-4.98

下载: 导出CSV

| 显示表格

3. 响应模型的建立

为寻找渣土塌落度和渗透系数与各因子间的定量规律,找出最佳的膨润土改良参数,采用二次多项式逐步回归-后退法,将 $α$ 值设为0.1,应用Design Expert软件对表2试验结果进行拟合并修正后的响应模型为：

$\begin{array}{l} \begin{array}{l} Y_{1} = X^{T} A_{1} X, Y_{2} = X^{T} A_{2} X, X = {(1, X_{1}, X_{2}, X_{3})}^{T}, \\ A_{1} = [\begin{matrix} 62 .2 & - 5 .14 & 7 .31 & - 35 .4 \\ 0.00 & - 0.15 7 & 2 .02 \\ - 0. 180 & 0 .549 \\ sym & 0.00 \end{matrix}], \end{array}} \\ A_{2} = [\begin{matrix} - 4 .99 & - 0.0 358 & 0.0 313 & - 0.0 682 \\ 0.00 & 0 .000149 & 0 .0106 \\ - 8.23 \times 10^{- 4} & 0.00 \\ sym & 0.00 \end{matrix}] 。 \end{array}$

(6)

式中 Y₁和Y₂分别为塌落度和渗透系数的预测响应值；A₁和A₂为计算信息矩阵；X₁为膨润土泥浆浓度（%）；X₂为膨润土泥浆掺入比（%）；X₃为盾构机推进速度（cm/min）。对模型进行方差分析,结果见表4。F值为F检验时的统计量值,P值为大于F值时的概率。P值用于分析对象显著性,P<0.01表示响应模型显著性极强。R²为决定系数,决定系数越接近1,说明模型拟合优度越高。优化后渣土塌落度模型P<0.0001,失拟项P=0.2472,决定系数R²=0.9685；优化后渣土渗透系数模型P<0.0001,失拟项P=0.0186,决定系数R²=0.9257。结果表明模型拟合度较高,可用于本试验的分析和预测。

表 3 回归模型方差分析表

Table 3. Analysis of variance of regression model

预测响应值	变异来源	平方和	均方	F值	P值	备注
Y₁	模型	64180.16	9168.59	52.78	< 0.0001	显著
	X₁	7894.86	7894.86	45.45	< 0.0001
	X₂	47051.44	47051.44	270.88	< 0.0001
	X₃	1629.43	1629.43	9.38	0.0098
	X₁ X₂	709.08	709.08	4.08	0.0662
	X₁ X₃	1178.79	1178.79	6.79	0.0230
	X₂ X₃	965.22	965.22	5.56	0.0362
	X₂²	4751.34	4751.34	27.35	0.0002
	失拟项	1516.83	216.69	1.91	0.2472	不显著
Y₂	模型	1.28	0.21	27.00	< 0.0001	显著
	X₁	1.06	1.06	134.01	< 0.0001
	X₂	0.01	0.01	1.12	0.3102
	X₃	0.02	0.02	2.08	0.1733
	X₁ X₂	0.06	0.06	8.11	0.0137
	X₁ X₃	0.03	0.03	4.13	0.0631
	X₂²	0.10	0.10	12.55	0.0036
	失拟项	0.10	0.01	7.76	0.0186	不显著

下载: 导出CSV

| 显示表格

表 4 响应优化目标范围

Table 4. Target ranges of response optimization

响应	塌落度/cm	lgK₄₀	膨润土单耗/(kg/环)
优化目标	100<Y₁<200,Y₁=150最为理想	-5.45<Y₂<-4.45	320<Y₃<1645

下载: 导出CSV

| 显示表格

4. 结果分析

4.1 塌落度

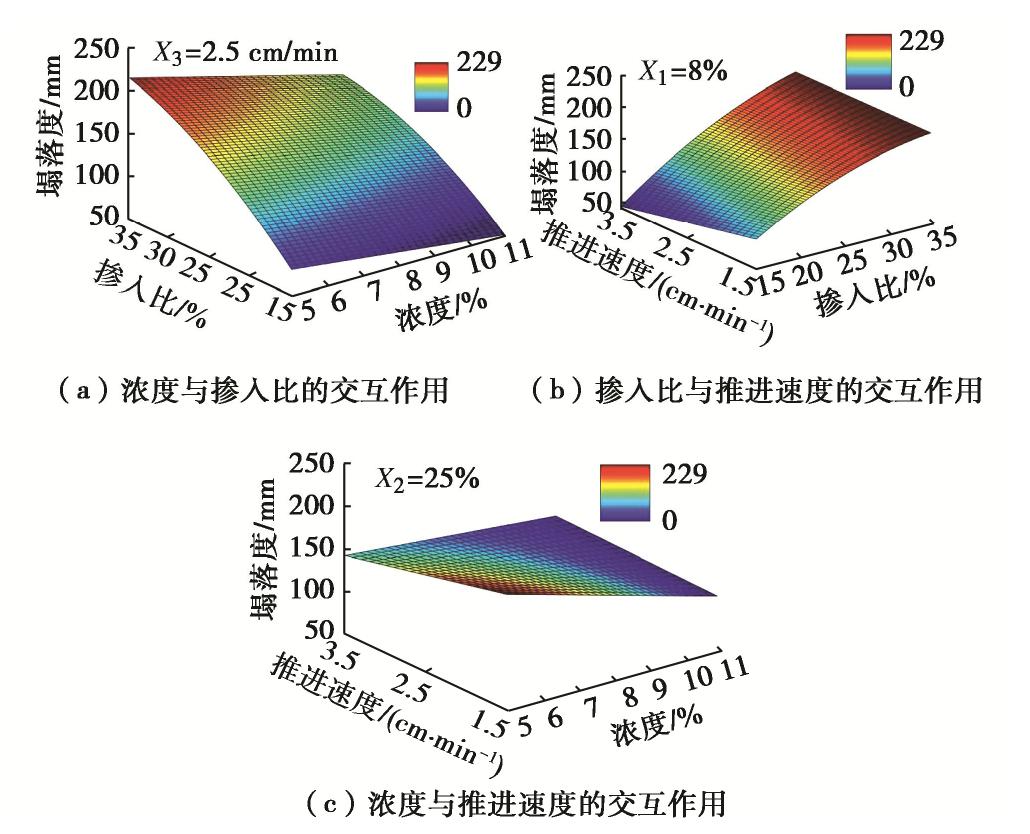
由表3的显著性检验可知,影响渣土塌落度的主要因素依次为： $X_{2}^{}$ （膨润土泥浆掺入比）> $X_{1}^{}$ （膨润土泥浆浓度）> $X_{3}^{}$ （盾构机推进速度）> $X_{2}^{2}$ > $X_{1}^{} X_{2}^{}$ > $X_{2}^{}$ $X_{3}^{}$ > $X_{1}^{} X_{3}^{}$ 。膨润土泥浆浓度值与渣土塌落度值负相关,膨润土泥浆浓度的增加对渣土塌落度值降低明显；膨润土泥浆掺入比与渣土塌落度值正相关,膨润土泥浆掺入比的增加可以增加渣土塌落度；盾构机推进速度与渣土塌落度值负相关,推进速度的增加会使渣土塌落度值减小。

膨润土泥浆浓度、掺入比和推进速度3个因素间交互作用的响应面如图6所示。从图6（a）可知,当推进速度固定在0水平,即X₃=2.5 cm/min时,若膨润土泥浆掺入比X₂∈（15,35）,塌落度增长率随着浓度X₁的增加持续减少,说明浓度的增加会抑制掺入比对渣土塌落度的贡献；从图6（b）可知,当膨润土泥浆浓度固定在0水平,即X₁=8%时,若膨润土泥浆掺入比X₂∈（15,35）,塌落度增长率随着推进速度X₃的增加持续减少,说明推进速度的增加会抑制掺入比对渣土塌落度的贡献；从图6（c）可知,当膨润土泥浆掺入比固定在0水平,即X₂=25%时,若膨润土泥浆浓度X₁∈（5,11）,塌落度下降率随着推进速度X₃的增加持续减少,说明推进速度的增加会抑制浓度对渣土塌落度的贡献。

图 6 塌落度响应曲面图

Figure 6. Response surface of slump

下载: 全尺寸图片幻灯片

4.2 渗透系数

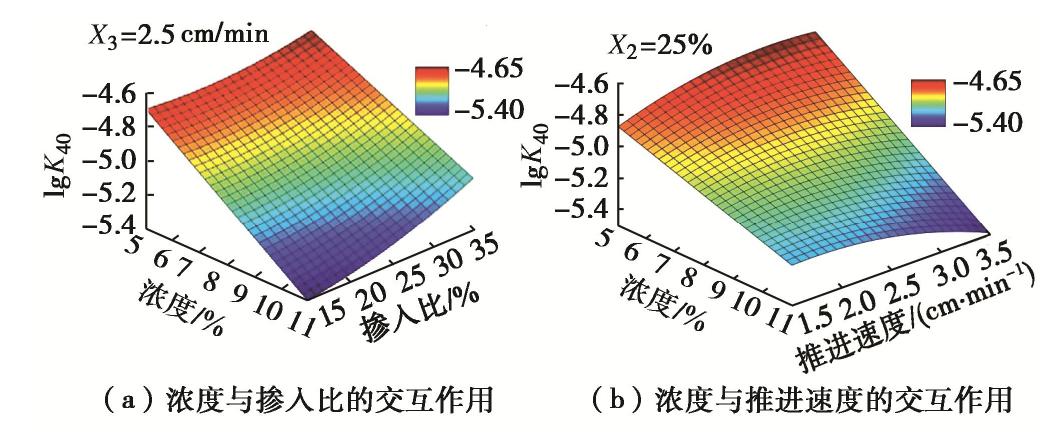
由表3的显著性检验可知,影响渣土渗透系数的主要因素依次为： $X_{1}$ （膨润土泥浆浓度）> $X_{3}$ （盾构机推进速度）> $X_{2}^{2}$ > $X_{1} X_{2}$ > $X_{1}$ $X_{3}$ > $X_{3}^{2}$ > $X_{2}^{}$ （膨润土泥浆掺入比）。膨润土泥浆浓度值与渣土渗透系数负相关,膨润土泥浆浓度的增加对渣土渗透系数降低明显；盾构机推进速度与渣土渗透系数正相关,推进速度的增加会使渣土渗透系数增加；膨润土泥浆掺入比与渣土渗透系数相关性受交互作用影响大,掺入比的增加可能会使渣土渗透系数增加,也可能会使渣土渗透系数减小。

膨润土泥浆浓度、掺入比和推进速度3个因素间交互作用的响应面如图7所示。

图 7 渗透系数响应曲面图

Figure 7. Response surface of permeability coefficient

下载: 全尺寸图片幻灯片

从图7（a）可知,当推进速度固定在0水平,即X₃=2.5 cm/min时,若膨润土泥浆浓度X₁∈（5,11）,掺入比与渣土渗透系数在高浓度下表现负相关,在低浓度下表现正相关,渗透系数增长率随着浓度X₁的增加持续减少,说明浓度的增加会抑制掺入比对渣土渗透系数的贡献；从图7（b）可知,当膨润土泥浆掺入比固定在0水平,即X₂=25%时,若膨润土泥浆浓度X₁∈（5,11）,渗透系数降低率随着推进速度X₃的增加持续减少,说明推进速度的增加会抑制泥浆浓度对渣土渗透系数的贡献。

5. 非线性多目标优化

5.1 优化方法

盾构隧道膨润土改良施工参数优化应基于以下原则：合理的塌落度、较小的渗透系数以及较低的改良成本（膨润土单耗）。每环管片膨润土泥浆消耗量Y₃（kg）为

$Y_{3} = ρ X_{1} X_{2} V$ 。

(6)

通过计算可知,响应模型定义域范围内, $Y_{3}$ 上限为1645 kg,下限为320 kg。

为获得最优的膨润土泥浆施工参数,在膨润土泥浆浓度、掺入比和每环膨润土消耗量响应优化分析的基础上,采用满意度函数（desirability function approach,DFA）的方法优化模型所得的工艺参数。由2.3节可知,塌落度属于望目型响应,即响应值越接近目标值满意度越高,其满意度函数为

$d_{i} (Y_{i}) = {\begin{array}{l} \frac{Y_{i} - L_{i}}{T_{i} - L_{i}} & {(L_{i} \leq Y_{i} \leq T)}_{i} \\ \frac{U_{i} - Y_{i}}{U_{i} - T_{i}} & (T_{i} \leq Y_{i} \leq U_{i}) \\ 0 & (其它) \end{array}$ 。

(7)

渗透系数和改良成本为望小型响应,即响应值越小满意度越高,其满意度函数为

$d_{i} (Y_{i}) = {\begin{cases} 1 (Y_{i} < L_{i}) \\ \frac{U_{i} - Y_{i}}{U_{i} - L_{i}} (L_{i} \leq Y_{i} \leq U_{i}) \\ 0 (T_{i} > U_{i}) \end{cases}$ 。

(8)

式中 $d_{i}$ 为第i个响应面的满意度函数； $Y_{i}$ 为第i个响应值； $L_{i}$ 为第i个响应值的规格下限； $U_{i}$ 为第i个响应值的规格上限； $T_{i}$ 为相应目标值。根据2.3节,取各响应值优化目标范围见表4。

在此基础上建立整体满意度函数为

$D = {(\prod_{i=1}^{3} d_{_{i}}^{r_{i}})}^{\frac{1}{\sum r_{i}}}$ ,

(9)

式中, $r_{i}$ 为权数,取决于各响应面在膨润土改良参数优化设计中的重要程度。假设各响应面回归模型重要程度相同,即r₁=r₂=r₃,

$D = \sqrt[3]{d_{1} d_{2} d_{3}}$ 。

(10)

渣土改良效果的整体满意度D是膨润土泥浆浓度、掺入比和推进速度的函数。该函数可作为改良参数优化的依据。

5.2 优化结果分析

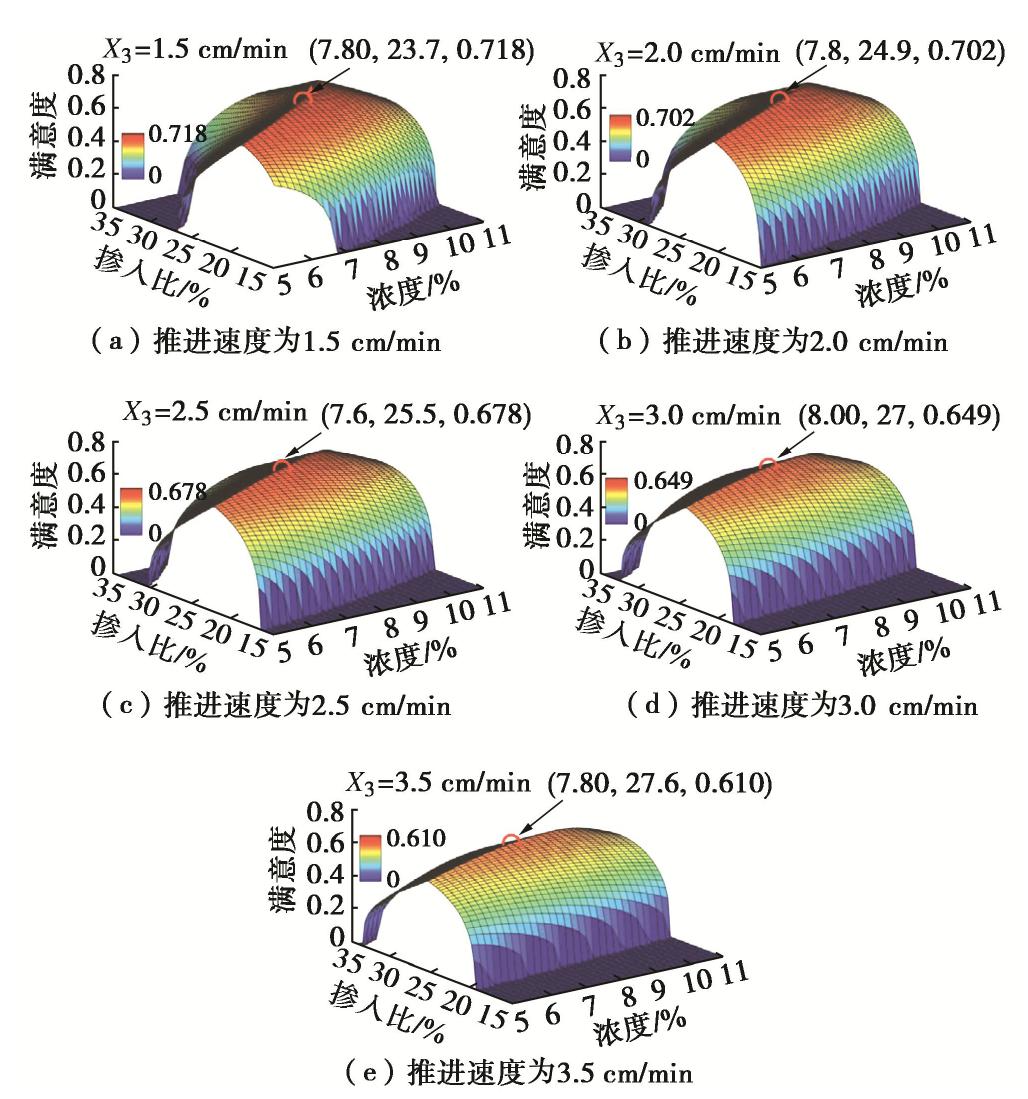
由于盾构推进速度由工况决定,故针对不同推进速度时的膨润土泥浆浓度和掺入比分别进行优化分析。根据式（10）计算推进速度X₃=1.5,2.0,2.5,3.0,3.5 cm/min时的整体满意度函数并作图见图8。由图8可知,渣土改良整体满意度在膨润土泥浆高浓度、低掺入比和低浓度、高掺入比的情况下都很低,不能应用于膨润土改良施工。

图 8 不同推进速度下满意度响应曲面图

Figure 8. Satisfaction response surface under different advancing speeds

下载: 全尺寸图片幻灯片

分别对不同推进速度下的满意度函数取极大值,将结果汇入表5。由表5可知,随着推进速度的提高,膨润土改良的整体满意度最大值会下降,说明为了保证良好的膨润土改良效果,盾构机推进速度不宜过快。

表 5 膨润土最优改良参数表

Table 5. Optimal parameters of bentonite improvement

推进速度/(cm·min^-1)	膨润土泥浆浓度/%	膨润土泥浆掺入比/%	整体满意度极大值
1.5	7.8	23.7	0.718
2.0	7.8	24.9	0.702
2.5	7.6	25.5	0.678
3.0	8.0	27.0	0.649
3.5	7.8	27.6	0.610

下载: 导出CSV

| 显示表格

6. 现场渣土改良应用分析

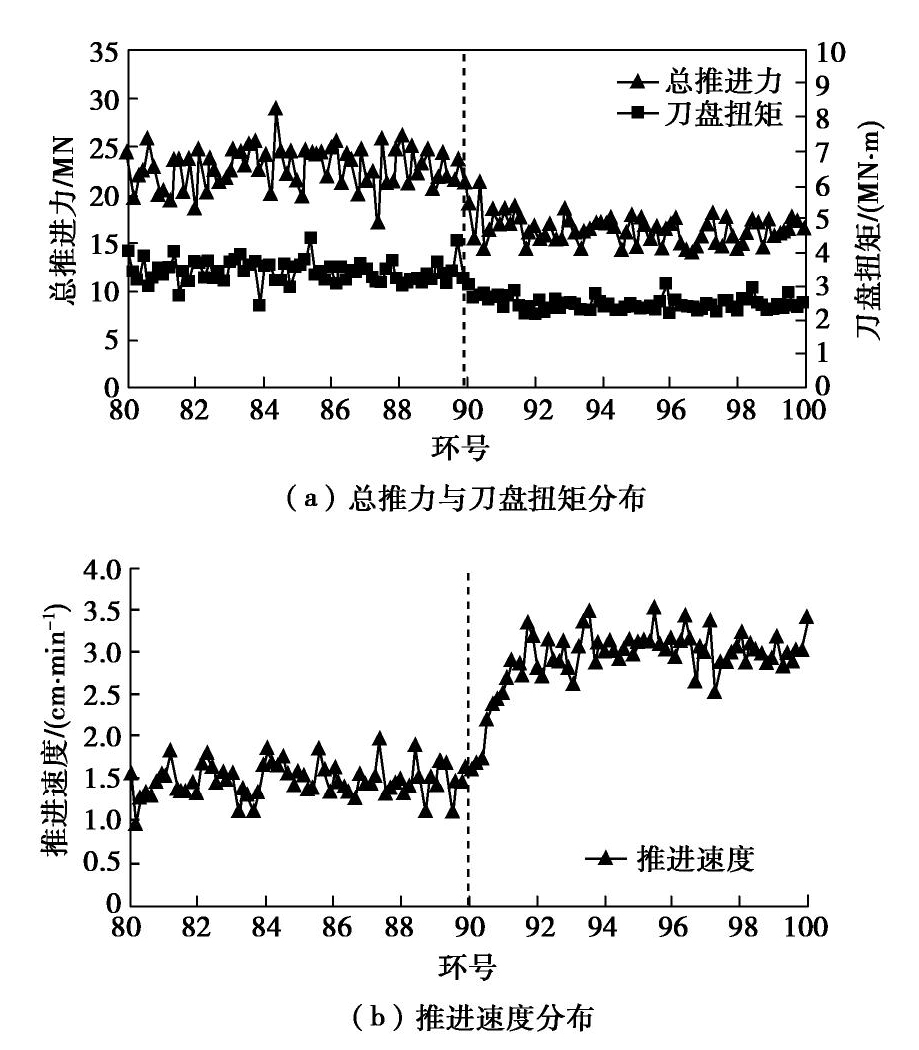
如图9所示,在盾构掘进81～90环,仅使用泡沫以45%的注入比进行土体改良。盾构推进过程中扭矩平均值3.2 MN·m,推力平均值23 MN,土压力波动大,掘进速度越来越慢,且喷涌现象频繁发生,严重影响工作进度。

图 9 试验段改良情况

Figure 9. Improvement of test sections

下载: 全尺寸图片幻灯片

将响应面-满意度函数得到的最优参数应用到91～100环进行掘进试验。与前10环相比,刀盘扭矩平均值降为2.4 MN·m,推力平均值降为18 MN,土压力趋于稳定,推进速度显著上升,喷涌现象不再发生,改良方案优化效果显著。

7. 结论

（1）设计了可用于研究盾构推进速度对渣土性能影响的盾构土舱相似模型,通过调节模型的刀盘转数模拟盾构推进速度的变化,具有良好的可操作性和便捷性。

（2）膨润土泥浆浓度、掺入比和盾构推进速度对强风化花岗岩地层渣土塌落度影响显著。膨润土泥浆浓度和盾构推进速度与塌落度值负相关；膨润土泥浆掺入比与塌落度值正相关。各因素间存在交互性。

（3）膨润土泥浆浓度、掺入比和盾构推进速度对强风化花岗岩地层渣土渗透系数影响显著。膨润土泥浆浓度与渗透系数负相关；盾构推进速度与渗透系数正相关。各因素间存在显著交互性,膨润土泥浆掺入比的增加可能会使渗透系数增加,也可能会使渗透系数减小。

（4）通过响应面-满意度函数的应用,将渣土塌落度、渗透系数和改良成本3个响应值优化问题转化为单一响应值优化,获得强风化花岗岩地层在不同盾构推进速度下的最优改良参数。

图 1 粒径级配曲线

Figure 1. Grain-size distribution curve

下载: 全尺寸图片幻灯片

图 2 土样制备

Figure 2. Preparation of soil samples

下载: 全尺寸图片幻灯片

图 3 盾构机土舱示意图

Figure 3. Schematic diagram of earth chamber of shield machine

下载: 全尺寸图片幻灯片

图 4 盾构机土舱相似模型

Figure 4. Similar model for EPB shield chamber

下载: 全尺寸图片幻灯片

图 5 改良效果对比

Figure 5. Comparison of improvement effect

下载: 全尺寸图片幻灯片

图 6 塌落度响应曲面图

Figure 6. Response surface of slump

下载: 全尺寸图片幻灯片

图 7 渗透系数响应曲面图

Figure 7. Response surface of permeability coefficient

下载: 全尺寸图片幻灯片

图 8 不同推进速度下满意度响应曲面图

Figure 8. Satisfaction response surface under different advancing speeds

下载: 全尺寸图片幻灯片

图 9 试验段改良情况

Figure 9. Improvement of test sections

下载: 全尺寸图片幻灯片

表 1 膨润土基本性质表

Table 1 Basic properties of bentonite

吸蓝量/(g·100g^-1)	胶质价/(mL·15g^-1)	膨胀倍数/(mL·g^-1)	pH值	细度（200目）
32	400	20	8.0~9.5	95

下载: 导出CSV

表 2 中心复合试验结果表

Table 2 Results of central composite tests

运行序	浓度/%	掺入比/%	推进速度/(cm·min^-1)	塌落度/mm	lgK₄₀
1	5	15	3.5	35	-4.83
2	8	8	2.5	8	-5.11
3	5	15	1.5	113	-4.89
4	11	35	1.5	140	-5.64
5	8	25	2.5	122	-4.98
6	11	15	1.5	56	-5.41
7	5	35	1.5	231	-4.68
8	5	35	3.5	201	-4.72
9	8	25	4.2	153	-4.60
10	8	25	2.5	147	-4.96
11	3	25	2.5	183	-4.57
12	8	25	2.5	151	-4.93
13	8	42	2.5	191	-5.17
14	13	25	2.5	106	-5.42
15	8	25	2.5	138	-5.04
16	11	15	3.5	30	-5.14
17	8	25	0.8	171	-5.01
18	8	25	2.5	147	-5.00
19	11	35	3.5	155	-5.39
20	8	25	2.5	141	-4.98

下载: 导出CSV

表 3 回归模型方差分析表

Table 3 Analysis of variance of regression model

预测响应值	变异来源	平方和	均方	F值	P值	备注
Y₁	模型	64180.16	9168.59	52.78	< 0.0001	显著
	X₁	7894.86	7894.86	45.45	< 0.0001
	X₂	47051.44	47051.44	270.88	< 0.0001
	X₃	1629.43	1629.43	9.38	0.0098
	X₁ X₂	709.08	709.08	4.08	0.0662
	X₁ X₃	1178.79	1178.79	6.79	0.0230
	X₂ X₃	965.22	965.22	5.56	0.0362
	X₂²	4751.34	4751.34	27.35	0.0002
	失拟项	1516.83	216.69	1.91	0.2472	不显著
Y₂	模型	1.28	0.21	27.00	< 0.0001	显著
	X₁	1.06	1.06	134.01	< 0.0001
	X₂	0.01	0.01	1.12	0.3102
	X₃	0.02	0.02	2.08	0.1733
	X₁ X₂	0.06	0.06	8.11	0.0137
	X₁ X₃	0.03	0.03	4.13	0.0631
	X₂²	0.10	0.10	12.55	0.0036
	失拟项	0.10	0.01	7.76	0.0186	不显著

下载: 导出CSV

表 4 响应优化目标范围

Table 4 Target ranges of response optimization

响应	塌落度/cm	lgK₄₀	膨润土单耗/(kg/环)
优化目标	100<Y₁<200,Y₁=150最为理想	-5.45<Y₂<-4.45	320<Y₃<1645

下载: 导出CSV

表 5 膨润土最优改良参数表

Table 5 Optimal parameters of bentonite improvement

推进速度/(cm·min^-1)	膨润土泥浆浓度/%	膨润土泥浆掺入比/%	整体满意度极大值
1.5	7.8	23.7	0.718
2.0	7.8	24.9	0.702
2.5	7.6	25.5	0.678
3.0	8.0	27.0	0.649
3.5	7.8	27.6	0.610

下载: 导出CSV

参考文献(12)

[1]	PEILA D, MARTINELLI D, TODARO C. Soil conditioning in EPB shield tunnelling-An overview of laboratory tests[J]. Geomechanics and Tunnelling, 2019, 12(5): 491-498. doi: 10.1002/geot.201900021
[2]	肖超, 阳军生, 王树英, 等. 土压平衡盾构改良渣土力学行为及其地层响应特征[J]. 中南大学学报(自然科学版), 2016, 47(7): 2432-2440. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201607034.htm XIAO Chao, YANG Jun-sheng, WANG Shu-ying, et al. Conditioned soils mechanical behavior of earth pressure balance shield tunneling and its impact on formation respons[J]. Journal of Central South University (Science and Technology), 2016, 47(7): 2432-2440. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201607034.htm
[3]	TANG S, ZHANG X, LIU Q. Prediction and analysis of replaceable scraper wear of slurry shield TBM in dense sandy ground: a case study of Sutong GIL Yangtze River Crossing Cable Tunnel[J]. Tunnelling and Underground Space Technology, 2020, 95: 103090. doi: 10.1016/j.tust.2019.103090
[4]	BARZEGARI G B, UROMEIHY A U, ZHAO J Z. Parametric study of soil abrasivity for predicting wear issue in TBM tunneling projects[J]. Tunnelling And Underground Space Technology, 2015, 48: 43-57. doi: 10.1016/j.tust.2014.10.010
[5]	HUANG Z H, WANG C W, DONG J D. Conditioning experiment on sand and cobble soil for shield tunneling[J]. Tunnelling and Underground Space Technology, 2019, 87: 187-194. doi: 10.1016/j.tust.2019.02.011
[6]	姜厚停, 龚秋明, 杜修力. 卵石地层土压平衡盾构施工土体改良试验研究[J]. 岩土工程学报, 2013, 35(2): 284-292. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201302014.htm JIANG Hou-ting, GONG Qiu-ming, DU Xiu-li. Experimental study on soil conditioning in cobble layer by use of earth pressure balanced machine[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 284-292. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201302014.htm
[7]	张润来, 宫全美, 周顺华, 等. 砂卵石地层土压平衡盾构施工渣土改良试验[J]. 同济大学学报(自然科学版), 2019, 47(5): 673-680. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ201905012.htm ZHANG Run-lai, GONG Quan-mei, ZHOU Shun-hua, et al. Test on improvement of residual soil by EPB shield in sandy pebble stratum[J]. Journal of Tongji University(Natural Science), 2019, 47(5): 673-680. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ201905012.htm
[8]	DING Y D Y, JIANG Y J Y, YANG Z Y Z. Soil conditioning of high water pressure sandy stratum for an EPB shield[J]. Journal of the Agromomy Faculty of Universidad del Zulia, 2019, 36(2): 215-229.
[9]	WANG S W S, LU X L X, WANG X W X. Soil improvement of EPBS construction in high water pressure and high permeability sand stratum[J/OL]. Advances in Civil Engineering, 2019. doi: 10.1155/2019/4503219.
[10]	BUDACH C, THEWES M. Application ranges of EPB shields in coarse ground based on laboratoryresearch[J]. Tunnelling and Underground Space Technology, 2015, 50: 296-304. doi: 10.1016/j.tust.2015.08.006
[11]	土工试验规程：SL237—1999[S]. 1999. Specification of Soil Test: SL237—1999[S]. 1999. (in Chinese)
[12]	朱伟, 秦建设, 魏康林. 土压平衡盾构喷涌发生机理研究[J]. 岩土工程学报, 2004, 26(5): 589-593. doi: 10.3321/j.issn:1000-4548.2004.05.003 ZHU Wei, QIN Jian-she, WEI Kang-lin. Research on the mechanism of the spewing in the EPB shield tunnelling[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(5): 589-593. (in Chinese) doi: 10.3321/j.issn:1000-4548.2004.05.003

施引文献(30)

期刊类型引用(14)

1.	王树英，钟嘉政，倪准林，郑响凑. 带压环境下泥浆-泡沫组合改良级配不良砂剪切特性研究. 岩土力学. 2024(10): 2879-2888 . 百度学术
2.	余俊，郑靖凡，张志中，李东凯，和振. 考虑推进过程的土压平衡盾构渗流场解析解及喷涌判别. 岩土工程学报. 2024(10): 2101-2110 . 本站查看
3.	汪雨珍，刘念武，梁锦涛，徐浩东. 膨润土含量对泥浆性能影响的室内测定试验研究. 大众标准化. 2024(19): 69-70+73 . 百度学术
4.	刘魁刚，郭易东，叶新丰，李振东. 基于非连续介质力学的多刀盘矩形顶管掘进性能分析. 铁道标准设计. 2024(11): 149-156 . 百度学术
5.	康瑞强，施成华，孙晓贺，李时杰，杨飞. 基于响应面-粒子群算法的大体积混凝土温度裂缝控制方法. 中南大学学报(自然科学版). 2024(12): 4505-4518 . 百度学术
6.	罗敏鹤，王旭春，刘绪壮，栾义浩，郝展鹏. 土压平衡盾构掘进喷涌处治分析与实践. 市政技术. 2023(02): 98-102+108 . 百度学术
7.	黄逢源，张康健，陈登开，张志强，贾斌. 富水复合地层土压平衡盾构渣土改良试验研究. 现代隧道技术. 2023(01): 262-269+280 . 百度学术
8.	占永杰，王树英，杨秀竹，王海波. 考虑级配影响的盾构泡沫改良粗粒土一维压缩理论计算模型. 岩土工程学报. 2023(08): 1644-1652 . 本站查看
9.	王璐，邢慧堂，朱伟，方治纲，钱勇进. 土压平衡盾构渣土泥浆化的防治及工程应用. 地下空间与工程学报. 2023(S1): 209-218 . 百度学术
10.	崔灿. 富水砂层土压平衡盾构渣土改良试验研究. 路基工程. 2023(05): 136-141 . 百度学术
11.	刘明阳，余宏淦，陶建峰，覃程锦，高浩寒，刘成良. 基于盾构机运行参数的局部切空间排列与Xgboost融合的地质类型识别. 中南大学学报(自然科学版). 2022(06): 2080-2091 . 百度学术
12.	占玉林，许江辉，许俊，邵俊虎，林智敏，何鹏. 基于响应面法和粒子群算法的桥梁高耸临时提升支架优化. 中国铁道科学. 2022(06): 39-46 . 百度学术
13.	潘涛. 盾构超近距离上穿诱发既有隧道纵向与水平变形研究. 华南地震. 2021(03): 33-39 . 百度学术
14.	雷华阳，刘旭，施福硕，许英刚. 顶管工程聚合物改性膨润土泥浆配比优化研究. 岩土工程学报. 2021(S2): 51-55 . 本站查看