复杂应力路径下饱和砂土静态液化失稳预测

黄茂松; 童森杰; 时振昊; 吕玺琳

doi:10.11779/CJGE202101002

复杂应力路径下饱和砂土静态液化失稳预测 English Version

黄茂松^{1, 2,},
童森杰^{1, 2},
时振昊^{1, 2, ,},
吕玺琳^{1, 2}

1.
同济大学岩土及地下工程教育部重点实验室,上海　200092
2.
同济大学地下建筑与工程系,上海　200092

基金项目:

国家自然科学基金项目 11972260

国家自然科学基金项目 41672270

详细信息

作者简介:
黄茂松(1965— ),男,浙江玉环人,博士,教授,博士生导师,主要从事岩土工程的科研和教学工作。E-mail:mshuang@tongji.edu.cn

通讯作者:
时振昊, E-mail: 1018tjzhenhao@tongji.edu.cn

中图分类号: TU43
计量
- 文章访问数: 414
- HTML全文浏览量: 34
- PDF下载量: 314
出版历程
- 收稿日期: 2020-02-04
- 网络出版日期: 2022-12-04
- 刊出日期: 2020-12-31

Prediction initiation of static liquefaction of saturated sand under complex stress paths

HUANG Mao-song^{1, 2,},
TONG Sen-jie^{1, 2},
SHI Zhen-hao^{1, 2, ,},
LÜ Xi-lin^{1, 2}

1.
Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, China
2.
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China

摘要

摘要: 饱和砂土应力-应变关系具有各向异性和状态相关特性,因此其静态液化的触发与应力路径密切相关。现有文献已提出多种静态液化判别准则,但其准确性往往仅在三轴应力路径下被进行校验。对于涉及主应力方向旋转和不同中主应力比的复杂应力路径,现有判别准则是否可以准确预测静态液化的触发有待进一步验证。为此,基于状态相关各向异性砂土本构模型,结合前人的空心圆柱扭剪单元体试验,比较了二阶功、弹塑性刚度矩阵对称部分和失稳模量3种准则对复杂应力路径下砂土静态液化失稳预测的效果。发现包括：基于弹塑性刚度矩阵对称部分的失稳触发表达式不依赖于加载路径,具有更好的通用性,其预测的失稳点早于或与实际失稳点吻合；失稳模量理论可预测实际液化失稳的位置,但判定表达式因加载条件不同而变化。获得了复杂应力路径下的失稳线,分析了静态液化触发前砂土可发挥峰值摩擦角受中主应力、主应力方向等因素的影响。
- 砂土 /
- 静态液化 /
- 各向异性 /
- 中主应力比 /
- 液化判别 /
- 失稳线
Abstract: The stress-strain relations of saturated sand are anisotropic and state-dependent, thus the initiation of its static liquefaction relies on stress paths. While various criteria have been proposed to predict the triggering of static liquefaction, their accuracy is normally examined under triaxial stress paths. When subjected to complex stress paths that involve the rotation of the principal stress directions and different relative magnitudes of the intermediate principal stress, the accuracy of these criteria remains to be an open question. Here the capacity of three criteria is evaluated, including the second-order work, symmetric part of the elastoplastic stiffness matrix and instability modulus, for predicting the static liquefaction under complex stress paths, by employing a state-dependent, anisotropic constitutive model and comparing against the hollow cylindrical torsional shear tests on Toyoura sand. It is found that: (1) The instability condition derived from the elastoplastic stiffness matrix does not depend on the stress paths, thus being more general, and the predicted liquefaction initiation is earlier than or coincident with the actual instability point. (2) The instability modulus approach can predict the initiation of static liquefaction, however, the instability conditions vary across different loading paths. The instability line is obtained, through which the influences of factors like the intermediate principal stress and the principal stress directions on the peak mobilized friction angle before liquefaction are studied.
- sand /
- static liquefaction /
- anisotropy /
- intermediate principal stress ratio /
- liquefaction criterion /
- instability line

HTML全文

0. 引言

持水特征曲线指土体持水状态（可用体积含水率、质量含水率或饱和度表达）与土中水的能量状态（可用吸力、势能或相对湿度表达）之间的关系^[1],描述了土中水（液相）与土（固相）间的能量平衡状态^[2]。

土体持水的物理化学机制有毛细、吸附与渗透。毛细机制与弯液面上的表面张力有关,受Young- Laplace方程控制（土体孔径越小其毛细吸力越大）,当土中水能量状态低至其空化点以下,毛细水汽化,相应毛细机制消失。吸附机制指（黏）土颗粒表面由于van der Waals力、双电层力、阳离子水化等造成的短程吸附作用导致的土中水能量降低,可用Kelvin方程描述。通常将毛细与吸附机制导致的土中水相对自由水状态而言势能的降低称为基质势（用负值表达）；将对应土体固相的持水/吸水能力（用正值表达）称为基质吸力；二者数值相等,符号相反。此外,渗透机制指溶解盐会降低土中水的能量状态,其能量降低程度与溶质类型和浓度相关。

SWRC表征土体持水能力,原本用于农业领域,随后的研究表明非饱和状态下的渗流、强度与变形等土力学行为^[1]乃至土的成分与结构等土质学特征^[2]均与SWRC密切相关,因而成为描述非饱和状态下土体性状的关键指标与工具,在非饱和土力学研究与工程应用中具有基础的、特殊的、关键的作用与位置,其研究成果亦非常丰富^[1-3],但大部分SWRC^[1-3]由轴平移方法获得,受陶土板进气值限制,其基质吸力目前仅能控制在1500 kPa以内,根据Kelvin方程（式（1））可知其对应的相对湿度RH为98.9%以上（环境温度25℃时）。然而,自然界中RH变化范围远比轴平移方法所能控制的RH范围大；例如中国主要城市各月RH统计^[4]显示,最低14%（拉萨,2月）,最高90%（长沙,10月与11月；海口,1月）；因而高吸力（RH低于95%或吸力高于7.1 MPa）下的土体持水特征研究具有特别的现实意义。

高吸力下土体持水特征测试常用方法主要有：滤纸法^[5-8]（适用于10～100 MPa）、冷镜湿度计法^[9]（适用于0～300 MPa）、饱和盐溶液等压湿度控制法^[10-12]（适用于3～400 MPa）、干湿空气混合湿度控制法^[13]（适用于7～600 MPa）等。前两种为吸力量测方法,难以控制吸力；后两种为吸力控制方法,适于测定完整的SWRC,但蒸汽平衡历时漫长,如文献[14]采用饱和盐溶液等压湿度控制法测定3.3～359.1 MPa吸力范围的膨胀土SWRC耗时319 d,阻碍了高吸力下土体持水特征的研究与应用。

近年来出现的动态露点等温线方法^[15-16]使得上述情况有所改观,该方法能够在较短时间（几天内）获得相对湿度在3%～95%范围的SWRC。为了给高吸力下相关土力学工程实践提供依据和参考,本文采用该方法：①对从黏土质砂到极高塑性黏土的9种土样开展高吸力下吸脱湿过程持水特征测试；②采用RH = 95%下的吸湿质量含水率w₉₅量化高吸力下持水能力,采用吸脱湿SWRC间滞回区域面积HHA量化高吸力下SWRC滞回效应强弱,采用同一吸力下吸脱湿SWRC含水率之差最大值Δw_max量化水力滞回导致的含水率偏差范围；③探讨w₉₅、HHA、Δw_max与液限w_L、塑性指数I_p、阳离子交换量CEC、比表面积SSA等土性参数间量化关系；④构建修正的Fredlund-Xing模型描述高吸力下吸脱湿过程SWRC。

1. 研究方案

1.1 试验土样

试验采用Wyoming膨润土、宁明膨胀土、荆门黄褐色膨胀土、Denver黏土岩、荆门棕褐色膨胀土、武汉黏土、三门峡粉质黏土、郑州粉土和开封黄河砂共9种土样,其物理性质指标测试结果见表1。

表 1 试验用土的物理性质指标

Table 1. Physical property indexes of soils

土样名称	颗粒相对质量密度^[17]	颗粒所占比例^[17]/%				液限^[17]/%	塑限^[17]/%	塑性指数	塑性^[18]	USCS 定名^[19]	比表面积EGME^[20]/(m²·g^-1)	CEC(NH₄⁺)^[17]/( mmol·kg^-1)	自由膨胀率^[21]/%	膨胀潜势^[21]
土样名称	颗粒相对质量密度^[17]	>0.075 mm	0.005~0.075 mm	0.002~0.005 mm	<0.002 mm	液限^[17]/%	塑限^[17]/%	塑性指数	塑性^[18]	USCS 定名^[19]	比表面积EGME^[20]/(m²·g^-1)	CEC(NH₄⁺)^[17]/( mmol·kg^-1)	自由膨胀率^[21]/%	膨胀潜势^[21]
Wyoming膨润土	2.70	5.1	14.2	3.8	77.0	217.7	33.1	184.5	极高	CH	500.1	621	775	强
宁明膨胀土	2.73	5.8	2.9	0.3	91.1	164.6	37.6	127.0	极高	CH	393.0	508	655	强
荆门黄褐色膨胀土	2.75	2.1	47.4	21.5	29.0	62.9	25.5	37.4	高	CH	236.5	309	75	中
Denver黏土岩	2.72	8.5	44.2	20.6	26.7	46.0	23.2	22.8	中等	CL	88.7	160	38	—
荆门棕褐色膨胀土	2.72	11.6	42.4	26.7	19.3	41.8	20.7	21.1	中等	CL	110.4	254	40	弱
武汉黏土	2.73	5.5	63.9	9.6	21.0	40.3	18.2	22.1	中等	CL	112.5	154	39	—
三门峡粉质黏土	2.72	0.5	82.8	5.7	11.1	35.2	19.1	16.1	中等	CL	108.5	149	30	—
郑州粉土	2.70	8.7	77.4	2.5	11.4	26.1	14.8	11.3	低	CL	27.7	50	9	—
开封黄河砂	2.68	62.6	36.0	0.2	1.3	—	—	—	—	SC	7.5	16	—	—

下载: 导出CSV

| 显示表格

1.2 蒸汽吸附分析仪工作原理

美国Meter公司生产的蒸汽吸附分析仪（Vapor Sorption Analyzer, VSA）见图1,用于测试动态的或平衡的水分吸附等温线（moisture sorption isotherms）,即给定温度下的SWRC。

图 1 蒸汽吸附分析仪

Figure 1. Vapor sorption analyzer

下载: 全尺寸图片幻灯片

VSA采用动态露点等温线（dynamic dew point isotherm, DDI）方法获得动态水分吸附等温线；采用控制湿度下测试样质量的方法（dynamic vapor sorption, DVS）获得静态（平衡）水分吸附等温线。其工作原理是：DDI方法既不控制含水率亦不控制RH,而是在用湿气流湿化/干气流脱湿过程中通过高精度天平测试样质量变化、通过冷镜露点法测RH得到动态水分吸附等温线。DVS方法是在控制RH条件下跟踪试样质量变化以获得静态（平衡）水分吸附等温线,每级湿度下的稳定（平衡）标准可用预设时间间隔或预设试样质量变化幅度。Likos等^[15]与Arthur等^[22]试验证实了DDI方法的精度与可靠性,系统试验研究表明DDI方法与DVS方法获得的SWRC无明显偏差。

VSA相对湿度控制范围是3%～95%（25℃下对应吸力范围为7.1～482.9 MPa）,试样质量建议范围为500～5000 mg,试样温度可控范围为15℃～60 ℃。

1.3 高吸力下持水特征试验方案

采用VSA测定9种土样高吸力下SWRC。将土样风干碾散过0.5 mm筛,置于烘箱中烘至衡量（105 ℃下烘干48 h）,取出置于干燥器内冷却至室温,每次取约1000 mg试验。试验方案与步骤如下：

（1）仪器准备

将VSA在工作台上调平,安装干燥管,水箱中注入去离子水,检查天平,标定相对湿度。

（2）设定SWRC量测步骤

鉴于采用DDI方法与DVS方法测土样SWRC具有很好的一致性^[22],且前者测试历时约为后者的1/25^[15],因此采用DDI方法。由于试样是完全烘干后的,质量含水率w为0,第1步设置初始RH为3%,最终RH为95%,用DDI方法采集吸湿过程w数据RH,即土样SWRC吸湿边界线；第2步设置初始RH为95%、最终RH为3%,目的是获得土样SWRC的脱湿曲线；由于脱湿曲线起始点为RH=95%对应点,所以并非脱湿边界线。此外,设定样品室温度为25℃。

（3）测定SWRC

将试样置入样品杯,放入试样室开始测试,测试由VSA自动执行。试验结束后,取出试样杯称试样质量,烘干后复测干土质量,并在计算机终端下载SWRC试验数据。

2. 试验结果分析

由于Kelvin方程（式(1)）确定了吸力ψ与RH间关系,VSA试验结果既可用w-RH关系亦可用w-ψ关系表达；鉴于非饱和土力学中常用w-ψ关系,因此将9种土样w-ψ关系表达的SWRC绘制在图2中,将每种土样试验历时,试验数据点数,吸湿起始点、吸湿结束点（脱湿起始点）、脱湿结束点对应的RH,ψ,w值列在表2中。

图 2 高吸力下的SWRC（RH = 3%~95%）

Figure 2. Soil-water retention curves under high suctions

下载: 全尺寸图片幻灯片

表 2 高吸力下SWRC的吸湿/脱湿起始点与结束点

Table 2. Start point/end point of adsorption/desorption of SWRCs under high suctions

土样名称	试验历时/min	试验数据点数	吸湿起始点			吸湿结束点（脱湿起始点）			脱湿结束点
土样名称	试验历时/min	试验数据点数	RH	ψ/kPa	w/%	RH	ψ/kPa	w₉₅/%	RH	ψ/kPa	w/%
Wyoming膨润土	3135	203	0.0375	451647	0.67	0.9457	7686	21.46	0.0350	461106	0.87
宁明膨胀土	3777	205	0.0324	471755	0.76	0.9472	7468	19.45	0.0343	463909	1.02
荆门黄褐色膨胀土	2982	204	0.0297	484119	1.28	0.9456	7700	13.40	0.0331	468823	1.96
Denver黏土岩	2113	201	0.0313	476506	0.79	0.9476	7410	6.79	0.0338	465943	1.14
荆门棕褐色膨胀土	2523	212	0.0299	483240	0.89	0.9474	7439	9.63	0.0245	510367	1.28
武汉黏土	2343	202	0.0294	485114	0.44	0.9455	7715	7.37	0.0326	470929	0.91
三门峡粉质黏土	2186	203	0.0244	510892	0.43	0.9478	7380	6.19	0.0327	470498	0.97
郑州粉土	1787	197	0.0246	509791	0.42	0.9500	7061	2.34	0.0245	510347	0.52
开封黄河砂	1295	148	0.0245	510383	0.65	0.9519	6786	1.28	0.0247	509237	0.67

下载: 导出CSV

| 显示表格

$ψ = - \frac{R T}{ν_{w}} \ln RH$ ,

(1)

式中 ψ为吸力（kPa）；R = 8.314 J/(K·mol),为通用气体常数；T为热力学温度,样品室温度25℃对应T = 298.15 K； $ν_{w}$ = 1.8×10^-5 m³/mol,为水的摩尔体积；RH为相对湿度,量纲为1。

由表2可见,9种土样中宁明膨胀土测试历时最长,为3777 min,即2.6 d,且有205个数据点。一方面说明试验历时为文献[14]中饱和盐溶液等压湿度控制法测试历时（319 d）的1/122,极大缩短了测试时间；另一方面说明数据点丰富,能够更好描述土样的持水特征。

从以下3方面探讨高吸力下的SWRC：①反映土样亲水性强弱的持水能力特征点w₉₅；②描述水力滞回效应强弱的SWRC滞回区域面积HHA；③反映水力滞回导致的含水率偏差范围的SWRC滞回效应最大值Δw_max。

2.1 高吸力下持水能力特征点w₉₅

由图2与表2可见：9种土样从完全干燥状态吸湿结束时（控制RH为95%）对应的质量含水率w₉₅差别相当大,高至Wyoming膨润土的21.46%,宁明膨胀土的19.45%,表明持水能力/亲水性非常强,低至开封黄河砂的1.28%,表明其持水能力/亲水性非常弱。由此可见,w₉₅作为RH = 95%下的吸湿质量含水率,是表征土样持水（吸水）能力的特征点,其数值反映了土样亲水性强弱。

将9种土样的w₉₅与表1给出的CEC对应绘制在图3中,可见w₉₅与CEC具有非常高的线性相关性,其线性拟合结果见式（2）,决定系数R²高达0.99。

$w_{95} = 0.035 CEC + 1.3$ 。

(2)

图 3 9种土的w₉₅-CEC关系

Figure 3. Relationship between w₉₅ and CEC of 9 kinds of soils

下载: 全尺寸图片幻灯片

鉴于《膨胀土地区建筑技术规范》^[21]采用CEC分别为340,260,170 mmol/kg作为判断土样膨胀潜势强（CEC > 340 mmol/kg）、中（CEC =260～340 mmol/kg）、弱（CEC = 170～260 mmol/kg）的界限,将其代入式（2）得到采用w₉₅判别土样膨胀潜势的相应界限分别为13.0%,10.2%,7.1%。即：w₉₅ > 13.0%,判别为强膨胀土；w₉₅=10.2%～13.0%,判别为中膨胀土；w₉₅=7.1%～10.2%,判别为弱膨胀土；w₉₅<7.1%,判别为非膨胀土。

下面对上述方法的可行性进行验证：表3为根据《膨胀土地区建筑技术规范》^[21]测定的Denver膨润土、信阳黏土、商用高岭土的CEC、自由膨胀率及确定的膨胀潜势。采用VSA获得的w₉₅亦列在表3中,Denver膨润土w₉₅为22.47%,大于13.0%,根据w₉₅判别为强膨胀土；信阳黏土w₉₅为8.77%,在7.1%～10.2%,根据w₉₅判别为弱膨胀土；商用高岭土w₉₅为1.03%,小于7.1 %,根据w₉₅判别为非膨胀土。表明采用w₉₅作为膨胀潜势判别标准与采用CEC的判别结果具有很好的一致性,至于如何提高其判别精度,则应收集更多的试验结果,确定更为可靠的强、中、弱膨胀潜势的w₉₅界限值。

表 3 3种土样膨胀潜势的判别指标

Table 3. Eestimation indexes of swelling potential of 3 kinds of soils

土样名称	CEC(NH₄⁺)^[17]/(mmol·kg^-1)	自由膨胀率^[21]/%	膨胀潜势^[21]	w₉₅/%
Denver膨润土	976	111	强	22.47
信阳黏土	206	40	弱	8.77
商用高岭土	4	—	—	1.03

下载: 导出CSV

| 显示表格

2.2 高吸力下SWRC滞回区域面积HHA

由图2可见,高吸力段(RH = 3%～95%),9种土样SWRC均呈现或强或弱的水力滞回行为,即相同吸力下脱湿路径上的w高于吸湿路径上的w。

SWRC水力滞回效应强弱可用脱湿与吸湿曲线间滞回区域面积HHA (hydraulic hysteresis area)描述。根据图2中的脱湿与吸湿曲线数据在Origin软件中数值积分获得9种土样滞回区域面积见表4。

表 4 高吸力下SWRC滞回效应特征参数（R_H = 3%~95%）

Table 4. Hysteresis properties of SWRCs under high suctions

土样名称	滞回区域面积HHA/kPa	HHA 相对值	Δw_max/%	ψ(Δw_max)/kPa	RH(Δw_max)	w_d(Δw_max)/%	w_w(Δw_max)/%	w相对误差/%
土样名称	滞回区域面积HHA/kPa	HHA 相对值	Δw_max/%	ψ(Δw_max)/kPa	RH(Δw_max)	w_d(Δw_max)/%	w_w(Δw_max)/%	$\frac{Δ w_{\max}}{w_{d}}$	$\frac{Δ w_{\max}}{w_{w}}$
Wyoming膨润土	13641	1.00	6.27	68737	0.6069	13.08	6.81	47.9	92.1
宁明膨胀土	10717	0.79	4.18	72744	0.5895	11.00	6.81	38.0	61.4
荆门黄褐色膨胀土	4512	0.33	1.77	37559	0.7612	9.87	8.10	17.9	21.9
Denver黏土岩	2367	0.17	0.69	37184	0.7633	4.80	4.11	14.4	16.8
荆门棕褐色膨胀土	3520	0.26	1.38	30993	0.7984	7.41	6.03	18.6	22.9
武汉黏土	3412	0.25	1.15	31077	0.7979	5.13	3.98	22.4	28.9
三门峡粉质黏土	3439	0.25	1.04	89267	0.5228	3.55	2.51	29.3	41.4
郑州粉土	1002	0.07	0.37	155335	0.3235	1.22	0.85	30.3	43.5
开封黄河砂	196	0.01	0.16	221700	0.1999	0.88	0.72	18.2	22.2

下载: 导出CSV

| 显示表格

由图2与表4可见：9种土样HHA差别显著,对于强膨胀土,Wyoming膨润土高达13641 kPa,宁明膨胀土亦高达10717 kPa；对于中膨胀土,荆门黄褐色膨胀土为4512 kPa；对于弱膨胀土,荆门棕褐色膨胀土为3520 kPa；武汉黏土、三门峡粉质黏土亦达到3412,3439 kPa；而郑州粉土低至1002 kPa；开封黄河砂仅有196 kPa,是Wyoming膨润土的1/70,滞回效应可忽略不计。

以上数据表明：HHA与土样膨胀潜势正相关,将9种土样的HHA与表1给出的CEC、SSA对应绘制在双y轴坐标系中,见图4,可见HHA与CEC、SSA均具有非常高的线性相关性,其过坐标原点的线性拟合结果为

图 4 9种土的CEC-SSA-HHA关系

Figure 4. CEC-SSA-HHA relationship of 9 kinds of soils

下载: 全尺寸图片幻灯片

$CEC = 0 .049 HHA$ ,

(3)

$SSA = 0 .037 HHA$ ,

(4)

式中,HHA与CEC线性相关的R²达到0.94,HHA与SSA线性相关的R²高达0.97。

CEC与SSA是强烈相关但有明显区别的土性指标。CEC指单位质量土样吸附的可交换阳离子总量,反映由于颗粒带负电荷导致的土样吸附阳离子的能力,更大的CEC意味着更强的膨胀潜势。SSA指单位质量土样具有的表面积,反映土样的颗粒级配与矿物成分,更大的SSA意味着更大的塑性,更强的膨胀潜势,更强的亲水性。HHA与CEC、SSA均正相关表明,滞回效应大小既受土样吸附阳离子能力的强烈影响,亦受土样比表面积控制,且从R²上看,其受土样比表面积影响更大。

将8种细粒土HHA与其液限w_L、塑性指数I_p绘制在双y轴坐标系中,见图5。

图 5 8种细粒土的w_L-I_p-HHA关系

Figure 5. w_L-I_p-HHA relationship of 8 kinds of fine-grained soils

下载: 全尺寸图片幻灯片

可见HHA与w_L、I_p均正相关,过坐标原点的线性拟合结果分别为

$w_{L} = 0 .015 HHA$ ,

(5)

$I_{p} = 0.012 HHA$ 。

(6)

式中,HHA与w_L线性相关的R²高达0.97,HHA与I_p线性相关的R²亦达到0.92,表明细粒土HHA与w_L具有更高的线性相关性。由于w_L、I_p代表土样塑性大小,表明HHA受土样塑性大小控制。

2.3 高吸力下SWRC滞回效应最大值Δw_max

SWRC滞回效应指水力滞回（脱/吸湿路径）对SWRC（此处是w-ψ关系）的影响,此处SWRC滞回效应最大值定义为相同ψ下,脱湿曲线对应含水率w_d与吸湿曲线对应含水率w_w之差的最大值Δw_max。根据该定义,在图2中搜索到每种土的Δw_max,及其对应的吸力ψ、RH、脱湿曲线含水率w_d、吸湿曲线含水率w_w,列入表4中。

由表4与图2可见,9种土样Δw_max存在较大差异：强膨胀土Δw_max相当大,如Wyoming膨润土为6.27%,宁明膨胀土为4.18%；中膨胀土,荆门黄褐色膨胀土为1.77 %；弱膨胀土,荆门棕褐色膨胀土为1.38%；中等塑性黏土,武汉黏土为1.15%,三门峡粉质黏土为1.04%,Denver黏土岩为0.69%；低塑性黏土,郑州粉土为0.37%；开封黄河砂仅为0.16%。对比表1可见,土样Δw_max值与w_L,I_p,CEC,SSA均正相关,反映了水力滞回导致的含水率偏差范围。取Δw_max与相应w_d、w_w的比值作为SWRC的含水率相对误差,计算9种土样Δw_max/w_d、Δw_max/w_w结果列于表4与图6。

图 6 由于水力滞回导致的含水率相对误差

Figure 6. Relative errors of water content due to hydraulic hysteresis

下载: 全尺寸图片幻灯片

表4与图6中,同一土样w_w小于w_d,因此采用吸湿曲线含水率w_w作为分母的相对误差比采用脱湿曲线含水率w_d作为分母的相对误差要大。由相对误差计算结果可见：在高吸力范围,不考虑水力滞回会导致持水特征曲线SWRC上质量含水率w最高92.1 %（Wyoming膨润土）的相对误差。

另一方面,如果工程中需要用当前含水率估算吸力,则同一w下,脱湿路径上吸力与吸湿路径上吸力的比值最高可达2.71（图2中Wyoming膨润土,w为6%,脱湿路径上吸力205959 kPa,吸湿路径上吸力76119 kPa,比值为2.71）,印证了高吸力下强膨胀土SWRC滞回效应之强烈。

2.4 高吸力下SWRC滞回行为机制探讨

由图2及2.2节、2.3节对SWRC滞回区域面积HHA与滞回效应最大值Δw_max的分析,可知高吸力下,9种土样中,高塑性（液限高、塑性指数大）、阳离子交换量大、比表面积大的土样滞回效应大,在此对高吸力下SWRC滞回行为机制展开探讨。

水力滞回行为机制解释主要有墨水瓶效应^[1]与接触角效应^[13],前者由于土中孔隙尺寸与形状（可用孔径r概化）的不均匀性所致,后者由于吸湿接触角 $α_{w}$ 通常大于脱湿接触角 $α_{d}$ 所致^[23]。墨水瓶效应与接触角效应均属毛细范畴,受Young-Laplace方程控制：

$ψ_{c} = u_{a} - u_{w} = \frac{2 T_{s} \cos α}{r}$ 。

(7)

式中 ψ_c为毛细吸力,可用孔隙气压力u_a与孔隙水压力u_w之差表达；T_s为水的表面张力； $α$ 为接触角；r为毛细半径。当吸力增大、土中水能量状态低到其空化点以下,毛细水汽化,（土中毛细水比自由水空化点更低,但其对应的ψ_c或RH尚无定论,一般而言RH低于80%,毛细水难以存在^[2]）,墨水瓶效应与接触角效应难以解释高吸力下的滞回行为。

Lu等^[24]给出了高吸力下SWRC滞回机制的一种解释：非膨胀黏土,脱湿与吸湿主要发生在颗粒表面,因而滞回效应较小。膨胀性土,脱湿与吸湿亦可发生于存在可交换阳离子的晶层之间,吸湿时阳离子水化吸附极性水分子,水分子需克服较大的,van der Waals力方能进入层间；脱湿时由于层间距离较大van der Waals力较弱,因此相同ψ下,吸湿路径对应较小的w,脱湿路径对应较大的w。在此结合文中数据探讨该解释的合理性：

高吸力下Wyoming膨润土HHA=13641 kPa,Δw_max=6.27 %,滞回效应最大；自由膨胀率为775 %,膨胀性最大；SSA高达500.1 m²/g,表明其包含了较大的层间比表面积^[25],CEC高达621 mmol/kg,表明其可交换阳离子总量大；印证了吸湿状况下膨胀土层间阳离子水化受van der Waals力阻碍致其含水率较低的机制解释。

相对而言,郑州粉土,SSA为27.7 m²/g,CEC为50 mmol/kg,比表面积小,可交换阳离子总量小。一方面其自由膨胀率（9%）为Wyoming膨润土的1.2 %,表明其为非膨胀土；另一方面,其HHA（1002 kPa）为Wyoming膨润土的7%,Δw_max（0.37%）为Wyoming膨润土的6%,滞回效应很小。印证了非膨胀土脱湿吸湿主要发生在颗粒表面（而非层间）致其滞回效应较小的机制解释。

以上讨论明晰了2.2节中的论述：高吸力下滞回效应既受CEC的强烈影响,亦受SSA控制,且从R²上看,其受SSA影响更大。至于是否考虑滞回效应,应视土样与工况等具体情况而定,鉴于Wyoming膨润土具有最大的HHA,可采用其作为标准,其它土样的HHA相对值亦列入表4中,可见从开封黄河砂的0.01到宁明膨胀土的0.79,HHA相对值可作为实际工况中是否考虑滞回效应的依据。

3. 高吸力下持水特征的本构描述

基于对以上9种土样高吸力下SWRC规律性的认知,经尝试,建议了Fredlund-Xing（1994）模型^[1]的修正形式描述高吸力下SWRC：

$\begin{matrix} w (ψ) = C (ψ) \frac{w_{u}}{{\ln [\exp (1) + {(\frac{(ψ - ψ_{b})}{a})}^{n}]}^{m}} \\ = [1 - \frac{\ln (1 + ψ / ψ_{r})}{\ln (1 + 10^{6} / ψ_{r})}] \frac{w_{u}}{{\ln [\exp (1) + {(\frac{(ψ - ψ_{b})}{a})}^{n}]}^{m}} 。 \end{matrix}$

(8)

式中 w为质量含水率（%）；ψ为吸力（kPa）；w(ψ)为质量含水率表达的SWRC；C(ψ)为修正系数函数,能够迫使SWRC通过零含水率对应吸力10⁶ kPa的点。4个参数a,n,m,ψ_r为Fredlund-Xing(1994)模型已有参数,a为与拐点位置相关的土性参数（kPa）；n为与拐点处斜率相关的土性参数,量纲为1,m为与曲率相关的土性参数,量纲为1,ψ_r为残余吸力（kPa）。

为描述高吸力下SWRC,将Fredlund-Xing模型中饱和质量含水率w₀用w_u替代,w_u为高吸力下SWRC质量含水率上边界（最大值）,相应吸力为ψ_b。增加土性参数ψ_b是式（8）与Fredlund-Xing模型形式上的主要区别,ψ_b单位为kPa,物理意义是高吸力下SWRC吸力下边界。由此可见,修正的Fredlund-Xing模型共有6个参数：w_u,ψ_b,ψ_r,a,n,m。为区分吸湿与脱湿过程,相应参数增加上标w（wetting,表示吸湿）或d（drying,表示脱湿）。

采用式（8）分别对9种土样高吸力下SWRC进行拟合,流程如下：

（1）采用表2给出的吸湿结束点（脱湿起始点）含水率w₉₅值作为w_u值,对应吸力值作为ψ_b值；w_u与ψ_b为吸脱湿过程共用参数值。

（2）对于吸湿过程,采用表2给出的吸湿起始点吸力值作为ψ_r值；至此,吸湿过程所需确定的参数仅余a,n,m。依据式（8）在Excel中通过规划求解功能对吸湿过程SWRC数据进行非线性拟合获得a,n,m最优解以及拟合结果的决定系数R²。

（3）对于脱湿过程,采用表2给出的脱湿结束点吸力值作为ψ_r值；依据式（8）在Excel中通过规划求解功能对脱湿过程SWRC数据进行非线性拟合获得a,n,m最优解以及R²。

前8种土样采用上述流程获得的模型参数与R²见表5,可见8种土样,无论脱湿吸湿,修正的Fredlund-Xing模型再现结果的R²均在0.99以上。为节约篇幅,其修正Fredlund-Xing模型数值再现结果亦放在图2中,可见式（8）相当好地再现了高吸力下8种土样脱湿与吸湿过程SWRC。

表 5 高吸力下修正Fredlund-Xing模型参数

Table 5. Modified Fredlund-Xing model parameters for 9 kinds of soils under high suctions

土样名称	共用参数		吸湿过程					脱湿过程
土样名称	w_u/%	ψ_b/kPa	ψ_r^w/kPa	a^w/kPa	n^w	m^w	R²	ψ_r^d/kPa	a^w/kPa	n^d	m^d	R²
Wyoming膨润土	21.46	7686	451647	248967	0.94	10.54	1.00	461106	90593	1.06	2.09	0.99
宁明膨胀土	19.45	7468	471755	245967	0.82	8.02	1.00	463909	90230	0.94	2.13	1.00
荆门黄褐色膨胀土	13.40	7700	484119	237692	0.61	4.34	1.00	468823	91452	0.82	1.90	1.00
Denver黏土岩	6.79	7410	476506	267853	0.57	4.14	1.00	465943	91075	0.66	1.79	1.00
荆门棕褐色膨胀土	9.63	7439	483240	87263	0.64	2.81	1.00	510367	86362	0.80	1.96	0.99
武汉黏土	7.37	7715	485114	81572	0.67	3.77	1.00	470929	80590	0.71	2.39	0.99
三门峡粉质黏土	6.19	7380	510892	213682	0.67	4.50	1.00	470498	91368	0.82	1.56	1.00
郑州粉土	2.34	7061	509791	30152	0.78	1.17	0.99	510347	31576	0.58	0.86	1.00
开封黄河砂	1.28	6786	—	76542	0.66	1.04	0.96	—	76542	0.66	1.04	0.96

下载: 导出CSV

| 显示表格

对第9种土样开封黄河砂,由图2可见其SWRC滞回行为非常小,因此采用同一组模型参数描述其SWRC,此外不考虑式（8）中修正系数函数C(ψ),即C(ψ) = 1,对吸脱湿SWRC数据进行非线性拟合获得a,n,m最优解见表5,同时描述其吸脱湿SWRC的R²达到0.96,由图2的再现结果可见式（8）非常好地对其SWRC进行了本构描述。

此外,对比表5中吸脱湿过程a,n,m值可见,对同种土样,相对脱湿过程,吸湿过程a值较大说明其拐点位置靠后,n值较低说明其拐点处斜率相对较小,m值较大说明其曲率较大。

由此可见,文中建议的Fredlund-Xing模型修正形式有6个参数：w_u,ψ_b,ψ_r值直接从实测SWRC数据确定,a,n,m值通过非线性拟合获得。Fredlund- Xing(1994)模型中4个参数（a,n,m,ψ_r）需通过非线性拟合获得,还有一个参数饱和质量含水率w₀需试验测定（从实测SWRC数据确定）,实际上有5个参数。文中建议的修正形式仅增加了一个参数ψ_b,且ψ_b与w_u、ψ_r直接从实测SWRC数据确定,只需非线性拟合3个参数（a,n,m）,且该修正形式能够很好地分别描述吸湿与脱湿过程中SWRC强烈的非线性行为。

4. 结论

（1）9种土样高吸力下吸湿与脱湿过程持水特征测试最长历时为2.6 d,有205个数据点,说明动态露点法极大缩短了高吸力下SWRC测试时间,且数据点丰富,能够更好描述土样持水特征。

（2）w₉₅作为RH = 95%下的吸湿质量含水率,是表征土样持水能力的特征点,反映土样亲水性强弱,w₉₅与CEC具有非常高的线性相关性,w₉₅作为膨胀潜势的判别标准是可行的。

（3）SWRC水力滞回效应强弱可用吸脱湿曲线间滞回区域面积HHA描述,HHA与CEC、SSA均有非常高的线性相关性,表明滞回效应强弱既受土样吸附阳离子能力的强烈影响,亦受土样SSA控制,且从R²看,其受SSA影响更大。HHA与w_L,I_p均正相关,表明HHA受土样塑性大小控制。

（4）SWRC滞回效应最大值可用同一ψ下脱湿与吸湿曲线对应w之差最大值Δw_max量化,土样Δw_max值与w_L,I_p,CEC,SSA均正相关,反映了水力滞回导致的w偏差范围。高吸力范围,不考虑水力滞回会导致SWRC上w最高92.1 %的相对误差。如工程中需要用当前w估算ψ,则同一w下,脱湿路径上ψ与吸湿路径上ψ的比值最高可达2.71。

（5）建议采用Fredlund-Xing模型的修正形式描述高吸力下SWRC,方程有6个参数,w_u,ψ_b,ψ_r值直接从实测SWRC数据确定,a,n,m值通过非线性拟合获得。对9种土样SWRC的修正Fredlund -Xing模型数值再现结果表明该方程可分别很好地描述吸湿与脱湿过程中SWRC强烈的非线性行为。

图 1 有效平均应力为零时的临界状态孔隙比随各向异性状态参数A的变化

Figure 1. Variation of critical state void ratio with anisotropic state-parameter A

下载: 全尺寸图片幻灯片

图 2 不排水三轴压缩路径下试验与模拟结果对比

Figure 2. Comparison between measured and simulated responses in undrained triaxial compression tests

下载: 全尺寸图片幻灯片

图 3 不排水定主应力方向剪切试验的试验与模拟结果对比

Figure 3. Comparison between measured and simulated responses in undrained shear tests with fixed directions of principal stresses

下载: 全尺寸图片幻灯片

图 4 不排水定中主应力比剪切试验的试验与模拟结果对比

Figure 4. Comparison between measured and simulated stress paths in undrained shear tests with fixed intermediate principal stress ratios

下载: 全尺寸图片幻灯片

图 5 等向固结单剪试验与模拟结果

Figure 5. Comparison between measured and simulated stress paths in undrained hollow cylindrical simple shear tests following isotropic consolidation

下载: 全尺寸图片幻灯片

图 6 　K₀固结单剪试验与模拟结果（K₀=0.5）

Figure 6. Comparison between measured and simulated stress paths in undrained hollow cylindrical simple shear tests following K₀ consolidation

下载: 全尺寸图片幻灯片

图 7 有效平均应力-广义剪应力空间内静态液化失稳线

Figure 7. Instability lines in space of effective mean normal stress and deviatoric stress

下载: 全尺寸图片幻灯片

表 1 Toyoura砂模型参数

Table 1 Model parameters of Toyoura sand

弹性参数	临界状态参数	剪胀参数	硬化参数	各向异性参数
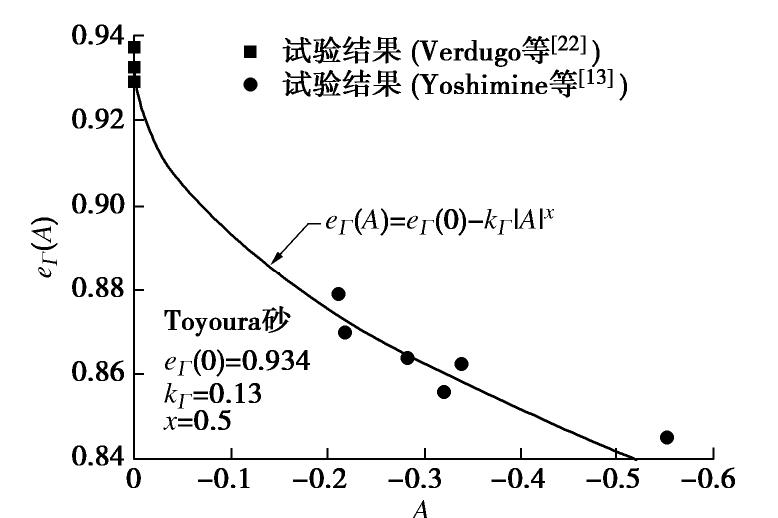
G₀=125, $ν$ =0.05	M_cs=1.25, e_г=0.934, λ_c=0.019, ξ=0.7	d₀=0.88, m=3.5	h₁=3.15, h₂=3.05, n=1.1	Δ=0.214, K_г=0.13, k_d=1.8, k_h=0.9, c=0.75, x=0.5,

下载: 导出CSV

参考文献(28)

[1]	SLADEN J A, DHOLLANDER R D, KRAHN J. Back analysis of the Nerlerk berm liquefaction slides[J]. Canadian Geotechnical Journal, 1985, 22(4): 579-588. doi: 10.1139/t85-077
[2]	ZENG S, LU X L, HUANG M S. Discrete element modeling of static liquefaction of shield tunnel face in saturated sand[J]. Acta Geotechnica, 2019, 14: 1643-1652. doi: 10.1007/s11440-019-00806-w
[3]	黄茂松, 李学丰, 钱建固. 各向异性砂土的应变局部化分析[J]. 岩土工程学报, 2012, 34(10): 1885-1892. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201210004.htm HUANG Mao-song, LI Xue-feng, QIAN Jian-gu. Strain localization of anisotropic sands[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(10): 1885-1892. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201210004.htm
[4]	黄茂松, 曲勰, 吕玺琳. 基于状态相关本构模型的松砂静态液化失稳数值分析[J]. 岩石力学与工程学报, 2014, 33(7): 1479-1487. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201407021.htm HUANG Mao-song, QU Xie, LÜ Xi-lin. Instability and static liquefaction analysis of loose sands with a state-dependent constitutive model[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(7): 1479-1487. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201407021.htm
[5]	MROZ Z, BOUKPETI N, DRESCHER A. Constitutive model for static liquefaction[J]. International Journal of Geomechanics, 2003, 3(2): 133-144. doi: 10.1061/(ASCE)1532-3641(2003)3:2(133)
[6]	吕玺琳, 赖海波, 黄茂松. 饱和土体静态液化失稳理论预测[J]. 岩土力学, 2014, 35(5): 1330-1333, 1339. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201405018.htm LÜ Xi-lin, LAI Hai-bo, HUANG Mao-song. Theoretically predicting instability of static liquefaction of saturated soils[J]. Rock and Soil Mechanics, 2014, 35(5): 1330-1333, 1339. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201405018.htm
[7]	ANDRADE J E. A predictive framework for liquefaction instability[J]. Géotechnique, 2009, 59(8): 673-682. doi: 10.1680/geot.7.00087
[8]	LASHKARI A. Prediction of flow liquefaction instability of clean and silty sands[J]. Acta Geotechnica, 2016, 11(5): 987-1014. doi: 10.1007/s11440-015-0413-9
[9]	BUSCARNERA G, DATTOLA G, DI PRISCO C. Controllability, uniqueness and existence of the incremental response: A mathematical criterion for elastoplastic constitutive laws[J]. International Journal of Solids and Structures, 2011, 48(13): 1867-1878. doi: 10.1016/j.ijsolstr.2011.02.016
[10]	NOVA R. Controllability of the incremental response of soil specimens subjected to arbitrary loading programmes[J]. Journal of the Mechanical Behavior of Materials, 1994, 5(2): 193-202. doi: 10.1515/JMBM.1994.5.2.193
[11]	BUSCARNERA G, WHITTLE A J. Model prediction of static liquefaction: influence of the initial state on potential instabilities[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(3): 420-432. doi: 10.1061/(ASCE)GT.1943-5606.0000779
[12]	WANATOWSKI D, CHU J. Static liquefaction of sand in plane strain[J]. Canadian Geotechnical Journal, 2007, 44(3): 299-313. doi: 10.1139/t06-078
[13]	YOSHIMINE M, ISHIHARA K, VARGAS W. Effects of principal stress direction and intermediate principal stress on undrained shear behavior of sand[J]. Soils and Foundations, 1998, 38(3): 179-188. doi: 10.3208/sandf.38.3_179
[14]	吕玺琳, 钱建固, 黄茂松. 不排水加载条件下K₀固结饱和砂土失稳预测[J]. 岩土工程学报, 2015, 37(6): 1010-1015. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201506007.htm LÜ Xi-lin, QIAN Jian-gu, HUANG Mao-song. Prediction of instability of K₀-consolidated saturated sands under undrained loading conditions[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(6): 1010-1015. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201506007.htm
[15]	LÜ X L, HUANG M S. Static liquefaction of sands under isotropically and K₀-consolidated undrained triaxial conditions[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, 141(1): 04014087. doi: 10.1061/(ASCE)GT.1943-5606.0001206
[16]	LÜ X L, HUANG M S, ANDRADE J E. Predicting the initiation of static liquefaction of cross-anisotropic sands under multiaxial stress conditions[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2017, 41(17): 1724-1740. doi: 10.1002/nag.2697
[17]	陈洲泉, 黄茂松. 砂土各向异性与非共轴特性的本构模拟[J]. 岩土工程学报, 2018, 40(2): 243-251. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201802005.htm CHEN Zhou-quan, HUANG Mao-song. Constitutive modeling of anisotropic and non-coaxial behaviors of sand[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(2): 243-251 (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201802005.htm
[18]	PAPADIMITRIOU A G, BOUCKOVALAS G D. Plasticity model for sand under small and large cyclic strains: A multiaxial formulation[J]. Soil Dynamics and Earthquake Engineering, 2002, 22: 194-204.
[19]	LI X S, DAFALIAS Y F. Constitutive modeling of inherently anisotropic sand behavior[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(10): 868-880. doi: 10.1061/(ASCE)1090-0241(2002)128:10(868)
[20]	ODA M, NAKAYAMA H. Introduction of inherent anisotropy of soil in the yield function[C]//Micromechanics of Granular Materials, 1988, Amsterdam: 81-89.
[21]	YANG Z X, LI X S, YANG J. Quantifying and modelling fabric anisotropy of granular soils[J]. Géotechnique, 2008, 58(4): 237-248. doi: 10.1680/geot.2008.58.4.237
[22]	VERDUGO R, ISHIHARA K. The steady state of sandy soils[J]. Soils and Foundations, 1996, 36(2): 81-91.
[23]	BEEN K, JEFFERIES M G. A state parameter for sands[J]. Géotechnique, 1985, 35(2): 99-112.
[24]	HILL R. A general theory of uniqueness and stability in elastic-plastic solids[J]. Journal of the Mechanics and Physics of Solids, 1958, 6(3): 236-249.
[25]	LADE P V. Static instability and liquefaction of loose fine sandy slopes[J]. Journal of Geotechnical Engineering, 1992, 118(1): 51-71.
[26]	LÜ X L, HUANG M S, ANDRADE J E. Modeling the static liquefaction of unsaturated sand containing gas bubbles[J]. Soils and Foundations, 2018, 58(1): 122-133.
[27]	ANDEADE J E. A predictive framework for liquefaction instability[J]. Géotechnique, 2009, 59(8): 673-682.
[28]	LI X S, DAFALIAS Y F. Dilatancy for cohesionless soils[J]. Géotechnique, 2000, 50(4): 449-460.