现代地基设计理论的创新与发展

杨光华

doi:10.11779/CJGE202101001

现代地基设计理论的创新与发展 English Version

杨光华

1.
广东省水利水电科学研究院,广东　广州　510635
2.
广东省岩土工程技术研究中心,广东　广州　510635

基金项目:

国家自然科学基金项目 52078143

详细信息

中图分类号: TU43
计量
- 文章访问数: 621
- HTML全文浏览量: 31
- PDF下载量: 563
出版历程
- 收稿日期: 2020-10-16
- 网络出版日期: 2022-12-04
- 刊出日期: 2020-12-31

Innovation and development of modern theories for foundation design

YANG Guang-hua

1.
Guangdong Research Institute of Water Resources and Hydropower, Guangzhou 510635, China
2.
The Geotechnical Engineering Technology Center of Guangdong Province, Guangzhou 510635, China

摘要

摘要: 主要介绍了依据现场原位压板载荷试验而建立的一套地基设计的新理论。地基设计中地基沉降计算与地基承载力合理确定的问题是土力学中的经典问题。现代土力学理论虽然发展了土的本构模型和现代数值计算方法,解决了非线性等复杂的计算难题,但实际工程设计中,目前采用的仍是传统的半理论半经验的方法,这是土力学理论创立近百年以来都没很好解决的一个问题。问题的根本原因是什么?应如何破解?本文认为对于结构性的硬土地基,传统理论依据室内土样试验求参数,由于取样扰动等的影响,这样得到的参数不能反映原位土的特性,从而使依据这些参数计算的结果与实际结果差异大。为解决这个难题,依据现场原位压板载荷试验曲线建立了切线模量法的计算模型并反算出模型的3个土体参数：初始切线模量 $E_{t0}$ $E_{t0}$ ,黏聚力 $c$ $c$ 和内摩擦角 $φ$ $φ$ 。该法所需参数少,物理意义明确,参数来源于现场原位试验,避免了取样扰动影响,精度可靠,可以计算基础沉降的非线性直到破坏的全过程。对于地基承载力,提出了用切线模量法计算实际基础的荷载沉降的p-s曲线,根据p-s曲线依据强度和变形双控的原则确定最合适的地基承载力的方法,实现变形控制设计,解决了以往直接由压板载荷试验曲线确定承载力存在的尺寸效应问题。对软土地基的沉降计算,在Duncan-Chang模型基础上,用压缩试验的e-p曲线构建了非线性沉降的实用计算方法,并建立了用压缩模量 $E_{s 1 - 2}$ $E_{s 1 - 2}$ 求e-p曲线的方法,这样只用压缩模量 $E_{s 1 - 2}$ $E_{s 1 - 2}$ 即可进行非线性沉降计算。由于一般饱和软土的 $E_{s 1 - 2}$ $E_{s 1 - 2}$ 为2～4 MPa,变化范围小,参数简单而较为可靠,从而使方法易于应用。该项研究为破解土力学的百年难题提供了新的思路,值得进一步发展完善,为现代地基设计提供更科学的新方法。
- 地基沉降 /
- 承载力 /
- 切线模量法 /
- 压板载荷试验
Abstract: A set of new theory of foundation design is introduced based on in-situ plate loading tests. The calculation of foundation settlement and the reasonable determination of bearing capacity in foundation design are the classic problems in soil mechanics. Although the modern soil mechanics theories have developed soil constitutive models and numerical methods to solve complex problems such as nonlinearities, the actual engineering design around the world is still using the traditional semi-theoretical and semi-empirical method. It is a problem that has not been solved well since the foundation of soil mechanics theory for nearly a hundred years. What is the root cause of the problem? How to solve it? It is believed that for the structured hard soils, the traditional theories are based on the indoor soil sample tests to obtain parameters. Due to the influences of sampling disturbances, the parameters obtained in this way cannot reflect the characteristics of the in-situ soils, so that the calculated results based on such parameters are not consistent with actual conditions and the results vary greatly. In order to solve this problem, the model for calculating the tangent modulus method is established based on the in-situ plate loading test curve, and the three soil parameters of the model are inversely calculated: initial tangent modulus $E_{t0}$ $E_{t0}$ , cohesion $c$ $c$ and internal friction angle $φ$ $φ$ . The proposed method requires few parameters and has clear physical meaning. The parameters are derived from the in-situ tests, avoiding the influences of sampling disturbance, and the accuracy is reliable. It can be used to calculate the whole process from the nonlinearity of foundation settlement to failure. For the bearing capacity of foundation, the relation curve of the pressure and settlement (p-s curve) of the actual foundation is calculated by the tangent modulus method. According to the p-s curve, a method to determine the most suitable bearing capacity of foundation based on the principles of dual-control of strength and deformation realizes the deformation control design. At the same time, this method can solve the problem of the size effect of the bearing capacity directly determined by the plate loading test curve in the past. For the settlement calculation of soft soil foundation, on the basis of the Duncan-Chang model, a practical method for calculating the nonlinear settlement is established using the e-p curve of the compression tests. And a method for calculating e-p curve with compressive modulus $E_{s 1 - 2}$ $E_{s 1 - 2}$ is established, so that only the compressive modulus $E_{s 1 - 2}$ $E_{s 1 - 2}$ can be used to calculate the nonlinear settlement. Since the compressive modulus $E_{s 1 - 2}$ $E_{s 1 - 2}$ of general saturated soft soils is about 2~ 4 MPa, the range of change is small, the parameters are simple and reliable, and the proposed method is easy to apply. This research provides a new idea for solving the century-old problems of soil mechanics and a more scientific new method for modern foundation design, which is worthy of further development and improvement.
- foundation settlement /
- bearing capacity /
- tangent modulus method /
- plate loading test

HTML全文

0. 引言

持水特征曲线指土体持水状态（可用体积含水率、质量含水率或饱和度表达）与土中水的能量状态（可用吸力、势能或相对湿度表达）之间的关系^[1],描述了土中水（液相）与土（固相）间的能量平衡状态^[2]。

土体持水的物理化学机制有毛细、吸附与渗透。毛细机制与弯液面上的表面张力有关,受Young- Laplace方程控制（土体孔径越小其毛细吸力越大）,当土中水能量状态低至其空化点以下,毛细水汽化,相应毛细机制消失。吸附机制指（黏）土颗粒表面由于van der Waals力、双电层力、阳离子水化等造成的短程吸附作用导致的土中水能量降低,可用Kelvin方程描述。通常将毛细与吸附机制导致的土中水相对自由水状态而言势能的降低称为基质势（用负值表达）；将对应土体固相的持水/吸水能力（用正值表达）称为基质吸力；二者数值相等,符号相反。此外,渗透机制指溶解盐会降低土中水的能量状态,其能量降低程度与溶质类型和浓度相关。

SWRC表征土体持水能力,原本用于农业领域,随后的研究表明非饱和状态下的渗流、强度与变形等土力学行为^[1]乃至土的成分与结构等土质学特征^[2]均与SWRC密切相关,因而成为描述非饱和状态下土体性状的关键指标与工具,在非饱和土力学研究与工程应用中具有基础的、特殊的、关键的作用与位置,其研究成果亦非常丰富^[1-3],但大部分SWRC^[1-3]由轴平移方法获得,受陶土板进气值限制,其基质吸力目前仅能控制在1500 kPa以内,根据Kelvin方程（式（1））可知其对应的相对湿度RH为98.9%以上（环境温度25℃时）。然而,自然界中RH变化范围远比轴平移方法所能控制的RH范围大；例如中国主要城市各月RH统计^[4]显示,最低14%（拉萨,2月）,最高90%（长沙,10月与11月；海口,1月）；因而高吸力（RH低于95%或吸力高于7.1 MPa）下的土体持水特征研究具有特别的现实意义。

高吸力下土体持水特征测试常用方法主要有：滤纸法^[5-8]（适用于10～100 MPa）、冷镜湿度计法^[9]（适用于0～300 MPa）、饱和盐溶液等压湿度控制法^[10-12]（适用于3～400 MPa）、干湿空气混合湿度控制法^[13]（适用于7～600 MPa）等。前两种为吸力量测方法,难以控制吸力；后两种为吸力控制方法,适于测定完整的SWRC,但蒸汽平衡历时漫长,如文献[14]采用饱和盐溶液等压湿度控制法测定3.3～359.1 MPa吸力范围的膨胀土SWRC耗时319 d,阻碍了高吸力下土体持水特征的研究与应用。

近年来出现的动态露点等温线方法^[15-16]使得上述情况有所改观,该方法能够在较短时间（几天内）获得相对湿度在3%～95%范围的SWRC。为了给高吸力下相关土力学工程实践提供依据和参考,本文采用该方法：①对从黏土质砂到极高塑性黏土的9种土样开展高吸力下吸脱湿过程持水特征测试；②采用RH = 95%下的吸湿质量含水率w₉₅量化高吸力下持水能力,采用吸脱湿SWRC间滞回区域面积HHA量化高吸力下SWRC滞回效应强弱,采用同一吸力下吸脱湿SWRC含水率之差最大值Δw_max量化水力滞回导致的含水率偏差范围；③探讨w₉₅、HHA、Δw_max与液限w_L、塑性指数I_p、阳离子交换量CEC、比表面积SSA等土性参数间量化关系；④构建修正的Fredlund-Xing模型描述高吸力下吸脱湿过程SWRC。

1. 研究方案

1.1 试验土样

试验采用Wyoming膨润土、宁明膨胀土、荆门黄褐色膨胀土、Denver黏土岩、荆门棕褐色膨胀土、武汉黏土、三门峡粉质黏土、郑州粉土和开封黄河砂共9种土样,其物理性质指标测试结果见表1。

表 1 试验用土的物理性质指标

Table 1. Physical property indexes of soils

土样名称	颗粒相对质量密度^[17]	颗粒所占比例^[17]/%				液限^[17]/%	塑限^[17]/%	塑性指数	塑性^[18]	USCS 定名^[19]	比表面积EGME^[20]/(m²·g^-1)	CEC(NH₄⁺)^[17]/( mmol·kg^-1)	自由膨胀率^[21]/%	膨胀潜势^[21]
土样名称	颗粒相对质量密度^[17]	>0.075 mm	0.005~0.075 mm	0.002~0.005 mm	<0.002 mm	液限^[17]/%	塑限^[17]/%	塑性指数	塑性^[18]	USCS 定名^[19]	比表面积EGME^[20]/(m²·g^-1)	CEC(NH₄⁺)^[17]/( mmol·kg^-1)	自由膨胀率^[21]/%	膨胀潜势^[21]
Wyoming膨润土	2.70	5.1	14.2	3.8	77.0	217.7	33.1	184.5	极高	CH	500.1	621	775	强
宁明膨胀土	2.73	5.8	2.9	0.3	91.1	164.6	37.6	127.0	极高	CH	393.0	508	655	强
荆门黄褐色膨胀土	2.75	2.1	47.4	21.5	29.0	62.9	25.5	37.4	高	CH	236.5	309	75	中
Denver黏土岩	2.72	8.5	44.2	20.6	26.7	46.0	23.2	22.8	中等	CL	88.7	160	38	—
荆门棕褐色膨胀土	2.72	11.6	42.4	26.7	19.3	41.8	20.7	21.1	中等	CL	110.4	254	40	弱
武汉黏土	2.73	5.5	63.9	9.6	21.0	40.3	18.2	22.1	中等	CL	112.5	154	39	—
三门峡粉质黏土	2.72	0.5	82.8	5.7	11.1	35.2	19.1	16.1	中等	CL	108.5	149	30	—
郑州粉土	2.70	8.7	77.4	2.5	11.4	26.1	14.8	11.3	低	CL	27.7	50	9	—
开封黄河砂	2.68	62.6	36.0	0.2	1.3	—	—	—	—	SC	7.5	16	—	—

下载: 导出CSV

| 显示表格

1.2 蒸汽吸附分析仪工作原理

美国Meter公司生产的蒸汽吸附分析仪（Vapor Sorption Analyzer, VSA）见图1,用于测试动态的或平衡的水分吸附等温线（moisture sorption isotherms）,即给定温度下的SWRC。

图 1 蒸汽吸附分析仪

Figure 1. Vapor sorption analyzer

下载: 全尺寸图片幻灯片

VSA采用动态露点等温线（dynamic dew point isotherm, DDI）方法获得动态水分吸附等温线；采用控制湿度下测试样质量的方法（dynamic vapor sorption, DVS）获得静态（平衡）水分吸附等温线。其工作原理是：DDI方法既不控制含水率亦不控制RH,而是在用湿气流湿化/干气流脱湿过程中通过高精度天平测试样质量变化、通过冷镜露点法测RH得到动态水分吸附等温线。DVS方法是在控制RH条件下跟踪试样质量变化以获得静态（平衡）水分吸附等温线,每级湿度下的稳定（平衡）标准可用预设时间间隔或预设试样质量变化幅度。Likos等^[15]与Arthur等^[22]试验证实了DDI方法的精度与可靠性,系统试验研究表明DDI方法与DVS方法获得的SWRC无明显偏差。

VSA相对湿度控制范围是3%～95%（25℃下对应吸力范围为7.1～482.9 MPa）,试样质量建议范围为500～5000 mg,试样温度可控范围为15℃～60 ℃。

1.3 高吸力下持水特征试验方案

采用VSA测定9种土样高吸力下SWRC。将土样风干碾散过0.5 mm筛,置于烘箱中烘至衡量（105 ℃下烘干48 h）,取出置于干燥器内冷却至室温,每次取约1000 mg试验。试验方案与步骤如下：

（1）仪器准备

将VSA在工作台上调平,安装干燥管,水箱中注入去离子水,检查天平,标定相对湿度。

（2）设定SWRC量测步骤

鉴于采用DDI方法与DVS方法测土样SWRC具有很好的一致性^[22],且前者测试历时约为后者的1/25^[15],因此采用DDI方法。由于试样是完全烘干后的,质量含水率w为0,第1步设置初始RH为3%,最终RH为95%,用DDI方法采集吸湿过程w数据RH,即土样SWRC吸湿边界线；第2步设置初始RH为95%、最终RH为3%,目的是获得土样SWRC的脱湿曲线；由于脱湿曲线起始点为RH=95%对应点,所以并非脱湿边界线。此外,设定样品室温度为25℃。

（3）测定SWRC

将试样置入样品杯,放入试样室开始测试,测试由VSA自动执行。试验结束后,取出试样杯称试样质量,烘干后复测干土质量,并在计算机终端下载SWRC试验数据。

2. 试验结果分析

由于Kelvin方程（式(1)）确定了吸力ψ与RH间关系,VSA试验结果既可用w-RH关系亦可用w-ψ关系表达；鉴于非饱和土力学中常用w-ψ关系,因此将9种土样w-ψ关系表达的SWRC绘制在图2中,将每种土样试验历时,试验数据点数,吸湿起始点、吸湿结束点（脱湿起始点）、脱湿结束点对应的RH,ψ,w值列在表2中。

图 2 高吸力下的SWRC（RH = 3%~95%）

Figure 2. Soil-water retention curves under high suctions

下载: 全尺寸图片幻灯片

表 2 高吸力下SWRC的吸湿/脱湿起始点与结束点

Table 2. Start point/end point of adsorption/desorption of SWRCs under high suctions

土样名称	试验历时/min	试验数据点数	吸湿起始点			吸湿结束点（脱湿起始点）			脱湿结束点
土样名称	试验历时/min	试验数据点数	RH	ψ/kPa	w/%	RH	ψ/kPa	w₉₅/%	RH	ψ/kPa	w/%
Wyoming膨润土	3135	203	0.0375	451647	0.67	0.9457	7686	21.46	0.0350	461106	0.87
宁明膨胀土	3777	205	0.0324	471755	0.76	0.9472	7468	19.45	0.0343	463909	1.02
荆门黄褐色膨胀土	2982	204	0.0297	484119	1.28	0.9456	7700	13.40	0.0331	468823	1.96
Denver黏土岩	2113	201	0.0313	476506	0.79	0.9476	7410	6.79	0.0338	465943	1.14
荆门棕褐色膨胀土	2523	212	0.0299	483240	0.89	0.9474	7439	9.63	0.0245	510367	1.28
武汉黏土	2343	202	0.0294	485114	0.44	0.9455	7715	7.37	0.0326	470929	0.91
三门峡粉质黏土	2186	203	0.0244	510892	0.43	0.9478	7380	6.19	0.0327	470498	0.97
郑州粉土	1787	197	0.0246	509791	0.42	0.9500	7061	2.34	0.0245	510347	0.52
开封黄河砂	1295	148	0.0245	510383	0.65	0.9519	6786	1.28	0.0247	509237	0.67

下载: 导出CSV

| 显示表格

$ψ = - \frac{R T}{ν_{w}} \ln RH$ ,

(1)

式中 ψ为吸力（kPa）；R = 8.314 J/(K·mol),为通用气体常数；T为热力学温度,样品室温度25℃对应T = 298.15 K； $ν_{w}$ = 1.8×10^-5 m³/mol,为水的摩尔体积；RH为相对湿度,量纲为1。

由表2可见,9种土样中宁明膨胀土测试历时最长,为3777 min,即2.6 d,且有205个数据点。一方面说明试验历时为文献[14]中饱和盐溶液等压湿度控制法测试历时（319 d）的1/122,极大缩短了测试时间；另一方面说明数据点丰富,能够更好描述土样的持水特征。

从以下3方面探讨高吸力下的SWRC：①反映土样亲水性强弱的持水能力特征点w₉₅；②描述水力滞回效应强弱的SWRC滞回区域面积HHA；③反映水力滞回导致的含水率偏差范围的SWRC滞回效应最大值Δw_max。

2.1 高吸力下持水能力特征点w₉₅

由图2与表2可见：9种土样从完全干燥状态吸湿结束时（控制RH为95%）对应的质量含水率w₉₅差别相当大,高至Wyoming膨润土的21.46%,宁明膨胀土的19.45%,表明持水能力/亲水性非常强,低至开封黄河砂的1.28%,表明其持水能力/亲水性非常弱。由此可见,w₉₅作为RH = 95%下的吸湿质量含水率,是表征土样持水（吸水）能力的特征点,其数值反映了土样亲水性强弱。

将9种土样的w₉₅与表1给出的CEC对应绘制在图3中,可见w₉₅与CEC具有非常高的线性相关性,其线性拟合结果见式（2）,决定系数R²高达0.99。

$w_{95} = 0.035 CEC + 1.3$ 。

(2)

图 3 9种土的w₉₅-CEC关系

Figure 3. Relationship between w₉₅ and CEC of 9 kinds of soils

下载: 全尺寸图片幻灯片

鉴于《膨胀土地区建筑技术规范》^[21]采用CEC分别为340,260,170 mmol/kg作为判断土样膨胀潜势强（CEC > 340 mmol/kg）、中（CEC =260～340 mmol/kg）、弱（CEC = 170～260 mmol/kg）的界限,将其代入式（2）得到采用w₉₅判别土样膨胀潜势的相应界限分别为13.0%,10.2%,7.1%。即：w₉₅ > 13.0%,判别为强膨胀土；w₉₅=10.2%～13.0%,判别为中膨胀土；w₉₅=7.1%～10.2%,判别为弱膨胀土；w₉₅<7.1%,判别为非膨胀土。

下面对上述方法的可行性进行验证：表3为根据《膨胀土地区建筑技术规范》^[21]测定的Denver膨润土、信阳黏土、商用高岭土的CEC、自由膨胀率及确定的膨胀潜势。采用VSA获得的w₉₅亦列在表3中,Denver膨润土w₉₅为22.47%,大于13.0%,根据w₉₅判别为强膨胀土；信阳黏土w₉₅为8.77%,在7.1%～10.2%,根据w₉₅判别为弱膨胀土；商用高岭土w₉₅为1.03%,小于7.1 %,根据w₉₅判别为非膨胀土。表明采用w₉₅作为膨胀潜势判别标准与采用CEC的判别结果具有很好的一致性,至于如何提高其判别精度,则应收集更多的试验结果,确定更为可靠的强、中、弱膨胀潜势的w₉₅界限值。

表 3 3种土样膨胀潜势的判别指标

Table 3. Eestimation indexes of swelling potential of 3 kinds of soils

土样名称	CEC(NH₄⁺)^[17]/(mmol·kg^-1)	自由膨胀率^[21]/%	膨胀潜势^[21]	w₉₅/%
Denver膨润土	976	111	强	22.47
信阳黏土	206	40	弱	8.77
商用高岭土	4	—	—	1.03

下载: 导出CSV

| 显示表格

2.2 高吸力下SWRC滞回区域面积HHA

由图2可见,高吸力段(RH = 3%～95%),9种土样SWRC均呈现或强或弱的水力滞回行为,即相同吸力下脱湿路径上的w高于吸湿路径上的w。

SWRC水力滞回效应强弱可用脱湿与吸湿曲线间滞回区域面积HHA (hydraulic hysteresis area)描述。根据图2中的脱湿与吸湿曲线数据在Origin软件中数值积分获得9种土样滞回区域面积见表4。

表 4 高吸力下SWRC滞回效应特征参数（R_H = 3%~95%）

Table 4. Hysteresis properties of SWRCs under high suctions

土样名称	滞回区域面积HHA/kPa	HHA 相对值	Δw_max/%	ψ(Δw_max)/kPa	RH(Δw_max)	w_d(Δw_max)/%	w_w(Δw_max)/%	w相对误差/%
土样名称	滞回区域面积HHA/kPa	HHA 相对值	Δw_max/%	ψ(Δw_max)/kPa	RH(Δw_max)	w_d(Δw_max)/%	w_w(Δw_max)/%	$\frac{Δ w_{\max}}{w_{d}}$	$\frac{Δ w_{\max}}{w_{w}}$
Wyoming膨润土	13641	1.00	6.27	68737	0.6069	13.08	6.81	47.9	92.1
宁明膨胀土	10717	0.79	4.18	72744	0.5895	11.00	6.81	38.0	61.4
荆门黄褐色膨胀土	4512	0.33	1.77	37559	0.7612	9.87	8.10	17.9	21.9
Denver黏土岩	2367	0.17	0.69	37184	0.7633	4.80	4.11	14.4	16.8
荆门棕褐色膨胀土	3520	0.26	1.38	30993	0.7984	7.41	6.03	18.6	22.9
武汉黏土	3412	0.25	1.15	31077	0.7979	5.13	3.98	22.4	28.9
三门峡粉质黏土	3439	0.25	1.04	89267	0.5228	3.55	2.51	29.3	41.4
郑州粉土	1002	0.07	0.37	155335	0.3235	1.22	0.85	30.3	43.5
开封黄河砂	196	0.01	0.16	221700	0.1999	0.88	0.72	18.2	22.2

下载: 导出CSV

| 显示表格

由图2与表4可见：9种土样HHA差别显著,对于强膨胀土,Wyoming膨润土高达13641 kPa,宁明膨胀土亦高达10717 kPa；对于中膨胀土,荆门黄褐色膨胀土为4512 kPa；对于弱膨胀土,荆门棕褐色膨胀土为3520 kPa；武汉黏土、三门峡粉质黏土亦达到3412,3439 kPa；而郑州粉土低至1002 kPa；开封黄河砂仅有196 kPa,是Wyoming膨润土的1/70,滞回效应可忽略不计。

以上数据表明：HHA与土样膨胀潜势正相关,将9种土样的HHA与表1给出的CEC、SSA对应绘制在双y轴坐标系中,见图4,可见HHA与CEC、SSA均具有非常高的线性相关性,其过坐标原点的线性拟合结果为

图 4 9种土的CEC-SSA-HHA关系

Figure 4. CEC-SSA-HHA relationship of 9 kinds of soils

下载: 全尺寸图片幻灯片

$CEC = 0 .049 HHA$ ,

(3)

$SSA = 0 .037 HHA$ ,

(4)

式中,HHA与CEC线性相关的R²达到0.94,HHA与SSA线性相关的R²高达0.97。

CEC与SSA是强烈相关但有明显区别的土性指标。CEC指单位质量土样吸附的可交换阳离子总量,反映由于颗粒带负电荷导致的土样吸附阳离子的能力,更大的CEC意味着更强的膨胀潜势。SSA指单位质量土样具有的表面积,反映土样的颗粒级配与矿物成分,更大的SSA意味着更大的塑性,更强的膨胀潜势,更强的亲水性。HHA与CEC、SSA均正相关表明,滞回效应大小既受土样吸附阳离子能力的强烈影响,亦受土样比表面积控制,且从R²上看,其受土样比表面积影响更大。

将8种细粒土HHA与其液限w_L、塑性指数I_p绘制在双y轴坐标系中,见图5。

图 5 8种细粒土的w_L-I_p-HHA关系

Figure 5. w_L-I_p-HHA relationship of 8 kinds of fine-grained soils

下载: 全尺寸图片幻灯片

可见HHA与w_L、I_p均正相关,过坐标原点的线性拟合结果分别为

$w_{L} = 0 .015 HHA$ ,

(5)

$I_{p} = 0.012 HHA$ 。

(6)

式中,HHA与w_L线性相关的R²高达0.97,HHA与I_p线性相关的R²亦达到0.92,表明细粒土HHA与w_L具有更高的线性相关性。由于w_L、I_p代表土样塑性大小,表明HHA受土样塑性大小控制。

2.3 高吸力下SWRC滞回效应最大值Δw_max

SWRC滞回效应指水力滞回（脱/吸湿路径）对SWRC（此处是w-ψ关系）的影响,此处SWRC滞回效应最大值定义为相同ψ下,脱湿曲线对应含水率w_d与吸湿曲线对应含水率w_w之差的最大值Δw_max。根据该定义,在图2中搜索到每种土的Δw_max,及其对应的吸力ψ、RH、脱湿曲线含水率w_d、吸湿曲线含水率w_w,列入表4中。

由表4与图2可见,9种土样Δw_max存在较大差异：强膨胀土Δw_max相当大,如Wyoming膨润土为6.27%,宁明膨胀土为4.18%；中膨胀土,荆门黄褐色膨胀土为1.77 %；弱膨胀土,荆门棕褐色膨胀土为1.38%；中等塑性黏土,武汉黏土为1.15%,三门峡粉质黏土为1.04%,Denver黏土岩为0.69%；低塑性黏土,郑州粉土为0.37%；开封黄河砂仅为0.16%。对比表1可见,土样Δw_max值与w_L,I_p,CEC,SSA均正相关,反映了水力滞回导致的含水率偏差范围。取Δw_max与相应w_d、w_w的比值作为SWRC的含水率相对误差,计算9种土样Δw_max/w_d、Δw_max/w_w结果列于表4与图6。

图 6 由于水力滞回导致的含水率相对误差

Figure 6. Relative errors of water content due to hydraulic hysteresis

下载: 全尺寸图片幻灯片

表4与图6中,同一土样w_w小于w_d,因此采用吸湿曲线含水率w_w作为分母的相对误差比采用脱湿曲线含水率w_d作为分母的相对误差要大。由相对误差计算结果可见：在高吸力范围,不考虑水力滞回会导致持水特征曲线SWRC上质量含水率w最高92.1 %（Wyoming膨润土）的相对误差。

另一方面,如果工程中需要用当前含水率估算吸力,则同一w下,脱湿路径上吸力与吸湿路径上吸力的比值最高可达2.71（图2中Wyoming膨润土,w为6%,脱湿路径上吸力205959 kPa,吸湿路径上吸力76119 kPa,比值为2.71）,印证了高吸力下强膨胀土SWRC滞回效应之强烈。

2.4 高吸力下SWRC滞回行为机制探讨

由图2及2.2节、2.3节对SWRC滞回区域面积HHA与滞回效应最大值Δw_max的分析,可知高吸力下,9种土样中,高塑性（液限高、塑性指数大）、阳离子交换量大、比表面积大的土样滞回效应大,在此对高吸力下SWRC滞回行为机制展开探讨。

水力滞回行为机制解释主要有墨水瓶效应^[1]与接触角效应^[13],前者由于土中孔隙尺寸与形状（可用孔径r概化）的不均匀性所致,后者由于吸湿接触角 $α_{w}$ 通常大于脱湿接触角 $α_{d}$ 所致^[23]。墨水瓶效应与接触角效应均属毛细范畴,受Young-Laplace方程控制：

$ψ_{c} = u_{a} - u_{w} = \frac{2 T_{s} \cos α}{r}$ 。

(7)

式中 ψ_c为毛细吸力,可用孔隙气压力u_a与孔隙水压力u_w之差表达；T_s为水的表面张力； $α$ 为接触角；r为毛细半径。当吸力增大、土中水能量状态低到其空化点以下,毛细水汽化,（土中毛细水比自由水空化点更低,但其对应的ψ_c或RH尚无定论,一般而言RH低于80%,毛细水难以存在^[2]）,墨水瓶效应与接触角效应难以解释高吸力下的滞回行为。

Lu等^[24]给出了高吸力下SWRC滞回机制的一种解释：非膨胀黏土,脱湿与吸湿主要发生在颗粒表面,因而滞回效应较小。膨胀性土,脱湿与吸湿亦可发生于存在可交换阳离子的晶层之间,吸湿时阳离子水化吸附极性水分子,水分子需克服较大的,van der Waals力方能进入层间；脱湿时由于层间距离较大van der Waals力较弱,因此相同ψ下,吸湿路径对应较小的w,脱湿路径对应较大的w。在此结合文中数据探讨该解释的合理性：

高吸力下Wyoming膨润土HHA=13641 kPa,Δw_max=6.27 %,滞回效应最大；自由膨胀率为775 %,膨胀性最大；SSA高达500.1 m²/g,表明其包含了较大的层间比表面积^[25],CEC高达621 mmol/kg,表明其可交换阳离子总量大；印证了吸湿状况下膨胀土层间阳离子水化受van der Waals力阻碍致其含水率较低的机制解释。

相对而言,郑州粉土,SSA为27.7 m²/g,CEC为50 mmol/kg,比表面积小,可交换阳离子总量小。一方面其自由膨胀率（9%）为Wyoming膨润土的1.2 %,表明其为非膨胀土；另一方面,其HHA（1002 kPa）为Wyoming膨润土的7%,Δw_max（0.37%）为Wyoming膨润土的6%,滞回效应很小。印证了非膨胀土脱湿吸湿主要发生在颗粒表面（而非层间）致其滞回效应较小的机制解释。

以上讨论明晰了2.2节中的论述：高吸力下滞回效应既受CEC的强烈影响,亦受SSA控制,且从R²上看,其受SSA影响更大。至于是否考虑滞回效应,应视土样与工况等具体情况而定,鉴于Wyoming膨润土具有最大的HHA,可采用其作为标准,其它土样的HHA相对值亦列入表4中,可见从开封黄河砂的0.01到宁明膨胀土的0.79,HHA相对值可作为实际工况中是否考虑滞回效应的依据。

3. 高吸力下持水特征的本构描述

基于对以上9种土样高吸力下SWRC规律性的认知,经尝试,建议了Fredlund-Xing（1994）模型^[1]的修正形式描述高吸力下SWRC：

$\begin{matrix} w (ψ) = C (ψ) \frac{w_{u}}{{\ln [\exp (1) + {(\frac{(ψ - ψ_{b})}{a})}^{n}]}^{m}} \\ = [1 - \frac{\ln (1 + ψ / ψ_{r})}{\ln (1 + 10^{6} / ψ_{r})}] \frac{w_{u}}{{\ln [\exp (1) + {(\frac{(ψ - ψ_{b})}{a})}^{n}]}^{m}} 。 \end{matrix}$

(8)

式中 w为质量含水率（%）；ψ为吸力（kPa）；w(ψ)为质量含水率表达的SWRC；C(ψ)为修正系数函数,能够迫使SWRC通过零含水率对应吸力10⁶ kPa的点。4个参数a,n,m,ψ_r为Fredlund-Xing(1994)模型已有参数,a为与拐点位置相关的土性参数（kPa）；n为与拐点处斜率相关的土性参数,量纲为1,m为与曲率相关的土性参数,量纲为1,ψ_r为残余吸力（kPa）。

为描述高吸力下SWRC,将Fredlund-Xing模型中饱和质量含水率w₀用w_u替代,w_u为高吸力下SWRC质量含水率上边界（最大值）,相应吸力为ψ_b。增加土性参数ψ_b是式（8）与Fredlund-Xing模型形式上的主要区别,ψ_b单位为kPa,物理意义是高吸力下SWRC吸力下边界。由此可见,修正的Fredlund-Xing模型共有6个参数：w_u,ψ_b,ψ_r,a,n,m。为区分吸湿与脱湿过程,相应参数增加上标w（wetting,表示吸湿）或d（drying,表示脱湿）。

采用式（8）分别对9种土样高吸力下SWRC进行拟合,流程如下：

（1）采用表2给出的吸湿结束点（脱湿起始点）含水率w₉₅值作为w_u值,对应吸力值作为ψ_b值；w_u与ψ_b为吸脱湿过程共用参数值。

（2）对于吸湿过程,采用表2给出的吸湿起始点吸力值作为ψ_r值；至此,吸湿过程所需确定的参数仅余a,n,m。依据式（8）在Excel中通过规划求解功能对吸湿过程SWRC数据进行非线性拟合获得a,n,m最优解以及拟合结果的决定系数R²。

（3）对于脱湿过程,采用表2给出的脱湿结束点吸力值作为ψ_r值；依据式（8）在Excel中通过规划求解功能对脱湿过程SWRC数据进行非线性拟合获得a,n,m最优解以及R²。

前8种土样采用上述流程获得的模型参数与R²见表5,可见8种土样,无论脱湿吸湿,修正的Fredlund-Xing模型再现结果的R²均在0.99以上。为节约篇幅,其修正Fredlund-Xing模型数值再现结果亦放在图2中,可见式（8）相当好地再现了高吸力下8种土样脱湿与吸湿过程SWRC。

表 5 高吸力下修正Fredlund-Xing模型参数

Table 5. Modified Fredlund-Xing model parameters for 9 kinds of soils under high suctions

土样名称	共用参数		吸湿过程					脱湿过程
土样名称	w_u/%	ψ_b/kPa	ψ_r^w/kPa	a^w/kPa	n^w	m^w	R²	ψ_r^d/kPa	a^w/kPa	n^d	m^d	R²
Wyoming膨润土	21.46	7686	451647	248967	0.94	10.54	1.00	461106	90593	1.06	2.09	0.99
宁明膨胀土	19.45	7468	471755	245967	0.82	8.02	1.00	463909	90230	0.94	2.13	1.00
荆门黄褐色膨胀土	13.40	7700	484119	237692	0.61	4.34	1.00	468823	91452	0.82	1.90	1.00
Denver黏土岩	6.79	7410	476506	267853	0.57	4.14	1.00	465943	91075	0.66	1.79	1.00
荆门棕褐色膨胀土	9.63	7439	483240	87263	0.64	2.81	1.00	510367	86362	0.80	1.96	0.99
武汉黏土	7.37	7715	485114	81572	0.67	3.77	1.00	470929	80590	0.71	2.39	0.99
三门峡粉质黏土	6.19	7380	510892	213682	0.67	4.50	1.00	470498	91368	0.82	1.56	1.00
郑州粉土	2.34	7061	509791	30152	0.78	1.17	0.99	510347	31576	0.58	0.86	1.00
开封黄河砂	1.28	6786	—	76542	0.66	1.04	0.96	—	76542	0.66	1.04	0.96

下载: 导出CSV

| 显示表格

对第9种土样开封黄河砂,由图2可见其SWRC滞回行为非常小,因此采用同一组模型参数描述其SWRC,此外不考虑式（8）中修正系数函数C(ψ),即C(ψ) = 1,对吸脱湿SWRC数据进行非线性拟合获得a,n,m最优解见表5,同时描述其吸脱湿SWRC的R²达到0.96,由图2的再现结果可见式（8）非常好地对其SWRC进行了本构描述。

此外,对比表5中吸脱湿过程a,n,m值可见,对同种土样,相对脱湿过程,吸湿过程a值较大说明其拐点位置靠后,n值较低说明其拐点处斜率相对较小,m值较大说明其曲率较大。

由此可见,文中建议的Fredlund-Xing模型修正形式有6个参数：w_u,ψ_b,ψ_r值直接从实测SWRC数据确定,a,n,m值通过非线性拟合获得。Fredlund- Xing(1994)模型中4个参数（a,n,m,ψ_r）需通过非线性拟合获得,还有一个参数饱和质量含水率w₀需试验测定（从实测SWRC数据确定）,实际上有5个参数。文中建议的修正形式仅增加了一个参数ψ_b,且ψ_b与w_u、ψ_r直接从实测SWRC数据确定,只需非线性拟合3个参数（a,n,m）,且该修正形式能够很好地分别描述吸湿与脱湿过程中SWRC强烈的非线性行为。

4. 结论

（1）9种土样高吸力下吸湿与脱湿过程持水特征测试最长历时为2.6 d,有205个数据点,说明动态露点法极大缩短了高吸力下SWRC测试时间,且数据点丰富,能够更好描述土样持水特征。

（2）w₉₅作为RH = 95%下的吸湿质量含水率,是表征土样持水能力的特征点,反映土样亲水性强弱,w₉₅与CEC具有非常高的线性相关性,w₉₅作为膨胀潜势的判别标准是可行的。

（3）SWRC水力滞回效应强弱可用吸脱湿曲线间滞回区域面积HHA描述,HHA与CEC、SSA均有非常高的线性相关性,表明滞回效应强弱既受土样吸附阳离子能力的强烈影响,亦受土样SSA控制,且从R²看,其受SSA影响更大。HHA与w_L,I_p均正相关,表明HHA受土样塑性大小控制。

（4）SWRC滞回效应最大值可用同一ψ下脱湿与吸湿曲线对应w之差最大值Δw_max量化,土样Δw_max值与w_L,I_p,CEC,SSA均正相关,反映了水力滞回导致的w偏差范围。高吸力范围,不考虑水力滞回会导致SWRC上w最高92.1 %的相对误差。如工程中需要用当前w估算ψ,则同一w下,脱湿路径上ψ与吸湿路径上ψ的比值最高可达2.71。

（5）建议采用Fredlund-Xing模型的修正形式描述高吸力下SWRC,方程有6个参数,w_u,ψ_b,ψ_r值直接从实测SWRC数据确定,a,n,m值通过非线性拟合获得。对9种土样SWRC的修正Fredlund -Xing模型数值再现结果表明该方程可分别很好地描述吸湿与脱湿过程中SWRC强烈的非线性行为。

致谢: 感谢广东省水利水电科学研究院岩土中心的同事及学生所做的工作,本项研究结合了多个实际工程开展试验研究。笔者从1997年发表论文开始这一个问题的探索,研究工作包括了从2004级开始的历届研究生的工作。

图 1 实际基础载荷沉降曲线与理想弹塑性曲线

Figure 1. Actual foundation load settlement curve and ideal elastoplastic curve

下载: 全尺寸图片幻灯片

图 2 压板载荷试验曲线

Figure 2. Curves of plate loading tests

下载: 全尺寸图片幻灯片

图 3 地基沉降计算的分层土

Figure 3. Layered soils calculated for foundation settlement

下载: 全尺寸图片幻灯片

图 4 侧限压缩试验及其e-p曲线

Figure 4. Confined compression tests and e-p curve

下载: 全尺寸图片幻灯片

图 5 压板载荷试验的p-s曲线

Figure 5. p-s curves of plate loading tests

下载: 全尺寸图片幻灯片

图 6 小尺寸压板荷载沉降过程

Figure 6. Load settlement process of plate with small sizes

下载: 全尺寸图片幻灯片

图 7 实际基础荷载沉降过程

Figure 7. Load settlement process of actual foundation

下载: 全尺寸图片幻灯片

图 8 分层总和法

Figure 8. Layer-wise summation method

下载: 全尺寸图片幻灯片

图 9 压板载荷试验曲线

Figure 9. Curves of plate loading tests

下载: 全尺寸图片幻灯片

图 10 土体分层

Figure 10. Layered soils

下载: 全尺寸图片幻灯片

图 11 割线模量法

Figure 11. Secant modulus method

下载: 全尺寸图片幻灯片

图 12 工程地质剖面

Figure 12. Engineering geological section

下载: 全尺寸图片幻灯片

图 13 3个压板载荷试验曲线

Figure 13. Curves of three plate loading tests

下载: 全尺寸图片幻灯片

图 14 双曲线线性化拟合

Figure 14. Fitting of hyperbola linearization

下载: 全尺寸图片幻灯片

图 15 拟合双曲线与试验曲线比较

Figure 15. Comparison between fitted hyperbola and test curve

下载: 全尺寸图片幻灯片

图 16 计算曲线与试验曲线比较

Figure 16. Comparison between calculated curves and test curve

下载: 全尺寸图片幻灯片

图 17 切线模量E_t随深度的变化

Figure 17. Change of tangent modulus E_t with depth

下载: 全尺寸图片幻灯片

图 18 切线模量法计算的沉降随深度的变化

Figure 18. Change of calculated settlement by tangent modulus method with depth

下载: 全尺寸图片幻灯片

图 19 ^#5压板载荷沉降p-s曲线（1.0 m×1.0 m）

Figure 19. p-s curves of No. 5 plate loading settlement (1.0 m×1.0 m)

下载: 全尺寸图片幻灯片

图 20 ^#2压板载荷沉降p-s曲线（1.5 m×1.5 m）

Figure 20. p-s curves of No. 2 plate loading settlement (1.5 m×1.5 m)

下载: 全尺寸图片幻灯片

图 21 ^#4压板载荷沉降p-s曲线（2.5 m×2.5 m）

Figure 21. p-s curves of No. 4 plate loading settlement (2.5 m×2.5 m)

下载: 全尺寸图片幻灯片

图 22 ^#1压板载荷沉降p-s曲线（3.0 m×3.0 m）

Figure 22. p-s curves of No. 1 plate loading settlement (3.0 m×3.0 m)

下载: 全尺寸图片幻灯片

图 23 ^#3压板载荷沉降p-s曲线（3.0 m×3.0 m）

Figure 23. p-s curves of No. 3 plate loading settlement (3.0m×3.0m)

下载: 全尺寸图片幻灯片

图 24 切线模量法计算的分层地基

Figure 24. Layered foundation calculated by tangent modulus method

下载: 全尺寸图片幻灯片

图 25 切线模量法计算的分层地基沉降比较

Figure 25. Comparison of settlements of layered foundation calculated by tangent modulus method

下载: 全尺寸图片幻灯片

图 26 切线模量法有限元计算与试验结果的比较

Figure 26. Comparison of finite element calculation between tangent modulus method and test results

下载: 全尺寸图片幻灯片

图 27 不同计算方法计算地基梁地基反力分布

Figure 27. Different methods to calculate distribution of reaction force of foundation beam and foundation

下载: 全尺寸图片幻灯片

图 28 不同方法计算的压缩模量比较

Figure 28. Comparison of compressive modulus calculated by different methods

下载: 全尺寸图片幻灯片

图 29 t=495 d时计算得到的堤基地表沉降断面图

Figure 29. Cross-section of surface settlement of embankment foundation (t=495 d)

下载: 全尺寸图片幻灯片

图 30 堤基地表中心点沉降时间曲线

Figure 30. Settling-time curves of surface at center of embankment foundation

下载: 全尺寸图片幻灯片

图 31 基础的p-s曲线

Figure 31. p-s curves of foundation

下载: 全尺寸图片幻灯片

图 32 切线模量法计算与试验曲线比较

Figure 32. Comparison between tangent modulus method and test curves

下载: 全尺寸图片幻灯片

图 33 2 m宽基础下的荷载沉降曲线

Figure 33. Load settlement curves of foundation of 2 m wide

下载: 全尺寸图片幻灯片

图 34 6 m宽基础下的荷载沉降曲线

Figure 34. Load settlement curves of foundation of 6 m wide

下载: 全尺寸图片幻灯片

表 1 P_1/4法的安全系数

Table 1 Values of safety factor of P_1/4 method

c/kPa	$φ$ $φ$ /(°)
c/kPa	0	5	10	15	20	25	30	35	40	45
0	—	—	1.86	2.13	2.80	4.18	5.62	7.84	15.6	21.7
10	1.52	1.78	2.09	2.38	2.94	4.01	5.28	7.25	13.1	19.1
20	1.65	1.87	2.16	2.47	2.99	3.94	5.12	6.95	11.9	17.6
30	1.70	1.90	2.20	2.52	3.02	3.90	5.03	6.77	11.2	—
40	1.73	1.93	2.22	2.55	3.04	3.88	4.97	6.64	—	—
50	1.75	1.95	2.23	2.57	3.05	3.86	4.93	—	—	—
中值	1.67	1.89	2.12	2.44	2.97	3.96	5.16	7.09	13.0	19.5

下载: 导出CSV

表 2 沉降计算经验系数

Table 2 Empirical coefficients of settlement calculation

基地附加应力	${\bar{E}}_{s}$ ${\bar{E}}_{s}$ /MPa
基地附加应力	2.5	4.0	7.0	15.0	20.0
p₀≥f_ak	1.4	1.3	1.0	0.4	0.2
p₀≤0.75f_ak	1.1	1.0	0.7	0.4	0.2

下载: 导出CSV

表 3 地层参数

Table 3 Parameters of strata

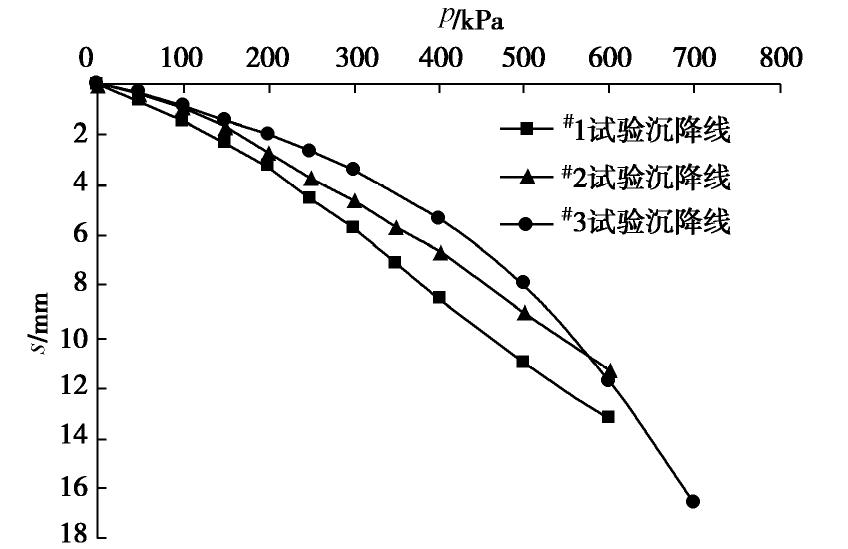
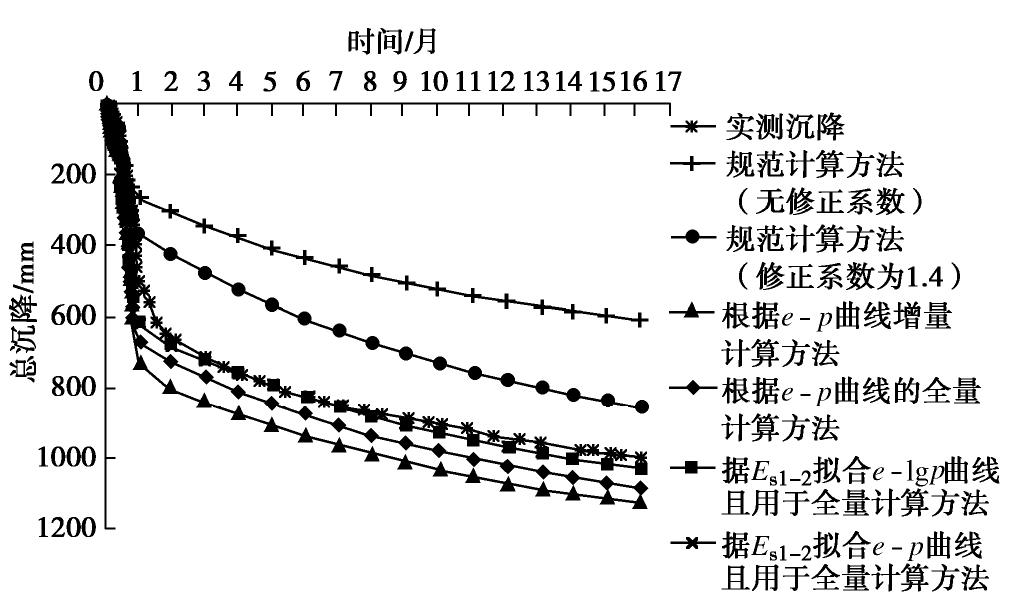
分层土号	岩性	湿密度 $ρ_{s}$ $ρ_{s}$ /(g·cm^-3)	天然含水率w/%	天然孔隙比e	塑性指数I_P	液性指数I_L	压缩系数 $a_{1 - 2}$ $a_{1 - 2}$ /MPa	压缩模量E_s/MPa	抗剪强度		标准击数N_63.5	推荐承载力f_k/kPa
分层土号	岩性	湿密度 $ρ_{s}$ $ρ_{s}$ /(g·cm^-3)	天然含水率w/%	天然孔隙比e	塑性指数I_P	液性指数I_L	压缩系数 $a_{1 - 2}$ $a_{1 - 2}$ /MPa	压缩模量E_s/MPa	c/kPa	$φ$ $φ$	标准击数N_63.5	推荐承载力f_k/kPa
1Qml	素填土	—	—	—	—	—	—	—	—	—	—	60~80
2Qal	细砂	—	—	—	—	—	—	—	—	—	—	60~70
3-①	粉质	1.83~2.12	16.3~29.5	0.475~0.943	8.8~14.1	0.50~0.53	0.265~0.653	2.61~5.77	26.09~91.87	2°10′~14°45′	5.3~13.6	160~180
Qel	黏土	(2.02)	(21.4)	(0.632)	(11.5)	0.50~0.53	(0.406)	(4.33)	26.09~91.87	2°10′~14°45′	(8.5)	160~180
3-②	粉土	1.84~21.0	15.9~22.5	0.540~0.776	6.3~11.4	0.26~0.76	0.245~0.754	2.10~6.65	14.7~75.49	7°8′~35°0′	16.0~32.4	240~260
Qel	粉土	(2.00)	(18.8)	(0.593)	(8.7)	0.26~0.76	0.245~0.754	(4.40)	14.7~75.49	7°8′~35°0′	(20.2)	240~260
注：（）内的值为平均值。

下载: 导出CSV

表 4 荔湾大厦计算与实测沉降比较

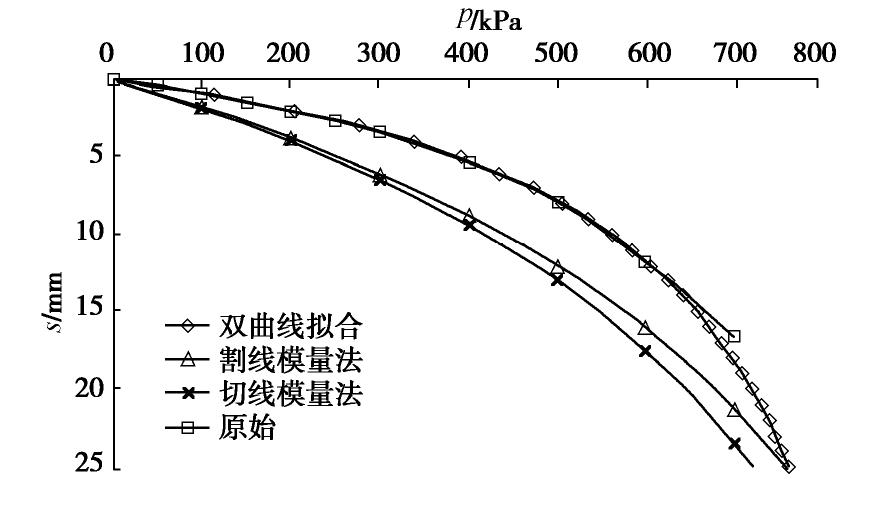
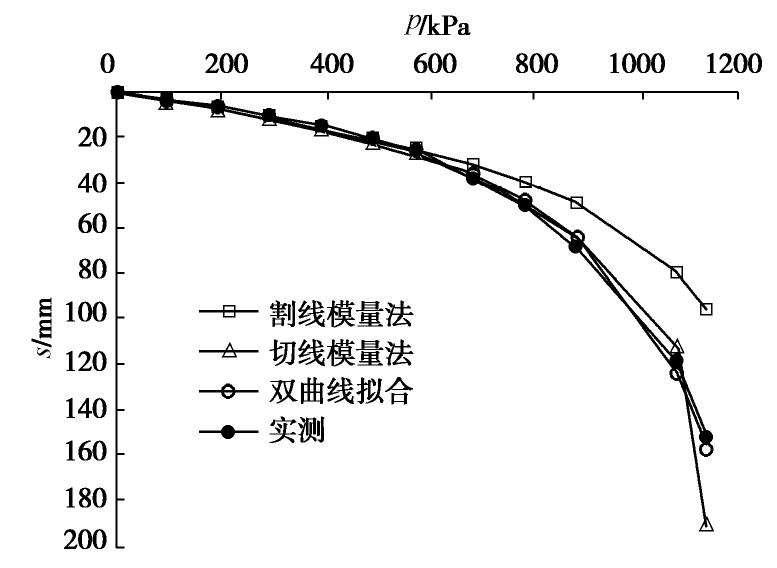
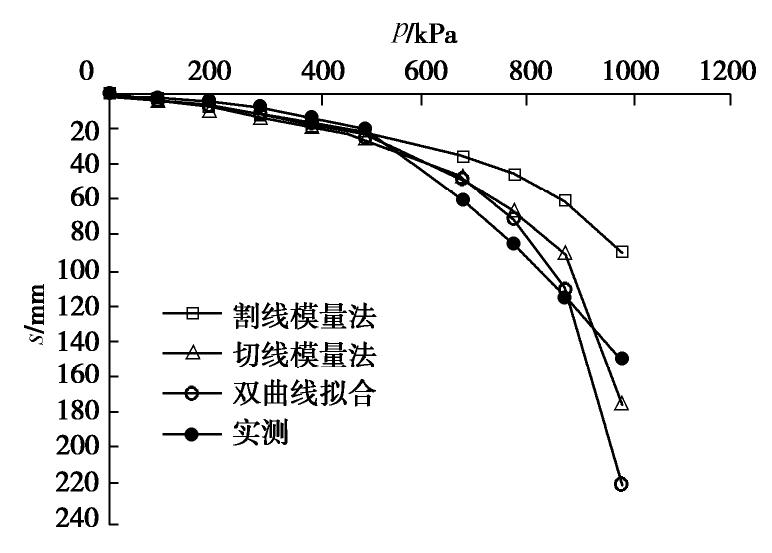
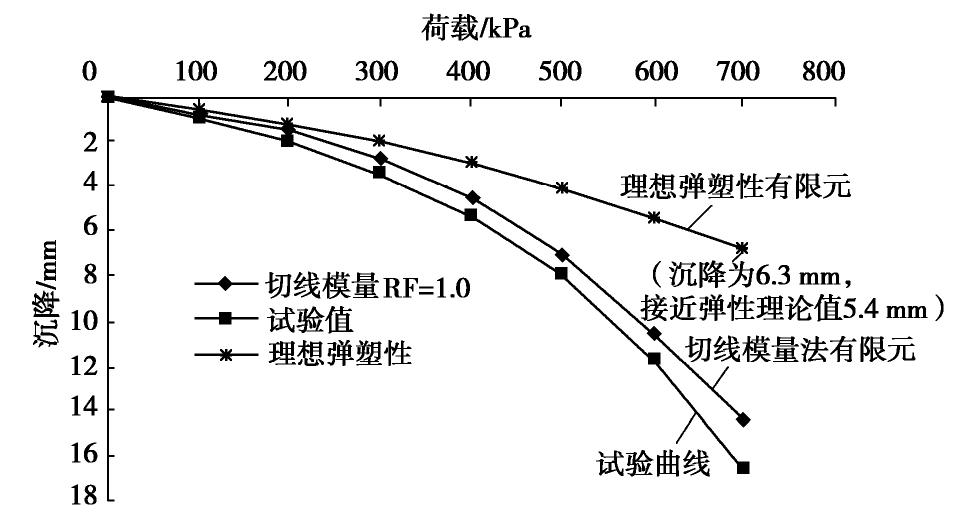
Table 4 Comparison between calculated and actual measured values of Liwan Building (mm)

实测平均沉降	用E_s计算	割线模量法		双曲线切线模量法
实测平均沉降	用E_s计算	用^#3试验数据计算	用平均试验数据计算	双曲线切线模量法
40	774.4	39.7	51.3	46.6

下载: 导出CSV

表 5 Poulos提供的各种方法计算沉降值与实测值比较

Table 5 Comparison between calculated settlements and measured values provided by Poulos

方法	s/mm
Terzaghi&Peck	39
Schmertmann	28
Burland&Burbridge	21
Elastic Theory $(E_{s} = 2 N)$ $(E_{s} = 2 N)$	18
Elastic Theory(PMT)	24
Elastic Theory(strain-dependent modulus)	32
Finite element	75
Measured	14

下载: 导出CSV

表 6 基于双曲线模型计算的地基土参数

Table 6 Parameters of foundation soils calculated based on hyperbolic model

压板试验编号	$E_{t0}$ $E_{t0}$ /MPa	$p_{u}$ $p_{u}$ /kPa	$φ$ $φ$ /(°)
^#5（1.0 m×1.0 m）	83.4	1399	39.5
^#2（1.5 m×1.5 m）	84.4	1202	37.2
^#4（2.5 m×2.5 m）	84.7	1340	35.8
^#1（3.0 m×3.0 m）	90.9	1405	35.2
^#3（3.0 m×3.0 m）	86.4	1128	33.8

下载: 导出CSV

表 7 根据压板试验反算的地基土的强度和变形参数

Table 7 Values of strength and deformation parameters of foundation soils back-calculated according to plate loading tests

压板试验编号	$E_{t0}$ $E_{t0}$ /MPa	$p_{u}$ $p_{u}$ /kPa	假定的 $φ$ $φ$ /(°)	反算所得的c/kPa
^#1试点	30.43	1505	20	70.2
^#2试点	25.51	1468	20	68.4
^#3试点	21.10	1527	20	71.2
平均值	25.68	1500	20	69.93

下载: 导出CSV

参考文献(47)

[1]	华南理工大学. 地基及基础[M]. 3版. 北京: 中国建筑工业出版社, 1998. South China University of Technology. Groundsill and Foundation[M]. 3rd ed. Beijing: China Architecture & Building Press, 1998. (in Chinese)
[2]	建筑地基基础设计规范：GB50007—2011[S]. 2012. Code for Design of Building Foundation: GB50007—2011[S]. 2012. (in Chinese)
[3]	陆培炎, 徐振华. 地基强度与变形的计算[M]. 西宁: 青海人民出版社, 1978. LU Pei-yan, XU Zhen-hua. Calculation of Foundation Strength and Deformation[M]. Xining: Qinghai People’s Publishing House Press, 1978. (in Chinese)
[4]	王红升, 周东久, 郭伦远. 理论公式确定地基容许承载力时安全系数的选择[J]. 河南交通科技, 1999(4): 31-32. https://www.cnki.com.cn/Article/CJFDTOTAL-HNJK199904009.htm WANG Hong-sheng, ZHOU Dong-jiu, GUO Lun-yuan. Safety coefficient selection in theory formula of subgrade allowance supporting capacity[J]. Science and Technology of Henan Cmmunication, 1999(4): 31-32. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HNJK199904009.htm
[5]	建筑地基基础设计规范：DBJ15—31—2016[S]. 2016. Design Code for Building Foundation: DBJ15—31—2016[S]. 2016. (in Chinese)
[6]	宰金珉, 翟洪飞, 周峰, 等. 按变形控制确定中、低压缩性地基土承载力的研究[J]. 土木工程学报, 2008, 41(8): 72-80. doi: 10.15951/j.tmgcxb.2008.08.012 ZAI Jin-min, ZHAI Hong-fei, ZHOU Feng, et al. Determination of the bearing capacity of soil foundation in medium and low compressive soils using deformation control[J]. China Civil Engineering Journal, 2008, 41(8): 72-80. (in Chinese) doi: 10.15951/j.tmgcxb.2008.08.012
[7]	李广信. 高等土力学[M]. 北京: 清华大学出版社, 2002. LI Guang-xin. Advanced Soil Mechanics[M]. Beijing: Tsinghua University Press, 2002. (in Chinese)
[8]	杨光华. 地基沉降计算的困难与突破[J]. 岩土工程学报, 2019, 42(10): 1893-1898. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201910016.htm YANG Guang-hua. Difficulties and breakthroughs in calculation of foundation settlement[J]. Chinese Journal of Geotechnical Engineering, 2019, 42(10): 1893-1898. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201910016.htm
[9]	TERZAGHI K, PECK R P. Soil Mechanics in Engineering Practice[M]. New York: John Wiley and Sons, 1948.
[10]	BRAJA D M. Shallow Foundations Bearing Capacity and Settlement[M]. 2nd ed. New York: CPC Press Taylor & Francis Group, 2009.
[11]	张在明. 等效变形模量的非线性特性的分析[J]. 岩土工程学报, 1997, 19(5): 56-59. doi: 10.3321/j.issn:1000-4548.1997.05.009 ZHANG Zai-ming, Analysis of nonlinear characteristics of equivalent deformation modulus[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(5): 56-59. (in Chinese) doi: 10.3321/j.issn:1000-4548.1997.05.009
[12]	北京地区建筑地基基础勘察设计规范：DBJ01—501—92[S]. 1992. Code for Investigation and Design of Building Foundation in Beijing Area: DBJ01—501—92[S]. 1992. (in Chinese)
[13]	焦五一. 地基变形计算的新参数——弦线模量的原理和应用[J]. 水文地质及工程地质, 1982(1): 30-33. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG198201007.htm JIAO Wu-yi. Principle and application of chord modulus: A new parameter for foundation deformation calculation[J]. Hydrogeology and Engineering Geology, 1982(1): 30-33. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG198201007.htm
[14]	深圳地区建筑地基基础设计试行规程：SJG1—88[S]. 1992. Testing Code for Design of Building Foundation in Shenzhen Area: SJG1—88[S]. 1992. (in Chinese)
[15]	建筑地基基础设计规范：DBJ15—31—2003[S]. 2003. Code for Design of Building Foundation: DBJ15—31— 2003[S]. 2003. (in Chinese)
[16]	高层建筑箱形与筏形基础技术规范：JGJ6—99[S]. 2002. Techincal Code for Tall Building Box Foundation and Raft Foundation: JGJ6—99[S]. 2002. (in Chinese)
[17]	杨光华. 基础非线性沉降的双曲线模型法[J]. 地基处理, 1997(1): 50-53. YANG Guang-hua. Hyperbola model in calculating the nonlinear settlement of foundation[J]. Ground Improvement, 1997(1): 50-53. (in Chinese)
[18]	杨光华. 地基非线性沉降计算的原状土切线模量法[J]. 岩土工程学报, 2006, 28(11): 1927-1931. doi: 10.3321/j.issn:1000-4548.2006.11.002 YANG Guang-hua. Nonlinear settlement computation of the soil foundation with the undisturbed soil tangent modulus method[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(11): 1927-1931. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.11.002
[19]	杨光华. 残积土上基础非线性沉降的双曲线模型的研究[C]//第七届全国岩土力学数值分析与解析方法讨论会论文集. 大连: 大连理工大学出版社, 2001: 168-171. YANG Guang-hua. Hyperbola Model Method in Calculating the Non-linear Settlement of Foundation on Granite Residual Soil[C]//Proceedings of the 7th National Conf on the Numerical Analysis and Analytical Method for Rock and Soil Mechanics. Dalian: Press of Dalian University of Technology, 2001: 168-171. (in Chinese)
[20]	杨光华, 王鹏华, 乔有梁. 地基非线性沉降计算的原状土割线模量法[J]. 土木工程学报, 2007, 40(5): 49-52. doi: 10.3321/j.issn:1000-131X.2007.05.007 YANG Guang-hua, WANG Peng-hua, QIAO You-liang. An undisturbed-soil secant modulus method for calculation of nonlinear of soil foundation[J]. China Civil Engineering Journal, 2007, 40(5): 49-52. (in Chinese) doi: 10.3321/j.issn:1000-131X.2007.05.007
[21]	杨光华. 地基沉降计算的新方法及其应用[M]. 北京: 科学出版社, 2013. YANG Guang-hua. The New Method to Calculate the Settlement of the Foundation and its Applications[M]. Beijing: The Science Publishing Company, 2013. (in Chinese)
[22]	杨光华. 地基沉降计算的新方法[J]. 岩石力学与工程学报, 2008, 27(4): 679-686. doi: 10.3321/j.issn:1000-6915.2008.04.005 YANG Guang-hua. New computation method for soil foundation settlement[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(4): 679-686. (in Chinese) doi: 10.3321/j.issn:1000-6915.2008.04.005
[23]	BRIAUD J L, GIBBENS R M. Predicted and measured behavior of five spread footings on sand[C]//Proceedings of a Prediction Symposium Sponsored by the Federal Highway Administration, Settlement’94 ASCE Conference, 1994, Texas.
[24]	YANG G H, LU Y D, ZHANG Y C, et al. Application of the tangengt modulus metheod in nonlinear settlement analysis of sand foundation[C]//Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, 2013.
[25]	杨光华, 王俊辉. 地基非线性沉降计算原状土切线模量法的推广和应用[J]. 岩土力学, 2011, 32(增刊1): 33-37. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S1007.htm YANG Guang-hua, WANG Jun-hui. Application of undisturbed soil tangent modulus method for computing nonlinear settlement of soil foundation[J]. Rock and Soil Mechanics, 2011, 32(S1): 33-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S1007.htm
[26]	杨光华, 骆以道, 张玉成, 等. 用简单原位试验确定切线模量法的参数及其在砂土地基非线性沉降分析中的验证[J]. 岩土工程学报, 2013, 35(3): 401-408. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201303002.htm YANG Guang-hua, LUO Yi-dao, ZHANG Yu-cheng, et al. Determination of parameters for tangent modulus method using simple in-situ test and its application in nonlinear settlement analysis on sandy soil[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(3): 401-408. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201303002.htm
[27]	刘琼, 杨光华, 刘鹏. 基于原位旁压试验的地基非线性沉降计算方法[J]. 广东水利水电, 2010(7): 4-6. https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD201007013.htm LIU Qiong, YANG Guang-hua, LIU Peng. Calculation method for nonlinear settlement of foundation based on in-situ pressure test[J]. Guangdong Water Resources and Hydropower Press, 2010(7): 4-6. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD201007013.htm
[28]	刘清华, 杨光华, 孙树楷. 切线模量法在分层地基沉降计算中的应用[J]. 广东水利水电, 2020(2): 6-12. https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD202002002.htm LIU Qing-hua, YANG Guang-hua, SUN Shu-kai. Application of tangent modulus method in settlement calculation of layered foundation[J]. Guangdong Water Resources and Hydropower Press, 2020(2): 6-12. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD202002002.htm
[29]	杨光华, 张玉成, 张有祥. 变模量弹塑性强度折减法及其在边坡稳定分析中的应用[J]. 岩石力学与工程学报, 2009, 28(7): 1506-1512. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200907028.htm YANG Guang-hua, ZHANG Yu-cheng, ZHANG You-xiang. Application of variable modulus elastic-plate strength reduction method and its application in slope stability analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(7): 1506-1512. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200907028.htm
[30]	王鹏华. 梁板地基非线性模型的研究及应用[D]. 广州: 华南理工大学, 2007. WANG Peng-hua, Research and Application of Nonlinear Model of Beam-Slab Foundation[D]. Guangzhou: South China University of Technology, 2007. (in Chinese)
[31]	杨光华, 李俊, 贾恺, 等. 改进的地基沉降计算的工程方法[J]. 岩石力学与工程学报, 2017, 36(增刊2): 4229-4234. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2017S2057.htm YANG Guang-hua, LI Jun, JIA Kai, et al. Improved settlement calculation method for engineering practice[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(S2): 4229-4234. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2017S2057.htm
[32]	杨光华. 软土地基非线性沉降计算的简化法[J]. 广东水利水电, 2001(1): 3-5. https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD200101000.htm YANG Guang-hua. Nonlinear settlement computation simplified method for soft foundation[J]. Guangdong Water Resources and Hydropower Press, 2001(1): 3-5. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD200101000.htm
[33]	杨光华, 李德吉, 李思平, 等. 计算软土地基非线性沉降的一个简化法[C]//第九届土力学及岩土工程学术会议论文集. 北京: 清华大学出版社, 2003: 506-510. YANG Guang-hua, LI De-ji, LI Si-ping, et al. A simplified method for nonlinear settlement computation of soft foundation[C]//Proceedings of the 9th Academic Conf on Soil Mechanics and Geotechnical Engineering. Beijing: Tsinghua University Press, 2003: 506-510. (in Chinese)
[34]	杨光华, 姚丽娜, 姜燕, 等. 基于e-p曲线的软土地基非线性沉降的实用计算方法[J]. 岩土工程学报, 2015, 37(2): 242-249. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201502007.htm YANG Guang-hua, YAO Li-na, JIANG Yan, et al. Pratical method for calculation nonlinear settlement of soft ground based on e-p curve[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(2): 242-249. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201502007.htm
[35]	杨光华, 黄致兴, 李志云, 等. 考虑侧向变形的软土地基非线性沉降计算的简化法[J]. 岩土工程学报, 2017, 39(9): 1697-1704. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201709023.htm YANG Guang-hua, HUANG Zhi-xing, LI Zi-yun, et al. Simplified method for nonlinear settlement calculation in soft soils considering lateral deformation[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(9): 1697-1704. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201709023.htm
[36]	彭长学, 杨光华. 软土e-p曲线确定的简化方法及在非线性沉降计算中的应用[J]. 岩土力学, 2008, 39(6): 1706-1710. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200806059.htm PENG Chang-xue, YANG Guang-hua. A simplified method for determining e-p curve of soft soil and its application to analyzing nonlinear settlement of foundation[J]. Rock and Soil Mechanics, 2008, 39(6): 1706-1710. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200806059.htm
[37]	陆培炎, 熊丽珍, 陈韶永, 等. 软土上一个土堤的试验分析[M]//陆炎培. 陆培炎科技著作及论文选集. 北京: 科学出版社, 2006. LU Pei-yan, XIONG Li-zhen, CHEN Shao-yong, et al. Test analysis of an earth embankment on soft soil[M]//LU Pei-yan. Selections of Lu Peiyan's Science and Technology Books and Papers. Beijing: Science Press, 2006. (in Chinese)
[38]	杨光华, 黄致兴, 姜燕, 等. 地基承载力的双控确定方法[J]. 岩土力学, 2016, 37(增刊2): 232-242. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S2028.htm YANG Guang-hua, HUANG Zhi-xing, JIANG Yan, et al. Double controlling method for determining bearing capacity of foundation soils[J]. Rock and Soil Mechanics, 2016, 37(S2): 232-242. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S2028.htm
[39]	杨光华, 姜燕, 张玉成, 等. 确定地基承载力的新方法[J]. 岩土工程学报, 2014, 36(4): 597-603. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201404002.htm YANG Guang-hua, JIANG Yan, ZHANG Yu-cheng, et al. New method for determination of bearing capacity of soil foundation[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(4): 597-603. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201404002.htm
[40]	YANG Guang-hua, JIANG Yan, XU Chuan-bao, et al. New method for determining foundation bearing capacity based on plate loading test[C]//Proceedings of China-Europe Conference on Geotechnical Engineering, 2018, Swwitzland.
[41]	杨光华. 地基的变形控制设计[M]//龚晓南. 岩土工程变形控制设计理论与实际. 北京: 中国建筑工业出版社, 2018. YANG Guang-hua. Deformation control design of foundation[M]//GONG Xiao-nan. Geotechnical Engineering Deformation Control Design Theory and Reality. Beijing: China Architecture & Building Press, 2018. (in Chinese)
[42]	杨光华, 孙树楷, 刘清华, 等. 强度和变形双控条件下基础尺寸的设计及优化[J]. 岩土工程学报, 2019, 41(增刊1): 5-8. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S1003.htm YANG Guang-hua, SUN Shu-kai, LIU Qing-hua, et al. Design and optimization of foundation sizes under dual control conditions of strength and deformation[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S1): 5-8. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S1003.htm
[43]	乔有梁, 杨光华, 张玉成, 等. 单桩非线性沉降计算的原状土切线模量法[J]. 广东水利水电, 2009(6): 22-24. https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD200906007.htm QIAO You-liang, YANG Guang-hua, ZHANG Yu-cheng, et al. Undisturbed soil tangent modulus method for calculation of single pile nonlinear settlement[J]. Guangdong Water Resources and Hydropower Press, 2009(6): 22-24. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD200906007.htm
[44]	杨光华, 苏卜坤, 乔有梁. 刚性桩复合地基沉降计算方法[J]. 岩石力学与工程学报, 2009, 28(11): 2193-2200. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200911006.htm YANG Guang-hua, SU Bu-kun, QIAO You-liang. Method for calculating settlement of rigid-pile composite foundation[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(11): 2193-2200. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200911006.htm
[45]	杨光华, 李德吉, 官大庶. 刚性桩复合地基优化设计[J]. 岩石力学与工程学报, 2011, 30(4): 818-825. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201104022.htm YANG Guang-hua, LI De-ji, GUANG Da-shu. Optimization design of pile composite foundation[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(4): 818-825. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201104022.htm
[46]	杨光华, 徐传堡, 李志云, 等. 软土地基刚性桩复合地基沉降计算的简化方法[J]. 岩土工程学报, 2017, 29(增刊2): 21-24. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2017S2007.htm YANG Guang-hua, XU Chuang-bao, LI Zhi-yun, et al. Simplified method for settlement calculation of rigid pile composite foundation in soft soils[J]. Chinese Journal of Geotechnical Engineering, 2017, 29(S2): 21-24. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2017S2007.htm
[47]	杨光华, 刘清华, 孙树楷, 等. 刚性桩复合地基承载力计算问题的探讨[J]. 广东水利水电, 2019(12): 1-7. https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD201912004.htm YANG Guang-hua, LIU Qing-hua, SUN Shu-kai, et al. Discussion on bearing capacity calculation of rigid pile composite foundation[J]. Guangdong Water Resources and Hydropower Press, 2019(12): 1-7. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD201912004.htm

施引文献(23)

期刊类型引用(7)

1.	王东，王智佼，陈伟祥，陈党辉. 不同锚孔出水量下预应力树脂锚索锚固剂组合试验研究. 四川建筑. 2024(01): 180-182 . 百度学术
2.	彭亚雄，周子霈，姚颖康，刘运思，左清军. 爆破作用下层状围岩隧道突变失稳判据研究. 中国安全科学学报. 2024(01): 171-178 . 百度学术
3.	刘晓颖，郭青林，张博，尚东娟，余静，裴强强. 降雪、温差作用下大尺寸砂岩风化模拟试验研究. 岩石力学与工程学报. 2024(06): 1519-1534 . 百度学术
4.	刘金芳，屈玉龙. 风化作用对侵蚀构造地貌碳质砂岩高边坡的影响. 科技与创新. 2023(05): 119-121+124 . 百度学术
5.	尹大伟，丁屹松，汪锋，江宁，谭毅，李宗蓄. 压力水浸泡下煤岩抗拉特性试验研究. 岩石力学与工程学报. 2023(S1): 3178-3191 . 百度学术
6.	王世鸣，熊咸瑞，王嘉琪，颜世军，吴秋红，翁磊. TSL材料防护作用下砂岩动态抗拉性能的试验研究. 振动与冲击. 2023(21): 192-199+218 . 百度学术
7.	陈伟，万文，赵延林，王卫军，吴秋红，吴小凡，谢森林. 高湿环境平行双裂隙砂岩单轴压缩破坏及裂纹扩展特性. 岩土工程学报. 2021(11): 2094-2104 . 本站查看

其他类型引用(16)

资源附件(0)

图(34) / 表(7)

计量

文章访问数: 621
HTML全文浏览量: 31
PDF下载量: 563
被引次数: 23

0. 引言
1. 研究方案
1.1 试验土样
1.2 蒸汽吸附分析仪工作原理
1.3 高吸力下持水特征试验方案
2. 试验结果分析
2.1 高吸力下持水能力特征点w95
2.2 高吸力下SWRC滞回区域面积HHA
2.3 高吸力下SWRC滞回效应最大值Δwmax
2.4 高吸力下SWRC滞回行为机制探讨
3. 高吸力下持水特征的本构描述
4. 结论

0. 引言
1. 研究方案
1.1 试验土样
1.2 蒸汽吸附分析仪工作原理
1.3 高吸力下持水特征试验方案
2. 试验结果分析
2.1 高吸力下持水能力特征点w₉₅
2.2 高吸力下SWRC滞回区域面积HHA
2.3 高吸力下SWRC滞回效应最大值Δw_max
2.4 高吸力下SWRC滞回行为机制探讨
3. 高吸力下持水特征的本构描述
4. 结论

参考文献(47)

施引文献(23)

资源附件(0)

现代地基设计理论的创新与发展 English Version

计量

出版历程

Innovation and development of modern theories for foundation design

0. 引言

1. 研究方案

1.1 试验土样

1.2 蒸汽吸附分析仪工作原理

1.3 高吸力下持水特征试验方案

2. 试验结果分析

2.1 高吸力下持水能力特征点w95

2.2 高吸力下SWRC滞回区域面积HHA

2.3 高吸力下SWRC滞回效应最大值Δwmax

2.4 高吸力下SWRC滞回行为机制探讨

3. 高吸力下持水特征的本构描述

4. 结论

期刊类型引用(7)

其他类型引用(16)

计量

出版历程

目录

0. 引言

1. 研究方案

1.1 试验土样

1.2 蒸汽吸附分析仪工作原理

1.3 高吸力下持水特征试验方案

2. 试验结果分析

2.1 高吸力下持水能力特征点w95

2.2 高吸力下SWRC滞回区域面积HHA

2.3 高吸力下SWRC滞回效应最大值Δwmax

2.4 高吸力下SWRC滞回行为机制探讨

3. 高吸力下持水特征的本构描述

4. 结论

2.1 高吸力下持水能力特征点w₉₅

2.3 高吸力下SWRC滞回效应最大值Δw_max

2.1 高吸力下持水能力特征点w₉₅

2.3 高吸力下SWRC滞回效应最大值Δw_max