Prediction of permeability coefficient of unsaturated lime-improved loess
-
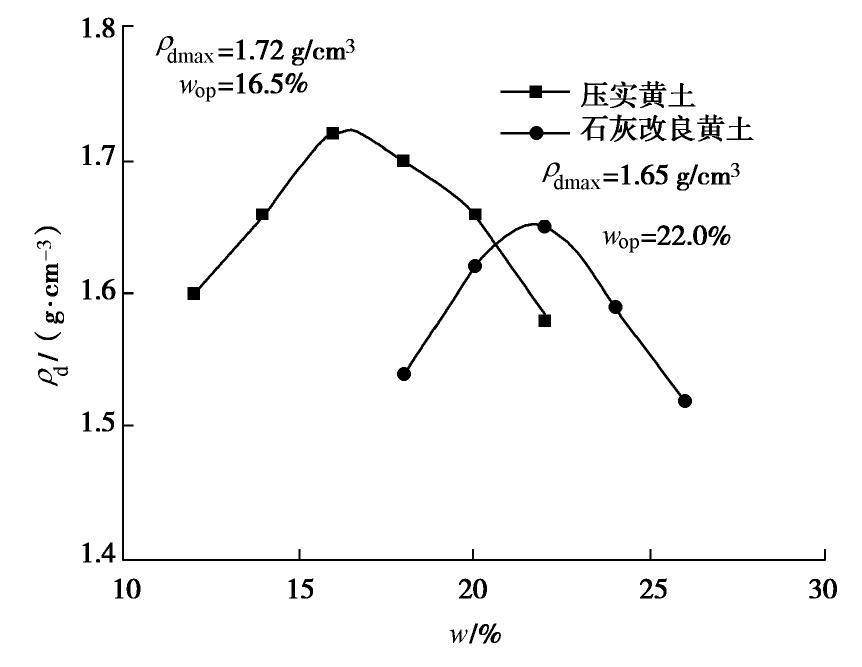
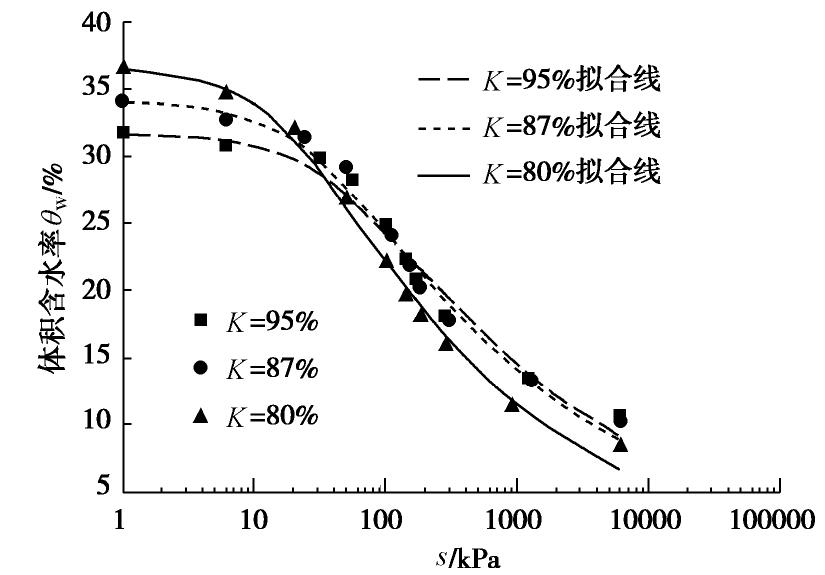
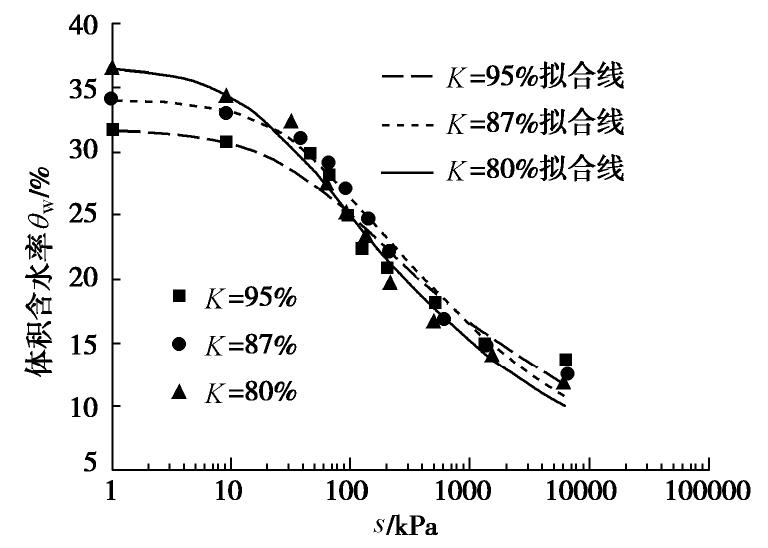
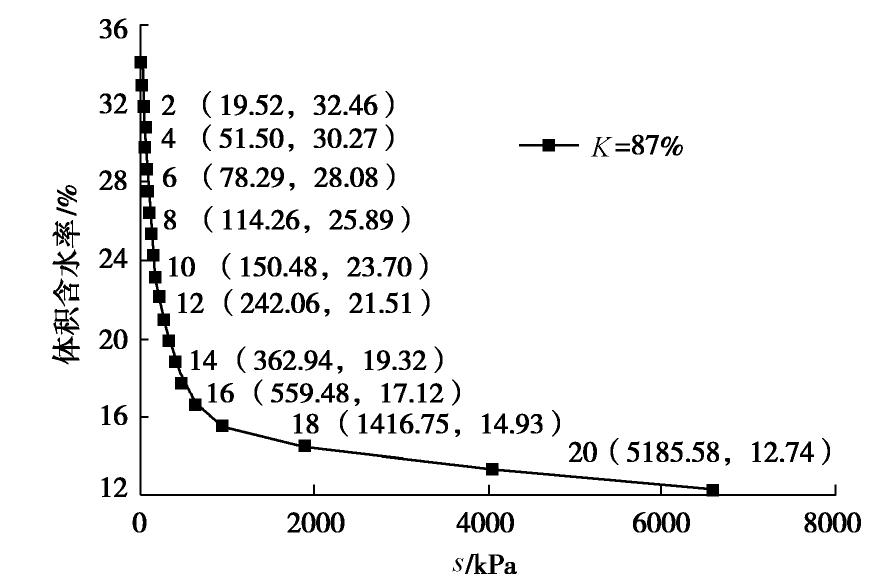
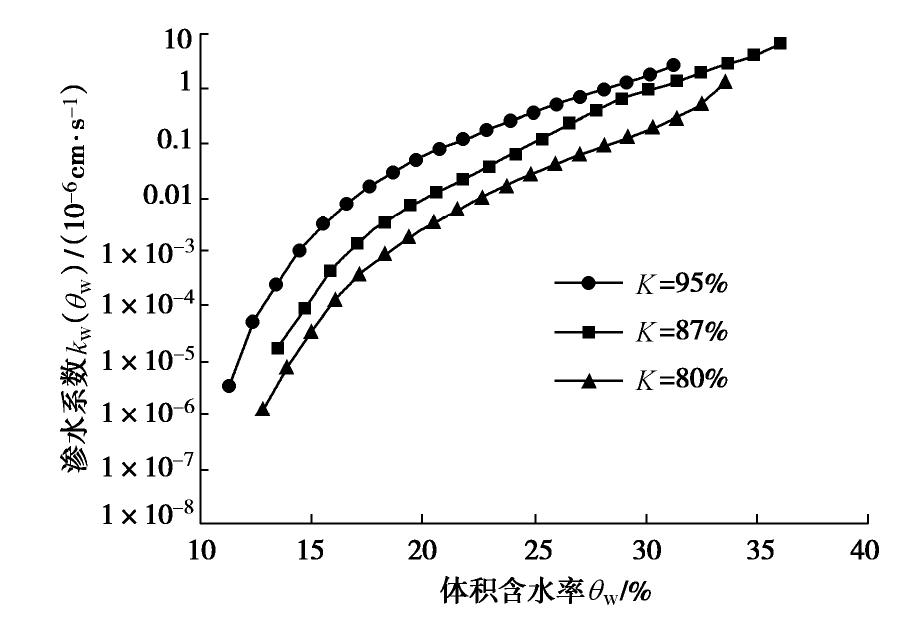
摘要: 针对黄土地区大部分黄土处于非饱和的状态,采用石灰改良非饱和黄土以解决非饱和黄土渗透性的问题。利用非饱和固结仪测得压实黄土和石灰改良黄土的土水特征曲线,采用Van Genuchten模型对试验数据进行拟合,同时测得饱和压实黄土和石灰改良黄土的饱和渗水系数,基于测得的土水特征曲线,采用Childs & Collis-George预测非饱和石灰改良黄土的渗水系数的模型,得到非饱和石灰改良黄土的体积含水率以及基质吸力和渗水系数之间的关系曲线,并通过微观结构来分析验证其机理。结果表明：压实度对非饱和石灰改良黄土土水特征曲线影响明显,压实度越大,进气值越大；石灰改良黄土的饱和渗水系数小于压实黄土；同一压实度,非饱和石灰改良黄土的渗水系数随体积含水率的增大而增大,随基质吸力的增大,呈先迅速减小后趋于平衡的趋势,吸力一定时,压实度越大,非饱和渗水系数越小；且渗水系数与基质吸力可用幂函数表示。为石灰改良黄土地基和路基等工程提供数值计算基础和理论支持。Abstract: In view of the fact that most loess in the loess regions is in an unsaturated state, lime is used to improve the unsaturated loess to solve the problem of permeability of unsaturated loess. The soil-water characteristic curves of the compacted loess and the lime-modified loess are measured by an unsaturated consolidation instrument, and the Van Genuchten model is used to fit the test data. The saturated permeability coefficients of the saturated compacted loess and the lime-modified loess are also measured. The obtained soil-water characteristic curve is modeled using the Childs & Collis-George model to predict the permeability coefficient of unsaturated lime-improved loess, and the relationship curves of the volumetric water content of unsaturated lime-improved loess, the matrix suction and the permeability coefficient are obtained so as to analyze the mechanism. The results show that the compaction degree has a significant effect on the soil-water characteristic curve of the unsaturated lime-modified loess. The larger the compaction degree, the larger the air intake value. The saturated permeability coefficient of the lime-modified loess is smaller than that of the compacted loess. Under the same compaction degree, the permeability coefficient of the lime-improved loess increases with the increase of the volumetric water content, and with the increase of the matrix suction, it first decreases rapidly and then tends to be equilibrium. When the suction is constant, the greater the compaction degree, the smaller the unsaturated permeability coefficient. The permeability coefficient and matrix suction can be expressed by a power function. The results may provide numerical calculation basis and theoretical support for lime-improved loess and roadbed projects.
-
0. 引言
土的渗透特性是土重要的工程性质之一,影响着土木工程的施工。目前无黏性土渗透特性的试验研究,多是采用竖向圆柱体模型槽进行,试验中土体受到的水流的作用方向是由下至上的竖直方向,而对于土体承受水平向渗流时土体渗透特性的研究不多[1],渗流方向对土体渗流变形特性的研究还尚未给予足够重视。对土渗流的研究表明,实际施工中渗流的优势方向往往是水平方向,通常土体水平向的渗透性大于竖向,而抵抗水平向渗透破坏的能力低于抵抗竖向渗透破坏的能力[2-6]。
本文针对粉砂竖向和水平向渗透特性研究存有的不足,利用自主设计的实验装置,对粉砂开展竖向和水平向渗流试验,对比分析了两种不同方向渗流场下粉砂的渗透特性。基于室内模拟试验,建立三维离散元与计算流体力学耦合的细观力学模型,对粉砂在竖向和水平向的渗流情况进行分析和计算。通过数值计算结果,对竖向和水平向渗流作用下的粉砂内部接触力、渗流速度及流场的分布规律进行细观分析,将数值模拟与室内试验的结果进行分析、比较。
1. 不同渗流方向下粉砂渗透变形室内试验模拟
1.1 试验仪器和方法
（1）试验仪器
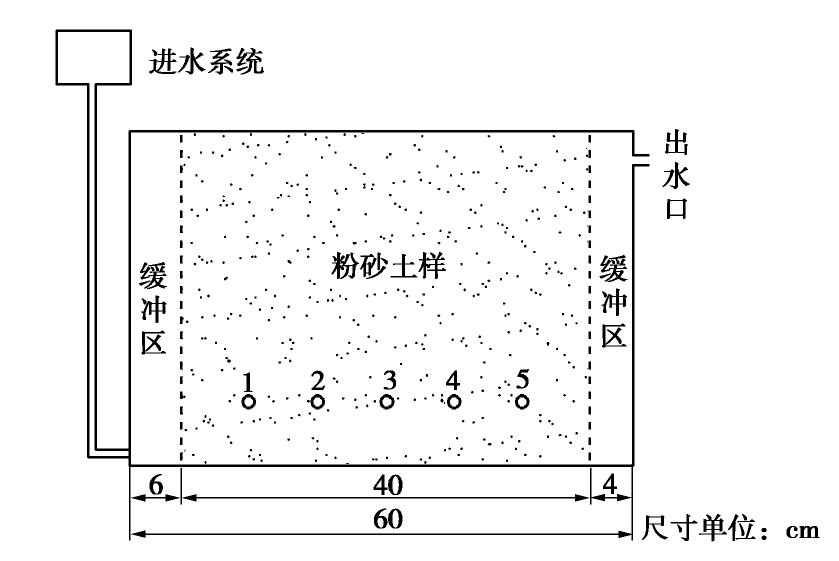
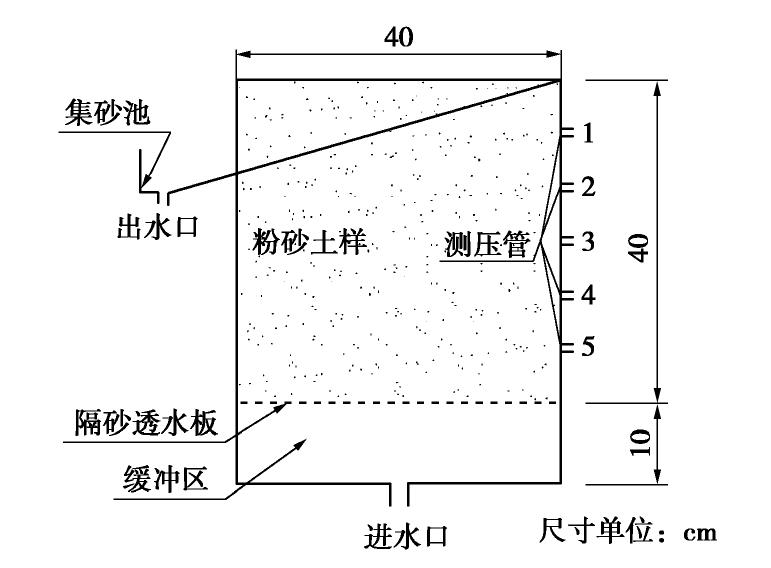
粉砂的竖向渗透变形试验借助实验室自主设计的圆柱形渗流试验仪进行,该装置示意图如图1所示。粉砂水平向渗流渗透变形特性的研究是在自主设计的水平渗流试验装置中进行的,见图2。模型由进水系统,装样区及排水系统3个主要部分组成。进水系统可以通过对进水水头高度的调节自由选择水头加载高度。
![]()
图 1 圆柱形渗流试验仪示意图Figure 1. Schematic diagram of instrument for cylindrical seepage tests（2）试验方法及步骤
粉砂烘干并分层装样。称样烘干24 g取出装样,每10 cm分为一层进行装样；排气饱和。装样完成,分次提升水箱供水高度对试验土样进行饱和,最后一次使水头抬升至与试样顶端齐平,静置24 h；逐级调整水头进行试验。逐级抬升水头高度,对测压管水头高度读数并记录,同时量测渗流量大小,记录试验进程中的渗流现象,直至该级渗流稳定,转入下一级水头；当试验过程中,流量忽然增大,并出现明显的渗流通道,可以认定为试样发生渗透破坏,不再继续加大水头高度,试验完成。
1.2 粉砂竖向和水平向渗流试验结果分析
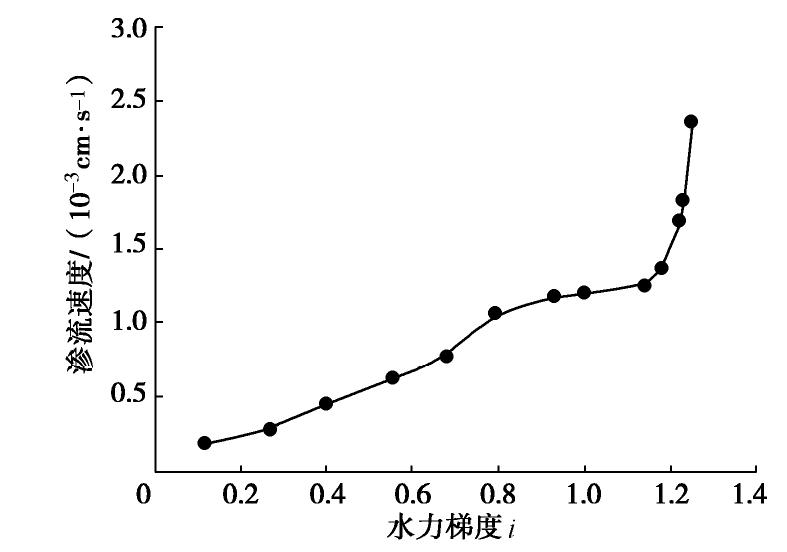
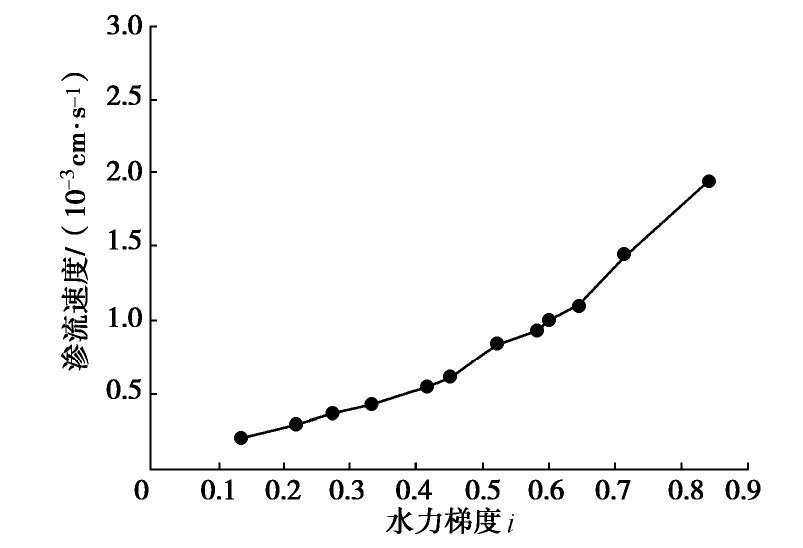
对粉砂在竖向渗流下的渗透流速受水力梯度影响下的变化规律进行研究,得到渗流速度随水力梯度变化的关系曲线,如图3所示。对粉砂在水平向渗流作用下的临界水力梯度进行研究,结果如图4所示。
![]()
图 3 竖向渗流下渗流速度随水力梯度变化曲线Figure 3. Relationship between seepage velocity and vertical hydraulic gradient![]()
图 4 水平向渗流下渗流速度随水力梯度变化曲线Figure 4. Relationship between seepage velocity and critical hydraulic gradient由图3得到,在水力梯度
<0.787时,渗流速度随水力梯度呈近似线性的变化,此时土样处于渗流稳定阶段；当水力梯度为1.1时,渗流速度忽然增大,粉砂颗粒流失量也徒增,此时土体发生渗透变形。图4粉砂在水平向渗流下的变化规律显示：水力梯度小于0.45时,粉砂土渗透流速随着水力梯度的增大呈线性增长,水流清澈,粉砂流出较少。当水力梯度增至0.52时,试样整体的流速瞬间增大,粉砂流出量明显增多且呈持续流失状态,此时粉砂土样内部颗粒运移不再规律,试样开始发生渗透破坏。 表1给出粉砂在两种渗流方向下的渗透系数、临界坡降与破坏坡降。粉砂在竖向渗流时的临界水力梯度为0.787,破坏水力梯度为1.10；而水平向渗流中,所能承受的临界水力梯度为0.45。在影响因素诸如种类、级配、密度、孔隙大小等相同的前提下,粉砂竖向渗流的临界水力梯度比水平向高出近44%。由于土体在受到水平向渗流时,平均渗透系数取决于最透水土层的厚度和渗透性；而对于竖向渗流,其平均渗透系数取决于最不透水土层的渗透性。加之,竖向渗流中重力作用与渗流方向一致,会产生对土层的压密作用,使得该渗流方向下的渗透系数小于水平向,而土体能够承受的水头高于水平向的渗流。
表 1 不同渗流方向下粉砂渗透系数、临界坡降和破坏坡降Table 1. Datat of permeability coeffieient of silt, critical slope and failure slope under different seepage directions渗流方向 渗透系数/(10-4 cm·s-1) 临界水力梯度 破坏水力梯度 竖向 6.13 0.787 1.10 水平 6.25 0.450 0.52 2. 不同渗流方向下粉砂渗透变形颗粒流模拟
对于固相颗粒,通过求解运动和动量方程模拟颗粒运动,采用离散元的颗粒流理论进行模拟；对于液相介质,采用均一化流体计算技术模拟其在孔隙中的运动,也就是通过求解平均Navier-Stokes方程模拟孔隙中流体的运动[7-9]。
2.1 数值模型
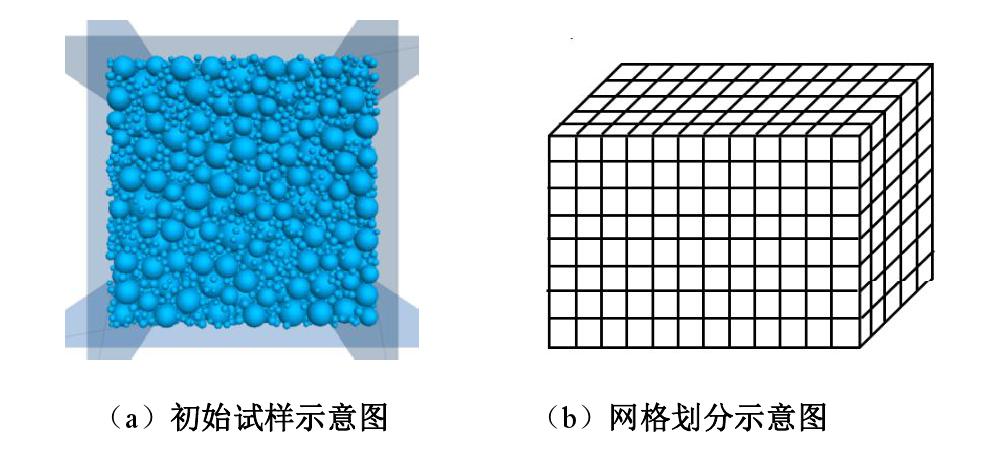
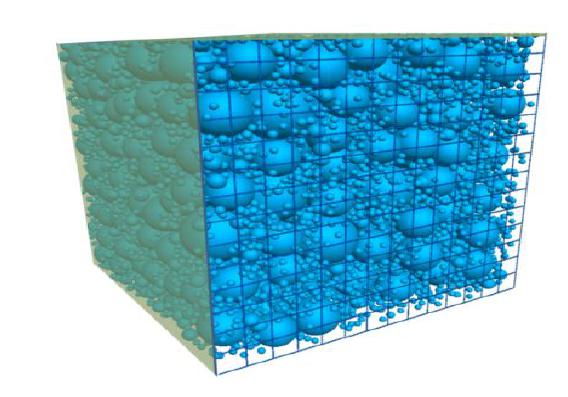
对粉砂土不同向渗流形态的模拟中,边界条件的界定也略有不同。竖向渗流下,颗粒周边的边界为固壁边界条件,上下为压力边界条件。水平向渗流下,模型的前后和上下边界为固壁边界条件,左右设置为压力边界条件和自由边界条件。生成的土体模型如图5所示。
对于竖向的渗流,按照试验中模型,上覆为自由边界,没有压重。对于水平向的渗流,试样在重力和浮力作用下保持平衡,当作用渗流力后,土中小颗粒将从模型右侧流出,因此在试样右侧设置了相互交叉垂直的线墙,如图6所示。
2.2 数值计算流程
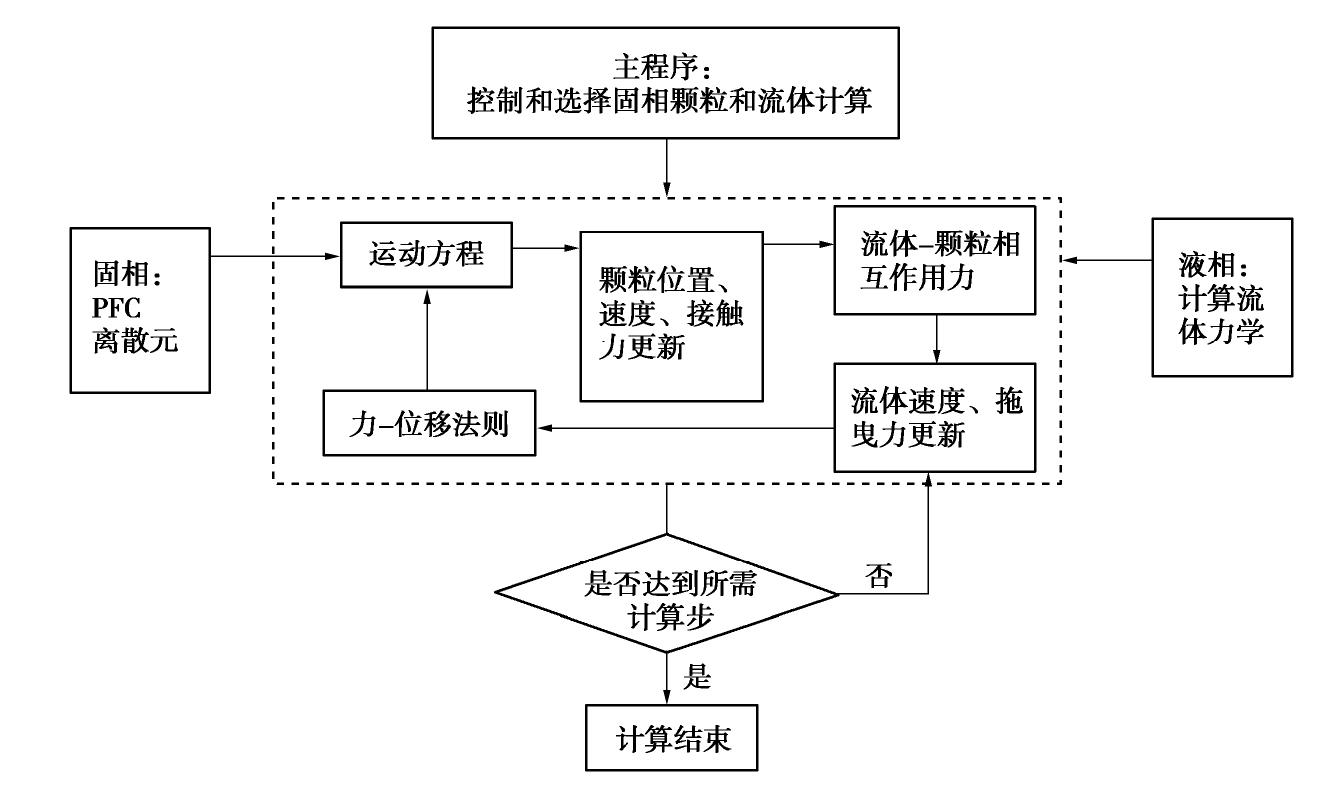
采用PFC3D对流固耦合问题进行计算流程如图7所示。
2.3 数值模拟结果
（1）粉砂土竖向和水平向渗流下渗透变形情况
a）粉砂竖向渗流下的渗透变形情况
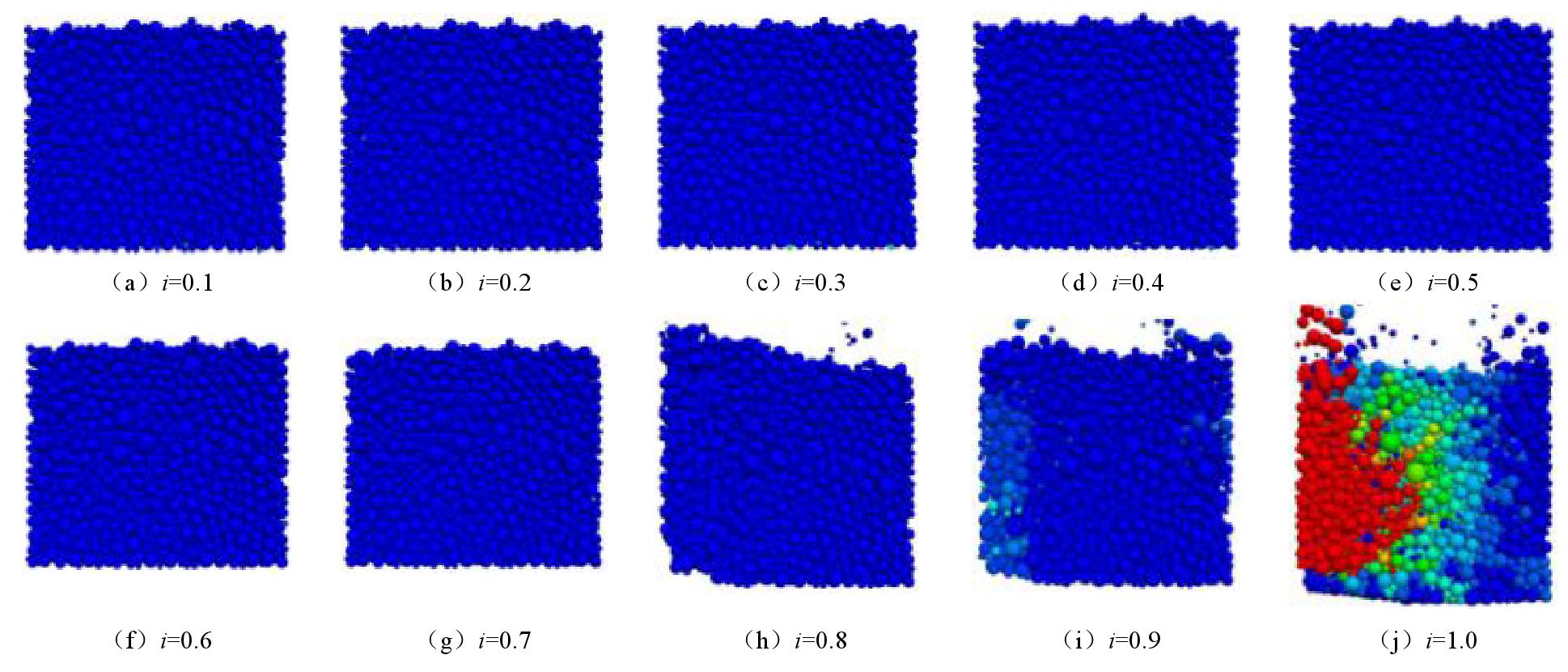
图8给出了粉砂在竖向渗流作用下,土样随水力梯度的变化情况。
![]()
图 8 竖向渗流下粉砂土随水力梯度变化情况Figure 8. Variation of silty sand with gradient under vertical seepage水力梯度从0.1,0.2,0.3,...,逐级增加,水力梯度施加至0.7时,粉砂几乎无变化；当水力梯度增至0.8时,土样出现从底部被整体抬升的趋势,发生少量细小颗粒流失的现象；水力梯度继续增至1.0时,土体发生了整体的抬升,土体表面颗粒簇发生整体迁移的现象。模拟结果表明,试样的临界水力梯度在0.8左右。
b）粉砂水平向渗流下的渗透变形情况
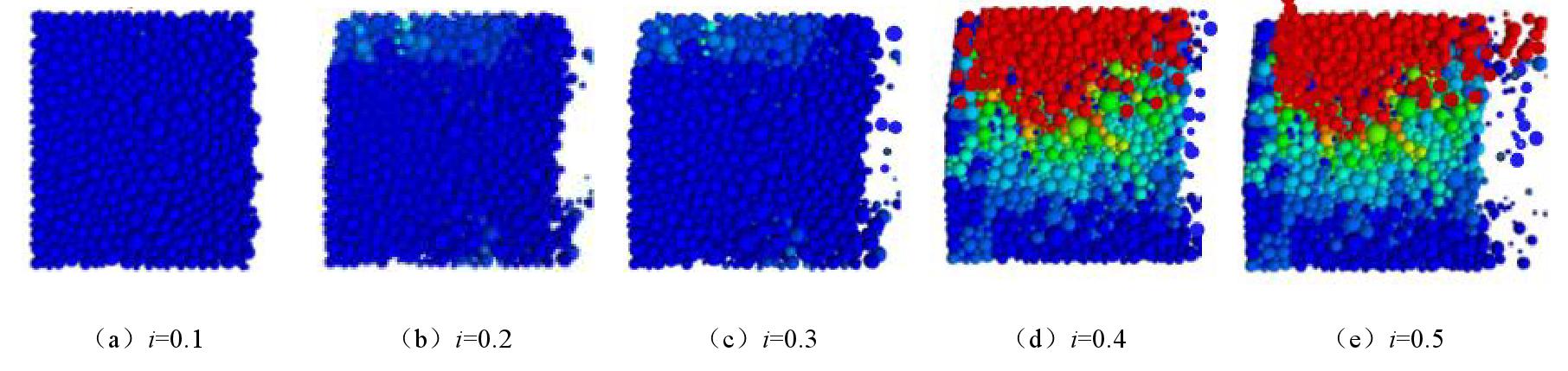
粉砂土的水平向渗流中水力梯度也是由0.1,0.2,0.3依次逐级抬升,图9给出了粉砂土在水平向渗流下试样随水力梯度变化的情况。
![]()
图 9 水平向渗流下粉砂土随水力梯度变化情况Figure 9. Variation of silt with gradient under horizontal seepage从图9中可以看出,当水力梯度增至0.3时,试样底部细小颗粒也开始发生迁移,水力梯度继续增大至0.4,此时试样发生颗粒成团的流失,土体发生了渗透变形。水力梯度加载至0.5时,土体颗粒发生了更加显著的整体性渗流破坏。根据模拟结果,得到粉砂土水平向渗流的临界水力梯度在0.4左右。
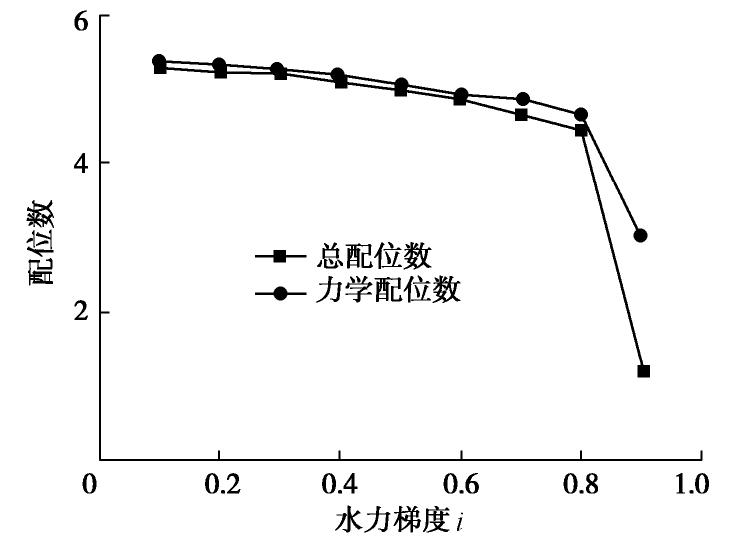
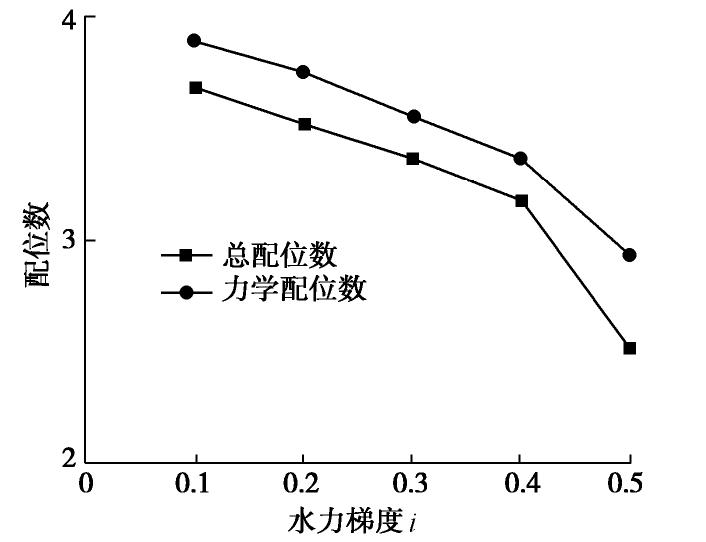
（2）粉砂土竖向和水平向渗流下配位数变化情况分析
土体的配位数表示了颗粒间的接触数,是表达土颗粒间接触情况的参数之一,总配位数是颗粒与颗粒之间以及颗粒与墙之间的平均接触数,反映出试样的压密程度；力学配位数为颗粒与颗粒之间接触数大于2时的颗粒接触数,反映额土骨架的压密程度。图10,11给出了粉砂土在竖向和水平向渗流作用下,配位数随水力梯度的变化情况。
![]()
图 10 竖向渗流下粉砂配位数随水力梯度变化Figure 10. Variation of coordination number with gradient under vertical seepage![]()
图 11 水平向渗流粉砂配位数随水力梯度变化Figure 11. Variation of coordination number with gradient under horizontal seepage图10,11可以看出,当竖向渗流的水力梯度为0.8,水平向渗流水力梯度为0.4时,土体的两个配位数都发生迅速的下降,说明此时的土体状态发生了较大的变化,即渗透变形发生。图中,总配位数和力学配位数都在随着水力梯度的增大而不断降低,总的配位数较力学配位数下降更快速,幅度也更大。这是由于水力梯度增大,颗粒发生了移动,颗粒的接触数减小,但在水力梯度增加至土体渗透变形前的整个过程中,总配位数下降幅度明显大于力学配位数,说明发生移动的多为小颗粒,小颗粒的运移使土体中接触数减少,随之小颗粒填充至骨架颗粒孔隙间,与大颗粒发生接触,保持了力学配位数的大小。
3. 结论
（1）粉砂在水平向能承受的渗流破坏作用一般低于竖向渗流。
（2）数值模拟结果与模拟试验过程中粉砂的渗流变化过程相符,数值方法所测得的临界水力梯度与试验测得的结果亦较为吻合。
（3）竖向和水平向渗流下,粉砂的总配位数和力学配位数均随着水力梯度的抬升而衰减,当土体发生渗透破坏,土体配位数出现迅速降低。
-
![]()
图 1 压实黄土和石灰改良黄土的击实曲线
Figure 1. Compaction curves of compacted loess and lime-modified loess
![]()
图 3 不同压实度非饱和压实黄土的土水特征曲线
Figure 3. Soil-water characteristic curves of unsaturated compacted loess with different dry densities
![]()
图 4 不同压实度非饱和石灰改良黄土的土水特征曲线
Figure 4. Soil-water characteristic curves of unsaturated lime-modified loess with different dry densities
![]()
图 5 饱和压实黄土和石灰改良黄土的渗水系数曲线
Figure 5. Curves of permeability coefficient of saturated compacted loess and lime-modified loess
![]()
图 6 非饱和石灰改良黄土的土水特征曲线
Figure 6. Soil-water characteristic curves of unsaturated lime-modified loess
![]()
图 7 非饱和石灰改良黄土的渗水系数与体积含水率的关系曲线
Figure 7. Curves of permeability coefficient and volumetric water content of unsaturated lime-modified loess
![]()
图 8 非饱和石灰改良黄土的渗水系数与吸力之间的关系曲线
Figure 8. Relationship between permeability coefficient and suction force of unsaturated lime-modified loess
![]()
图 9 不同压实度非饱和石灰改良黄土SEM图像
Figure 9. SEM images of unsaturated lime-modified loess with different compaction degrees
表 1 黄土基本物理性质指标
Table 1 Basic physical parameters of loess
天然干密度/(g·cm-3) 天然含水率/% 塑限/% 液限/% 塑性 指数Ip 土粒相对密度 颗粒组成/% <0.005 mm 0.005~0.075 mm >0.075 mm 1.28 15.2 19.0 28.6 9.6 2.71 15.5 74.3 10.2 
下载: 导出CSV
表 2 石灰主要化学成分
Table 2 Main chemical composition of lime
化学成分 百分含量/% 化学成分 百分含量/% CaO 72.12 MgO 3.90
下载: 导出CSV
表 3 非饱和石灰改良黄土V-G模型土性参数
Table 3 Soil parameters of V-G model for unsaturated lime-modified loess
土类 压实度K/% /% /% a b R2 压实黄土 95 31.74 12.84 45.46 1.25 0.978 87 34.13 12.21 31.57 1.25 0.985 80 36.62 10.73 20.16 1.30 0.993 石灰黄土 95 31.74 10.70 51.62 1.24 0.973 87 34.13 10.27 42.93 1.23 0.986 80 36.62 8.00 21.00 1.21 0.974
下载: 导出CSV
表 4 非饱和压实黄土及石灰改良黄土饱和渗水系数
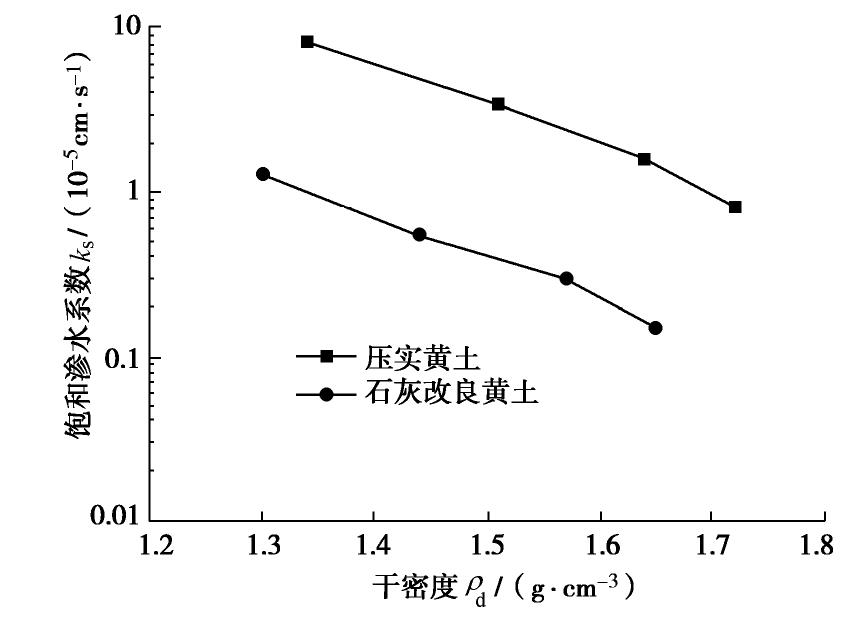
Table 4 Saturated permeability coefficients of unsaturated compacted loess and lime-modified loess
压实黄土 石灰改良黄土 压实度K/% 渗透系数ks/(10-5cm·s-1) 压实度K/% 渗透系数ks/(10-5cm·s-1) 100 0.82 1.61 100 0.15 0.30 95 95 87 3.50 87 0.55 80 8.20 80 1.30
下载: 导出CSV
表 5 非饱和石灰改良黄土渗水系数
Table 5 Permeability coefficients of unsaturated lime-modified loess
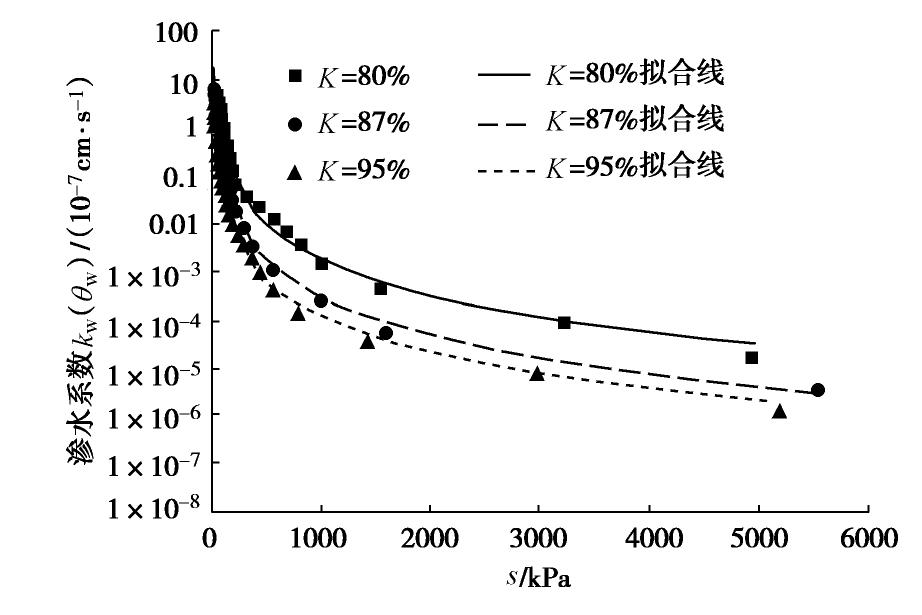
i K=80% K=87% K=95% s/kPa kw(θw)/(10-6 cm·s-1) s/kPa kw(θw)/(10-6 cm·s-1) s/kPa kw(θw)/(10-6 cm·s-1) 1 21.98 6.77 22.43 2.74 15.00 1.37 2 35.45 4.24 26.80 1.84 24.00 0.50 3 50.06 2.88 42.70 1.30 41.79 0.30 4 64.27 2.01 59.08 0.96 51.50 0.20 5 77.64 1.41 63.90 0.71 60.41 0.13 6 94.96 0.97 69.24 0.51 78.29 0.09 7 102.96 0.64 81.07 0.37 96.19 0.06 8 119.59 0.39 93.14 0.26 114.26 0.04 9 139.72 0.22 105.78 0.18 133.12 0.03 10 180.65 0.12 118.05 0.12 150.48 0.02 11 217.61 0.06 146.10 0.08 187.17 0.01 12 319.58 0.03 169.43 0.05 242.06 6.03×10-3 13 429.95 0.02 193.84 0.03 297.9 3.49×10-3 14 563.59 0.01 220.06 0.02 362.94 1.89×10-3 15 681.91 6.96×10-3 285.90 7.77×10-3 437.21 9.27×10-4 16 809.1 3.43×10-3 376.11 3.22×10-3 559.48 3.89×10-4 17 1000.76 1.42×10-3 560.37 1.05×10-3 787.17 1.31×10-4 18 1535.34 4.33×10-4 998.17 2.48×10-3 1416.75 3.42×10-5 19 3215.28 9.02×10-5 1592.64 5.19×10-5 2965.08 7.52×10-6 20 4935.80 1.68×10-5 5543.13 3.43×10-6 5185.58 1.24×10-6
下载: 导出CSV
表 6 渗水系数与基质吸力关系曲线的拟合参数
Table 6 Fitting values of permeability coefficient and matrix suction
压实度K/% 压实度ρd/(g·cm-3) a/10-3 b 80 1.32 4.48 2.466 87 1.44 3.13 2.669 95 1.57 3.07 2.771
下载: 导出CSV
-
[1] 刘祖典. 黄土力学与工程[M]. 西安: 陕西科技出版社, 1997. LIU Zu-dian. Mechanics and Engineering of Loess[M]. Xi'an: Shaanxi Science and Technology Press, 1997. (in Chinese)
[2] 胡再强, 梁志超, 吴传意, 等. 冻融循环作用下石灰改性黄土的力学特性试验研究[J]. 土木工程学报, 2019, 52(增刊1): 211-217. HU Zai-qiang, LIANG Zhi-chao, WU Chuan-yi, et al. Experimental study on mechanical properties of lime modified loess under freeze-thaw cycle[J]. China Civil Engineering Journal, 2019, 52(S1): 211-217. (in Chinese)
[3] 陈正汉, 谢定义, 王永胜. 非饱和土的水气运动规律及其工程性质研究[J]. 岩土工程学报, 1993(3): 9-20. doi: 10.3321/j.issn:1000-4548.1993.03.002 CHEN Zheng-han, XIE Ding-yi, WANG Yong-sheng. Experimental studies of lows of fluid motion suction and pore pressures in unsaturated soil[J]. Chinese Journal of Geotechnical Engineering, 1993(3): 9-20. (in Chinese) doi: 10.3321/j.issn:1000-4548.1993.03.002
[4] 徐永福, 兰守奇, 孙德安, 等. 一种能测量应力状态对非饱和土渗透系数影响的新型试验装置[J]. 岩石力学与工程学报, 2005, 24(1): 160-164. doi: 10.3321/j.issn:1000-6915.2005.01.027 XU Yong-fu, LAN Shou-qi, SUN De-an, et al. New apparatus for measurement of stress effect on permeability of unsaturated soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(1): 160-164. (in Chinese) doi: 10.3321/j.issn:1000-6915.2005.01.027
[5] 李永乐, 刘翠然, 刘海宁, 等. 非饱和土的渗透特性试验研究[J]. 岩石力学与工程学报, 2004, 23(22): 3861-3865. doi: 10.3321/j.issn:1000-6915.2004.22.023 LI Yong-le, LIU Cui-ran, LIU Hai-ning, et al. Testing study on permeability characteeistics of unsaturated soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(22): 3861-3865. (in Chinese) doi: 10.3321/j.issn:1000-6915.2004.22.023
[6] CHIU C F, NG C W W. A state-dependent elasto-plastic model for saturated and unsaturated soils[J]. Géotechnique, 2003, 53(9): 809-829. doi: 10.1680/geot.2003.53.9.809
[7] SAMINGAN A S. Mechanical and hydraulic properties of compacted tropical residual soils[J]. Polymer Korea, 2009, 33(33): 97-103.
[8] GARG N K, GUPTA M. Assessment of improved soil hydraulic parameters for soil water content simulation and irrigation scheduling[J]. Irrigation Science, 2015, 33(4): 247-264. doi: 10.1007/s00271-015-0463-7
[9] KUNZE R J, UEHARA G, GRAHAM K. Factors important in the calculation of hydraulic conductivity[J]. Soil Science Society of America Proceedings, 1968, 32(6): 760-765. doi: 10.2136/sssaj1968.03615995003200060020x
[10] 李萍, 李同录, 王红, 等. 非饱和黄土土-水特征曲线与渗透系数Childs & Collis-Geroge模型预测[J]. 岩土力学2013, 34(增刊2): 184-189. LI Ping, LI Tong-lu, WANG Hong, et al. Soil-water characteristic curve and permeability perdiction on Childs & Collis-Geroge model of unsaturated loess[J]. Soil and Rock Mechanics, 2013, 34(S2): 184-189. (in Chinese)
[11] 高登辉, 陈正汉, 邢义川, 等. 净平均应力对非饱和重塑黄土渗水系数的影响[J]. 岩土工程学报, 2018, 40(增刊1): 51-56. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2018S1010.htm GAO Deng-hui, CHEN Zheng-han, XING Yi-chuan, et al. Influence of net mean stress on permeability coefficient of unsaturated remolded loess[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(S1): 51-56. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2018S1010.htm
[12] VAN GENUCHTEN M T. A closed form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44: 892-898. doi: 10.2136/sssaj1980.03615995004400050002x
[13] FREDLUND D G, XING A. Equations for the soil water characteristic curve[J]. Can Geotech J, 1994, 31: 521-532. doi: 10.1139/t94-061
[14] FREDLUND D G. RAHARDJO. Soil Mechanics for Unsaturated Soils[M]. Wiley, 1993.
-
期刊类型引用(4)
1. 应宏伟，陈雨，王阳扬，刘冠. 含碎石芯软黏土复合试样大三轴试验研究. 湖南大学学报(自然科学版). 2024(11): 104-114 . 
百度学术
2. 邱俊峰，叶晨峰，陈峰，郑铖杰. 镍铁渣粉水泥固化砂土剪切强度与应力应变关系研究. 湖南文理学院学报(自然科学版). 2023(02): 78-82+95 . 百度学术
3. 殷天军，宁华宇，寇晓强. 深中通道沉管基础水下深层水泥搅拌桩应用全过程探讨. 中国港湾建设. 2022(07): 11-16 . 百度学术
4. 张振，郑文强，叶观宝，陈勇. 循环荷载下水泥土桩复合单元体变形特性及其地基长期沉降计算方法. 中国公路学报. 2022(11): 21-29 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 221
- HTML全文浏览量: 26
- PDF下载量: 64
- 被引次数: 6
