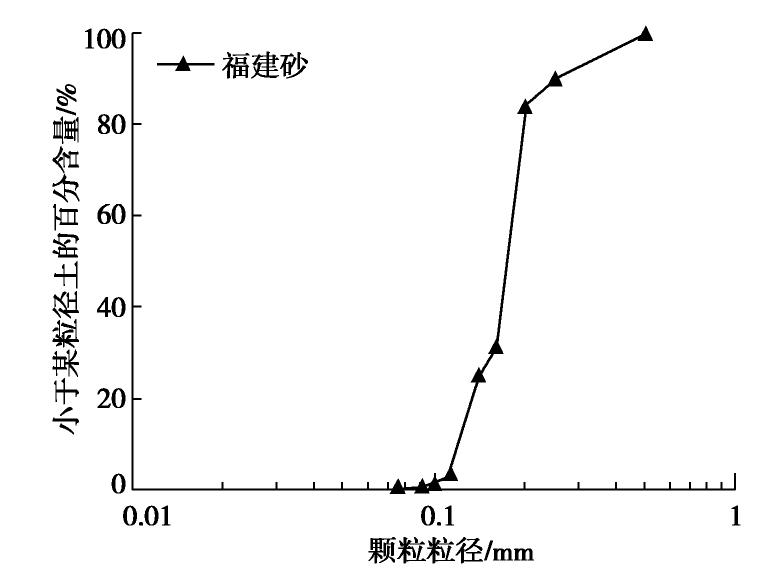
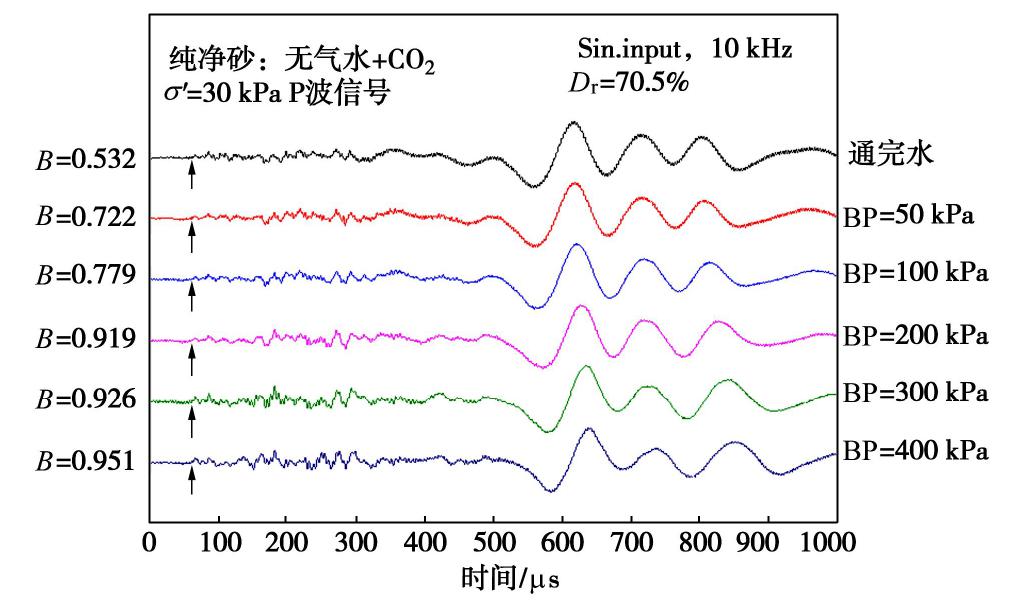
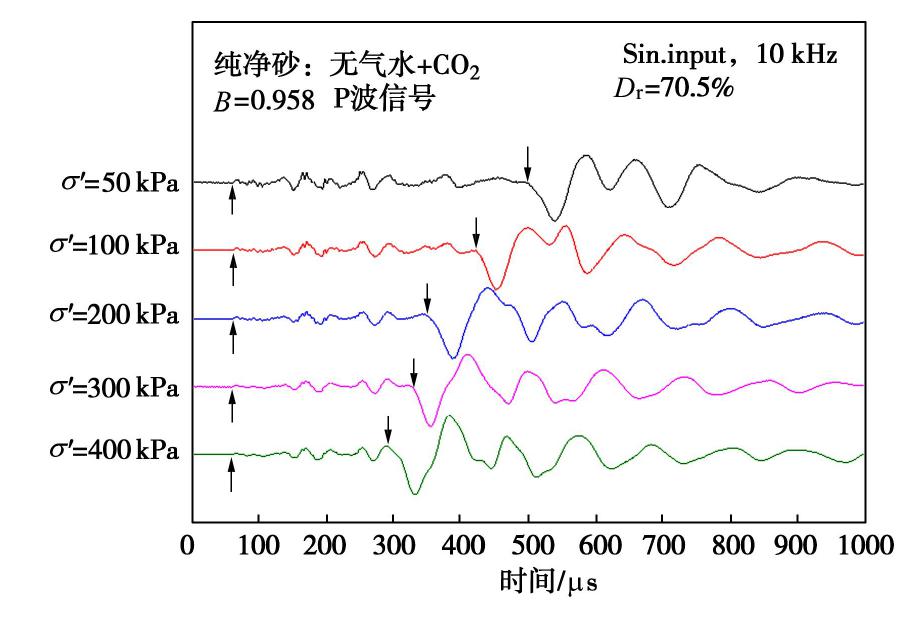
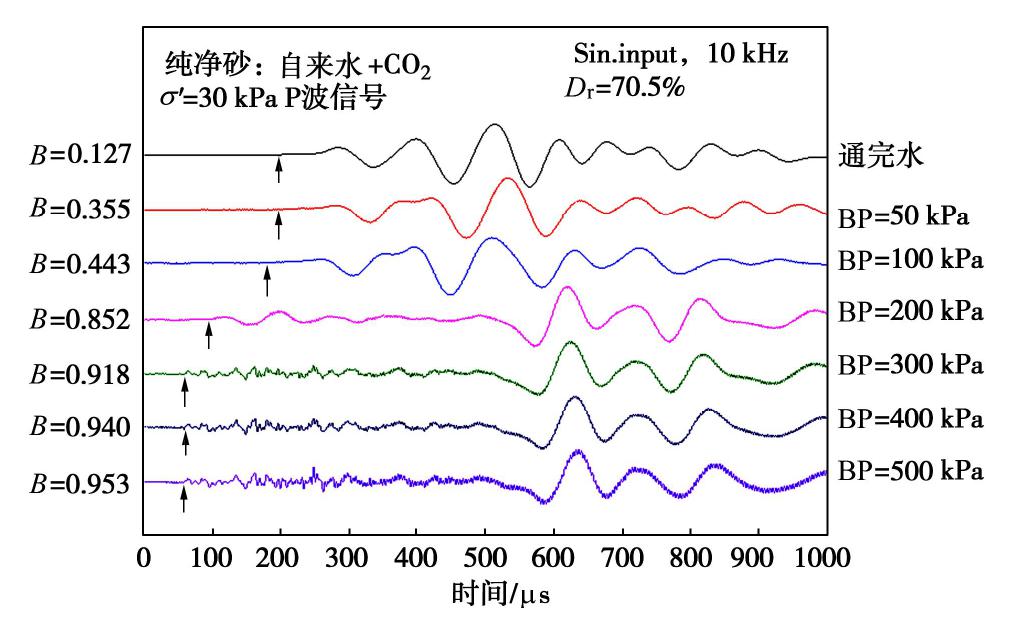
Investigation on relationship between P-wave velocity and B-value by bender element tests
-
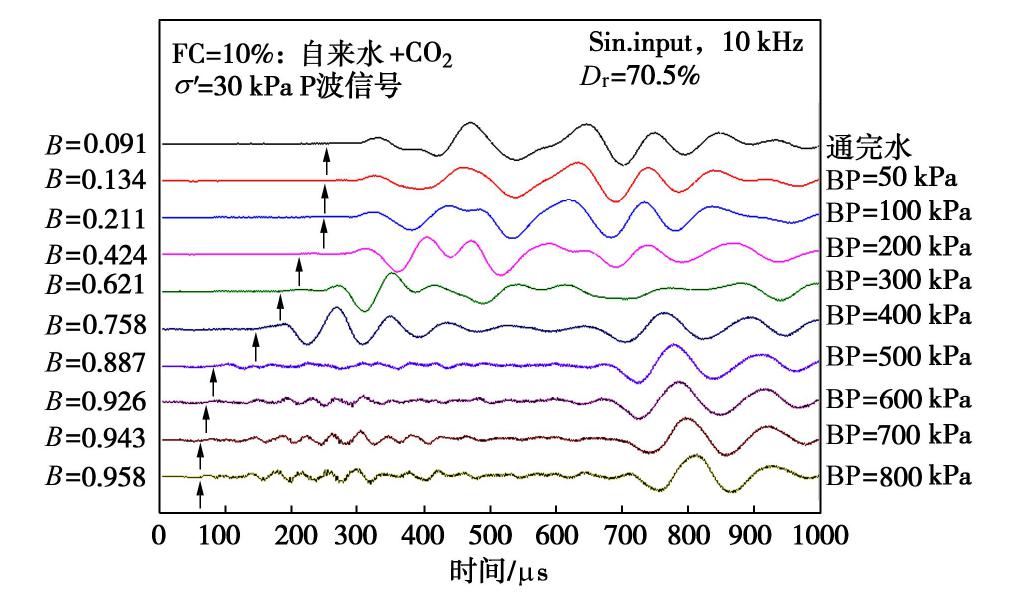
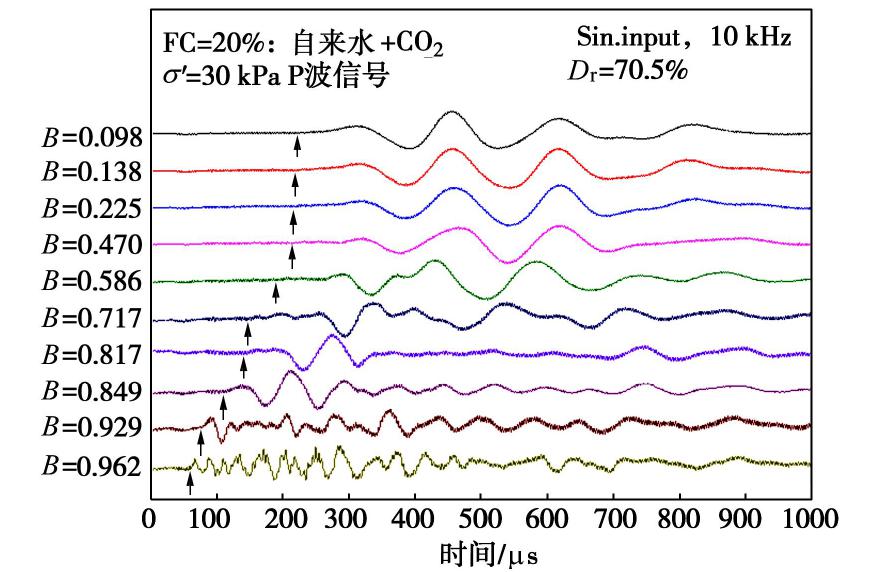
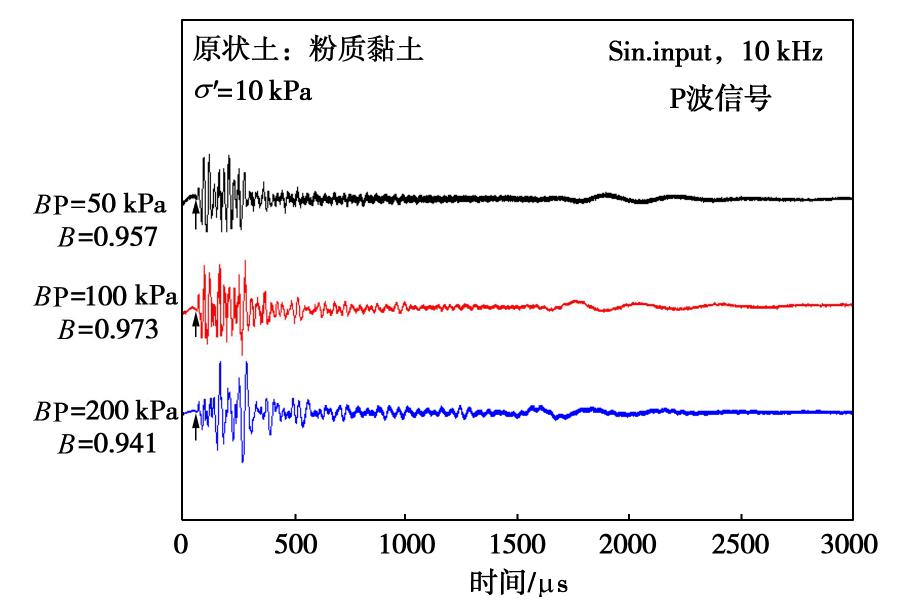
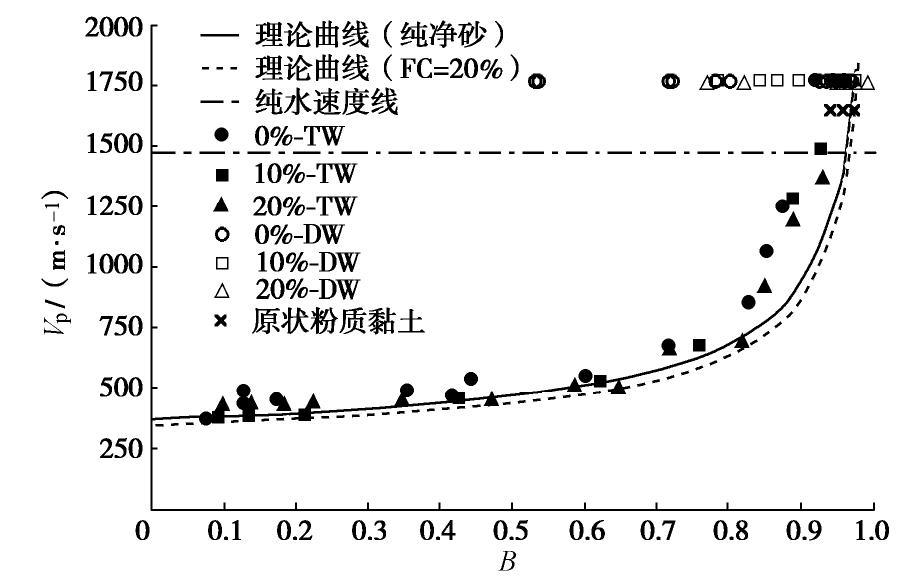
摘要: 利用带有弯曲元波速测试系统的GDS应力路径三轴仪,测定了土体中P波与孔隙水压力系数B值,研究了土体P波信号随着饱和度的演化过程,并对比分析了孔隙水类别(自来水或无气水)、砂样中黏粒含量、土体类别对P波波速Vp与B值关系的影响。研究结果表明:当孔隙水为无气水或砂样B值达到一定值时,P波信号由两大部分组成,第一部分较第二部分幅值小但频率高,且不受有效围压和输入波初始偏振方向影响,可确定为P1波。当孔隙水为无气水时,Vp与B值大小无关且保持最大波速不变;而孔隙水为自来水时,在B值较小时两者关系与理论曲线趋势相近,随着B值的增大,Vp与理论值差距越来越明显。另外,Vp最大值与黏粒含量无关,且受土体类别影响较小,均大于纯水中P波波速。Abstract: The P-wave velocity Vp and the pore water pressure coefficient B in saturated soils are measured by bender element system in a GDS stress path triaxial apparatus. The evolution of P-wave signals with saturation and the effects of fluid type (tap water or de-aired water), clay content and different soil types on the relationship between Vp and B-value are considered. It is concluded that when the fluid is de-aired water or B-value reaches a certain value, the P-wave signal is composed of two parts. The first part has a smaller amplitude but a higher frequency than the second part. The first part is not affected by the effective confining pressure and the initial polarization direction of the input wave, and therefore it can be deduced as P1 wave. When the fluid is de-aired water, Vp is independent of B-value and the maximum wave velocity is constant. When the fluid is tap water, the relationship between Vp and B-value is consistent with the theoretical prediction in general when the B-value is small. When the B-value becomes large, the difference between the measured Vp and the theoretical value becomes larger. Besides, the maximum Vp in soil is greater than that in pure water, which is independent of clay content and soil type.
-
0. 引言
作为七大环境公害之一,交通引起的环境振动问题愈发受到关注。对于环境振动问题的研究方法主要集中在现场测试、数值模拟和理论推导3个方面。在理论推导方面,1904年Lamb[1]发表了关于稳态解的Fourier法考虑4种典型振源的解析解积分表达式的经典论文,而后许多学者[2-3]在Lamb的基础上进行深入研究。但理论推导存在许多假设条件,从而导致与实际工程存在较大差异。因此实际工程评估时常采用现场测量与数值模拟相结合的方式。例如,蒋通等[4]在实测上海地铁3号线的基础上,利用有限元建立了车-桥子结构和框架-桩基础-地基子结构,并进行计算。然而,无论是现场实测还是数值模拟,多是针对具体某个工程而言。人们想通过最简单的测量而得到尽可能多的信息,于是振动预测应运而生。例如,Bornitz所提出了点振源环境振动理论衰减公式[5-6],它考虑了距离、土体几何阻尼以及材料阻尼的影响。
目前对于高速铁路运行所引起的环境振动的问题已有较多的论述,例如Xia等[7]对高速铁路引起的振动进行了现场实测,表明振动加速度会随列车车速的增加而增大;Yang等[8]提出半解析方法研究了高速列车引起的地基振动问题,分析了车速、跨度和支座刚度等参数对地基振动的影响。磁悬浮列车作为一种速度很快的交通方式,有较好的发展潜力。但关于由它运行引起的环境振动问题研究较少。此外,对于环境振动实测分析方面,文献主要探讨振动随距离衰减的特性。但随着地下城市空间的开发,放置在地下的精密仪器越来越多,许多工程对地下振动的要求越来越严格,故非常有必要对振动随深度的衰减特性进行研究。本文通过现场实测,分析磁悬浮列车运行引起的环境振动随距离及深度的衰减特性,为将来磁悬浮列车引起的环境振动问题以及远场环境振动随深度衰减的特性提供有益的参考。
1. 现场实测及数据预处理
1.1 工程概况
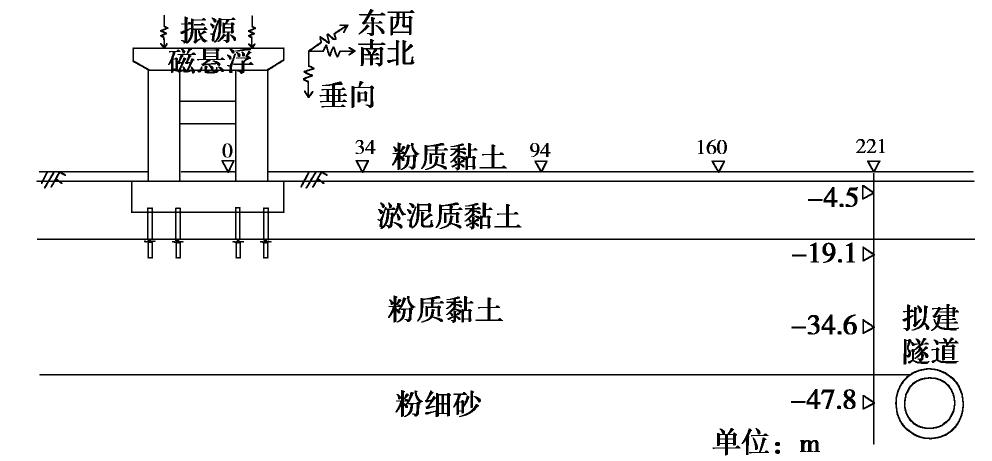
本研究依托上海硬X射线自由电子激光装置4号井振动评估项目,其振动控制标准为隧道底板微振动小于0.15
。4号井附近的振源主要有磁悬浮线路、16号地铁线路以及罗山路。地铁16号线和罗山路距离4号井较远(约350 m),故可利用16号线列车未经过而磁悬浮列车经过时的振动来研究磁悬浮列车引起的环境振动衰减规律。 1.2 测试仪器及监测布点
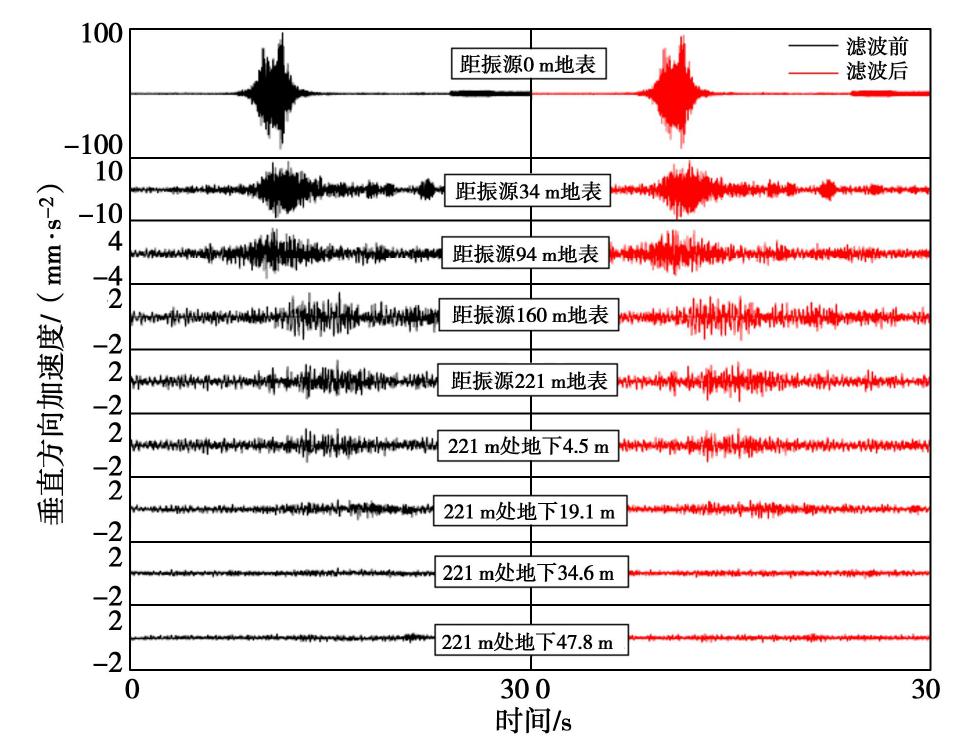
本次测试采用的仪器为中国工程力学研究所941 B型拾振器,该拾振器适合测试结构物及地面振动。由于土层振动频率一般为低频,不会高于100 Hz[6, 9],故本次测试采样频率为256 Hz,以达到精确的结果。为了解隧道附近的真实环境振动情况,从磁悬浮线路至4号井沿线布置5个地面测点,同时在4号井位置沿深度0,4.5,19.1,34.6,47.8 m布置5个测点,测试场地与测点布置如图1所示。
本次测量共获取10条磁悬浮列车经过时的振动数据,但其中一条磁悬浮列车与16号线地铁同时经过,故本次分析只选取9条磁悬浮列车单独通过时的振动数据。
1.3 实测数据预处理
实测数据由于受到各种干扰(如电磁场等)会偏离真实振动值,所以对数据进行分析前需要进行预处理。振动数据预处理主要包含滤波和消除趋势项。
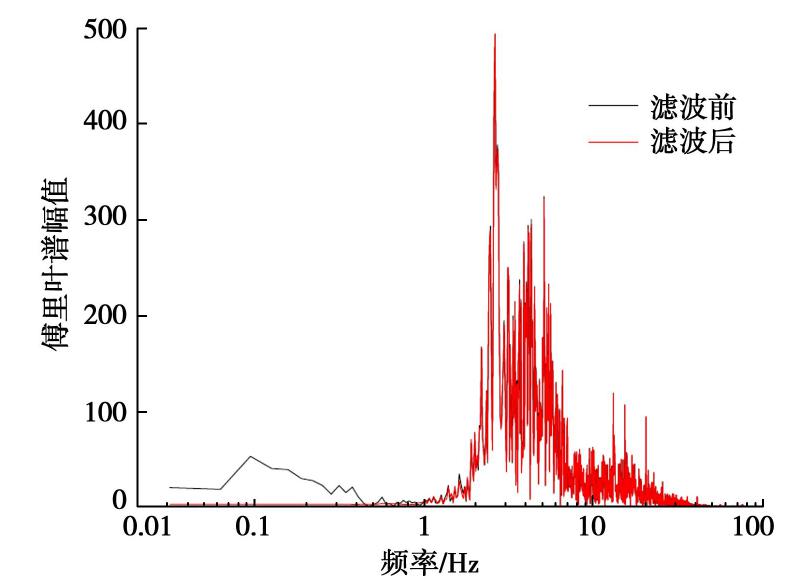
首先对振动数据进行快速傅里叶变换,在尽可能保证数据整体能量的前提下确定滤波的范围,再根据滤波范围调整并选取滤波器类型。本次振动数据处理采用的是无限长冲激响应IIR型滤波器中的切比雪夫Ⅰ型带通滤波器,带通截止频率为1~128 Hz(温度变化产生的低频干扰信号通常在0~1 Hz)。
图2给出了滤波前后不同测点垂向实测振动信号。由图可见振幅随着距离的增加明显衰减,同时滤波前后加速度时程曲线未明显变化。图3给出了距振源221 m地下4.5 m测点垂向加速度信号的频谱曲线。由图可知滤除的能量(频谱中图形与横坐标所围的面积)约为28,而主体部分能量约为25000,滤除的能量仅占主体能量的0.1%,说明该滤波方法是可行的。
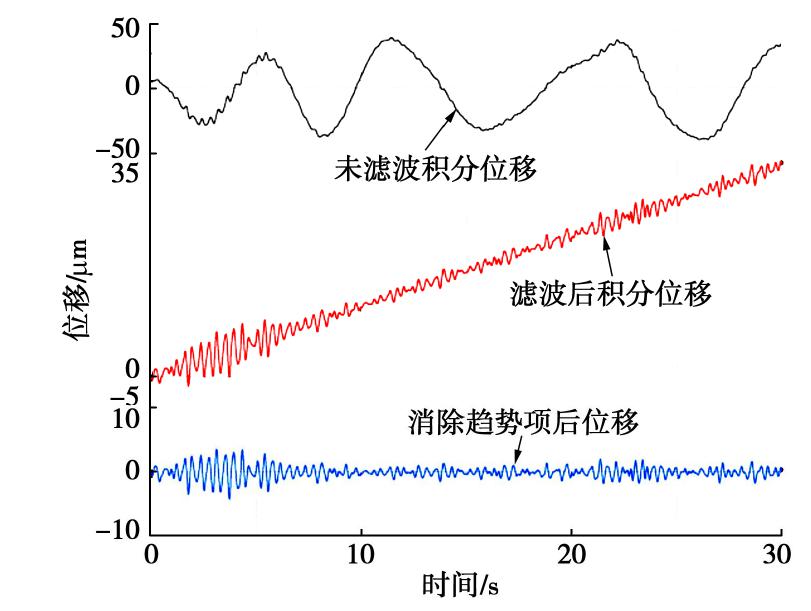
速度和位移通常可由实测的加速度进行时域积分或频域积分得到,然而积分时通常会出现零点漂移现象。信号中的低频成分对位移振动幅值有着十分大的影响,并且传感器由于温度变化也常会产生低频长周期(通常在0~1 Hz)的趋势项,从而影响测试数据的准确性。因此,对滤波后的加速度数据进行积分后还需要进行消除趋势项处理以获得准确的数据。
图4对比了基于滤波前后距振源221 m地下4.5 m测点垂向加速度数据积分得到的位移曲线以及消除趋势项后的位移曲线。由图4所示,直接对未滤波的加速度数据进行积分得到的位移曲线受到低频长周期(干扰信号)的影响很大,不能反映真实的振动位移。对滤波后的加速度数据进行积分,呈现位移单调增加的趋势项。经趋势项消除处理后,便可还原真实合理的振动信号,说明本文采用的预处理十分有效。
2. 环境振动实测结果与分析
2.1 振动随距离衰减特性
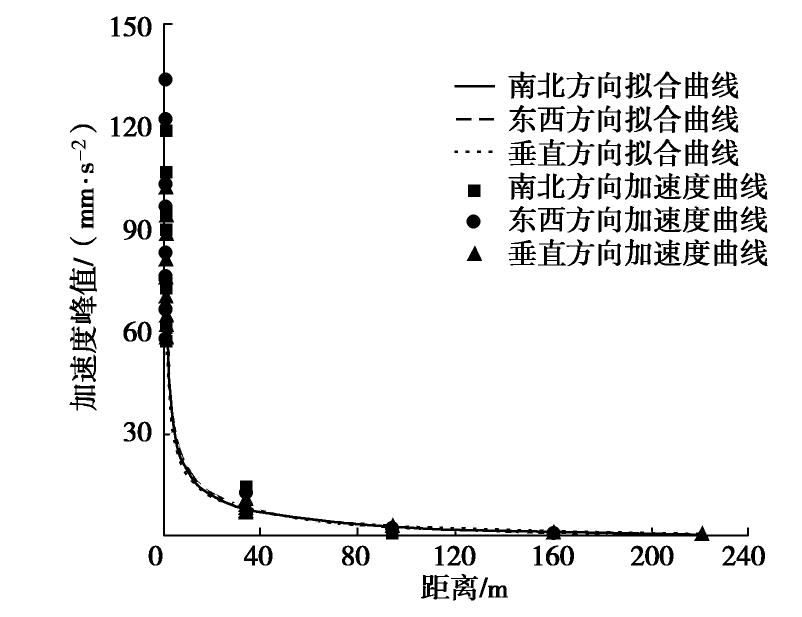
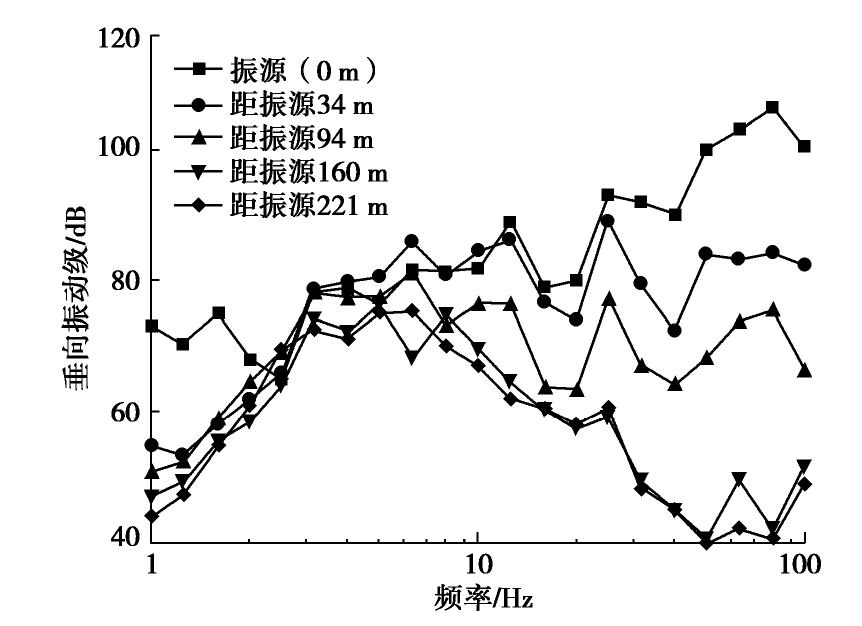
振动随距离的衰减特性多以加速度峰值作表征指标,并用Bornitz公式进行分析。图5给出了实测各个测点三方向的加速度峰值及其拟合曲线,可见振动随着距离的增加而减小,未发现振动放大区,也没有振动明显占优的方向。频域分析采用的是1/3倍频程谱,某次实测振动1/3倍频程谱如图6所示,可见振动随距离的增加,其优势频带不断降低,从振源的80~100 Hz优势频带不断减少至3.15~6 Hz。优势频带主要与振动介质有关,振源处的振动介质主要为混凝土,其产生振动的频率较高,而土体的优势频率低,一般是几赫兹左右,振源产生的高频经过土层这个低频滤波器不断滤波,使得优势频带不断降低,直到与土层的固有频率相近。上海硬X射线场地的优势频率在3~5 Hz左右[10-11],这与本次的实测结果一致。
本文对实测各方向的加速度峰值按Bornitz的点振源振动衰减公式进行拟合:
, (1) 式中,A0为振源处加速度峰值,R为距振源的距离,n为几何阻尼(辐射阻尼)系数,a为材料阻尼系数。拟合得到的南北向加速度峰值衰减公式为
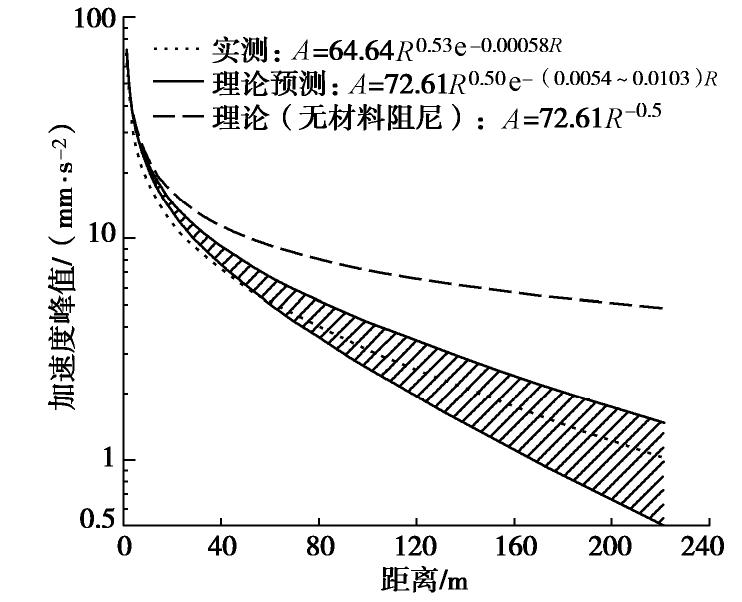
,东西向加速度峰值衰减公式为 ,垂向加速度峰值衰减公式为 。 下面选取垂向加速度峰值衰减规律对磁悬浮列车运行引起的环境微振动随距离的变化进行讨论。实测磁悬浮振源处地表垂向振动加速度峰值平均值A0=72.61 mm/s2。振动在远场中以瑞利波(面波)为主,高架引起的地表振动属于列阵点振源,远场中更偏向于点振源情况,根据Kim等[12]的研究(表1),本次磁悬浮列车引起的环境微振动的辐射阻尼系数取0.5;材料阻尼系数a主要取决于土体类型和振动频率,可由频率无关系数a0与场地振动优势频率f的乘积得到。根据Athanasopoulos等[13]、Yang等[14]建议的各类土的a0,可计算软土的频率无关系数a0大约为(1.80~2.05)×10-3,同时考虑本工程场地以及上海软土的优势频率在3~5 Hz,故取材料阻尼系数a=a0×f=(5.40~10.25)×10-3。图7对比了Bornitz理论预测曲线和实测拟合曲线,由图可见,在远场区域实测的拟合曲线与Bornitz理论预测曲线符合很好,而在近场区域Bornitz理论预测曲线比实测的要大2~8 mm/s2(衰减慢一些),这主要是因为实际振动存在体波的影响。体波衰减较瑞利波更快(体波几何阻尼衰减系数要大于瑞利波),而理论预测时认为振动以瑞利波为主,直接忽略的体波的影响,故理论预测曲线在近场区域更大一些。此外,不考虑材料阻尼时预测的振动会明显大于实测振动,表明尽管振动微小,也存在一定的土体材料阻尼,不能将其忽略,尤其是考虑远场环境振动时。
表 1 不同振源位置及类型的辐射阻尼系数值Table 1. Values of attenuation coefficient due to radiation damping for various combinations of source location and type振源位置 振源类型 波的类型 n 地表 点振源 体波 2.0 地表 点振源 面波 0.5 地表 线振源 体波 1.0 地表 线振源 面波 0.0 地下 点振源 体波 1.0 地下 线振源 体波 0.5 2.2 振动随深度衰减特性
一直以来,较少学者去研究振动随深度的衰减特性,主要是因为理论推出振动位移随深度衰减较快,且主要关心地表振动。随着社会发展,许多精密设备放在地下且对振动的要求越来越严格,远场深度微小的振动不可忽略。对于振动随深度衰减的研究,1970年Woods等[15]和Lysmer等[16]从理论上提出了竖向简谐作用下不同泊松比土中的水平振动和竖向振动位移振幅随深度的分布曲线。
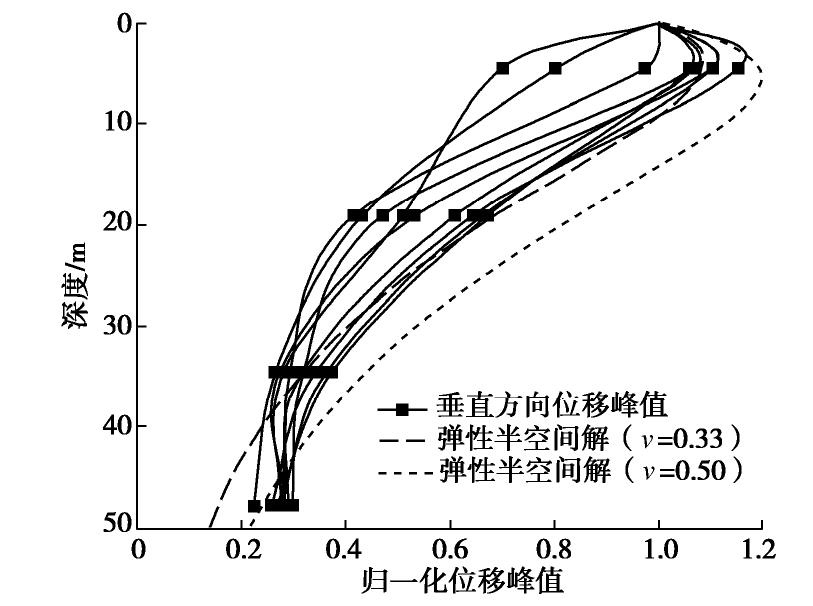
图8给出了以实测地表垂直向位移峰值作归一化后的振动位移峰值随深度的衰减曲线。由图可见,振动总体随深度的增加而减小,但在地下5 m处存在放大区,这与解析解得到的规律一致,两者符合较好。但解析解沿深度衰减的更快,在较深区域会低估实测的振动值。笔者认为原因是实际场地存在地脉动,在远场深处微小的振动情况下地脉动的影响不可忽略。
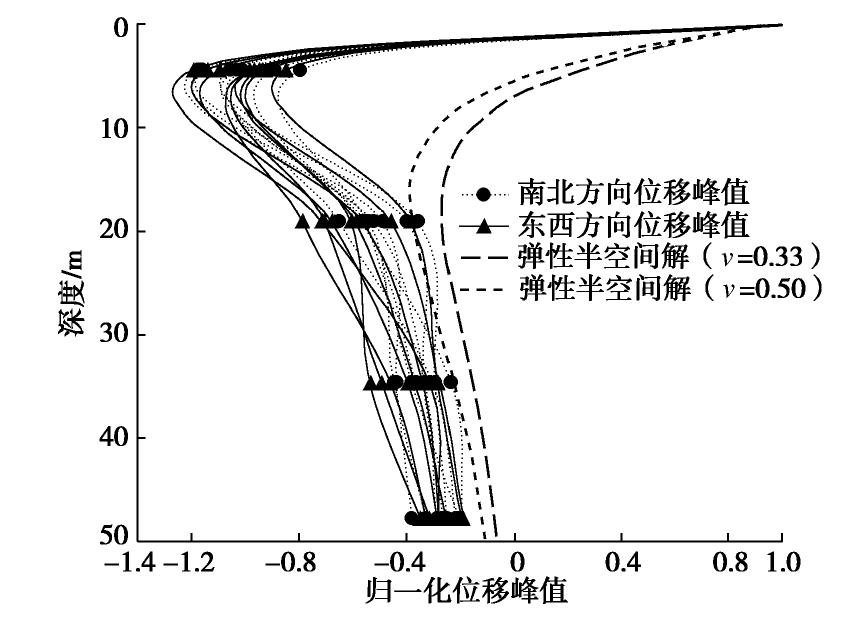
图9给出了实测水平方向振动位移峰值随深度的衰减曲线,可以看出水平方向在地下5 m处亦存在一定的放大,部分点甚至超过了其地面振动,可能的原因是由于分层地基中某些土层的固有瑞利波速与整个土层的瑞利波速度接近时(整个土层的瑞利波是根据频率从整个土层的瑞利波弥散曲线得到的),其瑞利波的位移会明显增大,类似于局部共振现象[11]。由图可见,解析解会明显低估了水平方向的振动,笔者认为原因有二:①实际场地是分层土层,瑞利波在土层中反射干涉会发生弥散效应,会增强深度水平方向的振动;②实际场地存在地脉动,地脉动在三方向量级相当,而解析解竖直方向的振动会明显大于水平方向的振动,实测振动包含地脉动后,水平方向的振动会被低估的更加明显。
3. 结论
本文通过现场试验研究磁悬浮列车引起的环境微振动随距离和土层深度的衰减,初步可得以下3点结论。
(1)实测磁悬浮列车引起的振动随距离的增加而减小,其远场土层优势频率在3~6 Hz。Bornitz的理论预测公式可较为准确的预测磁悬浮列车振动随距离的变化情况,特别是远场的振动,但会部分高估(2~8 mm/s2)近场区域的振动。
(2)实测磁悬浮列车引起的远场振动总体随深度的增加而减小,但振动在地下5 m处存在放大区。对于竖直位移振幅,弹性半空间解析解可以较好的反应其随深度的变化规律,但会低估较深区域的振动。对于水平位移振幅,弹性半空间解析解会明显低估远场深度方向的振动。
(3)环境振动衰减主要由几何阻尼为主,但土体材料阻尼的作用不能简单地忽略,尤其是远场区域。同时,预测远场深度方向的振动时,瑞利波的弥散特性和地脉动的影响不可忽略。
-
表 1 不同含量混合砂的基本参数
Table 1 Basic parameters of sand-clay mixtures
黏粒含量/% 相对密度 最大干密度/(g·cm-3) 最小干密度/(g·cm-3) 最大孔隙比 最小孔隙比 0 2.638 1.595 1.308 1.017 0.654 10 2.658 1.660 1.315 1.021 0.601 20 2.684 1.761 1.320 1.033 0.524 -
[1] SHERIF M A, ISHIBASHI I, TSUCHIYA C. Saturation effect on initial soil liquefaction[J]. Journal of the Geotechnical Engineering Division, 1977, 103(8): 914-917. doi: 10.1061/AJGEB6.0000477
[2] YOSHIMI Y, TANAKA K, TOKIMATSU K. Liquefaction resistance of a partially saturated sand[J]. Soils and Foundation, 1989, 29(3): 157-162. doi: 10.3208/sandf1972.29.3_157
[3] TSUKAMOTO Y, ISHIHARA K, NAKAZAWA H, et al. Resistance of partly saturated sand to liquefaction with reference to longitudinal and shear wave velocities[J]. Soils and Foundations, 2002, 42(6): 93-104. doi: 10.3208/sandf.42.6_93
[4] SKEMPTON A W. The pore-pressure coefficients A and B[J]. Géotechnique, 1954, 4(4): 143-147. doi: 10.1680/geot.1954.4.4.143
[5] YANG J. Pore pressure coefficient for soil and rock and its relation to compressional wave velocity[J]. Géotechnique, 2005, 55(3): 251-256. doi: 10.1680/geot.2005.55.3.251
[6] TAMURA S, TOKIMATSU K, ABE A, SATO M. Effect of air bubble on B-value and P-wave velocity of a partially saturated sand[J]. Soils and Foundations, 2002, 42(1): 121-129. doi: 10.3208/sandf.42.121
[7] NAESGAARD E, BRYNE P M, WIJEWICKREME D. Is P-wave velocity an indicator of saturation in sand with viscous pore fluid?[J]. International Journal of Geomechanics, 2007, 7(6): 437-443. doi: 10.1061/(ASCE)1532-3641(2007)7:6(437)
[8] HAKANATA M, MASUDA T. Experimental study on the relationship between degree of saturation and P-wave velocity in sandy soils[C]//Geotechnical Engineering for Disaster Mitigation and Rehabilitation, Part 4. Beijing: Science Press, 2008: 346-351.
[9] GU X Q, YANG J, HUANG M S. Laboratory investigation on relationship between degree of saturation, B-value and P-wave velocity[J]. Journal of Center South University, 2013, 20(7): 2001-2007. doi: 10.1007/s11771-013-1701-x
[10] POLITO C P, MARTIN J R. Effect of non-plastic fines on the liquefaction resistance of sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(5): 408-415. doi: 10.1061/(ASCE)1090-0241(2001)127:5(408)
[11] XENAKI V C, ATHANASOPOULOS G A. Liquefaction resistance of sand-silt mixture: an experimental investigation of the effect of fines[J]. Soil Dynamics and Earthquake Engineering, 2003, 23(3): 183-194.
[12] CHANG W J, HONG M L. Effect of clay content on liquefaction characteristics of gap-graded clayey sands[J]. Soils and Foundations, 2008, 48(1): 101-114. doi: 10.3208/sandf.48.101
[13] LINGS M L, GREENING P D. A novel bender/extender element for soil testing[J]. Géotechnique, 2001, 51(8): 713-717. doi: 10.1680/geot.2001.51.8.713
[14] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid: I Low frequency range: II Higher frequency range[J]. Journal of the Acoustic Society of America, 1956, 28(2): 168-191. doi: 10.1121/1.1908239
[15] PLONA T J. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies[J]. Applied Physics Letters, 1980, 36(4): 259-261. doi: 10.1063/1.91445
[16] GU X Q, YANG J, HUANG M S. Laboratory measurements of small strain properties of dry sands by bender element[J]. Soils and Foundations, 2013, 53(5): 735-745. doi: 10.1016/j.sandf.2013.08.011
[17] GU X Q, YANG J, HUANG M S, et al. Bender element tests in dry and saturated sand: signal interpretation and result comparison[J]. Soils and Foundations, 2015, 55(5): 952-963.
-
期刊类型引用(3)
1. 吴德顺,顾晓强,刘鑫. 上海地铁运行引起软土场地振动实测与预测模型研究. 结构工程师. 2023(05): 174-183 .  百度学术
百度学术
2. 蒋家文,张琦. 超导磁悬浮列车及超导技术的运用. 智能城市. 2021(18): 136-137 .  百度学术
百度学术
3. 邱乐侠,胡启洲,吴翊恺,吴啸宇. 基于多粒度粗糙集与多级可拓的高速磁浮系统综合评判. 交通运输工程与信息学报. 2021(04): 106-117 .  百度学术
百度学术
其他类型引用(6)



 下载:
下载: