Non-linear settlement calculation method based on soil parameters obtained from pressuremeter tests
-
摘要: 在常规的地基沉降计算方法中,通常由于室内试验确定的计算参数与实际土体参数存在一定的误差,导致理论计算结果与实际沉降相差较大。为了解决问题,考虑地基沉降的非线性,采用原位试验确定计算参数是一个可行的办法。旁压试验不仅操作简单、费用低,而且能测得不同深度的土体参数。在前人已有的研究成果基础上,研究了基于旁压试验获得沉降计算参数的非线性沉降计算方法。主要内容和成果有：①对目前常用沉降计算方法存在的不足和计算结果精度不高的原因进行了分析总结；②根据旁压试验的受力特点、原理及旁压孔壁土体应力分布规律,假定土体服从M-C屈服准则,从理论上推导沉降计算中需要的岩土体参数Et0,c,φ；③基于杨光华提出的非线性切线模量法,推导并给出了利用旁压试验成果计算地基非线性沉降的原理和步骤；④结合具体工程实例,验证了该方法,并与规范方法中分层总和法的结果进行了对比分析,结果表明基于原位测试结果确定岩土体参数的沉降计算值更符合实际。由于旁压试验在不同深度能够考虑土的非线性和土体剪切变形引起的沉降,通过这项探索性的研究为今后利用原位试验结果计算地基变形打下了基础,也为实际工程的计算分析提供借鉴。Abstract: In the conventional calculation method for foundation settlement, there is a certain error between the calculation parameters determined by laboratory tests and the actual soil parameters, which leads to a large difference between prediction and reality. To overcome this shortcoming and consider the nonlinearity of foundation settlement, it is feasible to determine the calculation parameters by in-situ tests. The pressuremeter tests are easy to operate and low cost and can be used to measure the soil parameters at different depths. Therefore, on the basis of the previous research results, a non-linear settlement calculation method based on the calculation parameters obtained from the pressuremeter tests is studied. The main contents and achievements are as follows: (1) the shortcomings of the current commonly used settlement calculation methods and the reasons for the low accuracy of the calculated results are analyzed and summarized. (2) According to the stress characteristics and principles of the pressure meter tests, and the distribution laws of soil stress of the pressure meter hole wall as well as the M-C yield criterion, the parameters Et0, c and φ needed in the settlement calculation are derived theoretically. (3) According to the non-linear tangent modulus method proposed by Yang Guang-hua, the principle and procedure of calculating the nonlinear settlement of foundation based on the results of pressuremeter tests are derived and given. (4) The proposed method is verified through projects, and the results are compared with those predicted by the codes (layer-wise summation method). The comparison shows that the prediction based on the parameters derived from in-situ tests is closer to the real settlement. Because the nonlinear soil and the settlement caused by shear deformation of soil can be considered in the pressuremeter tests at different depths, this exploratory study lays a foundation for the calculation of foundation deformation by the results of in-situ test in the future. It can also be regarded as a reference for other projects.
-
0. 引言
膨胀土具有较强的亲水性,对于处于季节冻土区的渠道工程、边坡工程等,反复冻融循环对膨胀土的劣化作用会极大影响工程稳定性[1-2]。已有的研究表明,冻融作用对土体的性质改变相对复杂,部分特征并无统一认识[3-4],典型的如内摩擦角,变大、变小、基本不变的结论均有。由于冻融循环作用下,不同土体响应机制的复杂性,针对膨胀土特定土体的冻融分析在工程实践中具有更好的指导意义。
目前针对膨胀土的冻融循环研究已有了较大进展,蔡正银等[2]以高寒渠道膨胀土为研究对象,在干湿冻融耦合的试验条件下系统讨论了冻融作用下膨胀土的裂隙演化规律。Lu等[5]、Tang等[6]则讨论了不同状态下的膨胀土与循环冻融次数相关的劣化规律,研究表明,随着冻融循环次数的增加,膨胀土的破坏强度、弹性模量、抗剪强度等力学指标劣化加剧,且第一次冻融循环下其劣化最为明显。
目前有关冻融循环下的损伤模型,更多是基于连续介质理论展开。损伤力学中的损伤因子D部分研究需要借助其他测试手段进行确定,如卢再华等[7]通过CT扫描技术定义损伤因子,其构建的损伤模型包含23个参数,均需测试确定。目前主流的损伤因子定义是在已有的应力应变测试成果上进行,其中假设土体微元满足weibull分布,基于应变等价原理开展损伤模型构建获得了广泛应用。杨明辉等[8]、李向东等[9]进行了基质吸力和外部荷载耦合状态下的非饱和土损伤模型构建。Tang等[6]基于多种技术手段综合研究了损伤程度与冻融循环次数之间的关系,并构建了冻融循环作用下的统一损伤模型。总结目前的土的损伤模型,其损伤定义时,主要考虑了弹性模量的退化,核心均集中到应力应变曲线的模拟,但是对于土体本身的性质如压硬性等考虑不足。
传统弹性力学中的应变是微应变,但是土工试验中的土体变形量较高,因此完全按照传统应变去研究其土体性质无法充分考虑土体的内在特质。基于此,通过引入自然应变的概念、weibull统计分布规律、应变等价原理等,推导构建适用于膨胀土的损伤模型,并以损伤模型为基础进行冻融损伤分析等工作。
1. 基于自然应变的冻融损伤模型
1.1 自然应变适用性
以图1中所示的岩土体为分析模型,其满足均质各向同性的基本假定,受荷时,假定无新的损伤发生,其应力应变关系用HOOK定律进行描述,
dσ=Kdε, (1) 式中,
σ 为岩土材料截面应力（压为正）,K为岩土体的刚度,ε 为当前应力状态下的应变量。根据弹性力学理论,岩土体的应变可为
dε=−dH/H, (2) 式中,H为当前应力状态下的试件高度。
式（2）计算的应变,Freed将其定义为自然应变或真实应变[10]。具体到应用阶段通过下式计算岩土体应变量更为广泛：
dε=−dH/H0, (3) 式中,H0为未受荷时的试件高度。对于高刚度材料,通常变形量较原来的形状较为微小,数量级相差在2个以上,此时式（2）,（3）基本等效。式（3）由于更简洁的表达形式,在岩土工程建设中具有广泛的应用场景。但对于部分软岩、松散土体、断裂结构、多孔介质等,全部采用式（3）去分析其力学特征,则可能会阻碍对岩土本质特征的正确认识。
对于土体而言,土颗粒是高刚度材料,由于空气和水的存在,其形成的多介质土体则不完全满足式（3）的适用条件。尤其是对于亲水性矿物含量高的膨胀土而言,饱和时,会极大的削弱土体的刚度,干湿循环、冻融循环的条件下,会进一步导致其刚度的降低。因此在分析其力学特征时,式（2）具有更好的适用性。
1.2 基于应变等价原理的冻融损伤变量
岩土体的损伤产生主要有受荷和环境影响2部分。针对产生损伤岩土体,目前常用的损伤变量定义方法是基于应变等价原理实现,即可将损伤状态的材料在有效应力作用下的应变与无损状态下的应变进行等效,其无损状态的材料所受的应力称为名义应力。原理图如图1所示,表达式为
ε=σE′=σ′E, (4) σA=σ′A′, (5) 式中,
σ 为损伤状态下的有效应力,A为损伤状态下有效承载面积,E'为损伤状态下的岩土体模量,σ'等效无损状态下的名义应力,A'等效无损状态下有效承载面积,E为等效无损状态下的岩土体模量。损伤变量可用岩土体模量来表示,
D=1−E'/E。 (6) 更一般的情况下,岩土体的损伤可用岩土体变形模量的损伤来定义,目前多数文献均采用此定义[6, 8-9]。
基于式（2）的自然应变概念,可进一步建立岩土体刚度和传统方法变形模量的关系,
E=σ1−exp(−σ/K)。 (7) 将式（7）代入式（6）,可得自然应变下的岩土体损伤变量为
D=1−K'/K, (8) 式中,K'为损伤状态下的土体刚度。式（6）,（8）的形式基本一致,但是代表的是两种不同应变概念下的损伤定义方式。对于高刚度材料,E=K,传统的应变定义是自然应变定义下的一种特殊情况。
对于环境损伤Df（冻融循环、干湿循环）和受荷损伤Ds耦合的情况,总的损伤变量D可表示为
D=1−(1−Df)(1−Ds)。 (9) 1.3 受荷损伤模型构建
假设土体内部微元服从概率分布,可用Weibull分布定量描述微元强度的分布特征[11],
φ(F)=mF0(FF0)m−1e−(FF0)m=dDsdF, (10) 式中,φ(F)为土体微元强度概率分布函数,F0,m为Weibull分布的参数,F为微元的强度。
对式（10）进行积分可得,受荷损伤的损伤变量Ds与土体微元强度F的关系,
Ds=1−exp[−(F/F0)m]。 (11) 土体微元的强度准则采用D-P准则进行计算[12]。土体微元的强度F为
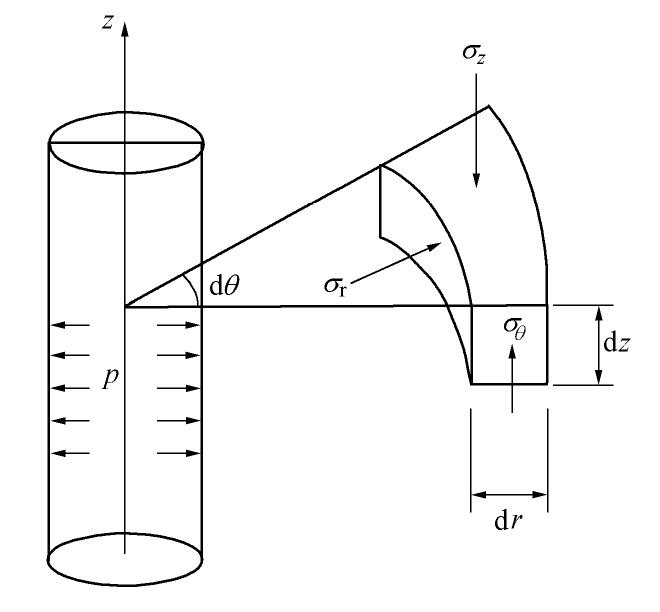
F=αI′1+√J′2, (12) 式中,
α 为材料参数,I′1 为有效应力状态下的应力第一不变量,J2'为有效应力状态下的偏应力第二不变量,α=2sinφ√3(3−sinφ) ,I′1=σ′1+2σ′3 ,J′2=13(σ′1−σ′3)2 ,} (13) 其中,φ土体微元内摩擦角,
σ′1 ,σ′3 为常规三轴条件下的竖向有效应力和有效围压。通过自然应变的概念,有效应力作用下的最大主应力方向的应变
ε′1 为ε′1=1−exp(−σ′1−σ′3K')(σ′1−σ′3)(σ′1−2μσ′3), (14) 式中,K'为土体的刚度,μ为泊松比。常规三轴试验时的固结过程,测得应力应变曲线主要是偏应力
(σ1−σ3) 和除去初始应变之后的应变ε1 ,基于应变等价原理,将有效应力进行转换,可将式（14）改写为σ1−σ3=−K0(1−Ds)ln(1−ε1), (15) 式中,K0为偏应力为0时的初始刚度。设孔隙水压力为PW,则联立式（12）～（15）,土体基于自然应变的损伤本构模型如下：
σ1−σ3=−K0ln(1−ε1)exp[−(FF0)m], (16) 其中,
F={2sinφ√3(3−sinφ)[(σ1−σ3)+3(σ3−PW)]+1√3(σ1−σ3)}⋅−K0ln(1−ε1)σ1−σ3。 (17) 2. 基于遗传算法的模型参数确定
从式（16）,（17）中可以发现,对于损伤参量无法直接测量的参数主要有初始刚度K0、土体微元内摩擦角φ、Weibull分布的参数F0和m。由于土体结构的复杂性,为避免误差累积,降低模型本身的精度,具体参数确定时采用智能算法遗传算法实现。遗传算法本质上属于生物进化算法,通过模拟生物进化中的优胜劣汰,对于具体的问题给出最优解[13]。对于给定的应力应变曲线,限定参数的取值范围,通过数值计算软件MATLAB编程,进行参数自动搜索,全局寻优,具体原理如图2所示。
3. 损伤模型验证
3.1 冻融循环试验数据
为进一步研究冻融循环后,膨胀土的损伤特性,利用Tang等[6]。的试验数据进行进一步的分析。试验土样充分饱水后进行冻融循环,-10℃保持12 h后,10℃保持12 h为1次冻融循环。试验采用常规三轴压缩试验,试验条件为固结排水,因此可不考虑超静孔隙水压力影响,试验围压为100 kPa。文献[6]采用的循环冻融次数NFT分别为0,1,3,7,11。试验结果如图3所示。
![]()
图 3 膨胀土冻融循环后的应力应变曲线Figure 3. Stress-strain curves of expansive soils after freeze-thaw3.2 损伤模型验证
通过MATLAB编程,遗传算法可实现损伤模型参数的自动获取。通过实测的应变应变数据模拟,得到到实测值和模拟值的对比如图4所示,模拟参数如表1所示。从图4中可明显的发现,基于自然应变推导的损伤模型可以很好的模拟膨胀土在不同冻融循环下的应力应变关系,模拟精度较高。
![]()
图 4 损伤模型应力应变曲线模拟值与实测值对比Figure 4. Comparison of simulated and measured values of stress-strain curves of damage model表 1 损伤模型拟合参数Table 1. Fitting parameters for damage modelNFT K0/MPa φ/(°) F0 m 0 15.96 35.31 154.05 0.3174 1 14.89 35.83 153.06 0.3205 3 12.96 34.18 146.31 0.3200 7 12.42 35.30 145.52 0.3202 11 11.90 34.86 143.63 0.3209 3.3 损伤模型参数分析
从表1可以明显发现,4个参数中初始刚度K0、参数F0呈现明显的劣化特征,土体微元内摩擦角φ,m相对变化不大。Weibull分布中的参数F0和m通常代表着宏观平均强度和均布系数。由于土体结构本身的劣化,对土体形成一定的损伤,导致F0的减小。由于冻融过程中,土颗粒的团聚效应,均布系数m有略微增加的趋势,验证了论文中本构模型对于分析冻融损伤的合理性。冻融损伤产生的一个重要原因就是孔隙的增加,结构劣化,因此膨胀土的冻融损伤同样表现在初始刚度K0的明显降低。
选取受冻融影响明显的初始刚度K0和参数F0作为分析对象,绘制其与冻融循环次数的关系曲线如图5所示。从图5中可以明显看出,初始刚度K0和参数F0的劣化规律均满足一定的负指数关系,随着冻融次数的增加,劣化速度减慢,逐渐趋于一稳定值。
![]()
图 5 损伤模型参数随冻融次数的变化曲线Figure 5. Variation of damage model parameters with number of freeze-thaw cycles4. 讨论
通过建立的自然应变损伤模型,高精度的模拟了膨胀土冻融循环后的应力应变曲线,以及分析了冻融损伤对模型参数的影响。为进一步研究冻融损伤的损伤演化过程,利用式（9）绘制损伤因子D的变化曲线如图6所示。通过图6可以看出,在应力应变曲线的后期,不同冻融循环下的损伤因子基本上趋于一致。在应力应变曲线前期,随着冻融循环次数的增加,冻融损伤速度也进一步加快。但是这种加快的趋势随循环次数的增加开始减弱。
事实上,基于自然应变的膨胀土损伤模型优势不仅在于模拟精度上的提升,而且可以解决传统应变模式下对于土体本身性质认识的局限性。通过自然应变损伤模型,将非损伤变形和损伤变形进行一定区分,绘制图7的应力变形曲线。
![]()
图 7 不同冻融循环下非损伤和损伤变形曲线Figure 7. Non-damage and damage deformation curves under different freeze-thaw cycles通过图7可以发现,非损伤变形部分呈现逐渐密实的状态,即对应加载过程中不存在土体损伤时的变形状态,变形曲线特征基本上与土体的侧限压缩试验对应。三轴压缩时,由于损伤变形贡献了主要的变形量,因此曲线特征基本上与损伤变形曲线一致。
5. 结论
通过引入自然应变的概念,基于Weibull统计理论和应变等价原理,构建了损伤模型。在模型验证的基础上进一步分析膨胀土的冻融损伤特征。通过研究得出以下结论。
（1）构建的自然应变损伤模型可高精度的模拟膨胀土不同冻融循环下的应力应变曲线特征。遗传算法在模型验证中自动化程度高,可实现参数的自动寻优。
（2）膨胀土初始刚度K0和参数F0的冻融劣化明显,与冻融循环次数呈负指数关系。内摩擦角呈现出一定的波动下降趋势,均布系数m有略微增加的趋势。
（3）从不同冻融循环下的损伤因子演化曲线可以看出,冻融损伤主要发生在应力应变曲线前期,且随着冻融循环次数增加,应力应变曲线前期的损伤速度有加快趋势。应力应变后期损伤过程则基本一致。
（4）绘制非损伤变形和损伤变形,非损伤变形呈现逐渐压密的状态,损伤变形贡献了更多的变形量。其变形特征与侧限压缩试验曲线和三轴压缩曲线具有较好的对应性。
-
![]()
图 6 亚层A的旁压p-V曲线与计算得到的p-s曲线
Figure 6. Comparison between p-V curve from pressuremeter tests and corresponding p-s curve predicted of a sub-layer A
![]()
图 7 亚层B的旁压p-V曲线与计算得到的p-s曲线
Figure 7. Comparison between p-V curve from pressuremeter tests and corresponding p-s curve predicted of a sub-layer B
![]()
图 8 亚层C的旁压p-V曲线与计算得到的p-s曲线
Figure 8. Comparison between p-V curve from pressuremeter tests and corresponding p-s curve predicted of a sub-layer C
![]()
图 9 建筑物基础实测沉降时间-曲线
Figure 9. Monitoring curve of foundation settlements with respect to time
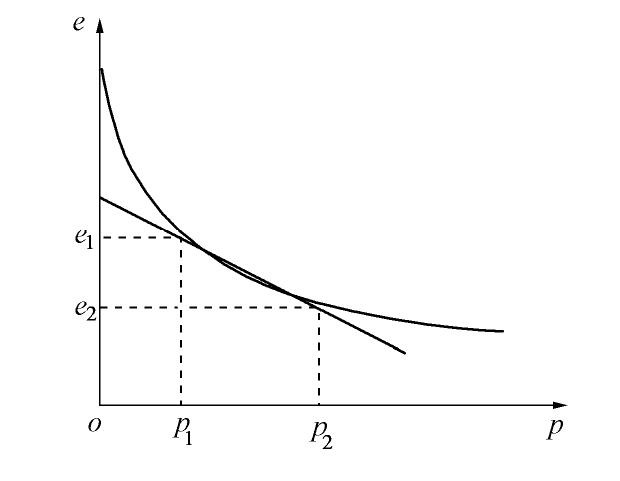
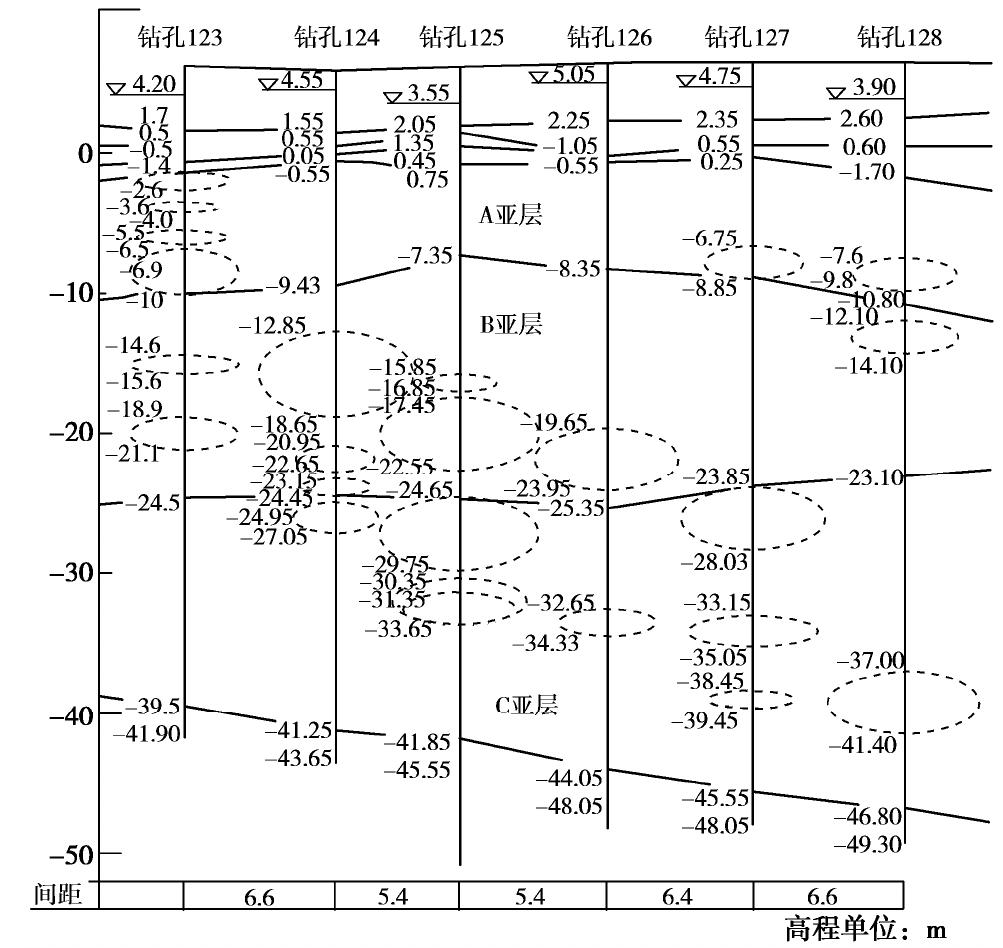
表 1 规范沉降计算方法中的经验系数
ψs Table 1 Empirical coefficients for settlement calculation from China's code
附加应力 E s/MPa 20 15 7 4 2.5 p0≤0.75 fk 0.2 0.4 0.7 1.0 1.1 p0≥fk 0.2 0.4 1.0 1.3 1.4 注： p0为基底的附加应力,Es为土的压缩模量。
下载: 导出CSV
表 2 主要物理力学指标
Table 2 Major physical parameters of soil
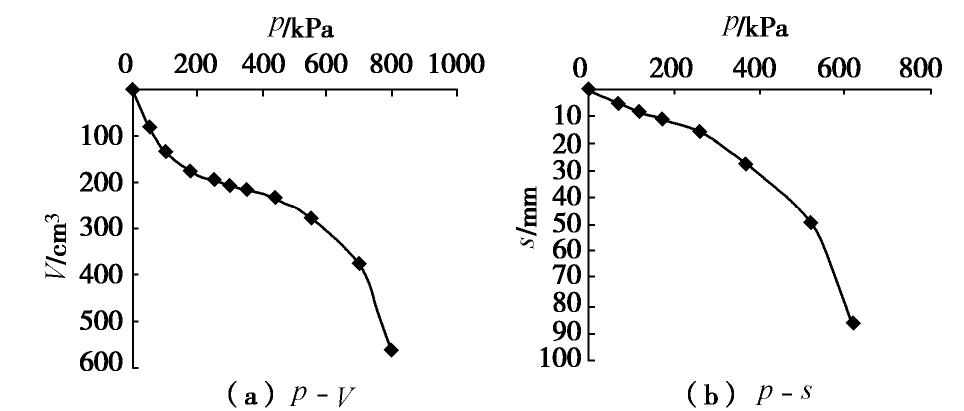
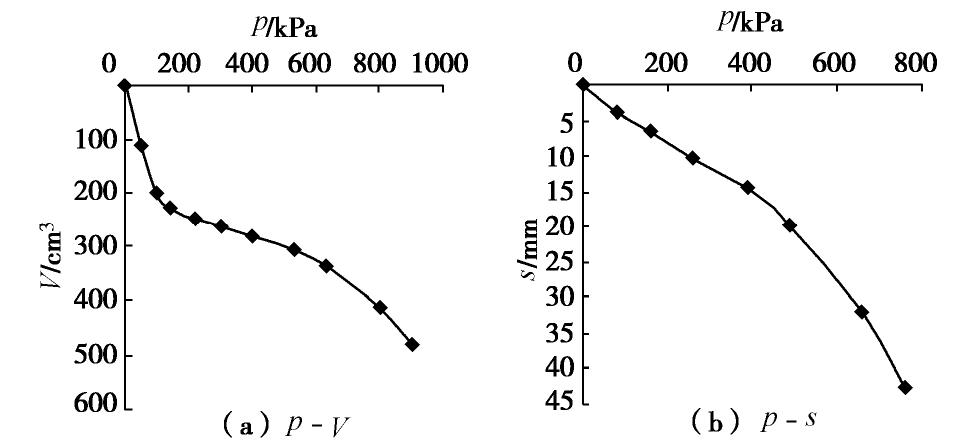
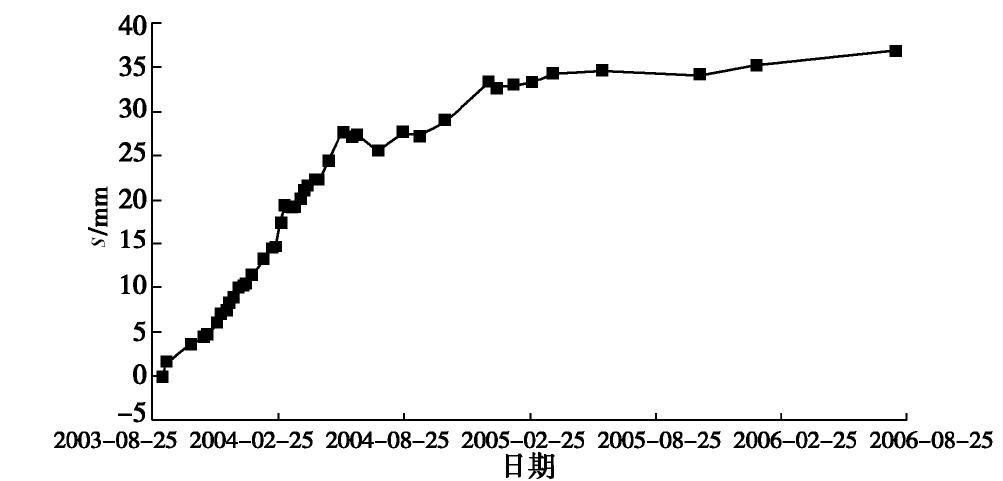
花岗岩残基砂质黏土 天然重度/(kN·m-3) 天然含水率/% 液性指数 标贯击数 天然孔隙比 旁压模量/MPa 极限压力/kPa 压缩模量/MPa 变形模量/MPa 承载力/kPa A亚层 18.5 30 0.12 13 0.895 14.1 1088 5.4 12 250 B亚层 19.4 25 0.10 21 0.743 34.8 2163 6.2 25 300 C亚层 19.9 20 0.01 32 0.631 76.1 3668 7.0 38 400
下载: 导出CSV
表 3 利用旁压结果计算的3个亚层参数
Table 3 Derived soil parameters for three sub-layers by pressuremeter tests
花岗岩残积砂质黏土 黏聚力c/kPa 内摩擦角φ/(°) 初始切线模量 Et0 /MPaA亚层 40.2 24 19 B亚层 56.0 26 30 C亚层 67.0 26 81
下载: 导出CSV
-
[1] 建筑地基基础设计规范：GB5007—2011[S]. 2002. Code for Design of Building Foundation: GB50007—2011[S]. 2012. (in Chinese)
[2] 杨光华. 地基非线性沉降计算的原状土切线模量法[J]. 岩土工程学报, 2006, 28(11): 1927-1931. doi: 10.3321/j.issn:1000-4548.2006.11.002 YANG Guang-hua. Nonlinear settlement computation of the soil foundation with the undisturbed soil tangent modulus method[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(11): 1927-1931. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.11.002
[3] 杨光华, 李思平, 杜秀忠, 等. 岩溶地区高层建筑基础筏板的工程实践[J]. 岩石力学与工程学报, 2006, 25(增刊2): 3363-3371. YANG Guang-hua, LI Si-ping, DU Xiu-zhong, et al. Practice of high-rise building with raft foundation in karst region[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(S2): 3363-3371. (in Chinese)
[4] 杨光华, 王鹏华, 乔有梁. 地基非线性沉降计算的原状土割线模量法[J]. 土木工程学报, 2007, 40(5): 49-52. doi: 10.3321/j.issn:1000-131X.2007.05.007 YANG Guang-hua, WANG Peng-hua, QIAO You-liang. An undisturbed-soil secant modulus method for calculation of nonlinear settlement of soil foundations[J]. China Civil Engineering Journal, 2007, 40(5): 49-52. (in Chinese) doi: 10.3321/j.issn:1000-131X.2007.05.007
[5] 建筑地基基础设计规范：DBJ 15—31—2003[S]. 2003. Design Code for Building Foundation: DBJ 15—31—2003[S]. 2003. (in Chinese)
[6] 李广信, 蔡飞. 旁压试验在计算碎石桩荷载沉降关系中的应用[J]. 勘察科学技术, 1993, 6: 30-34. https://www.cnki.com.cn/Article/CJFDTOTAL-KCKX199306010.htm LI Guang-xin, CAI Fei. Application of side pressure test in calculating load settlement relation of gravel pile[J]. Site Investigation Science and Technology, 1993, 12(2): 30-33. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KCKX199306010.htm
[7] 刘琼, 杨光华, 李德吉. 用旁压试验结果推算载荷试验p-s曲线[J]. 广东水利水电, 2008(8): 82-82. doi: 10.3969/j.issn.1008-0112.2010.07.002 LIU Qiong, YANG Guang-hua, LIU Peng. Nonlinear settlement computation of the soil foundation based on in-situ testing[J]. Guangdong Water Resources and Hydropower, 2010(7): 4-6. (in Chinese) doi: 10.3969/j.issn.1008-0112.2010.07.002
[8] 王长科. 用旁压试验原位测定土的强度参数[J]. 勘察科学技术, 1992(6): 25-27. https://www.cnki.com.cn/Article/CJFDTOTAL-KCKX199206007.htm WANG Chang-ke Strength parameters of soil determined by pressure test in situ[J]. Site Investigation Science and Technology, 1992(6): 25-27. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KCKX199206007.htm
[9] 杨光华. 基础非线性沉降的双曲线模型法[J]. 地基处理, 1997(1): 50-53. YANG Guang-hua. Hyperbola model in calculating the nonlinear settlement of foundation[J]. Ground Improvement, 1997(1): 50-53. (in Chinese)
[10] 杨光华. 地基沉降计算的新方法[J]. 岩石力学与工程学报, 2008, 27(4): 679-686. doi: 10.3321/j.issn:1000-6915.2008.04.005 ANG Guang-hua. New computation method for soil foundation settlement[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(4): 679-686. (in Chinese) doi: 10.3321/j.issn:1000-6915.2008.04.005
[11] 岩土工程勘察规范：DGJ 08—37—2002[S]. 2002. Geotechnical Engineering Investigation Code: DGJ 08—37—2002[S]. 2002. (in Chinese)
[12] 王长科. 用旁压试验推求土体强度指标的方法探讨[J]. 勘察科学技术, 1989(1): 1-3. https://www.cnki.com.cn/Article/CJFDTOTAL-KCKX198901000.htm WANG Chang-ke. Determination of Strength of soil by pressure test in situ[J]. Site Investigation Science and Technology, 1989(1): 1-3. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KCKX198901000.htm
[13] 杨光华. 根据经验地基承载力反算土的强度和变形参数[J]. 广东水利水电, 2002(1): 3-6. https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD200201000.htm YANG Guang-hua. According to the experience of foundation bearing capacity to inverse the strength and deformation parameters of soil[J]. Guangdong Water Resources and Hydropower, 2002(1): 3-6. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD200201000.htm
[14] 徐超, 石振明, 高彦斌, 等. 岩土工程原位测试[M]. 上海: 同济大学出版社, 2005. XU Chao, SHI Zheng-ming, GAO Yan-bin, et al. Geotechnical Engineering In-Situ Test[M]. Shanghai: Tongji University Press, 2005. (in Chinese)
[15] 杨光华, 骆以道, 张玉成, 等. 用简单原位试验确定切线模量法的参数及其在砂土地基非线性沉降分析中的验证[J]. 岩土工程学报, 2013, 35(3): 401-408. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201303002.htm ANG Guang-hua, LUO Yi-dao, ZHANG Yu-cheng, et al. Determination of parameters for tangent modulus methodusing simple in-situ test and its application in nonlinear settlement analysis on sandy soil[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 855-863.) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201303002.htm
[16] 刘琼, 杨光华, 刘鹏. 基于原位旁压试验的地基非线性沉降计算方法[J]. 广东水利水电, 2010(7): 4-6. https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD201007013.htm LIU Qiong, YANG Guang-hua, LIU Peng. Nonlinear settlement computation of the soil foundation based on in-situ testing[J]. Guangdong Water Resources and Hydropower, 2010(7): 4-6. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD201007013.htm
[17] 嘉益大厦课题研究小组. 厦门嘉益大厦基础设计研究报告[R]. Jiayi Building Research Group. Research Report on foundation design of Xiamen Jiayi building[R]. (in Chinese)
[18] 刘琼. 基于原位试验的地基非线性沉降计算方法的研究与应用[D]. 邯郸: 河北工程大学, 2009. LIU Qiong, Research and Application of Nonlinear Settlement Calculation Method Based on in Situ Test[D]. Handan: 2009. (in Chinese)
-
期刊类型引用(5)
1. 谢柏涵，孔元元，张学飞，孙东彦，王智慧. 冻融循环作用下盐渍土损伤模型的建立及验证. 人民长江. 2025(02): 183-189+200 . 
百度学术
2. 孙超，谷鸿雁，郭浩天. 冻融循环次数对粉质黏土强度劣化影响的试验研究. 吉林建筑大学学报. 2024(05): 66-71 . 百度学术
3. 吕思清，朱杰兵，汪斌，祝永锁. 冻融荷载耦合作用下含开口裂隙砂岩宏细观损伤模型研究. 岩石力学与工程学报. 2023(05): 1124-1135 . 百度学术
4. 李新宇，凌贤长，曲娜. 考虑温度效应的冻结膨胀土统计损伤模型. 吉林大学学报(工学版). 2023(08): 2339-2349 . 百度学术
5. 张雁，薛晓雨，杨晓蕴. 低温状态下纤维加筋膨胀土数值模拟试验. 中国科技论文. 2022(12): 1351-1357 . 百度学术
其他类型引用(5)
计量
- 文章访问数: 220
- HTML全文浏览量: 12
- PDF下载量: 150
- 被引次数: 10
