三轴剪切过程中粗粒料颗粒破碎变化规律研究

吴二鲁; 朱俊高; 黄维; 刘忠

doi:10.11779/CJGE202012021

三轴剪切过程中粗粒料颗粒破碎变化规律研究 English Version

吴二鲁^1,,
朱俊高^1, ,,
黄维²,
刘忠³

1.
河海大学岩土力学与堤坝工程教育部重点实验室,江苏　南京　210098
2.
中国电建集团华东勘测设计研究院有限公司,浙江　杭州　311122
3.
黄河水利委员会黄河水利科学研究院,河南　郑州　450003

基金项目:

国家重点研发计划项目 2017YFC0404801

国家自然科学基金项目 U1865104

国家自然科学基金项目 51479052

国家自然科学基金青年科学基金项目 51609098

详细信息

作者简介:
吴二鲁(1993—),男,博士研究生,主要从事土体基本性质及本构关系、土石坝工程研究。E-mail：170804010004@hhu.edu.cn

通讯作者:
朱俊高, E-mail：zhujungao@hhu.edu.cn

中图分类号: TU43
计量
- 文章访问数: 253
- HTML全文浏览量: 27
- PDF下载量: 136
出版历程
- 收稿日期: 2020-01-18
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-11-30

Evolution law of particle breakage of coarse-grained soil during triaxial shearing

1.
Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University, Nanjing 210098, China
2.
PowerChina Huadong Engineering Corporation Limited, Hangzhou 311122, China
3.
Yellow River Institute of Hydraulic Research, Zhengzhou 450003, China

摘要

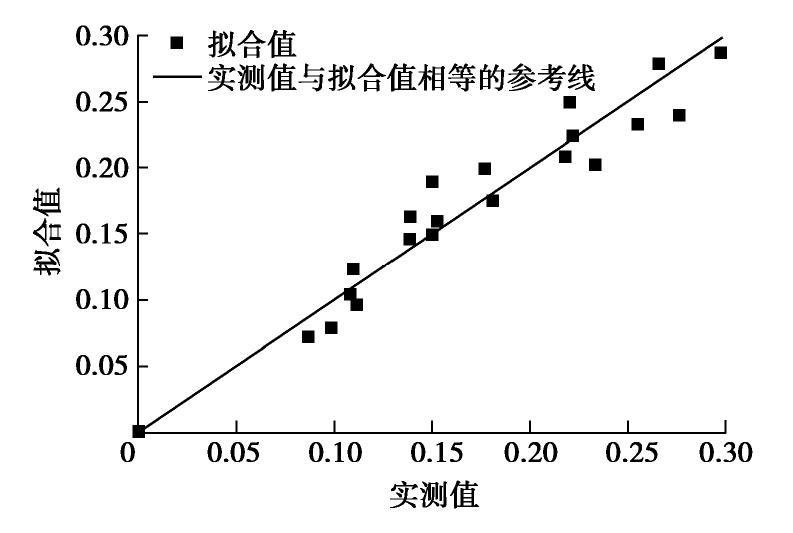
摘要: 准确预测粗粒料在加载过程中颗粒破碎的变化规律,并将其应用于粗粒料的本构模型中具有重要意义。合理定义和精确计算颗粒破碎指标是准确研究加载过程中粗粒料颗粒破碎变化规律的保障。引入Einav的分形破碎指标,认为在目前的颗粒破碎指标中该指标最适合用来对比评价粗粒料的颗粒破碎程度,并利用连续级配土的级配方程代替分形级配方程进行破碎指标的准确计算。在此基础上,选取已有文献中的试验数据,对粗粒料三轴剪切过程中的颗粒破碎变化规律进行了研究,建立了一个可以描述三轴剪切过程中颗粒破碎指标与剪应变及平均正应力之间关系的数学模型,并验证了该模型的适用性。
- 粗粒料 /
- 三轴剪切 /
- 颗粒破碎 /
- 级配方程 /
- 变化规律
Abstract: Accurate prediction of the evolution law of particle breakage during loading process is of great significance to building the constitutive model for coarse-grained soil. The reasonable definition and accurate calculation of particle breakage indices are the guarantee to exactly study the evolution law of particle breakage during loading process. The fractal breakage index of Einav is introduced and considered as the most suitable one to compare and evaluate the breakage degree of coarse-grained soil among breakage indices. It is realized to accurately calculate the fractal breakage index by replacing fractal gradation equation with the gradation equation for continuous gradation soil. On this basis, the evolution law of particle breakage of coarse-grained soil is studied by selecting the experimental data in the existing literatures. A mathematical model is established to describe the relationship among particle breakage indices, shear strain and average normal stress during triaxial shearing, and the applicability of this model is validated.
- coarse-grained soil /
- triaxial shearing /
- particle breakage /
- gradation equation /
- evolution law

HTML全文

0. 引言

重塑土是在经过压密或者压实作用后形成的具有一定重度、含水率的人工制备的土样,与原状土的各向异性相比,其性质较为均一。目前已有很多学者对重塑土的制备进行了深入研究^[1-6],但由于重塑土的结构性较弱,在实践工程中会出现计算结果与实际值存在较大误差的现象。在岩土工程技术领域中,随着交通流量的增加,荷载的多样性和复杂性对高速公路、铁路的地基在受到波浪、交通循环荷载等作用下的承载能力及稳定性的要求与日俱增,开展各种与实际情况更相近的主应力轴偏转试验研究成了新的突破口。

一方面,王杏杏等^[7]指出土的应力状态是由其结构决定的,而前期应力状态是由结构性来体现的。Lerouei等^[8]认为各地土的结构性对其力学性质的影响存在显著差异。因此,迫切需要对原状土进行相关室内试验研究。

另一方面,土工试验成果的质量取决于试样的扰动程度,试样的扰动主要由取样扰动和制样扰动两部分组成,试样在采取过程中产生扰动是不可避免的。根据试验方案及土质情况,采用水压式取土器对软土进行取样,采用该装置进行采样,不仅采样效率高,取土质量也较好^[8],一定程度上解决了取样过程中扰动的问题,因此,如何解决制样扰动问题就成了关注重点。

目前,原状土空心试样制备方法主要有两种方法：一种是以英国帝国理工大学为代表,通过渐进式修正的方法成功制备了伦敦超固结黏土空心试样,采用机械式进行制样,利用7种不同直径的钻杆依次进行钻孔取芯；另一种是以Talesnick等^[10]为代表,他们成功制备出了天然含水率高达80%～100%的高灵敏性软土空心试样,采用电渗式方法进行制样,利用一根穿通试样的电线切割试样内壁,从而使得内壁变得光滑,并且孔壁与内芯较易分离,对试样的扰动也较小。

综上所述,现有的制样方式仍存在一些缺陷,如传统机械制样方式,由于在钻孔的过程中需要更换不同直径的钻杆,故不可避免地会对土样产生扰动；而电渗法则需要利用电势降使试样中的水从正极流向负极,很大程度的影响了试样含水情况,且操作较为繁琐。因此,鉴于现有装置和技术的尚可改进之处,本文基于传统机械法提出了一种改进的空心圆柱试样的制备方法。

1. 新型原状软黏土空心圆柱试样制备装置开发

1.1 试样制备用土

试样用土取自杭州市紫金港,选择土质均匀、无杂质的处进行取土。测定土体基本物理特性指标,见表1。对现场取得的土样进行切削、钻芯等步骤后获得空心圆柱样,操作过程严格按照《土工试验规程》的规定进行。

表 1 试样的物理特征指标

Table 1. Physical characteristics of samples

土样类型	含水率w/%	干密度ρ_d/(g·cm^-3)	颗粒相对密度G_s	孔隙比e	饱和度S_r/%	液限w_L/%	塑性指数I_P
淤泥质黏土	47.00	11.60	2.74	1.34	96.50	37.60	17.56

下载: 导出CSV

| 显示表格

1.2 试样制备装置设计

试样制备装置主要由台式水钻机部分、可更换钻头部分、制样桶三部分组成（结构如图1（a）所示）；其中台式水钻机包括水钻机、升降支架及调节手柄等部件；升降支架设置在水钻机的下部；可更换钻头部分由转换接头及若干刀头组成,转换接头是用来将刀头安装在水钻机上的连接部件,通过调节手柄可以控制更换钻头部分的竖向移动；刀头包括直杆旋转式刀头（见图1（b））、螺旋杆刀头（见图1（c））以及长筒型环刀,其中长筒型环刀又分为侧向单开口式环刀（见图1（d））和侧向双开口式环刀（见图1（e））两种,其皆为可拆卸式；其中直杆旋转式刀头用于圆柱试样内孔的粗削,螺旋杆刀头用于圆柱试样圆形孔的粗削成型及掏土加工,而长筒型环刀用来对圆柱试样圆形孔进行精削；侧向单开口式环刀或侧向双开口式环刀为无缝不锈钢管,其外径略小于钻孔直径；侧向单开口式环刀的开口处位于刀体的中部,其开口弧度为环刀圆周长的1/3；侧向双开口式环刀的开口处位于刀体的中部,开口方式为对向开口,开口弧度为环刀圆周长的1/8。制样桶设置在制样桶支架上,而制样桶支架则固定在底部转盘上,制样桶的正下方是废土筒,转盘电机与底部转盘连接。

图 1 制样装置结构示意图

Figure 1. Sketch of new sample preparation device

下载: 全尺寸图片幻灯片

2. 试样制备过程

为了减少土样扰动,本次采用不锈钢薄壁取土法进行取土制样。先将薄壁管内外壁均匀涂抹硅油,而后将直径200 mm、高度750 mm的薄壁管压入土层中切取土样,土样切取完毕后,在土样筒的两端均匀的涂上黄油,并用塑料盖盖在土样筒上裹紧密封,随后蜡封保存,在标签上记录取样信息附于土样筒上,再用胶带密封。

下面结合图2具体介绍原状软黏土空心圆柱试样的制备流程：①将取样筒内土体按照原状实心圆柱土样削切方法成型,置于制样桶中,并采用推土器将所取土样缓慢进行推出,见图2（a）。②用钢丝锯将试样四周多余部分进行切除并修补土样外壁,为了防止在内壁钻孔过程中对土样产生扰动,采用三瓣膜将已修补完成后的外壁箍紧,如图2（b）所示。③采用3种不同的规格的钻孔器对内壁进行钻孔,钻孔器见图2（c）。④箍紧三瓣膜并固定上下盖板,然后将试样与三瓣膜放入固定架上,如图2（d）所示,安装完毕后见图（e）。⑤调整水钻机的升降支架,直至达到合适高度停止,在钻机头上安装转换接头,首先接上直杆旋转式刀头,手动调整调节手柄,直至制样桶上部距400 mm以上停止调整,并按下水钻机开关,控制转速在100～200 rad/m,下降速度100 mm/min,逐渐下降进行实心圆柱土样的钻芯加工。⑥关闭水钻机,换下水钻机上的直杆旋转式刀头,安装上螺旋杆刀头,再次手动调整调节手柄手动调,直至制样桶上部距400 mm以上停止,开启水钻机,将转速控制在60 rad/m,下降速度100 mm/min,逐渐下降进行实心圆柱土样的圆形孔加工。⑦关闭水钻机,再次将水钻机转接头上的直杆旋转式刀头换下,装上长筒型环刀,并均匀的涂抹少许机油在长筒型环刀内外上,将调节手柄手动调整至制样桶上部距离400 mm以上,开启转盘电机,控制转速在20～30 rad/m,同时开启水钻机,并控制转速低于50 rad/m,以50 mm为每次的下降量,逐渐下降长筒型环刀,上升至试样外部,采用下拉推土刮片排出桶内的土体。⑧最后关闭水钻机和转盘电机,将制样桶和削切完成的土样从底部转盘上取下,这样就成功地完成了试样制备。通过上述制备流程所制试样内外表面光滑,对试样土体扰动较小,能够满足试验需求。图2（f）为所制试样与橡胶样的对比图。⑨将土样置于饱和器中进行真空饱和。

图 2 试样制备流程图

Figure 2. Flowchart of sample preparation

下载: 全尺寸图片幻灯片

相较于之前的试样制备装置,该新型制样装置具有结构简单,操作便捷,脱模容易,可快速实现机械化制样等一系列优点,有效保证了制样的质量,为空心圆柱扭剪试验奠定了基础。

3. 原状试样力学性能均衡性验证

对上述所制试样采用空心圆柱扭剪仪来进行试验验证,通过测试同一条件下的一组平行试样来检验土体性状是否能够满足循环荷载下试验要求。

3.1 试验方案

空心圆柱扭剪仪（GCTS HCA）是目前公认的最符合实际受力情况的土动力学试验设备,能够很好地模拟循环荷载下的土样受荷复杂应力路径^[9]。开展不排水循环剪切试验,在试验过程中施加大小相同的内外围压,为了能够更加准确的模拟实际荷载状况,加载时保持循环扭矩MT和循环轴力的相位差,本次试验中有效围压均为50 kPa,采用K₀固结,具体的试验方案见表2。

表 2 不同频率下的空心扭剪试验方案

Table 2. Hollow torsion shear test programs under different frequencies

试样编号	有效围压/kPa	竖向循环应力幅值/%	循环剪应力幅值/%	竖向-扭剪循环应力耦合比	应力路径	频率	振次N
A-1	50	15	6	0.4	圆形	0.1	2500
A-2	50	15	6	0.4	圆形	0.1	2500
B-1	50	15	6	0.4	圆形	0.5	2500
B-2	50	15	6	0.4	圆形	0.5	2500

下载: 导出CSV

| 显示表格

3.2 试验结果分析对比

图3,4分别为不同频率下试样累积轴向应变与时间的关系曲线图。从图中可以看出,在频率0.1,0.5 Hz下试样轴向累积变形随振次的增加而逐渐增大,应变增长速率随振次的增大而逐渐减小,一定振次后,应变量逐渐趋于稳定,同一频率相同加载条件下,不同试样间的应变规律相同,试验结果较为一致。

图 3 0.1 Hz下试样A-1,A-2累积轴向应变发展曲线

Figure 3. Variation curves of cumulative axial strain of samples under 0.1 Hz

下载: 全尺寸图片幻灯片

图 4 0.5 Hz下试样B-1,B-2累积轴向应变发展曲线

Figure 4. Variation curve of cumulative axial strain of samples under 0.5 Hz

下载: 全尺寸图片幻灯片

图5,6分别为不同频率下试样孔压比与时间的关系曲线图。从图中可以看出,其发展趋势大致与轴向累积变形发展规律类似,在初始阶段时,孔压比曲线增长速率较高,随着振次的增加而逐渐降低,在一定振次之后,最终基本趋于稳定,同一频率相同加载条件下,不同试样间孔压累积发展曲线基本重合,试验结果较为一致。

图 5 0.1 Hz下试样A-1,A-2孔压发展规律

Figure 5. Variation rules of pore pressure of samples under 0.1 Hz

下载: 全尺寸图片幻灯片

图 6 0.5 Hz下试样B-1,B-2孔压发展规律

Figure 6. Variation rules of pore pressure of samples under 0.5 Hz

下载: 全尺寸图片幻灯片

图7,8分别为不同频率下试样软化指数与时间的关系曲线图,其中软化指数采用王军等^[11]定义的公式：

图 7 0.1 Hz下试样A-1,A-2软化指数图

Figure 7. Softening indices of dynamic stress ratio under 0.1 H

下载: 全尺寸图片幻灯片

图 8 0.5 Hz下试样B-1,B-2软化指数图

Figure 8. Softening indices of dynamic stress ratio under 0.5 Hz

下载: 全尺寸图片幻灯片

$\frac{G_{S N}}{G_{S 1}} = \frac{\frac{q_{\max} - q_{\min}}{ε_{N, \max} - ε_{N, \min}}}{\frac{q_{\max} - q_{\min}}{ε_{1, \max} - ε_{1, \min}}} = \frac{\frac{2 σ_{d}}{ε_{N, \max} - ε_{N, \min}}}{\frac{2 σ_{d}}{ε_{1, \max} - ε_{1, \min}}} = \frac{ε_{1, \max} - ε_{1, \min}}{ε_{N, \max} - ε_{N, \min}}$ 。

(1)

式中 q_max为每次循坏中的最大偏应力,q_min为每次循环中的最小偏应力； $ε_{1, \max}$ 为第一次循环中最大轴向应变, $ε_{1, \min}$ 为第一次循环中最小轴向应变； $ε_{N, \max}$ 为第N次循环中最大轴应变, $ε_{N, \min}$ 为第N次循环中最小轴应变。

从图7,8中可以看出,总体上软化指数是随着振次的增加而减小,其中频率0.5 Hz时土样软化指数衰减的速度是最快的,0.5 Hz下的最小软化指数为0.55,而当频率为0.1 Hz时,试样的软化系数衰减速度较慢,可以理解为土样在0.1 Hz时轴向应变较小。由此可知,在同样的加载条件和频率下,不同试样间的软化指数变化曲线基本重合,试验结果较为一致。

根据上述分析可知,采用本技术所制备的试样即保证了试样的结构性,也保证了试样内外壁光滑,能够满足室内试验要求,并且所得试验数据规律性良好,为今后分析原状软黏土的试验结果提供了保障。

4. 结论

（1）在对空心样进行掏孔时,该装置采用4种不同的削切环刀,先用直杆旋转式刀头进行粗削,再用小于内孔径的螺旋杆刀头进行掏土,可有效减小制样过程中对软黏土原状样的扰动。

（2）在精细削土加工过程中采用长筒型薄壁环刀,侧壁开口释放了削切附土内压,开刃侧可用于最后手动刮壁,使孔内壁光滑,确保不坍孔。

（3）采用转盘电机驱动的底部转盘上的制样桶,形成一整套制样仪,使得制样与成样过程统一,相较传统的手动削土速度大幅提高,成样内外径圆心一致。

（4）从土体力学性能的方面验证了该试样制备技术在复杂应力下研究土体性态演变规律的可行性,为复杂应力路径下研究原状软黏土基本性状提供了保障,具有很高的实用价值。

图 1 Hardin破碎指标定义

Figure 1. Definition of particle breakage index of Hardin

下载: 全尺寸图片幻灯片

图 2 Einav破碎指标定义

Figure 2. Definition of particle breakage index of Einav

下载: 全尺寸图片幻灯片

图 3 式（3）的适用性验证

Figure 3. Verification of applicability of Eq. (3)

下载: 全尺寸图片幻灯片

图 4 级配曲线面积S

Figure 4. Area of gradation curve

下载: 全尺寸图片幻灯片

图 5 B_E的实测值与拟合值

Figure 5. Measured and fitting data ofB_E

下载: 全尺寸图片幻灯片

图 6 堆石料B破碎指标的实测值与拟合值

Figure 6. Measured and fitting data of breakage index of coarse-grained soil B

下载: 全尺寸图片幻灯片

表 1 三轴剪切过程中的颗粒破碎试验数据

Table 1 Test data of particle breakage during triaxial shearing

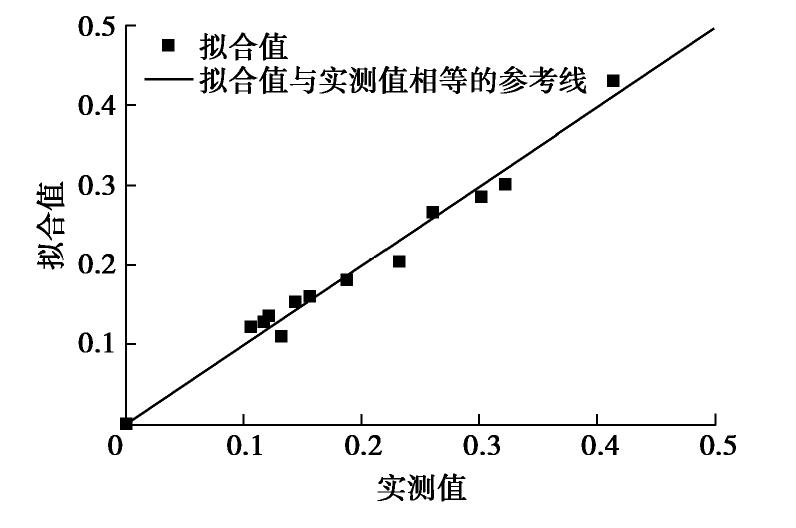
围压/kPa	剪应变ε_s/%	平均正应力p/kPa	B_E/%
0	0	0	0
500	1.87	1242	8.7
500	4.56	1422	11.1
500	8.44	1494	15.0
500	12.49	1469	15.3
500	16.01	1420	14.0
1000	1.75	2046	9.9
1000	4.60	2343	13.9
1000	7.20	2552	18.2
1000	10.66	2534	15.1
1000	15.19	2621	23.4
1500	1.90	2760	11.2
1500	7.34	3504	21.9
1500	9.31	3596	22.2
1500	12.47	3543	25.6
1500	14.35	3602	27.6
2000	1.85	3336	10.9
2000	4.55	4064	17.7
2000	7.26	4484	22.0
2000	10.75	4653	26.7
2000	13.76	4619	29.8

下载: 导出CSV

表 2 粗粒料B的颗粒破碎试验数据

Table 2 Test data of particle breakage of coarse-grained soil B

围压/kPa	剪应变ε_s/%	平均正应力p/kPa	B_E/%
0	0	0	0
200	4.41	570	10.6
200	9.95	580	14.4
200	13.40	560	15.6
500	3.37	1140	11.6
500	7.53	1300	18.7
500	14.30	1320	23.1
1000	2.60	1800	12.2
1000	8.56	2370	26.0
1000	15.20	2480	32.1
1500	1.63	2160	13.2
1500	5.34	3010	30.2
1500	16.30	3570	41.4

下载: 导出CSV

参考文献(33)

[1]	孙逸飞, 刘汉龙, 杨贵. 考虑颗粒破碎引起级配演变的粗粒料屈服函数研究[J]. 岩土力学, 2013, 34(12): 3479-3484. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201312021.htm SUN Yi-fei, LIU Han-long, YANG Gui. Yielding function for coarse aggregates considering gradation evolution induced by particle breakage[J]. Rock and Soil Mechanics, 2013, 34(12): 3479-3484. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201312021.htm
[2]	XU M, SONG E X, CHEN J F. A large triaxial investigation of the stress-path-dependent behavior of compacted rockfill[J]. Acta Geotechnica, 2012, 7(3): 167-175. doi: 10.1007/s11440-012-0160-0
[3]	ALONSO E E, TAPIAS M, GILI J. Scale effects in rockfill behaviour[J]. Geotechnical Letters, 2012, 3: 155-160.
[4]	贾宇峰, 迟世春, 林皋. 考虑颗粒破碎影响的粗粒土本构模型[J]. 岩土力学, 2009, 30(11): 3261-3267. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200911010.htm JIA Yu-feng, CHI Shi-chun, LIN Gao. Constitutive model for coarse granular aggregates incorporating particle breakage[J]. Rock and Soil Mechanics, 2009, 30(1): 3261-3267. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200911010.htm
[5]	GUO W L, CAI Z Y, WU Y L, et al. Estimations of three characteristic stress ratios for rockfill material considering particle breakage[J]. Acta Mechanica Solida Sinica, 2019, 32(2): 215-229. doi: 10.1007/s10338-019-00074-x
[6]	TAPIAS M, ALONSO E E, GILI J. A particle model for rockfill behavior[J]. Géotechnique, 2015, 65(12): 975-994. doi: 10.1680/jgeot.14.P.170
[7]	XIAO Y, LIU H L. Elastoplastic constitutive model for rockfill materials considering particle breakage[J]. International Journal of Geomechanics, 2017, 17(1): 04016041. doi: 10.1061/(ASCE)GM.1943-5622.0000681
[8]	XIAO Y, LIU H L, DING X M, et al. Influence of particle breakage on critical state line of rockfill material[J]. International Journal of Geomechanics, 2016, 16(1): 04015031. doi: 10.1061/(ASCE)GM.1943-5622.0000538
[9]	武颖利, 皇甫泽华, 郭万里, 等. 考虑颗粒破碎影响的粗粒土临界状态研究[J]. 岩土工程学报, 2019, 41(增刊2): 25-28. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S2008.htm WU Ying-li, HUANGFU Ze-hua, GUO Wan-li, et al. Influences of particle breakage on critical state of coarse-grained soils[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S2): 25-28. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S2008.htm
[10]	尹振宇, 许强, 胡伟. 考虑颗粒破碎效应的粒状材料本构研究：进展及发展[J]. 岩土工程学报, 2012, 34(12): 2170-2180. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201212006.htm YIN Zhen-yu, XU Qiang, HU Wei. Constitutive relations for granular materials considering particle crushing: review and development[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(12): 2170-2180. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201212006.htm
[11]	SALIM W, INDRARATNA B. A new elastoplastic constitutive model for coarse granular aggregates incorporating particle breakage[J]. Canadian Geotechnical Journal, 2004, 41(4): 657-671. doi: 10.1139/t04-025
[12]	贾宇峰, 迟世春, 林皋. 考虑颗粒破碎的粗粒土剪胀统一本构模型[J]. 岩土力学, 2010, 31(5): 1381-1388. doi: 10.3969/j.issn.1000-7598.2010.05.006 JIA Yu-feng, CHI Shi-chun, LIN Gao. Dilatancy unified constitutive model for coarse granular aggregates incorporating particle breakage[J]. Rock and Soil Mechanics, 2010, 31(5): 1381-1388. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.05.006
[13]	米占宽, 李国英, 陈生水. 基于破碎能耗的粗颗粒料本构模型[J]. 岩土工程学报, 2012, 34(12): 1801-1811. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201210008.htm MI Zhan-kuan, LI Guo-ying, CHEN Sheng-shui. Constitutive model for coarse granular materials based on breakage energy[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(12): 1801-1811. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201210008.htm
[14]	LADE P V, YAMAMURO J A, BOPP P A. Significance of particle crushing in granular materials[J]. Journal of Geotechnical Engineering, 1996, 122(4): 309-316. doi: 10.1061/(ASCE)0733-9410(1996)122:4(309)
[15]	LEE K L, FARHOOMAND L. Compressibility and crushing of granular soil in anisotropic triaxial[J]. Canadian Geotechnical Journal, 1976, 4(1): 68-86.
[16]	GUO W L, HUANG Y H, ANDY F, et al. Mathematical model revealing the evolution of particle breakage and particle-size distribution for rockfill during triaxial shearing[J]. European Journal of Environmental and Civil Engineering. doi: 10.1080/19648189.2018.1552898.
[17]	MARSAL R J. Large-scale testing of rockfill materials[J]. ASCE Journal of the Soil Mechanics and Foundation Engineering, 1967, 93(2): 27-43.
[18]	HARDIN B O. Crushing of soil particles[J]. Journal of Geotechnical Engineering, 1985, 111(10): 1177-1192.
[19]	EINAV I. Breakage mechanics-part I: theory[J]. Journal of the Mechanics and Physics of Solids, 2007, 55(6): 1274-1297.
[20]	COOP M R, SORENSEN K K, FREITAS T B, et al. Particle breakage during shearing of a carbonate sand[J]. Géotechnique, 2004, 54(3): 157-163.
[21]	陈镠芬, 高庄平, 朱俊高, 等. 粗粒土级配及颗粒破碎分形特性[J]. 中南大学学报(自然科学版), 2015, 46(9): 3446-3453. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201509038.htm CHEN Liu-fen, GAO Zhuang-ping, ZHU Jun-gao, et al. Gradation of coarse grained soil and fractal geometry character of particle breakage[J]. Journal of Central South University (Science and Technology), 2015, 46(9): 3446-3453. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201509038.htm
[22]	孔宪京, 刘京茂, 邹德高, 等. 紫坪铺面板坝堆石料颗粒破碎试验研究[J]. 岩土力学, 2014, 35(1): 35-40. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201401004.htm KONG Xian-jing, LIU Jing-mao, ZOU De-gao, et al. Experimental study of particle breakage of Zipingpu rockfill material[J]. Rock and Soil Mechanics, 2014, 35(1): 35-40. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201401004.htm
[23]	田海, 孔令伟, 赵翀. 基于粒度熵概念的贝壳砂颗粒破碎特性描述[J]. 岩土工程学报, 2014, 36(6): 1152-1159. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201406027.htm TIAN Hai, KONG Ling-wei, ZHAO Chong. Characterization of particle breakage with grading entropy on shell sand[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(6): 1152-1159. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201406027.htm
[24]	刘汉龙, 秦红玉, 高玉峰, 等. 堆石粗粒料颗粒破碎试验研究[J]. 岩土力学, 2005, 26(4): 562-566. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200504011.htm LIU Han-long, QIN Hong-yu, GAO Yu-feng, et al. Experimental study on particle breakage of rockfill and coarse aggregates[J]. Rock and Soil Mechanics, 2005, 26(4): 562-566. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200504011.htm
[25]	蔡正银, 李小梅, 关云飞, 等. 堆石料的颗粒破碎规律研究[J]. 岩土工程学报, 2016, 38(5): 923-929. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201605019.htm CAI Zheng-yin, LI Xiao-mei, GUAN Yun-fei, et al. Particle breakage rules of rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 923-929. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201605019.htm
[26]	张季如, 张弼文, 胡泳, 等. 粒状岩土材料颗粒破碎演化规律的模型预测研究[J]. 岩石力学与工程学报, 2016, 35(9): 1898-1905. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201609019.htm ZHANG Ji-ru, ZHANG Bi-wen, HU Yong, et al. Predicting the particle breakage of granular geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(9): 1898-1905. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201609019.htm
[27]	JIA Y F, XU B, CHI S C, et al. Research on the particle breakage of rockfill materials during triaxial tests[J]. International Journal of Geomechanics, 2017, 17(10): 04017085.
[28]	郭万里. 粗粒土颗粒破碎演化规律及本构模型研究[D]. 南京: 河海大学, 2018. GUO Wan-li. Study on the Particle Breakage Evolution and Constitutive Model of Coarse-Grained Soils[D]. Nanjing: Hohai University, 2018. (in Chinese)
[29]	YANGZ Y, JUO J L. Interpretation of sieve analysis data using the box-counting method for gravelly cobbles[J]. Canadian Geotechnical Journal, 2001, 38(6): 1201-1212. http://www.researchgate.net/publication/325670496_Interpretation_of_sieve_analysis_data_using_the_box-counting_method_for_gravelly_cobbles
[30]	XIAO Y, LIU H L, YANG G, et al. A constitutive model for the state-dependent behaviors of rockfill material considering particle breakage[J]. Science China Technological Science, 2014, 57(8): 1636-1646.
[31]	朱俊高, 郭万里, 王元龙, 等. 连续级配土的级配方程及其适用性研究[J]. 岩土工程学报, 2015, 37(10): 1931-1936. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201510029.htm ZHU Jun-gao, GUO Wan-li, WANG Yuan-long, et al. Equation for soil gradation curve and its applicability[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(10): 1931-1936. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201510029.htm
[32]	吴二鲁, 朱俊高, 王龙, 等. 粗粒料的单参数级配方程及其适用性研究[J]. 岩土力学, 2020, 41(3): 1-6. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202003013.htm WU Er-lu, ZHU Jun-gao, WANG Long, et al. Gradation equation with a parameter of coarse-grained soil and its applicability[J]. Rock and Soil Mechanics, 2020, 41(3): 1-6. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202003013.htm
[33]	ZHU J G, GUO W L, WEN Y F, et al. New gradation equation and qpplicability for particle-size distributions of various soils[J]. International Journal of Geomechanics, 2018, 18(2): 04017155.

施引文献(9)

期刊类型引用(3)

1.	梁绍敏，冯云田，赵婷婷，王志华. 颗粒材料破碎行为数值分析方法研究综述. 力学学报. 2024(01): 1-22 . 百度学术
2.	丁林楠，李国英. 基于分形级配方程的堆石料颗粒破碎SBG模型. 岩土工程学报. 2022(02): 264-270 . 本站查看
3.	吴二鲁，朱俊高，陆阳洋，钱彬. 基于颗粒破碎耗能的粗粒料剪胀方程研究. 岩土工程学报. 2022(05): 898-906 . 本站查看