Full-scale model tests and numerical investigations on bearing characteristics of superimposed lining structures under external loads
-
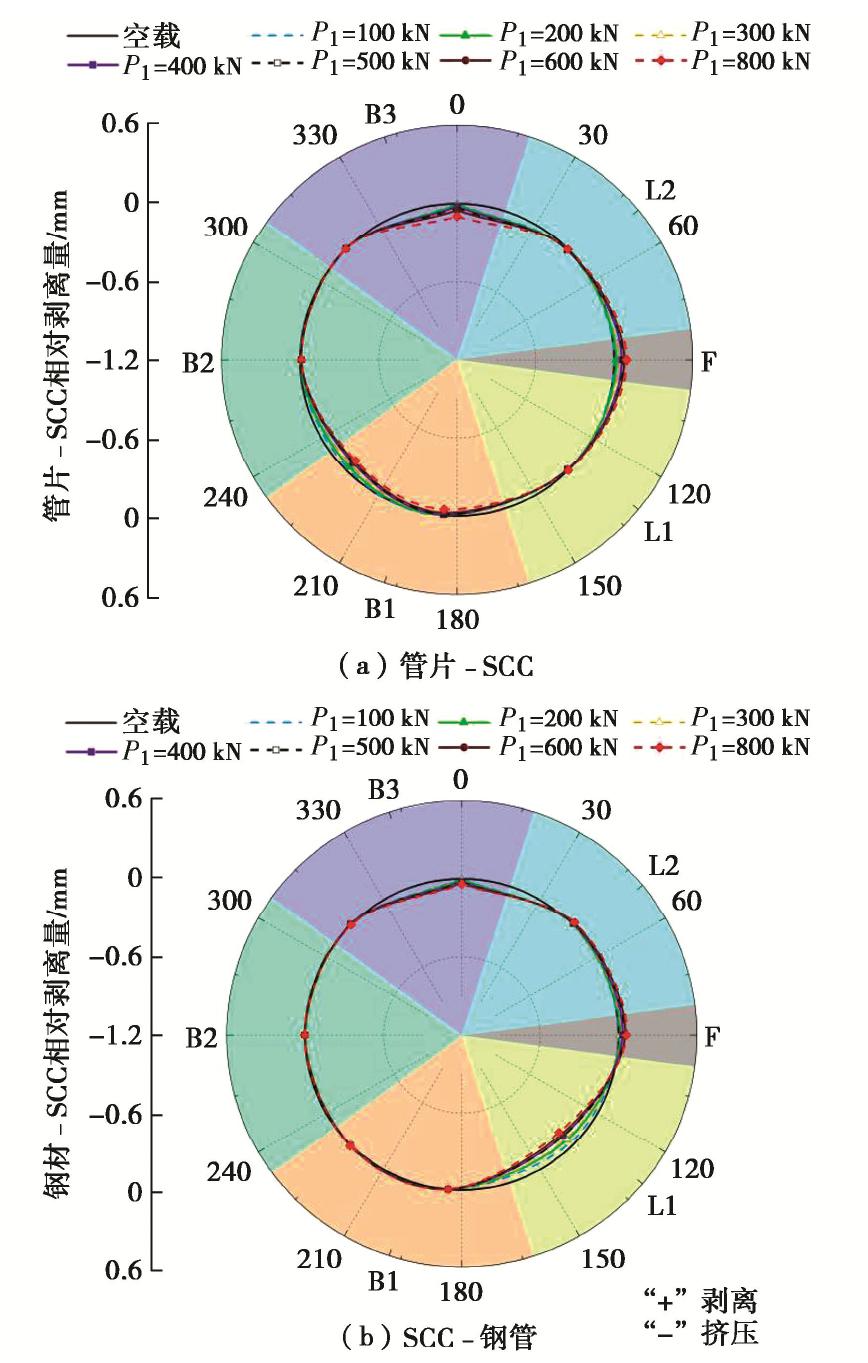
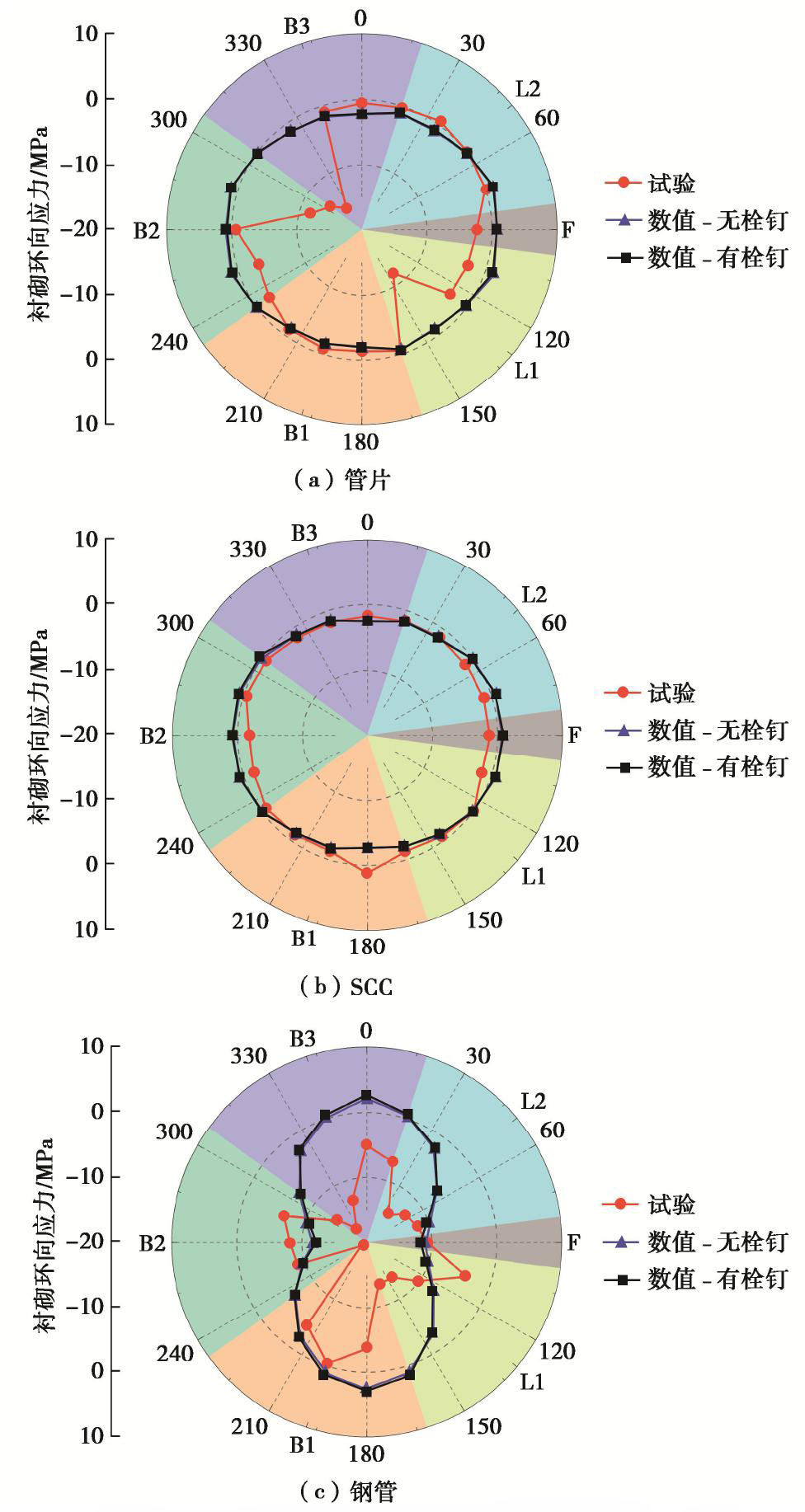
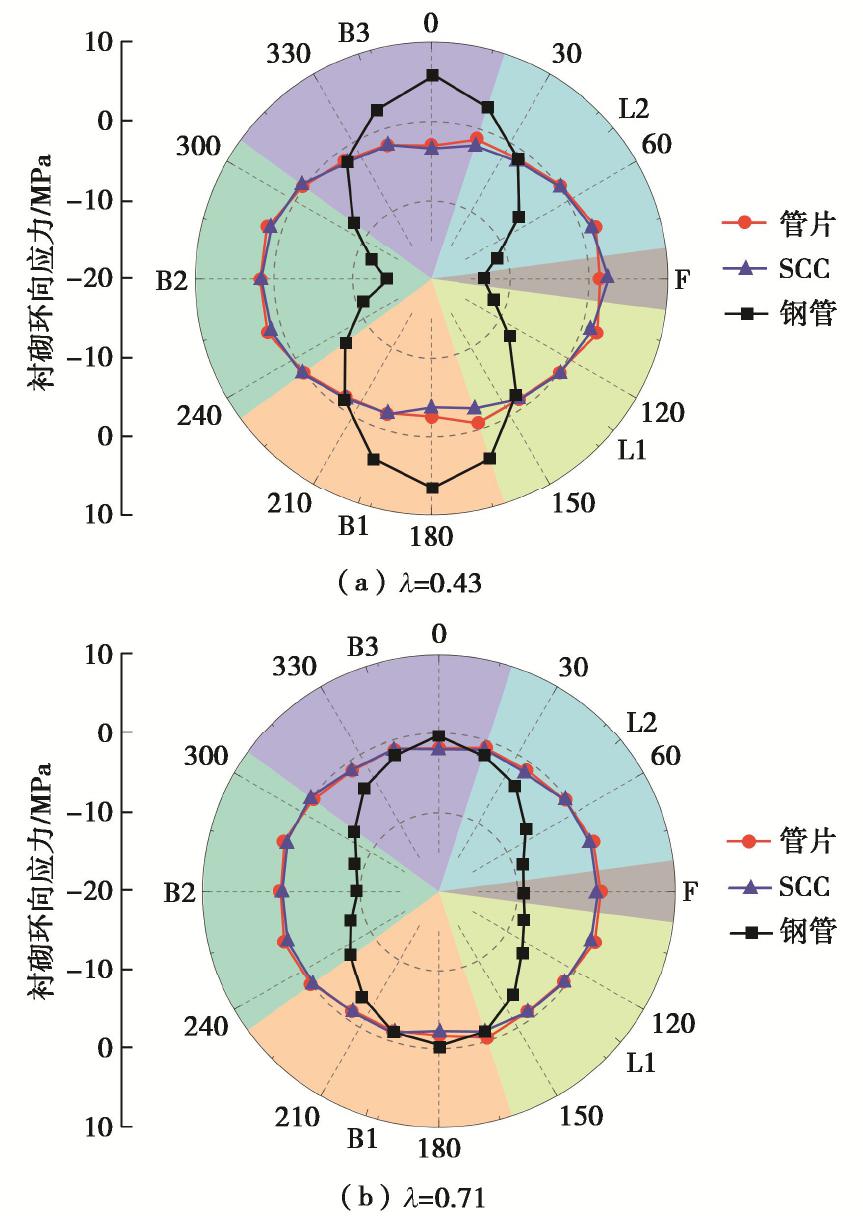
摘要: 设计了一种探究“管片-自密实混凝土（SCC）-钢管”叠合式衬砌结构横向力学行为与变形特性的大型足尺试验方法,初步揭示了叠合式衬砌结构在非均匀外载下的变形及力学响应规律；结合三维精细化有限元模型,探讨了栓钉布设、衬砌类型、侧压力系数等因素对结构承载机理的影响。结果表明：在非均匀外载作用下叠合式衬砌的环向应力相比分离式衬砌较小,变形呈现“横椭圆”模式,且随荷载非均匀性增加,其变形规律越显著；栓钉布设有效地增强了钢管-SCC的界面性能,但对结构环向应力影响甚微。Abstract: A full-scale mode test is proposed to study the transverse mechanical behaviors and deformation characteristics of segment-self compacted concrete (SCC)-steel superimposed linings. The deformation and mechanical response laws of composite lining structures under non-uniform external loads are revealed. Based on the 3D refined finite element model, the influences of studs, lining types and lateral pressure coefficient on the bearing capacity of the structures are discussed. The results show that the circumferential stress of the superimposed linings is lower than that of the separated ones under the action of non-uniform external loads, and the superimposed lining structures present a 'transverse ellipse’ deformation, and the deformation laws are more clear with the increase of load amplitude and non-uniformity. The studs can effectively enhance the interface performance of steel-SCC, but they have few effects on the circumferential stress of the structures.
-
0. 引言
黄土在中国分布广泛,是一类典型特殊土地基[1]。随着中国“一带一路”倡议和西部大开发战略实施,黄土地区工程建设急剧增加,越来越多工程建设面临基础抗拔问题,如输电线路杆塔和通信塔基础抗拔稳定性往往是其设计控制条件,抗拔基础承载性能已成为黄土地区工程建设的热点问题[2]。此外,黄土地区工程建设中,常因路径或场地条件限制,不得不将抗拔基埋置于斜坡地形的坡面。黄土斜坡边界条件使得抗拔基础低坡侧和高坡侧土体厚度不同,上拔荷载作用下,基础周围的上坡侧和下坡侧土体抗力有差异,黄土斜坡抗拔基础承载能力显著降低[3-4]。目前对黄土斜坡抗拔基础承载性能承载特性的研究相对薄弱。
国内外工程实践中,抗拔基础主要分为2大类：截面不随深度变化的直柱等截面基础和底部设计成扩大端的直柱扩底基础。本文基于黄土地区抗拔基础现场试验成果,阐述黄土平地直柱等截面基础和直柱扩底基础荷载-位移曲线特征、基础抗拔极限承载力确定准则、基础抗拔承载机理,并进一步对比分析黄土斜坡基础抗拔承载性能,可供工程设计参考。
1. 黄土平地抗拔基础荷载位移特征
在甘肃天水、定西和榆中3个黄土试验场地开展了18个直柱等截面基础和15个直柱扩底基础抗拔静载荷试验[5]。立柱直径0.9～1.5 m,扩底直径1.2～2.7 m,埋深1.8～10.0 m。所有试验均采用慢速维持荷载法,实测荷载-位移曲线如图1所示。
![]()
图 1 等直径直柱和直柱扩底基础荷载-位移曲线对比Figure 1. Comparison of uplift load-displacement curves for straight-sided and belled shaft foundations in flat loess ground从图1可以看出,等截面直柱基础和直柱扩底基础抗拔荷载-位移曲线均呈图2所示“缓变型”变化规律,可划分为3个特征阶段：初始弹性直线段、弹塑性曲线过渡段和直线破坏段。在初始弹性直线段OL1,荷载-位移曲线呈线性变化,抗拔土体以弹性变形为主。在弹塑性曲线过渡段L1L2,基础上拔位移随荷载增加呈非线性增加,位移变化速率增大。在直线破坏段L2L3,随上拔荷载持续增加,基础变形急剧增大,较小的荷载增量即产生较大的位移增量,直至基础抗拔承载能力丧失而破坏。
![]()
图 2 黄土基础抗拔荷载-位移曲线特征段及其承载力确定Figure 2. Characteristics of uplift load-displacement response and determination of uplift resistance of shaft foundations in loess表1给出了针对抗拔基础呈“缓变型”荷载-位移曲线的几种典型承载力确定准则（如图2所示）。为便于比较,以L1－L2两点法确定的极限承载力2LT作为基准,将试验过程中每一级试验荷载T除以2LT,从而对试验荷载进行归一化处理,并以T/2LT为y轴,相应试验荷载对应的位移为x轴,得到直柱等截面基础和直柱扩底基础抗拔归一化荷载-位移曲线对比如图1所示。结果表明,归一化荷载-位移曲线离散性明显小于实测数据[15]。
表 1 几种典型的拔极基础限承载力确定准则Table 1. Definitions of representative uplift interpretation criteria名称 类别 极限承载力定义 Chin双曲线法[6] 数学法 将实测荷载-位移曲线按照直线型方程s/T=ms+c拟合,T为上拔荷载,s为上拔位移,m为直线斜率,c为截距。取直线斜率的倒数倒数1/m为极限承载力,记为TCHIN Terzaghi和Peck法[7] 位移法 取上拔位移25.4 mm所对应荷载为极限承载力,记为TT&P Fuller和Hoy法[8] 位移法 取位移变化速率为0.14 mm/kN所对应的最小荷载为基础极限承载力,记为TF&H DeBeer法[9] 位移法 将荷载实测荷载-位移曲线转化为双对数坐标轴的荷载-位移曲线,取双对数坐标轴的荷载-位移曲线斜率变化点对应荷载为基础极限承载力,记为TDB 初始斜率法[10] 图解法 取与初始直线段斜率相同且平移3.8 mm后的直线与实测荷载-位移曲线交点所对应的荷载为基础极限承载力,记为TST 双切线交点法[11-12] 图解法 取过初始弹性段和直线破坏段直线交点的水平线与实测荷载-位移曲线交点所对应荷载为基础极限承载力,记为TTI L1-L2两点法[13-14] 图解法 根据图2所示荷载-位移曲线3阶段特征,取初始弹性直线段终点L1对应的荷载为弹性极限荷载,取破坏直线线段起点L2对应的荷载为基础极限承载力,分别记为TL1和TL2 进一步地,取按照图2和表1所示不同失效准确定的基础极限承载力除以2LT,以T/2LT均值为y轴,相应失效准则确定的极限承载力所对应位移的均值为x轴,得到直柱等截面基础和直柱扩底基础抗拔归一化荷载-位移特征曲线对比如图3所示。
![]()
图 3 黄土抗拔基础归一化抗拔荷载-位移特征曲线Figure 3. Comparison of normalized uplift load-displacement curves of straight-sided and belled shaft foundations in flat loess ground图3表明,不同失效准则所确定的基础极限承载力和位移值不同,从小到大顺序依次为：DeBeer法[9]、初始斜率法[10]、双切线交点法[11-12]、L1－L2两点法[13-14]、Terzaghi和Peck法[7]、Fuller和Hoy法[8],Chin双曲线法[6]最大,其过高估计了基础抗拔承载力。总体上看,L1－L2两点法取基础抗拔荷载-位移曲线初始弹直线性段终点荷载为弹性极限荷载,取破坏直线段起点荷载为基础塑性极限承载力,可较好地符合黄土抗拔基础荷载-位移曲线形态特征。
按L1－L2两点法,黄土直柱扩底和等直径直柱基础弹性极限荷载TL1对应位移1Ls均值分别为1.12,1.11 mm,二者较为接近,且对应1Ls/2Ls均值分别仅为0.04和0.08,抗拔弹性变形非常小。相应塑性极限荷载位移2Ls均值分别为25.75 mm和13.69 mm,基本满足一般结构物位移25 mm要求[16]。按L1－L2两点法确定的直柱扩底基础和等截面直柱基础弹性极限荷载1LT与塑性极限荷载2LT的比值分别为0.46和0.69。当试验中因加载能力限制而不能获得完整荷载-位移曲线时,可采用L1－L2两点法确定的弹性极限荷载1LT进行不同失效准则下基础抗拔极限承载力预估。对直柱等截面基础TST=1.371LT,TTI=1.471LT,2LT=1.521LT和TCHIN=1.721LT,对直柱扩底基础TST=1.721LT,TTI=2.021LT,2LT=2.211LT和TCHIN= 2.611LT。由此表明,在工程设计中如取黄土抗拔基础安全系数为2.5,则设计荷载下,黄土抗拔基础将均处于弹性承载状态。
2. 黄土平地基础抗拔承载机理
2.1 等截面直柱基础
黄土等截面直柱基础埋深一般较大,抗拔承载力主要由基础直柱与其周围土体间摩擦阻力提供,其抗拔承载过程如图4所示。
![]()
图 4 黄土平地条件下等截面直柱抗拔基础承载机理Figure 4. Uplift mechanism of straight-sided shaft foundations in flat loess ground当上拔荷载超过基础弹性极限承载力达到荷载-位移曲线L1点时,立柱接触面周围满足莫尔-库仑强度准则条件区域土体中出现间条状剪切面（图4（b））,并在空间上呈倒锥型斜面,基础沿接触面产生滑移较小。随上拔荷载继续增加,立柱周围土体中出现大致与界面平行的滑裂面（图4（c））,且随荷载增加而迅速发展、连续滑移,直至形成间条状剪切破坏面（图4（d））,荷载位移-曲线发展到L2点,达到抗拔基础极限承载力,基础立柱和黄土界面位移滑移值一般为13 mm左右,这与Kulhawy等[17]关于桩土界面圆柱形剪切破坏所需滑极限移值研究结果一致。当接近破坏时,荷载增加较小,位移迅速增大,下部呈圆柱形滑移而抽出破坏,靠近地表呈倒锥形破裂面（图4（e）,（f））。
2.2 直柱扩底基础
试验结果表明,直柱扩底基础极限抗拔承载力随深度变化存在临界深度hc。当基础抗拔埋深小于hc时呈浅基础破坏模式,抗拔土体滑动面一直延伸到地表,基础抗拔极限承载力随埋深增加而增加。当超过临界深度hc后,基础抗拔极限承载力随深度增加而提高的速率明显减小,临界埋深以上抗拔土体滑动面可延伸到地面,而在临界埋深以下,抗拔土体滑动面呈柱状。总体上看,黄土直柱扩底基础临界深度hc一般为扩底直径的3～4倍,呈扩大端土体压缩挤密产生弹性变形～基础周围土体塑性区形成、发展、贯通—土体整体剪切破坏的渐进过程,基础抗拔承载力主要由基础自重、滑动面剪切阻力及滑动面范围内土体重量组成。
图5为浅基础抗拔承载过程与破坏模式。初始加载阶段,荷载主要由基础自重和立柱周围土体侧摩阻力承担。随上拔荷载增加,立柱段摩阻力充分发挥并下移至扩大端,扩大端上方土体开始被压密而承载,荷载—位移曲线发展至L1点。上拔荷载持续增加,位移随荷载增加呈非线性变化且位移增加速率明显加大,扩大端周围土体由弹性状态转为塑性状态（图5（b））,并发生剪切变形,土体塑性区逐渐扩展（图5（c））,直至完全贯通（图5（d））,地表出现微裂缝并不断增大,抗拔土体滑裂面形成并延伸至地面,破坏时在地表产生环状和纵向裂缝（图5（e））。
![]()
图 5 黄土平地条件下浅埋扩底基础抗拔承载机理Figure 5. Uplift mechanism of belled shaft foundations in shallow failure mode on flat loess ground图6为深基础抗拔承载过程与破坏模式。与浅基础抗拔承载过程相同,当等截面段侧阻力发挥至弹性极限值后,扩大端周围土体压缩挤密,直至局部进入塑性状态。随上拔荷载持续增长,位移继续增大,等截面直柱段侧摩力逐渐发挥至极限值,相应地在上拔过程中扩大端周边土体继续受挤压,塑性区范围进一步发展扩大,直至贯通而发生受压破坏,基础抗拔承载力达到极限值。但与浅基础抗拔承载过程不同,抗拔承载力极限状态时,基础底部扩大头段形成椭圆状局部破坏,而等截面段形成一曲线破裂面并延伸至地面的较小范围,如图6（e）所示。
![]()
图 6 深埋扩底基础抗拔承载机理Figure 6. Uplift mechanism of belled shaft foundation in deep failure mode on flat loess ground3. 黄土斜坡基础抗拔承载性能
以甘肃定西市某黄土斜坡抗拔基础为例[3-4],试验场地坡度20°,共3个试验基础,其中等截面直柱基础SP1,直柱扩底基础BP1和BP2,基础结构尺寸及基顶位移均值随上拔荷载变化如图7所示。
![]()
图 7 黄土斜坡试验基础及其抗拔荷载-位移曲线Figure 7. Foundation structure and corresponding uplift load-displacement curves on sloped loess ground图7表明,黄土斜坡等截面直柱基础抗拔荷载-位移曲线呈“陡降型”变化,陡降起始点极限上拔承载力600 kN,对应位移为2.82 mm。基础立柱侧壁与周围土体界面滑移而抽出破坏。然而,直柱扩底基础与黄土平地基础抗拔荷载-位移曲线变化规律相同,也呈图2所示的“缓变型”3阶段变化规律。采用L1－L2两点法确定BP1、BP2基础弹性极限荷载1LT分别为830,1040 kN,相应塑性极限荷载2LT分别为1700,1800 kN。因此,扩底和增加埋深均可显著黄土斜坡基础抗拔性能。
试验前,在斜坡地基下坡侧和上坡侧地表以及基础顶部布置了电子位移传感器,监测相应测点位移变化。图8以斜坡基础BP1和BP2为例,给出了极限荷载下地表不同测点和基顶测点位移大小。
![]()
图 8 黄土斜坡直柱扩底基础地表及基顶位移分布Figure 8. Vertical displacements of ground surface and shaft head of belled foundations on sloped ground图8中基础顶部下坡侧位移传感器#1和#2均值要大于上坡侧传感器#3和#4的均值,因此每级上拔荷载作用下,基础顶部将产生竖向微小偏转,转角随荷载变化规律如图9所示。
![]()
图 9 沿上拔方向基础顶面转角随荷载变化曲线Figure 9. Relationship between instantaneous rotation angle of shaft head and applied uplift load由于基础BP2埋深大于BP1,相同上拔荷载作用下,BP2基顶转角要小于BP1。此外,图8中斜坡基础下坡侧黄土地表位移也明显大于上坡侧土体,抗拔土体破坏滑裂面形态及地表裂缝分布具有不对称性,如图10所示。
![]()
图 10 黄土斜坡直柱扩底基础地表裂缝分布Figure 10. Bulge and sketch of cracks after failure for belled shafts on sloped ground图10（a）中BP1呈浅基础破坏模式,基础破坏时地表裂缝延伸至地表呈环向和径向分布,并延伸向下坡侧较大范围,而上坡侧相对较小。相比较而言,BP2基础破坏时土体滑裂面延伸至地面,破裂面范围要远小于BP1基础,呈深基础破坏模式。因此,增加扩底基础埋深可有效提高黄土斜坡基础抗拔性能。
4. 结论
（1）黄土平地等截面直柱基础和直柱扩底基础抗拔荷载-位移曲线均呈3阶段变化规律：初始弹性直线段、弹塑性曲线过渡段和直线破坏段,L1－L2两点法可较好反映荷载-位移曲线变化特征。以L1－L2两点法确定的基础塑性极限荷载2LT为基准,对实测荷载-位移曲线进行归一化处理结果表明：直柱扩底和等截面直柱基础弹性极限荷载1LT对应位移均值分别为1.12,1.11 mm,塑性极限荷载2LT对应位移均值分别为25.75,13.69 mm。黄土抗拔基础设计安全系数取2.5,可使设计荷载作用下的黄土抗拔基础处于弹性承载状态。
（2）黄土等截面直柱基础和直柱扩底基础抗拔承载性能差异源于其承载机理的不同。前者抗拔承载力主要由基础直柱与周围土体间滑移而产生的侧阻力来提供,而后者呈扩大端土体压缩挤密发生弹性变形—塑性区形成、发展、贯通至土体整体剪切破坏的渐进过程,并可分为浅基础和深基础2种破坏模式,抗拔承载力主要由基础自重、滑动面剪切阻力及滑动面范围内土体重量组成。
（3）上拔荷载作用下,黄土斜坡地形等截面直柱基础和直柱扩底基础顶面沿上拔力方向均产生转角,下坡侧地表土体位移大于上坡侧,抗拔土体滑裂面及地表裂缝形成和发展具有不对称性。扩底和增加埋深可提高黄土斜坡基础抗拔承载性能。
致谢: 感谢中国建筑股份有限公司技术中心马程昊博士、北方工业大学何世钦博士课题组的支持,感谢清华大学张楚汉院士和安雪晖教授、重庆交通大学李鹏飞博士、华南理工大学陈高敬同学的帮助与讨论。 -
![]()
图 9 叠合式衬砌环向应力雷达图（
λ =0.57）Figure 9. Circumferential stresses of superimposed lining structures（
λ =0.57）![]()
图 10 无栓钉衬砌环向应力雷达图（
λ =0.57）Figure 10. Circumferential stresses of linings without studs（
λ =0.57）![]()
图 11 叠合式衬砌环向应力雷达图（无栓钉）
Figure 11. Circumferential stresses of superimposed lining structures (without studs)
表 1 测量方案
Table 1 Measurement schemes
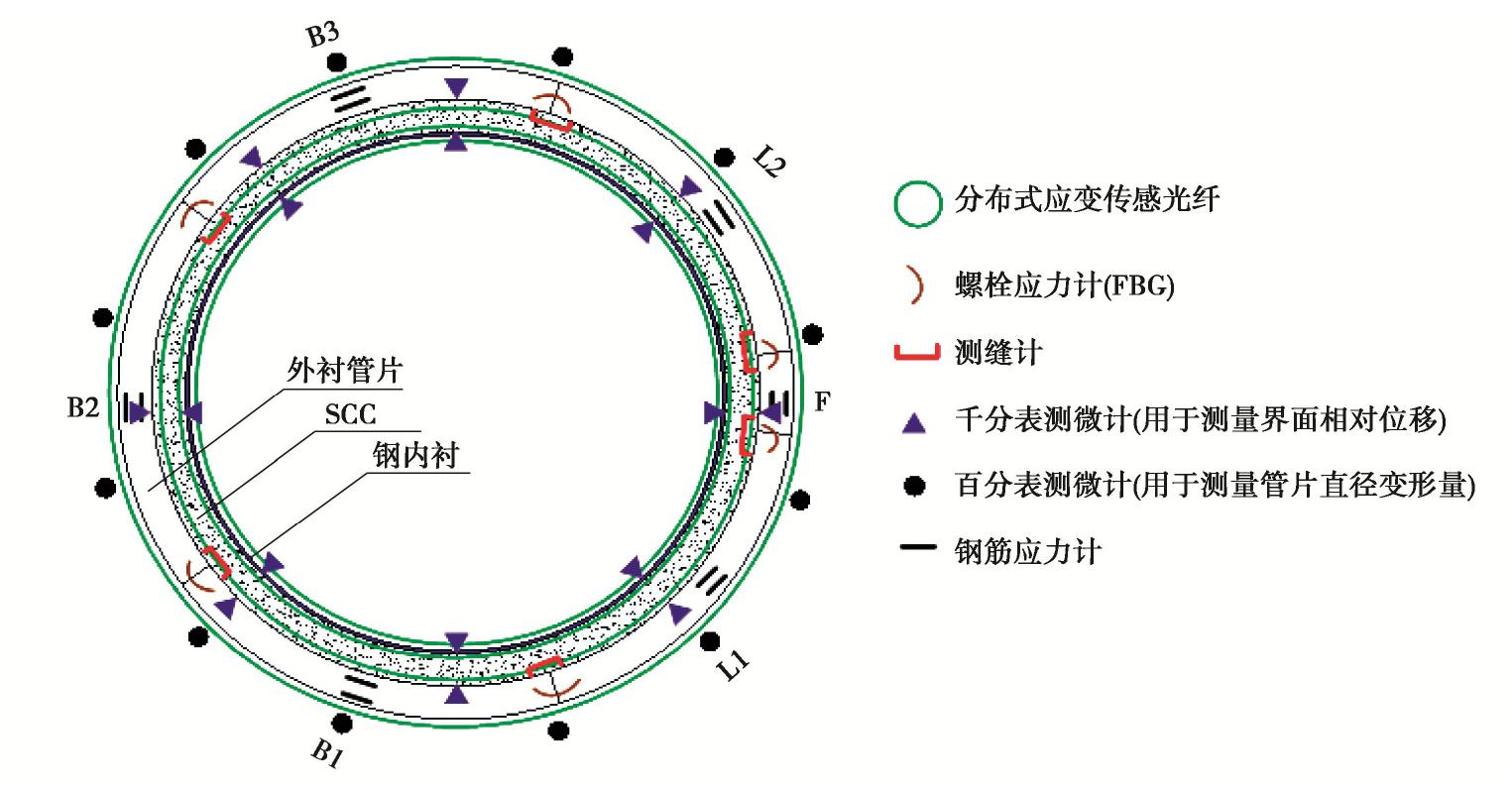
传感器类型 测量精度 布置位置 测量内容 元件数量 传统类 钢筋计（振弦式） 0.01 MPa 管片跨中截面（中环） 钢筋应力 内侧6支\外侧6支 数显百分表（机械式） 0.01 mm 管片外弧面（中环） 全周径向变形 12支 测缝计（振弦式） 0.001 mm 管片内弧面接头（中环） 纵缝张开量 12支 数显千分表（机械式） 0.001 mm 顶环管片端面 界面相对位移 16支（双向） 光纤类 光纤光栅裸栅应变计 1 με 管片下层连接螺栓 轴向应变 中环6支\顶环6支 分布式应变传感光缆 2με SCC（中环管片） SCC裂缝扩展 外侧1道\内侧1道 分布式应变传感光缆 2 με 钢管（中环管片） 全周环向应变 幅宽中央1道\环缝接头1道 
下载: 导出CSV
表 2 材料力学参数
Table 2 Mechanical parameters of materials
材料 抗拉/压强度/MPa 弹性模量/GPa 极限强度/MPa 屈服强度/MPa 混凝土 2.74/ 35.5 35.5 — — SCC 2.01 /20.1 30.0 — — 螺栓 — 206 700 450 钢筋 — 200 540 400 钢材 — 206 470 345
下载: 导出CSV
表 3 界面力学参数
Table 3 Mechanical parameters of interface
连接类型 kt/(N·m-3) kn/(N·m-3) fct/(N·m-2) 无栓钉 3.0×107 1.0×1011 4.0×106 含栓钉 8.0×108 1.0×1011 2.5×107 注： kt,kn,fct为切向刚度模量、法向刚度模量和抗拉强度。
下载: 导出CSV
表 4 衬砌最大环向应力
Table 4 Maximum circumferential stresses of linings
(MPa) 衬砌 管片 SCC 钢管 环向应力 拉应力 压应力 拉应力 压应力 拉应力 压应力 λ =0.431.99 -2.98 2.46 -3.69 6.59 -14.21 λ =0.571.31 -2.27 0.84 -2.64 2.69 -11.74 λ =0.710.71 -1.85 0.27 -2.10 — -9.68
下载: 导出CSV
-
[1] 广东省水利电力勘测设计研究院. 珠江三角洲水资源配置工程初步设计报告[R]. 广州: 广东省水利电力勘测设计研究院, 2018. Guangdong Hydropower Planning and Design Institute. Preliminary Design Report of Water Resources Allocation Project in the Pearl River Delta[R]. Guangzhou: Guangdong Hydropower Planning and Design Institute, 2018. (in Chinese)
[2] 严振瑞, 秦晓川, 张武, 等. 珠江三角洲水资源配置工程输水盾构隧洞形式优化设计研究[M]//水工隧洞技术应用与发展. 北京: 中国水利水电出版社, 2018. YAN Zhen-rui, QIN Xiao-chuan, ZHANG Wu, et al. Study on the optimization design of shield tunnel for water resources allocation project in the Pearl River Delta[M]//Application and Development of Hydraulic Tunnel Technology. Beijing: China Water Power Press, 2018. (in Chinese)
[3] 杨光华, 李志云, 徐传堡, 等. 盾构隧洞复合衬砌的荷载结构共同作用模型[J]. 水力发电学报, 2018, 37(10): 20-30. https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201810003.htm YANG Guang-hua, LI Zhi-yun, XU Chuan-bao, et al. Modeling load-structure interaction in shield tunnel composite lining[J]. Journal of Hydroelectric Engineering, 2018, 37(10): 20-30. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201810003.htm
[4] YANG F, CAO S R, QIN G. Mechanical behavior of two kinds of prestressed composite linings: A case study of the Yellow River Crossing Tunnel in China[J]. Tunnelling and Underground Space Technology, 2018, 79: 96-109. doi: 10.1016/j.tust.2018.04.036
[5] 张常光, 胡云世, 赵均海, 等. 深埋圆形水工隧洞弹塑性应力和位移统一解[J]. 岩土工程学报, 2010, 32(11): 1738-1745. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201011020.htm ZHANG Chang-guang, HU Yun-shi, ZHAO Jun-hai, et al. Elastic-plastic unified solutions for stresses and displacements of a deep buried circular hydraulic tunnel[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1738-1745. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201011020.htm
[6] FENG K, HE C, QIU Y, et al. Full-scale tests on bending behavior of segmental joints for large underwater shield tunnels[J]. Tunnelling and Underground Space Technology, 2018, 75: 100-116. doi: 10.1016/j.tust.2018.02.008
[7] 章青, 卓家寿. 盾构式输水隧洞的计算模型及其工程应用[J]. 水利学报, 1999(2): 19-22. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB902.003.htm ZHANG Qing, ZHUO Jia-shou. A computational model of shield tunnel for water conveyance[J]. Journal of Hydraulic Engineering, 1999(2): 19-22. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB902.003.htm
[8] YAN Q X, YAO C F, YANG W, et al. An improved numerical model of shield tunnel with double lining and its applications[J]. Advances in Materials Science and Engineering, 2015: 1-15.
[9] 王志国, 顾小兵, 程子悦, 等. 西江引水工程盾构输水隧洞设计[J]. 水利水电工程设计, 2016(1): 1-3. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSG201601001.htm WANG Zhi-guo, GU Xiao-bin, CHENG Zi-yue, et al. Design of shield water conveyance tunnel in Xijiang Water Diversion Project[J]. Design of Water Resources & Hydroelectric Engineering, 2016(1): 1-3. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSG201601001.htm
[10] ARNAU O, MOLINS C. Three dimensional structural response of segmental tunnel linings[J]. Engineering Structures, 2012, 44(6): 210-221.
[11] 张厚美, 过迟, 吕国梁. 盾构压力隧洞双层衬砌的力学模型研究[J]. 水利学报, 2001, 32(4): 28-33. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200104004.htm ZHANG Hou-mei, GUO Chi, LÜ Guo-liang. Mechanical model for shield presure tunnel with secondary linings[J]. Journal of Hydraulic Engineering, 2001, 32(4): 28-33. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB200104004.htm
[12] 黄鸿浩. “管片-SCC-钢衬”叠合式衬砌体系足尺结构试验设计与抗外载特性研究[D]. 广州: 华南理工大学大学, 2019. HUANG Hong-hao. Full-scale Experimental Investigation on Bearing Characteristic of Segment-SCC -Steel Superimposed Lining Structure Subjected to External Pressure[D]. Guangzhou: South China University of Technology, 2019. (in Chinese)
计量
- 文章访问数: 259
- HTML全文浏览量: 24
- PDF下载量: 111
