基于混合物理论的饱和岩石弹塑性模型

胡亚元

doi:10.11779/CJGE202012001

基于混合物理论的饱和岩石弹塑性模型 English Version

胡亚元

浙江大学滨海与城市岩土工程研究中心,浙江　杭州　310058

详细信息

作者简介:
胡亚元(1968—),男,博士,副教授,主要从事环境土工和岩土本构关系的研究工作。E-mail：huyayuan@zju.edu.cn

中图分类号: TU43
计量
- 文章访问数: 340
- HTML全文浏览量: 30
- PDF下载量: 218
出版历程
- 收稿日期: 2019-12-28
- 网络出版日期: 2022-12-05
- 刊出日期: 2020-11-30

Elastoplastic model for saturated rock based on mixture theory

HU Ya-yuan

Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China

摘要

摘要: 为了避免运用Skempton有效应力创建非线性本构模型时确定Biot系数的困难,选择工程混合物理论来建立饱和岩石的弹塑性模型。首先,根据工程混合物理论中的均匀化响应原理,揭示“固相基质体应变决定固相基质压力,骨架弹性和塑性应变决定Terzaghi有效应力和耗散Terzaghi有效应力,流相基质体应变决定孔压”的饱和多孔介质本构规律。其次,根据Hoek-Brown屈服准则和非关联流动准则,在已有岩石损伤模型基础上建立了饱和岩石弹塑性模型。最后,利用三轴排水和不排水剪切试验验证了饱和岩石弹塑性本构模型的合理性。研究表明,基于工程混合物理论的饱和岩石弹塑性模型能够较准确地模拟弹性阶段、弹塑性阶段和下降段应力应变全过程曲线的宏观力学性质,反映三轴不排水剪切试验条件下孔压随剪切加载先增加后减少的变化规律。由于工程混合物理论不直接采用Skempton有效应力建模,因而可以克服Biot非线性理论中确定Biot系数公式的困难,更容易建立饱和岩石弹塑性本构模型。
- 饱和岩石 /
- 工程混合物理论 /
- 弹塑性模型 /
- 骨架应力和骨架应变 /
- 基质压力和基质体应变
Abstract: In order to avoid the difficulties in evaluating the Biot's coefficient value of Skempton's effective stress used to formulate nonlinear constitutive model, the engineering mixture theory is chosen to build the elastoplastic model for saturated rock. Firstly, according to the principle of homogeneous response in the engineering mixture theory, the constitutive laws of saturated porous media are revealed as follows: "The solid matrix bulk strain determines solid matrix pressure, the skeleton elastic and plastic strains determine Terzaghi's effective stress and dissipate Terzaghi's effective stress, and the fluid matrix bulk strain determines pore pressure". Secondly, according to the Hoek-Brown yielding criterion and the non-associated flow rule, the saturated rock elastoplastic model is provided on the basis of the existing rock damage model. Finally, the proposed saturated rock elastoplastic model is validated by the triaxial drained and undrained shear test results. The researches show that the saturated rock elastoplastic model based on the engineering mixture theory can fairly accurately simulate the macroscopic mechanical behaviors of the overall stress-strain curve of rock including elastic stage, elastoplastic stage and descending stage, and illustrate the changing rule in the triaxial undrained shear tests that the pore pressure increases first and then decreases with the exteral shear stress. The engineering mixture theory does not use the Skempton's effective stress to build model, as a result, it can overcome the difficulties in determining the formula for Biot's coefficients in Biot's nonlinear model and is more convenient to establish the elastoplastic model for saturated rock.
- saturated rock /
- engineering mixture theory /
- elastoplastic model /
- skeleton stress and skeleton strain /
- matrix pressure and matrix bulk strain

HTML全文

0. 引言

在水利工程、石油工程、海洋工程、隧道工程和核废料处理工程等许多领域常涉及复杂环境作用下饱和岩石的多场耦合机理和相互作用问题,因此建立饱和岩石的本构关系具有重要的理论价值和广泛的应用价值^[1-7]。拟连续介质力学理论是饱和岩石力学广泛应用的建模方法之一。以往通常直接借用饱和土的Terzaghi有效应力原理来构建饱和岩石的本构关系。然而,许多岩体力学学者认为不能忽略饱和岩石固相基质（颗粒）的压缩性,因而不主张采用Terzaghi有效应力原理来建立饱和岩石的应力应变关系^[4-5]。张国新^[6]在仿真分析小湾水电站蓄水后的库区变形时发现,上游库岸变形按Terzaghi有效应力原理构建的模型计算为上浮24.5 mm,实测却是最大30 mm的沉降,造成这一错误的原因在于Terzaghi有效应力忽略了固相基质的压缩变形。为了弥补这一缺陷,赵阳升^[1]、张国新^[6]和周创兵等^[7]采用能够考虑固相基质压缩性的Biot线弹性理论来研究饱和岩石的流固耦合特性。许江等^[8]、张俊文等^[9]和HU等^[10]试验研究了水压和围压对饱和岩石变形和强度的影响,发现饱和岩石的受力变形具有明显的非线性和塑性性质。为了在Biot线弹性理论基础上反映饱和岩石的非线性和塑性特性,王伟等^[11]和谢妮等^[12]采用Skempton有效应力公式来建立饱和岩石的弹塑性本构方程。朱其志等^[13]和Chen等^[14]则另辟蹊径,采用细观力学来建立饱和岩石的弹塑性本构模型。上述研究深化了岩土工程界对饱和岩石力学特性的理解,有力地促进了饱和岩石本构模型的发展。

混合物理论以公理化体系来研究饱和多孔介质流固耦合的变形规律,在建模研究中具有独特的优势。然而经典混合物理论以在工程和试验中难以直接测量的组分应力和应变作为建模的状态变量,增加了确定本构方程具体形式及其模型参数的困难。因此直接采用混合物理论来研究饱和岩石本构模型的文献报道凤毛麟角。为了克服上述困难,经过近二三十年的发展,工程混合物理论应运而生^[15-22]。它既继承了传统混合物理论逻辑推理严密和力学基础扎实的优点,又兼顾工程实践简单实用需求,具有以下特点：①强调混合物理论必须跟研究对象的具体特点相结合,能够阐释岩土压硬剪胀等变形特性；②采用在工程和试验中便于测量和控制的应力应变量如有效应力和孔压等作为混合物本构理论框架的状态变量,以提高本构模型的实用性。采用能量守恒方程中的功共轭对来选择本构模型的应力应变量,以保证本构建模的严密性；③采用自由能势函数和耗散势函数来反映岩土可逆和不可逆变形的力学性质,统一阐释弹性和压硬剪胀等弹塑性变形规律；④强调孔隙变形在多场耦合机理中的关键作用,通过建立骨架体应变与固流两相体应变之间的数学物理关系来揭示流固两相耦合作用的力学机制。如陈正汉^[15-16]提出岩土力学的公理化体系,总结了岩土力学独特的本构原理,深刻揭示了理性力学只有与岩土力学的有效应力原理和具体工程性质相结合才能获得历史性突破。Houlsby^[17]假定固液两相基质不可压缩,从经典混合物能量守恒方程出发证明饱和土选用Terzaghi有效应力和非饱和土选用双应力变量建模的合理性。Borja^[18]在考虑组分基质压缩性条件下企图证明Skempton 有效应力是混合物能量方程的一个应力状态变量。赵成刚等^[19]和刘艳等^[20]从机械功共轭理论出发,提出采用3个应力变量才能更合理反映非饱和土的本构特性。胡亚元^[21-22]根据耗散势函数讨论了Drucker塑性公式和Iliushin塑性公式的适用范围,通过孔隙变形与固流两相变形之间的内在联系探究了流固耦合作用的力学机理^[21],揭示了Terzaghi有效应力原理的力学基础是固流两相的体积分数之和必须等于1,即Terzaghi有效应力公式是饱和多孔介质固流两相体积分数之和等于1这一几何关系在力学上的反映^[22],并应用均匀化响应原理^{[16, 22-24]}研究了饱和多孔介质能量表达式的合理形式,证明了Terzaghi有效应力、固相基质压力和流相基质压力是一组完备的饱和多孔介质本构方程的状态变量^[22]。胡亚元等^[25-26]采用Terzaghi有效应力、固相基质压力（或孔压）和流相基质压力建立了饱和多孔介质的超弹性本构方程,结合Lade等^[27]试验数据,建立了饱和多孔介质的非线性体积本构模型。本文将在上述研究基础之上,以工程混合物理论为指导,建立能够考虑剪胀效应的饱和岩石弹塑性本构模型,为完善和发展饱和岩石本构理论和实用模型添砖加瓦。

1. 饱和多孔介质一般本构理论

工程混合物理论认为,饱和多孔介质固流两相存在两种不同尺寸的构形：一种是组分实际存在的细观真实构形,如饱和岩土的固相颗粒和孔隙中的流体,它们所产生的应变在混合物中称为组分基质应变,固相基质应变用 $ε_{RS}$ 表示,流相基质应变用 $ε_{RF}$ 表示；另一种是组分按体积分数平均化后连续变化的宏观构形,它所产生的应变按经典混合物理论专业术语称为组分应变,固相应变用 $ε_{S}$ 表示,流相应变用 $ε_{F}$ 表示。

为行文简洁,文中下标 $S$ 表示固相,下标 $F$ 表示流相, $α = {S,F}$ 为组分变量。设 $ρ_{R α}$ 为 $α$ 组分的材料密度（在饱和岩土力学中也称为真实密度）, $ρ_{α}$ 为 $α$ 组分的平均密度, $ρ_{α} =$ $n_{α} ρ_{R α}$ , $n_{α}$ 为体积分数。对于饱和多孔两相介质,体积分数 $n_{α}$ 满足：

$n_{S} + n_{F} = 1$ 。

(1)

设 $σ_{S}$ 为饱和多孔介质中固相承受的应力张量； $σ_{Fm}$ 为流相承受的球应力； $P_{S}$ 为固相基质压力, $P_{S} = (σ_{S} : I) / (3 n_{S0})$ ； $u$ 为流相基质压力或称为孔压, $u = σ_{Fm} / n_{F0}$ ； $σ$ 为饱和多孔介质的总应力张量。根据工程混合物理论,在小应变条件下有^{[22, 25-26]}

$σ = σ_{S} + σ_{Fm} I = σ_{S} + (n_{F0} u) I$ 。

(2)

小应变条件下固流两相基质体应变 $ε_{RSV}$ , $ε_{RFV}$ 的定义为^{[22, 25-26]}

$ε_{RSV} = (ρ_{RS} - ρ_{RS0}) / ρ_{RS0}$ ,

(3)

$ε_{RFV} = (ρ_{RF} - ρ_{RF0}) / ρ_{RF0}$ 。

(4)

令固相应变为 $ε_{S}$ ,流相体应变为 $ε_{FV}$ ,小应变条件下固相组分的骨架应变 $ε_{Sf}$ 定义为^{[22, 25-26]}

$ε_{Sf} = ε_{S} - (ε_{RSV} / 3) I$ 。

(5)

设 $e = n_{F} / (1 - n_{F})$ ,为孔隙比。根据工程混合物理论,固相组分的骨架体应变 $ε_{SfV}$ （也称固相体积分数应变）和流相体应变 $ε_{FV}$ 表达如下^{[22, 25-26]}：

$ε_{SfV} = ε_{Sf} : I = (n_{S} - n_{S 0}) / n_{S} = (e_{0} - e) / (1 + e_{0})$ ,

(6)

$ε_{FV} = ε_{RFV} - (n_{S0} ε_{SfV}) / n_{F0}$ 。

(7)

在实际工程中,岩土工程界关心的是流体从多孔固体介质的流出或流入量。令 $ε_{SV} = ε_{S} : I$ ,定义孔隙中流体渗入量为 $ζ_{F} = n_{F0} (ε_{FV} - ε_{SV})$ 。对式（5）求迹后式（5）,（7）代入渗入量定义式,可得 $ζ_{F}$ 的表达式为

$ζ_{F} = n_{F0} (ε_{RFV} - ε_{RSV}) - ε_{SfV}$ 。

(8)

根据工程混合物理论,忽略热传递和热源,饱和多孔介质的内能平衡可表示为^[22]

$\dot{U} = n_{S0} P_{S} {\dot{ε}}_{RSV} + σ^{'} : {\dot{ε}}_{Sf} + n_{F0} u {\dot{ε}}_{RFV} + W_{F} \cdot (u \nabla n_{F} - {\hat{p}}_{F})$ ,

(9)

式中, $σ^{'}$ 为Terzaghi有效应力（ $σ^{'} = σ - u I$ ）, $W_{F} =$ ${\dot{x}}_{F} -$ ${\dot{x}}_{S}$ , ${\hat{p}}_{F}$ 为流固两相之间流速差异引起的动量供应量,在饱和岩土中主要表现为流体渗透引起的拖拽力等。式（9）表明,饱和多孔介质的内能等于固相骨架变形功、固相基质体积变形功、流相基质体积变形功和渗流引起的机械功之和。

饱和岩石的细观力学表明,岩石的不可逆变形主要来源于岩石微裂隙等孔隙的发展^{[1, 7, 13-14]}。式（6）又表明,孔隙率的变化与骨架体应变 $ε_{SfV}$ 成一一对应关系,由此可知岩石的不可逆变形为骨架变形。令 $ε_{Sf}^{p}$ 为不可逆骨架应变。首先根据热力学内变量本构理论可知^[17-22],饱和岩石的自由能变量可选为 $ε_{RSV}$ , $ε_{Sf}$ , $ε_{Sf}^{p}$ 和 $ε_{RFV}$ 。其次,以线弹性理论为基础,Geertsma^[23]发现当总应力等于孔隙水压力时饱和岩土与单相岩土体的本构关系相同,获得了饱和岩土的线弹性本构方程和有效应力公式；陈正汉等^{[16, 24]}揭示了当总应力和孔隙中某流体压力相等时,该流体所占据的孔隙可用固相材料替代的变形规律,获得了著名的非饱和岩土的有效应力原理。陈正汉还把这一规律推广到含有N个不相混流体的多孔介质领域,获得了相应的有效应力公式^{[16, 24]}。陈勉等^[28]研究了多重孔隙介质的有效应力定律,也得到了与陈正汉等^{[16, 24]}相同的结论。他们的研究揭示了如下规律：“当多孔介质混合物单元体中每一点的应变相等时,混合物单元体等效于单相均质单元体,单元体中每一点产生的应力亦相等；反之亦然”。由于在多孔介质混合物理论中需要经常使用这一性质,文献[22]把它称为均匀化响应原理。文献[22]还揭示了均匀化响应原理成立时不但多孔介质的孔隙率保持不变,而且多孔介质的骨架变形、固相基质变形和流相基质变形相互独立的力学性质。这一性质不但在线弹性理论中成立,而且在非线性和塑性理论中亦成立^[22],因此运用均匀化响应原理可以极大地简化多孔介质混合物的本构模型。当混合物受力变形符合均匀化响应原理时,饱和多孔介质的内能可由独立的3部分组成^[22]：①第一部分是固相基质体积变形产生的内能 $U_{RS}$ ,它取决于 $ε_{RSV}$ ；②第二部分是固相骨架变形产生的内能 $U_{Sf}$ ,根据热力学内变量本构理论,它取决于 $ε_{Sf}$ , $ε_{Sf}^{p}$ ；③第三部分是流相基质体积变形产生的内能 $U_{RF}$ ,它取决于 $ε_{RFV}$ 。根据热力学局部平衡原理,有^[22]

$\begin{matrix} \dot{U} = \frac{\partial U_{RS} (ε_{RSV})}{\partial ε_{RSV}} {\dot{ε}}_{RSV} + \frac{\partial U_{Sf} (ε_{Sf}, ε_{Sf}^{p})}{\partial ε_{Sf}} : {\dot{ε}}_{Sf} + \\ \frac{\partial U_{Sf} (ε_{Sf}, ε_{Sf}^{p})}{\partial ε_{Sf}^{p}} : {\dot{ε}}_{Sf}^{p} + \frac{\partial U_{RF} (ε_{RFV})}{\partial ε_{RFV}} {\dot{ε}}_{RFV} + θ \dot{η} \end{matrix}$ 。

(10)

因为式（9）与式（10）恒相等,根据变量 $ε_{RSV}$ , $ε_{Sf}$ , $ε_{Sf}^{p}$ 和 $ε_{RFV}$ 之间相互独立的性质可得

$P_{S} = \partial [U_{RS} (ε_{RSV})] / \partial ε_{RSV}$ ,

(11)

$σ^{'} = \partial [U_{Sf} (ε_{Sf}, ε_{Sf}^{p})] / \partial ε_{Sf}$ ,

(12)

$u = \partial [U_{RF} (ε_{RFV}) / n_{F0}] / \partial ε_{RFV}$ 。

(13)

从式（11）～（13）可以看出,固相基质压力由固相基质体应变唯一决定,有效应力由骨架弹性和塑性应变唯一决定,孔压由流相基质体应变唯一决定。令耗散应力 ${σ^{'}}^{p}$ 为

${σ^{'}}^{p} = - \partial [U_{Sf} (ε_{Sf}, ε_{Sf}^{p})] / \partial ε_{Sf}^{p}$ 。

(14)

引入 $H (σ^{'}, ε_{Sf}^{p}) = σ^{'} ε_{Sf} - U_{Sf} (ε_{Sf}, ε_{Sf}^{p})$ ,则根据式（12）,（14）有：

$\begin{array}{l} ε_{Sf} = \frac{\partial H_{Sf} (σ^{'}, ε_{Sf}^{p})}{\partial σ^{'}}, \\ {σ^{'}}^{p} = \frac{\partial H_{Sf} (σ^{'}, ε_{Sf}^{p})}{\partial ε_{Sf}^{p}} 。 \end{array}}$

(15)

对大多数弹塑性问题, $H_{Sf} (σ^{'}, ε_{Sf}^{p})$ 可表示为 $H_{Sf} (σ^{'}, ε_{Sf}^{p}) =$ $H_{Sf}^{e} (σ^{'}) + σ^{'} ε_{Sf}^{p}$ ,代入到式（15）有

$\begin{array}{l} ε_{Sf} = \partial [H_{Sf}^{e} (σ^{'})] / \partial σ^{'} + ε_{Sf}^{p}, \\ {σ^{'}}^{p} = σ^{'} 。 \end{array}}$

(16)

式（16）中的第二个等式表明耗散应力等于Terzaghi有效应力,因此 ${σ^{'}}^{p}$ 也称为耗散Terzaghi有效应力。由式（9）,（10）,（14）,（16）的第二式可得

$θ \dot{η} = W_{F} \cdot (u \nabla n_{F} - {\hat{p}}_{F}) + {σ^{'}}^{p} : {\dot{ε}}_{Sf}^{p}$ 。

(17)

把式（17）等式右边的第一项与渗流耗散势理论相结合可以建立广义达西定理^[29],具体见文后附录。把式（17）等式右边的第二项与塑性耗散势理论相结合可以建立塑性本构关系^[17-22]。由于整个推导过程十分繁复,不利于工程应用,因此本文直接采用经典塑性力学方法来建立饱和岩石的塑性本构模型。下文根据上述推导和经典弹塑性力学理论来建立饱和岩石的弹塑性本构模型。

2. 饱和岩石弹塑性本构模型

2.1 岩石基质本构方程

在土力学中把固相基质称为土颗粒,对应的是无孔隙土固体的变形力学特性。与土颗粒一样,岩石基质对应的是内部无孔隙时完整岩石的变形力学特性。岩石破坏往往发生在微裂隙等缺陷部位。由于构成孔隙的岩石骨架强度远小于完整岩石强度,因此一般认为岩石骨架破坏时,作为完整岩石的岩体基质仍处于弹性状态。故式（11）中与岩体基质体应变有关的内能可表示为 $U_{RS} (ε_{RSV}) = K_{S} ε_{RSV}^{2} / 2$ , $K_{S}$ 为固相基质的体积模量。将其代入到式（11）可得

$P_{S} = K_{S} ε_{RSV}$ 。

(18)

2.2 岩石骨架本构方程

从式（5）可知,岩石的骨架应变 $ε_{Sf}$ 等于岩石的固相应变 $ε_{S}$ 减去岩石基质平均应变 $ε_{RSV} I / 3$ 。式（15）表明 $ε_{Sf}$ 的变化取决于Terzaghi有效应力 $σ^{'}$ 和骨架塑性应变 $ε_{Sf}^{p}$ ,但由于构成孔隙的岩石骨架变形极其复杂,因此要明确地确定式（16）中 $H_{Sf}^{e} (σ^{'})$ 十分困难。故本文通过经典弹塑性力学和岩石室内试验直接确定 $ε_{Sf}$ , $ε_{Sf}^{p}$ 的本构方程。

设 $ε_{Sf}$ 的3个主应力分别为 $ε_{Sf1}$ , $ε_{Sf2}$ 和 $ε_{Sf3}$ ,由于 $ε_{Sf}$ 的变化取决于Terzaghi有效应力 $σ^{'}$ ,根据三轴岩石试验并借鉴文献[30, 31]研究成果,唯象地提出如下岩石骨架的损伤本构方程：

${σ^{'}}_{1} - {σ^{'}}_{3} = E_{H} ε_{Sf1} \exp [- {(ε_{Sf1} / ε_{a})}^{m}]$ ,

(19)

式中, $E_{H}$ 为无损伤时的弹性模量, $ε_{a}$ ,m为屈服微单元随分布变量 $ε_{Sf1}$ 变化的Weibull概率函数分布参数^[30]。笔者总结了数个砂岩的试验成果,发现 $E_{H}$ 计算式可表示为

$E_{H} = E_{H0} [1 + \frac{b (σ_{3} - χ P_{F})}{1 + a (σ_{3} - χ P_{F})}]$ ,

(20)

式中, $E_{H0}$ 为岩石骨架的初始无损伤杨氏模量, $a$ ,b,χc为影响 $E_{H}$ 值的模型参数。根据式（19）可得 ${σ^{'}}_{1} - {σ^{'}}_{3}$ 的峰值为

${({σ^{'}}_{1} - {σ^{'}}_{3})}_{f} = E_{H} \exp (- 1 / m) \sqrt[m]{(1 / m)} ε_{a}$ 。

(21)

饱和岩石的破坏准则满足Hoek-Brown破坏准则,

${({σ^{'}}_{1} - {σ^{'}}_{3})}_{f} = \sqrt{s σ_{c} {σ^{'}}_{3} + σ_{c}^{2}} = \sqrt{s σ_{c}} \sqrt{{σ^{'}}_{3} + σ_{c} / s}$ 。

(22)

故有

$ε_{a} = \frac{\sqrt{s σ_{c} {σ^{'}}_{3} + σ_{c}^{2}}}{E_{H}} \exp (1 / m) \sqrt[m]{m}$ 。

(23)

岩石的回弹和再压缩变形可表示为

${σ^{'}}_{1} - {σ^{'}}_{3} = E_{H} ε_{Sf1}^{e}$ 。

(24)

令函数 $x =roc(y, m)$ 是 $y = x \exp (- x^{m})$ 的反函数,则 $ε_{Sf1}$ 表示为

$ε_{Sf1} = ε_{a} roc (\frac{{σ^{'}}_{1} - {σ^{'}}_{3}}{ε_{a} E_{H}}, m)$ 。

(25)

岩石的塑性变形为

$ε_{Sf1}^{p} = ε_{a} roc (\frac{{σ^{'}}_{1} - {σ^{'}}_{3}}{ε_{a} E_{H}}, m) - \frac{{σ^{'}}_{1} - {σ^{'}}_{3}}{E_{H}}$ 。

(26)

以往的岩石损伤模型只考虑损伤导致弹性模量衰减,这类损伤模型无法解释岩石的剪胀效应,这是传统岩石损伤模型较大的一个缺陷。实际上岩石微单元在屈服损伤过程中会出现剪胀效应,导致屈服损伤因子出现各向异性,笔者认为各个方向的损伤程度可以结合式（19）和塑性势理论来描述,这是本论文改进传统损伤模型之处。借鉴土力学弹塑性模型中势函数的选择方式,势函数一般取为与屈服准则相类似的形式,故饱和岩石的势函数取为与Hoek-Brown破坏准则相类似的形式,

$g (σ^{'}, β) = {σ^{'}}_{1} - {σ^{'}}_{3} - β \sqrt{s_{v} σ_{c}} \sqrt{{σ^{'}}_{3} + σ_{c} / s}$ ,

(27)

式中, $β$ 为非相关联系数,

$s_{v} = {({σ^{'}}_{1} - {σ^{'}}_{3})}^{2} / [σ_{c} ({σ^{'}}_{3} + σ_{c} / s)]$ 。

(28)

由此可得

$d ε_{Sf1}^{p} = d λ \frac{\partial g}{\partial σ'_{1}} = d λ$ ,

(29)

$d ε_{Sf3}^{p} = d λ \frac{\partial g}{\partial {σ^{'}}_{3}} = - [1 + \frac{β ({σ^{'}}_{1} - {σ^{'}}_{3})}{2 ({σ^{'}}_{3} + σ_{c} / s)}] d ε_{Sf1}^{p}$ 。

(30)

设岩石骨架的泊松比为 $υ_{H}$ ,则骨架的弹性变形为

$d ε_{Sf1}^{e} = \frac{d {σ^{'}}_{1}}{E_{H}} - \frac{ν_{H} d {σ^{'}}_{2}}{E_{H}} - \frac{ν_{H} d {σ^{'}}_{3}}{E_{H}}$ ,

(31)

$d ε_{Sf2}^{e} = \frac{d {σ^{'}}_{2}}{E_{H}} - \frac{ν_{H} d {σ^{'}}_{1}}{E_{H}} - \frac{ν_{H} d {σ^{'}}_{3}}{E_{H}}$ ,

(32)

$d ε_{Sf3}^{e} = \frac{d {σ^{'}}_{3}}{E_{H}} - \frac{ν_{H} d {σ^{'}}_{1}}{E_{H}} - \frac{ν_{H} d {σ^{'}}_{2}}{E_{H}}$ 。

(33)

由式（29）～（33）,利用式（16）中的第一式得

$d ε_{Sf1} = \frac{d {σ^{'}}_{1}}{E_{H}} - ν_{H} \frac{d {σ^{'}}_{2} + d {σ^{'}}_{3}}{E_{H}} + d ε_{Sf1}^{p}$ ,

(34)

$d ε_{Sf2} = \frac{d {σ^{'}}_{2}}{E_{H}} - ν_{H} \frac{d {σ^{'}}_{1} + d {σ^{'}}_{3}}{E_{H}}$ ,

(35)

$d ε_{Sf3} = \frac{d {σ^{'}}_{3}}{E_{H}} - ν_{H} \frac{d {σ^{'}}_{1} + d {σ^{'}}_{2}}{E_{H}} - [1 + \frac{β ({σ^{'}}_{1} - {σ^{'}}_{3})}{2 ({σ^{'}}_{3} + σ_{c} / s)}] d ε_{Sf1}^{p}$ 。

(36)

2.3 岩石本构方程

令

$E_{b} = 9 E_{H} n_{S0} K_{S} / (9 n_{S0} K_{S} + E_{H})$ ,

(37)

$ν_{b} = (9 ν_{H} n_{S0} K_{S} - E_{H}) / (9 n_{S0} K_{S} + E_{H})$ ,

(38)

$K_{H} = E_{H} / 3 / (1 - 2 ν_{H})$ ,

(39)

$K_{b} = E_{b} / [3 (1 - 2 ν_{b})] = K_{H} n_{S0} K_{S} / (n_{S0} K_{S} + K_{H})$ ,

(40)

式中, $E_{b}$ 为岩石的杨氏模量, $ν_{b}$ 为岩石的泊松比, $K_{b}$ 为岩石的体积模量, $K_{H}$ 为岩石骨架的体积模量。饱和岩石本构方程由式（5）,（18）,（34）～（36）和有效应力公式 $σ^{'} = σ - u I$ 可得

$\begin{matrix} d ε_{S1} = d ε_{Sf1} + \frac{d ε_{RSV}}{3} = \frac{d σ_{1}}{E_{b}} - ν_{b} \frac{d σ_{2} + d σ_{3}}{E_{b}} + \\ (\frac{1}{3 K_{b}} - \frac{1}{3 K_{S}}) d u + d ε_{Sf1}^{p} \end{matrix}$ ,

(41)

$\begin{matrix} d ε_{S2} = d ε_{Sf2} + \frac{d ε_{RSV}}{3} = \frac{d σ_{2}}{E_{b}} - ν_{b} \frac{d σ_{1} + d σ_{3}}{E_{b}} + \\ (\frac{1}{3 K_{b}} - \frac{1}{3 K_{S}}) d u \end{matrix}$ ,

(42)

$\begin{matrix} d ε_{S3} = d ε_{Sf3} + \frac{d ε_{RSV}}{3} = - ν_{b} \frac{d σ_{1} + d σ_{2}}{E_{b}} + \frac{d σ_{3}}{E_{b}} + \\ (\frac{1}{3 K_{H}} - \frac{1}{3 K_{S}}) d u - [1 + \frac{β ({σ^{'}}_{1} - {σ^{'}}_{3})}{2 (σ'_{3} + σ_{c} / s)}] d ε_{Sf1}^{p} \end{matrix}$ 。

(43)

对式（26）微分并利用式（19）～（21）,（23）可得

(44)

（1）当塑性变形为零时, $d ε_{Sf1}^{p} = d ε_{Sf2}^{p} = d ε_{Sf3}^{p} = 0$ ,从式（41）～（43）可得Skempton有效应力为

$\begin{array}{l} σ_{i}^{*} = σ_{i} - （ 1 - K_{b} / K_{s}) u & （ i = 1, 2, 3 ） \end{array}$ 。

(45)

从而可把式（41）～（43）写为用Skempton有效应力表示的胡克定理：

$d ε_{S1} = [d σ_{1}^{*} - ν_{b} (d σ_{2}^{*} + d σ_{3}^{*})] / E_{b}$ ,

(46)

$d ε_{S2} = [d σ_{2}^{*} - ν_{b} (d σ_{1}^{*} + d σ_{3}^{*})] / E_{b}$ ,

(47)

$d ε_{S3} = [d σ_{3}^{*} - ν_{b} (d σ_{1}^{*} + d σ_{2}^{*})] / E_{b}$ 。

(48)

（2）当塑性变形不为零时, $d ε_{Sf1}^{p} \neq 0$ 和 $d ε_{Sf3}^{p} \neq 0$ ,从式（41）～（43）,（44）可知很难找到一个全量形式的Biot系数公式（从而也很难获得类似式（45）的全量形式的Skempton有效应力表达式）^[26],可以把应变唯一地表示为Skempton有效应力的函数。这一分析结果表明,基于混合物理论建立的饱和岩石本构模型不一定能用类似式（45）的全量形式的Skempton有效应力来表示,这是与采用Skempton有效应力作为状态变量来建模的Biot饱和多孔介质宏观理论不同的,这说明采用工程混合物理论建模具有独特性。

（3）从式（41）～（43）可以计算增量形式的（切线）Biot系数^[26],但获得的Biot系数具有各向异性,并且加卸载具有不同的值。而基于Biot理论的弹塑性本构模型为了建模方便往往选用全量形式的Skempton有效应力,所取的Biot系数值往往各向同性且加卸载一致。

2.4 流体渗流量本构方程

根据式（34）～（36）得

$d ε_{SfV} = \frac{d {σ^{'}}_{m}}{K_{H}} - \frac{β ({σ^{'}}_{1} - {σ^{'}}_{3})}{2 ({σ^{'}}_{3} + σ_{c} / s)} d ε_{Sf1}^{p}$ 。

(49)

与流相基质体积变形有关的内能表达式可表示为 $U_{RF} (ε_{RFV}) = n_{F0} K_{F} ε_{RFV}^{2} / 2$ , $K_{F}$ 为流相基质的体积弹性模量。把它代入到式（13）可得

$u = K_{F} ε_{RFV}$ 。

(50)

对式（8）进行微分,由式（18）、式（37）～（43）和式（50）得

$\begin{matrix} d ζ_{F} = (\frac{n_{F0}}{K_{F}} + \frac{1}{K_{b}} - \frac{1 + n_{F0}}{K_{S}}) d u - (\frac{1}{K_{b}} - \frac{1}{K_{S}}) d σ_{m} + \\ \frac{β ({σ^{'}}_{1} - {σ^{'}}_{3})}{2 ({σ^{'}}_{3} + σ_{c} / s)} d ε_{Sf1}^{p} \end{matrix}$ 。

(51)

3. 算例验证

3.1 三峡砂岩恒定孔压三轴排水剪切试验模拟

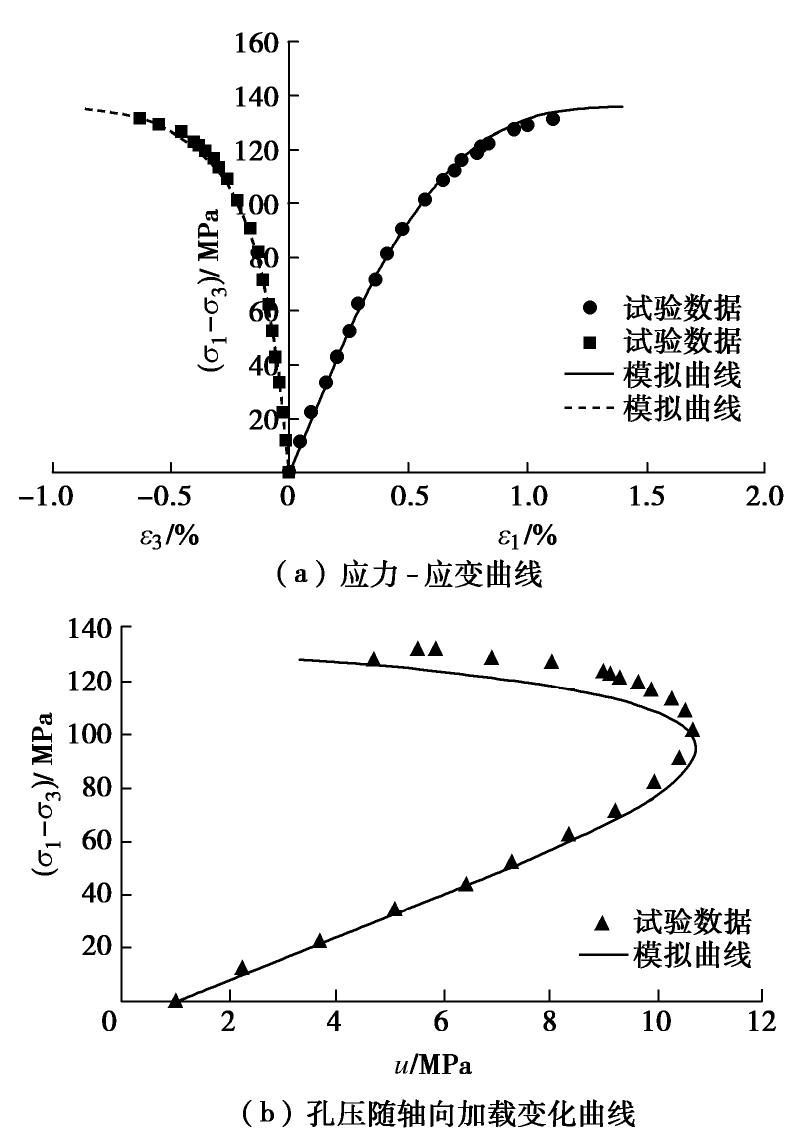
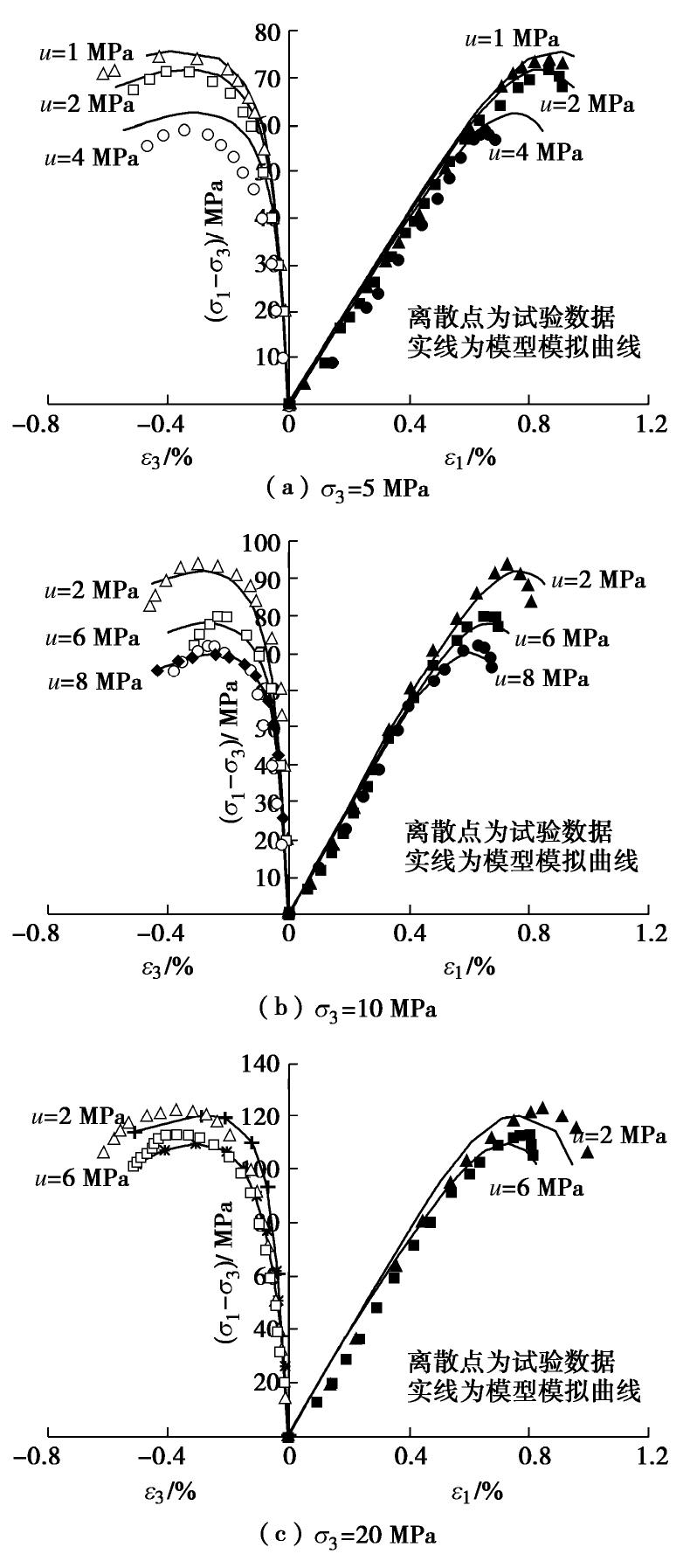
从第2节分析可知,建立完备的饱和岩石需要11个模型参数,其中,固相基质本构关系参数1个（固相基质体积模量 $K_{S}$ ）、固相骨架本构关系参数9个和流相基质本构关系参数1个（流相介质体积模量 $K_{F}$ ）。固相骨架本构关系的9个参数：①反映杨氏模量 $E_{H}$ 变化规律的参数 $E_{H0}$ ,a,b和 $χ$ ；②泊松比参数 $ν_{H}$ ；③反映骨架损伤的参数 $m$ ；④反映破坏强度准则的参数s, $σ_{c}$ ；⑤反映剪胀关系的参数β。上述模型参数可以根据确定完整岩石、流体和岩石经典损伤模型力学参数相同的方法来确定^{[11, 30-31]}。

杨红伟采用美国制造的MTS815岩石力学实验系统对三峡库区三叠系上统徐家河的细粒砂岩进行了三轴试验^[32],试验数据如图1中离散点所示,砂岩孔隙率为0.109,粒径0.1～0.5 mm,主要成分为石英、长石、燧石和白云母等。根据 $E_{H}$ 随围压和孔压的变化数据确定参数E_H0,a,b和 $χ$ ,根据峰值强度随有效应力变化数据确定参数s, $σ_{c}$ ,根据 $σ_{3}$ =5 MPa 和u=1 MPa试验曲线来率定损伤模型参数、塑性势参数、岩块基质体积模量和泊松比,所有模型参数：K_S为3.5k_H,K_F为2 GPa,E_H0为4.07 GPa,a为0.48,b为0.06, $χ$ 为0.109, $ν_{H}$ 为0.25,m为3.65,s为9.8 MPa, $σ_{c}$ 为60.8 MPa, $β$ =0.2。再根据这些参数来模拟所有试验曲线验证模型的客观性,模型计算模拟曲线和试验数据对比图见图1。

图 1 模型应力应变模拟曲线和试验数据对比

Figure 1. Comparison between simulated stress-strain curves by model and experimental data

下载: 全尺寸图片幻灯片

从图1可以看出,模型模拟曲线与试验数据比较吻合。当主应力差较小时,饱和岩石的总变形量和塑性变形量均较小,岩石轴向和横向变形大致随应力线性增加；当主应力差较大时,岩石轴向和横向变形继续增大,应力应变曲线呈现出非线性变化,产生明显的塑性变形和剪胀效应；当轴向应变继续增大时,剪胀效应更为明显,但饱和岩石承受的主应力差不再继续增加,而是出现峰值强度后迅速减小直至破坏。如图1所示,饱和岩石的这些主要力学特性均能在本文饱和岩石弹塑性模型中得到合理明确的反映。

3.2 浙江红砂岩三轴不排水剪切试验模拟

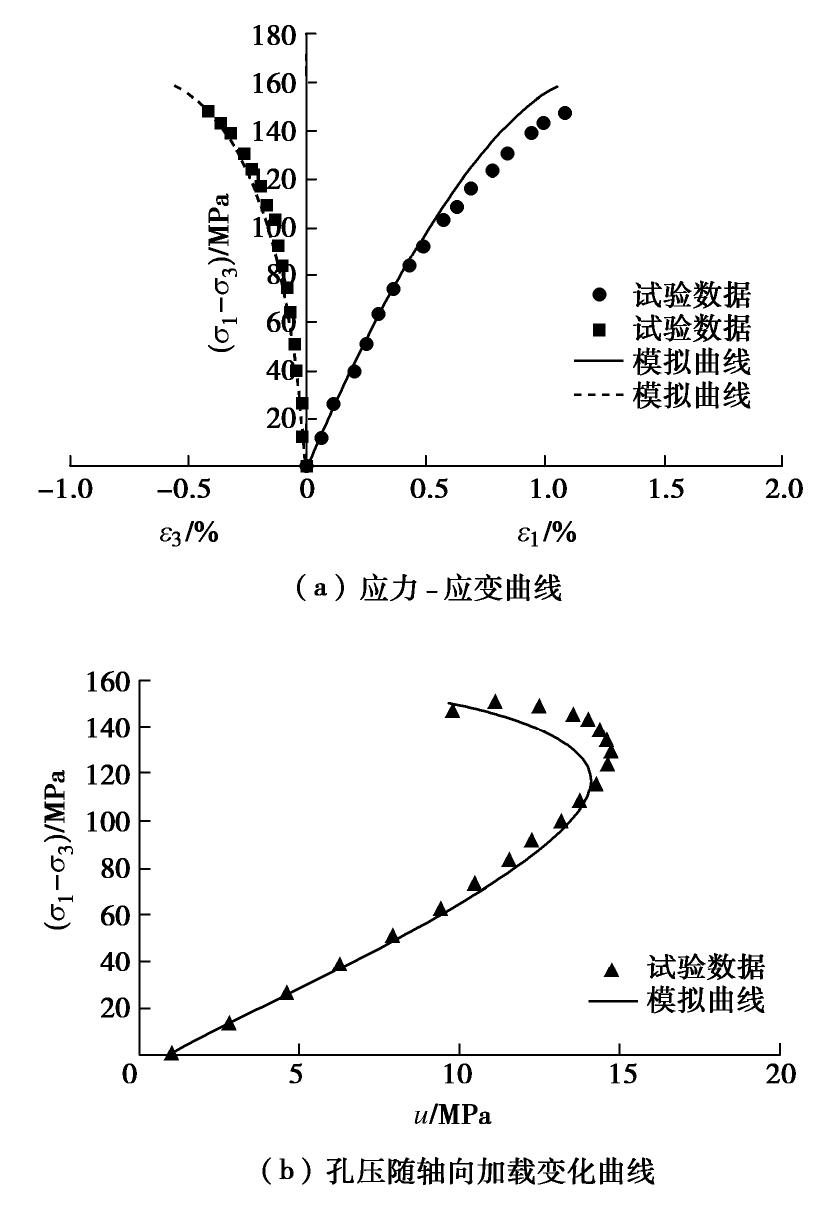
HU等^[10]对浙江红砂岩进行三轴不排水试验。现利用本文本构模型,对初始孔压力u₀=1 MPa、围压为30,50 MPa条件下得到的三轴不排水应力-应变曲线和孔隙水压力曲线进行数值模拟。该红砂岩孔隙率为0.12,模拟所用的模型参数：K_S为27.3 GPa,K_F为2 GPa,E_H0为24.0 GPa,a为0,b为0, $ν_{H}$ 为0.25,m为1.7,s为9.5 MPa, $σ_{c}$ 为63 MPa, $β$ 为0.1,参数先根据峰值强度随有效应力变化数据确定参数s, $σ_{c}$ ,然后根据 $σ_{3}$ =30 MPa试验曲线来率定无损伤弹性模量、损伤模型参数、塑性势参数、岩块基质体积模量和泊松比。再根据这些参数来模拟所有试验曲线验证模型的客观性,所得结果如图2,3所示。

图 2

$σ_{3}$ =30 MPa下模型模拟曲线和试验数据对比

Figure 2. Comparison between simulated curves by model and experimental data under

$σ_{3}$ of 30 MPa

下载: 全尺寸图片幻灯片

图 3

$σ_{3}$ =50 MPa下模型模拟曲线和试验数据对比

Figure 3. Comparison between simulated curve by model and experimental data under

$σ_{3}$ of 50 MPa

下载: 全尺寸图片幻灯片

从图2,3中可以看出：①模型能够比较准确地模拟岩石的受力变形性能,无论是轴向应变还是横向应变,应力-应变曲线峰前的弹性阶段和塑性阶段都得到了较为准确的描述。②由于饱和岩石具有明显的剪胀特性,在三轴不排水剪切过程中,岩石体应变呈现出从压缩到膨胀的过程,相应地孔隙水压力随着轴向加载呈现出先增大后减小的变化规律。本文模型能较好地模拟这一过程,图中孔隙水压力随剪切变化的模拟曲线与试验数据具有较好的一致性。

4. 结论

（1）由工程混合物理论和均匀化响应原理^{[16, 22-24]},提出“固相基质体应变决定固相基质压力,骨架弹性应变和塑性应变决定Terzaghi有效应力和耗散Terzaghi有效应力,流相基质体应变决定孔压”的饱和多孔介质本构规律。

（2）采用骨架应力、固相基质压力和流相基质压力作为本构应力变量,骨架应变、固相基质体应变和流相基质体应变作为本构应变变量,在已有的岩石损伤模型基础上,根据Hoek-Brown屈服准则和非关联流动准则,建立了饱和岩石弹塑性模型。在建模过程中,未采用Skempton有效应力,因而避免了采用Biot宏观力学理论建立非线性模型时难于确定Skempton有效应力中Biot参数的困难。

（3）把本文饱和岩石弹塑性模型用于模拟三轴排水和不排水试验,模拟曲线与试验曲线基本吻合,说明本文本构模型具备合理模拟饱和岩石受力变形和孔压变化的能力。

附录

达西是在静止状态下进行渗流试验的,不考虑体力,由混合物理论的流相动量守恒方程可得^[18]：

$\nabla (- n_{F} u) + {\hat{p}}_{F} = - n_{F} \nabla u - u \nabla n_{F} + {\hat{p}}_{F} = 0$ 。

(A1)

假定渗流耗散势函数为 $ϕ = n_{F} n_{F0} W_{F}^{2} / (2 b_{F})$ ,b_F是广义渗透系数,根据式（17）有

$u \nabla n_{F} - {\hat{p}}_{F} = \frac{\partial ϕ}{\partial W_{F}} = n_{F} n_{F0} W_{F} / b_{F}$ 。

(A2)

把式（A2）代入到式（A1）得

$n_{F0} W_{F} = - b_{F} \nabla u$ 。

(A3)

式（A3）即是达西试验的渗流方程式。

致谢: 感谢审稿专家提出的宝贵意见。笔者把本文所建立的饱和岩石本构模型称为“西湖/孤山模型”,以纪念这几十年来孤苦寂寥筚路蓝缕的科研生涯。

图 1 模型应力应变模拟曲线和试验数据对比

Figure 1. Comparison between simulated stress-strain curves by model and experimental data

下载: 全尺寸图片幻灯片

图 2 $σ_{3}$ $σ_{3}$ =30 MPa下模型模拟曲线和试验数据对比

Figure 2. Comparison between simulated curves by model and experimental data under $σ_{3}$ $σ_{3}$ of 30 MPa

下载: 全尺寸图片幻灯片

图 3 $σ_{3}$ $σ_{3}$ =50 MPa下模型模拟曲线和试验数据对比

Figure 3. Comparison between simulated curve by model and experimental data under $σ_{3}$ $σ_{3}$ of 50 MPa

下载: 全尺寸图片幻灯片

参考文献(32)

[1]	赵阳升. 多孔介质多场耦合作用及其工程响应[M]. 北京: 科学出版社, 2010. ZHAO Yang-sheng. Multi-field Coupling Action of Porous Media and its Application Responces[M]. Beijing: Science Press, 2010. (in Chinese)
[2]	王媛, 徐志英, 速宝玉. 裂隙岩体渗流与应力耦合分析的四自由度全耦合法[J]. 水利学报, 1998(7): 55-59. doi: 10.3321/j.issn:0559-9350.1998.07.012 WANG Yuan, XU Zhi-ying, SU Bao-yu. Four-freedom complete method for the seepage-stress coupled analysis in fissured rock masses[J]. Journal of Hydraulic Engineering, 1998(7): 55-59. (in Chinese) doi: 10.3321/j.issn:0559-9350.1998.07.012
[3]	盛金昌, 速宝玉, 王媛, 等. 裂隙岩体渗流-弹塑性应力耦合分析[J]. 岩石力学与工程学报, 2000, 19(3): 304-309. doi: 10.3321/j.issn:1000-6915.2000.03.010 SHENG Jin-chang, SU Bao-yu, WANG Yuan, et al. Coupling analysis of elasto-plastic stress and fluid flow in jointed rock masses[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(3): 304-309. (in Chinese) doi: 10.3321/j.issn:1000-6915.2000.03.010
[4]	李广信. 关于有效应力原理的几个问题[J]. 岩土工程学报, 2011, 33(2): 316-320. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201102028.htm LI Guang-xin. Some problems about principle of effective stress[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(2): 316-320. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201102028.htm
[5]	陈晶晶, 雷国辉. 决定饱和岩土材料变形的有效应力及孔压系数[J]. 岩土力学, 2012, 33(12): 3696-3703. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201212028.htm CHEN Jing-jing, LEI Guo-hui. Effective stress and pore pressure coefficient controlling the deformation of saturated geomaterials[J]. Rock and Soil Mechanics, 2012, 33(12): 3696-3703. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201212028.htm
[6]	张国新. 多孔连续介质渗透压力对变形应力影响的数值模拟方法探讨[J]. 水利学报, 2017, 48(6): 640-650. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201706002.htm ZHANG Guo-xin. Study on numerical simulation method used in analyzing the effect of seepage pressure in continuous medium with pores on deformation and stress[J]. Journal of Hydraulic Engineering, 2017, 48(6): 640-650. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201706002.htm
[7]	周创兵. 复杂岩体多场广义耦合分析导论[M]. 北京: 中国水利水电出版社, 2008. ZHOU Chuang-bing. An Introduction to Multi-Field Generalized Coupling Analysis on Complex Rock Mass[M]. Beijing: China Water & Power Press, 2008. (in Chinese)
[8]	许江, 杨红伟, 彭守建, 等. 孔隙水压力-围压作用下砂岩力学特性的试验研究[J]. 岩石力学与工程学报, 2010, 29(8): 1618-1623. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201008016.htm XU Jiang, YANG Hong-wei, PENG Shou-jian, et al. Experimental study of mechanical property of sandstone under pore water pressure and confining pressure[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1618-1623. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201008016.htm
[9]	张俊文, 宋治祥, 范文兵, 等. 应力-渗流耦合下砂岩力学行为与渗透特性试验研究[J]. 岩石力学与工程学报, 2019, 38(7): 1364-1372. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201907007.htm ZHANG Jun-wen, SONG Zhi-xiang, FAN Wen-bing, et al. Experimental study on mechanical behavior and permeability characteristics of sandstone under stress-seepage coupling[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(7): 1364-1372. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201907007.htm
[10]	HU D W, ZHOU H, ZHANG F, et al. Evolution of poroelastic properties and permeability in damaged sandstone[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(6): 962-973. doi: 10.1016/j.ijrmms.2010.06.007
[11]	王伟, 田振元, 朱其志, 等. 考虑孔隙水压力的岩石统计损伤本构模型研究[J]. 岩石力学与工程学报, 2015, 34(增刊2): 3676-3682. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2015S2008.htm WANG Wei, TIAN Zhen-yuan, ZHU Qi-zhi, et al. Study of statistical damage constitutive model for rock considering pore water pressure[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S2): 3676-3682. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2015S2008.htm
[12]	谢妮, 徐礼华, 邵建富, 等. 法向应力和水压力作用下岩石单裂隙水力耦合模型[J]. 岩石力学与工程学报, 2011, 30(增刊2): 3796-3803. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2011S2056.htm XIE Ni, XU Li-hua, SHAO Jian-fu, et al. Coupled hydro-mechanical modeling of rock fractures subject to both normal stress and fluid pressure[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(S2): 3796-3803. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2011S2056.htm
[13]	朱其志, 王岩岩, 仇晶晶, 等. 准脆性岩石水力耦合不排水多尺度本构模型[J]. 河海大学学报(自然科学版), 2018, 46(2): 165-170. https://www.cnki.com.cn/Article/CJFDTOTAL-HHDX201802014.htm ZHU Qi-zhi, WANG Yan-yan, QIU Jing-jing, et al. Multiscale hydro-mechanical constitutive model for qusi-brittle rocks under undrained condition[J]. Journal of Hohai University (Natural Sciences), 2018, 46(2): 165-170. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HHDX201802014.htm
[14]	CHEN Y F, HU S H, WEI K, et al. Experimental characterization and micromechanical modeling of damage-induced permeability variation in Beishan granite[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 71: 64-76.
[15]	陈正汉. 岩土力学的公理化理论体系[J]. 应用数学和力学, 1994, 15(10): 901-910. https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX410.007.htm CHEN Zheng-han. An axiomatics of geomechanics[J]. Applied Mathematics and Mechanics (English Edition), 1994, 15(10): 901-910. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX410.007.htm
[16]	陈正汉. 非饱和土与特殊土力学的基本理论研究[J]. 岩土工程学报, 2014, 36(2): 201-272. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201402002.htm CHEN Zheng-han. On basic theories of unsaturated soils and special soils[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(2): 201-272. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201402002.htm
[17]	HOULSBY G T. The work input to an unsaturated granular material[J]. Géotechnique, 1997, 47(1): 193-196.
[18]	BORJA R I. On the mechanical energy and effective stress in saturated and unsaturated porous continua[J]. International Journal of Solids and Structures, 2006, 43: 1764-1786.
[19]	赵成刚, 刘艳. 连续孔隙介质土力学及其在非饱和土本构关系中的应用[J]. 岩土工程学报, 2009, 31(9): 1324-1335. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200909005.htm ZHAO Cheng-gang, LIU Yan. Continuum porous medium soil mechanics and its application in constitutive relationship of unsaturated soils[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(9): 1324-1335. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC200909005.htm
[20]	刘艳, 赵成刚, 蔡国庆. 理性土力学与热力学[M]. 北京: 科学出版社, 2016: 66-84. LIU Yan, ZHAO Cheng-gang, CAI Guo-qing. Rational Soil Mechanics and Thermodynamics[M]. Beijing: Science Press, 2016: 66-84. (in Chinese)
[21]	胡亚元. 关于率无关塑性力学和广义塑性力学的评述[J]. 岩土工程学报, 2005, 27(1): 128-131. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC20050100N.htm HU Ya-yuan. Comment on rate-independent plasticity and generalized plasticity[J]. China Journal of Geotechnical Engineering, 2005, 27(1): 128-131. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC20050100N.htm
[22]	胡亚元. 饱和多孔介质的超黏弹性本构理论研究[J]. 应用数学和力学, 2016, 37(6): 584-598. https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX201606004.htm HU Ya-yuan. Study on the super viscoelastic constitutive theory for saturated porous media[J]. Applied Mathematics and Mechanics, 2016, 37(6): 584-598. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX201606004.htm
[23]	GEERTSMA J. The effect of fluid pressure decline on volumetric changes of porous rocks[J]. Society of Petroleum Transactions, 1957, 210: 331-339.
[24]	陈正汉, 谢定义, 刘祖典. 非饱和土固结的混合物理论(I)[J]. 应用数学和力学, 1993, 14(2): 127-137. https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX199302004.htm CHEN Zheng-han, XIE Ding-yi, LIU Zu-dian. Consolidation theory of unsaturated soil based on the theory of mixture(I)[J]. Applied Mathematics and Mechanics, 1993, 14(2): 127-137. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX199302004.htm
[25]	HU Ya-yuan. Isothermal hyperelastic model for saturated porous media based on poromechanics[C]//Proceedings of China-Europe Conference on Geotechnical Engineering (Volume 1), 2018, Springer.
[26]	胡亚元, 王超. 双应力变量的饱和多孔介质非线性体积本构关系[J]. 上海交通大学学报, 2019, 53(7): 797-804. https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT201907006.htm HU Ya-yuan, WANG chao. Nonlinear volumetric constitutive relations of saturated porous media in terms of double stress variables[J]. Journal of Shanghai Jiaotong University, 2019, 53(7): 797-804. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SHJT201907006.htm
[27]	LADE P V, DE Boer R. The concept of effective stress for soil, concrete and rock[J]. Géotechnique, 1997, 47(1): 61-78.
[28]	陈勉, 陈至达. 多重孔隙介质的有效应力定律[J]. 应用数学与物理学, 1999, 20(11): 1121-1127. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201901004.htm CHEN Mian, CHEN Zhi-da. Effective stress laws for multi-porosity media[J]. Applied Mathematics and Mechanics, 1999, 20(11): 1121-1127. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201901004.htm
[29]	胡亚元. 双变量耦合作用对非饱和岩土波动特性的影响研究[J]. 振动与冲击, 2018, 37(10): 208-217. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201810030.htm HU Ya-yuan. Effect of double-variable coupling on the fluctuating characteristics of unsaturated rock and soil[J]. Journal of Vibration and Shock, 2018, 37(10): 208-217. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDCJ201810030.htm
[30]	赵怡晴, 刘红岩, 吕淑然, 等. 基于宏观和细观缺陷耦合的节理岩体损伤本构模型[J]. 中南大学学报, 2015, 46(4): 1489-1496. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201504041.htm ZHAO Yi-qing, LIU Hong-yan, LU Shu-ran, et al. Damage constitutive model of jointed rock mass based on coupling of macroscopic and meso-scopic defects[J]. Journal of Central South University, 2015, 46(4): 1489-1496. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201504041.htm
[31]	曹文贵, 杨尚, 张超. 考虑弹性模量变化的岩石统计损伤本构模型[J]. 水文地质工程地质, 2017, 44(3): 42-48. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201703008.htm CAO Wen-gui, YANG Shang, ZHANG Chao. Astatistical damage constitutive model of rocks considering the variation of the elastic modulus[J]. Hydrogeology and Engineering Geology, 2017, 44(3): 42-48. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201703008.htm
[32]	杨红伟. 循环载荷作用下岩石与孔隙水耦合作用机理研究[D]. 重庆: 重庆大学, 2011. YANG Hong-wei. Study on Coupling Mechanism of Rock and Pore Water under Cyclic Loading[D]. Chongqing: Chongqing University, 2011. (in Chinese)

施引文献(16)

期刊类型引用(7)

1.	胡亚元，袁书行. 盐溶液饱和岩土的本构理论及在黏土中的应用. 岩土工程学报. 2024(02): 223-234 . 本站查看
2.	赵兴东. 黄金矿山深井开采研究进展与发展趋势. 黄金. 2024(08): 1-18 . 百度学术
3.	张菂，李源，张伟，赵伟乔，秦忠培，郭少峰. 2023年8月西代村跨断层短水准异常分析. 地震地磁观测与研究. 2024(06): 83-91 . 百度学术
4.	张根宝，张超，白允，杨楚卿. 空隙岩石非线性变形细观唯象分析及本构模型. 公路交通科技. 2023(02): 135-144 . 百度学术
5.	贺文海，王恒，赵佳鑫. 矿井辅助运输巷道底板数学模型构建及其力学特性研究. 煤炭技术. 2023(08): 17-21 . 百度学术
6.	胡亚元，周焕慧. 饱和块状混合回填土地基的一维固结分析. 岩土工程学报. 2022(04): 632-642 . 本站查看
7.	刘武，过申磊，陆倩，郑连阁，袁文俊. 基于TOUGHREACT的岩石水力损伤耦合数值模型研究. 岩土工程学报. 2021(07): 1306-1314+1380 . 本站查看