Analytical study on water inflow and pore water pressure of tunnels under drainage
-
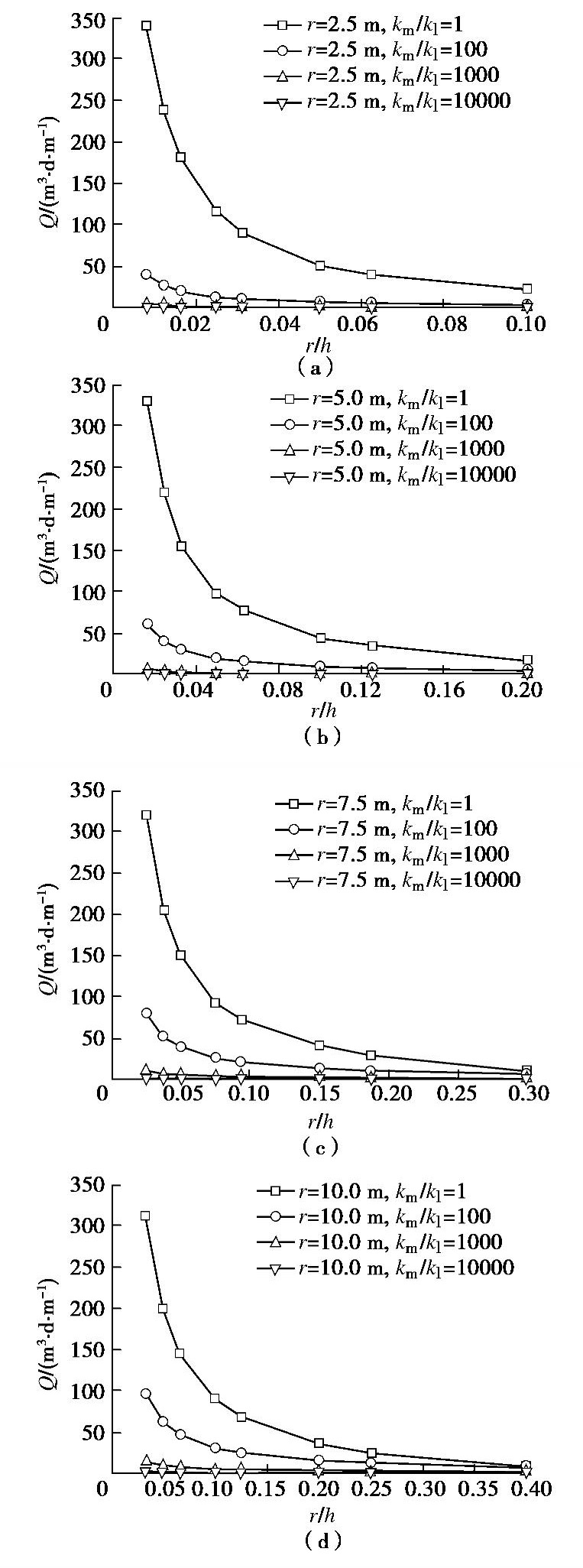
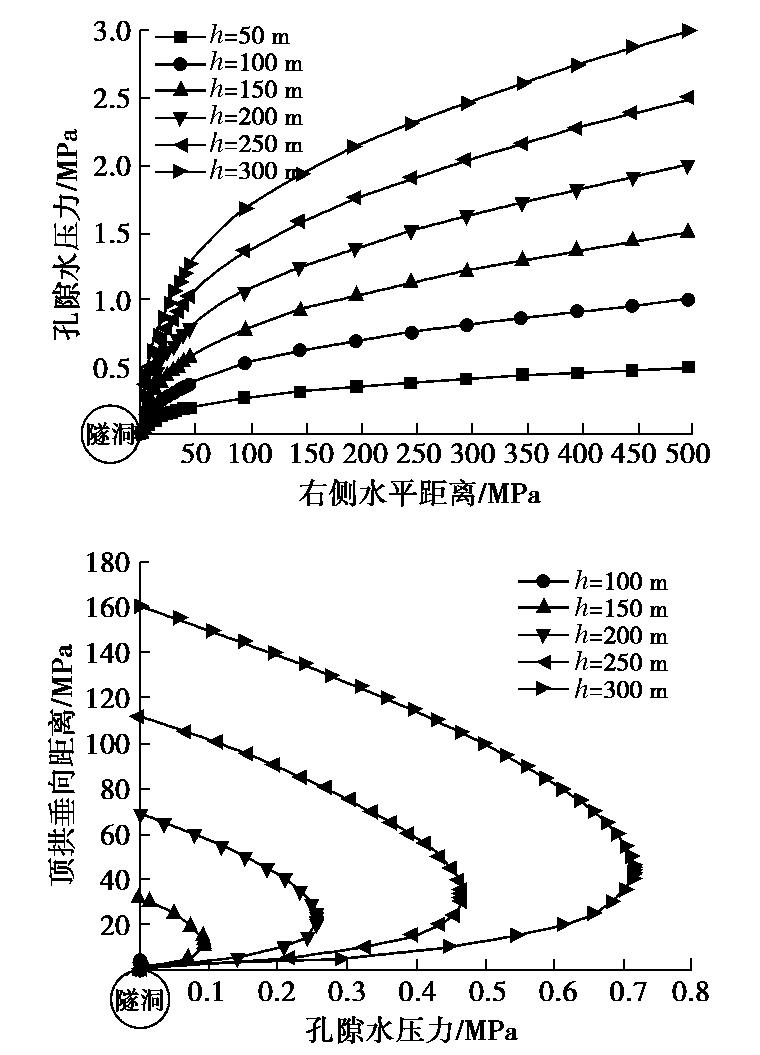
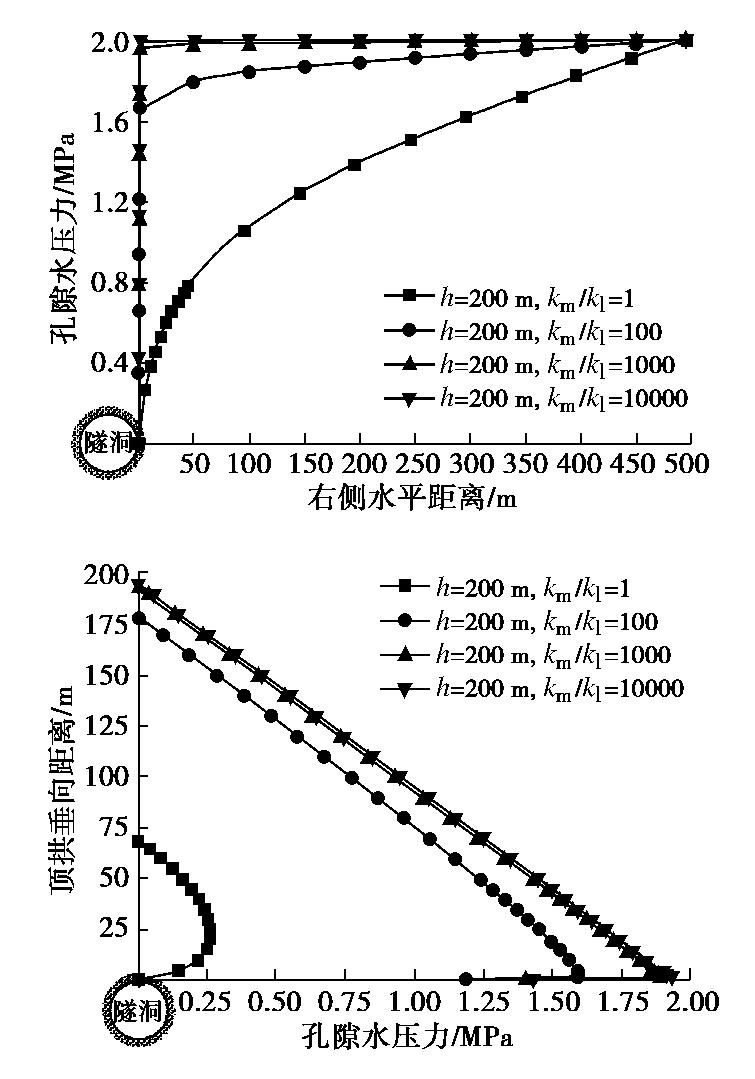
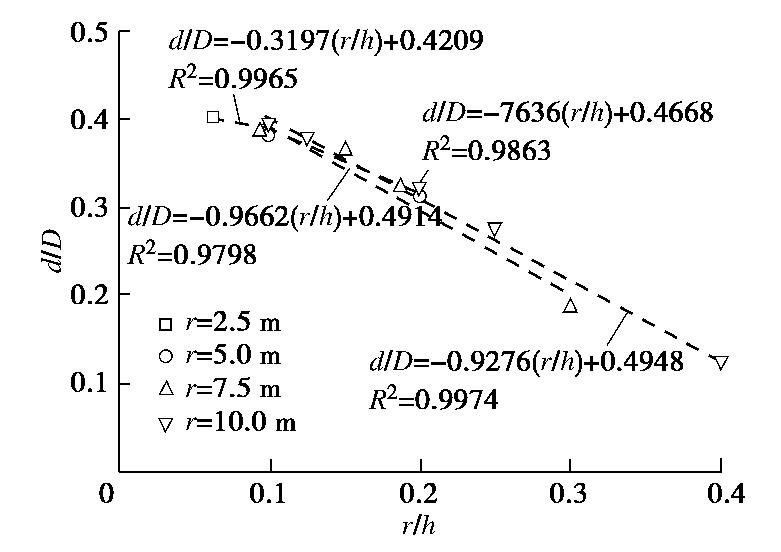
摘要: 隧洞涌水和孔隙水压力计算一直是地下工程领域最为关注的焦点问题,然而对于疏干条件下隧洞涌水量及衬孔隙水压力的变化规律仍未得到很好的解决。针对浅埋、深埋及衬砌隧洞分别进行解析分析,然后利用数值计算方法反算出关键参数(影响距离、等效地下水位及衬砌等效地下水位)的计算公式,进一步提出了隧洞涌水量的解析公式,探讨了孔隙水压力的分布规律。结果表明,疏干条件下隧洞涌水量取决于隧洞半径、初始地下水位高度及围岩与衬砌相对渗透性,其中围岩与衬砌相对渗透性起到决定性因素;衬砌圈显著改变了隧洞涌水量大小与外水压力分布规律,随着相对渗透性的增大,孔压解析解与数值解的拟合程度逐渐提高;通过与传统解析公式及数值的相互对比,提出的解析公式真实刻画了浅埋、深埋和衬砌隧洞渗流场特征,计算结果更加合理和准确。Abstract: The calculation of water inflow and pore water pressure of tunnels is always the focus of underground engineering. However, the effect of water inflow and pore water pressure of tunnels under drainage has not been well solved. The analytical analysis of shallow, deep and lined tunnels is carried out respectively. Then, the expressions for the key parameters (influencing distance, equivalent underground water level and equivalent underground water level of linings) are obtained by using the numerical method, and the analytical formulae for water inflow into tunnels are put forward. Finally, the distribution rules of pore water pressure are discussed. The results show that the water inflow into tunnels depends on the tunnel radius, the initial groundwater level and the relative permeability of the surrounding rock and linings, among which the relative permeability of the surrounding rock and linings plays a key role. The lining ring significantly changes the amount of water inflow and distribution of pore water pressure of tunnels. With the increase of the relative permeability, the fitting degree between the analytical solution and the numerical solution of pore water pressure increases gradually. Compared with traditional analytical solution and numerical solution, the proposed analytical formula more truly describes the seepage field characteristics of shallow, deep and lined tunnels, and the calculated results are more reasonable and accurate.
-
Keywords:
- tunnel /
- water inflow /
- pore water pressure /
- analytical formula /
- numerical simulation
-
0. 引言
中国地处环太平洋地震带以及欧亚地震带之间,其地震活动呈现出高频性、高强度、浅震源等特点,当地震发生在人口稠密的地区时,会带来惨重的经济和社会损失。对工程进行抗震研究,减轻地震灾害的影响将变得十分重要。
在对工程进行地震响应分析过程中,考虑到现实情况的复杂性,常采用数值方法进行计算[1]。动力时程分析法可以较好地揭示结构在地震全时段内的响应规律[2],随着计算机硬件设备的不断发展,该方法得到了一定的认可。应用有限元方法进行动力时程分析过程中,为降低计算成本,提高计算效率,往往要将地层取出规定大小的有限区域来进行计算,并在此区域外施加人工边界来模拟无限地基的情况[3]。其中人工边界包括无限元边界、黏性边界和黏弹性边界等形式,而黏弹性人工边界因具有好的低频和高频稳定性,应用方便,被广泛使用[4]。
在进行工程抗震分析时,根据波动理论,考虑到地壳密度随地层深度的增加而增加,普遍认为地震波在地表附近的传播方向接近竖向[5],故而常常探讨地震波在垂直入射下情况。但现实情况下,根据地层条件的不同,地震波往往存在一定的入射角度。Jin等[6]和Takahiro等[7]通过对各地震动记录进行反演分析,得出了不同的地震波入射角度。因此,若仅考虑垂直入射的情况对结构进行地震响应分析,或将带来不能忽视的误差[8]。因此,考虑地震波斜入射也具有一定的现实意义。而在此方面,许多学者[9-11]同样进行了很多相关的研究。
而对于水平层状场地地震波斜入射问题,刘晶波等[12-13]提出了一维化时域有限元计算方法;赵密等[14-15]和尹侯权等[16]利用弹性介质的应力–位移本构关系建立了人工边界处应力与速度的阻抗边界条件,替代黏性边界条件,改进P-SV波斜入射时成层半空间自由场的时域算法;王笃国等[17-18]应用频域传递矩阵结合等效线性化方法,求解了地震波斜入射下水平层状场地的地震响应。而直接运用黏弹性边界理论,因时间延迟计算较为繁琐,缺乏深入研究。
对于地震波斜入射中时间延迟的计算,目前普遍采用立体几何的方式对地震波路径逐一进行求解,或采用坐标变换[19]的方式对计算过程进行一定成度的简化。然而,当面对水平层状场地等特殊情况时,存在地震波多次反射和透射的情况,此方法不易迭代,计算成本较高。
对此,本文尝试建立一种新的时间延迟计算方法,以当前地震波属性表征其生成路径全过程上的时间延迟;在此基础上,推导黏弹性边界下水平层状场地地震波斜入射方法,进而实现合理有效的地震动数值计算。最后建立有限元计算模型,利用此方法对单脉冲作用下的数值解与理论解进行对比,验证方法的准确性和适用性。
1. 黏弹性边界地震动输入
黏弹性人工边界的思想就是将弹簧和黏滞阻尼器并联,形成一种弹簧-阻尼器物理元件,并将其施加在边界上。要使用这种边界,首先要将地震波转化成人工边界上各处所对应的等效荷载,其中包括产生内行场反应所需要抵抗的人工边界物理元件上的结点力,以及因产生内行场反应而需抵抗近场介质所需的结点力[20-21]。当黏弹性边界可以将计算区域内向外传播的散射波完全吸收时,人工边界的节点上便会形成因地震作用而产生的自由场运动。
这样,地震动的输入问题便转化为在人工边界的节点上所作用的自由场运动问题,通等效节点力的方式施加在所求模型的边界上。
等效节点力的计算公式为
Fb=(Kbub+Cb˙ub+σbn)Al。 (1) 在弹簧刚度矩阵Kb和阻尼系数矩阵Cb的取值方面,许多学者都进行了研究,同时给出了一定的建议,但不同方法对结果影响不大。对此,本文选用文献[22]的方法进行计算。
在水平层状场地的计算过程中,式(1)的自由场位移向量ub和自由场速度向量˙ub需要根据斯涅尔方程得到地震波在成层界面上的转换情况,并分析其与入射波之间的时空关系,进而利用波的叠加原理进行求解,这其中便涉及到时间延迟的计算问题。在此方面,当前的计算方法较为复杂,求解较为困难。下面针对水平层状场地时间延迟的计算进行分析。
2. 时间延迟计算方法
针对水平层状场地,本文假定各层地层均匀弹性,在水平方向上无限延伸。根据地震波波动理论可知,平面P波斜入射时,在地层界面处生成反射P波、反射SV波、透射P波和透射SV波;平面SV波斜入射时,如入射角度不超过临界角,将生成反射P波、反射SV波、透射P波和透射SV波。因此,为将时间延迟计算公式进行统一,在这里假设入射波为m,反射波n,透射波l,其中m,n,l为平面P波或平面SV波,入射波、反射波及透射波的方向角分别为α,β,γ,T0时刻入射波波前与入射波传播方向垂直,仅区分反射和透射两种情况进行讨论。
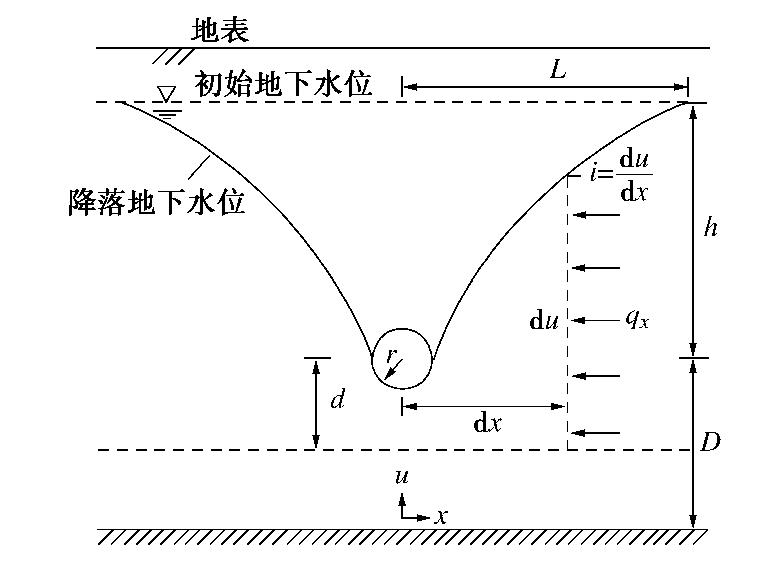
对反射波,如图 1所示,α和β满足:
sinαv1=sinβv2, (2) 式中,v1,v2分别为入射波m和反射波n在对应地层内的传播速度。
假设Xf(x0,y0)为所求模型边界上的一点,AB为零时刻的波前面,则反射波n在该点处的时间延迟为
Δt=t1+t2, (3) t1=ODv1, (4) t2=OXfv2, (5) 式中,t1,t2分别为计算所需入射波m和反射波n的时间延迟。
在此,过A点做ON垂线,与ON延长线交于点C。由几何关系得
OD=AOsinα, (6) OC=AOsinβ, (7) t1=ODv1=OCv2, (8) Δt=t1+t2=OC+OXfv2=CXfv2。 (9) 设点U(x1,y1)∈AC,则式(9)可改写为
Δt=1v2[(x1−x0)cosβ+(y1−y0)sinβ]。 (10) 对透射波,如图 2所示,α和γ满足:
sinαv1=sinγv3, (11) 式中,v3为透射波l在对应地层内的传播速度。
假设Xt(x2,y2)为所求模型边界上的一点,AB为零时刻的波前面,则透射波l在该点处的时间延迟为
Δt=t1+t3, (12) t1=ODv1, (13) t3=OXtv3, (14) 式中,t3为计算所需透射波的时间延迟。
在此,过A点做ON垂线,与ON延长线交于点C′。由几何关系得
OD=AOsinα, (15) OC′=AOsinγ, (16) t1=ODv1=OC′v3, (17) Δt=t1+t3=OC′+OXtv3=CXtv3。 (18) 设点V(x3,y3)∈AC′,式(18)可改写为
Δt=1v3((x3−x2)cosγ+(y3−y2)sinγ)。 (19) 至此,反射波n和透射波l的时间延迟计算公式中已经不含有其对应入射波m的任何参数,所有参数均为当前地震波的参数,且形式较为统一,便于进行迭代计算。
由于点U(x1,y1)∈AC,点V(x3,y3)∈AC′,不妨将其均取为波前与地层界面相交的A点,作为所求地震波的等效零时刻点,由此便可以得到时间延迟的计算公式为
Δti=1vi(Δxicosθi+Δyisinθi), (20) 式中,Δxi,Δyi为所求点与A点坐标差,θi为所求地震波传播方向与竖向的夹角,vi为所求地震波在对应地层中的传播速度。
将其引申至三维模型,如图 3所示,波前与地层界面相交于A1A2,故A点可为A1A2上的任意一点,为便于计算可将其设为特殊点。此时时间延迟计算公式:
Δti=1vi[ΔxiΔyiΔzi][cosαicosβicosγi], (21) 式中,αi,βi,γi分别为所求地震波传播方向与3个坐标轴的夹角。
3. 水平层状场地地震波斜入射
对于水平层状场地而言,地震波斜入射边界条件的计算重点在于等效节点力的求解上,而地震波在成层界面的反射透射导致其计算过程较为困难。因此,通过将上述时间延迟计算思路应用于水平层状场地的情况,采用迭代方式实现水平层状场地地震动的计算问题。
利用文献[23]中地震波在成层界面上的对应关系,在计算过程中,对任意地震波,可通过将其产生过程中每一次转换所得到的振幅比值进行连乘来记录其与原入射波之间的幅度比值,即Ei=∏AiBiCiDi。其中A,B,C,D分别表示同类反射波、转换反射波、同类透射波、转换透射波与入射波幅值的比值。同时,由于地震波遇到成层界面时将会发生反射和透射现象,故在实际计算过程中存在终止条件的选择问题。在此取计算精度δ,忽略所得地震波与原入射波的比值小于δ的分量(即Ei<δ)及其后的地震波。考虑到地震是扩散衰减的,应用此方法进行计算无需担心收敛问题。δ的大小将在一定程度上影响计算精度和计算时效,故应在对二者进行权衡,但与动力有限元计算相比,此处计算量占比较小,无需过多斟酌。对地震波求解完成后,即可进一步计算黏弹性边界上各个节点的节点力,并施加在模型上。计算流程如图 4所示。
以第k层地层边界面上的一点N(xn,yn,zn)为例,求解黏弹性边界水平层状场地地震波斜入射下的等效节点力。
假设Ⅰ1为该层地层中与Z轴正向夹角大于90°的平面P波,Ⅰ2为该层地层中与Z轴正向夹角小于90°的平面P波,Ⅰ3为该层地层中与Z轴正向夹角大于90°的平面SV波,Ⅰ4为该层地层中与Z轴正向夹角小于90°的平面SV波。计算过程中,应注意地震波传播过程中正方向的连续性,以保证公式的准确性。
假设u0为基岩入射波的位移时程,则N点处自由场位移:
uNx=∑i∈I1,I2Eiu0(t−Δti)sinαi+∑i∈I3,I4Eiu0(t−Δti)cosαi, (22) uNy=0, (23) uNz=−∑i∈I1Eiu0(t−Δti)cosαi+∑i∈I2Eiu0(t−Δti)cosαi+ ∑i∈I3Eiu0(t−Δti)sinαi−∑i∈I4Eiu0(t−Δti)sinαi 。 (24) 将式(22)~(24)对时间求导可以得到N点处自由场速度:
˙uNx=∑i∈I1,I2Ei˙u0(t−Δti)sinαi+∑i∈I3,I4Ei˙u0(t−Δti)cosαi, (25) ˙uNy=0, (26) ˙uNz=−∑i∈I1Ei˙u0(t−Δti)cosαi+∑i∈I2Ei˙u0(t−Δti)cosαi+ ∑i∈I3Ei˙u0(t−Δti)sinαi−∑i∈I4Ei˙u0(t−Δti)sinαi。 (27) 在计算自由场应力时,可以根据波的叠加效应分别对模型的每个侧面及底面进行分析。
当对模型任意一点(x,y,z),都有xn≥x时,N点处自由场应力:
σNx=−∑i∈I1,I2λk+2Gksin2αicpkEi˙u0(t−Δti)− ∑i∈I1,I2Gksin2αicskEi˙u0(t−Δti) , (28) σNy=0, (29) σNz=∑i∈I1Gksin2αicpkEi˙u0(t−Δti)−∑i∈I2Gksin2αicpk⋅Ei˙u0(t−Δti)+∑i∈I3Gkcos2αicskEi¨u0(t−Δti)− ∑i∈I4Gkcos2αicskEi˙u0(t−Δti) 。 (30) 当对模型任意一点(x,y,z),都有xn≤x时,N点处自由场应力:
σNx=∑i∈I1,I2λk+2Gksin2αicpkEi˙u0(t−Δti)+ ∑i∈I1,I2Gksin2αicskEi˙u0(t−Δti) , (31) σNy=0, (32) σNz=−∑i∈I1Gksin2αicpkEi˙u0(t−Δti)+∑i∈I2Gksin2αicpk⋅ Ei˙u0(t−Δti)−∑i∈I3Gkcos2αicskEi˙u0(t−Δti)+ ∑i∈I4Gkcos2αicskEi˙u0(t−Δti) 。 (33) 当对模型任意一点(x,y,z),都有yn≥y时,N点处自由场应力:
σNx=0, (34) σNy=−∑i∈I1,I2λkcpkEi˙u0(t−Δti), (35) σNz=0。 (36) 当对模型任意一点(x,y,z),都有yn≤y时,N点处自由场应力:
σNx=0, (37) σNy=∑i∈I1,I2λkcpkEi˙u0(t−Δti), (38) σNz=0。 (39) 当对模型任意一点(x,y,z),都有zn≤z时,N点处自由场应力:
σNx=−∑i∈I1Gksin2αicpkEi˙u0(t−Δti)+∑i∈I2Gksin2αicpk⋅ Ei˙u0(t−Δti)−∑i∈I3Gkcos2αicskEi˙u0(t−Δti)+ ∑i∈I4Gkcos2αicskEi˙u0(t−Δti) , (40) σNy=0, (41) σNz=∑i∈I1,I2λk+2Gkcos2αicpkEi˙u0(t−Δti)− ∑i∈I3,I4Gksin2αicskEi˙u0(t−Δti) 。 (42) 式(22)~(42)中的Δti可根据式(21)进行计算。将式(22)~(42)代入等效节点力的计算公式,即可求得黏弹性边界下分层地层地震波斜入射过程中施加在模型边界节点上的等效节点力。在此基础上,依托现有的黏弹性边界地震动输入理论,利用常用的有限元计算软件和计算方法,即可对水平层状场地进行地震动有限元分析。
4. 方法验证
为验证本文方法的有效性和准确性,使用相关有限元计算软件建立如图 5所示的计算模型。考虑两层水平层状场地结构进行模拟,模型上层H1=100 m,下层H2=150 m。长度L和宽度D均取250 m。采用T=0.25 s的狄拉克脉冲函数作为入射波,其位移的时程关系曲线如图 6所示,先考虑模型两层密度ρ1=ρ2=2.0×103 kg/m3,弹性模量E1=E2=1 GPa,泊松比μ1=μ2=0.2的特殊情况,取入射角α为10°,20°平面P波和α为5°,15°平面SV波作为入射波,输入的时间间隔取0.005 s,对比本文方法与文献[19]方法的异同。
分别采用两种方法得到有限元计算输入文件,图 7给出了文件的MD5计算结果,两种方法得到的MD5完全相同,说明文件一致,因此本文方法在有限次终止时与文献[19]方法的结果保持一致。
考虑一般情况,取上层密度ρ1=2.0×103 kg/m3,弹性模量E1=1 GPa,泊松比μ1=0.2;下层密度ρ2=2.0×103 kg/m3,泊松比μ2=0.2,弹性模量E2=1.5 GPa,分别取入射角α为10°,20°平面P波和α为5°,15°平面SV波作为入射波。
取δ=0.01,图 8给出了模型在不同角度及不同类型入射波下地表中点处的水平(X方向)和竖向(Z方向)的位移时程,并与理论解进行对比。理论解采用频域传递矩阵法[24]结合快速傅里叶变换得到[14]。从图中可以看出,模型解与理论解吻合较好,相对误差较小,说明此方法在求解水平层状场地地震波斜入射方面具有良好的精度和准确性。
图 9以入射角α=20°的平面P波为例给出了模型在不同时刻下的位移场云图,从图中可以看出,本文的方法所引起地层内部变形规律与边界一致,变化较为均匀合理,且云图中的位移角度与地震波的斜入射的理论值基本上是吻合的,验证了本方法在计算水平层状场地地震波斜入射过程中的可靠性。
5. 结论
(1)提出了新的时间延迟计算方法。使用解析方式推导时间延迟的计算公式,使公式更加简化。在进行时间延迟的求解过程中,可通过所求目标地震波的具体信息及其所在地层的具体条件直接求解,摒弃以往计算方式中对所求地震波的全部来源依次进行计算的方式,使时间延迟公式统一,增强时间延迟计算方法的适用性。
(2)推导了基于等效零时刻点迭代的水平层状场地地震波斜入射方法。对于黏弹性边界下水平层状场地地震波波动输入问题,推导了基于本文时间延迟计算方法的人工边界上等效节点力的计算公式,进而得到了黏弹性边界下水平层状场地地震动输入的计算公式,拓展了黏弹性边界理论在水平层状场地斜入射地震动上的应用。
(3)进行方法验证。使用该方法建立水平层状场地三维有限元模型,求解两层地层结构地震波斜入射下的响应。将结果与理论值进行对比,验证了该方法的准确性和实用性。
-
-
[1] 刘志春, 王梦恕. 隧道工程因素对地下水环境影响研究[J]. 岩土力学, 2015, 36(增刊2): 281-288. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2015S2038.htm LIU Zhi-chun, WANG Meng-shu. Research on impact of tunnel engineering factors on groundwater environment[J]. Rock and Soil Mechanics, 2015, 36(S2): 281-288. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2015S2038.htm
[2] 潘东东, 李术才, 许振浩, 等. 岩溶隧道承压隐伏溶洞突水模型试验与数值分析[J]. 岩土工程学报, 2018, 40(5): 828-836. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201805009.htm PAN Dong-dong, LI Shu-cai, XU Zhen-hao, et al. Model tests and numerical analysis for water inrush caused by karst caves filled with confined water in tunnels Chinese[J]. Journal of Geotechnical Engineering, 2018, 40(5): 828-836. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201805009.htm
[3] HARR M E, Groundwater and Seepage[M]. New York: Dover Publications, 1962: 249-264.
[4] 吴建, 周志芳, 李鸣威, 等. 隧洞涌水量预测计算方法研究进展[J]. 工程地质学报, 2019, 27(4): 890-902. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201904023.htm WU Jian, ZHOU Zhi-fang, LI Ming-wei, et al. Advance on the methods for predicting water inflow into tunnels[J]. Journal of Engineering Geology, 2019, 27(4): 890-902. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201904023.htm
[5] GOODMAN R E, MOYE D G, VAN SCHALKWYK A, et al. Ground Water Inflows During Tunnel Driving[M]. California: College of Engineering, University of California, 1964.
[6] LEI S. An analytical solution for steady flow into a Ttonnel[J]. Groundwater, 1999, 37(1): 23-26. doi: 10.1111/j.1745-6584.1999.tb00953.x
[7] RAYMER J H. Predicting groundwater inflow into hard-rock tunnels: estimating the high-end of the permeability distribution[C]//2001 Rapid Excavation and Tunneling Conference, 2001, Littleton: 1027-1038.
[8] EL TANI M. Circular tunnel in a semi-infinite aquifer[J]. Tunnelling and Underground Space Technology, 2003, 18(1): 49-55. doi: 10.1016/S0886-7798(02)00102-5
[9] MOON J, FERNANDEZ G. Effect of excavation-induced groundwater level drawdown on tunnel inflow in a jointed rock mass[J]. Engineering Geology, 2010, 110(3/4): 33-42.
[10] 苏凯, 陈锐, 周亚峰, 等. 圆形隧洞渗流量计算的解析方法及其应用[J]. 岩石力学与工程学报, 2017, 36(增刊1): 3332-3341. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2017S1024.htm SU Kai, CHEN Rui, ZHOU Ya-feng, et al. Analytical method for calculating the groundwater inflow of circular tunnel and its application[J]. Rock and Soil Mechanics, 2017, 36(S1): 3332-3341. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2017S1024.htm
[11] EL TANI M, KAMALI A, GHOLAMI M A. Analytic assessment of the water table drawdown, seepage, and back pressure at rudbar PSPP[J]. Rock Mechanics and Rock Engineering, 2019, 52(7): 2227-2243.
[12] HOOGHOUDT S B. Bijdragen Tot De Kennis Van Eenige Natuurkundige Grootheden Van Den Grond: Algemeene Beschouwing Van Het Probleem Van De Detailontwatering En De Infiltratie Door Middel Van Parallel Loopende Drains, Greppels, Slooten En Kanalen[R]. Hague: Algemeene Landsdrukkerij, 1940: 515-707.
[13] FERNANDEZ G, MOON J. Excavation-induced hydraulic conductivity reduction around a tunnel-part 1: Guideline for estimate of ground water inflow rate[J]. Tunnelling and Underground Space Technology, 2010, 25(5): 560-566.
[14] FERNANDEZ G, MOON J. Excavation-induced hydraulic conductivity reduction around a tunnel-part 2: Verification of proposed method using numerical modeling[J]. Tunnelling and Underground Space Technology, 2010, 25(5): 567-574.
[15] 周亚峰, 苏凯, 伍鹤皋. 水工隧洞钢筋混凝土衬砌外水压力取值方法研究[J]. 岩土力学, 2014, 35(增刊2): 198-203. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2014S2027.htm ZHOU Ya-feng, SU Kai, WU He-gao. Study of external water pressure estimation method for reinforced concrete lining of hydraulic tunnels[J]. Rock and Soil Mechanics, 2014, 35(S2): 198-203. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2014S2027.htm
[16] DAI Y, ZHOU Z. Steady seepage simulation of underground oil storage caverns based on Signorini type variational inequality formulation[J]. Geosciences Journal, 2015, 19(2): 341-355.
[17] 郑宏, 刘德富, 李焯, 等. 一个新的有自由面渗流问题的变分不等式提法[J]. 应用数学和力学, 2005, 26(3): 363-371. https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX200503016.htm ZHENG Hong, LIU De-fu, LEE C F, et al. New variational inequality formulation for seepage problems with free surfaces[J]. Applied Mathematics and Mechanics, 2005, 26(3): 363-371. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX200503016.htm
-
期刊类型引用(2)
1. 杜闯,高启辉,宋帅. 地震波斜入射下港珠澳大桥沉管隧道地震响应分析. 河北工业大学学报. 2024(03): 76-86 .  百度学术
百度学术
2. 邓捷程,吕龙,孙海忠,吕玺琳. 基于等效线性土体模型的地基与结构整体地震响应模拟. 结构工程师. 2023(03): 85-91 .  百度学术
百度学术
其他类型引用(0)




 下载:
下载: