Analysis of surface vibration effect on tunnel excavation section induced by tunneling blasting
-
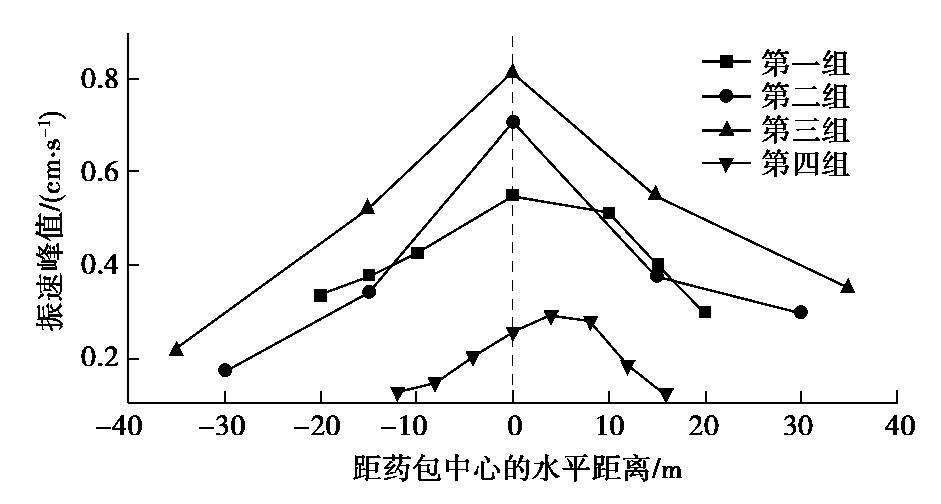
摘要: 针对目前在隧道已开挖区段地表振动效应理论研究的不足,从理论方面对隧道的地表振动效应进行了研究,并利用现场实测数据加以验证和分析。首先,对隧道掘进爆破模型进行简化,将掏槽孔的爆破简化为一系列球形药包的爆破,再利用保角映射将隧道已开挖段地表质点的振动问题转化为半空间内一系列球形药包的地表振动问题,最终得出已开挖段地表质点的振动速度计算方法。通过实际工程,对比了理论和实测的隧道轴线振速峰值分布曲线,验证了理论计算方法的可行性,同时利用理论计算方法探讨了隧道埋深对隧道轴线振速峰值的分布规律,发现隧道埋深较浅时,已开挖段振速峰值大于未开挖段的现象较明显,随着埋深的增加,该现象逐渐消失。Abstract: In view of the shortage of theories on the surface vibration effect in the excavated section of the tunnel, the surface vibration effect of the tunnel is analyzed based on theoretical and field measured data. Firstly, the blasting model for a tunnel is simplified, and the blasting of cut holes is simplified to a series of spherical charge blasting. Then the surface vibration in the excavated section of the tunnel is transformed into the surface vibration of spherical charge by conformal mapping. Finally, the method for calculating the vibration velocity of surface particles in the excavated section is obtained. Through practical projects, The feasibility of the theoretical method is verified by comparing the theoretical and measured peak velocity distribution curves. The distribution laws of the tunnel depth on the peak velocity of the tunnel axis are discussed by using the theoretical method. It is found that when the tunnel depth is shallow, the peak velocity of the excavated section larger than that of the unexcavated section is obvious. With the increase of the depth, the phenomenon gradually disappears.
-
Keywords:
- tunnel /
- blasting /
- vibration effect /
- excavation section /
- distribution of peak vibration velocity
-
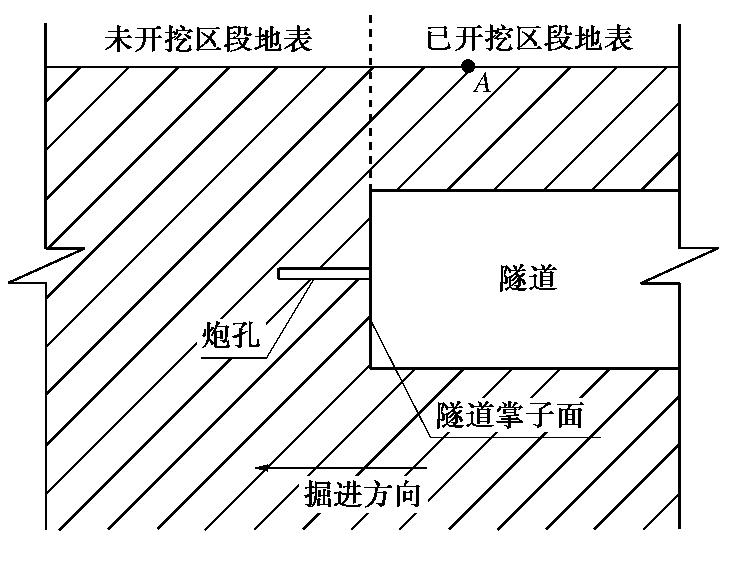
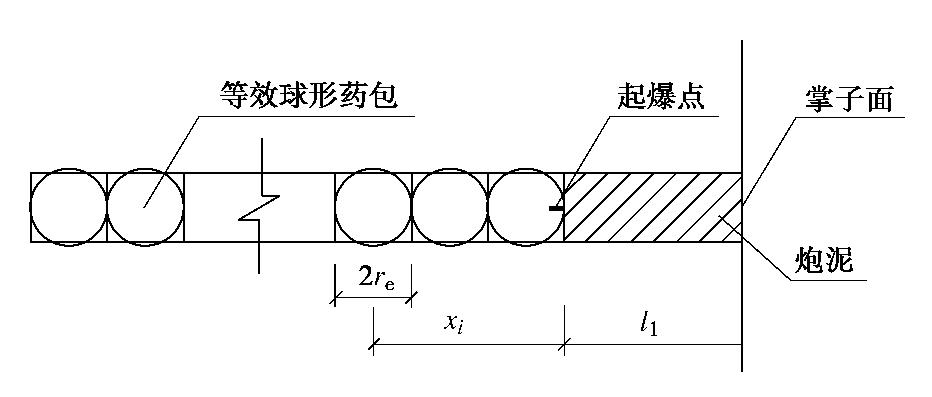
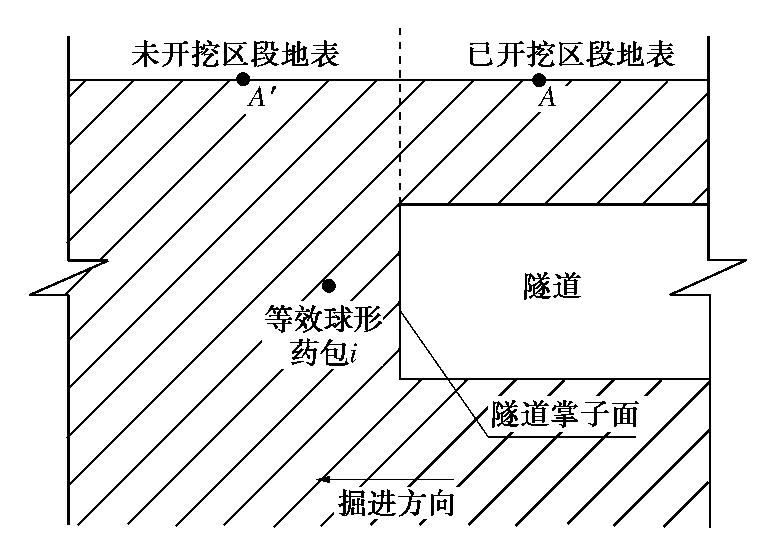
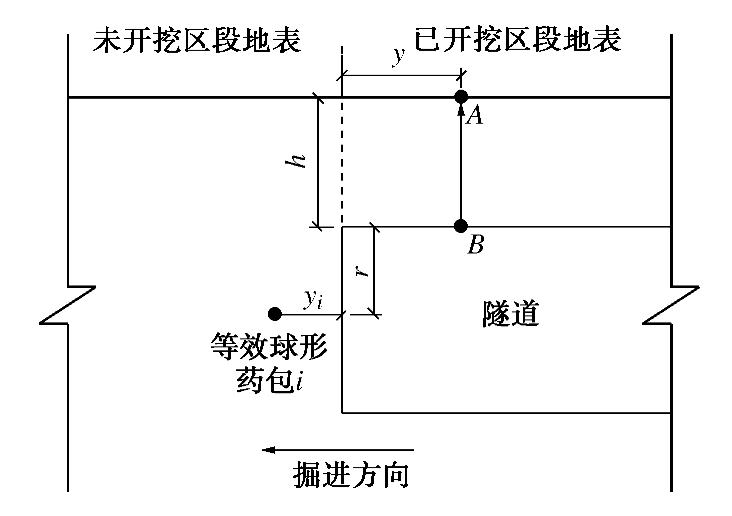
0. 引言
随着中国基础设施建设的快速发展，在非饱和盐渍土地区进行盐渍土的改良以及工程土障建设中，均涉及到水-热-气-传质等多物理场多相的耦合作用。Reshetin等[1]基于扩散定律和温度、湿度和蒸汽含量之间的函数关系，建立了关于温度场与湿度场的动力学数学模型，但数学模型中没有考虑非饱和土中水力梯度变化对耦合作用的影响。Jia等[2]在建立传热传质耦合模型时，考虑到水蒸汽对传热传质效应的影响。基于压力梯度和温度梯度等多种驱动因素建立了多种有关非饱和多孔介质的水-热耦合的数学模型，但忽略了非饱和多孔介质中水力梯度随时间和空间的变化规律且对气相的组分划分较为笼统[3-6]，Mohammad等[7]考虑干燥气体与水蒸气的迁移对能量守恒的影响，但在在能量迁移的方式中忽略了对流作用影响。He等[8]在非饱和土水-热-力多场耦合的数学模型，没有考虑多场多相耦合作用中溶质的存在对多孔介质中水分场、温度场迁移规律的影响。
多孔介质中水-热-盐迁移现象是各影响因素相互耦合的过程，且迁移规律随时间和空间不断变化。Cleall等[9]，HERNÁNDEZ-LÓPEZ等[10]通过试验孔隙的曲率因子和土体温度梯度的增强因子对水蒸汽通量有较大影响，Chen等[11]发现随着盐分在一端的大量聚集，溶液中的盐分会在盐分梯度作用下继续向该处迁移。周凤玺等[12-13]建立了完善热-湿-盐多物理场多相耦合的数学模型。但模型仅考虑均质非饱和多孔介质中的热湿盐多场耦合，并没有对复合非饱和土中的水-热-盐迁移规律进行进一步的研究且缺乏试验验证。
本文全面研究了复合非饱和土中的液态水、液相中的干燥气体和盐分以及孔隙中水蒸气等对水分场、盐分场和温度场随时间变化在空间上的分布规律的影响，并在能量守恒中考虑盐分、干燥气体以及各组分导热系数等分项对温度场的影响，建立了非稳态条件下复合非饱和土中多场多相耦合的状态方程。通过试验分单层验证了数学模型的准确性而后对复合非饱和土中水-盐-热的多场耦合问题进行参数分析。
1. 数学模型
1.1 质量守恒方程
$$ \frac{\partial ({\phi }^{\pi }{\rho }_{\alpha }^{\pi })}{\partial t}+\nabla \cdot ({\phi }^{\pi }{\rho }_{\alpha }^{\pi }{\boldsymbol{v}}^{\alpha })+\nabla \cdot {\boldsymbol{j}}_{\alpha }^{\pi }={\dot{m}}_{\alpha }^{\pi }\text{，} \text{，} $$ (1) 式中，$ {\boldsymbol{j}}_\alpha ^\pi $为α组分在π相的非对流通量矢量，$ {\phi ^\pi } $为π相的体积分数，$ \rho _\alpha ^\pi $为α组分在π相的质量分数，$ {{\boldsymbol{v}}^\alpha } $为α组分的速度矢量[12-13]。
由式（1）可得水分平衡方程为
$$ \frac{{\partial (n{S^{\text{l}}}\rho _{\text{w}}^{\text{l}})}}{{\partial t}} + \frac{{\partial (n{S^{\text{g}}}\rho _{\text{w}}^{\text{g}})}}{{\partial t}} + \nabla\cdot {\text{(}}n{S^{\text{g}}}\rho _{\text{w}}^{\text{g}}{{\boldsymbol{v}}^{\text{g}}}{\text{)}} + \nabla\cdot {\boldsymbol{j}}_{\text{w}}^{\text{g}} + \\ \;\;\;\;\;\nabla \cdot (n{S}^{\text{l}}{\rho }_{\text{w}}^{\text{l}}{\boldsymbol{v}}^{\text{l}})+\nabla \cdot ({\rho }_{\text{w}}^{\text{l}}{q}^{\text{l}})+\nabla \cdot ({\rho }_{\text{w}}^{\text{g}}{q}^{\text{g}})=0\text{ }\text{，} $$ (2) 式中，饱和度$ {S^{\text{l}}} $为孔隙水压力Pl与孔隙气压力Pg的函数，存在表达式Pl + Pg = 1。液相、气相通量[12-13]存在表达式：
$$ {q^{\bf{l}}} =- {K^{\bf{l}}}(\nabla {P_{\bf{l}}} + \rho _{\text{w}}^{\bf{l}}g) \text{，} $$ (3) $$ {q^\text{g}} =- {K^\text{g}}(\nabla {P_\text{g}} + {\rho ^\text{g}}g) \text{，} $$ (4) 式中，Kl，Kg为水动力参数[12-13]，g为重力加速度矢量。
非对流水通量遵循Philip等[14]所建立的模型，气相中水蒸汽非对流通量的变化可以归因于系统中水分的变化和系统中温度的变化：
$$ {\boldsymbol{j}}_{\text{w}}^{\text{g}} = {\boldsymbol{j}}_{{\text{vw}}}^{\text{g}} + {\boldsymbol{j}}_{{\text{vT}}}^{\text{g}} =- {D_{{\text{vw}}}}\nabla {P_{\text{l}}} + {D_{{\text{vw}}}}\nabla {P_{\text{g}}} - {D_{{\text{vT}}}}\nabla T 。 $$ (5) 其中由温度和水分引起的分子扩散系数存在表达式[12-13]：
$$ {D_{{\text{vT}}}} = n{S^{\text{g}}}\rho _{\text{w}}^{\text{g}}{D_{{\text{atm}}}}v\tau {f_{{\text{Tv}}}}\left[ {\frac{{4974.0}}{{{T^2}}} + \frac{{{M_{\text{w}}}\psi }}{{R{T^2}\rho _{\text{w}}^{\text{l}}}}} \right] \text{，} $$ (6) $$ {D_{{\text{vw}}}} = n{S^{\text{g}}}\rho _{\text{w}}^{\text{g}}{D_{{\text{atm}}}}v\tau \frac{{{M_{\text{w}}}}}{{RT\rho _{\text{w}}^{\text{l}}}} \text{，} $$ (7) 式中，Datm为水蒸汽分子的扩散系数，Datm = 2.16×10-5(T/273.15)1.8，τ为曲率因子[12-13]。
结合式（1）可得干燥气体的质量平衡方程为
$$ \frac{{\partial (nH{S^{\text{l}}}\rho _{\text{a}}^{\text{l}})}}{{\partial t}} + \nabla\cdot ({\phi ^{\text{l}}}\rho _{\text{a}}^{\text{l}}{{\boldsymbol{v}}^{\text{l}}}) + \nabla\cdot {\boldsymbol{j}}_{\text{a}}^{\text{l}} +\\ \;\;\;\;\;\; \frac{\partial (n{S}^{\text{g}}{\rho }_{\text{a}}^{\text{g}})}{\partial t}+\nabla \cdot ({\phi }^{\text{g}}{\rho }_{\text{a}}^{\text{g}}{v}^{\text{g}})+\nabla \cdot {j}_{\text{a}}^{\text{g}}=0\text{ }。 $$ (8) 干燥气体在液相中不发生扩散，即$ {\boldsymbol{j}}_{\text{a}}^{\text{l}} = 0 $。非对流项中的干燥气体的非对流通量与水蒸气的非对流通量存在表达式$ {\boldsymbol{j}}_{\text{a}}^{\text{g}} =- {\boldsymbol{j}}_{\text{w}}^{\text{g}} $，水中气体的密度存在[12-13]：
$$ \rho _{\text{a}}^{\text{l}} \approx \rho _{\text{a}}^{\text{g}} = {\rho _{\text{a}}} = \frac{{{M_{\text{a}}}}}{{RT}}({P_{\text{g}}} - {P_{\text{v}}}) \text{，} $$ (9) 式中，Pv为水蒸气压力，Ma为干气摩尔质量，R为气体常数。
结合式（1）可以得出液相中盐分的质量守恒方程为
$$ \frac{{\partial ({\phi ^{\text{l}}}\rho _{\text{p}}^{\text{l}})}}{{\partial t}} + \nabla\cdot (\rho _{\text{w}}^{\text{l}}\omega {q^{\text{l}}}) + \nabla\cdot {\boldsymbol{j}}_{\text{p}}^{\text{l}} = 0 。 $$ (10) 由于研究土壤液相中盐分得浓度较低，不考虑溶质的溶解与析出。液相中溶质非对流通量$ {\boldsymbol{j}}_{\text{p}}^{\text{l}} $可以表示为
$$ {\boldsymbol{j}}_{\text{p}}^{\text{l}} =- n{S^{\text{l}}}\rho _{\text{w}}^{\text{l}}\tau {D_{\text{p}}}\nabla \omega \text{，} $$ (11) 1.2 能量平衡方程
系统中能量平衡的一般形式为[15]
$$ \frac{{\partial {\mathit{\Phi} _\text{h}}}}{{\partial t}} + Q + \nabla\cdot {q_\text{h}} = 0 \text{，} $$ (12) 式中，Φh为内能，Q为潜热，$ \nabla\cdot {q_\text{h}} $表示热对流和传导。
考虑局部平衡以及不同组分温度相等的条件下，土壤的内能变化可表示为
$$ \frac{{\partial {\mathit{\Phi} _\text{h}}}}{{\partial t}} = \left[ {{\text{(}}1 - n{\text{)}}{\rho ^\text{s}}{c_\text{s}} + nH{S^\text{l}}{\rho _\text{a}}{c_\text{a}} + } \right. \\ \;\;\;\;\;\;\;\; n{S}^{\text{g}}{\rho }_{\text{a}}{c}_{\text{a}}+n{S}^{\text{l}}{\rho }_{\text{w}}^{\text{l}}{c}_{\text{w}}^{\text{l}}+n{S}^{\text{g}}{\rho }_{\text{w}}^{\text{g}}{c}_{\text{w}}^{\text{g}}]\frac{\partial T}{\partial t}\text{ }。 $$ (13) 在非饱和土中由汽化和凝结引起的能量变化可表示为
$$ Q = \dot m_\text{w}^\text{g}{H_{\text{gw}}} \text{，} $$ (14) 式中，$ {H_\text{gw}} $为液相中水分的汽化焓[16]，$ {H_{\text{gw}}} = {L_{\text{gw}}} - $ $ (c_\text{w}^\text{l} - c_\text{w}^\text{g}) $$ (T - {T_0}) $，$ \dot m_\text{w}^\text{g} $为蒸发率。
热流方程包括固相热传导、液相对流、气相对流，存在表达式[14]：
$$ \begin{aligned} q_{\mathrm{h}}= & q^{\mathrm{T}}+\rho_\alpha^\pi E_{\mathrm{T} \alpha}^\pi q^\alpha+E_{\mathrm{T} \alpha}^\pi {\boldsymbol{j}}_\alpha^\pi \\ = & -\left(\lambda_{\mathrm{s}}^{1-n} \lambda_{\mathrm{w}}^{n S^l} \lambda_{\mathrm{p}}^{n S^{\mathrm{p}}}\right) \nabla T+\left(\rho_a c_a+\rho_{\mathrm{w}}^{\mathrm{g}} c_{\mathrm{w}}^{\mathrm{g}}\right)\left(T-T_0\right) q^{\mathrm{g}}+ \\ & \left(c_{\mathrm{w}}^{\mathrm{g}}-c_a\right)\left(T-T_0\right) {\boldsymbol{j}}_{\mathrm{w}}^{\mathrm{g}}+c_{\mathrm{p}}^1 \boldsymbol{j}_{\mathrm{p}}^{\mathrm{1}}\left(T-T_0\right)+ \\ & \left(\rho_a c_a H+\rho_{\mathrm{w}}^1 c_{\mathrm{w}}^1\right)\left(T-T_0\right) q^1。 \end{aligned} $$ (15) 以往的研究忽略温度对溶液热容与导热系数的影响，溶液热容和导热系数与溶质的浓度有关[17]
$$ \left.\begin{array}{l} c_{\mathrm{w}}^{\prime}=\beta_2 c_{\mathrm{s}}+c_{\mathrm{w}}, \\ \lambda_{\mathrm{w}}=\beta_3 c_{\mathrm{s}}+\lambda_{\mathrm{l}}, \end{array}\right\}$$ (16) 式中，$ {\beta _2} $= -167，$ {\beta _3} $= 0.00493。
1.3 复合非饱和土非稳态问题求解
方程（2），（8），（10），（12）给出了复合非饱和土中水-气-盐-热多场耦合过程的控制方程，耦合方程是将孔隙水压力、孔隙气压力、温度、含盐率及其一阶偏导为未知量的封闭方程。将控制方程进行拉普拉斯变换后通过数值方法计算可得控制方程的频域解，而后基于Hausdoff矩问题将频域解$ u(x) $转化为时域解$ {q_N}(t) $。
Hausdoff矩问题存在积分关系式
$$ {\displaystyle {\int }_{0}^{1}{x}^{n}u(x)\text{d}x={\mu }_{n}}\text{ (}n=0,1,2,\cdot \cdot \cdot \text{) }。 $$ (17) Hausdorff矩问题是一个典型的不适定问题，$ u(x) $的正则化近似解为
$$ {p_N}(x) = \sum\limits_{i = 0}^N {{\lambda _i}{L_i}(x)} 。 $$ (18) 最终Laplace逆变换的近似解为
$$ {q_N}{\text{(}}t{\text{)}} \equiv {p_N}({{\text{e}}^{ - t}}) = \sum\limits_{i = 0}^N {{\lambda _i}{L_i}({{\text{e}}^{ - t}})} 。 $$ (19) 基于式（19）Hausdoff矩问题的稳定化算法获得Laplace逆变换的解。
2. 试验验证
试验采用的土样是取自甘肃省兰州市的粉质黏土，该土样的颗粒相对质量密度为2.70 g/cm3，渗透系数约为2.89×10-6 m/s。将土样压制成高为280 mm、直径为200 mm，试验土柱的孔隙率n为0.3。初始时刻试验土柱的温度为25℃，顶板与底板的温度分别设为30，15℃。两端的孔隙气压力为101 kPa、初始质量含水率为10 %、初始含盐率为7%。
表 1，2分别给出了试验粉质黏土土样各物理成分的热力学参数和Van Genuchten（VG）模型[13，15]参数。经试验和计算可得粉质黏土土样在VG模型中所对应的拟合参数分别为nvg=1.69，mvg=0.0147。图 1~3分别给出了试样中水分，盐分和温度的分布规律，并与本文所提出的教学模型进行验证，两者吻合较好。
表 1 多孔介质中各物理成分的热力学参数Table 1. Thermodynamic parameters of physical components in porous media参数 数值 参数 数值 $ {c_{\text{a}}} $/(J·kg-1·K-1) 1000 $ {L_{{\text{gw}}}} $/(J·kg-1) 2413000 $ c_{\text{w}}^{\text{l}} $/(J·kg-1·K-1) 4180 $ {k_0} $/(m·s-1) 2.89×10-6 $ c_{\text{w}}^{\text{g}} $/(J·kg-1·K-1) 1900 g/(m·s-2) 9.8 $ c_{\text{p}}^{\text{l}} $/(J·kg-1·K-1) 3750 $ \rho _{\text{w}}^{\text{g}} $/(kg-1·m-3) 1000 $ {\lambda _{\text{g}}} $/(W·m-1·K-1) 0.024 $ {M_{\text{a}}} $/(kg-1·mol-1） 0.0288 $ {\lambda _{\text{s}}} $/(W·m-1·K-1) 2.93 $ {M_{\text{w}}} $/(kg-1·mol-1) 0.018016 $ {\lambda _{\text{l}}} $/(W·m-1·K-1) 0.56 $ R $/(J·mol-1·K-1) 8.3144 表 2 粉质黏土VG模型参数Table 2. VG model parameters of silty clay参数 数值 参数 数值 $ n $ 0.3 $ {n_{{\text{vg}}}} $ 1.698 $ S_{{\text{res}}}^{\text{l}} $ 0.15 v 1.4 $ S_{{\text{sat}}}^{\text{l}} $ 0.85 $ {f_{\tau {\text{v}}}} $ 1.2 $ {m_{{\text{vg}}}} $ 0.411 $ {P_{\text{s}}} $/kPa 68 3. 参数分析
表 2，3[18]分别给出了粉质黏土与砂土的VG模型参数。非饱和黏土上覆非饱和砂土的高度为300 mm保持不变，对砂土不同厚度、渗透系数等条件下复合非饱和土中的水分、盐分随时间变化的分布情况以及变化规律进行分析。砂土的孔隙率为0.5，上覆粉质黏土的孔隙率为0.3、土体上下边界的温度分别为27℃，3℃，上下边界的孔隙气压力均为102 kPa。复合非饱和土初始时刻的温度为15℃、初始时刻的孔隙气压力为102 kPa，为了让迁移规律更加明显砂土与黏土中初始的孔隙水压力设为-800 kPa、含盐率为0.12%。
表 3 砂土的VG模型参数Table 3. VG model parameters of sand soil参数 数值 参数 数值 n 0.5 $ {n_{{\text{vg}}}} $ 2.45 $ S_{{\text{res}}}^{\text{l}} $ 0.07 v 2 $ S_{{\text{sat}}}^{\text{l}} $ 0.93 $ {f_{\tau {\text{v}}}} $ 1.4 $ {m_{{\text{vg}}}} $ 0.59 $ {P_{\text{s}}} $/kPa 32 图 4，5分别给出了在砂土厚度分别为50，100，150 mm，且复合非饱和土厚度始终为300 mm条件下，复合土体中孔压和溶质的分布情况。从图 4中可以明显地看出随着砂土厚度的增加，复合土体中砂土中的盐分是降低的。图 5给出了距热端25，75，125，75，225，275 mm位置处复合非饱和土孔隙水压力随时间的变化情况。随着砂土厚度增大，相同位置处复合非饱和土热端的孔隙水压力越小，继而含水率越小。当孔隙率为0.5的砂土厚度越大，砂土对复合非饱和土中盐分迁移和水分迁移阻碍能力就越大。
![]()
图 4 不同砂土厚度下含盐率的变化Figure 4. Variation of salt content under different sand thicknesses![]()
图 5 不同砂土厚度下不同位置处孔隙水压力随时间变化Figure 5. Variation of pore water pressure with time at different locations under different sand thicknesses为了分析砂土渗透系数对复合非饱和土中水-热-盐耦合行为的影响，当砂土与粉质黏土的孔隙率以及复合非饱和土体的边界和初始条件保持不变。图 6绘出了砂土厚度为100 mm，复合非饱和土厚度为300 mm，砂土的渗透系数分别为1.2×10-4，4.2×10-4，8.2×10-4 m/s条件下，复合非饱和土体中盐分的变化情况。由图中曲线可以看出：随着砂土渗透系数的增大，复合非饱和土热端处溶液中的盐分浓度是增加。图 7给出了距低温端25，75，125，175，225，275 mm位置处孔隙水压力随时间的变化情况，随着砂土渗透系数增大，相同位置处复合非饱和土热端处的孔隙水压力越小，继而含水率越小。
![]()
图 6 不同渗透系数下含盐率的变化Figure 6. Change of salt content under different permeability coefficients![]()
图 7 不同渗透系数下不同位置处孔隙水压力随时间变化Figure 7. Change of pore water pressure with time at different positions under different permeability coefficients4. 结论
文章建立了完善的双层非饱和多孔介质中水-热-盐耦合运移的数学模型，并进行相应的参数分析和试验研究。
（1）复合非饱和土中，盐分在温度梯度的作用下逐渐向热端聚集，水分在温度梯度的作用下逐渐向冷端聚集。
（2）随着砂土厚度的增大，复合非饱和土低温端聚集的水分是逐渐增加的，高温端的水分是逐渐减少的。高温端砂土中聚集的盐分会随着砂土厚度的增大而逐渐降低，低温端粉质黏土中的盐分随着砂土厚度的增大而增加。
（3）随着砂土渗透系数的增大，复合非饱和土低温端的水分降低。高温端砂土中聚集的盐分会随着砂土渗透系数的增大而逐渐增加，低温端粉质黏土中的盐分随着砂土渗透系数的增大而减小。
-
![]()
图 7 测振仪器部分测点布置图
Figure 7. Layout of partial measuring points of vibration measuring instruments
![]()
图 9 不同埋深下隧道轴线振速峰值分布图
Figure 9. Distribution of peak vibration velocity along tunnel axis under different burial depths
表 1 各级岩石的
β 取值Table 1 Values of
β of rock at each level参数 岩体类别 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ RMR 81~100 61~80 41~60 21~40 0~20 β 0~19 20~39 40~59 60~79 80~100 
下载: 导出CSV
-
[1] 张自光, 仇文革, 陈瑜嘉. 花岗岩地层地铁隧道爆破施工地表振动效应随埋深变化规律研究[J]. 四川建筑科学研究, 2015, 41(2): 115-119. https://www.cnki.com.cn/Article/CJFDTOTAL-ACZJ201502031.htm ZHANG Zi-guang, QIU Wen-ge, CHEN Yu-jia. Study on the law of vibration effects of ground resulted from blasting construction varying with buried depth of metro tunnels in granite stratum[J]. Sichuan Building Science, 2015, 41(2): 115-119. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ACZJ201502031.htm
[2] 张震, 周传波, 路世伟, 等. 超浅埋地铁站通道爆破暗挖地表振动传播特征[J]. 中南大学学报(自然科学版), 2017, 48(8): 2119-2125. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201708021.htm ZHANG Zhen, ZHOU Chuan-bo, LU Shi-wei, et al. Propagation characteristics of ground vibration induced by subsurface blasting excavation in an ultra-shallow buried underpass[J]. Journal of Central South University (Science and Technology), 2017, 48(8): 2119-2125. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201708021.htm
[3] 王超, 周传波, 路世伟, 等. 城市暗挖隧道爆破地震波传播规律研究[J]. 科学技术与工程, 2017, 17(6): 158-162. doi: 10.3969/j.issn.1671-1815.2017.06.028 WANG Chao, ZHOU Chuan-bo, LU Shi-wei, et al. Propagation pattern of blasting vibration in the surrounding rock of metro tunnel[J]. Science Technology and Engineering, 2017, 17(6): 158-162. (in Chinese) doi: 10.3969/j.issn.1671-1815.2017.06.028
[4] 樊浩博, 邱军领, 谢永利, 等. 下穿村庄隧道爆破振动对地表建筑的影响[J]. 解放军理工大学学报(自然科学版), 2016, 17(3): 209-214. https://www.cnki.com.cn/Article/CJFDTOTAL-JFJL201603002.htm FAN Hao-bo, QIU Jun-ling, XIE Yong-li, et al. Blast-induced ground vibration from tunnel under crossing a village[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2016, 17(3): 209-214. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JFJL201603002.htm
[5] 张继春, 曹孝君, 郑爽英, 等. 浅埋隧道掘进爆破的地表震动效应试验研究[J]. 岩石力学与工程学报, 2005, 24(22): 4158-4163. doi: 10.3321/j.issn:1000-6915.2005.22.024 ZHANG Ji-chun, CAO Xiao-jun, ZHEN Shuang-ying, et al. Experimental study on vibration effects of ground due to shallow tunnel blasting[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(22): 4158-4163. (in Chinese) doi: 10.3321/j.issn:1000-6915.2005.22.024
[6] 郭建群, 张继春, 许海亮, 等. 人和场隧道掘进爆破的地震效应试验研究[J]. 中国铁道科学, 2003, 24(4): 92-95. doi: 10.3321/j.issn:1001-4632.2003.04.018 GUO Jian-qun, ZHANG Ji-chun, XU Hai-liang, et al. Seismic effects on drive-blasting in renhechang tunnel[J]. China Railway Science, 2003, 24(4): 92-95. (in Chinese) doi: 10.3321/j.issn:1001-4632.2003.04.018
[7] 许海亮. 浅埋隧道掘进爆破地震效应试验研究[D]. 成都: 西南交通大学, 2003: 33-36. XU Hai-liang. The Experimental Investigation on Seismic Effect of Shallow Tunnels[D]. Chengdu: Southwest Jiaotong University, 2003: 33-36. (in Chinese)
[8] 曹孝君. 浅埋隧道爆破的地表震动效应研究[D]. 成都: 西南交通大学, 2006: 59-71. CAO Xiao-jun. Study on Viberation Effects of Ground Resulted from Blasting in Shallow Tunnel[D]. Chengdu: Southwest Jiaotong University, 2006: 59-71. (in Chinese)
[9] 冯阳阳. 浅埋隧道爆破地表振动传播规律试验研究[D]. 成都: 西南科技大学, 2015: 21-27. FENG Yang-yang. Experimental Study on Ground Vibration Propagation Law of Shallow Buried Tunnel[D]. Chengdu: Southwest University of Science and Technology, 2015: 21-27. (in Chinese)
[10] 邹新宽, 张继春, 潘强, 等. 浅埋小净距隧道掘进爆破引起的地表振动特性模拟分析[J]. 防灾减灾工程学报, 2016, 36(4): 646-651. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201604021.htm ZOU Xin-kuan, ZHANG Ji-chun, PAN Qiang, et al. Ground vibration analysis of shallow-buried and small-interval tunnel resulting from blasting by numerical simulation[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(4): 646-651. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201604021.htm
[11] 刘光汉, 周建敏, 余红兵. 浅埋隧道掘进爆破空洞效应研究[J]. 采矿技术, 2017, 17(5): 112-113. https://www.cnki.com.cn/Article/CJFDTOTAL-SJCK201705038.htm LIU Guang-han, ZHOU Jian-min, YU Bing-hong. Study on cavity effect of blasting in shallow tunnel[J]. Mining Technology, 2017, 17(5): 112-113. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJCK201705038.htm
[12] 肖文芳, 李宇珅, 方凯明, 等. 地铁隧道钻爆施工地表振动速度特征研究[J]. 工程爆破, 2018, 24(1): 72-77. https://www.cnki.com.cn/Article/CJFDTOTAL-GCBP201801012.htm XIAO Wen-fang, LI Yu-sheng, FANG Kai-ming, et al. Study on vibration velocity effects of ground induced by metro tunnel drilling and blasting construction[J]. Engineering Blasting, 2018, 24(1): 72-77. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCBP201801012.htm
[13] 王海亮, 陈吉辉. 隧道上台阶分区爆破振动规律[J]. 山东科技大学学报(自然科学版), 2018, 37(3): 43-50. https://www.cnki.com.cn/Article/CJFDTOTAL-SDKY201803006.htm WANG Hai-liang, CHEN Ji-hui. Vibration law of partition blasting in upper bench of tunnel[J]. Journal of Shandong University of Science and Technology (Natural Science), 2018, 37(3): 43-50. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SDKY201803006.htm
[14] 傅洪贤, 赵勇, 谢晋水, 等. 隧道爆破近区爆破振动测试研究[J]. 岩石力学与工程学报, 2011, 30(2): 335-340. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201102017.htm FU Hong-xian, ZHAO Yong, XIE Jin-shui, et al. Study of blasting vibration test of area near tunnel blasting source[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(2): 335-340. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201102017.htm
[15] 刘小鸣, 陈士海. 隧道掘进中掏槽孔爆破引起的地表振动波形预测[J]. 岩土工程学报, 2019, 41(9): 1731-1737. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909020.htm LIU Xiao-ming, CHEN Shi-hai. Prediction of surface vibration waveform caused by cuthole blasting in tunnel excavation[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1731-1737. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909020.htm
[16] 刘小鸣, 陈士海. 群孔微差爆破的地表振动波形预测及其效应分析[J]. 岩土工程学报, 2020, 42(3): 551-560. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202003022.htm LIU Xiao-ming, CHEN Shi-hai. Prediction and effect analysis of surface vibration waveform for group hole delay blasting[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(3): 551-560. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202003022.htm
计量
- 文章访问数: 285
- HTML全文浏览量: 24
- PDF下载量: 125
