基于统计损伤原理的岩石加速蠕变模型研究

刘文博; 张树光; 陈雷; 孙博一; 路平平

doi:10.11779/CJGE202009014

基于统计损伤原理的岩石加速蠕变模型研究 English Version

刘文博^{1, 3,},
张树光^{1, 2, ,},
陈雷³,
孙博一³,
路平平³

1.
广西岩土力学与工程重点实验室,广西　桂林　541004
2.
桂林理工大学土木与建筑工程学院,广西　桂林　541004
3.
辽宁工程技术大学土木工程学院,辽宁　阜新　123000

基金项目:

国家自然科学基金项目 51274109

广西自然科学基金项目 2020GXNSFAA159125

详细信息

作者简介:
刘文博(1990—),男,甘肃兰州人,博士研究生,主要从事岩石力学与地下工程方面的工作。E-mail：15393162288@163.com

通讯作者:
张树光, E-mail：zhangshuguang168@163.com

中图分类号: TU451
计量
- 文章访问数: 384
- HTML全文浏览量: 37
- PDF下载量: 164
出版历程
- 收稿日期: 2019-11-05
- 网络出版日期: 2022-12-07
- 刊出日期: 2020-08-31

Accelerated creep model for rock based on statistical damage principle

LIU Wen-bo^{1, 3,},
ZHANG Shu-guang^{1, 2, ,},
CHEN Lei³,
SUN Bo-yi³,
LU Ping-ping³

1.
Guangxi Key Laboratory of Geomechanics and Geotechnical Engineering, Guilin 541004, China
2.
School of Civil and Architectural Engineering, Guilin University of Technology, Guilin 541000, China
3.
School of Civil Engineering, Liaoning Technical University, Fuxin 123000, China

摘要

摘要: 针对现有蠕变理论模型无法较好地描述岩石黏塑性阶段的加速蠕变特性及如何确定岩石加速蠕变阶段的启动条件等问题,对取自阜新恒大煤矿深部围岩开展了室内三轴蠕变试验,分析了岩石在蠕变变形规律。为了使建立的模型不仅较好地描述岩石蠕变特性,也可以较好与经典蠕变曲线各阶段相对应,通过经典的蠕变变形示意定义了各个分段临界点的指标,进而建立了一种考虑加速蠕变变形的新型岩石黏弹塑性蠕变模型。结果表明：在考虑岩土类内部缺陷发育的基础上,采用统计损伤理论来构建岩石加速蠕变模型,使得试验曲线也与模型曲线具有良好的吻合度,说明了基于统计损伤原理建立的岩石加速蠕变模型,来反映岩石蠕变全过程曲线是正确的；这也证明了采用统计损伤变量和经典蠕变曲线定义的临界点指标的正确性。岩石蠕变加载过程也是一种岩石内部微元体损伤破坏的过程,在材料微观结构上表现为不可逆性。通过将蠕变曲线分阶段,来定义分段临界点的损伤变量的表达形式,结合统计损伤理论和Perzyna黏塑性模型,对传统的西原体模型进行适当的改进,建立非线性蠕变损伤模型,从而更好地体现了损伤受岩石内部应力应变状态影响和损伤演化规律。
- 统计损伤理论 /
- 黏弹塑性蠕变模型 /
- 启动条件 /
- 加速蠕变 /
- 阈值
Abstract: Aiming at the problems that the existing creep theoretical models cannot describe the accelerated creep characteristics of the viscoplastic phase of rock and how to determine the start conditions of its accelerated creep phase, the triaxial creep tests are carried out on the deep surrounding rocks taken from Hengda Coal Mine of Fuxin. The creep deformation laws of rock are analyzed. In order to make the model describe the creep characteristics of the rock well and correspond to each stage of the classic creep curve, and by defining the index of each segment critical point based on the classical creep deformation, a new visco-elastoplastic creep model for rock considering accelerated creep is established. The results show that on the basis of considering the development of internal defects in rock and soil, the statistical damage theory can be used to formulate the accelerated creep model for rock. It is proved that the proposed model based on the statistical damage principle is correct in reflecting the whole curve of rock creep. The correctness of the critical point index defined by statistical damage variables and classic creep curves is also proved. The loading process of rock creep is also a kind of damage and destruction process of micro-elements inside the rock, which is irreversible in the material microstructure. By dividing the creep curve into stages, the expression form for the damage variable of the segmentation critical point is defined. By combining the statistical damage theory with the Perzyna viscoplastic model, the traditional Nishihara model is appropriately improved so as to establish the nonlinear creep damage model to better reflect the influences of the stress and strain state of the rock and the damage evolution laws.
- statistical damage theory /
- viscoelastic-plastic creep model /
- start condition /
- accelerated creep /
- threshold

HTML全文

0. 引言

砂岩等硬岩在深部复杂地质环境中呈现出的力学性质与在浅部地质环境中表现出的力学性质有所差异,例如硬岩在深部地质中呈现出浅部地质中未有的流变性质,以及力学特性由线性变化向非线性变化转化,故为了保证工程围岩的长期稳定性和工程中施工人员的安全,需要对岩石的流变性质进行深入研究^[1]。同时,岩石在外部荷载以及多因素耦合条件下的长期变形特性更加复杂,往往采用传统流变元件组合等方法建立的蠕变模型已经无法较好地描述岩石的变形特性。近年来学者们更多采用损伤理论、连续性力学等理论,通过建立一个可以反映岩石内部力学性质劣化的内变量,使得构建的流变模型更加科学合理^[2-3]。

近些年,学者们对岩石的流变特性以及如何建立一个合适可行的流变模型做出了以下研究：张树光等^[4]认为岩石材料的力学参数会随着应力和时间的双重影响产生劣化,构建了力学参数与应力和时间的关系式,进而建立了一种新的关于材料性质劣化的模型；杨秀荣等^[5]在大量含水岩石蠕变试验的基础上,发现了含水岩石的力学参数不仅在时间作用下产生劣化,而且其力学特性在岩石内部水分侵蚀作用下也会产生劣化,故在上述假设基础上建立了含水岩石的时效劣化蠕变模型；张泽林等^[6]为了得到含水率对泥岩长期变形特性的影响机制,采用引入含水率损伤元件的方法,建立出一种基于含水率影响的流变元件,并对其长期强度特性与含水率之间的关系进行了描述；梅胜尧等^[7]发现岩石在加速蠕变变形过程中,岩石内部裂隙的闭合对蠕变变形规律具有一定的影响,构建了一个裂隙闭合的元件,进而建立了符合含裂隙岩石的流变模型。

针对以往的流变模型研究,建立的模型虽然都可较好地描述岩石蠕变特性,但模型未能较好与经典蠕变曲线各阶段相对应,且未提出较为合适的蠕变分界点定义。因此,在开展岩石流变室内试验的基础上,对岩石的流变破坏机理进行剖析；进而采用对蠕变曲线分段设置临界点的手段,结合统计损伤理论和Perzyna黏塑性模型,以岩石内部损伤微元体为研究对象,建立一种新型的黏弹塑性蠕变本构模型。

1. 基于统计损伤理论的加速蠕变模型建立

1.1 一维蠕变模型建立

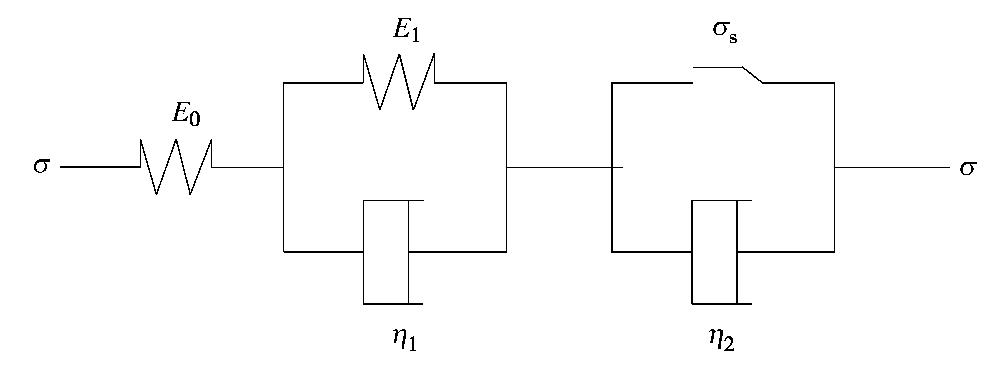
在传统流变模型中,西原模型对岩石的流变特性描述较好,但还是未能描述岩石的加速蠕变特性。它的物理模型表示如图1所示^[8]。

图 1 西原模型

Figure 1. Nishihara model

下载: 全尺寸图片幻灯片

。

$ε = {\begin{cases} \frac{σ}{E_{0}} + \frac{σ}{E_{1}} 1 - \exp (- \frac{E_{1}}{η_{1}} t) (σ \leq σ_{s}) \\ \frac{σ}{E_{0}} + \frac{σ}{E_{1}} 1 - \exp (- \frac{E_{1}}{η_{1}} t) + \frac{σ - σ_{s}}{η_{2}} t (σ > σ_{s}) \end{cases} 。$

(1)

式中 E₀为弹性模量；E₁为黏弹性模量；η₁和η₂为黏滞系数； $σ$ 为总应力； $ε$ 为总应变； $σ_{s}$ 为长期强度；t为蠕变时长。

笔者选用Perzyna黏塑性模型来代替西原体原有黏塑性模型^[9],其黏塑性应变率 ${\dot{ε}}_{vp}$ 为

${{\dot{ε}}_{vp}} = η 〈 φ (F) 〉 {m}$ 。

(2)

式中 ${\dot{ε}}_{vp}$ 为黏塑性应变率；η为黏塑性黏滞系数；F为岩石屈服函数；{m}黏塑性流动方向。其中,φ(F)为F的任意函数,一般可以表示为^[10]

$φ (F) = {(\frac{F}{σ_{s1}})}^{α}$ ,

(3)

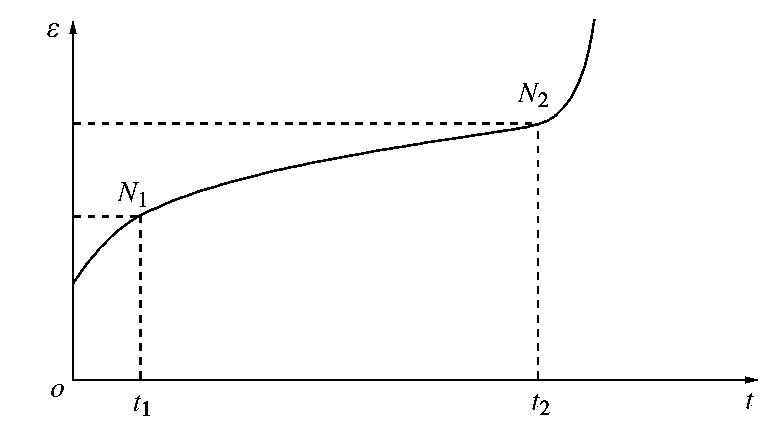
式中, $α$ 为参数, $σ_{s1}$ 为初始屈服强度。

一般情况下,岩石内部缺陷的发育是造成其变形的主要原因,而统计损伤力学是采用材料内部损伤微元与微元总个数的比值来描述材料的损伤程度,故可以采用损伤力理论来反映黏塑性蠕变阶段屈服函数劣化规律,以及描述岩石黏塑性蠕变变形的特性。笔者采用图2所示的蠕变变形分段示意,来定义各个分段临界点的指标。当岩石由衰减蠕变阶段进入到稳定蠕变阶段时,对应的蠕变时间为t₁,内部损伤破坏微元体为N₁（下限值为N₁^*）；当岩石由稳定蠕变阶段进入到加速蠕变阶段时,对应的蠕变时间为t₂,内部损伤破坏微元体为N₂（下限值为N₂^*）。

图 2 蠕变分段临界示意图

Figure 2. Critical diagram of creep segmentation

下载: 全尺寸图片幻灯片

选用Weibull分布来对岩石的微元强度体进行描述,其随机分布概率密度函数 $f (F)$ 为^[11]

$f (F) = \frac{n}{F_{0}} {(\frac{F}{F_{0}})}^{n - 1} \exp (- {(\frac{F}{F_{0}})}^{n})$ ,

(4)

式中,n,F₀为分布参数。

当岩石受到外荷载数值达到屈服强度值时,岩石内部微元体损伤数目为 $N_{f}$ ,即

$N_{f} = \int_{0}^{F} N f (x) d x$ ,

(5)

式中,N为总微元体的个数, $N_{f}$ 为损伤微元体的个数。

根据式（4）和式（5）得出在蠕变时间为t₁时,临界点处岩石损伤微元体数目N₁为

$\begin{matrix} N_{1} = \int_{0}^{F (σ)} N f (x) d x \\ = {\int_{0}^{F (σ)} \frac{n}{F_{0}} (\frac{x}{F_{0}}) n^{m - 1} \exp (- {(\frac{x}{F_{0}})}^{n}) d x |}_{F (σ) = F_{1} (σ)} \end{matrix}$ ,

(6)

式中, $F (σ)$ 为稳定蠕变阶段对应的应力状态函数。

结合式（6）得出临界点的下限值 $N_{1}^{*}$ 为

$\begin{matrix} N_{1}^{*} = \int_{0}^{F (σ_{s})} N f (x) d x \\ = {\int_{0}^{F (σ_{s})} \frac{n}{F_{0}} {(\frac{x}{F_{0}})}^{n - 1} \exp (- {(\frac{x}{F_{0}})}^{n}) d x |}_{F (σ_{s}) = F_{1} (σ_{s})} \end{matrix}$ ,.

(7)

式中, $σ_{s}$ 为长期强度, $N_{1}^{*}$ 实际计算时可近似取衰减蠕变微元损伤个数达到的极限最大值。

在蠕变任意时刻下,岩石内部微元损伤个数可以用式（6）来表示。因此,岩石的黏塑性蠕变速率 ${\dot{ε}}_{vp}$ 可以表示为

${{\dot{ε}}_{vp}} = η [\frac{N_{f}}{N_{1}^{*}}] {m} (N_{f} > N_{1}^{*})$ ,

(8)

式中, $η$ 为黏滞性系数,其中,{m}=1^[12]。

上述模型中虽然可较好地确定出岩石的黏塑性应变率,但是岩石内部微元损伤体的个数和岩石微元体总个数不能准确确定出,故此模型还具有一定的局限性。为了更好地划分岩石蠕变变形各个阶段以及定义蠕变变形各个阶段临界点的启动条件,采用统计损伤力学的理论将岩石内部微元损伤体的个数和岩石微元体总个数之间的关系进行转化,即根据Kachanov对损伤的定义可知^[13],材料的损伤一般可以由其内部损伤单元个数和材料总单元个数比值来表示,即

$D = \frac{N_{f}}{N}$ 。

(9)

将式（4）,（5）和式（9）代入到式（8）中,进行化简得到

${{\dot{ε}}_{vp}} = η_{2} [\frac{1 - \exp (- {(F (σ^{*}) / F_{0})}^{n} ）}{D_{1}^{*}}] (D > D_{1}^{*})$ ,

(10)

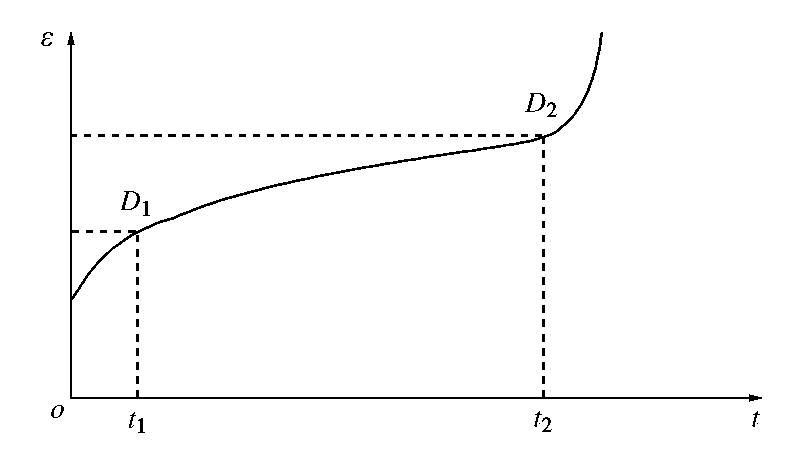
式中,D₁为临界点岩石产生微元损伤个数为N₁^*时的损伤变量值, $σ^{*}$ 为有效应力。

结合图2蠕变分段的定义可知,当蠕变时间为t₁时,对应岩石内部损伤变量为D₁（下限值为D₁^*）；当蠕变时间为t₂时,对应内部损伤变量为D₂（下限值为D₂^*）如图3所示。

图 3 改进的蠕变分段临界示意图

Figure 3. Critical diagram of improved creep segmentation

下载: 全尺寸图片幻灯片

岩石的应力与有效应力之间的关系可以表示为

$[σ^{*}] = [σ] / (1 - D)$ 。

(11)

则可以得到岩石内部微元体的屈服函数为

$F (σ^{*}) = F (σ) / (1 - D)$ 。

(12)

基于统计损伤力学理论的黏塑性应变率模型可以表示为

${{\dot{ε}}_{vp}} = η_{2} [\frac{1 - \exp (- {(σ / (1 - D) / F_{0})}^{n})}{D_{1}^{*}}] (D > D_{1}^{*})$ 。

(13)

岩石蠕变应变可以表示为应力和时间的函数,在岩石蠕变试验中,由于施加荷载是固定的,故蠕变应变只是关于时间变化的函数。因此,在考虑岩石应力损伤的条件下,岩石的黏塑性蠕变应变为

$ε_{vp} (σ, t) = \frac{σ ε (t)}{1 - D}$ ,

(14)

式中, $ε_{vp}$ 为黏塑性蠕变应变, $ε (t)$ 为关于时间的蠕变应变函数。

根据岩石黏塑性应变与时间的变化规律可知^[14],可以采用多项进行无线逼近黏塑性蠕变应变与时间曲线为

$\begin{matrix} ε (t) = f (t) = a_{0} + a_{1} t + \dots + a_{i} t^{i} + \dots + a_{k} t^{k} & (k = 0 ～ M) \end{matrix}$ ,

(15)

式中,f(t)为关于时间的多项式函数,i为多项式的幂次,a_i为常数。

当蠕变时间t=t₁～t₂时,蠕变应变为稳定蠕变变形（蠕变应变与时间变化规律基本呈现线性趋势）,则蠕变应变与时间变化规律的表达式为

$ε (t) = f (t) = a_{0}$ ,

(16)

式中,a₀为常数。

将式（14）～（16）代入到式（13）中得到

${{\dot{ε}}_{vp}} = η_{2} {\frac{1 - \exp [- {(ε_{vp} (σ, t) / a_{0} F_{0})}^{n}]}{D_{1}^{*}}} (D_{2}^{*} \geq D > D_{1}^{*}) 。$

(17)

当岩石的蠕变变形处于衰减蠕变变形与稳定蠕变变形的临界损伤点时,岩石的临界值下限损伤变量D₁^*为

$D_{1}^{*} = 1 - \exp [- {(ε_{vp}^{t_{1}} / a_{0} F_{0})}^{n}] (D_{2}^{*} \geq D > D_{1}^{*})$ ,

(18)

式中, $ε_{vp}^{t_{1}}$ 为临界点t₁时刻下对应的岩石黏塑性蠕变应变值。

由于在t₁时刻之前,岩石产生的黏塑性蠕变值 $ε_{vp}^{}$ 小于t₁时刻对应的黏塑性蠕变值 $ε_{vp}^{t_{1}}$ ,故在岩石发生稳定蠕变之前,存在D<D₁^*。同时,由于岩石的蠕变是随着时间逐渐变化的,此时岩石产生的损伤和在t₁时刻下产生的损伤对应的分布参数是一致的。

由于式（17）无法进行积分,将采用泰勒展开式将式（17）右边进行展开,可得

$\begin{array}{l} \exp {- {[ε_{vp} (σ, t) / a_{0} F_{0}]}^{n}} \\ = 1 - {[ε_{v p} (σ, t) / a_{0} F_{0}]}^{n} + o (ε_{vp}^{2}) \end{array}$ ,

(19)

式中, $o (ε_{vp}^{2})$ 为黏塑性蠕变应变 $ε_{vp}$ 的高阶无穷小。

将式（19）代入到式（17）中,得到

${{\dot{ε}}_{vp}} = η_{2} [\frac{{[ε_{vp} (σ, t) / a_{0} F_{0}]}^{n} + o (ε_{vp}^{2})}{D_{1}^{*}}] (D_{2}^{*} \geq D > D_{1}^{*}) 。$

(20)

当t→0时,存在 $ε_{vp}$ =0,则对式（20）进行积分得

$ε_{vp} = {[(\frac{η_{2}}{D_{1}^{*}} t) (n - 1)]}^{\frac{1}{1 - n}} {(a_{0} F_{0})}^{\frac{n}{n - 1}}$ 。

(21)

综上所述,得到改进后岩石蠕变本构方程为

$ε = {\begin{cases} \frac{σ}{E_{0}} + \frac{σ}{E_{1}} 1 - \exp (- \frac{E_{1}}{η_{1}} t) (D \leq D_{1}^{*}), \\ \frac{σ}{E_{0}} + \frac{σ}{E_{1}} 1 - \exp (- \frac{E_{1}}{η_{1}} t) + {[(\frac{η_{2}}{D_{1}^{*}} t_{1}) (n - 1)]}^{\frac{1}{1 - n}} \cdot \\ {(a_{0} F_{0})}^{\frac{n}{n - 1}} (D_{2}^{*} \geq D > D_{1}^{*}) 。 \end{cases}$

(22)

黏塑性蠕变应变与时间曲线f(t)是一个关于时间变化的函数,且岩石在同一种应力状态作用下加速蠕变破坏的模式极为相似。当t<t₂时,岩石的蠕变应变与时间变化规律呈现出非线性特性,故蠕变应变与时间变化规律的表达式为^[15]

$ε (t) = f (t) = a_{0} + a_{1} t$ ,

(23)

式中,a₁为常数。

因此,将式（23）和式（14）代入到式（13）中,得到岩石的黏塑性蠕变应变为

${{\dot{ε}}_{vp}} = η_{3} {\frac{1 - \exp [- {(ε_{vp} (σ, t) / ({a^{'}}_{0} + a_{1} t) {F^{'}}_{0})}^{n^{'}}]}{D_{2}^{*}}} (D > D_{2}^{*}),$

(24)

式中, ${F^{'}}_{0}$ , $n^{'}$ 为黏塑性蠕变阶段分布参数。

由于式（24）无法进行积分,采用泰勒展开式现将式（24）右边进行展开,可得

$\begin{matrix} \exp {- {[ε_{vp} (σ, t) / ({a^{'}}_{0} + a_{1} t) {F^{'}}_{0}]}^{n^{'}}} \\ = 1 - {[ε_{v p} (σ, t) / ({a^{'}}_{0} + a_{1} t) {F^{'}}_{0}]}^{n^{'}} + o (ε_{vp}^{2}) \end{matrix}$ 。

(25)

将式（25）代入到式（24）中,对式（24）进行积分得到黏塑性应变模型为

$ε_{vp} = \frac{{[a_{1} {({F^{'}}_{0} ({a^{'}}_{0} + a_{1} (t - t_{2})))}^{n^{'}} (n^{'} - 1)]}^{^{\frac{1}{n - 1}}}}{C {[a_{1} {({F^{'}}_{0} ({a^{'}}_{0} + a_{1} (t - t_{2})))}^{n} (n^{'} - 1)]}^{^{\frac{1}{1 - n^{'}}}} + \frac{η_{3}}{D_{2}^{*}} ({a^{'}}_{0} + a_{1} (t - t_{2}))},$

(26)

式中,C为积分参数。

综上所述,得到岩石一维状态下的黏弹塑性蠕变本构模型为

$ε = \frac{σ}{E_{0}} + \frac{σ}{E_{1}} [1 - \exp (- \frac{E_{1}}{η_{1}} t)] (D \leq D_{1}^{*})$ ,

(27)

$\begin{matrix} ε = \frac{σ}{E_{0}} + \frac{σ}{E_{1}} 1 - \exp (- \frac{E_{1}}{η_{1}} t) + (a_{0} F_{0}) \frac{n}{n - 1} \cdot \\ {[(\frac{η_{2}}{D_{1}^{*}} t) (n - 1)]}^{\frac{1}{1 - n}} (D_{2}^{*} \geq D > D_{1}^{*}) \end{matrix}$ ,

(28)

$\begin{matrix} ε = \frac{σ}{E_{0}} + \frac{σ}{E_{1}} 1 - \exp (- \frac{E_{1}}{η_{1}} t) + ε_{vp} + \\ {[(\frac{η_{2}}{D_{1}^{*}} t_{1}) (n - 1)]}^{\frac{1}{1 - n}} {(a_{0} F_{0})}^{\frac{n}{n - 1}} (D > D_{2}^{*}) \end{matrix}$ 。

(29)

1.2 三维蠕变模型建立

采用类比法将一维蠕变本构模型转化为三维本构模型,得到基于统计损伤理论的可以描述加速蠕变过程的三维加速蠕变本构模型为

$ε = \frac{σ_{1} - σ_{3}}{3 G_{0}} + \frac{σ_{1} + 2 σ_{3}}{9 K} + \frac{σ_{1} - σ_{3}}{3 G_{1}} [1 - \exp (- \frac{G_{1}}{{η^{'}}_{1}} t)] (D \leq D_{1}^{*}),$

(30)

$\begin{array}{l} ε = \frac{σ_{1} - σ_{3}}{3 G_{0}} + \frac{σ_{1} + 2 σ_{3}}{9 K} + \frac{σ_{1} - σ_{3}}{3 G_{1}} [1 - \exp (- \frac{G_{1}}{{η^{'}}_{1}} t)] + \\ {[(\frac{{η^{'}}_{2}}{D_{1}^{*}} t) (n - 1)]}^{\frac{1}{1 - n}} {(a_{0} F_{0})}^{\frac{n}{n - 1}} (D_{2}^{*} \geq D > D_{1}^{*}) \end{array}$ ,

(31)

$\begin{array}{l} ε = \frac{σ_{1} - σ_{3}}{3 G_{0}} + \frac{σ_{1} + 2 σ_{3}}{9 K} + \frac{σ}{3 G_{1}} [1 - \exp (- \frac{G_{1}}{{η^{'}}_{1}} t)] + A + \\ {[(\frac{{η^{'}}_{2}}{D_{1}^{*}} t_{1}) (n - 1)]}^{\frac{1}{1 - n}} {(a_{0} F_{0})}^{\frac{1}{n - 1}} (D > D_{2}^{*}) \end{array}$ ,

(32)

$A = \frac{{[a_{1} {({F^{'}}_{0} (a_{0} + a_{1} (t - t_{2})))}^{n^{'}} (n^{'} - 1)]}^{^{\frac{1}{n - 1}}}}{C {[a_{1} {({F^{'}}_{0} (a_{0} + a_{1} (t - t_{2})))}^{n} (n^{'} - 1)]}^{^{\frac{1}{1 - n^{'}}}} + \frac{{η^{'}}_{3}}{D_{2}^{*}} (a_{0} + a_{1} (t - t_{2}))},$

(33)

式中,G₁和G₂为剪切模量,K为体积模量, ${η^{'}}_{1}$ , ${η^{'}}_{2}$ , ${η^{'}}_{3}$ 为三维状态下的黏滞性系数。

2. 室内蠕变试验

2.1 室内三轴压缩试验

本文所用砂岩采自阜新市恒大煤矿,岩石试样按照岩石相关试验规程要求进行精加工,制作成h=100 mm,D=50 mm标准圆柱形试件如图4。采用比重杯法测得岩石的密度为2.352 g/cm³,用排水法测得岩石的孔隙率为1.151%（测定3个试样取平均值）。

图 4 岩样和设备

Figure 4. Rock samples and devices

下载: 全尺寸图片幻灯片

需要通过相应条件下的三轴压缩试验,来确定出蠕变试验的应力施加方案。其中,三轴压缩试样方案为：①为保证岩石和试验系统的充分接触,施加一个较小的轴向压力；②以500 N/s的加载速率将围压加到预定值；③以500 N/s的加载速率施加轴压,在此过程必须保持围压不变；④待到岩石变形破坏后,停止施加轴压；⑤将试验数据保存并导出。

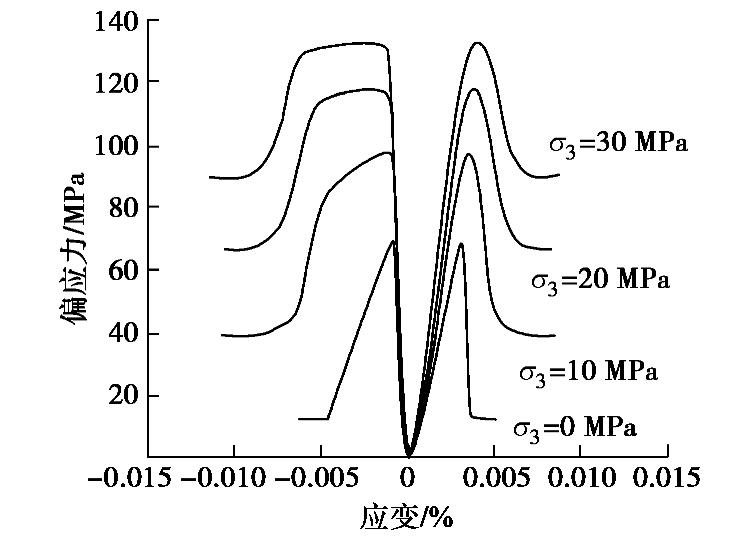
绘制出不同围压作用下应力–应变曲线如图5所示。

图 5 应力–应变曲线

Figure 5. Stress-strain curves

下载: 全尺寸图片幻灯片

根据图5的应力–应变曲线数据,总结出三轴压缩试验结果见表1所示。

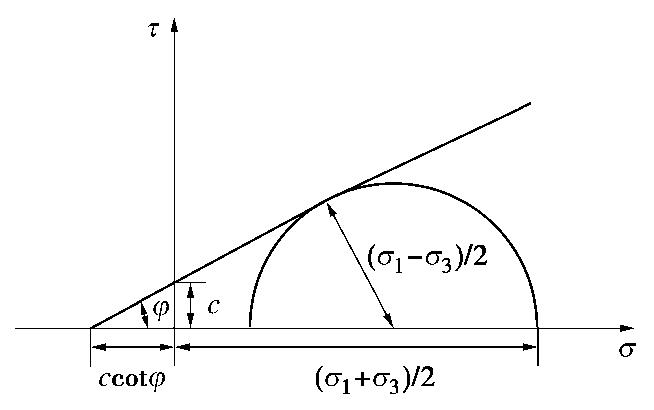
表 1 试验结果

Table 1. Test results

围压/MPa	轴向峰值强度/MPa	偏应力强度/MPa	轴向峰值应变/10^-4%	径向峰值应变/10^-4%	E₅₀/GPa
0	76.073	76.073	3.21	-7.488	21.814
10	108.226	98.226	3.64	-9.7464	26.216
20	138.601	118.601	3.71	-10.2	32.814
30	163.557	133.557	3.89	-12.1	36.224
注：表中E₅₀为轴向应变等于峰值应变50%时对应的弹性模量。

下载: 导出CSV

| 显示表格

一般采用莫尔应力圆（如图6）与包络线的关系来确定岩石的强度参数值。

图 6 莫尔应力圆

Figure 6. Mohr stress circle

下载: 全尺寸图片幻灯片

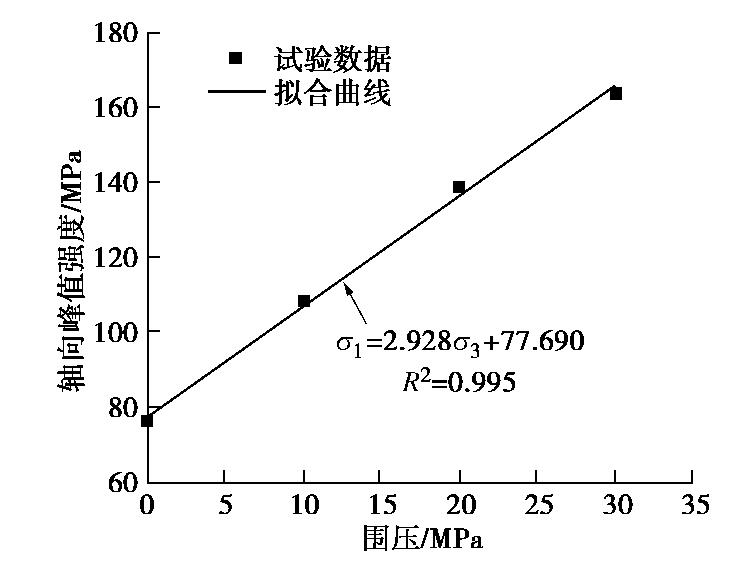
根据表1中岩石在不同围压作用下的峰值强度值^[16-17],绘制出围压与峰值强度的关系曲线如图7。

图 7 围压与峰值强度的关系

Figure 7. Relationship between confining pressure and peak intensity

下载: 全尺寸图片幻灯片

由图7可知,围压与峰值强度之间关系满足线性变化关系,拟合的直线方程的斜率为2.928,截距为77.690。根据围压与峰值强度之间关系方程与莫尔应力圆理论可知,岩石的黏聚力c为22.701 MPa,内摩擦角φ为29.395°。

2.2 室内三轴蠕变试验

加载蠕变试验具体步骤为：①保证所有试样取自同一块岩体,将明显外部缺陷的试样剔除,且通过波速测试仪将波速一致的岩样作为试样对象；②根据室内三轴压缩试验最大偏应力来确定蠕变试验的应力等级水平,应力初始水平选取加载三轴试验峰值强度的60%。为了方便施加应力,起始值选取整数值,以后每一级荷载分别取加载三轴试验峰值强度的70%,80%和90%；③先以500 N/s加载速度施加围压至预定值,待稳定后再以相同加载速度施加轴压至预定值,当岩石的径向变形小于0.03 mm/24h时,进行下一级荷载的施加,重复上述步骤直至岩石破坏；④待试验完成后,首先将围压卸载至零,然后卸载轴压至零,将压力舱内液压油抽回到设备中,升起压力舱取出岩石试样进行保存,试验数据保存间隔为5 s,最终导出试验数据即可。

其中,不同围压作用下的岩石的轴向蠕变变形历时曲线如图8所示。

图 8 各级应力下轴向蠕变曲线

Figure 8. Axial creep curves under stress at each level

下载: 全尺寸图片幻灯片

由图8可知,在围压恒定时逐级加载轴向应力时,岩石在加载瞬间会出现一个瞬时变形,且瞬时变形随着轴向应力地不断增大而增大,但是由于岩石在初始时刻其内部孔隙完全张开,在加载时孔隙逐渐闭合为瞬时变形提供一定的变形量,随着孔隙的完全闭合和之后应力水平增大迫使其产生裂纹破裂,对于瞬时应变量的作用逐步减小,故瞬时应变在岩石试样整体变形量中的比例也随之逐步减少；岩石的蠕变变形不断占总变形量越来越多,说明了岩石内部空隙不断发育,导致岩石劣化特性愈加明显。但是对比分析瞬时应变和蠕变应变可知,瞬时应变占总变形的比重远远大于蠕变应变占总变形的比重,说明了瞬时应变对岩石造成损伤大于蠕变对岩石造成的损伤。以围压30 MPa为例,当应力大于110 MPa时,岩石出现了明显加速蠕变阶段,加速蠕变时间随着应力水平增大逐渐减小,说明了应力的增大加剧了岩石内部损伤发育和裂隙的扩展,使得岩石更容易产生破坏^[18]。

3. 参数识别

3.1 临界点参数确定

蠕变时刻t₁和蠕变变形 $ε_{t1}$ ,以及蠕变时刻t₂和蠕变变形 $ε_{t2}$ ,这4个参数均可以由蠕变历时曲线得出。不同围压、不同应力水平作用下岩石的临界点参数值见表2（以围压20 MPa为例）^[19-20]。

表 2 岩石的临界点参数值

Table 2. Values of critical point parameters of rocks

应力水平/MPa	t₁/h	ε_t1/%	t₂/h	ε_t2/%
40	—	—	—	—
50	9.78	0.132	—	—
60	7.45	0.245	—	—
70	1.06	0.373	4.09	0.404

下载: 导出CSV

| 显示表格

3.2 模型计算值与试验值对比

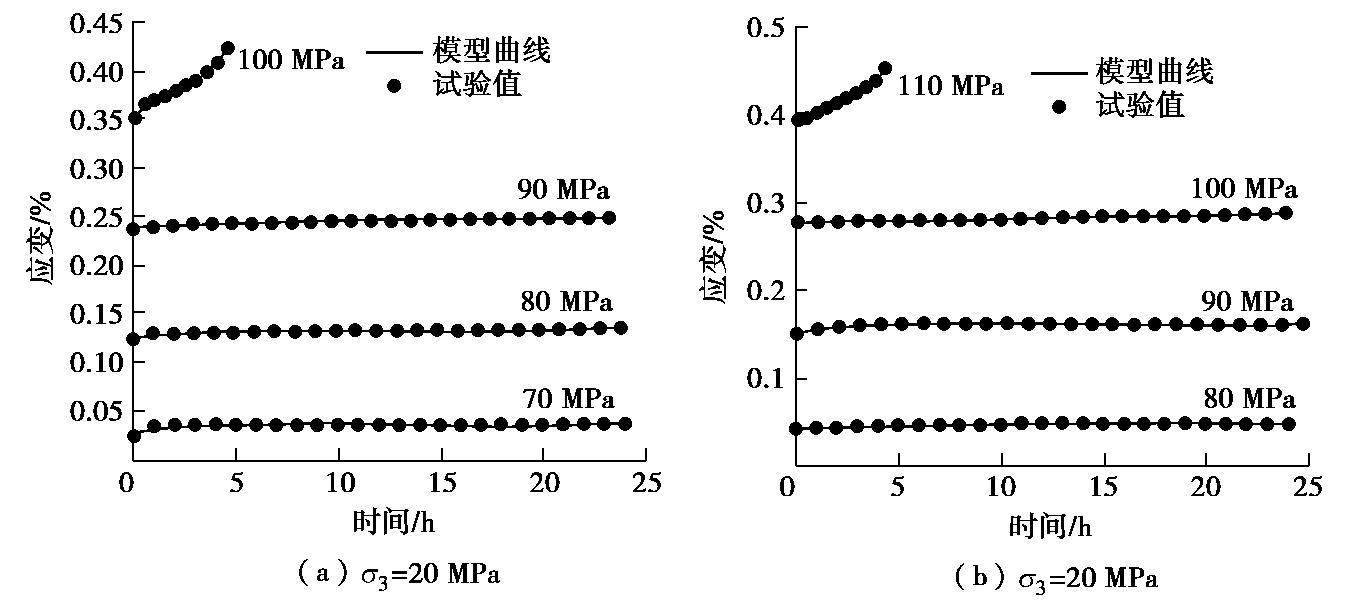
基于最小二乘法^[21-23]对围压20 MPa下蠕变试验曲线进行参数辨识,得到模型参数值见表3。得到蠕变模型曲线与试验曲线的对比如图9所示。

表 3 岩石的拟合参数值

Table 3. Fitting values of rock parameters

应力水平/MPa	参数
应力水平/MPa	G₀/GPa	K/GPa	G₁/GPa	${η^{'}}_{1}$ /(GPa·h)	${η^{'}}_{2}$ /(GPa·h)	${η^{'}}_{3}$ /(GPa·h)	F₀	n	${F^{'}}_{0}$	$n^{'}$	a₀	${a^{'}}_{0}$	a₁	C	相关系数R²	方差平方和
70	106.899	162.033	228.235	134.970	—	—	—	—	—	—	—	—	—	—	0.998	7.643×10^-7
80	113.228	193.810	466.039	280.073	779.849	—	6.566	2.034	—	—	—	—	—	—	0.985	1.017×10^-4
90	118.231	226.017	1391.242	197.300	1190.656	—	6.079	4.409	—	—	—	—	—	—	0.978	5.553×10^-5
100	45.980	192.896	94.388	94.999	1002.345	2485.416	5.444	8.131	3.824	0.932	-2.880	2.621	-0.153	2.345	0.972	2.196×10^-4

下载: 导出CSV

| 显示表格

图 9 试验结果和模型对比

Figure 9. Comparison between test results and models

下载: 全尺寸图片幻灯片

由图9可知,试验曲线和模型曲线具有良好的吻合度,这说明了基于统计损伤原理建立的岩石加速蠕变模型,来反映岩石蠕变全过程曲线是正确的。

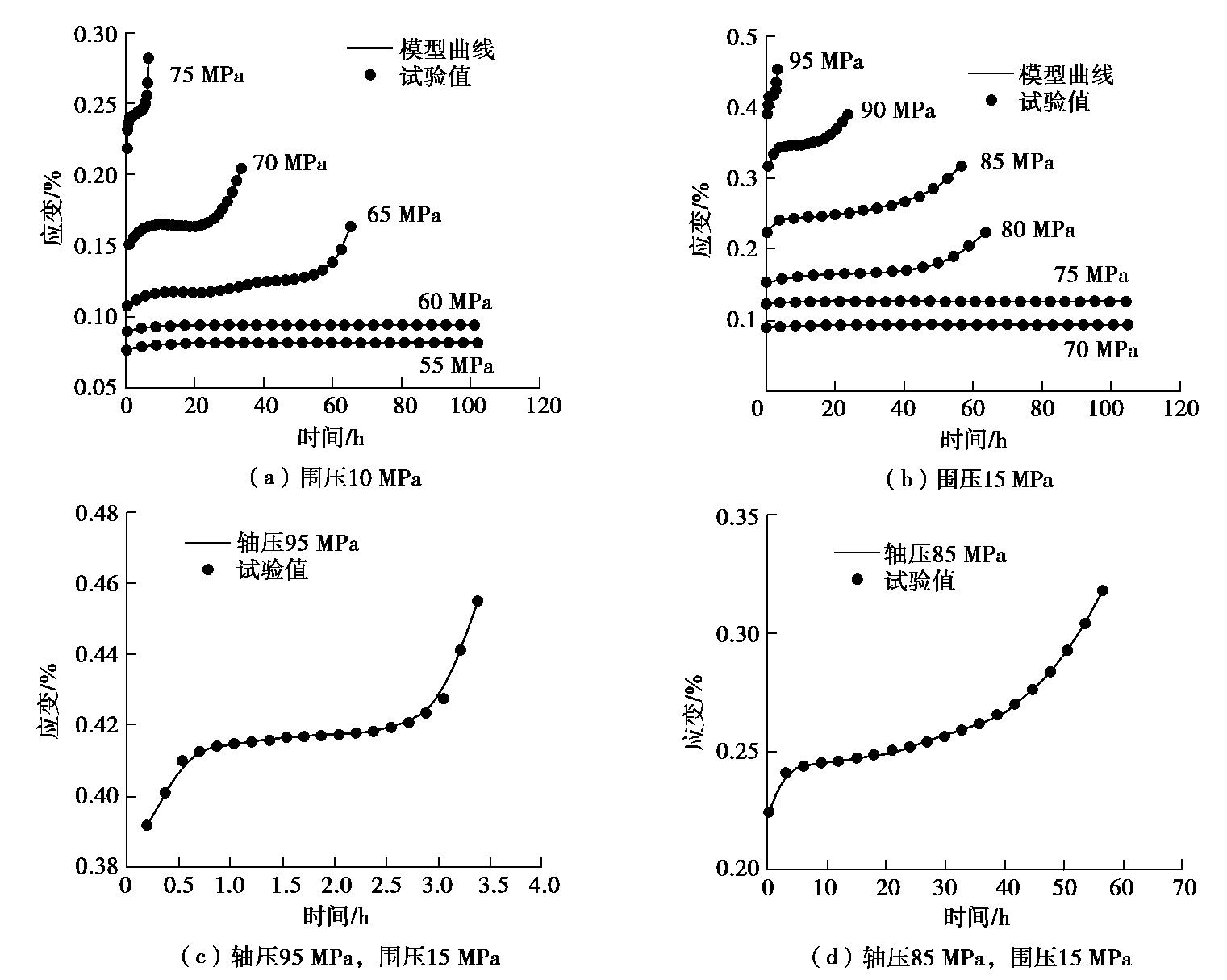
本文将采用笔者在文献[4]的中加速蠕变试验数据来进一步验证该模型的正确性。绘制出不同围压和应力作用下的含加速蠕变试验曲线与模型曲线对比如图10所示。其中,特别将围压15 MPa、轴压为95,85 MPa的试验曲线单独进行对比。

图 10 引用文献[4]中蠕变试验曲线与模型曲线对比

Figure 10. Comparison between creep test results and model curves in Reference [4]

下载: 全尺寸图片幻灯片

由图10可知,引用文献中的试验曲线也与模型曲线具有良好的吻合度（只是关于加速蠕变变形曲线的吻合度相对其他曲线的拟合度较低）,说明了基于统计损伤原理建立的岩石加速蠕变模型,来反映岩石蠕变全过程曲线是正确的。

综上所述,岩石蠕变加载过程也是一种岩石内部微元体损伤破坏的过程,在材料微观结构上表现为不可逆性。通过将蠕变曲线分阶段,来定义分段临界点的损伤变量的表达形式,结合统计损伤理论和Perzyna黏塑性模型,对传统的西原体模型进行适当的改进,建立非线性蠕变损伤模型,从而更好地体现了受损伤岩石内部应力–应变状态和损伤演化规律,对于解决实际工程围岩长期稳定性具有指导意义。

4. 结论

（1）基于细观统计损伤理论,采用临界统计损伤变量对加速蠕变和稳定蠕变的启动条件进行了定义,这为构建加速蠕变模型奠定了基础。

（2）岩石蠕变加载过程也是一种岩石内部微元体损伤破坏的过程,在材料微观结构上表现为不可逆性。

（3）通过将蠕变曲线分阶段,来定义分段临界点的损伤变量的表达形式,结合统计损伤理论和Perzyna黏塑性模型,对传统的西原体模型进行适当的改进,建立非线性蠕变损伤模型,从而更好地体现了损伤受岩石内部应力应变状态影响和损伤演化规律。

图 1 西原模型

Figure 1. Nishihara model

下载: 全尺寸图片幻灯片

图 2 蠕变分段临界示意图

Figure 2. Critical diagram of creep segmentation

下载: 全尺寸图片幻灯片

图 3 改进的蠕变分段临界示意图

Figure 3. Critical diagram of improved creep segmentation

下载: 全尺寸图片幻灯片

图 4 岩样和设备

Figure 4. Rock samples and devices

下载: 全尺寸图片幻灯片

图 5 应力–应变曲线

Figure 5. Stress-strain curves

下载: 全尺寸图片幻灯片

图 6 莫尔应力圆

Figure 6. Mohr stress circle

下载: 全尺寸图片幻灯片

图 7 围压与峰值强度的关系

Figure 7. Relationship between confining pressure and peak intensity

下载: 全尺寸图片幻灯片

图 8 各级应力下轴向蠕变曲线

Figure 8. Axial creep curves under stress at each level

下载: 全尺寸图片幻灯片

图 9 试验结果和模型对比

Figure 9. Comparison between test results and models

下载: 全尺寸图片幻灯片

图 10 引用文献[4]中蠕变试验曲线与模型曲线对比

Figure 10. Comparison between creep test results and model curves in Reference [4]

下载: 全尺寸图片幻灯片

表 1 试验结果

Table 1 Test results

围压/MPa	轴向峰值强度/MPa	偏应力强度/MPa	轴向峰值应变/10^-4%	径向峰值应变/10^-4%	E₅₀/GPa
0	76.073	76.073	3.21	-7.488	21.814
10	108.226	98.226	3.64	-9.7464	26.216
20	138.601	118.601	3.71	-10.2	32.814
30	163.557	133.557	3.89	-12.1	36.224
注：表中E₅₀为轴向应变等于峰值应变50%时对应的弹性模量。

下载: 导出CSV

表 2 岩石的临界点参数值

Table 2 Values of critical point parameters of rocks

应力水平/MPa	t₁/h	ε_t1/%	t₂/h	ε_t2/%
40	—	—	—	—
50	9.78	0.132	—	—
60	7.45	0.245	—	—
70	1.06	0.373	4.09	0.404

下载: 导出CSV

表 3 岩石的拟合参数值

Table 3 Fitting values of rock parameters

应力水平/MPa	参数
应力水平/MPa	G₀/GPa	K/GPa	G₁/GPa	${η^{'}}_{1}$ ${η^{'}}_{1}$ /(GPa·h)	${η^{'}}_{2}$ ${η^{'}}_{2}$ /(GPa·h)	${η^{'}}_{3}$ ${η^{'}}_{3}$ /(GPa·h)	F₀	n	${F^{'}}_{0}$ ${F^{'}}_{0}$	$n^{'}$ $n^{'}$	a₀	${a^{'}}_{0}$ ${a^{'}}_{0}$	a₁	C	相关系数R²	方差平方和
70	106.899	162.033	228.235	134.970	—	—	—	—	—	—	—	—	—	—	0.998	7.643×10^-7
80	113.228	193.810	466.039	280.073	779.849	—	6.566	2.034	—	—	—	—	—	—	0.985	1.017×10^-4
90	118.231	226.017	1391.242	197.300	1190.656	—	6.079	4.409	—	—	—	—	—	—	0.978	5.553×10^-5
100	45.980	192.896	94.388	94.999	1002.345	2485.416	5.444	8.131	3.824	0.932	-2.880	2.621	-0.153	2.345	0.972	2.196×10^-4

下载: 导出CSV

参考文献(23)

[1]	黄海峰, 巨能攀, 黄敏, 等. 朱俊霖软岩非线性蠕变损伤模型及其试验研究[J]. 水文地质工程地质, 2017, 44(3): 49-60. HUANG Hai-feng, JU Neng-pan, HUANG Min, et al. Nonlinear creep damage model of soft rock and its experimental study[J]. Hrdrogeology and Engineering Geology, 2017, 44(3): 49-60. (in Chinese)
[2]	梁冰, 张涛, 王俊光, 等. 片麻岩蠕变特性试验研究[J]. 实验力学, 2018, 33(3): 451-46. https://www.cnki.com.cn/Article/CJFDTOTAL-SYLX201803014.htm LIANG Bin, ZHANG Tao, WANG Jun-guang, et al. Experimental study of geneiss creep properties[J]. Journal of Experimental Mechanics, 2018, 33(3): 451-46. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SYLX201803014.htm
[3]	蒲成志, 曹平, 张春阳. 考虑时效损伤劣化的变参数非线性蠕变损伤模型[J]. 工程力学, 2017, 34(6): 17-27. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201706005.htm PU Chengzhi, CAO Ping, ZHANG Chun-yang, et al. Variable parameters non-linear creep damage model of Rock with consideration of aging damage and deterioration[J]. Engineering Mechanics, 2017, 34(6): 17-27. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201706005.htm
[4]	张树光, 刘文博, 陈雷, 等. 基于力学参数时效性的非定常蠕变模型[J]. 中国矿业大学学报, 2019, 48(5): 993-1002. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD201905007.htm ZHANG Shu-guang, LIU Wen-bo, CHEN Lei, et al. Unsteady creep model based on time-dependentness of mechanical parameters[J]. Journal of China University of Mining and Technology, 2019, 48(5): 993-1002. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD201905007.htm
[5]	杨秀荣, 姜谙男, 江宗斌. 含水状态下软岩蠕变试验及损伤模型研究[J]. 岩土力学, 2018, 39(增刊1): 167-174. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2018S1021.htm YANG Xiu-rong, JIANG An-nan, JIANG Zong-bin. Creep test and damage model of soft rock under water containing condition[J]. Rock and Soil Mechanics, 2018, 39(S1): 167-174. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2018S1021.htm
[6]	张泽林, 吴树仁, 王涛, 等. 甘肃天水泥岩剪切蠕变行为及其模型研究[J]. 岩石力学与工程学报, 2019, 38(增刊2): 3603-3617. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2019S2035.htm ZHANG Ze-lin, WU Shu-ren, WANG Tao, et al. Study on shear creep behavior and its model of mudstone in Tianshui, Gansu Province[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(S2): 3603-3617. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2019S2035.htm
[7]	梅胜尧, 王伟, 秦志军, 等. 考虑裂隙塑性的岩石非线性分数阶蠕变模型[J]. 河海大学学报(自然科学版), 2019, 47(6): 548-554. https://www.cnki.com.cn/Article/CJFDTOTAL-HHDX201906011.htm MEI Sheng-yao, WANG Wei, QIN Zhi-jun, et al. A nonlinear creep model based on fractional order theory considering the plasticity of fissures for rocks[J]. Journal of Hohai University(Natural Sciences), 2019, 47(6): 548-554. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HHDX201906011.htm
[8]	刘泉声, 罗慈友, 彭星新, 等. 软岩现场流变试验及非线性分数阶蠕变模型研究[J]. 煤炭学报, 2020, 45(4): 1348-1356. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB202004017.htm LIU Quan-sheng, LUO Ci-you, PENG Xing-xin, et al. Research on field rheological test and nonlinear fractional derivative creep model of weak rock mass[J]. Journal of China Coal Society, 2020, 45(4): 1348-1356. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB202004017.htm
[9]	ZHOU H W, WANG C P, HAN B B, et al. A creep constitutive model for salt rock based on fractional derivatives[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(1): 116-121.
[10]	ZHU H H, YE B, CAI Y C, et al. An elasto-viscoplas-tic model for soft rock around tunnels considering overconsolidationand structure effects[J]. Computers and Geotechnics, 2013, 50: 6-16.
[11]	LI S Y, LAI Y M, ZHANG S J. An improved statistical damage constitutive model for warm frozen clay based on Mohr-Coulomb criterion[J]. Cold Regions Science and Technology, 2009, 57(12): 154-159.
[12]	LIU W B, ZHANG S G. Creep Parameter Determination and model establishment considering stress and time effects[J]. Geotechnical and Geological Engineering, 2019, 38(2): 1509-1520.
[13]	KACHNOV M. Effective elastic properties of cracked solids:critical review of some basic concepts[J]. Applied Mechanics Review, 1992, 45(8): 304-335.
[14]	沈才华, 张兵, 王文武. 一种基于应变能理论的黏弹塑性蠕变本构模型[J]. 岩土力学, 2014, 35(12): 3430-3436. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201412012.htm SHEN Cai-hua, ZHANG Bing, WANG Wen-wu. A new viscoela-stoplastic creep constitutive model based on strain energy theory[J]. Rock and Soil Mechanics, 2014, 35(12): 3430-3436. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201412012.htm
[15]	ZHOU H W, WANG C P, MISHNAEVSKY L Jr, et al. A fractional derivative approach to full creep regions in salt rock[J]. Mechanics of Time-Dependent Materials, 2013, 17(3): 413-425.
[16]	刘开云, 薛永涛, 周辉. 参数非定常的软岩非线性黏弹塑性蠕变模型[J]. 中国矿业大学学报, 2018, 47(4): 921-928. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD201804030.htm LIU Kai-yun, XUE Yong-tao, ZHOU Hui. Anonlinear viscoelastic-plastic creep model of soft rock with unsteady parameters[J]. Journal of China University of Mining & Technology, 2018, 47(4): 921-928. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGKD201804030.htm
[17]	RUTTER E H. On the creep testing of rocks at constant stress and constant force[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1972, 9(2): 191-195.
[18]	张树光, 孙成鑫, 王有涛, 等. 海棠山隧道砂岩变参数蠕变特性研究[J]. 公路交通科技, 2016, 33(10): 105-110. https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK201610016.htm ZHNAG Shu-guang, SUN Cheng-xin, WANG You-tao, et al. Study on variable parameter creep characteristics of sandstone in Haitangshan Tunnel[J]. Journal of Highway and Transportation Research and Development, 2016, 33(10): 105-110. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GLJK201610016.htm
[19]	刘文博, 张树光, 李若木. 一种基于能量耗散理论的岩石加速蠕变模型[J]. 煤炭学报, 2019, 44(9): 2741-2750. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201909014.htm LIU Wen-bo, ZHANG Shu-guang, LI Ruo-mu. Research on accelerated creep model of rock based on energy dissipation theory[J]. Journal of China Coal Society, 2019, 44(9): 2741-2750. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB201909014.htm
[20]	XU T, ZHOU G, HEAP M J, et al. The modeling of time-dependent deformation and fracturing of brittle rocks under varying confining and pore pressures[J]. Rock Mechanics and Rock Engineering, 2018, 51(10): 3241-3263.
[21]	何志磊, 朱珍德, 朱明礼, 等. 基于分数阶导数的非定常蠕变本构模型研究[J]. 岩土力学, 2016, 37(3): 737-744. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201603017.htm HE Zhi-lei, ZHU De-zhen, ZHU Ming-li, et al. An unsteady creep constitutive model based on fractional order derivatives[J]. Rock and Soil Mechanics, 2016, 37(3): 737-744. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201603017.htm
[22]	韩阳, 谭跃虎, 李二兵, 等. 岩石非定常Burgers蠕变模型及其参数识别[J]. 工程力学, 2018, 35(3): 201-217. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201803024.htm HAN Yang, TAN Yue-hu, LI Er-bin, et al. Non-stationary Burgers creep model of rock and its parameter identification[J]. Engineering Mechanics, 2018, 35(3): 201-217. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201803024.htm
[23]	张德, 刘恩龙, 刘星炎, 等. 基于修正Mohr-Coulomb屈服准则的冻结砂土损伤本构模型[J]. 岩石力学与工程学报, 2018, 37(4): 978-986. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201804020.htm ZHANG De, LIU En-long, LIU Xing-yan, et al. A damage constitutive model for frozen sandy soils based on modified Mohr-Coulomb yield criterion[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(4): 978-986. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201804020.htm

施引文献(52)

期刊类型引用(19)

1.	刘桃根，胡凯，李玲，王伟. 天然和饱水红砂岩三轴压缩蠕变变形试验研究. 三峡大学学报(自然科学版). 2025(01): 9-15 . 百度学术
2.	于超云，黄生辉，吴祥业，田宇航，李俊昆. 冻融循环对不同饱和度红砂岩力学特性和破坏特征的影响. 矿业研究与开发. 2025(02): 162-170 . 百度学术
3.	赵越，牛心玉，齐晓磊，华玉涵. 水化-冻融耦合作用下大理岩蠕变长期强度. 吉林大学学报(地球科学版). 2025(01): 188-198 . 百度学术
4.	赵越，司运航，张译丹，赵京禹. 水化-冻融耦合条件下大理岩蠕变损伤本构模型. 吉林大学学报(地球科学版). 2024(01): 231-241 . 百度学术
5.	张鑫，吉海峰，金生莲，朱彦鹏，王浩，黄安平. 强风化岩流态固化土抗压强度试验研究. 水利与建筑工程学报. 2024(04): 85-91 . 百度学术
6.	苏浩然. 冻融循环作用下岩石损伤研究综述. 低碳世界. 2024(11): 187-189 . 百度学术
7.	谢昊天，徐颖，郑强强，于美鲁，谢守冬，李成杰. 冻融循环作用下饱水砂岩强度衰减及细观结构特征. 煤炭科学技术. 2024(12): 84-93 . 百度学术
8.	杨志全，甘进，樊详珑，朱颖彦，杨溢，丁渝池. 岩石冻融损伤机理研究进展及展望. 防灾减灾工程学报. 2023(01): 176-188 . 百度学术
9.	赵志波. 冻融条件下隧道围岩单轴蠕变力学特性试验及本构模型. 黑龙江科技大学学报. 2023(02): 299-305 . 百度学术
10.	王冠强，于怀昌，席伟，程广利，牛睿. 预制裂隙对砂岩蠕变力学特性及声发射前兆特征影响试验研究. 华北水利水电大学学报(自然科学版). 2023(02): 72-79 . 百度学术
11.	苗浩东，任富强. 冻融循环作用下不同含水率砂岩抗拉特性研究. 工矿自动化. 2023(05): 133-138+152 . 百度学术
12.	闫建兵，张小强，宋选民，王开，姜玉龙，岳少飞. 低围压条件下无烟煤三轴蠕变特性试验研究（英文）. Journal of Central South University. 2023(05): 1618-1630 . 百度学术
13.	许军策，浦海，沙子恒. 低温下不同饱和度冻结砂岩动态力学行为试验研究. 煤炭科学技术. 2023(09): 88-99 . 百度学术
14.	王前朋，范宣梅，王文松，杜三林，郭劲松，温鑫. 青藏高原片麻岩宏微观冻融损伤特性试验研究. 科学技术与工程. 2023(31): 13515-13524 . 百度学术
15.	贾蓬，卢佳亮，毛松泽，郭子铭，王茵. 不同饱和度冻融砂岩动态冲击压缩特性及损伤机制研究. 岩石力学与工程学报. 2023(12): 2908-2918 . 百度学术
16.	张正全. 不同含水率的砂化白云岩力学特性研究. 科技与创新. 2022(04): 79-82 . 百度学术
17.	高越. 寒区隧道围岩冻融损伤试验研究. 资源信息与工程. 2022(01): 97-100+103 . 百度学术
18.	王子一，康向涛，江明泉，周浪. 冻融循环作用下砂岩劣化试验研究. 矿业研究与开发. 2022(05): 139-143 . 百度学术
19.	张安琪，袁磊，舒中潘，张军，周飞. 不同含水率花岗岩冻融循环作用下的抗压性能及强度损伤特性研究. 资源信息与工程. 2022(05): 64-68 . 百度学术